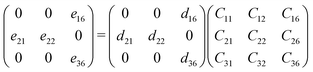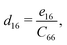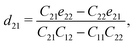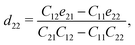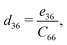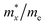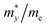Two-dimensional ternary pentagonal BCX (X = P, As, and Sb): promising photocatalyst semiconductors for water splitting with strong piezoelectricity†
Received
8th October 2023
, Accepted 15th November 2023
First published on 25th November 2023
Abstract
Seeking high-performance energy conversion materials is one of the most important issues in designing 2D materials. In the framework of density functional theory, we propose a series of ternary monolayers, penta-BCX (X = P, As, and Sb), and systematically investigate their structural stability, mechanical, piezoelectric, and photocatalytic properties. All three materials are semiconductors with a bandgap ranging from 2.56 eV to 3.24 eV, so they could be promising catalysts for the photolysis of water. Penta-BCX exhibits significant piezoelectric properties attributed to their non-centrosymmetric structure and low in-plane Young's modulus, which are expected to efficiently drive photocatalytic water decomposition. Moreover, the bandgap, band edge position, and light absorption of penta-BCX can be modulated by tensile or compressive strain to enhance their photocatalytic performance in the visible light and ultraviolet regions.
1 Introduction
As fossil fuels continue to be consumed, the resulting energy shortages are leading to disputes and environmental pollution. Catalytic technologies, such as electrocatalysis, photocatalysis, and piezoelectric catalysis, have made significant progress in developing clean energy. Photocatalysis, in particular, has shown great promise in converting solar energy into chemical energy for sustainable energy and environmental remediation. However, most photocatalysts face challenges such as poor light absorption, low charge carrier mobility, and fast electron–hole pair recombination, which limit their energy conversion efficiency.1,2
An emerging strategy proposes inducing a piezoelectric field inside a semiconductor by spontaneous polarization or by applying an external field.3 This integration of piezoelectricity, photonic excitation, and semiconductor properties can tune or control charge transport behavior. A strong and persistent piezoelectric field is not only effective in separating electron/hole pairs excited by light, but also is a key factor in stimulating catalytic reactions.4–6 Experimentally verified materials that can be used for piezo-photocatalytic water splitting include perovskite-structured materials,7–10 transition metal chalcogenides,11–13 metal–organic frameworks,14 graphite carbon nitride,15 and some layered materials.16 Simultaneous light and mechanical stimulation significantly enhance the H2 output compared to single photocatalysis or piezoelectric catalysis.17 However, it should be mentioned that visible-light-driving of the photocatalyst is crucial. To improve the limited light absorption of piezoelectric ZnO, Hong et al. enhanced the piezo-photocatalytic activity by coupling piezoelectric ZnO with a visible-light-active CuS photocatalyst.18 Liu et al. combined ReS2 with BaTiO3 to enhance light absorption and promote charge transfer by forming interfacial Re–O covalent bonds and decreasing the Schottky barrier.19 Under this strategy, several heterostructures with excellent piezoelectricity, light absorption ability, and charge transfer presented outstanding photo-piezoelectric catalytic efficiency.20–25
However, suitable piezoelectric semiconductor materials with visible light activity and the ability to couple both piezoelectric and photoexcitation effects are still lacking, making the search for such materials critical. Recently, ternary pentagonal monolayer BCN, BNSi and BCP have been theoretically predicted to be stable, all of them are piezoelectric semiconductors, and the band edge position meets the conditions of photocatalytic hydrolysis, so they may have the potential to be excellent hydrolysis photocatalysts.26–28 It is necessary to explore more boron–carbon-based ternary pentagonal monolayer materials. In this paper, we have verified the dynamic, thermal and mechanical stability of penta-BCX (X = P, As, and Sb), investigated their mechanical, electronic, optical and piezoelectric properties, revealed their suitability for photocatalytic hydrolysis applications, and predicted that their photocatalytic performance could be enhanced by coupling piezoelectric effects.
2 Calculation methods
Within the framework of density functional theory (DFT), all first-principles calculations were performed using the Vienna ab initio Simulation Package (VASP) based on plane waves.29,30 The plane waves with a cut-off kinetic energy of 600 eV were used to approximate the electron wave functions. The Perdew–Burke–Ernzerhof (PBE) was used as the exchange–correlation function under the generalized gradient approximation (GGA),31 and the projector augmented wave potential was used to describe ion–electron interaction.32 To acquire accurate electronic properties and energy band gap, the Heyd–Scuseria Ernzerhof (HSE06) hybrid functional approach was utilized.33 The van der Waals (vdW) interactions were described by Grimme's DFT-D3 correction.34 A Γ-centered 9 × 9 × 1 and 17 × 17 × 1 Monkhorst–pack k-grid for reciprocal space were used for geometric optimization and self-consistent total energy calculations.35 A 20 Å vacuum space was inserted in the direction perpendicular to avoid any interaction in the non-periodic direction. After fixing the vacuum layer, the convergence thresholds of total energy and atomic force were set to 10−6 eV and 10−3 eV Å−1, respectively. Ab initio molecular dynamics (AIMD) simulations were conducted by using the NVT canonical ensemble with a Nosé–Hoover thermostat.36 Note that the machine-learning interatomic potentials package can also be combined with machine learning to establish high-precision interatomic interactions in a more cost-effective manner.37,38
The thermodynamic stability is examined by calculating the cohesive energy (Ecoh), which is defined as
| | | Ecoh = (EBCX − 2EB − 2EC − 2EX)/6, | (1) |
in which
EBCX,
EB,
EC, and
EX are the energy of the BCX monolayer, and a free B, C, and X atom, respectively. A more negative
Ecoh value indicates better thermodynamic stability of the structure.
According to the deformation potential theory, the carrier mobility (μ) of a 2D structure is defined as:39,40
| | 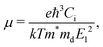 | (2) |
in which
ħ and
k are the reduced Planck constant and the Boltzmann constant, respectively.
T refers to the temperature.
Ci refers to the elastic constant,
m* is the effective mass of the carrier in the transport direction, and
md is the average effective mass in the two directions given by
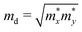
.
E1 stands for the deformation potential constant of the valence band maximum (VBM) for a hole, or the conduction band minimum (CBM) for an electron along the transportation direction, obtained by
E1 = ∂
Eedge/∂
ε, where
Eedge represents the shift of the band edge position with respect to the strain.
The relationship between the piezoelectric stress tensor eij, the piezoelectric strain tensor dik and elastic stiffness constant Ckj can be defined as: eij = dikCkj.41 Due to the P21 point group symmetry of the penta-BCX structure, the corresponding coefficients are:28
| | 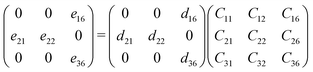 | (3) |
The non-zero independent piezoelectric strain coefficients d16, d21, d22, and d36 are derived as:28
| | 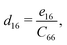 | (4) |
| | 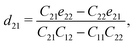 | (5) |
| | 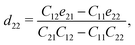 | (6) |
| | 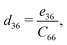 | (7) |
3 Results and discussion
3.1 Structure, stability and mechanical properties
The top and side views of the optimized penta-BCX (X = P, As, and Sb) structure are shown in Fig. 1, and BCX is used to denote planar penta-BCX in the following. The single cell contains two B atoms, two C atoms and two X atoms. Optimized structural parameters, including lattice constants (a, b), bond length (l) and thickness (δ), are summarized in Table 1, where the structural parameters of the BCP are in agreement with those previously reported.28 As the atomic radius of the group V elements increases, the lattice constants of the 2D structures as well as the thickness increase.
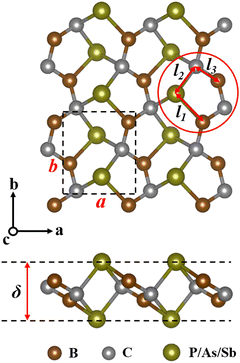 |
| | Fig. 1 The top and side views of pentagonal BCX (X = P, As, and Sb) monolayers. The black dashed square denotes the unit cell. | |
Table 1 The lattice constants (a and b, in Å), bond length (l1, l2, and l3, in Å), thickness (δ, in Å) and cohesive energy (Ecoh, in eV) of the BCX monolayers. Available reporting data for the BCP sheet are also included
| System |
a
|
b
|
l
1
|
l
2
|
l
3
|
δ
|
E
coh
|
| BCP |
3.65 |
4.11 |
1.96 |
1.92 |
1.56 |
2.47 |
−5.65 |
| BCAs |
3.71 |
4.24 |
2.09 |
2.07 |
1.53 |
2.73 |
−5.38 |
| BCSb |
3.96 |
4.41 |
2.31 |
2.27 |
1.53 |
3.02 |
−5.19 |
| BCP28 |
3.67 |
4.12 |
1.96 |
1.92 |
1.56 |
2.47 |
−5.61 |
As seen in Table 1, the obtained Ecoh are in the range from −5.19 eV to −5.65 eV. Compared with other similar pentagonal materials, Ecoh of BCX is lower than that of SiCN (−4.36 eV),42 and comparable with that of BCN (−6.18 eV),26 indicating their energetic stability. The dynamical stability of BCX can be obtained by calculating the phonon dispersion relationships along the high symmetry directions of the first Brillouin region. As shown in Fig. 2(a) and (b) and Fig. S1(a) (ESI†), for the monolayers considered, the dynamical matrix is completely free of imaginary eigenvalues. Our results of BCP are in line with the available literature.28 Considering the reported AIMD simulations of BCP,28 we have chosen a high temperature of 1200 K to study the thermal stability of BCX. As illustrated in Fig. 2(c) and (d), total energy fluctuations of BCAs and BCSb become gradually stable over time, and the final geometries do not suffer significant distortion after 10 ps, confirming their thermal stability.
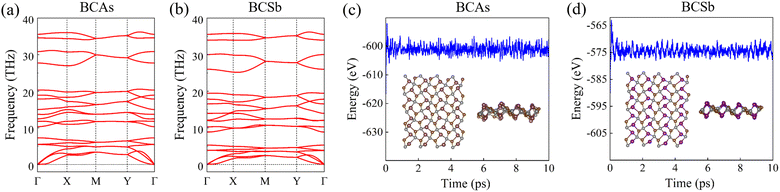 |
| | Fig. 2 (a) and (b) The phonon spectra, (c) and (d) the energy profile in AIMD simulations at 1200 K of BCAs and BCSb monolayers. The insets are snapshots taken after 10 ps. | |
The mechanical stability of the BCX structures was analyzed based on the energy-strain relationship, and the elastic constants obtained are listed in Table S1 (ESI†), which fully satisfy the Born criteria: C11C22 − C122 > 0 and C66 > 0.43 Using the same calculation method as our previous paper,44 we plotted Young's modulus and Poisson's ratio of BCX as a function of θ in Fig. S2(a) and (b) (ESI†). They both exhibit similar butterfly-like characteristics to those reported for BCP.28 Compared with BCN (220 N m−1),26 BNSi (113 N m−1),27 MoS2 (120 N m−1),45 and h-BN (271 Nm−1),46 BCX monolayers with flexible and anisotropic mechanical properties are prone to exhibit greater piezoelectricity.
3.2 Electronic structure and photocatalytic properties
The electronic properties of BCX were investigated by calculating the electronic energy band structure, and atomic projected density of states (PDOS), and the band-decomposition charge density distribution with the HSE06 functional. As shown in Fig. S1(b) (ESI†), the BCP has an indirect band gap of 3.08 eV, which is consistent with the previously reported 2.97 eV.28 As shown in Fig. 3(a) and (c), BCAs and BCSb are indirect bandgap semiconductors with the CBM located at the Γ point in the first Brillouin zone and the VBM located at the path Γ–X. It can be seen from PDOS that the VBM is mainly contributed by X atoms and the CBM is mainly contributed by B and X atoms. The charge density distribution shown in Fig. 3(b) and (d) reveals that X atoms and B atoms do contribute the electronic states near the Fermi energy level, which is consistent with the PDOS results. In addition, the asymmetric charge density distribution generated by strong orbital hybridization leads to spontaneous polarization of BCX.
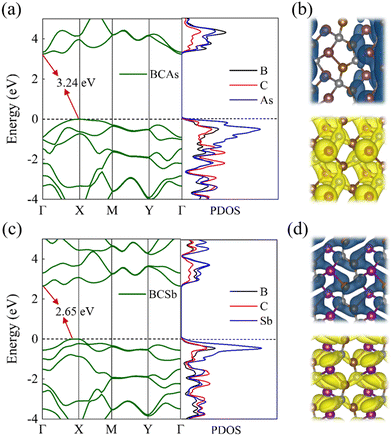 |
| | Fig. 3 (a)–(c) The band structure and the density of states, (b) and (d) the highest occupied band and the lowest unoccupied band of the BCX monolayers. (The isosurface value is 0.007 Å−3.) | |
We then align the band edge positions of BCX related to the vacuum level, which are extracted from the local potential distribution within the monolayer. The energy of the VBM and CBM with respect to the vacuum can be calculated as: EVBM = φ − EF, ECBM = EVBM + Eg, where φ, EF, and Eg are the electrostatic potential in a vacuum level, the Fermi level, and the band gap, respectively. As a superior photocatalyst for water decomposition, its band edge must straddle the redox potential of water, which depends on the pH value of the water decomposition reaction. The standard reduction potential of H+/H2 can be estimated by: EH+/H2 = −4.44 + pH × 0.059, while the oxidation potential of O2/H2O can be obtained by EO2/H2O = −1.23 +EH+/H2. The pH equals 0, 7, and 14 for acidic, neutral, and alkali conditions, respectively. Fig. 4 illustrates a schematic view of the band edges of BCX monolayers for photocatalytic water splitting. For comparison, data on reported 2D BNSi27 and BCN26 materials are included. Note that the VBM energy of BCSb is higher than the oxidation potential of water at pH = 0, so it is only suitable for driving water decomposition under neutral and alkaline conditions. Superior to BCN,26 the potential positions of BCP and BCAs are high enough to drive redox reactions at all pH values.
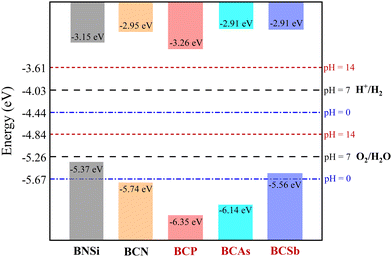 |
| | Fig. 4 The location of the VBM and CBM of the BCX monolayer. The redox potentials of water splitting at pH = 0 (blue dot-dashed lines), pH = 7 (black dashed lines), and pH = 14 (red dotted lines) are guides for the eyes. The data marked in red are calculated in the present work, and in the black are taken from ref. 26 and 27. | |
To characterize the electronic transport characteristics of BCX monolayers, effective mass (me, mh) and mobility (μe, μh) of charge carriers were computed. Due to the lack of symmetry of BCX, the carrier mobility along directions x and y is anisotropic. The results are summarized in Table 2, where the charge mobility usually has a large value in the y direction. Compared with the experimentally synthesized MoS2 (77.30/193.60 cm2 V−1 s−1)47 and penta-PdSe2 (534.55/229.01 cm2 V−1 s−1),48 the higher and anisotropic carrier mobility can effectively reduce the recombination rate of photogenerated carriers, which is desirable for the photocatalytic water splitting reaction process. The optical absorption capacity of 2D materials plays an essential role in photocatalytic applications. To study the optical absorption spectra of BCX nanosheets along the in-plane optical polarization, the complex dielectric constants were calculated for a given frequency. Fig. 5 shows the in-plane optical absorption coefficients of BCSb (the spectra for BCP and BCAs are shown in Fig. S3, ESI†). It is clear that only the BCSb monolayer possesses the ability to adsorb visible light, and its optical adsorption coefficient is very small, whether along the xx or yy direction.
Table 2 Relative effective mass (m*/m0) of electron (e) and hole (h), deformation potential constant (E1, in eV), and carrier mobilities (μ, in cm2 V−1 s−1) for pentagonal BCX monolayers at room temperature
| BCX |
Carrier |
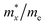
|
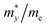
|
E
1,x
|
E
1,y
|
μ
x
|
μ
y
|
| BCP |
e |
0.50 |
1.07 |
7.62 |
3.25 |
48.08 |
396.32 |
| h |
1.90 |
2.57 |
3.42 |
3.65 |
20.57 |
43.06 |
| BCAs |
e |
0.42 |
3.19 |
7.80 |
2.34 |
43.20 |
1190.52 |
| h |
0.34 |
7.23 |
3.37 |
3.83 |
8.07 |
43.47 |
| BCSb |
e |
0.36 |
1.02 |
3.99 |
5.44 |
275.16 |
198.51 |
| h |
0.27 |
5.30 |
1.28 |
2.23 |
383.75 |
1042.80 |
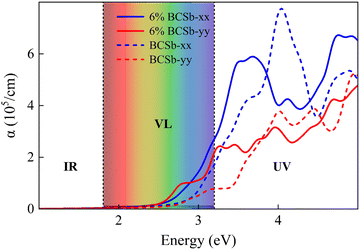 |
| | Fig. 5 In-plane optical absorption coefficients of unstrained (in dotted line) and strained (in solid line) BCSb. The energy ranges for the IR (infrared), VL (visible light), and UV (ultraviolet) regions are marked. | |
3.3 Strain engineering
Tensile or compressive strain can modulate the electronic structure by changing the distance between atoms.49,50 As shown in Fig. 6, as the in-plane biaxial strain increases, the bandgap values are tuned, and the VBM and CBM positions of BCX span the redox potentials at different pH. This can meet different potential requirements, which is conducive to its application in photocatalytic hydrolysis. The ideal photocatalyst should absorb as much visible and UV light as possible. Under 6% tensile strain, the absorption spectra are red-shifted in both directions, and the absorption in the UV region is also enhanced, as shown in Fig. 5. A similar red-shift phenomenon occurs for strained BCP and BCAs in Fig. S3 (ESI†). The stability of these materials under tensile strain was double checked by AIMD simulations (see Fig. S4, ESI†). These structures show no significant deformation or fracture, and the total energy oscillates steadily within a certain small range. This indicates that the strained BCX exhibits high thermodynamic stability.
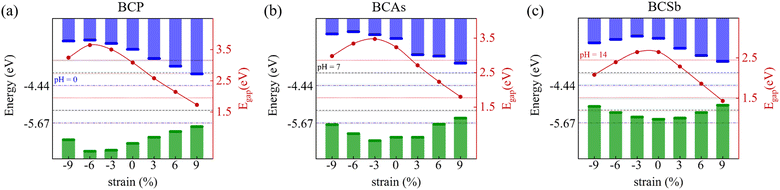 |
| | Fig. 6 Variation of the band gaps and band edge positions of (a) BCP, (b) BCAs, and (c) BCSb monolayers under various biaxial strains. | |
3.4 Intrinsic piezoelectricity
Materials can exhibit piezoelectric behavior only when they lack inversion symmetry and have an electronic band gap. As a unique material property, piezoelectricity is described as the interconversion of mechanical and electrical energy in a non-centrosymmetric structure. The piezoelectric effect is accurately described by solving the third-order tensor to obtain the piezoelectric constants in different directions using the correlation between the strain (or stress) and the electric field. As shown in Table 3, BCX possesses remarkable in-plane piezoelectric responses to both tensile and shear strains, with the strongest in-plane piezoelectric effect factor, d21, being an order of magnitude larger than that of BCN and CNP.41,51 Compared with h-BN (0.60 pm V−1)52 and MoS2 (3.73 pm V−1),52 BCX shows a piezoelectricity advantage, suggesting that BCX is an ideal candidate for powerful piezoelectric catalytic effect piezo-photocatalysis. The strain produced by the piezoelectric effect is in the elastic strain category, and obviously its strong piezoelectricity is closely related to the low elastic modulus of the material.
Table 3 Piezoelectric stress tensor eij (in 10−10 C m−1), and piezoelectric strain tensor dij (in pm V−1) of BCX monolayers. Available reporting data for BCP, BCN, and CNP are also included
| System |
e
21
|
e
22
|
e
16
|
e
36
|
d
21
|
d
22
|
d
16
|
d
36
|
| BCP |
−2.56 |
1.34 |
−1.07 |
0.34 |
−13.65 |
6.39 |
−1.32 |
0.46 |
| BCAs |
−2.44 |
1.35 |
−0.85 |
0.30 |
−8.82 |
3.99 |
−1.36 |
0.48 |
| BCSb |
−2.48 |
1.97 |
−0.64 |
0.28 |
−9.56 |
4.79 |
−1.38 |
0.60 |
| BCP28 |
−2.53 |
1.35 |
−1.00 |
0.35 |
−13.57 |
6.33 |
−1.31 |
0.46 |
| BCN41 |
1.93 |
−1.24 |
1.80 |
−0.08 |
0.88 |
−0.68 |
1.72 |
−0.08 |
| CNP51 |
2.37 |
−1.21 |
1.78 |
−0.11 |
1.39 |
−0.69 |
1.80 |
−0.10 |
4 Conclusions
In summary, the BCX (X = P, As, and Sb) monolayers were verified to be dynamically, thermally, and mechanically stable by first-principles calculations. BCP, BCAs, and BCSb monolayers have low in-plane Young's modulus and asymmetric charge density distribution, exhibiting anisotropic mechanical properties and strong piezoelectricity. All three materials are indirect bandgap semiconductors with suitable band gaps, high anisotropic carrier mobility and good optical absorption in the UV region. In addition, strain can modulate the bandgap, band edge position and light absorption, thus enhancing their photocatalytic performance in the VL and UV regions. We predict that BCX monolayers could be used as piezo-photocatalysts, and may have broad application prospects in flexible devices and piezoelectric devices.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work is supported by the Natural Science Foundation of China (Grants No. 11874033 and 12374061) and the KC Wong Magna Foundation in Ningbo University. The computations were supported by the high performance computing center at Ningbo University.
References
- W. Lubitz and W. Tumas, Chem. Rev., 2007, 107, 3900–3903 CrossRef CAS PubMed.
- T. Yu, C. Wang, X. Yan, G. Yang and U. Schwingenschlogl, J. Phys. Chem. Lett., 2021, 12, 2464–2470 CrossRef CAS PubMed.
- K. Hong, H. Xu, H. Konishi and X. Li, J. Phys. Chem. Lett., 2010, 1, 997–1002 CrossRef CAS.
- T. Lv, J. Li, N. Arif, L. Qi, J. Lu, Z. Ye and Y. Zeng, Matter, 2022, 5, 2685–2721 CrossRef CAS.
- Z. Liang, C. Yan, S. Rtimi and J. Bandara, Appl. Catal., B, 2019, 241, 256–269 CrossRef CAS.
- C. Wang, C. Hu, F. Chen, T. Ma, Y. Zhang and H. Huang, Nano Energy, 2022, 108093 Search PubMed.
- X. Ma, Y. Gao, B. Yang, X. Lou, J. Huang, L. Ma and D. Jing, Mater. Today Nano, 2023, 21, 100289 CrossRef CAS.
- K. Rajan, P. Gotipamul, S. Khanna, S. Chidambaram and M. Rathinam, Mater. Lett., 2021, 296, 129902 CrossRef.
- D. Yu, Z. Liu, J. Zhang, S. Li, Z. Zhao, L. Zhu, W. Liu, Y. Lin, H. Liu and Z. Zhang, Nano Energy, 2019, 58, 695–705 CrossRef CAS.
- C. Hu, H. Huang, F. Chen, Y. Zhang, H. Yu and T. Ma, Adv. Funct. Mater., 2020, 30, 1908168 CrossRef CAS.
- J. Wang, C. Hu, Y. Zhang and H. Huang, Chin. J. Catal., 2022, 43, 1277–1285 CrossRef CAS.
- M. Zhang, S. Nie, T. Cheng, Y. Feng, C. Zhang, L. Zheng, L. Wu, W. Hao and Y. Ding, Nano Energy, 2021, 90, 106635 CrossRef CAS.
- J. Wu, Y. Sun, W. Chang and J. Lee, Nano Energy, 2018, 46, 372–382 CrossRef CAS.
- C. Zhang, D. Lei, C. Xie, X. Hang, C. He and H. Jiang, Adv. Mater., 2021, 33, 2106308 CrossRef CAS PubMed.
- C. Hu, F. Chen, Y. Wang, N. Tian, T. Ma, Y. Zhang and H. Huang, Adv. Mater., 2021, 33, 2101751 CrossRef CAS PubMed.
- H. Lei, H. Zhang, Y. Zou, X. Dong, Y. Jia and F. Wang, J. Alloys Compd., 2019, 809, 151840 CrossRef CAS.
- Y. Zhao, X. Huang, F. Gao, L. Zhang, Q. Tian, Z. Fang and P. Liu, Nanoscale, 2019, 11, 9085–9090 RSC.
- D. Hong, W. Zang, X. Guo, Y. Fu, H. He, J. Sun, L. Xing, B. Liu and X. Xue, ACS Appl. Mater. Interfaces, 2016, 8, 21302–21314 CrossRef CAS PubMed.
- W. Liu, P. Wang, Y. Ao, J. Chen, X. Gao, B. Jia and T. Ma, Adv. Mater., 2022, 34, 2202508 CrossRef CAS PubMed.
- X. Huang, R. Lei, J. Yuan, F. Gao, C. Jiang, W. Feng, J. Zhuang and P. Liu, Appl. Catal., B, 2021, 282, 119586 CrossRef CAS.
- S. Jia, Y. Su, B. Zhang, Z. Zhao, S. Li, Y. Zhang, P. Li, M. Xu and R. Ren, Nanoscale, 2019, 11, 7690–7700 RSC.
- Z. Li, H. Fu, X. Wang, X. Chen, T. Li, Y. Cui, N. Li and H. Luo, Colloids Surf., A, 2022, 652, 129820 CrossRef CAS.
- M. Xu, M. Lu, G. Qin, X. Wu, T. Yu, L. Zhang, K. Li, X. Cheng and Y. Lan, Angew. Chem., Int. Ed., 2022, 61, e202210700 CrossRef CAS PubMed.
- W. Shen, N. Li, S. Zuo, M. Wu, G. Sun, Q. Li, M. Shi and J. Ma, Ceram. Int., 2022, 48, 15899–15907 CrossRef CAS.
- X. Xu, X. Lin, F. Yang, S. Huang and X. Cheng, J. Phys. Chem. C, 2020, 124, 24126–24134 CrossRef CAS.
- M. Kilic and K. Lee, Phys. Rev. Appl., 2022, 18, 014066 CrossRef CAS.
- M. Varjovi, M. Kilic and E. Durgun, Phys. Rev. Mater., 2022, 6, 034004 CrossRef CAS.
- C. Hou, Y. Shen, W. Sun, Y. Chen, D. Ni and Q. Wang, J. Mater. Chem. C, 2022, 10, 10302–10309 RSC.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- A. Krukau, O. Vydrov, A. Izmaylov and G. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- H. Monkhorst and J. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- G. Martyna, M. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- I. S. Novikov, K. Gubaev, E. V. Podryabinkin and A. V. Shapeev, Mach. Learn.: Sci. Technol., 2020, 2, 025002 Search PubMed.
- B. Mortazavi, B. Javvaji, F. Shojaei, T. Rabczuk, A. V. Shapeev and X. Zhuang, Nano Energy, 2021, 82, 105716 CrossRef CAS.
- J. Chen, J. Xi, D. Wang and Z. Shuai, J. Phys. Chem. Lett., 2013, 4, 1443–1448 CrossRef CAS PubMed.
- S. Sun, F. Meng, H. Wang, H. Wang and Y. Ni, J. Mater. Chem. A, 2018, 6, 11890–11897 RSC.
- K. Zhao, Y. Guo, Y. Shen, Q. Wang, Y. Kawazoe and P. Jena, J. Phys. Chem. Lett., 2020, 11, 3501–3506 CrossRef CAS PubMed.
- S. Sharma, I. Qattan, M. Jaishi and D. Paudyal, ACS Appl. Energy Mater., 2022, 4, 2561–2569 CrossRef CAS.
- J. Wang, S. Yip, S. Phillpot and D. Wolf, Phys. Rev. Lett., 1993, 71, 4182 CrossRef CAS PubMed.
- L. Liu, X. Kang, S. Gao and X. Duan, Nanoscale, 2023, 15, 9123–9129 RSC.
- Q. Peng and S. De, Phys. Chem. Chem. Phys., 2013, 15, 19427–19437 RSC.
- R. Andrew, R. Mapasha, A. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 100, 209901 CrossRef.
- H. Phuc, N. Hieu, B. Hoi, N. Hieu, T. Thu, N. Hung, V. Ilyasov, N. Poklonski and C. Nguyen, J. Electron. Mater., 2018, 47, 730–736 CrossRef CAS.
- C. Long, Y. Liang, H. Jin, B. Huang and Y. Dai, ACS Appl. Energy Mater., 2018, 2, 513–520 CrossRef.
- G. Wang, M. Si, A. Kumar and R. Pandey, Appl. Phys. Lett., 2014, 104, 213107 CrossRef.
- X. Zhong, Y. Yap, R. Pandey and S. Karna, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 193403 CrossRef.
- W. Sun, Y. Shen, Y. Guo, Y. Chen and Q. Wang, Appl. Surf. Sci., 2021, 554, 149499 CrossRef CAS.
- K. Duerloo, M. Ong and E. Reed, J. Phys. Chem. Lett., 2012, 3, 2871–2876 CrossRef CAS.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  a,
Shan
Gao
*ab and
Xiangmei
Duan
a,
Shan
Gao
*ab and
Xiangmei
Duan
 *ab
*ab
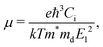
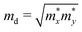 . E1 stands for the deformation potential constant of the valence band maximum (VBM) for a hole, or the conduction band minimum (CBM) for an electron along the transportation direction, obtained by E1 = ∂Eedge/∂ε, where Eedge represents the shift of the band edge position with respect to the strain.
. E1 stands for the deformation potential constant of the valence band maximum (VBM) for a hole, or the conduction band minimum (CBM) for an electron along the transportation direction, obtained by E1 = ∂Eedge/∂ε, where Eedge represents the shift of the band edge position with respect to the strain.