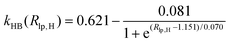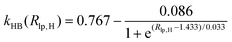Development of a QM/MM(ABEEM) method for the deprotonation of neutral and cation radicals in the G-tetrad and GGX(8-oxo-G) tetrad†
Yue
Wang‡
,
Linlin
Liu‡
,
Yue
Gao
,
Jiayue
Zhao
,
Cui
Liu
 *,
Lidong
Gong
*,
Lidong
Gong
 * and
Zhongzhi
Yang
* and
Zhongzhi
Yang

School of Chemistry and Chemical Engineering, Liaoning Normal University, Dalian, 116029, People's Republic of China. E-mail: liuc@lnnu.edu.cn; gongjw@lnnu.edu.cn; Tel: +86 411-82158977
First published on 28th November 2023
Abstract
The rapid deprotonation of G˙+ in the DNA strand impedes positive charge (hole) transfer, whereas the slow deprotonation rate of G˙+ in the G-tetrad makes it a more suitable carrier for hole conduction. The QM/MM(ABEEM) combined method, which involves the integration of QM and the ABEEM polarizable force field (ABEEM PFF), was developed to investigate the deprotonation of neutral and cation free radicals in the G-tetrad and GGX(8-oxo-G) tetrad (xanthine and 8-oxoguanine dual substituted G-tetrad). By incorporating valence-state electronegativity piecewise functions χ*(r) and implementing charge local conservation conditions, QM/MM(ABEEM) possesses the advantage of accurately simulating charge transfer and polarization effect during deprotonation. The activation energy calculated by the QM method of X˙ is the lowest among other bases in the GGX(8-oxo-G) tetrad, which is supported by the computation of the average electronegativity calculated by ABEEM PFF. By utilizing QM/MM(ABEEM) with a two-way free energy perturbation method, the deprotonation activation energy of X˙ in the GGX(8-oxo-G) tetrad is determined to be 33.0 ± 2.1 kJ mol−1, while that of G˙+ in the G-tetrad is 20.7 ± 0.6 kJ mol−1, consistent with the experimental measurement of 20 ± 1.0 kJ mol−1. These results manifest that X˙ in the GGX(8-oxo-G) tetrad exhibits a slower deprotonation rate than G˙+ in the G-tetrad, suggesting that the GGX(8-oxo-G) tetrad may serve as a more favorable hole transport carrier. Furthermore, the unequal average electronegativities of bases in the GGX(8-oxo-G) tetrad impede the deprotonation rate. This study provides a potential foundation for investigating the microscopic mechanism of DNA electronic devices.
1. Introduction
The unique one-dimensional π stacking base pair array structure of double-stranded DNA makes it have the chemical function of mediating charge transfer.1,2 It is observed that positive charge (hole) transports along DNA strands.3–6 Charge transfer through DNA strands has attracted much attention in the last few decades due to its biological importance and potential application in molecular electronics.7,8 In double-stranded DNA, guanine (G) has the lowest oxidation potential (+1.47 V) and is the most susceptible of all to being oxidized and generating the guanine radical cation (G˙+).9–12 Some studies have shown that the deprotonation of G˙+ will compete with hole transfer.7,13–15 The deprotonation rate of G˙+ is about 106–107 s−1, which determines that the maximum distance of hole transfer in double-stranded DNA is only about 200.0 Å.16,17 Therefore, the behavior of rapid G˙+ deprotonation in double-stranded DNA becomes the main factor that hinders its application in electronics.The human genome contains a large number of G sequences especially in the oncogenic promoter, minisatellite repeats, and telomeric region.18–23 These G-rich sequences pair in a non-canonical manner to form stable four-stranded DNA structures with different folding topologies, called G-quadruplexes.24 The deprotonation rate of G˙+ in the G-quadruplex is about 105 s−1, which is slower than that of double-stranded DNA. It effectively extends the distance of hole transfer. The G-quadruplex is a more promising structure for hole transfer and is instructive for improving medical electronic devices. It is widely found in regions with important functions such as telomeres, promoters of disease genes, and immunoglobulin switch regions.25–27
Numerous studies have been conducted to incorporate guanine analogs into the G-tetrad to design novel G-tetrad structures. 28–31 This work involves two types of naturally occurring base damages: 8-oxoguanine and xanthine. 8-Oxoguanine (abbreviated as 8-oxo-G) is formed by intracellular oxidative damage to the guanine base. Xanthine (abbreviated as X) is a guanine analog and forms via the nitrosative deamination of the guanine base.32
The NMR study shows that there is a structure of the GGX(8-oxo-G) tetrad in solution, and the complementary arrangement between X and 8-oxo-G is confirmed.33 The GGX(8-oxo-G) tetrad can retain the original folding topology reasonably and its inherent characteristics can be studied through electrospray ionization mass spectrometry, ultraviolet absorption spectrum, and circular dichroism.34 However, the charge transfer rate of deprotonation is so fast, and detailed deprotonation behavior cannot be captured directly and accurately in the experiment, so it is impossible to judge the microscopic mechanism such as the reaction path and charge distribution associated with proton transfer. Theoretical methods have particular advantages in the study of such a rapid process, and we will focus on the deprotonation of free radical cations in the GGX(8-oxo-G) tetrad and G-tetrad via molecular dynamics simulations.
At present, the QM/MM method is widely used to simulate biological macromolecular systems.35–40 Many force fields are employed in QM/MM, and a polarizable force field (PFF) has been developed to accurately simulate the polarization effect and charge transfer effect, such as CHARMM,41 AMBER Pol,42,43 CHARMM Drude,44,45 AMOEBA,46 X-POL,47 OPLS48 and so on. Yang et al. have developed the atom-bond electronegativity equalization method fluctuating charge PFF (ABEEM PFF) and combined it with QM to establish the QM/MM(ABEEM) method.49–56 When the environment changes, the system energy and the partial charges of atoms, chemical bonds, and lone-pair (lp) electron sites will be recalculated in terms of ABEEM PFF. The ABEEM PFF can reasonably describe the charge transfer effect and polarization effect and has been widely used in the study of gas-phase water clusters, ionic aqueous solutions, inorganic and organic molecules,57–59 and biomolecules such as peptides, proteins, and nucleic acids.60
In this paper, four deprotonation paths of the GGX(8-oxo-G) tetrad were designed to study the deprotonation mechanism, and the optimal deprotonation path was determined as X˙. The QM/MM(ABEEM) method was used to simulate the deprotonation of G˙+ in the G-tetrad and X˙ in the GGX(8-oxo-G) tetrad, respectively. The charge transfer effect and polarization effect in deprotonation will be handled by setting valence-state electronegativity piecewise functions χ*(r) and local charge conservation conditions. Moreover, molecular dynamics (MD) simulations with the two-way free energy perturbation method were used to calculate the activation energy. This research can provide valuable microscopic insight into the deprotonation mechanism of neutral and cation radicals in the G-tetrad and GGX(8-oxo-G) tetrad and may serve as the potential basis for the design of DNA electronic devices.
2. Models and methods
The transition state was searched at the M06-2X/6-31G(d) level using the Berny algorithm,61 and the intrinsic reaction coordinate (IRC) method was performed for verification. The activation energy was calculated at the same level. The density functional M06-2X was chosen because of its capacity to account for dispersion and polarization effect in the systems of hydrogen bonds62 and open-shell systems containing free radicals.63This calculation is mainly composed of two parts: QM and QM/MM(ABEEM) calculations. The workflow diagram is shown in Fig. 1. The GAUSSIAN 09 package was employed to perform all the QM calculations.64
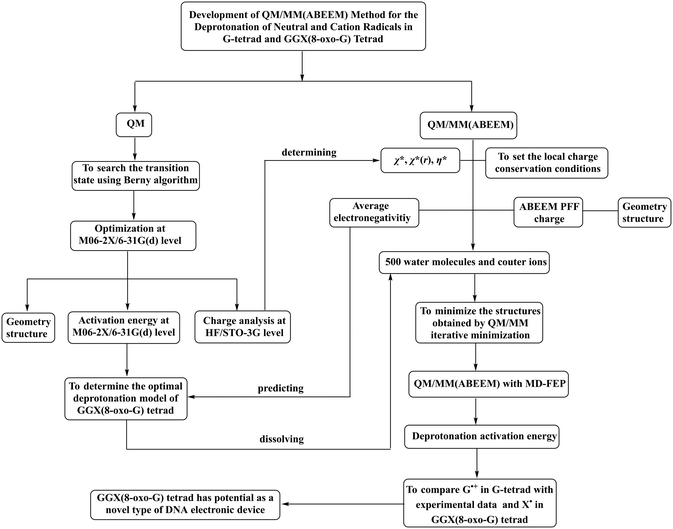 | ||
| Fig. 1 Flowchart of investigation on the deprotonation of neutral and cation radicals in the G-tetrad and GGX(8-oxo-G) tetrad. | ||
2.1. Establishment of models
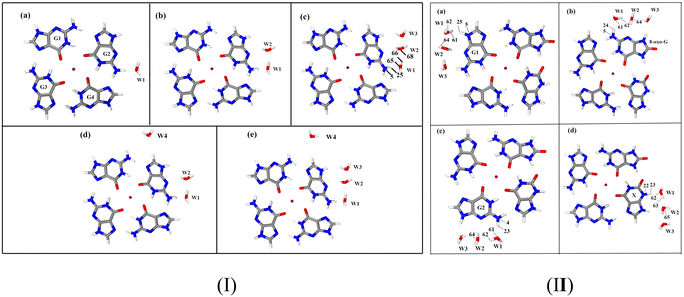
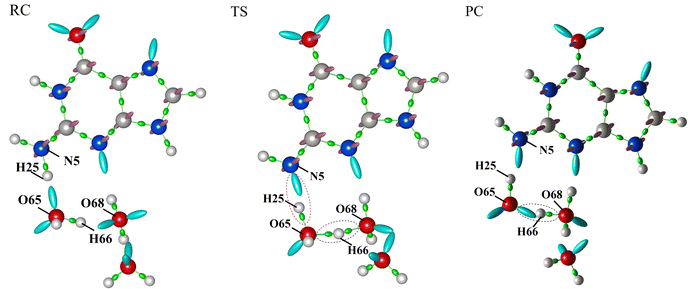
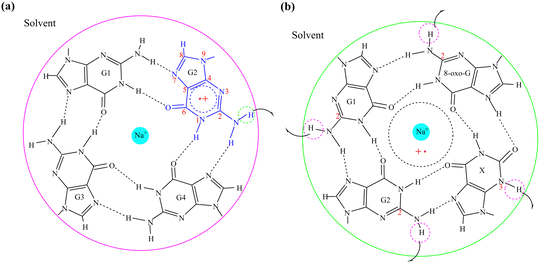
The activation energy of G˙+ deprotonation in the human telomeric G-quadruplex AG3(T2AG3)3 is similar to that of 1-methyl deoxyguanosine.65,66 It indicates that the conformation of the G-quadruplex has little effect on the activation energy of G˙+ deprotonation. Hence, it is reasonable to use a simplified model of a single layer of the G-tetrad plane. The calculation efficiency is improved and the accuracy of the deprotonation details is ensured.The N2–H (the international label of the base), as shown in Fig. 2(a), is the deprotonation site of G˙+ in the G-tetrad.13Fig. 3I plots the arrangement of explicit water molecules in the deprotonation model of G˙+ in the G-tetrad. In the central cavity of the G-tetrad, a Na+ ion is added with a distance of about 2.2 Å from the O atom of the carbonyl to maintain the stability of the system and help achieve convergence of QM calculation.
 | ||
| Fig. 2 The deprotonation sites of (a) G˙+ in the G-tetrad; (b) G1˙+, G2˙, 8-oxo-G˙+, and X˙ in the GGX(8-oxo-G) tetrad. | ||
Proper arrangement of X and 8-oxo-G dual substituted G-tetrad can retain the original folding topology and reverse hydrogen bond polarity. Moreover, the GGX(8-oxo-G) tetrad was selected because it also exists in both protonated and deprotonated states at physiological pH.33
The deprotonation site of X˙ is N3–H and those of 8-oxo-G˙+, G1˙+, G2˙ are all N2–H (Fig. 2(b)). In order to distinguish the two guanine bases, the one adjacent to 8-oxo-G is referred to as G1, and the other G2. The four possible deprotonation paths are shown in Fig. 3II. The deprotonation behavior was investigated by adding three water molecules near the deprotonation site of each base separately to explore the most ideal deprotonated base.
2.2. QM/MM(ABEEM) method
According to the basic idea of the QM/MM method, a system is divided into the QM and MM regions. In this work, a G-tetrad, a GGX(8-oxo-G) tetrad, a Na+ ion and three water molecules were selected as the QM region, and the surrounding water environment and counter ions were selected as the MM region. The total energy expression of a system is expressed as| Etotal = EQM + EMM + EelecQM/MM + EvdWQM/MM | (1) |
In the QM/MM(ABEEM) method, EelecQM/MM and EvdWQM/MM are expressed as eqn (2) and (3), respectively.
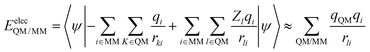 | (2) |
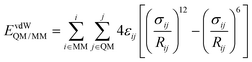 | (3) |
In the calculation of EelecQM/MM, the charge distribution of the QM region is obtained under the influence of the MM region. The charge distribution of the MM region also considers the effect of the QM region. The electrostatic interaction between sites after polarization is calculated by EelecQM/MM.
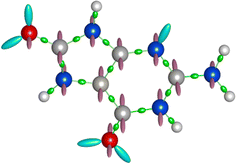
The ABEEM based on density functional theory (DFT)67 and the electronegativity equalization method (EEM)68 can quickly and accurately obtain the charge distribution and total energy of the system, where the electron density in the ABEEM of a molecule can be divided into four parts: atom, σ bond, π bond, and lp electrons sites. The charge sites of 8-oxo-G are shown in Fig. 4, including 16 atom sites on the atomic nucleus, 17 σ bond sites, which locate at the ratio of covalent radii between bonded atoms; 24 π bond sites perpendicular to the σ bond plane, placing above and below the double-bond atoms at the covalent radius of double-bond atoms; 6 lp electrons sites at the covalent radius of double-bond atoms, with angles determined by the hybrid orbital type. The ABEEM PFF labels of the above sites are listed in Fig. S2 (ESI†).
Yang et al. introduced the ABEEM49,69–71 into MM and established ABEEM PFF,51,52 in which the potential energy is expressed as eqn (4). At present, it has been widely used in a pure water system, ion aqueous solution, protein, nucleic acid system, etc.
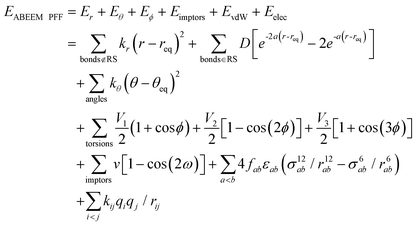 | (4) |
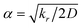 ). In the Eϕ, using Fourier expansion, where V1, V2 and V3 are the force constants and ϕ is the dihedral angle. The trigonometric function was used in Eimptors, where v and ω are the force constant and non-coplanar dihedral angle, respectively. The 12-6 Lennard-Jones was used in the EvdW, where εab, σab, and rab are Lennard-Jones well depth, diameter parameters and the distance between the a atom and the b atom, respectively. When the interaction between a and b atoms in a molecule is 1–2 or 1–3 relations, fab = 0; for 1–4 relation, fab = 0.5, and for 1–5 or other relations, fab = 1. The Eelec adopting Coulomb interaction is the distinguishing characteristic of ABEEM PFF, wherein the ABEEM PFF accurately computes the charge distribution by meticulously considering the electrostatic interactions among the atom, bond (comprising of σ and π bonds), and lp electrons sites. qi and qj are partial charges of the i atom and j atom, respectively. For 1–2 and 1–3 relations of atom pairs in a molecule, kij = 0; kij = kHB(Rlp,H) (hydrogen bond fitting function) when i and j are in the hydrogen bond interaction region (HBIR), and in all other cases, kij = 0.57.
). In the Eϕ, using Fourier expansion, where V1, V2 and V3 are the force constants and ϕ is the dihedral angle. The trigonometric function was used in Eimptors, where v and ω are the force constant and non-coplanar dihedral angle, respectively. The 12-6 Lennard-Jones was used in the EvdW, where εab, σab, and rab are Lennard-Jones well depth, diameter parameters and the distance between the a atom and the b atom, respectively. When the interaction between a and b atoms in a molecule is 1–2 or 1–3 relations, fab = 0; for 1–4 relation, fab = 0.5, and for 1–5 or other relations, fab = 1. The Eelec adopting Coulomb interaction is the distinguishing characteristic of ABEEM PFF, wherein the ABEEM PFF accurately computes the charge distribution by meticulously considering the electrostatic interactions among the atom, bond (comprising of σ and π bonds), and lp electrons sites. qi and qj are partial charges of the i atom and j atom, respectively. For 1–2 and 1–3 relations of atom pairs in a molecule, kij = 0; kij = kHB(Rlp,H) (hydrogen bond fitting function) when i and j are in the hydrogen bond interaction region (HBIR), and in all other cases, kij = 0.57.
During the MD simulations in explicit water, there are hydrogen bonds among water molecules. W2 forms hydrogen bonds with W1 and W3 in the form of H3O+, respectively. The kHB(Rlp,H), listed in Table 1, is employed and optimized to deal with different types of hydrogen bonds between water molecules, where Rlp,H represents the distance between lp electrons of the O atom and H atom, and the functional relationships between kHB(Rlp,H) and Rlp,H are shown in Fig. S1 (ESI†).
The partial charges in ABEEM PFF fluctuate with the change of ambient environments and geometry to represent the polarization effect, and particularly those in the atoms involved in bond formation and breaking undulate to a great extent during the deprotonation. It is difficult to describe in terms of a constant χ*, so the valence-state electronegativity piecewise function χ*(r)72,73 is introduced for concerned atoms to describe the fluctuant charge distributions during the deprotonation.
The χ*(r) is the function of the distance r between the concerned atoms, meanwhile, charge transfer and polarization effect are simulated with the change of r. The linear regression and least squares methods are employed to fit the QM charge distributions along the IRC and obtain the χ*(r). The QM charge distribution from the HF/STO-3G level served as the reference. The STO-3G basis set does not exaggerate the overlap of inter-atomic basis functions and overestimate the polarization effect,70 and it has been generally used in the ABEEM PFF for enzyme system,74,75 graphene–water system,76 base pair,77 water clusters,78,79etc.
The following atoms as active sites are represented by the atomic number displayed in the GaussView software.64 During the deprotonation of G˙+ in the G-tetrad, including N5 and H25 in G˙+, O65 and H66 in W1, and O68 in W2; while in the deprotonation of X˙ in the GGX(8-oxo-G) tetrad, N22 and H23 in X˙, O62 and H63 in W1, and O65 in W2 are mainly concerned. The χ*(r) of the above atoms are listed in Tables S1–S10 (ESI†).
The effective electronegativity equations of the atom, σ bond, π bond, and lp electrons are expressed in eqn (5)–(8), respectively.
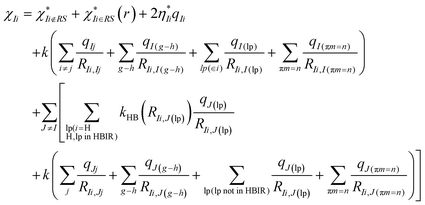 | (5) |
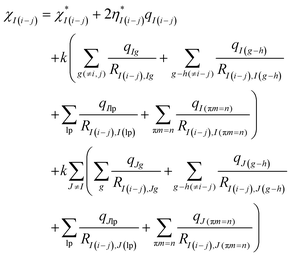 | (6) |
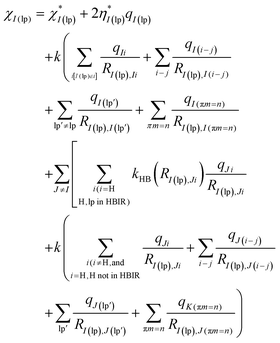 | (7) |
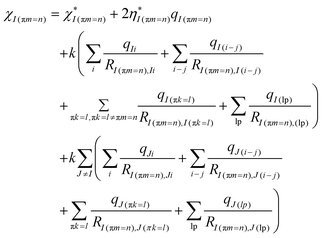 | (8) |
The EEM holds eqn (9).
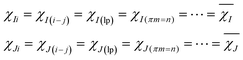 | (9) |
The local charge conservation conditions are used, where the charge transfer between molecules is forbidden. The different local charge conservation conditions were set for reactant (RC), transition state (TS), and product (PC), respectively. During the deprotonation of G˙+ in the G-tetrad: (1) from RC to TS, the net charge of G˙+ is 1.00 |e|; (2) in TS, the net charge of W2 and W1 is 1.00 |e|; (3) from TS to PC, the net charge of the three water molecules is 1.00 |e|. Under all the above conditions, the net charge of Na+ is always 1.00 |e|, and other molecules setting are electrically neutral.
2.3. Details of molecular dynamics simulation-free energy perturbation
Free energy perturbation (FEP) theory presented by Zwanzig80 was used to calculate the deprotonation activation energy in this study. From RC to TS, the potential energy was partitioned into multiple intermediate states, with the energy of each state expressed as a function of the coupling coefficient λ. According to the structures intercepted every three steps along IRC, the λ, scaled from 0 to 1, was evenly spaced into 17 in the deprotonation.The change from state 1 to state 2 was divided into 1 → λ → λ + 1 → ⋯ → 2. The free energy difference of each stage with small changes was calculated separately and summed up finally. The difference in the total free energy between RC and TS can be expressed as:
| ΔFRC→TS = ΔGRC→TSQM + ΔARC→TS | (10) |
From RC to TS, the reaction is segmented reasonably to obtain the exact value of ΔARC→TS, and determine the lowest energy reaction path. The free energy difference between any points λ and (λ + 1) can be expressed as:
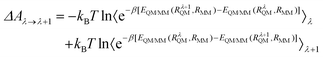 | (11) |
The corresponding difference in total free energy between RC and TS can be described as:
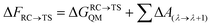 | (12) |
The free energy of a point i on the reaction coordinate as well as the free energy change values of λi → λi+1 and λi → λi−1 were obtained using the two-wide sampling method.
Systems were neutralized by the introduction of 2 Cl− ions and solvated using the ABEEM-7P water model in a truncated cubic box accommodating 500 water molecules. To minimize the geometry of the deprotonation system efficiently, the convergence criteria81 was adopted for QM/MM iterative minimization. Minimization was completed when the maximum energy deviation in the QM region was less than 5 × 10−4 a.u., and root mean square (RMS) in the MM region was less than 1 × 10−2 kcal mol−1 Å−1. Based on the structures obtained by QM/MM iterative minimization, taking the lengths of breaking and forming bonds as variables, the minimum energy reaction path in a two-dimensional coordinate space was determined.
The activation energy of deprotonation was calculated by MD simulations with two-way free energy perturbation (MD-FEP),82 and all the MD-FEP calculations were performed at NVT ensemble in QM/MM(ABEEM) using the modified Tinker 6.2 program. An energy compensation term of 0.6 kcal mol−1 was added to the activation energy for consistency by the experimental method.73,83 The Verlet integral and periodic boundary conditions were used.84,85 The cutoff was set to 12.3 Å and the nearest mirror image was adopted. The integral length was set to 1.0 fs and charge distribution was recalculated every 1.0 ps. Final simulations were run in the absence of position restraints at 298 K86 for 500 ps.40,87 The last 100 ps data were used for statistical the correlation properties, and then to obtain the fluctuation range.
3. Results and discussion
Two water molecules, labeled as W1 and W2, are placed in the first hydration shell, adjacent to N2–H and N3 of G˙+ in the hydrogen-bonding conformation. Regardless of the adjustments made to the positions and orientations of the water molecules, proton transfer is not observed in either the 1H2O or 2H2O models of G˙+ in the G-tetrad. In the 3H2O model, W3 signifies the influence of the second hydration shell, interacting only weakly via hydrogen bonding with W2. Proton transfer is observed in this model, suggesting that W3 assists in anchoring the proton at W2.To further validate the 3H2O model, it is necessary to consider more water molecules or explore additional conformations of this model. A previous study considered adding a water molecule to the C8-H site of an adjacent base (G4). The results show that this additional water molecule weakens the ability of W1 to transport protons, resulting in activation energy inconsistent with experimental data.88 Therefore, the discussion on this site is not to be repeated. The N9 site is connected to the pentosyl group in the real environment, resulting in no space for additional water molecules. The only viable site for adding water molecules is at C8–H.
According to the literature about G-quadruplex crystal structures,89,90 water molecules mainly form strong hydrogen bonds with the N2–H and N3 of the G base. Therefore, based on the 2H2O model, the water molecule (W4) is added at the C8–H far away from the deprotonation site to establish the 3H2O-b model. In the 3H2O-b model, proton transfer is not observed, underscoring the necessity of W3. When W4 is added at C8-H based on the 3H2O model to establish the 4H2O model, the calculated results are similar to those of 3H2O. This suggests that water molecule far from the deprotonation site does not significantly impact deprotonation. Clearly, the 3H2O model is reasonable.
3.1. Analysis of activation energy
The activation energy of the four deprotonation paths of the GGX(8-oxo-G) tetrad is selected as the criteria to determine the optimal deprotonation model. At the M06-2X/6-31G(d) level, the deprotonation activation energies of G1˙+, 8-oxo-G˙+, G2˙ and X˙ in the GGX(8-oxo-G) tetrad are 40.6, 41.9, 43.9 and 36.6 kJ mol−1, respectively. The activation energy of X˙ is lower than the other free radicals, so X˙ in the GGX(8-oxo-G) tetrad is the most favorable for deprotonation.The average electronegativity ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) of the G-tetrad and GGX(8-oxo-G) tetrad was calculated by the QM/MM(ABEEM) method. The
of the G-tetrad and GGX(8-oxo-G) tetrad was calculated by the QM/MM(ABEEM) method. The ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) value of each base in the G-tetrad is equal, while that of the X base in the GGX(8-oxo-G) tetrad is higher than other bases (Table 4). Higher
value of each base in the G-tetrad is equal, while that of the X base in the GGX(8-oxo-G) tetrad is higher than other bases (Table 4). Higher ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) is more attractive for electrons and will be favorable for the leaving of a proton. Therefore, it is reasonable to take the X base as the most favorable base for the deprotonation. This is also consistent with the results of the deprotonation activation energies by the QM method. Thus, X˙ in the GGX(8-oxo-G) tetrad is determined as the optimal deprotonation model to perform further QM/MM(ABEEM) and MD simulations.
is more attractive for electrons and will be favorable for the leaving of a proton. Therefore, it is reasonable to take the X base as the most favorable base for the deprotonation. This is also consistent with the results of the deprotonation activation energies by the QM method. Thus, X˙ in the GGX(8-oxo-G) tetrad is determined as the optimal deprotonation model to perform further QM/MM(ABEEM) and MD simulations.
In addition, a close correlation between ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) and activation energy is found in this study. As is demonstrated in Table 4, the
and activation energy is found in this study. As is demonstrated in Table 4, the ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) of the bases in the GGX (8-oxo-G) tetrad increase continuously, which indicates the abilities of the bases to absorb electrons and deprotonation become increasingly stronger. At this point, the activation energy progressively decreases, thereby enhancing the likelihood of the deprotonation reaction, which is consistent with the findings from
of the bases in the GGX (8-oxo-G) tetrad increase continuously, which indicates the abilities of the bases to absorb electrons and deprotonation become increasingly stronger. At this point, the activation energy progressively decreases, thereby enhancing the likelihood of the deprotonation reaction, which is consistent with the findings from ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) calculations. In view of the complexity of calculating activation energy, ABEEM PFF can accurately and efficiently predict the optimal deprotonation base in the GGX (8-oxo-G) tetrad.
calculations. In view of the complexity of calculating activation energy, ABEEM PFF can accurately and efficiently predict the optimal deprotonation base in the GGX (8-oxo-G) tetrad.
The deprotonation activation energy of G˙+ in the G-tetrad and X˙ in the GGX(8-oxo-G) tetrad obtained by MD-FEP herein is 20.7 and 33.0 kJ mol−1, respectively. The result of G˙+ in the G-tetrad is in good agreement with the experimental measurement (20.0 ± 1.0 kJ mol−1). The deprotonation activation energy of X˙ is evidently larger than that of G˙+ in the G-tetrad. By comparing the activation energy and ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) of G˙+ in the G-tetrad with those of X˙ in the GGX(8-oxo-G) tetrad, it is found that the unequal
of G˙+ in the G-tetrad with those of X˙ in the GGX(8-oxo-G) tetrad, it is found that the unequal ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) between bases in GGX(8-oxo-G) tetrad retard the deprotonation rate.
between bases in GGX(8-oxo-G) tetrad retard the deprotonation rate.
3.2. Charge analysis
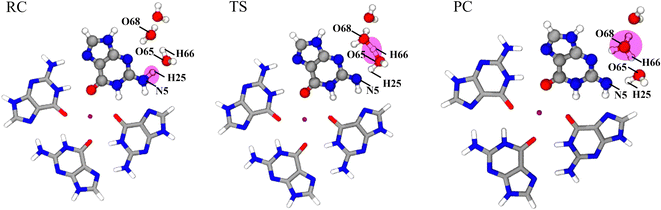
Charge distribution is important to describe interactions between molecules during deprotonation. Proton transfer must be accompanied by significant fluctuations in charge distribution. During the deprotonation of G˙+ in the G-tetrad, the charge of the whole system is 2.00 |e|. Charge distributions of each base, Na+, and water molecules in the G-tetrad are listed in Table 2. It shows that the positive charge in RC is mainly distributed on Na+ and G˙+, and the other bases and water molecules are all nearly neutral. In TS, the proton does not localize at W1 but forms a proton bridge between W1 and W2 (0.75 |e|). From TS to PC, the H+ proceeds to transport along the proton bridge and, finally, is stabilized at W2 (0.60 |e|). To sum up, the proton transfer path of G˙+ in the G-tetrad is from G(N1–H)˙+ to H5O2+(W1⋯H⋯W2) to H3O+(W2⋯H).| Structure | RC | TS | PC |
|---|---|---|---|
| G1 | 0.15 | 0.10 | 0.09 |
| G˙+ | 0.80 | — | — |
| G(–H)˙ | — | 0.14 | 0.14 |
| G3 | 0.11 | 0.10 | 0.09 |
| G4 | 0.11 | 0.11 | 0.11 |
| W1 | 0.05 | — | 0.16 |
| W1⋯H⋯W2 | — | 0.75 | — |
| W2 | 0.02 | — | — |
| W2⋯H | — | — | 0.60 |
| W3 | 0.05 | 0.09 | 0.10 |
| Na+ | 0.71 | 0.71 | 0.71 |
Tables S11–S13 (ESI†) shows the charge distributions during the deprotonation of 8-oxo-G˙+, G1˙+ and G2˙ in the GGX(8-oxo-G) tetrad, respectively. In the RC of the deprotonation of 8-oxo-G˙+, charges are mainly distributed on 8-oxo-G˙+ (0.80 |e|) and Na+ (0.71 |e|). In TS, the proton is trapped by W1 and W2 (0.73 |e|), and the neutral radical, 8-oxo-G(–H)˙, is formed. In PC, the proton is transferred to W2. Other bases (G1, G2, X) and water molecules (W1, W2, W3) are almost neutral. From RC to PC, 8-oxo-G˙+ transfers 0.68 |e| to surrounding water molecules, where W2 eventually receives 0.58 |e|, and the rest 0.10 |e| transfers to other water molecules. The proton transfer path is from 8-oxo-G(N2–H)˙+ to H5O2+(W1⋯H⋯W2) to H3O+(W2⋯H), and the charge transfer ratio is 1.00.
Deprotonation occurred in G1˙+ is similar to the behavior observed in 8-oxo-G˙+. From RC to PC, W2 ultimately receives a charge of 0.58 |e|, with 0.49 |e| originating from G1˙+ and the remaining 0.09 |e| deriving from other bases. The direction of proton transfer is from G1(N2–H)˙+ to H5O2+(W1⋯H⋯W2) to H3O+(W1⋯H), and the charge transfer ratio is 0.85.
In the RC of the deprotonation of G2˙ in the GGX(8-oxo-G) tetrad, the charge of 8-oxo-G is 0.99 |e|, while that of G2˙ is −0.09 |e|. From RC to TS, it is worth noting that the charge of 8-oxo-G is reduced from 0.99 |e| to 0.04 |e|. A large amount of positive charge is distributed on a proton bridge formed by W1 and W2 (0.74 |e|). In PC, H+ bonds with W2, forming H3O+ (0.59 |e|). According to changes of charge distributions, it is inferred that the proton transfer path is from 8-oxo-G+ to G2(N2–H)˙ to H5O2+(W1⋯H⋯W2) to H3O+(W2⋯H). The deprotonation reaction steps of G2˙ are more than those of 8-oxo-G˙+ and G1˙+, and then the corresponding activation energy is the highest.
Table 3 shows the charge distributions of deprotonation of X˙ in the GGX(8-oxo-G) tetrad. In RC, X˙, G1, G2 and surrounding water are nearly neutral, and the most of charges are distributed on 8-oxo-G and Na+. With the proton leaving, X˙ eventually becomes a radical anion X(–H)˙− with a charge of −0.61 |e|. In TS, positive charge is mainly distributed on H5O2+ (0.75 |e|). From RC to PC, charge distributions of G1, G2, 8-oxo-G, Na+ and W3 do not change obviously. In PC, the proton is stabilized at W2 (0.62 |e|). The proton transfer path is from X(N3–H)˙ to H5O2+(W1⋯H⋯W2) to H3O+(W2⋯H), which is same to that of G˙+ in G-tetrad. When compared to the charge distributions of the other three deprotonation models in GGX(8-oxo-G) tetrad, the deprotonation of X˙ yields a negatively charged groove (−0.65 |e|), which can be attributed to its highest average electronegativity, consequently resulting in the lowest deprotonation activation energy. Other base radicals are almost neutral after deprotonation. The properties of each base in the GGX(8-oxo-G) tetrad are summarized in Table 4.
| Structure | RC | TS | PC |
|---|---|---|---|
| G1 | 0.12 | 0.11 | 0.11 |
| G2 | 0.11 | 0.10 | 0.10 |
| 8-oxo-G | 0.84 | 0.84 | 0.84 |
| X˙ | 0.10 | — | — |
| X(–H)˙− | — | −0.61 | −0.65 |
| W1 | 0.04 | — | 0.16 |
| W1⋯H⋯W2 | — | 0.75 | — |
| W2 | 0.02 | — | — |
| W2⋯H | — | — | 0.62 |
| W3 | 0.05 | 0.09 | 0.10 |
| Na+ | 0.71 | 0.71 | 0.71 |
![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif)
|
Activation energy (kJ mol−1) | Charge transfer ratio | Reaction path | |
|---|---|---|---|---|
| X | 9.08 | 36.6 | 0.80 | X˙ → H5O2+ → H3O2+ |
| G1 | 8.41 | 40.6 | 1.00 | G1˙+ → H5O2+ → H3O2+ |
| 8-oxo-G | 8.32 | 41.9 | 0.85 | 8-oxo-G˙+ → H5O2+ → H3O2+ |
| G2 | 8.20 | 43.9 | 0.61 | 8-oxo-G+ → G2˙ → H5O2+ → H3O2+ |
During the deprotonation of G˙+ in the G-tetrad and X˙ in the GGX(8-oxo-G) tetrad, the linear correlations of the charge distributions, calculated by QM/MM(ABEEM) and QM methods, of each structure are above 0.97 (Tables S14 and S15, ESI†). Special attention was paid to RC, TS, and PC, the linear correlations of the charge distributions between them are shown in Fig. S3 and S4 (ESI†).
The concerned atoms involved in bond-forming and bond-breaking are N5, H25, O65, H66, and O68 in the G˙+ deprotonation of the G-tetrad, while N22, H23, O62, H63, and O65 in the X˙ deprotonation of the GGX(8-oxo-G) tetrad. The fluctuations of partial charges of these atoms are shown in Fig. 5. In RC, H25+ and H23+ are located at N5 and N22, respectively, and the partial charges of each atom do not change obviously. From RC to TS, H25+ moves to O65 as well as H23+ moves to O62. The trends of partial charges of O65 and O62 atoms rise sharply, and N5 and N22 show a decreasing trend. From TS to PC, the trends of partial charges of O68 and O65 are rising and then gradually descending. The fluctuation of the partial charge is most pronounced in the vicinity of the TS. In PC, the partial charge of each atom undergoes minimal alteration.
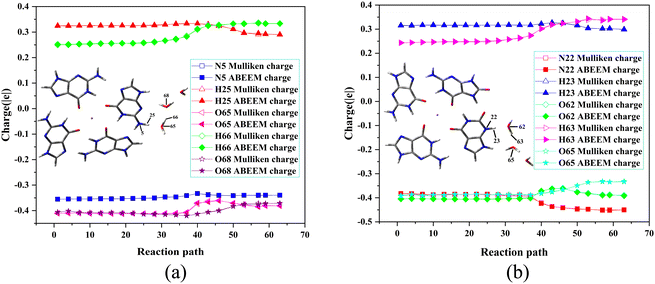 | ||
| Fig. 5 Fluctuations of the partial charges during the deprotonation of (a) G˙+ in the G-tetrad and (b) X˙ in the GGX(8-oxo-G) tetrad by QM/MM(ABEEM) and QM methods. | ||
The linear correlations of above the atoms between the QM charge and the ABEEM charge are both above 0.99 (Fig. S5 and S6, ESI†). The reasonable and reliable ABEEM charge is employed in QM/MM(ABEEM)/MD-FEP.
3.3. Structure analysis
The σ bond and lp electron sites of the atoms involved in the formation and breaking of chemical bonds would change with deprotonation, which can be accurately simulated by the QM/MM(ABEEM) method. Fig. 6 shows the deprotonation of G˙+ in the G-tetrad, and N5 always maintains sp3 hybridization. From RC to TS, the σ bond (N5–H25) of N5 is replaced by the lp electrons. O65 and H25 are connected by the σ bond, and O65 of W1 also always maintains sp3 hybridization. From TS to PC, H66 leaves W1, and O65 forms new lp electrons. In PC, O68 of W2 maintains sp3 hybridization with three σ bonds. It should be noted that the number of lp electrons of O68 changed from two pairs to one pair.Fig. 7 shows the optimized structures of RC, TS, and PC in the deprotonation of G˙+ in the G-tetrad. The molecules involved in deprotonation are represented by a ball and stick model, and the other bases are represented by the tube model. The proton is marked in red. In RC, the proton is located on G˙+, and W1, W2 and W3 are located around N1–H. From RC to TS, the distance between N5 and H25 increases from 1.069 Å to 1.594 Å. The distance between H25 and O65 of W1 decreases from 1.597 Å to 1.036 Å. In TS, H66 forms a proton bridge, W1⋯H66⋯W2 (H5O2+). From TS to PC, the proton continues to approach W2, which is finally stabilized at W2 to form H3O+. From RC to PC, the distance of H66–O65 increases from 0.993 Å to 1.320 Å, and that of H66–O68 decreases from 1.701 Å to 1.111 Å.
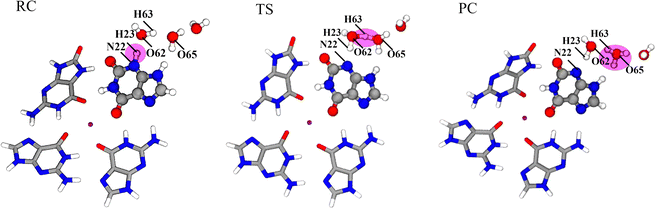
The proton transfer of X˙ in the GGX(8-oxo-G) tetrad has been shown in Fig. 8. From RC to TS, the distance of N22-H23 increases from 1.069 Å to 1.594 Å as well as the proton moves away from X˙ to W1. With H63 of W1 moving to W2, the distances of H23–O62 and H63–O62 change from 1.597 Å and 0.993 Å to 1.036 Å and 1.207 Å, respectively. In TS, H+ is between W1 and W2. In PC, H+ is completely stabilized at W2 to bond with O65, and the H63-O65 is decreased from 1.701 Å to 1.113 Å.
Fig. S7–S9 (ESI†) shows the optimized structures of RC, TS, and PC in 8-oxo-G˙+, G1˙+, and G2˙. From the perspective of structures, the neutral and cation radicals in the GGX(8-oxo-G) tetrad show similarity in proton transfer. The proton transfer paths are all from corresponding neutral and cation radicals to W2. The X˙ as the optimal deprotonation path in the GGX(8-oxo-G) tetrad has been further analyzed in detail.
During the deprotonation of X˙ in the GGX(8-oxo-G) tetrad, variations of the atom, σ bond, π bond, and lp electrons sites of RC, TS, and PC have been shown in Fig. S10 (ESI†). In RC, N22 in X˙ is sp3 hybridized and connects to H23 by a σ bond. From RC to TS, H23 is away from N22 to bond with O62 of W1. The σ bond between N22 and H23 is replaced by the lp electrons. Due to the approach of H23, a pair of lp electrons in O62 is replaced by a σ bond, and the O62 in W1 remains sp3 hybridization. From TS to PC, H63 moves away from O62 to bond with O65 of W2, forming H3O+. A pair of lp electrons of O65 becomes a σ bond, and the hybridization type of O65 still remains sp3.
4. Conclusions
This work focuses on the development of the QM/MM(ABEEM) method to accurately investigate the microscopic mechanism of deprotonation of neutral and cation radicals in G-tetrad and GGX(8-oxo-G) tetrad. The QM/MM(ABEEM) method is based on the charge local conservation conditions and valence-state electronegativity piecewise function χ*(r), which fully takes into account the polarization effect and accurately simulates charge transfer. In order to determine the parameters for ABEEM PFF, the atomic partial charges were calculated by QM/MM(ABEEM) and QM methods. The deprotonation activation energy was calculated in the explicit water model. The impact of the average electronegativity of the G-tetrad and GGX(8-oxo-G) tetrad on the deprotonation rate was investigated, and the changes in each site and atomic partial charges during proton transfer were thoroughly analyzed.In this study, five deprotonation models of G˙+ in G-tetrad were proposed, and the influence of the number and position of water molecules on deprotonation was investigated. The rationality of the 3H2O model has been verified. Four deprotonation paths of the GGX(8-oxo-G) tetrad were simulated. The activation energies calculated by the QM method for the four paths indicated that the X base was the most suitable for deprotonation. This finding is also in line with the outcome of the average electronegativity of X with a higher average electronegativity compared to the other bases in the GGX(8-oxo-G) tetrad. ABEEM PFF can accurately and efficiently predict that the optimal deprotonation base is X in the GGX(8-oxo-G) tetrad. The deprotonation activation energies of G˙+ in the G-tetrad and X˙ in the GGX(8-oxo-G) tetrad are 20.7 ± 0.6 and 33.0 ± 2.1 kJ mol−1, respectively, using QM/MM(ABEEM)/MD-FEP calculations. The result of G˙+ in the G-tetrad aligns well with the experimental measurement (20 ± 1.0 kJ mol−1). The above results suggest that the deprotonation rate of X˙ in the GGX(8-oxo-G) tetrad is lower than that of G˙+ in the G-tetrad. Additionally, compared to the equal average electronegativities of bases in the G-tetrad, the unequal average electronegativity within the GGX(8-oxo-G) tetrad impedes deprotonation and reduces competition with hole transfer, ultimately enhancing hole transfer efficiency. Therefore, the GGX(8-oxo-G) tetrad has potential as a novel type of DNA electronic device.
Abbreviations
| Quantum mechanics | (QM) |
| Molecular mechanics | (MM) |
| Chemistry at HARVARD macromolecular mechanics | (CHARMM) |
| Assisted model building with energy refinement | (AMBER) |
| Fixed-charge force field | (FFF) |
| Polarizable force field | (PFF) |
| Atom-bond electronegativity equalization method fluctuating charge polarizable force field | (ABEEM PFF) |
| A transferable intermolecular potential seven points approach including fluctuating charge and flexible model | (ABEEM-7P) |
| Electronegativity equalization method | (EEM) |
| Free energy perturbation | (FEP) |
| Molecular dynamics | (MD) |
| Nuclear magnetic resonance | (NMR) |
| Root mean square | (RMS) |
| Root mean square deviation | (RMSD) |
| Intrinsic reaction coordinate | (IRC) |
| Lone-pair | (lp) |
| Guanine | (G) |
| Guanine radical cation | (G˙+) |
| Guanine neutral radical | (G(–H)•) |
| 8-Oxoguanine | (8-oxo-G) |
| 8-Oxoguanine radical cation | (8-oxo-G˙+) |
| 8-Oxoguanine neutral radical | (8-oxo-G(–H)•) |
| Xanthine | (X) |
| Xanthine neutral radical | (X˙) |
| Xanthine radical anion | (X(–H)•−) |
| Xanthine and 8-oxoguanine dual substituted a G-tetrad | (GGX(8-oxo-G)) |
| Tetrad composed of two 8-oxoguanines and two xanthines | (XOXO) |
| Reactant | (RC) |
| Transition state | (TS) |
| Product | (PC) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors greatly thank Professor Jay William Ponder for providing the Tinker program; the authors also acknowledged the support from the National Natural Science Foundation of China (No. 22277046 and 22377048) and the Foundation of Liaoning Province Education Administration (No. LJKZ0983, LJKMZ202214)References
- K. Kawai and T. Majima, Acc. Chem. Res., 2013, 46, 2616–2625 CrossRef CAS PubMed.
- R. N. Barnett, C. L. Cleveland, A. Joy, U. Landman and G. B. Schuster, Science, 2001, 294, 567–571 CrossRef CAS.
- T. Kubař, R. Gutiérrez, U. Kleinekathöfer, G. Cuniberti and M. Elstner, Phys. Status Solidi B, 2013, 250, 2277–2287 CrossRef.
- P. A. Sontz, N. B. Muren and J. K. Barton, Acc. Chem. Res., 2012, 45, 1792–1800 CrossRef CAS PubMed.
- J. C. Genereux and J. K. Barton, Chem. Rev., 2010, 110, 1642–1662 CrossRef CAS PubMed.
- B. Giese, Acc. Chem. Res., 2000, 33, 631–636 CrossRef CAS PubMed.
- C. L. Cleveland, R. N. Barnett, A. Bongiorno, J. Joseph, C. S. Liu, G. B. Schuster and U. Landman, J. Am. Chem. Soc., 2007, 129, 8408–8409 CrossRef CAS PubMed.
- K. Kawai, Y. Osakada and T. Majima, ChemPhysChem, 2009, 10, 1766–1769 CrossRef CAS PubMed.
- A. Kupan, A. Saulière, S. Broussy, C. Seguy, G. Pratviel and B. Meunier, ChemBioChem, 2006, 7, 125–133 CrossRef CAS PubMed.
- H. Ding and M. M. Greenberg, J. Am. Chem. Soc., 2007, 129, 772–773 CrossRef CAS PubMed.
- J. L. Jie, K. H. Liu, L. Wu, H. M. Zhao, D. Song and H. M. Su, Sci. Adv., 2017, 3, e1700171 CrossRef PubMed.
- Y. Wang, H. Zhao, C. Yang, J. Jie, X. Dai, Q. Zhou, K. Liu, D. Song and H. Su, J. Am. Chem. Soc., 2019, 141, 1970–1979 CrossRef CAS PubMed.
- L. D. Wu, K. H. Liu, J. L. Jie and H. M. Su, J. Am. Chem. Soc., 2015, 137, 259–266 CrossRef CAS PubMed.
- K. Kawai, H. Kodera, Y. Osakada and T. Majima, Nat. Chem., 2009, 1, 156–159 CrossRef CAS PubMed.
- K. Kobayashi, R. Yamagami and S. Tagawa, J. Phys. Chem. B, 2008, 112, 10752–10757 CrossRef CAS PubMed.
- T. Takada, K. Kawai, M. Fujitsuka and T. Majima, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 14002–14006 CrossRef CAS PubMed.
- P. T. Henderson, D. Jones, G. Hampikian, Y. Kan and G. B. Schuster, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 8353–8358 CrossRef CAS PubMed.
- D. J. Patel, A. T. Phan and V. Kuryavyi, Nucleic Acids Res., 2007, 35, 7429–7455 CrossRef CAS PubMed.
- J. L. Huppert and S. Balasubramanian, Nucleic Acids Res., 2007, 35, 406–413 CrossRef CAS PubMed.
- J. Eddy and N. Maizels, Nucleic Acids Res., 2006, 34, 3887–3896 CrossRef CAS PubMed.
- A. K. Todd, M. Johnston and S. Neidle, Nucleic Acids Res., 2005, 33, 2901–2907 CrossRef CAS PubMed.
- A. Verma, K. Halder, R. Halder, V. K. Yadav, P. Rawal, R. K. Thakur, F. Mohd, A. Sharma and S. Chowdhury, J. Med. Chem., 2008, 51, 5641–5649 CrossRef CAS PubMed.
- J. L. Huppert and S. Balasubramanian, Nucleic Acids Res., 2005, 33, 2908–2916 CrossRef CAS PubMed.
- A. T. Phan, FEBS J., 2010, 277, 1107–1117 CrossRef CAS PubMed.
- G. Biffi, D. Tannahill, J. McCafferty and S. Balasubramanian, Nat. Chem., 2013, 5, 182–186 CrossRef CAS PubMed.
- S. Neidle, FEBS J., 2010, 277, 1118–1125 CrossRef CAS PubMed.
- D. P. Gamblin, P. Garnier, S. van Kasteren, N. J. Oldham, A. J. Fairbanks and B. G. Davis, Angew. Chem., Int. Ed., 2004, 43, 827–833 CrossRef PubMed.
- J. Sagi, J. Biomol. Struct. Dyn., 2014, 32, 477–511 CrossRef CAS PubMed.
- A. Virgilio, V. Esposito, A. Randazzo, L. Mayol and A. Galeone, Nucleic Acids Res., 2005, 33, 6188–6195 CrossRef CAS PubMed.
- V. Esposito, A. Randazzo, G. Piccialli, L. Petraccone, C. Giancola and L. Mayol, Org. Biomol. Chem., 2004, 2, 313–318 RSC.
- V. Kuryavyi, A. Kettani, W. M. Wang, R. Jones and D. J. Patel, J. Mol. Biol., 2000, 295, 455–469 CrossRef CAS PubMed.
- D. M. Wilson, T. M. Sofinowski and D. R. McNeill, Front. Biosci., 2003, 8, 963–981 CrossRef PubMed.
- V. V. Cheong, B. Heddi, C. J. Lech and A. T. Phan, Nucleic Acids Res., 2015, 43, 10506–10514 CAS.
- Y. H. Wang, J. L. Jie, H. M. Zhao, Y. Bai, P. X. Qin and D. Song, Acta Chim. Sin., 2018, 76, 475–482 CrossRef CAS.
- Q. Cui, T. Pal and L. Xie, J. Phys. Chem. B, 2021, 125, 689–702 CrossRef CAS PubMed.
- X. Lu, D. Fang, S. Ito, Y. Okamoto, V. Ovchinnikov and Q. Cui, Mol. Simul., 2016, 42, 1056–1078 CrossRef CAS PubMed.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- H. M. Senn and W. Thiel, Curr. Opin. Chem. Biol., 2007, 11, 182–187 CrossRef CAS PubMed.
- A. Heyden, H. Lin and D. G. Truhlar, J. Phys. Chem. B, 2007, 111, 2231–2241 CrossRef CAS PubMed.
- T. Ishida and S. Kato, J. Am. Chem. Soc., 2003, 125, 12035–12048 CrossRef CAS PubMed.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, Jr, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- P. K. Weiner and P. A. Kollman, J. Comput. Chem., 1981, 2, 287–303 CrossRef CAS.
- D. A. Case, T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, K. M. Merz Jr., A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688 CrossRef CAS PubMed.
- H. Li, V. Ngo, M. C. Da Silva, D. R. Salahub, K. Callahan, B. Roux and S. Y. Noskov, J. Phys. Chem. B, 2015, 119, 9401–9416 CrossRef CAS PubMed.
- J. A. Lemkul, J. Huang, B. Roux and A. D. MacKerell, Jr., Chem. Rev., 2016, 116, 4983–5013 CrossRef CAS PubMed.
- R. A. Corrigan, G. Qi, A. C. Thiel, J. R. Lynn, B. D. Walker, T. L. Casavant, L. Lagardere, J. P. Piquemal, J. W. Ponder, P. Y. Ren and M. J. Schnieders, J. Chem. Theory Comput., 2021, 17, 2323–2341 CrossRef CAS PubMed.
- W. S. Xie, L. C. Song, D. G. Truhlar and J. L. Gao, J. Chem. Phys., 2008, 128, 234108 CrossRef PubMed.
- B. Doherty and O. Acevedo, J. Phys. Chem. B, 2018, 122, 9982–9993 CrossRef CAS PubMed.
- C. S. Wang and Z. Z. Yang, J. Chem. Phys., 1999, 110, 6189–6197 CrossRef CAS.
- C. S. Wang, D. X. Zhao and Z. Z. Yang, Chem. Phys. Lett., 2000, 330, 132–138 CrossRef CAS.
- Z. Z. Yang, Y. Wu and D. X. Zhao, J. Chem. Phys., 2004, 120, 2541–2557 CrossRef CAS PubMed.
- D. X. Zhao, C. Liu, F. F. Wang, C. Y. Yu, L. D. Gong, S. B. Liu and Z. Z. Yang, J. Chem. Theory Comput., 2010, 6, 795–804 CrossRef CAS PubMed.
- Y. Xu, C. Liu, C. J. Han, M. Y. Pan, Z. Q. Sun, B. Y. Han and Z. Z. Yang, Chem. Res. Chin. Univ., 2019, 40, 288–297 CAS.
- C. Liu, J. Zhao, Z. Z. Yang and D. X. Zhao, J. Chem. Theory Comput., 2020, 16, 7618–7631 CrossRef CAS PubMed.
- C. Liu, C. Lv, Y. Y. Yao, X. Du, D. X. Zhao and Z. Z. Yang, J. Chem. Theory Comput., 2021, 17, 3525–3538 CrossRef CAS PubMed.
- J. Zhang, L. D. Gong and Z. Z. Yang, J. Comput. Biophys. Chem., 2022, 21, 485–498 CrossRef CAS.
- F. Y. Zhao, L. Cui, L. D. Gong and Z. Z. Yang, Acta Chim. Sin., 2011, 69, 1141–1150 CAS.
- P. Qian, W. Song, L. N. Lu and Z. Z. Yang, Int. J. Quantum Chem., 2010, 110, 1923–1937 CrossRef CAS.
- H. Shi, L. D. Gong, C. Liu, L. N. Lu and Z. Z. Yang, J. Phys. Chem. A, 2020, 124, 5963–5978 CrossRef CAS PubMed.
- C. Liu, Y. Li, B. Y. Han, L. D. Gong, L. N. Lu, Z. Z. Yang and D. X. Zhao, J. Chem. Theory Comput., 2017, 13, 2098–2111 CrossRef CAS PubMed.
- H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218 CrossRef CAS.
- J. Gu, J. Wang and J. Leszczynski, Chem. Phys. Lett., 2011, 512, 108–112 CrossRef CAS.
- A. Galano and J. R. Alvarez-Idaboy, Phys. Chem. Chem. Phys., 2012, 14, 12476–12487 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A. 02, 2009 Search PubMed.
- L. D. Wu, K. H. Liu, J. L. Jie, D. Song and H. M. Su, J. Am. Chem. Soc., 2015, 137, 259–266 CrossRef CAS PubMed.
- L. D. Wu, J. L. Jie, K. H. Liu and H. M. Su, Acta Chim. Sin., 2014, 72, 1182–1186 CrossRef CAS.
- L. J. Sham and W. Kohn, Phys. Rev. A, 1965, 140, 1133 CrossRef.
- W. J. Mortier, S. K. Ghosh and S. Shankar, J. Am. Chem. Soc., 1986, 108, 4315–4320 CrossRef CAS.
- Z. Z. Yang and C. S. Wang, J. Phys. Chem. A, 1997, 101, 6315–6321 CrossRef CAS.
- Z. Z. Yang, J. J. Wang and D. X. Zhao, J. Comput. Chem., 2014, 35, 1690–1706 CrossRef CAS PubMed.
- Z. Z. Yang and B. Q. Cui, J. Chem. Theory Comput., 2007, 3, 1561–1568 CrossRef CAS PubMed.
- C. Liu, H. Jiang, Y. Li, B. Xue, Y. Y. Yao and Z. Z. Yang, Phys. Chem. Chem. Phys., 2023, 25, 3432–3448 RSC.
- C. Liu, Y. Ren, X. Q. Gao, X. Du and Z. Z. Yang, J. Comput. Chem., 2022, 43, 2139–2153 CrossRef CAS PubMed.
- L. N. Lu, C. Liu, Z. Z. Yang and D. X. Zhao, J. Mol. Graphics Modell., 2022, 114, 108190 CrossRef CAS PubMed.
- L. N. Lu, C. Liu and Z. Z. Yang, J. Phys. Chem. A, 2020, 124, 8614–8632 CrossRef CAS PubMed.
- L. L. He, Y. Li, D. X. Zhao, L. Yu, C. L. Zhao, L. N. Lu, C. Liu and Z. Z. Yang, J. Phys. Chem. C, 2019, 123, 5653–5666 CrossRef CAS.
- C. Liu, Y. Li, B. Y. Han, L. D. Gong, L. N. Lu, Z. Z. Yang and D. X. Zhao, J. Chem. Theory Comput., 2017, 13, 2098–2111 CrossRef CAS PubMed.
- P. Qian and Z. Z. Yang, Sci. China, Ser. B: Chem., 2007, 50, 190–204 CrossRef CAS.
- C. L. Zhao, D. X. Zhao, Q. Y. Jiang, H. X. Zhang, S. Li and Z. Z. Yang, J. Phys. Chem. B, 2020, 124, 2450–2464 CrossRef CAS PubMed.
- R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420–1426 CrossRef CAS.
- T. Ishida and S. Kato, J. Am. Chem. Soc., 2003, 125, 12035–12048 CrossRef CAS PubMed.
- C. I. Cave-Ayland, C. K. Skylaris and J. W. Essex, J. Chem. Theory Comput., 2017, 13, 415–424 CrossRef CAS PubMed.
- H. Li, D. Wang, X. Zhao, L. N. Lu, C. Liu, L. D. Gong, D. X. Zhao and Z. Z. Yang, J. Comput. Chem., 2019, 40, 1141–1150 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684 CrossRef CAS.
- P. A. Bash, M. J. Field and M. Karplus, J. Am. Chem. Soc., 1987, 109, 8092–8094 CrossRef CAS.
- Y. M. Yang, W. J. Yang, H. M. Su, W. H. Fang and X. B. Chen, Phys. Chem. Chem. Phys., 2018, 20, 13598–13606 RSC.
- G. N. Parkinson, M. P. H. Lee and S. Neidle, Nature, 2002, 417, 876–880 CrossRef CAS PubMed.
- M. P. Horvath and S. C. Schultz, J. Mol. Biol., 2001, 310, 367–377 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: The hydrogen bond fitting functions, ABEEM PFF labels of 8-oxo-G˙+ in the GGX(8-oxo-G) tetrad, the linear correlations of the charge distributions of G˙+ in the G-tetrad and X˙ in the GGX(8-oxo-G) tetrad; positions of protons in the optimized structures, and variations of each site; valence-state electronegativity piecewise functions, charge distributions of 8-oxo-G˙+, G1˙+, and G2˙ in the GGX(8-oxo-G) tetrad and the linear correlations at key stationary points calculated by QM/MM(ABEEM) and QM methods. See DOI: https://doi.org/10.1039/d3cp04357f |
| ‡ These authors contributed equally. |
| This journal is © the Owner Societies 2024 |