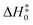Quantitative kinetics of the atmospheric reaction between isocyanic acid and hydroxyl radicals: post-CCSD(T) contribution, anharmonicity, recrossing effects, torsional anharmonicity, and tunneling†
Dai-Dan
Deng
a and
Bo
Long
 *ab
*ab
aCollege of Physics and Mechatronic Engineering, Guizhou Minzu University, Guiyang 550025, China. E-mail: wwwltcommon@sina.com
bCollege of Materials Science and Engineering, Guizhou Minzu University, Guiyang 550025, China
First published on 23rd November 2023
Abstract
Hydroxyl radicals (OH) are the most important atmospheric oxidant, initiating atmospheric reactions for the chemical transformation of volatile organic compounds. Here, we choose the HNCO + OH reaction as a prototype reaction because it contains the fundamental reaction processes for OH radicals: H-abstraction reaction by OH and OH addition reaction. However, its kinetics are unknown under atmospheric conditions. We investigate the reaction of HNCO with OH by using the GMM(P).L method close to the accuracy of single, double, triple, and quadruple excitations and noniterative quintuple excitations with a complete basis set (CCSDTQ(P)/CBS) as benchmark results and a dual-level strategy for kinetics calculations. The calculated rate constant of HNCO + OH is in good agreement with the experimental data available at the temperatures between 620 and 2500 K. We find that the rate constant cannot be correctly obtained by using experimental data to extrapolate the atmospheric temperature ranges. We find that the post-CCSD(T) contribution is very large for the barrier height with the value of −0.85 kcal mol−1 for the H-abstraction reaction, while the previous investigations were done up to the CCSD(T) level. Moreover, we also find that recrossing effects, tunneling, torsional anharmonicity, and anharmonicity are important for obtaining quantitative kinetics in the OH + HNCO reaction.
1. Introduction
Isocyanic acid (HNCO) is a potentially toxic air pollutant identified as a significant risk to human health1,2 emitted into the atmosphere from combustion processes and human activities.3–6 For example, HNCO is mainly produced during the pyrolysis of nitrogen-containing biomass materials proceeding through wildfires and agricultural fires.7–9 Low temperature coal combustion processes and the photochemistry of amine and amide species can also lead to the formation of HNCO.10–12 In addition, the combustion of fossil fuels (gasoline, coal and diesel), as well as the oxidation of nicotine, produce HNCO.13–15 Most recently, indoor sources of HNCO have been identified, such as chlorine bleach cleaning, cooking, and cigarette smoking.16–19 Therefore, understanding the chemical transformations of HNCO is particularly important for atmospheric modeling.In the atmosphere, HNCO is mainly removed by heterogeneous uptake, dry deposition, and reaction with OH.20–23 The reaction between HNCO and OH has been investigated by experimental and theoretical methods.24–29 However, the kinetics of HNCO + OH is unclear in the atmosphere, as experimental kinetics were only measured at temperatures between 620 and 2500 K; this does not cover atmospheric temperatures. Additionally, theoretical investigations were only done up to the CCSD(T) level.30 Therefore, it is unknown whether post-CCSD(T) calculations are required to obtain quantitative barrier height in the HNCO + OH reaction. Moreover, in the kinetics calculations, transition state theory was only used to calculate the kinetics at the atmospheric temperature.31,32 However, all the crossing effects, torsional anharmonicity, and anharmonicity have not been considered. Our previous investigations have shown that these factors could be key parameters for obtaining quantitative atmospheric kinetics from the theoretical methods.33–37 Further investigations are required to obtain quantitative kinetics of HNCO + OH in the atmosphere.
In this article, quantum chemical methods and reaction rate theory have been used to obtain quantitative atmospheric kinetics of HNCO + OH. First, we examined the convergence of geometrical optimizations and calculated zero-point vibrational energies for coupled cluster theory with single and double excitations and quasiperturbative connected triple excitations with simplified explicit correlation (CCSD(T)-F12a).38 Second, we consider the convergence between the basis set and excitation level for the couple cluster theory method to reach accuracy close to full CI in single point energy calculations. Finally, all the factors related to kinetics calculations are considered. We choose the HNCO + OH reaction as a prototype reaction because it contains the fundamental reaction processes for OH radicals: H-abstraction reaction by OH and OH addition reaction. Therefore, the present findings should have abroad implications in obtaining the quantitative kinetics for the reactions of the compounds with a carbon–nitrogen double bond in the atmosphere.
2. Computational methods
2.1. Electronic structure best estimates
In principle, it is required to examine the excitation level and basis set in couple cluster theory to obtain reliable optimized geometries and zero-point vibrational energies. However, it is prohibitive to use the post-CCSD(T) method for optimized geometries and frequency calculations. Furthermore, previous investigations have shown that the CCSD(T) level can obtain optimized geometries and zero-point vibrational energies quantitatively.33–35 Therefore, we only examine the convergence of the basis set for optimized geometries and frequency calculations in CCSD(T) calculations. For the HNCO + OH reaction, the benchmark calculations were done for all geometry optimizations and frequency calculations, including transition states (TS) and products by using W2X42//CCSD(T)-F12a/cc-pVTZ-F12,39,40 W2X//CCSD(T)-F12a/cc-pVDZ-F12, and W2X//CCSD(T)-F12b/jun′-cc-pVDZ.41The single point energies were carried out by using W3X-L42, MW2-F1243, MW2-F12.L44, and W2X. In addition, we used GMM(P).L44 to reach an accuracy close to CCSDTQ(P)/CBS in eqn (1).
| EGMM(P).L = ΔEMW2-F12.L + ΔET-(T) + ΔE(Q)-T + ΔEQ-(Q) + ΔE(P)-Q + ESO | (1) |
In the above equation, ΔET-(T) and ΔE(Q)-T are the CCSDT-CCSD(T) and CCSDT(Q)-CCSDT components, respectively, which are extrapolated to the complete basis set limit (CBS) by using cc-pVDZ and cc-pVTZ basis sets. The specific extrapolation formula is EL = ECBS + A/L3, where L = 2 for cc-pVDZ and 3 for cc-pVTZ. ΔEQ-(Q) is the CCSDTQ-CCSDT(Q) component calculated by using the VDZ(d) basis set in W3X-L,42 where VDZ(d) is defined as cc-pVDZ without polarization functions for hydrogens. ΔE(P)-Q is the CCSDTQ(P)-CCSDTQ component computed by using cc-VDZ45 defined as cc-pVDZ without polarization functions for any atom. Eso is the lowering of the energy by spin–orbit coupling. The OH radical has two low-lying electronic states (2Π3/2 and 2Π1/2) separated by 140 cm−1.46 Thus, the spin–orbit coupling energy is −0.20 kcal mol−1 for the OH radical included in all calculations. This increases the barrier heights and energies of all the reactions investigated here by 0.20 kcal mol−1. Here, GMM(P).L//CCSD(T)-F12a/cc-pVTZ-F12 acts as our best estimate.
2.2. Electronic structure density functional choices
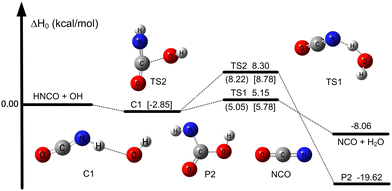
All geometry optimizations and harmonic vibrational frequency calculations of reactants, the pre-reactive complex, transition states (TS), and products were computed by using the M05-2X47/aug-cc-pVTZ48 method. As can be seen from Table 1, the mean unsigned deviation (MUD) of activation enthalpies (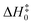 ) for the M05-2X/aug-cc-pVTZ functional method has the smallest error derivation of 0.54 kcal mol−1, compared with the benchmark value.
) for the M05-2X/aug-cc-pVTZ functional method has the smallest error derivation of 0.54 kcal mol−1, compared with the benchmark value.
| Methods | |||
|---|---|---|---|
| TS1b | TS2c | MUDd | |
| a All reactant energies used to compute barrier heights and enthalpies in this table include a spin–orbit contribution of −0.20 kcal mol−1, and this raised all reported barrier heights and enthalpies of activation by 0.20 kcal mol−1. b The transition state for hydrogen atom of HNCO abstracted by OH. c The transition state for OH addition to the carbon atom of HNCO. For TS2, GMM(P).L energy is obtained by using the following equation: ETS2GMM(P).L = ΔETS2MW2-F12.L + ΔETS2(W3X-L)-W2X + (ETS1GMM(P).L − ETS1(W3X-L)-W2X) + ESO. d The mean unsigned deviation. | |||
| GMM(P).L//CCSD(T)-F12a/cc-pVTZ-F12 | 5.05 | 8.22 | 0.00 |
| W3X-L//CCSD(T)-F12a/cc-pVTZ-F12 | 5.15 | 8.30 | 0.09 |
| M05-2X/aug-cc-pVTZ | 5.25 | 9.20 | 0.54 |
| CCSD(T)-F12a/cc-pVTZ-F12//M08HX/MG3S | 5.78 | 8.78 | 0.65 |
| W2X//CCSD(T)-F12a/cc-pVTZ-F12 | 5.73 | 8.91 | 0.69 |
| W2X//CCSD(T)-F12a/cc-pVDZ-F12 | 5.95 | 8.92 | 0.80 |
| W2X//CCSD(T)-F12b/jun′-cc-pVDZ | 5.97 | 8.93 | 0.81 |
| MW2-F12//CCSD(T)-F12a/cc-pVTZ-F12 | 5.89 | 9.08 | 0.85 |
| MW2-F12.L//CCSD(T)-F12a/cc-pVTZ-F12 | 5.91 | 9.10 | 0.87 |
2.3. Vibrational frequencies
The vibration frequencies in all wave function and density functional methods were scaled to improve the calculated zero-point vibrational energies. Two different methods have been used to obtain the scale factors. The first is the standard scale factor, which is obtained by fitting experimental zero-point vibrational energies, as listed in Table S1 (ESI†).49Previous work has shown that these standard scale factors are not sufficiently accurate for some transition states.50–52 Here, we used the MPW1K53/MG3S54 electronic structure method by combining with hybrid degeneracy-corrected second-order vibrational perturbation theory (HDCVPT)55,56 to calculate vibrational anharmonicity. The specific reaction scale factors that we obtained are listed in Table 2. The specific reaction scale factors were calculated using the formula (2):
| λZPE = λAnhλH | (2) |
| HNCOc | OHc | TS1c | TS2c | |
|---|---|---|---|---|
| a λ Anh equals the ratio of anharmonic zero-point vibrational energies to harmonic zero-point vibrational energy from the MPW1K/MG3S method. b λ ZPE equals the product of λAnh and the general parameter λH, and these calculations are based on a previous study.81 c λ H is 0.998 for CCSD(T)-F12a/cc-pVTZ-F12. | ||||
| ZPE(Harm) | 13.850 | 5.558 | 18.743 | 21.796 |
| ZPE(Anh) | 13.712 | 5.511 | 18.140 | 21.476 |
| λ Anh | 0.990 | 0.992 | 0.968 | 0.985 |
| λ ZPE | 0.988 | 0.990 | 0.966 | 0.983 |
For CCSD(T)-F12a/cc-pVTZ-F12, the scale factor of the standard method is 0.984 in Table S2 (ESI†). The specific reaction scale factors for HNCO, OH and TS2 are 0.988, 0.990 and 0.983 respectively in Table 2, which closely approach 0.984. However, the specific reaction scale factor for TS1 is 0.966, which is remarkably different from the value of 0.984. This uncovers that the specific reaction scale factor is required for improving the calculated zero-point vibrational energies.
2.4. Kinetics methods
We calculated rate constants by utilizing a dual-level strategy.60–62 The direct kinetics calculations at the M05-2X/aug-cc-pVTZ level were performed by using canonical variational transition state theory (CVT), in which the tunneling transmission coefficient is computed by using small-curvature tunneling (SCT) approximation.63–66 The rate constant was calculated using the following eqn (3).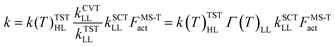 | (3) |
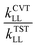 , kSCTLL is the tunneling transmission coefficient calculated by using small-curvature tunneling (SCT) approximation at the M05-2X/aug-cc-pVTZ level from the pre-reactive complex to the corresponding product, and FMS-Tact is the multi-structural torsional anharmonicity factor calculated by using the multi-structural method with torsional anharmonicity based on a coupled torsional potential.67 In kinetics calculations, the minimum energy path (MEP) was calculated from the pre-reactive complex to the corresponding product by using curvilinear coordinates at the M05-2X/aug-cc-pVTZ level. HL represents the higher-level electronic structure calculations, while LL represents the lower-level electronic structure calculations. Here, HL is GMM(P).L//CCSD(T)-F12a/cc-pVTZ-F12 and LL is M05-2X/aug-cc-pVTZ. We used the specific reaction scale factors in Table 2 to calculate k(T)TSTHL. And for the calculation of the kSCTLL and Γ(T)LL, we used the standard scale factor, which is 0.964 for M05-2X/aug-cc-pVTZ in Table S1 (ESI†). Meanwhile, we also considered the torsional anharmonicity factor for the reaction of HNCO + OH. More details are provided in the ESI.†
, kSCTLL is the tunneling transmission coefficient calculated by using small-curvature tunneling (SCT) approximation at the M05-2X/aug-cc-pVTZ level from the pre-reactive complex to the corresponding product, and FMS-Tact is the multi-structural torsional anharmonicity factor calculated by using the multi-structural method with torsional anharmonicity based on a coupled torsional potential.67 In kinetics calculations, the minimum energy path (MEP) was calculated from the pre-reactive complex to the corresponding product by using curvilinear coordinates at the M05-2X/aug-cc-pVTZ level. HL represents the higher-level electronic structure calculations, while LL represents the lower-level electronic structure calculations. Here, HL is GMM(P).L//CCSD(T)-F12a/cc-pVTZ-F12 and LL is M05-2X/aug-cc-pVTZ. We used the specific reaction scale factors in Table 2 to calculate k(T)TSTHL. And for the calculation of the kSCTLL and Γ(T)LL, we used the standard scale factor, which is 0.964 for M05-2X/aug-cc-pVTZ in Table S1 (ESI†). Meanwhile, we also considered the torsional anharmonicity factor for the reaction of HNCO + OH. More details are provided in the ESI.†
2.5. Software
All the electronic structure calculations were carried out using the M05-2X method with the aug-cc-pVTZ basis set in the Gaussian 09 suite of programs68 and using coupled cluster methods CCSD(T)-F12a/cc-pVTZ-F12, CCSD(T)-F12a/cc-pVDZ-F12 and CCSD(T)-F12b/jun′-cc-pVDZ in the Molpro 2019 code.69 The rate constants were calculated using the Polyrate 2017-C70 and Gaussrate 2017-B71 codes. The torsional anharmonicity72 was computed using the MSTor code.733. Results and discussion
3.1. The electronic structure of the HNCO + OH reaction
As previously reported in the literature,30 there are four different reaction pathways for the reaction between HNCO and OH in Fig. S1 (ESI†). One is an H-abstraction reaction and the other three are the addition reactions (i.e., addition of OH to the carbon, nitrogen, and oxygen sites of HNCO). We thus did the calculations by using CCSD(T)-F12a/cc-pVTZ-F12//M08-HX/MG3S to investigate the four reaction pathways, as described in Fig. S1 (ESI†). We find OH addition to the nitrogen and oxygen site of HNCO with much higher enthalpies of activation of 22 kcal mol−1 or more in Fig. S1 (ESI†); this leads to these two reaction pathways being unimportant in our present investigation. Therefore, we only consider the hydrogen atom abstracted by OH (TS1) and the addition reaction of OH to the carbon atom of HNCO (TS2), as shown in Fig. 1 and Fig. S1 (ESI†). The reaction between HNCO and OH firstly undergoes the same pre-reactive complex C1 and then proceeds the respective transition states TS1 and TS2, as listed in Fig. 1 and Fig. S2 and S3 (ESI†).Table S2 (ESI†) shows that the optimized transition structures are reliable, as the mean unsigned deviation (MUD) for the barrier height ΔV‡ is 0.01 kcal mol−1, compared with W2X//CCSD(T)-F12a/cc-pVTZ-F12 theoretical results. This shows that the optimized geometries are well converged at the CCSD(T)/CBS level. Moreover, we find that the relative zero-point vibrational energies (RZPVE) significantly depend on the basis set in CCSD(T)-F12 calculations for H-abstraction reaction (TS1), as listed in Table S3 (ESI†). The difference between CCSD(T)-F12a/cc-pVTZ-F12 and CCSD(T)-F12a/cc-pVDZ-F12 for RZPVE is 0.23 kcal mol−1 in Table S3 (ESI†); this is also observed in the previous investigations.74
The enthalpies of activation of the TS1 and TS2 at 0 K are computed to be 5.8 and 8.8 kcal mol−1 respectively calculated by CCSD(T)-F12a/cc-pVTZ-F12//M08-HX/MG3S (see Table 1), which are in well agreement with the previously reported values of 6.0 and 8.7 kcal mol−1 by Rosanka et al.,30 respectively, as calculated by CCSD(T)/CBS(DTQ)//M06-2X/aug-cc-pVTZ. For the H-abstraction reaction, the value (5.8 kcal mol−1) was reported by Sengupta and Nguyen,28 calculated by QCISD(T)/6-311G++(d,p). While these values agree with one another, the effects of higher-order excitations than CCSD(T) are not considered. Therefore, we used higher-level approaches to do single point energy calculations.
As shown in Fig. 1 and Table 1, the enthalpies of activation at 0 K for TS1 and TS2 are computed to be 5.05 and 8.22 kcal mol−1 respectively for H-abstraction and OH addition reactions by GMM(P).L//CCSD(T)-F12a/cc-pVTZ-F12. However, the mean unsigned derivation (MUD) of MW2-F12.L//CCSD(T)-F12a/cc-pVTZ-F12 for TS1 and TS2 is 0.87 kcal mol−1 without post-CCSD(T) contribution; this corresponds to Boltzmann factors of 5.8, 4.3 at 250, 298 K, respectively. It is noted that the post-CCSD(T) contribution for TS1 is −0.85 kcal mol−1, while for TS2, it is −0.88 kcal mol−1; this is almost equally important for H-abstraction and OH addition reactions for post-CCSD(T). Therefore, the present findings show that the post-CCSD(T) contribution is very large for obtaining a quantitative barrier for H-abstraction reaction and OH addition reaction for the compounds with a carbon–nitrogen double bond involved. Moreover, there are abundant compounds with carbon–nitrogen double bonds in the atmosphere.75 However, the similar reactions of OH were only done at the CCSD(T) level.76
Table 3 shows that the contributions of the CCSDT-CCSD(T) component, the CCSDTQ-CCSDT(Q) component, and the CCSDTQ(P)-CCSDTQ component are quite small. However, the contribution of the CCSDT(Q)-CCSDT component is very large with the value of −0.74 kcal mol−1, which is particularly necessary for obtaining quantitative barrier heights in the HNCO + OH reaction.
| Method | ΔV‡ |
|---|---|
| a Using the extrapolation formula EL = ECBS + A/L3, where L = 2, 3 for cc-pVDZ, cc-pVTZ, respectively. b VDZ(d) is defined as cc-pVDZ with no polarization functions on hydrogens, which can be obtained from the literature.22 c cc-VDZ is defined as cc-pVDZ with no polarization functions on any atom; it is also called cc-pVDZ(NP), which can be obtained from the literature.26 d GMM(P).L is a revised version of the developed GMM(P) method for approximating CCSDTQ (P)//CBS. | |
| MW2-F12.L | 6.78 |
| CCSDT-CCSD(T)/cc-pVDZ | −0.26 |
| CCSDT-CCSD(T)/cc-pVTZ | −0.18 |
| CCSDT-CCSD(T)/CBSa | −0.14 |
| CCSDT(Q)-CCSDT/cc-pVDZ | −0.50 |
| CCSDT(Q)-CCSDT/cc-pVTZ | −0.67 |
| CCSDT(Q)-CCSDT/CBSa | −0.74 |
| CCCSDTQ-CCSDT(Q)/VDZ(d)b | 0.08 |
| CCSDTQ(P)-CCSDTQ/cc-VDZc | −0.05 |
| Spin–orbit coupling | 0.20 |
| GMM(P).Ld | 6.13 |
We also consider the effect of the specific reaction scale factor on the enthalpies of activation to correct high-frequency anharmonicity, as listed in Table S4 (ESI†), the contributions of the specific reaction scale factor lead to the decrease of the barrier height by 0.38 and 0.11 kcal mol−1 for the H-abstraction and OH addition reactions in Fig. 1, respectively; this shows that high-frequency anharmonicity is important for obtaining quantitative barrier heights in the OH + HNCO reaction.77
3.2. Kinetics
We calculated the rate constants for the TS1 and TS2 reaction channels between 190 and 3000 K, as provided in Table 4, and for more details as listed in Tables S5 and S6 (ESI†). Notably, for TS1, the rate constant is a slight negative temperature dependence below 220 K, even though it has a positive reaction barrier. We have fitted the total rate constants by using the following formulas in eqn (4) and (5):63,78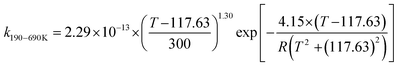 | (4) |
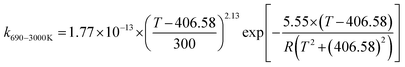 | (5) |
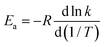 | (6) |
| T (K) | k total (cm3 molecule−1 s−1) | E a (kcal mol−1) |
|---|---|---|
| a k total and Ea are the total rate constants and Arrhenius activation energies of the HNCO + OH reaction, respectively. | ||
| 190 | 1.80 × 10−15 | −0.06 |
| 298 | 3.00 × 10−15 | 0.17 |
| 540 | 1.97 × 10−14 | 1.96 |
| 840 | 9.63 × 10−14 | 6.15 |
| 1140 | 2.92 × 10−13 | 8.19 |
| 1440 | 6.77 × 10−13 | 10.18 |
| 1740 | 1.32 × 10−12 | 11.99 |
| 2040 | 2.27 × 10−12 | 13.66 |
| 2340 | 3.58 × 10−12 | 15.24 |
| 2640 | 5.29 × 10−12 | 16.74 |
| 2940 | 7.43 × 10−12 | 18.20 |
| 3000 | 7.90 × 10−12 | 18.49 |
The computed activation energy is listed in Table 4, which shows that it increases by 18.6 kcal mol−1 over the temperature range studied (more information can be seen in Table S7, ESI†). Furthermore, it is negative under 290 K.
3.3. The effects of anharmonicity on rate constants
We use the standard scale factor and specific reaction scale factor to calculate the rate constants of OH + HNCO at 190–3000 K, as listed in Table S8 (ESI†). For H abstraction (TS1) reaction, the ratio of the rate constant between 190 and 3000 K is 3.0 to 1.3, with a more pronounced effect only at lower temperatures, while for the OH addition (TS2) reaction, the rate constant ratio is within a factor of 1.4 over the entire temperature range. Thus, the effect of the anharmonicity may be negligible for OH addition reaction (TS2) because it has been shown that anharmonicity only decreases the barrier height of TS2 by 0.11 kcal mol−1 in Fig. 1. This comparison suggests that a larger reaction rate is obtained by using specific reaction scale factors for H abstraction (TS1) reaction at lower temperatures.3.4. The effects of torsional anharmonicity on rate constant
For the H-abstraction reaction, we find that our calculated rate constants decrease by a factor of about 2 over the entire temperature range, when considering the effect of torsional anharmonicity in Table S5 (ESI†). However, for the OH addition reaction (TS2), the effect of torsional anharmonicity is unimportant.3.5. The effects of tunneling and recrossing on the rate constants
The recrossing transmission coefficients and tunneling transmission coefficients are provided in Tables S5 and S6 (ESI†). For the H-abstraction reaction (TS1), the recrossing effects need to be taken into account because the rate constants decreased by up to 27% with the increase of the temperature (see Tables S5 and S6, ESI†). In addition, the H-abstraction process has remarkable tunneling, making the reaction faster, especially below 350 K. For example, the tunneling is very large, reaching 3 orders of magnitude at lower temperatures. It is noted that SCT may cause some error bars at lower temperatures; this may lead to some uncertainty for calculated rate constants. For the OH addition reaction (TS2), the recrossing effects are negligible since the rate constant decreases only by up to 10% over the entire temperature range. However, the tunneling has only a minor effect on rate constant with factors of 4.3–1.5 in the temperature range 190–330 K for the addition reaction and as the temperature gradually increases, the values are close to 1.After accounting for the effects of various factors on the rate constants, our predictions reproduce the rate coefficients with an average error of 1.6 times compared to the experimental measurements between 624 and 875 K by Tully et al.27 and the average error is a factor of 1.5 compared to the experimental measurements by Wooldridge et al.29 over the whole temperature range of 620–1860 K. Moreover, our predictions also closely align with the temperature range between 2120 and 2500 K estimated by Mertens et al.25 with an average error of 1.4 times, whereas Rosanka et al.'s30 predictions are up to a factor of 2.7, compared with Mertens et al.'s predictions. These results demonstrate the accuracy of our calculations. The total rate constant that we calculated at 298 K is 3.0 × 10−15 cm3 molecule−1 s−1, while the rate constants for the extrapolation of the experimental values of Tully et al. and Wooldridge et al. are 1.2 × 10−15 and 7.2 × 10−16 cm3 molecule−1 s−1, respectively. This shows that direct extrapolation of experimental measurements would be subject to greater uncertainty.
3.6. Atmospheric lifetimes
We present the atmospheric lifetime of HNCO with respect to the concentration of OH at different altitudes from 0 to 50 km (see Table 5). Because OH concentration in the atmosphere slightly varies with altitude, the atmospheric lifetime of HNCO with respect to OH varies from 1.7 to 48.6 years. However, in the aqueous phase, the atmospheric lifetimes of HNCO in the aqueous phase, dry deposition, and aerosol-deposited processes vary from a few hours to over a month,1,20 1–2 days,80 and 6–12 days.23 This shows that HNCO is removed by the heterogenous processes in the atmosphere.| H (Km) | T (K) | [OH]a (molecules cm−3) | k total (cm3 molecule−1 s −1) | τ (year) |
|---|---|---|---|---|
a
H (the altitude), T (the temperature), and [OH] (the OH concentration) are from ref. 82.
b
k is the bimolecular rate constant of HNCO + OH.
c
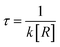 , where R is the concentration of OH. , where R is the concentration of OH.
|
||||
| 0 | 290.2 | 3.0 × 106 | 2.82 × 10−15 | 3.8 |
| 5 | 250.5 | 1.0 × 106 | 2.11 × 10−15 | 15.0 |
| 10 | 215.6 | 5.7 × 105 | 1.79 × 10−15 | 31.0 |
| 15 | 198.0 | 4.2 × 105 | 1.74 × 10−15 | 43.3 |
| 20 | 208.0 | 3.7 × 105 | 1.76 × 10−15 | 48.6 |
| 25 | 216.1 | 6.6 × 105 | 1.80 × 10−15 | 26.7 |
| 30 | 221.5 | 1.6 × 106 | 1.83 × 10−15 | 10.8 |
| 35 | 228.1 | 3.7 × 106 | 1.88 × 10−15 | 4.6 |
| 40 | 240.5 | 6.8 × 106 | 1.99 × 10−15 | 2.3 |
| 45 | 251.9 | 8.5 × 106 | 2.13 × 10−15 | 1.7 |
| 50 | 253.7 | 6.8 × 106 | 2.16 × 10−15 | 2.2 |
4. Conclusions
In summary, hydroxyl radicals (OH) are the most important atmospheric oxidant, initiating the atmospheric reactions for atmospheric molecules and radicals. The fundamental parameter is kinetics for understanding their chemical transformations in the atmosphere. Although experimental methods can be used to obtain the kinetics of atmospheric reactions, they are limited to specific conditions; this often leads to the kinetics under atmospheric conditions being unavailable. Theoretical methods actually provide an alternative tool for obtaining quantitative kinetics in the atmosphere. However, one often uses low-accuracy electronic structure methods and incomplete kinetics models.We investigated the reaction of OH with isocyanic acid by using the recently developed dual-level strategy to obtain its quantitative kinetics by doing benchmark calculations using GMM(P).L energy in combination with CCSD(T)-F12a/cc-pVTZ-F12 geometries and frequencies for TS1 and TS2. We find that the post-CCSD(T) contribution is very important to obtain quantitative barrier heights for the reaction and the main contribution is the CCSDT(Q)-CCSDT component, which is up to −0.74 kcal mol−1. We obtain recrossing transmission coefficients and tunneling transmission coefficients by using canonical variational transition state theory with small curvature tunneling (CVT/SCT). Moreover, these two coefficients are important for the H-abstraction reaction, while they can be neglected for the OH addition reaction. The total rate constant we calculated at 298 K is 3.0 × 10−15 cm3 molecule−1 s−1, which is a factor of 2 and a factor of 4 different from the experimentally extrapolated values of Tully et al.27 and Wooldridge et al.,29 respectively. This shows that direct extrapolation of experimental values at high temperatures to low temperatures is subject to a larger error bar. Moreover, we calculate the atmospheric lifetime of HNCO with respect to the concentration of OH at different altitudes from 0 to 50 km, which is about two years or even longer. Compared to heterogeneous processes, we therefore demonstrate that heterogeneous processes of HNCO are the dominant removal process for HNCO.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (42120104007 and 41775125, and 91961123), by the Guizhou Provincial Science and Technology Projects, China (CXTD [2022]001) and (GCC[2023]026), and by the Science and Technology Foundation of Guizhou Provincial Department of Education, China (no. KY[2021]014).References
- M. D. Leslie, M. Ridoli, J. G. Murphy and N. Borduas-Dedekind, Environ. Sci.: Processes Impacts, 2019, 21, 793–808 RSC.
- Z. Wang, B. Yuan, C. Ye, J. Roberts, A. Wisthaler, Y. Lin, T. Li, C. Wu, Y. Peng, C. Wang, S. Wang, S. Yang, B. Wang, J. Qi, C. Wang, W. Song, W. Hu, X. Wang, W. Xu, N. Ma, Y. Kuang, J. Tao, Z. Zhang, H. Su, Y. Cheng, X. Wang and M. Shao, Environ. Sci. Technol., 2020, 54, 11818–11826 CrossRef CAS PubMed.
- J. M. Roberts, P. R. Veres, T. C. Vandenboer, C. Warneke, M. Graus, E. J. Williams, B. Lefer, C. A. Brock, R. Bahreini, F. Öztürk, A. M. Middlebrook, N. L. Wagner, W. P. Dubé and J. A. De Gouw, J. Geophys. Res.: Atmos., 2014, 119, 1060–1072 CrossRef CAS.
- J. M. Roberts, P. Veres, C. Warneke, J. A. Neuman, R. A. Washenfelder, S. S. Brown, M. Baasandorj, J. B. Burkholder, I. R. Burling, T. J. Johnson, R. J. Yokelson and J. De Gouw, Atmos. Meas. Tech., 2010, 3, 981–990 CrossRef CAS.
- P. Veres, J. M. Roberts, I. R. Burling, C. Warneke, J. De Gouw and R. J. Yokelson, J. Geophys. Res.: Atmos., 2010, 115, D23302 CrossRef.
- P. J. Young, L. K. Emmons, J. M. Roberts, J.-F. Lamarque, C. Wiedinmyer, P. Veres and T. C. Vandenboer, J. Geophys. Res.: Atmos., 2012, 117, D10308 Search PubMed.
- Q. Ren and C. Zhao, Environ. Sci. Technol., 2012, 46, 4236–4240 CrossRef CAS PubMed.
- J. M. Roberts, P. R. Veres, A. K. Cochran, C. Warneke, I. R. Burling, R. J. Yokelson, B. Lerner, J. B. Gilman, W. C. Kuster, R. Fall and J. De Gouw, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 8966–8971 CrossRef CAS PubMed.
- K.-M. Hansson, J. Samuelsson, C. Tullin and L.-E. Åmand, Combust. Flame, 2004, 137, 265–277 CrossRef CAS.
- P. F. Nelson, C.-Z. Li and E. Ledesma, Energy Fuels, 1996, 10, 264–265 CrossRef CAS.
- C. Wang, J. M. Mattila, D. K. Farmer, C. Arata, A. H. Goldstein and J. P. D. Abbatt, Environ. Sci. Technol., 2022, 56, 7598–7607 CrossRef CAS PubMed.
- H. Zhan, X. Yin, Y. Huang, H. Yuan and C. Wu, Fuel, 2017, 207, 438–448 CrossRef CAS.
- P. M. Nicholls and P. F. Nelson, Energy Fuels, 2000, 14, 943–944 CrossRef CAS.
- J. J. B. Wentzell, J. Liggio, S.-M. Li, A. Vlasenko, R. Staebler, G. Lu, M.-J. Poitras, T. Chan and J. R. Brook, Environ. Sci. Technol., 2013, 47, 7663–7671 CrossRef CAS PubMed.
- S. H. Jathar, C. Heppding, M. F. Link, D. K. Farmer, A. Akherati, M. J. Kleeman, J. A. De Gouw, P. R. Veres and J. M. Roberts, Atmos. Chem. Phys., 2017, 17, 8959–8970 CrossRef CAS.
- D. J. Price, D. A. Day, D. Pagonis, H. Stark, A. V. Handschy, L. B. Algrim, S. L. Miller, J. A. De Gouw, P. J. Ziemann and J. L. Jimenez, ACS Earth Space Chem., 2021, 5, 2252–2267 CrossRef CAS.
- J. C. Ditto, J. P. D. Abbatt and A. W. H. Chan, Environ. Sci. Technol., 2022, 56, 7741–7750 CrossRef CAS PubMed.
- B. You, W. Zhou, J. Li, Z. Li and Y. Sun, Environ. Int., 2022, 170, 107611 CrossRef CAS PubMed.
- C. Wang, J. M. Mattila, D. K. Farmer, C. Arata, A. H. Goldstein and J. P. D. Abbatt, Environ. Sci. Technol., 2022, 56, 7598–7607 CrossRef CAS PubMed.
- M. C. Barth, A. K. Cochran, M. N. Fiddler, J. M. Roberts and S. Bililign, J. Geophys. Res.: Atmos., 2013, 118, 8688–8701 CrossRef CAS.
- N. Borduas, B. Place, G. R. Wentworth, J. P. D. Abbatt and J. G. Murphy, Atmos. Chem. Phys., 2016, 16, 703–714 CrossRef CAS.
- J. Zhong, L. Li, M. Kumar, X. C. Zeng, J. Zhang and J. S. Francisco, J. Am. Chem. Soc., 2022, 144, 5315–5322 CrossRef CAS PubMed.
- J. M. Roberts and Y. Liu, Atmos. Chem. Phys., 2019, 19, 4419–4437 CrossRef CAS.
- D. L. Baulch, C. T. Bowman, C. J. Cobos, R. A. Cox, T. Just, J. A. Kerr, M. J. Pilling, D. Stocker, J. Troe, W. Tsang, R. W. Walker and J. Warnatz, J. Phys. Chem. Ref. Data, 2005, 34, 757–1397 CrossRef CAS.
- J. D. Mertens, A. Y. Chang, R. K. Hanson and C. T. Bowman, Int. J. Chem. Kinet., 1992, 24, 279–295 CrossRef CAS.
- W. Tsang and J. T. Herron, J. Phys. Chem. Ref. Data, 1991, 20, 609–663 CrossRef CAS.
- F. P. Tully, R. A. Perry, L. R. Thorne and M. D. Allendorf, Symp. Int. Combust., 1989, 22, 1101–1106 CrossRef.
- D. Sengupta and M. T. Nguyen, J. Chem. Phys., 1997, 106, 9703–9707 CrossRef.
- M. S. Wooldridge, R. K. Hanson and C. T. Bowman, Int. J. Chem. Kinet., 1996, 28, 361–372 CrossRef CAS.
- S. Rosanka, G. H. T. Vu, H. M. T. Nguyen, T. V. Pham, U. Javed, D. Taraborrelli and L. Vereecken, Atmos. Chem. Phys., 2020, 20, 6671–6686 CrossRef CAS.
- D. G. Truhlar, W. L. Hase and J. T. Hynes, J. Phys. Chem., 1983, 87, 2664–2682 CrossRef CAS.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, J. Phys. Chem., 1996, 100, 12771–12800 CrossRef CAS.
- B. Long, J. L. Bao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2017, 19, 8091–8100 RSC.
- B. Long, Y. Xia and D. G. Truhlar, J. Am. Chem. Soc., 2022, 144, 19910–19920 CrossRef CAS PubMed.
- B. Long, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2019, 141, 611–617 CrossRef CAS PubMed.
- B. Long, J. L. Bao and D. G. Truhlar, Nat. Commun., 2019, 10, 2003 CrossRef PubMed.
- Y. Sun, B. Long and D. G. Truhlar, Research, 2023, 6, 0143 CrossRef CAS PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- G. Czakó, I. Szabó and H. Telekes, J. Phys. Chem. A, 2014, 118, 646–654 CrossRef PubMed.
- E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027–3034 CrossRef CAS PubMed.
- B. Chan and L. Radom, J. Chem. Theory Comput., 2015, 11, 2109–2119 CrossRef CAS PubMed.
- N. Sylvetsky, K. A. Peterson, A. Karton and J. M. L. Martin, J. Chem. Phys., 2016, 144, 214101 CrossRef PubMed.
- B. Long, Y. Wang, Y. Xia, X. He, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2021, 143, 8402–8413 CrossRef CAS PubMed.
- B. Chan and L. Radom, J. Chem. Theory Comput., 2013, 9, 4769–4778 CrossRef CAS PubMed.
- G.-X. Li, T. Gao, D. Chen, Y.-X. Li, Y.-G. Zhang and Z.-H. Zhu, Chin. Phys., 2006, 15, 998 CrossRef CAS.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382 CrossRef PubMed.
- T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed.
- R. Meana-Pañeda, X. Xu, H. Ma and D. G. Truhlar, J. Phys. Chem. A, 2017, 121, 1693–1707 CrossRef PubMed.
- L. G. Gao, J. Zheng, A. Fernández-Ramos, D. G. Truhlar and X. Xu, J. Am. Chem. Soc., 2018, 140, 2906–2918 CrossRef CAS PubMed.
- J. Wu, L. G. Gao, Z. Varga, X. Xu, W. Ren and D. G. Truhlar, Angew. Chem., 2020, 132, 10918–10922 CrossRef.
- B. J. Lynch, P. L. Fast, M. Harris and D. G. Truhlar, J. Phys. Chem. A, 2000, 104, 4811–4815 CrossRef CAS.
- B. J. Lynch, Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2003, 107, 1384–1388 CrossRef CAS.
- J. Bloino, M. Biczysko and V. Barone, J. Chem. Theory Comput., 2012, 8, 1015–1036 CrossRef CAS PubMed.
- K. M. Kuhler, D. G. Truhlar and A. D. Isaacson, J. Chem. Phys., 1996, 104, 4664–4671 CrossRef CAS.
- J. Bloino, M. Biczysko and V. Barone, J. Chem. Theory Comput., 2012, 8, 1015–1036 CrossRef CAS PubMed.
- K. M. Kuhler, D. G. Truhlar and A. D. Jsaacson, J. Chem. Phys., 1996, 104, 4664–4671 CrossRef CAS.
- H. S. Yu, L. J. Fiedler, I. M. Alecu and D. G. Truhlar, Comput. Phys. Commun., 2017, 210, 132–138 CrossRef CAS.
- B. Long, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2016, 138, 14409–14422 CrossRef CAS PubMed.
- B. Long, J. L. Bao and D. G. Truhlar, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6135–6140 CrossRef CAS PubMed.
- Y. Xia, B. Long, A. Liu and D. G. Truhlar, Fundamental Res., 2023 DOI:10.1016/j.fmre.2023.02.012.
- J. L. Bao, R. Meana-Pañeda and D. G. Truhlar, Chem. Sci., 2015, 6, 5866–5881 RSC.
- T. Yu, J. Zheng and D. G. Truhlar, J. Phys. Chem. A, 2012, 116, 297–308 CrossRef CAS PubMed.
- J. L. Bao, P. Sripa and D. G. Truhlar, Phys. Chem. Chem. Phys., 2016, 18, 1032–1041 RSC.
- J. L. Bao and D. G. Truhlar, Chem. Soc. Rev., 2017, 46, 7548–7596 RSC.
- J. Zheng and D. G. Truhlar, J. Chem. Theory Comput., 2013, 9, 1356–1367 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision C.01, Gaussian, Inc., Wallingford, CT, 2010, https://www.gaussian.com/g_prod/g09.html Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- J. Zheng, L. J. W. Bao, R. Meana-Pañeda, S. Zhang, B. J. Lynch, J. C. Corchado, Y.-Y. Chuang, P. L. Fast, W.-P. Hu, Y.-P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. Fernandez Ramos, B. A. Ellingson, V. S. Melissas, J. Villa, I. Rossi, L. Coitino, J. Pu, T. V. Albu, R. Steckler, B. C. Garrett, A. D. Issacson and D. G. Truhlar, Polyrate – version 2017-C, University of Minnesota, Minneapolis, 2018 Search PubMed.
- J. Zheng, L. J. W. Bao, S. Zhang, J. C. Corchado, Y.-Y. Chuang, E. L. Coitiño, B. A. Ellingson and D. G. Truhlar, Gaussrate – version 2017-B, University of Minnesota, Minneapolis, 2018 Search PubMed.
- J. Zheng and D. G. Truhlar, J. Chem. Theory Comput., 2013, 9, 1356–1367 CrossRef CAS PubMed.
- J. Zheng, R. Meana-Pañeda and D. G. Truhlar, Comput. Phys. Commun., 2013, 184, 2032–2033 CrossRef CAS.
- Y. Xia, B. Long, S. Lin, C. Teng, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2022, 144, 4828–4838 CrossRef CAS PubMed.
- C. J. Nielsen, H. Herrmann and C. Weller, Chem. Soc. Rev., 2012, 41, 6684–6704 RSC.
- M. A. Ali and J. R. Barker, J. Phys. Chem. A, 2015, 119, 7578–7592 CrossRef PubMed.
- B. Long, Y. Xia, Y.-Q. Zhang and D. G. Truhlar, J. Am. Chem. Soc., 2023, 145, 19866–19876 CrossRef CAS PubMed.
- J. L. Bao, X. Zhang and D. G. Truhlar, Phys. Chem. Chem. Phys., 2016, 18, 16659–16670 RSC.
- D. G. Truhlar, J. Chem. Educ., 1978, 55, 309–311 CrossRef CAS.
- P. J. Young, L. K. Emmons, J. M. Roberts, J.-F. Lamarque, C. Wiedinmyer, P. Veres and T. C. Vandenboer, J. Geophys. Res.: Atmos., 2012, 117, D10308 Search PubMed.
- J. Zheng, R. Meana-Pañeda and D. G. Truhlar, J. Am. Chem. Soc., 2014, 136, 5150–5160 CrossRef CAS PubMed.
- G. Brasseur and S. Solomon, Aeronomy of the middle atmosphere 3rd revised and enlarged, Springer, New York, 2005 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: References for spin–orbit coupling and electronic partition functions; scale factors for the vibrational frequencies; activation enthalpies at 0 K and barrier heights for TS1 and TS2; the relative zero-point vibrational energies of TS1 and TS2; rate constants, activation energies recrossing transmission coefficients, and tunneling transmission coefficients; cartesian coordinates of optimized structures; the enthalpy profile of the OH reaction with HNCO; the absolute energies of the different calculations. See DOI: https://doi.org/10.1039/d3cp04385a |
| This journal is © the Owner Societies 2024 |