Quantum hardware calculations of the activation and dissociation of nitrogen on iron clusters and surfaces†
Georgia
Christopoulou
 *a,
Cono
Di Paola
a,
Floris Eelke
Elzinga
b,
Aurelie
Jallat
b,
David
Muñoz Ramo
a and
Michal
Krompiec
a
*a,
Cono
Di Paola
a,
Floris Eelke
Elzinga
b,
Aurelie
Jallat
b,
David
Muñoz Ramo
a and
Michal
Krompiec
a
aQuantinuum, Terrington House, 13-15 Hills Road, CB2 1NL, Cambridge, UK. E-mail: Georgia.Christopoulou@quantinuum.com
bEquinor ASA, Martin Linges vei 33, Fornebu, Norway
First published on 31st January 2024
Abstract
Catalytic processes are the cornerstone of chemical industry, and catalytic conversion of nitrogen to ammonia remains one of the largest industrial processes implemented. Rational design of catalysts and catalytic reactions largely depends on approximate computational chemistry methods, such as density functional theory, which, however, suffer from limited accuracy, especially for strongly-correlated materials. Rigorous ab initio methods which account for static and dynamic electron correlation, while arbitrarily accurate for small systems, are generally too expensive to be applied to modelling of catalytic cycles, due to prohibitive time and space computational complexity with respect to the size of the active space. Recent advances in quantum computing give hope for enabling access to accurate ab initio methods at scale. Herein, we present a prototype hybrid quantum-classical workflow for modeling chemical reactions on surfaces, applied to proof-of-concept models of activation and dissociation of nitrogen on small Fe clusters and a single-layer (221) iron surface. First, we determined the structures of species present in the catalytic cycle at DFT level and studied their electronic structure using CASSCF. We show that it is possible to decouple the half-filled Fe-3d band from the Fe–N and N–N bond orbitals, thereby reducing the active space significantly. Subsequently, we translated the CASSCF wavefunctions into corresponding qubit quantum states, using the Adaptive Variational Quantum Eigensolver, and estimated their energies using a state vector simulator, H1-1E quantum emulator and (for selected systems) H1-1 quantum computer. We demonstrated that if a sufficiently small active orbital space is chosen, ground state energies obtained with classical methods and with the quantum computer are in reasonable agreement. We argue that once quantum computing methods are scaled up so that larger active spaces are accessible, they can offer a tremendous practical advantage to the computational catalysis community.
1 Introduction
Quantum computing and quantum simulations are creating transformative possibilities by exploiting the principles of quantum mechanics in new ways to process and generate information. Although classical computational chemistry has shown great progress in predicting and describing the properties of a wide range of systems, simulating some chemical systems is still classically difficult. Therefore, there is a great interest in applying quantum algorithms to solve these problems efficiently, especially for the so-called strongly correlated systems.1 These are systems usually described by wavefunctions with a high degree of entanglement. Strong correlation is ubiquitous in the study of chemical kinetics and catalysis at the atomistic level, as well as in the modelling of light–matter interactions, magnetic materials, novel semiconductors, Mott insulators and high-temperature superconductors.2 Today's “workhorses” among computational methods for catalysis and kinetics, while extremely useful for many use cases, are not accurate enough to drive process or materials discovery and optimisation. Quantum computing will transform this landscape by unlocking the practical potential of accurate first-principles computational methods that currently—on classical CPUs—rely on Density Functional Theory (DFT) and steeply scaling wavefunction methods in estimating total energies.3–5Several early applications of quantum computers and quantum simulations have already been presented,6–13 and the initial results are quite promising. Today's quantum computers, with their 2-digit qubit counts and ever-improving gate fidelities, are sometimes referred to as NISQ (“Noisy Intermediate-Scale Quantum”) or “near-term” devices.14 Their computing power can be measured in terms of quantum volume, which refers to the maximum number of operations a quantum computer can perform before the signal disappears into noise. Near-term quantum algorithms for molecular ground state problems, such as Adapt-VQE15 and UCCSD-VQE,16–18 leverage variational techniques and parameterized quantum circuits to approximate molecular ground state energies on quantum computers, offering promising approaches for quantum chemistry simulations with existing or near-future quantum hardware. Efforts to tackle the challenge of the excited state issue involve the exploration of novel approaches like quantum subspace expansion19 (QSE) and quantum self-consistent equation-of-motion20 (Q-SC-EOM). These methods harness the distinctive computational powers of quantum computers to precisely simulate and investigate excited electronic states within molecular systems. Additionally, effective Hamiltonian techniques and embedding-type approaches such as doubly unitary coupled cluster21 (DUCC) and transcorrelated Hamiltonian methods22–24 are being explored on quantum computers, using their computational power to address complex electronic correlations and enable efficient simulations of large molecular systems with improved accuracy and scalability.
However, the quantum hardware available today needs to be further improved for quantum technology to have a significant impact on a range of industries, including the chemical industry. We believe that sufficiently large, fault-tolerant quantum computers will surpass the capabilities of currently available classical machines to simulate large, highly correlated systems.25,26 Moreover, before such large, fault-tolerant computers are available, further improvements in algorithms are expected, which would further reduce runtimes and resource requirements. Advanced modelling capabilities, such as those offered by quantum computing, will not only provide new insights into the fundamentals but, thanks to their ever-increasing accuracy, will also accelerate progress in research by enabling fast in silico experimental testing of new ideas, thus reducing the number of costly “trial-and-error” experiments in the laboratory.
With this in mind, the aim of this study is to demonstrate the workflow of a typical surface science ab initio simulation on quantum computers. To this end, we focused on the activation and dissociation of nitrogen on iron clusters. Although the production of ammonia is the oldest and one of the largest catalytic processes in the chemical industry, it still requires high temperatures and pressures. Therefore, considerable efforts are being made to develop novel catalysts and methods for milder, more environmentally friendly activation of nitrogen.27–30 Catalytic cycles on conventional catalysts for ammonia synthesis have been rationalised via DFT models.31 However, predictive simulation of these processes requires first-principles methods that correctly describe the strongly correlated properties of the catalysts. Strong magnetic interactions, such as those found in the Haber–Bosch catalysts, are thought to be important for their catalytic activity.32,33 The FeMo cofactor, nature's solution for ammonia synthesis,34 is beyond the reach of current computational chemistry methods35 and is considered a prime target for quantum-accelerated computational chemistry.36 Moreover, with reference to the currently available literature,37 it is believed that Fe3 and Fe4 clusters on the θ-Al2O3(010) surface can be successfully used as a heterogeneous catalyst for ammonia synthesis.
Larger model systems such as iron clusters and surfaces require quantum phase estimation (QPE) algorithms. However, their resource requirements are too large for the currently available quantum computers. Variational algorithms are considered the most suitable techniques for NISQ devices. In these algorithms, a hybrid quantum-classical setup is constructed in which a relatively flat-parameterised quantum circuit performs heavy tasks such as encoding correlated molecular wavefunctions to calculate the expected value of the energy, while the classical computer collects the quantum computer data to optimise the parameters within the variational loop. In this study, the variational quantum eigensolver (VQE) algorithm38 was used, which is one of the most commonly used variational algorithms to perform quantum chemical simulations on NISQ devices.
This work is structured as follows. In Section 2, the classical and quantum computational methods of the simulations are discussed. In Section 3 we provide all the results on the iron clusters and surfaces with nitrogen, starting with classical calculations to find the best way to simplify the system for calculations with quantum algorithms. Finally, in the last section (Section 4), we present a detailed summary of our results and future work.
2 Methods
To model the activation and dissociation of nitrogen on iron clusters and surfaces, we used a wide range of classical and quantum computational methods. First, we built the atomistic models and optimised them classically, and then used these data to build our quantum models. This section is structured as follows: first, we describe the computational details and classical optimisation methods used for the iron clusters and surfaces. Then we present the methods and technical details for the quantum calculations including the Hamiltonian construction and the details of the quantum hardware used. In the last section, we mention all the equations and approaches used in the various energy calculations.2.1 Hartree–Fock, CASSCF and DFT calculations
Atomistic models of nitrogen activation on iron were built by running simulations for the bulk metal and for the single/multi-layer surface slabs using the Quantum Espresso (QE) Kohn–Sham Density Functional Theory (DFT) package.39,40 Spin-polarised simulations were performed using DFT-D3 van der Waals dispersion correction41 to optimise the geometry of the structures of interest. In all DFT calculations, we employed the Perdew–Burke–Ernzerhof (PBE) GGA exchange–correlation functional together with projector augmented-wave (PAW) pseudopotentials.42 Wavefunction and charge density cut-offs of 36–47 Ry and 221–448 Ry, respectively, were used together with a Brillouin zone sampling mesh of (12 × 12 × 12) for the bulk system and a Marzari–Vanderbilt smearing of 0.04 Ry. Single-point calculations were performed at the restricted open-shell Hartree–Fock (ROHF) and CASSCF levels of theory and with the Los Alamos National Laboratory (lanl2dz) effective core potential (ECP) and the basis set in PySCF.43,44A cubic box of at least 10 Å for the iron clusters and 35 Å of vacuum on top of single/multi-layer surfaces (z-axis) were adopted to avoid any density overlap along non-periodic directions. The PBE0 functional was also used here, which mixes the PBE exchange energy and the Hartree–Fock (HF) exchange energy in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio together with the full PBE correlation energy. In addition to building the structures, the Nudged Elastic Band (NEB) method45 available in the Quantum Espresso package39,40 was used to find transition states and minimum energy paths between known reactants and products. A loose force convergence threshold of approximately 0.05 eV Å−1 was also used.
1 ratio together with the full PBE correlation energy. In addition to building the structures, the Nudged Elastic Band (NEB) method45 available in the Quantum Espresso package39,40 was used to find transition states and minimum energy paths between known reactants and products. A loose force convergence threshold of approximately 0.05 eV Å−1 was also used.
Periodic HF mean-field calculations were performed using the Los Alamos National Laboratory (lanl2dz) basis/pseudopotentials of the double-ζ type for both nitrogen and iron atoms, as implemented in PySCF. For the clusters, first, a ROHF calculation and then a CASSCF calculation was performed, each time using the CI coefficients and orbitals from the previous CASSCF calculation as the initial guess. To ensure convergence of the total energy, a general second-order solver called the Co-Iterative Augmented Hessian (CIAH) method, implemented in PySCF, was used. The same setup was applied to the iron surface models by sampling the Brillouin zone only at the Γ-point and using a Gaussian auxiliary basis set for density fitting in the form available in PySCF.
2.2 Atomic valence active space (AVAS) orbital localisation
To construct the active orbital space for post-Hartree–Fock and quantum calculations, we used our own implementation of Regional Embedding (RE),46 a variant of the AVAS method.47 In AVAS, the active space is constructed by selecting a list of atomic orbitals (projectors) defined as spherically averaged ground state HF wavefunctions of free atoms in a minimal basis (MINAO). In the RE variant and only for the virtual orbitals, basis functions of the current computational basis are used. An overlap matrix of the occupied orbitals is calculated, which is projected into the space of these selected atomic orbitals:[SA]ij = 〈i|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |j〉 |j〉 | (1) |
| SAU = U diag(σ1,…,σNocc) | (2) |
The new set of rotated molecular orbitals in the basis of the fragment projectors defines a sorted descending set of eigenvalues for the occupied and unoccupied orbitals. These values represent the AVAS overlap threshold in the range between 1.0 (highest overlap) and 0.0 (lowest overlap).
2.3 ADAPT-VQE and NEVPT2 methods
Adaptive variational quantum eigensolver (ADAPT-VQE) is an extension of the traditional VQE algorithm that aims to address challenges in efficiently finding the ground state energy of quantum systems, particularly in the realm of quantum chemistry. In the standard VQE, a parameterized quantum circuit is repeatedly executed, and its parameters are adjusted to minimize a cost function, eventually converging to an estimate of the ground state energy. Adapt VQE builds upon this framework by introducing an adaptive strategy during the optimization process. This adaptability allows the algorithm to dynamically alter its optimization approach based on the characteristics of the quantum system it is analyzing.The key innovation of Adapt-VQE lies in its ability to intelligently respond to the specific properties of the quantum system under consideration. By adjusting its optimization strategy on-the-fly, the algorithm can navigate more efficiently through complex energy landscapes, potentially leading to faster convergence and improved accuracy in estimating ground state energies. This adaptability is particularly advantageous when dealing with diverse and challenging quantum chemistry problems, providing a promising avenue for enhancing the practical utility of variational quantum algorithms in real-world applications.15
NEVPT2 (N-electron valence perturbation theory of second order) is a powerful quantum chemical method employed to calculate accurate electronic energies and properties of molecular systems, particularly for systems with significant electron correlation effects.48,49 It is a perturbative approach that extends beyond the limitations of simple wave function methods by systematically incorporating electron correlation effects that are crucial for describing the electronic structure of molecules. In NEVPT2, the reference wave function is typically obtained from a lower-level method, such as a single-reference method like Hartree–Fock, and the correlation effects are then treated as perturbations. The second-order perturbation theory accounts for dynamic electron correlation, offering a more accurate description of electron–electron interactions than the reference method alone.
One notable feature of NEVPT2 is its ability to handle multi-reference systems where a single determinant wave function is insufficient to represent the electronic structure adequately. By incorporating a reference wave function that includes multiple determinants, NEVPT2 can capture complex electronic correlations, making it a versatile tool for studying molecular systems with diverse electronic behaviors. NEVPT2 is commonly used as an energy correction method because it calculates the contribution of dynamic electron correlation. This correction is crucial for obtaining more accurate predictions of molecular properties, especially in cases where electron correlation plays a significant role. The perturbative nature of NEVPT2 allows it to be computationally tractable while providing a substantial improvement in the accuracy of electronic structure predictions.
2.4 Technical details for the quantum calculations
To calculate the total single-point energies of products, transition states and reactants to evaluate the reaction energies, quantum simulators and state-of-the-art quantum hardware were used. This was achieved by using a stack of PySCF,43 InQuanto50 and Pytket51 as well as Qulacs52 statevector simulator, Qiskit Aer simulator53 and the ‘H1-1’ quantum device and its emulator.The second-quantized Hamiltonians for the VQE calculations were obtained by Hartree–Fock calculations in the PySCF extension of InQuanto using the lanl2dz basis set and the corresponding ECP, localising the orbitals with AVAS, and transforming the Hamiltonian to the MO representation in InQuanto. The terms with coefficients smaller than a certain threshold (i.e. below 10−8) were then removed.
For the state preparation, we applied the Adaptive Derivative-Assembled Pseudo-Trotter (ADAPT15) approach, which uses the Unitary Coupled Cluster Singles Doubles formalism (UCCSD) excitation pool and the ‘Chemically Aware’54 circuit synthesis method. The Jordan–Wigner transformation was used. In the final step, all circuits are optimised and compiled with pytket for the target backend. The ADAPT-VQE algorithm was run on the Qulacs statevector simulator to build the ansatz and determine its parameters. The expectation value of the energy was then evaluated using Hamiltonian averaging. We measured the Pauli terms by appending measurement circuits directly to the system register and using Partition Measurement Symmetry Verification (PMSV) error mitigation.55 NEVPT2 dynamical correlation was applied to the iron surface models only and evaluated using the CASSCF reduced density matrices.
The measurement circuits were then prepared, optimised and delivered for processing on quantum emulators and hardware using pytket. For our 6-qubit calculations, we used the emulation and processing of the Quantinuum H-Series, ‘H1-1’, 20-qubit device. The ‘H1-1’ device is constantly being developed and upgraded. The experiments presented in this study were conducted from March to May 2023. The device specifications can be found online.56
2.5 General details of the energy calculations
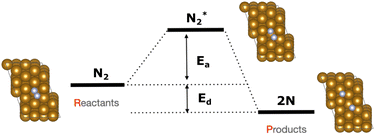
The focus of this study is on the calculation of the activation and dissociation energies of nitrogen on iron clusters and surfaces. Fig. 1 shows the quantities we would like to calculate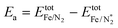 | (3) |
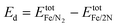 | (4) |
In the quantum emulator and hardware experiments, the approximate correlation energy Ecorr is calculated, which is defined as the difference between post-HF and HF energies. The ΔE(θ) can be defined as
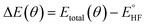 | (5) |
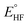 denotes the HF energy which is calculated with the classical computer and Etotal(θ) refers to the total energy calculated on quantum hardware or simulator, which may be affected by noise and/or stochastic errors. If these errors are small enough, the value of ΔE(θ) calculated with optimal parameters θ is a good approximation to Ecorr, which must be a negative value. However, quantum noise in the NISQ device can cause ΔE(θ) to even take on a positive value, since noise-induced high energy excited states can contaminate the calculated ground state wavefunction.
denotes the HF energy which is calculated with the classical computer and Etotal(θ) refers to the total energy calculated on quantum hardware or simulator, which may be affected by noise and/or stochastic errors. If these errors are small enough, the value of ΔE(θ) calculated with optimal parameters θ is a good approximation to Ecorr, which must be a negative value. However, quantum noise in the NISQ device can cause ΔE(θ) to even take on a positive value, since noise-induced high energy excited states can contaminate the calculated ground state wavefunction.
2.6 Technical details of emulator experiments
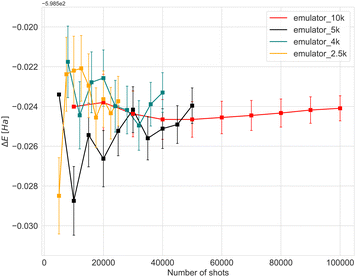
Before running experiments on the quantum computer, we performed a thorough analysis and benchmarking using classical quantum simulators, to investigate the convergence with respect to the number of measurements (“shots”) and the effect of quantum errors (noise). The quantum circuits were built using the exponents (fermionic excitations) selected by the ADAPT-VQE algorithm. The start geometry of the Fe3N2 cluster was used in all the benchmark simulations.Simulating an actual machine is a key step towards understanding the resources needed to run on hardware. Fig. 2 shows the relationship between the number of shots and the accuracy of calculations performed using the initial geometry for the Fe4N2 cluster. The cost of a hardware experiment depends on the type and number of gates used for the circuits, as well as the total time required for all processes to be compiled. In Fig. 2, an approach called batching has been used, where we repeat each experiment with a target number of shots ten times. In the case of 4k shots, for example, the target number is 4k, and after 10 repetitions, we have an experiment with 40k shots in total. The energy and error bars shown in Fig. 2 and 3 are the mean and standard deviation, which were obtained at the end of each repetition. We can see that error bars get significantly smaller when there are enough samples. For the case of a hardware device, only a single batch of experiments will be run. To limit the effect of noise when estimating expectation values, PMSV (Partition Measurement Symmetry Verification) noise mitigation method has been employed. This reduces experimental noise by removing shots in which a symmetry-breaking error has occurred. Here, the mirror planes (Z2) and electron-number conservation (U1) symmetries have been used which can be represented by a single Pauli string that tracks the parity of the wavefunction.
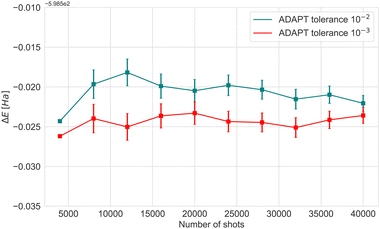
To reduce circuit depth and limit the magnitude of noise, we investigated the effect of relaxing the ADAPT convergence threshold from 10−3 to 10−2, see Fig. 3. Clearly, increasing the threshold negatively affects accuracy, but the maximum energy difference was 0.07 Ha, which we consider to be within the acceptable limits for VQE experiments. Taking into consideration the different results and the limited availability of the actual hardware device, the optimal choice was to conduct experiments with 4000 shots.
Finally, six qubits with three parameters and twenty 2-qubit gates were used in the circuits designed for the start and final geometry. The deepest circuit in this study, the TS geometry utilised six qubits as well, but this time four parameters and thirty-nine controlled-NOT gates were used. The convergence of the expectation value of energy with respect to the number of measurements in the absence of noise is discussed in ESI.†
3 Results
3.1 Simulations of iron clusters
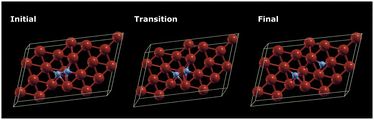
It is shown37,57,58 that Fe clusters promote N2 reduction. Thus, the applicability of our hybrid quantum-classical workflow was first tested on small iron clusters. For the Fe4 cluster (Fig. 4(a)), which is the smallest 3D iron cluster, different multiplicities of the ground state have been found in the literature.37,59,60 Therefore, the geometry of Fe4 was optimised for several possible spin multiplicities (7, 9, 11 and 13) and we found that the state with multiplicity 7 has the lowest energy. Here we focus on the catalytic behaviour of the Fe4 clusters, while we also studied the Fe3 cluster and its relevant products by adding two nitrogen atoms similar to the case of Fe4 (ESI†). As with the Fe3 cluster, after optimising the Fe4 system, the Fe4N2 clusters were constructed by adding two nitrogen atoms and re-optimising (initial geometry, Fig. 4(b)) or by stretching only the nitrogen atoms and re-optimising to obtain the final geometry (Fig. 4(c)).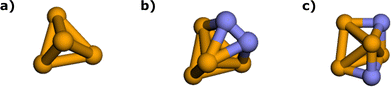 | ||
| Fig. 4 Visualisation of the optimised geometries of the (a) Fe4 cluster (b) N2 adsorption on Fe4 and (c) N2 dissociation on Fe4 using InQuanto-NGLView. Colour code: orange for Fe and blue for N. | ||
To calculate the activation energy Ea we had to determine the structure of the transition state (TS), N2 for the Fe4 cluster. The results for Fe4N2 with eleven NEB images are shown in Fig. 5. The activation energy calculated here is in the range of values found in the literature.37,60
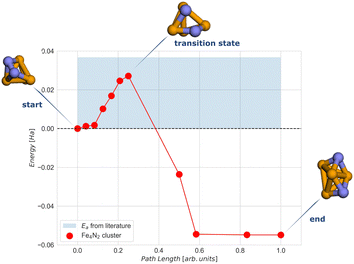 | ||
| Fig. 5 NEB simulation of the minimum energy path for the dissociation of the N2 molecule on the Fe4N2 cluster. The light blue region represents the range of activation energy values available in the literature.37,60 Colour code: orange for Fe and blue for N. | ||
If one constructs the active space from (partially) filled Fe d orbitals and the N–N occupied and virtual orbitals, no excitations from Fe 3d to N–N σ or π orbitals are found in the CI wavefunction. We have also separately verified that excitations from the occupied N–N orbitals to the empty Fe-3d orbitals do not contribute. This means that the excitations in the Fe d manifold and in the N–N bond are not coupled and that a reduced active space can be created consisting of orbitals of the dinitrogen system and selected Fe orbitals interacting with it, i.e. excluding all half-filled 3d-like orbitals on Fe.
As can be seen in Table 1, the contribution of the excited determinants in the wavefunction is at least 10% and only the first, second and third active orbitals are significantly active. ESI† contains an illustration of these orbitals. For the construction of the AVAS active space, we selected 2p orbitals of the two nitrogen atoms and doubly occupied or empty 3d orbitals of the five iron atoms. The overlap threshold for occupied orbitals was 0.9, while the threshold for virtual orbitals was set at 0.97. The half-filled orbitals of Fe atoms were frozen and thus excluded from the active space.
| Alpha occ-orbitals | Beta occ-orbitals | CI coefficient |
|---|---|---|
| [012] | [012] | 0.98709 |
| [013] | [013] | −0.12552 |
| [013] | [023] | 0.03952 |
| [013] | [014] | −0.04160 |
| [023] | [013] | 0.03952 |
| [014] | [013] | −0.04160 |
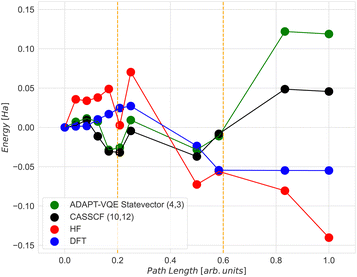
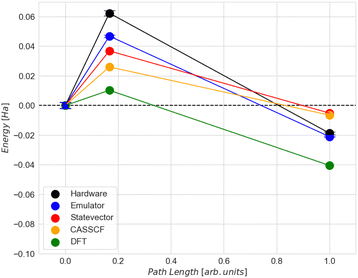
The CASSCF and the classical VQE statevector results are quite unexpected. As can be seen in Fig. 6, the energy of the final state is higher than that of the initial and transition states. Also, the trend of the CASSCF and VQE energy graphs does not follow the DFT. The most likely reason for this is that the potential energy surfaces at the CASSCF and DFT levels of theories are qualitatively different, especially at the middle and the end of the NEB path. However, the middle section of the CASSCF and VQE curves still exhibits a peak, which can be taken as an approximation to the transition state. Therefore, we decided to focus only on the range between images 6 and 9, i.e. between two dashed orange lines shown in Fig. 6. Thus, for the next calculations, the initial state is the 6th image, the transition state is the 7th image and the final state is the 9th image of NEB calculation. The energy difference between the zero point energy (NEB image 1) and the present NEB image is used to determine energies in Fig. 6.
Comparing the energy results computed classically with the ADAPT-VQE statevector to those from emulator and hardware experiments, we can see that the highest level of accuracy is achieved for the final state in both the emulator and hardware (Table 2). However, it is about 7 times worse than the so-called “chemical accuracy” target of 1 kcal mol−1 (1.6 mHa).
| State | State vector (Ha) | ‘H1-1E’ emulator (Ha) | Deviation (mHa) | ‘H1-1’ hardware (Ha) | Deviation (mHa) |
|---|---|---|---|---|---|
| Initial | −598.561 | −598.523 | 38 | −598.524 | 0.74 |
| Transition | −598.523 | −598.476 | 47 | −598.461 | 14 |
| Final | −598.556 | −598.544 | 12 | −598.542 | 1.6 |
3.2 Simulations of iron surfaces
The high quality of the experimental output obtained on the Quantinuum ‘H1-1’ device (and ‘H1-1E’ noisy emulator) has shown encouraging results, indicating that this workflow is suitable for larger simulations. Thus, our next target was to study the activation and dissociation of nitrogen on iron surfaces.To model the dissociation on the Fe catalyst, the equilibrium value of the lattice parameter was first calculated. A final value of 2.829 Å was found, which is very close to the lattice parameter available in the literature of about 2.832 Å.61 Then, the orientation of the simulated surface was determined. It has been shown61 by comparing the relative difference in intrinsic reactivity of various iron facets that the reaction rate, relative to the (100) facet follows the order of (221) > (311) > (111) > (211) > (310) > (210) > (110), with 5.59, 5.13, 4.92, 4.32, 4.19, 2.40, and 1.90 orders of magnitude higher than the (100) facet, respectively. Thus, we opted for the (221) direction, even though this was not the simplest case. We constructed the atomistic structure by selecting the number of repeated unit cells along the X and Y axes of the slab, determining the number of layers, and specifying the vacuum thickness above and below the structure (along the non-periodic ‘z’ axis).
We found that a (3 × 3 × 1) monolayer slab with a total amount of about 20 Å of vacuum, equally distributed around the model, was large enough to prevent density overlapping between neighbouring cells along the Z axis and ensure enough surface space for the adsorption of a single molecule. The slab was generated using the model-building functions of the Atomic Simulation Environment (ASE).62 Even though we can consider the 3 × 3 × 1 slab good enough for testing purposes, more “realistic” models should include at least 7 layers to mimic the bulk behaviour in the innermost region, as suggested by Kaushal et al.63 and Krupski et al.64
In this study, we adopted the geometries proposed by Zhang et al.61 as initial and final states. This choice was influenced by the close agreement of the lattice parameter obtained in our PBE/PAW pseudo-potential study using the Equation of States (EOS) approach within the Quantum ESPRESSO (QE) package. Fig. 8(a) provides an overview of the complete slab, encompassing 66 iron atoms.
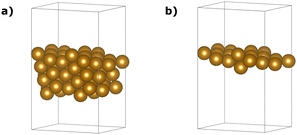 | ||
| Fig. 8 The slab (a) and the one-layer (b) atomistic models were used in this work to mimic the Fe(221) surface. | ||
Maintaining consistency with our DFT setup, we performed geometry relaxation on the iron slab first as depicted in Fig. 8(a), and after achieving convergence, proceeded to relax the deposited adsorbates based on the geometries suggested in reference ref. 61. This process generated the initial and final images for our 8-image NEB calculation, where only the degrees of freedom of the nitrogen atoms were allowed to change while mapping the minimal energy path. The resulting NEB path was further refined around the saddle point using the Climbing Image approach65 to ensure accurate determination of the Transition State (TS) structure. The relative energies to the initial state for the N2 dissociation on the 66-atom iron slab are presented in Fig. 9, indicated by full red circles.
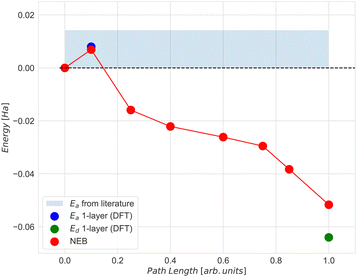 | ||
| Fig. 9 NEB simulation of the minimum energy path for the dissociation of N2 molecule on top of the 3-layer Fe(221) model. For comparison, the activation energy (Ea, indicated by the blue dot) and dissociation energy (Ed, indicated by the green dot) were calculated at the DFT level with respect to the initial state for the 1-layer Fe(221) model and are also presented. The light blue area represents the range of values for the activation energy available in literature.61 | ||
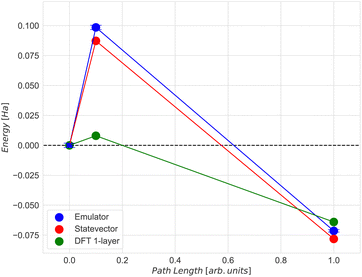
Given our primary interest in the applicability of quantum computers to surface reactions, we decided to simplify the slab model for the following quantum experiments. We reduced its thickness to encompass solely the surface iron atoms, resulting in a 22-atom single layer system depicted in Fig. 8(b). Considerations regarding the stability of larger models were deferred to another context. This choice was reinforced by two key observations: (1) the additional residual electron density generated during adsorption and dissociation mainly concentrated on the surface at the contact site between iron and nitrogen atoms (refer to the density difference in the ESI† for the larger model); (2) the relative energy of the transition state did not significantly change with varying thickness of the two iron systems (Fig. 9, path length = 0.1, full blue circle). This is likely due to an effective screening of iron atoms when the landing site is on the Fe (221) “step” region, as supported by the apparent increase of stability of the final state with one nitrogen atom sitting in the hollow of the single layer terrace region (Fig. 9, path length = 1.00, full green circle). The initial (image 1), transition (image 2), and final (image 8) states for the single layer model were subsequently utilized for all subsequent calculations.
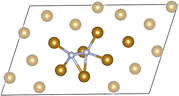 | ||
| Fig. 10 The selected sub-system of the single-layer atomistic model (Fe20N2). Colour code: gold for Fe and silver for N. | ||
The agreement between the energies computed with the ADAPT-VQE statevector simulator and those from the ‘H1-1E’ emulator experiments is quite good. The initial geometry has a difference of only 0.74 mHa, as seen in Table 3. By comparing the dissociation energy, it can be seen (Fig. 12) that the results from DFT are very consistent to those from ADAPT-VQE for both the statevector and the emulator. In contrast to DFT results, the activation energy is much overestimated. As mentioned before, the origin of this error in the activation energy may be attributed to the noise in quantum hardware and also the noise model implemented in the emulator. Furthermore, the shape of the potential energy surface at the ADAPT-VQE level differ to that obtained with DFT. In Fig. 11 and Figs. 5 and 6 of ESI†, where DFT density difference calculations are employed to screen the N–N bond, it is evident that the density of the iron layers does not have an impact on this reaction. While the literature commonly suggests incorporating a minimum of 7 layers in more realistic models to simulate bulk behaviour in the innermost region,63,64 the specific characteristics of this system, such as the packing morphology of iron atoms at the adsorption “step” site, enable us to employ a considerably simplified model with just one layer without a substantial loss of descriptive accuracy for the activation energy.
| State | State vector (Ha) | Emulator (Ha) | Deviation (mHa) |
|---|---|---|---|
| Initial | −2546.783 | −2546.785 | 1.6 |
| Transition | −2546.696 | −2546.686 | 9.6 |
| Final | −2546.861 | −2546.866 | 5.1 |
4 Conclusions and future work
We have presented proof-of-concept calculations of the static correlation energies of molecular and periodic models of species involved in the catalytic activation of nitrogen on iron. We have attempted to replicate state-of-the-art results in quantum chemistry by using quantum algorithms on noisy quantum computers with few qubits to demonstrate the current state of quantum computing for chemistry. We focused on 6-qubit computations in the Jordan–Wigner encoding representing 3-orbital active spaces of 2 chemical systems with 3 states each. Efficient circuits were prepared for Hamiltonian averaging by using the ADAPT-VQE ansatz, compiled and processed on backends by using pytket. We applied post-selection symmetry verification error mitigation to reduce the impact of quantum errors. Overall, our results showed an accuracy of about 12 mHa for the best-case cluster systems, which is typical for quantum simulations on current hardware, but about 7 times worse than the so-called “chemical accuracy” of 1 kcal mol−1 (1.6 mHa). For the single-layer surface model, the results were much better, as chemical accuracy was achieved for the initial state. These results are very encouraging, even if they do not yet allow us to prove the advantage of quantum solutions for the simulation of complex catalytic systems.Quantum machinery was not applied to the entire atomistic model – that would be not only expensive but also unnecessary; rather, we used it to describe the immediate vicinity of the reaction site. This is made possible by carefully transforming the mean-field orbitals so that a compact active space is constructed. Crucially, we have found that it is possible to decouple the half-filled Fe-3d band from the Fe–N and N–N bond orbitals, as their mutual correlation turns out to be negligible.
In the case of the single-layer iron surface with 22 atoms, the charge density difference calculations confirmed our hypothesis that we can use only the top iron layer instead of the whole slab and still be able to capture correlation energy equivalent to the CASSCF. As our relative energy results showed, the VQE results were very successful in reproducing the DFT energy trend when studying the activation and dissociation of nitrogen on iron surfaces. Even though this was an approximation, it has clearly shown that large surface models are not necessary and that fragmentation can instead be an accurate way to deal with similar cases.
Future studies of these systems, using both quantum and classical methods, may provide further insight into elementary steps of catalytic ammonia synthesis. A suggestion to better understand the iron catalyst would be to use a simpler facet such as 111 or 211. Even though facets like 221 are more reactive, a simpler facet is an easier problem for today's quantum computers. Other catalysts could be also explored. Examples include ruthenium-based catalysts, which are the most commonly used catalysts for ammonia synthesis after iron, as Ru supported on CaFH can achieve ammonia synthesis at an exceptionally low temperature (50 °C), electron-based catalysts such as an ionic O2− compound in which electrons act as the anion, cobalt-based, as it has been found that Co supported on CeO2 or carbon and promoted with Ba has very high activity, nickel-based, which has high activity at low temperatures, and metal nitride catalysts consisting of binary nitride systems based on uranium, cerium, vanadium, molybdenum and rhenium.66–69
In addition to investigating other related systems, future work should focus on building up the methodology to reduce errors and increase the size of the calculated systems. It is clear that the Variational Quantum Eigensolver running on noisy quantum processors cannot provide the required accuracy, nor is it applicable to larger problems. A transition to phase estimation algorithms is necessary but requires fault-tolerant quantum computation, which is not yet available. Whether stochastic approximations to phase estimation that can tolerate a certain amount of noise can fill this gap remains to be answered.70
While the quantum advantage for Hamiltonian simulation of strongly correlated systems has been postulated in principle due to the exponential scaling of classical brute-force algorithms, its practical implementation depends on the cost comparison between a classical approximate heuristic algorithm and the quantum method (including the cost of preparing the initial state) for a given use case.1 Therefore, follow-up studies could use state-of-the-art approximate classical FCI solvers (such as Stochastic Heat-Bath Configuration Interaction,71 or the Density Matrix Renormalisation Group72) to (1) investigate how complex the electronic states of catalytic species are, (2) determine the scaling of classical approximate ab initio methods for such systems, and (3) develop prototype end-to-end workflows applicable to large and dense Hamiltonians.
Author contributions
G. C. directly obtained the results presented in the study. C. D. P. and M. K. assisted with the reaction path calculations. F. E. Z. and A. J. contributed the use case and helped scope the project and conceptualise the study. G. C., C. D. P., M. K. and D. M. R. interpreted the data. M. K. conceptualised the study and supervised the work. G. C. and M. K. wrote and organised the paper. All coauthors participated in joint discussions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge financial and domain knowledge support from Equinor ASA. The authors thank Evgeny Plekhanov, Kesha Sorathia and Duncan Gowland for their comments on the manuscript. The authors also thank Isobel Hooper, Brian Neyenhuis and Jenni Strabley for assistance in the hardware experiments.Notes and references
- S. Lee, J. Lee, H. Zhai, Y. Tong, A. M. Dalzell, A. Kumar, P. Helms, J. Gray, Z.-H. Cui, W. Liu, M. Kastoryano, R. Babbush, J. Preskill, D. R. Reichman, E. T. Campbell, E. F. Valeev, L. Lin and G. K.-L. Chan, arXiv, 2022, preprint, arXiv:2208.02199 DOI:10.48550/arXiv.2208.02199.
- C. J. Stein and M. Reiher, Mol. Phys., 2017, 115, 2110–2119 CrossRef CAS.
- E. Grumbling and M. Horowitz, Quantum Computing, National Academies Press, 2019 Search PubMed.
- M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition, Cambridge University Press, 2010 Search PubMed.
- D. Claudino, Int. J. Quantum Chem., 2022, e26990 CrossRef CAS.
- K. Bharti, A. Cervera-Lierta, T. H. Kyaw, T. Haug, S. Alperin-Lea, A. Anand, M. Degroote, H. Heimonen, J. S. Kottmann, T. Menke and W. K. Mok, Rev. Mod. Phys., 2022, 94(1), 015004 CrossRef CAS.
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. C. Benjamin and X. Yuan, Rev. Mod. Phys., 2020, 92, 015003 CrossRef CAS.
- B. P. Lanyon, J. D. Whitfield, G. G. Gillett, M. E. Goggin, M. P. Almeida, I. Kassal, J. D. Biamonte, M. Mohseni, B. J. Powell and M. Barbieri, et al. , Nat. Chem., 2010, 2, 106–111 CrossRef CAS PubMed.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre and N. P. Sawaya, et al. , Chem. Rev., 2019, 119, 10856–10915 CrossRef CAS PubMed.
- B. Bauer, S. Bravyi, M. Motta and G. K.-L. Chan, Chem. Rev., 2020, 120, 12685–12717 CrossRef CAS PubMed.
- V. von Burg, G. H. Low, T. Häner, D. S. Steiger, M. Reiher, M. Roetteler and M. Troyer, Phys. Rev. Res., 2021, 3, 033055 CrossRef CAS.
- J. J. Goings, A. White, J. Lee, C. S. Tautermann, M. Degroote, C. Gidney, T. Shiozaki, R. Babbush and N. C. Rubin, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2203533119 CrossRef CAS PubMed.
- V. E. Elfving, B. W. Broer, M. Webber, J. Gavartin, M. D. Halls, K. P. Lorton and A. Bochevarov, arXiv, 2020, preprint, arXiv:2009.12472 DOI:10.48550/arXiv.2009.12472.
- J. Preskill, Quantum, 2018, 2, 79 CrossRef.
- H. R. Grimsley, S. E. Economou, E. Barnes and N. J. Mayhall, Nat. Commun., 2019, 10, 3007 CrossRef PubMed.
- H. R. Grimsley, D. Claudino, S. E. Economou, E. Barnes and N. J. Mayhall, J. Chem. Theory Comput., 2019, 16, 1–6 CrossRef PubMed.
- Y. Shen, X. Zhang, S. Zhang, J.-N. Zhang, M.-H. Yung and K. Kim, Phys. Rev. A: At., Mol., Opt. Phys., 2017, 95, 020501 CrossRef.
- R. Xia and S. Kais, Quantum Sci. Technol., 2020, 6, 015001 CrossRef.
- J. R. McClean, M. E. Kimchi-Schwartz, J. Carter and W. A. De Jong, Phys. Rev. A: At., Mol., Opt. Phys., 2017, 95, 042308 CrossRef.
- A. Asthana, A. Kumar, V. Abraham, H. Grimsley, Y. Zhang, L. Cincio, S. Tretiak, P. A. Dub, S. E. Economou and E. Barnes, et al. , Chem. Sci., 2023, 14, 2405–2418 RSC.
- M. Metcalf, N. P. Bauman, K. Kowalski and W. A. De Jong, J. Chem. Theory Comput., 2020, 16, 6165–6175 CrossRef CAS PubMed.
- M. Motta, T. P. Gujarati, J. E. Rice, A. Kumar, C. Masteran, J. A. Latone, E. Lee, E. F. Valeev and T. Y. Takeshita, Phys. Chem. Chem. Phys., 2020, 22, 24270–24281 RSC.
- I. O. Sokolov, W. Dobrautz, H. Luo, A. Alavi and I. Tavernelli, Phys. Rev. Res., 2023, 5, 023174 CrossRef CAS.
- S. McArdle and D. P. Tew, arXiv, 2020, preprint, arXiv:2006.11181 DOI:10.48550/arXiv.2006.11181.
- Y. Su, D. W. Berry, N. Wiebe, N. Rubin and R. Babbush, PRX Quantum, 2021, 2, 040332 CrossRef.
- Z. Ding and L. Lin, PRX Quantum, 2023, 4, 020331 CrossRef.
- R. Schlögl, Angew. Chem., Int. Ed., 2003, 42, 2004–2008 CrossRef PubMed.
- Y. Tanabe and Y. Nishibayashi, Coord. Chem. Rev., 2013, 257, 2551–2564 CrossRef CAS.
- L. Wang, M. Xia, H. Wang, K. Huang, C. Qian, C. T. Maravelias and G. A. Ozin, Joule, 2018, 2, 1055–1074 CrossRef CAS.
- V. S. Marakatti and E. M. Gaigneaux, ChemCatChem, 2020, 12, 5838–5857 CrossRef CAS.
- C. D. Zeinalipour-Yazdi, J. S. J. Hargreaves, S. Laassiri and C. R. A. Catlow, R. Soc. Open Sci., 2021, 8, 210952 CrossRef CAS PubMed.
- C. Biz, M. Fianchini and J. Gracia, ACS Catal., 2021, 11, 14249–14261 CrossRef CAS.
- J. Munarriz, V. Polo and J. Gracia, Chem. Phys. Chem., 2018, 19, 2843–2847 CrossRef CAS PubMed.
- O. Einsle, JBIC, J. Biol. Inorg. Chem., 2014, 19, 737–745 CrossRef CAS PubMed.
- Z. Li, J. Li, N. S. Dattani, C. J. Umrigar and G. K.-L. Chan, J. Chem. Phys., 2019, 150, 024302 CrossRef PubMed.
- J. Lee, D. W. Berry, C. Gidney, W. J. Huggins, J. R. McClean, N. Wiebe and R. Babbush, PRX Quantum, 2021, 2, 030305 CrossRef.
- J.-C. Liu, X.-L. Ma, Y. Li, Y.-G. Wang, H. Xiao and J. Li, Nat. Commun., 2018, 9, 1610 CrossRef PubMed.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. Obrien, Nat. Commun., 2014, 5, 1–7 Search PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Condens. Matter Phys., 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Condens. Matter Phys., 2017, 29, 465901 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340 Search PubMed.
- Q. Sun, X. Zhang, S. Banerjee, P. Bao, M. Barbry, N. S. Blunt, N. A. Bogdanov, G. H. Booth, J. Chen, Z.-H. Cui, J. J. Eriksen, Y. Gao, S. Guo, J. Hermann, M. R. Hermes, K. Koh, P. Koval, S. Lehtola, Z. Li, J. Liu, N. Mardirossian, J. D. McClain, M. Motta, B. Mussard, H. Q. Pham, A. Pulkin, W. Purwanto, P. J. Robinson, E. Ronca, E. R. Sayfutyarova, M. Scheurer, H. F. Schurkus, J. E. T. Smith, C. Sun, S.-N. Sun, S. Upadhyay, L. K. Wagner, X. Wang, A. White, J. D. Whitfield, M. J. Williamson, S. Wouters, J. Yang, J. M. Yu, T. Zhu, T. C. Berkelbach, S. Sharma, A. Y. Sokolov and G. K.-L. Chan, J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed.
- H. Jónsson, G. Mills and K. W. Jacobsen, Classical and Quantum Dynamics in Condensed Phase Simulations, 1998 Search PubMed.
- B. T. G. Lau, G. Knizia and T. C. Berkelbach, J. Phys. Chem., 2021, 12, 1104–1109 CAS.
- E. R. Sayfutyarova, Q. Sun, G. K.-L. Chan and G. Knizia, J. Chem. Theory Comput., 2017, 13, 4063–4078 CrossRef CAS PubMed.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- M. Krompiec and D. M. Ramo, arXiv, 2022, preprint, arXiv:2210.05702 DOI:10.48550/arXiv.2210.05702.
- A. Tranter, C. Di Paola, D. Zsolt Manrique, D. Muñoz Ramo, D. Gowland, E. Plekhanov, G. Greene-Diniz, G. Christopoulou, G. Prokopiou, H. Keen, I. Polyak, I. Khan, J. Pilipczuk, J. Kirsopp, K. Yamamoto, M. Tudorovskaya, M. Krompiec, M. Sze and N. Fitzpatrick, InQuanto: Quantum Computational Chemistry, 2022, https://www.quantinuum.com/computationalchemistry/inquanto,https://medium.com/cambridge-quantum-computing/introduction-to-the-inquanto-computational//-chemistry-platform-for-quantum//-computers-4fced08d66cc.
- S. Sivarajah, S. Dilkes, A. Cowtan, W. Simmons, A. Edgington and R. Duncan, Quantum Sci. Technol., 2020, 6, 14003 CrossRef.
- Y. Suzuki, Y. Kawase, Y. Masumura, Y. Hiraga, M. Nakadai, J. Chen, K. M. Nakanishi, K. Mitarai, R. Imai, S. Tamiya, T. Yamamoto, T. Yan, T. Kawakubo, Y. O. Nakagawa, Y. Ibe, Y. Zhang, H. Yamashita, H. Yoshimura, A. Hayashi and K. Fujii, Quantum, 2021, 5, 559 CrossRef.
- Qiskit contributors, Qiskit: An Open-source Framework for Quantum Computing, 2023.
- I. T. Khan, M. Tudorovskaya, J. J. M. Kirsopp, D. M. Ramo, P. W. Warrier, D. K. Papanastasiou and R. Singh, J. Chem. Phys., 2023, 158, 214114 CrossRef CAS PubMed.
- K. Yamamoto, D. Z. Manrique, I. T. Khan, H. Sawada and D. M. Ramo, Phys. Rev. Res., 2022, 4, 1–9 Search PubMed.
- Quantinuum contributors, GitHub – CQCL/quantinuum-hardware-specifications: Repository for sharing Quantinuum's hardware specifications data, 2023, https://github.com/CQCL/quantinuum-hardware-specifications.
- S. F. McWilliams and P. L. Holland, Acc. Chem. Res., 2015, 48, 2059–2065 CrossRef CAS PubMed.
- I. Čorić, B. Q. Mercado, E. Bill, D. J. Vinyard and P. L. Holland, Nature, 2015, 526, 96–99 CrossRef PubMed.
- A. Pakiari and M. Mousavi, J. Phys. Chem. A, 2010, 114, 10209–10216 CrossRef CAS PubMed.
- G. L. Gutsev, S. M. Aldoshin, L. G. Gutsev and B. R. Ramachandran, J. Phys. Chem. A, 2021, 125, 7891–7899 CrossRef CAS PubMed.
- B.-Y. Zhang, H.-Y. Su, J.-X. Liu and W.-X. Li, ChemCatChem, 2019, 11, 1928–1934 CrossRef CAS.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys. Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- A. K. Kaushal, S. Mullick and P. K. Ahluwalia, AIP Conf. Proc., 2011, 1349, 693–694 CrossRef CAS.
- K. Krupski, M. Moors, P. Jóźwik, T. Kobiela and A. Krupski, Materials, 2015, 8, 2935–2952 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- N. Morlanés, W. Almaksoud, R. K. Rai, S. Ould-Chikh, M. M. Ali, B. Vidjayacoumar, B. E. Al-Sabban, K. Albahily and J.-M. Basset, Catal. Sci. Technol., 2020, 10, 844–852 RSC.
- J. Humphreys, R. Lan and S. Tao, Adv. Sustainable Syst., 2021, 2, 2000043 CAS.
- A. Daisley, J. Hargreaves, R. Hermann, Y. Poya and Y. Wang, Catal. Today, 2020, 357, 534–540 CrossRef CAS.
- C. D. Zeinalipour-Yazdi, J. S. Hargreaves, S. Laassiri and C. R. A. Catlow, R. Soc. Open Sci., 2021, 8, 210952 CrossRef CAS PubMed.
- S. Paesani, A. Gentile, R. Santagati, J. Wang, N. Wiebe, D. Tew, J. O'Brien and M. Thompson, Phys. Rev. Lett., 2017, 118, 100503 CrossRef CAS PubMed.
- J. Li, M. Otten, A. A. Holmes, S. Sharma and C. J. Umrigar, J. Chem. Phys., 2018, 149, 214110 CrossRef PubMed.
- A. Baiardi and M. Reiher, J. Chem. Phys., 2020, 152, 040903 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05167f |
| This journal is © the Owner Societies 2024 |