New-generation electron-propagator methods for vertical electron detachment energies of molecular anions: benchmarks and applications to model green-fluorescent-protein chromophores†
Ernest
Opoku
 ,
Filip
Pawłowski
and
J. V.
Ortiz
,
Filip
Pawłowski
and
J. V.
Ortiz
 *
*
Department of Chemistry and Biochemistry, Auburn University, Auburn, AL 36849-5312, USA. E-mail: ezo0009@auburn.edu; flp0008@auburn.edu; ortiz@auburn.edu
First published on 8th March 2024
Abstract
Ab initio electron-propagator calculations continue to be useful companions to experimental investigations of electronic structure in molecular anions. A new generation of electron-propagator methods recently has surpassed its antecedents’ predictive accuracy and computational efficiency. Interpretive clarity has been conserved, for no adjustable parameters have been introduced in the preparation of molecular orbitals or in the formulation of approximate self-energies. These methods have employed the diagonal self-energy approximation wherein each Dyson orbital equals a canonical Hartree–Fock orbital times the square root of a probability factor. Numerical tests indicate that explicitly renormalized, diagonal self-energies are needed when Dyson orbitals have large valence nitrogen, oxygen or fluorine components. They also demonstrate that even greater accuracy can be realized with generalizations that do not employ the diagonal self-energy approximation in the canonical Hartree–Fock basis. Whereas the diagonal methods have fifth-power arithmetic scaling factors, the non-diagonal generalizations introduce only non-iterative sixth-power contractions. Composite models conserve the accuracy of the most demanding combinations of self-energy approximations and flexible basis sets with drastically reduced computational effort. Composite-model results on anions that resemble the chromophore of the green fluorescent protein illustrate the interpretive capabilities of explicitly renormalized self-energies. Accurate predictions on the lowest vertical electron detachment energy of each anion confirm experimental data and the utility of the diagonal self-energy approximation.
1. Introduction
Electron-propagator calculations have been a frequent and persistent accompaniment to reports of anion photoelectron spectra.1–7 The theory that underlies these calculations may be expressed in terms of an eigenvalue equation with an effective one-electron operator.8–11 In addition to the kinetic, nuclear-attraction, Coulomb and exchange components found in the Hartree–Fock equations, the self-energy operator also appears. The latter term describes orbital relaxation and differential correlation effects on electron detachment energies. The form of the exact self-energy operator is known and ab initio approximations to it have been widely applied. When electron-propagator calculations are performed on an anionic reference state, electron detachment energies emerge as eigenvalues of a non-local, energy-dependent operator. In addition, the one-electron eigenfunctions are proportional to Dyson orbitals. The proportionality factor, known as a probability factor or pole strength, may be determined from the energy derivative of the self-energy contribution to the eigenvalue. Spectral intensities in the sudden approximation may be calculated with transition integrals between continuum functions and Dyson orbitals.11 The eigenvalue equation offers a convenient generalization of Koopmans's identity for the lowest electron detachment energies of closed-shell molecules and ions. Electron-propagator methodology conserves a one-electron picture of chemical bonding to the greatest extent possible in an exact, ab initio theory. It also provides diagnostics based on probability factors when that picture becomes invalid and well-defined procedures for describing qualitatively important correlation effects.Whereas older self-energy approximations have aided interpretations of spectra since the 1970s,12–15 a new generation of electron-propagator methods has surpassed their accuracy and computational efficiency. These advantages have entailed no sacrifice of interpretability, for no adjustable parameters have been introduced in the preparation of orbitals or in the self-energy formulae. For a given level of computational effort, determined by the arithmetic scaling of bottleneck operations, a higher level of accuracy has been realized.5,16–19 For example, the three older, outer valence Green's function (OVGF, versions A, B and C) self-energies15,20,21 and a recently developed method have identical fifth-power bottlenecks. (See Table 1 for a complete set of self-energy acronyms; Table 2 lists the scaling of arithmetic bottlenecks for each method.) The latter alternative, the approximately renormalized linear third order (L3+B) self-energy, has produced lower mean absolute errors in several recent tests versus standard data.5,16–19 Even higher levels of accuracy have been achieved with methods that introduce more steps with the same scaling factor. In addition, new-generation self-energies with only cubically scaling computational demands have closely approached the accuracy of the best OVGF options. Several other widely applied methods have now been surpassed in a similar manner. Examples of older diagonal approximations include the diagonal second order (D2) and approximately renormalized partial third order22–24 (P3+) self-energies. Among the older non-diagonal, renormalized examples are the strict20 (3+) and standard25 Dyson versions of the third order algebraic diagrammatic construction26 [ADC(3)]. Comparisons have also been made to a fully ab initio member of the G0W0 family methods27 that employs canonical Hartree–Fock orbitals and Tamm–Dancoff excitations.28 This G0W0@HF-TDA method has a diagonal self-energy that comprises ring terms in all orders and therefore is denoted by DR below. These conclusions are based on numerical tests versus the QTP,16,18 GW100,17 OPV2419 and VEDE555 data bases of electron binding energies.
| Acronyma | Full name |
|---|---|
| a New-generation methods are in bold type. N = non-diagonal; nD = non-Dyson; R = explicitly renormalized; + = approximately renormalized. | |
| Diagonal self-energies | |
| D2 | Diagonal second order |
| os-D2 | Opposite-spin D2 |
| nD-D2 | non-Dyson D2 |
| os-nD-D2 | Opposite-spin non-Dyson D2 |
| D3 | Diagonal third order |
| nD-D3 | non-Dyson D3 |
| OVGF | Outer-Valence Green's Function (Versions A, B and C) |
| nD-OVGF | non-Dyson OVGF (Versions A, B and C) |
| P3 | Partial third order |
| P3+ | Approximately renormalized partial third order |
| Q3 | Quasiparticle third order |
| Q3+ | Approximately renormalized quasiparticle third order |
| L3 | Linear third order |
| nD-L3 | non-Dyson L3 |
| L3+ | Approximately renormalized linear third order (Versions A, B and C) |
| nD-L3+ | non-Dyson L3+ (Versions A, B and C) |
| RP3 | Explicitly renormalized partial third order |
| RQ3 | Explicitly renormalized quasiparticle third order |
| RL3 | Explicitly renormalized linear third order |
| nD-RL3 | non-Dyson RL3 |
| DR | Diagonal (renormalized) ring approximation (HF-TDA-G0W0) |
| Non-diagonal self-energies | |
| ND2 | Non-diagonal, second order |
| 2ph-TDA | Two-particle-one-hole Tamm–Dancoff approximation |
| 3+ | Non-diagonal third order |
| ADC(3) | Third order algebraic diagrammatic construction |
| NR2 | Non-diagonal, renormalized, second order |
| BD-T1 | Brueckner doubles with triple field operators |
| NRP3 | Non-diagonal extension of RP3 |
| NRQ3 | Non-diagonal extension of RQ3 |
| NRL3 | Non-diagonal extension of RL3 |
| Method class | Methodsb | Arithmetic bottleneck | Bottleneck steps | Largest ERIc subset |
|---|---|---|---|---|
| a O = # occupied orbital, V = # virtual orbitals, NE = energy iterations, NI = inverse-expansion or linear-equation iterations for diagonal methods and Hamiltonian-vector multiplications for non-diagonal methods. b New methods in bold type. c ERI = electron repulsion integral. d Reduction by a factor of NE occurs in non-Dyson (nD) versions. e The O2V4 arithmetic bottleneck occurs in the Brueckner doubles, coupled-cluster, reference-state calculation; the subsequent electron-propagator bottleneck is OV4. f N I OV4 iterative steps for 3+, ADC(3) and NRL3; NI O3V2 iterative steps for NR2, NRP3 and NRQ3. | ||||
| Diagonal 2nd order | D2, os-D2 | OV2 | NE | O2V2 |
| RSPT2, nD-D2, os-nD-D2 | OV2 | Non-iterative | O2V2 | |
| Diagonal post 2nd order | RSPT3 | OV4 | Non-iterative | V4 |
| D3, OVGF | OV4 | NEd | V4 | |
| P3, P3+, Q3, Q3+ | O2V3 | Non-iterative | OV3 | |
| L3, L3+ | OV4 | NEd | V4 | |
| RP3, RQ3 | O2V3 | Non-iterative | OV3 | |
| RL3 | OV4 | NINEd | V4 | |
| DR | O2V3 | NINE | O2V2 | |
| Non-diagonal | ND2 | OV3 | NI | OV3 |
| 2ph-TDA | OV4 | NI | V4 | |
| 3+ | O2V4 | Non-iterativef | V4 | |
| ADC(3) | O2V4 | NIf | V4 | |
| NR2 | O3V3 | Non-iterativef | OV3 | |
| BD-T1 | O2V4 | BDe | V4 | |
| NRP3, NRQ3, NRL3 | O2V4 | Non-iterativef | V4 | |
Underlying the efficient fifth-power and third-power scaling factors of these methods is the diagonal self-energy approximation. By neglecting off-diagonal elements of the self-energy operator in the canonical Hartree–Fock orbital basis, sixth-power algorithms may be avoided. (For example, coupled-cluster and configuration interaction methods that include double orbital substitutions are in the sixth-power category.) This advantage has enabled widespread application of electron-propagator methodology to the interpretation of spectra. The price that is paid for this expedient is a constraint on the resulting Dyson orbitals, for they become proportional to canonical Hartree–Fock orbitals.
The latest methodological developments restore non-diagonal elements of the self-energy matrix while retaining all terms that appeared in their diagonal antecedents.18 This restoration allows the Dyson orbitals to be expressed in their most general form, a linear combination of basis functions, e.g., the canonical Hartree–Fock orbitals. The validity of the diagonal approximation may be tested via comparisons of electron binding energies and Dyson orbitals. Numerical data of this kind for anionic reference states is presented in this work for the first time.
These tests are performed on a previously devised set of 55 vertical electron detachment energies (VEDEs) pertaining to 36 closed-shell anions.5 Nuclei from the first three periods (elements X and Z) are represented in the X−, XZ−, XHn− and HXZ− anions of the VEDE55 set. Basis-set extrapolated data on VEDEs computed with a high level of theory constitute the standard of comparison. Calculations performed with each of the self-energy approximations are used to obtain basis-set-extrapolated results. Error measures and arithmetic scaling factors are the criteria that determine the best combinations of accuracy and computational efficiency.
To rapidly approximate results obtained with the best self-energy approximations and the most flexible basis sets, several composite methods has been devised and tested.5,19 These techniques assume the additivity of basis-set and correlation corrections to lower-level calculations.29 In this work, new composite models with explicitly renormalized diagonal or non-diagonal renormalized self-energy components are introduced. The success of these models indicates that calculations of high accuracy are feasible for considerably larger molecules and ions.
The 2008 Nobel Prize in Chemistry recognized the discovery of the green fluorescent protein (GFP), the foundation of myriad optical characterizations of biological structures.30 Electron propagator techniques developed in this work may be applied to the chromophoric center that is responsible for the intense fluorescence of GFP. This fragment of the protein is a closed-shell anion that contains a phenolate moiety covalently bound to an imidazolinone ring. Recent anion photoelectron spectroscopy experiments have measured the VEDEs of the p-hydroxybenzylidene-2,3-dimethylimidazoline anion (p-HBDI−) and two substituted analogues.31–39 The latter anions display two substitutions on the phenolate ring with fluorine (DF-HBDI−) or methoxy (syn-DM-HBDI−) groups. Experiments have also been performed on the three phenolate anions (PhO−, DF-PhO−, syn-DM-PhO−) that are formed when a hydrogen atom resides in the ipso position.40–44 Applications to these anions of the new, composite electron-propagator models demonstrate their interpretive capabilities, confirm precise spectral data, and provide information to stimulate further experimentation.
2. Theory and computational methods
2.1 Electron propagator theory
Many kinds of electron-propagator calculations are executed by software organized around the Dyson quasiparticle equation. (Commercially available software with electron-propagator capabilities has been in use for thirty years.45) This pseudo-eigenvalue equation involves a one-electron operator that is energy-dependent and non-local. With the introduction of an orthonormal orbital basis, it can be cast in terms of matrices (in bold type) as follows:| [F + Σ′(EX)]C(EX) = EXC(EX) | (1) |
| Fpq = hpq(1) + 〈pr||qs〉ρrs, | (2) |
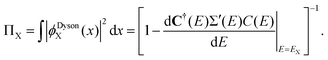 | (3) |
Probability factors vary between zero and unity. Intensities in the sudden approximation52 are proportional to probability factors and squared moduli of transition matrix elements between normalized Dyson orbitals and continuum functions. In the exact electron propagator, the sum of the probability factors equals the number of electrons. A convenient criterion of one-electron (e.g., Koopmans-like) character for an electron binding energy is a probability factor greater than or equal to 0.85. Correlation final states53 (e.g., simple shake-ups) have lower probability factors.
When a basis of canonical Hartree–Fock orbitals is assumed, the uncorrelated and correlated parts of F are represented respectively as FHF and Σ(∞). In this case,
| Fpq = FHFpq + Σpq(∞) = δpqεpq + Σpq(∞), | (4) |
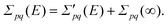 | (5) |
When the absolute value of E increases without bound, the limit of the total self-energy equals its energy-independent part. A diagonal matrix of canonical Hartree–Fock orbital energies (ε) and the self-energy matrix consequently appear in the Dyson quasiparticle equation:
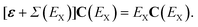 | (6) |
When other orbital basis sets (e.g., Kohn–Sham) are chosen, the Hartree–Fock exchange operator may be incorporated in the self-energy term. In the canonical Hartree–Fock basis, constant self-energy terms vanish in first and second order in the Møller–Plesset fluctuation potential.54 Neglect of the self-energy operator in eqn (6) recovers the Koopmans-identity approximation55 for electron binding energies and Dyson orbitals that equal canonical Hartree–Fock orbitals.
For the smallest electron detachment energies and the largest electron attachment energies of closed-shell species, off-diagonal elements of Σ(E) in eqn (6) are often neglected. The diagonal self-energy approximation reduces arithmetic operations and forces Dyson orbitals to be proportional to canonical Hartree–Fock orbitals. Unit eigenvectors from eqn (6) simplify the probability factor of eqn (3), for the energy derivative of only a single self-energy matrix element is needed.
Several levels of diagonal self-energy approximations have been implemented and examined in numerical tests. All involve perturbative self-energy corrections to Koopmans results that may be classified according to orders of the Møller–Plesset fluctuation potential. The simplest class involves only second-order terms and requires arithmetic operations that scale cubically with the size of the system. Next in computational difficulty are the third-order methods, which have fifth-power arithmetic scaling. A third level comprises approximately renormalized methods that require almost no additional computational effort. This class employs only second-order and third-order terms to estimate certain classes of corrections in all higher orders. At the fourth and highest level are diagonal methods that explicitly evaluate the higher-order terms.
A new generation of diagonal self-energies spans all four levels and includes members that surpass their respective predecessors’ accuracy.5,16–19 Opposite-spin (os) second-order methods achieve higher accuracy by avoiding the tendency of full second-order calculations to exaggerate orbital relaxation and final-state differential correlation. Whereas full third-order and second-order results have similar absolute errors but with opposite signs, the recently introduced third-order methods are clearly more accurate. They provide a better reference for approximately renormalized self-energies that achieve smaller error measures than those of their predecessors. Their explicitly renormalized counterparts compete successfully against an ab initio version of G0W0 (DR), wherein ring self-energy terms are included in all orders. Mean absolute errors decline from 0.2 eV at the second-order level to below 0.1 eV at the explicitly renormalized level. These advances are achieved without the introduction of adjustable parameters in the generation of an orbital basis or in the self-energy formulae.
New-generation third-order methods and their renormalized extensions are founded on a different approach to deriving self-energy approximations. Elements of the generalized Fock and energy-dependent self-energy matrices may be expressed in terms of a super-operator Hamiltonian matrix, Ĥ. Sub-blocks of this matrix appear in general expressions of F and Σ′(E):
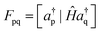 | (7) |
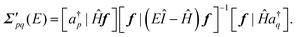 | (8) |
When Ĥ acts on an ionization operator, z, it forms a commutator with the Hamiltonian, i.e., Ĥz = Hz − zH.56 In derivations of previous approximations, the secondary ionization operator manifold, f, and perturbative improvements to reference-state density matrices were introduced. Operators and density matrices that sufficed to produce all self-energy terms up to a desired order were chosen. For example, to generate all third-order terms in F, ρ in second order must be invoked. To recover some of the third-order terms in Σ′(E), first-order corrections to the two-electron reduced density matrices are used to evaluate [f|Ĥa†] and its adjoint. Non-vanishing first-order couplings between f and a† occur only for triple field-operator products (f3) with two creators (a† operators) and one annihilator (a). Products of two occupied (h for hole) creators and one unoccupied (p for particle) annihilator occur in the 2hp sector of f3. The 2ph sector comprises products of two unoccupied creators and one occupied annihilator. Only the Hartree–Fock three-electron reduced density matrix is needed for the inverted matrix in eqn (8). These choices suffice for the 3+ self-energy, which is also known as the strict version of the third-order algebraic diagrammatic construction or ADC(3). By discarding all fourth-order and higher-order terms, the third-order self-energy is recovered. Many higher order terms are also included in the 3+ self-energy; they are discarded in calculations that employ the third-order self-energy.
To obtain new-generation third-order methods, a fixed super-operator metric is introduced where the overlap between the z1 and z2 ionization operators reads
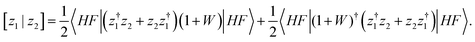 | (9) |
This choice forces the super-operator Hamiltonian matrix to be Hermitian. Its intermediate normalization enables total energy expressions based on contour integrations to be size-extensive.57 The latter property differs from the Hermitization procedure of equation-of-motion theory.58 Whereas the latter strategy can Hermitize spurious terms, the new metric may be used to recover many-body energy expressions. To obtain third-order contributions to Σ(E), the following approximation is made:
| W ≈ T2(1) + T1(2). | (10) |
First-order double substitutions and second-order single substitutions occur linearly in all super-operator matrix elements. No elements that are bi-linear (i.e., quadratic when real) in reference-state substitution amplitudes are present. In accord with eqn (9), matrix elements that are linear in these amplitudes are multiplied by one half. Self-energy terms that are free of reference-state correlation amplitudes (e.g., ring and ladder summations) remain the same.
Omission of self-energy terms of fourth and higher orders results in the linear, third-order (L3) self-energy. The most promising of its approximately renormalized extensions (L3+B) performs separate renormalization estimates for the 2hp and 2ph members of f3. The explicitly renormalized version (RL3) contains all terms present in L3 as well as ring, ladder and mixed ring-ladder terms in all orders.
For electron detachment energies, self-energy terms beyond second order that involve 2ph operators define computational bottlenecks but often have relatively little numerical importance.22,23,59,60 Omission of these terms at the three levels discussed in the previous paragraph defines the quasiparticle third order (Q3) method and its approximately (Q3+) and explicitly (RQ3) renormalized extensions. OV4 bottlenecks characterize L3, L3+B, and RL3 calculations of all electron binding energies. Q3, Q3+ and RQ3 calculations of electron detachment energies have O2V3 bottlenecks and no need for ERIs with four virtual indices. In several numerical tests, only minor increases in mean absolute errors with respect to the L methods have occurred for their three Q counterparts.
The OV4 bottleneck for electron detachment energies can be minimized by ignoring the energy dependence of self-energy terms generated by 2ph operators. By substituting the Koopmans guess for E in these terms, the non-Dyson (nD) versions of L3, L3+B and RL3 may be defined.
Each of the summations (or diagrams) in the diagonal self-energy formulae may be interpreted in terms of electron-pair correlation and orbital relaxation concepts.61,62 For electron detachment energies, second-order and third-order terms generated by 2ph operators in the f3 set are associated with initial-state differential correlation. Pair correlation energies present in the initial state that are absent in the final state are responsible for these self-energy terms. Terms in Σii(E) that descend only from final-state orbital relaxation are easily identified when E = εi, where i is an occupied spin-orbital index. Ring, ladder and certain other summations that include T2 (i.e., double substitution) correlation amplitudes have terms where one or more occupied orbital indices equal i. Whereas these terms correspond solely to orbital relaxation, the remaining ones in these 2hp diagrams originate from final-state differential correlation. Additional electron-pair correlation that arises from the newly vacant i spin-orbital is responsible for the latter terms. Energy-independent, third-order self-energy terms arise from orbital relaxation in final-state electron-pair correlation energies.
Instead of solving for electron binding energies and Dyson orbitals with the Dyson quasiparticle equation, one may diagonalize the super-operator Hamiltonian matrix, Ĥ. Eigenvalues of Ĥ equal electron binding energies. Eigenvector elements corresponding to simple creation operators (a†) equal orbital basis coefficients in the Dyson orbitals. A variety of techniques for the diagonalization of Hermitian matrices of high rank has been employed.63–65 The Dyson quasiparticle equation may be regarded as a partitioned version66 (with a† and f sectors) of the diagonalization of Ĥ.
This approach is advantageous for self-energies that are non-diagonal and renormalized. The former property is realized by including all simple creators in the space of ionization operators. Renormalization is achieved by including off-diagonal matrix elements of (f|(EÎ − Ĥ)f). Expansion of the inverse of the latter matrix about its diagonal, zeroth order component generates terms in all orders of the fluctuation potential. (See eqn (8).)
Non-diagonal, renormalized (NR) generalizations of the L3, RL3, Q3 and RQ3 self-energies have been introduced recently.18 In numerical tests on ionization energies of closed-shell molecules, they have produced lower errors than their diagonal predecessors. These methods also require non-iterative, sixth-power matrix multiplications for the evaluation of second-order terms in the (f|Ĥa†) matrices and their adjoints. In the NRL3 method, the super-operator metric of eqn (9) is assumed. The (a†|Ĥa†), (f|Ĥa†) and (f|Ĥf) matrices are evaluated respectively in third, second and first orders in the fluctuation potential. All terms present in the L3 and RL3 self-energies are also present in the NRL3 self-energy. Neglect of second-order (f2ph|Ĥa†) and first-order (f2ph|(EÎ − Ĥ)f2ph) terms yields the NRQ3 version of Ĥ for electron detachment energies. The orders of the NRL3 blocks of Ĥ are the same as in the 3+ method20 [i.e., the strict version of ADC(3)],15,26 but there are no terms that are bi-linear in the reference-state correlation amplitudes of eqn (10). No constant self-energy terms that depend on T2 amplitudes are included. [Constant terms that are quadratic in these amplitudes appear in 3+ and ADC(3).] In the NR versions of Ĥ, terms that are linear in reference-state correlation amplitudes are multiplied by one half. Programs that currently execute any version of ADC(3) therefore may be easily modified to perform NRL3, NRQ3 or NRP3 calculations.
2.2 Comparison to equation-of-motion, coupled-cluster theory
Electron-propagator and equation-of-motion, coupled-cluster67 (EOM-CC) methods have several common features that are characteristic of many-body theories.68 Both approaches to the calculation of spectra generate algebraically connected formulae that preserve correct separation limits. In many-body theories, separation of a molecule into two remote fragments (αβ → α + β) produces transitions that equal those of the individual fragments.Whereas EOM-CC theory leads to separate equations for energies of electron detachment and attachment, f operators of both types interact in the Dyson quasiparticle equation. For example, the second-order self-energy has energy-dependent 2hp and 2ph terms that correspond respectively to final-state and initial-state correlation effects for electron detachment energies. The roles of the two terms are reversed for electron attachments. A single energy-dependent, non-local potential encompasses both cases. An intermediate approach occurs in nD versions of self-energies, wherein energy-dependence is eliminated for initial-state terms, as in EOM-CC theory.
In Dyson and nD versions of electron-propagator theory, the superoperator Hamiltonian matrix is Hermitian. Eigenvalues of these matrices (i.e., electron binding energies) therefore are real. Left and right eigenvectors are adjoints of each other. Dyson orbitals therefore are unambiguously defined. The effective Hamiltonian matrix of EOM-CC theory is non-Hermitian. Its eigenvalues are not necessarily real, but this formal deficiency is seldom encountered in calculations on closed-shell molecules. Left and right eigenvectors that include the amplitudes of the Dyson orbitals are not adjoints of each other. Well-defined transition probabilities must involve both eigenvectors.
EOM-CC calculations of transition energies are typically preceded by determination of the reference state's coupled-cluster wavefunction. In EOM-CCSD calculations,69 this preliminary result requires iterations with an O2V4 arithmetic scaling factor. This sixth-power stage is followed by fifth-power iterations that pertain to electron binding energies. An approximation to the EOM-CCSD method avoids the reference-state optimization by substitution of first-order cluster amplitudes to realize fifth-power scaling.70 Optimizations of reference-state wavefunctions respectively acquire eighth-power and tenth-power scaling factors when triple and quadruple substitutions are included. In tests versus EOM-CCSDT/cc-pVTZ vertical ionization energy standards, EOM-CCSD produced larger error measures than NR2, BD-T1 and several, less costly, new-generation electron-propagator methods.16,18
2.3 Computational methods
Geometries of all 36 closed-shell molecular anions in the test set corresponding to 55 VEDEs were taken from previous studies.5,71 The test set consists of molecular anions whose nuclei are drawn from the first three periods. Simple hydrides (XHn−), atoms (X−), di-atomics (XZ−), and tri-atomic hydrides (HXZ−) are included in an unbiased manner. ERIs are transformed to the canonical Hartree–Fock basis and stored on disk. Table 2 presents the most extensive subsets of ERIs needed for each self-energy approximation. Core orbitals are excluded from self-energy summations. All computations were executed with the development version of Gaussian wherein all electron propagator methods have been implemented.72 Electron propagator calculations have been performed on all the test anions using the aug-cc-pVDZ, aug-cc-pVTZ, and aug-cc-pVQZ basis sets. The standard test set of VEDEs was inferred from ΔCCSD(T) (i.e., total energy differences based on coupled-cluster theory with single and double replacements and approximate triple replacements73) inverse quartically extrapolated [i.e., (l + ½)−4] total energies obtained with augmented quadruple and triple ζ basis sets.74 Contour plots of Dyson orbitals have been generated with GaussView.75Table 4 and Fig. 4 and 5 display statistics obtained from composite electron propagator methods. Eight composite methods denoted by CMX (where X = 1–8) have been developed for VEDEs:
| ECM1 = EnD-L3+Baug-cc-pVDZ + Eos-nD-D2CBS(DT) − Eos-nD-D2aug-cc-pVDZ | (11) |
| ECM2 = EQ3+aug-cc-pVDZ + Eos-nD-D2CBS(DT) − Eos-nD-D2aug-cc-pVDZ | (12) |
| ECM3 = EnD-L3+Baug-cc-pVTZ + Eos-nD-D2CBS(TQ) − Eos-nD-D2aug-cc-pVTZ | (13) |
| ECM4 = EQ3aug-cc-pVTZ + Eos-nD-D2CBS(TQ) − Eos-nD-D2aug-cc-pVTZ | (14) |
| ECM5 = EnD-RL3aug-cc-pVDZ + Eos-nD-D2CBS(DT) − Eos-nD-D2aug-cc-pVDZ | (15) |
| ECM6 = EnD-RL3aug-cc-pVTZ + Eos-nD-D2CBS(TQ) − Eos-nD-D2aug-cc-pVTZ | (16) |
| ECM7 = EQ3+aug-cc-pVTZ + EnD-L3+Baug-cc-pVDZ − EQ3+aug-cc-pVDZ + Eos-nD-D2CBS(TQ) − Eos-nD-D2aug-cc-pVTZ | (17) |
| ECM8 = ENRL3aug-cc-pVDZ + Eos-nD-D2CBS(DT) − Eos-nD-D2aug-cc-pVDZ | (18) |
Complete basis set (CBS) results in the composite methods are based on a two-point (double–triple or triple–quadruple) inverse quartic extrapolation, i.e., (l + ½)−4, scheme. Data in the ESI† confirm that quartically extrapolated data are very close to their cubically (i.e., l−3) extrapolated counterparts.5
Geometries of the three small GFP anions (phenolate and substituted analogues)40 were optimized with MP2 in conjunction with the aug-cc-pVTZ basis set. The geometries of the large GFP anions (p-hydroxybenzylidene-2,3-dimethyl-4-imidazolinone and substituted analogues)31,32 were optimized with the B3LYP/6-311++G(2d,p) model.76
3. Results and discussion
3.1 Tests on vertical electron detachment energies of small anions
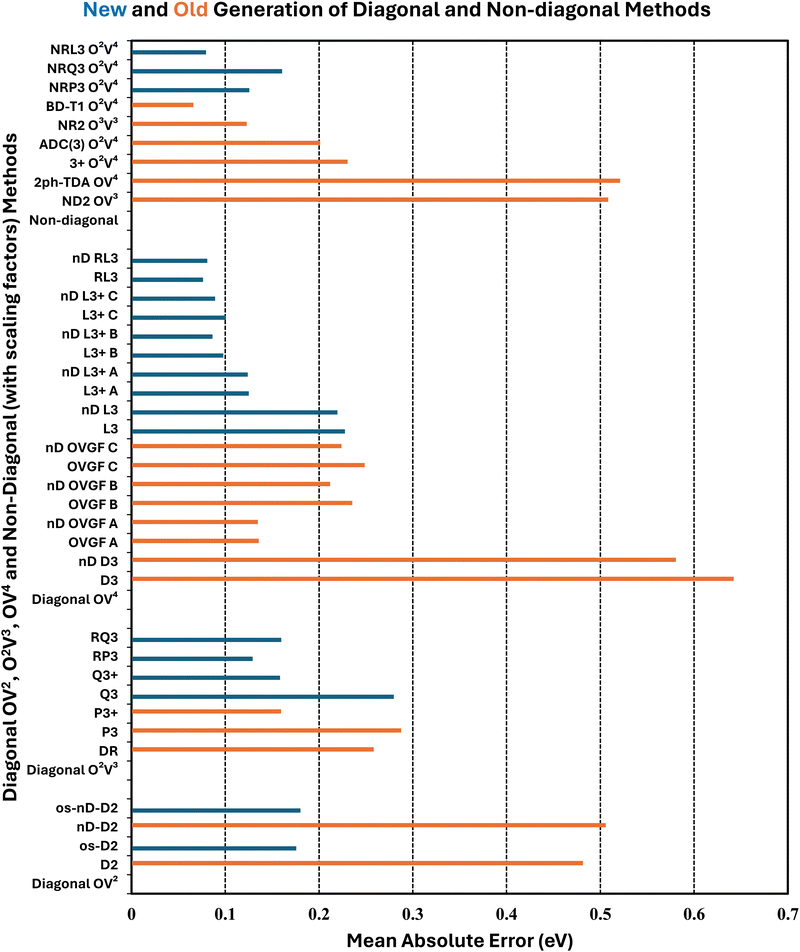
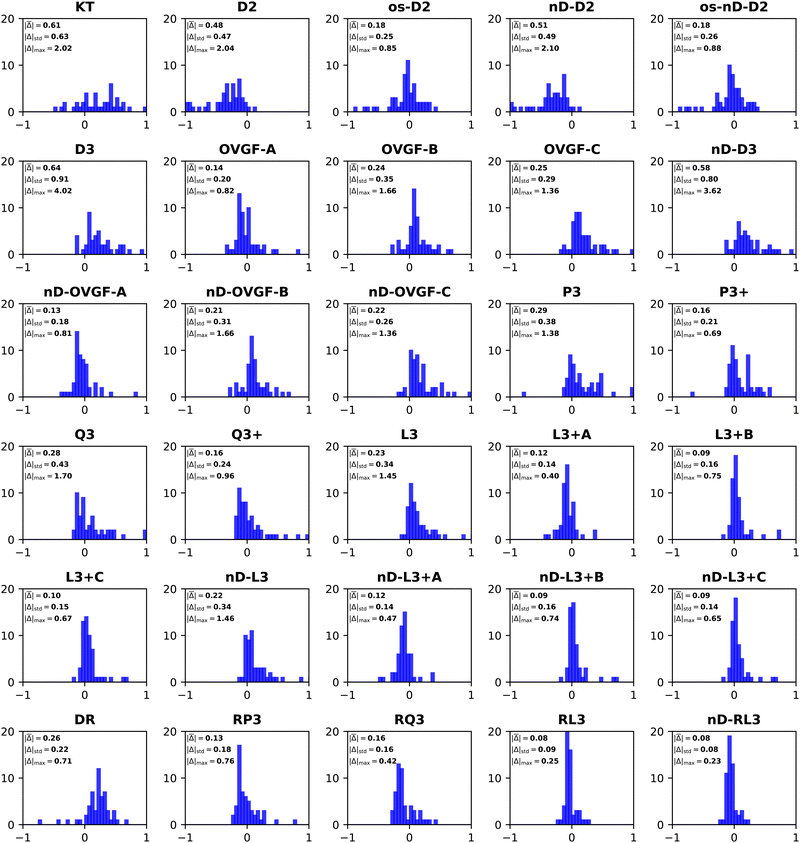
Error statistics that compare self-energy approximations to ΔCCSD(T) standards obtained with the same basis set have been compiled for three cases: aug-cc-pVDZ, aug-cc-pVTZ and aug-cc-pVQZ. These data do not differ significantly from comparisons that are based on inverse quartically extrapolated results. Table 3 and Fig. 1–3 display this information. In a previous work on the same set of 55 VEDEs, inverse cubic extrapolations were employed and data for the NR methods were absent.5| Method class | Methoda | Mean unsigned errorb | Mean signed error | Standard deviation | Maximum unsigned error |
|---|---|---|---|---|---|
| a New methods in bold type. b Optimal methods in bold type. | |||||
| Uncorrelated | KT | 0.613 | 0.537 | 0.628 | 2.017 |
| Diagonal 2nd order | D2 | 0.482 | −0.477 | 0.466 | 2.043 |
| os-D2 | 0.176 | −0.059 | 0.251 | 0.853 | |
| nD-D2 | 0.506 | −0.501 | 0.487 | 2.104 | |
| os-nD-D2 | 0.180 | −0.070 | 0.256 | 0.882 | |
| Diagonal post 2nd order | DR | 0.258 | 0.199 | 0.221 | 0.711 |
| D3 | 0.642 | 0.624 | 0.910 | 4.018 | |
| nD-D3 | 0.581 | 0.564 | 0.808 | 3.622 | |
| OVGF-A | 0.136 | −0.009 | 0.196 | 0.822 | |
| OVGF-B | 0.235 | 0.189 | 0.347 | 1.654 | |
| OVGF-C | 0.249 | 0.230 | 0.291 | 1.363 | |
| nD-OVGF-A | 0.135 | −0.029 | 0.192 | 0.810 | |
| nD-OVGF-B | 0.212 | 0.158 | 0.311 | 1.655 | |
| nD-OVGF-C | 0.224 | 0.207 | 0.270 | 1.358 | |
| P3 | 0.288 | 0.235 | 0.387 | 1.577 | |
| P3+ | 0.159 | 0.094 | 0.212 | 0.781 | |
| Q3 | 0.280 | 0.200 | 0.431 | 1.696 | |
| Q3+ | 0.158 | 0.051 | 0.242 | 0.965 | |
| L3 | 0.228 | 0.213 | 0.347 | 1.450 | |
| nD-L3 | 0.220 | 0.206 | 0.340 | 1.457 | |
| L3+A | 0.125 | −0.070 | 0.149 | 0.464 | |
| L3+B | 0.098 | 0.071 | 0.169 | 0.748 | |
| L3+C | 0.101 | 0.076 | 0.158 | 0.669 | |
| nD-L3+A | 0.124 | −0.085 | 0.135 | 0.466 | |
| nD-L3+B | 0.086 | 0.060 | 0.158 | 0.735 | |
| nD-L3+C | 0.089 | 0.065 | 0.144 | 0.653 | |
| RP3 | 0.129 | −0.006 | 0.176 | 0.764 | |
| RQ3 | 0.160 | −0.082 | 0.159 | 0.417 | |
| RL3 | 0.076 | −0.031 | 0.087 | 0.253 | |
| nD-RL3 | 0.081 | −0.045 | 0.083 | 0.227 | |
| Non-diagonal | ND2 | 0.508 | −0.423 | 0.418 | 2.077 |
| 2ph-TDA | 0.521 | −0.521 | 0.244 | 1.128 | |
| 3+ | 0.230 | 0.207 | 0.323 | 1.407 | |
| ADC(3) | 0.201 | 0.153 | 0.239 | 0.823 | |
| NR2 | 0.123 | −0.056 | 0.136 | 0.514 | |
| BD-T1 | 0.066 | 0.043 | 0.089 | 0.345 | |
| NRP3 | 0.126 | −0.055 | 0.142 | 0.519 | |
| NRQ3 | 0.161 | −0.104 | 0.146 | 0.382 | |
| NRL3 | 0.079 | −0.046 | 0.090 | 0.305 | |
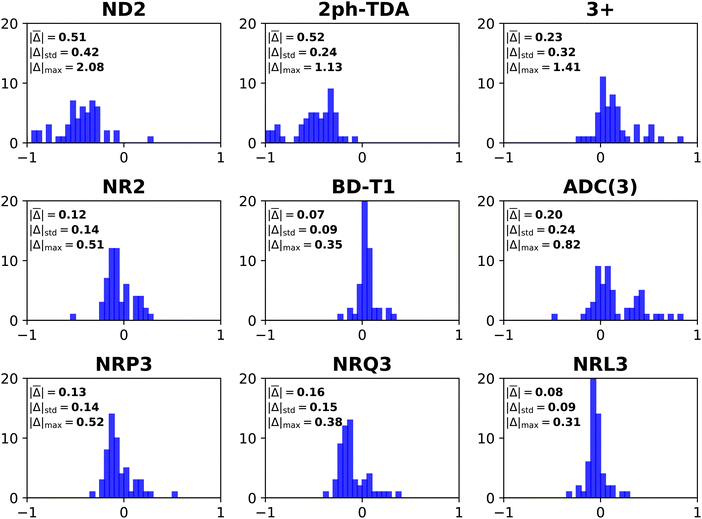 | ||
| Fig. 3 Histograms of error distributions (eV) versus ΔCCSD(T)/CBS standards: non-diagonal EP methods. | ||
Whereas MAEs in Table 3 for D2 and nD-D2 are near 0.5 eV, much lower values emerge from os-D2 and os-nD-D2 calculations. The two latter cubically scaling methods produce MAEs below 0.2 eV and are practically free after the ERI transformation. They contain no adjustable parameters and may be analyzed in terms of simple electron-pair correlations and orbital relaxation concepts. Fig. 2 reveals that the two os methods’ errors are more evenly distributed between underestimates and overestimates of VEDEs. Both methods produce absolute errors above 0.3 eV for the same eight anions. (This set comprises VEDEs of AlO−, CP−, F−, HBN−, HCC−, NH2−, OH−, and SiN−). In most of these cases, the Dyson orbital is localized near an electronegative center, i.e. N, O or F.
Some additional computational effort is necessary for the three Q approximations. Without any estimates of terms beyond third-order, Q3 attains a MAE below 0.3 eV. Its approximately renormalized extension, Q3+, achieves a MAE that is slightly smaller than those of the two os, second-order diagonal methods. Q3 and Q3+ have non-iterative O2V3 arithmetic scaling and therefore the O(Nbasis)4 computational bottleneck still occurs in the partial transformation of ERIs. With an iterative O2V3 bottleneck, the renormalized DR method produces a larger MAE of 0.26 eV. The latter alternative has the advantage (versus Q3, Q3+ and RQ3) of not needing ERIs with three virtual indices. DR's histogram displays a greater tendency to overestimate than to underestimate VEDEs. RQ3 is a more accurate alternative with the same iterative bottleneck. Its MAE of 0.16 eV is almost identical to that of Q3+, but its standard deviation and maximum unsigned error are significantly lower. Among the methods with bottlenecks below that of MP2's partial integral transformation, RQ3 is least likely to produce absolute errors over 0.3 eV. Whereas Q3+ fails according to the latter criterion for six VEDEs, RQ3 fails for only those of two anions, AlO− and F−.
The next level of arithmetic scaling, OV4, pertains to D3 and its approximately renormalized OVGF extensions. D3's MAE is worse than that of D2. Whereas D2 underestimates VEDEs, D3 overestimates them. OVGF-A and its nD variant reduce the MAE to 0.14 eV. The other two OVGF alternatives and their nD variants are less successful. With the same computational effort, L3 produces a MAE that is about a third as large as the MAE of D3. The approximately renormalized L3+B extension and its nD variant generate MAEs of 0.10 and 0.09 eV respectively. Whereas L3+B produces absolute errors above 0.3 eV in four cases, its explicitly renormalized counterpart, RL3, produces none−. RL3 and its nD variant have MAEs of 0.08 eV and markedly lower standard deviations and maximum errors the L3+B. The histograms of the diagonal self-energies with OV4 bottlenecks clearly indicate the superior reliability of RL3 and nD-RL3.
Comparisons between diagonal methods with OV4 arithmetic scaling and non-diagonal methods pertain to the two top sectors of Fig. 1. ND2 and 2ph-TDA are decidedly disadvantageous. The strict (3+) and standard (Schirmer-Angonoa25) Dyson versions of ADC(3) produce MAEs near 0.2 eV. The latter method has iterative O2V4 scaling that occurs in its evaluation of ρ. Only the NR2 and BD-T1 methods with non-iterative O3V3 and iterative O2V4 scaling, respectively, remain competitive with the best diagonal alternatives.
RQ3 and its non-diagonal extension NRQ3 produce almost identical error measures. Their maximum errors are only ∼0.4 eV; both produce absolute errors above 0.3 eV in only two cases. The histograms of RQ3 and NRQ3 also closely resemble each other. NRQ3 requires a non-iterative O2V4 step not found in RQ3, but, like all non-diagonal methods, it yields a more general expression of the Dyson orbitals.
RL3 and NRL3 behave in a similar manner, but they attain higher accuracy than RQ3 and NRQ3. MAEs do not rise from NRL3 to RL3, i.e., when the diagonal approximation is made. NRL3 produces only one absolute error above 0.3 eV. (NRL3's error for HPCl− is only 0.305 eV.) With MAEs near 0.08 eV, RL3 and NRL3 approach the limits of the accuracy of the ΔCCSD(T) standard.
A closer inspection of the results confirms that errors greater than or equal to 0.3 eV become less numerous with increased arithmetic effort. The cases of F− and OH− are notorious in the history of electron propagator calculations on anions. Absolute errors of D2 and OVGF range from 0.8 to 2.0 eV for F− and from 0.4 to 1.7 eV for OH−. Improvements of approximately 0.1 eV occur between Q3+, RQ3 and NRQ3 and L3+B, RL3 and NRL3, respectively. Third-order and higher-order terms that describe initial-state differential correlation are therefore significant; exaggerations at the second-order level are thereby redressed. From L3+B to RL3 or NRL3, absolute errors for F− and OH− decline respectively from 0.7 to 0.2 and from 0.5 to 0.1 eV. These results imply that the crucial improvement over L3+B is replacing approximate with explicit renormalization and that the diagonal approximation introduces only minor errors. Explicit renormalization, as realized in RL3 and NRL3 calculations, is indicated for VEDEs whose Dyson orbitals are localized near N, O or F nuclei.
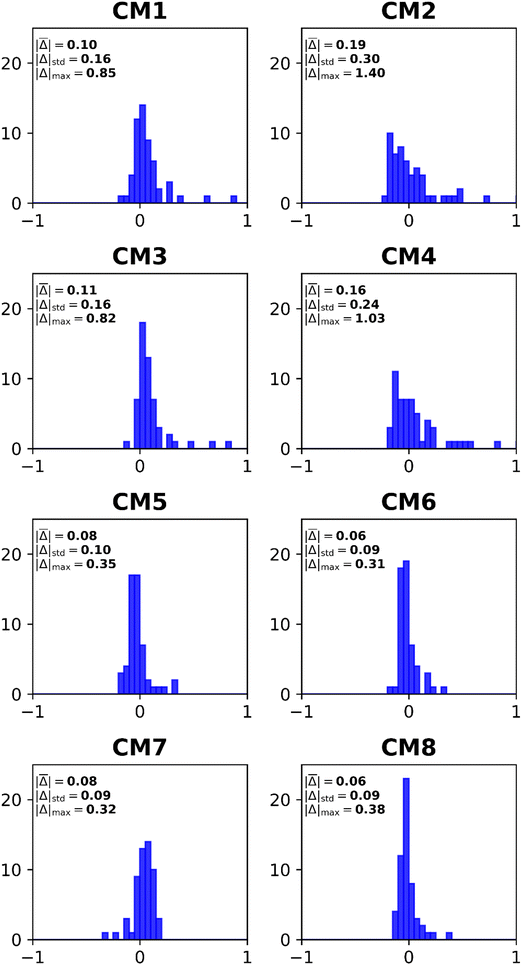
3.2 Composite models
Basis-set effects on electron-propagator poles are often approximately constant with respect to changes in self-energy approximations.29 Composite models (CM) assume the validity of this assumption while attempting to achieve high accuracy with reduced computational effort. Eqn (11)–(18) define the components of eight composite models. Table 4 and Fig. 4 display error measures. Histograms are shown in Fig. 5. All composite models employ os-nD-D2 calculations to estimate complete-basis-set extrapolations based on double–triple or triple–quadruple ζ data. In CM1-CM6 and in CM8, the higher-order method may be Q3+, nD-L3+B, or nD-RL3; two basis sets are used in each model. CM7 employs nD-L3+B, Q3+ and os-nD-D2 data and involves three basis sets. CM1 and CM2 differ in their use of L3+B and Q3+, respectively. Both models employ double and triple ζ basis sets. The MAE of the slower CM1 model is about 0.1 eV, whereas CM2's MAE is closer to 0.2 eV. Upgrading basis sets to triple and quadruple ζ (see CM3 and CM4 results.) has little effect on the MAEs. When the better self-energy is nD-RL3, an explicitly renormalized diagonal method, MAEs decline below 0.1 eV with double-triple ζ and with triple-quadruple ζ data. (See CM5 and CM6 results.) The previously introduced CM7 model makes small improvements over CM1 and CM3. In CM8, the non-diagonal renormalized NRL3 is introduced at the double ζ level. This model yields the lowest MAE.| Composite model (CM) | Mean unsigned error | Mean signed error | Standard deviation | Maximum unsigned error |
|---|---|---|---|---|
| CM1 | 0.101 | 0.072 | 0.163 | 0.851 |
| CM2 | 0.185 | 0.054 | 0.301 | 1.400 |
| CM3 | 0.107 | 0.098 | 0.159 | 0.820 |
| CM4 | 0.162 | 0.065 | 0.244 | 1.030 |
| CM5 | 0.079 | −0.024 | 0.101 | 0.346 |
| CM6 | 0.065 | −0.010 | 0.085 | 0.309 |
| CM7 | 0.080 | 0.034 | 0.094 | 0.321 |
| CM8 | 0.059 | −0.005 | 0.086 | 0.377 |
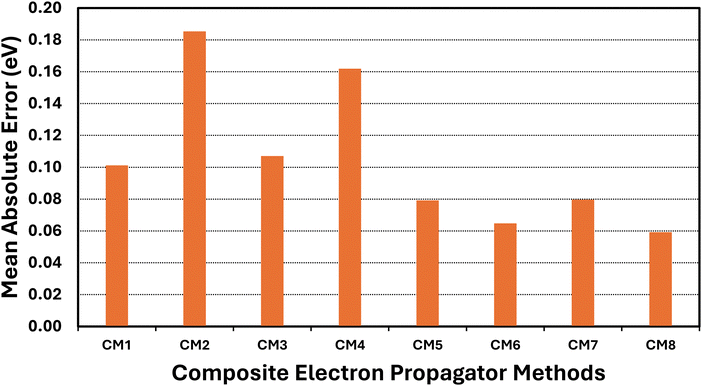 | ||
| Fig. 4 Mean absolute errors (eV) of composite EP methods versus ΔCCSD(T)/CBS standards and arithmetic scaling factors. | ||
A comparison of the CM1–CM4 histograms leads to two conclusions. First, errors grow when Q3+ replaces L3+B as the more advanced self-energy. Second, only minor improvements occur when the triple–quadruple ζ combination replaces the double–triple ζ combination. The CM5 and CM6 histograms demonstrate that large errors are almost eliminated when the nD-RL3 self-energy is used instead of Q3+ or L3+B. Both models produce an absolute error above 0.3 eV only for AlO−. Basis-set improvements (compare CM5 and CM6) make only small changes to the profile of errors. The extra calculations required by CM7 produce improvements over CM1 and CM3. Only one large error occurs: the VEDE of SiN−. The sharpest profile pertains to CM8, which fails only for the difficult AlO− case.
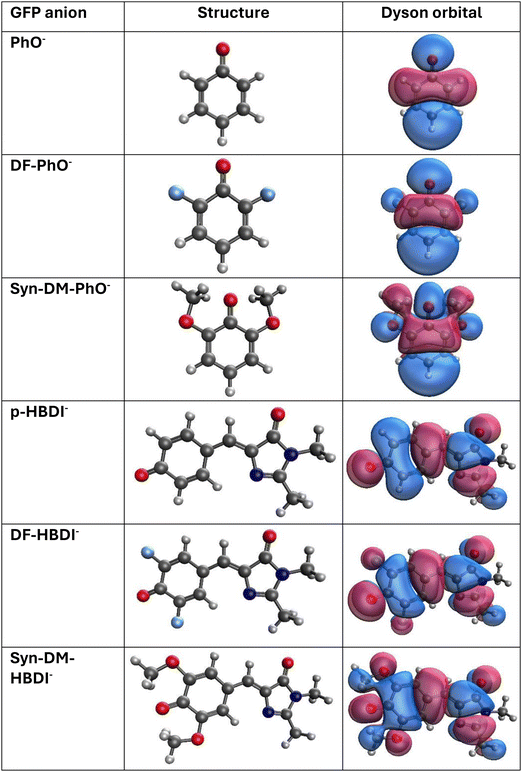
3.3 GFP model anions
The lowest VEDEs of six GFP model anions are displayed in Table 5. Composite models with explicitly renormalized diagonal (CM5) or non-diagonal renormalized (CM8) self-energy components are in excellent agreement with experiment in all cases. For PhO− and p-HBDI−, the CM8 predictions lie within the experimental error bars. Similar success obtains for CM5 in the PhO− case. Discrepancies between the two models are somewhat larger (∼0.05 eV) for the three phenolate anions than for the three anions which closely resemble GFP's chromophore. Both models account for basis-set effects beyond the aug-cc-pVTZ level. Agreement between CM5 and CM6 results obtained for the VEDE55 data set strongly suggests that further basis-set improvements are unlikely to produce significant changes.| Anion | Final state | Experiment | CM5 | CM8 | Previous calculations |
|---|---|---|---|---|---|
| a Anion photoelectron spectroscopy and EOM-CCSD/aug-cc-pVDZ calculations.40 b Anion photoelectron spectroscopy.31 c EOM-CCSD with aug-cc-pVDZ for p-HBDI− and DF-HBDI− and with 6-311++G(d,p) for syn-DM-HBDI−.31 d OVGF/6-311++G(3df,3pd).32 e XMCQDPT2/aug-cc-pVTZ.32 f EOM-CCSD/aug-cc-pVDZ.78 g EOM-CCSD/aug-cc-pVTZ.78 h ΔCCSD(T)/aug-cc-pVTZ.78 i ΔωB97X-D/aug-cc-pVDZ.78 | |||||
| PhO− | 2B1 | 2.26 ± 0.03a | 2.28 | 2.23 | 2.06a 2.08f 2.25g 2.27h |
| DF-PhO− | 2B1 | 2.61 ± 0.03a | 2.71 | 2.66 | 2.50a |
| Syn-DM-PhO− | 2B1 | ∼2.35a | 2.42 | 2.37 | 2.20a |
| p-HBDI− | 2A′′ | 2.74 ± 0.04b | 2.80 | 2.78 | 2.66c 2.78d 2.74e 2.65i |
| DF-HBDI− | 2A′′ | 2.98 ± 0.04b | 3.05 | 3.04 | 2.93c 3.02d 2.99e |
| Syn-DM-HBDI− | 2A′′ | 2.7 ± 0.04b | 2.82 | 2.81 | 2.61c 2.77d 2.69e |
Previous calculations (see Table 5) indicate that results obtained with the aug-cc-pVDZ basis are approximately 0.2 eV lower than those obtained with the aug-cc-pVTZ basis. Augmented basis sets of quadruple ζ and higher quality are likely to increase extrapolated VEDEs by at least 0.1 eV. (Data at the os-D2/aug-cc-pVQZ level confirm this estimate.) None of the previous calculations includes an estimate of the effects of larger basis sets. Iterative procedures with O2V4 arithmetic scaling accompany EOM-CCSD69 and ΔCCSD(T) calculations; the latter method also has a non-iterative, seventh power step. The bottlenecks steps of the renormalized terms in CM5 and CM8 have lower arithmetic scaling and need be performed only at the aug-cc-pVDZ level.
Delocalized π Dyson orbitals with b1 or a” irreducible representation labels correspond to the lowest VEDEs of the six anions. (See Fig. 6 for NRL3/aug-cc-pVDZ Dyson orbitals.) Antibonding phase relationships between oxygen and nearby carbon ring functions are present in each case. Basis functions centered on the fluoride and methoxy oxygen nuclei have appreciable amplitudes in the substituted anions. These contributions to Dyson orbitals indicate that explicitly renormalized self-energies are likely to produce better results than approximately renormalized self-energies. This hypothesis is confirmed by the ∼0.05 eV reduction of VEDEs that is realized by nD-RL3 versus nD-L3+B. A reduction of similar magnitude versus nD-RL3 accompanies the use of NRL3 for the three phenolates, but not for the three larger anions. These corrections are essential for the high accuracy attained by the CM5 and CM8 calculations.
Probability factors provide deeper insight into the strength of relaxation and correlation effects. For the three phenolates, nD-L3+B, nD-RL3 and NRL3 probability factors with the aug-cc-pVDZ basis are 0.92, 0.90 and 0.86, respectively. In the NRL3 calculations, the reference canonical Hartree–Fock orbital has a coefficient of 0.99 in the normalized Dyson orbitals. These data confirm the qualitative validity of the diagonal self-energy approximation. Relaxation and correlation effects are somewhat stronger for the three HBDI− anions, where the same three self-energies produce probability factors of 0.90, 0.87 and 0.83. The latter figure is below the conventional 0.85 threshold for the validity of the diagonal approximation. Despite this marginal result, the reference orbital's coefficient in the Dyson orbital exceeds 0.99. The diagonal self-energy approximation is qualitatively valid, but off-diagonal couplings allow greater flexibility in the description of relaxation and correlation.
4. Conclusions
For VEDEs of closed-shell anions, the os-D2 and os-nD-D2 methods offer an excellent compromise of trivial post-Hartree–Fock computational effort and mean absolute errors below 0.2 eV. These methods are likely to be useful in interpreting and predicting anion photoelectron spectra and other experiments that measure vertical electron detachment energies. For large systems wherein full transformations of electron repulsion integrals are infeasible, they provide a unique opportunity for prediction and detailed analysis. Surveys of large data sets assembled for the optimization of properties also may be undertaken efficiently. Large errors (i.e., above 0.3 eV) are relatively frequent at this level of theory. This disadvantage may become more tolerable when partial transformations with fourth-power scaling are implemented for the highly constrained set of required integrals.The RQ3 method still has a lower arithmetic bottleneck for electron detachment energies than the preceding partial electron repulsion integral transformation. It requires transformed integrals with three virtual indices in only one matrix multiplication step. In comparison with os-D2, os-nD-D2 and Q3+, RQ3 has a diminished tendency to produce large errors.
The best options at the next level of computational effort are the approximately renormalized L3+B and nD-L3+B self-energies. Their mean absolute errors for the present data set are below 0.1 eV. At the cost of more OV4 iterations, the RL3 method and its nD variant attained practically the same mean absolute error with no absolute errors above 0.25 eV.
Diagonal, explicitly renormalized self-energies and their non-diagonal, renormalized generalizations produce vertical electron detachment energies and corresponding mean absolute errors that are in close agreement. This result provides a foundation for employment of the diagonal methods in calculations on closed-shell anions. Dyson orbitals and probability factors also agree very well. Non-diagonal self-energies yield Dyson orbitals with a single dominant contribution from a high-lying canonical Hartree–Fock orbital. The success of RL3 and its approximately renormalized simplification, L3+B, is not founded on a fortuitous cancellation of errors connected to the diagonal approximation.
When Dyson orbitals are localized near N, O or F nuclei, large errors are less likely with explicitly renormalized instead of approximately renormalized methods. Such cases may be anticipated by the presence of lone pairs in Lewis structures of the anions. For this class of anions, the RQ3, RL3 or nD-RL3 methods are preferable to os-D2, os-nD-D2, Q3+ and L3+B.
Results of difficult calculations that require large basis sets and self-energies with high arithmetic scaling factors can be accurately approximated with composite models. These methods assume the additivity of basis-set effects and self-energy improvements and therefore require only a set of less demanding calculations. Explicitly renormalized diagonal and non-diagonal renormalized methods produce lower average measures of error in composite models and reduce the number of large errors.
Composite-model calculations have been applied successfully to a set of six anions that resemble the GFP chromophore. Models with explicitly renormalized self-energies produce fast, accurate predictions of vertical electron detachment energies that include basis-set extrapolations. These predictions are directly comparable to experimental data and lie within 0.1 eV of experimental error bounds for the lowest final state.
This study demonstrates the capabilities of composite models and their new-generation self-energy components for prediction and interpretation of electron-detachment experiments on closed-shell anions. Closely related methods for electron attachment energies of closed-shell molecules have been applied successfully to organic photovoltaic molecules.19 Definitive tests that include diagonal and non-diagonal self-energies and consider closed-shell molecules with positive electron affinities are in progress.
The dominance of a single Slater determinant in the reference state is assumed in most many-body theories, including the electron-propagator methods examined in this work. Despite this assumption, excellent results for the ionization energies of ozone, a molecule with high multiconfigurational character, have been obtained with the BD-T1 approximation.77 Methylene is another small molecule with qualitatively important configuration interaction in its ground, singlet state. Its vertical ionization energy (10.396 ± 0.003 eV, see NIST tables) is accurately predicted by L3+B (10.423) and RL3 (10.398) with the aug-cc-pVQZ basis. The limitations of single-reference electron-propagator methods have yet to be established in numerical tests.
Data availability
Data on calculated vertical electron detachment energies that support the findings of this study are available within the manuscript and the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Manuel Díaz-Tinoco for valuable discussions and the Alabama Supercomputer Center for computing resources.References
- J. Simons and W. D. Smith, J. Chem. Phys., 1973, 58, 4899–4907 CrossRef CAS.
- J. Simons, Annu. Rev. Phys. Chem., 1977, 28, 15–45 CrossRef CAS.
- J. Simons, Theor. Chem., 1978, 3, 1–3 CAS.
- J. Simons, Int. J. Quantum Chem., Quantum Chem. Symp., 1982, 16, 575–581 CAS.
- E. Opoku, F. Pawłowski and J. V. Ortiz, J. Phys. Chem. A, 2023, 127, 1085–1101 CrossRef CAS PubMed.
- M. Díaz-Tinoco, H. H. Corzo and J. V. Ortiz, J. Chem. Theory Comput., 2018, 14, 5881–5895 CrossRef PubMed.
- A. Pérez-González, A. Galano and J. V. Ortiz, J. Phys. Chem. A, 2014, 118, 6125–6131 CrossRef PubMed.
- J. V. Ortiz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 123–142 CAS.
- J. V. Ortiz, in Annual Reports in Computational Chemistry, ed. D. A. Dixon, Elsevier, 2017, vol. 13, pp.139–182 Search PubMed.
- H. H. Corzo and J. V. Ortiz, in Adv. Quantum Chem., ed. J. R. Sabin and E. J. Brändas, Academic Press, 2017, vol. 74, pp. 267–298 Search PubMed.
- J. V. Ortiz, J. Chem. Phys., 2020, 153, 070902 CrossRef CAS PubMed.
- J. Linderberg and Y. Öhrn, Propagators in Quantum Chemistry, Second Edition, Wiley-Interscience, Hoboken NJ, 2004 Search PubMed.
- P. Jørgensen and J. Simons, Second Quantization-Based Methods in Quantum Chemistry, Academic Press, New York, 1981 Search PubMed.
- J. Schirmer, Many-Body Methods for Atoms, Molecules and Clusters, Springer International Publishing AG, 2018 Search PubMed.
- W. von Niessen, J. Schirmer and L. S. Cederbaum, Comput. Phys. Rep., 1984, 1, 57–125 CrossRef CAS.
- E. Opoku, F. Pawłowski and J. V. Ortiz, J. Chem. Phys., 2021, 155, 204107 CrossRef CAS PubMed.
- E. Opoku, F. Pawłowski and J. V. Ortiz, J. Chem. Theory Comput., 2022, 18, 4927–4944 CrossRef CAS PubMed.
- E. Opoku, F. Pawłowski and J. V. Ortiz, J. Chem. Phys., 2023, 159, 124109 CrossRef CAS PubMed.
- E. Opoku, F. Pawłowski and J. V. Ortiz, J. Chem. Theory Comput., 2024, 20, 290–306 CrossRef CAS PubMed.
- J. V. Ortiz, in Computational Chemistry: Reviews of Current Trends, ed. J. Leszczynski, World Scientific, Singapore, 1997, vol. 2, pp.1–61 Search PubMed.
- V. G. Zakrzewski, J. V. Ortiz, J. A. Nichols, D. Heryadi, D. L. Yeager and J. T. Golab, Int. J. Quantum Chem., 1996, 60, 29–36 CrossRef.
- J. V. Ortiz, J. Chem. Phys., 1996, 104, 7599–7605 CrossRef CAS.
- J. V. Ortiz, Int. J. Quantum Chem., 2005, 105, 803–808 CrossRef CAS.
- A. M. Ferreira, G. Seabra, O. Dolgounitcheva, V. G. Zakrzewski and J. V. Ortiz, in Quantum-Mechanical Prediction of Thermochemical Data, ed. J. Cioslowski, Springer, Netherlands, Dordrecht, 2001, pp.131–160 Search PubMed.
- J. Schirmer and G. Angonoa, J. Chem. Phys., 1989, 91, 1754–1761 CrossRef CAS.
- J. Schirmer, L. S. Cederbaum and O. Walter, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 28, 1237–1259 CrossRef CAS.
- L. Reining, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1344 Search PubMed.
- S. J. Bintrim and T. C. Berkelbach, J. Chem. Phys., 2021, 154, 041101 CrossRef CAS PubMed.
- M. Díaz-Tinoco, O. Dolgounitcheva, V. G. Zakrzewski and J. V. Ortiz, J. Chem. Phys., 2016, 144, 224110 CrossRef PubMed.
- R. Y. Tsien, Annu. Rev. Biochem., 1998, 67, 509–544 CrossRef CAS PubMed.
- J. L. Woodhouse, A. Henley, R. Lewin, J. M. Ward, H. C. Hailes, A. V. Bochenkova and H. H. Fielding, Phys. Chem. Chem. Phys., 2021, 23, 19911–19922 RSC.
- A. V. Bochenkova, C. R. S. Mooney, M. A. Parkes, J. L. Woodhouse, L. Zhang, R. Lewin, J. M. Ward, H. C. Hailes, L. H. Andersen and H. H. Fielding, Chem. Sci., 2017, 8, 3154–3163 RSC.
- Y. Toker, D. B. Rahbek, B. Klærke, A. V. Bochenkova and L. H. Andersen, Phys. Rev. Lett., 2012, 109, 128101 CrossRef CAS PubMed.
- D. A. Horke and J. R. R. Verlet, Phys. Chem. Chem. Phys., 2012, 14, 8511–8515 RSC.
- C. R. S. Mooney, M. E. Sanz, A. R. McKay, R. J. Fitzmaurice, A. E. Aliev, S. Caddick and H. H. Fielding, J. Phys. Chem. A, 2012, 116, 7943–7949 CrossRef CAS PubMed.
- S. H. M. Deng, X.-Y. Kong, G. Zhang, Y. Yang, W.-J. Zheng, Z.-R. Sun, D.-Q. Zhang and X.-B. Wang, J. Phys. Chem. Lett., 2014, 5, 2155–2159 CrossRef CAS PubMed.
- C. R. S. Mooney, M. A. Parkes, L. Zhang, H. C. Hailes, A. Simperler, M. J. Bearpark and H. H. Fielding, J. Chem. Phys., 2014, 140, 205103 CrossRef PubMed.
- C. W. West, J. N. Bull, A. S. Hudson, S. L. Cobb and J. R. R. Verlet, J. Phys. Chem. B, 2015, 119, 3982–3987 CrossRef CAS PubMed.
- C. McLaughlin, M. Assmann, M. A. Parkes, J. L. Woodhouse, R. Lewin, H. C. Hailes, G. A. Worth and H. H. Fielding, Chem. Sci., 2017, 8, 1621–1630 RSC.
- J. L. Woodhouse, A. Henley, M. A. Parkes and H. H. Fielding, J. Phys. Chem. A, 2019, 123, 2709–2718 CrossRef CAS PubMed.
- C. S. Anstöter, C. R. Dean and J. R. R. Verlet, Phys. Chem. Chem. Phys., 2017, 19, 29772–29779 RSC.
- R. F. Gunion, M. K. Gilles, M. L. Polak and W. C. Lineberger, Int. J. Mass Spectrom. Ion Processes, 1992, 117, 601–620 CrossRef CAS.
- J. B. Kim, T. I. Yacovitch, C. Hock and D. M. Neumark, Phys. Chem. Chem. Phys., 2011, 13, 17378–17383 RSC.
- H.-T. Liu, C.-G. Ning, D.-L. Huang, P. D. Dau and L.-S. Wang, Angew. Chem., Int. Ed., 2013, 52, 8976–8979 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, P. M. W. Gill, B. G. Johnson, M. A. Robb, J. R. Cheeseman, T. A. Keith, G. A. Petersson, J. A. Montgomery Jr., K. Raghavachari, M. A. Al-Laham, V. G. Zakrzewski, J. V. Ortiz, J. B. Foresman, J. Cioslowski, B. B. Stefanov, A. Nanayakkara, M. Challacombe, C. Y. Peng, P. Y. Ayala, W. Chen, M. W. Wong, J. L. Andres, E. S. Replogle, R. Gomperts, R. L. Martin, D. J. Fox, J. S. Binkley, D. J. Defrees, J. Baker, J. P. Stewart, M. Head-Gordon, C. Gonzalez and J. A. Pople, Gaussian 94, Gaussian, Inc., Pittsburgh PA, 1995 Search PubMed.
- S. Canuto, K. Coutinho, B. J. C. Cabral, V. G. Zakrzewski and J. V. Ortiz, J. Chem. Phys., 2010, 132, 214507 CrossRef PubMed.
- O. Dolgounitcheva, V. G. Zakrzewski, L. Streit and J. V. Ortiz, Mol. Phys., 2014, 112, 332–339 CrossRef CAS.
- K. D. Jordan, V. K. Voora and J. Simons, Theor. Chem. Acc., 2014, 133, 1–15 Search PubMed.
- R. A. Donnelly and J. Simons, J. Chem. Phys., 1980, 73, 2858–2866 CrossRef CAS.
- M. Mishra, P. Froelich and Y. Öhrn, Chem. Phys. Lett., 1981, 81, 339–346 CrossRef CAS.
- M. K. Mishra and A. Venkatnathan, Int. J. Quantum Chem., 2002, 90, 1334–1347 CrossRef CAS.
- T. Åberg, Phys. Rev., 1967, 156, 35–41 CrossRef.
- S. J. Desjardins, A. D. O. Bawagan, Z. F. Liu, K. H. Tan, Y. Wang and E. R. Davidson, J. Chem. Phys., 1995, 102, 6385–6399 CrossRef CAS.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- T. Koopmans, Physica, 1934, 1, 104–113 CrossRef.
- O. Goscinski and B. Lukman, Chem. Phys. Lett., 1970, 7, 573–576 CrossRef CAS.
- J. V. Ortiz, Int. J. Quantum Chem., Quantum Chem. Symp., 1995, 29, 331–337 CrossRef CAS.
- D. J. Rowe, Rev. Mod. Phys., 1968, 40, 153–166 CrossRef.
- A. M. Ferreira, G. Seabra, O. Dolgounitcheva, V. G. Zakrzewski and J. V. Ortiz, Understanding Chem. React., 2001, 22, 131–160 CAS.
- J. V. Ortiz, J. Chem. Phys., 1998, 108, 1008–1014 CrossRef CAS.
- B. T. Pickup and O. Goscinski, Mol. Phys., 1973, 26, 1013–1035 CrossRef CAS.
- G. Born, H. A. Kurtz and Y. Öhrn, J. Chem. Phys., 1978, 68, 74–85 CrossRef CAS.
- J. Baker and B. T. Pickup, Chem. Phys. Lett., 1980, 76, 537–541 CrossRef CAS.
- J. Baker and B. T. Pickup, Mol. Phys., 1983, 49, 651–662 CrossRef CAS.
- H. G. Weikert, H. D. Meyer, L. S. Cederbaum and F. Tarantelli, J. Chem. Phys., 1996, 104, 7122–7138 CrossRef CAS.
- P. O. Löwdin, Phys. Rev., 1965, 139, 357–372 CrossRef.
- R. J. Bartlett, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 126–138 CAS.
- I. Shavitt and R. J. Bartlett, Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory, Cambridge University Press, New York, 2009 Search PubMed.
- J. F. Stanton and J. Gauss, J. Chem. Phys., 1994, 101, 8938–8944 CrossRef CAS.
- M. Nooijen and J. G. Snijders, J. Chem. Phys., 1995, 102, 1681–1688 CrossRef CAS.
- M. Diaz-Tinoco, H. H. Corzo and J. V. Ortiz, J. Chem. Theory Comput., 2018, 14, 5881–5895 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian development version, Revision I.14, Gaussian Inc., Wallingford CT, 2018 Search PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView, Version 6, Semichem Inc., Shawnee Mission, KS, 2016 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- F. Pawłowski and J. V. Ortiz, J. Phys. Chem. A, 2021, 125, 3664–3680 CrossRef PubMed.
- K. B. Bravaya and A. I. Krylov, J. Phys. Chem. A, 2013, 117, 11815–11822 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00441h |
| This journal is © the Owner Societies 2024 |