Controlling achiral and chiral conformations of benzyl alcohol by ortho-halogenation, collisional relaxation and dimerisation

Abstract

Ortho-Halogenated benzyl alcohol can exist in two different low energy chiral conformations, only one of them with an OH–X contact (X = Cl, Br, I). A third, achiral conformation is enabled by the halogen substitution. We show by IR spectroscopy in supersonic jets that the achiral monomer is less stable than the chiral conformation with OH–X contact, but both can be produced in similar amounts using helium as a carrier gas. The robust OH transition observed for the achiral monomer is a sensitive benchmark for the conformational energy sequence, since the chiral conformation without OH–X contact is at least an order of magnitude less abundant, although it is often predicted by DFT to be slightly more stable and separated from the achiral conformation by a low barrier. This competing chiral conformation must be energetically higher by at least a few tenths of a kJ mol⁻¹ to be consistent with experimental observations. That is indeed predicted by high-level energy calculations at the DFT-optimised structures. The most stable dimers of ortho-halogenated benzyl alcohols involve torsionally homo- and heterochiral pairings of the two OH groups, where the hydrogen bond-accepting OH group forms a cooperative intramolecular OH–X contact. The achiral monomer conformation is suppressed in these dimers. A homochiral dimer is formed almost exclusively for Cl, whereas its heterochiral variant is progressively co-stabilised with increasing halogen size. The stretching wavenumber of the donor OH in the dimers depends on the relative chirality of the donor and acceptor conformations. The consistent picture that emerges for Cl, Br and I substitution in ortho-position of benzyl alcohol is discussed in the context of interconversion barriers, heavy atom tunneling, π–π stacking, suppression of OH–π bonding, chirality synchronisation, and shortcomings of DFT approaches in reproducing the observations. The homochiral aggregation preference observed for simple benzyl alcohol is conserved and even enhanced upon ortho-halogenation, albeit partly by different interactions.

---

1 Introduction

Benzyl alcohol is among the dynamically most interesting alcohols.¹ In the monomeric state, it shows degenerate heavy atom tunneling between mirror image conformations.² This differs from most other alcohols, where tunneling between equivalent conformations largely occurs by hydrogen motion.³ Beyond the tightly interconnected manifold of transiently chiral benzyl alcohol conformations, an approximately mirror-symmetric (C_s) isomer has been frequently postulated,^4–7 but never safely detected at low temperature.

The strong influence of ortho-fluorination on the conformational properties of benzyl alcohol has been spectroscopically studied in solution at room temperature.⁷ It was found that the role of mirror-symmetric conformations was not strongly influenced by the fluorine substitution. However, thermal excitation and solvent effects complicate the direct comparison of experiment with spectroscopic gas phase predictions. In the cold gas phase, no isomer beyond the one with an internal hydrogen bond to the fluorine could be detected.⁸ A mirror symmetric isomer was not considered in that work. To fill this gap, and to extend to halogens below F in the periodic table, the present work investigates vacuum-isolated ortho-chloro- to ortho-iodobenzyl alcohol monomers in supersonic jet expansions.

Such expansions also facilitate the formation of dimers. Their cold vibrational spectra can be probed by UV/IR double resonance, which allows for size and conformational selectivity,⁹ and also by direct infrared absorption,^10,11 where dimers are easily distinguished from monomers by concentration variation and spectral position but different conformations are simultaneously observed. In both cases, the conformational abundance ratio is dictated by the relative (Gibbs) energy of the species, but conversion between conformers may freeze at different effective temperatures anywhere between the nozzle temperature and the final rotational temperature, depending on the expansion conditions and the interconversion barrier. The chirality synchronisation¹² in the dimer of benzyl alcohol as a particularly interesting conformational conversion has been investigated thoroughly.¹³ It is a special variant of chirality discrimination in the gas phase¹⁴ which applies to two transiently chiral species. Again, we present the first spectra for jet-cooled dimers of transiently chiral ortho-chloro- to ortho-iodobenzyl alcohol and show that the preferred aggregation involves two (different) chiral conformations of the monomer with the same handedness of the OH group relative to the backbone of the molecule. This synchronisation of transient chirality is evidently rather effective under jet expansion conditions for CH₂OH units attached to an aromatic ring.

The homochirality preference of the benzyl alcohol dimer continues for larger clusters¹⁵ and may also be compared to the crystal structure preferences. For benzyl alcohol, homochiral chains of cooperative OH⋯O hydrogen bonds are found.¹⁶ The same is observed for ortho-chlorobenzyl alcohol¹⁷ and ortho-bromobenzyl alcohol.¹⁸ The ortho-iodobenzyl alcohol crystal structure shows 50% disorder which means that there are probably two different conformers present in the crystal.^18,19 This makes it difficult to determine the homo- or heterochirality and to compare the ortho-iodobenzyl alcohol crystal structure to the crystal structures of other ortho-benzyl alcohols.

2 Methods

2.1 Experimental techniques

For investigating the cold gas phase spectra of 2-chlorobenzyl alcohol (BLD Pharmatech, Kaiserslautern, Germany, 99.95%), 2-bromobenzyl alcohol (BLD Pharmatech, Kaiserslautern, Germany, 99%) and 2-iodobenzyl alcohol (BLD Pharmatech, Kaiserslautern, Germany, 99.75%) an FTIR jet setup was used that is specifically designed for measuring substances with lower vapour pressure. A supersonic coexpansion of helium (Nippon Gases, Düsseldorf, Germany, ≥99.996%) carrier gas (with a small percentage of argon (Linde, Pullach, Germany, ≥99.999%) added in Fig. 12) and a small fraction of the alcohol is created by filling the helium into a 69 L reservoir at a pressure of 1.5 bar. From there the gas is pulsed through a heatable substance chamber where the less volatile alcohols (supported on molecular sieve) are entrained into the carrier gas flow. The resulting gas mixture is expanded through a 60 mm × 0.2 mm heatable slit nozzle into the vacuum chamber. To ensure a low background pressure of the expansion the vacuum chamber is connected to a buffer volume that is continuously pumped (500 m³ h⁻¹). The Bruker IFS 66v/S FTIR spectrometer synchronised to the pulses includes CaF₂ lenses, a KBr beamsplitter and a ceramic glower as light source. The absorption is detected by a L-N₂ cooled Judson InSb detector. A spectral resolution of 2 cm⁻¹ is chosen as a compromise between gas consumption and intrinsic width of the vibrational transitions. The presented spectra are averaged over 140 to 490 interferometer scans, where one scan is equal to one pulse of the gas mixture. More information about this setup can be found in ref. 20 and 21.

2.2 Computational techniques

The potential energy hypersurface was explored with the CREST²² program to locate a large number of conformers which were then pre-optimised using the B97-3c functional.²³ All conformers up to a relative electronic energy of 10 kJ mol⁻¹ were re-optimised with the B3LYP^24–26 functional, using the D3 dispersion correction²⁷ including Becke–Johnson damping,^28–31 three-body terms and the def2-TZVP³² or def2-QZVP³² basis set (for iodine: effective core potential def2-ECP³³). IR wavenumbers and intensities were calculated in the harmonic approximation.

Nudged elastic band climbing image³⁴ (NEB-CI) calculations and subsequent transition state optimisations were done using the same functional and options using def2-TZVP³² and def2-QZVP.³²

DLPNO-CCSD(T)³⁵ single point calculations were performed using the “TightPNO” settings, the aug-cc-pVQZ^36–38 basis set (for iodine: aug-cc-pVQZ-PP^33,39 and effective core potential SK-MCDHF-RSC⁴⁰) at the optimised B3LYP geometries.

Geometry optimisations, single point calculations, NEB, transition state optimisations and relaxed scans were carried out using ORCA version 5.0.3.⁴¹ Computational details can be found in the ESI† (Table S1), including the choice of atomic masses (Table S2, ESI†).

2.3 Nomenclature

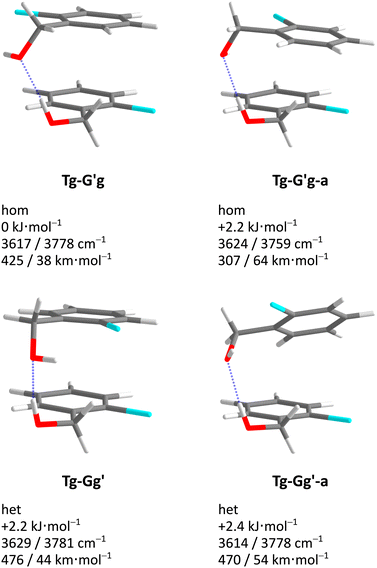
Acronyms used for the investigated molecules are B for benzyl alcohol, Cl for 2-chlorobenzyl alcohol, Br for 2-bromobenzyl alcohol and I for 2-iodobenzyl alcohol. The simplicity and systematics of the vibrational spectra invites a coarse-grained conformational nomenclature, which builds on relative chirality because no permanently chiral compounds are investigated. Whenever two gauche torsional angles in a monomer or dimer are opposite in sign, a prime is added to one of them. The (X)CCCO torsional angle involving the substituted ortho carbon is classified with a capital letter G (gauche) or T (trans), depending on whether its magnitude falls within 0–120° or 120–240°, when the appropriate enantiomer is chosen. The same is done for the CCOH torsional angle with a lower case g or t. Thus, a Gg′ monomer has (X)CCCO and CCOH dihedral angles of opposite sign. Dimers are labelled in donor–acceptor sequence. For chiral monomers and dimers, the enantiomer with the minimal number of primes (in the donor) is discussed. A Tg–G′g 2-chlorobenzyl alcohol dimer (Fig. 1, equivalent to Tg′–Gg′ but avoiding the ′ in the donor) is one where the donor oxygen points away from its ortho C–Cl bond and the donor hydrogen leads out of the plane, coordinating the OH group of the acceptor which is positioned in between the two stacking aromatic rings. This OH group forms a weak intramolecular hydrogen bond to the ortho C–Cl. Because the sign of the two g angles is the same, we denote this dimer hom(ochiral). It has the two Cl atoms pointing in opposite directions, which may contribute to its stability in terms of dipole–dipole interactions. The corresponding het(erochiral) diastereomer Tg–Gg′ involves a mirror image of the acceptor (Fig. 2) and has the two chlorine atoms on the same side. Due to the flatness of the two aromatic rings, several minima with the same monomer conformation may be stabilised and the higher ones are denoted with a terminal a, b etc., if needed.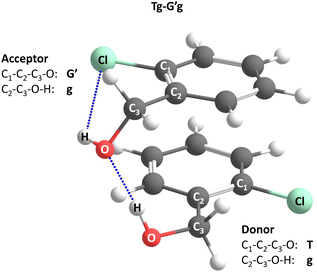

Fig. 1 Illustration of the torsional nomenclature for dimers, using the global minimum structure Tg–G′g. See text for explanations.

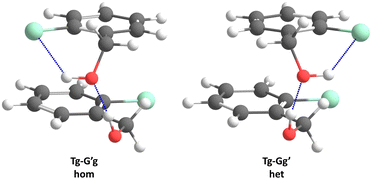Fig. 2 Comparison of the most stable hom(ochiral) with the most stable het(erochiral) Cl dimer structure. The enantiomeric acceptor units lead to a large difference in the Cl–Cl atom distance.

3 Results and discussion

3.1 Computational results

Before introducing the infrared spectra, robust computational trends for the halogenated benzylalcohols and their dimers shall be discussed.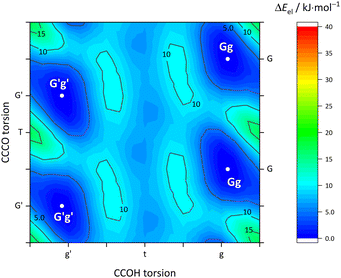

3.1.1 Monomer conformations. It is instructive to start with an approximate 2D torsional contour map of Cl with respect to the CCCO (upper case designator) and CCOH (lower case designator) torsional angles and to compare it to the well-studied B case.¹³ Relaxed torsional scans at B97-3c level are sufficient for our purpose, because the zero point energy variation anyway distorts the quantitative conformational landscape and the effect of chlorination is pronounced. Fig. 3 shows the deep conformational trough connecting all relevant Cl conformations Gg–Gg′–Tg′–Tt–Tg–G′g–G′g′ in a sequential way, where every step involves the change of a single torsional angle and is energetically more or less feasible (deep blue color). In contrast, any conversion through a vanishing CCCO angle is highly unfeasible (yellow and red) due to the repulsion between the O and the Cl atom. The contrast to unsubstituted B (Fig. 4) could hardly be starker. Here, the most feasible conformational conversion involves a concerted torsional switch from Gg to G′g′ (across the plot boundary) which gives rise to heavy atom tunneling motion through a shallow (2 kJ mol⁻¹) transition state.^{1,2,6,11,13,42,43} The entire torsional landscape is much more accessible, as emphasized by the dominantly blue color coding. Ortho-Halogenation removes the symmetry and introduces a penalty for short oxygen–halogen contacts. This turns the direct inversion path for B into a sixfold barrier-crossing event for Cl. The enantiomeric global minima Gg′ and G′g which are stabilised by hydrogen bonding are still separated by four sequential surmountable barriers. This is more than for meta-substituted benzyl alcohols.⁴³ In the center of the Gg′–G′g conversions, a well-defined all-planar (deviations from planarity below 0.1°) minimum Tt emerges. Note that in the case of B, the planar Tt structure is a shallow saddle-point connecting two quasi-planar enantiomeric minima. NCI⁴⁴ analysis (Fig. S3, ESI†) suggests that the planarisation of Tt in Cl has to do with the attraction of the two methylene hydrogens to the halogen atom.

Fig. 3 Contour plot of the two dimensional orca relaxed full cycle scan of the CCCO angle and the CCOH angle of the Cl monomer at B97-3c level with a stepsize of 20°. The shown electronic energy difference is referred to the structure with the lowest calculated energy (Gg′, respectively G′g conformer).

Fig. 4 As Fig. 3 (including the energy scale) but for the B monomer. G and G′ labels are now interchangeable due to symmetry.

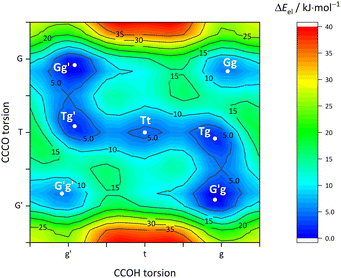
Fig. 5 describes the relevant conformational minima from the 2D contour plots after optimisation at higher level together with their relative zero-point corrected energy and harmonic OH stretching wavenumber. G′g profits from the internal hydrogen bond, whereas Tg and Tt are essentially isoenergetical, also considering that without zero-point energy correction they still differ by 0.6 kJ mol⁻¹. Because their predicted OH stretching wavenumber is quite different, experimental spectra should be able to clearly distinguish and thus energetically rank the two competing conformations. This is particularly easy because the barrier connecting the two is only about 1.5 kJ mol⁻¹ including ZPVE.

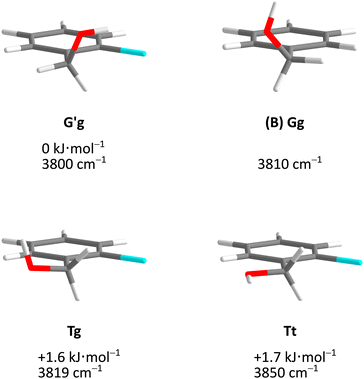Fig. 5 Optimised Cl monomer structures (Tables S3–S5, ESI†) with harmonically zero-point-corrected relative energies and unscaled harmonic OH stretching wavenumbers at B3LYP-D3(BJ)/def2-QZVP level. The Br and I monomers show analogous structures but different relative energies (Fig. 7). The Gg conformation of B monomer is shown for comparison.

The maximum barrier to be overcome from G′g to Gg′ via Tg, Tt and Tg′ is significantly higher, as illustrated in Fig. 6. This is due to the sizeable heavy atom torsion barrier, which is not lowered much by zero point energy correction. Very relevant for benchmarking purposes, the Tt conformer profits much from replacing the DFT electronic energy by a coupled cluster wavefunction value. Now, Tg is no more competitive with Tt, which should be verifiable due to their markedly different IR signature and low interconversion threshold. In any case, the complexity of the chirality inversion path in Cl compared to the concerted heavy atom tunneling racemisation path for B is remarkable, but the barriers stay small enough to allow for some conformational dynamics in Cl during the supersonic expansion.

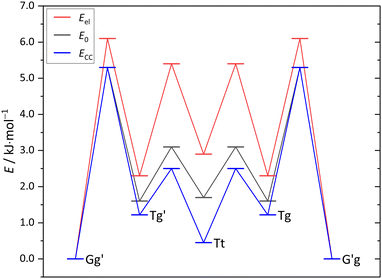Fig. 6 Cl monomer energies for minima and transition states (Tables S6, S7 and Fig. S2 in the ESI†) at B3LYP-D3(BJ)/def2-QZVP level without ZVPE (E_el), with ZVPE (E₀) and with the electronic energy being replaced by the DLPNO-CCSD(T)/aug-cc-pVQZ//B3LYP-D3(BJ)/def2-QZVP value (E_CC).

The pronounced difference between B and its halogenated variants is also reflected in the energy difference between the metastable T conformations and the global minimum structure (Fig. 7, including zero-point energy correction). While quasiplanar Tt is high up in energy and Tg does not correspond to a stable structure for B, consistent with their non-observation, chlorination brings Tt and Tg down to less than 2 kJ mol⁻¹ energy penalty already at DFT level, and thus into reach for our supersonic jet spectra. Correction of the electronic energy at CCSD(T) level further lowers the energy in particular for Tt, such that it should be well populated in the jet expansion. For heavier halogen atoms, the T stabilisation trend gradually reverses, but Tt remains energetically in reach even for I. These predictions, which do not depend critically on zero point energy correction (Fig. S1, ESI†), encourage the spectroscopic study of the monomers. As suggested by the simulated spectra in Fig. 8, the conformations should be easily distinguishable. Furthermore, only the global minimum conformation is predicted to be sensitive to the halogen type.

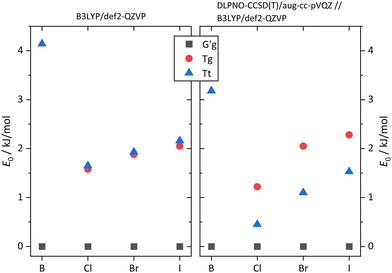Fig. 7 Computed energetic order of the monomer conformers for B, Cl, Br, I calculated at B3LYP-D3(BJ)/def2-QZVP level (left) compared to results from calculations at DLPNO-CCSD(T)/aug-cc-pVQZ//B3LYP-D3(BJ)/def2-QZVP level (right). All energies include B3LYP-D3(BJ)/def2-QZVP ZPVE. For results without ZPVE, see Fig. S1 in the ESI.†

Fig. 8 Comparison between the calculated harmonic wavenumbers and IR intensities for the monomer conformers of Cl, Br, I, calculated at B3LYP-D3(BJ)/def2-QZVP level.

3.1.2 Dimer conformations. The experimentally relevant conformational landscape of the dimers of ortho-halogenated benzyl alcohols is simpler than that of benzyl alcohol dimers.^3,13 In an energy window of 4 kJ mol⁻¹, there are two pairs of stacking variants (Fig. 9). The lower energy pair involves homochiral OH group orientations relative to the heavy atom monomer scaffolds and because the two structures are rather similar, it is expected that a supersonic jet expansion collapses the less stable one (Tg–G′g-a) into the most stable arrangement Tg–G′g. The higher energy pair replaces the acceptor molecule with its mirror image and thus leads to a heterochiral combination of the two OH torsions. This brings the two Cl atoms closer to each other and only the slightly lower energy variant is expected to be populated. The barriers for interconversion within each of the conformational pairs are predicted below 2 kJ mol⁻¹ (for Cl, B3LYP-D3(BJ)/def2-QZVP, see Fig. S5, S6, S12 and S13, ESI†) and can be easily surmounted. Due to the typically facile inversion of the benzyl group chirality¹³ and a predicted driving force of more than 2 kJ mol⁻¹ in the case of Cl dimers, it is even conceivable that a heterochiral encounter, which happens statistically with 50% likelihood for this transiently chiral species, is converted into the lower energy homochiral pairing during the expansion. However, the barrier for interconversion is sizeable (B3LYP-D3(BJ)/def2-QZVP predicts a barrier of ca. 17 kJ mol⁻¹ with ZVPE, see Fig. S5, S6 and Table S14, ESI†), due to the required flipping of the aromatic ring stacking to separate the Cl atoms. Therefore, experiment must decide whether one or two dimer conformations are observed. This is realistic, because theory predicts that the hom and het pairings should be spectrally distinguishable (Fig. 9) at least for the intensified hydrogen-bonded OH stretching mode. Although the position of this mode is non-systematic among all four conformations, the hom pairing is predicted to give rise to a systematic downshift if relaxation into the most stable hom and het conformations is assumed (see Fig. S4, ESI†). Because the double-harmonic prediction of the IR intensity for these hom and het dimer variants is comparable, the signal strength is a faithful measure for the relative population of the diastereomeric complexes. DFT theory also predicts that the hom/het energy gap starts to close with increasing size of the halogen atom (Fig. 10) and the transition state increases in energy (Fig. S7, ESI†), such that the chances to observe the het dimer increase with increasing halogen size.

Fig. 9 Optimised Cl dimer structures (Tables S8–S11, ESI†) with harmonically zero-point-corrected relative energies, unscaled harmonic OH stretching wavenumbers and calculated IR intensities (hydrogen bond donor/hydrogen bond acceptor) at B3LYP-D3(BJ)/def2-QZVP level. Included are all structures up to a relative energy of 4 kJ mol⁻¹. The Br and I dimers show similar structures but different relative energies (Fig. 10).

Fig. 10 Computed relative energies of the main dimer conformers for Cl, Br, I, calculated at B3LYP-D3(BJ)/def2-QZVP level with (E₀) and without (E_el) ZPVE.

3.2 Experimental results

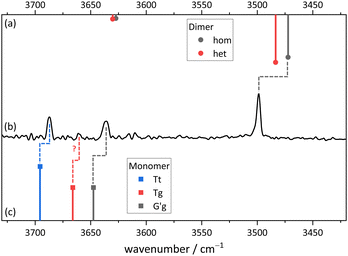
Fig. 11 compares the theoretical expectations in the double-harmonic expectation with experiment for Cl, after employing a rounded scaling factor of 0.96. Three strong OH stretching transitions find straightforward interpretations. In the monomer region, the spacing between two bands matches that between the global minimum G′g conformation (downshifted due to hydrogen bonding) and the planar Tt conformation which was elusive for B. Surprisingly, their experimental intensities match the theoretical ones, indicating a similar abundance of both conformers in the jet expansion. Tentatively, a weak band in between may be attributed to the third monomer conformation Tg in an order of magnitude inferior abundance. The scarcity of the Tg signal in the presence of Tt shows that DFT predictions of isoenergetic Tt and Tg conformations are inaccurate. The strongest and strongly downshifted band fits the prediction for the hydrogen bond donor in the most stable dimer Tg–G′g, although the accuracy of harmonic DFT predictions is not sufficient to prove its homochirality, given that the heterochiral counterpart is only predicted 12 cm⁻¹ higher in wavenumber. Even an experimental hom-het overlap cannot be ruled out completely. The corresponding acceptor OH stretching vibration is predicted to have an order of magnitude lower intensity. It may overlap one of the monomer transitions or – less likely – be the exclusive cause of the small peak tentatively assigned to Tg.

Fig. 11 Simulated stick spectra of (a) the Cl dimer and (c) the Cl monomer conformers (harmonic wavenumbers calculated at B3LYP-D3(BJ)/def2-QZVP level scaled by 0.96, relative intensity based on calculated IR band strength) compared to (b) the measured FTIR spectrum in the OH stretching region of Cl.

While this assignment based on consistently underestimating scaled harmonic DFT wavenumber predictions is plausible (a scaling factor of 0.97 would lead to predictions which consistently overestimate the experimental wavenumbers), it needs to be verified and aligned with further computational and experimental evidence. An important piece of evidence is shown in Fig. 12. By adding argon to the helium expansion, the relaxation of the Tt monomer to the global minimum G′g structure is expected to be enhanced.⁴⁵ Indeed, the signal assigned to Tt is now substantially attenuated and also the tentative weak Tg absorption is no more detectable. This strongly supports the robust global minimum character of G′g and it also confirms that Tt is lower in energy than Tg. The latter result is far from robust in the theoretical predictions, but it is consistent with the highest level calculations. We can thus unambiguously show the existence of the B-elusive Tt conformation and prove its energetical rank as the second-most stable structure.

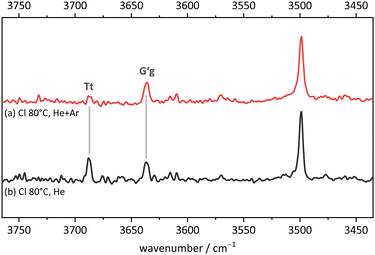Fig. 12 FTIR spectrum in the OH stretching region of 2-chlorobenzyl alcohol (Cl). (a) expanded with helium and argon and (b) with helium only (for experimental details see ESI†). The relative depletion of the Tt signal with Ar addition shows that G′g has a lower energy and is separated from Tt by a moderate size barrier.

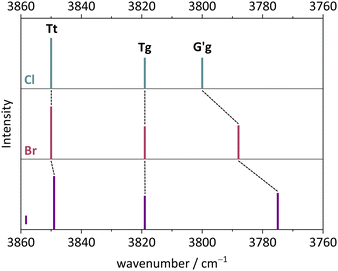
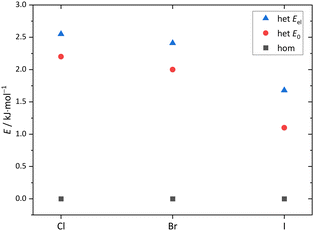
The monomer conformational assignments are further supported by the halogenation trend, which was predicted in Fig. 8. As the experimental spectral series for Cl, Br and I (Fig. 13) shows, only the G′g band exhibits a noticeable wavenumber trend with halogen size, as predicted and expected for an intramolecular hydrogen bond. The same figure shows that the hom dimer peak observed for Cl decreases in intensity with halogen size, but remains largely unchanged in position. Instead, a second peak emerges at somewhat higher wavenumber, where the het dimer counterpart is predicted (compare Fig. S4 in the ESI†). This matches the increasing energetical competitiveness of the het dimer with halogen size (Fig. 10) and/or suggests that the het-hom interconversion barrier increases with halogen size. Indeed, DFT calculations suggest that the lowest identified barrier steadily increases from Cl over Br to I (Fig. S7, ESI†) and there may be a combination of thermodynamic and kinetic effects at play. Assuming that the het/hom predicted energy difference for Br is correct, a 20% population of the het dimer (Fig. 13) means that the het-to-hom interconversion freezes around 150 K. For I, either the computed energy difference is overestimated or the observed hom/het ratio corresponds to nearly statistical and thus kinetically controlled dimerisation without significant subsequent isomerisation. This is not unreasonable for the substantial barrier which has to be overcome once the dimer is sufficiently cooled by collisions. For Cl, with no trace of the het isomer, freezing of the conformational relaxation may happen at temperatures lower than 150 K, if there is no accidental band overlap hiding the het dimer. Therefore, the halogens appear to tune the diastereomeric dimer relaxation behaviour from easy relaxation (Cl) over hindered relaxation (Br) to early freezing (I). However, the computed high racemisation barriers invite a reinvestigation by high-resolution structural methods to verify that the heterochiral Cl dimer is not present in significant abundance. All experimental wavenumbers together with the proposed assignments are listed in Table S16 in the ESI.†

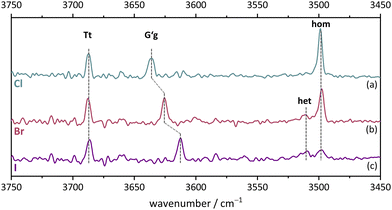Fig. 13 FTIR spectra in the OH stretching region of Cl, Br, I. (a) 2-Chlorobenzyl alcohol, (b) 2-bromobenzyl alcohol, (c) 2-iodobenzyl alcohol. For measurement conditions of the underlying helium expansions, see Table S15, for theoretical predictions, see Fig. S4 in ESI.†

In summary, there is an excellent match between dispersion-corrected DFT predictions and experiments for both monomers and dimers of ortho-halogenated benzylalcohols, once one accepts that the energetic order of the Tt and Tg conformations is inverted and more pronounced than predicted, in line with coupled cluster corrections to the energy sequence.

4 Conclusions

Replacement of an ortho hydrogen in benzyl alcohol by a halogen atom introduces a new intramolecular hydrogen bond contact which is more attractive than the weak OH interaction with the aromatic ring. Somewhat counterintuitively, it also lowers the relative energy of a (pseudo)planar conformation which does not profit from this hydrogen bond contact and which had remained elusive in jet studies of benzyl alcohol. It does so to such an extent that this structure without internal hydrogen bonding remains strongly populated in a supersonic jet expansion, at least for helium as a carrier gas. Its population can however be depleted by adding a small fraction of argon as a relaxation promoter.

Important findings of the present work include:

1. Ortho-Halogenation of benzyl alcohol favours a transiently chiral conformation with intramolecular OH hydrogen bond to the halogen.

2. In supersonic jets, a planar and thus achiral conformation without OH hydrogen bond can be prepared in similar abundance or largely avoided, depending on the collision partner during the expansion.⁴⁵ It had remained spectroscopically elusive for simple benzyl alcohol.^6,13

3. A chiral conformation without internal hydrogen bond is energetically higher than the planar one, although DFT calculations tend to predict otherwise. Coupled cluster corrections achieve consistency with experiment. Thus, ortho-halogenated benzyl alcohols serve as experimental benchmarks⁴⁶ for predicted conformational energy rankings.

4. Heavy-atom tunneling between enantiomers, which is prominent in benzyl alcohol,² is likely quenched by the ortho-halogenation, as this introduces a sequence of four isomerisation barriers instead of one.

5. When two ortho-halogenated benzyl alcohols dimerise, the donor is forced into a chiral conformation without intramolecular hydrogen bond by the stacking of the two aromatic rings, whereas the acceptor keeps its intramolecular hydrogen bond. Aryl-halogen interactions⁴⁷ appear to be less decisive.

6. In contrast to simple benzyl alcohol, OH–π hydrogen bonding is not crucial for dimerisation after ortho-halogenation.

7. Heterochiral pairing of two halogenated benzyl alcohol units becomes increasingly competitive with increasing size of the halogen atom, whereas homochiral pairing and thus positive chirality synchronisation¹² between the two monomers is always observed.

8. Preferential homochirality was extensively discussed for clusters of unsubstituted benzyl alcohol and previously observed in the solid state of ortho-halogenated benzyl alcohols. The present work underscores this preference at the molecular level.

Extension of this work to fluorinated benzyl alcohols,⁸ to para- and meta-halogenated benzyl alcohols,^43,48 and to other acceptor molecules including persistent organic radicals is planned. For the latter, ortho-halogenated benzyl alcohols offer flexible, tunable solvents which control the accessibility of the radical center including dynamical nuclear polarisation effects.⁴⁹

Data availability

The data supporting this article have been included as part of the ESI.† In addition, the original infrared spectra are made available at the GROdata repository at https://doi.org/10.25625/YXUUF0.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 389479699/GRK2455. Computational ressources from the GWDG and the Faculty of Chemistry are acknowledged. We thank Katharina Rachuy for helping with the literature search for the crystal structures.

Notes and references

1. R. Glaser and G. R. Nichols, J. Org. Chem., 2000, 65, 755–766.
2. K. A. Utzat, R. K. Bohn, J. A. Montgomery, H. H. Michels and W. Caminati, J. Phys. Chem. A, 2010, 114, 6913–6916.
3. R. Medel, Phys. Chem. Chem. Phys., 2021, 23, 17591–17605.
4. P. J. Krueger and B. F. Hawkins, Can. J. Chem., 1973, 51, 3250–3262.
5. N. Guchhait, T. Ebata and N. Mikami, J. Am. Chem. Soc., 1999, 121, 5705–5711.
6. B. J. Miller, H. G. Kjaergaard, K. Hattori, S.-I. Ishiuchi and M. Fujii, Chem. Phys. Lett., 2008, 466, 21–26.
7. E. Bogdan, G. Compain, L. Mtashobya, J.-Y. Le Questel, F. Besseau, N. Galland, B. Linclau and J. Graton, Chem. – Eur. J., 2015, 21, 11462–11474.
8. L. Evangelisti, L. B. Favero and W. Caminati, J. Mol. Struct., 2010, 978, 279–281.
9. M. Mons, E. G. Robertson and J. P. Simons, J. Phys. Chem. A, 2000, 104, 1430–1437.
10. M. Herman, R. Georges, M. Hepp and D. Hurtmans, Int. Rev. Phys. Chem., 2000, 19, 277–325.
11. J. Altnöder, S. Oswald and M. A. Suhm, J. Phys. Chem. A, 2014, 118, 3266–3279.
12. A. Zehnacker and M. A. Suhm, Angew. Chem., Int. Ed., 2008, 47, 6970–6992.
13. R. Medel and M. A. Suhm, Phys. Chem. Chem. Phys., 2020, 22, 25538–25551.
14. A. R. Al-Rabaa, K. L. Barbu, F. Lahmani and A. Zehnacker-Rentien, J. Photochem. Photobiol., A, 1997, 105, 277–282.
15. R. Medel, A. Camiruaga, R. T. Saragi, P. Pinacho, C. Pérez, M. Schnell, A. Lesarri, M. A. Suhm and J. A. Fernández, Phys. Chem. Chem. Phys., 2021, 23, 23610–23624.
16. S. K. Nayak, R. Sathishkumar and T. N. G. Row, CrystEngComm, 2010, 12, 3112 . Note that the position of the hydroxy hydrogen atom in the single molecule cutout in Fig. 4 of the reference is not in agreement with the crystal structure.
17. L. Dunbar, A. R. Kennedy and J. Reglinski, CCDC 942082: Experimental Crystal Structure Determination; 2-chloro-benzyl alcohol, 2013,  DOI:10.5517/cc10m9rp.
18. T. Misiaszek, K. Knapik, A. Gagor and M. Trzebiatowska-Gusowska, J. Mol. Struct., 2013, 1054–1055, 117–122.
19. A. Prathap, A. Ravi, J. R. Pathan and K. M. Sureshan, CrystEngComm, 2019, 21, 5310–5316.
20. J. Altnöder, J. J. Lee, K. E. Otto and M. A. Suhm, ChemistryOpen, 2012, 1, 269–275.
21. B. Hartwig, M. Lange, A. Poblotzki, R. Medel, A. Zehnacker and M. A. Suhm, Phys. Chem. Chem. Phys., 2020, 22, 1122–1136.
22. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
23. J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104.
24. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
25. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
26. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
27. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
28. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101.
29. E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101.
30. E. R. Johnson and A. D. Becke, J. Chem. Phys., 2006, 124, 174104.
31. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
32. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
33. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123.
34. V. Ásgeirsson, B. O. Birgisson, R. Bjornsson, U. Becker, F. Neese, C. Riplinger and H. Jónsson, J. Chem. Theory Comput., 2021, 17, 4929–4945.
35. C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101.
36. R. A. Kendall, T. H. Dunning, Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
37. D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1993, 98, 1358–1371.
38. A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, Jr., J. Chem. Phys., 1999, 110, 7667–7676.
39. K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112.
40. K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877–13883.
41. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
42. V. V. Varfolomeeva and A. V. Terentev, Russ. J. Phys. Chem. A, 2010, 84, 1592–1597.
43. T. V. Alves, L. Simón-Carballido, F. R. Ornellas and A. Fernández-Ramos, Phys. Chem. Chem. Phys., 2016, 18, 8945–8953.
44. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
45. R. S. Ruoff, T. D. Klots, T. Emilsson and H. S. Gutowsky, J. Chem. Phys., 1990, 93, 3142–3150.
46. R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 11011–11018.
47. H.-J. Schneider, Angew. Chem., Int. Ed., 2009, 48, 3924–3977.
48. S. Tang, Z. Xia, A. Maris and W. Caminati, Chem. Phys. Lett., 2010, 498, 52–55.
49. M. Levien, L. Yang, A. van der Ham, M. Reinhard, M. John, A. Purea, J. Ganz, T. Marquardsen, I. Tkach, T. Orlando and M. Bennati, Nat. Commun., 2024, 15, 5904.

---

Footnote

† Electronic supplementary information (ESI) available: More computational and experimental details and results. See DOI: https://doi.org/10.1039/d4cp03203a

---