Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Germanium distributions in zeolites derived from neural network potentials†
Indranil
Saha
,
Andreas
Erlebach
 ,
Petr
Nachtigall‡
,
Petr
Nachtigall‡
 ,
Christopher J.
Heard
,
Christopher J.
Heard
 and
Lukáš
Grajciar
and
Lukáš
Grajciar
 *
*
Department of Physical and Macromolecular Chemistry, Faculty of Science, Charles, University in Prague, 12483, Czech Republic. E-mail: lukas.grajciar@natur.cuni.cz
First published on 28th August 2024
Abstract
Germanosilicate zeolites have played a pivotal role in the recent surge in synthesis of novel zeolite topologies. This success has been attributed to the combined effect of the high hydrolytic lability and specific distribution of germanium within the zeolitic framework, e.g., favoring the double four-ring (D4R) structural units. While experimental determination of germanium distributions remains limited, their in silico investigation has been hampered by the high computational cost of ab initio calculations. To overcome these limitations, we have developed neural network potentials (NNPs) that can efficiently explore a wide range of distributions in germanosilicate zeolites, while maintaining the accuracy of the ab initio (dispersion-corrected GGA DFT) training dataset. Through comprehensive screening of low-energy germanium distributions for five zeolite topologies (UTL, BEC, UOV, IWW and *CTH) across a broad range of Si/Ge ratios, we have identified a key factor governing the distribution of germanium in these D4R-containing zeolites, which is the tendency of germanium to cluster. The clustering initiates at the D4R units, leading to a preference to occupy these units at low to medium Ge loading (Si/Ge ≥ 5). However, at high Ge loading, the Ge tends to phase separate into Ge-rich and Ge-poor regions, regardless of the specific structural unit. The zeolite topology was shown to be capable of modulating these trends in germanium distribution (e.g., UTL strongly favors D4R occupation even for low Si/Ge ratios), which suggests the possibility to develop design strategies for targeted zeolite synthesis. The NNPs presented herein enable rapid evaluation of these design strategies across a wide range of candidate zeolite structures and experimentally relevant Si/Ge ratios.
1 Introduction
Zeolites are a diverse class of crystalline microporous silicates, with a wide range of pore shapes, connectivities and framework topologies. These materials are of enormous industrial importance for their superior adsorption, ion exchange, and catalysis properties, and the benefits of tuning these properties to particular applications provide a strong incentive to tailor their synthesis.1 With the advent of the assembly–disassembly–organization–reassembly (ADOR) process2 around ten years ago, a novel approach to generate so-called unfeasible zeolites3 became available. The process makes use of the specific (non-statistical) distribution of framework heteroatoms, generally germanium, to direct preferential hydrolysis of layered precursors into separate, two-dimensional intermediates, followed by targeted recondensation into condensed phases.4 This procedure allows for access to zeolite topologies that are unavailable by other synthetic routes, and indeed has led to the discovery of several new zeolite topologies. From many previous studies, it has been established that the presence of germanium has a major role in guiding zeolite synthesis through the ADOR process.5 Specifically, it is the preferential occupation of germanium atoms into cubic double 4-ring (D4R) sites that leads to the separability of layers, in e.g. zeolite UTL, for which the ADOR approach has been most successful.An elegant study by O'Keefe and Yaghi6 linked the possibility to form zeolite structures containing Ge, Si or both, to the geometric preference of various bond angles for Ge and Si in Si8−nGenO20 cubic subunits. Villaescusa et al.7 subsequently synthesised the D4R subunit analogue, Ge8O12(OH)8F−. Such idealised views of the D4R as an isolated, Ge-rich subunit, while beneficial as models, do not, however, capture the effects of confinement within the zeolite framework.
In order to ultimately guide the synthesis, an understanding of the properties of D4Rs, along with an accurate description of the distribution of germanium atoms inside the zeolite framework is needed. However, the relative stability of various substitution positions and the degree of germanium incorporation into the D4R is not definitely understood, nor are additional factors, including the generality of this preference across zeolite topologies, the role of the Si/Ge ratio, or the effect of D4R asymmetry on the occupation of D4Rs.
It is not simple to get precise information about the germanium distribution from the experiments – most characterization has come via19F NMR,8,9 in which the occupation fraction of D4R by germanium is estimated from the chemical shifts of fluoride ions residing within the D4R cage. However, this method has insufficient precision10–12 to fully determine the Ge content of D4R sites, or to distinguish between various cage units in the zeolite. The precision of X-ray powder diffraction (PXRD) measurements is higher, however, the mean germanium occupations were reported only for a limited number of zeolites and Si/Ge ratios,10,13–17 with the refinement of the PXRD signal being far from straightforward in some cases.16
As a result of this limited available knowledge, computational studies have contributed to the prediction of stable germanium distributions, and to understanding the principles behind their stability. Density functional calculations have been performed for several Ge-zeolite topologies, including UTL18 and BEC (ITQ-17),19 showing that at low Ge content, the D4R sites are energetically preferred, with a slight preference for Ge–O–Ge clustering over disconnected Ge distributions. The high expense of DFT calculations however limited these investigations to selected configurations and low Ge content. Attempts to statistically sample the large configuration space of Ge in BEC and ITQ-7 using inexpensive empirical potentials also showed a preference for D4R sites8,14,20 and a dependence of that preference on Ge loading, implying a collective structure-directing effect of Ge. However, the preference for Ge–O–Ge clustering was not observed, owing to limitations in the accuracy of the force-field at high Ge concentrations.
More recent studies11,12,21,22 have examined the effect of ionic species which are present in the synthesis mixture of germanosilicate zeolites, namely fluoride ions (F−) and organic structure-directing agents (OSDAs). It was observed that F− is relatively immobile within D4R units of zeolites AST and ITH and its presence has a significant effect on the relative stabilities of different Ge distributions. Similarly, the presence of the F−/OSDA was found to give rise to larger differences in energy than those due to the choice of germanium distributions. Hence, these species represent an important template for the occupation of D4Rs.
Overall, the vast number of configurations, the small energy differences between them, and the complex role of zeolite topology mean that determining a comprehensive detailed probability distribution of Ge within zeolites remains a challenging task. In this study, our aim is to statistically analyze the arrangement of germanium (Ge) atoms across a spectrum of Si/Ge ratios, within a broad set of framework topologies (UTL, BEC, CTH, UOV, and IWW). To achieve this, we employ a methodology centred around newly developed machine learning potentials (MLPs), which drastically extend the scope of calculations, allowing for a comprehensive view of the preferential locations, distributions of Ge, and their trends across a diverse range of frameworks.
2 Computational methods and models
2.1 Neural network potential (NNP) training
Training neural network potentials (NNPs) capable of general Ge-zeolite modelling first requires the generation of a DFT dataset spanning all relevant parts of the configuration space. Previously, we demonstrated the development of general NNPs for silica and siliceous zeolites, including their reactive phase transformations, by selecting structurally distinct configurations from zeolite databases and active-learning simulations.23 The structure selection used farthest point sampling (FPS)24 with the smooth overlap of atomic positions (SOAP) descriptor to quantify the similarity between atomic environments.25In this work, we focus on accurately modelling close-to-equilibrium (EQ) configurations of Ge-substituted zeolites. Therefore, we did not include high-energy structures required for the NNP training of reactive events in the current dataset. First, to cover the purely siliceous interactions, we used a subset of 22k EQ structures from the previously created23 silica database (33k structures in total, including high-energy structures). These structures were obtained from structure optimizations of a hypothetical zeolite database and lattice deformations applied to ten hypothetical and five existing zeolites (CHA, SOD, IRR, MVY, MTF) (see ref. 23 for details). This approach proved successful in generating a training database for the general modelling of zeolites.
Subsequently, to cover the germanosilicate interactions, 10k EQ configurations were chosen by SOAP–FPS and Si atoms were randomly replaced by Ge atoms according to a randomly chosen Ge fraction (between 0 and 1, but with at least one Si/Ge atom in the unit cell). In addition, to sample EQ Ge-zeolites more systematically, we applied a set of lattice deformations to the aforementioned 15 frameworks, each with 9 randomly generated Ge substitutions covering Ge fractions between 0.25 and 0.75. We used all 70 permutations of possible strain tensors with strain rates of 1.5%, 3%, 4.5%, and 6% (see also ref. 23 for further details). Lastly, we used the same set of deformations for two GeO2 polymorphs with tetrahedral Ge coordination (quartz-like structure) and hexagonally coordinated Ge (rutile-like structure).
All created structures were used for DFT single-point calculations, yielding a training dataset of 64k configurations with Si/Ge ratios ranging from 0.3 to 9. This dataset is publicly available under: https://doi.org/10.5281/zenodo.13357083. Since our focus is on simulations of EQ structures that mostly show force magnitudes of a few eV Å−1, we excluded all structures with forces higher than 15 eV Å−1. The DFT simulations used the Vienna Ab initio Simulation Package (VASP, version 5.4.4)26–29 along with the PBE exchange–correlation functional30 and the D3 dispersion correction31 with Becke–Johnson (BJ) damping.32 We employed the projector augmented-wave (PAW) method33,34 with the standard (recommended) potentials and a plane-wave energy cutoff of 400 eV. For every unit cell, the k-point density was not lower than 0.1 Å−1 along each reciprocal lattice vector.
NNP training and simulations used the Python package SchNet-Pack35 together with the atomistic simulation environment (ASE).36 We trained the ensemble of six NNPs using the same setup of the SchNet architecture37 as in our previous work starting from the initial silica models:23 a cutoff of 6 Å, six interaction blocks, 128 feature vector elements, and distance expansion with 60 Gaussians. The generated DFT database was randomly split into training (80%), validation (10%), and test sets (10%). We employed the ADAM optimizer38 with 8 structures per batch for minimization of the mean squared error of energy and forces (with a trade-off factor of 0.01, see also ref. 23). The learning rate was halved if the value of the validation loss did not decrease in 15 epochs (from 10−4 to 10−6).
We quantified the accuracy of the trained NNPs using the test set of the created DFT database, yielding energy and force root mean square errors (RMSE) within the training domain of 4.2 meV per atom and 51 eV Å−1, respectively (see Table S1†). These errors are lower compared to NNPs that were also trained to model reactive events (5 meV per atom, 150 eV Å−1).23,39 In addition, we calculated the NNP (out-of-domain) errors for a randomly selected subset (5249 structures in total) taken from the basin-hopping Monte Carlo simulations of germanium distributions (see below) for zeolite frameworks that were not part of the training database. We performed single-point calculations for this subset and obtained only mildly larger force errors for these test cases of about 70 eV Å−1. However, the energy RMSE, which is more relevant in this work, which focuses on the Monte Carlo simulations sampling low-energy structures, is considerably lower (1.7 meV per atom) compared to the test set errors, demonstrating a good generalization capability of the NNPs (see Table S2†).
To directly evaluate the accuracy of the NNPs with respect to the reference DFT level for the same type of simulations performed in this work, Fig. 1 compares the relative energies of several Ge distributions and contents in UTL calculated using both the NNP and the DFT (PBE-D3(BJ)) geometry optimizations. The relative energies are given with respect to the lowest energy configuration obtained for the respective Ge concentration (1 to 8 Ge atoms per 38 T-sites unit cell). We found a very good agreement between the NNP and DFT calculated energies (MAE of 2.2 kJ mol−1 and RMSE of 3.1 kJ mol−1), with Pearson correlation coefficients 40 ranging from 0.77 to 0.94. All structures used for error evaluation, including DFT and NNP calculated energies and forces, are available under: https://doi.org/10.5281/zenodo.13357083.
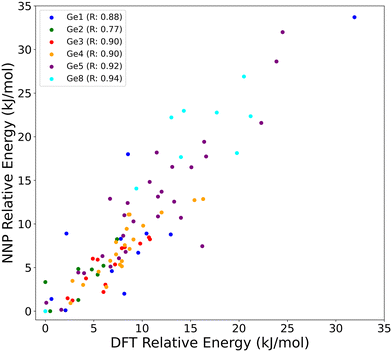 | ||
| Fig. 1 Comparison between the relative energies [kJ mol−1] of UTL models with various Ge contents (1, 2, 3, 4, 5, 8 per unit cell – each represented by a distinct colour) calculated using the reference DFT and the NNP model. For each germanium content, the energies are calculated relative to the most stable distribution at a given content, which serves as a reference (zero). The correlation between the DFT and NNP results is quantified using the Pearson correlation coefficient (R).40 The MAE and RMSE of the NNP energies with respect to the DFT reference for this dataset are 2.2 and 3.1 kJ mol−1, respectively. | ||
As the last benchmark test, we evaluated, at both NNP and DFT level (PBE-D3(BJ) employing the plane-wave energy cutoff of 800 eV), multiple structural parameters (unit cell parameters, unit cell volumes, average T–O–T angles and T–O bond lengths) for five zeolite topologies (AST, ASV, STW, BEC and UTL) considering, in the majority of cases, Si/Ge ratios ranging from purely siliceous models all the way to germanium oxide polymorphs (see Tables 1 and S6 to S15†). For each model with Si/Ge ∉ {0, ∞} we ran basin hopping Monte Carlo simulations (see section 2.2 for details) for at least 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps to obtain a germanium distribution corresponding to the tentative global minimum structure, for which we carried out the unit cell optimization both at the NNP and DFT level and obtained the structural parameters for comparison. We found that the unit cell volumes at the NNP level are on average slightly underestimated (mean relative error of −1.5%), with the performance mildly varying among the topologies (the largest errors of approx. 4% for AST, with BEC and STW showing errors below 1%) but following the same qualitative trends as the reference DFT as a function of Si/Ge ratio. Also, at the NNP level, the average Ge–O–Ge angles are on average two degrees smaller and the Ge–O bonds approximately 0.02 Å shorter than their DFT counterparts, which represents only a minor deviation from the reference, with the NNP values again following the same trends as DFT as a function of the Si/Ge ratio, i.e., the NNP values are almost constantly offsetted from the DFT values. Further details on other structural properties (e.g., Si–O–Si angles and Si–O bond lengths) can be found in the ESI† (Tables S11 to S15). Note also, that similar discrepancies, e.g., in unit cell volume predictions, can be observed as a result of using a different value of plane-wave energy cutoff, a different GGA exchange–correlation functional, a different dispersion correction (see Table S5†), or a different program package (compare, e.g., our results for AST zeolite with the data from ref. 21). Hence, the herein-reported NNP errors fall within the existing uncertainties of the standard solid state (GGA-level) DFT calculations (Table S5†).
000 steps to obtain a germanium distribution corresponding to the tentative global minimum structure, for which we carried out the unit cell optimization both at the NNP and DFT level and obtained the structural parameters for comparison. We found that the unit cell volumes at the NNP level are on average slightly underestimated (mean relative error of −1.5%), with the performance mildly varying among the topologies (the largest errors of approx. 4% for AST, with BEC and STW showing errors below 1%) but following the same qualitative trends as the reference DFT as a function of Si/Ge ratio. Also, at the NNP level, the average Ge–O–Ge angles are on average two degrees smaller and the Ge–O bonds approximately 0.02 Å shorter than their DFT counterparts, which represents only a minor deviation from the reference, with the NNP values again following the same trends as DFT as a function of the Si/Ge ratio, i.e., the NNP values are almost constantly offsetted from the DFT values. Further details on other structural properties (e.g., Si–O–Si angles and Si–O bond lengths) can be found in the ESI† (Tables S11 to S15). Note also, that similar discrepancies, e.g., in unit cell volume predictions, can be observed as a result of using a different value of plane-wave energy cutoff, a different GGA exchange–correlation functional, a different dispersion correction (see Table S5†), or a different program package (compare, e.g., our results for AST zeolite with the data from ref. 21). Hence, the herein-reported NNP errors fall within the existing uncertainties of the standard solid state (GGA-level) DFT calculations (Table S5†).
| Lattice parameters | Volume | T–O–T | T–O | |||
|---|---|---|---|---|---|---|
| Si–O–Si | Si–O–Ge | Ge–O–Ge | Si–O | Ge–O | ||
| 0.9% | 1.6% | 1.5° | 1.3° | 2.3° | 0.001 Å | 0.024 Å |
2.2 Global structure search and models considered
The global structure search was carried out using the basin hopping Monte Carlo (BHMC) simulations, a stochastic optimization technique proposed by Wales and Doye.41 The approach involves iterative exploration of the configuration space by randomly perturbing atomic positions and performing local optimization combined with the Metropolis–Hasting acceptance criterion. Firstly, the siliceous frameworks (UTL, UOV, CTH–polymorph A, IWW, BEC) taken from the IZA database were optimized at the NNP level allowing the unit cell vectors and volume to change (see ESI† Tables S3 and S4). The BHMC simulations were carried out using the atomic simulation environment (ASE),36 with a random swap of Ge and Si atoms used as a move class followed by a local geometry optimization. The convergence criterion for the local geometry optimization was set to a maximum force of 10−2 eV Å−1 on atoms. The temperature of the simulation was set to 300 K. To ensure a diverse set of starting configurations, ten independent simulations of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 basin-hopping steps were run for each zeolite framework and each Si/Ge ratio, amounting to a total of 105 sampled configurations for each combination of a zeolite and Si/Ge ratio. Running ten independent simulations also allows us to quantify the statistical uncertainty (see ESI† Fig. S2 and S3) in the observables discussed below.
000 basin-hopping steps were run for each zeolite framework and each Si/Ge ratio, amounting to a total of 105 sampled configurations for each combination of a zeolite and Si/Ge ratio. Running ten independent simulations also allows us to quantify the statistical uncertainty (see ESI† Fig. S2 and S3) in the observables discussed below.
2.3 Custom metrics for the characterization of germanium distributions
To quantify the relative concentration of germanium in different types of T sites (ESI† Fig. S1), we use the metric occupation frequency [%], defined as, | (1) |
To probe the filling of the D4R sites irrespective of the Si/Ge ratio, we use Ge fraction in D4R [%], which describes what fraction of the D4R unit is occupied on average by the germanium. It is defined as,
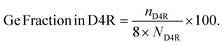 | (2) |
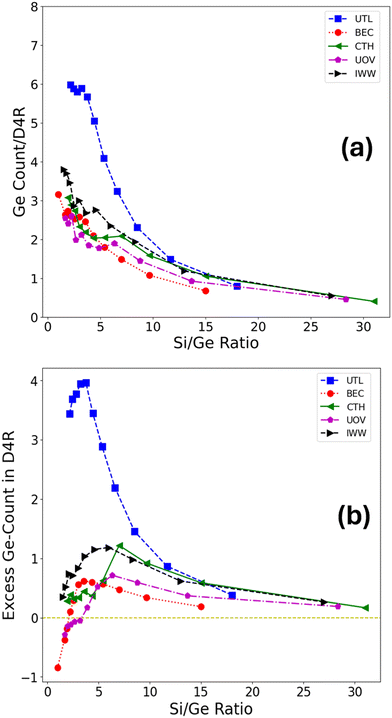
Here, nD4R is the average number of Ge atoms in the D4R unit(s) in the simulation cell, and ND4R is the number of D4R units in the simulation cell, each of which is made up of eight T sites (see Fig. 2a as an example of use). The Ge count/D4R is then just nD4R/ND4R.
The Ge fraction in D4R (and Ge count/D4R) are extensive properties with respect to the germanium content in the framework, hence, to define an intensive property that characterizes the preference of germanium to cluster in D4R (or other) T sites irrespective of the germanium content, we define an excess occupation as,
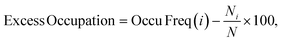 | (3) |
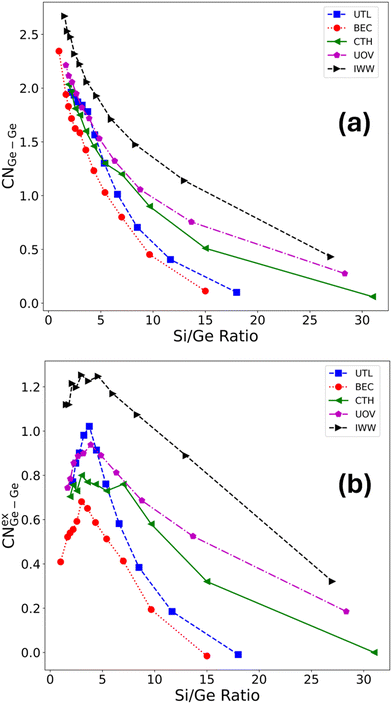
To quantify the clustering of germanium, we used the Ge–Ge coordination number (CNGe–Ge), evaluated from the Ge–Ge radial distribution function (see ESI† Fig. S4) considering only the nearest neighbour T sites, i.e., applying a cut-off of approximately 3.5 Å. This evaluates how many germanium atoms have other germanium atoms as their nearest neighbours (four being the maximum in the tetrahedral coordination environment). Similarly to the case of Ge fraction in D4R above, the CNGe–Ge, is an extensive property with respect to the germanium loading. Hence, we introduce an intensive property, namely, where excess Ge–Ge coordination number CNexGe–Ge defined as,
| CNexGe–Ge = CNGe–Ge − CNuniform, | (4) |
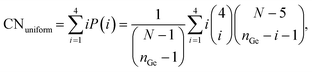 | (5) |
Here, P(i) stands for the probability of a Ge atom having a coordination number of i (= 1, 2, 3, 4 since it is tetrahedral), nGe is the total number of germanium in simulation cell, and N is the total number of T sites in the cell.
3 Results and discussion
3.1 General trends
Germanium atoms are expected to preferentially occupy the D4R units in the zeolitic frameworks. To investigate whether this is generally true, we first evaluated the average D4R Ge count across a broad range of Si/Ge ratios, as well as across five distinct zeolite topologies (UTL, BEC, CTH, IWW, UOV), each of which contains D4R units in their structure (see Fig. 2). These topologies were selected as those for which significant experimental efforts have been made to transform them according to the ADOR process, with mixed results. A comparison of our findings with these experimental observations will be discussed in section 3.5. The occupation of D4R units in general increases with germanium content (i.e., with decreasing Si/Ge ratio). However, with the exception of UTL, the increase is rather small, such that even for very low Si/Ge ratios of ≈1–2, the D4Rs are occupied only up to around 40%, which corresponds to around 2–3 Ge atoms per D4R unit, despite there being sufficient germanium content in the sample to fill all D4R sites. Only for UTL the D4R occupation increases significantly and peaks at around six germanium atoms per D4R for Si/Ge ≤ 5. Second, to directly quantify the average preference of germanium for D4R occupation, we evaluated an excess Ge count in D4R units (see section 2.3), which measures the difference between the observed germanium occupation in D4Rs (Fig. 2a) and the one based on purely random (uniform) germanium distribution across all T-sites. Fig. 2b confirms that for all considered frameworks and for almost all Si/Ge ratios considered the germanium prefers to occupy the D4R units. However, this preference is, with the exception of the UTL framework, rather weak, populating the D4R units by only up to one germanium atom more than what one would obtain by randomly placing germanium atoms in the framework. Moreover, after reaching this maximum value of over-occupation at Si/Ge of ≈4–7, the preference for D4R occupation plummets, in some cases (BEC and UOV) to the point of disfavoring D4R occupation by germanium altogether (corresponding to negative values of the excess Ge count). Hence, our simulations confirm the observation that germanium prefers to occupy D4R units, however, we find, that with the exception of UTL, the preference is weak and is most pronounced for low to intermediate germanium loading, i.e., Si/Ge ≥ 5 (see Fig. 2 and S9† depicting excess occupation).The preferential occupation of the D4R units can also be viewed as a manifestation of a general tendency of germanium atoms to cluster, i.e., to phase-separate, upon its introduction to the silicate framework. To probe the clustering tendency of germanium irrespective of the specific structural unit, we evaluated how many germanium atoms have other germanium atoms as their nearest neighbours (four being the maximum in the tetrahedral coordination environment), i.e., we calculated the Ge–Ge coordination number (see section 2.3 for the definition). We observe a rather steep increase in Ge–Ge coordination number (CN) with germanium content (Fig. 3a), which does not level off even for very high germanium loading (Si/Ge ≤ 3). This trend is consistent for all frameworks, and notably, UTL is no longer an outlier. Thus, a strong, general propensity for germanium to cluster extensively is observed, despite relatively low degrees of D4R population overall.
Similarly to the case of D4R occupation by germanium, we introduced the excess Ge–Ge coordination number (see section 2.3 for definition), which partially decouples the increase in germanium clustering from the increase in germanium content, by measuring the difference between the observed Ge–Ge CN values and those based on the assumption of purely random (uniform) germanium distribution across all T-sites (see Fig. 3b). Fig. 3b confirms that germanium prefers to cluster for all Si/Ge ratios considered, with a germanium atom being surrounded by between 0.4 and 1.2 more germanium atoms as nearest neighbours than would be predicted based on a random germanium distribution, at intermediate to high germanium loading (Si/Ge ≤ 8). Compared to the D4R occupation preference (see Fig. 2b), the germanium clustering peaks at lower Si/Ge ratios (≈3–4) and either stays flat after that (CTH) or decreases only mildly (IWW, UTL, BEC, UOV). The clustering preference can be related to the increased energetic stabilization associated with phase separation of germanium as exemplified by a strong positive correlation (with Pearson correlation coefficient40R ≈ 0.5–0.8) between stabilization of the structure and a total count of Ge–O–Ge bonds (see ESI† Fig. S8 and S51), an alternative measure of clustering used in the literature.11 In brief, our simulations suggest a significant clustering tendency of germanium, irrespective of the specific structural unit, across all the Si/Ge ratios considered.
In summary, we identified two phenomena driving the character of the germanium distributions in D4R-containing zeolites, the general clustering tendency of germanium and a specific preference of germanium towards occupation of D4R units. At low to intermediate germanium loading (approximately Si/Ge ≥ 5) the preference for D4R occupation is the main driving force, as it also allows for significant clustering at such loading. This is exemplified by the finding that the largest Ge–Ge CN values are calculated for D4R T-sites at such Si/Ge ratios (see ESI† Fig. S5–S7). At high germanium loading (approximately Si/Ge < 5), the germanium clustering in T-sites other than in D4R units starts to be favoured significantly, slowing down or even diminishing the population of germanium in D4R units. In the following, we focus on the particular manifestation of these general trends for each specific topology as well as on the specific role of various topological features (such as heterogeneity of D4R units and topology dimensionality) on the germanium distributions.
3.2 The effect of zeolite topology
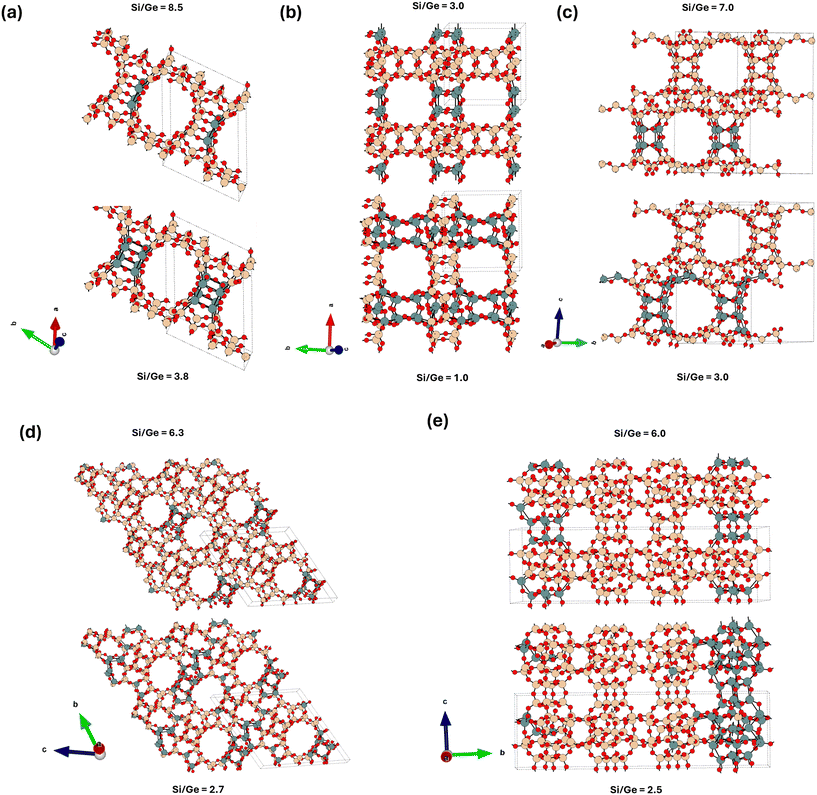
To succinctly characterize the germanium distribution for each zeolite framework across a broad range of Si/Ge ratios in more detail (Fig. 4 and 5), we focus below only on a few descriptors, : i) the relative occupations of various classes of T-sites (D4R, framework and adjacent – see section 2 and ESI† Fig. S1 for definition), ii) the relative occupations of each individual D4R unit in the unit cell: representing asymmetry in D4R occupations, iii) the global structure optima (GSO) for the germanium loading at specific Ge loadings. Further relevant characterizations, e.g., a broader set of low-energy structures, will be only briefly discussed, with the details provided in the ESI.†To determine the asymmetry in D4R occupation within a given topology, we must label the individual D4Rs. However, with the exception of UOV, all the D4Rs in each of the considered topologies are crystallographically equivalent. To solve this, for each snapshot, we assign a label to each D4R based on its relative occupation, from the least occupied to the most occupied. Then, the average occupation for each label is calculated over the entire trajectory (Fig. 5). This allows us to compare, for example, the average maximum and minimum occupations of symmetry equivalent D4Rs within a given topology.
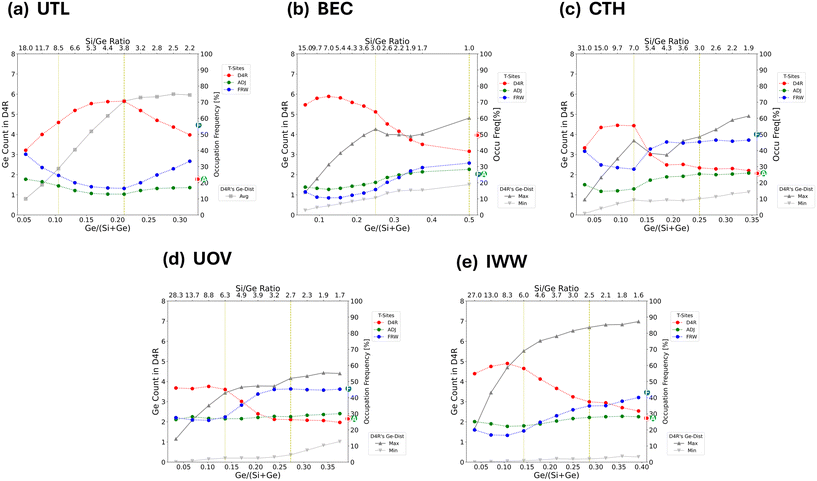 | ||
| Fig. 5 Plots characterizing the average germanium distributions across a broad range of Si/Ge ratios for (a) UTL, (b) BEC, (c) CTH, (d) UOV, and (e) IWW topologies. Two specific Si/Ge ratios are highlighted, corresponding to the Ge loading sufficient to fill half (dotted yellow vertical line) and all (dashed yellow vertical line) of the D4R T-sites, whose global structure optima are depicted in Fig. 4. Each plot focuses on two aspects of the average germanium distributions: i) (using the primary y-axis) the asymmetry in the occupation of D4R, represented by grey lines for the most (max) and least (min) occupied D4Rs. For UTL, the unit cell contains only one D4R unit, the average (avg) germanium occupation of which is plotted (compare with Fig. 2). ii) (using the secondary y-axis) The occupation frequency [in %] (see section 2.3 for definition) of germanium atoms in different types of T sites – D4R (red), adjacent (green), framework (blue) (see also ESI† Fig. S1). The encircled letters D/A/F on the secondary y-axis denote the total fraction of T sites of each class (D4R/adjacent/framework) for the given topology. | ||
Fig. 5 shows the variation of occupation of all classes of site (D4R, adjacent and framework sites), in addition to the asymmetry, which is depicted as a comparison between maximum and minimum D4R occupation. By comparing two specific germanium loadings: sufficient to fill half, and sufficient to fill all D4R units, we find that there are two apparent modes of germanium distribution: i) strong preference for D4R occupation (half-filling of D4Rs), and ii) the spread of the occupation towards the framework T-sites (complete filling of D4R). These modes are clearly discernible from the relative occupations of the different classes of T-sites (Fig. 5), which, with the exception of UTL, show that the relative occupations of D4Rs peak approximately at Si/Ge ratios corresponding to the half-filling of D4R units and then plummet and stabilize again approximately at the Si/Ge ratios corresponding to complete-filling of D4R units. This behaviour of D4R occupations is approximately mirrored by the occupations of framework T-sites, with the occupation of the adjacent T-sites being close to constant across all the Si/Ge ratios. For Si/Ge ratios corresponding to more than the complete-filling of the D4R units (again with the exception of UTL), the occupations of various classes of T-sites are rather stable and tend to their respective (purely statistical) class multiplicities (highlighted in Fig. 5 on the right ordinate axis).
Both cases lead to clear phase-separation of the germanium from silicon, leading to the formation of germanium-poor and germanium-rich ‘layers’ coplanar with the [0b0] plane. However, the phase separation perpendicular to the CFI layers (e.g., coplanar with [00c]) is shown to be less favourable (ESI† Fig. S20).
3.3 Finite-size effects
The size of the periodic simulation cell is a model parameter that is expected to affect the germanium distribution, in particular, if small simulation cells and high germanium loading are considered. To quantify the effect herein, we enlarged the simulation cells (Table S4†) for all but the UOV framework (along with IWW, UOV has a very large primitive cell with a volume above 5000 Å3 – see Tables S3†) and ran the basin hopping MC simulations for three (high) germanium loadings for each of the enlarged cells. The comparison of the various characteristics (Ge fraction in D4R unit, Ge–Ge CN, etc.) of the average germanium distribution between the primitive and the super-cell simulations (Table 2, Fig. S38 and S39†) confirms the expectation that the finite size effects are the most pronounced (changing the selected characteristics by 10–40%) for rather small primitive cells, such as for those of UTL and BEC (<3000 Å3), while being smaller for CTH and IWW frameworks with larger primitive cells (>4000 Å3). Nevertheless, even for UTL and BEC, the finite size effects do not qualitatively change the main observations reported above (section 3.2). The main consequence of the adoption of the larger simulation cells appears to be a (minor) increase in germanium clustering irrespective of the T site (measured by the total coordination number) at the expense of the germanium localization in the D4R units.| UTL | BEC | CTH | IWW | ||
|---|---|---|---|---|---|
| Ge fraction (in D4R) | −14 | −23 | 16 | 2 | |
| Total CN (Ge–Ge) | 25 | 19 | 9 | −1 | |
| Occu Freq | D4R | −12 | −26 | 16 | 4 |
| Adj | 14 | 39 | −5 | −10 | |
| Frw | 30 | 11 | −8 | 3 | |
The largest super-cell effects are observed for the UTL framework, for which the super-cell is four times larger than the primitive cell and which contains four D4R units (ESI† Table S4), allowing us to probe the heterogeneity of D4R unit occupation in UTL as well. The super-cell contains two dense IPC-2 layers connected from each side by a pair of D4R units (Fig. 6), and similarly to the CTH case (section 3.2.3), the germanium prefers to form a germanium-rich (pair) of D4R units and the germanium-poorer D4R units, partially phase-separating approximately perpendicular to the [a00] direction (see Fig. 6 and also ESI† Fig. S41, S42, and S47). However, compared to CTH, germanium in UTL still strongly prefers to localize in D4R units, with the larger population of the IPC layers observed only for a very low Si/Ge ratio of 2.8. In the case of BEC, the adoption of a larger simulation cell leads only to intensification and the earlier (at lower Ge content) onset of the trends observed already for the primitive cell, namely, the formation of alternating germanium-rich and germanium-poor ‘layers’ coplanar with [00c] plane formed from germanium-rich and germanium-poor ‘rods’ co-linear either with [a00] or [0b0] direction (see ESI† Fig. S44). Only at Si/Ge = 1, germaniums start to cluster also along the [00c] direction. For IWW and CTH, the changes in the average germanium distribution due to the enlargement of the simulation cell are almost negligible.
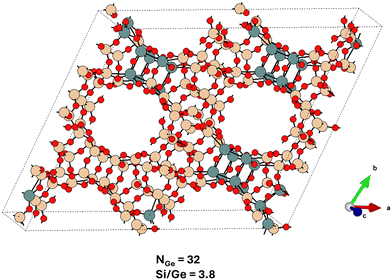 | ||
| Fig. 6 The global structure optimum for the UTL system with Si/Ge = 3.8 adopting a large simulation cell (Table S4†) – compare with Fig. 4. The Ge content at this Si/Ge ratio allows for a complete filling of D4R units with germanium atoms, however, a partial spillover of Ge atoms towards the non-D4R T sites is observed. The structure is viewed approximately along the c-axis. | ||
3.4 Generalizations and the modelling context
Both the preference of germanium for D4R occupation as well as for the formation of germanium clusters – typically evaluated using a total count of Ge–O–Ge bonds – have already been discussed and tested in the literature. The germanium preference for D4R occupation was confirmed in a few periodic DFT investigations (UTL,18 BEC,19 ITH12) for very low germanium loading (1–2 Ge atoms per unit cell), for which the exhaustive enumeration of germanium distribution is possible, and it has been associated with the particular distribution of the T–O–T angles in the D4R units. For the larger concentration of germanium, the sampling was limited to a few tens of expert-chosen distributions, which in addition strongly favoured a significant population of the D4R T-sites to start with (ITH,12 BEC19) or explicitly focused on the population of the D4Rs only (SOV,22 SOR,11 AST21). Even the older works using empirical force fields considered only a few hundred randomly generated structures for BEC14 and a range of other frameworks (AST, ASV, BEA, LTA, ISV).42 By contrast, in this work, we extensively probed the germanium distribution space across a broad range of germanium concentrations. We also quantify the preference of germanium for D4R units as a function of zeolite topology, and show that it is strong for low to intermediate germanium loading (approx. Si/Ge ≥ 5) but significantly weakens for high germanium loading, where other than D4R T-sites become strongly populated. Also, we show that even for low to intermediate germanium loading the germanium population in other than D4R T-sites is on average non-negligible (up to 50% of the Ge atoms are in non-D4R sites), despite the fact that most stable structures (the global structure optima), typically considered as the most representative structures in the literature, do contain a disproportionately high amount of germanium in the D4R units (Fig. 4). The distributions containing Ge atoms spilled-over to the non-D4R sites are both relatively stable and there are many of them, i.e., they have a high “density of states”, which makes them important for the total distribution at a finite temperature, i.e., we observe the increased role of the configuration entropy. There are also other more specific aspects to consider regarding the preference of germanium for D4R occupation, namely the role of heterogeneity in D4R populations once there are more D4R units present in the simulation cell. These D4R units can be either crystallographically equivalent or inequivalent. The heterogeneity of D4R units in the former case has been probed recently for SOV22 and SOR11 topologies (for a specific Si/Ge ratio and considering low tens of configurations). The results support the observation made herein about the large asymmetry in occupation of the individual D4R units in the simulation cell (Fig. 5). The authors related it to the clustering propensity of germanium, evaluated based on the number of the Ge–O–Ge links in different configurations. A strong positive correlation between the stability of the particular germanium distribution and the degree of germanium clustering is indeed confirmed herein for all zeolite topologies and across a broad range of Si/Ge ratios (see ESI† Fig. S8 and S51). An example of the heterogeneity in D4R occupations and a consequence of the tug-of-war between the germanium clustering and the D4R preference is the formation of the phase-separated germanium-rich and germanium-poor layers for CTH. The CTH topology is composed of rather thick dense CFI layers with at least four T-sites separating the D4Rs across the layer, but only three T-sites separating the D4R units along the layer. Hence, for the same Ge loading, a larger degree of Ge clustering can be achieved when the germanium atoms are spilled over in-between the germanium-rich D4Rs arranged along the layer than across the layer. Besides this distribution pattern, we may also distinguish some preference for the “spillover” germanium to spread along the specific directions (in the framework/adjacent sites) that are rich in S4R units, i.e., along the chain of S4R units in UOV and along the S4R-containing framework sites in the vicinity of the T2-site-edges of the two neighbouring D4Rs units in IWW (see ESI† Fig. S21–S23). For a topology with crystallographically inequivalent D4Rs units – UOV – we observe a strong dependence of the germanium occupation on the type of the D4R unit with the Ge occupation being the largest for “T3–T6” D4R and the smallest for “T14–T18” D4R unit. An explanation for this observation may be the larger lattice strain at the “T3–T6” D4R unit, with a few 5 M-rings in the close vicinity (the vertex symbols of T3 and T6 sites are 4·5·4·6·4·10), to be contrasted with the more flexible environments of the “T14–T18” and “T17–T19” D4R units surrounded by 6 M- or larger rings. We may hypothesize that such markedly different preferences for Ge occupation of the crystallographically inequivalent D4R units can be utilized to induce the hydrolytic instability into a specific crystallographic direction, i.e., the direction along which the (more) strained D4R units are arranged.An important issue that our models do not address is the role of fluoride anions and organic structure-directing agents (OSDAs). Earlier works,11,12,21,22 which consider only a limited amount of configurations, have shown that the role of fluoride/OSDA is significant and that their inclusion in the model commonly leads to an increased preference for germanium occupation of the D4R units and to the lowering of the asymmetry in Ge occupations among the D4R units present in the unit cell. Gramatikov et al.11,22 also showed that the stability of the configurations depends heavily on fluoride location and OSDA orientation, which could not be extensively sampled using the costly periodic DFT calculations. In addition, one can expect that the size and the chemical composition of the OSDA as well as the zeolite topology would play a sizable role as well. Hence, it appears that, until a more general ML potential, similar to the examples proposed recently,39,43,44 capable of comprehensive sampling of configuration space that also encompasses fluoride/OSDAs is available, it is difficult to draw reliable, quantitative predictions regarding the germanium distributions for any of the (D4R-containing) zeolite frameworks. Also, during zeolite synthesis, besides the thermodynamic stability, kinetic factors may play a role, which are not captured by Monte Carlo simulations focusing on low-energy structures. Despite these limitations, the qualitative agreement of our calculations with some of the experimental observations (see section 3.5 below) suggest that even by employing only the bare-framework models, one can capture an important aspect of germanium distributions, which may turn out to be decisive for some of the topologies.
3.5 Comparison with experimental data
UTL is a quintessential example of the ADOR-able zeolite (commonly prepared with Si/Ge = 4–6) and our calculations confirm a very strong preference for germanium to occupy the D4R units, which is indeed exceptional amongst the zeolite topologies considered herein (see Fig. 2). Also, we observe, in line with experimental interpretations,45 a strong preference of germanium to cluster within the particular D4R unit, e.g., in the S4R subunits (see ESI† Fig. S18). A similarly good correspondence between experimental46 and NNP-based predictions are observed for unit cell volumes and lattice parameters (approx. 1% error – see Table S10 in ESI†). Interestingly, the germanium-containing UTL zeolite has been shown to undergo a spectrum of transformations47 with significantly varying products, ranging from a complete removal of all the D4R units (IPC-4/PCR)48 to the removal of S4R sub-units from only a fraction of D4R units (IPC-7 (ref. 49)). This variability of products is commonly associated with the varying conditions of the hydrolysis and of the subsequent rearrangement, however, the heterogeneity of the germanium distribution amongst the D4R units, e.g., such as the presence of germanium-rich and germanium-poor UTL-like layers reported above (section 3.3), can be expected also to play a role. The existence of the UTL-like layers with varying germanium content may serve as a simple explanation for the observation of the partial hydrolysis products composed from a mixture of different connections between the UTL-like layers49 such as IPC-6 (*PCS) with layers connected by the S4R units or oxygen bridges and IPC-7 with layers connected by D4R or S4R units.There are numerous reports,14,15,45 including those for UTL, which use 19F MAS NMR spectra to determine the germanium distribution (counts) among the F− containing-D4R units (note that, commonly, the D4R units are the only structural units assumed to be occupied by germanium a priori). However, a few recent computational studies for STW,10 ITH12 and SOR11 germanosilicates show convincingly, that using the 1D NMR spectra, one is able to differentiate at best only amongst the purely siliceous D4Rs, those D4Rs containing isolated Ge atoms and those with at least one Ge–O–Ge link. In addition, even the ability to determine the location of F− anion within the framework (e.g., whether it is located in the D4R unit or in other parts of the framework) using 19F NMR was indicated12 to be limited to the purely siliceous case, i.e., the 19F NMR does not differentiate well between the cases with F− located in D4R or other structural units (e.g. in the [4·56] cage of ITH), unless the unit is purely siliceous. Therefore, we refrain from discussing the experimental data on germanium distributions, which are based only on the 19F MAS NMR spectra in the following.
For the BEC topology, a few studies13,14,16 reported average occupations based on PXRD measurements, which can be directly compared with our computational results presented above. In particular, Sastre et al.14 synthesized BEC samples that covered a broad range of Si/Ge ratios from ≈7 down to 1. The unit cell volumes reported for these BEC samples are close to the NNP predictions (errors are within 2% – see Table S7†). Also, their data show a strong preference for D4R occupations at lower Ge loadings, up to approximately 3–4 Ge atoms per D4R unit (Si/Ge ≈ 3), which is replaced by a surge in occupation of adjacent and framework sites for high Ge contents, with the germanium occupation of adjacent and framework T sites becoming almost the same to that of the D4R site at Si/Ge = 1. Importantly, the authors also report that even at higher Si/Ge ratios, the germanium occupation of other than D4R sites is not completely negligible and accounts for a few tenths of per cent of the total Ge loading. These observations, also supported by an earlier report13 from the same group, are qualitatively in line with our simulations (see Fig. 5 and S16†), with our predictions only mildly underestimating the D4R populations, which, e.g., leads to a break-even point between D4R and non-D4R T-site occupations to be observed slightly earlier (Si/Ge ≈ 1.9) then for the experiments (Si/Ge ≈ 1). The more recent PXRD data from Smeets et al.16 for BEC with Si/Ge = 5.1 localized, after a challenging diffraction pattern refinement, Ge atoms exclusively in D4R units – the discrepancy in the germanium occupation of D4R units between the work of Smeets et al. and the works discussed above may stem from the different OSDAs used for the BEC synthesis, since the role of OSDA in stabilization of different Ge distributions can be significant.11,22 Also, we note, that BEC zeolite has not been reported to give novel structural derivatives using the ADOR strategy, which is to be expected as BEC has a tetragonal symmetry (with crystallographically identical D4R units arranged along orthogonal directions). We confirm this by our calculations, observing the formation of ‘layer-like’ Ge-rich rods along both of these two directions (see sections 3.2.2 and 3.3). Alternatively, the unsuccessful ADOR may be attributed to the very high content of D4R T sites (50% of all T sites), hydrolysis of which would lead to extensive framework destruction, thereby preventing the rearrangement of the remaining components into a new zeolite framework.
Similarly to BEC, multiple initial attempts45,50,51 to obtain novel zeolitic structures using the ADOR strategy failed for IWW germanosilicate. For IWW with approx. Si/Ge ≥ 5, the framework was found to retain 3D connectivity and crystallinity, undergoing only limited degermanation accompanied by the creation of defects. This resistance to delamination was associated45 with the presence of Si-rich D4R units. For higher Ge content (Si/Ge ≈ 3–4), IWW50 underwent more significant structural changes, leading to the generation of a narrowly-distributed mesoporosity (peaked at approx. 3 nm) that remained even after subsequent calcination treatment, which resulted in regeneration of almost purely siliceous IWW. Also, the partially hydrolyzed intermediate could not be swelled by the surfactant, indicating that the IWW layers in the hydrolyzed intermediate are still connected via the Si–O bridges. Only the subsequent work of Kasneryk et al.52 using the acidic vapour-phase-transport approach managed to succeed in generating a new zeolite topology (IPC-18 with IWW layers connected by S4R units only) from the IWW parent zeolite. But even in this work, a significant structural rearrangement including the IWW layer as well as its significant distortion are reported. The herein observed large asymmetry in D4R unit occupation by germanium (Fig. 5), i.e., the retention of almost purely siliceous D4Rs in IWW, as well as phase-separation of germanium into Ge-rich and Ge-poor rods/planes perpendicular to the IWW layers, and a sizable germanium population in the T sites within the IWW layers, may serve as possible explanations for the experimental difficulties in IWW delamination (due to Si-rich D4Rs), the narrowly-distributed mesoporosity (due to leaching of Ge-rich rods/planes), and the reportedly very large rearrangement/distortion of the IWW layers (due to sizable Ge population in the layers). However, Liu et al.15 claim, based on the PXRD refinement for IWW with Si/Ge = 4.3, that almost all germanium is located in the D4Rs, amounting to approx. 4.5 Ge per D4R unit on average, which is approximately 1.5–2 more Ge atoms than predicted by us (Fig. 2). While some underestimation of D4R population is possible (see also the discussion above for the BEC case), e.g., due to the role of OSDA, we would expect that such a high content of Ge atoms in D4R units should allow for the IWW delamination, which is not observed experimentally, unless the Si/Ge ratio drops to as low as 1.53
UOV with Si/Ge ≈ 3 was reported5,17,52 to successfully transform into a new IPC-12 structure (UOV layers connected with the oxygen bridges only) using the ADOR strategy. However, the hydrolyzed intermediate could not be swollen5 using the surfactant and a strong signal corresponding to F− anions in purely siliceous D4R units was present5,17 in the 19F MAS NMR spectra, all of which indicate a heterogeneity in germanium population across the D4R units. This is broadly in agreement with our simulations which predict the presence of Ge-rich and Ge-poor D4Rs units for UOV with Si/Ge < 6–7 (Fig. 4, 5, S21 and S34†). Also, we predict a significant population of germanium in the UOV layers at least for Si/Ge < 3–4 (Fig. 5), which is consistent with the observed17 lability of the UOV framework at ambient conditions at very low Ge loadings (Si/Ge ≈ 1.4) leading to a loss of crystallinity and formation of GeO2. Yet, Kasneryk et al.17 showed that even a modest change in one of the synthesis parameters (Si/Ge ratio in the synthesis gel) – which does not change the Si/Ge ratio of the final UOV samples – can lead to non-negligible effects on the 19F MAS NMR spectra and the propensity of UOV to undergo ADOR transformation. This is presumably a consequence of some differences in the Ge distributions between these UOV samples, the origin of which is, as discussed in detail above (section 3.4), beyond the prediction capabilities of the models adopted herein.
The CTH(–A) structure adopted herein, never observed as a pure ordered material in the experiments, is an ordered member of the disordered framework structure family denoted as *CTH, or also known as an intergrowth family CIT-13, which are a set of polymorphs that differ in the connectivity pattern54 between CFI layers and a row of D4R units. The Ge-rich (Si/Ge ≈ 4) samples of the intergrowth *CTH were reported to undergo the ADOR-type transformation, leading to the formation of daughter zeolites with CFI layers connected by S4R55 or direct O-linkages.55–57 However, a significantly increased efficacy of the alkaline-based delamination was noted in some of these studies,56,57 hinting at the presence of the Si–O–Si connections between the CFI layers within the D4R units. This partially counters the previous PXRD-based structure refinement58 for mildly higher Si/Ge = 5.6 that places the most Ge atoms (≈80%) into D4R units, i.e., about four Ge atoms per D4R unit at this Si/Ge ratio. These seemingly contrasting observations may be interpreted as a consequence of the heterogeneity in D4R occupations, which we also observe in our simulations (Fig. 5). However, our computational predictions (Fig. 5) seem to moderately underestimate the germanium population of the D4R units around this Si/Ge ratio (≈50%) at the expense of increased population of the T sites inside the CFI layers, which may be related the effect11,22 of fluoride/OSDA.
Lastly, we probed the generality of our NNPs for three other non-ADORable topologies composed almost solely from the D4R units; ASV, AST and STW (see in ESI,† Tables S6 and S11 for STW, S8 and S13 for AST, S9 and S14 for ASV). In particular, for STW topology, Rigo et al.,10 reported average Ge occupations of all symmetrically inequivalent T sites based on PXRD measurements for two Si/Ge ratios (Si/Ge = 1.5 and 0.6), which can be directly compared with our computational results (see Fig. S17†). Similar to BEC, our predictions are in qualitative agreement with the experimental occupations, favouring occupation of T1/T2 and T3/T4 sites over the T5 site, the only non-D4R T site. Also, our predictions for STW are closer to the experimental occupations than the effective Hamiltonian approach proposed by Rigo et al.10 We also evaluated (see section 2.1) and compared a number of structural parameters (unit cell volumes, lattice parameters, T–O–T angles and T–O bond lengths) with the available experimental (and computational) data for AST,21,59,60 ASV60–62 and STW.10,63 Note, however, that the direct comparison is problematic as most experimental data are reported for samples containing fluoride and OSDA, while our computational models are devoid of these occluded species, with the inclusion of occluded species having a sizable effect on the structural parameters such as unit cell volumes and lattice parameters.21 Nevertheless, for STW, the NNP (and DFT) predictions are close to the experimental observations, e.g., the predicted unit cell volumes differ by less than 2–3%, but larger discrepancies (e.g., 5–10% in volume) are observed for ASV and AST in their pure germanate forms.
4 Conclusions
We have generated and verified a transferable neural network based potential that is capable of comprehensive sampling of germanium distributions in germanosilicate zeolites across a broad range of framework topologies and Si/Ge ratios. The potential was applied to determine the preferential location of germanium at ambient conditions in five D4R-containing zeolites (UTL, BEC, UOV, IWW and *CTH), utilizing a global structure search method: basin-hopping Monte Carlo. The extensive sampling of the low-energy germanium distributions showed that the main determinant of the distribution stability is the degree of germanium clustering, which typically leads to phase-separation into Ge-rich and Ge-poor parts of the framework at high Ge loadings, largely irrespective of the specific structural unit. At low to medium Ge loadings (approx. Si/Ge ≥ 5) the D4R units clearly stand out as the “nucleation” centers for the germanium clustering, which results in a strong preference of germanium to occupy the D4R units at such Si/Ge ratios. Yet, the consequence of a strong tendency of germanium to cluster is the significant asymmetry in D4R occupations at all Ge loadings, i.e., while some of the D4R units are Ge-rich, others remain Ge-poor across a range of Si/Ge ratios. These general trends are mildly modulated by the topological effects with, e.g., UTL exhibiting a significant preference for D4R occupation by germanium, while in UOV the germanium occupation of D4R unit is barely preferred. Our calculations hint at some synthesis design handles that may be exploited in selective hydrolysis, e.g., the introduction of crystallographically inequivalent D4R units, which are observed to result in markedly different Ge occupations.Despite the fact that our description is limited to bare germanosilicate frameworks, and does not consider the role of fluoride anions and organic structure directing agents (OSDAs), these intrinsic germanium distribution trends are able to provide qualitative explanations for some important aspects observed in experiments, e.g., a difficulty to delaminate some topologies (possibly due to existing Si–O–Si links in D4R units connecting the layers), the formation of the ADOR-based daughter zeolites that are composed of a mixture of different layer connections (possibly due to the asymmetry of D4R Ge-occupations) and the formation of narrowly-distributed mesoporosity upon partial hydrolysis (possibly due to a presence of Ge-rich rods/planes at low Si/Ge ratios). Hence, we believe, that this model will allow for rapid screening of zeolite topologies for targeted transformations, such as the ADOR strategy.48
Data availability
The trained neural network potentials (NNPs), the DFT (PBE + D3(BJ)) training data, the generalization tests, as well as the scripts (analysis, post-processing, etc.) and the ensemble of zeolite structures obtained from basin hopping Monte Carlo simulation for all zeolite topologies and Si/Ge ratios considered are publicly available in a Zenodo repository under CC-BY-NC-SA 4.0 license: https://doi.org/10.5281/zenodo.13357083. The additional data supporting this article have also been included as part of the ESI,† including information on generalization tests, details on zeolite models adopted, convergence tests for basin hopping Monte Carlo, Ge–Ge partial radial distribution functions, correlations between stability and Ge–O–Ge bond count, additional low-energy structures, and more detailed characterizations of the germanium distributions (Ge–Ge coordination number, Ge count in D4R, occupation frequency per T site type, asymmetry of D4R units, etc.).Author contributions
LG and PN acquired the funding. LG, CJH, AE conceptualised and administered the project. CJH, AE generated and curated the the reference DFT data for the generation of the training database, AE trained the neural network potential. AE also carried out initial tests of the basin-hopping Monte Carlo simulations. IS carried out the production basin hopping Monte Carlo simulations. IS and AE analysed the data, LG helped with the data analysis and devised the custom metrics for germanium distribution analysis. IS prepared the article graphics. LG supervised the investigation. IS wrote the original draft of the manuscript. LG, AE, and CJH carried out the manuscript review and editing.Conflicts of interest
There are no conflicts to declare from any author.Acknowledgements
Charles University Centre of Advanced Materials (CUCAM) (OP VVV Excellent Research Teams, project number CZ.02.1.01/0.0/0.0/15_003/0000417) is acknowledged. LG acknowledges the support of the Czech Science Foundation (23-07616S). This work was supported by the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID: 90254) and the ERC_CZ project LL 2104 (CJH). The authors thank Miroslav Položij and Mengting Jin for preliminary calculations and useful discussions.Notes and references
- S. Mintova, M. Jaber and V. Valtchev, Chem. Soc. Rev., 2015, 44, 7207–7233 RSC.
- P. Eliášová, M. Opanasenko, P. S. Wheatley, M. Shamzhy, M. Mazur, P. Nachtigall, W. J. Roth, R. E. Morris and J. Čejka, Chem. Soc. Rev., 2015, 44, 7177–7206 RSC.
- M. Mazur, P. S. Wheatley, M. Navarro, W. J. Roth, M. Položij, A. Mayoral, P. Eliášová, P. Nachtigall, J. Čejka and R. E. Morris, Nat. Chem., 2016, 8, 58–62 CrossRef CAS PubMed.
- D. N. Rainer, C. M. Rice, S. J. Warrender, S. E. Ashbrook and R. E. Morris, Chem. Sci., 2020, 11, 7060–7069 RSC.
- V. Kasneryk, M. Shamzhy, M. Opanasenko, P. S. Wheatley, S. A. Morris, S. E. Russell, A. Mayoral, M. Trachta, J. Čejka and R. E. Morris, Angew. Chem., Int. Ed., 2017, 56, 4324–4327 CrossRef CAS PubMed.
- M. O'Keeffe and O. M. Yaghi, Chem. – Eur. J., 1999, 5, 2796–2801 CrossRef.
- L. A. Villaescusa, P. Lightfoot and R. E. Morris, Chem. Commun., 2002, 2220–2221 RSC.
- A. Pulido, G. Sastre and A. Corma, ChemPhysChem, 2006, 7, 1092–1099 CrossRef CAS PubMed.
- X. Liu, Y. Chu, Q. Wang, W. Wang, C. Wang, J. Xu and F. Deng, Solid State Nucl. Magn. Reson., 2017, 87, 1–9 CrossRef CAS PubMed.
- R. T. Rigo, S. R. Balestra, S. Hamad, R. Bueno-Perez, A. R. Ruiz-Salvador, S. Calero and M. A. Camblor, J. Mater. Chem. A, 2018, 6, 15110–15122 RSC.
- S. P. Gramatikov, P. S. Petkov and G. N. Vayssilov, Inorg. Chem. Front., 2022, 9, 3747–3757 RSC.
- M. Fischer, C. Bornes, L. Mafra and J. Rocha, Chem. – Eur. J., 2022, 28, e202104298 CrossRef CAS PubMed.
- A. Corma, M. T. Navarro, F. Rey, J. Rius and S. Valencia, Angew. Chem., 2001, 113, 2337–2340 CrossRef.
- G. Sastre, J. A. Vidal-Moya, T. Blasco, J. Rius, J. L. Jordá, M. T. Navarro, F. Rey and A. Corma, Angew. Chem., Int. Ed., 2002, 41, 4722–4726 CrossRef CAS PubMed.
- X. Liu, U. Ravon, F. Bosselet, G. Bergeret and A. Tuel, Chem. Mater., 2012, 24, 3016–3022 CrossRef CAS.
- S. Smeets, L. Koch, N. Mascello, J. Sesseg, L. McCusker, M. Hernández-Rodríguez, S. Mitchell and J. Pérez-Ramírez, CrystEngComm, 2015, 17, 4865–4870 RSC.
- V. Kasneryk, M. Shamzhy, M. Opanasenko, P. S. Wheatley, R. E. Morris and J. Čejka, Dalton Trans., 2018, 47, 3084–3092 RSC.
- S. O. Odoh, M. W. Deem and L. Gagliardi, J. Phys. Chem. C, 2014, 118, 26939–26946 CrossRef CAS.
- P. Kamakoti and T. A. Barckholtz, J. Phys. Chem. C, 2007, 111, 3575–3583 CrossRef CAS.
- G. Sastre, A. Cantin, M. J. Diaz-Cabañas and A. Corma, Chem. Mater., 2005, 17, 545–552 CrossRef CAS.
- M. Fischer, J. Phys. Chem. C, 2018, 123, 1852–1865 CrossRef.
- S. P. Gramatikov, P. S. Petkov, Z. Wang, W. Yang and G. N. Vayssilov, Front. Chem. Sci. Eng., 2024, 18, 58 CrossRef CAS.
- A. Erlebach, P. Nachtigall and L. Grajciar, npj Comput. Mater., 2022, 8, 174 CrossRef CAS.
- G. Imbalzano, A. Anelli, D. Giofré, S. Klees, J. Behler and M. Ceriotti, J. Chem. Phys., 2018, 148, 241730 CrossRef PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B, 2013, 87, 184115 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B, 1994, 49, 14251 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758 CrossRef CAS.
- K. Schütt, P. Kessel, M. Gastegger, K. Nicoli, A. Tkatchenko and K.-R. Müller, J. Chem. Theory Comput., 2018, 15, 448–455 CrossRef PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, et al. , J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- D. P. Kingma and J. Ba, arXiv, 2014, preprint, arXiv:1412.6980, DOI:10.48550/arXiv.1412.6980.
- A. Erlebach, M. Šípka, I. Saha, P. Nachtigall, C. J. Heard and L. Grajciar, Nat. Commun., 2024, 15, 4215 CrossRef CAS.
- J. Lee Rodgers and W. A. Nicewander, Am. Stat., 1988, 42, 59–66 CrossRef.
- D. J. Wales and J. P. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- G. Sastre, A. Pulido and A. Corma, Microporous Mesoporous Mater., 2005, 82, 159–163 CrossRef CAS.
- C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728 CrossRef PubMed.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, Nat. Mach. Intell., 2023, 5, 1031–1041 CrossRef.
- N. Kasian, A. Tuel, E. Verheyen, C. E. Kirschhock, F. Taulelle and J. A. Martens, Chem. Mater., 2014, 26, 5556–5565 CrossRef CAS.
- J.-L. Paillaud, B. Harbuzaru, J. Patarin and N. Bats, Science, 2004, 304, 990–992 CrossRef CAS.
- J. Zhang, O. Veselý, Z. Tošner, M. Mazur, M. Opanasenko, J. Čejka and M. Shamzhy, Chem. Mater., 2021, 33, 1228–1237 CrossRef CAS.
- W. J. Roth, P. Nachtigall, R. E. Morris, P. S. Wheatley, V. R. Seymour, S. E. Ashbrook, P. Chlubná, L. Grajciar, M. Položij and A. Zukal, et al. , Nat. Chem., 2013, 5, 628–633 CrossRef CAS PubMed.
- P. S. Wheatley, P. Chlubná-Eliášová, H. Greer, W. Zhou, V. R. Seymour, D. M. Dawson, S. E. Ashbrook, A. B. Pinar, L. B. McCusker and M. Opanasenko, et al. , Angew. Chem., 2014, 126, 13426–13430 CrossRef.
- P. Chlubná-Eliášová, Y. Tian, A. B. Pinar, M. Kubú, J. Čejka and R. E. Morris, Angew. Chem., 2014, 126, 7168–7172 CrossRef.
- L. Burel, N. Kasian and A. Tuel, Angew. Chem., 2014, 126, 1384–1387 CrossRef.
- V. Kasneryk, M. Shamzhy, J. Zhou, Q. Yue, M. Mazur, A. Mayoral, Z. Luo, R. E. Morris, J. Čejka and M. Opanasenko, Nat. Commun., 2019, 10, 5129 CrossRef PubMed.
- K. Lu, J. Huang, M. Jiao, Y. Zhao, Y. Ma, J. Jiang, H. Xu, Y. Ma and P. Wu, Microporous Mesoporous Mater., 2021, 310, 110617 CrossRef CAS.
- International Zeolite Association, Database of Zeolite Structures, http://www.izastructure.org/databases/, Accessed 2021-03-02.
- D. S. Firth, S. A. Morris, P. S. Wheatley, S. E. Russell, A. M. Slawin, D. M. Dawson, A. Mayoral, M. Opanasenko, M. Položij and J. Čejka, et al. , Chem. Mater., 2017, 29, 5605–5611 CrossRef CAS.
- J. H. Kang, D. Xie, S. I. Zones and M. E. Davis, Chem. Mater., 2019, 31, 9777–9787 CrossRef CAS.
- X. Liu, W. Mao, J. Jiang, X. Lu, M. Peng, H. Xu, L. Han, S.-A. Che and P. Wu, Chem. – Eur. J., 2019, 25, 4520–4529 CrossRef CAS.
- J. H. Kang, D. Xie, S. I. Zones, S. Smeets, L. B. McCusker and M. E. Davis, Chem. Mater., 2016, 28, 6250–6259 CrossRef CAS.
- Y. Wang, J. Song and H. Gies, Solid State Sci., 2003, 5, 1421–1433 CrossRef CAS.
- G. Sastre and A. Corma, J. Phys. Chem. C, 2010, 114, 1667–1673 CrossRef CAS.
- H. Li and O. Yaghi, J. Am. Chem. Soc., 1998, 120, 10569–10570 CrossRef CAS.
- G. Sastre and J. D. Gale, Chem. Mater., 2003, 15, 1788–1796 CrossRef.
- A. Rojas and M. A. Camblor, Angew. Chem., Int. Ed., 2012, 51, 3854–3856 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Information on generalization tests, details on zeolite models adopted, convergence tests for basin hopping Monte Carlo, Ge–Ge partial radial distribution functions, correlations between stability and Ge–O–Ge bond count, additional low-energy structures, and more detailed characterizations of the germanium distributions are provided. Additional data (neural network potentials, training database, neural network potential testing data, analysis and post-processing scripts, zeolite structures from basin hopping Monte Carlo, etc.) are provided in the Zenodo repository at https://doi.org/10.5281/zenodo.13357083. See DOI: https://doi.org/10.1039/d4cy00763h |
| ‡ Deceased. |
| This journal is © The Royal Society of Chemistry 2024 |