 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Generative BigSMILES: an extension for polymer informatics, computer simulations & ML/AI†
Ludwig
Schneider
 *a,
Dylan
Walsh
*a,
Dylan
Walsh
 b,
Bradley
Olsen
b,
Bradley
Olsen
 b and
Juan
de Pablo
b and
Juan
de Pablo
 *a
*a
aPritzker School of Molecular Engineering, University of Chicago, 5740 S. Ellis Ave, Chicago, IL, USA. E-mail: depablo@uchicago.edu; ludwigschneider@uchicago.edu
bDepartment of Chemical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA, USA
First published on 17th November 2023
Abstract
The BigSMILES notation, a concise tool for polymer ensemble representation, is augmented here by introducing an enhanced version called generative BigSMILES. G-BigSMILES is designed for generative workflows, and is complemented by tailored software tools for ease of use. This extension integrates additional data, including reactivity ratios (or connection probabilities among repeat units), molecular weight distributions, and ensemble size. An algorithm, interpretable as a generative graph is devised that utilizes these data, enabling molecule generation from defined polymer ensembles. Consequently, the G-BigSMILES notation allows for efficient specification of complex molecular ensembles via a streamlined line notation, thereby providing a foundational tool for automated polymeric materials design. In addition, the graph interpretation of the G-BigSMILES notation sets the stage for robust machine learning methods capable of encapsulating intricate polymeric ensembles. The combination of G-BigSMILES with advanced machine learning techniques will facilitate straightforward property determination and in silico polymeric material synthesis automation. This integration has the potential to significantly accelerate materials design processes and advance the field of polymer science.
1 Introduction
Polymers consist of thousands of repeating monomers, whose exact sequence or length poses a significant challenge to representation by traditional line notations. These notations, which depict each individual atom, such as International Chemical Identifier (InChI),1,2 SELF-referencing embedded string (SELFIES),3 or Simplified Molecular Input Line Entry System (SMILES),4 can rapidly become excessively lengthy and unwieldy for polymers. CurlySMILES5 provides a variant of the SMILES notation that aims to address this challenge by employing a compact representation for recurring elements. This is achieved through the enclosure of such elements within curly brackets, giving rise to the notation's distinctive name.‡ The inherently stochastic nature of polymeric materials necessitates a description in terms of ensembles of molecules, as opposed to a single-molecule representation, which is the approach that has been followed to date in traditional notations.BigSMILES7–9 provides an alternative solution, and relies on a line notation that is tailored specifically for polymeric systems. This notation captures individual molecular fragments and their interconnections via bond descriptors, making it a more appropriate choice for polymer representation. BigSMILES has gained acceptance for its user-friendliness and accessibility to both humans and machines. Its successful integration into various polymer informatics ecosystems, such as CRIPT,10 serves as a testament to its usefulness. As shown in Fig. 2a, BigSMILES extends the functionality of SMILES by portraying a polymer as a sequence of interconnected monomers. However, it suffers from the fact that it is purely descriptive and lacks generative capabilities.
In its original form, a single BigSMILES string represents a subset of the chemical space, which is often expansive and inclusive of “improbable polymer molecules”. For instance, a BigSMILES notation for a random copolymer ensemble frequently encompasses the homopolymers of its individual components. However, BigSMILES is not designed to assign likelihoods to structures within the chemical space, leading to an equal representation of all possible ensemble realizations, including those that are highly improbable. This characteristic restricts the amount of information that BigSMILES can convey about a polymeric material, which naturally consists of a spectrum of more and less probable structures.
The aim of this work is to enhance BigSMILES with a compact notation that encapsulates the inherent stochasticity of a polymer ensemble. BigSMILES was chosen as the foundation due to its user-friendly notation, which is comprehensible to both humans and machines. Crucially, our proposed extension maintains compatibility with the original BigSMILES notation, allowing for the additional information to be easily omitted if so desired. In order to assign likelihoods to polymer ensembles and molecules, information about the molecular architecture and composition is essential. The enhanced notation, known as generative BigSMILES, or G-BigSMILES, incorporates details such as molecular weight distributions, reactivity ratios (which are probabilities of repeat unit connections), and the size of ensemble realizations. Fig. 1 offers a conceptual illustration of how generative BigSMILES refines the broader space delineated by original BigSMILES and assigns likelihoods to individual polymers within the ensemble. Our ESI† includes multiple case studies that underscore the efficacy of G-BigSMILES for specification of precise composition ensembles.
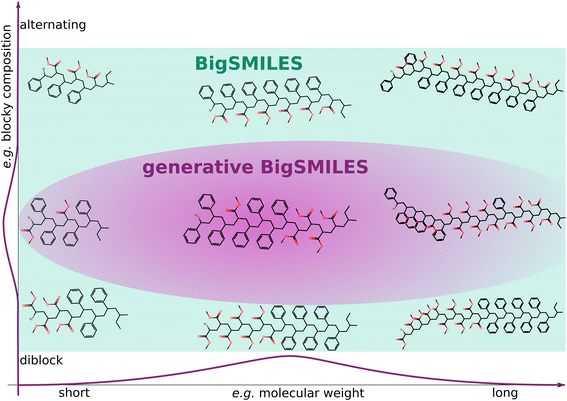 | ||
| Fig. 1 Schematic representation of the distinction between the original BigSMILES and the enhanced G-BigSMILES notation. While BigSMILES delineates a subset of the chemical space by describing the participating monomers and their connections, G-BigSMILES refines a subset of this space and attributes varying likelihoods to potential realizations within an ensemble. This advanced notation notably includes the molecular weight distribution and provides detailed information regarding the likelihood of specific compositions and sequences. As an illustrative example, we showcase a PS-PMMA ensemble. In contrast to the original BigSMILES notation, which cannot differentiate molecular weight or blockiness, G-BigSMILES narrows this example to a random sequence. Please refer to the PS-PMMA example in the ESI† for additional details. | ||
The capability to translate additional information into concrete realizations of polymer ensembles using a precise algorithm is crucial, particularly for applications such as automated computer simulations.11 However, it is important to recognize that this generation deviates from the chemical reaction pathway and can only approximate reality with idealized models. This function enables the generation of initial conditions for a simulation box directly from a single line notation input, thereby facilitating automated exploration of the chemical space in the search for novel polymeric materials. This process can also be reversed to assign generation probabilities to molecules within a specific ensemble, an essential feature for certain machine learning applications as it allows for the evaluation of a molecule's likelihood of belonging to a target ensemble. Both of these algorithms, along with a reference implementation, are detailed in the subsequent sections.
First, we delve into the extension of the notation, followed by a comprehensive discussion of the generating algorithm and, finally, we explore the interpretation of this notation and its potential applications.
2 Results
The BigSMILES line notation has been formally documented and published in the scientific literature7 and is currently in active use within community polymer projects.10 In the present context, we offer a succinct overview of key elements that are pertinent to the proposed extension and the generation of polymers. For a thorough introduction and detailed rationale, we direct readers to the relevant literature.A BigSMILES string is essentially a SMILES string in which atoms, or a series of atoms, can be depicted as stochastic elements (Fig. 2a). These elements are enclosed within curly brackets and are comprised of a comma-separated list of repeat units and end units. A repeat unit is represented by a SMILES fragment combined with a set of bond descriptors, which clarify the potential chemical bonding between repeating units. In contrast, an end unit, distinguished from regular repeat units by the use of a semi-colon, serves to terminate the molecule by providing a singular bond descriptor. Bond descriptors can take the form of unidirectional [$] or directional [<], [>] symbols, thereby enabling connections exclusively between dissimilar bond descriptors.
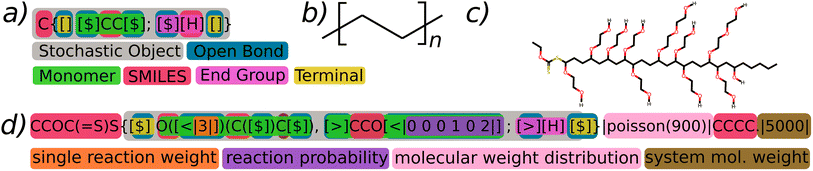 | ||
| Fig. 2 In panel (a), a simplified representation of poly-(ethylene) is presented, highlighting the stochastic object in grey, open descriptors in blue, terminal bond descriptors in yellow, monomeric repeat units in green, end groups in hot pink, and SMILES fragments in red. Panel (b) illustrates the conventional graphical depiction of the corresponding polymer structure (it's notable that the value of n is unspecified in BigSMILES (a)). Panel (d) introduces G-BigSMILES with the generative extension, featuring a representative single reaction weight denoted in orange, a more detailed reaction probability shown in purple, a specification of the molecular weight distribution in light pink, and a system molecular weight specification in brown. Panel (c) demonstrates a representative molecular representation that is part of the ensemble described in panel (d). A thorough step-by-step explanation of the generation process for such molecules can be found in Fig. 3. It is important to underscore that the example BigSMILES notation chosen is not intended to represent chemical realism but is used solely for illustrative purposes.§ | ||
2.1 Generative BigSMILES notation
With the generative BigSMILES extension (refer to Fig. 2d), we enhance the stochastic object and bond descriptors in BigSMILES notation by incorporating additional text, enclosed within || characters. This extension provides the necessary information to generate a system of molecules. The | character was specifically chosen for this purpose, as it is not used in the SMILES and BigSMILES notations, thereby ensuring seamless compatibility between the notations. By simply eliminating all characters between the | markers, the G-BigSMILES can be reverted back to the original BigSMILES notation.The G-BigSMILES notation contributes the following information to a BigSMILES string:
(1) Stochastic objects are expanded to incorporate information about their molecular weight distribution (shown in pink in Fig. 2).
(2) Bond descriptors are enhanced to manage the connection probabilities within stochastic objects (shown in orange and purple in Fig. 2).
(3) We introduce a notation that incorporates the quantification of the number of molecules in an ensemble realization, depicted in brown in Fig. 2, while also allowing for the specification of mixtures comprising different molecular species.
In the following sections, we offer a comprehensive introduction to each of these extensions and explain how they enable the generation of complete molecular systems. Our discussion covers both the theoretical aspects of the notation and the generation algorithm, and it refers to a reference implementation available at https://github.com/InnocentBug/bigSMILESgen.
2.2 Generation algorithm
The G-BigSMILES notation is inherently linked with its interpretation as an algorithm. It is formulated to enable the generation of molecular ensembles from this notation. This section outlines the details of our notation enhancements and the interpretation processes applied by the generation algorithm.Importantly, G-BigSMILES reinstates the comprehensive structural representation of molecules that is inherent in original line notations such as SMILES and InChI. This is achieved by facilitating the generation of the molecular structures.
In the reference implementation, we provide support for the following molecular weight distributions that represent idealization of realistic distributions.
(1) Schulz–Zimm distribution: represented as |schulz_zimm(Mw, Mn)|,14 it corresponds to the probability mass function (PMF)
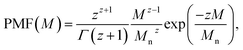 | (1) |
(2) Flory–Schulz distribution: textually represented as |flory_schulz(a)|,15 this distribution corresponds to the PMF
| PMF(Mw) = a2Mw(1 − a)Mw−1, | (2) |
(3) Gaussian distribution: denoted as |gauss(m, s)|, this distribution is specified by the mean m and standard deviation s. The probability density function (PDF) is
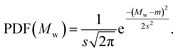 | (3) |
(4) Uniform distribution: denoted as |uniform(l, u)|, this distribution is defined by the lower bound l and upper bound u. The distribution is constant within the interval [l, u] and zero outside of it.
(5) Poisson: denoted as |poisson(N)|, this distribution is defined by the number average chain length N. The PDF is13
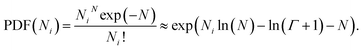 | (4) |
(6) Log-normal distribution: represented textually as |log_normal(Mn, Đ)|, the PDF is
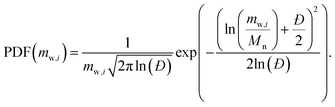 | (5) |
The log-normal distribution models narrow molecular weight dispersities (Đ ∈ [1, 2]) effectively.16
A user chooses a distribution based on either theoretical insights into reaction kinetics, e.g. the Schulz–Zimm distribution for controlled polymerization, or in a manner that aligns with an experimental molecular weight distribution, thereby determining parameters for that distribution. Regardless of the choice, this distribution remains a simplification of reality, and its effects on relevant properties must be rigorously evaluated.
Generating a molecule from a polymer ensemble with a specified molecular weight distribution involves a two-step process. Initially, a random molecular weight, denoted as Mw0, is drawn from the specified distribution. Then, the stochastic object is generated iteratively, until the molecular weight surpasses Mw0. During this process, after each addition of a repeat unit, the generated molecule is hypothetically terminated with the prescribed end groups. If the resulting molecule exceeds the weight Mw0, the generation is deemed complete. If not, the termination is reversed and the generation of repeat units continues. This termination condition is graphically illustrated in Fig. 3(ii) with a flowchart. The ESI† includes explicit tests that demonstrate the reference implementation is able to generate ensembles with the expected molecular weight distributions.
While all extension elements of G-BigSMILES are optional to conserve the underlying BigSMILES string, specifying a molecular weight distribution is required to generate molecules from a G-BigSMILES string.
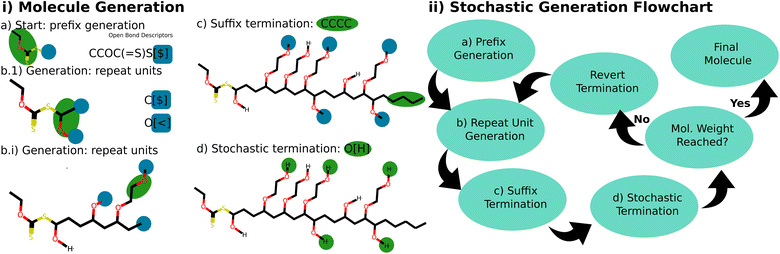 | ||
Fig. 3 This figure portrays the generation process of a stochastic molecule. (i) Generation of an example molecule, where the latest addition is highlighted in green, and open bond descriptors are accented in blue. (a) Molecule generation begins with the prefix CCOC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S)S[$]. (b.1) A backbone O([<])(C([$])C[$]) repeat unit is attached by selecting one of the available open-bond descriptors [$] based on their weight. With two open bond descriptors available for the next generation ([$], [<]), one is chosen randomly according to their weight (1, 2). If [$] is selected, the backbone grows; if [<] is chosen, the bottlebrush's side chain grows instead. (b.i) The propagation continues for multiple steps. Notably, the bottlebrush arm unit with bond descriptor CCO[<|0 0 0 1 0 2|] selects its next bond descriptor based on the listed weight specified, rather than the overall weight. Here, a 1 in 3 choice is made to continue the arm's growth, or a 2 in 3 choice is made to terminate the arm with a hydrogen atom. This serves a dual purpose: it ensures arm units connect only to arm units, and it allows for stochastic termination of the arms. In this example, some of the bottlebrush arms are already terminated, while others still feature an open bond descriptor. (c) The generation persists until the desired molecular weight is attained. At this juncture, the backbone is terminated with the suffixed butane end group. (d) The stochastic object is finalized by terminating all other open bond descriptors (bottlebrush arms) to a stochastic end group, once again based on the weight of the bond descriptors of the available end groups (hydrogen). The corresponding G-BigSMILES notation, CCOC( S)S[$]. (b.1) A backbone O([<])(C([$])C[$]) repeat unit is attached by selecting one of the available open-bond descriptors [$] based on their weight. With two open bond descriptors available for the next generation ([$], [<]), one is chosen randomly according to their weight (1, 2). If [$] is selected, the backbone grows; if [<] is chosen, the bottlebrush's side chain grows instead. (b.i) The propagation continues for multiple steps. Notably, the bottlebrush arm unit with bond descriptor CCO[<|0 0 0 1 0 2|] selects its next bond descriptor based on the listed weight specified, rather than the overall weight. Here, a 1 in 3 choice is made to continue the arm's growth, or a 2 in 3 choice is made to terminate the arm with a hydrogen atom. This serves a dual purpose: it ensures arm units connect only to arm units, and it allows for stochastic termination of the arms. In this example, some of the bottlebrush arms are already terminated, while others still feature an open bond descriptor. (c) The generation persists until the desired molecular weight is attained. At this juncture, the backbone is terminated with the suffixed butane end group. (d) The stochastic object is finalized by terminating all other open bond descriptors (bottlebrush arms) to a stochastic end group, once again based on the weight of the bond descriptors of the available end groups (hydrogen). The corresponding G-BigSMILES notation, CCOC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S)S{[$] O([<|3|])(C([$])C[$]), [>]CCO[<|0 0 0 1 0 2|]; [>][H] [$]}|poisson(900)| CCCC, is outlined in Fig. 2d. (ii) Flow chart overview of the generation algorithm for stochastic objects. S)S{[$] O([<|3|])(C([$])C[$]), [>]CCO[<|0 0 0 1 0 2|]; [>][H] [$]}|poisson(900)| CCCC, is outlined in Fig. 2d. (ii) Flow chart overview of the generation algorithm for stochastic objects. | ||
2.2.2.1 Initiating the generation of a new molecule. The initiation of a stochastic element can take two distinctive routes, contingent on whether it is preceded by another object or if it stands as the first object in the sequence.
When a stochastic object follows another object, the preceding object represents a segment of the final molecule and must have exactly one open bond descriptor. This antecedent object could be a simple SMILES prefix, illustrated in Fig. 3a, or another stochastic object. In both scenarios, the left terminal bond descriptor of the stochastic object must not be empty, and this determines how the prefix is continued through the stochastic object. More details on this generation process are offered in the upcoming section on repeat unit generation.
Alternatively, when the stochastic object is the first in the sequence to be generated, the left terminal bond descriptor is empty. This case requires the specification of end groups for the molecule. An end group is selected based on the weight of its one bond descriptor, in a similar fashion to the repeat unit generation process, to initiate the generation of a new molecule. This selection leaves exactly one open bond descriptor, after which the generation of repeat units can commence.
2.2.2.2 Generation of repeat units within a stochastic object. During the process of generating repeat units, partially constructed molecules invariably maintain at least one open bond descriptor.¶
Each bond descriptor within the generative notation carries a corresponding weight. By default, this weight is set to unity and explicit designation is omitted in the string, but it can be explicitly defined in the generative notation using the format [<|weight|] (accentuated in orange in Fig. 2d). Any positive number can be designated as the weight. The second step commences when an open bond descriptor is available, requiring selection of a new repeat unit and its corresponding reacting bond descriptor. This selection of the next open bond descriptor is randomly chosen according to the weight assigned to them. While we assign weights to the reactions, the compatibility of the BigSMILES notation for bond descriptors takes precedence over the assigned weights. This step provides two control procedures. The weights are specifically allocated to bond descriptors, not to the repeating units (monomers). This technique enables a high degree of control, even at the level of the individual monomers. For instance, distinct weights can be assigned within a single monomer using unidirectional bond descriptors, denoted as [$]. This allows us to finely modulate the distribution of head–tail, head–head, and tail–tail configurations along the polymer backbone.
In a straightforward scenario, the open bond descriptor of the already generated molecule is denoted by a weight value (highlighted in orange in Fig. 2d). The subsequent bond descriptor is selected from all compatible bond descriptors of the new repeat units, determined by their respective weights. For instance, in Fig. 2d, the [<|3|] bond descriptor of the backbone repeat unit carries a weight exceeding 1. As a result, the branch point is frequently given priority to enhance the growth of the bottlebrush arms over the backbone's growth. This exemplifies how weight adjustment can influence the frequency distribution of repeat units in the generated ensemble. The single weight bond descriptor notation is primarily useful if the monomer composition is known, but the individual reaction probabilities are unknown and can be assumed as uniformly random. The ESI† provides an example, where we verify that the reference implementation is capable of reproducing the desired monomer compositions with this notation. If the reaction probabilities between the different bond descriptors are known, either experimentally or computationally, the advanced notation of the subsequent section is preferred.
2.2.2.3 Advanced specification of bond descriptor weights. While the straightforward weight specification is recommended for linear polymers and does not require weights for selecting open bond descriptors in the first step, complex scenarios involving random polymers often need more precise control. In these cases, the weights provide a simple way to specify the relative composition of each repeat unit in the polymer.
For more intricate molecules, further control over step two – the selection of the subsequent reacting partner – is typically desired. This can be accomplished by specifying the probability of the reacting bond descriptor using a list of reaction weights r, formatted as [<|r1 r2 r3r4 …] (emphasized in purple in Fig. 2d). Each ri can be any positive number, and the length of this list should match the number of bond descriptors in the stochastic object, including end groups. Refer to the ESI† for an example of how to identify which weight corresponds to which bond descriptor in the stochastic object. The numerical values of ri denote the weight with which the corresponding bond descriptor is likely to react next. These weights are not normalized in the notation, but if normalized by the sum of 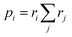 , they describe the probability to form a connection from this bond descriptor to the next bond descriptor in the molecule. It is important to remember that any ri that would connect incompatible bond descriptors must always be zero.
, they describe the probability to form a connection from this bond descriptor to the next bond descriptor in the molecule. It is important to remember that any ri that would connect incompatible bond descriptors must always be zero.
The normalization constant, 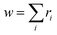 , represents the bond descriptor weight, and governs the probability of selecting open bond descriptors in the initial reaction step. Using
, represents the bond descriptor weight, and governs the probability of selecting open bond descriptors in the initial reaction step. Using 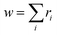 as the weight provides a succinct notation, with the ESI† detailing the combination of these elements. This approach ensures exact control over the reaction probability of each bond descriptor and can replicate experimentally observed reaction probabilities. Fig. 2d illustrates a bottlebrush polymer with a backbone unit, a branch point, and an arm repeat unit deviating from the backbone. We elucidate the G-BigSMILES’ mechanism for managing growth of both entities. The ESI† provides a detailed example for PS-PMMA, which emphasizes how a single reaction weight controls the PS
as the weight provides a succinct notation, with the ESI† detailing the combination of these elements. This approach ensures exact control over the reaction probability of each bond descriptor and can replicate experimentally observed reaction probabilities. Fig. 2d illustrates a bottlebrush polymer with a backbone unit, a branch point, and an arm repeat unit deviating from the backbone. We elucidate the G-BigSMILES’ mechanism for managing growth of both entities. The ESI† provides a detailed example for PS-PMMA, which emphasizes how a single reaction weight controls the PS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PMMA composition ratio, and the list notation refines the individual PS and PMMA microblock arrangements.
PMMA composition ratio, and the list notation refines the individual PS and PMMA microblock arrangements.
The weight of the branch point, denoted as [<|3|], exceeds that of the bond descriptors (depicted as [$]), which control the backbone growth. This weight discrepancy ensures that a branch point is typically followed by an arm extension unit.
The arm extension unit incorporates directional bond descriptors, such as the second one with assigned weights <|0 0 0 1 0 2|. This provides a refined mechanism to manipulate the arm's growth. The initial sequence of zeros ensures that the backbone does not extend from the arms, and the fifth zero indicates that the bond descriptor cannot react with itself.||
The first weight of 1 introduces a 1 in 3 chance for the arm to be extended by another arm segment. The final weight of 2 indicates a 2 in 3 probability of terminating the arm by connecting it with a stochastic end group (in this case: [H]). This weight distribution is critical in governing the molecular weight distribution of the arms, where the molecular weight follows a geometric distribution with a termination probability, p, of 2/3.
When employing reaction probabilities to control termination, e.g. assigning non-zero probabilities to end groups, the molecular weight distribution becomes limited to a geometric distribution. In the case of this bottle brush example, we control the molecular weight of the arms using this method. However, since the backbone bond descriptors do not utilize this approach, hence the molecular weight of the entire stochastic object is governed by the specification at the end, which follows a Poisson distribution. Therefore, it is possible to combine both termination methods, but caution must be exercised to avoid prematurely terminating stochastic objects with reaction weights if it is not desired. If the arms of a bottle brush are intended to follow a different molecular weight distribution, this can be achieved through nested stochastic objects. For a detailed discussion, please refer to the section titled Limitations.
2.2.2.4 Weight sum and termination controls. The total sum of the listed weights is three (<|0 0 0 1 0 2|), identical to the weight of the branch point ([<|3|]). This equality indicates that extending an existing arm is equally probable as initiating a new arm from the branch point, though both are more likely than extending the backbone.
The backbone growth termination is exclusively dictated by the predetermined molecular weight distribution of the stochastic element, as there are no compatible stochastic end groups for the backbone's bond descriptors.
From an algorithmic standpoint, the generation of repeat units is akin to a Markov process, with each step relying solely on its predecessor. However, the decision to halt the repeat unit generation and start termination is guided by the molecular weight distribution. The size of the already generated molecular graph significantly influences this step, making it non-Markovian.
2.2.2.5 Initiating stochastic object termination. Once the generated repeat units within a stochastic object exceed the targeted molecular weight, the termination process commences in two stages.
The first stage encompasses suffix termination, as depicted in Fig. 3c. If the stochastic object's right bond descriptor is not empty, it is designed to connect to a subsequent object. To facilitate this linkage, one of the open bond descriptors compatible with the right terminal bond descriptor is chosen. This selection mirrors the process of picking an open bond descriptor in the first step of repeat unit generation. The chosen open bond descriptor is then earmarked for the upcoming suffix connection, excluding it from the stochastic termination process.
2.2.2.6 Stochastic termination of stochastic object. The second phase involves stochastic termination, as showcased in Fig. 3d. All remaining open bond descriptors are coupled with end groups to finalize the stochastic group. This procedure resembles repeat unit generation, but with the crucial difference that only end groups, not repeat units, are appended to the generated graph.
This step, considered independently, aligns with a Markov process. However, the decision to transition to the termination phase hinges on the previously generated molecule. While this generation scheme shares similarities with Hidden Markov Models (HMMs),17,18 it does not conform to the HMM category as the probability of switching between the hidden states (repeat unit generation and termination) is governed by the non-Markovian molecular weight distribution.
For computer simulations, it is advantageous to specify not only a collection of polymer molecules, but also the number of atoms that each instance of this collection represents. Such information can be important for determining the number of molecules in a simulation box. Incorporating these data directly into the line notation offers two key benefits: (a) it enables generation of a complete simulation box without the need for additional information and, (b) it signals the impact of finite-size effects on associated properties. This functionality extends beyond computer simulations and, for example, can serve to highlight differences between single-molecule properties and bulk properties.
We propose an enhancement of the BigSMILES notation that utilizes the disconnection feature of SMILES notation to signify the number of molecules in a system representing the ensemble. In its most basic form, a molecule is suffixed with a dot (safe in SMILES) and then a specification in the format |system_molecule_weight|. In this context, system_molecule_weight is a real number that encapsulates the total molecular weight of all molecules preceding the dot, that is, the cumulative molecular weights of those molecules. For the generation of individual molecules (bigsmiles_gen.Molecule in the reference implementation), specifying the system molecular weight is optional. However, for a full system description (bigsmiles_gen.System), its definition is required for generation.
2.3 Representing molecular mixtures
The extended notation offers the capability to represent not only a single type of molecule but also mixtures comprising different molecule types. This allows for the depiction of diverse scenarios, such as a mixture of a polymer and its solvent, or a blend of homo- and diblock copolymers (dbc).For instance, consider the expression homo_bigsmi.|tot_wt_homo|dbc_bigsmi.|tot_wt_dbc|. This notation signifies that the combined molecular weight of all homo polymers is represented by tot_wt_homo. For example, if the average molecular weight of a homo polymer is 104 g mol−1 and tot_wt_homo is 105 g mol−1, we would expect an average of 10 homo polymer chains in this ensemble realization. The total molecular weight of the diblock copolymer follows a similar treatment, resulting in an ensemble comprising a mixture of homo polymers and diblock copolymers.
For a more realistic and detailed example, please refer to the ESI.†
2.4 Determining molecule ensemble probabilities
With the G-BigSMILES notation it is possible to ascertain the likelihood of a specific molecule being generated by a polymer ensemble. Utilizing the exact generation scheme of G-BigSMILES, we can investigate all plausible generation paths leading to the target molecule. We traverse the molecule, retracing the generation steps while documenting the associated probabilities at each juncture. Often, multiple generation paths are possible, and only those that lead to the full generation of the molecule possess a non-zero overall generation probability. Probabilities along a generation path are multiplied, while probabilities of different possible paths are summed up. This results in a single probability representing the likelihood of generating the molecule from the given ensemble. We note that the computational cost of this algorithm can be prohibitively high for large, branched molecules.For stochastic objects, their termination is guided by the previously discussed molecular weight notation. In reconstructing the molecular graph, it is essential to compute the likelihood of terminating generation after adding a repeat unit. If a currently generated stochastic object has a molecular weight M and the ensuing repeat unit has a weight w, the termination probability, pt, can be determined by integrating the molecular weight distribution's probability density function (PDF), pmw(x), over the range M to M + w: 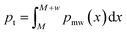 . Importantly, pt is independent from the graph traversal probability, and their product gives the overall generation probability for that stochastic object. Fig. 4 includes two examples illustrating this generation probability, termed “p(ensemble)”. The algorithm's reference implementation is also provided.
. Importantly, pt is independent from the graph traversal probability, and their product gives the overall generation probability for that stochastic object. Fig. 4 includes two examples illustrating this generation probability, termed “p(ensemble)”. The algorithm's reference implementation is also provided.
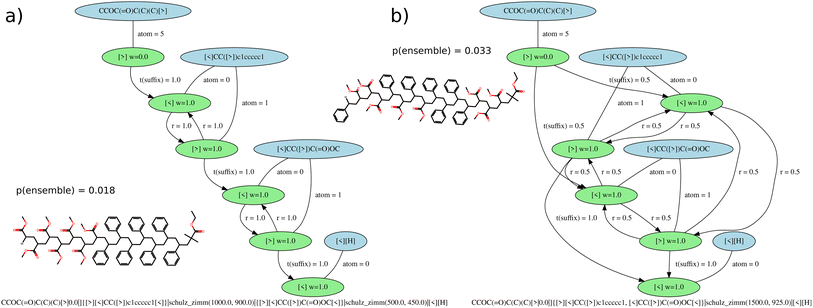 | ||
Fig. 4 Reaction graphs for (a) PS-b-PMMA and (b) PS-r-PMMA molecular ensembles. The blue elements represent SMILES tokens linked to repeat or end units. The green elements signify the bond descriptors of these units, with a label indicating their weight. The edges connecting SMILES tokens to their bond descriptors bear the atom index of the bond descriptor. The edges between bond descriptors carry labels signifying transition weights: r denotes the reaction weights between individual bond descriptors, t(suffix) weights correspond to the reaction weights during suffix termination (Fig. 3c), and t(stochastic) weights correspond to stochastic termination (Fig. 3d). For illustrative purposes, we have included a random drawing from each ensemble and calculated the generation probability (p(ensemble)) for each molecule. To aid visualization, we have scaled down the molecular weights Mw and Mn relative to realistic ensembles. Importantly, the BigSMILES descriptions, in the absence of the generative extension, can be identical for both ensembles, as showcased by CCOC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)C(C)(C){[<] [<]CC([>])c1ccccc1, [<]CC([>])(C)C( O)C(C)(C){[<] [<]CC([>])c1ccccc1, [<]CC([>])(C)C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC [>]}[H]. Nonetheless, due to microphase separation, the diblock copolymer is anticipated to display markedly different properties compared to the random copolymer. O)OC [>]}[H]. Nonetheless, due to microphase separation, the diblock copolymer is anticipated to display markedly different properties compared to the random copolymer. | ||
The generation probability offers a handy metric to gauge how well a collection of polymer molecules represents a given ensemble. It allows for the quantification of how accurately a simulation box filled with polymers depicts the complete polymer ensemble. Moreover, within the context of Auto-Encoders for machine learning, it's essential to evaluate the similarity between a generated set of molecules and a specified ensemble. More on this topic is explored in the upcoming section Machine learning representation.
Given an ensemble characterized by the G-BigSMILES notation, the ensemble probability serves as a robust metric for comparing molecules. However, generation probabilities can vary substantially between ensembles. For instance, if a molecule is present in both ensembles A and B, a higher generation probability in A than in B does not necessarily signify a greater likelihood of the molecule originating from A. This discrepancy might arise if A contains a singular valid molecule (yielding a generation probability of 1 for this molecule and 0 for all other molecules), whereas B supports multiple molecules, thus diluting the generation probability of any individual molecule. The difference here lies in the ensemble diversity, not the origin of the molecule. Therefore, using only generation probabilities to infer the most likely originating ensemble for a molecule can be deceptive.
2.5 Visualizing polymer ensembles as generation graphs
The algorithmic nature of generative BigSMILES allows the molecule generation process to be visualized as a graph structure. Representing BigSMILES as graphs has been previously discussed in the literature.7,8 Here, a slightly different approach is taken, which focuses on the capability of the graph to generate ensemble molecules, respecting the reaction probabilities. In this graphical representation, the bond descriptors serve as nodes, each connected to its corresponding monomers. The edges of the graph connect compatible bond descriptors, and their assigned weights indicate the reaction probabilities during the generation process. Fig. 4 illustrates such graphs for two distinct G-BigSMILES notations. These generation graphs are instrumental in visually capturing and representing polymer ensembles, providing an intuitive understanding for both human observers and machine algorithms. The process of analyzing a generation graph involves tracing the evolution of a molecule.The initial step involves pinpointing an end-group. This is achieved by selecting a SMILES fragment, depicted in blue in Fig. 4, which harbors a single bond descriptor, showcased in green. This bond descriptor is then tracked to its respective atom label, indicating the atom within the SMILES string that connects to the bond descriptor. The path then extends to the subsequent reaction partner. In cases that involve a prefix and a stochastic object, the connection is labeled t(suffix), and the associated reaction probability is appended.
Upon identification of the next bond descriptor, we integrate the corresponding monomer (highlighted in blue) into the molecule. The bond point is reflected in the edges as atom.
Following this, an open bond descriptor is chosen from all monomers, a decision that is influenced by the probability weighted by the factor w. This bond descriptor guides us to the next reaction partner. Whether we intend to incorporate another repeat unit (determined by rate r), terminate with a stochastic end group (denoted by t(stochastic)), or opt for a suffix termination (represented by t(suffix)), this algorithm facilitates the generation of the entire molecule.
Furthermore, examining the different weights assigned to the transitions within the graph can offer insightful understandings of the topology. In section Machine learning, we explain how machines can interpret these graphs to generate a latent space embedding for polymer ensembles.
It is important to recognize that the graph representation alone cannot entirely replicate the generation of polymer molecules. The non-Markovian nature of the generation process, which relies on previously generated fragments, isn't adequately captured in a static graph and necessitates a separate encoding system.
3 Discussion
In this section, we underscore the multifaceted applications and benefits of using generative BigSMILES notation.3.1 Generative BigSMILES as a detailed descriptor
While BigSMILES serves as a label for polymeric materials, the G-BigSMILES enhances this function. It contains detailed information and provides greater constraints within the chemical space compared to BigSMILES, enabling more specific representation and eliminating unintended interpretations. Therefore, G-BigSMILES could prove instrumental in labeling materials for databases, such as CRIPT.103.2 Streamlining automated workflows in simulation and experimentation
The integration of a one-line notation to trigger automated workflows is paramount. This notation can act as an essential input for experimental and computational simulation workflows. By using G-BigSMILES as an input, these workflows can process and characterize a sample, leading to an automated acquisition of material properties.Several aspects of the simulation, including forcefield parameter assignment, equilibration, and characterization, can already be automated.11,19,20 Existing workflows typically require assumptions about polymer ensembles or additional input parameters to govern the generation process. G-BigSMILES notation, however, sidesteps this need, thereby facilitating the description of a much wider range of possible polymer ensembles than those typically implemented. For a description of how reliable initial conditions for computer simulations can be generated product molecules of G-BigSMILES, readers are referred to our previous publication about automated simulation discovery.11
3.3 Machine learning
This improvement bolsters the creation of standardized workflows capable of handling a broad variety of potential polymer ensembles. The use of a one-line notation streamlines automation and ensures transparency for both humans and computers. The compatibility of G-BigSMILES notation with machine learning algorithms turns it into a powerful tool for future applications.For example, an active learning agent employing an optimization policy could leverage the results of prior workflow iterations to generate a new polymer ensemble defined by G-BigSMILES. This newly generated G-BigSMILES can then serve as input for the next workflow iteration.
A significant merit of this iterative process is its readability by both humans and machines. Consequently, scientists can effortlessly supervise the automated workflow iterations, thus offering an efficient method for directing and optimizing polymer synthesis and characterization processes.
To the best of our knowledge, despite notable progress in recent years,23–28 none of the current embedding technologies have fully achieved this goal. While the G-BigSMILES notation itself does not directly contribute to the development of new encoding strategies (which is beyond the scope of this manuscript), we wish to emphasize its potential for future advancements in this field. The G-BigSMILES notation offers valuable insights into describing and generating polymer ensembles, which can inspire novel approaches to encoding and representation that may ultimately lead to more effective ML-based design strategies for polymeric materials.
On the other hand, the BigSMILES notation without the generative extension can also be used to construct similar generation graphs, albeit without the inclusion of edge weights representing reaction probabilities which comes with inherent limitations.27 The advancement of ML technologies has facilitated the processing of such graph structures using graph neural networks, specifically message-passing graph neural networks.29,30 One common approach to represent such graphs in a latent space is through the use of Auto-Encoders.31 This approach has been employed in molecular contexts where the graph represents individual molecules composed of chemical fragments.28 These techniques pave the way for potential applications of graph neural networks in analyzing and modeling generative G-BigSMILES graphs for polymer ensembles.
In this context, the reaction graph, as introduced in section Visualizing polymer ensembles as generation graphs and Fig. 4, can be encoded using a message-passing graph neural network acting as an encoder, which maps the graph into a latent space. From the latent space, a decoder network can then convert it back into a graph structure. To train this approach, the objective is to maximize the similarity between the output of the decoder and the input of the encoder. In this case, the input corresponds to a polymer ensemble described by G-BigSMILES and represented as a reaction graph, while the output can be a generated ensemble of polymer molecules. The generation probability discussed earlier (see section Determining molecule ensemble probabilities) can be utilized to maximize the probability of subsequently generated molecules belonging to the input ensemble or directly compare the reaction graphs.
The generation graph of G-BigSMILES differs fundamentally from atom-based graphs used for individual molecule encoding. In atom-based graphs, the count of vertices and edges grows with molecular size, posing challenges for encoding larger molecules like polymers. However, the G-BigSMILES generation graph size is determined by the number of unique chemical repeat units, not their repetitions in the molecule. Consequently, G-BigSMILES graphs are notably smaller than atom-based ones, making the application of established ML methods more feasible. Since the G-BigSMILES generation graph greater focus on molecular architecture compared to chemical details, consequently we expect this approach to be particularly adept at representing questions from polymer physics.
This approach has the potential to accurately represent large, stochastic, and non-trivial polymer ensembles for ML applications, particularly for polymeric materials where a precise representation of polymer chain architectures is crucial for properties such as viscoelasticity. Adopting a standardized notation, like the proposed G-BigSMILES, not only facilitates comparisons between different approaches but also offers a convenient means to specify a wide range of diverse polymer ensembles. These diverse ensembles can serve as valuable training data for ML models in the field, enhancing their ability to capture the complexity and intricacies of polymer systems.
3.4 Limitations
The G-BigSMILES notation aims to capture a broad range of realistic polymer ensembles. However, its simplified nature imposes limitations; it is not possible to describe all possible polymer ensembles, and in some cases only approximate representations are realized. For instance, cross-linked polymer materials cannot be generated using the G-BigSMILES notation. The notation's mechanism of establishing connections between generating molecules and new repeat or end units does not account for cross-link connections between open bond descriptors within the same molecule. This limitation could be addressed in future revisions by considering spatial proximity between cross-linkers, which is crucial for cross-link formation but absent in the current generation process focused solely on polymer architecture.G-BigSMILES utilizes idealized models to describe polymer ensembles. For instance, the molecular weight distributions applied to stochastic objects reflect idealized situations that are not always consistent with what is observed during experimental characterization. Likewise, the reaction probabilities used to define transition probabilities for bond descriptors are simplifications and should be interpreted in the context of their respective measurement methods.
Crucially, these idealized model parameters are often associated with uncertainties and the specifics of their derivation. Such idealization inevitably impacts the described and generated polymer ensembles, potentially leading to deviations between experimental and, for instance, simulation realizations.
This limitation is an intentional design choice aimed at maintaining the notation's compactness. However, additional context and metadata, such as parameter uncertainties and details about parameter determination, should be accompanied by the line notation.
The CRIPT project is a potential platform for contextualizing G-BigSMILES.10 Its data model facilitates the specification of parameter histories and methods of acquisition. Moreover, it allows for the association of corresponding measurements with the polymer material. This feature can help underscore deviations and confirmations between the idealized model and the actual realization, further enriching the analytical process.
Canonization for G-BigSMILES remains a challenge; while for BigSMILES progress has been made towards canonzation,8 there is no canonized form of G-BigSMILES available at this time. However, by determining generation probabilities, it becomes possible to establish similarities between different ensembles. For instance, if the generation probability of each molecule generated from ensemble a is identical to that of ensemble b (∀ma: pa (ma) = pb (ma)), and the same holds true for molecules generated from ensemble b (∀mb: pa(mb) = pb(mb)), then both ensembles can be considered identical. The incorporation of generation probabilities enables a more nuanced understanding of the relationship between different polymer ensembles described by generative G-BigSMILES.
(1) The notation does not support nested stochastic objects, which poses a challenge in describing bottlebrush polymers where such nesting is often encountered. Bottlebrush polymers can still be described and generated with the current implementation, just the molecular weight distribution is limited as shown in the earlier example.
(2) Ladder polymer notation is not supported, limiting the ability to represent this specific class of polymers using G-BigSMILES.
(3) Each SMILES fragment within the notation must represent a valid molecule description. This prevents the representation of complex constructs, such as scenarios where stochastic elements are present within ring molecules or stochastic branches.
By addressing these limitations in future iterations, G-BigSMILES offers the potential to become a highly versatile and comprehensive tool for description of a wider range of polymer structures and ensembles.
4 Conclusion
The introduction of the generative BigSMILES, G-BigSMILES, notation represents a significant advancement towards the standardized and concise representation of polymer ensembles. It offers a systematic and comprehensive framework for describing polymer architectures, their connectivity, and the probabilistic pathways of their generation. By incorporating essential information such as reaction probabilities, monomer compositions, and molecular weight distributions, the generative G-BigSMILES notation enables the generation of a wide range of polymeric ensembles.G-BigSMILES can be understood as a generative graph embellished with transition probabilities. This extends the concept of traditional graph representations by incorporating molecular weight distributions for stochastic polymers. Such an interpretation paves the way for the application of machine learning techniques in embedding stochastic polymer ensembles. This has far-reaching implications for a variety of applications, such as property prediction and active learning methods.
Additionally, along with the definition of the G-BigSMILES notation, we present an algorithm capable of generating polymer ensembles and assigning probabilities to polymers within the ensemble by reversing the algorithm. We offer both algorithms in a reference implementation for ease of use.
The fusion of the G-BigSMILES notation with recent advances in machine learning and encoding strategies offers considerable promise. Importantly, it could streamline material design processes and facilitate discovery of next-generation polymeric materials with custom-designed properties.
In conclusion, the G-BigSMILES notation introduced here represents an improvement in notations for polymer science. Its application, combined with modern machine learning techniques, contributes to the ongoing development of accelerated materials design strategies for novel polymeric materials with improved features and functionality.
Data availability
The code for G-BigSMILES can be found at https://github.com/InnocentBug/bigSMILESgen. The version of the code employed for this study is version 0.1.1. All data used throughout the article can be reproduced with the SI.ipynb at the same location.Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. Schneider gratefully acknowledges the support of the Eric and Wendy Schmidt AI in Science Postdoctoral Fellowship, a Schmidt Futures program. This work was supported by the National Science Foundation Convergence Accelerator award number 2134795.Notes and references
- S. Heller, A. McNaught, S. Stein, D. Tchekhovskoi and I. Pletnev, J. Cheminform., 2013, 5, 1–9 CrossRef.
- S. R. Heller, A. McNaught, I. Pletnev, S. Stein and D. Tchekhovskoi, J. Cheminform., 2015, 7, 1–34 CrossRef CAS.
- M. Krenn, Q. Ai, S. Barthel, N. Carson, A. Frei, N. C. Frey, P. Friederich, T. Gaudin, A. A. Gayle, K. M. Jablonka, R. F. Lameiro, D. Lemm, A. Lo, S. M. Moosavi, J. M. Nápoles-Duarte, A. Nigam, R. Pollice, K. Rajan, U. Schatzschneider, P. Schwaller, M. Skreta, B. Smit, F. Strieth-Kalthoff, C. Sun, G. Tom, G. Falk von Rudorff, A. Wang, A. D. White, A. Young, R. Yu and A. Aspuru-Guzik, Patterns, 2022, 3, 100588 CrossRef CAS PubMed.
- N. M. O'boyle, R. Guha, E. L. Willighagen, S. E. Adams, J. Alvarsson, J.-C. Bradley, I. V. Filippov, R. M. Hanson, M. D. Hanwell and G. R. Hutchison, et al. , J. Cheminform., 2011, 3, 1–15 CrossRef PubMed.
- A. Drefahl, J. Cheminform., 2011, 3, 1–7 CrossRef CAS.
- L. Schneider and M. Müller, Comput. Phys. Commun., 2019, 235, 463–476 CrossRef CAS.
- T.-S. Lin, C. W. Coley, H. Mochigase, H. K. Beech, W. Wang, Z. Wang, E. Woods, S. L. Craig, J. A. Johnson and J. A. Kalow, et al. , ACS Cent. Sci., 2019, 5, 1523–1531 CrossRef CAS PubMed.
- T.-S. Lin, N. J. Rebello, G.-H. Lee, M. A. Morris and B. D. Olsen, ACS Polym. Au, 2022, 2, 486–500 CrossRef CAS.
- W. Zou, A. M. Monterroza, Y. Yao, S. C. Millik, M. M. Cencer, N. J. Rebello, H. K. Beech, M. A. Morris, T.-S. Lin and C. S. Castano, et al. , Chem. Sci., 2022, 13, 12045–12055 RSC.
- D. J. Walsh, W. Zou, L. Schneider, R. Mello, M. E. Deagen, J. Mysona, T.-S. Lin, J. J. de Pablo, K. F. Jensen, D. J. Audus and B. D. Olsen, ACS Cent. Sci., 2023, 9, 330–338 CrossRef CAS PubMed.
- L. Schneider, M. Schwarting, J. Mysona, H. Liang, M. Han, P. M. Rauscher, J. M. Ting, S. Venkatram, R. B. Ross and K. Schmidt, et al. , Mol. Syst. Des. Eng., 2022, 7, 1611–1621 RSC.
- T. Congdon, P. Shaw and M. I. Gibson, Polym. Chem., 2015, 6, 4749–4757 RSC.
- P. J. Flory, J. Am. Chem. Soc., 1940, 62, 1561–1565 CrossRef CAS.
- P. C. Hiemenz and T. P. Lodge, Polymer Chemistry, CRC press, 2007 Search PubMed.
- P. J. Flory, J. Am. Chem. Soc., 1936, 58, 1877–1885 CrossRef CAS.
- D. J. Walsh, M. A. Wade, S. A. Rogers and D. Guironnet, Macromolecules, 2020, 53, 8610–8620 CrossRef CAS.
- S. R. Eddy, Nat. Biotechnol., 2004, 22, 1315–1316 CrossRef CAS PubMed.
- B. Schuster-Böckler and A. Bateman, Curr. Protoc. Bioinform., 2007, 18 DOI:10.1002/0471250953.bia03as18.
- Y. Hayashi, J. Shiomi, J. Morikawa and R. Yoshida, npj Comput. Mater., 2022, 8, 222 CrossRef CAS.
- S. Kim, C. M. Schroeder and N. E. Jackson, ACS Polym. Au., 2023, 3(4), 318–330 CrossRef CAS PubMed.
- D. J. Audus, A. McDannald and B. DeCost, ACS Macro Lett., 2022, 11, 1117–1122 CrossRef CAS.
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley and M. Mathea, et al. , J. Chem. Inf. Model., 2019, 59, 3370–3388 CrossRef CAS PubMed.
- M. Guo, W. Shou, L. Makatura, T. Erps, M. Foshey and W. Matusik, Adv. Sci., 2022, 9, 2101864 CrossRef CAS PubMed.
- C. Kuenneth, W. Schertzer and R. Ramprasad, Macromolecules, 2021, 54, 5957–5961 CrossRef CAS.
- D. Bhattacharya, D. C. Kleeblatt, A. Statt and W. F. Reinhart, Soft Matter, 2022, 18, 5037–5051 RSC.
- R. A. Patel, C. H. Borca and M. A. Webb, Mol. Syst. Des. Eng., 2022, 7, 661–676 RSC.
- M. Aldeghi and C. W. Coley, Chem. Sci., 2022, 13, 10486–10498 RSC.
- W. Jin, R. Barzilay and T. Jaakkola, International Conference on Machine Learning, 2020, pp. 4839–4848 Search PubMed.
- J. Zhou, G. Cui, S. Hu, Z. Zhang, C. Yang, Z. Liu, L. Wang, C. Li and M. Sun, Open J. Artif. Intell., 2020, 1, 57–81 Search PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Mach. learn. Quantum Phys., 2020, 199–214 CAS.
- Y. Wang, H. Yao and S. Zhao, Neurocomputing, 2016, 184, 232–242 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00147d |
| ‡ Note that variations of the CurlySMILES notation specifically designed for polymeric systems already exist in the realm of generative implementations. These are incorporated within the polymer simulation package SOMA.6 However, this notation is most appropriate for coarse-grained descriptions, where one can neglect the intricate molecular connectivity details of repeating units. |
| § The bottlebrush polymer is synthesized through a three-step process. First, vinyl acetate undergoes RAFT polymerization to produce poly(vinyl acetate).12 In the second step, poly(vinyl acetate) is hydrolyzed to form poly(vinyl alcohol).12 In the third step, poly(vinyl alcohol) serves as an initiator for the ring opening polymerization of ethylene oxide, resulting in the formation of the bottlebrush polymer.13 |
| ¶ It is important to underscore a special case where generation could terminate prematurely, leading to the absence of open bond descriptors. This scenario will be discussed in a subsequent section. |
| || Aside from the zero weight, the bond descriptors are also incompatible. |
| This journal is © The Royal Society of Chemistry 2024 |
