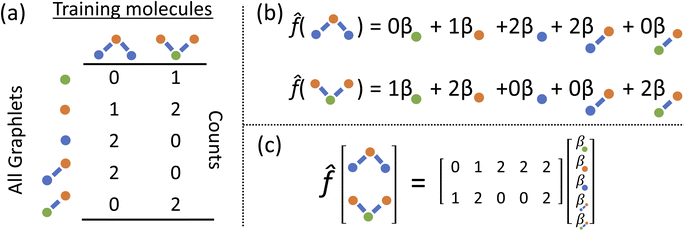Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Linear graphlet models for accurate and interpretable cheminformatics†
Michael
Tynes‡§
 *ab,
Michael G.
Taylor
a,
Jan
Janssen
*ab,
Michael G.
Taylor
a,
Jan
Janssen
 a,
Daniel J.
Burrill
ab,
Danny
Perez
a,
Daniel J.
Burrill
ab,
Danny
Perez
 a,
Ping
Yang
a,
Ping
Yang
 *a and
Nicholas
Lubbers
*a and
Nicholas
Lubbers
 *c
*c
aTheoretical Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA. E-mail: mtynes@uchicago.edu; pyang@lanl.gov
bCenter for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
cComputer, Computational, and Statistical Sciences Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA. E-mail: nlubbers@lanl.gov
First published on 16th August 2024
Abstract
Advances in machine learning have given rise to a plurality of data-driven methods for predicting chemical properties from molecular structure. For many decades, the cheminformatics field has relied heavily on structural fingerprinting, while in recent years much focus has shifted toward leveraging highly parameterized deep neural networks which usually maximize accuracy. Beyond accuracy, to be useful and trustworthy in scientific applications, machine learning techniques often need intuitive explanations for model predictions and uncertainty quantification techniques so a practitioner might know when a model is appropriate to apply to new data. Here we revisit graphlet histogram fingerprints and introduce several new elements. We show that linear models built on graphlet fingerprints attain accuracy that is competitive with the state of the art while retaining an explainability advantage over black-box approaches. We show how to produce precise explanations of predictions by exploiting the relationships between molecular graphlets and show that these explanations are consistent with chemical intuition, experimental measurements, and theoretical calculations. Finally, we show how to use the presence of unseen fragments in new molecules to adjust predictions and quantify uncertainty.
1 Introduction
Chemical property prediction from molecular graphs is a long-established approach that has evolved into a complex discipline, especially so following the recent revolutions in machine learning (ML).1–3 Historically, cheminformatics has treated molecular graphs (also referred to as 2D chemical information) using schemes that count the presence of substructural patterns to generate feature representations known as molecular fingerprints,1–9 which can then be used in a variety of Machine Learning (ML) pipelines for chemical property prediction. Deep learning (DL) approaches such as message passing and graph neural networks have come to overshadow other ML methods due to their state-of-the-art performance across a variety of tasks.10–12 However, these performance improvements have come at the expense of increased training cost and decreased model interpretability, and addressing these drawbacks is an active area of research.13–19 Considering the limitations of DL, we show here that prediction using graph fragments still has a place in the modern chemistry-applied ML arsenal by revisiting fragment generation, and by constructing new approaches to model building, chemical property prediction explanation, and uncertainty quantification.Model interpretability is often invaluable when ML is applied in the sciences both because it helps scientists understand when and how models make errors, thereby building trust in model predictions, and because it can help uncover trends in predictions, which can lead to enhanced scientific understanding. Methods for interpreting ML models in the context of chemistry and materials problems are reviewed thoroughly in ref. 18, 20 and we review key points here. In the ML interpretability literature, intrinsically interpretable models18,20 are those wherein the model functional form and mechanisms for prediction are transparent and meaningful. An often-cited example of such a model is linear regression, where each coefficient has a clear interpretation as the contribution of an individual feature to a prediction (even when these features may be difficult to interpret). In contrast, many ML models – e.g., deep neural networks (DNNs) – are too large or complicated to be interpreted directly and are thus referred to as black-box methods. Such methods can still be interpreted through post hoc procedures which are applied to models after training or to their predictions. Examples of such techniques include local linear surrogates which examine the contribution of input features near a given input point21 and similar local explanations called SHapley Additive exPlanations (SHAP) based on game-theory.22–24 DNNs are often interpreted by methods that examine the gradients of their predictions, e.g. through integrated gradients25 or the deep Taylor decomposition.26 Such post hoc methods have been applied to molecular property prediction and have been used to give explanations in terms of atoms,27 bonds,28 and higher-order molecular subgraphs.29
Some argue that because DNNs often provide the most accuracy across ML models and that numerous post hoc DNN explanation methods exist, these methods should be favored over intrinsically explainable models, which are commonly thought to be comparatively weak predictors.18 However, this perceived accuracy-interpretability tradeoff is often exaggerated and is sometimes orthogonal to observed trends.19 Furthermore, many post hoc interpretability methods have theoretical weaknesses that are empirically borne out by counter-intuitive and untrustworthy explanations. For example, ref. 30 discusses that numerous post hoc methods are not locally Lipschitz continuous, meaning that extremely small perturbations in model input can yield large changes in explanations, a phenomenon which makes explanations appear inconsistent to a human observer. More recently, ref. 31 showed that post hoc methods based on the deep Taylor decomposition can be manipulated to produce arbitrary explanations. Such findings have led to calls to use simpler, explainable models when possible.19
Intrinsically explainable models often have comparable predictive power to black box models, especially when constructed carefully.19 This general observation has been demonstrated recently in a materials science context where interpretable (multi-)linear models were applied material property prediction problems and achieved accuracy close to state-of-the-art nonlinear approaches.32 One of these model families was constructed by counting atomic n-grams present in a crystal lattice unit cell and assigning coefficients to their presence, inspired by the cluster expansion. Here we develop an analogous representation for organic molecules which we call the atom-induced molecular subgraph, or graphlet, representation, wherein a molecule is represented by constituent n-atom connected subgraphs. A similar representation was recently developed by ref. 9 and used to sample and characterize large chemical spaces of more than billions of molecules.33–35 Here we show that such a representation can be combined with linear models for competitive and interpretable prediction.
We construct accurate, explainable linear models which, inspired by the many-body expansion,36–38 approximate molecular properties as functions of molecular graphlets organized by their body-order, i.e., the number of atoms in each graphlet. We show that so-constructed linear models perform competitively with nonlinear black box models across a variety of structure–property prediction tasks. We then show that this approach can naturally be used to produce coherent, additive explanations by projecting higher-order model coefficients onto atoms or bonds within their molecular context, and empirically find correlation between these projections and both chemical intuition and chemical theory. Finally, we examine how graphlet train and test statistics can be used to estimate distribution shift39 and thereby quantify prediction uncertainty.
2 Methods
We develop a method for molecular representation and model fitting using the principle of the many-body expansion, in which we aim to write a property of a molecule as a linear combination of coefficients associated with all of the graphlets of the molecule weighted by their number of occurrences in the molecular graph. This is illustrated in Fig. 1. In this section, we outline the mathematical framework for constructing and counting these graphlets (Section 2.2). We then discuss hierarchical regression by body order (Section 2.3), show how graphlet coefficients can be combined to give model explanations (Section 2.4), and finally, how the presence of unseen fragments in molecules not seen during training can be used to both adjust model predictions and quantify uncertainty (Section 2.5). After formally describing our methods, we discuss the molecular property prediction tasks and datasets we used to evaluate them (Section 2.6) and then finally, we give a few remarks on our implementation (Section 2.7), which is open-source and freely available.2.1 Graphlet fingerprint approach
Graphlets are defined as isomorphism classes of connected subgraphs induced by choosing a set of nodes and all of the edges connecting those nodes in a graph.40 We define a graphlet fingerprint as a vector of counts of occurrences of graphlets in a molecular graph. This is similar to other fingerprinting approaches, which enumerate molecular subgraphs of a given family up to some size parameter. For example, Daylight-like5 fingerprints enumerate linear paths on the molecular graph up to a maximum path length with optional path branching6 and Extended Connectivity FingerPrints (ECPF or Morgan, the latter after Morgan's original formulation7) enumerate atom-centered radial subgraphs up out to a maximum radius.8 In contrast, rather than restricting the process that generates subgraphs, we base our machine learning counts of all molecular graphlets up to some size N.Graphlet fingerprints, like other fingerprint approaches, are built upon pre-defined type labels assigned to the atoms and bonds in a molecular graph. We label nodes by atomic species, formal charge, and aromaticity. This implies that every node type has a precise degree which is constant across all instances in all molecular graphs. Edges are labeled according to bond type as either single, double, triple, or aromatic. As a result, the graphlet statistics form a typed version of Dk degree statistics.41 This rich typing scheme helps to capture information more efficiently at lower maximum graphlet size; as an example, with only species based typing an N+ atom with 4 bonds is not distinguished from an N atom with 3 bonds until using a graphlet size of at least 5. Valence-based rich typing of atoms can resolve the difference between these atoms at a graphlet size of 1.
Graphlets are enumerated by a recursive algorithm similar to the explicit subgraph enumeration routine described in ref. 42 and 9, during which we identify and count membership in isomorphism classes through our hashing technique described in the next section.
2.2 Graphlet fingerprint mathematical description
In mathematically precise terms, we construct graphlet fingerprints as histograms of members of induced subgraph isomorphism classes present in a molecular graph. We consider a molecular graph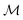 to be a set of atoms
to be a set of atoms  and a set of bonds
and a set of bonds 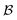 between those atoms, that is
between those atoms, that is 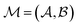 . An induced molecular subgraph is a subgraph of
. An induced molecular subgraph is a subgraph of  formed by choosing a subset of atoms
formed by choosing a subset of atoms  and all of the bonds between the atoms in
and all of the bonds between the atoms in 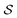 , which we label as
, which we label as 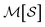 .
.
To construct molecular graphlets, we consider the family of sets of atoms in 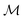 for whom the induced subgraph is connected, denoted
for whom the induced subgraph is connected, denoted
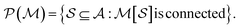 | (1) |
Loosely speaking, one can think of 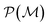 as playing the role of a cumulant expansion over the induced subgraphs formed by the power set of
as playing the role of a cumulant expansion over the induced subgraphs formed by the power set of 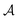 . Molecular graphlets are the classes of isomorphic subgraphs present in
. Molecular graphlets are the classes of isomorphic subgraphs present in 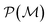 . It will be useful to consider induced subgraphs restricted to a given number of atoms, N, denoted as
. It will be useful to consider induced subgraphs restricted to a given number of atoms, N, denoted as
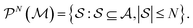 | (2) |
The graphlet fingerprint is the histogram CN of isomorphic induced subgraphs up to subgraph size N. With the Iverson brackets 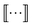 representing the indicator function and
representing the indicator function and  denoting the set of graph isomorphism classes, the components of CN are
denoting the set of graph isomorphism classes, the components of CN are
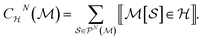 | (3) |
To efficiently track graphlet isomorphism classes 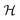 , we build an integer-valued labeling (in other words, hashing) function H and produce counts of these labels. We construct a concrete histogram cN with components labeled h as
, we build an integer-valued labeling (in other words, hashing) function H and produce counts of these labels. We construct a concrete histogram cN with components labeled h as
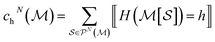 | (4) |
To build this hashing function, we require pre-defined atom labels, 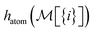 , and pair labels,
, and pair labels, 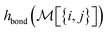 (atom and bond labels for the pair), as well as a labeling function hrec, which can identify a histogram ch by sorting the labels in the histogram and pairing them with the accompanying count. To label graphlets of arbitrary size, we construct a recursive labeling function H with hrec using hatom and hbond as base cases:
(atom and bond labels for the pair), as well as a labeling function hrec, which can identify a histogram ch by sorting the labels in the histogram and pairing them with the accompanying count. To label graphlets of arbitrary size, we construct a recursive labeling function H with hrec using hatom and hbond as base cases:
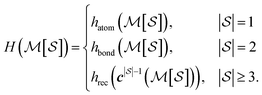 | (5) |
In plain words, we label graphlet isomorphism classes by their own histograms of graphlets: triplets are labeled in terms of bonds and atoms, and four-vertex graphlets are labeled in terms of triplets, bonds, and atoms, etc. To our knowledge, this labeling scheme not been presented in any prior work. Because it is recursive, it has the advantage of allowing memoization while building the graphlet set. Whether or not the concrete labeling function H is a faithful realization of the ideal isomorphism classes 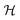 is a complex question related to the long-standing graph reconstruction conjecture,43–46 which is notably true for some particular classes of graphs, false for others, and not settled for a great many cases. For the molecules and subgraph sizes studied here we have found no counterexamples.
is a complex question related to the long-standing graph reconstruction conjecture,43–46 which is notably true for some particular classes of graphs, false for others, and not settled for a great many cases. For the molecules and subgraph sizes studied here we have found no counterexamples.
2.3 Hierarchical regression
We explore fitting linear regression models hierarchically, first to subgraphs with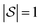 , and then
, and then 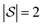 , and so on. Let us think of the graphlet histograms cN of graphlets up to
, and so on. Let us think of the graphlet histograms cN of graphlets up to 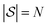 as members of a space
as members of a space 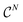 . This space can be decomposed as a direct sum of vector spaces
. This space can be decomposed as a direct sum of vector spaces 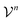
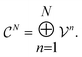 | (6) |
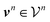 are counts of graphlets of size precisely equal to n. Using this notation, we construct an order-N hierarchical model to predict y as
are counts of graphlets of size precisely equal to n. Using this notation, we construct an order-N hierarchical model to predict y as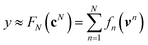 | (7) |
Using ŶN = FN(cN) for arbitrary values of N, each constituent model fn is trained to minimize the same loss function evaluated against the residual y − Ŷn−1, that is to minimize 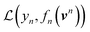 with
with
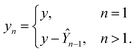 | (8) |
Put less mathematically, using the graphlet approach, we can build a function up by first applying regression to the graphlet counts generated by atoms, and then to the graphlet counts generated by bonds, and then to the graphlet counts generated by connected triples, and so on, up to some graphlet size N, where the model at size n learns a correction to the model at size n – 1. This same hierarchical approach can be analogously applied to the other 2D graph fingerprints we examine. For path-based fingerprints, the hierarchical levels indexed by n correspond to the number of steps in the graph walks or, equivalently, the number of bonds. For circular fingerprints, the hierarchical levels n indicate the set of fragment features with radius equal to n.
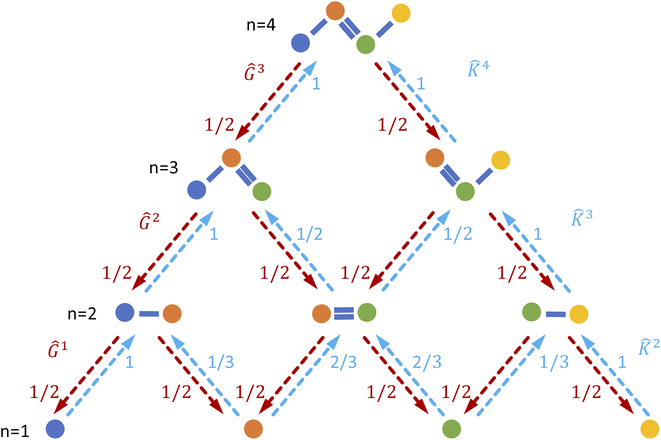
2.4 Interpretation projections
We produce local (per molecule) interpretations of our graphlet-based linear models by exploiting the inclusion of smaller graphlets within larger graphlets. Using the graphlet inclusion relationships in a particular molecular graph, we project the linear model coefficients associated with each graphlet onto the molecule's atoms or bonds. The projected values describe the contribution of each atom or bond to the model prediction, given its context within the molecular graph. These atom- or bond-projected values sum to the model prediction value for this molecule, a property we refer to as additivity. A visualization of the inclusion relationship structure is presented in Fig. 2. The remainder of this section describes how we produce the pictured graph and use it to perform projections in formal notation.We consider the directed acyclic graph (DAG) of inclusion relationships between graphlets of varying size, defined as
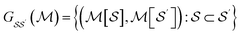 | (9) |
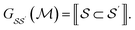 | (10) |
For brevity, we will omit the 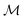 and write these matrix elements as
and write these matrix elements as 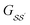 , but the matrix remains associated with a particular molecule.
, but the matrix remains associated with a particular molecule.
We principally deal with the inclusions of size n graphlets within size n + 1 graphlets, which form an N-partite DAG with partitions for each graphlet size from n = 1, …, N. We refer to the partitions as levels. Much like in a feedforward neural network, each adjacent pair of levels is connected by a set of edges. These edges are a subset of those in G; the adjacency matrix Gn connecting nodes from level n + 1 to level n corresponds to
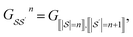 | (11) |
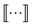 subscripts indicate taking only rows and columns of G that respectively correspond to size n and size n + 1 fragments. A column of Gn describes which size n graphlets are included in each size n + 1 graphlet. We use the matrices Gn to perform our projections from higher to lower levels of the DAG. The DAG described by these matrices, and their upward analogs to be introduced shortly, is visualized for a fictitious molecule in Fig. 2.
subscripts indicate taking only rows and columns of G that respectively correspond to size n and size n + 1 fragments. A column of Gn describes which size n graphlets are included in each size n + 1 graphlet. We use the matrices Gn to perform our projections from higher to lower levels of the DAG. The DAG described by these matrices, and their upward analogs to be introduced shortly, is visualized for a fictitious molecule in Fig. 2.
We want our projections onto atoms or bonds to be additive, that is, to sum to the prediction of the linear model, so we want the transformation corresponding to each Gn to be sum conserving. To accomplish this, when projecting contributions from a size n + 1 graphlet to its size n graphlets, we evenly distribute this contribution across all of the size n graphlets. Mathematically, we can ensure this by normalizing the columns of Gn to sum to 1. We write the column-normalized adjacency matrix as Ĝn with columns defined as
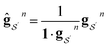 | (12) |
To develop our projections, we must think carefully about our linear model form. A linear model with weights β acting on graphlet histogram cN to estimate y is written as,
| ŷ = β·cN. | (13) |
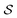 in a molecule, written as
in a molecule, written as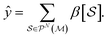 | (14) |
When projecting “downwards” from larger to smaller fragments, denote the projection value on a set of atoms as 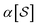 . We write the vector of these projection, α, and coefficient, β, values associated with all
. We write the vector of these projection, α, and coefficient, β, values associated with all 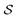 of size n in a molecule as
of size n in a molecule as 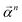 and
and 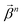 . With this notation, we define the projection from level n + 1 to n as
. With this notation, we define the projection from level n + 1 to n as
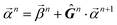 | (15) |
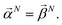 | (16) |
Eqn (15) is sufficient to produce atom-level explanations by computing 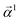
For bond-level explanations, we introduce the reverse “upwards” projection from level n – 1 to n. To do so, we reverse the direction of the edges in the DAGs described above. The edges are now weighted by the total “valence” (in graph terms, the total edge weight) of one graphlet within another. Loosely speaking, these valence weights are the counts of bonds subsumed in the larger graphlet. More formally, the matrix K with elements given by
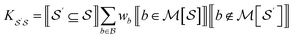 | (17) |
![[K with combining circumflex]](https://www.rsc.org/images/entities/b_char_004b_0302.gif) n with columns summing to 1. In the case where n = 2, edges toward atom pairs connected by integral bonds are weighted by the number of electron pairs, and aromatic bonds have weight of
n with columns summing to 1. In the case where n = 2, edges toward atom pairs connected by integral bonds are weighted by the number of electron pairs, and aromatic bonds have weight of 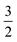 . This allows us to define natural “upward” projections
. This allows us to define natural “upward” projections 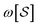 as
as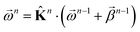 | (18) |
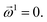 | (19) |
A diagram of this scheme for interpretability projections is shown in Fig. 2. As a concrete example of this definition, a 2-graphlet (bond) containing a carbon and nitrogen that are double-bonded to each other will receive 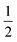 of the carbon-associated β and (2 out of 4 bonds) and
of the carbon-associated β and (2 out of 4 bonds) and 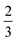 of the nitrogen-associated β (2 out of 3 bonds) in an upward projection.
of the nitrogen-associated β (2 out of 3 bonds) in an upward projection.
We combine the upward and downward projections at level n, denoted by 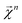 , as
, as
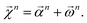 | (20) |
For any level n,
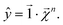 | (21) |
This equation represents the fact that our explanation vectors χ are additive in the sense that the sum of the explanation reproduces the prediction; the explanation breaks the prediction into component pieces. We primarily consider 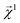 which corresponds to breaking up the prediction Ŷ into atom-centered terms and
which corresponds to breaking up the prediction Ŷ into atom-centered terms and 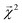 corresponding Ŷ decomposed into bond-centered terms, although one can compute
corresponding Ŷ decomposed into bond-centered terms, although one can compute 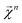 for any n = 1, …, N.
for any n = 1, …, N.
2.5 Uncertainty quantification and prediction adjustment based on unseen graphlets
When evaluating graphlet-based regression models on new molecules, it is likely that these molecules will contain graphlets not present during training. We can use the presence of these unseen fragments both to construct uncertainty quantification (UQ) measures and, when appropriate, adjust our predictions to account for systematic biases introduced by the absence of fitted model coefficients associated with the unseen graphlets. These uncertainty metrics could be applied in active learning47 and Bayesian optimization48 workflows to discover new molecules and materials.We examine various methods of constructing uncertainty metrics based on unseen graphlets. While yet more approaches are possible, we explored using the total number of unseen graphlets, the fraction of unseen graphlets, and an auxiliary uncertainty regression model to weight the relative importance of unseen fragments of size s.
We can exploit statistical information in the distribution of graphlet coefficients to adjust predictions when a test molecule has unseen graphlets. We examine this in the context of predicting energies, where each graphlet is associated with a coefficient that can be thought of as the energy contribution of each graphlet. Ignoring unseen graphlets present in a new molecule causes the magnitude of a molecule's energy to be mispredicted. We adjust for this bias by finding the mean coefficients ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) s for each size s = 1, …, N, constructing a histogram of counts dsN of unseen all fragments of size s, regardless of the fragment structure. The adjusted prediction ŷadj is then written as
s for each size s = 1, …, N, constructing a histogram of counts dsN of unseen all fragments of size s, regardless of the fragment structure. The adjusted prediction ŷadj is then written as
ŷadj = β·cN + ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/b_i_char_e10e.gif) ·dN ·dN | (22) |
2.6 Overview of data sources and experiments
We evaluate models built using graphlet fingerprints on fifteen molecular datasets from several sources to assess the general applicability of the graphlet approach.To examine regression performance, we first examine prediction on roughly 130k atomization energies from the QM9 (ref. 49) dataset computed using Density Functional Theory (DFT) and compare performance against a range of fingerprint-based regression methods applied to this dataset, including one applied by ref. 50. Later, we use splits of this dataset to evaluate our uncertainty quantification and prediction adjustment approaches. We then evaluate our method's performance on solubility prediction using four datasets from ref. 51 with sizes ranging roughly from 400 to 900 molecules and compare our results to those therein. Finally, we evaluate regression performance on nine drug discovery related quantities in datasets with sizes ranging roughly from 700 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules from ref. 52 and compare performance to leaderboards hosted online.53
000 molecules from ref. 52 and compare performance to leaderboards hosted online.53
To evaluate our interpretability projections, we qualitatively examine solubility predictions on the datasets from ref. 51 and, more quantitatively, correlate bond-projected energies to roughly 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bond dissociation energies calculated on a set of molecules from ref. 54.
000 bond dissociation energies calculated on a set of molecules from ref. 54.
2.7 Implementation
We implemented our fingerprints using a custom python package, , which we have open-sourced and made freely available at http://www.github.com/lanl/minervachem/.
, which we have open-sourced and made freely available at http://www.github.com/lanl/minervachem/.  uses RDKit55 and networkx56 to represent molecules and graphlets. Graphlet counts are represented as scipy57 sparse matrices for model fitting. Linear and hierarchical modelling procedures in
uses RDKit55 and networkx56 to represent molecules and graphlets. Graphlet counts are represented as scipy57 sparse matrices for model fitting. Linear and hierarchical modelling procedures in  are implemented with scikit-learn.58 Nonlinear models are implemented with the Light Gradient Boosting Machine (LightGBM) library.59 LightGBM model hyperparameters were optimized using the Fast Library for Auto Machine Learning (FLAML)60 and include the number of boosted tree estimators, the maximum number of leaves per estimator, the maximum number of samples per leaf, the fraction of features considered by each tree, the learning rate, and L1 and L2 regression parameters. Internally to minvervachem, visualizing projected coefficients uses RDKit plotting methods, and visualizing projection DAGs is done in networkx.
are implemented with scikit-learn.58 Nonlinear models are implemented with the Light Gradient Boosting Machine (LightGBM) library.59 LightGBM model hyperparameters were optimized using the Fast Library for Auto Machine Learning (FLAML)60 and include the number of boosted tree estimators, the maximum number of leaves per estimator, the maximum number of samples per leaf, the fraction of features considered by each tree, the learning rate, and L1 and L2 regression parameters. Internally to minvervachem, visualizing projected coefficients uses RDKit plotting methods, and visualizing projection DAGs is done in networkx.  also implements the pairwise difference regression (PADRE) meta-algorithm.61
also implements the pairwise difference regression (PADRE) meta-algorithm.61
3 Results
Our results show competitive model predictive performance, strong interpretability, and uncertainty quantification that is well-correlated to absolute error. In Section 3.1, we see that graphlet-based linear models fit to DFT atomization energies exceed the performance of both linear and nonlinear models built on other fingerprints and exceed the accuracy of these DFT calculations with respect to experiment. In Section 3.2, we show that projecting coefficients from these models to bonds gives bond-level attributions that are both similar to experimentally-derived bond dissociation energies (BDEs) and are correlated with DFT-derived BDEs. In Section 3.3, we see predictive performance on solubilities in various solvents that is competitive with nonlinear models from the literature, and in Section 3.4 that interpreting the coefficients from these models projected to atoms agrees with chemical intuition. In Section 3.5, we see competitive performance across nine drug-discovery-related molecular property prediction tasks from the Therapeutic Data Commons leaderboards.52,53 In Section 3.6, we use information about unseen fragments to improve prediction quality on unseen molecules by up 38% in a fragment holdout experiment. Finally, in Section 3.7, we use unseen fragment information to construct uncertainty quantification metrics that show good correlation with absolute prediction error.3.1 High accuracy on diverse chemical systems
We present computational experiments on the QM9 dataset that are designed to evaluate the performance of graphlet fingerprint-based linear models compared to other fingerprinting methods and to nonlinear modeling approaches. We restricted the target QM9 property to atomization energy as a case study to examine our graphlet-based linear modeling approach, as our approach was inspired by many-body expansion energy models. For linear regression models, we fit L2-regularized models on graphlet fingerprint representations with maximum graphlet size s ranging from 1 to 9. For comparison with a nonlinear model, we included gradient boosting as implemented by the LightGBM library.59 To compare with other fingerprinting methods, we included RDKit and Morgan fingerprints as implemented in the RDKit library.55 RDKit fingerprints are an implementation of path-based, Daylight-like fingerprints, and Morgan fingerprints are radial/circular fingerprints, both discussed earlier in Section 2.1 and in ref. 6. We used count-based unfolded representations for both types of fingerprints and allowed branching for RDKit fingerprints. We also varied s from 1 to 9 for these fingerprints, where s is the maximum number of bonds present in an RDKit fingerprint and the maximum radius in a Morgan fingerprint. At each fragment size, we performed a hyperparameter optimization and measured test performance on a 0.64/0.16/0.2 train/val/test split. For the ridge regression model we searched for the L2 strength parameter over ranges described in ESI Section S1.1.† For the LightGBM we used the FLAML procedure,60 which aims to intelligently find hyperparameters (which are listed in Section 2.7) given a wall-time budget, which we set to 30 min for each level in the hierarchical models and s × 30 min in the non-hierarchical case. We also compare our model to the best fingerprint-based model for the atomization energy task presented in ref. 50.Overall, graphlet-based linear models show stronger performance than both nonlinear models and models constructed with other fingerprints, as seen in Fig. 3 which summarizes our QM9 experiments (additional learning curves including training performance are given in ESI Fig. S1 and S2†). First, considering hierarchical models, performance improves consistently with fragment size to a mean absolute error (MAE) of less than 5 kcal mol−1 for all models. The best of these models uses graphlet fingerprints and attains a test MAE of 1.74 kcal mol−1. Although this is not quite the 1 kcal mol−1 widely considered to be chemical accuracy,62 it is less than the error of the DFT used to calculate these values of ΔHat.50 The RDKit fingerprint-based model follows this performance, with an MAE of 2.15 kcal mol−1. The performance of these two fingerprint variants is likely similar because they capture similar chemical information, i.e., atom-induced subgraphs vs. branched-path fingerprints which can be though of as edge-induced subgraphs. We hypothesize that the stronger performance of both graphlet and RDKit fingerprints over Morgan fingerprints is because they are a richer representation than the Morgan fingerprints, having many more features at a given size. We further hypothesize that the performance improvement of graphlet fingerprints over RDKit fingerprints is due to the relative redundancy present in RDKit fingerprints: because they are walk based, there are many RDKit fingerprint fragments corresponding to the same exact set of atoms for which there is necessarily only one graphlet.
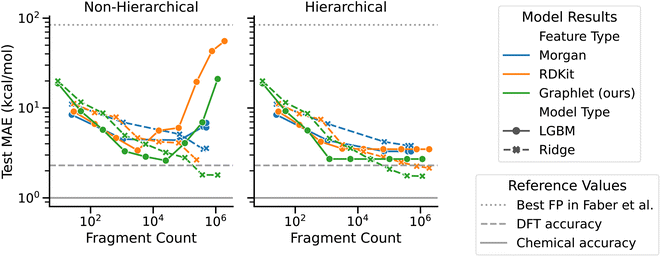 | ||
| Fig. 3 Test set performance vs. fragment count by model type, feature type, and hierarchicality on the QM9 ΔHat task. The horizontal axis is shown in number of fragments rather than fingerprint size because the size parameter has different meanings across fingerprint types. The dashed horizontal line at 2.3 kcal mol−1 indicates the accuracy of the DFT calculations that produced these ΔHat values compared to experiment.50 The solid horizontal line at 1 kcal mol−1 gives a common benchmark of “quantum chemical accuracy” at 1 kcal mol−1. The dotted horizontal line at 84.2 kcal mol−1 shows the best MAE attained by fingerprint-based models in ref. 50. | ||
The nonlinear LightGBM models outperform linear models with small fragment counts, but this relationship is reversed as fragment count increases. This is possibly because LightGBM does not capture the additivity of fragment energies reflected in the many body expansion ansatz, which, by contrast, is well-captured by linear models. Instead of assigning an energy to each graphlet, the LightGBM model must examine a large set of features to sift through the combinations which produce good estimates of total energy. This hypothesis is consistent with the rapid increase in error of non-hierarchical LightGBM models with fragment count, which have to consider all fragments at once. Hierarchicality also eliminates feature correlation induced by the inclusion of smaller fragments within large ones, which may explain the trend of slightly better performance among the hierarchical models in general and the much stronger performance of LightGBM using the hierarchical approach.
All models constructed here outperform the best fingerprint-based model performance reported in ref. 50, most by one to two orders of magnitude, regardless of fingerprint type, highlighting the importance of carefully selecting fingerprint parameters. Ref. 50 uses binary ECP4 (Morgan) fingerprints out to radius 4 folded to a fingerprint length of 1024. At radius 4, we find roughly 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Morgan fragments in the training set when using unfolded fingerprints (see ESI Table S1† for the exact number of fragments observed at each size for each fingerprint type). This close to 500× ratio between unique fragments and fingerprint entries likely explains the limitations of the model from ref. 50.
000 Morgan fragments in the training set when using unfolded fingerprints (see ESI Table S1† for the exact number of fragments observed at each size for each fingerprint type). This close to 500× ratio between unique fragments and fingerprint entries likely explains the limitations of the model from ref. 50.
3.2 Interpreting energy models on bonds
The energy models built in Section 3.1 provide an opportunity to investigate whether the bond-level projections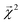 (defined in eqn (20)) of an energy prediction correlate with bond dissociation energies (BDEs). We examine the relationship between
(defined in eqn (20)) of an energy prediction correlate with bond dissociation energies (BDEs). We examine the relationship between 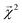 and both experimentally and theoretically-derived BDEs, in both cases using a linear model fit with graphlet fingerprints up to size 7 on approximately 128
and both experimentally and theoretically-derived BDEs, in both cases using a linear model fit with graphlet fingerprints up to size 7 on approximately 128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules from QM9 (the details of the data split and model construction are discussed in Section 3.2.2).
000 molecules from QM9 (the details of the data split and model construction are discussed in Section 3.2.2).
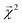 and experimental BDEs for three example molecules – ethane, ethene, and ethyne – are shown in Fig. 4. Both quantities, reported in kcal mol−1, appear on the same scale. The expected trend of increasing C–C bond energy with bond order is captured. This can be explained largely in terms of the explicit single, double, and triple bond fragment coefficients. More interestingly, the subtle trend in C–H bond energy with C–C bond order is also partially captured. In this case, the inclusion of these bonds within higher-order graphlets increased the values of
and experimental BDEs for three example molecules – ethane, ethene, and ethyne – are shown in Fig. 4. Both quantities, reported in kcal mol−1, appear on the same scale. The expected trend of increasing C–C bond energy with bond order is captured. This can be explained largely in terms of the explicit single, double, and triple bond fragment coefficients. More interestingly, the subtle trend in C–H bond energy with C–C bond order is also partially captured. In this case, the inclusion of these bonds within higher-order graphlets increased the values of 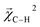 .
.
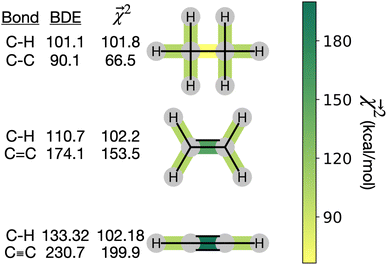 | ||
Fig. 4 Bond-level model interpretability: the projection of a ΔHat model onto bonds 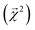 along experimental bond dissociation energies (BDE) for ethane, ethene, and ethyne obtained from ref. 63. Energies are in units of kcal mol−1. along experimental bond dissociation energies (BDE) for ethane, ethene, and ethyne obtained from ref. 63. Energies are in units of kcal mol−1. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 single-bond BDEs from roughly 40
000 single-bond BDEs from roughly 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules calculated at the M06-2X/def2-TZVP level of theory. Of these, approximately 5000 molecules (with roughly 50
000 molecules calculated at the M06-2X/def2-TZVP level of theory. Of these, approximately 5000 molecules (with roughly 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 associated BDEs) are present in QM9. For consistency with QM9, we recalculated the dissociation energies of the bonds in these molecules at the B3LYP/6-31G(2df,p) level of theory. The calculations converged for over 99% of these roughly 50
000 associated BDEs) are present in QM9. For consistency with QM9, we recalculated the dissociation energies of the bonds in these molecules at the B3LYP/6-31G(2df,p) level of theory. The calculations converged for over 99% of these roughly 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bonds, and serve as a reference for our bond-projected predictions
000 bonds, and serve as a reference for our bond-projected predictions 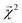 .
.
We construct a holdout set of BDEs to evaluate whether the correlation between 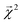 is subject to a generalization gap. Half of the 5000 molecules present in both the theoretical BDE dataset and QM9 were held out from training. We then trained a graphlet-based hierarchical linear model to all QM9 molecules except those present in this holdout set (approximately 128k molecules), using a maximum graphlet size of 7.
is subject to a generalization gap. Half of the 5000 molecules present in both the theoretical BDE dataset and QM9 were held out from training. We then trained a graphlet-based hierarchical linear model to all QM9 molecules except those present in this holdout set (approximately 128k molecules), using a maximum graphlet size of 7.
The bond-projected predictions 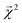 from these models show reasonable agreement with the theoretically calculated BDEs, especially considering that only single bond dissociations are present. On the held out bonds, we attain a Pearson r of 0.46 over all of the bonds, shown in Fig. 5 (notably, there is very little generalization gap in these correlations, as shown in ESI Fig. S3 and S4†). To test whether this correlation is driven by the relative strengths of single bonds between each element pair (an instance of Simpson's paradox64), we separate the data by element pairs and compute the correlations, shown in Table 1. Within the element pairs, the strength of the relationship between
from these models show reasonable agreement with the theoretically calculated BDEs, especially considering that only single bond dissociations are present. On the held out bonds, we attain a Pearson r of 0.46 over all of the bonds, shown in Fig. 5 (notably, there is very little generalization gap in these correlations, as shown in ESI Fig. S3 and S4†). To test whether this correlation is driven by the relative strengths of single bonds between each element pair (an instance of Simpson's paradox64), we separate the data by element pairs and compute the correlations, shown in Table 1. Within the element pairs, the strength of the relationship between 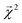 and BDE varies widely, with relatively strong performance for C–C bonds, weak performance for H–O bonds, and moderate performance for the remaining element pairs. Thus, our interpretability scheme recapitulates trends even within most individual bond types. In particular, heavy-atom to heavy-atom bond energies are better correlated with the BDE in comparison to hydrogen-heavy-atom bonds; the variance of the bond explanation for hydrogen atoms is noticeably smaller than the variance of bond explanations for heavy atoms. When interpreting these correlations, it is important to remember that this is a test of empirical correlation between qualitatively similar phenomena; the model was not trained in any way to predict BDEs – rather, it predicts total energies, and the bond-wise interpretation of these predictions is significantly correlated to the BDE. The model is unaware of open-shell molecules, radicals, or ions that are produced in breaking those bonds.
and BDE varies widely, with relatively strong performance for C–C bonds, weak performance for H–O bonds, and moderate performance for the remaining element pairs. Thus, our interpretability scheme recapitulates trends even within most individual bond types. In particular, heavy-atom to heavy-atom bond energies are better correlated with the BDE in comparison to hydrogen-heavy-atom bonds; the variance of the bond explanation for hydrogen atoms is noticeably smaller than the variance of bond explanations for heavy atoms. When interpreting these correlations, it is important to remember that this is a test of empirical correlation between qualitatively similar phenomena; the model was not trained in any way to predict BDEs – rather, it predicts total energies, and the bond-wise interpretation of these predictions is significantly correlated to the BDE. The model is unaware of open-shell molecules, radicals, or ions that are produced in breaking those bonds.
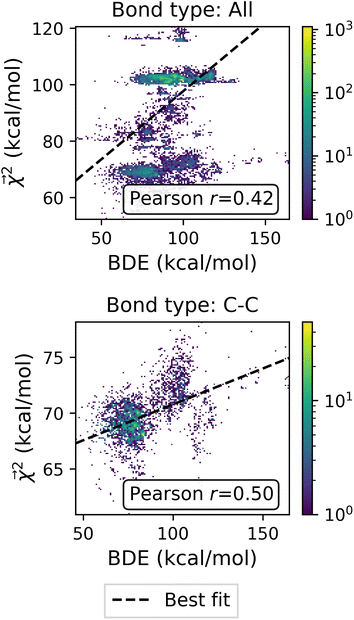 | ||
Fig. 5 Relationship between Bond Dissociation Energies (BDEs) computed with DFT and the bond-level interpretations  for a model fit to atomization energy on the QM9 dataset. for a model fit to atomization energy on the QM9 dataset. | ||
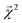 of the linear model and theoretical bond dissociation energies by element pair. Coefficients are calculated on molecules from the holdout set, and the number of bonds is denoted by n. Each correlation is statistically significant, with p < 10−12, except for the smallest category of H–O bonds, for which the correlation is not significant (p > 0.05)
of the linear model and theoretical bond dissociation energies by element pair. Coefficients are calculated on molecules from the holdout set, and the number of bonds is denoted by n. Each correlation is statistically significant, with p < 10−12, except for the smallest category of H–O bonds, for which the correlation is not significant (p > 0.05)
| Bond | n | Pearson r |
|---|---|---|
| All | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 695 695 |
0.4198 |
| C–H | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980 980 |
0.1414 |
| C–C | 4699 | 0.4968 |
| C–N | 1064 | 0.3043 |
| C–O | 1440 | 0.2266 |
| H–N | 990 | 0.2298 |
| H–O | 522 | −0.0584 |
3.3 Competitive performance for solubility prediction
To evaluate the applicability of graphlet-based linear models beyond energy prediction, we evaluate them on a dataset of hundreds of experimental log solubilities in four solvents: acetone, benzene, ethanol, and water, as presented in ref. 51. We compare our model performance directly with ML model performance presented in ref. 51 using the same datasets and prediction tasks with datasets ranging in size from roughly 400 to 900 molecules. Molecular log solubilities in each solvent are considered separate tasks and each have their own ML models, with the water solubility prediction task broken into three tasks based on varying log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S cutoffs – (1) “Water”: only molecules with −4 < log
S cutoffs – (1) “Water”: only molecules with −4 < log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S < –1 are included, (2) “Water (wide)”: all molecules are included, and (3) “Water (wide-narrow)”: only the test set is filtered to −4 < log
S < –1 are included, (2) “Water (wide)”: all molecules are included, and (3) “Water (wide-narrow)”: only the test set is filtered to −4 < log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S < –1. We use the same train/test splitting procedure as reported in ref. 51 and further split the training set into an 80/20 train/val split to optimize the maximum graphlet size and model hyperparameters. For linear models we searched for the L2 parameter in a range of 10−5 to 102, and LightGBM was optimized with FLAML with a time budget of 2 min.
S < –1. We use the same train/test splitting procedure as reported in ref. 51 and further split the training set into an 80/20 train/val split to optimize the maximum graphlet size and model hyperparameters. For linear models we searched for the L2 parameter in a range of 10−5 to 102, and LightGBM was optimized with FLAML with a time budget of 2 min.
Overall, we found that the graphlet fingerprints coupled with linear models predict small molecule solubility in four solvents competitively with nonlinear models from ref. 51, which were trained on expensive DFT- and experiment-based features. Fig. 6 shows test RMSE (log molarity) for each model presented in ref. 51 and for graphlet-based linear and LightGBM models.
 | ||
| Fig. 6 Model performance on the solubility datasets from ref. 51. Root mean squared errors are in units of log molarity. Models from ref. 51 are shown in shades of red in the left-hand side of each panel, models from this work are shown in shades of blue, offset on the right-hand side of each panel. | ||
Graphlet-fingerprint-based models are competitive on all datasets save for benzene, and are among the best for the water (wide) and water (wide-narrow) sets, while being both inexpensive and easy to interpret based on structural motifs (interpretations of solubility predictions are discussed in the following section, and shown in Fig. 7). Compared to nonlinear LightGBM models, linear models are unexpectedly strong on these tasks. This demonstrates that, surprisingly, our molecular representation coupled with linear models is useful outside the context of predicting extensive properties like energy.
The interesting sub-result of improved performance of the graphlet-based models when moving from the water to water (wide-narrow) suggests a robustness to overfitting. In the former task, only molecules of log-solubility ranging from −4 to −1 are included. In the latter task, the test set is the same, but the training set additionally includes molecules in the wider log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S range of −12 to 2. In principle, the test task is statistically identical, but in the wide-narrow version, more information is given for training. Most of the models from ref. 51 nonetheless perform worse on the test task in the wide-narrow version; the new information somehow confounds the models. In contrast, our graphlet approach behaves intuitively – when given more data, it makes strictly better predictions on the same test set.
S range of −12 to 2. In principle, the test task is statistically identical, but in the wide-narrow version, more information is given for training. Most of the models from ref. 51 nonetheless perform worse on the test task in the wide-narrow version; the new information somehow confounds the models. In contrast, our graphlet approach behaves intuitively – when given more data, it makes strictly better predictions on the same test set.
We note again the relatively low expense of our approach compared to the models in ref. 51; because the latter models rely on features that involve DFT and experimental measurements, applying the model to an arbitrary new chemical can be limited by the speed to calculate, find, or measure these quantities. In contrast, a fingerprinting approach such as graphlet fingerprints can be applied to completely new molecules in timescales far less than a second. For these tasks, there are on the order of hundreds to thousands of graphlet features; precise counts are given in ESI Table S2.†
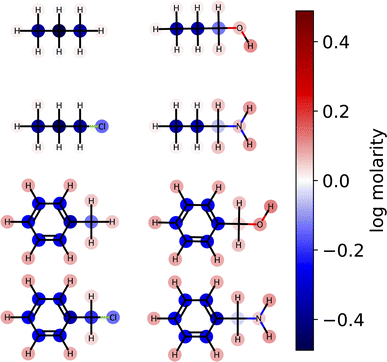
3.4 Atom-level interpretation of solubility models
Here, we examine the interpretability of graphlet fingerprints using linear models by computing the atom-projections of the predictions and examining the qualitative agreement between structural trends in the projections and chemical intuition about solubility. In particular, we choose propyl and benzyl backbones, by themselves and in combination with alcohol, amine, and chloro functional groups. Fig. 7 shows the interpretation
and examining the qualitative agreement between structural trends in the projections and chemical intuition about solubility. In particular, we choose propyl and benzyl backbones, by themselves and in combination with alcohol, amine, and chloro functional groups. Fig. 7 shows the interpretation 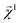 , that is, the atom-level-projected contributions from our linear water solubility model described in Section 3.3. Note how each functional group contributes to the overall molecular solubility. As expected, alcohol and amine groups are shown to be responsible for increasing solubility, and chloro groups are responsible for lowering solubility. ESI Fig. S5† shows interpretations for additional molecules selected from the intersection of the acetone and water solubility datasets.
, that is, the atom-level-projected contributions from our linear water solubility model described in Section 3.3. Note how each functional group contributes to the overall molecular solubility. As expected, alcohol and amine groups are shown to be responsible for increasing solubility, and chloro groups are responsible for lowering solubility. ESI Fig. S5† shows interpretations for additional molecules selected from the intersection of the acetone and water solubility datasets.
3.5 ADMET leaderboards
To further assess general applicability of graphlet-fingerprint-based models, we evaluate their performance on nine drug-discovery-relevant regression tasks from the Therapeutic Data Commons (TDC).52,53 These tasks include the prediction of a variety of biochemical attributes relevant to drug design, including chemical properties such as lipophilicity and aqueous solubility along with human-biological properties, such as toxicity and half-life in blood, which are not chemically absolute.These tasks form an important and challenging collection of properties which are useful because candidate drugs must perform satisfactorily with respect to a host of variables apart from biochemical mechanism of the drug itself, but to Absorption, Distribution, Metabolism, Excretion, and Toxicity (ADMET) properties that characterize how the molecule interacts with important aspects of human biochemistry. In ESI Section S5† we briefly overview the individual tasks addressed in this work; for details please see the TDC information.
These properties are contained in datasets of roughly 1000 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules. We followed the same train/val/test split recommended by the TDC. This is a challenging generalization evaluation which holds out all molecules built upon a particular scaffold (molecular backbone) and conducting training and hyperparameter optimization on the remaining molecules. The performance is averaged over 5 random training/validation splits. We fit both the LightGBM and ridge models with graphlet fingerprints.
000 molecules. We followed the same train/val/test split recommended by the TDC. This is a challenging generalization evaluation which holds out all molecules built upon a particular scaffold (molecular backbone) and conducting training and hyperparameter optimization on the remaining molecules. The performance is averaged over 5 random training/validation splits. We fit both the LightGBM and ridge models with graphlet fingerprints.
Table 2 shows our performance compared to the existing leaderboard entries at the time of writing. A visualization of all of the models' performance for all leaderboard tasks is present in ESI Fig. S6 and S7.† Models using graphlet fingerprints score in the upper half of the leaderboard for seven out of nine of the tasks. Notably, all these high-scoring models used the LightGBM regressor; ridge regression did not perform impressively in these tests and was in the lower half of the leaderboard for five of the nine tasks. This is surprising in the context of ridge regression's strong performance on solubility prediction in Section 3.3, but less surprising in that we expect non-linear, non-extensive models to perform better on biological properties that may not be easy to represent linearly as a sum of all graphlet contributions.
| Task | LightGBM perf. | LightGBM rank | Ridge perf. | Ridge rank | Perf. metric |
|---|---|---|---|---|---|
| LD50 | 0.603 | 3/19 | 0.632 | 8/19 | MAE |
| AqSol | 0.803 | 5/16 | 1.105 | 15/16 | MAE |
| Lipo | 0.519 | 5/17 | 0.516 | 4/17 | MAE |
| PPBR | 8.729 | 6/17 | 10.699 | 15/17 | MAE |
| Caco2 | 0.316 | 7/19 | 0.306 | 6/19 | MAE |
| VDss | 0.500 | 8/17 | 0.448 | 13/17 | Spearman's ρ |
| Half life | 0.217 | 12/18 | 0.229 | 11/18 | Spearman's ρ |
| CL-Hepa | 0.341 | 13/16 | 0.349 | 12/16 | Spearman's ρ |
| CL-Micro | 0.525 | 14/18 | 0.600 | 4/18 | Spearman's ρ |
3.6 Exploiting interpretability to account for new information
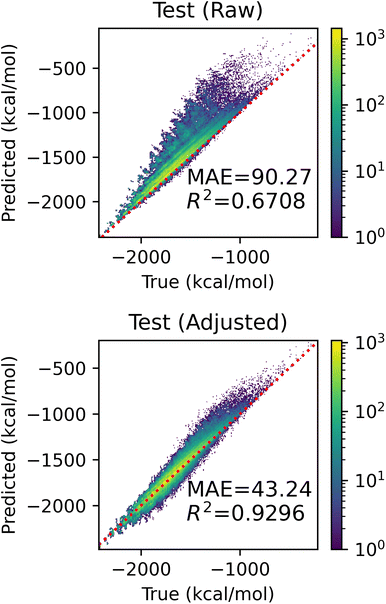
In this section, we evaluate the effectiveness of the adjustment based on unseen fragments discussed in Section 2.5. We conducted a series of experiments on the QM9 dataset, holding out all molecules with graphlets of size ≤2 that appeared in at least 1000 and at most 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules – 22 fragments in total. We expect small graphlets to have large influence on model performance, as their coefficients tend to be larger in our models. Visualizations of these fragments and their counts in QM9 can be found in ESI Fig. S8.† For each held-out fragment, we fit a linear model with graphlet fingerprints up to size 5 on molecules that did not contain this held out fragment. We measured the performance of raw and adjusted predictions on molecules containing the held-out fragment. Fig. 8 shows the aggregated holdout molecule predictions from these 22 experiments. The upper panel shows that models make drastic errors when predicting on molecules with unseen small fragments, yielding an MAE of 90.20 kcal mol−1, and the lower panel shows that the adjustment reduced error by 52% to 42.96 kcal mol−1 and improved R2 by over 38% from 0.67 to 0.93 by exploiting the simple assumption that unknown fragments are similar in nature to known ones on average. This proof-of-concept result demonstrates how an interpretable model can be readily manipulated to incorporate further knowledge and intuition.
000 molecules – 22 fragments in total. We expect small graphlets to have large influence on model performance, as their coefficients tend to be larger in our models. Visualizations of these fragments and their counts in QM9 can be found in ESI Fig. S8.† For each held-out fragment, we fit a linear model with graphlet fingerprints up to size 5 on molecules that did not contain this held out fragment. We measured the performance of raw and adjusted predictions on molecules containing the held-out fragment. Fig. 8 shows the aggregated holdout molecule predictions from these 22 experiments. The upper panel shows that models make drastic errors when predicting on molecules with unseen small fragments, yielding an MAE of 90.20 kcal mol−1, and the lower panel shows that the adjustment reduced error by 52% to 42.96 kcal mol−1 and improved R2 by over 38% from 0.67 to 0.93 by exploiting the simple assumption that unknown fragments are similar in nature to known ones on average. This proof-of-concept result demonstrates how an interpretable model can be readily manipulated to incorporate further knowledge and intuition.
3.7 Uncertainty quantification
As discussed in Section 2.5, the presence of unseen fragments in new molecules can also be used to quantify model uncertainty. There are numerous ways one could utilize this information for UQ, including (1) using the count of unseen fragments or (2) using their frequency. One could also (3) build an explicit model of uncertainty based on unseen fragments. We evaluate all three of these approaches on a graphlet-based linear model trained on a small sample of 1000 random molecules and their atomization energies from the QM9 dataset. The remaining molecules are used as a test set for all three UQ methods.The explicit uncertainty model is a linear regression mapping the number of fragments of each size to the absolute residuals. This model is fit with non-negative least squares, guaranteeing non-negative residual prediction and giving coefficients with a natural interpretation as the contribution of a single unseen fragment of a given size to the model uncertainty in units of the regression target. The resulting model coefficients are given in ESI Table S3.†
We measure the performance of these uncertainty quantification methods with both correlation coefficients and confidence curves. Confidence curves (CCs) show how the model error changes as data points (here, molecules) with the highest uncertainty are excluded from the test set.65,66 Confidence curves for different UQ metrics are compared quantitatively by comparing their integrals in the so-named AUC metric: the less area under the CC, the better the performance of the UQ metric. To give a more intuitive meaning to the AUC, the Area Under the Confidence Oracle (AUCO) metric presented in ref. 65 considers the area between the confidence curve and an oracle curve, that is the true ordering of the points by decreasing absolute error and is the best-case CC for a UQ metric. As AUCO approaches zero, the confidence curve approaches the oracle curve, so smaller AUCO values are better. To provide an even more intuitive functional of the CC, we consider both an oracle and an anti-oracle which randomly discards points. This serves as a baseline that any well-performing UQ metric should outperform. Because the anti-oracle throws away points randomly, the anti-oracle has an expected CC equal to the test set MAE. The area between the anti-oracle and oracle (ABAO) thus represents a baseline AUCO. The confidence curve efficiency metric CCeff is then defined as
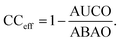 | (23) |
Values of CCeff close to one occur in the best case when the CC approaches the oracle CC, values near zero occur when the UQ metric is no better than random guessing, and negative values occur when the UQ metric is worse than random assignment. In this way, we can think of CCeff as being related to the AUC in the same way that R2 relates to MSE; a perfect CCeff is 1, an uninformative CCeff is 0.
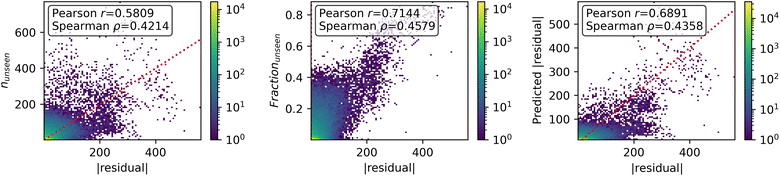
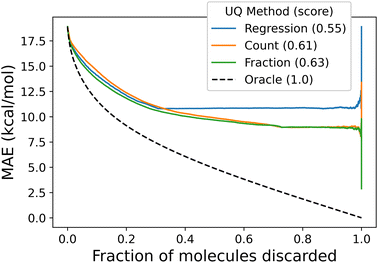
All of the proposed measures of uncertainty based on unseen fragments have moderate to strong correlation with absolute residuals, shown in Fig. 9. Confidence curves and CCeff values are shown in Fig. 10. The fraction of unseen fragments performs the strongest under both correlation coefficients and our confidence curve efficiency metric.
4 Discussion
Regression on molecular graphlets is a simple yet powerful technique yielding overall strong performance at little computational cost; even our s = 9 models of QM9 with over 1 M features (graphlet isomorphism classes) were trained on a single compute node in less than 48 hours, including hyperparameter search. For most of the datasets examined in this work, accurate graphlet-based models can be trained in the order of minutes. Such models built on molecular graphlets are also highly locally interpretable via atom- and bond-level projected coefficients, and the presence of unseen fragments can be used to adjust for model biases and quantify model uncertainty. In many cases, linear models built on graphlets are comparable to nonlinear ones – we prefer the former due to their stronger interpretability.We contrast the straightforward interpretability of our approach with complications associated with applying post hoc interpretability methods to models built on molecular fingerprints, which can lead to inconsistencies and confusions. For example, some research23,24 examines SHAP values on the subgraphs corresponding to fingerprint fragments. In this case, in addition to the inconsistency of SHAP discussed in ref. 30, SHAP explanations can include contributions associated with the absence of a particular fragment, thereby explaining properties of molecules based on what they are not. This is reasonable from a statistical perspective, but cannot provide a mechanistic explanation in terms only of the contents of the molecular graph being examined; if an interpretability method entangles the molecule with the training dataset, the resulting interpretation can be unintuitive. By contrast, interpreting linear model coefficients instead focuses only on the fragments that are present in the given molecule and model coefficients for components that are not present are irrelevant to the prediction. We also note that care must be taken to always use unfolded fingerprints when attempting to explain model predictions, or else the one-to-many correspondence between features and molecular fragments67–69 significantly complicates interpretation, if not rendering it fully impossible.
Still, even linear models with large numbers of coefficients can be difficult to interpret, motivating our projection interpretability scheme. In our graphlet models, the typical number of features can easily be in the thousands, and even up to a million features in the case of QM9 with large maximum fragment sizes. Also complicating interpretation of the model is the set of inclusion relationships between the fragments. To combat these issues, we used two techniques. First, we used a hierarchical fitting approach which aims to capture the largest amount of variation using the simplest graphlets, effectively attempting to impose a many-body hierarchy on the learned models. Second, we developed the interpretation projection technique to build atom, bond, or higher-body-order-graphlet level interpretations. We note that a similar interpretation method to our projection scheme is presented in ref. 70, wherein the SHAP attributions of all of the fingerprint fragments containing a given atom are summed, giving an atom-level SHAP contribution; our projections could be considered to be a more general version of this technique. An advantage of our approach used with linear graphlet models is that it is additive in the sense of eqn (21); the explanation breaks the prediction into component parts which add to recapitulate the prediction. Additivity over the feature space is also guaranteed by SHAP, but because this includes the features which are absent from the molecule having nonzero SHAP values as described above, the projection of SHAP values onto atoms or bonds is not additive, that is, the projections do not add to the final prediction.
We also performed uncertainty quantification using the unseen graphlets types not present in training. Our approaches have some similarity to UQ metrics based on the distance of an unseen point to its nearest neighbor(s) in the training set, which have long been applied in molecular property prediction, including with fingerprints71 and more recently with latent neural network representations.72 However, our approach does not require comparison to the training dataset, thus scales to arbitrarily large datasets; the cost of evaluating the UQ metric does not increase with the training set size, which is desirable in general and especially in applications such as molecular screening which may require very many uncertainty evaluations.
Some similarity may be noted between our work and that of atom-in-molecule-ons (AMONs),73 because each involves analysis of substructures. AMONs constitute a framework for the comparison of 3D configurations; in that lens, they are a composition of a selective (as opposed to exhaustive) fragmentation into subgraphs, and molecular similarity kernels.74 3D information about target molecules is typically used for contexts where the target property varies with respect to the input coordinates-for example, conformational energy variations; the cheminformatics applications presented in this work are distinct because they do not depend on conformation.
We note some advantages of graphlet fingerprints over other fingerprints, some of which are noted in ref. 9. Graphlet fingerprints may be considered at once more complete than Morgan-like fingerprints and more compact or less redundant than RDKit fingerprints. This is visible in the feature counts in Fig. 3, also shown in the ESI, Table S1.† Due to the radial nature, many substructures have no direct representation in Morgan fingerprints. Notably, Morgan fingerprints cannot explicitly represent individual bonds, which important chemical and physical meanings. Thus, bond-level interpretations like those in 3.2 are impossible with Morgan fingerprints. Likewise, RDKit fingerprints cannot directly represent atoms: paths of length one-bonds are the smallest fragments in RDKit fingerprints. RDKit fingerprints are also redundant in their representation of fragments in individual molecules when multiple bond paths connect the same set of atoms. For example, in a molecule with a ring containing n atoms, there is precisely one graphlet-based fingerprint fragment containing exactly those atoms, yet RDKit fingerprints will produce n – 1 fingerprint elements containing that same set of atoms, each one missing one bond from the ring. This leads to many-to-one correspondence between model coefficients and atom subsets, which presents a challenge to directly interpreting these coefficients. This redundancy may also challenge machine learning methods, as the fingerprint vectors will be highly correlated, even when models are fit hierarchically by fragment size. Hierarchical fitting helps to alleviate this redundancy by assigning model contributions to the lowest fragment size possible.
Regarding computational efficiency, we note that Morgan fingerprints are less costly to compute on large molecules with large fragment sizes due to their highly restrictive radial fragment definition. Graphlet fingerprints scale similarly in cost with molecule and fragment size to RDKit fingerprints, though are slightly less costly due to the aforementioned lack of redundancy with respect to subsets of atoms. This is unsurprising, as RDKit fingerprints can be thought of as edge-induced subgraphs rather than node-induced subgraphs.
We note that identifying and counting graphlets has long shown promise in other application areas of machine learning. A kernel based on the number of shared graphlets between graphs has been used to predict functional residues of proteins.75 Due to the potentially combinatoric cost of counting all graphlets on arbitrarily connected graphs, these methods often incorporate random sampling of small graphlets.76 Examining the symmetry relationships between nodes within graphlets has been exploited to understand protein–protein interactions77 and interactions between MicroRNA and small molecules.78 Various spectral methods based on graphlets have been developed79 and applied to problems such as biological network comparison.80,81 Recently, graphlet substructure relationships have been used to improve performance of graph neural networks.45
5 Conclusion
In this manuscript, we have revisited the mathematics of graphlet-based fingerprinting techniques. We introduced several new components, including a new recursive hashing algorithm, hierarchical fitting approach, interpretability scheme, and uncertainty quantification/prediction adjustment method. We have applied the methods widely, comparing the performance of molecular graphlet fingerprints coupled with linear and nonlinear regressors to a variety of molecular featurization techniques from the literature. These include similar topological fingerprints such as the RDKit and Morgan fingerprints on QM9, hand-crafted DFT and experimental features on solubility datasets, and a variety of methods, including deep learning methods such as attention-based and graph neural networks on the ADMET regression tasks from the Therapeutic Data Commons. We find that the graphlet approach fares better than other topological fingerprint techniques, and is generally comparable in accuracy to the other techniques in the recent literature. This result gives counterpoint to recent efforts advocating for the use of black-box algorithms followed by post hoc interpretability algorithms.18At the same time, we have shown that the transparent nature of fingerprint techniques comes with many additional advantages. For one, we show that hierarchical linear modeling in the graphlet approach, using a many-body expansion hypothesis, in some circumstances produces a more accurate model which is far more stable to the maximum graphlet size hyperparameter. We also show how graphlet inclusion relationships can be used to assign precise interpretations which decompose the model prediction across the input molecular structure. This was shown to produce reasonable correlation with chemical theory and chemical intuition in the case of both 2-body (bond) and 1-body (atom) projections. Finally, we showed how the interpretability of graphlet-fingerprint-based linear models provides natural methods for uncertainty quantification as well as model adjustments which address distribution shift, in particular, adjustments that estimate the effect of new topological structures arising in test molecules.
Future work could take on a variety of directions. For one, having shown comparable performance to methods from recent literature on a very wide array of tasks, the graphlet featurization approach is suitable for application to new chemical datasets. Methodologically, the uncertainty quantification and interpretability methods discussed in this work are but the tip of the iceberg; a variety of more complex schemes could be explored, and some of them might prove to produce better interpretations or more well-calibrated uncertainty estimates. We believe a comparison of the both the interpretability and UQ metrics presented here to others is warranted, along with evaluation of the UQ methods with other frequently used methods.82 The problem of modeling uncertainty and constructing interpretations when using these features in combination with external features (such as ab initio properties) remains unsolved; in some sense, any feature that is itself a function of the molecular structure cannot present information that is orthogonal to the graphlet histogram, and so a method to project the information gained by models through these features back onto the molecular graph would need to be devised in order to extend the notions of interpretations presented here. In this work, we have concentrated on modeling data whose domain is scalar, that is, where the prediction target for each molecule is a single number. However, the graphlet distribution can be localized to their location in the graph, and so the graphlet technique could be modified to predict information such as the partial atomic charges within a molecule. Finally, the large number of graphlet types in a fingerprint (up to ≈106 in this work) points to the possibility of using intelligent strategies for pruning the set of features of interest.83
Before concluding, we remind the reader that we have released the code for our approach as an open source package,  , at https://github.com/lanl/minervachem, along with tutorials outlining how to build models using the methods described here. We hope that future developments by ourselves and others will be made available through the library.
, at https://github.com/lanl/minervachem, along with tutorials outlining how to build models using the methods described here. We hope that future developments by ourselves and others will be made available through the library.
Data availability
The source code for the package which implements the methods developed in this manuscript, including constructing graphlet fingerprints, building hierarchical models, and building graphlet model explanations, can be found on github at http://www.github.com/lanl/minervachem/ along with tutorial notebooks demonstrating how to use the library, and version info for dependency packages used in the creation of this work. No new datasets were created with this work; all datasets analyzed in this work were generated previously and can be found in their respective bibliographic ref. 49 and 51–54.
package which implements the methods developed in this manuscript, including constructing graphlet fingerprints, building hierarchical models, and building graphlet model explanations, can be found on github at http://www.github.com/lanl/minervachem/ along with tutorial notebooks demonstrating how to use the library, and version info for dependency packages used in the creation of this work. No new datasets were created with this work; all datasets analyzed in this work were generated previously and can be found in their respective bibliographic ref. 49 and 51–54.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We thank the following individuals, in no particular order, for helpful discussions concerning this work, including Alon Perkus, Eric Mojlness, Pieter Swart, Nathan Lemons, Alice E. A. Allen, Sakib Matin, Kipton Barros, and Joshua Schrier. Los Alamos National Laboratory (LANL) is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (contract no. 89233218CNA000001). We acknowledge the support by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Separation Science Program under contract number 2022LANLE3M1 and Heavy Element Chemistry Program under contract number 2022LANLE3M2. M. T. acknowledges funding from student fellowships sponsored by the Seaborg Institute and the Center for Nonlinear Studies (CNLS). M. T. is also supported by U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Computational Science Graduate Fellowship under Award Number(s) DE-SC0023112. D. J. B. acknowledges a postdoctoral fellowship with the Center of Nonlinear Studies at LANL. We acknowledge the LANL's Director's Postdoc Fellowship (M. G. T.: LANL-LDRD-20210966PRD4; J. J.: LANL-LDRD-20220815PRD4). This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 using NERSC award BES-ERCAP0022265. Computational experiments were conducted in part using LANL's CCS-7 Darwin cluster. This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.References
- M. Hann and R. Green, Chemoinformatics — a new name for an old problem?, Curr. Opin. Chem. Biol., 1999, 3, 379–383 CrossRef CAS PubMed
.
- P. Willett, Chemoinformatics: a history, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 46–56 CAS
.
- T. Engel, Basic Overview of Chemoinformatics, J. Chem. Inf. Model., 2006, 46, 2267–2277 CrossRef CAS PubMed
.
- L. C. Ray and R. A. Kirsch, Finding chemical records by digital computers, Science, 1957, 126, 814–819 CrossRef CAS PubMed
.
- Daylight Theory: Fingerprints – Screening and Similarity, https://www.daylight.com/dayhtml/doc/theory/theory.finger.html, accessed: 2023-10-03.
- G. Landrum, Fingerprints in the RDKit, https://www.rdkit.org/UGM/2012/Landrum_RDKit_UGM.Fingerprints.Final.pptx.pdf, accessed 4-Oct-2023.
- H. L. Morgan, The generation of a unique machine description for chemical structures-a technique developed at chemical abstracts service, J. Chem. Doc., 1965, 5, 107–113 CrossRef CAS
.
- D. Rogers and M. Hahn, Extended-connectivity fingerprints, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed
.
- L. Bellmann, P. Penner and M. Rarey, Connected subgraph fingerprints: representing molecules using exhaustive subgraph enumeration, J. Chem. Inf. Model., 2019, 59, 4625–4635 CrossRef CAS PubMed
.
- W. P. Walters and R. Barzilay, Applications of deep learning in molecule generation and molecular property prediction, Acc. Chem. Res., 2020, 54, 263–270 CrossRef PubMed
.
- O. Wieder, S. Kohlbacher, M. Kuenemann, A. Garon, P. Ducrot, T. Seidel and T. Langer, A compact review of molecular property prediction with graph neural networks, Drug Discovery Today: Technol., 2020, 37, 1–12 CrossRef PubMed
.
- Z. Li, M. Jiang, S. Wang and S. Zhang, Deep learning methods for molecular representation and property prediction, Drug Discov. Today, 2022, 103373 CrossRef PubMed
.
- V. Gupta, K. Choudhary, F. Tavazza, C. Campbell, W.-k. Liao, A. Choudhary and A. Agrawal, Cross-property deep transfer learning framework for enhanced predictive analytics on small materials data, Nat. Commun., 2021, 12, 6595 CrossRef CAS PubMed
.
- J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Approaching coupled cluster accuracy with a general-purpose neural network potential through transfer learning, Nat. Commun., 2019, 10, 2903 CrossRef PubMed
.
- F. H. Vermeire and W. H. Green, Transfer learning for solvation free energies: From quantum chemistry to experiments, Chem. Eng. J., 2021, 418, 129307 CrossRef CAS
.
-
Z. Wang, Z. Dai, B. Póczos and J. Carbonell, Characterizing and avoiding negative transfer, Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019, pp. 11293–11302 Search PubMed
.
- N. Hoffmann, J. Schmidt, S. Botti and M. A. Marques, Transfer learning on large datasets for the accurate prediction of material properties, Digital Discovery, 2023, 2, 1368–1379 RSC
.
- G. P. Wellawatte, H. A. Gandhi, A. Seshadri and A. D. White, A Perspective on Explanations of Molecular Prediction Models, J. Chem. Theory Comput., 2023, 19, 2149–2160 CrossRef CAS PubMed
.
- C. Rudin, Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead, Nat. Mach. Intell., 2019, 1, 206–215 CrossRef PubMed
.
- F. Oviedo, J. L. Ferres, T. Buonassisi and K. T. Butler, Interpretable and explainable machine learning for materials science and chemistry, Acc. Mater. Res., 2022, 3, 597–607 CrossRef CAS
.
-
M. T. Ribeiro, S. Singh and C. Guestrin, Why should i trust you?” Explaining the predictions of any classifier, Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, 2016, pp. 1135–1144 Search PubMed
.
- S. M. Lundberg and S.-I. Lee, A unified approach to interpreting model predictions, Adv. Neural Inf. Process. Syst., 2017, 30, 4768–4777 Search PubMed
.
- F. O. Sanches-Neto, J. R. Dias-Silva, L. H. Keng Queiroz Junior and V. H. Carvalho-Silva, “py SiRC”: Machine Learning Combined with Molecular Fingerprints to Predict the Reaction Rate Constant of the Radical-Based Oxidation Processes of Aqueous Organic Contaminants, Environ. Sci. Technol., 2021, 55, 12437–12448 CrossRef CAS PubMed
.
- Y. Ding, M. Chen, C. Guo, P. Zhang and J. Wang, Molecular fingerprint-based machine learning assisted QSAR model development for prediction of ionic liquid properties, J. Mol. Liq., 2021, 326, 115212 CrossRef CAS
.
-
M. Sundararajan, A. Taly and Q. Yan, Axiomatic attribution for deep networks, International conference on machine learning, 2017, pp. 3319–3328 Search PubMed
.
- G. Montavon, S. Lapuschkin, A. Binder, W. Samek and K.-R. Müller, Explaining nonlinear classification decisions with deep taylor decomposition, Pattern Recogn., 2017, 65, 211–222 CrossRef
.
- S. Ishida, K. Terayama, R. Kojima, K. Takasu and Y. Okuno, Prediction and interpretable visualization of retrosynthetic reactions using graph convolutional networks, J. Chem. Inf. Model., 2019, 59, 5026–5033 CrossRef CAS PubMed
.
- A. Mastropietro, G. Pasculli, C. Feldmann, R. Rodríguez-Pérez and J. Bajorath, EdgeSHAPer: Bond-centric Shapley value-based explanation method for graph neural networks, Iscience, 2022, 25, 105043 CrossRef PubMed
.
-
P. Xiong, T. Schnake, M. Gastegger, G. Montavon, K. R. Muller and S. Nakajima, Relevant Walk Search for Explaining Graph Neural Networks, 2023 Search PubMed
.
- D. Alvarez-Melis and T. S. Jaakkola, On the robustness of interpretability methods, arXiv, 2018, preprint, arXiv:1806.08049, DOI:10.48550/arXiv.1806.08049.
-
L. Sixt and T. Landgraf, A rigorous study of the deep taylor decomposition, Transactions on Machine Learning Research, 2022 Search PubMed
.
- A. E. Allen and A. Tkatchenko, Machine learning of material properties: Predictive and interpretable multilinear models, Sci. Adv., 2022, 8, eabm7185 CrossRef CAS PubMed
.
- L. Bellmann, P. Penner and M. Rarey, Topological similarity search in large combinatorial fragment spaces, J. Chem. Inf. Model., 2020, 61, 238–251 CrossRef PubMed
.
- L. Bellmann, P. Penner, M. Gastreich and M. Rarey, Comparison of combinatorial fragment spaces and its application to ultralarge make-on-demand compound catalogs, J. Chem. Inf. Model., 2022, 62, 553–566 CrossRef CAS PubMed
.
- L. Bellmann, R. Klein and M. Rarey, Calculating and optimizing physicochemical property distributions of large combinatorial fragment spaces, J. Chem. Inf. Model., 2022, 62, 2800–2810 CrossRef CAS PubMed
.
- K. Yao, J. E. Herr and J. Parkhill, The many-body expansion combined with neural networks, J. Chem. Phys., 2017, 146, 014106 CrossRef PubMed
.
- N. Lubbers, J. S. Smith and K. Barros, Hierarchical modeling of molecular energies using a deep neural network, J. Chem. Phys., 2018, 148, 241715 CrossRef PubMed
.
- I. Batatia, S. Batzner, D. P. Kovács, A. Musaelian, G. N. Simm, R. Drautz, C. Ortner, B. Kozinsky and G. Csányi, The design space of E (3)-equivariant atom-centered interatomic potentials, arXiv, 2022, preprint, arXiv:2205.06643, DOI:10.48550/arXiv.2205.06643.
-
J. Quinonero-Candela, M. Sugiyama, A. Schwaighofer and N. D. Lawrence, Dataset Shift in Machine Learning, Mit Press, 2008 Search PubMed
.
- N. Pržulj, D. G. Corneil and I. Jurisica, Modeling interactome: scale-free or geometric?, Bioinformatics, 2004, 20, 3508–3515 CrossRef PubMed
.
-
P. Mahadevan, D. Krioukov, K. Fall and A. Vahdat, Systematic topology
analysis and generation using degree correlations, ACM SIGCOMM Computer Communication Review, 2006, vol. 36, pp. 135–146 Search PubMed
.
-
S. Wernicke, Efficient detection of network motifs, IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2006, vol. 3, pp. 347–359 Search PubMed
.
-
S. Ulam, A collection of mathematical problems, Interscience Publishers, New York, 1960 Search PubMed
.
- J. A. Bondy and R. L. Hemminger, Graph reconstruction—a survey, J. Graph Theor., 1977, 1, 227–268 CrossRef
.
- G. Bouritsas, F. Frasca, S. Zafeiriou and M. M. Bronstein, Improving graph neural network expressivity via subgraph isomorphism counting, IEEE Trans. Pattern Anal. Mach. Intell., 2022, 45, 657–668 Search PubMed
.
- B. Bollobás, Almost every graph has reconstruction number three, J. Graph Theor., 1990, 14, 1–4 CrossRef
.
- J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, Less is more: Sampling chemical space with active learning, J. Chem. Phys., 2018, 148, 241733 CrossRef PubMed
.
- K. Wang and A. W. Dowling, Bayesian optimization for chemical products and functional materials, Curr. Opin. Chem. Eng., 2022, 36, 100728 CrossRef
.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Quantum chemistry structures and properties of 134 kilo molecules, Sci. Data, 2014, 1, 1–7 Search PubMed
.
- F. A. Faber, L. Hutchison, B. Huang, J. Gilmer, S. S. Schoenholz, G. E. Dahl, O. Vinyals, S. Kearnes, P. F. Riley and O. A. Von Lilienfeld, Prediction errors of molecular machine learning models lower than hybrid DFT error, J. Chem. Theor. Comput., 2017, 13, 5255–5264 CrossRef CAS PubMed
.
- S. Boobier, D. R. Hose, A. J. Blacker and B. N. Nguyen, Machine learning with physicochemical relationships: solubility prediction in organic solvents and water, Nat. Commun., 2020, 11, 1–10 CrossRef PubMed
.
-
K. Huang, T. Fu, W. Gao, Y. Zhao, Y. Roohani, J. Leskovec, C. W. Coley, C. Xiao, J. Sun and M. Zitnik, Therapeutics data commons: Machine learning datasets and tasks for drug discovery and development, NeurIPS, 2021 Search PubMed
.
- Therapeutics Data Commons: ADMET Leaderboards, https://tdcommons.ai/benchmark/admet_group/overview/, accessed: 2023-07-24.
- P. C. John, Y. Guan, Y. Kim, B. D. Etz, S. Kim and R. S. Paton, Quantum chemical calculations for over 200,000 organic radical species and 40,000 associated closed-shell molecules, Sci. Data, 2020, 7, 244 CrossRef PubMed
.
- G. Landrum, RDKit: Open-Source Cheminformatics. http://www.rdkit.org, accessed 2-Feb-2020.
-
A. Hagberg, P. Swart and D. S Chult, Exploring network structure, dynamics, and function using NetworkX, 2008 Search PubMed
.
- P. Virtanen,
et al., SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed
.
- F. Pedregosa,
et al., Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed
.
- G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, Q. Ye and T.-Y. Liu, Lightgbm: A highly efficient gradient boosting decision tree, Adv. Neural Inf. Process. Syst., 2017, 30, 3149–3157 Search PubMed
.
-
C. Wang, Q. Wu, M. Weimer and E. Zhu, FLAML: A Fast and Lightweight AutoML Library, MLSys, 2021 Search PubMed
.
- M. Tynes, W. Gao, D. J. Burrill, E. R. Batista, D. Perez, P. Yang and N. Lubbers, Pairwise difference regression: a machine learning meta-algorithm for improved prediction and uncertainty quantification in chemical search, J. Chem. Inf. Model., 2021, 61, 3846–3857 CrossRef CAS PubMed
.
- M. Bogojeski, L. Vogt-Maranto, M. E. Tuckerman, K.-R. Müller and K. Burke, Quantum chemical accuracy from density functional approximations via machine learning, Nat. Commun., 2020, 11, 5223 CrossRef CAS PubMed
.
- S. J. Blanksby and G. B. Ellison, Bond dissociation energies of organic molecules, Acc. Chem. Res., 2003, 36, 255–263 CrossRef CAS PubMed
.
- E. H. Simpson, The interpretation of interaction in contingency tables, J. Roy. Stat. Soc., 1951, 13, 238–241 CrossRef
.
- G. Scalia, C. A. Grambow, B. Pernici, Y.-P. Li and W. H. Green, Evaluating Scalable Uncertainty Estimation Methods for Deep Learning-Based Molecular Property Prediction, J. Chem. Inf. Model., 2020, 60, 2697–2717 CrossRef CAS PubMed
.
- X. Huang, J. Yang, L. Li, H. Deng, B. Ni and Y. Xu, Evaluating and Boosting Uncertainty Quantification in Classification, arXiv, 2019, preprint, arXiv:1909.06030, DOI:10.48550/arXiv.1909.06030.
- I. Cortés-Ciriano, Q. U. Ain, V. Subramanian, E. B. Lenselink, O. Méndez- Lucio, A. P. IJzerman, G. Wohlfahrt, P. Prusis, T. E. Malliavin and G. J. van Westen, others Polypharmacology modelling using proteochemometrics (PCM): recent methodological developments, applications to target families, and future prospects, MedChemComm, 2015, 6, 24–50 RSC
.
- I. Cortes-Ciriano, Bioalerts: a python library for the derivation of structural alerts from bioactivity and toxicity data sets, J. Cheminf., 2016, 8, 1–6 Search PubMed
.
- D. S. Murrell, I. Cortes-Ciriano, G. J. Van Westen, I. P. Stott, A. Bender, T. E. Malliavin and R. C. Glen, Chemically Aware Model Builder (camb): an R package for property and bioactivity modelling of small molecules, J. Cheminf., 2015, 7, 1–10 Search PubMed
.
- C. Humer, H. Heberle, F. Montanari, T. Wolf, F. Huber, R. Henderson, J. Heinrich and M. Streit, ChemInformatics Model Explorer (CIME): exploratory analysis of chemical model explanations, J. Cheminf., 2022, 14, 21 Search PubMed
.
- R. P. Sheridan, B. P. Feuston, V. N. Maiorov and S. K. Kearsley, Similarity to molecules in the training set is a good discriminator for prediction accuracy in QSAR, J. Chem. Inf. Comput. Sci., 2004, 44, 1912–1928 CrossRef CAS PubMed
.
- J. P. Janet, C. Duan, T. Yang, A. Nandy and H. J. Kulik, A quantitative uncertainty metric controls error in neural network-driven chemical discovery, Chem. Sci., 2019, 10, 7913–7922 RSC
.
- B. Huang and O. A. von Lilienfeld, Quantum machine learning using atom-in-molecule-based fragments selected on the fly, Nat. Chem., 2020, 12, 945–951 CrossRef CAS PubMed
.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Machine learning of accurate energy-conserving molecular force fields, Sci. Adv., 2017, 3, e1603015 CrossRef PubMed
.
- V. Vacic, L. M. Iakoucheva, S. Lonardi and P. Radivojac, Graphlet kernels for prediction of functional residues in protein structures, J. Comput. Biol., 2010, 17, 55–72 CrossRef CAS PubMed
.
-
N. Shervashidze, S. Vishwanathan, T. Petri, K. Mehlhorn and K. Borgwardt, Efficient graphlet kernels for large graph comparison, Artificial intelligence and statistics, 2009, pp. 488–495 Search PubMed
.
- X.-D. Wang, J.-L. Huang, L. Yang, D.-Q. Wei, Y.-X. Qi and Z.-L. Jiang, Identification of human disease genes from interactome network using graphlet interaction, PLoS One, 2014, 9, e86142 CrossRef PubMed
.
- N.-N. Guan, Y.-Z. Sun, Z. Ming, J.-Q. Li and X. Chen, Prediction of potential small molecule-associated microRNAs using graphlet interaction, Front. Pharmacol., 2018, 9, 1152 CrossRef CAS PubMed
.
-
R. Kondor, N. Shervashidze and K. M. Borgwardt, The graphlet spectrum, Proceedings of the 26th Annual International Conference on Machine Learning, 2009, pp. 529–536 Search PubMed
.
- N. Pržulj, Biological network comparison using graphlet degree distribution, Bioinformatics, 2007, 23, e177–e183 CrossRef PubMed
.
- S. F. Windels, N. Malod-Dognin and N. Pržulj, Graphlet Laplacians for topology-function and topology-disease relationships, Bioinformatics, 2019, 35, 5226–5234 CrossRef CAS PubMed
.
- M. H. Rasmussen, C. Duan, H. J. Kulik and J. H. Jensen, Uncertain of uncertainties? A comparison of uncertainty quantification metrics for chemical data sets, J. Cheminf., 2023, 15, 121 CAS
.
- A. M. Krajewski, J. W. Siegel and Z.-K. Liu, Efficient Structure-Informed Featurization and Property Prediction of Ordered, Dilute, and Random Atomic Structures, arXiv, 2024, preprint, arXiv:2404.02849, DOI:10.48550/arXiv.2404.02849.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00089g |
| ‡ Current address: Analytics, Intelligence, and Technology Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA. |
| § Current address: Department of Computer Science, The University of Chicago, Chicago, IL 60637, USA. |
| This journal is © The Royal Society of Chemistry 2024 |