Data-driven exploration of silver nanoplate formation in multidimensional chemical design spaces

Abstract

We present an autonomous data-driven framework that iteratively explores the experimental design space of silver nanoparticle synthesis to obtain control over the formation of a desired morphology and size. The objective of the method is to identify design rules such as the effects of the design variables on the structure of the nanoparticle. The framework balances multimodal characterization methods (i.e. UV-vis spectroscopy, SAXS, TEM), taking into account the cost of performing a measurement and the quality of information gained. By integrating with an AI agent, we identify important design variables in the synthesis of small colloidally stable plate-like silver particles and outline how each variable affects plate thickness, radius, polydispersity, and relative concentration. Our findings are consistent with the literature, demonstrating that the framework could be further applied to new systems that have not been well characterized and understood. The framework is generalizable and allows tangible knowledge extraction from the high-throughput experimental runs while still considering inherent stochasticity.

---

Introduction

Silver nanoparticles have shown to be extremely useful for purposes such as catalysis,¹ therapeutics,² drug delivery,³ and surface-enhanced Raman spectroscopy (SERS).⁴ It is also well known that the optical properties of silver nanoparticles depend on their shape and size,⁵ thus the ability to synthesize particles of a specific structure is highly desirable. The literature on the synthesis of silver nanoparticles is vast including physical, photochemical, and chemical methods.⁶ Still, it is often difficult to obtain control over their shape and size due to a limited understanding of the processes that affect the final structure. For example, nucleation, growth, aggregation, and Ostwald ripening, are often affected by both thermodynamic and kinetic parameters associated with reaction conditions.⁷ Because of this, the experimental design space used to synthesize these nanoparticles is often large and complex.⁸ In the chemical synthesis of silver nanoparticles, factors such as light, temperature, age of stock solutions, and duration of the reaction affect the nanoparticle's structure. Finally, due to the limited understanding of the processes that affect the final structure, the relationship between the experimental design parameters (e.g., the concentration of reagents, temperature) and the final structure is often determined by trial and error, which is time-consuming and laborious.⁹

Large and multidimensional experimental design spaces are common in material synthesis. Recently, the combination of artificial intelligence, automation, and a characterization method has emerged as a powerful method to achieve control over the results of nanoparticle synthesis.¹⁰ Automation can be used to synthesize nanoparticles in high-throughput and then screen for a desired structure or property using a characterization method, which facilitates the collection of large datasets. While it is often difficult for a human to interpret the generated large datasets, artificial intelligence algorithms have been successfully used to make decisions for experimental design,^10,11 build predictive models,¹² and extract knowledge via model interpretation.¹³ One common application of artificial intelligence and automation is the concept of a closed-loop design or “retrosynthesis”, where optimization algorithms (e.g., Bayesian optimization¹⁰ or genetic algorithms¹⁴) work together with robots (e.g., liquid handling robots¹⁰ or microfluidic devices¹⁵) and one or more characterization methods (e.g., UV-vis spectroscopy) to iteratively discover the reagent compositions and conditions that yield a desired material or structure.

Many attempts to demonstrate this concept with inorganic nanoparticle synthesis have been successful.^10,16,17 Despite these successes, there are several limitations to closed-loop systems. For example, in most of the above-mentioned frameworks, the experimental design space, which is usually specified by variations in reagent concentrations, is chosen based on values extracted from the literature. This is in direct conflict with the ultimate goal of the closed-loop approach which is to accelerate the discovery of novel materials. Thus, it is unlikely that existing literature would contain information on the design parameters for the completely new materials we aim to discover. Another limitation is the lack of interpretability of the data that is generated from the experiment. Since an optimization algorithm drives the experiment and causes the data to be biased to samples that are close to the target, almost no information on the effect of the experimental design parameters on the structure or property of the material (i.e. outcomes) is obtained that is interpretable by humans. Understanding these relationships is important to obtain a better understanding of the reaction mechanisms that occur during the experiment, which can be useful for modifying the design space, optimizing material structure, or extracting higher-level knowledge that can then be applied to other problems.

In addition to closed-loop systems, another method to study large and complex design spaces is to combine design of experiments (DOE) concepts and high throughput experimentation to perform systematic studies of large design spaces. Some sampling methods include full factorial designs and Latin hypercube sampling, which can increase interpretability when combined with data science and artificial intelligence methods.¹⁸ However, an important disadvantage of such systematic studies is that they do not scale well in high-dimensional experimental design spaces which is defined in terms of the number of tunable design variables. As the number of variables or dimensions gets larger, the number of experiments that need to be performed to sufficiently explore the design space increases drastically.¹⁹ In addition, just like in closed-loop systems, the design space used in systematic studies needs to be chosen very carefully to maximize the amount of information gained from the experiment, which is again difficult to implement in completely new and unknown material systems.

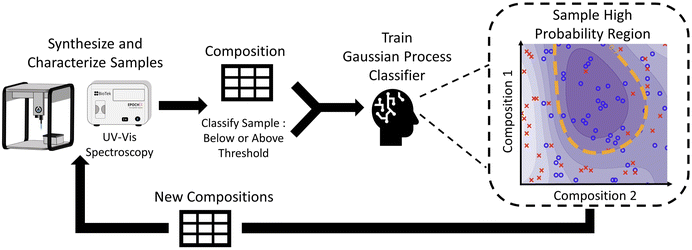
The objective of this work is to demonstrate a hierarchical data-driven framework that can efficiently explore large multidimensional experimental design spaces of material synthesis to converge onto targeted outcomes. This framework combines the advantages of a fully automated closed-loop system, by sampling iteratively, and systematic studies (similar to traditional DOE), by being interpretable. To demonstrate our framework, we chose the synthesis of silver nanoparticles, where we aim to identify regions where nanoparticles of a specific shape (i.e., small plate-like particles) can be formed with greater accuracy and control. In addition, after identifying particles of the desired shape, we seek to extract information on the relationship between the design parameters and structural features of the nanoparticles such as feature size and polydispersity. In this work, we leverage the power of a liquid-handling robot to perform the synthesis of silver nanoparticles in high-throughput sampling campaigns. For the characterization of samples, we use a hierarchical analysis campaign starting with UV-vis spectroscopy as a fast and inexpensive proxy for the nanoparticle's structure, small-angle X-ray scattering as a more expensive but direct characterization method, and transmission electron microscopy (TEM) as the most expensive but most information-rich characterization method. Due to the compromise between costs and structural detail that is gained from each of these complementary methods, we also seek to apply a hierarchical experimental design to maximize the value of the information that is obtained while minimizing the total costs. Our data-driven exploration starts with UV-vis spectroscopy, as the fastest and least expensive technique, to infer the shape of nanoparticles based on their plasmonic resonance. We analyze vast amounts of spectra collected over a very large design space and use a distance metric to determine which samples are small, colloidally stable, monodisperse, plate-like particles. The data is then used to train a Gaussian process classifier which is used to iteratively explore regions of the design space that allow us to synthesize nanoparticles of the targeted morphology (i.e. silver nanoplates). Once we constraint the design space to primarily form particles with the target shape, we perform small angle X-ray scattering (SAXS) on these samples to obtain quantitative information on the size of features (i.e. radius and thickness) as well as the polydispersity and relative concentration of particles. We then use transmission electron microscopy, which is the most expensive and time-intensive technique, to verify models and to help validate the SAXS data. Finally, interpretable design rules are extracted from the aggregate data to identify the effect of design parameters on the structural features of 2D silver nanoparticles.

Materials and methods

Materials

Silver nanoparticles were synthesized using polyvinylpyrrolidone (PVP) 40 kDa, tannic acid, ascorbic acid (≥99%), silver nitrate (≥99%), sodium borohydride (≥98%), and methyl cellulose (4000 cP). All chemicals were purchased from Sigma Aldrich (St. Louis, MO, USA) and used as received. Deionized water was used in all syntheses from a Direct-Q 3 UV water purification system with a resistivity of 18.2 MΩ (Millipore Corporation, Bedford, MA, USA).

Silver nanoparticle synthesis

We used a procedure similar to that described in Samanta et al.²⁰ to synthesize nanoparticles. The first step was to synthesize silver seeds. To do this, 0.50 mL of a 10 mM silver nitrate solution and 4.5 mL of water were added to 15 mL of 9.35 mM ice-cold methyl cellulose solution. Under rigorous stirring, 0.050 mL of 10 mM sodium borohydride solution was added and the color of the solution immediately turned dark yellow. The seeds were left for 2 hours under stirring before use. All stock solutions were created in 20 mL scintillation vials. The synthesis of silver nanoparticles was performed in clear 96-well polystyrene microplates (Corning, NY, USA) with a maximum well volume of 350 μL at approximately 22 degrees Celsius. Water was added to each sample so a total volume of 325 μL could be achieved. The order in which the reagents were added is as follows: PVP, water, tannic acid, ascorbic acid, silver nitrate, and silver seeds. Samples were made simultaneously in batches of 48 samples, meaning that a given reagent was added to every well, in the specified volumes, before changing the pipette tip and performing the same step with the next reagent. After the addition of tannic acid, ascorbic acid, silver nitrate, and silver seeds, a mixing step was performed in each well by repeatedly aspirating and dispensing 100 μL of sample three times. The pipette tip was then washed by performing this same mixing step in three different reservoirs of deionized water to avoid cross-contamination of the stock solutions and of the samples. All pipetting was performed by an Opentrons (Brooklyn, NY, USA) OT2 liquid handling robot. The OT2 control code can be found at (https://github.com/pozzo-research-group/papers/tree/main/Silver%20Nanoplates) to perform the pipetting commands.

UV-vis spectroscopy

Samples were characterized using an Epoch 2 microplate spectrophotometer (BioTek, Winooski, VT, USA) from 350 nm to 800 nm in increments of 5 nm. Background subtraction was performed by subtracting the optical extinction of a water sample with the same volume (325 μL). UV-vis spectroscopy was performed 24 hours after the synthesis of the silver nanoparticles to allow enough time for the complete growth of the particles, which continued to evolve over several hours after the reagents were added.

Small angle X-ray scattering

SAXS was performed on a Xenocs Xeuss 3.0 (Grenoble, France) instrument with an X-ray energy of 8.04 keV (wavelength 1.54 Å) using a copper Kα microfocus source. Data was collected in three configurations: low-q (0.003–0.007 Å⁻¹) for 7 minutes, mid-q (0.007–0.020 Å⁻¹) for 3 minutes, and high-q (0.020–0.100 Å⁻¹) for 2 minutes. Samples were automatically loaded into a 2 mm diameter quartz capillary flow cell using the “Biocube” sample environment and the robotic loading capabilities of the Xeuss instrument. After each measurement, the capillary was flushed with water for 15 seconds and dried for 50 seconds with compressed air using the robotic arm. It was discovered that this cleaning protocol prevented fouling in the capillary after changing samples. Background reduction was performed with the XSCAT software by subtracting the scattering of water in the same capillary flow cell and the data was merged automatically using a Python code. The models used to fit the data were implemented with Sasmodels (http://www.github.com/SasView/sasmodels). Code to automatically merge data and fit SAXS data can be found in the online repository (https://github.com/pozzo-research-group/papers/tree/main/Silver%20Nanoplates).

Transmission electron microscopy

Transmission electron microscopy (TEM) samples were prepared by casting 10 μL over a carbon-coated film, 200 mesh, copper grids which were purchased from Electron Microscopy Sciences (Hatfield, PA, USA). No centrifugation or other sample preparation was performed. The grids were then imaged on an FEI Tecnai F20 at 200 kV. Image analysis was performed by individually measuring all the plate diameters in the TEM images with the ImageJ software.²¹

Scanning electron microscopy

Scanning electron microscopy (SEM) was performed using an Apreo-S instrument (Thermo Fisher, Waltham, MA, USA). Samples were first diluted 100 times and then 5 μL aliquots were deposited on clean silicon wafers.

Machine learning and data analysis

Machine learning algorithms were used for several purposes. A Gaussian process classifier was used to explore the nanoparticle morphologies in the experimental design space. A Gaussian process regressor was used to create contour plots. Both algorithms were implemented in Python with the sci-kit learn library. A radial basis function kernel was selected. Code to reproduce the algorithms can be found in the online repository (https://github.com/pozzo-research-group/papers/tree/main/Silver%20Nanoplates).

Results and discussion

For the data-driven exploration, we used three different characterization techniques that have different costs, throughput, and information content. UV-vis spectroscopy was used in the Fast spectroscopic exploration section to determine the experimental design parameters that give the highest probability of forming small, colloidally stable, monodisperse, plate-like particles. SAXS was then used in the SAXS Structural Exploration section to determine how design parameters affect the thickness, radius, polydispersity, and scale, a parameter proportional to the concentration of the plate-like particles. Finally, transmission electron microscopy (TEM), which is the most expensive and intensive of the characterization tools, was used on select samples to validate observations via direct imaging. In each section, we provide a description of how each characterization method is used followed by a discussion of the results.

Fast spectroscopic exploration

Our first objective is to narrow down the design space to find regions where small, colloidally stable, monodisperse, plate-like structures are formed in high purity. This first step is advantageous because it enables starting experiments from an arbitrarily large design space, as intended for the application of these systems in the discovery of novel materials. The viable design space, which is bounded or limited by the maximum concentrations of stock solutions and the maximum/minimum volumes that can be transferred by the robotic tool, is shown in Table 1.

Table 1 Experimental design parameters used to synthesize silver nanoparticles. The volumes of each regent can be independently varied from 0–60 μL in increments of 1 μL. Water was added to each sample to obtain a volume of 325 μL. The lowest concentration achieved is 0.09 μM for the silver seeds and 0.006 mM for the other reagents. Reagent concentrations are reported assuming a total volume of 325 μL

Reagent	Stock concentration (mM)	Volume range (uL)	Concentration range (mM)
PVP	2.00	0–60	0.000–0.370
Tannic acid	2.00	0–60	0.000–0.370
Ascorbic acid	2.00	0–60	0.000–0.370
Silver nitrate	2.00	0–60	0.000–0.370
Silver seeds	0.03	0–60	0.000–0.001

---

In order to maximize the chances of obtaining a diverse set of morphologies and sizes, several reducing agents and stabilizers were selected based on common silver nanoparticle synthesis reagents. Instead of relying on the literature for stock solution concentrations, a relatively high, but reasonable, concentration of 2 mM was chosen for all reagents except for silver seeds because the method used for the seed synthesis could not achieve such a high concentration. A high stock solution concentration ensures that a large design space can be searched by the algorithm.

An experiment was also performed to determine the effect of the order and time of reagent addition on the final nanoparticle's structure (ESI S20†). In summary, it was found that the order of addition had a major effect on the final structure, but the time of addition only affected certain sample compositions when the order of addition was: silver nitrate, seeds, ascorbic acid, tannic acid, PVP. Experiments evaluating the order and/or time of reagent addition can be easily evaluated and explored using robotic systems but this is otherwise very challenging to explore due to the manual labor involved. Data-driven workflows driven by robotic tools enable effective analysis of colloidal systems where timed-intervention affects the final structure.²² Despite this, we decided to constrain our experimental design space to exclusively explore the concentrations of the reagents.

UV-vis spectroscopy was chosen as the primary screening step because of its low cost and high-throughput capabilities to characterize plasmonic samples. It is well known that this method can be used to indirectly determine a metallic nanoparticle's structure by measuring its localized surface plasmon resonance (LSPR), which results in the local enhancement of an oscillating electric field due to nanoscale confinements. In a UV-vis spectrum, this is usually the wavelength where the peak extinction occurs. Using LSPR to determine the size of a nanoparticle must be done cautiously since the LSPR is also affected by other factors such as particle assembly/aggregation, the solvent or medium, the orientation of the electric field, impurities, etc⁵, which makes it difficult to attribute variations of the LSPR exclusively to particle size. The shape of a UV-vis spectrum can also be used to determine the nanoparticle's shape. While suffering from similar limitations (e.g. sensitivity to aggregation), the shape of a UV-vis spectrum has significant variation when used to differentiate between nanoparticle shapes (i.e. spheres, rods or plates). For example, the spectrum of a nanorod has transverse and longitudinal peaks, a sphere has a single peak, and an aggregate of particles has a very broad peak.²³ In addition to particle shape, UV-vis spectroscopy can identify conditions that do not lead to any reaction or nanoparticle formation. For example, the spectrum of a sample where no nanoparticles are formed will have low extinction, similar to that of water. It can be challenging to determine which experimental parameters are most effective in producing nanoparticles when working with a large design space. Therefore, the shape of the UV-vis spectra was used as a fast and effective screening method to identify regions leading to nanoparticle morphologies of interest. This approach proved helpful in identifying the most promising candidates for further study.

The analysis of functional data such as UV-vis spectroscopy curves is challenging due to the high-dimensional space. Scalar-value features such as peak position and peak width are frequently used to characterize nanoparticle shapes; however, in an experimental spectrum of real samples, the shape of the spectrum represents an ensemble average of all individual nanoparticle signals. Thus, polydispersity, which is a measure of particle size distributions and variations in shape, can change the width of the primary peak in a spectrum. To account for this information and provide a generic method that is agnostic to prior knowledge about observing all the different features of the synthesized morphology, we use information in the form of shape rather than selecting a few scalar features that narrowly represent the full shape of the spectrum.

In our experiment, we expected that we would synthesize hundreds of samples that would later have to be autonomously classified as small, colloidally stable, monodisperse, plate-like particles or not. To carry out this task, a distance metric was established that used the UV-vis spectroscopy curve of each sample. Before creating this distance metric, the targeted UV-vis spectroscopy curve of small, colloidally stable, monodisperse, plate-like particles was simulated using the discrete dipole approximation for the scattering (nanoDDSCAT)²⁴ with a refractive index of 1.33 corresponding to water. Because we were concerned with initially classifying particles based on shape, we simulated the spectra of several small plates of different radii and used them as targets. In addition to nanoplates, the formation of spherical silver nanoparticles is also likely using the experimental design parameters.² Therefore, the extinction spectrum of silver nanospheres of different sizes was also simulated to identify the spectrum of these undesired structures. Using data from simulations, a distance metric that rewards spectra that are close to that of plates and penalizes those that are close to spheres was created. A threshold distance was carefully chosen so that spectra with distances lower than this value would be classified as “Below Threshold” and samples with distances greater than the threshold would be classified as “Above Threshold”. Since the selection of the distance threshold could vary, we accept that there will be samples that have some of the small, colloidally stable, monodisperse, and/or plate-like characteristics that are cut off by the distance threshold. This is because we expect the targeted characteristics to change gradually within an experimental design space, unlike a binary design space where there is a sudden change between regions with particles that have all the targeted characteristics and regions that do not.

From the simulations shown in Fig. 1, the simulated spectra of both spheres and plates have a similar shape (i.e. single peak). The main difference is the wavelength where the peak is located. The position of the peaks of spheres of 20 to 40 nm in diameter varies from about 390 nm to 410 nm, while that of the plates of the same size varies from 480 nm to 590 nm. These observations are consistent with the explanation that anisotropic morphologies have longer plasmon lengths which in turn shifts its spectrum's peak position to higher wavelengths.²⁵ Using these observations, a distance metric was created to classify UV-vis spectra. This distance metric is composed of four terms shown in eqn (1). Each distance term was scaled with a coefficient so that all the terms had values that ranged within the same order of magnitude. This was to ensure that the contributions of each term to the final distance metric were comparable. The effect of each coefficient on the final distance metric was also investigated and this is demonstrated in the ESI (S4).†

d = (7 × d_AP) + (2 × d_peak) + (85 × d_area) + (1 × d_intesnity) (1)

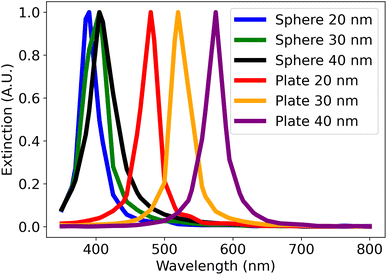Fig. 1 The simulated spectra of spheres and plates using nanoDDSCAT. The legend refers to the diameter of simulated the plates and spheres. All simulated plates have a thickness of 7 nm.

• d_AP refers to the Amplitude Phase distance as described in Vaddi et al.¹⁰ This distance primarily accounts for the shape of the spectra by decomposing the required distance into x-component (phase) and y-component (amplitude). The amplitude and phase components are then computed by an iterative two-step optimization procedure to compute the amount of x and y-component distance between the query and target spectra. This approach represents spectra as points in a high-dimensional function space. The amplitude distance is defined using a function norm between the query and target after separating the phase component. The phase distance is calculated by measuring the distance between the identity phase component (which means no change along the x-axis of the query spectrum) and the phase component of the query spectrum that is needed to derive it from the target spectrum. We refer interested readers to the ESI† or the original paper and references therein for more details.

• d_peak refers to the wavelength of the peak intensity. Since the simulated spectra of spheres and plates in Fig. 1 have similar shapes, this distance term penalizes spectra that have a peak position lower than 450 nm, which are most likely to belong to spheres. This term adds a penalty of 100 to the total distance score if the primary peak's wavelength is lower than 450 nm.

• d_area refers to the area under the curve, which encourages monodispersity. This facilitates the interpretation of data when determining how the reagents affect the size of the plates. This term is determined by integrating the UV-vis spectrum and adding this value to the distance score.

• d_intensity refers to the intensity below 450 nm. Since the simulated spectra of plates have low intensity at these wavelengths, this term was added to help in the classification of plates. This term is determined by finding the maximum intensity of the UV-vis spectrum at wavelengths less than 450 nm and adding this value to the distance score.

The distance metric was used as the primary reward function for the workflow presented in Fig. 2. In the initial iteration, the compositions for 48 samples were randomly selected from the predetermined design space and synthesized using an Opentrons OT2 robot, which took around 3 hours. After one day, UV-vis spectroscopy characterization was performed, and the distance metric was used to classify each sample. The information on the composition and classification of each sample was then used to train a Gaussian process classifier. Due to the probabilistic nature of a Gaussian process, we could identify regions in the design space where the probability of forming small, colloidally stable, monodisperse plate-like structures was greater than a certain limit, which was chosen to be 90%. It is important to clarify that this 90% limit is a hyperparameter independent from the distance threshold, but both can be used to bias how strongly the algorithm forms the targeted structure. Next, we randomly selected 48 new samples from these high-probability regions to obtain the next iteration of compositions to synthesize. In this closed-loop system, the Gaussian process gets more accurate as data is obtained, which allows it to improve its prediction of where samples with high concentrations of the desired plates are most likely to be formed. It was observed that convergence was achieved after performing a total of six iterations.

Fig. 2 The workflow for fast spectroscopic exploration. samples were synthesized with an Opentrons OT-2 liquid handling robot and then characterized using UV-vis spectroscopy. Each UV-vis spectrum that was obtained was classified, using the distance metric, into whether it had characteristics of small, colloidally stable, monodisperse, plate-like particles. This information was then used to train a Gaussian process classifier. Using this classifier, the region where desired plates are most likely to be formed was identified, and samples for the next iteration were randomly chosen from this region. This method can be applied in high-dimensional design spaces, but a two-dimensional design space is shown in the figure for visualization purposes.

Results of fast spectroscopic exploration

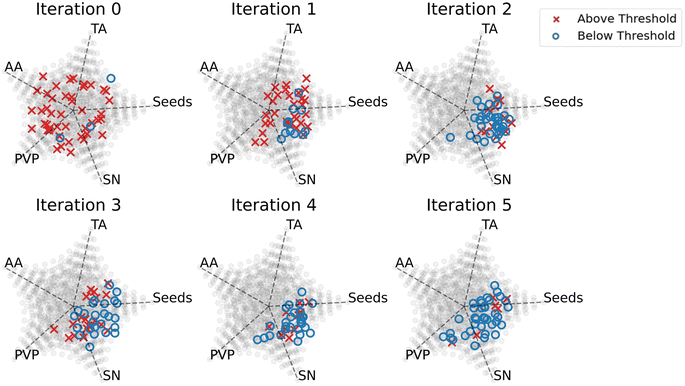
The primary goal for the interpretation of data in this section was to determine the design rules that the Gaussian process classifier learned to synthesize plate-like particles. Understanding these design rules can be helpful when performing future experiments that attempt to synthesize plate-like particles. Fig. 3 shows the changes in the samples' composition over the iterations and gives insight into how the Gaussian process classifier updated its predictions throughout the experiment. Since we used random sampling, each iteration consists of samples that, collectively, are an unbiased representation of the region in the design space where plates are formed. The ability to randomly sample in different regions of the design space gives rise to the interpretability of our data-driven exploration and distinguishes it from other closed-loop retrosynthesis systems.

Fig. 3 This figure shows the volume fractions of each sample that was synthesized in each iteration. Each iteration contains 48 samples. The plot of each iteration is a 2-dimensional representation of a 5-dimensional space. Each corner of the pentagon represents a reagent: ascorbic acid (AA), tannic acid (TA), silver seeds (Seeds), silver nitrate (SN), and polyvinylpyrrolidone (PVP). Samples that are located closer to a corner indicate a higher volume fraction of the reagent labeled in the respective corner. Samples located near the center of the plot, indicated by the intersection of the dotted black lines, suggest equal volume fractions of all reagents. The grey dots are visual aids to show the shape of the plot. A red “x” represents a sample that was classified as “Above Threshold” using the distance metric. A blue “o” represents a sample that was classified as “Below Threshold”. There were 3/48 samples labeled “Below Threshold” in iteration 0, 11/48 in iteration 1, 34/48 in iteration 2, 26/48 in iteration 3, 36/48 in iteration 4, and 41/48 in iteration 5.

In Fig. 3, we attempt to visualize the multivariate effect of the reagents on the shape of the nanoparticle by representing the volume fractions of the 5 reagents using multidimensional scaling plots, adapted from Li et al.²⁶ Iteration 0 in Fig. 3 was the first iteration, meaning that it was sampled randomly without any input from the Gaussian process classifier. Because of this, the samples were dispersed, and a high number of samples that had distances above the threshold were synthesized. In iteration 1, the Gaussian process classifier influenced the sampling by sampling in the region with low-volume fractions of ascorbic acid. However, there were still many samples that had distances above the threshold. In iteration 2, the sampling was biased towards low-volume fractions of ascorbic acid and tannic acid, moderate-volume fractions of PVP, and high-volume fractions of silver nitrate and silver seeds. In this iteration, the majority of the samples were plate-like and had distances below the threshold. The design rules learned from iteration 2 were maintained through iteration 5, which indicates convergence to a set of rules.

There are several explanations for why these design rules led to the synthesis of small, colloidally stable, monodisperse, plate-like particles. According to Yang et al., slow growth kinetics of the nanoparticles is essential for the formation of plate-like particles, which means that weaker reducing agents are favorable over stronger ones.²⁷ In our experiment, ascorbic acid was the strongest reducing agent followed by tannic acid and then PVP. This could explain why moderate-volume fractions of PVP and low-volume fractions of tannic acid and ascorbic acid were selected for the formation of plates. In addition to being a weak reducing agent, PVP can also bind to the Ag(111) facet of the plate (i.e., the axial direction) via van der Waals interactions and induce growth in the radial direction.²⁸ The data also shows that high concentrations of silver seeds and silver nitrate were needed to form our targeted particles. In our distance metric, we simulated small plates (20–40 nm), and we included a term to bias towards monodispersity. High-volume fractions of silver seeds result in a large number of nucleation sites for the nanoparticles to grow and high-volume fractions of silver nitrate are necessary for the production of the silver atoms that grow on these sites.²⁹ This combination of reagents would thus result in a high concentration of small monodisperse plates.

The classified UV-vis spectra of all the samples were plotted and shown in Fig. 4. The spectra that were classified as “Below Threshold” have similar shapes (i.e., single narrow peak) and peak intensity positions (i.e., greater than 450 nm) to the simulated plates in Fig. 1. In addition, the variance in the peak intensity positions indicates that plates of different sizes are being synthesized, which means that the effect of the reagents on the plate size can be explored in the next section. The spectra of the samples that were classified as “Above Threshold” are also shown in Fig. 4. These spectra have vastly different shapes such as ones with broad peaks, ones with high extinction at high wavelengths, and also ones that are similar to the simulated sphere spectra in Fig. 1. The successful classification of UV-vis spectra shown in Fig. 4 supports the implementation of our chosen distance metric. Geometric metrics, such as the aspect ratio of plates or spheres, could also be great metric descriptors of morphology. However, determining metrics such as the aspect ratio of a particle usually requires microscopy, which is typically a low throughput and costly technique. Instead, we rely on using bulk classification metrics (e.g. UV-vis, SAXS) that can be used as proxies for the ensemble geometry of particles. As seen by the results of our classification, UV-vis spectroscopy was able to differentiate samples that formed small, monodisperse, (triangular or circular) plate-like particles from other kinds of morphologies and sizes. Therefore, UV-vis spectroscopy is an effective and cost-effective technique for this classification. We would also like to clarify that, for this work, we focused on demonstrating the hierarchical analysis method, which could be applied to any particle of interest. We chose to focus on making small monodisperse plate-like particles. However, the methodology could be used for any other particle shape of interest with modification of the simulations and the definition of the distance metric.

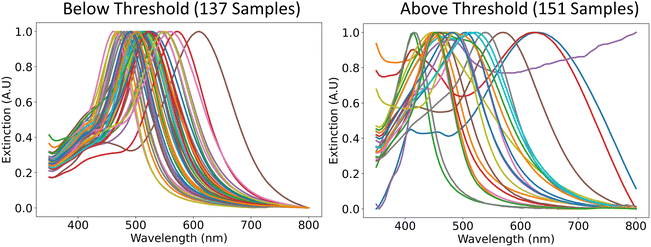Fig. 4 Representative UV-vis spectra of the samples that were classified as “Below Threshold” and the ones that were classified as “Above Threshold”.

SAXS structural exploration

From Fast spectroscopic exploration, we selected 137 samples that were classified as “Below Threshold” based on their UV-vis spectroscopy curve. To determine how the concentration of the reagents affects the size of the plates, we took SAXS measurements on these samples. Unlike UV-vis spectroscopy, SAXS is a direct method of characterizing nanoparticle structure in the dispersion state due to its sensitivity to structural parameters in this size range. The scattering can be mathematically modeled as the Fourier transform of the continuous electron density in all sample orientations,³⁰ and because of this, geometric models can be used to fit experimental data to obtain information on size, shape, shape fraction, polydispersity, or concentration. Like other scattering techniques, SAXS data has the limitation of being degenerate, which means that many structures can have the same SAXS curve. This is due to the phase problem where the detector can only measure the intensity of the scattered x-rays and not the phase, which contains the majority of the structural information.³⁰ Because of this, it is well known that the choice of geometric model used to fit the data must be supported with data from other characterization methods or other pieces of information.³¹ In our method we only perform SAXS on samples that we hypothesize are plates based on the shape of their UV-vis spectroscopy curve. After collecting the SAXS data, we can then perform electron microscopy on a few samples to confirm this hypothesis.

Supported by evidence primarily from UV-vis spectroscopy, the geometric model used to fit the SAXS data was a dilute cylinder model because a cylinder with a radius much larger than its length is representative of a plate. Although the shape of particles is most frequently rounded, in certain samples we also observe nanoplates with triangular shapes. In SAXS analysis these were approximated with a circular plate model because of the low difference between the scattering patterns for somewhat polydisperse samples. However, their presence could have a significant effect on the spectroscopic properties. The fundamental equation for small angle X-ray scattering is shown in eqn (2). The variable n refers to the number density of the particles, Δρ refers to the contrast, V refers to the volume of a single particle, S(q) refers to the structure factor, and P(q) refers to the form factor.³²

I(q) = nΔρ²V²P(q)S(q) + background (2)

This equation was simplified with the following expression:

A = nΔρ²V² (3)

Since Δρ and V are constant:

A ∝ n (4)

By substituting eqn (3) back in eqn (2), assuming that the nanoparticles are dilute(S(q) = 1), assuming a background of 0, and using the form factor of a plate, the scattering equation for a plate was created. The subscript “p” refers to a plate.

I(q) = A_pP_p(R,T,PD,q) (5)

Using sasmodels (http://www.github.com/SasView/sasmodels), the parameters in eqn (5) were obtained by fitting the model to the experimental data. From the form factor P_p(R, T, PD, q), the radius R, the lognormal polydispersity of the radius PD, and the thickness T of the plates were obtained. The scale parameter A was also obtained, which is a parameter proportional to the concentration of the particles in the solution.

After fitting all the data with a plate model, it was discovered that 23 out of the 137 fits were sub-optimal by the residuals or errors of the fits. To fit these datasets, a combined model of a plate and sphere (eqn (6)) was used only on the data from the 23 samples. In eqn (6), the subscript “p” refers to a plate and “s” refers to a sphere.

I(q) = A_pP_p(PD,R,T,q) + A_sP_s(R,q) (6)

This method of hierarchical fitting ensures that the most simple model (i.e., polydisperse plates) is used first to fit the data. This means the data that agreed with this simple model most likely come from samples that contain polydisperse plates. As we update the model by adding spheres, we risk overfitting the data and are less confident in the structural parameters obtained from these fits. While the plate and sphere model improved the fits of the 23 samples that did not fit the polydisperse plate model, they were not used in further data analysis, since the objective of this work is to study the structural features of nanoplates.

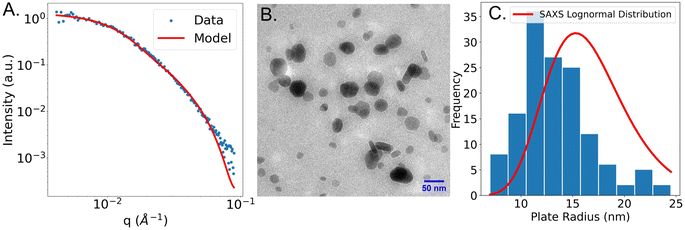
After fitting the SAXS data with the models, we randomly chose a sample that was fit using the polydisperse plate model. Electron microscopy was performed to validate the model choice that was used. The SAXS curve of the sample that was fit using a plate model and an image of the sample is shown in Fig. 5B below.

Fig. 5 This figure shows the data from the randomly chosen sample that was fit using a plate model. (A) The SAXS curve and the plate model that was used to fit the data. (B) An electron microscopy image from the set of images that were taken of the sample. (C) A histogram of the plate radii from all the images that were taken. The lognormal distribution with the plate radius and polydispersity obtained from SAXS is plotted in red.

Fig. 5A shows the experimental SAXS scattering curve of a plate-like sample and the plate model used to fit the experimental data. From the fit, an average plate radius of 16.2 nm, a lognormal plate radius polydispersity of 0.24, and a plate thickness of 7.2 nm was obtained. Fig. 5B shows a TEM image taken of the same sample. From that image, circular plates of different radii are observed. It is likely that some plates are stacked on top of each other, which causes some plates to have darker contours in the image. It is also possible that spheres are stacked on top of plates. However, we believe, based on evidence from UV-vis spectroscopy and SAXS, that the sample is primarily composed of plates. In addition, some plates stand on their edges which could explain the rod-like shape in TEM. This analysis is consistent with that of similar silver nanoplates in Gestraud et al.³³ The image in Fig. 5B is a representative image from a much larger set. By measuring the plate radii using all images (included in the ESI S11–S18†), a histogram of the plate radius was created and compared to the lognormal distribution obtained from SAXS. The comparison between the radius distribution derived from TEM and SAXS is shown in Fig. 5C. From the TEM images, the radius of 140 individual plates was measured. The mean radius was 13.3 nm and the lognormal radius polydispersity was 0.26. The lognormal radius polydispersity obtained from microscopy and SAXS have a good agreement, but the plate radius obtained from SAXS is slightly larger than that from microscopy. There are several reasons for this discrepancy. The first reason for the disagreement between SAXS and TEM could be that data obtained from SAXS is often biased towards larger particles because of their stronger scattering signal.³⁴ Another reason is the difficulty in distinguishing between thickness and radius in the TEM images since the particles can be imaged in all possible orientations.

Results of SAXS structural exploration

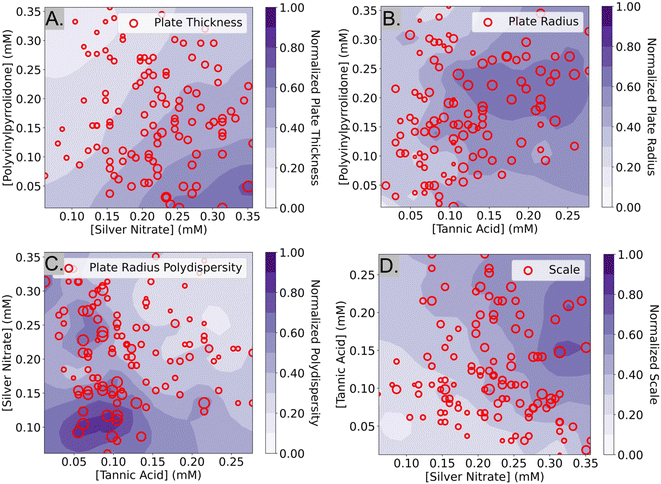
The interpretation of structural features from samples obtained via SAXS was performed in several steps. The first step relates the composition of the synthesis to the plate thickness, scale parameter, radius, and polydispersity. We first use histograms to visualize the different types of plates that were formed in our experiment. We then attempt to discover relationships between the concentrations of the reagents and the structural features using contour plots. This information can be used to obtain a better understanding of the role of each reagent in the synthesis of silver nanoplates. Understanding the roles of each reagent could be useful to modify the experimental design space in case a target structure cannot be synthesized.

Plate thickness, plate radius, plate radius polydispersity, and scale

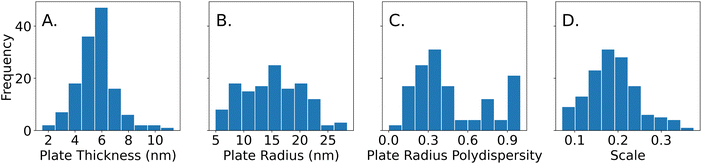
The histograms in Fig. 6 show the plate thicknesses, plate radius, lognormal radius polydispersity, and scale parameter of the 114 samples that were obtained from SAXS data that were fit using the polydisperse plate model. Since compositions were randomly sampled, the histograms are representative of the samples in the targeted design space of plate-like particles learned by the Gaussian process classifier after the Fast spectroscopic exploration step. The plate thicknesses ranged from 2.4 nm to 11.4 nm with a mean of 5.7 nm and a standard deviation of 1.3 nm. Most of the thicknesses (about 90%) are less than 7 nm. The plate radius ranges from 5.0 nm to 34.0 nm with a mean of 15.8 nm and a standard deviation of 5.1 nm. The plate radii seem to be somewhat normally distributed. The lognormal polydispersity of the plate radii ranges from 0 to 1 with a mean of 0.45 and a standard deviation of 0.28. Most of the samples seem to have a polydispersity of less than 0.5, but there are some with a polydispersity of 1.0. A polydispersity of greater than 0.5 can be considered excessive and likely caused by another factor such as aggregation or low concentrations that limit the quality and reliability of the SAXS data. Despite this, the samples with high polydispersity were kept for the analysis, since they were a minority of all the samples (31 out of 114 samples). Finally, the concentration of the particles was determined by the scale parameter in eqn (4), which is proportional to the concentration of the particles in the solution. It ranges from 0.07 to 0.38 and seems to be normally distributed with a mean of 0.18 and a standard deviation of 0.06. All this information can inform us of the sizes of the plates that are most commonly synthesized by the algorithm used in the Fast spectroscopic exploration section and their size limits.

Fig. 6 A histogram of the plate thickness (A), plate radius (B), lognormal plate radius polydispersity (C), and scale (D) that were obtained from the 114 samples that were fitted with the polydisperse plate model.

To determine the effects of the experimental design parameters on the structural features of the samples, the 5-dimensional design space was simplified into 2 dimensions. SHAP, a method to explain machine learning models,³⁵ was first used to identify the top two most important reagents that contributed to each of the measured structural features. This ignores data on the concentrations of the other three reagents but increases the interpretability since it is much easier to visualize data in two dimensions. From SHAP, it was determined that PVP and silver nitrate were the strongest contributors to variations in plate thickness, while tannic acid and PVP contributed the most to variations in plate radius. A Gaussian process regressor was trained with the top two contributing factors (i.e. reagents) and the structural parameter to obtain a contour plot that shows how the regions in the design space affect each structural parameter.

In the contour plot of plate thickness (Fig. 7A) there is a noticeable pattern where low concentrations of PVP and high concentrations of silver nitrate resulted in thicker plates. A reason for this could be that higher concentrations of silver nitrate lead to higher amounts of silver atoms available in the solution. Low concentrations of PVP result in larger plates because PVP can act as a stabilizer to prevent large particles from forming. As discussed before, it has been reported that PVP preferentially binds to the Ag(111) facet (i.e., the axial direction) via van der Waals interactions due to the larger surface area. This explains why lower concentrations of PVP result in thicker plates. In Fig. 7B, tannic acid and PVP were identified as the top two most influential reagents on plate radius. From Fig. 7B, it seems that the region where samples with the largest plate radii are obtained is in the darker purple region, between 0.10–0.25 mM tannic acid and 0.15–0.25 mM PVP. This indicates that relatively high concentrations of both tannic acid and PVP are essential for the formation of large silver nanoplates, but excessive amounts result in a reduced size. As discussed previously, tannic acid and PVP can act as both reducing agents and stabilizers that control the size and shape of the nanoplates.^36–38 Low concentrations of reducing agents could result in smaller nanoparticles by limiting the number of silver atoms available in the solution. However, we hypothesize that high concentrations of these reagents could hinder the growth of the nanoplates by inducing steric hindrance effects on the surface of the particles.²⁸ Another reason why high concentrations of both PVP and tannic acid are detrimental to the plate radius could be due to the cross-linking of the reagents. During the synthesis, it was observed that when high concentrations of tannic acid were mixed with PVP, the solution became turbid. The cross-linking of tannic acid and PVP is likely caused by the pyrogallol compounds in tannic acid interacting with PVP via hydrogen bonding³⁹ or π–π stacking.⁴⁰ Therefore, it is hypothesized that high concentrations of tannic acid could contribute to a lower plate radius by inducing cross-linking and reducing the number of PVP and tannic acid molecules available for the reaction. Finally, the largest plates of the samples labeled “Below Threshold” are around 30–34 nm in radius and are located in the central region of Fig. 7B, supporting the hypothesis that moderate concentrations of tannic acid and PVP lead to large plates.

Fig. 7 Contour plots of the top two most influential reagents on plate thickness (A), plate radius (B), lognormal plate radius polydispersity (C), and the scale parameter of the particles (D), which is proportional to the concentration of the particles. The structural information was obtained by fitting a polydisperse plate model to SAXS data. The marker size is directly correlated to the value of the structural feature, and the contours represent the design space learned by the Gaussian process regressor.

In Fig. 7C, a contour plot of the effect of the top two reagents on the lognormal polydispersity of the plate radius is shown. It was determined that silver nitrate and tannic acid had the greatest effect on this feature and that high concentrations of both reagents increase the probability of synthesizing monodisperse plates. Due to the lack of studies involving the effect of silver nitrate and tannic on the polydispersity of plate radius, no comparisons to the literature were made. In equation Fig. 7D, the effect of tannic acid and silver nitrate on the scale parameter of the particles is shown. The contour plot shows that high amounts of silver nitrate and tannic acid increase the scale parameter of the particles. This is consistent with the explanation that silver nitrate is the precursor of the silver ions in the reaction and that tannic acid acts as a reducing agent. In summary, we have described many testable hypotheses that could explain the observations in our experiment. While these hypotheses have not been experimentally verified in this manuscript, we aim to tackle that in a follow-up work.

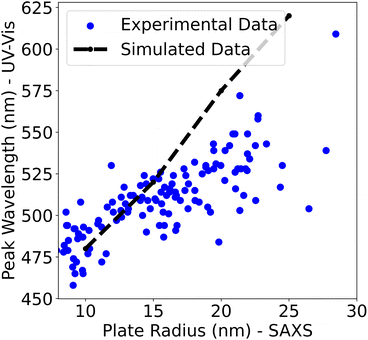
UV-vis spectroscopy as a proxy for particle size

In the Fast spectroscopic exploration section of this paper, it was claimed that UV-vis spectroscopy was limited in determining the size of a nanoparticle. Since both a UV-vis spectrum and a SAXS scattering curve were obtained for each sample, that claim could be evaluated. By assuming that the plate radius determined by SAXS was the “true” value, the radius determined by SAXS and the peak wavelength of the sample's UV-vis spectra were plotted. Only the 114 samples that were determined to be polydisperse plates are shown in the plot. In addition to this, the peak wavelength positions of the simulated UV-vis spectra using nanoDDSCAT²⁴ were added to the plot to compare how the peak wavelength position changes as the plates get bigger in simulations compared to experiments.

From Fig. 8, it is evident that the peak wavelength position increases as the plate radius increases. This is seen in both the experimental data and the simulations and confirms that the peak wavelength position of the spectra is positively correlated with the size of the nanoparticle. However, it seems that the nanoDDSCAT simulation overestimates the peak wavelength position compared to the experimental data. An explanation for this could be the presence of organic molecules in the solution such as PVP or tannic acid which could account for this disagreement.

Fig. 8 The comparison between the plate radius determined by the peak wavelength position from UV-vis spectroscopy and the radius determined by SAXS. The data from the simulated plates are also plotted assuming that the radius determined from SAXS is the “true” radius.

In summary, Fig. 8 shows that the peak wavelength positions from UV-vis spectra are directly correlated with the size of the nanoparticle. However, caution must be exercised when using the peak wavelength position to determine the absolute size of a nanoparticle especially when analyzing samples with impurities or with anisotropically shaped nanoparticles. This underscores the importance of SAXS for determining the size of silver nanoparticles in dispersion since X-rays are only sensitive to the size and morphology of these electron-dense nanoparticles. Dynamic light scattering (DLS) is another technique that is sensitive to the size and shape of nanoparticles and is often more accessible than SAXS. However, DLS relies on size measurements based on the diffusion of particles, which has a much lower structural resolution and is model-dependent. Thus, the interpretation of DLS data requires an assumption of either spherical particles to convert a diffusion coefficient into a diameter or an assumption of a shape (e.g., plates) and an aspect ratio to quantitatively interpret the size from the diffusion coefficient. For these reasons, SAXS is more powerful for the analysis of silver nanoparticles as we report in this study.

Conclusions

We performed a data-driven exploration of the synthesis of silver nanoplates, which combines the iterative sampling capabilities of a closed-loop system and the straightforward data interpretation and visualization of a systematic study. Our closed-loop system goes beyond solving an optimization problem and focuses on the generation of scientific knowledge. To do this, we take advantage of multimodal and complementary characterization methods. Our data-driven method balances the use of characterization techniques based on cost and information gained. UV-vis spectroscopy was used as a fast proxy to determine how to synthesize silver nanoplates, while SAXS, a more expensive but direct characterization method, was used for information on the structural features of these nanoplates. In summary, using a Gaussian process classifier and UV-vis spectroscopy, we started from a relatively large design space and narrowed it down to a region where plate-like particles are most likely to be formed. In this region of interest, random sampling and SAXS were used to obtain simplified contour plots containing information on the effect of the top two most contributing chemical reagents on the structural features of nanoplates. Our findings on the compositions of the reagents that are necessary to form plate-like nanoparticles as well as the effect of these reagents on the nanoparticle's structural features are consistent with the literature. Because of this, we envision that all the methods that were used for the synthesis, data science, and characterization can be applied to other, more complex, systems to accelerate the discovery of novel materials.

Data availability

Data and processing scripts for this paper, including the algorithms used for the exploration of the design space and SAXS data fitting are available at (https://github.com/pozzo-research-group/papers/tree/main/Silver Nanoplates).

Author contributions

All the authors contributed equally to conceptualization, Methodology, problem formulation, and reviews. H. T. C developed the theoretical and algorithmic framework for the data-driven exploration, and experimental pipeline, and performed all the experimental synthesis and sample characterization. L. D. P. contributed to the supervision and project administration.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the DOE Energy Frontiers Research Center (EFRC) the Center for the Science of Synthesis Across Scales (DE-SC0019288). Shape-based metric analysis by K. V. was funded by the US Department of Energy (DOE), Office of Science, and Office of Basic Energy Sciences (BES) under the award number DE-SC0019911. The authors acknowledge the use of facilities and instrumentation supported by the U.S. National Science Foundation through the Major Research Instrumentation (MRI) program (DMR-2116265) and the UW Molecular Engineering Materials Center (MEM-C), a Materials Research Science and Engineering Center (DMR-2308979). Part of this work was conducted at the Molecular Analysis Facility, a National Nanotechnology Coordinated Infrastructure (NNCI) site at the University of Washington, which is supported in part by funds from the National Science Foundation (awards NNCI-2025489, NNCI-1542101). Part of this work was conducted with instrumentation provided by the Joint Center for Deployment and Research in Earth Abundant Materials (JCDREAM). This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. SasView contains code developed with funding from the European Union's Horizon 2020 research and innovation program under the SINE2020 project, grant agreement no. 654000.

Notes and references

1. Z.-J. Jiang, C.-Y. Liu and L.-W. Sun, J. Phys. Chem. B, 2005, 109, 1730–1735.
2. X.-F. Zhang, Z.-G. Liu, W. Shen and S. Gurunathan, Int. J. Mol. Sci., 2016, 17, 1534.
3. P. Prasher, M. Sharma, H. Mudila, G. Gupta, A. K. Sharma, D. Kumar, H. A. Bakshi, P. Negi, D. N. Kapoor, D. K. Chellappan, M. M. Tambuwala and K. Dua, Colloid Interface Sci. Commun., 2020, 35, 100244.
4. A. I. Pérez-Jiménez, D. Lyu, Z. Lu, G. Liu and B. Ren, Chem. Sci., 2020, 11, 4563–4577.
5. L. M. Liz-Marzán, Langmuir, 2006, 22, 32–41.
6. S. Iravani, H. Korbekandi, S. Mirmohammadi and B. Zolfaghari, Res. Pharm. Sci., 2014, 9, 385–406.
7. A. R. Tao, S. Habas and P. Yang, Small, 2008, 4, 310–325.
8. K. J. Lachowski, H. T. Chiang, K. Torkelson, W. Zhou, S. Zhang, J. Pfaendtner and L. D. Pozzo, Langmuir, 2023, 39, 15878–15888.
9. H. Tao, T. Wu, S. Kheiri, M. Aldeghi, A. Aspuru-Guzik and E. Kumacheva, Adv. Funct. Mater., 2021, 31, 2106725.
10. K. Vaddi, H. T. Chiang and L. D. Pozzo, Digital Discovery, 2022, 1, 502–510.
11. S. Y. Schmid, K. Lachowski, H. T. Chiang, L. Pozzo, J. De Yoreo and S. Zhang, Angew. Chem., Int. Ed., 2023, 62, e202309725.
12. M. Ansari and A. D. White, J. Chem. Inf. Model., 2023, 63, 2546–2553.
13. Y. Liu, M. Ziatdinov and S. V. Kalinin, ACS Nano, 2022, 16, 1250–1259.
14. D. Salley, G. Keenan, J. Grizou, A. Sharma, S. Martín and L. Cronin, Nat. Commun., 2020, 11, 2771.
15. A. A. Volk, R. W. Epps, D. T. Yonemoto, B. S. Masters, F. N. Castellano, K. G. Reyes and M. Abolhasani, Nat. Commun., 2023, 14, 1403.
16. F. Mekki-Berrada, Z. Ren, T. Huang, W. K. Wong, F. Zheng, J. Xie, I. P. S. Tian, S. Jayavelu, Z. Mahfoud and D. Bash, et al. , npj Comput. Mater., 2021, 7, 1–10.
17. Y. Jiang, D. Salley, A. Sharma, G. Keenan, M. Mullin and L. Cronin, Sci. Adv., 2022, 8, eabo2626.
18. K. J. Lachowski, K. Vaddi, N. Y. Naser, F. Baneyx and L. D. Pozzo, Digital Discovery, 2022, 1, 427–439.
19. M. Politi, F. Baum, K. Vaddi, E. Antonio, J. Vasquez, B. P. Bishop, N. Peek, V. C. Holmberg and L. D. Pozzo, Digital Discovery, 2023, 2, 1042–1057.
20. S. Samanta, P. Sarkar, S. Pyne, G. P. Sahoo and A. Misra, J. Mol. Liq., 2012, 165, 21–26.
21. S. Caroline, R. Wayne and E. Kevin, Nat. Methods, 2012, 671.
22. K. J. Lachowski, H. T. Chiang, K. Torkelson, W. Zhou, S. Zhang, J. Pfaendtner and L. D. Pozzo, Langmuir, 2023, 39, 15878–15888.
23. A. Siehr, B. Xu, R. A. Siegel and W. Shen, Soft Matter, 2019, 15, 7122–7126.
24. P. K. Jain, N. Sobh, J. Smith, A. N. Sobh, S. White, J. Faucheaux and J. Feser, nanoDDSCAT, 2014, https://nanohub.org/resources/dda, Accessed on 2023-09-16.
25. C. Boukouvala and E. Ringe, J. Phys. Chem. C, 2019, 123, 25501–25508.
26. Y. J. Li, A. Savan, A. Kostka, H. S. Stein and A. Ludwig, Mater. Horiz., 2018, 5, 86–92.
27. Y. Yang, W. Wang, X. Li, W. Chen, N. Fan, C. Zou, X. Chen, X. Xu, L. Zhang and S. Huang, Chem. Mater., 2013, 25, 34–41.
28. R. Mravljak and A. Podgornik, ACS Omega, 2023, 8, 2760–2772.
29. Z. YI, J. bo ZHANG, H. HE, X. bin XU, B. chi LUO, X. bo LI, K. LI, G. NIU, X. lan TAN, J. shan LUO, Y. jian TANG, W. dong WU and Y. gen YI, Trans. Nonferrous Met. Soc. China, 2012, 22, 865–872.
30. C. J. Gommes, S. Jaksch and H. Frielinghaus, J. Appl. Crystallogr., 2021, 54, 1832–1843.
31. B. R. Pauw, J. Phys.: Condens. Matter, 2013, 25, 383201.
32. C. M. Jeffries, J. Ilavsky, A. Martel, S. Hinrichs, A. Meyer, J. S. Pedersen, A. V. Sokolova and D. I. Svergun, Nat. Rev. Methods Primers, 2021, 1, 70.
33. C. Gestraud, P. Roblin, J. F. Morris, M. Meireles and Y. Hallez, CrystEngComm, 2020, 22, 1769–1778.
34. S. Wu, X. Zuo and Y. Sun, J. Appl. Crystallogr., 2023, 56, 1739–1750.
35. S. M. Lundberg and S.-I. Lee, Advances in Neural Information Processing Systems 30, Curran Associates, Inc., 2017, pp. 4765–4774.
36. K. M. Koczkur, S. Mourdikoudis, L. Polavarapu and S. E. Skrabalak, Dalton Trans., 2015, 44, 17883–17905.
37. I. Washio, Y. Xiong, Y. Yin and Y. Xia, Adv. Mater., 2006, 18, 1745–1749.
38. T. Ahmad, J. Nanotechnol., 2014, 2014, 954206.
39. H. Fan, L. Wang, X. Feng, Y. Bu, D. Wu and Z. Jin, Macromolecules, 2017, 50, 666–676.
40. C. Chen, H. Yang, X. Yang and Q. Ma, RSC Adv., 2022, 12, 7689–7711.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00211c

---