Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cost-informed Bayesian reaction optimization†
Alexandre A.
Schoepfer‡
 abc,
Jan
Weinreich‡
abc,
Jan
Weinreich‡
 ac,
Ruben
Laplaza
ac,
Ruben
Laplaza
 ac,
Jerome
Waser
ac,
Jerome
Waser
 *bc and
Clemence
Corminboeuf
*bc and
Clemence
Corminboeuf
 *ac
*ac
aLaboratory for Computational Molecular Design, Institute of Chemical Sciences and Engineering, École Polytechnique Fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland. E-mail: clemence.corminboeuf@epfl.ch
bLaboratory of Catalysis and Organic Synthesis, Institute of Chemical Sciences and Engineering, École Polytechnique Fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland. E-mail: jerome.waser@epfl.ch
cNational Center for Competence in Research-Catalysis (NCCR-Catalysis), École Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland
First published on 1st October 2024
Abstract
Bayesian optimization (BO) is an efficient method for solving complex optimization problems, including those in chemical research, where it is gaining significant popularity. Although effective in guiding experimental design, BO does not account for experimentation costs: testing readily available reagents under different conditions could be more cost and time-effective than synthesizing or buying additional ones. To address this issue, we present cost-informed BO (CIBO), an approach tailored for the rational planning of chemical experimentation that prioritizes the most cost-effective experiments. Reagents are used only when their anticipated improvement in reaction performance sufficiently outweighs their costs. Our algorithm tracks available reagents, including those recently acquired, and dynamically updates their cost during the optimization. Using literature data of Pd-catalyzed reactions, we show that CIBO reduces the cost of reaction optimization by up to 90% compared to standard BO. Our approach is compatible with any type of cost, e.g., of buying equipment or compounds, waiting time, as well as environmental or security concerns. We believe CIBO extends the possibilities of BO in chemistry and envision applications for both traditional and self-driving laboratories for experiment planning.
1 Introduction
Reaction optimization is a challenging task that is often tackled “one factor at a time” by sequentially optimizing individual parameters such as catalyst, temperature, or additives. While this strategy simplifies the problem, it remains both time and resource-intensive. Moreover, promising combinations of parameters may be overlooked. For instance, an additive and ligand, which were discarded when tested individually, may yield optimal results when combined.As an alternative, data-driven computational tools, such as machine learning (ML), have recently been used to guide experimental effort aimed at achieving the best possible performance by predicting reaction yield or selectivity from substrates, catalysts, and reaction conditions.1–6 Amongst different ML frameworks, Bayesian optimization (BO) is ideally suited for this task.7,8 Given initial data, BO leverages predictions and their corresponding uncertainties to suggest the next experiments evaluated as the most promising. As such, BO-driven reaction optimization has seen notable success in the last few years, especially in automated laboratory and high-throughput experimentation (HTE) settings.3,9–16 In such situations, all materials being considered (i.e., substrates, catalysts, additives, solvents) are typically procured prior to experimentation, at which point BO is used to identify the best reagents and reaction conditions.1,3,17,18
Yet, the implementation of BO and other ML frameworks in more traditional (i.e., not high-throughput) laboratories is still limited.19–22 In these settings, defining and acquiring all necessary materials prior to the optimization, especially when dealing with unexplored chemistry, is not ideal. A further complication is that classical BO methods usually attribute the same cost to all suggested experiments. In reaction optimization, where e.g., catalyst ligands and reaction conditions have to be adjusted simultaneously, this assumption is also unsuitable as the cost of an experiment (in terms of money, time investment, or risk) can vary drastically depending on whether a ligand is already available in the laboratory, commercially available, reported in the literature, or has never been synthesized before. Thus, experiments suggested by BO may be impractical or even non-feasible and human filtering might be necessary. On the other hand, testing already available ligands with different reaction conditions may yield a comparable improvement with lower cost, especially in the preliminary stages of reaction optimization when less is known about the chemistry.
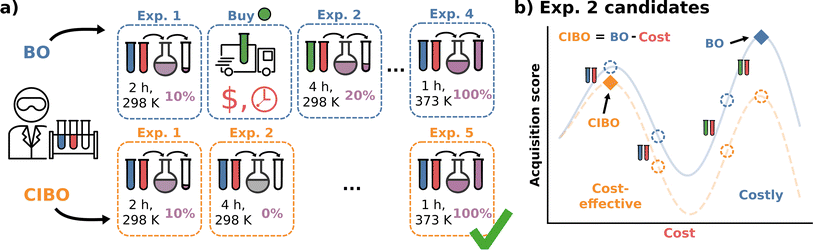
To overcome this limitation, we introduce cost-informed Bayesian optimization (CIBO), a BO framework that incorporates cost into the decision-making process to achieve practical and rational batch experimentation planning. CIBO optimizes a single objective by incorporating contextual information into the decision-making process. For instance, if two equally informative experiments are possible, CIBO suggests the one with the lower cost (Fig. 1). Additionally, it maintains a digital inventory that dynamically updates experiment costs based on the resources currently available. For example, once a ligand is purchased, it can be used for several experiments.
Previous methods aimed at optimizing reaction cost and performance relied on multi-objective approaches or included constraints on the overall cost.16,18,23,24 Multi-objective methods typically balance competing objectives like yield, selectivity, and cost, often using complex scalarizing methods to manage trade-offs (e.g., Pareto fronts). CIBO also contrasts with (non-multi-objective) methods that have been proposed in chemistry (vide infra), as well as in other fields, such as cost-aware BO in computer science.25–27 Those are based on different strategies and include, for instance, contextual BO,28 addressing environmental effects, as well as direct modifications of the acquisition function.29–31 Methods that favor low-cost experiments for a given budget have been suggested,32–36 but with the costs kept fixed throughout the optimization. Resource management optimization is a related problem that has been investigated, albeit not with BO.37–40 More recent works have focused on the cost of changing between different experimental setups to account for the associated expenses41–48 or on human-in-the-loop strategies.49 Finding cost-efficient routes in the context of retro-synthesis planning has also been explored50–54 although the focus is placed on proposing plausible and practical pathways rather than on optimizing the conditions of individual reactions.
To our knowledge, a reaction optimization framework accounting for both the cost of experiments contextually and the fact that these costs are dynamically updated over time has not been introduced. Here, we demonstrate the performance of CIBO using two HTE datasets of Pd-catalyzed reactions and find that, despite occasionally requiring additional experiments to match standard BO, the overall cost of the optimization is significantly reduced. Our benchmarks evaluate cost using the price of commercially available reagents. However, CIBO is compatible with any cost definition, such as the number of steps or estimated time required for synthesizing reported ligands, as well as sustainability metrics for solvents or compounds. In the latter case, the platform will prioritize options with lower environmental impact.55–57 Overall, CIBO promises an efficient and sustainable alternative to existing design-of-experiment methods.58,59
2 Methods
2.1 Cost-informed Bayesian optimization
BO is an effective method for optimizing noisy functions that are expensive or time-consuming to evaluate.60 At its core lies a surrogate model that predicts the value of the function (mean μ) and the uncertainty of the prediction (standard deviation σ). Acquisition functions are used to identify promising experiments in the design space.61 This is done by considering all possible experiments and weighting their potential to maximize μ, balancing the trade-off between exploring uncertain areas of the design space (exploration) and exploiting areas known to yield high values (exploitation). In addition to performing one experiment at a time, batch BO proposes a joined set (i.e., a batch of experiments) which provides the largest expected improvement when performed in parallel.Given the previous definition, BO does not account for the varying costs of the resources involved in the optimization. Instead of buying or synthesizing additional substances, chemists may first choose to vary easily controllable conditions (e.g., temperature, reaction time), resulting in lower costs and a better-informed decision before acquiring additional compounds. Finding the best experimental conditions for the smallest budget is different from identifying the best value–cost trade-off in the optimized reaction. The latter is relevant when large amounts of the compounds involved need to be acquired repeatedly: e.g., large-scale synthesis. The former, and current case, is relevant when the budget (in terms of cost, time, or other) for the experimentation campaign itself is important.
Our method, cost-informed Bayesian optimization (CIBO), balances minimizing experimentation cost with maximizing measured improvement (see Fig. 1). It results in experiments that more closely mimic the optimization process in a chemistry lab, only acquiring a compound if the expected improvement justifies the cost. CIBO stands out from standard BO by promoting the search for more cost-effective experiments while not constraining its search space (i.e., an expensive ligand may still be selected if its expected improvement is justified). We account for experimentation costs by including them in the acquisition function,62,63 scaling the cost adjustment with the expected improvement values. Given the set of all possible experiments {e}, we use the batch noisy expected improvement (qNEI) acquisition function {αe}, computed from the predicted μ and σ from the surrogate model to determine the next batch 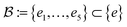 for each iteration.64,65 Here ej is the j-th experiment in batch
for each iteration.64,65 Here ej is the j-th experiment in batch 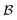 with acquisition function value αj ≡ αej. Note that there is exactly one αj per experiment ej. For a batch of experiments, here Ne = 5 per batch, we consider the current cost of each compound involved. As user input, only the compound prices per gram, per mol, per bottle, or other user-defined costs pj are required.
with acquisition function value αj ≡ αej. Note that there is exactly one αj per experiment ej. For a batch of experiments, here Ne = 5 per batch, we consider the current cost of each compound involved. As user input, only the compound prices per gram, per mol, per bottle, or other user-defined costs pj are required.
For simplicity, we cover the case of one compound j per experiment ej. Batches are ordered with respect to the norm of 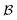 , defined by the sum of the acquisition function values αi in each batch,
, defined by the sum of the acquisition function values αi in each batch,
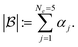 | (1) |
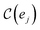 as follows:
as follows: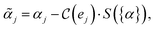 | (2) |
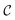 probes whether compound j was bought at price pj in a previous iteration or added to the same batch before, i.e.,
probes whether compound j was bought at price pj in a previous iteration or added to the same batch before, i.e.,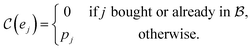 | (3) |
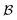 but under different experimental conditions. For simplicity, throughout this work we assume that compounds in the inventory are never exhausted. However, our framework could be set to deduct exact quantities from the inventory until nothing remains.
but under different experimental conditions. For simplicity, throughout this work we assume that compounds in the inventory are never exhausted. However, our framework could be set to deduct exact quantities from the inventory until nothing remains.
In eqn (2), we introduced a scaling function S that depends on all acquisition function values {α} evaluated on all experiments not yet included in the surrogate model and the current prices {p} for each ligand,
| S:= λ·max{α}/avg{p}, | (4) |
After computing the modified acquisition values for each potential experiment in a batch ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) 1, …
1, … ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) 5, we evaluate the updated norm value,
5, we evaluate the updated norm value,
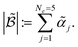 | (5) |
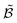 , offering the best cost–benefit ratio, is then selected for the next iteration.
, offering the best cost–benefit ratio, is then selected for the next iteration.
Note that our approach does not penalize exploration per se, but rather favors the most inexpensive ways to explore before committing to higher-cost experiments. Further details of our implementation are available in the ESI Section S1.†
2.2 Datasets and models
To demonstrate the potential of CIBO, we attempt to maximize reaction yield in the most cost-efficient manner for two literature datasets: Pd-catalyzed direct C–H arylation (DA, Fig. 2a)3 and Pd-catalyzed Buchwald–Hartwig cross-couplings of amine nucleophiles using a droplet platform (CC, Fig. 2b).17 Being the most expensive element of the optimization, CIBO should avoid using unnecessary ligands to reach a high yield.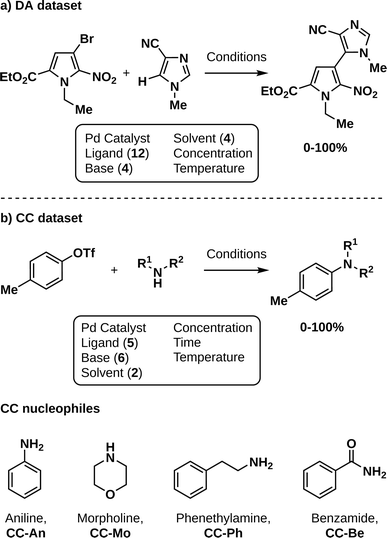 | ||
| Fig. 2 Reaction schemes of the two datasets used in this work. (a) Direct arylation (DA) with yields ranging from 0–100%.3 (b) Cross-coupling (CC) with yields ranging from 0–100%.17 The four nucleophiles explored in the latter dataset are depicted below, each leading to a subset (An, Mo, Ph, Be). | ||
In both cases, we use Gaussian process regression with a Jaccard–Tanimoto kernel (see ESI Section S2 for more details†) as the surrogate model in the optimization. The batch size is always fixed to five,3,18 but we note any other value could be used according to the preferred experimental setup. As the cost, we use the price per gram of material (dollars per gram $/g, see ESI Section S3 for details†), since chemical suppliers provide most chemicals gram-wise.
For consistency and to make the task challenging, we start the optimization using models trained only on a small subset of experiments performed with chemicals with low overall cost or performance (iteration zero, vide infra). The cost of the initial experiments is included in the total cost. For simplicity, we assume that we never run out of chemicals in the inventory, which applies both to the reagents used in the initial experiments and to newly acquired ones. The results are averaged over 100 separate runs using the same initialization.66
The DA dataset consists of 1728 measurements where the monophosphine ligand, base, solvent, concentration, and temperature are varied to optimize the formation of one product. The cost of chemicals was reported previously18 and was converted to dollars per gram for this work. We considered concentration and temperature to be variables with no additional cost. In general, the costs of the base and solvent are negligible compared to the ligand. The optimization begins with the surrogate model trained exclusively on the 144 experiments in the dataset that use the dimethylphenylphosphine ligand, which is inexpensive and the worst-performing ligand overall. The minimal spending to obtain the best results corresponds to $144 for this dataset.
For the CC dataset, four different amine nucleophiles, aniline (An), morpholine (Mo), phenethylamine (Ph), and benzamide (Be), are each coupled with p-tolyl triflate yielding different products over 363 reactions (around 90 per nucleophile). Each is considered an individual reaction in which the ligand (precatalyst), base (concentration and equivalents), solvent, temperature, and time all change.23 The prices for all chemicals involved were obtained from supplier websites and converted to dollars per gram if necessary. Concentrations, equivalents, temperature, and time are varied without additional cost. On average, nine experiments are used at the start of each optimization. For the Ph and Be subsets of CC we initialize using tBuXPhos as a ligand (for the precatalyst) and DBU as a base, the cheapest combination. For An, we chose to initialize with EPhos and TEA as the cheapest initialization would have resulted in perfect yield. For Mo no measurements with tBuXPhos were performed. Thus, we initialize with tBuBrettPhos and DBU. For the CC experiments, the cost of the solvents and bases were also taken into account, since the dataset contains only a few different ligands per nucleophile. The minimal spending to obtain the best results is $69 for An, $1382 for Mo, $97 for Ph, and $591 for Be respectively. A full list of chemical abbreviations is presented in Table S1.†
3 Results
3.1 Direct arylation
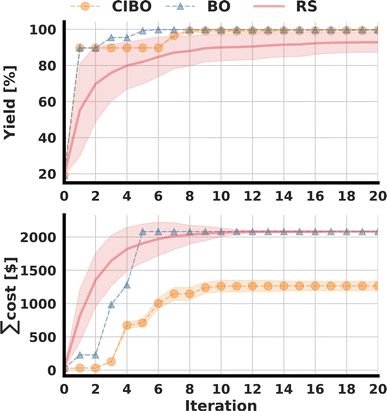
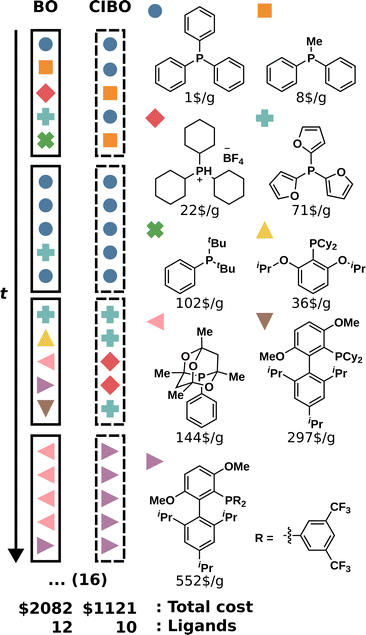
Following the original publication, the optimization was run for 20 total iterations (100 experiments).3 The best-observed yield for several batched iterations, as well as the total amount spent, are shown in Fig. 3. CIBO achieves a yield of over 99% after eight iterations, compared to five iterations in standard BO. However, the total cost of running the five iterations (25 experiments) suggested by BO is, on average $1592, whereas the cost of running the eight iterations proposed by CIBO (40 experiments) is, on average, $1156, 38% less. After 20 iterations, standard BO bought all possible ligands (12), amounting to a cost of $2082, while CIBO bought two fewer ligands (10), for a total spending of $1221, thereby saving more than 40%. Considering the error of the surrogate model (see ESI Section S1†) it is prudent not to buy additional ligands after reaching a yield above 99%. Following this logic, past that point (in the tenth iteration), CIBO suggests optimizing reaction conditions instead of buying expensive ligands.To study the difference in experimentation planning between BO and CIBO, we visualize the ligand batch composition of the first four iterations (see Fig. 4) for one of the five repetitions. CIBO batches are less diverse than BO in terms of ligands: CIBO suggests at most two different ligands per batch. In the first iteration, BO suggests acquiring five ligands in addition to dimethylphenylphosphine, compared to only two for CIBO. For a detailed analysis of the effect of initialization, see ESI Section S5.†
Finally, we investigated the influence of the weighting factor λ (see eqn (4)) on the results and found the expected behavior: increasing λ substantially decreases the costs and vice versa. However, this comes with a trade-off in yield optimization and an additional increase in the number of iterations required to obtain the yield for a smaller cost weighting (see ESI Section S4 for details†).
3.2 Cross-coupling
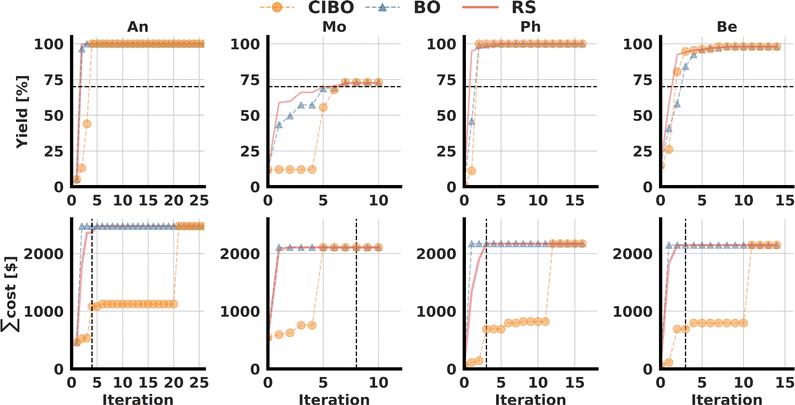
The top row shows the best yield found as a function of the batch iteration, and the bottom row displays the cumulative costs. The black dotted line in the top row indicates the target yield at 70%. The resulting terminal iteration (vertical black line) in the bottom row indicates the total budget spent with CIBO.The dataset is split into subsets of the four different amine nucleophiles (see Fig. 2b) resulting in four distinct optimization problems. As before, we consider the best-observed yield and total cost per iteration. The total dollar amount spent, listed in the first row of Table 1, depends on the nucleophile subset, since not all ligand (precatalyst)/base combinations were tested experimentally for each nucleophile. Due to the limited available data, the optimization is continued until the experimental data is exhausted, and the results are averaged over 100 different runs.
| An | Mo | Ph | Be | |
|---|---|---|---|---|
| Cost all reagents | $2474 | $2105 | $2170 | $2144 |
| CIBO spent | $1124 | $2105 | $142 | $690 |
| Saved wrt. BO | $1350 (54%) | 0 | $2028 (93%) | $1454 (68%) |
| Saved reagents | 5/9 | 0/7 | 4/8 | 3/8 |
As shown in the bottom row of Fig. 5 standard BO suggests buying all available ligand and base combinations immediately following the first iteration – irrespective of their costs. CIBO acquires less expensive reagents first and recommends experiments under varying conditions before finally buying all reagents – if no other experiments are left in the dataset. By inspecting the amount of money spent versus the number of iterations, Fig. 5, it is apparent that CIBO suggests more expensive molecules only as a last option. If possible, CIBO optimizes the yield based on reagent/condition combinations that can be performed with minimal or zero additional cost. The case of Be is illustrative: after iteration four, over 30 experiments are performed without acquiring any additional reagents, resulting in a cost plateau. Similar observations are made for An and Ph (Fig. 5a and c) where the optimization achieved a yield of 100% after only a few iterations, followed by iterations where CIBO does not acquire additional reagents.
The goal of every experimentation series always depends on the context. We define a stopping criterion when at least 70% yield is achieved, as this was deemed to be high yield in the original CC publication.17 In Table 1 we show the cost and reagent savings compared to standard BO when using this criterion. In all cases, except for Mo, the cost is reduced by over 50%, and fewer compounds were acquired.
For Mo, CIBO performs as well as BO in terms of yield optimization for the same cost, but only because the highest performing ligand is also the most expensive that must be acquired to achieve high yield. For Ph, CIBO requires no new ligands but manages to find a perfect yield by buying a much cheaper base (BTTP). This results in a savings of 93% compared to the standard BO experiments that acquire all ligands in a single step.
4 Conclusion
We introduced cost-informed Bayesian optimization (CIBO), a variant of BO that balances cost and ease of experimentation with a global optimization objective. Akin to BO, the algorithm retains the flexibility to identify the most promising experiments but takes a more cost-efficient optimization path by updating the acquisition function according to the current inventory status.This work focuses on limiting the economic cost engendered by the purchase of compounds needed to carry out an experiment, but CIBO is general and amenable to any user-defined cost, including logistical availability, synthesizability, number of synthetic steps, structural complexity, safety, time, environmental impact, and sustainability. The framework is also compatible with evolving costs and could, for example, be coupled with an online catalog. Finally, CIBO may also be adapted to planning and optimizing successive reactions and accounting for resource management.35,48,67
Overall CIBO is more broadly applicable than standard BO in conditions for which the cost of each experiment extensively varies (e.g., large ligand price differences). We envision the method to be useful for the reaction optimization and development in both traditional and self-driving laboratories.58,59
Data availability
CIBO, an accompanying tutorial, and all the data used in this work are available at https://github.com/lcmd-epfl/cibo.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors thank EPFL for computational resources. This publication was created as part of NCCR Catalysis (grant number 180544), a National Centre of Competence in Research funded by the Swiss National Science Foundation. We also thank Dr Puck van Gerwen, Dr Ksenia Briling, and Dr Matthew Wodrich for fruitful discussions.References
- D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Predicting reaction performance in C–N cross-coupling using machine learning, Science, 2018, 360, 186–190 CrossRef CAS PubMed.
- A. F. Zahrt, J. J. Henle, B. T. Rose, Y. Wang, W. T. Darrow and S. E. Denmark, Prediction of higher-selectivity catalysts by computer-driven workflow and machine learning, Science, 2019, 363, eaau5631 CrossRef CAS PubMed.
- B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Bayesian reaction optimization as a tool for chemical synthesis, Nature, 2021, 590, 89–96 CrossRef CAS PubMed.
- P. Schwaller, A. C. Vaucher, R. Laplaza, C. Bunne, A. Krause, C. Corminboeuf and T. Laino, Machine intelligence for chemical reaction space, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1604 Search PubMed.
- E. Shim, A. Tewari, T. Cernak and P. M. Zimmerman, Machine Learning Strategies for Reaction Development: Toward the Low-Data Limit, J. Chem. Inf. Model., 2023, 63, 3659–3668 CrossRef CAS PubMed.
- B. Ranković, and P. Schwaller, BoChemian: Large language model embeddings for Bayesian optimization of chemical reactions, NeurIPS 2023 Workshop on Adaptive Experimental Design and Active Learning in the Real World, 2023 Search PubMed.
- J. Guo, B. Ranković and P. Schwaller, Bayesian optimization for chemical reactions, Chimia, 2023, 77, 31–38 CrossRef CAS PubMed.
- B. Ranković, R.-R. Griffiths, H. B. Moss and P. Schwaller, Bayesian optimisation for additive screening and yield improvements – beyond one-hot encoding, Digital Discovery, 2024, 3, 654–666 RSC.
- A. M. Schweidtmann, A. D. Clayton, N. Holmes, E. Bradford, R. A. Bourne and A. A. Lapkin, Machine learning meets continuous flow chemistry: Automated optimization towards the Pareto front of multiple objectives, Chem. Eng. J., 2018, 352, 277–282 CrossRef CAS.
- A. D. Clayton, A. M. Schweidtmann, G. Clemens, J. A. Manson, C. J. Taylor, C. G. Niño, T. W. Chamberlain, N. Kapur, A. J. Blacker, A. A. Lapkin and R. A. Bourne, Automated self-optimisation of multi-step reaction and separation processes using machine learning, Chem. Eng. J., 2020, 384, 123340 CrossRef CAS.
- N. H. Angello, V. Rathore, W. Beker, A. Wołos, E. R. Jira, R. Roszak, T. C. Wu, C. M. Schroeder, A. Aspuru-Guzik, B. A. Grzybowski and M. D. Burke, Closed-loop optimization of general reaction conditions for heteroaryl Suzuki-Miyaura coupling, Science, 2022, 378, 399–405 CrossRef CAS PubMed.
- K. E. McCullough, D. S. King, S. P. Chheda, M. S. Ferrandon, T. A. Goetjen, Z. H. Syed, T. R. Graham, N. M. Washton, O. K. Farha, L. Gagliardi and M. Delferro, High-throughput experimentation, theoretical modeling, and human intuition: Lessons learned in metal–organic-framework-corted catalyst design, ACS Cent. Sci., 2023, 9, 266–276 CrossRef CAS PubMed.
- C. J. Taylor, K. C. Felton, D. Wigh, M. I. Jeraal, R. Grainger, G. Chessari, C. N. Johnson and A. A. Lapkin, Accelerated chemical reaction optimization using multi-task learning, ACS Cent. Sci., 2023, 9, 957–968 CrossRef CAS.
- M. Seifrid, R. Pollice, A. Aguilar-Granda, Z. Morgan Chan, K. Hotta, C. T. Ser, J. Vestfrid, T. C. Wu and A. Aspuru-Guzik, Autonomous chemical experiments: Challenges and perspectives on establishing a self-driving lab, Acc. Chem. Res., 2022, 55, 2454–2466 CrossRef CAS.
- R. J. Hickman, P. Bannigan, Z. Bao, A. Aspuru-Guzik and C. Allen, Self-driving laboratories: A paradigm shift in nanomedicine development, Matter, 2023, 6, 1071–1081 CrossRef CAS PubMed.
- A. Ramirez, E. Lam, D. P. Gutierrez, Y. Hou, H. Tribukait, L. M. Roch, C. Copéret and P. Laveille, Accelerated exploration of heterogeneous CO2 hydrogenation catalysts by Bayesian-optimized high-throughput and automated experimentation, Chem Catal., 2024, 4, 100888 CrossRef CAS.
- L. M. Baumgartner, J. M. Dennis, N. A. White, S. L. Buchwald and K. F. Jensen, Use of a droplet platform to optimize Pd-catalyzed C–N coupling reactions promoted by organic bases, Org. Process Res. Dev., 2019, 23, 1594–1601 CrossRef CAS.
- J. A. G. Torres, S. H. Lau, P. Anchuri, J. M. Stevens, J. E. Tabora, J. Li, A. Borovika, R. P. Adams and A. G. Doyle, A multi-objective active learning platform and web app for reaction optimization, J. Am. Chem. Soc., 2022, 144, 19999–20007 CrossRef CAS.
- F. Strieth-Kalthoff, F. Sandfort, M. Kühnemund, F. R. Schäfer, H. Kuchen and F. Glorius, Machine learning for chemical reactivity: The importance of failed experiments, Angew. Chem., Int. Ed., 2022, 61, e202204647 CrossRef CAS PubMed.
- J. Schleinitz, M. Langevin, Y. Smail, B. Wehnert, L. Grimaud and R. Vuilleumier, Machine learning yield prediction from NiCOlit, a small-size literature data set of nickel catalyzed C–O couplings, J. Am. Chem. Soc., 2022, 144, 14722–14730 CrossRef CAS PubMed.
- M. P. Maloney, C. W. Coley, S. Genheden, N. Carson, P. Helquist, P.-O. Norrby and O. Wiest, Negative data in data sets for machine learning training, Org. Lett., 2023, 25, 2945–2947 CrossRef CAS.
- V. Voinarovska, M. Kabeshov, D. Dudenko, S. Genheden and I. V. Tetko, When yield prediction does not yield prediction: An overview of the current challenges, J. Chem. Inf. Model., 2023, 64, 42–56 CrossRef PubMed.
- K. C. Felton, J. G. Rittig and A. A. Lapkin, Summit: Benchmarking machine learning methods for reaction optimisation, Chem.: Methods, 2021, 1, 116–122 CAS.
- R. J. Hickman, M. Aldeghi, F. Häse and A. Aspuru-Guzik, Bayesian optimization with known experimental and design constraints for chemistry applications, Digital Discovery, 2022, 1, 732–744 RSC.
- E. H. Lee, V. Perrone, C. Archambeau, and M. Seeger, Cost-aware Bayesian Optimization, arXiv, 2020, preprint, arXiv:200310870, DOI:10.48550/arXiv.2003.10870.
- Z. Z. Foumani, M. Shishehbor, A. Yousefpour and R. Bostanabad, Multi-fidelity cost-aware Bayesian optimization, Comput. Methods Appl. Mech. Eng., 2023, 407, 115937 CrossRef.
- Q. Xie, R. Astudillo, P. Frazier, Z. Scully, and A. Terenin, Cost-aware Bayesian optimization via the Pandora’s Box Gittins index, arXiv, 2024, preprint, arXiv:240620062, DOI:10.48550/arXiv.2406.20062.
- A. Krause and C. Ong, Contextual Gaussian process bandit optimization, Adv. Neural Inf. Process. Syst., 2011, 2447–2455 Search PubMed.
- J. Snoek, H. Larochelle and R. P. Adams, Practical Bayesian Optimization of Machine Learning Algorithms, Adv. Neural Inf. Process. Syst., 2012, 2951–2959 Search PubMed.
- J. Berk, V. Nguyen, S. Gupta, S. Rana, and S. Venkatesh, Exploration enhanced expected improvement for Bayesian optimization, Joint European Conference on Machine Learning and Knowledge Discovery in Databases, 2018, pp 621–637 Search PubMed.
- R. Tachibana, K. Zhang, Z. Zou, S. Burgener and T. R. Ward, A Customized Bayesian Algorithm to Optimize Enzyme-Catalyzed Reactions, ACS Sustain. Chem. Eng., 2023, 11, 12336–12344 CrossRef CAS.
- N. Dolatnia, A. Fern, and X. Fern, Bayesian optimization with resource constraints and production, Proceedings of the ICAPS, 2016, vol. 26, pp. 115–123 Search PubMed.
- E. H. Lee, V. Perrone, C. Archambeau, and M. Seeger, Cost-aware Bayesian optimization, ICML 2020 Workshop on AutoML, 2020 Search PubMed.
- P. Luong, D. Nguyen, S. Gupta, S. Rana and S. Venkatesh, Adaptive cost-aware Bayesian optimization, Knowl.-Based Syst., 2021, 232, 107481 CrossRef.
- E. H. Lee, D. Eriksson, V. Perrone, and M. Seeger, A nonmyopic approach to cost-constrained Bayesian optimization, Proceedings of the Thirty-Seventh Conference on Uncertainty in Artificial Intelligence, 2021, pp 568–577 Search PubMed.
- S. Belakaria, J. R. Doppa, N. Fusi, and R. Sheth, Bayesian optimization over iterative learners with structured responses: A budget-aware planning approach, Proceedings of The 26th International Conference on Artificial Intelligence and Statistics, 2023, pp 9076–9093 Search PubMed.
- H. Gao, C. W. Coley, T. J. Struble, L. Li, Y. Qian, W. H. Green and K. F. Jensen, Combining retrosynthesis and mixed-integer optimization for minimizing the chemical inventory needed to realize a WHO essential medicines list, React. Chem. Eng., 2020, 5, 367–376 RSC.
- P. Rodriguez Diaz, J. A. Killian, L. Xu, A. S. Suggala, A. Taneja, and M. Tambe, Flexible budgets in restless bandits: A primal-dual algorithm for efficient budget allocation, Proceedings of the AAAI Conference on Artificial Intelligence, 2023, vol. 37, pp. 12103–12111 Search PubMed.
- J. Zuo, and C. Joe-Wong, Combinatorial multi-armed bandits for resource allocation, 2021 55th Annual Conference on Information Sciences and Systems (CISS), 2021, pp 1–4 Search PubMed.
- B. Thananjeyan, K. Kandasamy, I. Stoica, M. Jordan, K. Goldberg, and J. Gonzalez, Resource allocation in multi-armed bandit exploration: Overcoming sublinear scaling with adaptive parallelism, Proceedings of the 38th International Conference on Machine Learning, 2021, pp 10236–10246 Search PubMed.
- P. Vellanki, S. Rana, S. Gupta, D. Rubin, A. Sutti, T. Dorin, M. Height, P. Sanders and S. Venkatesh, Process-constrained batch Bayesian optimisation, Adv. Neural Inf. Process. Syst., 2017, 3414–3423 Search PubMed.
- J. P. Folch, S. Zhang, R. Lee, B. Shafei, D. Walz, C. Tsay, M. van der Wilk and R. Misener, SnAKe: Bayesian optimization with pathwise exploration, Adv. Neural Inf. Process. Syst., 2022, 35226–35239 Search PubMed.
- S. S. Ramesh, P. G. Sessa, A. Krause and I. Bogunovic, Movement penalized Bayesian optimization with application to wind energy systems, Adv. Neural Inf. Process. Syst., 2022, 27036–27048 Search PubMed.
- A. X. Yang, L. Aitchison, and H. B. MossMONGOOSE: Path-wise smooth Bayesian optimisation via meta-learning, arXiv, 2023, preprint, arXiv:230211533, DOI:10.48550/arXiv.2302.11533.
- J. P. Folch, J. A. C. Odgers, S. Zhang, R. M. Lee, B. Shafei, D. Walz, C. Tsay, M. van der Wilk, and R. Misener, Practical path-based Bayesian optimization, NeurIPS 2023 Workshop on Adaptive Experimental Design and Active Learning in the Real World, 2023 Search PubMed.
- P. Liu, H. Wang, and W. Qiyu, Bayesian optimization with switching cost: Regret analysis and lookahead variants, Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, IJCAI-23, 2023, pp 4011–4018 Search PubMed.
- R. Liang, H. Hu, Y. Han, B. Chen and Z. Yuan, CAPBO: A cost-aware parallelized Bayesian optimization method for chemical reaction optimization, AIChE J., 2024, 70, e18316 CrossRef CAS.
- J. P. Folch, C. Tsay, R. M. Lee, B. Shafei, W. Ormaniec, A. Krause, M. van der Wilk, R. Misener, and M. Mutný, Transition constrained Bayesian optimization via Markov decision processes, arXiv, 2024, preprint, arXiv:240208406, DOI:10.48550/arXiv.2402.08406.
- A. Biswas, Y. Liu, N. Creange, Y.-C. Liu, S. Jesse, J.-C. Yang, S. V. Kalinin, M. A. Ziatdinov and R. K. Vasudevan, A dynamic Bayesian optimized active recommender system for curiosity-driven partially Human-in-the-loop automated experiments, npj Comput. Mater., 2024, 10, 29 CrossRef.
- M. H. S. Segler, M. Preuss and M. P. Waller, Planning chemical syntheses with deep neural networks and symbolic AI, Nature, 2018, 555, 604–610 CrossRef CAS PubMed.
- K. Molga, P. Dittwald and B. A. Grzybowski, Navigating around Patented Routes by Preserving Specific Motifs along Computer-Planned Retrosynthetic Pathways, Chem, 2019, 5, 460–473 CAS.
- S. Hong, H. H. Zhuo, K. Jin, G. Shao and Z. Zhou, Retrosynthetic planning with experience-guided Monte Carlo tree search, Commun. Chem., 2023, 6, 120 CrossRef PubMed.
- B. A. Koscher, et al., Autonomous, multiproperty-driven molecular discovery: From predictions to measurements and back, Science, 2023, 382, eadi1407 CrossRef CAS PubMed.
- J. C. Fromer and C. W. Coley, An algorithmic framework for synthetic cost-aware decision making in molecular design, Nat. Comput. Sci., 2024, 4, 440–450 CrossRef.
- V. Tulus, J. Pérez-Ramírez and G. Guillén-Gosálbez, Planetary metrics for the absolute environmental sustainability assessment of chemicals, Green Chem., 2021, 23, 9881–9893 RSC.
- F. P. Byrne, S. Jin, G. Paggiola, T. H. M. Petchey, J. H. Clark, T. J. Farmer, A. J. Hunt, C. R. McElroy and J. Sherwood, Tools and techniques for solvent selection: green solvent selection guides, Sustainable Chem. Processes, 2016, 4, 7 CrossRef.
- S. Mitchell, A. J. Martín, G. Guillén-Gosálbez and J. Pérez-Ramírez, The Future of Chemical Sciences is Sustainable, Angew. Chem., Int. Ed., 2024, e202318676 CAS.
- F. Häse, L. M. Roch and A. Aspuru-Guzik, Next-generation experimentation with self-driving laboratories, Trends Chem., 2019, 1, 282–291 CrossRef.
- B. P. MacLeod, et al., Self-driving laboratory for accelerated discovery of thin-film materials, Sci. Adv., 2020, 6, eaaz8867 CrossRef CAS.
- C. E. Rasmussen, Gaussian Processes in Machine Learning, Lecture Notes in Computer Science, Springer, 2004, vol. 3176 Search PubMed.
- L. P. Kaelbling, M. L. Littman and A. W. Moore, Reinforcement learning: A survey, J. Artif. Intell. Res., 1996, 4, 237–285 CrossRef.
- R. Garnett, Bayesian Optimization, Cambridge University Press, 2023 Search PubMed.
- H. Raiffa, and R. Schlaifer, Applied Statistical Decision Theory; Division of Research, Graduate School of Business Administration, Harvard University, 1961, ch. 4 Search PubMed.
- D. R. Jones, M. Schonlau and W. J. Welch, Efficient global optimization of expensive black-box functions, J. Glob. Optim., 1998, 13, 455–492 CrossRef.
- M. Balandat, B. Karrer, D. R. Jiang, S. Daulton, B. Letham, A. G. Wilson and E. Bakshy, BoTorch: A framework for efficient Monte-Carlo Bayesian optimization, Adv. Neural Inf. Process. Syst., 2020, 21524–21538 Search PubMed.
- CIBO is based on the batch noisy expected improvement (qNEI) function, which uses random initialization, Results change negligibly over the 100 independent runs, but we present the averaged results for completeness.
- X. Yue, and R. A. Kontar, Why Non-myopic Bayesian Optimization is Promising and How Far Should We Look-ahead? A Study via Rollout, Proceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics, 2022, pp 2808–2818 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00225c |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |