Open Access Article
Open Access ArticleHH130: a standardized database of machine learning interatomic potentials, datasets, and its applications in the thermal transport of half-Heusler thermoelectrics†
Yuyan
Yang‡
a,
Yifei
Lin‡
a,
Shengnan
Dai
*a,
Yifan
Zhu
bcd,
Jinyang
Xi
 a,
Lili
Xi
a,
Lili
Xi
 a,
Xiaokun
Gu
a,
Xiaokun
Gu
 e,
David J.
Singh
f,
Wenqing
Zhang
bcg and
Jiong
Yang
e,
David J.
Singh
f,
Wenqing
Zhang
bcg and
Jiong
Yang
 *a
*a
aMaterials Genome Institute, Shanghai Engineering Research Center for Integrated Circuits and Advanced Display Materials, Shanghai University, Shanghai 200444, China. E-mail: musenc@shu.edu.cn; jiongy@t.shu.edu.cn
bDepartment of Materials Science and Engineering, Southern University of Science and Technology, Shenzhen, Guangdong 518055, China
cState Key Laboratory of High Performance Ceramics and Superfine Microstructure, Shanghai Institute of Ceramics, Chinese Academy of Sciences, Shanghai 200050, China
dUniversity of Chinese Academy of Sciences, Beijing 100049, China
eInstitute of Engineering Thermophysics, School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
fDepartment of Physics and Astronomy, University of Missouri, Columbia, MO 65211, USA
gShenzhen Municipal Key-Lab for Advanced Quantum Materials and Devices, Guangdong Provincial Key Lab for Computational Science and Materials Design, Southern University of Science and Technology, Shenzhen, Guangdong 518055, China
First published on 11th October 2024
Abstract
High-throughput screening of thermoelectric materials from databases requires efficient and accurate computational methods. Machine-learning interatomic potentials (MLIPs) provide a promising avenue, facilitating the development of database-driven thermal transport applications through high-throughput simulations. However, the present challenge is the lack of standardized databases and openly available models for precise large-scale simulations. Here, we introduce HH130, a standardized database for 130 half-Heusler (HH) compounds in MatHub-3d (http://www.mathub3d.net), containing both MLIP models and datasets for the thermal transport of HH thermoelectrics. HH130 contains 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 891 total configurations (∼245 configurations per HH) and 390 MLIP models (three models per HH), generated using the dual adaptive sampling method to cover a wide range of thermodynamic conditions, and can be openly accessed on MatHub-3d. Comprehensive validation against first-principles calculations demonstrates that the MLIP models accurately predict energies, forces, and interatomic force constants (IFCs). The MLIP models in HH130 enabled us to efficiently perform four-phonon interactions for 80 HHs with phonon frequencies closely matching ab initio results. It is found that HHs with an 8 valence electron count (VEC) per unit cell generally exhibit lower lattice thermal conductivities (κLs) compared to those with an 18 VEC, due to a combination of low 2nd-order IFCs and large scattering phase spaces in the former group. Additionally, we identified several HHs that demonstrate significant reductions in κL due to four-phonon interactions. HH130 provides a robust platform for high-throughput computation of κL and aids in the discovery of next-generation thermoelectrics through machine learning.
891 total configurations (∼245 configurations per HH) and 390 MLIP models (three models per HH), generated using the dual adaptive sampling method to cover a wide range of thermodynamic conditions, and can be openly accessed on MatHub-3d. Comprehensive validation against first-principles calculations demonstrates that the MLIP models accurately predict energies, forces, and interatomic force constants (IFCs). The MLIP models in HH130 enabled us to efficiently perform four-phonon interactions for 80 HHs with phonon frequencies closely matching ab initio results. It is found that HHs with an 8 valence electron count (VEC) per unit cell generally exhibit lower lattice thermal conductivities (κLs) compared to those with an 18 VEC, due to a combination of low 2nd-order IFCs and large scattering phase spaces in the former group. Additionally, we identified several HHs that demonstrate significant reductions in κL due to four-phonon interactions. HH130 provides a robust platform for high-throughput computation of κL and aids in the discovery of next-generation thermoelectrics through machine learning.
1 Introduction
Since the introduction of the Materials Genome Initiative (MGI)1 in 2011, methods for exploring novel materials have advanced beyond traditional trial-and-error approaches.2–4 Databases based on first-principles calculations have emerged, including the Materials Project (MP),5,6 the Automatic-FLOW for Materials Discovery (AFLOW),7–9 the Open Quantum Materials Database (OQMD),10,11 the Joint Automated Repository for Various Integrated Simulations (JARVIS),12 the MatHub-3d13–15 and others. These databases provide fundamental information about materials, such as crystal parameters, electronic density of states, formation energies, and phase fields. MatHub-3d is a materials data repository containing over 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 electronic structures and 10
000 electronic structures and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 electrical transport properties, specifically designed for thermoelectric applications.
000 electrical transport properties, specifically designed for thermoelectric applications.
Currently, computational materials databases primarily rely on first-principles calculations and related results. However, this limits the range of properties for which large volumes of data can be obtained. Although there are some existing databases based on machine learning methods, such as AFLOW-ML16–19 and JARVIS-ML,20–22 there remains a lack of computational results that are based directly on the structures of materials and can be precisely applied to larger-scale simulations. MLIPs, which parameterize the interaction between atoms, are highly promising novel direction machine learning methods due to their reusable models and training datasets and their demonstrable high fidelity to the underlying first-principles calculations.23,24 This combination of transferability and precision enables large scale studies of complex materials and efficient high throughput searches. Mortazavi et al. utilized MLIPs to compute phonon dispersion relations in two-dimensional materials and made the MLIP model and training dataset publicly accessible.25 Liu et al. developed an open-access MLIP model for SnSe to precisely capture its temperature-dependent phonon transport properties.26 Accelerated thermal transport simulation is also a primary application of MLIP models, as thermal transport is crucial in various fields such as thermoelectrics,27,28 thermal barriers,29 and thermal management materials.30 Ouyang et al. used accurate machine learning neuroevolution potentials to calculate the κL of AgX (X = Cl, Br, I) including four-phonon scattering.31 However, significant challenges are the computational difficulty of generating accurate validated MLIPs and the absence of standardized MLIP databases and open-access MLIP models.
Here, a standardized open-access database, HH130, has been established on MatHub-3d. This can be applied to the simulation of thermal transport in HHs. We demonstrate this database by investigating the thermal transport properties of HHs for thermoelectric performance. Out of the 273 HHs in MatHub-3d, 130 HHs meet two criteria, band gap > 0.1 eV and no imaginary frequencies in phonon dispersion. These are selected for our high-throughput computational materials study. MLIP models for the 130 HH compounds from MatHub-3d (IDs of each material are shown in Table S1†) have been trained. To cover a wide range of thermodynamic conditions, the dual adaptive sampling (DAS)32 method is adopted to construct the HH130 database. HH130 consists of 390 MLIP models (three models per HH) and 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 891 configurations (∼245 configurations per HH).
891 configurations (∼245 configurations per HH).
The MLIP models from HH130 enabled us to efficiently perform four-phonon thermal conductivity calculations for 80 HHs with phonon frequencies similar to those obtained from ab initio calculations. We find that HHs with an 8 VEC typically exhibit lower κL than those with an 18 VEC. This phenomenon arises from a combination of low 2nd-order IFCs and large scattering phase spaces. Specifically, low 2nd-order IFCs lead to reduced phonon group velocities, while large scattering phase spaces increase phonon scattering rates in the HHs with an 8 VEC. It may also be noted that low 2nd-order IFCs indicate weak bonding, which is often associated with anharmonicity.33,34 Additionally, we screened several HHs that exhibit substantial reductions in κL due to four-phonon interactions. Among these, LiAgTe exhibits the highest reduction (54.4%), owing to its large four-phonon scattering phase space. All trained MLIP models and datasets in HH130 are publicly available on the website http://www.mathub3d.net/, providing a robust foundation for future data mining. The establishment of HH130 has expanded the data scope of MatHub-3d beyond first-principles results, demonstrating novel possibilities for integrating machine learning with thermal transport research.
2 Methods
For our research, we utilize the DAS method to construct an effective configuration dataset for each HH compound. This method comprises an inner adaptive loop and an outer loop: the inner loop explores the local configuration space under relatively narrow thermodynamic conditions, while the outer loop spans a broad temperature range. The main difference between the DAS method and other active learning sampling methods is its adaptive approach, which automatically updates the threshold of ensemble ambiguity using atomic forces. The ensemble ambiguity ā(x) for configuration x is calculated by using35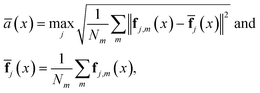 | (1) |
Based on the above formula, the convergence criterion for the inner loop is defined as
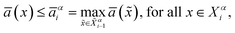 | (2) |
![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) αi−1 is the set of configurations added to the training dataset in the (i − 1)th iteration.
αi−1 is the set of configurations added to the training dataset in the (i − 1)th iteration.
The inner loop of DAS primarily consists of three steps: (1) training Nm MLIP models based on the updated training dataset; (2) exploring the configuration space under specified thermodynamic conditions through MD simulations and sampling according to the adaptive threshold of ensemble ambiguity; (3) labeling the sampled configurations using density functional theory (DFT)36,37 calculations, and subsequently adding them to the training dataset.
In the MLIP model training section, we select the moment tensor potential (MTP)38,39 as the local environment descriptor to fit the training dataset due to its high accuracy and low computational cost.40 The moment tensor descriptors have the following form:
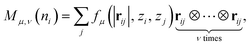 | (3) |
In the exploration of configuration space and sampling section, we use the LAMMPS package41 to conduct MD simulation with the MLIP model that has the lowest loss on the training dataset. The optimized configurations of the 130 HHs and their DFT-calculated phonon dispersions are all obtained from MatHub-3d.13–15 All of the ab initio calculations are carried out by using the Vienna ab initio Simulation Package (VASP)42 with the projector augmented wave method.43 The Perdew–Burke–Ernzerhof form of the generalized gradient approximation served as the exchange-correlation functional.44 For each HH compound, the initial training dataset is constructed by sampling every two steps from a 20 fs ab initio molecular dynamics (AIMD)45 simulation at 300 K, with a timestep of 1 fs. This dataset is then used to train the initial MLIP models, initiating the DAS process. All DFT calculations, including AIMD, employ a plane-wave energy cutoff of 400 eV and an energy convergence criterion of 10−5 eV, with the k-point mesh set to 1 × 1 × 1. During the sampling process, all MD simulations and DFT calculations used 192-atom 4 × 4 × 4 supercells.
The phonon dispersion calculations are done using the Phonopy package.46,47 The κLs, derived using the Boltzmann transport equation (BTE) method, are computed with the ShengBTE package based on a full iterative solution.48 In the framework of the BTE, the κL tensor can be expressed as:48
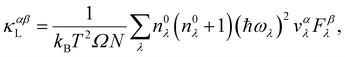 | (4) |
In this work, the relaxation time was obtained with both three-phonon (3ph) and four-phonon (4ph) scattering. The scattering rates for the 3ph and 4ph processes were calculated using the scattering probability matrices:49
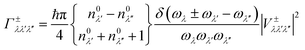 | (5) |
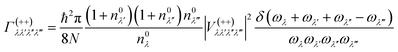 | (6) |
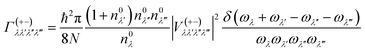 | (7) |
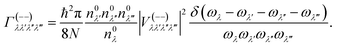 | (8) |
Eqn (5) corresponds to 3ph processes, and eqn (6) to (8) correspond to 4ph processes, with energy conservation enforced by using the Dirac delta function δ.
To calculate the κL using MLIP, the higher-order IFCs are determined through the finite displacement method. We considered up to the fifth-nearest neighboring atoms for the 3rd-order IFCs and second-nearest neighboring atoms for the 4th-order IFCs. The cutoff distances for both 3rd- and 4th-order IFCs are identical for DFT and MLIP. The BTE with 3ph scattering is solved using a 20 × 20 × 20 q-point grid, while the BTE with 4ph scattering is solved using a 12 × 12 × 12 q-point grid. To calculate the phonon renormalization and coherent κL for TiCoSb,50 we conducted MD simulations using the MLIP model and employed the obtained snapshots to fit the higher-order IFCs in the Hiphive software package.51
3 Results and discussion
To predict HH compounds with excellent thermal transport properties in the context of thermoelectric application, we established the HH130 database and designed a comprehensive process for material screening and calculation standards. The HH130 workflow comprises three main parts: material selection, training MLIP models, and material property prediction, as illustrated in Fig. 1. HH compounds XYZ are ternary solids with a cubic structure (space group no. 216, F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m). Their crystalline structure can be visualized as a combination of rock salt and zinc blende structures. The Wyckoff positions of the X, Y, and Z atoms are 4a (0, 0, 0), 4c (1/4, 1/4, 1/4), and 4b (1/2, 1/2, 1/2), respectively. The elements for HH compounds are shown in Fig. S1.†
3m). Their crystalline structure can be visualized as a combination of rock salt and zinc blende structures. The Wyckoff positions of the X, Y, and Z atoms are 4a (0, 0, 0), 4c (1/4, 1/4, 1/4), and 4b (1/2, 1/2, 1/2), respectively. The elements for HH compounds are shown in Fig. S1.†
The training datasets for the 130 HH compounds are obtained through the DAS method. Two temperature sampling blocks, 250 K to 400 K and 650 K to 800 K, are established with 50 K intervals. Based on the temperature dependence of the lattice constants, a 3% thermal expansion is considered for the sampling volume at each temperature. For each HH compound, we simultaneously trained three MTP models with random initialization under identical conditions. The DAS program selects the model with the lowest loss on the training dataset to run MD simulations, each lasting 2.5 ps with a time step of 0.5 fs. Configurations are sampled every 20 steps and added to the candidate configuration set. From this set, effective configurations are selected for labeling based on the adaptive threshold of ensemble ambiguity, with a maximum of 10 configurations chosen for labeling. Finally, the DFT-labeled configurations are added to the training dataset for model updates.
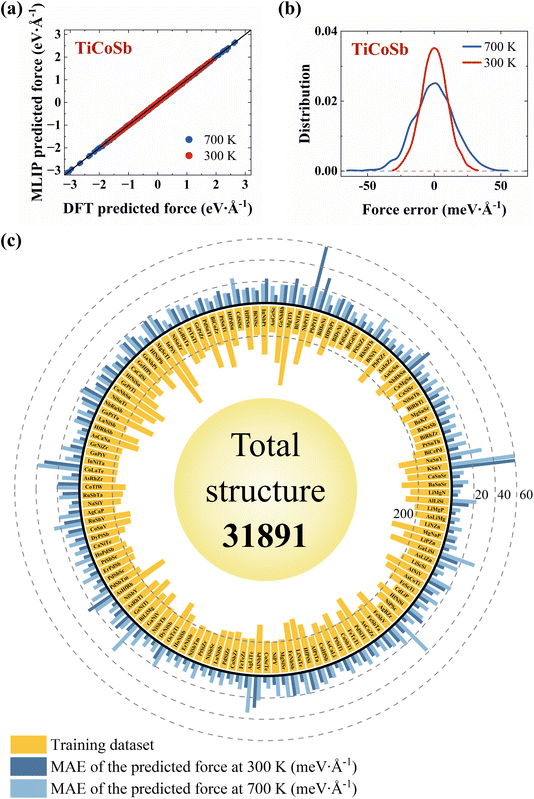
To verify the accuracy of the MLIP models, the energies and forces of randomly selected configurations, as calculated by MLIP, are compared with those calculated by DFT. At each temperature (300 K or 700 K, both within the temperature sampling blocks), a 0.1 ns MD simulation is first conducted. Following this, an additional 4.5 ps simulation is performed, during which configurations are sampled every 0.5 ps to ensure they are relatively novel to the model. This process results in a total of 10 test configurations. In TiCoSb, the comparison of forces between the DFT and MLIP calculated configurations at 300 K and 700 K is shown in Fig. 2a. The average mean absolute errors (MAEs) of the energies are 1.91 meV per atom and 1.20 meV per atom, respectively. The corresponding MAEs of the forces are 7.84 meV Å−1 and 12.17 meV Å−1. These errors follow a near-zero normal distribution, indicating the high accuracy of MLIP in predicting forces (Fig. 2b).
The MAEs of the forces for 130 HHs at 300 K and 700 K are shown in Fig. 2c. At 300 K and 700 K, the average MAEs of the energies are 0.98 meV per atom and 0.62 meV per atom, and the average MAEs of the forces are 11.73 meV Å−1 and 16.42 meV Å−1, respectively. The corresponding error distributions are shown in Fig. S2.† The MLIP trained using a single room-temperature sampling block exhibits a relatively dispersed distribution of MAEs. In contrast, training with both room-temperature and high-temperature sampling blocks significantly reduces the MAEs of energies to below 1 meV per atom for most systems, while the MAEs of forces are below 20 meV Å−1. Overall, the energies and forces predicted by MLIP are in good agreement with those obtained by DFT calculations. The final training datasets for 130 HH compounds, along with the number of configurations, are shown in Fig. 2c. The total number of configurations is 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 891, with an average of 245 per HH compound.
891, with an average of 245 per HH compound.
As summarized in Table 1, the HH130 includes sample information, MLIP model details, and open-access files from MatHub-3d for 130 HH compounds. The sampling covers temperatures ranging from 250 K to 400 K and 650 K to 800 K, spanning both low- and high-temperature ranges. The MLIP model section lists the employed descriptors and cutoff radius. The MTP descriptors effectively capture various material properties during training. To achieve an optimal balance between accuracy and efficiency, we selected an MTP model with a level of 18 and a cutoff radius of 6 Å based on our tests (as shown in Tables S2 and S3†). Additionally, the open-access section provides the trained MLIP models and training datasets, which are available on MatHub-3d. Three independent MLIP models are provided for each HH compound to assess prediction uncertainty. The training datasets record atomic coordinates, energies, forces, and stress tensors sampled during training, which facilitate the validation of the potentials against the first-principles calculations.
| Sample information | Materials | 130 HHs |
| Temperatures | [250, 300, 350, and 400 K] | |
| [650, 700, 750, and 800 K] | ||
| MLIP model details | Descriptors | MTP |
| Cutoff radius | 6.0 Å | |
| Open-access files from MatHub-3d | MLIP models | 3 MLIP models per HH |
| Training datasets | Atomic coordinates | |
| Energies | ||
| Forces | ||
| Stress tensors | ||
| Input files | INCAR.vasp | |
| KPOINTS.vasp | ||
| POTCAR.spec | ||
| in.lammps |
The public availability of MLIP models and their corresponding training datasets in HH130 expands the scope of data provided by MatHub-3d, extending beyond purely first-principles results. The provided MTP models can be used directly and accurately for large-scale MD simulations of HH compounds. Moreover, these models are highly accurate in predicting atomic forces and stress tensors for most systems in the training dataset. The accuracy makes them suitable for precise predictions of lattice dynamics and modulus properties.
The remainder of this paper provides demonstrations of the prediction of 2nd-, 3rd-, and even 4th-order IFCs, as well as the simulation of κL, using the MLIP models from the HH130 database. Based on these simulations, we can elucidate the trends in the κL of HH compounds using the generated large dataset, as shown below. Besides, from a technical standpoint, even accounting for the total time required to generate the training datasets (including training, sampling, and DFT labeling), the efficiency of calculating 3rd- and 4th-order IFCs using MLIP remains approximately an order of magnitude higher than that of traditional DFT calculations (as shown in Tables S4 and S5†).
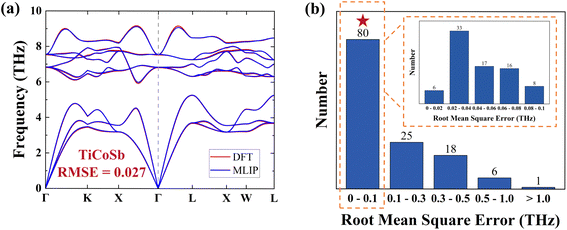
To evaluate the model's suitability for accurate prediction of IFCs, we calculated the 2nd-order IFCs and harmonic phonon dispersions using the finite displacement method within MLIP, comparing them to DFT data from MatHub-3d. Fig. 3a shows that the TiCoSb phonon dispersion calculated by MLIP is very similar to the DFT result. To facilitate statistical analysis of the differences across all HH compounds, we calculated the root mean square error (RMSE) of the phonon dispersion for each HH compound, based on the frequencies at corresponding points in the DFT and MLIP results. 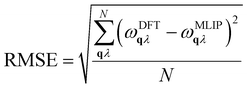 , where ωqλ is the frequency corresponding to a phonon mode with wave vector q and branch λ, and N is the number of q points in the first Brillouin zone. The RMSE of TiCoSb phonon dispersion is 0.027 THz. Fig. 3b displays the RMSEs of phonon dispersions for 130 HH compounds. Among these, the RMSEs for 123 HH compounds range from 0 to 0.5, demonstrating the high accuracy of MLIP in predicting 2nd-order IFCs.
, where ωqλ is the frequency corresponding to a phonon mode with wave vector q and branch λ, and N is the number of q points in the first Brillouin zone. The RMSE of TiCoSb phonon dispersion is 0.027 THz. Fig. 3b displays the RMSEs of phonon dispersions for 130 HH compounds. Among these, the RMSEs for 123 HH compounds range from 0 to 0.5, demonstrating the high accuracy of MLIP in predicting 2nd-order IFCs.
Given the high demand for accurate higher-order IFCs, 80 HH compounds with phonon dispersion RMSEs less than 0.1 THz were selected to calculate κL. Calculating the κL including higher-order scatterings, requires higher-order IFCs (such as 3rd- and 4th-order IFCs), which account for the majority of the calculation time. This often necessitates thousands of single-point DFT force calculations, depending on the cutoff distance and symmetry relationship.52 MLIP models capable of accurately predicting forces are employed to calculate higher-order IFCs, significantly reducing the high-throughput calculation costs.53–55 To assess our MLIP model's accuracy in predicting κL, we computed the κL of TiCoSb using 3rd-order IFCs with the MLIP model. The predictions closely match the κL at the DFT level, as well as the experimental results (Fig. S3†).
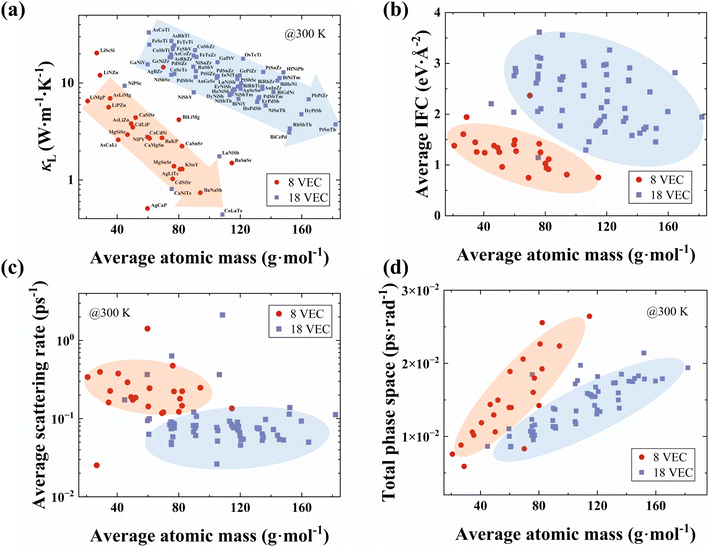
The κL values at 300 K for the 80 HH compounds, considering both 3ph and 4ph scattering, are presented in Fig. 4a (the results with only 3ph scattering are shown in Fig. S4†). The κL values range from 0.44 to 33.16 W m−1 K−1. This wide range underscores substantial variability in the thermal transport properties of HHs. Based on the stability characteristics of HH semiconductors with an 8 or 18 VEC proposed by Carrete et al.,56 we classified the 80 HH compounds into two group: 23 with an 8 VEC and 57 with an 18 VEC. This classification is important for understanding the underlying physical mechanisms affecting κL. As shown in Fig. 4a, the κL for both categories of HH compounds decreases with increasing average atomic mass as expected from consideration of the effect of mass on phonon group velocities. Furthermore, the κL of HH compounds with an 8 VEC is generally lower than that of those with an 18 VEC, suggesting that the number of VEC plays a key role in the thermal transport properties of HHs.
To further investigate the reasons behind the difference in κL between 8- and 18-VEC HHs, we analyzed the phonon group velocities and scattering rates for both groups based on the BTE. The average phonon group velocities for 8-VEC HHs are generally lower than that for 18-VEC HHs (as illustrated in Fig. S5†). Furthermore, the magnitude of the phonon group velocity depends on the 2nd-order IFCs (|Φαβij|), where i and j represent the atomic indices, and α and β denote the directions. To gain a deeper understanding of phonon behavior, we calculated and averaged the 2nd-order IFCs for each HH compound (the methodology for averaging the 2nd-order IFCs is shown in the ESI†). The average IFCs as a function of average atomic mass are depicted in Fig. 4b. At the same average atomic mass, the equivalent average 2nd-order IFCs for 8-VEC HHs are smaller than those for 18-VEC HHs, which aligns with observed trends in κLs and phonon group velocities. Thus 8-VEC HHs tend to be more weakly bonded than 18-VEC compounds. This comparison underscores the influence of the VEC on the IFCs, thereby enhancing the understanding of the lower κLs observed in 8-VEC HHs.
Next, the average scattering rate for all HHs was obtained based on the method by Dai et al.,57 as shown in Fig. 4c. This average scattering rate is derived from the total phonon scattering rates, considering both the 3ph and 4ph scattering. The results reveal that 8-VEC HHs exhibit higher average scattering rates compared to 18-VEC HHs. To explore the underlying physical mechanisms, we examined the relationship between the total scattering phase space (considering both 3ph and 4ph scattering) and the average atomic mass. As shown in Fig. 4d, 8-VEC HHs exhibit larger total scattering phase spaces than 18-VEC HHs. This trend is consistent in the individual 3ph and 4ph scattering phase spaces, as illustrated in Fig. S6.† Thus, the combination of low 2nd-order IFCs, leading to low phonon group velocities, and large scattering phase spaces, resulting in high phonon scattering rates, contributes to the lower κL observed in HH compounds with an 8 VEC.
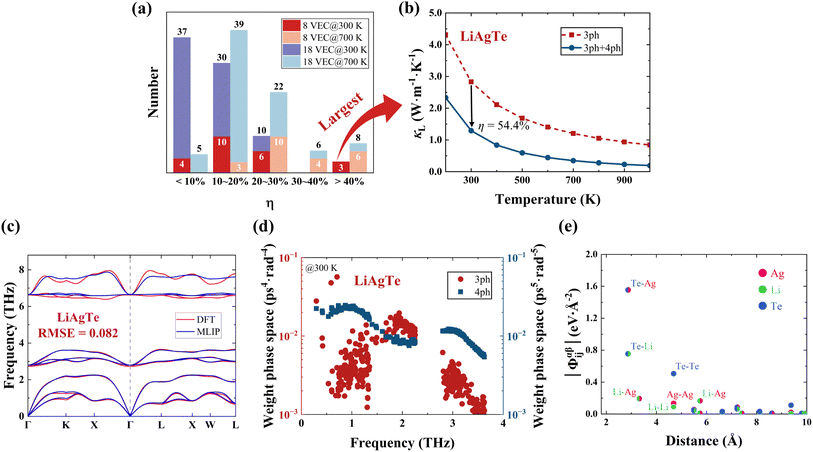
To gain quantitative insights into the influence of 4ph scattering and the number of VEC on the κL, we calculated the reduction rate in κL (η) due to 4ph scattering for the 80 HHs classified with an 8 and an 18 VEC, as shown in Fig. 5a. Here, η is defined as:
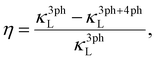 | (9) |
Next, the reasons for the large η in LiAgTe were analyzed. As the cumulative κL tends to be stable at high frequencies, we calculated the cumulative κL below 4 THz at 300 K (Fig. S7†). Between 0.4 and 1.5 THz, the cumulative κ3phL increases rapidly, while κ3ph+4phL increases more slowly, indicating that 4ph interactions within this frequency range significantly contribute to the η. Fig. 5c displays the phonon dispersion of LiAgTe calculated by using DFT and MLIP, which has only 0.082 THz RMSE. It has relatively flat and concentrated phonon dispersion in the low-frequency region and an ∼1 THz phonon gap between acoustic and optical phonons. These behaviors are reported to enhance 4ph interaction.53,58 In order to observe the specific scattering processes, Fig. 5d presents the 3ph and 4ph scattering weight phase spaces59 at 300 K for LiAgTe. Similar to the cumulative κL, the 4ph scattering weight phase space is obviously larger than that of 3ph scattering in the 0.4 to 1.5 THz range. The large 4ph scattering weight phase space enhances the 4ph scattering rate, leading to a significant reduction in κL. It is interesting that the aaaa process is the most prevalent in the 4ph process. Furthermore, we assessed the effect of phonon group velocity on κL by calculating the norm of the 2nd-order IFC matrix, as shown in Fig. 5e. The equivalent average IFC is 0.94 eV Å−2, notably lower than the average of 2.03 eV Å−2 for the 80 HH compounds. Therefore, in the case of LiAgTe, its low κL is due to, on one hand, low phonon velocities from small 2nd-order IFCs, and on the other hand, strong 4ph interactions from large 4ph scattering phase spaces.
4 Conclusions
The HH130 database includes open-access MLIP models and training datasets for 130 HH compounds, encompassing 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 891 configurations with atomic coordinates, energies, forces, and stress tensors. These MLIP models, formulated as MTP and fitted using the DAS method, demonstrate high accuracy in predicting energies and forces, as confirmed by validation against DFT calculations. Utilizing the MLIP models from HH130, we investigated the effects of 4ph scattering and the number of VEC on the κL of HH compounds, revealing the complex relationship between atomic interactions and thermal transport properties. The analysis highlights substantial variability in κL among 80 HH compounds, with values ranging from 0.44 to 33.16 W m−1 K−1 at 300 K. 8-VEC HHs typically exhibit lower κL values than 18-VEC HHs due to smaller 2nd-order IFCs and larger scattering phase spaces, which contribute to the smaller phonon group velocities and higher scattering rates, respectively. Additionally, we screened several HH compounds that exhibit significant reductions in κL as a result of 4ph scattering. As temperature increases, 4ph processes become more pronounced. LiAgTe exhibits the highest η among the 80 HHs, due to its large 4ph scattering phase space. This comprehensive analysis elucidates the complex mechanisms governing thermal transport in HH compounds. The κL data presented in this work were computed using the finite displacement method implemented in the Phonopy and ShengBTE packages. Notably, the MLIP models for each HH compound can be utilized in conventional MD simulations, enabling the easy extraction of temperature-dependent IFCs and the corresponding particle-like κL and coherent κL (see the results for TiCoSb in Fig. S8†). The establishment of HH130 has expanded the data scope provided by MatHub-3d, and bridged the gap between accuracy and efficiency in computational thermoelectric research on a larger scale.
891 configurations with atomic coordinates, energies, forces, and stress tensors. These MLIP models, formulated as MTP and fitted using the DAS method, demonstrate high accuracy in predicting energies and forces, as confirmed by validation against DFT calculations. Utilizing the MLIP models from HH130, we investigated the effects of 4ph scattering and the number of VEC on the κL of HH compounds, revealing the complex relationship between atomic interactions and thermal transport properties. The analysis highlights substantial variability in κL among 80 HH compounds, with values ranging from 0.44 to 33.16 W m−1 K−1 at 300 K. 8-VEC HHs typically exhibit lower κL values than 18-VEC HHs due to smaller 2nd-order IFCs and larger scattering phase spaces, which contribute to the smaller phonon group velocities and higher scattering rates, respectively. Additionally, we screened several HH compounds that exhibit significant reductions in κL as a result of 4ph scattering. As temperature increases, 4ph processes become more pronounced. LiAgTe exhibits the highest η among the 80 HHs, due to its large 4ph scattering phase space. This comprehensive analysis elucidates the complex mechanisms governing thermal transport in HH compounds. The κL data presented in this work were computed using the finite displacement method implemented in the Phonopy and ShengBTE packages. Notably, the MLIP models for each HH compound can be utilized in conventional MD simulations, enabling the easy extraction of temperature-dependent IFCs and the corresponding particle-like κL and coherent κL (see the results for TiCoSb in Fig. S8†). The establishment of HH130 has expanded the data scope provided by MatHub-3d, and bridged the gap between accuracy and efficiency in computational thermoelectric research on a larger scale.
Data availability
Data for this article, including trained MLIP models (three models per HH compound), datasets, necessary input files, and primitive cell structures of the 130 HH compounds are available from the download interface of the MatHub-3d database at http://www.mathub3d.net. The direct download link is http://www.mathub3d.net/static/database/HH130.zip. The dual adaptive sampling (DAS) code (which includes the workflow for training, sampling, and labeling) used in this work is available on GitHub at https://doi.org/10.1103/PhysRevB.104.094310 and https://github.com/hlyang1992/das. Additionally, the moment tensor potential (MTP) package is available at https://mlip.skoltech.ru/download/.Author contributions
Yuyan Yang: conceptualization, methodology, writing – original draft. Yifei Lin: conceptualization, methodology, writing – original draft. Shengnan Dai: conceptualization, methodology, supervision, writing – review & editing. Yifan Zhu: conceptualization, methodology. Jinyang Xi: conceptualization, supervision, funding acquisition, writing – review & editing. Lili Xi: conceptualization, supervision, funding acquisition, writing – review & editing. Xiaokun Gu: conceptualization, methodology. David J. Singh: supervision, writing – review & editing. Wenqing Zhang: supervision, funding acquisition, writing – review & editing. Jiong Yang: conceptualization, project administration, supervision, funding acquisition, writing – review & editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 52172216 and 92163212). The computing resources supporting this work include the Shanghai Technical Service Center of Science and Engineering Computing in Shanghai University, the Hefei Advanced Computing Center, and the Center for Computational Science and Engineering at Southern University of Science and Technology. J. Y. acknowledges the support from the Shanghai Engineering Research Center for Integrated Circuits and Advanced Display Materials.References
-
C. H. Ward, presented in part at Aeromat 23 Conference and Exposition, American Society for Metals, USA, 2012 Search PubMed
.
- A. Agrawal and A. Choudhary, APL Mater., 2016, 4, 053208 CrossRef
.
- J. J. de Pablo, B. Jones, C. L. Kovacs, V. Ozolins and A. P. Ramirez, Curr. Opin. Solid State Mater. Sci., 2014, 18, 99–117 CrossRef
.
- M. L. Green, C. L. Choi, J. R. Hattrick-Simpers, A. M. Joshi, I. Takeuchi, S. C. Barron, E. Campo, T. Chiang, S. Empedocles, J. M. Gregoire, A. G. Kusne, J. Martin, A. Mehta, K. Persson, Z. Trautt, J. Van Duren and A. Zakutayev, Appl. Phys. Rev., 2017, 4, 011105 Search PubMed
.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef
.
- A. Jain, G. Hautier, C. J. Moore, S. Ping Ong, C. C. Fischer, T. Mueller, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2011, 50, 2295–2310 CrossRef CAS
.
- S. Curtarolo, W. Setyawan, G. L. W. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang, O. Levy, M. J. Mehl, H. T. Stokes, D. O. Demchenko and D. Morgan, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS
.
- S. Curtarolo, W. Setyawan, S. Wang, J. Xue, K. Yang, R. H. Taylor, L. J. Nelson, G. L. W. Hart, S. Sanvito, M. Buongiorno-Nardelli, N. Mingo and O. Levy, Comput. Mater. Sci., 2012, 58, 227–235 CrossRef CAS
.
- R. H. Taylor, F. Rose, C. Toher, O. Levy, K. Yang, M. Buongiorno Nardelli and S. Curtarolo, Comput. Mater. Sci., 2014, 93, 178–192 CrossRef
.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS
.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 15010 CrossRef CAS
.
- K. Choudhary, K. F. Garrity, A. C. E. Reid, B. DeCost, A. J. Biacchi, A. R. Hight Walker, Z. Trautt, J. Hattrick-Simpers, A. G. Kusne, A. Centrone, A. Davydov, J. Jiang, R. Pachter, G. Cheon, E. Reed, A. Agrawal, X. Qian, V. Sharma, H. Zhuang, S. V. Kalinin, B. G. Sumpter, G. Pilania, P. Acar, S. Mandal, K. Haule, D. Vanderbilt, K. Rabe and F. Tavazza, npj Comput. Mater., 2020, 6, 173 CrossRef
.
- M. Yao, Y. Wang, X. Li, Y. Sheng, H. Huo, L. Xi, J. Yang and W. Zhang, Sci. Data, 2021, 8, 236 CrossRef CAS PubMed
.
- X. Li, Z. Zhang, J. Xi, D. J. Singh, Y. Sheng, J. Yang and W. Zhang, Comput. Mater. Sci., 2021, 186, 110074 CrossRef CAS
.
- Y. Jin, X. Wang, M. Yao, D. Qiu, D. J. Singh, J. Xi, J. Yang and L. Xi, npj Comput. Mater., 2023, 9, 190 CrossRef CAS
.
- O. Isayev, C. Oses, C. Toher, E. Gossett, S. Curtarolo and A. Tropsha, Nat. Commun., 2017, 8, 15679 CrossRef CAS PubMed
.
- F. Legrain, J. Carrete, A. van Roekeghem, S. Curtarolo and N. Mingo, Chem. Mater., 2017, 29, 6220–6227 CrossRef CAS
.
- V. Stanev, C. Oses, A. G. Kusne, E. Rodriguez, J. Paglione, S. Curtarolo and I. Takeuchi, npj Comput. Mater., 2018, 4, 29 CrossRef
.
- E. Gossett, C. Toher, C. Oses, O. Isayev, F. Legrain, F. Rose, E. Zurek, J. Carrete, N. Mingo, A. Tropsha and S. Curtarolo, Comput. Mater. Sci., 2018, 152, 134–145 CrossRef CAS
.
- K. Choudhary, B. DeCost and F. Tavazza, Phys. Rev. Mater., 2018, 2, 083801 CrossRef CAS PubMed
.
- K. Choudhary, K. F. Garrity, V. Sharma, A. J. Biacchi, A. R. Hight Walker and F. Tavazza, npj Comput. Mater., 2020, 6, 64 CrossRef
.
- K. Choudhary, K. F. Garrity and F. Tavazza, J. Phys.: Condens. Matter, 2020, 32, 475501 CrossRef CAS
.
- V. L. Deringer, M. A. Caro and G. Csányi, Adv. Mater., 2019, 31, 1902765 CrossRef CAS PubMed
.
- Y. Mishin, Acta Mater., 2021, 214, 116980 CrossRef CAS
.
- B. Mortazavi, I. S. Novikov, E. V. Podryabinkin, S. Roche, T. Rabczuk, A. V. Shapeev and X. Zhuang, Appl. Mater. Today, 2020, 20, 100685 CrossRef
.
- H. Liu, X. Qian, H. Bao, C. Y. Zhao and X. Gu, J. Phys.: Condens. Matter, 2021, 33, 405401 CrossRef CAS PubMed
.
- J. Yang, L. Xi, W. Qiu, L. Wu, X. Shi, L. Chen, J. Yang, W. Zhang, C. Uher and D. J. Singh, npj Comput. Mater., 2016, 2, 15015 CrossRef CAS
.
- T. Zhu, Y. Liu, C. Fu, J. P. Heremans, J. G. Snyder and X. Zhao, Adv. Mater., 2017, 29, 1605884 CrossRef PubMed
.
- B. Liu, Y. Liu, C. Zhu, H. Xiang, H. Chen, L. Sun, Y. Gao and Y. Zhou, J. Mater. Sci. Technol., 2019, 35, 833–851 CrossRef CAS
.
- A. L. Moore and L. Shi, Mater. Today, 2014, 17, 163–174 CrossRef CAS
.
- N. Ouyang, Z. Zeng, C. Wang, Q. Wang and Y. Chen, Phys. Rev. B, 2023, 108, 174302 CrossRef CAS
.
- H. Yang, Y. Zhu, E. Dong, Y. Wu, J. Yang and W. Zhang, Phys. Rev. B, 2021, 104, 094310 CrossRef CAS
.
- J. Zhang, L. Song, M. Sist, K. Tolborg and B. B. Iversen, Nat. Commun., 2018, 9, 4716 CrossRef PubMed
.
- T. B. E. Grønbech, H. Kasai, J. Zhang, E. Nishibori and B. B. Iversen, Adv. Funct. Mater., 2024, 34, 2401703 CrossRef
.
- L. Zhang, D.-Y. Lin, H. Wang, R. Car and W. E, Phys. Rev. Mater., 2019, 3, 023804 CrossRef CAS
.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef
.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef
.
- A. V. Shapeev, Multiscale Model. Simul., 2016, 14, 1153–1173 CrossRef
.
- I. S. Novikov, K. Gubaev, E. V. Podryabinkin and A. V. Shapeev, Mach. Learn.: Sci. Technol., 2021, 2, 025002 Search PubMed
.
- Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. Behler, G. Csányi, A. V. Shapeev, A. P. Thompson, M. A. Wood and S. P. Ong, J. Phys. Chem. A, 2020, 124, 731–745 CrossRef CAS PubMed
.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS PubMed
.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS
.
- A. Togo, J. Phys. Soc. Jpn., 2022, 92, 012001 CrossRef
.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS
.
- Z. Han, X. Yang, W. Li, T. Feng and X. Ruan, Comput. Phys. Commun., 2022, 270, 108179 CrossRef CAS
.
- L. Ji, A. Huang, Y. Huo, Y.-M. Ding, S. Zeng, Y. Wu and L. Zhou, Phys. Rev. B, 2024, 109, 214307 CrossRef
.
- F. Eriksson, E. Fransson and P. Erhart, Adv. Theory Simul., 2019, 2, 1800184 CrossRef
.
- L. Lindsay, D. A. Broido and T. L. Reinecke, Phys. Rev. B, 2013, 87, 165201 CrossRef
.
- Y. Xia, V. I. Hegde, K. Pal, X. Hua, D. Gaines, S. Patel, J. He, M. Aykol and C. Wolverton, Phys. Rev. X, 2020, 10, 041029 CAS
.
- J. Brorsson, A. Hashemi, Z. Fan, E. Fransson, F. Eriksson, T. Ala-Nissila, A. V. Krasheninnikov, H.-P. Komsa and P. Erhart, Adv. Theory Simul., 2022, 5, 2100217 CrossRef CAS
.
- B. Mortazavi, E. V. Podryabinkin, I. S. Novikov, T. Rabczuk, X. Zhuang and A. V. Shapeev, Comput. Phys. Commun., 2021, 258, 107583 CrossRef CAS
.
- J. Carrete, W. Li, N. Mingo, S. Wang and S. Curtarolo, Phys. Rev. X, 2014, 4, 011019 CAS
.
- S. Dai, C. Liu, J. Ning, C. Fu, J. Xi, J. Yang and W. Zhang, Mater. Today Phys., 2023, 31, 100993 CrossRef CAS
.
- Y. Li, J. Chen, C. Lu, H. Fukui, X. Yu, C. Li, J. Zhao, X. Wang, W. Wang and J. Hong, Phys. Rev. B, 2024, 109, 174302 CrossRef CAS
.
- W. Li and N. Mingo, Phys. Rev. B, 2015, 91, 144304 CrossRef
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00240g |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |