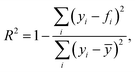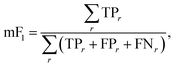Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Learning material synthesis–process–structure–property relationship by data fusion: Bayesian co-regionalization N-dimensional piecewise function learning†
A. Gilad
Kusne
 *ab,
Austin
McDannald
*ab,
Austin
McDannald
 a and
Brian
DeCost
a and
Brian
DeCost
 a
a
aMaterials Measurement Science, Division of the National Institute of Standards and Technology, Gaithersburg, MD 20899, USA. E-mail: aaron.kusne@nist.gov; austin.mcdannald@nist.gov; brian.decost@nist.gov
bMaterials Science and Engineering, Department of the University of Maryland, College Park, MD 20742, USA
First published on 27th September 2024
Abstract
Autonomous materials research labs require the ability to combine and learn from diverse data streams. This is especially true for learning material synthesis–process–structure–property relationships, key to accelerating materials optimization and discovery as well as accelerating mechanistic understanding. We present the Synthesis–process–structure–property relAtionship coreGionalized lEarner (SAGE) algorithm. A fully Bayesian algorithm that uses multimodal coregionalization and probability to merge knowledge across data sources into a unified model of synthesis–process–structure–property relationships. SAGE outputs a probabilistic posterior including the most likely relationship given the data along with proper uncertainty quantification. Beyond autonomous systems, SAGE will allow materials researchers to unify knowledge across their lab toward making better experiment design decisions.
1. Introduction
Lack of advanced materials stymies many next-generation technologies such as quantum computing, carbon capture, and low-cost medical imaging. However, fundamental challenges stand in the way of discovering novel and optimized materials including (1) the challenge of a high-dimensional, complex materials search space and (2) the challenge of integrating knowledge across instruments and labs, i.e., data fusion. The first challenge arises from the need to explore ever–more complex materials as simpler material systems are exhausted. Here material system refers to the materials resulting from a set of material synthesis and processing conditions. With each new material synthesis or processing condition, the number of potential experiments grows exponentially – rapidly escape the feasibility of Edisonian-type studies, forming a high-dimensional search space. As a result, any data is typically sparse relative to the search space. The search space is also highly complex due to the underlying complex relationship between material synthesis and process conditions and the resulting material structure and functional properties, i.e., the material synthesis-process-structure–property relationship (SPSPR).Knowledge of this SPSPR plays a fundamental role across materials research, whether the research is performed by hand or through an automated or autonomous system. Researchers use knowledge of the SPSPR as a blueprint to navigate the high-dimensional complex search space toward novel and optimized materials and to explore the underlying mechanistic origins of material properties. As a result, an algorithm that properly unifies diverse materials data into SPSPR models may accelerate all these activities, impacting much of materials research. For example, such an algorithm can exploit the SPSPR to dramatically improve prediction accuracy of a target functional property, despite sparsity of data. This improved prediction would then better guide subsequent research, which would in turn boost SPSPR knowledge.
Building the SPSPR blueprint involves combining knowledge of material synthesis and process conditions, lattice structure (and potentially microstructure), as well as the diverse set of functional properties required to meet the technological requirements. This requires integrating data across different instruments and measurement modalities, each dependent on differing physical principles. Additionally, measurements can vary based on instrument calibration, measurement parameter settings, environmental conditions such as temperature and humidity, and each instrument user's measurement process. Even instruments of the same make and model differ based on unique biases, uncertainties, and data artifacts.
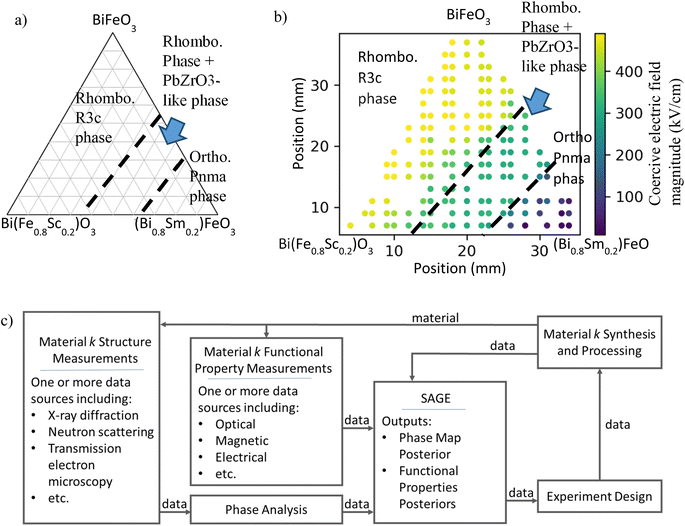
As a very common example, researchers often start their search for improved materials with the phase map of the target material system. A phase map (or ‘phase diagram’ for equilibrium materials) visualizes the synthesis–structure relationship. An example phase map is shown in Fig. 1a for the (Bi,Sm)(Sc,Fe)O3 material system.1 Here the phase map relates material composition (the target synthesis conditions) to resulting lattice structure, described in terms of phases, i.e., composition-structure prototypes. The phase map is divided into phase regions – contiguous regions of synthesis-process space (experiments of varying synthesis and process conditions) that result in materials of the same set of phases. The regions are separated by phase boundaries (dashed black lines). Material phase information is predictive of many functional properties. Materials with property extrema tend to occur either within specific phase regions (e.g., magnetism and superconductivity) or along phase boundaries (e.g., caloric-cooling materials). Thus, a materials researcher can use phase maps to guide their studies toward synthesis and process conditions that are expected to produce materials with more promising properties.
Fig. 1b visualizes a (Bi,Sm)(Sc,Fe)O3 SPSPR by combining the phase map with the functional property of coercive electric field magnitude (CEFM).2,3 Circles indicate experimentally characterized materials and circle color indicates measured CEFM. The CEFM is highly dependent on both synthesis conditions and phase, with the highest values occurring with ‘open’ hysteresis loops in the rhombohedral R3c phase region. Additionally, the composition dependence of CEFM significantly differs between phase regions, with greater variation occurring in the R3c and Pnma phase regions than the intermediary region. In general, discontinuities in functional property values may also occur at phase boundaries. Thus, functional properties can be represented as piecewise functions of the synthesis parameters (in this case composition), with each ‘piece’ of the piecewise function associated with a phase region. This allows for significant changes in function behavior from region to region and/or discontinuities to occur at phase boundaries.
For this example, data for materials synthesis and structure are used to build a phase map, and that phase map is then used to guide understanding of target property data. Knowledge is one directional, from structure to functional property. With a proper SPSPR learning algorithm, these diverse data could be combined in a unified model where knowledge of the phase map would improve analysis and prediction of functional properties and vice versa. For example, significant changes in functional properties may indicate a phase boundary and thus improve analysis and prediction of materials structure. Such an algorithm would boost overall materials research prediction accuracy and subsequent research, but such an algorithm has been lacking.
To overcome the dual challenges of a complex, high-dimensional search space and data fusion in SPSPR learning, we present the synthesis–process–structure–property relAtionship coreGionalized lEarner (SAGE). The SAGE algorithm is available as part of the Hermes library, https://github.com/usnistgov/hermes and as a standalone library https://github.com/KusneNIST/SAGE. SAGE is a Bayesian machine learning (ML) algorithm that combines three features: (1) ML-based segmentation of the synthesis-processing space using material synthesis, process, and phase data. Segments are phase regions, and the collection of phase regions forms the synthesis–process–phase map. The synthesis–process–phase map is then used to extrapolate the synthesis–process–structure relationship to new materials, (2) piecewise regression to fit and extrapolate synthesis–process–property relationships, and (3) coregionalization. Coregionalization allows multimodal, disparate knowledge of structure1 and property,2 both gathered across the shared domain of synthesis and processing conditions, to be combined to exploit shared trends. Here the term multi-modal refers to learning from disparate data sources (similar to its use in the common machine learning challenge of learning from text, audio, and image data). SAGE combines these three features to learn the most likely SPSPR model given material synthesis, process, structure, and property data. Multi-modal learning arises from exploiting both structure and functional property data to improve phase mapping (rather than using just the structure data) and both structure and functional property data to improve functional property regression (rather than just using the functional property data). Here the language of probability is used to unify knowledge across multi-modal data with assumptions represented as priors and data combined through likelihoods. Additionally, SAGE's Bayesian framework allows for full uncertainty quantification and propagation.
Much of machine learning focuses on algorithms that provide “point estimate” outputs, i.e., they provide analysis or prediction without uncertainty. Proper uncertainty quantification and propagation requires explicitly expressing uncertainties in all variables and data, and then propagating these uncertainties through all computations to provide the uncertainty in the algorithm's outputs. A set of statistical learning algorithms such as Gaussian process regression were analytically developed to explicitly and properly manage uncertainties.4 Due to the complexity (and wide-spread use) of many algorithms, computational methods are often employed to approximate output uncertainties without significantly changing the main algorithm.5 Alternatively statistical methods such Bayesian inference can be used to build probabilistic models. With Bayesian inference, uncertainties are explicitly expressed and combined with Bayes rule to output the posterior probability (a probabilistic representation of uncertainty) – the probability distribution of the model given the data.6 When analytically intractable, sampling methods such as Markov Chain Monty Carlo (MCMC) can be used to estimate these posterior probabilities.6 Implementing these techniques is made easier through probabilistic programming languages such as Pyro and Turing.7,8 SAGE employes Bayesian inference and MCMC for uncertainty quantification and propagation.
A schematic of SAGE is provided in Fig. 1c. Here SAGE takes in data streams from the material synthesis and processing systems, structure characterization instruments, as well as functional property characterization instruments. Each structure data stream is first processed using a phase analysis algorithm as described below. SAGE then learns the SPSPR from the combined phase analysis data streams and the functional property data streams. SAGE's output SPSPR posterior can be broken down into posteriors over the synthesis–process–structure phase map and the functional properties. These posteriors can then be integrated into either an experiment recommendation engine or a closed-loop autonomous materials laboratory,9 which can guide subsequent experiments and measurements in structure and functional property. For example, an autonomous system could target maximizing knowledge of the SPSPR or optimizing a material for a set of target functional properties.
Each of SAGE's features has a diverse history. The first feature of ML-based phase mapping has a seen the development of an array of algorithms over the last few decades.3,10–14 These algorithms combine two tasks, (1) data analysis: analyzing structure data to identify phase abundances or phase regions and (2) extrapolation: extrapolating phase knowledge from measured materials to unmeasured materials. Data analysis techniques (i.e., phase or phase region identification) include matrix factorization, peak detection, graphical model segmentation, constraint programming, mixed integer programming, and deep learning, among others.3,15–23 For an example of such an algorithm applied to the provided datasets, including a thorough description of these datasets, we refer the reader to ref. 3. Extrapolation algorithms have focused primarily on the use of graph-based models or Gaussian processes (GP).16,17,24,25 (For a brief overview of Gaussian processes, see Section 4.2.6 Gaussian processes) For the present work, we assume the task of structure data analysis is addressed with one of the many available algorithms. We indicate the use of one of these algorithms with the function m(Ds) applied to structure dataset Ds, as described below. SAGE therefore begins with knowledge of phase and focuses on the task of extrapolating phase map knowledge through Bayesian coregionalized synthesis and process space segmentation.
Piecewise function regression algorithms have a much longer history. This includes the common challenge of detecting data discontinuities – also known as jumps or changepoints, which can be generalized to higher dimensions as edges,26 change-boundaries, and change-surfaces. Changepoint detection algorithms are quite diverse, using function derivatives, filter convolution, Bayesian inference, and more recently, adaptive design.27 Common methods for piecewise regression include linear piecewise algorithms and splines. We point the reader to review articles in these fields.28,29 Specifically for GPs, multiple piecewise modeling methods exist30 including the use of the changepoint kernel (below called GP-CP).31
The field of coregionalization developed from geospatial science to learn functions with shared trends over the same physical domain.32,33 Data for each target function is not required to be collected for the same set of points in the input domain.33 For example, if one seeks to learn f1:x → y and f2:x → s, data D1 = {(xk, yk)}Nk=1 and D2 = {(xl, sl)}Ml=1, the set of input locations {xk}Nk=1 and {xl}Ml=1 are not required to correspond to the same locations. Alternative methods for jointly learning related functions include multi-task learning, co-kriging, including multi-task Gaussian processes5,34 as well as constraint programming methods and Bayesian methods.33,35,36 These algorithms focus on exploiting similarities between functions over the full underlying shared domain, assume the set of output functions are similar (e.g., all continuous), and assume that each experiment is characterized similarly. Recent work tackles learning heterogenous sets of functions such as a mix of continuous, categorical, and binary outputs.37 These algorithms assume a correlation between a set of latent functions that contribute to the observed output functions.
Our challenge is unique. While we seek to jointly learn the synthesis–process–structure relationship and synthesis–process–property relationships, the correlation of interest between these relationships is purely that of discontinuities, rather than correlations over the full synthesis–process domain. We assume that phase boundaries indicate potential change surfaces in functional properties, and vice versa. We wish to jointly learn these phase boundaries and utilize them to define piecewise functions for the functional properties, allowing for different property behavior in different phase regions. Prior algorithms fail for this challenge as the synthesis–process–structure relationship and those of synthesis–process–properties are not correlated over the full synthesis–process domain (this is also true for latent function representations). Additionally, SAGE utilizes coregionalization to allow different measurements to be performed at different locations in the shared synthesis and process domain. This is commonly the case when materials synthesis and processing experiments take equal or less time than the measurements or when combining data collected at different times or by different labs.
To the authors' knowledge, the only algorithm that addresses the same challenge is the closed-loop autonomous materials exploration and optimization (CAMEO) algorithm.16 CAMEO first learns phase boundaries from synthesis, process, and structure data and then utilizes this knowledge to define the change boundaries in the piecewise function used to fit and model functional property data. This two-step approach was employed in driving an X-ray diffraction-based autonomous (robot) materials research system in the study of phase-change memory material. The study resulted in the discovery of the current best-in-class phase-change memory material – the first autonomous discovery of a best-in-class solid state material.16 SAGE improves on CAMEO by allowing full Bayesian uncertainty quantification and propagation, thus providing simultaneous information sharing between the structure and property measurements. SAGE jointly solves for the SPSPR to better exploit shared trends across structure and property data and improve SPSPR knowledge. SAGE is offered as a module of CAMEO, i.e., CAMEO-SAGE.
The present data science challenge is generalizable beyond learning SPSPR. One can use SAGE to address the more common issue of having successful and failed experiments across a shared experiment parameter domain. SAGE would then learn and exploit knowledge of the success–failure boundary to improve prediction of properties of either type of experiments. Additionally, SAGE addresses data fusion across instruments, measurement modalities and labs. The common approach to this data fusion challenge is to map data from different sources into the same data space, allowing comparison. For example, data fusion for X-ray diffraction (XRD) measurements from two different XRD instruments requires removing source-based data artifacts including instrument effects that are convolved into the data. To do this, that data must then be mapped from the instrument specific, source-based independent variable space (2θ) to an instrument-free independent variable space (q), while also accounting for differences in finite resolution in 2θ space, absolute intensities and counting times, beam wavelength dispersion, and background signals, amongst other considerations. In general, data mapping to an instrument (also lab, weather, etc.) invariant space requires a significant amount of meta data that is often not available.
An alternative is to independently analyze the data from each source and then combine the derived knowledge across sources. SAGE allows such limited-metadata data fusion. The idea behind coregionalization, as implemented in SAGE, is that the boundaries identified by one measurement method are also boundaries in the other measurement methods – regardless of if those measurement methods are all nominally the same technique (e.g., several different XRD instruments) or different techniques (e.g., an XRD instrument and electrical coercivity measurements). For example, for structure data, one performs phase mapping analysis for each data source and then SAGE coregionalization combines knowledge across sources. A similar benefit exists for functional property data by treating data from each source as a different target property, e.g., coercivity_data_source_1 and coercivity_data_source_2. Additionally, SAGE may be applied to cases where only structure data or only functional property data is obtained.
The contributions of this work are:
• Extending Bayesian coregionalization algorithms to 1-dimensional and N-dimensional joint segmentation and piecewise regression.
• Associated constraint programming algorithms for coregionalized joint segmentation and piecewise regression.
• Demonstration of Bayesian algorithms for learning SPSPR in a unified model.
SAGE is a physics-informed (also known as inductive-bias informed) machine learning algorithm.38 A wide array of methods exists for integrating prior physical knowledge into machine learning methods, including engineering descriptors,39,40 latent mappings,12 constrained solution spaces,41 kernels,42 among many others. For example, a physics-informed algorithm was designed for autonomous, closed-loop control over neutron scattering to accelerate characterization of temperature-dependent magnetic structure.43 The authors represent the temperature-dependent structure as a stochastic process with neutron scattering-defined measurement uncertainties as well as a mean function prior defined by magnetics physics. The algorithm resulted in a fivefold acceleration in measurement efficiency. However, no previous algorithms provide the contributions listed above. Such physics-informed methods provide greater performance and lend greater interpretability to the machine learning model – providing more physically meaningful solutions.
While the provided implementation of SAGE is a surrogate model, its framework allows easy modification to embed greater prior knowledge and to increase interpretability. Target functional properties are currently defined through samples of multivariate normal distributions, similar to a Gaussian process. To increase interpretability, users can replace these samples with samples of potentially descriptive parametric models (as well as a parameter that selects between the models). SAGE will then identify the most likely model and posteriors over its parameter values. In this way a user can exploit SAGE's built-in coregionalization of functional property with phase mapping (i.e., enforced SPSPR) to boost data analysis. Additionally, one can modify parameter priors. For example, setting segmentation length scales to a Gamma distribution to increase bias for small or larger phase regions.
2. Results
We demonstrate SAGE for 1D and 2D example challenges. For both 1D and 2D, we first investigate performance for 2 edge cases, each with artificial phase maps of 2 phase regions and one artificial target functional property. In the first edge case, structure data is more informative of the change boundary and in the second edge case the functional property data is more informative of the change boundary. These edge cases demonstrate SAGE's ability to exploit knowledge across both structure and functional property data to improve prediction of both. We then provide an example of SAGE's multi-data source coregionalization capabilities with a challenge of 2 structure data sources and 2 functional property data sources. This is followed by a real-world application to the (Bi,Sm)(Sc,Fe)O3 and FeGaPd3 material systems.As described above, SAGE performs the two tasks jointly of (1) segmenting the synthesis–process domain X into phase regions i.e., a phase map and (2) regression of the functional properties. SAGE tackles both tasks by exploiting shared knowledge (i.e., multimodal knowledge) across the structure and functional property data. We compare SAGE to a set of common algorithms and modified SAGE algorithms as described below (see section Additional models). SAGE's phase mapping capabilities are compared to that of GPC, the modified SAGE algorithm SAGE-1D-PM, and SAGE-ND-PM using only synthesis–process and structure data to segment the synthesis–process space. SAGE's functional property regression capability is compared to that of GPR, GP-CP, and the modified SAGE algorithms SAGE-1D-FP and SAGE-ND-FP using only synthesis–process and functional property data. Here the GP-CP algorithm seeks to perform functional property regression while also identifying change points (i.e., phase boundaries) without access to structure data. SAGE's capabilities for jointly performing phase mapping and functional property regression from synthesis, process, structure, and property data is compared to the CAMEO's regression algorithm which first uses synthesis–process and structure data to identify a phase map and then employs the phase map in piecewise regression for functional property data.
For each experiment, an algorithm is given a subset of materials data – for each challenge, all algorithms are given the same set of data (as visualized by red and black markers for 1D challenges and red markers for 2D challenges in the figures below) – and each algorithm is then used to predict one of or both of (based on its capabilities): (1) the phase map over the synthesis–process domain X, (2) functional properties over X. For 1D challenges this is over a 100-point grid and for 2D challenges a 40 × 40-point grid (see Fig. 2 and 3 for ranges). For instance, GPC takes a subset of data in X and the associated structure data and then predicts the phase map over the associated X grid; GPR takes a subset of data for X and associated functional properties data to provide functional property regression over the X grid.
Phase mapping performance is measured by comparing predicted phase map labels to ground truth (over the grid) using the micro F1 accuracy score. Ground truth for the 1D and 2D cases can be seen in the red and black dashed curves of Fig. 2 and the color-coded values of Fig. 3. Functional property regression performance is quantified by comparing predicted regression models with the ground truth using the typical coefficient of determination R2. A description of these measures can be found in the Methods section. Furthermore, the performance of MCMC-computed algorithms is based on their posterior mean and the performance of variational inference-based algorithms (e.g., GPs) is based on their maximum likelihood estimate (MLE) mean as given in Table 1.
| Phase map performance, micro F1 accuracy score [arb. Units] | ||||||
|---|---|---|---|---|---|---|
| 1D challenges | SAGE-1D (post. mean) | SAGE-1D-PM (post. mean | SAGE-1D-FP (post. mean) | GP-CP (max likelihood) | GP classification (max likelihood) | CAMEO prediction |
| 1D edge case 1 | 1.00 | 1.00 | 0.89 | 0.82 | 1.00 | 1.00 |
| 1D edge case 2 | 0.99 | 0.89 | 0.99 | 0.90 | 0.90 | 0.86 |
| Phase map performance, micro F1 accuracy score [arb. Units] | ||||||
|---|---|---|---|---|---|---|
| 2D challenges | SAGE-ND (post. mean) | SAGE-ND-PM (post. mean) | SAGE-ND-FP (post. mean) | — | GP classification (max likelihood) | CAMEO |
| 2D edge case 1 | 0.98 | 0.97 | 0.85 | — | 0.98 | 0.94 |
| 2D edge case 2 | 0.98 | 0.92 | 0.97 | — | 0.93 | 0.53 |
| (Bi,Sm)(Sc,Fe)O3 | 0.97 | 0.94 | 0.61 | — | 0.89 | 0.99 |
| FeGaPd | 0.95 | 0.93 | 0.13 | 0.99 | 0.96 | |
| Functional property performance R2 [arb. units] | ||||||
|---|---|---|---|---|---|---|
| 1D challenges | SAGE-1D (post. mean) | — | SAGE-1D-FP (post. mean) | GP-CP (max likelihood) | — | CAMEO prediction |
| 1D edge case 1 | 0.99 | — | 0.98 | 0.96 | — | 1.0 |
| 1D edge case 2 | 1.00 | — | 1.00 | 0.98 | — | 0.92 |
| Functional property performance R2 [arb. units] | ||||||
|---|---|---|---|---|---|---|
| 2D challenges | SAGE-ND (post. mean) | — | SAGE-ND-FP (post. mean) | — | GP regression (max likelihood) | CAMEO |
| 2D edge case 1 | 0.88 | — | 0.53 | — | 0.67 | 0.86 |
| 2D edge case 2 | 0.89 | — | 0.87 | — | 0.62 | 0.67 |
| (Bi,Sm)(Sc,Fe)O3 | 0.91 | — | 0.27 | — | 0.84 | 0.87 |
| FeGaPd | 0.91 | 0.87 | 0.90 | 0.91 | ||
2.1. 1D examples
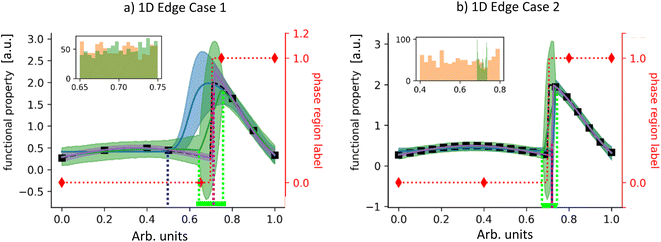
The 1D challenges are shown in Fig. 2 with the target functional property shown as a black dashed curve and the phase map shown as a dotted red curve that switches between a value of 0 and 1 at x = 0.7. For the first edge case, structure data (red diamonds) is more informative of the phase boundary, compared to functional property data (black squares). The reverse is true for the second edge case. To compare functional property prediction performance, in Fig. 2a and b we plot: (1) SAGE-1D's functional property posterior mean (solid green line) and 95% confidence interval (shaded green area), (2) an off-the-shelf GP with the changepoint kernel31 (GP-CP, blue line and shaded area) which uses maximum likelihood estimate (MLE), and (3) a plot of SAGE-1D's maximum likelihood sample (MLS, magenta line and shaded area) – the MCMC sample with the maximum computed likelihood. This sample contains an explicit changepoint value and associated piecewise GP regression. For phase boundary prediction comparison, we plot: (1) SAGE-1D's phase boundary posterior distribution (green inset histogram) and (2) SAGE-1D-PM's posterior distribution (orange inset histogram).For the first edge case, SAGE-1D MLS combines structure and functional property knowledge to outperform GP-CP in predicting both functional property and phase boundary. SAGE-1D's slanted transition at the phase boundary (Fig. 2a) indicates a range of potential phase boundary locations between the two structure data points (range is also indicated by the dotted green lines). SAGE-1D and SAGE-1D-PM have similar performance in identifying the phase boundary location, providing similar posteriors (inset). SAGE-1D employs phase boundary uncertainty to better quantify its regression uncertainty as indicated by the wider confidence intervals.
For the second edge case, SAGE-1D MLS and GP-CP have similar regression performance due to the highly informative functional property data. However, SAGE-1D outperforms SAGE-1D-PM in locating the phase boundary, as it exploits functional property data to greatly narrow in on potential locations. A further comparison between SAGE-1D, GP-CP, SAGE-1D-PM, SAGE-1D-FP, and GP classification are presented in Table 1. Knowledge of the changepoint location is limited to the two nearest data points, either functional property or structure data. As a result, functional property prediction performance is measured outside the range of the two nearest data points.
2.2. 2D examples
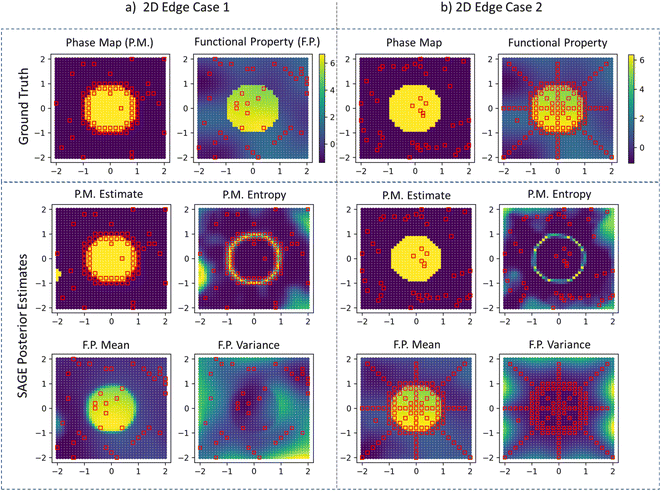
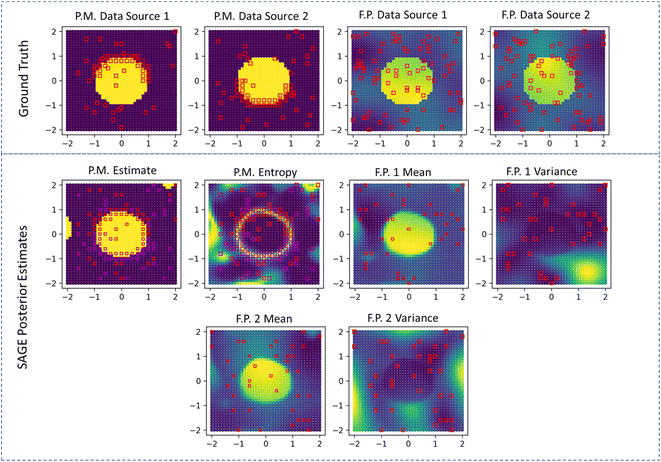
We observe similar behavior in the 2D demonstration of SAGE-ND as shown in Fig. 3. The location of structure data (red squares on phase map plots) and functional property data (red squares on functional property plots) are indicated. For phase map prediction, SAGE-ND is compared to SAGE-ND-PM, SAGE-ND-FP, and GP classification. For functional property prediction, SAGE-ND is compared to SAGE-ND-FP and off-the-shelf GP regression. Performance scores are reported in Table 1. SAGE-ND outperforms the other methods in both phase mapping and functional property prediction for both edge cases. In edge case 2, despite highly informative functional property data, SAGE-ND outperforms off-the-shelf GP regression due to its ability to properly deal with the change in property and change in hyperparameters across the phase boundary.In Fig. 4 we demonstrate the ND algorithm for the 2D case with 2 structure data sources and 2 functional property sources. Here the first structure data source provides more information for the upper part of the phase boundary and the second source provides more information for the lower part of the boundary. SAGE-ND unifies knowledge across all four data sources to obtain good prediction of both phase map and the two functional properties.
2.3. Materials example
For the first materials challenge demonstration, SAGE-ND is applied to learn a SPSPR for a (Bi,Sm)(Sc,Fe)O3 composition spread dataset of Raman spectra structure measurements and CEFM as shown in Fig. 5. As structure data is collected primarily to learn the phase map, we present the case where structure data is more informative of the phase boundaries than the functional property data. Phase mapping and CEFM predictions estimates are shown in Fig. 5a1 and 5b1 and uncertainties in Fig. 5a2 and 5b2 respectively.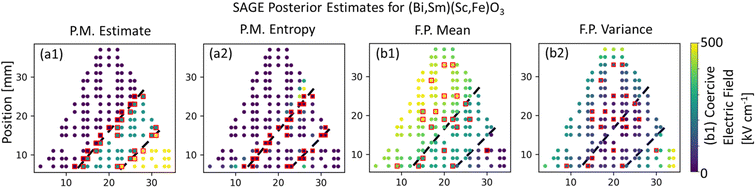 | ||
| Fig. 5 SAGE-ND applied to (Bi,Sm)(Sc,Fe)O3 dataset, where structure data is more informative of the phase boundaries. Fig. 1 shows the ground truth. (a1) Phase map estimate indicated by color coding with structure data indicated with red squares and phase boundaries indicated by dashed black lines. (a2) Entropy-measured uncertainty in the phase map of (a1), (b1) CEFM estimate with functional property data indicated with red squares. (b2) Variance-measured uncertainty for the CEFM estimate. SAGE-ND utilizes the more informative structure data to identify the phase regions and utilizes this information to better identify the varying CEFM behavior in each phase region. | ||
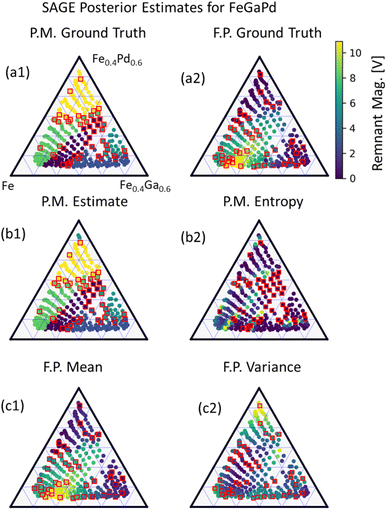
For the second materials challenge demonstration, SAGE-ND is applied to learn a SPSPR for a FeGaPd3 composition spread dataset of X-ray diffraction structure measurements and remanent magnetization as shown in Fig. 6. Ground truth phase mapping and remanent magnetization are shown in Fig. 6a1 and 6a2, respectively. SAGE prediction estimates are shown in Fig. 6b1 and 6c1 and uncertainties in Fig. 6b2 and 6c2, respectively.
For both material systems, a comparison of SAGE-ND with SAGE-ND-PM, SAGE-ND-FP, GP classification, GP regression, and CAMEO are shown in Table 1. For the (Bi,Sm)(Sc,Fe)O3 dataset, SAGE-ND provides 97% (or 0.97 out of 1.00) or greater phase mapping accuracy, though not the top accuracy among algorithms. For (Bi,Sm)(Sc,Fe)O3, CAMEO outperforms SAGE-ND by 2% and for FeGaPd, GPC outperforms SAGE-ND by 4%. For functional property predictions, SAGE-ND provides the best (or tied for best) performance.
Better performance for predicting functional properties over phase mapping is to be expected as there is greater information of the phase boundaries from the structure data than the functional property data. Thus, SAGE exploits knowledge from the structure data (knowledge of the synthesis–process–structure relationship) to boost functional property prediction.
While SAGE-ND does not always provide the best results, it does provide proper uncertainty quantification compared to CAMEO. Additionally, if the SAGE assumption that the target functional property behavior is dependent on phase is true for the material system of interest, SAGE exploits this relationship to improve uncertainty quantification using both structure and functional property data compared to methods (e.g., GP methods) that can only utilize either structure or functional property data. SAGE is also the only algorithm which provides a single model for quantifying both prediction and uncertainty for the synthesis–process–structure–property relationship.
3. Conclusion
SAGE allows one to combine knowledge of material structure and material property from multiple data sources into one unified SPSPR model, exploiting shared data trends to maximize knowledge of the phase diagram and functional properties. The Bayesian inference methodology allows for appropriate quantification of uncertainty. By providing probabilistic descriptions of data of varying quality or fidelity (whether theory-derived or experimental), these uncertainties can then be propagated through the model by sampling the data distributions along with the model parameters and/or by replacing the piecewise GPs with heteroskedastic GPs. Additionally, correlations between functional properties can also be exploited by replacing the functional property-representing independent piecewise GPs with a coregionalized multi-output GP. These points will be the focus of future work.Model output estimates and uncertainties can be employed in active learning-driven recommendation engines or closed-loop autonomous systems, to ensure optimum selection of subsequent experiments. For example, the phase map estimate and uncertainty can guide subsequent structure measurements toward improved phase map knowledge while the paired functional property estimates and uncertainties guide materials optimization. With each experiment increasing knowledge of separate portions of the SSPR, SAGE can play a part in unifying knowledge across a research lab toward the discovery of advanced materials.
4. Methods
We present coregionalization algorithms for combining multiple data sources for materials synthesis, process, structure, and property to learn the SPSPR over the shared synthesis and processing domain x ∈ X. Structure data from data source i is represented by Ds,i = {xk, zk,i}Nk=1i for material xk (data pair indexed with k) and its associated structure descriptor zk,i, with Ni data pairs collected from data source i. The full set of structure data is labeled Ds, where the subscript s indicated structure-associated data. Similarly, property data from data source j is represented by Dp,j = {xl,yl,j}Nl=1j for material xl and its associated material property measurement yl,j, and where subscript p indicates functional-property-associated data. Ds,i,k and Dp,j,k are the i-sourced structure data for xk and the j-sourced functional property data for xl. For this work we assume each data source provides data for one property. The full set of functional property data is labeled Dp. This representation allows for duplicate measurements of the same material from different data sources. The function m(Ds) maps dataset Ds to a set of phase map labels. It is one of the many such algorithms described above, and as such is not part of SAGE.4.1. Constraint programming
The constraint programming algorithm (eqn (1)) is defined by finding the set of parameters θ = {θs,θp} that minimize the objective function Obj. The phase map is described by the function fs(x,θs) which maps each point x in the target synthesis-process space X to a set of phase labels s, fs:x → s, where θs is the associated set of parameters. The functional property is described by the piecewise function fp(x, fs, θp) which maps each point x to a set of functional properties y, i.e., fp:x → y. This function is dependent on the set of parameters θp and its piecewise nature is dependent on fs. The functions ds and dp compute the relationship – typically the loss, between the function fs and data Ds or between fp and data Dp, respectively. For example, dp can combine a measure of goodness of fit of fp and model complexity, e.g., the Bayesian information criteria.44 To quantify loss for structure data, the data Ds must also be mapped to a set of phase map labels, here performed by the function m(Ds) (As discussed above, this function is one of the many found in the literature). Minimizing the objective involves: (1) identifying potential values for parameters θs, (2) solving for m(Ds) and fs, (3) identifying potential values for parameters θp, (4) solving for fp, and (5) computing the overall loss for the objective function. This iterative approach allows a target property estimate to inform the subsequent optimization of fs(x).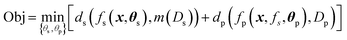 | (1) |
If the loss functions are additive across datasets, we have:
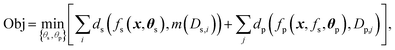 | (2) |
One implementation has fs map each point to an integer label associated with a given phase region. The function ms is then required to map the structure data to potential phase region labels similar to those of.3,10–13,15 Alternatively, one may want the overall algorithm to identify phase abundances for each material x. For this case, ms identifies phase abundances and maps x to phase region labels. Abundance regression can then be performed by including abundances in the list of target properties yp.
The Bayesian model presented below can be solved using such an objective function. Here, ds and dp are the negative log likelihood functions:
| ds = −ln[p(fs(x, θs)|m(Ds)], | (3) |
| dp = −ln[p(fp(x, fs, θp)|Dp,j)], | (4) |
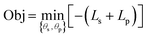 where Ls and Lp are the sum log likelihoods over all structure or all functional property observations, respectively. The notation p() represents a pdf, p(a|b) describes the pdf of a given b, and for the equations below, a ∼ p(b) indicates drawing independent and identically distributed samples from p(b). Solving for {θs, θp} may be done under the variational inference approximation. The results presented her focus on Markov Chain Monte Carlo (MCMC) computed posteriors. The variational inference approximation can be used to initialize MCMC and speed up calculations.
where Ls and Lp are the sum log likelihoods over all structure or all functional property observations, respectively. The notation p() represents a pdf, p(a|b) describes the pdf of a given b, and for the equations below, a ∼ p(b) indicates drawing independent and identically distributed samples from p(b). Solving for {θs, θp} may be done under the variational inference approximation. The results presented her focus on Markov Chain Monte Carlo (MCMC) computed posteriors. The variational inference approximation can be used to initialize MCMC and speed up calculations.
4.2. Bayesian models
We provide two Bayesian models, one for challenges where X is one dimensional (i.e., only one synthesis or process parameter is investigated) and one where X is of arbitrary dimension. Rather than minimizing loss, the aim of these models is to maximize the sum log likelihood L over the set of parameters and observed data (e.g., minimize sum of negative log likelihood as above). Here, MCMC is used to compute a posterior for each model parameter. Additionally, one can incorporate prior physical knowledge by modifying parameter prior probability density functions (pdf). For example, if one believes there to be many small phase regions, the uniform prior for ls can be replace with a Gamma distribution. Large expected fluctuations in a functional property can be included through modifying the sr,j prior. Both the 1-dimensional and N-dimensional models output an estimate for the posterior of the SPSPR and each parameter (given the model and data) – providing both an estimate and uncertainty, compared to the constraint programming algorithm which outputs a point estimate (estimates of the uncertainty can also be obtained). The posteriors can be used in further Bayesian analysis as demonstrated below. The MCMC Bayesian inference method for evaluating the models consists of: (1) sampling function parameters, (2) using the samples to define fs and fp, and then (3) compute the log likelihood L.Model 1 provides the general model. One samples the function parameter priors for θs and θp = {θp,j,r} for each j of J functional properties (or function property data source) and each r of R phase regions. fp,j is a piecewise random process with different behavior fp,j,r for each functional property in each phase region, i.e., different kernel hyperparameters for each phase region. fs is used to compute the categorical distribution p(r(x)) of phase regions labels for each point x. p(r(x)) is used to compute the sum log likelihood Ls of structure data observations and identify phase region label probabilities for each functional property observation data point xp. The sum log likelihood of the observed functional properties Lp is computed using these probabilities and the piecewise fp,j. The total likelihood L is then returned, guiding Bayesian inference sampling. The implementations and associated code can be used with an arbitrary number of data sources. Sampling from GPs uses the Cholesky decomposition method to improve MCMC stability.4
After Bayesian inference is run, i.e., each b sample of B total MCMC samples are collected, the Bayesian posteriors for the phase map and functional-properties-describing functions are approximated. Here the categorical distribution describing the phase map is computed by taking meanb[pb(r)], the posterior mean over the sampled categorical distributions. The phase map estimate ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) and uncertainty e
and uncertainty e![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) are then computed with
are then computed with ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) = argmaxr[pM] and e
= argmaxr[pM] and e![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) = entropyr[pM]. Each functional property is described by the posterior multivariate normal distribution N(meanb[fp,j,b], stdb[fp,j,b]) with additional measurement noise meanb[np,j,b].
= entropyr[pM]. Each functional property is described by the posterior multivariate normal distribution N(meanb[fp,j,b], stdb[fp,j,b]) with additional measurement noise meanb[np,j,b].
The SAGE algorithms make use of latent functions. One set of latent functions are used to identify the probabilities of each point x belonging to a specific phase region. These probabilities are then multiplied by an additional set of latent functions describing target functional properties, in effect weighting these second set of functions to bound them to target phase regions. Through this combination of latent functions, one can identify regions in X that may contain significant changes in phase and/or functional properties and may be of interest for further experiments. Statistical analysis of multiple samples of latent functions provides a posterior distribution for phase map and piecewise functional properties.
The presented implementation is developed from that of ref. 25. The functional property in each phase region is represented by an independent radial basis function kernel Gaussian process, with θp including: lr,j kernel length scale, sr,j kernel standard deviation (also known as ‘scale’), and sj measured noise standard deviation. For this work, we assume that sj is the same for property j across all phase regions. For each property, the region-specific functions fp,j,r are sampled from GP(θp,j,r) and then combined using the probabilistic weights p(r) to give the piecewise functions fp,j. fp,j describes the sample mean and nj the sample noise of the multivariate distribution N(fp,j, nj) used to describe a potential generating random process. Data likelihood is then given by p(Dp,j|N(fp,j, nj)).
Example implementation:
We compare SAGE to off the shelf GP algorithms and modified versions of SAGE. We compare SAGE's phase mapping (PM) performance with a version of SAGE which only takes structure data input. For 1D challenges this is Model 4 ‘SAGE-1D-PM’ and for 2D challenges this is Model 6 ‘SAGE-ND-PM’. We compare SAGE's functional property (FP) prediction performance with versions that only take in functional property data, i.e., piecewise Gaussian process regression. For 1D challenges this is Model 5 ‘SAGE-1D-FP’ and for 2D challenges Model 7 ‘SAGE-ND-FP’. For these algorithms that rely on just one input data type, it is expected that for exhaustive data, performance will be high, while for partial data, the joint SAGE model will outperform these models. These additional algorithms are available as part of the SAGE library.
• Model 4, SAGE-1D-PM: this algorithm mirrors SAGE-1D but excludes functional property regression. The algorithm is described the same as Model 2 lines 1–4 and returns Ls.
• Model 5, SAGE-1D-FP: this algorithm mirrors SAGE-1D but excludes the phase mapping loss term. It is thus a 1-dimensional piecewise GP. The algorithm is described the same as Model 2 lines 1–3 and 5–11 and returns Lp.
• Model 6, SAGE-ND-PM: this algorithm mirrors SAGE-ND but excludes the task of functional property regression. The algorithm is described the same as Model 3 lines 1–6 and returns Ls.
• Model 7, SAGE-ND-FP: this algorithm mirrors SAGE-ND but excludes the phase mapping loss term. It is thus an N-dimensional piecewise GP. The mode is described the same as Model 3 lines 1–5 and 7–14 and returns Lp.
• GP-CP; GPR; GPC: the implementations use the radial basis function kernel for regression and the Matern 5/2 kernel and MultiClass likelihood for classification. All use the truncated Newton method for optimization.
• CAMEO – only piecewise regression task. This model follows that of []. A Gaussian random field (GRF) is defined for the material system including both characterized and potentially characterized materials. The GRF is applied to the structure data to segment the material system and that segmentation is then combined with off-the-shelf Gaussian process regression, using different hyperparameters for each phase region.
4.2.4.1. Regression: coefficient of determination, R2.
where yi is a ground truth value of target y(xi) located at point xi indexed with i, fi is the associated algorithm-based predicted value, and ȳ is the mean over all y values. Implemented with scikit-learn's r2_score function.
4.2.4.2. Phase mapping: micro F1-Score.
where TPr, FPr, and FNr are the count of true positive, false positive, and false negative classification values for each region r. Here positive defines points in X predicted to have label r and negative defines points predicted to not have label r, i.e., one-vs-all classification.
SAGE was run on a laptop (6 core 2.7 GHz, 32 GB memory, NVIDIA‡ Quadro P620) and runs within a few minutes, e.g., less than 2 minutes for the (Bi,Sm)(Sc,Fe)O3 material system example. All implementations are built to boost performance through parallelization across multiple CPUs by changing the “number of available cores” and “number of chains”. This dramatically accelerates computation. For example, using parallelization across a 100 CPU node allows MCMC samples for each CPU to be reduced by an order of 100. The choices of MCMC sample number indicated below were found to provide convergence in the posterior predictions.
Here we provide initial values or uniform prior ranges for the implementation. If a parameter is not mentioned, it is the default initial value or range of the library used.
• GPs
○ All GP implementations are written in gpflow.45
○ 1D CP-GP: initial length scale = 0.2; initial change point steepness = 100; noise variance = 0.01; max iterations = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000;
000;
○ 2D GPR: initial lengthscales = 1; noise variance = 0.005 and range [0.001, 0.01]; max iterations = 1000;
○ 1D and 2D GPC: max iterations = 1000;
• All MCMC algorithms
○ Number warmup samples = 100; number samples = 1000; target acceptance probability = 0.8; max tree depth = 5; jitter = 1 × 10−6
○ SAGE-1D, SAGE-1D-PM, SAGE-1D-FP are written in numpyro46 with parameters: sr,j = [0.01, 2.]; lr,j [0.2,1.]; nj = [0.001,0.01]; Change point bounds, i.e., θs = [0.5, 1.]
○ SAGE-ND, SAGE-ND-PM, SAGE-ND-FP are written in numpyro Jax with parameters.
■ SVI initialization of phase map: number of samples = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000; Adam step size = 0.05;
000; Adam step size = 0.05;
■ MCMC algorithm: ss = [5.,10.]; ls = [0.1,2.]; sr,j = [0.1, 2.]; lr,j = [1,2.]; nj = [0.001,0.1]; br,j = [−2., 2.]
○ SAGE-ND Multiple data sources:
■ SVI initialization of phase map: number of samples: 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000; Adam step size = 0.01; ss = [5.,10.]; ls = [1.,2.];
000; Adam step size = 0.01; ss = [5.,10.]; ls = [1.,2.];
■ MCMC algorithm: number of warmup steps: 100; number of samples: 2000; number of chains = 100; ss = [5.,10.]; ls = [0.1,2.]; sr,j = [0.1, 2.]; lr,j = [0.1,5.]; nj = [0.001,0.1]; br,j = [−2., 2.]
• CAMEO: uses the same parameters as in ref. 16.
 is the prior mean function and
is the prior mean function and 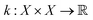 is a kernel function describing the relationship between f(xi) and f(xj). The prior is combined with a likelihood probability distribution p(y|f) used to describe the expected relationship between y and f, typically used to describe the expected noise in y given f. The prior and likelihood are combined using Bayes rule to identify a posterior given the data (x, y). When the prior and likelihood are both multivariate normal distributions, the posterior is also a multivariate normal distribution and an analytical solution for the posterior exists.
is a kernel function describing the relationship between f(xi) and f(xj). The prior is combined with a likelihood probability distribution p(y|f) used to describe the expected relationship between y and f, typically used to describe the expected noise in y given f. The prior and likelihood are combined using Bayes rule to identify a posterior given the data (x, y). When the prior and likelihood are both multivariate normal distributions, the posterior is also a multivariate normal distribution and an analytical solution for the posterior exists.
Numerous kernel functions exist including the radial basis function which is commonly used for regression and the Matern kernels which are commonly used in classification tasks. These kernel functions have parameters (often called hyperparameters) and the GP algorithm typically uses maximum likelihood to identify the most likely value of these parameters given the data. Additionally, numerous likelihood functions exist for various data challenges based on the expected noise in the data. For the regression case of expected normally distributed noise, the likelihood may be a multivariate normal distribution. Specific likelihood functions exist for the challenges of binary and multi-class classification. For more information on GPs, their theory, implementation, and use, please see the excellent resource.4
Data availability
The code, analysis scripts, and datasets supporting this article have been uploaded as part of the ESI.†Author contributions
The authors contributed to the provided work in the following order, with greatest contribution listed first. Initial concept: AGK. Theory: AGK, BD, AM. Implementation: AGK, BD, AM. Testing: AGK, AM, BD. Writing the paper: AGK, AM, BD.Conflicts of interest
There are no conflicts to declare.References
- D. Kan, C. J. Long, C. Steinmetz, S. E. Lofland and I. Takeuchi, Combinatorial search of structural transitions: Systematic investigation of morphotropic phase boundaries in chemically substituted BiFeO3, J. Mater. Res., 2012, 27(21), 2691–2704 CrossRef CAS.
- D. Kan, L. Pálová, V. Anbusathaiah, C. J. Cheng, S. Fujino and V. Nagarajan, et al., Universal Behavior and Electric-Field-Induced Structural Transition in Rare-Earth-Substituted BiFeO3, Adv. Funct. Mater., 2010, 20(7), 1108–1115 CrossRef CAS.
- A. G. Kusne, D. Keller, A. Anderson, A. Zaban and I. Takeuchi, High-throughput determination of structural phase diagram and constituent phases using GRENDEL, Nanotechnology, 2015, 26(44), 444002 CrossRef CAS PubMed.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, Cambridge, Mass, The MIT Press, 2005, p. 272 Search PubMed.
- T. Hastie, R. Tibshirani, J. Friedman, T. Hastie, J. Friedman and R. Tibshirani, The Elements of Statistical Learning, Springer, 2009, vol. 2, https://link.springer.com/content/pdf/10.1007/978-0-387-84858-7.pdf Search PubMed.
- A. Gelman, J. B. Carlin, H. S. Stern and D. B. Rubin, Bayesian Data Analysis, Chapman and Hall/CRC, 1995, https://www.taylorfrancis.com/books/mono/10.1201/9780429258411/bayesian-data-analysis-andrew-gelman-donald-rubin-john-carlin-hal-stern Search PubMed.
- E. Bingham, J. P. Chen, M. Jankowiak, F. Obermeyer, N. Pradhan and T. Karaletsos, et al., Pyro: Deep universal probabilistic programming, J. Mach. Learn. Res., 2019, 20(1), 973–978 Search PubMed.
- H. Ge, K. Xu and Z. Ghahramani, Turing: A Language for Flexible Probabilistic Inference, In Proceedings of the Twenty-First International Conference on Artificial Intelligence and Statistics, PMLR, 2018, pp. 1682–1690, https://proceedings.mlr.press/v84/ge18b.html Search PubMed.
- E. Stach, B. DeCost, A. G. Kusne, J. Hattrick-Simpers, K. A. Brown and K. G. Reyes, et al., Autonomous experimentation systems for materials development: A community perspective, Matter, 2021, 4(9), 2702–2726 CrossRef.
- J. K. Bunn, S. Han, Y. Zhang, Y. Tong, J. Hu and J. R. Hattrick-Simpers, Generalized machine learning technique for automatic phase attribution in time variant high-throughput experimental studies, J. Mater. Res., 2015, 30(07), 879–889 CrossRef CAS.
- J. R. Hattrick-Simpers, J. M. Gregoire and A. G. Kusne, Perspective: Composition–structure–property mapping in high-throughput experiments: Turning data into knowledge, APL Mater., 2016, 4(5), 053211 CrossRef.
- D. Chen, Y. Bai, W. Zhao, S. Ament, J. Gregoire and C. Gomes, Deep Reasoning Networks for Unsupervised Pattern De-mixing with Constraint Reasoning, in Proceedings of the 37th International Conference on Machine Learning, PMLR, 2020, pp. 1500–1509, https://proceedings.mlr.press/v119/chen20a.html Search PubMed.
- C. P. Gomes, J. Bai, Y. Xue, J. Björck, B. Rappazzo and S. Ament, et al., CRYSTAL: a multi-agent AI system for automated mapping of materials' crystal structures, MRS Commun., 2019, 9(2), 600–608 CrossRef CAS.
- S. V. Kalinin, M. P. Oxley, M. Valleti, J. Zhang, R. P. Hermann and H. Zheng, et al., Deep Bayesian local crystallography, npj Comput. Mater., 2021, 7(1), 181 CrossRef.
- A. G. Kusne, T. Gao, A. Mehta, L. Ke, M. C. Nguyen and K. M. Ho, et al., On-the-fly machine-learning for high-throughput experiments: search for rare-earth-free permanent magnets, Sci. Rep., 2014, 6367 CrossRef PubMed , https://www.nature.com/articles/srep06367.
- A. G. Kusne, H. Yu, C. Wu, H. Zhang, J. Hattrick-Simpers and B. DeCost, et al., On-the-fly closed-loop materials discovery via Bayesian active learning, Nat. Commun., 2020, 11(1), 5966 CrossRef CAS PubMed.
- R. LeBras, T. Damoulas, J. M. Gregoire, A. Sabharwal, C. P. Gomes and R. B. van Dover, Constraint reasoning and Kernel clustering for pattern decomposition with scaling, in Principles and Practice of Constraint Programming–CP 2011, Springer, 2011, pp. 508–522 Search PubMed.
- C. P. Gomes, J. Bai, Y. Xue, J. Björck, B. Rappazzo and S. Ament, et al., CRYSTAL: a multi-agent AI system for automated mapping of materials' crystal structures, MRS Commun., 2019, 9(2), 600–608 CrossRef CAS.
- Y. Iwasaki, A. G. Kusne and I. Takeuchi, Comparison of dissimilarity measures for cluster analysis of X-ray diffraction data from combinatorial libraries, npj Comput. Mater., 2017, 3(1), 1–9 CrossRef CAS.
- S. K. Suram, Y. Xue, J. Bai, R. Le Bras, B. Rappazzo and R. Bernstein, et al., Automated phase mapping with AgileFD and its application to light absorber discovery in the V–Mn–Nb oxide system, ACS Comb. Sci., 2017, 19(1), 37–46 CrossRef CAS PubMed.
- V. Stanev, V. V. Vesselinov, A. G. Kusne, G. Antoszewski, I. Takeuchi and B. S. Alexandrov, Unsupervised phase mapping of X-ray diffraction data by nonnegative matrix factorization integrated with custom clustering, npj Comput. Mater., 2018, 4(1), 1–10 CrossRef.
- P. M. Maffettone, L. Banko, P. Cui, Y. Lysogorskiy, M. A. Little and D. Olds, et al., Crystallography companion agent for high-throughput materials discovery, Nat. Comput. Sci., 2021, 1(4), 290–297 CrossRef PubMed.
- Autonomous Experimental Design and Execution | Handbook on Big Data and Machine Learning in the Physical Sciences, https://www.worldscientific.com/doi/abs/10.1142/9789811204579_0013 Search PubMed.
- S. Ament, M. Amsler, D. R. Sutherland, M. C. Chang, D. Guevarra and A. B. Connolly, et al., Autonomous materials synthesis via hierarchical active learning of nonequilibrium phase diagrams, Sci. Adv., 2021, eabg4930 CrossRef CAS PubMed , https://www.science.org/doi/abs/10.1126/sciadv.abg4930.
- A. G. Kusne and A. McDannald, Scalable multi-agent lab framework for lab optimization, Matter, 2023, 6(6), 1880–1893 CrossRef.
- J. Jing, S. Liu, G. Wang, W. Zhang and C. Sun, Recent advances on image edge detection: A comprehensive review, Neurocomputing, 2022, 503, 259–271 CrossRef.
- C. Park, P. Qiu, J. Carpena-Núñez, R. Rao, M. Susner and B. Maruyama, Sequential adaptive design for jump regression estimation, IISE Trans., 2023, 55(2), 111–128 CrossRef.
- S. Aminikhanghahi and D. J. Cook, A survey of methods for time series change point detection, Knowl. Inf. Syst., 2017, 51(2), 339–367 CrossRef PubMed.
- C. Truong, L. Oudre and N. Vayatis, Selective review of offline change point detection methods, Signal Process., 2020, 167, 107299 CrossRef.
- Y. Saatçi, R. D. Turner and C. E. Rasmussen, Gaussian process change point models, In Proceedings of the 27th International Conference on Machine Learning (ICML-10), 2010, pp. 927–934 Search PubMed.
- J. Lloyd, D. Duvenaud, R. Grosse, J. Tenenbaum and Z. Ghahramani, Automatic construction and natural-language description of nonparametric regression models, In Proceedings of the AAAI Conference on Artificial Intelligence, 2014 Search PubMed.
- A. G. Journel and C. J. Huijbregts, Mining geostatistics, Academic press, London, 1978, vol. 600 Search PubMed.
- M. A. Alvarez, L. Rosasco and N. D. Lawrence, Kernels for vector-valued functions: A review, Foundations and Trends® in Machine Learning, 2012, vol. 4(3), pp. 195–266 Search PubMed.
- E. V. Bonilla, K. Chai and C. Williams, Multi-task Gaussian process prediction, Advances in neural information processing systems, ed. J. Platt, D. Koller, Y. Singer and S. Roweis, Curran Associates, Inc., 2007, vol. 20 Search PubMed.
- C. A. Micchelli and M. Pontil, On learning vector-valued functions, Neural computation, 2005, 17(1), 177–204 CrossRef PubMed.
- C. Carmeli, E. De Vito and A. Toigo, Vector valued reproducing kernel Hilbert spaces of integrable functions and Mercer theorem, Anal. Appl., 2006, 4(04), 377–408 CrossRef.
- J. J. Giraldo and M. A. Álvarez, A Fully Natural Gradient Scheme for Improving Inference of the Heterogeneous Multioutput Gaussian Process Model, IEEE Trans. Neural Netw. Learn. Syst., 2022, 33(11), 6429–6442 Search PubMed.
- N. Baker, F. Alexander, T. Bremer, A. Hagberg, Y. Kevrekidis, H. Najm, et al.Workshop Report on Basic Research Needs for Scientific Machine Learning: Core Technologies for Artificial Intelligence, USDOE Office of Science (SC), Washington, D.C. (United States), 2019, https://www.osti.gov/biblio/1478744/ Search PubMed.
- O. Isayev, D. Fourches, E. N. Muratov, C. Oses, K. Rasch and A. Tropsha, et al., Materials Cartography: Representing and Mining Materials Space Using Structural and Electronic Fingerprints, Chem. Mater., 2015, 27(3), 735–743 CrossRef CAS.
- B. F. Grosso, N. A. Spaldin and A. M. Tehrani, Physics-Guided Descriptors for Prediction of Structural Polymorphs, J. Phys. Chem. Lett., 2022, 13(31), 7342–7349 CrossRef CAS PubMed.
- M. Schmidt and H. Lipson, Distilling free-form natural laws from experimental data, science, 2009, 324(5923), 81–85 CrossRef CAS PubMed.
- Z. Wang, W. Xing, R. Kirby and S. Zhe, Physics informed deep kernel learning, In: International Conference on Artificial Intelligence and Statistics, PMLR, 2022, pp. 1206–1218, https://proceedings.mlr.press/v151/wang22a.html Search PubMed.
- A. McDannald, M. Frontzek, A. T. Savici, M. Doucet, E. E. Rodriguez and K. Meuse, et al., On-the-fly autonomous control of neutron diffraction via physics-informed Bayesian active learning, Applied Physics Reviews, 2022, 9(2), 021408 CrossRef CAS.
- E. Wit, E. van den Heuvel and J. W. Romeijn, ‘All models are wrong…’: an introduction to model uncertainty, Statistica Neerlandica, 2012, 66(3), 217–236 CrossRef.
- A. G. de G. Matthews, M. Van Der Wilk, T. Nickson, K. Fujii, A. Boukouvalas and P. León-Villagrá, et al., GPflow: A Gaussian Process Library using TensorFlow, J. Mach. Learn. Res., 2017, 18(40), 1–6 Search PubMed.
- NumPyro documentation — NumPyro documentation, https://num.pyro.ai/en/latest/index.html# Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00048j |
| ‡ NIST disclaimer: certain commercial equipment, instruments, or materials are identified in this paper to foster understanding. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the materials or equipment identified are necessarily the best available for the purpose. |
| This journal is © The Royal Society of Chemistry 2024 |