 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetics of the reactions of the Criegee intermediate CH2OO with water vapour: experimental measurements as a function of temperature and global atmospheric modelling†
Rachel E.
Lade
a,
Mark A.
Blitz
 ab,
Matthew
Rowlinson
c,
Mathew J.
Evans
ab,
Matthew
Rowlinson
c,
Mathew J.
Evans
 cd,
Paul W.
Seakins
cd,
Paul W.
Seakins
 a and
Daniel
Stone
a and
Daniel
Stone
 *a
*a
aSchool of Chemistry, University of Leeds, Leeds, LS2 9JT, UK. E-mail: d.stone@leeds.ac.uk
bNational Centre for Atmospheric Science, University of Leeds, Leeds, LS2 9JT, UK
cWolfson Atmospheric Chemistry Laboratories, Department of Chemistry, University of York, York YO10 5DQ, UK
dNational Centre for Atmospheric Science, University of York, York YO10 5DQ, UK
First published on 30th September 2024
Abstract
The kinetics of reactions between the simplest Criegee intermediate, CH2OO, and water vapour have been investigated at temperatures between 262 and 353 K at a total pressure of 760 Torr using laser flash photolysis of CH2I2–O2–N2–H2O mixtures coupled with broadband time-resolved UV absorption spectroscopy. Results indicate that the reaction with water monomers represents a minor contribution to the total loss of CH2OO under the conditions employed in this work, with an estimated rate coefficient for CH2OO + H2O (R1) of (9.8 ± 5.9) × 10−17 cm3 molecule−1 s−1 at 298 K and a temperature dependence described by k1 = (3.2 ± 1.1) × 10−13 exp(−(2410 ± 270)/T) cm3 molecule−1 s−1. The reaction of CH2OO with water dimers, CH2OO + (H2O)2 (R2), dominates under the conditions employed in this work. The rate coefficient for R2 has been measured to be k2 = (9.5 ± 2.5) × 10−12 cm3 molecule−1 s−1 at 298 K, with a negative temperature dependence described by k2 = (2.85 ± 0.40) × 10−15 exp((2420 ± 340)/T) cm3 molecule−1 s−1, where rateR2 = k2[CH2OO][(H2O)2]. For use in atmospheric models, we recommend description of the kinetics for R2 in terms of the product of the rate coefficient k2 and the equilibrium constant KDeq (k2,eff = k2KDeq) for water dimer formation to allow the rate of reaction to be expressed in terms of water monomer concentration as rateR2 = k2,eff[CH2OO][H2O]2 to avoid explicit calculation of dimer concentrations and impacts of differences in values of KDeq reported in the literature. Results from this work give k2,eff = (1.96 ± 0.51) × 10−32 cm6 molecule−2 s−1 at 298 K with a temperature dependence described by k2,eff = (2.78 ± 0.28) × 10−38 exp((4010 ± 400)/T) cm6 molecule−2 s−1. No significant impacts of a reaction between CH2OO and three water molecules were observed in this work, potentially as a result of the relative humidities used in this work (up to 57% at 298 K). Atmospheric implications of the results have been investigated using the global chemistry transport model GEOS-Chem. Model simulations indicate that the reaction with water dimers dominates the loss of CH2OO in the atmosphere and limits the impacts of other reactions of CH2OO, with the reaction with water dimers representing >98% of the total loss of CH2OO in the troposphere.
Environmental significanceCriegee intermediates are key species in atmospheric chemistry, produced following the ozonolysis of unsaturated volatile organic compounds. The chemistry of Criegee intermediates influences atmospheric composition, and as a consequence, air quality and climate. The reactions of the simplest Criegee intermediate CH2OO with water monomers and dimers are expected to dominate its atmospheric chemistry, but there have been few experimental studies over a range of conditions relevant to the atmosphere. In our work we have performed a detailed experimental study of the kinetics of CH2OO reactions with water monomers and dimers over a wide range of temperatures relevant to the atmosphere, with atmospheric impacts of the reactions determined using the global chemistry transport model GEOS-Chem. |
Introduction
Criegee intermediates (CIs) are reactive zwitterionic species with the general formula R1R2COO produced in the atmosphere following the ozonolysis of unsaturated volatile organic compounds (VOCs). Ozonolysis reactions are typically exothermic by ∼250–300 kJ mol−1, producing CIs with high internal energies.1 The nascent CI may undergo unimolecular decomposition to form important trace species such as OH, HO2 and CO,2 or stabilisation through collisional energy transfer with surrounding gas molecules to form stabilised Criegee intermediates (SCIs). SCIs have longer atmospheric lifetimes than the nascent excited CIs, allowing them to participate in a wide range of chemical reactions. Bimolecular reactions of SCIs with water vapour3,4 and SO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5,6 are of particular interest as they have the potential to impact atmospheric budgets of secondary organic aerosols (SOA), gas phase sulfuric acid, and sulfate aerosol, thereby influencing air quality and climate. Reaction with water vapour is expected to dominate the atmospheric chemistry of the simplest SCI, CH2OO, but there is uncertainty over the role of reactions involving water monomers (H2O, R1), water dimers ((H2O)2, R2), or potentially three water molecules (likely via CH2OO·H2O + (H2O)2 or CH2OO·(H2O)2 + H2O, represented as CH2OO + 3H2O in R3) with a wide range of values reported for the kinetics of R1 and R2
5,6 are of particular interest as they have the potential to impact atmospheric budgets of secondary organic aerosols (SOA), gas phase sulfuric acid, and sulfate aerosol, thereby influencing air quality and climate. Reaction with water vapour is expected to dominate the atmospheric chemistry of the simplest SCI, CH2OO, but there is uncertainty over the role of reactions involving water monomers (H2O, R1), water dimers ((H2O)2, R2), or potentially three water molecules (likely via CH2OO·H2O + (H2O)2 or CH2OO·(H2O)2 + H2O, represented as CH2OO + 3H2O in R3) with a wide range of values reported for the kinetics of R1 and R2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7–10 and significant uncertainties regarding the products and product yields.11–15
7–10 and significant uncertainties regarding the products and product yields.11–15| CH2OO + H2O → Products | (R1) |
| CH2OO + (H2O)2 → Products | (R2) |
| CH2OO + 3H2O → Products | (R3) |
The development of photolytic precursors for the production of Criegee intermediates,16,17 including CH2OO,18,19 has led to the development of direct detection techniques for Criegee intermediates and improvements in our understanding of the reaction kinetics of a number of Criegee intermediate reactions relevant to the atmosphere.5,20,21 Welz et al.18 produced CH2OO following the 248 nm laser flash photolysis of diiodomethane, CH2I2, and investigated its potential reaction with water vapour, using tuneable VUV synchrotron photoionisation mass spectrometry (PIMS), at a total pressure of 4 Torr. Welz et al. observed no significant change in the decay of CH2OO on addition of water vapour at concentrations up to 3.1 × 1016 molecule cm−3, leading to the conclusion of an upper limit for k1 of 4 × 10−15 cm3 molecule−1 s−1 at 298 K. A subsequent study by Ouyang et al.22 examined the impact of water vapour on the production of NO3 following the 248 nm photolysis of CH2I2–O2–N2–NO2 mixtures, based on the assumption that NO3 was produced via CH2OO + NO2, which suggested a reaction of CH2OO with water vapour. However, a number of studies have since indicated that NO3 is produced via secondary chemistry in the system,4,23 leading to uncertainty in the result.
Photolytic production of CH2OO was also used by Stone et al.5 in a series of experiments monitoring the production of formaldehyde, HCHO, from CH2OO reactions via laser-induced fluorescence (LIF) spectroscopy. No significant change in the rate of HCHO production was observed on addition of water vapour at concentrations up to 1.7 × 1017 molecule cm−3 at a total pressure of 200 Torr, with a small change in HCHO yield attributed to fluorescence quenching by water and results indicating an upper limit of 9 × 10−17 cm3 molecule−1 s−1 for k1 at 295 K.
The effects of water vapour on CH2OO chemistry have also been investigated in studies of ozonolysis reactions through the competition with the reaction of CH2OO with SO2.7,8 Berndt et al.3 monitored the production of sulfuric acid, which is produced rapidly following the production of SO3via CH2OO + SO2,24–26 during ethene ozonolysis experiments conducted in a flow tube at 293 K over a range of water vapour concentrations. A quadratic relationship was observed between the rate coefficient describing the loss of CH2OO and the water monomer concentration, with a linear relationship demonstrated with the concentration of water dimers, (H2O)2, indicating that the dominant reaction of CH2OO was with water dimers (R2) rather than water monomers (R1). Berndt et al. reported a value of k2 = (1.07 ± 0.04) × 10−11 cm3 molecule−1 s−1. Later work by Berndt et al.27 investigated the kinetics of CH2OO reactions in the presence of water vapour using a free-jet flow system at 297 K by detecting H2SO4 formed following the reaction of CH2OO with SO2, and reported k1 = (3.2 ± 1.2) × 10−16 cm3 molecule−1 s−1. Newland et al.10 also investigated the impact of water vapour on CH2OO + SO2 by monitoring the consumption of SO2 in ethene ozonolysis experiments at the EUPHORE atmospheric simulation chamber, with results also indicating a more rapid reaction of CH2OO with water dimers than water monomers and giving k1 = (1.2 ± 0.4) × 10−15 cm3 molecule−1 s−1 and k2 = (5.2 ± 6.7) × 10−13 cm3 molecule−1 s−1 at 298 K using the current IUPAC recommendation of 3.7 × 10−11 cm3 molecule−1 s−1 for the rate coefficient for the reaction of CH2OO with SO2.
Direct measurements of CH2OO have also been made in the presence of excess water vapour using laser flash photolysis of CH2I2–O2–N2–H2O mixtures coupled with time-resolved broadband UV absorption spectroscopy.15,28 Results from several studies have now demonstrated a quadratic dependence of the pseudo-first-order rate coefficient describing the loss of CH2OO on the water vapour concentration4,15,28,29 thus also indicating that the reaction of CH2OO with water dimers dominates over reaction with water monomers. Lewis et al.4 reported a rate coefficient for reaction of CH2OO with water dimers of (4.0 ± 1.2) × 10−12 cm3 molecule−1 s−1 at 294 K, with no significant dependence on pressure in the range 50 to 400 Torr. Chao et al.28 reported a value for k2 of (6.5 ± 0.8) × 10−12 cm3 molecule−1 s−1 at 298 K that also showed no significant dependence on pressure between 100 and 500 Torr.
The temperature dependence of k2 was subsequently investigated by Smith et al.29 using UV absorption spectroscopy between 283 and 324 K, with results giving k2 = (7.4 ± 0.6) × 10−12 cm3 molecule−1 s−1 at 298 K, in agreement with the work of Chao et al.,28 and a negative temperature dependence.30 Further experiments have been performed using UV absorption spectroscopy by Wu et al.31 at temperatures between 290 and 346 K, which showed high precision in measurements of water vapour concentrations and CH2OO signal and led to the conclusion that observed kinetics of CH2OO removal in the presence of water vapour result from a combination of reactions involving one, two, or three water molecules. Experiments by Wu et al. were carried out at higher relative humidities than those employed in other studies, reaching close to 100% at each temperature investigated, and Wu et al. reported that the measurements at the highest relative humidities correspond to reaction with three water molecules, most likely involving CH2OO·H2O + (H2O)2 or CH2OO·(H2O)2 + H2O rather than a direct reaction of CH2OO with water trimers ((H2O)3), while experiments at low relative humidity provided information relating to the reaction with the water monomer. Wu et al. reported a positive temperature dependence for the reaction of CH2OO with the water monomer, and a negative temperature dependence for the reaction of CH2OO with water dimers that is in broad agreement with the behaviour observed by Smith et al.29 The reaction involving three water molecules also displayed a negative temperature dependence, with results indicating that this reaction could play an important role at high relative humidities at temperatures of 298 K and below.
There is a growing consensus that chemistry of CH2OO in the presence of water vapour is rapid, with a significant role for a reaction with water dimers, which, despite low water dimer concentrations (3.0 × 1014 molecule cm−3 for a relative humidity of 50% at 298 K) compared to water monomers in the atmosphere, is likely to dominate atmospheric losses of CH2OO. Although the study by Welz et al.18 did not observe any evidence for the reaction between CH2OO and water dimers, the water dimer concentrations at the low pressure (4 Torr) used by Welz et al. would have limited the impact of the reaction. The HCHO LIF experiments performed by Stone et al.5 did enable the use of higher water vapour concentrations, and thus significant water dimer concentrations. However, the impact of water vapour on production of HCHO may have been limited if HCHO is not a direct product of CH2OO reactions with water, and the reduction in HCHO signal which was attributed to quenching may have resulted from the production of other products. Product studies in ozonolysis reactions have reported the formation of HCHO, among other potential products,13,32 but more recent time-resolved product measurements, using laser flash photolysis of CH2I2–O2 in the presence of water vapour, have observed the production of hydroxymethyl hydroperoxide (HOCH2OOH, HMHP) by rotational spectroscopy33 and PIMS,15 with the PIMS study indicating HMHP as the dominant product of R1 and R2.15 Theory34–44 has also indicated that HMHP is a major product of R1 and R2, and supports the experimental results which suggest the dominant reaction is with water dimers. Subsequent chemistry of HMHP can lead to the production of formic acid (HCOOH), H2O2, and HCHO, which has been investigated by Nguyen et al.13 using measurements made in an atmospheric simulation chamber at 295 K and 1 atm at relative humidities between 4 and 76%. Measurements of HCHO, OH and HO2 were made in the chamber using LIF spectroscopy,45 while hydroperoxides (such as HMHP) and acids (such as HCOOH) were measured by chemical ionisation mass spectrometry (CIMS). At relative humidities below ∼40%, HMHP was observed to be the dominant product, followed by HCOOH and H2O2. However, at relative humidities above ∼40%, Nguyen et al. observed a significant decrease in the yield of HMHP, accompanied by an increase in the yield of HCOOH. Modelling of the observed yields for HMHP and HCOOH led to the conclusion that R1 leads to production of 73% HMHP, 21% HCOOH + H2O, and 6% HCHO + H2O2, while R2 leads to production of 54% HCOOH + H2O, 40% HMHP, and 6% HCHO + H2O2. The product distribution reported by Nguyen et al. forms the basis of the current mechanism adopted in the global atmospheric chemistry transport model (CTM) GEOS-Chem.
There is general agreement regarding the atmospheric significance of CH2OO reactions involving water, but there are discrepancies in product distributions and measured kinetics at room temperature, and the temperature dependence of the kinetics has only been investigated over a relatively narrow temperature range. In this work we report the results of experiments performed using laser flash photolysis of CH2I2–O2–N2–H2O mixtures coupled with time-resolved broadband UV absorption spectroscopy at temperatures in the range 262 to 353 K at 760 Torr. We also report atmospheric implications of the experimental results based on GEOS-Chem model simulations of CH2OO chemistry.
Experimental
The kinetics of CH2OO loss in the presence of water vapour have been studied as a function of temperature between 262 and 353 K at 760 Torr, using laser flash photolysis of CH2I2–O2–N2–H2O gas mixtures coupled with time-resolved broadband UV absorption spectroscopy. The experimental apparatus has been described in detail previously21,46 and so only a brief overview is given here.Gases (N2 (BOC, 99.998%) and O2 (BOC, 99.5%)) were mixed in a gas manifold at known concentrations using calibrated mass flow controllers (MFCs). Water vapour was added to the system by passing a known flow of N2 gas through a bubbler containing deionised water held in a water bath at 70 °C. The concentration of water vapour was measured at the exit of the reaction cell by a relative humidity (RH) probe (Michell Instruments PCMini52) that was calibrated against a dew point hygrometer (Buck Research Instruments, CR-4 chilled mirror hygrometer) (see ESI† for further details). The precursor CH2I2 (Alfa Aesar, 99%) was introduced into the gas mixture by flowing a fraction of the N2–O2–H2O flow over liquid CH2I2 contained in a bubbler before combining with the remaining N2–O2–H2O flow and passing the gas mixture into the reaction cell. The concentration of CH2I2 in the gas mixture could be controlled by a needle valve placed before the bubbler and was determined experimentally by measuring the UV intensity transmitted through the cell in experiments with and without CH2I2 present in the gas mixture flowing through the cell. Experiments were performed under pseudo-first-order conditions. Initial concentrations were: [H2O] = (0–5.5) × 1017 molecule cm−3, [CH2I2] = (3.8–6.4) × 1013 molecule cm−3, and [O2] = (1.2–2.7) × 1018 molecule cm−3.
The reaction cell was a 100 cm long jacketed glass tube with an inner diameter of 3 cm and fused silica windows at both ends. Experiments were carried out at temperatures between 262 and 353 K, with the temperature of the system controlled by circulating a thermofluid (HUBE6479 DW-THERM) from a thermoregulator (Huber Unistat 360) through the outer jacket of the cell. The temperature of the system was calibrated by flowing N2 through the reaction cell, under conditions identical to those used in kinetic experiments, and measuring the temperature using a K-type thermocouple at 5 cm increments along the length of the reaction cell.20 The total flow rate in the cell was 3700 sccm (standard cm3min−1), giving a residence time in the cell of 13.1 s, with relatively slow flows required in order to maximise saturation of the gas flow as it passed through the water bubbler. Experiments were performed at a total pressure of 760 Torr, which was controlled by throttling the exit of the cell to the pump and measured by a capacitance manometer (MKS instruments).
Chemistry was initiated using an excimer laser (KrF, Lambda-Physik CompEx 210) operating at a wavelength of 248 nm with a typical laser fluence of 15–25 mJ cm−2, giving initial CH2OO concentrations in the range (2.0–8.3) × 1011 molecule cm−3. The pulse repetition rate was set at 0.075 Hz to ensure there was enough time for a fresh gas mixture to be introduced to the reaction cell before the laser fired again.
UV light for the absorption measurements was provided by a laser-driven light source (LDLS, Energetiq EQ-99X) that provided ∼10 mW cm−2 of light at wavelengths between 200 and 800 nm. The light was collimated using an off-axis parabolic mirror (ThorLabs MPD129-F01 UV enhanced aluminium) and multi-passed nine times through the reaction cell by ten Al mirrors (Knight optical MCQ1200-C concave mirror UV enhanced, reflectivity >85% in the UV), each of 12 mm diameter, which were positioned outside the windows of the cell on a custom mirror mount.46 Each mirror in the multipass arrangement could be adjusted to align the probe beam such that there is maximum overlap with the 248 nm excimer beam, giving a total effective path length of l = (595 ± 53) cm (details regarding the determination of the effective path length are described in our previous work20).
In order to reduce the detection of scattered light from the photolysis laser, the probe beam exiting the cell was passed through a sharp cut-on filter (RazorEdge ultrasteep long-pass edge filter 248 nm), which effectively blocks light at wavelengths below 250 nm, and focussed onto a fibre optic. The fibre optic directed light through a 25 μm slit onto a spectrograph with a diffraction grating of 600 grooves mm−1 (Princeton Instruments, FER-GRT-060-500) which imaged the light onto a charge-coupled device (CCD) (Princeton Instruments, FER-SCI-1024BRX) detector with a spectral resolution (full width half maximum (FWHM)) of 1.1 nm. The CCD was cooled to −45 °C by a Peltier device to reduce the effects of dark current, and, prior to the start of experiments, a background spectrum was also measured to account for any remaining dark current on the device.
Light was imaged onto ten of rows on the CCD and transferred at specified time intervals either directly to the PC for analysis for measurements of stable gas mixtures, or onto a storage region on the CCD for time resolved measurements before transfer to the PC for analysis. The typical time resolution of kinetic experiments ranged between 70 μs and 165 μs (typically much shorter than the ms timescale of the kinetic decays), with the measurement and transfer to the storage region on the CCD leading to a Gaussian instrument response function (IRF) that has been described in previous work21 and was accounted for during data analysis. The intensity data for time-resolved experiments were typically averaged over 125 photolysis shots, with the time delay between the operation of the camera and the firing of the excimer laser controlled by a delay generator (SRS model DG 535).
The absorbance, Aλ,t, was determined for each wavelength λ and time point t from the measured intensities using the Beer–Lambert Law (eqn (1)):
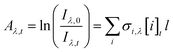 | (1) |
Fig. 1 shows a typical absorbance spectrum observed following photolysis, which contains contributions from the Criegee intermediate, CH2OO, the CH2I2 precursor (which exhibits a negative absorbance owing to depletion on photolysis), and iodine monoxide (IO) radicals which are produced in the system as a result of secondary chemistry.21,49 Reference spectra for CH2OO,21 CH2I2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 and IO48 were interpolated onto the experimental wavelength grid and least squares fit to the total observed absorbance using eqn (1) to determine the concentration of each species at each time point. Fig. 1 also shows a typical fit to the observed absorbance following photolysis.
47 and IO48 were interpolated onto the experimental wavelength grid and least squares fit to the total observed absorbance using eqn (1) to determine the concentration of each species at each time point. Fig. 1 also shows a typical fit to the observed absorbance following photolysis.
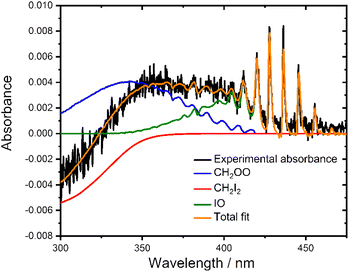 | ||
Fig. 1 Observed absorbance (black), total fit (orange) and individual contributions of CH2OO21 (blue), CH2I2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 (red) and IO48 (green) obtained by performing a least squares fit of reference cross-sections to the observed absorbance at t = 1 ms after photolysis at p = 760 Torr and T = 298 K with [CH2I2]0 = 4.1 × 1013 molecule cm−3. [CH2OO]t = 6.4 × 1011 molecule cm−3, Δ[CH2I2]t = −3.8 × 1012 molecule cm−3 and [IO]t = 7.3 × 1011 molecule cm−3. 47 (red) and IO48 (green) obtained by performing a least squares fit of reference cross-sections to the observed absorbance at t = 1 ms after photolysis at p = 760 Torr and T = 298 K with [CH2I2]0 = 4.1 × 1013 molecule cm−3. [CH2OO]t = 6.4 × 1011 molecule cm−3, Δ[CH2I2]t = −3.8 × 1012 molecule cm−3 and [IO]t = 7.3 × 1011 molecule cm−3. | ||
Results
Fig. 2 shows typical concentration–time profiles for CH2OO for a range of water vapour concentrations, demonstrating a more rapid loss of CH2OO as the water vapour concentration is increased. Experiments were performed under pseudo-first-order conditions, with water vapour concentrations in excess over CH2OO, and the temporal behaviour of CH2OO thus described by eqn (2).| [CH2OO]t = [CH2OO]0 exp(−k′t) | (2) |
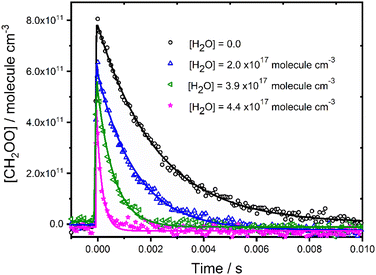 | ||
| Fig. 2 Concentration–time profiles for CH2OO in the presence and absence of water vapour at p = 760 Torr and T = 298 K. Solid lines represent unweighted fits to eqn (2) convoluted with the instrument response function. For [H2O] = 0, the fit gave [CH2OO]0 = 8.3 × 1011 molecule cm−3 and k′ = (313 ± 7) s−1; for [H2O] = 2.0 × 1017 molecule cm−3, the fit gave [CH2OO]0 = 6.6 × 1011 molecule cm−3 and k′ = (1247 ± 37) s−1; for [H2O] = 3.9 × 1017 molecule cm−3, the fit gave [CH2OO]0 = 5.8 × 1011 molecule cm−3 and k′ = (2669 ± 120) s−1; for [H2O] = 4.4 × 1017 molecule cm−3, the fit gave [CH2OO]0 = 5.7 × 1011 molecule cm−3 and k′ = (3722 ± 245) s−1. | ||
Fig. 3 shows that there is a non-linear dependence of the observed pseudo-first-order rate coefficients (k′), obtained by fitting with eqn (2), on the water vapour concentration. Similar behaviour has been observed in previous work, with the non-linear dependence attributed to reaction of CH2OO with water dimers (R2)3,4,10,15,28,31,50 or a reaction involving three water molecules (R3)31 dominating over the reaction of CH2OO with water monomers (R1). For a system involving reactions R1, R2, and R3, the observed pseudo-first-order rate coefficients k′ are given by eqn (3):
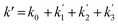 | (3) |
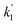 ,
, 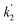 , and
, and 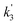 are the pseudo-first-order rate coefficients for R1, R2, and R3, respectively. We define k2 as the bimolecular rate coefficient for R2, which involves explicit calculation of the dimer concentration in rateR2 = k2[CH2OO][(H2O)2], and k2,eff as an effective rate coefficient given by the product of k2 and the equilibrium constant for dimer formation (KDeq), such that rateR2 = k2KDeq[CH2OO][H2O]2 = k2,eff[CH2OO][H2O]2. This removes the need for explicit calculation of the water dimer concentration and allows for simpler parameterisation of the kinetics for use in atmospheric models which relies only on the monomer concentration. For R3, we define k3,eff such that rateR3 = k3,eff[CH2OO][H2O]3 which removes need for knowledge of the exact reaction mechanism, i.e. whether the reaction proceeds via CH2OO·H2O + (H2O)2 or CH2OO·(H2O)2 + H2O. The quadratic and cubic relationships with water monomer concentrations for R2 and R3, respectively, lead to the potential for the observed non-linear dependence of k′ on the water monomer concentration.
are the pseudo-first-order rate coefficients for R1, R2, and R3, respectively. We define k2 as the bimolecular rate coefficient for R2, which involves explicit calculation of the dimer concentration in rateR2 = k2[CH2OO][(H2O)2], and k2,eff as an effective rate coefficient given by the product of k2 and the equilibrium constant for dimer formation (KDeq), such that rateR2 = k2KDeq[CH2OO][H2O]2 = k2,eff[CH2OO][H2O]2. This removes the need for explicit calculation of the water dimer concentration and allows for simpler parameterisation of the kinetics for use in atmospheric models which relies only on the monomer concentration. For R3, we define k3,eff such that rateR3 = k3,eff[CH2OO][H2O]3 which removes need for knowledge of the exact reaction mechanism, i.e. whether the reaction proceeds via CH2OO·H2O + (H2O)2 or CH2OO·(H2O)2 + H2O. The quadratic and cubic relationships with water monomer concentrations for R2 and R3, respectively, lead to the potential for the observed non-linear dependence of k′ on the water monomer concentration.
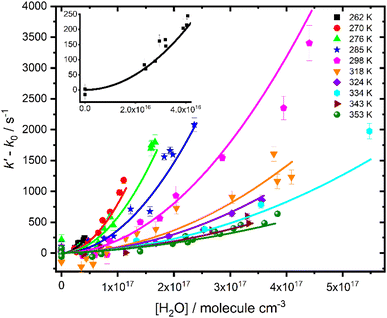 | ||
| Fig. 3 Pseudo-first-order rate coefficients as a function of water monomer concentration for experiments carried out at 760 Torr and temperatures between 262 and 353 K. The solid lines represent an unweighted global fit to eqn (3). The error bars represent the error in the fits to eqn (2). The inset shows data from experiments carried out at 262 K for clarity. Data for each temperature are shown separately in the ESI.† | ||
Fits to results for k′ were performed over all relative humidities and temperatures studied in this work, with k1, k2,eff and k3,eff described by Arrhenius expressions in which A and Ea were treated as global parameters for each reaction. However, the fits were insensitive to k3,eff, indicating that losses of CH2OO owing to reaction with three water molecules were not significant under the conditions employed in this work. Subsequent fits to the data were performed to determine k0, k1, and k2,eff, with k3,eff set to zero. Further details regarding analysis of the possible reaction involving three water molecules are given in the ESI.†
Fig. 3 shows the fit results for k′, which gave k1 = (3.2 ± 1.1) × 10−13 exp(−(2410 ± 270)/T) cm3 molecule−1 s−1 and k2,eff = (2.78 ± 0.28) × 10−38 exp((4010 ± 400)/T)cm6 molecule−2 s−1, where uncertainties represent a combination of the statistical error and the systematic errors resulting from uncertainties in relative humidity measurements and gas flow rates (see ESI†). Results for k2,eff correspond to k2 = (2.85 ± 0.40) × 10−15 exp((2417 ± 338)/T) cm3 molecule−1 s−1 using the temperature-dependent equilibrium constant for water dimer formation (KDeq), and associated uncertainties, reported by Ruscic et al.51 The results are consistent with suggestions made in previous work3,4,10,15,28,29 that the dominant loss of CH2OO in the presence of water vapour occurs via reaction with water dimers (R2). No significant differences were obtained in results for kinetics of R2 between global fits over all conditions and local fits to kinetics at each temperature (see ESI†). The reaction of CH2OO with water monomers (R1) was a minor contribution to the total loss of CH2OO for all conditions employed in this work, with results for k1 primarily defined by experiments performed at temperatures of 324 K and above. The kinetics of R1 were thus less well defined than those for R2, which represented the major contribution to the total CH2OO loss at high relative humidities at all temperatures, and results for k1 should be considered as estimates owing to the challenges associated with separating the impacts of k0 and k1.
Fig. 4 compares the results for k1 obtained in this study with measurements, upper limits based on experimental observations, and theoretical calculations reported in previous work, with experimental results at ∼298 K summarised in Table 1. Results for k1 obtained in this work are systematically lower than those measured previously, but are consistent with the prediction of a positive barrier to reaction,34–42 and are in agreement with calculated values of k1 reported by Long et al.43 at temperatures above 324 K, where results obtained in this work are more reliable. Previous direct experimental measurements of k1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15,27,31 at ∼298 K, range between (2.4 ± 1.6) × 10−16 cm3 molecule−1 s−1
15,27,31 at ∼298 K, range between (2.4 ± 1.6) × 10−16 cm3 molecule−1 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 and (4.2 ± 1.6) × 10−16 cm3 molecule−1 s−1,31 compared to the value of (9.8 ± 5.9) × 10−17 cm3 molecule−1 s−1 indicated in this work. Theory predicts values between 5.8 × 10−18 cm3 molecule−1 s−1
15 and (4.2 ± 1.6) × 10−16 cm3 molecule−1 s−1,31 compared to the value of (9.8 ± 5.9) × 10−17 cm3 molecule−1 s−1 indicated in this work. Theory predicts values between 5.8 × 10−18 cm3 molecule−1 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 and 7.08 × 10−15 cm3 molecule−1 s−1,44 with the most recent theoretical study giving k1 = 7.08 × 10−15 cm3 molecule−1 s−1.43 The temperature dependence for k1 indicated in this work is more significant than the temperature dependence reported by Wu et al.31
34 and 7.08 × 10−15 cm3 molecule−1 s−1,44 with the most recent theoretical study giving k1 = 7.08 × 10−15 cm3 molecule−1 s−1.43 The temperature dependence for k1 indicated in this work is more significant than the temperature dependence reported by Wu et al.31
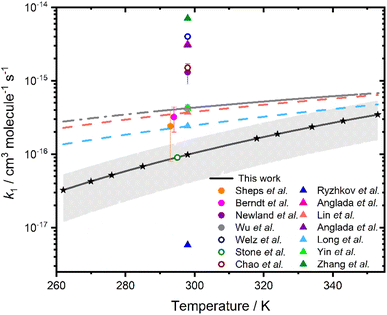 | ||
| Fig. 4 Rate coefficients k1 as a function of temperature. The global fit to results obtained in this work is shown by the solid black line, with uncertainties determined from a combination of the statistical error and the systematic errors resulting from uncertainties in gas flow rates and in the concentration of [H2O] shown by the shaded region. Stars represent the temperatures at which measurements were made. Results from previous studies are also included, where filled circles represent experimentally measured rate coefficients,10,15,27,31 hollow circles represent experimentally determined upper limits,5,18,28 and triangles represent rate coefficients calculated from theory.34–38,41,44 The solid grey line shows the data reported by Wu et al.,31 with the dashed grey line showing the extrapolation of the data reported by Wu et al. over the temperature range investigated in this work. The coral and light blue dashed lines are the parameterisations calculated by Lin et al.38 and Long et al.,41 respectively. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 and the k1 value in the first set of model updates was 2.8 × 10−16 cm3 molecule−1 s−1 at 298 K
13 and the k1 value in the first set of model updates was 2.8 × 10−16 cm3 molecule−1 s−1 at 298 K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30
30
| T/K | p/Torr | Experimental technique | k 1/10−17 cm3 molecule−1 s−1 | Reference |
|---|---|---|---|---|
| 298 | 4 | LFP/PIMS | ≤400 | Welz et al.18 |
| 295 | 200 | LFP/LIF | ≤9 | Stone et al.5 |
| 297 | 760 | Ozonolysis/CI-APi-TOF-MS | 32 ± 12 | Berndt et al.27 |
| 298 | 50–400 | LFP/UV abs | ≤150 | Chao et al.28 |
| 298 | 760 | RR. Ethene ozonolysis | 130 ± 40 | Newland et al.10 |
| 293 | 30–100 | LFP/UV abs | 24 ± 16 | Sheps et al.15 |
| 298 | 300 | LFP/UV abs | 42 ± 5 | Wu et al.31 |
| 298 | 760 | LFP/UV abs | 9.8 ± 5.9 | This work |
Whilst there are significant uncertainties in k1, the kinetics of R2 are well-defined from the fits shown in Fig. 3. Fig. 5 shows the temperature dependence of k2,eff, which is in good agreement with previous measurements3,28,50 over the temperature ranges in common, with this work extending the temperature range over which the kinetics have been investigated. At 298 K, this work indicates k2,eff = (1.96 ± 0.51) × 10−32 cm6 molecule−2 s−1, which corresponds to k2 = (9.5 ± 2.5) × 10−12 cm3 molecule−1 s−1 using the temperature-dependent equilibrium constant for water dimer formation reported by Ruscic et al.51Table 2 compares results for k2 and k2,eff obtained at 298 K in this work with those reported previously, with good agreement between the results reported here and the results of Berndt et al.,3 Smith et al.,29 Chao et al.28 and Sheps et al.15 The value for k2,eff reported by Wu et al.31 at 298 K is a factor of ∼1.8 lower than that reported here, but there is good agreement in the total pseudo-first-order rate coefficients as a function of water monomer concentration observed in this work and reported by Wu et al. (see ESI† for further details). Although Wu et al.31 reported an impact of a reaction between CH2OO and three water molecules, it was noted that there was little impact of the reaction involving three water molecules for water monomer concentrations below 4.8 × 1017 molecule cm−3 at 298 K, which is higher than the highest water concentrations used in this work at 298 K. The differences in kinetics for R2 between the results of Wu et al. and other studies, including this work, are impacted by differences in kinetics for R1 as well as contributions from R3, making direct comparison of rate coefficients for individual reactions difficult. Rate coefficients reported by Newland et al.10 for R2 at 298 K are notably lower than those reported elsewhere, but these experiments were carried out over a relatively narrow range of relative humidities (1.5 to 20%), leading to low water dimer concentrations and relatively limited impact of the dimer reaction. Lewis et al.4 also reported lower values than those obtained in this work and in other studies using flash photolysis with UV absorption,15,28,29 potentially resulting from overestimation of the water vapour, and thus water dimer, concentrations, which were based on flow rates and vapour pressure and assumed 100% saturation of the gas flow with water vapour. Results reported here, and in other studies using flash photolysis with UV absorption,28,29,31 measured the relative humidity of the gas flow, providing greater certainty in the water vapour and dimer concentrations.
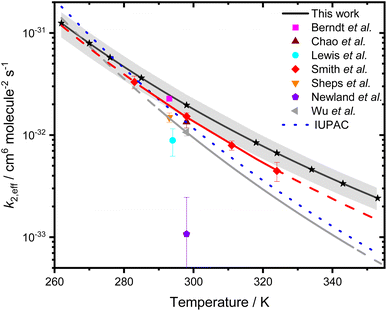 | ||
| Fig. 5 k 2,eff as a function of temperature. The global fit to results obtained in this work is shown by the solid black line, with uncertainties determined from a combination of the statistical error and the systematic errors resulting from uncertainties in gas flow rates and in the concentration of [H2O] shown by the shaded region. Stars represent the temperatures at which measurements were made. The solid grey line shows the data reported by Wu et al.,31 with the dashed grey line showing the extrapolation of the data reported by Wu et al. over the temperature range investigated in this work. The red solid line represents a fit to the data reported by Smith et al.,50 with the dashed red line showing the extrapolation of the data reported by Smith et al. over the temperature range investigated in this work. The blue dotted line represents the current IUPAC recommendation,30 which is based on the data reported by Smith et al. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 and the k2 value in the first set of model updates was 6.4 × 10−12 cm3 molecule−1 s−1 at 298 K
13 and the k2 value in the first set of model updates was 6.4 × 10−12 cm3 molecule−1 s−1 at 298 K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30
30
| T/K | p/Torr | Experimental technique | k 2/10−12 cm3 molecule−1 s−1 | k 2,eff/10−32 cm6 molecule−2 s−1 | Reference |
|---|---|---|---|---|---|
| 293 | 760 | IfT-LFT (H2SO4) measurements | 10.7 ± 0.40 | 2.28 ± 0.09 | Berndt et al.3 |
| 298 | 100–500 | LFP/UV abs | 6.5 ± 0.8 | 1.34 ± 0.17 | Chao et al.28 |
| 294 | 50–400 | LFP/UV abs | 4.0 ± 1.2 | 0.89 ± 0.27 | Lewis et al.4 |
| 298 | 200–600 | LFP/UV abs | 7.4 ± 0.6 | 1.53 ± 0.12 | Smith et al.29 |
| 293 | 30–100 | LFP/UV abs | 6.6 ± 0.7 | 1.49 ± 0.16 | Sheps et al.15 |
| 298 | 760 | RR. Ethene ozonolysis | 0.52 ± 0.67 | 0.11 ± 0.14 | Newland et al.10 |
| 298 | 300 | LFP/UV abs | 5.17 ± 0.40 | 1.07 ± 0.08 | Wu et al.31 |
| 298 | 760 | LFP/UV abs | 9.52 ± 2.49 | 1.96 ± 0.51 | This work |
The temperature-dependent behaviour observed for k2,eff is in agreement with previous experimental29,31 and theoretical34,35 work. Rate coefficients obtained in this work are in agreement with those reported by Smith et al. and Wu et al. over the common temperature ranges, but there are some discrepancies between the measurements made at the highest temperature employed in this work, and extrapolation of the results reported by Smith et al. and Wu et al.,31 as shown in Fig. 5. Observations of a negative temperature dependence for the kinetics of R2, and of the dominance of R2 over R1, are consistent with theoretical studies of R1 and R2.34,35,37,38 Calculations of the potential energy surfaces for R1 and R2, summarised in Table 3 and Fig. 6,34–43 indicate that both reactions proceed via the formation of pre-reaction complexes which then undergo rearrangement to form HMHP as the dominant product of both reactions, although experimental work has indicated that there may be other reaction channels or rapid subsequent chemistry of the HMHP product leading to the production of species including HCOOH, HCHO and H2O2. For R1, rearrangement of the pre-reaction complex to HMHP involves a transition state which is higher in energy than the initial reactants (i.e. there is an overall positive barrier to reaction). In contrast, the pre-reaction complex for R2 is more stable than that for R1 by a factor of ∼2 (Table 3 and Fig. 6), and the subsequent transition state to product formation is lower in energy than the initial reactants. The difference in barrier heights leads to the dominance of R2 over R1, and the submerged barrier for R2 leads to the observed negative temperature dependence.
| Method | PRC R1/kJ mol−1 | TS R1/kJ mol−1 | PRC R2/kJ mol−1 | TS R2/kJ mol−1 | k 1/cm3 molecule−1 s−1 | k 2/cm3 molecule−1 s−1 | Ref. |
|---|---|---|---|---|---|---|---|
| a Level of theory used to optimise geometries and energies for reactant, PRCs, and products. b Level of theory used to optimise geometries and energies for the transition states. | |||||||
| CCSD(T)/6-311G(d,p) | −30.1 | 9.6 | — | — | — | — | 39 |
| CCSD(T)/6-311+G(2d,2p) | −32.6 | 7.9 | — | — | — | — | 40 |
| CCSD(T)/6-311+G(2d,2p) | −30.9 | 14.2 | −65.7 | −36.8 | 5.8 × 10−18 | 1.1 × 10−12 | 34 |
| CTST | |||||||
| CCSD(T)/aug-cc-pVTZ | −26.0 | 8.5 | — | — | 3.12 × 10−15 | — | 36 |
| C/VTST | |||||||
| W3X-L//CCSD(T)-F12a/TZ-F12 | −26.2 | 14.7 | — | — | 2.41 × 10−16 | — | 41 |
| MP-CVT/SCT | |||||||
| CCSD(T)/aug-cc-PVTZ | −25.7 | 6.3 | −44.8 | −35.5 | 3.05 × 10−15 | 1.67 × 10−10 | 35 |
| VTST | |||||||
| CCSD(T)//M06-2X/6-311+G(2d,2p) | −28.5 | 11.2 | −63.7 | −45.3 | — | 6.71 × 10−12 | 42 |
| CTST | |||||||
| QCISD(T)/CBS//6-311+G(2d,2p) | −27.3 | 11.8 | −46.2 | −27.3 | 3.7 × 10−16 | 5.4 × 10−12 | 38 |
| VPT2 | |||||||
| B3LYP/6-311+G(2d,2p) | −26.4 | 12.8 | −42.4 | −24.6 | 4.26 × 10−16 | 2.91 × 10−12 | 37 |
| VPT2 | |||||||
| CCSD(T)/6-311+G(3df,2dp) | −25.9 | 14.2 | −32.0 | −8.4 | 7.08 × 10−15 | 1.15 × 10−12 | 44 |
| CTST | |||||||
| W3X-L//CCSD(T)- F12a/cc-pVDZ-F12a | — | — | −45.5 | −22.9 | — | 6.73 × 10−12 | 43 |
| W3X-L//CCSD(T)-F12a/cc-pVTZ-F12b | |||||||
| CUS | |||||||
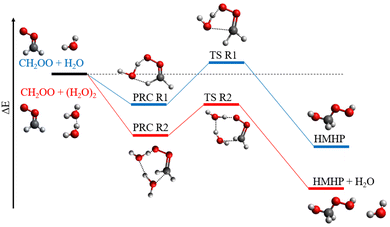 | ||
| Fig. 6 Schematic potential energy surface for the reactions of CH2OO with H2O (blue) and (H2O)2 (red). PRC = pre-reaction complex, TS = transition state, HMHP = hydroxymethyl hydroperoxide. | ||
Atmospheric implications
The reaction of CH2OO with water dimers is expected to dominate the atmospheric chemistry of CH2OO.3,15,28,29 Model simulations were performed with the global 3D atmospheric chemistry transport model (CTM) GEOS-Chem (version 14.2.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52) to assess the impact of this work on our understanding of CH2OO in the atmosphere. The model was run for 2 years (2018–2019) driven by MERRA-2 meteorology53 with a 4.0° × 4.5° spatial resolution and 72 vertical levels. The first year was considered as model spin up and discarded. The model contains detailed VOC oxidation chemistry54 including Criegee intermediate reactions.14 Biogenic emissions of VOCs were taken from MEGANv2.1,55 biomass burning emissions from GFED4s,56 while anthropogenic emissions use the Community Emissions Data System (CEDS).57
52) to assess the impact of this work on our understanding of CH2OO in the atmosphere. The model was run for 2 years (2018–2019) driven by MERRA-2 meteorology53 with a 4.0° × 4.5° spatial resolution and 72 vertical levels. The first year was considered as model spin up and discarded. The model contains detailed VOC oxidation chemistry54 including Criegee intermediate reactions.14 Biogenic emissions of VOCs were taken from MEGANv2.1,55 biomass burning emissions from GFED4s,56 while anthropogenic emissions use the Community Emissions Data System (CEDS).57
The Criegee intermediate chemistry in the base model was described in 2015![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 and subsequently updated by Bates et al.54 in 2021 to the current CH2OO chemistry in the base model shown in Table 4. Model runs in this work have been performed with the base chemistry and then with two sets of updates. The first update represents the state of current understanding, and involves updates to the rate coefficients for the reactions of CH2OO with H2O, (H2O)2, and NO2 to the values currently recommended by IUPAC,30 and to the rate coefficients of reactions with O3 and SO2 to the values reported in our previous work.20,21 In the first update we have also removed the reactions of CH2OO with NO or CO as the kinetics of these reactions are highly uncertain, and the reactions are not expected to represent significant losses for CH2OO. The second update to the model changes the rate coefficient for reactions R1 and R2 from those currently recommended by IUPAC to those determined in the experiments described in this work. The complete set of CH2OO chemistry used in the model is described in Table 4. Comparisons between the temperature-dependent rate coefficients for CH2OO + H2O and CH2OO + (H2O)2 in the three model simulations are given in the ESI (Fig. S8†). Kinetics for the reaction of CH2OO with water vapour in the base GEOS-Chem mechanism were estimated from the relative rates of CH2OO reactions with SO2 and water monomers, with a temperature dependence estimated from the temperature dependence of the equilibrium between water monomers and dimers, as described in previous work.13,54,61 Rate coefficients for R2 measured in this work are typically two orders of magnitude greater than those estimated in the simulations for the base case, leading to significant changes in the behaviour of CH2OO in the model.
58 and subsequently updated by Bates et al.54 in 2021 to the current CH2OO chemistry in the base model shown in Table 4. Model runs in this work have been performed with the base chemistry and then with two sets of updates. The first update represents the state of current understanding, and involves updates to the rate coefficients for the reactions of CH2OO with H2O, (H2O)2, and NO2 to the values currently recommended by IUPAC,30 and to the rate coefficients of reactions with O3 and SO2 to the values reported in our previous work.20,21 In the first update we have also removed the reactions of CH2OO with NO or CO as the kinetics of these reactions are highly uncertain, and the reactions are not expected to represent significant losses for CH2OO. The second update to the model changes the rate coefficient for reactions R1 and R2 from those currently recommended by IUPAC to those determined in the experiments described in this work. The complete set of CH2OO chemistry used in the model is described in Table 4. Comparisons between the temperature-dependent rate coefficients for CH2OO + H2O and CH2OO + (H2O)2 in the three model simulations are given in the ESI (Fig. S8†). Kinetics for the reaction of CH2OO with water vapour in the base GEOS-Chem mechanism were estimated from the relative rates of CH2OO reactions with SO2 and water monomers, with a temperature dependence estimated from the temperature dependence of the equilibrium between water monomers and dimers, as described in previous work.13,54,61 Rate coefficients for R2 measured in this work are typically two orders of magnitude greater than those estimated in the simulations for the base case, leading to significant changes in the behaviour of CH2OO in the model.
| Reaction | Products | Base model | First set of updates | Second set of updates | |||
|---|---|---|---|---|---|---|---|
| Rate coefficient/cm3 molecule−1 s−1 (second-order reactions) or cm6 molecule−2 s−1 (third-order reactions) | Loss/% | Rate coefficient/cm3 molecule−1 s−1 (second-order reactions) or cm6 molecule−2 s−1 (third-order reactions) | Loss/% | Rate coefficient/cm3 molecule−1 s−1 (second-order reactions) or cm6 molecule−2 s−1 (third-order reactions) | Loss/% | ||
| CH2OO + H2O | 0.73 HMHP + 0.21 HCOOH + 0.21 H2O + 0.06 HCHO + 0.06 H2O2 | 1.7 × 10−15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 13 |
64.74 | 2.8 × 10−16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30 |
3.77 | 3.2 × 10−13 exp(–2410/T) | 0.82 |
| CH2OO + H2O + H2O | 0.40 HMHP + 0.54 HCOOH + 0.54 H2O + 0.06 HCHO + 0.06 H2O2 | 2.88 × 10−35 × exp(1319/T)13 | 32.45 | 7.35 × 10−18 × exp(4076/T)30 | 96.03 | 2.78 × 10−38 exp(4010/T) | 98.32 |
| CH2OO + O3 | HCHO + 2O2 | 1.4 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 59 59 |
0.03 | 3.60 × 10−13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 60 |
0.01 | 3.60 × 10−13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 21 |
0.03 |
| CH2OO + SO2 | HCHO + SO3 | 3.70 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 59 59 |
2.79 | 3.72 × 10−11 × (T/298)−2.05![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
0.19 | 3.72 × 10−11 × (T/298)−2.05![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
0.83 |
| CH2OO + NO2 | HCHO + NO3 | 1.00 × 10−15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 14 |
<0.01 | 3.00 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30 |
<0.01 | 3.00 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30 |
<0.01 |
| CH2OO + NO | HCHO + NO2 | 1.00 × 10−14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 14 |
<0.01 | — | — | — | — |
| CH2OO + CO | HCHO + CO2 | 1.20 × 10−15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 14 |
0.01 | — | — | — | — |
Fig. 7 shows the impact of the changes made in the first update, compared to the base model run, on annual mean surface layer concentrations for CH2OO and several key atmospheric species. The model shows significant decreases in CH2OO in most locations, with mean surface layer concentrations decreased by 64.2% compared to the base model run owing to the faster kinetics for CH2OO + (H2O)2 used in the updated model. However, there are some regional differences to the global mean trend, with hot and dry regions over areas including Australia and parts of Africa and the Middle East displaying significant increases in the concentration of CH2OO. In these regions, the impacts of updates to k2,eff are limited as a result of low water dimer concentrations owing to low water monomer concentrations and the temperature dependence of the equilibrium between H2O and (H2O)2, with the observed impact dominated by the decreased values for k1 used in the updated model.
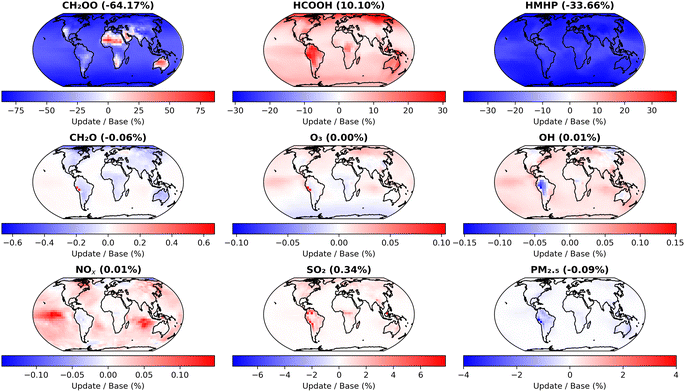 | ||
| Fig. 7 Impacts of changes made in the first set of GEOS-Chem updates (Table 4, ‘First set of updates’), compared to the base model run (Table 4, ‘Base model’), on annual mean surface layer mixing ratios for CH2OO and several key atmospheric species. The first set of model updates incorporate current IUPAC recommendations for k1 and k2,eff, as well as updates to rate coefficients for reactions of CH2OO with O3, SO2, and NO2. | ||
The first set of model updates also affect concentrations of products formed in CH2OO reactions with H2O and (H2O)2, which are based on the work of Nguyen et al.13 and thus consider the yields of products on longer timescales than the initial production of HMHP from the elementary reactions R1 and R2. In the first set of model updates, the annual mean surface layer concentration for HCOOH is increased by 10.1%, while that for HMHP is decreased by 33.7% owing to an increase in importance of the dimer reaction, which favours production of HCOOH over HMHP. Concentrations of other key atmospheric species display smaller changes, with SO2 showing regional surface layer increases of over 6% but an overall annual mean surface layer change of 0.3%, and PM2.5 (particulate matter of less than 2.5 μm diameter) showing decreases of up to 4% regionally but with a decrease in the overall annual mean surface layer of 0.1%.
The impacts of the second set of model updates, which make use of the results obtained in this work, are shown in Fig. 8. Further decreases in CH2OO concentrations are observed, with a reduction in the annual mean surface layer concentration of 3.7% compared to that obtained in the model run using the first set of updates, with little regional variation, and 61.8% compared to the base model run. However, changes to other species are more limited, with an increase in HCOOH of only 0.4% and a decrease in HMHP of only 3.0% compared to the overall annual mean surface concentrations obtained in the model run using the first set of updates. Species such as SO2 and PM2.5 display little difference compared to the results obtained with the first set of model updates.
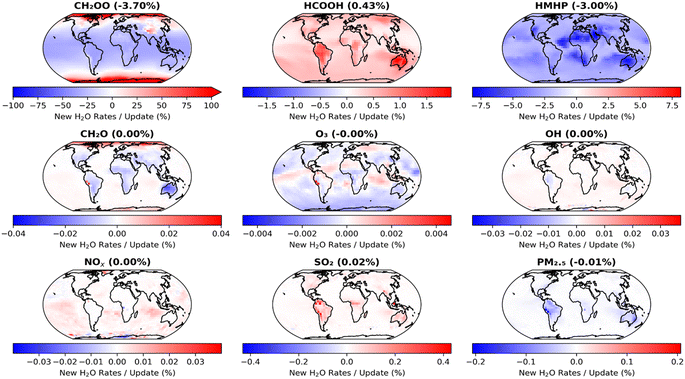 | ||
| Fig. 8 Impacts of changes made in the second set of GEOS-Chem updates (Table 4, ‘Second set of updates’), compared to the results obtained with the first set of updates (Table 4, ‘First set of updates’), on annual mean surface layer mixing ratios for CH2OO and several key atmospheric species. The second set of model updates make use of the results obtained in this work for k1 and k2,eff. | ||
Fig. 9 shows annual mean surface layer mixing ratios of CH2OO obtained for the model run updated with results obtained in this work. The annual surface layer mixing ratio of CH2OO peaks at 1.5 × 10−2 ppq, which is equivalent to a number density of 3.7 × 102 molecule cm−3 at 298 K and 760 Torr, with an annual mean of 3.5 × 10−4 ppq. Mixing ratios of CH2OO are highest over landmasses where the emissions of unsaturated VOCs into the atmosphere are highest, and lowest over remote oceanic regions. Vertically, the highest mixing ratios (1.9 × 10−2 ppq) are seen in the tropical upper troposphere, where convective lifting brings unsaturated VOCs into contact with high O3 concentrations in a region with low concentrations of water vapour. The mean lifetime of CH2OO in the updated model is 0.45 s, reaching a minimum of 9.8 × 10−4 s in the marine surface layer and a maximum of >2 s in the upper troposphere owing to low water concentrations. In the updated model, the tropospheric annual mean global loss of CH2OO is dominated by the reaction with water dimers, which represents 98.3% of the total CH2OO loss, with a further 0.8% of the total loss occurring through reaction with water monomers. Reactions of CH2OO with species other than water account for less than 1% of the total loss, other than in a few regions, primarily northern Eurasia, where this reaches up to 4%. The updated simulations restrict the importance of non-water reactions significantly, although there may be more localised impacts which are not realised in this work owing to the spatial resolution of the simulations.
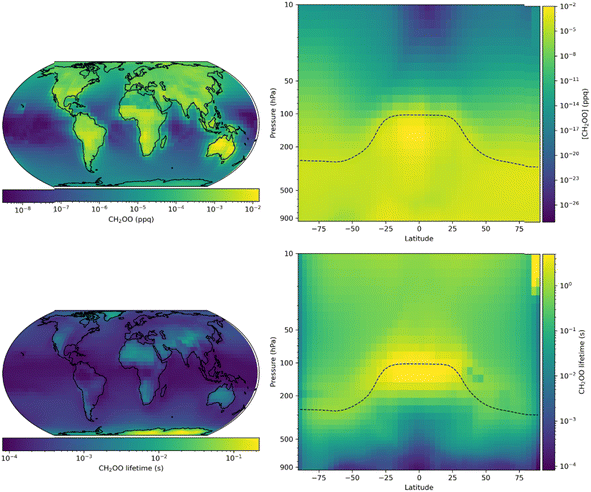 | ||
| Fig. 9 Annual mean CH2OO surface layer mixing ratios and zonal distributions (top panel) and lifetime (bottom panel) for GEOS-Chem simulations using the second set of model updates, which make used of results obtained in this work for k1 and k2,eff (Table 4, ‘Second set of updates’). | ||
Conclusions
The kinetics of the reaction of the simplest Criegee intermediate, CH2OO, with water vapour have been investigated using laser flash photolysis coupled with time-resolved broadband UV absorption spectroscopy at temperatures between 262 and 353 K at a total pressure of 760 Torr. The reaction of CH2OO with water monomers (R1) represents a minor contribution to the total loss of CH2OO under the conditions employed in this work, with an estimated value for k1 of (9.8 ± 5.9) × 10−17 cm3 molecule−1 s−1 at 298 K and a temperature dependence described by k1 = (3.2 ± 1.1) × 10−13 exp(−(2410 ± 270)/T) cm3 molecule−1 s−1. The results show that the reaction with water dimers (R2) dominates the loss of CH2OO, with k2 = (9.5 ± 2.5) × 10−12 cm3 molecule−1 s−1 at 298 K, with a temperature dependence described by k2 = (2.85 ± 0.40) × 10−15 exp((2420 ± 340)/T) cm3 molecule−1 s−1, where use of k2 requires calculation of the water dimer concentration to determine the rate of reaction. The kinetics of R2 can also be expressed in terms of an effective rate coefficient, k2,eff, which is given by the product k2KDeq, allowing calculation of the rate of reaction in terms of the square of the water monomer concentration rather than the water dimer concentration, giving k2,eff = (1.96 ± 0.51) × 10−32 cm6 molecule−2 s−1 at 298 K and a temperature dependence described by k2,eff = (2.78 ± 0.28) × 10−38 exp((4010 ± 400)/T)cm6 molecule−2 s−1. No significant impact of a reaction between CH2OO and three water molecules was observed in this work. The kinetic results are consistent with theoretical studies which predict the existence of a positive barrier to reaction for R1 and a submerged barrier for R2. Simulations performed using the global CTM GEOS-Chem updated with the experimental results obtained in this work indicate that the reaction of CH2OO with water dimers is expected to dominate the atmospheric chemistry of CH2OO, limiting the impacts of reactions of CH2OO with other species. Uncertainties in the product yields of CH2OO reactions with water monomers and dimers remain, which limit our understanding of the atmospheric impacts of CH2OO chemistry.Data availability
Relevant data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Natural Environment Research Council (NERC) for funding (grant reference NE/P012876/1).References
- D. Johnson and G. Marston, The gas-phase ozonolysis of unsaturated volatile organic compounds in the troposphere, Chem. Soc. Rev., 2008, 37(4), 699–716 RSC.
- D. Stone, K. Au, S. Sime, D. J. Medeiros, M. Blitz, P. W. Seakins, Z. Decker and L. Sheps, Unimolecular decomposition kinetics of the stabilised Criegee intermediates CH2OO and CD2OO, Phys. Chem. Chem. Phys., 2018, 20(38), 24940–24954 RSC.
- T. Berndt, J. Voigtländer, F. Stratmann, H. Junninen, R. L. Mauldin III, M. Sipilä, M. Kulmala and H. Herrmann, Competing atmospheric reactions of CH2OO with SO2 and water vapour, Phys. Chem. Chem. Phys., 2014, 16(36), 19130–19136 RSC.
- T. R. Lewis, M. A. Blitz, D. E. Heard and P. W. Seakins, Direct evidence for a substantive reaction between the Criegee intermediate, CH2OO, and the water vapour dimer, Phys. Chem. Chem. Phys., 2015, 17(7), 4859–4863 RSC.
- D. Stone, M. Blitz, L. Daubney, N. U. M. Howes and P. Seakins, Kinetics of CH2OO reactions with SO2, NO2, NO, H2O and CH3CHO as a function of pressure, Phys. Chem. Chem. Phys., 2014, 16(3), 1139–1149 RSC.
- N. U. M. Howes, Z. S. Mir, M. A. Blitz, S. Hardman, T. R. Lewis, D. Stone and P. W. Seakins, Kinetic studies of C1 and C2 Criegee intermediates with SO2 using laser flash photolysis coupled with photoionization mass spectrometry and time resolved UV absorption spectroscopy, Phys. Chem. Chem. Phys., 2018, 20(34), 22218–22227 RSC.
- M. Suto, E. R. Manzanares and L. C. Lee, Detection of sulfuric acid aerosols by ultraviolet scattering, Environ. Sci. Technol., 1985, 19(9), 815–820 CrossRef CAS.
- K. H. Becker, J. Bechara and K. J. Brockmann, Studies on the formation of H2O2 in the ozonolysis of alkenes, Atmos. Environ., Part A, 1993, 27(1), 57–61 CrossRef.
- K. E. Leather, M. R. McGillen, M. C. Cooke, S. R. Utembe, A. T. Archibald, M. E. Jenkin, R. G. Derwent, D. E. Shallcross and C. J. Percival, Acid-yield measurements of the gas-phase ozonolysis of ethene as a function of humidity using Chemical Ionisation Mass Spectrometry (CIMS), Atmos. Chem. Phys., 2012, 12(1), 469–479 CrossRef CAS.
- M. J. Newland, A. R. Rickard, M. S. Alam, L. Vereecken, A. Muñoz, M. Ródenas and W. J. Bloss, Kinetics of stabilised Criegee intermediates derived from alkene ozonolysis: reactions with SO2, H2O and decomposition under boundary layer conditions, Phys. Chem. Chem. Phys., 2015, 17(6), 4076–4088 RSC.
- A. S. Hasson, G. Orzechowska and S. E. Paulson, Production of stabilized Criegee intermediates and peroxides in the gas phase ozonolysis of alkenes: 1. Ethene, trans-2-butene, and 2,3-dimethyl-2-butene, J. Geophys. Res.: Atmos., 2001, 106(D24), 34131–34142 CrossRef CAS.
- G. E. Orzechowska and S. E. Paulson, Photochemical Sources of Organic Acids. 1. Reaction of Ozone with Isoprene, Propene, and 2-Butenes under Dry and Humid Conditions Using SPME, J. Phys. Chem. A, 2005, 109(24), 5358–5365 CrossRef CAS.
- T. B. Nguyen, G. S. Tyndall, J. D. Crounse, A. P. Teng, K. H. Bates, R. H. Schwantes, M. M. Coggon, L. Zhang, P. Feiner, D. O. Milller, K. M. Skog, J. C. Rivera-Rios, M. Dorris, K. F. Olson, A. Koss, R. J. Wild, S. S. Brown, A. H. Goldstein, J. A. de Gouw, W. H. Brune, F. N. Keutsch, J. H. Seinfeld and P. O. Wennberg, Atmospheric fates of Criegee intermediates in the ozonolysis of isoprene, Phys. Chem. Chem. Phys., 2016, 18(15), 10241–10254 RSC.
- D. B. Millet, M. Baasandorj, D. K. Farmer, J. A. Thornton, K. Baumann, P. Brophy, S. Chaliyakunnel, J. A. de Gouw, M. Graus, L. Hu, A. Koss, B. H. Lee, F. D. Lopez-Hilfiker, J. A. Neuman, F. Paulot, J. Peischl, I. B. Pollack, T. B. Ryerson, C. Warneke, B. J. Williams and J. Xu, A large and ubiquitous source of atmospheric formic acid, Atmos. Chem. Phys., 2015, 15(11), 6283–6304 CrossRef CAS.
- L. Sheps, B. Rotavera, A. J. Eskola, D. L. Osborn, C. A. Taatjes, K. Au, D. E. Shallcross, M. A. H. Khan and C. J. Percival, The reaction of Criegee intermediate CH2OO with water dimer: primary products and atmospheric impact, Phys. Chem. Chem. Phys., 2017, 19(33), 21970–21979 RSC.
- C. A. Taatjes, O. Welz, A. J. Eskola, J. D. Savee, A. M. Scheer, D. E. Shallcross, B. Rotavera, E. P. F. Lee, J. M. Dyke, D. K. W. Mok, D. L. Osborn and C. J. Percival, Direct Measurements of Conformer-Dependent Reactivity of the Criegee Intermediate CH3CHOO, Science, 2013, 340(6129), 177 CrossRef CAS.
- H.-L. Huang, W. Chao and J. J.-M. Lin, Kinetics of a Criegee intermediate that would survive high humidity and may oxidize atmospheric SO2, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(35), 10857–10862 CrossRef CAS.
- O. Welz, J. D. Savee, D. L. Osborn, S. S. Vasu, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Direct Kinetic Measurements of Criegee Intermediate (CH2OO) Formed by Reaction of CH2I with O2, Science, 2012, 335(6065), 204 CrossRef CAS.
- J. Peltola, P. Seal, A. Inkila and A. J. Eskola, Time-resolved, broadband UV-absorption spectrometry measurements of Criegee intermediate kinetics using a new photolytic precursor: unimolecular decomposition of CH2OO and its reaction with formic acid, Phys. Chem. Chem. Phys., 2020, 22, 11797–11808 RSC.
- L. Onel, R. Lade, J. Mortiboy, M. A. Blitz, P. W. Seakins, D. E. Heard and D. Stone, Kinetics of the gas phase reaction of the Criegee intermediate CH2OO with SO2 as a function of temperature, Phys. Chem. Chem. Phys., 2021, 23(35), 19415–19423 RSC.
- Z. S. Mir, T. R. Lewis, L. Onel, M. A. Blitz, P. W. Seakins and D. Stone, CH2OO Criegee intermediate UV absorption cross-sections and kinetics of CH2OO + CH2OO and CH2OO + I as a function of pressure, Phys. Chem. Chem. Phys., 2020, 22(17), 9448–9459 RSC.
- B. Ouyang, M. W. McLeod, R. L. Jones and W. J. Bloss, NO3 radical production from the reaction between the Criegee intermediate CH2OO and NO2, Phys. Chem. Chem. Phys., 2013, 15(40), 17070–17075 RSC.
- R. L. Caravan, M. A. H. Khan, B. Rotavera, E. Papajak, I. O. Antonov, M.-W. Chen, K. Au, W. Chao, D. L. Osborn, J. J.-M. Lin, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Products of Criegee intermediate reactions with NO2: experimental measurements and tropospheric implications, Faraday Discuss., 2017, 200, 313–330 RSC.
- L. Vereecken, H. Harder and A. Novelli, The reaction of Criegee intermediates with NO, RO2, and SO2, and their fate in the atmosphere, Phys. Chem. Chem. Phys., 2012, 14(42), 14682–14695 RSC.
- K. T. Kuwata, E. J. Guinn, M. R. Hermes, J. A. Fernandez, J. M. Mathison and K. Huang, A Computational Re-examination of the Criegee Intermediate–Sulfur Dioxide Reaction, J. Phys. Chem. A, 2015, 119(41), 10316–10335 CrossRef CAS.
- Y.-Y. Wang, M. R. Dash, C.-Y. Chung and Y.-P. Lee, Detection of transient infrared absorption of SO3 and 1,3,2-dioxathietane-2,2-dioxide [cyc-(CH2)O(SO2)O] in the reaction CH2OO+SO2, J. Chem. Phys., 2018, 148(6), 064301 CrossRef.
- T. Berndt, R. Kaethner, J. Voigtländer, F. Stratmann, M. Pfeifle, P. Reichle, M. Sipilä, M. Kulmala and M. Olzmann, Kinetics of the unimolecular reaction of CH2OO and the bimolecular reactions with the water monomer, acetaldehyde and acetone under atmospheric conditions, Phys. Chem. Chem. Phys., 2015, 17(30), 19862–19873 RSC.
- W. Chao, J.-T. Hsieh, C.-H. Chang and J. J.-M. Lin, Direct kinetic measurement of the reaction of the simplest Criegee intermediate with water vapor, Science, 2015, 347(6223), 751 CrossRef CAS.
- M. C. Smith, C.-H. Chang, W. Chao, L.-C. Lin, K. Takahashi, K. A. Boering and J. J.-M. Lin, Strong Negative Temperature Dependence of the Simplest Criegee Intermediate CH2OO Reaction with Water Dimer, J. Phys. Chem. Lett., 2015, 6(14), 2708–2713 CrossRef CAS.
- R. A. Cox, M. Ammann, J. N. Crowley, H. Herrmann, M. E. Jenkin, V. F. McNeill, A. Mellouki, J. Troe and T. J. Wallington, Evaluated kinetic and photochemical data for atmospheric chemistry: Volume VII – Criegee intermediates, Atmos. Chem. Phys., 2020, 20(21), 13497–13519 CrossRef CAS.
- Y.-J. Wu, K. Takahashi and J. J.-M. Lin, Kinetics of the Simplest Criegee Intermediate Reaction with Water Vapor: Revisit and Isotope Effect, J. Phys. Chem. A, 2023, 127(39), 8059–8072 CrossRef CAS.
- K. H. Becker, K. J. Brockmann and J. Bechara, Production of hydrogen peroxide in forest air by reaction of ozone with terpenes, Nature, 1990, 346(6281), 256–258 CrossRef CAS.
- M. Nakajima and Y. Endo, Observation of hydroxymethyl hydroperoxide in a reaction system containing CH2OO and water vapor through pure rotational spectroscopy, J. Chem. Phys., 2015, 143(16), 164307 CrossRef.
- A. B. Ryzhkov and P. A. Ariya, A theoretical study of the reactions of parent and substituted Criegee intermediates with water and the water dimer, Phys. Chem. Chem. Phys., 2004, 6(21), 5042–5050 RSC.
- J. M. Anglada and A. Solé, Impact of the water dimer on the atmospheric reactivity of carbonyl oxides, Phys. Chem. Chem. Phys., 2016, 18(26), 17698–17712 RSC.
- J. M. Anglada, J. González and M. Torrent-Sucarrat, Effects of the substituents on the reactivity of carbonyl oxides. A theoretical study on the reaction of substituted carbonyl oxides with water, Phys. Chem. Chem. Phys., 2011, 13(28), 13034–13045 RSC.
- C. Yin and K. Takahashi, Effect of unsaturated substituents in the reaction of Criegee intermediates with water vapor, Phys. Chem. Chem. Phys., 2018, 20(30), 20217–20227 RSC.
- L.-C. Lin, H.-T. Chang, C.-H. Chang, W. Chao, M. C. Smith, C.-H. Chang, J. Lin and K. Takahashi, Competition between H2O and (H2O)2 reactions with CH2OO/CH3CHOO, Phys. Chem. Chem. Phys., 2016, 18(6), 4557–4568 RSC.
- P. Aplincourt and M. F. Ruiz-López, Theoretical Investigation of Reaction Mechanisms for Carboxylic Acid Formation in the Atmosphere, J. Am. Chem. Soc., 2000, 122(37), 8990–8997 CrossRef CAS.
- R. Crehuet, J. M. Anglada and J. M. Bofill, Tropospheric Formation of Hydroxymethyl Hydroperoxide, Formic Acid, H2O2, and OH from Carbonyl Oxide in the Presence of Water Vapor: A Theoretical Study of the Reaction Mechanism, Chem.–Eur. J., 2001, 7(10), 2227–2235 CrossRef CAS.
- B. Long, J. L. Bao and D. G. Truhlar, Atmospheric Chemistry of Criegee Intermediates: Unimolecular Reactions and Reactions with Water, J. Am. Chem. Soc., 2016, 138(43), 14409–14422 CrossRef CAS.
- L. Chen, W. Wang, L. Zhou, W. Wang, F. Liu, C. Li and J. Lü, Role of water clusters in the reaction of the simplest Criegee intermediate CH2OO with water vapour, Theor. Chem. Acc., 2016, 135(11), 252 Search PubMed.
- B. Long, Y. Wang, Y. Xia, X. He, J. L. Bao and D. G. Truhlar, Atmospheric Kinetics: Bimolecular Reactions of Carbonyl Oxide by a Triple-Level Strategy, J. Am. Chem. Soc., 2021, 143(22), 8402–8413 CrossRef CAS.
- T. Zhang, X. Lan, R. Wang, S. Roy, Z. Qiao, Y. Lu and Z. Wang, The catalytic effects of H2CO3, CH3COOH, HCOOH and H2O on the addition reaction of CH2OO + H2O → CH2(OH)OOH, Mol. Phys., 2018, 116(14), 1783–1794 CrossRef CAS.
- T. B. Nguyen, J. D. Crounse, R. H. Schwantes, A. P. Teng, K. H. Bates, X. Zhang, J. M. St. Clair, W. H. Brune, G. S. Tyndall, F. N. Keutsch, J. H. Seinfeld and P. O. Wennberg, Overview of the Focused Isoprene eXperiment at the California Institute of Technology (FIXCIT): mechanistic chamber studies on the oxidation of biogenic compounds, Atmos. Chem. Phys., 2014, 14(24), 13531–13549 CrossRef.
- T. Lewis, D. E. Heard and M. A. Blitz, A novel multiplex absorption spectrometer for time-resolved studies, Rev. Sci. Instrum., 2018, 89(2), 024101 CrossRef.
- J. B. Burkholder, S. P. Sander, J. Abbatt, J. R. Barker, C. Cappa, J. D. Crounse, T. S. Dibble, R. E. Huie, C. E. Kolb, M. J. Kurylo, V. L. Orkin, C. J. Percival, D. M. Wilmouth, and P. H. Wine, Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation No. 19, JPL Publication 19-5, Jet Propulsion Laboratory, Pasadena, 2019, http://jpldataeval.jpl.nasa.gov Search PubMed.
- M. H. Harwood, J. B. Burkholder, M. Hunter, R. W. Fox and A. R. Ravishankara, Absorption Cross Sections and Self-Reaction Kinetics of the IO Radical, J. Phys. Chem. A, 1997, 101(5), 853–863 CrossRef CAS.
- W.-L. Ting, Y.-H. Chen, W. Chao, M. C. Smith and J. J.-M. Lin, The UV absorption spectrum of the simplest Criegee intermediate CH2OO, Phys. Chem. Chem. Phys., 2014, 16(22), 10438–10443 RSC.
- M. C. Smith, C.-H. Chang, W. Chao, L.-C. Lin, K. Takahashi, K. A. Boering and J. J.-M. Lin, Strong Negative Temperature Dependence of the Simplest Criegee Intermediate CH2OO Reaction with Water Dimer, J. Phys. Chem. Lett., 2015, 6(14), 2708–2713 CrossRef CAS.
- B. Ruscic, Active Thermochemical Tables: Water and Water Dimer, J. Phys. Chem. A, 2013, 117(46), 11940–11953 CrossRef CAS.
- I. Bey, D. J. Jacob, R. M. Yantosca, J. A. Logan, B. D. Field, A. M. Fiore, Q. Li, H. Y. Liu, L. J. Mickley and M. G. Schultz, Global modeling of tropospheric chemistry with assimilated meteorology: Model description and evaluation, J. Geophys. Res.: Atmos., 2001, 106, 23073–23095 CrossRef CAS.
- R. Gelaro, W. McCarty, M. J. Suárez, R. Todling, A. Molod, L. Takacs, C. A. Randles, A. Darmenov, M. G. Bosilovich, R. Reichle, K. Wargan, L. Coy, R. Cullather, C. Draper, S. Akella, V. Buchard, A. Conaty, A. M. da Silva, W. Gu, G.-K. Kim, R. Koster, R. Lucchesi, D. Merkova, J. E. Nielsen, G. Partyka, S. Pawson, W. Putman, M. Rienecker, S. D. Schubert, M. Sienkiewicz and B. Zhao, The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2), J. Clim., 2017, 30(14), 5419–5454 CrossRef.
- K. H. Bates, D. J. Jacob, K. Li, P. D. Ivatt, M. J. Evans, Y. Yan and J. Lin, Development and evaluation of a new compact mechanism for aromatic oxidation in atmospheric models, Atmos. Chem. Phys., 2021, 21(24), 18351–18374 CrossRef CAS.
- A. B. Guenther, X. Jiang, C. L. Heald, T. Sakulyanontvittaya, T. Duhl, L. K. Emmons and X. Wang, The Model of Emissions of Gases and Aerosols from Nature version 2.1 (MEGAN2.1): an extended and updated framework for modeling biogenic emissions, Geosci. Model Dev., 2012, 5(6), 1471–1492 CrossRef.
- G. R. van der Werf, J. T. Randerson, L. Giglio, T. T. van Leeuwen, Y. Chen, B. M. Rogers, M. Mu, M. J. E. van Marle, D. C. Morton, G. J. Collatz, R. J. Yokelson and P. S. Kasibhatla, Global fire emissions estimates during 1997–2016, Earth Syst. Sci. Data, 2017, 9(2), 697–720 CrossRef.
- R. M. Hoesly, S. J. Smith, L. Feng, Z. Klimont, G. Janssens-Maenhout, T. Pitkanen, J. J. Seibert, L. Vu, R. J. Andres, R. M. Bolt, T. C. Bond, L. Dawidowski, N. Kholod, J. I. Kurokawa, M. Li, L. Liu, Z. Lu, M. C. P. Moura, P. R. O'Rourke and Q. Zhang, Historical (1750–2014) anthropogenic emissions of reactive gases and aerosols from the Community Emissions Data System (CEDS), Geosci. Model Dev., 2018, 11(1), 369–408 CrossRef CAS.
- M. E. Jenkin, J. C. Young and A. R. Rickard, The MCM v3.3.1 degradation scheme for isoprene, Atmos. Chem. Phys., 2015, 15(20), 11433–11459 CrossRef CAS.
- K. H. Bates and D. J. Jacob, A new model mechanism for atmospheric oxidation of isoprene: global effects on oxidants, nitrogen oxides, organic products, and secondary organic aerosol, Atmos. Chem. Phys., 2019, 19(14), 9613–9640 CrossRef CAS.
- L. Onel, M. Blitz, P. Seakins, D. Heard and D. Stone, Kinetics of the Gas Phase Reactions of the Criegee Intermediate CH2OO with O3 and IO, J. Phys. Chem. A, 2020, 124(31), 6287–6293 CrossRef CAS.
- P. O. Wennberg, K. H. Bates, J. D. Crounse, L. G. Dodson, R. C. McVay, L. A. Mertens, T. B. Nguyen, E. Praske, R. H. Schwantes, M. D. Smarte, J. M. St Clair, A. P. Teng, X. Zhang and J. H. Seinfeld, Gas-Phase Reactions of Isoprene and Its Major Oxidation Products, Chem. Rev., 2018, 118(7), 3337–3390 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Hygrometer calibration and measurements of water vapour; description of the instrument response function; mixed-order analysis; concentration–time profiles for CH2I2 and IO; description of the analysis in terms of k2,eff and use of literature values for KDeq; investigation of the potential reaction between CH2OO and three water molecules; experimental uncertainties; comparison of global and local fit results for k2,eff; comparison of observations with previous work; values for k1 and k2,eff used in GEOS-Chem simulations; summary of experimental data. See DOI: https://doi.org/10.1039/d4ea00097h |
| This journal is © The Royal Society of Chemistry 2024 |
