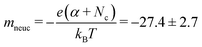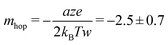Open Access Article
Open Access ArticleArtificial nociceptor using an Ag/Ag2S/Pt atomic switch†
Anwesha
Mahapatra
and
Alpana
Nayak
 *
*
Department of Physics, Indian Institute of Technology Patna, Bihta, India-801103. E-mail: anayak@iitp.ac.in
First published on 9th April 2024
Abstract
Pain is an essential sensation for any living organism to thrive in the everchanging environment, and hence an important aspect to be added to the capabilities of realistic machine intelligence. Here we present an Ag/Ag2S/Pt atomic switch as an artificial nociceptor whose voltage dependent conductance modulation is similar to that of a stimuli dependent pain sensation. Different rate limiting processes for the voltage dependent switching time illustrate its analogy to varying response times for different types of nociceptors. Distinct pain levels have been encoded in terms of quantized conductance, which is associated with opened NMDAR channels of the nociceptor network. This work emphasizes the signal dependent conductance modulation of the Ag/Ag2S/Pt atomic switch in order to mimic the biological pathway for pain sensation that will advance the defence mechanism in neuromorphic devices.
A. Introduction
The integration of artificial intelligence and robotics has paved the way for machines to interact with and navigate the physical world with increasing sophistication.1 However, the absence of a mechanism to perceive and respond to potentially harmful stimuli limits their ability to operate in a dynamic and unpredictable environment. Recently, artificial nociceptors utilizing diffusive memristors2 with maladaptive3 responses have garnered a lot of attention in the field of neuromorphic devices. In response to potentially or actually harmful stimuli (like harmful chemicals, and high temperatures2/pressure4 or light5), specialized sensory neurons called nociceptors generate electrical impulses that are transmitted to the central nervous system. The activation of N-methyl-D-aspartate receptors (NMDAR) has been linked to elevated and elongated pain sensitivity in peripheral and central neural systems, according to recent biological research.6 When the noxious signal is strong enough to cause NMDAR channel activation in the post synaptic terminal, the network becomes more sensitive with less threshold value for activation, responding more potently than it would in a normal state. Similar activation modulation occurs in atomic switch devices when the conductance value becomes greater than the first quantization of conductance7i.e.,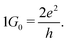 8 An atomic switch is a nano-ionic device that shows a resistive switching memory effect9–11 at the atomic scale. Silver sulphide (Ag2S), a silver chalcogenide compound, is an ionic crystal that exhibits mixed ion-electron conductivity due to the combined contribution of electrons and interstitial silver ions in the conduction mechanism.12,13 With sulphur atoms rigidly sitting in a fixed place, the silver atoms are mobile in the solid electrolyte participating in the filament formation, eliminating the problem of parasitic reaction, as occurs in oxygen-based systems. Ag2S possesses its acanthite state (α-Ag2S) with a band gap around 1 eV, and behaves like an n-type semiconductor at the ambient temperature.14 α-Ag2S is a polymorph with a monoclinic crystal structure. On the other hand, the octahedral and tetrahedral interstitial lattice points in the high-temperature argentite (β-Ag2S) are taken by Ag+ ions, while the S atoms are organized in a rigid, slightly deformed BCC structure.15 β-Ag2S is superionic due to the liquid-like behaviour of the silver sub-lattice, with a high ion mobility and electron conductivity (band gap 0.4 eV).16 In addition to temperature, an electric field can lead to the α-Ag2S to β-Ag2S phase transition.17 The heterostructure of an Ag/Ag2S nano-crystal makes it a good candidate for resistive switching-based memory devices with temperature sensitivity due to the reversible process of an α-Ag2S to β-Ag2S transformation along with a conducting channel formation18 under an electric field. The Ag/Ag2S/Pt structure is well established and well known for atomic switch applications with room temperature quantized conductance and neuromorphic hardware.19 In recent works, Ag/Ag2S-based flexible memristors have shown excellent endurance (105 switching cycles) and retention (104 s) proving its suitability for device applications.20 Ag2S is also known for its temperature-dependent conduction modulation18 and optoelectronic properties.21 Along with ease of fabrication and good reproducibility, these properties make the Ag/Ag2S/Pt atomic switch suitable for bio-inspired electronics.
8 An atomic switch is a nano-ionic device that shows a resistive switching memory effect9–11 at the atomic scale. Silver sulphide (Ag2S), a silver chalcogenide compound, is an ionic crystal that exhibits mixed ion-electron conductivity due to the combined contribution of electrons and interstitial silver ions in the conduction mechanism.12,13 With sulphur atoms rigidly sitting in a fixed place, the silver atoms are mobile in the solid electrolyte participating in the filament formation, eliminating the problem of parasitic reaction, as occurs in oxygen-based systems. Ag2S possesses its acanthite state (α-Ag2S) with a band gap around 1 eV, and behaves like an n-type semiconductor at the ambient temperature.14 α-Ag2S is a polymorph with a monoclinic crystal structure. On the other hand, the octahedral and tetrahedral interstitial lattice points in the high-temperature argentite (β-Ag2S) are taken by Ag+ ions, while the S atoms are organized in a rigid, slightly deformed BCC structure.15 β-Ag2S is superionic due to the liquid-like behaviour of the silver sub-lattice, with a high ion mobility and electron conductivity (band gap 0.4 eV).16 In addition to temperature, an electric field can lead to the α-Ag2S to β-Ag2S phase transition.17 The heterostructure of an Ag/Ag2S nano-crystal makes it a good candidate for resistive switching-based memory devices with temperature sensitivity due to the reversible process of an α-Ag2S to β-Ag2S transformation along with a conducting channel formation18 under an electric field. The Ag/Ag2S/Pt structure is well established and well known for atomic switch applications with room temperature quantized conductance and neuromorphic hardware.19 In recent works, Ag/Ag2S-based flexible memristors have shown excellent endurance (105 switching cycles) and retention (104 s) proving its suitability for device applications.20 Ag2S is also known for its temperature-dependent conduction modulation18 and optoelectronic properties.21 Along with ease of fabrication and good reproducibility, these properties make the Ag/Ag2S/Pt atomic switch suitable for bio-inspired electronics.
In this work, we have mimicked the properties of the NMDAR pathway linked to a nociceptor using an Ag/Ag2S/Pt atomic switch by applying different electrical signals similar to nocuous stimuli.22 A flexible top electrode, i.e., a conductive atomic force microscope (C-AFM) tip has been used to realize the gap-type atomic switch structure.23 This allows real-time and real-space observations of the process arising between the tip and the sample.24 Synaptic delay in the NMDAR pathway25 of the nociceptor network and its modulation with pain intensity has been related to the voltage dependency of the switching time of the atomic switch.
B. Methods
The sample Ag2S was prepared by exposing a freshly polished silver plate to sulphur vapor at 130 °C for 15 min.26 Field emission scanning electron microscopy (FESEM) and energy dispersive X-ray spectroscopy (EDS) were carried out to examine the surface morphology. For conductive atomic force microscopy (C-AFM) based characterization, Bruker multimode 8 has been used in the contact mode with a feedback set point of 10 nN, and a current limit of 1 μA. An SCM-PIT-V2 tip is used as the Pt electrode. As the precipitation occurred on the surface and the tip moved back, the simultaneous change in the z-position of the tip was recorded with time. The morphology of the surface was imaged before and after every switching event. For the pulse measurements, an Agilent 5500 AFM and a Keithley 4200 parameter analyzer were used, which allowed higher current ranges (100 μA and 1 mA).C. Results and discussions
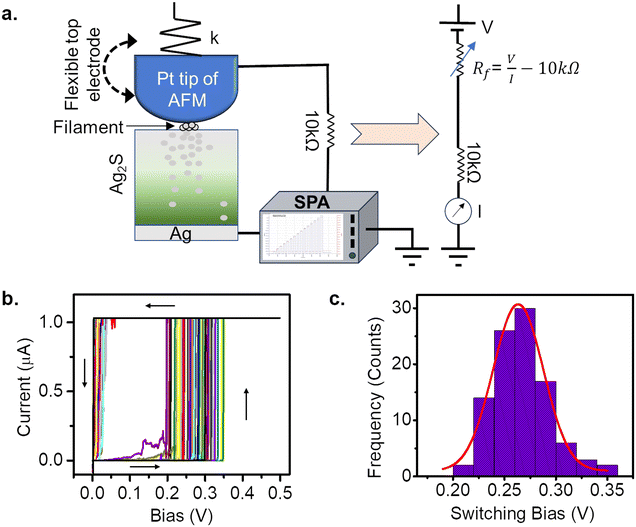
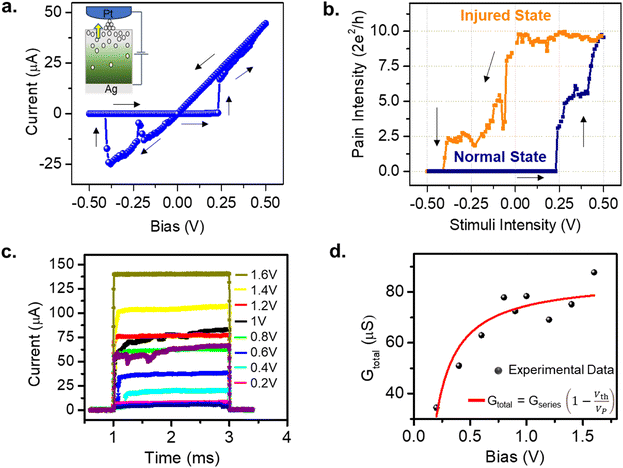
The atomic switch is realized as the Pt coated AFM tip approached the Ag2S thin film grown on the Ag substrate, as described in Fig. 1a. The AFM tip acts as a flexible top electrode, which allows precipitation on the surface, beneath the tip. One such observation has been illustrated in the Supplementary Information in Fig. S1.†Fig. 1b is the I–V response to bias sweeps of 0 V → 0.5 V → 0 V taken on 100 different positions on an Ag2S surface. The histogram of the switching voltages obtained in these measurements is shown in Fig. 1c. A Gaussian fit (red) to the data shows a peak at 0.25 V with a standard deviation of 0.02 V, which is expected due to the roughness of the Ag2S surface.26,27 The FESEM and AFM images of the Ag2S surface revealed crystal sizes of sub-micrometre order (Fig. S2†). The switching voltage (or the threshold Vth) is defined as a voltage value at which the atomic switch reaches a minimum of 1G0 (i.e., 2e2/h). It is to be noted that the threshold value depends on the sweep rate in the case of voltage sweep applications and the pulse amplitude in the case of voltage pulse applications. In this measurement, a switching voltage of 0.25 V is reproducible for a given sweep rate as long as the conditions of the silver substrate (purity and roughness), sulphurization conditions (temperature and time/amount of exposer to the sulphur vapour) remain the same. Such an atomic switch can be regarded as an artificial nociceptor whose response to the amplitude and time of the stimuli, quantized levels of conductance, and desensitization with reverse stimuli are presented here. The conductance of the atomic switch has been used to quantify the strength of the pain signal generated by a nociceptor.To draw the analogy of the atomic switch with a stimuli-dependent pain response of biological nociceptors, a pinched hysteresis for an applied sweep of 0 V → 0.5 V → 0 V → −0.5 V → 0 V has been obtained (Fig. 2a). The corresponding device structure is shown in the inset. The current value jumped from sub-nano Amperes to tens of micro-Amperes at 0.25 V. The equivalent pain perception is expressed in terms of the pain intensity (i.e., the system conductance, 2e2/h) as a function of stimuli intensity (i.e., bias strength, V) in Fig. 2b. The navy-blue line indicates the response of a normal state (forward sweep), whereas the orange line corresponds to an injured state (backward sweep). In the normal state, the conductance values are low for sub-threshold voltages, and increase above 1G0 (in this case, 10G0) for higher voltages. In the injured state, the high conductance is retained even for sub-threshold values. This resembles the elevated pain response for non-nocuous stimuli (sub-threshold voltages) by an activated nociceptor. For example, gentle tapping on a burnt skin seems more painful than a normal skin sensation.
Another essential feature of a nociceptor is its maladaptive behaviour. Maladaptivity yields a heightened response to a stronger pain stimulus, which is important for defense mechanism to survive in an unpredictable environment. This behaviour is demonstrated in our system by measuring the current responses for increased amplitudes of the input pulses with a given width. One such measurement is shown in Fig. 2c, where we applied voltage pulses with amplitudes (Vp) ranging from 0.2 V to 1.6 V, for a pulse width of 2 ms. As the pulse amplitude increased linearly in steps of 0.2 V, the current response grew from 7.03 to 139.25 μA. The total conductance Gtotal has been calculated and plotted with respect to voltage amplitude in Fig. 2d. From the equivalent circuit diagram shown in Fig. 1a, we can write
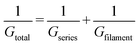 | (1) |
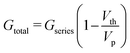 | (2) |
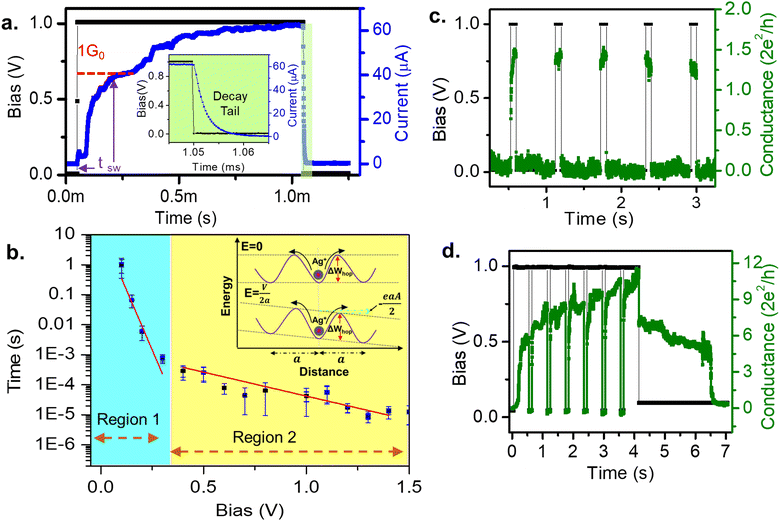
Nociceptors are known to signal faster for stronger pain stimuli. The delay plasticity in pain sensation has been studied by measuring the variation of switching time with pulse amplitude. Fig. 3a shows a typical switching time measurement for a pulse amplitude of 1 V. The switching time is defined as the time required to reach 1G0 after the pulse initiation. This can be compared with the synaptic/response delay28,29 of a nociceptor. At the end of the pulse, the current decays exponentially (inset of Fig. 3a), similar to the NMDAR pathway's calcium current tail25 that plays an important role to modulate the next signal response. Variation of the switching time (tsw) with different pulse amplitudes (Vp) has been plotted in Fig. 3b, which shows an exponential decrease in switching time with increasing pulse amplitude. This is similar to the faster pain sensation with a heightened stimuli strength, as observed in a biological nociceptor. Further, the tswvs. Vp plot shows two distinct slopes indicative of two different rate-limiting mechanisms.30–32 Region 1 is found to be the nucleation-limited process30,33,34 and region 2 is limited by the hopping rate. Similarly, in biology, different ranges of response speeds are found in thermal, mechanical, chemical and silent nociceptors due to the heterogeneity of the constituent ion-channels in the nociceptor network.35,36
First, the nucleation rate (Jn) in the Ag/Ag2S/Pt nociceptor has been determined by using an atomistic model for the electro-crystallization under a positive applied potential to the Ag substrate, given by
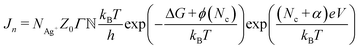 | (3) |
![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) are the number of Ag+ ions, the number of active sites, the Zeldovich factor, and the transmission probability, respectively. kBT, ΔG, ϕ(Nc), and eV represent the thermal energy, free activation enthalpy of the charge transfer reaction at V = 0, specific surface energy of the critical nucleus, and applied voltage potential, respectively. Nc denotes the number of atoms in the critical nucleus and α represents the charge transfer coefficient. h and e are Planck's constant and the elementary charge, respectively. For the measurements carried out under the same thermodynamic conditions, we can assume
are the number of Ag+ ions, the number of active sites, the Zeldovich factor, and the transmission probability, respectively. kBT, ΔG, ϕ(Nc), and eV represent the thermal energy, free activation enthalpy of the charge transfer reaction at V = 0, specific surface energy of the critical nucleus, and applied voltage potential, respectively. Nc denotes the number of atoms in the critical nucleus and α represents the charge transfer coefficient. h and e are Planck's constant and the elementary charge, respectively. For the measurements carried out under the same thermodynamic conditions, we can assume 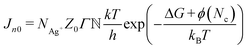 to be constant. Hence eqn (3) reduces to
to be constant. Hence eqn (3) reduces to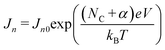 | (4) |
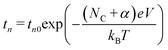 | (5) |
From this slope, we calculated values of α = 0.7 and Nc = 0, attributing the superionic β-phase of the Ag2S formed under the high electric field during the switching process.13,37
Next, for estimating the Ag+ ionic hopping current (Jh) we have used the Mott–Gurney law30 given by
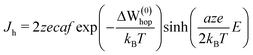 | (6) |
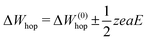 (Fig. 3b, inset). This leads to a hyperbolic sine term in eqn (6).
(Fig. 3b, inset). This leads to a hyperbolic sine term in eqn (6).
Under constant thermodynamic conditions, we can consider that 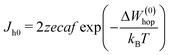 is a constant value. Thus eqn (6) reduces to
is a constant value. Thus eqn (6) reduces to
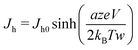 | (7) |
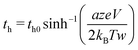 | (8) |
in our experiment. Typically the average value of a is 0.3–0.5 nm and w is 1.5–2.5 nm.30 Hence, for hopping being solely the rate-limiting process, the condition is
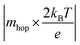 <0.2, which is of value 0.12 in our case. Overall, we can draw the analogy that the decrease in the switching time with increased pulse amplitude is a fingerprint for the nociceptor-like behaviour of the atomic switch. This indicates the greater the strength of the nocuous stimuli is, the faster the nociceptor indicates the pain sensation.
<0.2, which is of value 0.12 in our case. Overall, we can draw the analogy that the decrease in the switching time with increased pulse amplitude is a fingerprint for the nociceptor-like behaviour of the atomic switch. This indicates the greater the strength of the nocuous stimuli is, the faster the nociceptor indicates the pain sensation.
Further, an interesting analogy can be drawn from the relaxation dynamics of a nociceptor. If a stimulus arrives before the system retrieves from the previous injury, the pain sensation is found to increase. Moreover, a prolonged stimuli heightens the pain sensation. Both these features can be seen in our system (Fig. 3c and d). In Fig. 3c we have plotted the response for a pulse train consisting of five pulses with a 1 V amplitude, 100 ms width, and 750 ms interval. The resulting conductance value was 1.5G0 for each of the pulses. After every pulse end, a sufficient time interval of 750 ms allowed the system to relax back to its initial low conductance state, thus not affecting the response for the following pulse. On the other hand, Fig. 3d depicts the response for seven pulses of amplitude 1V and width 500 ms applied at 100 ms intervals. Note that for the same amplitude, the conductance value reached up to 6G0 for the first pulse, in contrast to the 1.5G0 value in Fig. 3c, due to the increased width of the signal. Again, due to the short interval of 100 ms between the consecutive pulses, the next pulse arrives before the system relaxes back to its initial conductance value. Thus, for the consecutive pulses, the conductance values increased from 8 to 10.3G0. This successfully mimics the heightened pain sensation (i.e., conductance) with frequent and prolonged stimuli (i.e., frequency and width of the pulse) of the biological nociceptor.4,5
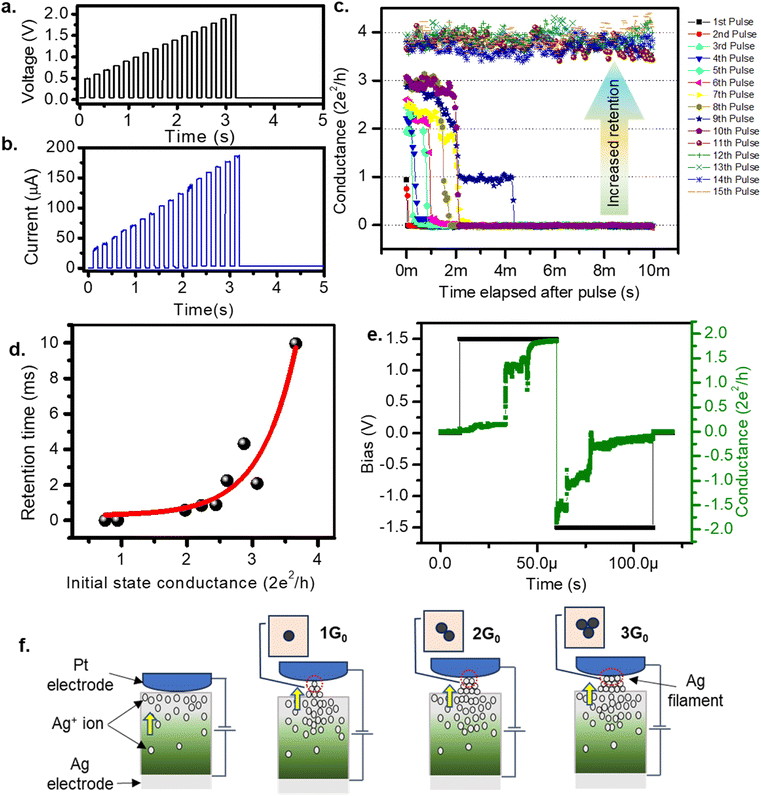
Room temperature quantization of conductance7 is one of the most intriguing aspects of the atomic switch,39 as successful observations of 1 to 10G0 have been reported.40 Similarly, in biology, the quantity of NMDAR channels in an active region is documented up to ten units.41 Therefore, we suggest that discrete pain levels, represented by opened NMDAR channels in biology, can be analogous to quantized conductance states in an atomic switch. Fig. 4a shows the input voltage of fifteen pulses with successive increments in amplitude from 0.5 V to 2 V, in steps of 0.1 V, with an interval of 10 ms. The corresponding current response is shown in Fig. 4b. The current reaches a high value during the pulse and decays to a low value in the interval after each pulse. The peak value of the current, during the pulse, increased from 30 to 185 μA. The low current observed after each pulse was not the initial value, instead it grew from 0.003 to 3.589 μA for the tenth pulse, which was retained for an observation time of 2 s after the end of the fifteenth pulse. These retained current values when expressed in terms of conductance (Fig. 4c) display clearly how the conductance decayed during the interval between two successive pulses. The initial conductance (1G0) after the first two pulses spontaneously decayed at the end of the pulse. This indicates the system only sensed the stimuli, without retaining any memory. When the system was raised to a conductance state of 2G0 or higher, the decay rate was slower and eventually leveled off to a permanent retention value of 4G0 at the end of the tenth pulse, which was retained for 2 s of observation time even after the fifteenth pulse. Since the conductance level is analogous to the pain level, retention of a higher conductance means a prolonged pain sensation for heightened pain stimuli. These conductance values and their corresponding retention times are plotted in Fig. 4d which is fitted to an exponential growth function (shown by the red line). This plot indicates that the states with conductance values ≤1G0 tend to decay instantaneously. Achieving a conductance level ≥2G0 is necessary for the system to enter a prolonged pain sensation (i.e., a retained conductance value). The stability of a higher G0 state is further verified by observing the conductance values for input of two successive pulses of opposite polarity with an amplitude of 1.5 V and width of 50 μs (Fig. 4e). For the positive polarity, the conductance value rose to 2G0, which was retained until a negative polarity diminished the value back to initial one.
We hereby reasonably argue that the opening of one NMDAR channel in a nociceptor can be represented by 1G0 of our system. Flexibility with a greater number of pain levels is achieved by opening more than one NMDAR channels corresponding to G > 1G0. In the atomic switch, the narrowest region of the conducting filament connecting the two electrodes resembles a quantum point contact.40 For ballistic transport in this region, the Landauer theory gives G = NchβG0, where Nch is the number of 1D opened conduction channels connecting the electrode and β takes a value between 0 and 1 (β = 1 in our case). Nch = 1 for a single atom contact and it takes values 2, 3,4, etc., for the corresponding number of atoms contacted as illustrated in Fig. 4f. Thus, the room temperature quantization of conductance in atomic switch provides the advantage of coding distinct pain levels depending on the signal strength, mimicking the NMDAR associated nociceptor of a mammalian nervous system.
D. Conclusions
In this work, we have proficiently demonstrated that an atomic switch can mimic the properties of a biological nociceptor. The conductance levels of the atomic switch are considered to be equivalent to the pain levels of a nociceptor. The high conductance ON-state of the atomic switch has been compared to the injured nociceptor, which signals elevated pain for sub-threshold values. The threshold is an important concept for implementing the maladaptive behaviour of the nociceptor, below which it signals no threats from the stimuli. Above the threshold value, the conductance, i.e., the pain sensation of the system, increases with the increasing stimuli strength. We have estimated the threshold value in our system. The possibility of more than one rate-limiting process in the switching time indicates the resemblance to varying response times for different nociceptors. The relaxation dynamics of our system mimic the heightened pain sensation (i.e., conductance) with frequent and prolonged stimuli (i.e., frequency and width of the pulse) of the biological nociceptor. To encode versatile high precision pain levels in the artificial nociceptor, quantized conductance states have been associated with opened NMDAR-channels of a biological network.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AN acknowledges the DST FIST project: SR/FST/PS-I/2018/34 for funding.References
- V. Dunjko and H. J. Briegel, Machine learning & artificial intelligence in the quantum domain: A review of recent progress, Rep. Prog. Phys., 2018, 81(7), 074001, DOI:10.1088/1361-6633/aab406.
- J. H. Yoon, et al., An artificial nociceptor based on a diffusive memristor, Nat. Commun., 2018, 9(1), 1–10, DOI:10.1038/s41467-017-02572-3.
- Y. G. Song, et al., Artificial Adaptive and Maladaptive Sensory Receptors Based on a Surface-Dominated Diffusive Memristor, Adv. Sci., 2022, 9(4), 1–10, DOI:10.1002/advs.202103484.
- G. Ding, et al., Filament Engineering of Two-Dimensional h-BN for a Self-Power Mechano-Nociceptor System, Small, 2022, 18(16), 1–15, DOI:10.1002/smll.202200185.
- Y. Gong, et al., Ultrasensitive Flexible Memory Phototransistor with Detectivity of 1.8×10 13 Jones for Artificial Visual Nociceptor, Adv. Intell. Syst., 2022, 4(8), 1–11, DOI:10.1002/aisy.202100257.
- Y. J. Liu, et al., NMDARs mediate peripheral and central sensitization contributing to chronic orofacial pain, Front. Cell. Neurosci., 2022, 16, 1–23, DOI:10.3389/fncel.2022.999509.
- F. Balestra and G. Ghibaudo, Electronic transport in low-dimensional structures, 1989 Search PubMed.
- K. Krishnan, M. Muruganathan, T. Tsuruoka, H. Mizuta and M. Aono, Highly Reproducible and Regulated Conductance Quantization in a Polymer-Based Atomic Switch, Adv. Funct. Mater., 2017, 27(10), 1–10, DOI:10.1002/adfm.201605104.
- D. S. Jeong, et al., Emerging memories: Resistive switching mechanisms and current status, Rep. Prog. Phys., 2012, 75(7), 076502, DOI:10.1088/0034-4885/75/7/076502.
- T. Ohno, T. Hasegawa, A. Nayak, T. Tsuruoka, J. K. Gimzewski and M. Aono, Sensory and short-term memory formations observed in a Ag2S gap-type atomic switch, Appl. Phys. Lett., 2011, 99(20), 203108, DOI:10.1063/1.3662390.
- T. Ohno, T. Hasegawa, T. Tsuruoka, K. Terabe, J. K. Gimzewski and M. Aono, Short-term plasticity and long-term potentiation mimicked in single inorganic synapses, Nat. Mater., 2011, 10(8), 591–595, DOI:10.1038/nmat3054.
- D. Karashanova and N. Starbov, Surface assisted electric transport in Ag 2 S thin films, Appl. Surf. Sci., 2006, 252(8), 3011–3022, DOI:10.1016/j.apsusc.2005.05.007.
- M. Kundu, K. Terabe, T. Hasegawa and M. Aono, Effect of sulfurization conditions and post-deposition annealing treatment on structural and electrical properties of silver sulfide films, J. Appl. Phys., 2006, 99(10), 103501, DOI:10.1063/1.2199067.
- S. Kashida, N. Watanabe, T. Hasegawa, H. Iida, M. Mori and S. Savrasov, Electronic structure of Ag2S, band calculation and photoelectron spectroscopy, Solid State Ionics, 2003, 158(1–2), 167–175, DOI:10.1016/S0167-2738(02)00768-3.
- N. Frick, M. Hosseini, D. Guilbaud, M. Gao and T. H. LaBean, Modeling and characterization of stochastic resistive switching in single Ag2S nanowires, Sci. Rep., 2022, 12(1), 1–10, DOI:10.1038/s41598-022-09893-4.
- M. Morales-Masis, S. J. van der Molen, W. T. Fu, M. B. Hesselberth and J. M. van Ruitenbeek, Conductance switching in Ag(2)S devices fabricated by in situ sulfurization, Nanotechnology, 2009, 20(9), 95710, DOI:10.1088/0957-4484/20/9/095710.
- C. Liang, K. Terabe and T. Hasegawa, Resistance switching of an individual Ag 2 S/Ag nanowire heterostructure, Nanotechnology, 2007, 485202, DOI:10.1088/0957-4484/18/48/485202.
- S. I. Sadovnikov, M. G. Kostenko, A. I. Gusev and A. V. Lukoyanov, Low-Temperature Predicted Structures of Ag2S (Silver Sulfide), Nanomaterials, 2023, 13(19), 2638, DOI:10.3390/nano13192638.
- T. Hasegawa, et al., Learning abilities achieved by a single solid-state atomic switch, Adv. Mater., 2010, 22(16), 1831–1834, DOI:10.1002/adma.200903680.
- Y. Zhu, J. S. Liang, X. Shi and Z. Zhang, Full-Inorganic Flexible Ag2S Memristor with Interface Resistance-Switching for Energy-Efficient Computing, ACS Appl. Mater. Interfaces, 2022, 14(38), 43482–43489, DOI:10.1021/acsami.2c11183.
- R. A. Ismail, H. A. Rawdhan and D. S. Ahmed, High-responsivity hybrid a-Ag2S/Si photodetector prepared by pulsed laser ablation in liquid, Beilstein J. Nanotechnol., 2020, 11, 1596–1607, DOI:10.3762/bjnano.11.142.
- Y. Zhang, et al., Modeling and emulation of artificial nociceptor based on TiO2 threshold switching memristor, Mater. Sci. Eng., B, 2022, 290, 2023, DOI:10.1016/j.mseb.2023.116360.
- A. Suzuki, T. Tsuruoka and T. Hasegawa, Time-Dependent Operations in Molecular Gap Atomic Switches, Phys. Status Solidi B, 2019, 1900068, 1–10, DOI:10.1002/pssb.201900068.
- Y. M. Kim, J. Lee, D. J. Jeon, S. E. Oh and J. S. Yeo, Advanced atomic force microscopy-based techniques for nanoscale characterization of switching devices for emerging neuromorphic applications, Appl. Microsc., 2021, 51(1), 7, DOI:10.1186/s42649-021-00056-9.
- B. L. Sabatini and W. G. Regehr, Timing of synaptic transmission, Annu. Rev. Physiol., 1999, 61, 521–542, DOI:10.1146/annurev.physiol.61.1.521.
- A. Mahapatra, I. Pradhan, D. Roy and A. Nayak, Unveiling the analogies between the atomic switch and NMDA receptor-based signal transmission of biological synapse, Jpn. J. Appl. Phys., 2022, 61, SM1008, DOI:10.35848/1347-4065/ac6c16.
- A. Mahapatra, I. Pradhan, P. P. Samal, H. Paul, P. Mishra and A. Nayak, Field-mediated neural transmission within an Ag2S gap-type atomic switch, Appl. Surf. Sci., 2023, 652, 2024, DOI:10.1016/j.apsusc.2024.159309.
- B. Katz and R. Miledi, The Measurement of Synaptic Delay, and the Time Course of Acetylcholine Release At the Neuromuscular Junction, Proc. R. Soc. London, Ser. B, 1965, 161(985), 483–495, DOI:10.1098/rspb.1965.0016.
- F. Sandin and M. Nilsson, Synaptic Delays for Insect-Inspired Temporal Feature Detection in Dynamic Neuromorphic Processors, Front. Neurosci., 2020, 14, 150, DOI:10.3389/fnins.2020.00150.
- S. Menzel, U. Böttger, M. Wimmer and M. Salinga, Physics of the Switching Kinetics in Resistive Memories, Adv. Funct. Mater., 2015, 25(40), 6306–6325, DOI:10.1002/adfm.201500825.
- A. Nayak, et al., Rate-limiting processes determining the switching time in a Ag2S atomic switch, J. Phys. Chem. Lett., 2010, 1(3), 604–608, DOI:10.1021/jz900375a.
- S. A. Chekol, S. Menzel, R. W. Ahmad, R. Waser and S. Hoffmann-Eifert, Effect of the Threshold Kinetics on the Filament Relaxation Behavior of Ag-Based Diffusive Memristors, Adv. Funct. Mater., 2021, 2111242, DOI:10.1002/adfm.202111242.
- I. Pradhan, A. Mahapatra, P. P. Samal, P. Mishra, P. Kumar and A. Nayak, Liquid-Liquid Interface-Assisted Self-Assembly of Ag-Doped ZnO Nanosheets for Atomic Switch Application, J. Phys. Chem. Lett., 2024, 15(1), 165–172, DOI:10.1021/acs.jpclett.3c02791.
- S. Mallik, et al., Quantized conductance behaviour observed in an atomic switch using triptycene-based polymers, J. Mater. Chem. C, 2022, 10(36), 13225–13233, 10.1039/d2tc00771a.
- E. E. Benarroch, Ion channels in nociceptors, Neurology, 2015, 84(11), 1153–1164, DOI:10.1212/wnl.0000000000001382.
- R. Giniatullin, Ion channels of nociception, Int. J. Mol. Sci., 2020, 21(10), 1–6, DOI:10.3390/ijms21103553.
- I. Valov, et al., Atomically controlled electrochemical nucleation at superionic solid electrolyte surfaces, Nat. Mater., 2012, 11(6), 530–535, DOI:10.1038/nmat3307.
- P. Meuffels and H. Schroeder, Comment on ‘exponential ionic drift: Fast switching and low volatility of thin-film memristors’ by D.B. Strukov and R.S. Williams in Appl. Phys. A (2009) 94: 515-519, Appl. Phys. A: Mater. Sci. Process., 2011, 105(1), 65–67, DOI:10.1007/s00339-011-6578-7.
- K. Terabe, T. Hasegawa, T. Nakayama and M. Aono, Quantized conductance atomic switch, Nature, 2005, 47–50, DOI:10.1038/nature03190.
- Y. Li, et al., Conductance Quantization in Resistive Random Access Memory, Nanoscale Res. Lett., 2015, 10(1), 420, DOI:10.1186/s11671-015-1118-6.
- A. Bracciali, M. Brunelli, E. Cataldo and P. Degano, Stochastic models for the in silico simulation of synaptic processes, BMC Bioinf., 2008, 9(SUPPL. 4), 1–14, DOI:10.1186/1471-2105-9-S4-S7.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lf00035h |
| This journal is © The Royal Society of Chemistry 2024 |