Open Access Article
Open Access ArticleSynthesis of zeolitic imidazolate framework-8 using an electric field in a gelled medium†
Norbert
Német
ab,
Gábor
Holló
c,
Nadia
Valletti
d,
Szabolcs
Farkas
a,
Brigitta
Dúzs
e,
Ákos
Kukovecz
 f,
Gábor
Schuszter
f,
Gábor
Schuszter
 g,
István
Szalai
h,
Federico
Rossi
g,
István
Szalai
h,
Federico
Rossi
 d and
István
Lagzi
d and
István
Lagzi
 *ai
*ai
aDepartment of Physics, Institute of Physics, Budapest University of Technology and Economics, Műegyetem rkp 3, Budapest H-1111, Hungary. E-mail: lagzi.istvan.laszlo@ttk.bme.hu; Fax: +361-463-4180; Tel: +361-463-1341
bDepartment of Organic Chemistry and Technology, Budapest University of Technology and Economics, Műegyetem rkp 3, Budapest H-1111, Hungary
cDepartment of Fundamental Microbiology, University of Lausanne, Biophore Building, Lausanne 1015, Switzerland
dDepartment of Physical Sciences, Earth and Environment, University of Siena, piazzetta Enzo Tiezzi 1, Siena 53100, Italy
eDepartment of Chemistry, University of Mainz, Duesbergweg 10-14, Mainz 55128, Germany
fInterdisciplinary Excellence Center, Department of Applied and Environmental Chemistry, University of Szeged, Rerrich Béla tér 1, Szeged H-6720, Hungary
gDepartment of Physical Chemistry and Materials Science, University of Szeged, Rerrich Béla tér 1, Szeged H-6720, Hungary
hLaboratory of Nonlinear Chemical Dynamics, Institute of Chemistry, Eötvös Loránd University, Pázmány Péter stny. 1/A, Budapest H-1117, Hungary
iHU-REN–BME Condensed Matter Physics Research Group, Budapest University of Technology and Economics, Műegyetem rkp 3., Budapest H-1111, Hungary
First published on 20th December 2023
Abstract
Using the ion migration in various gel mediums governed by a direct electric field is a well-known technique, especially in analytical chemistry, to separate charged chemical species. This approach is also suitable for generating different-sized crystals and controlling the pattern formation in gels. Here we present a synthesis of zeolitic imidazolate framework-8 in an agarose gel driven by a direct electric field. We investigate the effect of an applied electric current on the macroscopic pattern formed in the gel, morphology, size, and dispersity of the ZIF-8 crystals. Upon increasing the electric current, the average size of the particles and dispersity of the samples decreased along the gel tube from the liquid–gel interface of the anodic side. This trend is opposite to the results obtained in synthesising particles utilizing only diffusion for mass transport. The electric field caused peak-doubling in the X-ray diffraction (XRD) pattern. To support the experimental observations, we developed a reaction–diffusion–migration model, which qualitatively describes the pattern formation observed in experiments.
1 Introduction
Metal–organic frameworks (MOFs) are a class of organic–inorganic hybrid crystalline coordination materials investigated over the past two decades.1,2 These structured networks comprise metal ions (copper, zinc, cadmium, cobalt, and other transition metals) interconnected through organic linkers, predominantly aromatic or heteroaromatic in nature. This coordination results in the creation of diverse building blocks and crystal structures. MOFs have a wide range of applications due to their high porosity and specific surface area, these have been used in gas storage and separation (gas chromatography),3–5 furthermore, in drug delivery applications,6 microreactors7,8 and heterogeneous catalysts for organic reactions.9 Nowadays, they have been applied also in electronics as semiconductors.10Several synthesis methods have been developed for the generation of MOFs, including electrochemical synthesis,11 solvothermal,12 sonochemical,13 ionothermal,14 flow-driven,15 mechanochemical,16 microwave-,17 and diffusion-assisted.18
Several works have already been published on the diffusion-assisted production of MOFs in solid gels.19–22 In these cases, the inner electrolyte solution containing metal salts is uniformly dispersed within a gel matrix. Simultaneously, the outer electrolyte solution, containing organic linker molecules, is stratified on top of the gel. This outer solution permeates into the gel, leading to the formation of crystals of MOFs. The advantage of this technique is that the diffusion flux of the reagents controls the nucleation and growth of the crystals. The propagating supersaturation front initiated at the liquid–gel interface produces crystals with a size ranging between ∼100 nm and a few tens of μm along the reaction tube. The vast of the traditional methods generate sub-micron particles, and one experimental condition produces only particles with a given average size.23
In this paper, we report the synthesis of the zeolitic imidazolate framwork-8 (ZIF-8) in an agarose gel using an electric field. ZIFs are a subclass of MOFs that are topologically isomorphic with zeolites. Controlling and engineering particles and chemical structures by applying an electric field is a widely used technique.24–31 The electric field contributes to the mass transport of the charged chemical species in the system, and thus affecting the nucleation and crystal growth. Due to an enhanced ionic migration, the morphology, average size, and size distribution of the particles can be controlled by the electric current. We used electron microscopy, X-ray diffraction (XRD), and gas adsorption measurements to characterize the produced crystals. We found that an electric field can control the size and crystallinity of the particles in the reaction medium. To support the concept, we developed a mathematical model which qualitatively describes the experimental findings.
2 Experimental section
Agarose powder (Sigma-Aldrich, Type I-A, low EEO) and 2-methylimidazole (2-MIM, Sigma-Aldrich) were dissolved in a mixture of Type II distilled water and N,N-dimethylformamide (DMF, Sigma-Aldrich) with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio containing 1 mM of potassium nitrate (Emsure) acting as an inert conductive salt. The mixture was continuously stirred using a magnetic stirrer (300 rpm) at 80–85 °C until complete dissolution of the agarose (∼ 10 min). The gel contained 1% w/v of agarose and 300 mM of 2-MIM. The homogenous solution (4.5 mL) was gently injected into the U-shaped glass tubes (with a diameter of 0.9 cm) creating a curved gel column with a length of ∼ 7 cm. The gelation process was accomplished in a refrigerator at ∼ 5 °C. After gelation (∼ 24 h), the gel was kept for 1 hour at room temperature (21 ± 0.5 °C). Then the solutions containing 30 mM of zinc acetate (Sigma-Aldrich) and 300 mM 2-MIM (both dissolved in a mixture of Type II distilled water and DMF in a ratio of 1
1 ratio containing 1 mM of potassium nitrate (Emsure) acting as an inert conductive salt. The mixture was continuously stirred using a magnetic stirrer (300 rpm) at 80–85 °C until complete dissolution of the agarose (∼ 10 min). The gel contained 1% w/v of agarose and 300 mM of 2-MIM. The homogenous solution (4.5 mL) was gently injected into the U-shaped glass tubes (with a diameter of 0.9 cm) creating a curved gel column with a length of ∼ 7 cm. The gelation process was accomplished in a refrigerator at ∼ 5 °C. After gelation (∼ 24 h), the gel was kept for 1 hour at room temperature (21 ± 0.5 °C). Then the solutions containing 30 mM of zinc acetate (Sigma-Aldrich) and 300 mM 2-MIM (both dissolved in a mixture of Type II distilled water and DMF in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) were gently injected on the top of the separate gel surfaces, i.e., one solution on one side, the other solution on the other side of the U-shaped gel column. Both solutions contained 1 mM potassium nitrate. We added the solution of 2-MIM to the cathodic side to avoid diffusion of 2-MIM from the gel to the solution through the liquid–gel interface, which would have caused an inhomogeneous distribution of the 2-MIM in the gel before the generation of ZIF-8 crystals. Platinum wires were used as electrodes, and positive and negative electrodes were placed in the solutions of the zinc ions and 2-MIM, respectively. The galvanostatic condition was applied throughout the experiments. We also carried out control experiments in the absence of an electric field. The experimental setup can be found in the ESI† (Fig. S1). After three days, the rest of the solutions and gel were removed from the tube and cut into segmented pieces. Each piece of the gel was dissolved in 2.5 mL of DMF and was centrifuged for 15 minutes at 6000 rpm (Hettich ROTOFIX 32A). The extracted white precipitate was washed with distilled water once and DMF twice and dried overnight. The particle size distribution was determined based on the SEM micrographs using the ImageJ program.32 The ZIF-8 samples were characterized by scanning electron microscopy (SEM) and powder X-ray diffraction (PXRD). The specific surface area and pore volume were determined using Brunauer–Emmett–Teller (BET) and Barrett–Joyner–Halenda (BJH) methods, respectively.
1) were gently injected on the top of the separate gel surfaces, i.e., one solution on one side, the other solution on the other side of the U-shaped gel column. Both solutions contained 1 mM potassium nitrate. We added the solution of 2-MIM to the cathodic side to avoid diffusion of 2-MIM from the gel to the solution through the liquid–gel interface, which would have caused an inhomogeneous distribution of the 2-MIM in the gel before the generation of ZIF-8 crystals. Platinum wires were used as electrodes, and positive and negative electrodes were placed in the solutions of the zinc ions and 2-MIM, respectively. The galvanostatic condition was applied throughout the experiments. We also carried out control experiments in the absence of an electric field. The experimental setup can be found in the ESI† (Fig. S1). After three days, the rest of the solutions and gel were removed from the tube and cut into segmented pieces. Each piece of the gel was dissolved in 2.5 mL of DMF and was centrifuged for 15 minutes at 6000 rpm (Hettich ROTOFIX 32A). The extracted white precipitate was washed with distilled water once and DMF twice and dried overnight. The particle size distribution was determined based on the SEM micrographs using the ImageJ program.32 The ZIF-8 samples were characterized by scanning electron microscopy (SEM) and powder X-ray diffraction (PXRD). The specific surface area and pore volume were determined using Brunauer–Emmett–Teller (BET) and Barrett–Joyner–Halenda (BJH) methods, respectively.
3 Results and discussion
In a typical experiment, the organic linker (2-MIM) was homogeneously distributed in the agarose gel in the U-shaped glass tube. On the two boundaries of the gel, we had a zinc and a 2-MIM solution, respectively. The gel contained the same water/DMF (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) solvent mixture as the zinc ions and organic linker solutions. Organic solvents (such as DMF, methanol, and acetonitrile) facilitate the deprotonation of 2-MIM and, thus, the coordination of the zinc ions with 2-MIM linkers. Zinc acetate and other zinc-containing salts can be easily dissolved in an aqueous system, but DMF has an advantageous effect on controlling particle size in the crystallization of MOFs.33
1) solvent mixture as the zinc ions and organic linker solutions. Organic solvents (such as DMF, methanol, and acetonitrile) facilitate the deprotonation of 2-MIM and, thus, the coordination of the zinc ions with 2-MIM linkers. Zinc acetate and other zinc-containing salts can be easily dissolved in an aqueous system, but DMF has an advantageous effect on controlling particle size in the crystallization of MOFs.33
We carried out several control experiments in the absence of an electric field to investigate the formation of ZIF-8 crystals in the gel column. We fixed the ratio of zinc ions and 2-MIM to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 because the excess of the linker facilitates the formation of ZIF-8. The concentration of the zinc cations was varied between 5 and 30 mM (Fig. S2, ESI†). 30 mM was the highest possible concentration due to the limited solubility of zinc acetate in the water/DMF mixture. As expected, we achieved the highest precipitation yield when working with the highest concentration of zinc ions. Therefore, we used 30 mM of zinc acetate and 300 mM 2-MIM in this study.
10 because the excess of the linker facilitates the formation of ZIF-8. The concentration of the zinc cations was varied between 5 and 30 mM (Fig. S2, ESI†). 30 mM was the highest possible concentration due to the limited solubility of zinc acetate in the water/DMF mixture. As expected, we achieved the highest precipitation yield when working with the highest concentration of zinc ions. Therefore, we used 30 mM of zinc acetate and 300 mM 2-MIM in this study.
In all experiments, the concentrations of the agarose gel, potassium nitrate, zinc ion, and organic linker were kept unchanged, and only the electric current was varied between 0 and 200 μA.
When applied, the electric field enhanced the mass transport of zinc ions into the gel. Fig. 1 reports the effect of an increasing electric field on the macroscopic appearance of the pattern of the ZIF-8 in the gel and the morphology of the generated particles. The precipitation process always started near the liquid–gel interface at the anodic side. In the absence of an electric field (pure diffusion, I = 0), the ZIF-8 formed continuously from the liquid–gel interface on the anodic side. At the same time, the size and dispersity of ZIF-8 particles increased along the diffusion path (Fig. 1a), which is in good accordance with the findings observed in other reaction–diffusion systems (Fig. S3, ESI†).34 When we increased the electric current, two phenomena occurred. First, the length of the precipitation zone increased, which can be explained by the enhanced ionic migration of zinc ions towards the cathode. Secondly, a precipitation-free zone appeared near the anode side, and its length increased as the electric current increased (Fig. 1b–f and Fig. S4, ESI†).
The electric field affected the morphology of the formed particles. Upon increasing the electric current above a certain threshold, the appearance of an amorphous precipitate was observed in the precipitation zone near the anode (Fig. 1b–f). Interestingly, farther from the anode, the size of the particles decreased, and the dispersity of the samples became lower (Fig. S3 and Table S2, ESI†). This unexpected pattern contrasts with the typical trends observed in reaction-diffusion systems.34 In the pure reaction–diffusion scenario, the supersaturation is higher near the liquid–gel interface due to the high diffusive flux of the invading chemical species (in our case, these are zinc ions) than farther from it. This is because higher supersaturation results in smaller particles with high particle concentrations. However, farther from the liquid–gel interface, the decreased supersaturation (governed by diffusion) creates bigger particles with a lower particle concentration. In the presence of an electric field, the enhanced mass transport of the zinc ions can create higher supersaturation in segments farther from the liquid–gel interface, generating small particles. Under moderate electric currents, we identified an optimal value (I = 50 μA) that resulted in ZIF-8 particles with an average size of approximately 4 μm. This size is twice as large as was observed in cases where only diffusion is involved (Fig. 1a, d and Fig. S4, ESI†). (Fig. 1a, d and Fig. S5, ESI†).
The results of the PXRD, BET, and BJH methods provided further characterization of the ZIF-8 crystals. PXRD measurements revealed an XRD peak doubling caused by an electric field. Fig. 2 shows the obtained PXRD patterns in the absence (Fig. 2a) and presence (Fig. 2b and c) of an electric field. In all cases, the samples were crystalline; however, in the presence of an electric field, a new diffraction appeared in the patterns (at 11.1°) near the reflection {0 0 2} (at 10.5°). This could be due to the polarization of the solvent molecules in the crystal structure that causes electrostatic screening between the corresponding crystal planes resulting in a smaller distance between the planes. At a higher electric current used, the intensity of the new peak is increased, which supports this hypothesis. A similar peak doubling effect was observed for chloride-containing hydrocalumites, following the insertion of interlamellar chloride in place of carbonate or nitrate ions. In this case, the reflection {0 0 4} of hydrocalumite doubled due to slight variations in the hydration of the different double hydroxide layers.35
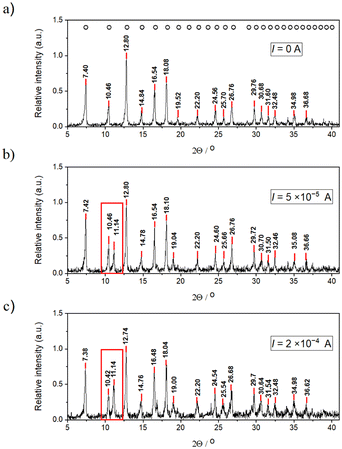 | ||
| Fig. 2 PXRD patterns of the ZIF-8 crystals extracted from the agarose gel using various electric currents, (a) I = 0 (segments A and B in Fig. 1a), (b) I = 50 μA (segments B and C in Fig. 1d), and (c) I = 200 μA (segments B and C in Fig. 1f). The open circles above the peaks in panel (a) indicate the reported diffractions of ZIF-8.38 The red box indicates the appearance of a new PXRD peak close to the reflection {0 0 2} in the presence of an electric field. | ||
In the absence of an electric field, the specific surface area and pore volume of the crystals were 1100 m2 g−1 and 0.55 cm3 g−1, respectively. These obtained data are in good accordance with the data reported in the literature using traditional synthesis methods.36,37 At a moderate electric current (I = 50 μA), the specific surface area decreased to 550 m2 g−1. However, the pore volume increased to 0.96 cm3 g−1. At the highest current (I = 200 μA), we obtained 400 m2 g−1 and 0.08 cm3 g−1 for the specific surface area and pore volume, respectively. This indicates that a high electric current does not facilitate the formation of high-quality ZIF-8 crystals.
To support our experimental findings, we developed a reaction–diffusion-ionic migration model incorporating the formation of ZIF-8 from zinc cations and 2-MIM. The mathematical model is based on the reaction–diffusion and the Nernst–Planck equations to describe the formation of ZIF-8 with the ionic migration of the charged chemical species in a gel medium:39,40
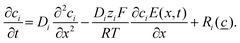 | (1) |
This equation contains diffusion, migration, and reaction kinetic terms, where Di is the diffusion coefficient, ci is the concentration, zi is the valence, and Ri(![[c with combining low line]](https://www.rsc.org/images/entities/char_0063_0332.gif) ) is the reaction kinetic term of the ith chemical species in the system. F, R, and T are the Faraday constant, the ideal gas constant, and the thermodynamic temperature, respectively.
) is the reaction kinetic term of the ith chemical species in the system. F, R, and T are the Faraday constant, the ideal gas constant, and the thermodynamic temperature, respectively.
The electric field is described by the following equation, which ensures electroneutrality:
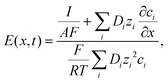 | (2) |
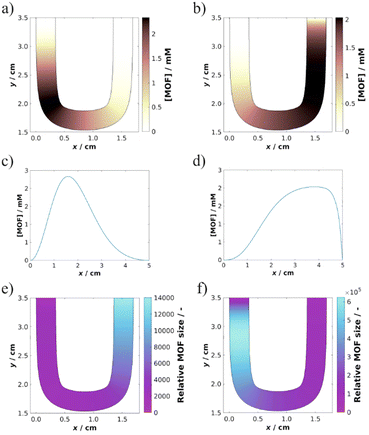
We simulated the generation of ZIF-8 and the size of the particles in the case of pure diffusion (I = 0) and at the highest electric current used in the experiments (I = 20 μA). Further details of the simulations (kinetic model, numerical method, and model parameters) can be found in the ESI† (Table S1).
In the kinetic model (see ESI†), we assumed that the electrically neutral 2-MIM forms a positively charged intermediate with zinc ion (4 L + M2+ → C2+), which later produces ZIF-8 particles.41Fig. 3 shows the results of the numerical simulations. In the absence of an electric field, the precipitation zone is located closer to the liquid–gel interface at the anodic side (Fig. 3a and c), and its length is smaller compared to the result obtained in the case in the presence of an electric field (Fig. 3b and d). In accordance with the experimental observation, the precipitation zone moves towards the cathodic side, and its length increases. The numerical model qualitatively reproduced these two essential properties of the system. The key ingredient here is that the intermediate species has a positive charge and moves towards the cathode, like zinc cations. This extra mass transport over the diffusion causes the precipitation to start farther from the liquid–gel interface at the anodic side, and the length of the zone becomes greater in the presence of an electric field due to the enhanced mass transport of the charged chemical species. The model could also reproduce the trend of the variation of the average size of the particles in the gel in the absence and presence of an electric field (Fig. 3e and f and Table S2, ESI†).
We also carried out experiments by replacing the electrodes. In this reversed scenario, we could not obtain any precipitate in the gel, even at the lowest electric current. The color of the solution of 2-MIM (anodic side) turned yellow with time due to the oxidation of 2-MIM (Fig. S6, ESI†).37
4 Conclusions
In conclusion, we have presented that an electric field can affect the crystallization of ZIF-8 particles in a gelled medium by facilitating the migration of charged chemical species. By increasing the electric field strength, the length of the precipitation domain became greater expanding towards the cathode, and the length of the zone containing fewer particles at the anodic side also increased. In the case of low electric current, both the average size of the ZIF-8 particles and the dispersity of the samples increased along the gel tube from the liquid–gel interface of the anodic side. This finding is similar to the results obtained in the synthesis utilizing only diffusion for mass transport. By increasing the electric current, the trend reversed. Namely, the size and dispersity decreased. However, at the highest electric current used (200 μA), particles lost their crystalline shape and became amorphous. Based on the PXRD measurements, in the presence of an electric field, we observed a peak-doubling in the pattern near the reflection {0 0 2}. The numerical model (incorporating diffusion, ion migration, and kinetics of ZIF-8 formation) captures the experimentally observed macroscopic characteristics. Based on the model simulation and experimental observation, we could provide indirect evidence that the intermediate product in the formation of ZIF-8 in aqueous solutions has a positive charge, indicating that in this step, the zinc ion coordinates protonated (uncharged) 2-MIM molecules. Our method provides a facile and scalable way to adjust particle morphology in spatially inhomogeneous conditions. It allows us to control the application-related physical–chemical properties of MOFs using a reaction–diffusion framework combined with an electric field.Author contributions
N. N., N. V., G. H., I. S., F. R., and I. L. conceived the research and designed the experiments. N. N. and N. V. performed the experiments, and all authors interpreted data. G. S. performed the SEM and PXRD measurements. Á. K. performed gas adsorption measurements (BET and BJH methods). G. H. preformed the numerical simulations. S. F. and B. D. performed statistical analysis of the ZIF-8 particles based on SEM micrographs. N. N. and I. L. wrote the manuscript, and all authors commented on it.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research, Development and Innovation Office of Hungary (K131425, K134687, K146071, and K138844), the National Research, Development, and Innovation Fund of Hungary under the grants of TKP2021-EGA-02, and ÚNKP-22-3-II-BME-13 New National Excellence program of the Ministry for Culture and Innovation from the source of the National Research, Development and Innovation Fund.References
- S. L. James, Chem. Soc. Rev., 2003, 32, 276 RSC.
- J. L. C. Rowsell and O. M. Yaghi, Microporous Mesoporous Mater., 2004, 73, 3–14 CrossRef CAS.
- H. Li, L. Li, R.-B. Lin, W. Zhou, Z. Zhang, S. Xiang and B. Chen, EnergyChem., 2019, 1, 100006 CrossRef.
- K. Yusuf, A. Aqel and Z. ALOthman, J. Chromatogr. A, 2014, 1348, 1–16 CrossRef CAS PubMed.
- J.-R. Li, R. J. Kuppler and H.-C. Zhou, Chem. Soc. Rev., 2009, 38, 1248–1256 RSC.
- J. Cao, X. Li and H. Tian, Curr. Med. Chem., 2020, 27, 5949–5969 CrossRef CAS PubMed.
- D. Tian, X. Zhang, H. Shi, L. Liang, N. Xue, J.-H. Wang and H. Yang, J. Am. Chem. Soc., 2021, 143, 16641–16652 CrossRef CAS PubMed.
- D. Tian, R. Hao, X. Zhang, H. Shi, Y. Wang, L. Liang, H. Liu and H. Yang, Nat. Commun., 2023, 14, 3226 CrossRef CAS.
- M.-L. Hu, V. Safarifard, E. Doustkhah, S. Rostamnia, A. Morsali, N. Nouruzi, S. Beheshti and K. Akhbari, Microporous Mesoporous Mater., 2018, 256, 111–127 CrossRef CAS.
- C. G. Silva, A. Corma and H. García, J. Mater. Chem., 2010, 20, 3141 RSC.
- A. Martinez Joaristi, J. Juan-Alcañiz, P. Serra-Crespo, F. Kapteijn and J. Gascon, Cryst. Growth Des., 2012, 12, 3489–3498 CrossRef CAS.
- P. Pachfule, R. Das, P. Poddar and R. Banerjee, Cryst. Growth Des., 2011, 11, 1215–1222 CrossRef CAS.
- C. Vaitsis, E. Kanellou, P. K. Pandis, I. Papamichael, G. Sourkouni, A. A. Zorpas and C. Argirusis, Sustainable Chem. Pharm., 2022, 29, 100786 CrossRef CAS.
- E. R. Parnham and R. E. Morris, Acc. Chem. Res., 2007, 40, 1005–1013 CrossRef CAS PubMed.
- Z. Liu, J. Zhu, C. Peng, T. Wakihara and T. Okubo, React. Chem. Eng., 2019, 4, 1699–1720 RSC.
- D. Chen, J. Zhao, P. Zhang and S. Dai, Polyhedron, 2019, 162, 59–64 CrossRef CAS.
- J. Klinowski, F. A. A. Paz, P. Silva and J. Rocha, Dalton Trans., 2011, 40, 321–330 RSC.
- J. Lim, E. J. Lee, J. S. Choi and N. C. Jeong, ACS Appl. Mater. Interfaces, 2018, 10, 3793–3800 CrossRef CAS PubMed.
- S. Farkas, M. S. Fonyi, G. Holló, N. Német, N. Valletti, Á. Kukovecz, G. Schuszter, F. Rossi and I. Lagzi, J. Phys. Chem. C, 2022, 126, 9580–9586 CrossRef CAS.
- D. Saliba, M. Ammar, M. Rammal, M. Al-Ghoul and M. Hmadeh, J. Am. Chem. Soc., 2018, 140, 1812–1823 CrossRef CAS PubMed.
- V. S. Vineetha and P. P. Pradyumnan, Mater. Res. Innovations, 2023, 27, 405–410 CrossRef.
- R. Zakhia Douaihy, M. Al-Ghoul and M. Hmadeh, Small, 2019, 15, 1901605 CrossRef.
- Y.-R. Lee, M.-S. Jang, H.-Y. Cho, H.-J. Kwon, S. Kim and W.-S. Ahn, Chem. Eng. J., 2015, 271, 276–280 CrossRef CAS.
- X. Xu, K. K. Caswell, E. Tucker, S. Kabisatpathy, K. L. Brodhacker and W. A. Scrivens, J. Chromatogr. A, 2007, 1167, 35–41 CrossRef CAS.
- A. H. Sharbaugh and A. H. Sharbaugh, J. Chem. Educ., 1989, 66, 589 CrossRef CAS.
- I. Lagzi, Phys. Chem. Chem. Phys., 2002, 4, 1268–1270 RSC.
- R. Sultan and R. Halabieh, Chem. Phys. Lett., 2000, 332, 331–338 CrossRef CAS.
- S. V. Amrutha, A. Sebastian, P. Sibeesh, S. Punacha and T. K. Shajahan, J. Phys. Chem. C, 2022, 126, 19618–19626 CrossRef CAS.
- H. Ševčíková, I. Schreiber and M. Marek, J. Phys. Chem., 1996, 100, 19153–19164 CrossRef.
- B. K. Agarwalla, S. Galhotra and J. K. Bhattacharjee, J. Math. Chem., 2014, 52, 188–197 CrossRef CAS.
- J. Carballido-Landeira, P. Taboada and A. P. Muñuzuri, Soft Matter, 2012, 8, 2945 RSC.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- A. A. Tezerjani, R. Halladj and S. Askari, RSC Adv., 2021, 11, 19914–19923 RSC.
- R. M. Walliser, F. Boudoire, E. Orosz, R. Tóth, A. Braun, E. C. Constable, Z. Rácz and I. Lagzi, Langmuir, 2015, 31, 1828–1834 CrossRef CAS PubMed.
- K. Karádi, T.-T. Nguyen, A. A. Ádám, K. Baán, A. Sápi, Á. Kukovecz, Z. Kónya, P. Sipos, I. Pálinkó and G. Varga, Green Chem., 2023, 25, 5741–5755 RSC.
- A. Paul, I. K. Banga, S. Muthukumar and S. Prasad, ACS Omega, 2022, 7, 26993–27003 CrossRef CAS PubMed.
- M. Itatani, N. Német, N. Valletti, G. Schuszter, P. Prete, P. Lo Nostro, R. Cucciniello, F. Rossi and I. Lagzi, ACS Sustainable Chem. Eng., 2023, 11, 13043–13049 CrossRef CAS PubMed.
- M. He, J. Yao, Q. Liu, K. Wang, F. Chen and H. Wang, Microporous Mesoporous Mater., 2014, 184, 55–60 CrossRef CAS.
- I. Bena, F. Coppex, M. Droz and Z. Rácz, J. Chem. Phys., 2005, 122, 024512 CrossRef CAS PubMed.
- I. Rubinstein, Electro-Diffusion of Ions, SIAM, Philadelphia, 1990 Search PubMed.
- M. Jian, B. Liu, R. Liu, J. Qu, H. Wang and X. Zhang, RSC Adv., 2015, 5, 48433–48441 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma00690e |
| This journal is © The Royal Society of Chemistry 2024 |