Open Access Article
Open Access ArticlePhenazine-integrated conjugated microporous polymers for modulating the mechanics of supercapacitor electrodes†
Mohammed G.
Kotp
a,
Johann
Lüder
ab,
Shiao-Wei
Kuo
 a and
Ahmed F. M.
EL-Mahdy
a and
Ahmed F. M.
EL-Mahdy
 *ac
*ac
aDepartment of Materials and Optoelectronic Science, National Sun Yat-Sen University, Kaohsiung, 80424, Taiwan. E-mail: ahmedelmahdy@mail.nsysu.edu.tw
bCenter for Theoretical and Computational Physics, National Sun Yat-Sen University, Kaohsiung 80424, Taiwan
cChemistry Department, Faculty of Science, Assiut University, Assiut 71516, Egypt
First published on 21st December 2023
Abstract
Conjugated microporous polymers (CMPs) are attractive materials in numerous interesting fields owing to their microporosity, tunable physicochemical properties, and extended π-conjugated skeletons. However, their limited electrical conductivity restricts their progress as dynamic supercapacitor electrodes. Moreover, dynamic redox building units based on CMPs forming outstanding electrode materials are still unexplored. In the current study, we synthesize and characterize two conjugated microporous polymers (CMPs), abbreviated as TPA-QP and TPA-TBP, which incorporate various redox-active phenazine linkers coupled with triphenylamine (TPA), and then demonstrate them as new supercapacitor electrodes. TPA CMPs display improved surface areas and thermal stabilities of up to 815 m2 g−1 and 77.7%, respectively. The physical and electrochemical properties of these CMPs vary depending on the nature of incorporated phenazine units and CMPs, which provide more active sites and show high capacitance as revealed experimentally and computationally. The TPA CMPs exhibit a superb three-electrode capacitance of 356 F g−1 at a current density of 1 A g−1 with an exceptional stability of 97%, which is comparable to those of earlier reported porous materials. A symmetric double-electrode device incorporating the TPA-QP CMP shows an improved specific capacitance of 235.5 F g−1 at 1 A g−1. The current paper provides a fruitful strategy for synthesizing dynamic electrochemical and redox-active CMPs for futuristic supercapacitors.
1. Introduction
Supercapacitors have been attracting enormous attention recently as energy storage instruments because of their good stabilities, high charge and discharge rates, long lifetimes (up to 105 cycles), and high power densities.1–5 They appear to be particularly suitable for application in electric vehicles, elevators, cranes, and power supply units.6–9 Many diverse materials, including hydroxides, active organic moieties, carbonaceous materials, and metal oxides and sulfides, have been introduced as supercapacitor electrodes.10–13 Supercapacitor electrodes based on inorganic moieties can be hazardous and environmentally destructive, while supercapacitor electrodes based on electroactive organic materials are attractive because of their availability, flexibility, sustainability, and eco-friendliness.13–17 Moreover, the supercapacitances of organic moieties can be modulated through the insertion of heteroatoms or other variations in their structures, with their chemical flexibility broadening their utility in energy storage.15,18–22 In particular, the introduction of nitrogenic sub-blocks within organic moieties can greatly improve their supercapacitance.23,24Phenazines are heterocyclic anthracene derivatives that usually display electrochemical and physical features similar to quinone derivatives. Indeed, phenazines feature a high content of redox-active sites, and their structures are quite similar to those of anthraquinones. Moreover, their reduction can occur through a two-electron mechanism or proton-coupled electron transfer. The redox potentials of phenazines are influenced by the nature of any appended functional groups. For example, functionalizing phenazine derivatives with OH, sulfonate, and carboxylate moieties can modulate their redox voltages in aqueous media.25 Winsberg et al.26 appended a bipolar organic molecule to TEMPO and phenazine derivatives for use as the cathode and anode, respectively, of a redox flow battery (RFB) that exhibited a high cell potential (up to 1.2 V). Wang et al.27 reported phenazine derivatives functionalized with OH and amino groups for aqueous RFBs, with the redox voltages of these materials being influenced by the position and number of OH units. Furthermore, because organic carbonaceous polymers display high structural diversity, good redox properties, and safety, while forming stable radical polymers, they are also efficient materials for storing energy. An obvious question arises: what will be the effect of incorporating phenazine units into such polymers?
Because of their exceptionally variable porosity, metal–organic frameworks (MOFs), conjugated microporous polymers (CMPs), and covalent–organic frameworks (COFs) are the developing polymers for supercapacitors as well as energy storage devices.28–32 In fact, CMPs have properties distinct from those of other porous organic polymers because of their π-conjugated structures and microporous nature and a wide variety of potential building units.33 CMPs have recently been found to display excellent performance in heterogeneous catalysis, photodegradation of dyes, photooxidative coupling of amines, oxidation of sulfides, hydrogen evolution (as photocatalytic materials), and supercapacitors (as electrodes).34–41 Moreover, through simple modification of their chemistry, CMPs can be prepared with high voltage windows and alterable redox performance.42–46 Although both phenazines and CMPs have been examined individually for their characteristics in energy storage, to the best of our knowledge the use of phenazine-based CMPs as supercapacitor electrodes has never been deeply discussed previously.
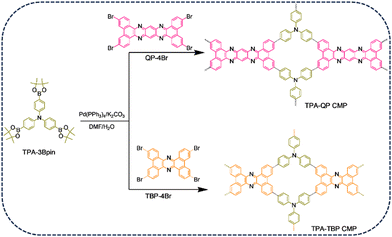
In this present study, we coupled the phenazine derivatives, 3,6,14,17-tetrabromodibenzo[a,c]-dibenzo[5,6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7,8]quinoxalino-[2,3-i]phenazine (QP-4Br) and tetrabromotetrabenzo phenazine (TBP-4Br), possessing different topologies,47 with tris(4-(4,4,5,5-tetramethyl-1,3,2-dioxaborolan-2-yl)phenyl)amine (TPA-3Bpin) to form TPA-QP and TPA-TBP CMPs, respectively (Scheme 1). Owing to their potential charge-transfer ability, phenazine-based derivatives have been applied as promising materials in several applications. Thus, their inherent porosity, charge mobility, and dynamic redox activity make phenazine-based CMPs ideal candidates for supercapacitor electrodes. Interestingly, phenazine can exhibit an improved specific capacitance of up to 356 F g−1; however, in-depth practical and theoretical studies based on the origin of their redox activities have not been reported to date. Furthermore, the TPA-QP CMP can store charges effectively in three-electrode and two-electrode supercapacitors.
7,8]quinoxalino-[2,3-i]phenazine (QP-4Br) and tetrabromotetrabenzo phenazine (TBP-4Br), possessing different topologies,47 with tris(4-(4,4,5,5-tetramethyl-1,3,2-dioxaborolan-2-yl)phenyl)amine (TPA-3Bpin) to form TPA-QP and TPA-TBP CMPs, respectively (Scheme 1). Owing to their potential charge-transfer ability, phenazine-based derivatives have been applied as promising materials in several applications. Thus, their inherent porosity, charge mobility, and dynamic redox activity make phenazine-based CMPs ideal candidates for supercapacitor electrodes. Interestingly, phenazine can exhibit an improved specific capacitance of up to 356 F g−1; however, in-depth practical and theoretical studies based on the origin of their redox activities have not been reported to date. Furthermore, the TPA-QP CMP can store charges effectively in three-electrode and two-electrode supercapacitors.
2. Experimental details
2.1. Materials
All chemicals used in our experiments were of analytical grade, and so they were used without further treatment. Furthermore, we used double distilled water in our work; further details were provided in the ESI.†2.2. Synthesis of tris(4-bromophenyl)amine (TPA-3Br)
We followed the previous report for the synthesis of TPA-3Br.37 In typical procedures, as clarified in Scheme S1 (ESI†), firstly, a 250 mL round bottom flask was charged with triphenylamine (5 g, 4.08 mmol) and DMF (120 mL). Secondly, dissolved NBS (12 g, 12.32 mmol) in DMF (60 mL) was added slowly into the flask and then the reaction was left under continuous stirring overnight in an ice bath. Finally, the product was extracted with dichloromethane (DCM) and then washed again with methanol to obtain a white solid. FTIR scan: 3064, 1570, 1266, and 816 cm−1. 1H NMR scan (400 MHz, 25 °C, CDCl3): δ 7.35 ppm (d, 6H), and 6.921 ppm (d, 6H). 13C NMR scan (CDCl3, 25 °C, 500 MHz): 146.7 ppm, 132.8, 126.01, and 116.38 ppm.2.3. Synthesis of TPA-3Bpin
As clarified in Scheme S2 (ESI†) and according to a typical procedure described in a previous report,48 a 250 mL round bottom flask was charged with previously synthesized TPA-3Br (734 mg, 1.54 mmol), bis(pinacolato)diboron (1.56 g, 6.14 mmol), bis[(diphenylphosphine)-ferrocene]dichloropalladium (101 mg, 0.138 mmol), potassium acetate (4.8 g, 46 mmol), and dry dioxane (50 mL). Flask contents were refluxed overnight under an N2 environment, then cooled and extracted with DCM. Finally, the residue was completely purified by column chromatography in PE-DCM (v/v, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to obtain a white solid. FTIR scan: 2927, 1598, 1517, 1400, and 1140 cm−1. 1H NMR scan (400 MHz, CDCl3), δ (ppm): 7.68 (d, 6H), 7.05 ppm (d, 6H), and 1.34 ppm (s, 36 H). 13C NMR scan (CDCl3, 25 °C, 500 MHz): 150.26, 136.59, 124.34, 84.18, and 24.94 ppm.
1) to obtain a white solid. FTIR scan: 2927, 1598, 1517, 1400, and 1140 cm−1. 1H NMR scan (400 MHz, CDCl3), δ (ppm): 7.68 (d, 6H), 7.05 ppm (d, 6H), and 1.34 ppm (s, 36 H). 13C NMR scan (CDCl3, 25 °C, 500 MHz): 150.26, 136.59, 124.34, 84.18, and 24.94 ppm.
2.4. Synthesis of QP-4Br
3,6,14,17-Tetrabromodibenzo[a,c]-dibenzo[5,6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7,8]-quinoxaline-[2,3-i]phenazine (QP-Br) was synthesized according to a published report47 and as briefed in Scheme S3 (ESI†). A 100 mL round two neck flask was charged with 3,6-dibromophenanthrene-9,10-dione (0.760 g, 2.10 mmol), benzene-1,2,4,5-tetraamine tetrahydrochloride (0.280 g, 1.00 mmol), EtOH (6 mL) and acetic acid (20 mL) and then refluxed up to 100 °C under nitrogen pressure. After that, triethylamine (1 mL) was injected slowly into the flask, and a red color appeared. The flask was left under reflux at 130 °C for another 6 hours. Finally, the product was filtered and dried at 80 °C for further use. FTIR scan: 3051, 1698, 1578, and 1488 cm−1.
7,8]-quinoxaline-[2,3-i]phenazine (QP-Br) was synthesized according to a published report47 and as briefed in Scheme S3 (ESI†). A 100 mL round two neck flask was charged with 3,6-dibromophenanthrene-9,10-dione (0.760 g, 2.10 mmol), benzene-1,2,4,5-tetraamine tetrahydrochloride (0.280 g, 1.00 mmol), EtOH (6 mL) and acetic acid (20 mL) and then refluxed up to 100 °C under nitrogen pressure. After that, triethylamine (1 mL) was injected slowly into the flask, and a red color appeared. The flask was left under reflux at 130 °C for another 6 hours. Finally, the product was filtered and dried at 80 °C for further use. FTIR scan: 3051, 1698, 1578, and 1488 cm−1.
2.5. Synthesis of TBP-4Br
Tetrabromotetrabenzophenazine (TBP-4Br) was synthesized according to a previous report47 and as briefed in Scheme S4 (ESI†). A 250 mL round bottom flask was charged with 3,6-dibromophenanthrene-9,10-diamine chloride (0.88 g, 2.0 mmol), 3,6-dibromophenanthrene-9,10-dione (3,6-DBPD, 0.73 g, 2.0 mmol), ethanol (6 mL), and acetic acid (20 mL) and then the flask temperature was raised to 100 °C. Then, triethylamine (1 mL) was slowly injected into the reaction mixture. Furthermore, the reaction flask was refluxed at 130 °C for 6 hours. Finally, the reaction was cooled to room temperature and then diluted with acetic acid and water before separation and drying. FTIR profile: 3003, 1711, 1599, and 1494 cm−1.2.6. Synthesis of the TPA-QP CMP
As clarified in Scheme S5 (ESI†), the TPA-QP CMP was synthesized via the Suzuki coupling reaction. In brief, a Schlenk tube was charged with TPA-3Bpin (200 mg, 0.32 mmol), TBP-4Br (192.1 mg, 0.24 mmol), K2CO3 (332.6 mg, 2.4 mmol), and Pd(PPh3)4 (50 mg, 0.04 mmol), and then they were evacuated for 15 min. Then, DMF (10.34 mL) and water (1.3 mL) were added to the reaction tube, followed by three cycles of thawing for 15 min each time. Furthermore, the reaction tube was left under magnetic stirring (400 rpm) at 130 °C for 72 hours; after this period, we observed a reddish-brown color. Finally, the product was centrifuged and washed several times with water, methanol, THF, and acetone (using a Soxhlet system) and then dried at 100 °C for further use. FTIR scan: 3008, 1705, and 1598 cm−1.2.7. Synthesis of the TPA-TBP CMP
The TPA-TBP CMP was synthesized via the Suzuki coupling reaction as displayed in Scheme S6 (ESI†). A Schlenk tube was charged with TPA-3Bpin (200 mg, 0.32 mmol), TBP-4Br (167.5, 0.24 mmol), Pd(PPh3)4 (50 mg, 0.04 mmol), and K2CO3 (332.6 mg, 2.4 mmol). The tube contents were degassed for 15 min before adding DMF (10.34 mL) and water(1.3 mL). Before raising the temperature of the reaction tube to 130 °C, the reaction tube was exposed to 3 turns of thaw cycles (15 min per cycle). After 72 hours of continuous stirring at 130 °C, the reaction mixture was cooled to room temperature and then filtered and washed several times with water, methanol, THF, and acetone. Finally, a yellow solid was obtained after the drying process at 100 °C for further usage. FTIR scan: 3003, 1710, and 1603 cm−1.2.8. Working electrode purging
Before usage, the glassy carbon electrode (GCE) was cleaned through sonication for 30 minutes in a water bath and again cleansed with 0.05 μm alumina powder and EtOH and finally dried in air.2.9. Electrochemical characterization
The electrochemical performances of our CMPs were estimated using an Autolab potentiostat (PGSTAT204) in an aqueous electrolyte (1 M KOH). The working electrode and the counter electrode were based on the GCE and Pt wire, respectively, and on the other hand, Hg/HgO (RE-1B, BAS) was employed as a reference electrode, and so every potential was referenced to this Hg/HgO electrode. Samples were synthesized via the mixing of 2 mg of CMP and 2 mg of activated carbon dispersed in water (800 μL) and ethanol (191 μL) via sonication for 30 min, and then 9 μL of Nafion (10% wt%) was charged under continuous sonication for another 1 hour. The tip of the working electrode was coated with 5 μL of the previously synthesized mixture and then dried under vacuum at 70 °C for 30 min. Electrochemical properties were determined via cyclic voltammetry (CV) at sweep rates between 5 and 200 mV s−1 and the galvanostatic charge–discharge (GCD) method in the potential range (0:−1 V) at current densities between 1 and 20 A g−1. The specific capacitances of our CMPs were determined through a GCD diagram using eqn (1).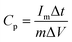 | (1) |
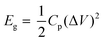 | (2) |
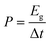 | (3) |
2.10. Coin cell design
The working electrodes of coin cells were designed using a slurry of CMPs (50 wt%), carbon (50 wt%), and Nafion binder (10 wt%) in ethanol (2 mL), coated with carbon foil, and then cut into circle shapes. Afterward, these electrodes were assembled in a coin supercapacitor by constructing two symmetric working electrodes, a carbon separator, and an electrolyte of 1 M KOH.The electrochemical behaviors were determined via CV at various sweep rates (from 5 to 200 mV s−1) and GCD methodology in a potential window of (−0.3 to +0.6 V) at current densities ranging from 1 to 20 A g−1. Importantly, the GCD profile was used to detect the specific capacitance of this coin cell using eqn (1).
2.11. Computational setup
Ab initio simulations within the Kohn–Sham density functional theory (DFT) framework49,50 were performed using the Gaussian software package.51 The hybrid functional B3LYP was used to obtain accurate electronic structure information. Electronic wave functions were represented with the Lanl2DZ basis set. All structures were fully allowed to relax. The convergence criteria for forces were 3 × 10−4 a.u. In addition, van der Waals corrections in the form of Grimme-D3 were added to account for possible weak binding configurations in the structure survey containing 40 initial configurations of a K atom adsorbed on each of the CMPs. The adsorption energies (Ead) were calculated using eqn (4).| Ead = ECMP+K − ECMP − EK | (4) |
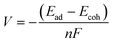 | (5) |
3. Results and discussion
3.1. Materials design and molecular characterization
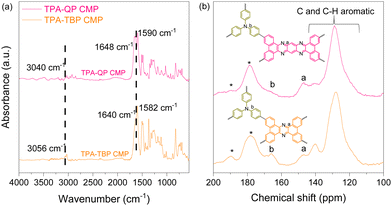
To design novel triphenylamine and phenazine based CMPs featuring various topologies, TPA-3Br, TPA-3Bpin, QP-4Br, and TBP-4Br were synthesized as reported earlier and these novel CMPs were investigated via Fourier transform infrared (FTIR), 1H NMR, and 13C NMR spectroscopy techniques (Schemes S1–S4 and Fig. S1–S8, ESI†).37,47 We applied classical Suzuki coupling reactions, catalyzed by palladium(0), to achieve the synthesis of innovative TPA-QP and TPA-TBP CMPs within 72 h (Schemes S5 and S6, ESI†). FTIR and solid-state (SS) 13C cross-polarization (CP)/magic angle spinning (MAS) nuclear magnetic resonance (NMR) spectroscopy reveal the chemical structures of our CMPs. The FTIR spectrum of the TPA-QP CMP features signals for aromatic C–H, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, and C
N, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds at 3040, 1648, and 1590 cm−1, respectively; the spectrum of the TPA-TBP CMP also features these signals at 3056, 1640, and 1582 cm−1, respectively (Fig. 1a). The absence of signals for B–C or Br–C units confirms the complete coupling of the phenazine units with the CMPs. The 13C SS-NMR spectra of both CMPs (Fig. 1b) confirm the presence of C–N units of the TPA moieties and C
C bonds at 3040, 1648, and 1590 cm−1, respectively; the spectrum of the TPA-TBP CMP also features these signals at 3056, 1640, and 1582 cm−1, respectively (Fig. 1a). The absence of signals for B–C or Br–C units confirms the complete coupling of the phenazine units with the CMPs. The 13C SS-NMR spectra of both CMPs (Fig. 1b) confirm the presence of C–N units of the TPA moieties and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds of phenazine units, with signals at 165 and 147 ppm, respectively, in addition to signals for aryl carbon nuclei in the range of 140–120 ppm.
N bonds of phenazine units, with signals at 165 and 147 ppm, respectively, in addition to signals for aryl carbon nuclei in the range of 140–120 ppm.
As seen in Fig. S9 (ESI†), XPS scans were carried out to determine the relative chemical compositions of the surface and electronic states of nitrogen and carbon in CMP materials. Realistically, unsaturated carbon atoms at carbonaceous edge sites may form structural defects due to nitrogen in the CMP. These flaws are highly reactive with physically adsorbed oxygen, forming oxygen-containing groups when exposed to air.44 The carbon–oxygen bonds in the C 1s spectrum and the wide-scan spectra of the CMP samples demonstrate oxygen functional groups, according to the XPS analysis (Fig. S9a and b, ESI†). Plots of the high-resolution XPS spectra of C1s and N 1s for the two CMP samples are displayed in Fig. S9b and c (ESI†). Three distinct peaks can be seen in the deconvoluted C1s spectra of the TPA-QP and TPA-TBP CMPs (Fig. S9b, ESI†). These three types of C states are identified by the fitting findings for the C 1s spectra of the TPA-QP and TPA-TBP CMP samples, which respectively include sp2 carbons (CC, 283.44 eV), sp2 carbon-containing nitrogen atoms (CN, 285.2 eV), and carbon atoms connected to oxygen (C–O, 285.1 eV). Additionally, deconvolution of the N 1s spectra of TPA-QP and TPA-TBP CMPs reveals an abundance of pair nitrogen forms with centers at approximately 398.22 and 399.36 eV, respectively. These states are attributed to the tertiary N of the TPA moiety alongside sp2-nitrogen, which connects to two carbon atoms in a hexagonal ring (pyridinic-N of the phenazine ring, which donates one π-electron to the aromatic π-system) (Fig. S9c, ESI†). Based on quantitative analysis, the TPA-QP CMP frameworks exhibit the highest abundance of the pyridinic-N chemical state (Table S1, ESI†).
Thermogravimetric analysis (TGA) of our synthesized TPA-QP and TPA-TBP CMPs revealed that they have high thermal decomposition temperatures (Td) for 10% weight-loss (554.8 and 563.1 °C, respectively) and high char yields (77.7 and 77.3%, respectively) (Fig. S10, ESI†). The thermal robustness of these CMPs presumably arose from the high planarity of their phenazine units, facilitating π-stacking processes in the CMP layers. Indeed, the thermal stabilities of these phenazine-based CMPs are superior to those of previously reported CMPs, whose decomposition temperatures have all been less than 400 °C.
3.2. Porosity and morphology
Nitrogen sorption/desorption isotherms confirm the microporous nature of our TPA-QP and TPA-TBP CMPs at 77 K (Fig. 2a and b). These materials show typical type I isotherms with sharp rises at low pressure. The Brunauer–Emmett–Teller surface area (SBET) of the TPA-QP CMP (815 m2 g−1) is almost four times greater than that of the TPA-TBP CMP (238 m2 g−1), presumably due to high fusions of QP units, which improve π-stacking, and planarity of the TPA-QP CMP. Moreover, the pore volumes of the TPA-QP and TPA-TBP CMPs are 1.3 and 0.3 cm3 g−1, respectively. Based on nonlocal density functional theory (DFT), we calculated the pore diameters of TPA-QP and TPA-TBP CMPs to be 1.7 and 2.1 nm, respectively (Fig. 2c and d).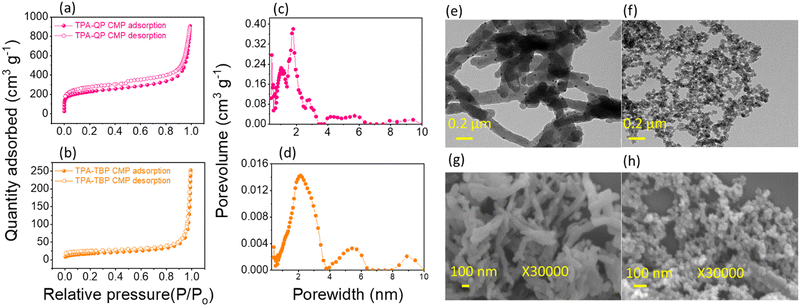 | ||
| Fig. 2 (a) and (b) N2 sorption isotherms at 77 K, (c) and (d) pore-size distributions, and (e) and (f) TEM and (g) and (h) FE-SEM images of the TPA-QP and TPA-TBP CMPs. | ||
We used high-resolution transmission and scanning electron microscopy (TEM and SEM, respectively) to visualize the morphologies of our phenazine CMPs. The TEM images of the TPA-QP CMP indicate that it has a well-ordered nanorod morphology, with the length of nanorods reaching up to several micrometers with a diameter of 52 nm (Fig. 2e). In contrast, TEM revealed that the TPA-TBP CMP has a spherical morphology, with diameters ranging between 16 and 20 nm (Fig. 2f). We attribute the rod-like morphology of the TPA-QP CMP to the coplanarity of its adjacent QP units, achieved through hydrogen bonding between the H and N atoms or possibly even between the H and Br atoms. Moreover, coplanar interactions with neighboring QP units presumably strengthen the packing of the QP-based polymer through face-to-face π-stacking. Because the planarity of TBP-4Br is lower than that of QP-4Br, with a concomitant shorter distance between aromatic planes, it assembles into the TPA-TBP CMP in the form of spheres.47 The nanorod and nano-spherical morphologies of the TPA-QP and TPA-TBP CMPs, respectively, are confirmed through field-effect SEM (FE-SEM; Fig. 1g and h).
Notably, TPA-QP and TPA-TBP CMPs showed amorphous character based on PXRD measurements (Fig. S11, ESI†).
3.3. Electrochemical properties
CMPs have gained a good reputation for their use as supercapacitor electrodes because of their ability to incorporate building blocks displaying diverse characteristics, as well as due to their high surface areas, uniform pore sizes, and variety of morphologies.52 We examined the electrochemical performance of our TPA-QP and TPA-TBP CMPs through cyclic voltammetry (CV), using a three-electrode system with 1 M aqueous KOH as the electrolyte. We recorded the CV curves of asymmetric supercapacitors based on the TPA-QP and TPA-TBP CMPs at various scan rates between 5 and 200 mV s−1 in the potential range between 0 and −1 V (Fig. 3a and b). The rectangular shapes of the CV plots of these phenazine-based CMPs, even at the highest scan rate of 200 mV s−1, provided a preliminary confirmation of their high capacitive performance, with facile kinetics and high rates, suggesting their suitability for application in supercapacitors.53,54 The CV curves of the TPA-QP CMP (Fig. 3a) are quasi-rectangular, indicating that its capacitance behavior is due to electric double layer capacitance (EDLC). Moreover, redox peaks within the CV curves emphasize the pseudocapacitive behavior of the TPA-QP CMP, resulting from the abundance of reversible redox imine groups in the QP units, electrode–electrolyte interactions, and adsorption sites for K+ ions. Consequently, we attribute the capacitance of the TPA-QP electrode to a hybrid of both EDLC and pseudocapacitive mechanisms (Fig. 3a). In contrast, a lack of electrolyte adsorption sites offered by the TBP units meant that the capacitance of the TPA-TBP CMP (Fig. 3b) mainly relies on its surface area; hence, it displays a major EDLC storage mechanism for energy storage.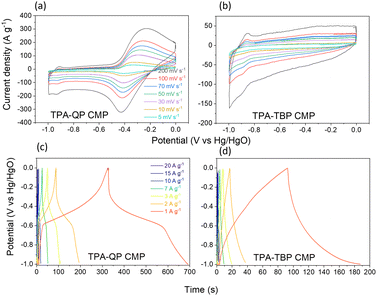 | ||
| Fig. 3 (a) and (b) CV and (c) and (d) GCD profiles of the TPA-QP and TPA-TBP CMPs, scanned in 1 M KOH. | ||
We performed ab initio calculations within the framework of Kohn–Sham DFT to gain insight into the electrochemical properties of the TPA-TBP and TPA-QP CMPs. The materials were modeled along with their monomer units.
Fig. 4 presents the optimized structures of the monomer units. The pores in the TPA-QP CMP have a length of 37.4 Å, a width of 17.1 Å, and a height, due to bending, of 13.2 Å. The dibenzo[a,c]dibenzo[5,6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7,8]quinoxalino[2,3-i]phenazine and triphenylamine rings are bent in opposite directions out of the molecular plane. The inner pores have a quasi-elliptic shape, with estimated axis lengths of 8.1 and 6.0 Å. The pores in the TPA-TBP CMP have a length of 28.9 Å and a width of 15.8 Å. Its phenazine- and triphenylamine-like subunits are bent out of the molecular plane by approximately −4.1 and +6.7 Å, respectively, spanning a total height (i.e., out-of-plane distortion) of approximately 11 Å. The inner pores of the TPA-TBP CMP are similar to those of the TPA-QP CMP, with a quasi-elliptic shape having estimated axis lengths of 8.1 and 6.0 Å. We modeled the redox activity of the CMPs through the adsorption of K+ cations, testing 40 different adsorption sites in each case. The energetically most favorable adsorption sites are similar but differ in their binding energies. In both CMPs, the K+ cations are bound to the pyridine-like rings with a distance of approximately 2.7 Å. The binding energy in the TPA-QP CMP was −1.62 eV and in the TPA-TBP CMP, it was −0.89 eV. Notably, the bending of the subunits in the TPA-QP CMP decreases, resulting in a height of 6.6 Å; in contrast, the bending in the TPA-TBP CMP is not significantly affected. The amounts of charge transfer, based on Mulliken charge analysis, between the K+ cations and the TPA-QP and TPA-TBP CMPs are approximately 0.87 and 0.85 e−, respectively, indicative of a slightly stronger redox process in the former. There is a notable difference (ca. 0.8 eV) in the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) gaps (HLGs) of the TPA-QP and TPA-TBP CMPs (2.08 and 2.86 eV, respectively). Notably, their HOMO energy levels are similar (−5.3 and −5.2 eV, respectively), while their LUMO energy levels differed by 0.9 eV (−3.2 and −2.3 eV, respectively).
7,8]quinoxalino[2,3-i]phenazine and triphenylamine rings are bent in opposite directions out of the molecular plane. The inner pores have a quasi-elliptic shape, with estimated axis lengths of 8.1 and 6.0 Å. The pores in the TPA-TBP CMP have a length of 28.9 Å and a width of 15.8 Å. Its phenazine- and triphenylamine-like subunits are bent out of the molecular plane by approximately −4.1 and +6.7 Å, respectively, spanning a total height (i.e., out-of-plane distortion) of approximately 11 Å. The inner pores of the TPA-TBP CMP are similar to those of the TPA-QP CMP, with a quasi-elliptic shape having estimated axis lengths of 8.1 and 6.0 Å. We modeled the redox activity of the CMPs through the adsorption of K+ cations, testing 40 different adsorption sites in each case. The energetically most favorable adsorption sites are similar but differ in their binding energies. In both CMPs, the K+ cations are bound to the pyridine-like rings with a distance of approximately 2.7 Å. The binding energy in the TPA-QP CMP was −1.62 eV and in the TPA-TBP CMP, it was −0.89 eV. Notably, the bending of the subunits in the TPA-QP CMP decreases, resulting in a height of 6.6 Å; in contrast, the bending in the TPA-TBP CMP is not significantly affected. The amounts of charge transfer, based on Mulliken charge analysis, between the K+ cations and the TPA-QP and TPA-TBP CMPs are approximately 0.87 and 0.85 e−, respectively, indicative of a slightly stronger redox process in the former. There is a notable difference (ca. 0.8 eV) in the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) gaps (HLGs) of the TPA-QP and TPA-TBP CMPs (2.08 and 2.86 eV, respectively). Notably, their HOMO energy levels are similar (−5.3 and −5.2 eV, respectively), while their LUMO energy levels differed by 0.9 eV (−3.2 and −2.3 eV, respectively).
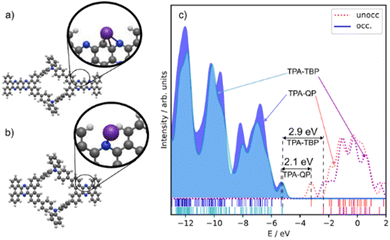 | ||
| Fig. 4 (a) and (b) Optimized structures of the (a) TPA-QP and (b) TPA-TBP monomers; insets: respective positions of attached K+ cations. (c) DOS and HLGs of the TPA-QA and TPA-TBP monomers. | ||
The adsorption energy is related to potentials through the Nernst equation (eqn (4)). The reference potential of K+/K was estimated from its cohesive energy of −0.94 eV.55 The predicted potential for the TMP-QP CMP is +0.68 V and for the TPA-TBP CMP, it is −0.22 V. A negative potential suggests non-working operation conditions. These values agree with the experimental data from the CV curves. Lower peak potentials in CV curves can be due to, for example, changes in solvation affecting the reference potential of K+/K. When aligning the computed potential with the CV data for the TPA-QP CMP, the resulting shift of the TPA-TBP CMP would still be non-working. Calculations at different levels of theory (PBE and B3LYP), in addition to the B3LYP + vdW calculations, are in qualitative agreement, with voltages of 0.52 V (B3LYP) and 0.72 V (PBE) for the TPA-QP CMP and non-working conditions for the TPA-TBP CMP.
We examined the galvanostatic charge/discharge (GCD) cycling of our TPA-QP and TPA-TBP CMPs at various current rates between 1 and 20 A g−1 (Fig. 3c and d). The GCD curve of the TPA-QP CMP has a triangular shape with tenuous bending, suggesting a combination of EDLC and pseudocapacitance mechanics.56 Indeed, the discharging time of the TPA-QP CMP is longer than that of the TPA-TBP CMP, consistent with the higher capacitance of the former (Fig. 3c and d). From the GCD curves and eqn (1), we calculated the specific capacitances of the TPA-QP and TPA-TBP CMPs at a current density of 1 A g−1 to be 356 and 88 F g−1, respectively (Fig. 5a). We attribute the high supercapacitance of our CMPs to their high surface areas, porosities, and content of N atoms, all of which facilitated the electrolyte to access the electrode surface.57
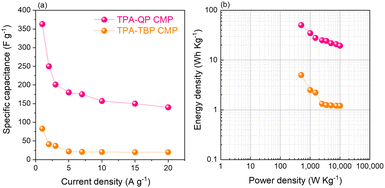 | ||
| Fig. 5 Corresponding specific capacitances of TPA-QP and TPA-TBP CMP cells (a) and Ragone plot of TPA-QP and TPA-TBP CMP cells (b). | ||
Moreover, the abundance of adsorption sites for K+ ions and the high surface area within the TPA-QP CMP played the most important roles in enhancing its supercapacitance and facilitating surface wettability for electrolyte ion transfer as theoretically elucidated. Notably, the capacitances of CMPs can decrease upon increasing the current density, due to rate limitations for the adsorption of ions into the active materials. Ragone plots based on eqn (2) and (3) in the voltage window between −1 and 0 V confirmed that the power density of the TPA-QP CMP is higher than that of the TPA-TBP CMP (Fig. 5b). Notably, the TPA-QP and TPA-TBP CMPs display energy densities of 50.42 and 5 W h kg−1 respectively at a current density of 500 W kg−1. Furthermore, these Ragone plots reveal that the power densities of cells based on our TPA-QP and TPA-TBP CMPs can reach higher than those of other reported capacitors as clarified in Table S2 (ESI†). The energy and power densities of the TPA-QP CMP are higher than those of the TPA-TBP CMP, presumably because of the higher surface area of the former. Although poor stability can be a drawback of conducting polymers, due to their swelling and shrinking, during charging/discharging cycling,58 our TPA-QP and TPA-TBP CMPs display high durability, even after 2000 cycles at a current density of 10 A g−1 (Fig. S12, ESI†), with retention capacitances of up to 97 and 90%, respectively. Furthermore, electrochemical impedance spectroscopy (EIS) (Fig. S13, ESI†) reveals the excellent structural stability of their electrical interfaces during cycling, in addition to their low electron resistances. As such, the specific capacitances of the TPA-QP and TPA-TBP CMPs are higher than those of several recently reported porous polymers (e.g., TBN-TPE and TBN-Car CMPs and a TBN-Car-CMP/SWCNT blend). For example, DeBlase et al.,59 reported specific capacitances of up to 202 F g−1 at a current density of 1 A g−1 for N-doped porous nanofibers, while Park et al.,60 reported a value of 71 F g−1 at a corresponding current density of 1 A g−1 for a nanoparticulate CMP (N-CMP). Table S3 (ESI†) compares the capacitances of previously reported materials with those of our phenazine CMPs.
The aforementioned capacitive impact on the overall capacity of the TPA-QP CMP has been determined using the following eqn (6) and (7):
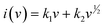 | (6) |
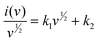 | (7) |
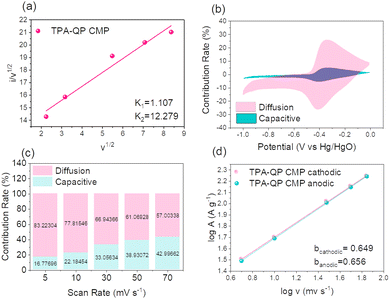
Fig. 6b demonstrates that the TPA-QP CMP contributed 16.77% of its total capacity through capacitive impacts at a rate of 5 mV s−1, hence validating the TPA-QP CMP's suitable capacitive service. Realistically, from 5 mV s−1 to 70 mV s−1, the capacitive impact grew with the scan rate, reaching values of 42.99% for the TPA-QP CMP (Fig. 6c). This results from the ion diffusion into the CMP network taking place faster during rapid scan rates.
In order to better understand the capacitive impact of the TPA-QP CMP, we utilized the power equation (eqn (8)) to examine the correlation between current (i) and the scan rate (v).
| i = avb | (8) |
Importantly, the coin cell CR2032 based on the TPA-QP CMP proves its validation over the potential window of −0.3 to +0.6 V and showed an improved capacitance of up to 235.5 F g−1 at 1 A g−1 in addition to an energy density of 32.7 W h Kg−1 (Fig. S14, ESI†).
4. Conclusion
In this study, we have used classical Suzuki condensations to prepare two new redox-active CMPs containing triphenylamine and phenazine linkers (TPA-QP and TPA-TBP CMPs). These CMPs possessed high thermal stabilities, smooth morphologies, and high surface areas. In particular, the TPA-QP CMP showed an excellent electrochemical capacitance due to the higher percentage of adsorption units for electrolyte ions (K+) within its molecular structure, in addition to its higher surface area. We theoretically discussed the importance of adsorption sites for electrolyte ions (K+) with phenazine CMP electrodes. These phenazine-based CMPs displayed a highly stable capacitance, even after 2000 cycles, with over 97% of the original capacitance retained when operated at a current density of 10 A g−1. We suspect that we should be able to exploit the high capacitance of the TPA-QP CMP shortly for several applications. Furthermore, in addition to identifying highly efficient supercapacitor electrodes, this study suggests a viable strategy for tuning the energy storage mechanisms of ultracapacitors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported financially by the Ministry of Science and Technology, Taiwan, under contracts NSTC 112-2221-E-110-005-MY3, 111-2221-E-110-003, and 112-2218-E-110-007.Notes and references
- G. Pacchioni, Nat. Rev. Mater., 2019, 4, 625 CrossRef CAS.
- P. Zhang, M. Wang, Y. Liu, S. Yang, F. Wang, Y. Li, G. Chen, Z. Li, G. Wang and M. Zhu, J. Am. Chem. Soc., 2021, 143, 10168–10176 CrossRef CAS PubMed.
- J. Yu, C. Yu, X. Song, Q. Zhang, Z. Wang, Y. Xie, Y. Liu, W. Li, Y. Ding and J. Qiu, J. Am. Chem. Soc., 2023, 25, 13828–13838 CrossRef.
- L. Qing and J. Jiang, ACS Nano, 2023, 17, 17122–17130 CrossRef CAS PubMed.
- X. Wang, X. Lu, B. Liu, D. Chen, Y. Tong and G. Shen, Adv. Mater., 2014, 26, 4763–4782 CrossRef CAS PubMed.
- F. Li, Y. Gao, Y. Wu, Y. Xia, C. Wang, J. Hu and Z. Huang, Energy Convers. Manage., 2023, 293, 117480 CrossRef.
- S. Satpathy, N. K. Misra, D. Kumar Shukla, V. Goyal, B. K. Bhattacharyya and C. S. Yadav, J. Energy Storage, 2023, 57, 106198 CrossRef.
- F. Tao, Z. Fu, H. Gong, B. Ji and Y. Zhou, Energy, 2023, 283, 129173 CrossRef.
- W. Jin, Y. Gao, H. Zhang and B. Jin, IEEE Trans. Veh. Technol., 2023, 72, 11437–11445 Search PubMed.
- Q. Huang, A. Zeb, Z. Xu, S. Sahar, J.-E. Zhou, X. Lin, Z. Wu, R. C. K. Reddy, X. Xiao and L. Hu, Coord. Chem. Rev., 2023, 494, 215335 CrossRef CAS.
- R. I. Mohanty, A. Mukherjee, P. Bhanja and B. K. Jena, J Energy Storage, 2023, 72, 108730 CrossRef.
- I. Hussain, I. Shaheen, R. Ahmad, I. Ali, K. Hussain, S. S. Hussain, N. S. Alsaiari, K. M. Katubi, S. M. Eldin and M. Z. Ansari, Chemosphere, 2023, 314, 137660 CrossRef CAS PubMed.
- B. Zheng, X. Lin, X. Zhang, D. Wu and K. Matyjaszewski, Adv. Funct. Mater., 2020, 30, 1907006 CrossRef CAS.
- A. Yadav, H. Kumar, R. Sharma and R. Kumari, Surf. Interfaces, 2023, 39, 102925 CrossRef CAS.
- P. Poizot, J. Gaubicher, S. Renault, L. Dubois, Y. Liang and Y. Yao, Chem. Rev., 2020, 120, 6490–6557 CrossRef CAS PubMed.
- M. M. Ayad, W. A. Amer, M. G. Kotp, I. M. Minisy, A. F. Rehab, D. Kopecký and P. Fitl, RSC Adv., 2017, 7, 18553–18560 RSC.
- M. M. Ayad, W. A. Amer and M. G. Kotp, Mol. Catal., 2017, 439, 72–80 CrossRef CAS.
- M. G. Kotp, C.-L. Chang and A. F. M. EL-Mahdy, J. Water Process Eng., 2023, 53, 103675 CrossRef.
- P. Thondaiman, C. J. Raj, R. Manikandan, V. Cristobal, C. Kaya and B. C. Kim, Sustain. Mater. Technol., 2023, e00742 CAS.
- T. A. Gaber, L. R. Ahmed and A. F. M. EL-Mahdy, J. Mater. Chem. A, 2023, 11, 19408–19417 RSC.
- J. Zhan and A. F. M. EL-Mahdy, Chem. Eng. J., 2023, 473, 145124 CrossRef CAS.
- Y. Liao, H. Wang, M. Zhu and A. Thomas, Adv. Mater., 2018, 30, 1705710 CrossRef PubMed.
- M. B. Arvas, H. Gürsu, M. Gencten and Y. Sahin, J Energy Storage, 2021, 35, 102328 CrossRef.
- M. Ahmed, M. G. Kotp, T. H. Mansoure, R.-H. Lee, S.-W. Kuo and A. F. M. EL-Mahdy, Microporous Mesoporous Mater., 2022, 333, 111766 CrossRef CAS.
- A. Hollas, X. Wei, V. Murugesan, Z. Nie, B. Li, D. Reed, J. Liu, V. Sprenkle and W. Wang, Nat. Energy, 2018, 3, 508–514 CrossRef CAS.
- J. Winsberg, C. Stolze, S. Muench, F. Liedl, M. D. Hager and U. S. Schubert, ACS Energy Lett., 2016, 1, 976–980 CrossRef CAS.
- C. Wang, X. Li, B. Yu, Y. Wang, Z. Yang, H. Wang, H. Lin, J. Ma, G. Li and Z. Jin, ACS Energy Lett., 2020, 5, 411–417 CrossRef CAS.
- D. Y. Lee, D. V. Shinde, E.-K. Kim, W. Lee, I.-W. Oh, N. K. Shrestha, J. K. Lee and S.-H. Han, Microporous Mesoporous Mater., 2013, 171, 53–57 CrossRef CAS.
- S. A. Patil, P. K. Katkar, M. Kaseem, G. Nazir, S.-W. Lee, H. Patil, H. Kim, V. K. Magotra, H. B. Thi, H. Im and N. K. Shrestha, Nanomaterials, 2023, 13, 1587 CrossRef CAS PubMed.
- A. I. Inamdar, H. S. Chavan, G. Shin, J. Han, S. Yeon, S. Park, S. A. Patil, N. K. Shrestha, H. Kim and H. Im, Int. J. Energy Res., 2022, 46, 17220–17229 CrossRef CAS.
- H. Zuo, J. Duan, B. Lyu, W. Lyu, Y. Li, X. Mei and Y. Liao, Macromol. Rapid Commun., 2023, 2300238 Search PubMed.
- D. Y. Lee, S. J. Yoon, N. K. Shrestha, S.-H. Lee, H. Ahn and S.-H. Han, Microporous Mesoporous Mater., 2012, 153, 163–165 CrossRef CAS.
- W. Zhang, H. Zuo, Z. Cheng, Y. Shi, Z. Guo, N. Meng, A. Thomas and Y. Liao, Adv. Mater., 2022, 34, 2104952 CrossRef CAS PubMed.
- T.-L. Lee, A. M. Elewa, M. G. Kotp, H.-H. Chou and A. F. M. EL-Mahdy, Chem. Commun., 2021, 57, 11968–11971 RSC.
- J.-S. M. Lee and A. I. Cooper, Chem. Rev., 2020, 120, 2171–2214 CrossRef CAS PubMed.
- M. G. Mohamed, A. F. M. EL-Mahdy, M. G. Kotp and S.-W. Kuo, Mater. Adv., 2022, 3, 707–733 RSC.
- M. G. Kotp, S. U. Sharma, J.-T. Lee, A. F. M. EL-Mahdy and S.-W. Kuo, J. Taiwan Inst. Chem. Eng., 2022, 134, 104310 CrossRef CAS.
- M. G. Kotp, N. L. Torad, J. Lüder, A. El-Amir, W. Chaikittisilp, Y. Yamauchi and A. F. M. EL-Mahdy, J. Mater. Chem. A, 2023, 11, 764–774 RSC.
- M. G. Kotp, A. M. Elewa, A. F. M. EL-Mahdy, H.-H. Chou and S.-W. Kuo, ACS Appl. Energy Mater., 2021, 4, 13140–13151 CrossRef CAS.
- Y. Liu, X. Jiang, L. Chen, Y. Cui, Q.-Y. Li, X. Zhao, X. Han, Y.-C. Zheng and X.-J. Wang, J. Mater. Chem. A, 2023, 11, 1208–1215 RSC.
- F. Chu, Y. Hu, K. Zhang, X. Li, G. Zhao, X. Huang and G. Wang, J. Colloid Interface Sci., 2023, 634, 159–168 CrossRef CAS PubMed.
- M. G. Kotp, A. F. M. EL-Mahdy, T.-L. Yang and S.-W. Kuo, Microporous Mesoporous Mater., 2022, 331, 111669 CrossRef CAS.
- A. F. M. EL-Mahdy, J. Lüder, M. G. Kotp and S.-W. Kuo, Polymers, 2021, 13, 1385 CrossRef CAS PubMed.
- M. G. Kotp, N. L. Torad, H. Nara, W. Chaikittisilp, J. You, Y. Yamauchi, A. F. M. EL-Mahdy and S.-W. Kuo, J. Mater. Chem. A, 2023, 11, 15022–15032 RSC.
- W. Du, X. Du, M. Ma, S. Huang, X. Sun and L. Xiong, Adv. Funct. Mater., 2022, 32, 2110871 CrossRef CAS.
- R. Iqbal, G. Yasin, M. Hamza, S. Ibraheem, B. Ullah, A. Saleem, S. Ali, S. Hussain, T. A. Nguyen and Y. Slimani, Coord. Chem. Rev., 2021, 447, 214152 CrossRef CAS.
- W. Liu, M. Ulaganathan, I. Abdelwahab, X. Luo, Z. Chen, S. J. Rong Tan, X. Wang, Y. Liu, D. Geng, Y. Bao, J. Chen and K. Ping Loh, ACS Nano, 2018, 12, 852–860 CrossRef CAS PubMed.
- Y. Zhang, X. Bao, M. Xiao, H. Tan, Q. Tao, Y. Wang, Y. Liu, R. Yang and W. Zhu, J. Mater. Chem. A, 2015, 3, 886–893 RSC.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsuji, Gaussian 16, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- W. Lyu, C. Yan, Z. Chen, J. Chen, H. Zuo, L. Teng, H. Liu, L. Wang and Y. Liao, ACS Appl. Energy Mater., 2022, 5, 3706–3714 CrossRef.
- A. Alabadi, X. Yang, Z. Dong, Z. Li and B. Tan, J. Mater. Chem. A, 2014, 2, 11697–11705 RSC.
- Y. Kou, Y. Xu, Z. Guo and D. Jiang, Angew. Chem., 2011, 123, 8912–8916 CrossRef.
- G. I. Csonka, J. P. Perdew, A. Ruzsinszky, P. H. Philipsen, S. Lebègue, J. Paier, O. A. Vydrov and J. G. Ángyán, Phys. Rev. B, 2009, 79, 155107 CrossRef.
- L. Ma, R. Liu, H. Niu, L. Xing, L. Liu and Y. Huang, ACS Appl. Mater. Interfaces, 2016, 8, 33608–33618 CrossRef CAS PubMed.
- F. Hu, J. Wang, S. Hu, L. Li, W. Shao, J. Qiu, Z. Lei, W. Deng and X. Jian, ACS Appl. Mater. Interfaces, 2017, 9, 31940–31949 CrossRef CAS PubMed.
- G. A. Snook, P. Kao and A. S. Best, J. Power Sources, 2011, 196, 1–12 CrossRef CAS.
- C. R. Deblase, K. Hernández-Burgos, K. E. Silberstein, G. G. Rodríguez-Calero, R. P. Bisbey, H. D. Abruña and W. R. Dichtel, ACS Nano, 2015, 9, 3178–3183 CrossRef CAS PubMed.
- S. Y. Park, C. W. Kang, S. M. Lee, H. J. Kim, Y.-J. Ko, J. Choi and S. U. Son, Chem. – Eur. J., 2020, 26, 12343–12348 CrossRef CAS PubMed.
- E. Lim, C. Jo, H. Kim, M.-H. Kim, Y. Mun, J. Chun, Y. Ye, J. Hwang, K.-S. Ha and K. C. Roh, ACS Nano, 2015, 9, 7497–7505 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma00979c |
| This journal is © The Royal Society of Chemistry 2024 |