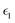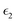Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Three component superlattice enhanced stability for photovoltaic applications: a first principles study
Amanda
Liu
 and
Xuan
Luo
and
Xuan
Luo
 *
*
National Graphene Research and Development Center, Springfield, Virginia 22151, USA. E-mail: xluo@ngrd.org
First published on 24th May 2024
Abstract
The use of superlattices is an attractive method to improve the stability and optoelectronic properties for enhanced photovoltaic performance. In this study, we construct ten superlattices composed of three unit cells of methylammonium tin halide perovskites MASnI3, MASnBr3, and MASnCl3, a structure never considered before. First-principles density functional theory (DFT) calculations are perfomed on the new trilayer superlattice to explore the effects of stacking order on its structural, electronic, and optical properties. The results show that all studied materials exhibit improved thermodynamic stability and adjustable bandgaps, demonstrating the effectiveness of the superlattice structures. In particular, MASnI3/MASnI3/MASnI3, MASnI3/MASnBr3/MASnI3, and MASnI3/MASnCl3/MASnI3 have small binding energies and bandgaps of 1.56, 1.58, and 1.46 eV respectively, which are suitable for high-efficiency photovoltaic materials. The absorption spectrum and photovoltaic parameters also reveal their high optical absorption (over 105 cm−1) in the entire visible light region and theoretical efficiences reaching over 20%, proving the potential of these three superlattices as novel nontoxic perovskite materials for photovoltaic and optoelectronic applications.
Introduction
The exhaustion of fossil fuel resources has attracted considerable attention to the development of solar energy as a renewable and sustainable energy.1 Although silicon currently dominates the market with an efficiency of 27.6%,2 it requires extremely high purity to function well in electronic devices.3 Consequently, researchers have turned their focus on perovskite solar cells (PSCs) which exhibit great potential to become the next generation photovoltaic technology.4 Unlike their silicon counterparts, perovskite-based photovoltaics are characterized by a higher defect tolerance, making it possible for PSCs to achieve high performing devices.5,6 In recent years, organic–inorganic halide perovskites have demonstrated a rapid improvement of power conversion efficiency (PCE), from 3.8% in 2009 to 26.1% today.7,8 Methylammonium (MA) lead iodide (MAPbI3) has emerged as the most promising candidate for PSCs with its tunable bandgap, strong light absorption, and high PCE exceeding 25%.9–11 However, lead-based perovskites face many limitations, most notably from the toxic nature of lead (Pb) and poor stability which restricts their commercial applications.12Overcoming these problems has motivated researchers to seek new alternative materials. The general structure for metal halide perovskites is ABX3, where A is an organic or inorganic cation, B is a metal cation, and X is a halogen anion. An effective method to reduce the toxicity and degradation issues is to change the composition of elements in the ABX3 structure by mixing or partially substituting the metal cations.13 It has been reported that Sn2+ and Ge2+ may be considered as potential environmentally friendly replacements for lead due to their similar electronic configurations and interesting optoelectronic properties.14 Roknuzzaman et al. investigated the physical properties of lead-free MABX3 (B = Sn, Ge; X = I, Br, Cl) compared with its Pb containing counterparts MAPbX3 (X = I, Br, Cl) and found Sn to be the most effective Pb replacement due to its excellent electrical and optical properties.15,16 Noel et al. has also experimentally fabricated a completely lead free perovskite solar cell yielding efficiencies of over 6% by using MASnI3 as the absorber layer.17 These results led Sn-based materials to be of great interest as low toxicity lead-free perovskites for photovoltaics and optoelectronics.
Besides changing the composition of the general perovskite structure through substitution or doping, the use of superlattice materials are promising for a variety of applications.18 Previous research has revealed how the unique superlattice structuring and periodicity can influence the geometric and electronic properties to design low bandgap semiconductors.19,20 There has been a large number of theoretical and experimental research performed on inorganic perovskite superlattices.21–24 Applying these superlattice structures to current hybrid organic–inorganic perovskites could be a potential strategy for developing stable and high-performance perovskites. Singh et al. successfully synthesized MAPbI3/MASnI3 to understand the electronic transport properties and demonstrated how constructing superlattices provides the opportunity for bandgap engineering.25 As shown in the work of Li et al., different layered superlattice structures combining MAPbI2BF4 and CsPbI2BF4 with conventional perovskites (CsPbI3, MAPbI3, and FAPbI3) also indicated high stability with excellent optical absorption properties.26 In addition to the electronic and optical properties, superlattice-monolayer structures have obtained a thermoelectric figure of merit much higher than existing monolayer and 2D thermoelectric materials reported so far.27 The Seebeck coefficient and lattice thermal conductivity should be further studied with such heterostructures to maximize thermoelectric performance.
Research has shown that the bandgaps of perovskites can be tuned by the compositional engineering of the halide ion.28,29 Moreover, altering the halogen atom can also increase the stability of the atomic structure of mixed-halide perovskites as well as absorb broadly across the solar spectrum.30,31 However, no related superlattice investigations have been done for lead-free halide materials. Thus, this study utilizes its uniqueness to construct a superlattice structure of tin-based organic–inorganic trihalide perovskites MASnX3/MASnY3/MASnZ3, where each material is composed of the halide ion I, Br, or Cl, independently.
In this density functional theory (DFT) study, we analyze the impact of changing the halide species of each superlattice layer on the material's properties. The structural, electronic, and optical properties of MASnX3/MASnY3/MASnZ3 (X, Y, and Z = I, Br, or Cl) were studied using first-principles calculations. To better understand the photovoltaic mechanism, the binding energy, electronic structure, bandgap, partial density of states, and optical absorption spectra have been analyzed. We will report our computational method, calculated results, and a discussion of our findings as well as their use for future studies.
Methods
Computational details
We performed first-principle calculations based on density functional theory (DFT) using the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE)32 format implemented in the ABINIT33 code. We use the projected augmented wave (PAW) method34 to generate pseudopotentials using the ATOMPAW code.35,36 The electron configurations and radius cut-offs used to generate these PAW pseudopotentials are listed in Table 1.| Element | Electron configuration | Radius cut-off (bohr) |
|---|---|---|
| Hydrogen (H) | 1s2 | 1.00 |
| Carbon (C) | 2s22p2 | 1.50 |
| Nitrogen (N) | 2s22p3 | 1.20 |
| Tin (Sn) | 5s25p24d10 | 2.50 |
| Iodide (I) | 5s25p5 | 2.30 |
| Bromide (Br) | 4s24p5 | 2.20 |
| Chloride (Cl) | 3s23p5 | 1.80 |
The kinetic energy cut-off and Monkhorst–Pack k-point grid were converged for each material through self-consistent field (SCF) total energy calculations. The SCF iterations were terminated when the total energy difference was less than the set criterion of 1.0 × 10−10 Hartree twice consecutively. The kinetic energy cut-off, Monkhorst–Pack k-point grid, and vacuum height of the superlattice were considered converged once the total energy difference between consecutive datasets were less than 1.0 × 10−4 Hartree (about 3 meV) twice.
With the converged kinetic energy cut-off, k-point grid, and vacuum, the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method37 was used to perform structural relaxation calculations to optimize the atomic structure. The atomic positions and the cell parameters were then relaxed until the force on each atom was below 5.0 × 10−5 hartree bohr−1 (about 3 meV Å−1). After relaxation, the electronic structure and optical properties were analyzed.
Material
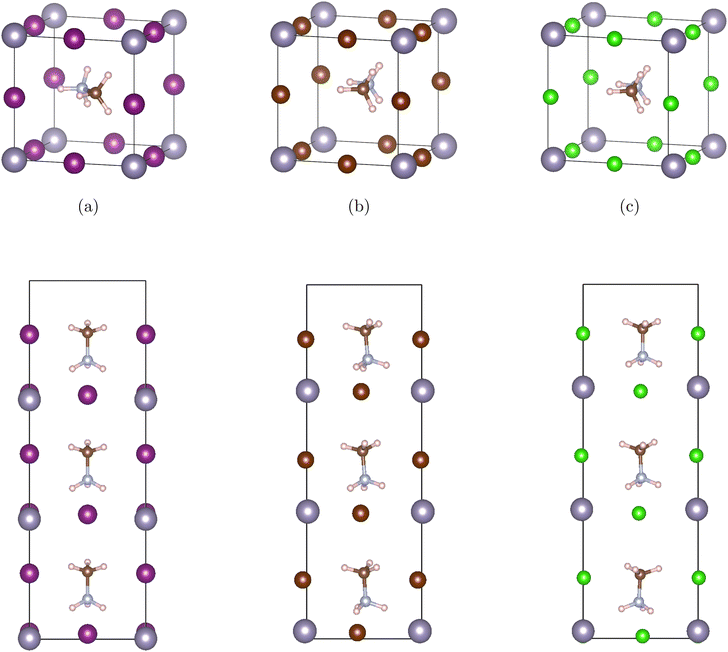
Our materials are based on the organic–inorganic halide perovskites MASnX3 (X = I, Br, Cl). The initial lattice constant and position of bulk cubic MASnI3 were retrieved from previous research.38,39 In cubic ABX3 perovskite structures, the A atom is in Wyckoff position 1b with fractional coordinates (0.5 0.5 0.5), the B atom resides in 1a (0 0 0), and X atoms in the 3d Wyckoff position (0.5 0 0), (0 0.5 0), (0 0 0.5). For the current organic–inorganic perovskites, the A atom is occupied by MA and each unit cell contains 28 atoms. Fig. 1 (top) shows the bulk (a) MASnI3, (b) MASnBr3, and (c) MASnCl3 structures.The corresponding superlattices of the cubic halide perovskites can be seen in Fig. 1 (bottom). The structures are constructed by stacking three cubic cells of MASnX3 (X = I, Br, Cl) to create a superlattice composed of 3 pristine perovskites. With this method, we formed 10 total superlattices from a combination of conventional halide perovskites. These materials, after fully optimized, are employed in band structure and Bethe–Salpeter (BSE) calculations.
Binding energy
Since the supercells of most of the considered superlattice structures differ, it is important to study the stability of the superlattice structures. The relative stability of these hybrid structures can be calculated based on the binding energies (Eb):40| Eb = E[MASnX3/MASnY3/MASnZ3] − E[MASnX3] − E[MASnY3] − E[MASnZ3] | (1) |
Electronic structure
The electronic structure was analyzed through the band structure and density of states (DOS). We calculated the band structure of the lead-free halide perovskite superlattices along the high-symmetry k-points of the first Brillouin zone Γ(0 0 0), X(0 0.5 0), M(0.5 0.5 0), X(0.5 0 0). Using the optimized lattice parameters and atomic structures, we calculated the partial density of states (PDOS) for all compounds to further understand the nature and formation of the energy bands.In this current research, DFT calculations with GGA–PBE generally underestimate bandgaps for most crystalline solids relative to their experimental value, which has been accepted internationally for the result of the function itself. In order to predict the experimental bandgap from the standard DFT calculation for practical applications of solar cells, we correct the theoretical bandgap values using the equation:41
| Ecg(corrected) = (Eg(GGA–PBE) × 1.358 + 0.125) × 0.998 + 0.014 | (2) |
Optical calculations
The macroscopic dielectric function is calculated using the Beth–Salpeter approach from the ABINIT software. A standard excitonic calculation within the Tamm–Dancoff approximation (TDA) using the Haydock iterative technique is performed. In the Beth–Salpeter calculation, the iterative method was stopped when the difference between two consecutive evaluations of dielectric function was less than 0.05 eV and the screening was formatted with an unsymmetrical k-mesh (shifted along the primitive axis by 0.11, 0.21, and 0.31). With these conditions, we computed the dielectric constants.The optical properties of perovskite materials can be expressed by the complex dielectric function:
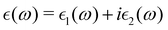 | (3) |
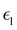 and
and 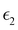 are the real and imaginary parts of the dielectric function, respectively. The real and imaginary coefficients can be calculated with the Kramers–Kronig relations:42,43
are the real and imaginary parts of the dielectric function, respectively. The real and imaginary coefficients can be calculated with the Kramers–Kronig relations:42,43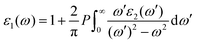 | (4) |
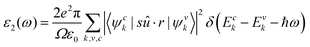 | (5) |
Using 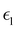 and
and 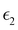 , the extinction coefficient k(ω) is represented by the following equation.44 The absorption coefficient α(ω) can then be calculated with respect to k(ω) and the wavelength (λ):
, the extinction coefficient k(ω) is represented by the following equation.44 The absorption coefficient α(ω) can then be calculated with respect to k(ω) and the wavelength (λ):
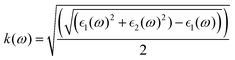 | (6) |
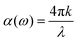 | (7) |
Photovoltaic paramaters
For perovskite superlattices with an optical bandgap Eg, the short circuit current, open circuit voltage, and theoretical power conversion efficiency can be calculated by assuming that all photons with energy larger than Eg are absorbed and produce electron–hole pairs.45 The short-circuit current density JSC is calculated by integrating the product of the material's absorbance A(E) and the incident solar spectrum Isun(E) over the relevant energy range:46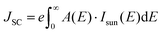 | (8) |
The open circuit voltage VOC can be estimated with the formula:47
| eVOC = (Eg − Eloss) | (9) |
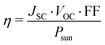 | (10) |
Results and discussion
Structural properties
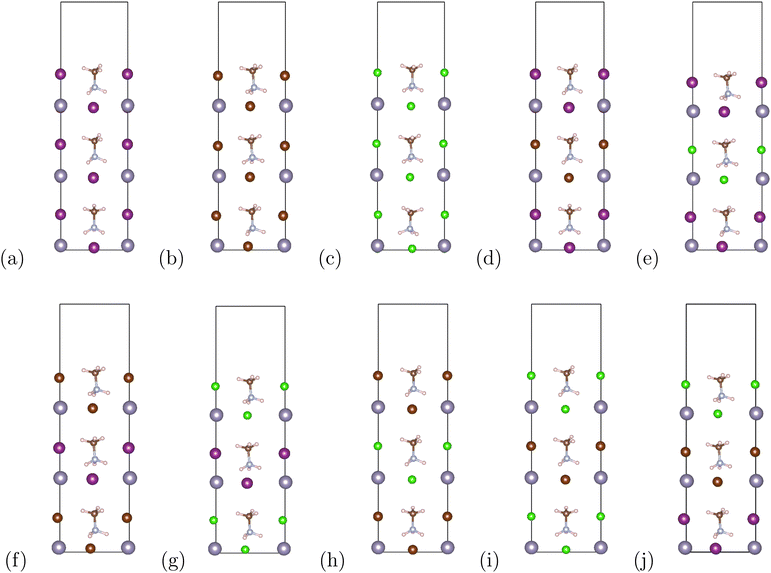
The organic–inorganic hybrid perovskite superlattices MASnX3/MASnY3/MASnZ3 possess a structure of three conventional MASnX3 perovskites. The vacuum was converged with a value of 7 Bohr and the atomic structures were relaxed. The energy cutoff was converged at 24 Hartree and k-point mesh at 4 × 4 × 1. Based on the optimized lattice parameters, we construct 10 symmetrical superlattices, as shown in Fig. 2 which displays the side views of these mixed halide structures.Our converged lattice parameters and their available experimental data are listed in Table 2. To our knowledge, only the perovskites of the form MASnX3 have been synthesized experimentally. It can be seen that for those compounds, the relaxed lattice constants are in a fair agreement with the reported experimental values, with all having less than 4% difference from the experimental data. The superlattices mainly preserve the structure and lattice parameters of the pristine perovskites. For example, the thickness of planar MASnI3/MASnI3/MASnI3 is stretched slightly from 6.239 Å in cubic MASnI3 to 6.392 Å in the superlattice. From Table 2, we can also observe that with the replacement of I to Br and Cl, the optimized lattice parameters of the superlattices present an evident shrink due to the decreasing atomic radius at the halogen site.
| Current materials | Lattice constants (Å) | |||||
|---|---|---|---|---|---|---|
| a | b | c | Exp. | % Error | E b | |
| MASnI3 | 6.239 | 6.239 | 6.239 | 6.24351 | 0.06 | — |
| MASnBr3 | 6.126 | 6.126 | 6.126 | 5.90552 | 3.74 | — |
| MASnCl3 | 5.926 | 5.926 | 5.926 | 5.76053 | 2.88 | — |
| MASnI3/MASnI3/MASnI3 | 6.392 | 6.392 | 23.091 | — | — | −0.40 |
| MASnBr3/MASnBr3/MASnBr3 | 6.128 | 6.128 | 22.136 | — | — | −0.03 |
| MASnCl3/MASnCl3/MASnCl3 | 5.934 | 5.934 | 21.437 | — | — | −0.11 |
| MASnI3/MASnBr3/MASnI3 | 6.355 | 6.355 | 22.957 | — | — | −0.30 |
| MASnI3/MASnCl3/MASnI3 | 6.353 | 6.353 | 22.949 | — | — | −0.33 |
| MASnBr3/MASnI3/MASnBr3 | 6.316 | 6.316 | 22.815 | — | — | −0.16 |
| MASnCl3/MASnI3/MASnCl3 | 6.272 | 6.272 | 22.657 | — | — | −0.22 |
| MASnBr3/MASnCl3/MASnBr3 | 6.078 | 6.078 | 21.956 | — | — | −0.05 |
| MASnCl3/MASnBr3/MASnCl3 | 6.035 | 6.035 | 21.801 | — | — | −0.08 |
| MASnI3/MASnBr3/MASnCl3 | 6.258 | 6.258 | 22.606 | — | — | −0.19 |
The binding energies of the superlattices are also listed in Table 2. We first calculated the total energies of structures with a surface to determine its effect on the binding energies. After comparing the energy differences with the bulk superlattices, we found that surface energy was negligible and disregarded its influence. All of the considered superlattices had negative binding energies, indicating they are more stable than each of the perovskite structures alone and exhibit good thermodynamic stability.26,54 It is also reflective of the suitable lattice constants match between the different perovskite compounds compromising the superlattice because lattice mismatch could destabilize the crystal structure.55 It can be seen that according to eqn (2), the binding energies of MASnI3/MASnI3/MASnI3, MASnI3/MASnBr3/MASnI3, and MASnI3/MASnCl3/MASnI3 are more negative compared to the other materials, indicating that these superlattices are the most stable.
Electronic properties
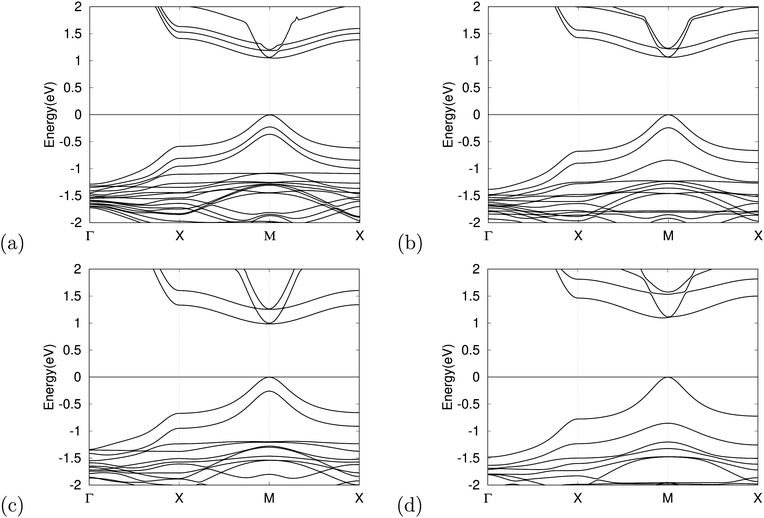
The band structure has an important impact on the optical properties, which is crucial in evaluating potential materials for solar cell applications. For this reason, we calculated the band structures of the optimized MASnX3/MASnY3/MASnZ3 perovskite structures for X, Y, and Z = I, Br, or Cl each. Fig. 3 shows the band structures of single halogen (MASnI3)3 and some mixed-halide superlattices plotted from −2 to +2 eV with the Fermi level at the VBM set to zero. It can be seen that both the valence band maximum (VBM) and the conduction band minimum (CBM) are located at point M in the reciprocal space, meaning all compounds are direct bandgap semiconductors. The calculated results of the bandgaps using the GGA–PBE approximation and the corrected bandgaps of the considered 10 compounds range from 1.46–3.86 eV, as presented in Table 3. Therefore, the bandgap of the considered superlattices can be tuned over almost the entire range of the visible light spectrum by changing the halogen species.| Material | E g (eV) | E c g (eV) |
|---|---|---|
| MASnI3/MASnI3/MASnI3 | 1.05 | 1.56 |
| MASnI3/MASnCl3/MASnI3 | 0.98 | 1.46 |
| MASnI3/MASnBr3/MASnI3 | 1.07 | 1.58 |
| MASnI3/MASnBr3/MASnCl3 | 1.10 | 1.62 |
| MASnCl3/MASnI3/MASnCl3 | 1.11 | 1.64 |
| MASnBr3/MASnI3/MASnBr3 | 1.21 | 1.77 |
| MASnBr3/MASnCl3/MASnBr3 | 1.56 | 2.25 |
| MASnBr3/MASnBr3/MASnBr3 | 1.89 | 2.70 |
| MASnCl3/MASnBr3/MASnCl3 | 1.92 | 2.74 |
| MASnCl3/MASnCl3/MASnCl3 | 2.75 | 3.86 |
The bandgap of absorber materials is one of the key characteristics to assure high efficiency for solar cells and plays a vital role in improving device performance. The superlattice structures composed purely of MASnBr3 and MASnCl3 layers have bandgap values above 2.2 eV, meaning they are less suitable for use as solar cell materials, but they have the potential to be developed as materials for other optical devices.56,57 In order to achieve a theoretical efficiency of >25%, the bandgap value should be within the range 0.9 1.6 eV.58 MASnI3/MASnI3/MASnI3 and MASnI3/MASnBr3/MASnI3 have bandgaps of 1.56 and 1.58 eV, which are within this range. It is seen that replacing halogens in different layers can both increase and decrease the bandgap effectively. By changing the halogen ion in the middle perovskite material to Cl, we successfully tuned the bandgap of MASnI3/MASnCl3/MASnI3 to 1.46 eV, making it an optimal candidate for the light-absorber layer in single-junction perovskite solar cells following the Shockley–Queisser limit.59
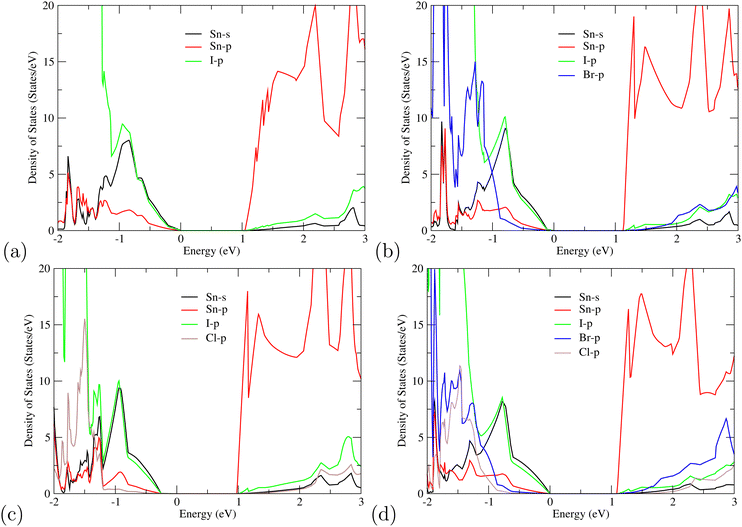
For further understanding of the electronic properties of superlattice perovskites, we also computed the density of states (DOS) in Fig. 4. Similar to other organic halides, the MA cations do not contribute directly to the band edges of the valence band nor of the conduction band.52 This indicates that the probability of electron transition of MA is very small and its main function is to maintain the stability of the perovskite structure. Thus, only the valence orbital contributions of Sn and halogen atoms around the Fermi level are presented. For the single-halide (MASnX3)3 perovskites, the valence bands are mainly contributed by the X-p orbital, as seen from MASnI3/MASnI3/MASnI3 in Fig. 4(a). For mixed-halide superlattices like MASnI3/MASnBr3/MASnCl3, Fig. 4(d) shows the valence bands mainly composed of I-5p, Br-4p, and Cl-3p orbitals, with higher energy levels from the I-5p orbital. Overall, the valence band near the Fermi surface is contributed by the p states of halogens (I-5p, Br-4p, and Cl-3p) and a small amount of Sn-5s while the CBM is composed of mostly Sn-5p orbital and some of the halogen p orbital. When the electrons are excited by light, it will transition from the anti-bonding orbitals hybridized by I-5p, Br-4p, and Cl-3p to the Sn-5p orbital. The results of the PDOS provide further evidence that the bandgap of the studied compounds can easily be tuned by replacing the halogen content, as the halogens are observed to contribute towards the density of states at both the VBM and CBM simultaneously.
Optical properties and photovoltaic performance
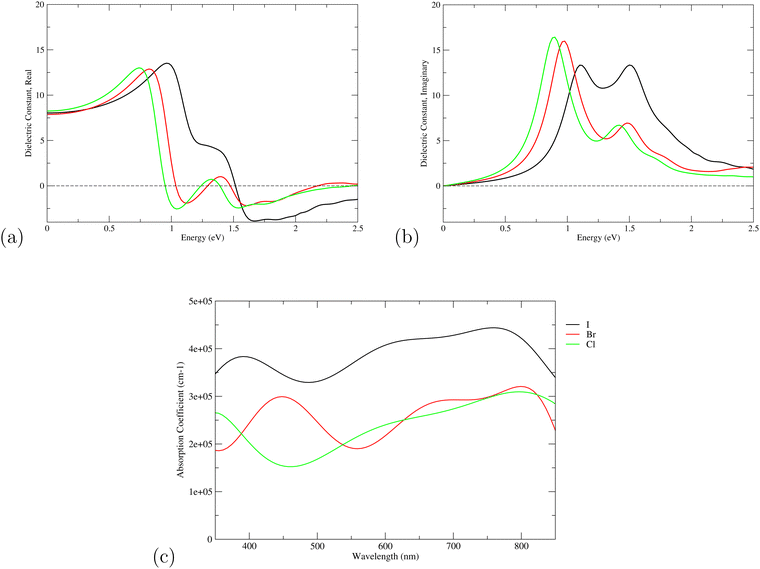
Optical properties such as the absorption coefficient and dielectric function are very important quantities for estimating the overall photovoltaic performance of perovskite solar cells. We focused on calculating the light absorption properties for the three superlattices with the most optimal bandgaps between 0.9–1.6 eV: MASnI3/MASnI3/MASnI3, MASnI3/MASnBr3/MASnI3, and MASnI3/MASnCl3/MASnI3. The response of a material to incident electromagnetic radiation can be characterized by the dielectric function. The dielectric function for zero photon energy is also known as the static dielectric function or dielectric constant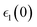 . Large dielectric constants with high optical absorption across a wide range of the solar spectrum are critical for efficient photovoltaic devices.60 Compared to the electronic bandgap, materials with lower bandgap values possess higher dielectric constants, with a maximum dielectric constant (8.25) found in MASnI3/MASnCl3/MASnI3 and a minimum in MASnI3/MASnBr3/MASnI3 (7.87), which reflects the findings of other theoretical research.61 For MASnI3/MASnI3/MASnI3, the static dielectric constant 8.03 in this work is in good agreement with the dielectric constant of 8.2 for MASnI3 calculated by Umari et al.62 This variation could help to design materials with optimum qualities for photovoltaic applications.
. Large dielectric constants with high optical absorption across a wide range of the solar spectrum are critical for efficient photovoltaic devices.60 Compared to the electronic bandgap, materials with lower bandgap values possess higher dielectric constants, with a maximum dielectric constant (8.25) found in MASnI3/MASnCl3/MASnI3 and a minimum in MASnI3/MASnBr3/MASnI3 (7.87), which reflects the findings of other theoretical research.61 For MASnI3/MASnI3/MASnI3, the static dielectric constant 8.03 in this work is in good agreement with the dielectric constant of 8.2 for MASnI3 calculated by Umari et al.62 This variation could help to design materials with optimum qualities for photovoltaic applications.
The dielectric function of the selected perovskite superlattices MASnX3/MASnY3/MASnZ3 is shown in Fig. 5, with the real part 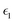 in (a) and the imaginary part
in (a) and the imaginary part 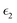 in (b). The dielectric constants are plotted against light intensities from 0 to 2.5 eV with intervals of 0.02 eV. The results reveal that the real and imaginary parts of the dielectric function for all three materials are very similar to each other in the energy range of 0–2.5 eV. From Fig. 5(a), the three perovskite compounds successively reach their peaks at around 1.0 eV, and a max of 13.5, 12.9, and 13 eV is found for Y = I, Br, and Cl, respectively. The real component denotes the amount of energy stored in any medium, demonstrating that MASnI3/MASnI3/MASnI3 has a better absorption capacity to visible light. The negative values in the real curve indicate that the materials change from dielectric behavior to metallic behavior.63 The obtained curves from the imaginary component are plotted in Fig. 5(b), with the thresholds starting around 1.1, 1.0, and 0.9 eV, agreeing with previous trends seen in the dielectric spectra of MASnI3.64 The imaginary part of the dielectric constant is directly related to the electronic structure of materials and describes the absorption characteristics.65 MASnI3/MASnBr3/MASnI3 and MASnI3/MASnCl3/MASnI3 follow similar absorption peaks as MASnI3/MASnI3/MASnI3, with one strong peak around 1.0 eV and a second peak around 1.5 eV.
in (b). The dielectric constants are plotted against light intensities from 0 to 2.5 eV with intervals of 0.02 eV. The results reveal that the real and imaginary parts of the dielectric function for all three materials are very similar to each other in the energy range of 0–2.5 eV. From Fig. 5(a), the three perovskite compounds successively reach their peaks at around 1.0 eV, and a max of 13.5, 12.9, and 13 eV is found for Y = I, Br, and Cl, respectively. The real component denotes the amount of energy stored in any medium, demonstrating that MASnI3/MASnI3/MASnI3 has a better absorption capacity to visible light. The negative values in the real curve indicate that the materials change from dielectric behavior to metallic behavior.63 The obtained curves from the imaginary component are plotted in Fig. 5(b), with the thresholds starting around 1.1, 1.0, and 0.9 eV, agreeing with previous trends seen in the dielectric spectra of MASnI3.64 The imaginary part of the dielectric constant is directly related to the electronic structure of materials and describes the absorption characteristics.65 MASnI3/MASnBr3/MASnI3 and MASnI3/MASnCl3/MASnI3 follow similar absorption peaks as MASnI3/MASnI3/MASnI3, with one strong peak around 1.0 eV and a second peak around 1.5 eV.
The absorption coefficient of solar cells can reflect the ability of the material to absorb light of various wavelengths. Generally, the most important wavelength range is the visible light region (400–800 nm) and near ultraviolet range. Hence, the calculated absorption coefficients of the three considered superlattices are plotted against the wavelengths 350–850 nm, as shown in Fig. 5(c). From the absorption spectra, it can be seen that MASnI3/MASnI3/MASnI3 has more superior absorption than the other two superlattices. MASnI3/MASnI3/MASnI3 has a maximum absorption coefficient of 4.5 × 105 cm−1 at a wavelength of around 700 nm and another smaller peak at 400 nm, both belonging to the visible region of the solar spectrum. Similarly, MASnI3/MASnBr3/MASnI3 has two peaks, with high absorption in the 400–500 nm region and a second peak approaching 800 nm. MASnI3/MASnCl3/MASnI3 has its main heights at around 350 nm and 800 nm, indicating the perovskite also exhibits good ultraviolet absorption. These results are consistent with the absorption spectra of MASnX3 (X = Cl, Br, I) perovskites, with a high absorption coefficient of above 105 cm−1 in the high ultraviolet and visible light region.66 With the change from I to Br to Cl, the curves seem to be red-shifted and move towards larger wavelengths of the visible region. This trend is also evident in the real and imaginary part of the dielectric function as the substitution from Br to Cl corresponds with smaller photon energies. From these figures, it can be seen that perovskites containing heavier halogen anions generally exhibit higher absorption coefficients, which are key parameters for both optical sensory and photovoltaic cell applications.67 Moreover, the optical absorption coefficient reaches 1 × 105 for the perovskite materials in the entire wavelength range 300–800 nm, meaning the corresponding 300 nm thick perovskite could absorb 90% of the incident light and be used in several highly efficient planar heterojunction devices.68,69 Therefore, these three perovskite superlattices have excellent optical performance in the entire range of visible light and are predicted to exhibit high efficiencies for photovoltaic devices.
The theoretical efficiencies of the materials with optimal bandgaps are further considered to evaluate the photovoltaic applications of superlattice perovskites for solar cell devices. From eqn (8)–(10), we calculated the values of VOC, JSC, and η for MASnI3/MASnCl3/MASnI3, MASnI3/MASnI3/MASnI3, and MASnI3/MASnBr3/MASnI3. The parameters are directly related to the bandgap as open-circuit voltage decreases while the short-circuit current and maximum power conversion efficiency increase with bandgap. As seen in Table 4, MASnI3/MASnCl3/MASnI3 has the smallest VOC but larger JSC and η due to its small bandgap. For MASnI3/MASnI3/MASnI3, it is observed that the calculated JSC and η are 23.87 mA cm−2 and 20.05%, which are higher than the experimental observations of 16.8 mA cm−2 and 6.4% with MASnI3 as the absorber layer.70 Similarly, experimental based results show that a maximum PCE of 4.27% is achieved using MASnBr3 as the perovskite layer in the solar cell.71 Our results indicate the superior photovoltaic performance of the superlattice perovskites compared to pristine perovskites and their potentials in maintaining high PCEs as light absorption layers for photovoltaic devices. These findings likely reflect real-world factors, but more work should be done to verify the theoretical performance in a practical setting. For instance, future research on the fabrication of such structures is needed to experimentally grow the superlattices with precise control over the location of the layers to match our theoretical atomic structures in order to further demonstrate their photovoltaic applications.
| Material | V OC (V) | J SC (mA cm−2) | η (%) |
|---|---|---|---|
| MASnI3/MASnCl3/MASnI3 | 0.96 | 26.41 | 20.28 |
| MASnI3/MASnI3/MASnI3 | 1.05 | 23.87 | 20.05 |
| MASnI3/MASnBr3/MASnI3 | 1.08 | 22.35 | 19.31 |
Conclusion
We constructed ten different superlattice structures by combining the conventional halide perovskites MASnI3, MASnBr3, and MASnCl3. The crystal structure, binding energy, band structure, partial density of states, optical absorption, and photovoltaic properties of the tin-based lead-free perovskite superlattices MASnX3/MASnY3/MASnZ3 (X, Y, Z = I, Br, Cl) were investigated by first-principles density functional theory (DFT) calculations. All superlattice structures are thermodynamically stable due to their negative binding energies and direct bandgap semiconductors with bandgap energies ranging from 1.46 to 3.86 eV, making many of these materials potentially suitable for a broad range of optoelectronic devices. A decrease of electronic bandgap is observed while changing the halogen composition of each pristine perovskite layer, meaning variations in the halogen contents in these materials can be used to tune the bandgap for various applications.Of the ten superlattices considered, three displayed optimal bandgaps between 0.9 and 1.6 eV: MASnI3/MASnI3/MASnI3 with a bandgap of 1.56 eV, MASnI3/MASnBr3/MASnI3 with 1.58 eV, and MASnI3/MASnCl3/MASnI3 with 1.46 eV. Their optical properties reveal that the materials possess high dielectric constants and large absorption coefficients between 2–5 × 105 cm−1. With the increasing of larger halide ions, the absorption spectra of the compounds red-shift and the absorption coefficient in the visible light range shows an increasing trend. The photovoltaic parameters were also evaluated and the calculations show that the estimated theoretical PCE of the superlattice structures reach up to 20.28%. These results suggest that the efficiency and absorption of superlattice perovskites can be improved by controlling the thickness and composition of perovskites.
The overall analysis of the properties of tin based perovskite superlattices suggests that MASnI3/MASnI3/MASnI3, MASnI3/MASnBr3/MASnI3, and MASnI3/MASnCl3/MASnI3 are promising solar cell materials that display a close to ideal bandgap as well as excellent absorption properties desired for stable and high efficiency photovoltaic devices. These three compounds can be utilized in future pervoskite research to enhance the design of nontoxic light absorbing perovskite materials and encourage further development of photovoltaic devices.
Author's contributions
Amanda Liu carried out DFT calculations and data collection, created data visualization, and prepared the writing – original draft and writing – review and editing. Xuan Luo aided in designing the methodology and contributed to writing – review and editing.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We would like to thank Dr Gefei Qian for his technical support and helpful discussions throughout our research.References
- M. Batmunkh, Advances in Emerging Solar Cells, Nanomaterials, 2020, 10(3), 534 CrossRef CAS PubMed.
- L. R. Karna, R. Upadhyay and A. Ghosh, All-inorganic perovskite photovoltaics for power conversion efficiency of 31%, Sci. Rep., 2023, 13, 15212 CrossRef CAS PubMed.
- A. Blakers, N. Zin, K. R. McIntosh and K. Fong, High Efficiency Silicon Solar Cells, Energy Proc., 2013, 33, 1–10 CrossRef.
- P. Zhang, M. Li and W.-C. Chen, A Perspective on Perovskite Solar Cells: Emergence, Progress, and Commercialization, Front. Chem., 2022, 10, 802890 CrossRef CAS PubMed.
- M. Shahiduzzaman, M. I. Hossain, M. Akhtaruzzaman, M. Nakano, M. Karakawa, J.-M. Nunzi and T. Taima, Comprehensive Guide on Organic and Inorganic Solar Cells, in Cell Engineering Solar, ed. M. Akhtaruzzaman and V. Selvanathan, Academic Press, 2022, pp. 273–317 Search PubMed.
- G.-W. Kim and A. Petrozza, Defect Tolerance and Intolerance in Metal-Halide Perovskites, Adv. Energy Mater., 2020, 10, 2001959 CrossRef CAS.
- S. Liu, V. P. Biju, Y. Qi, W. Chen and Z. Liu, Recent progress in the development of high-efficiency inverted perovskite solar cells, NPG Asia Mater., 2023, 15, 27 CrossRef CAS.
- J. A. L. D. Cheng P and Y. An, New Nanophotonics Approaches for Enhancing the Efficiency and Stability of Perovskite Solar Cells, Adv. Mater., 2024, 2309459 CrossRef PubMed.
- C. Lin, Stabilizing Organic-Inorganic Lead Halide Perovskite Solar Cells With Efficiency Beyond 20, Front. Chem., 2020, 8, 592 CrossRef CAS PubMed.
- F. F. Targhi, Y. S. Jalili and F. Kanjouri, MAPbI3 and FAPbI3 perovskites as solar cells: case study on structural, electrical and optical properties, Results Phys., 2018, 10, 616–627 CrossRef.
- M. E. Laamari, A. Cheknane, A. Benghia and H. S. Hilal, Optimized opto-electronic and mechanical properties of orthorhombic methylamunium lead halides (MAPbX3) (X = I, Br and Cl) for photovoltaic applications, Sol. Energy, 2019, 182, 9–15 CrossRef CAS.
- M. Shahbazi and H. Wang, Progress in research on the stability of organometal perovskite solar cells, Sol. Energy, 2016, 123, 74–87 CrossRef CAS.
- A. H. Slavney, R. W. Smaha, I. C. Smith, A. Jaffe, D. Umeyama and H. I. Karunadasa, Chemical Approaches to Addressing the Instability and Toxicity of Lead–Halide Perovskite Absorbers, Inorg. Chem., 2017, 56, 46–55 CrossRef CAS PubMed.
- S. Chatterjee and A. J. Pal, Influence of metal substitution on hybrid halide perovskites: towards lead-free perovskite solar cells, J. Mater. Chem. A, 2018, 6, 3793–3823 RSC.
- M. Roknuzzaman, K. K. Ostrikov, K. Chandula Wasalathilake, C. Yan, H. Wang and T. Tesfamichael, Insight into lead-free organic-inorganic hybrid perovskites for photovoltaics and optoelectronics: a first-principles study, Org. Electron., 2018, 59, 99–106 CrossRef CAS.
- M. Sulaman, S. Yang, Z. Zhang, A. Imran, A. Bukhtiar, Z. Ge, Y. Tang, Y. Jiang, L. Tang and B. Zou, Lead-free tin-based perovskites nanocrystals for high-performance self-driven bulk-heterojunction photodetectors, Mater. Today Phys., 2022, 27, 100829 CrossRef CAS.
- N. K. Noel, S. D. Stranks, A. Abate, C. Wehrenfennig, S. Guarnera, A.-A. Haghighirad, A. Sadhanala, G. E. Eperon, S. K. Pathak, M. B. Johnston, A. Petrozza, L. M. Herz and H. J. Snaith, Lead-free organic–inorganic tin halide perovskites for photovoltaic applications, Energy Environ. Sci., 2014, 7, 3061–3068 RSC.
- P. Xiong, B. Sun, N. Sakai, R. Ma, T. Sasaki, S. Wang, J. Zhang and G. Wang, 2D Superlattices for Efficient Energy Storage and Conversion, Adv. Mater., 2020, 32, 1902654 CrossRef CAS PubMed.
- M. Jiang, H. Y. Xiao, S. M. Peng, L. Qiao, G. X. Yang, Z. J. Liu and X. T. Zu, Effects of stacking periodicity on the electronic and optical properties of GaAs/AlAs superlattice: a first-principles study, Sci. Rep., 2020, 10, 4862 CrossRef CAS PubMed.
- S. Zhang, H. Xiao, S. Peng, G. Yang, Z. Liu, X. Zu, S. Li, D. Singh, L. Martin and L. Qiao, Band-Gap Reduction in (BiCrO3)m/(BiFeO3)n Superlattices: Designing Low-Band-Gap Ferroelectrics, Phys. Rev. Appl., 2018, 10, 044004 CrossRef CAS.
- J. H. Lee, U. V. Waghmare and J. Yu, First-principles effective Hamiltonian for ferroelectric polarization in BaTiO3/SrTiO3 superlattices, J. Appl. Phys., 2008, 103, 124106 CrossRef.
- Y. Zhou and K. M. Rabe, Determination of ground-state and low-energy structures of perovskite superlattices from first principles, Phys. Rev. B, 2014, 89(21), 214108 CrossRef.
- L. Qiao, et al., Dimensionality Controlled Octahedral Symmetry-Mismatch and Functionalities in Epitaxial LaCoO3/SrTiO3 Heterostructures, Nano Lett., 2015, 15, 4677–4684 CrossRef CAS PubMed.
- L. Qiao and X. Bi, Dielectric phase transition and relaxor behavior in BaTiO3/LaNiO3 superlattice, CrystEngComm, 2011, 13, 1693–1696 RSC.
- R. Singh, R. Kottokkaran, V. L. Dalal and G. Balasubramanian, Engineering band gap and electronic transport in organic–inorganic halide perovskites by superlattices, Nanoscale, 2017, 9, 8600–8607 RSC.
- D. Li, D. Li, H. Zhang, A. Yang and C. Liang, High-Performance Photovoltaic Materials Based on the Superlattice Structures of Organic–Inorganic Halide Perovskite and Superhalogen Hybrid Perovskite, J. Phys. Chem. Lett., 2020, 11, 5282–5294 CrossRef CAS PubMed.
- G. Ding, C. Wang, G. Gao, K. Yao, C. Dun, C. Feng, D. Li and G. Zhang, Engineering of charge carriers via a two-dimensional heterostructure to enhance the thermoelectric figure of merit, Nanoscale, 2018, 10, 7077–7084 RSC.
- A. Varadwaj, P. R. Varadwaj and K. Yamashita, Revealing the Chemistry between Band Gap and Binding Energy for Lead-/Tin-Based Trihalide Perovskite Solar Cell Semiconductors, ChemSusChem, 2018, 11, 449–463 CrossRef CAS PubMed.
- X. Wang, M. Li, B. Zhang, H. Wang, Y. Zhao and B. Wang, Recent progress in organometal halide perovskite photodetectors, Org. Electron., 2018, 52, 172–183 CrossRef CAS.
- J. Hieulle, X. Wang, C. Stecker, D.-Y. Son, L. Qiu, R. Ohmann, L. K. Ono, A. Mugarza, Y. Yan and Y. Qi, Unraveling the Impact of Halide Mixing on Perovskite Stability, J. Am. Chem. Soc., 2019, 141, 3515–3523 CrossRef CAS PubMed.
- C. Wehrenfennig, G. E. Eperon, M. B. Johnston, H. J. Snaith and L. M. Herz, High charge carrier mobilities and lifetimes in organolead trihalide perovskites, Adv. Mater., 2014, 26, 1584–1589 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- X. Gonze, et al., ABINIT: first-principles approach of materials and nanosystem properties, Comput. Phys. Commun., 2009, 180, 2582–2615 CrossRef CAS.
- P. Blochl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- N. A. W. Holzwarth, A. R. Tackett and G. E. Matthews, A Projector Augmented Wave (PAW) code for electronic structure calculations, Part I: atompaw for generating atomcentered functions, Comput. Phys. Commun., 2001, 135, 329–347 CrossRef CAS.
- A. Tackett, N. Holzwarth and G. Matthews, A Projector Augmented Wave (PAW) code for electronic structure calculations, Part II: pwpaw for periodic solids in a plane wave basis, Comput. Phys. Commun., 2001, 135, 348–376 CrossRef CAS.
- J. D. Head and M. C. Zerner, A Broyden—Fletcher—Goldfarb—Shanno optimization procedure for molecular geometries, Chem. Phys. Lett., 1985, 122, 264–270 CrossRef CAS.
- J. Li and P. Rinke, Atomic structure of metal-halide perovskites from first principles: the chicken-and-egg paradox of the organic-inorganic interaction, Phys. Rev. B, 2016, 94, 045201 CrossRef.
- T. Oku, Solar Cells, ed. L. A. Kosyachenko, IntechOpen, Rijeka, 2015, ch. 3 Search PubMed.
- R. Singh and G. Balasubramanian, Impeding phonon transport through superlattices of organic–inorganic halide perovskites, RSC Adv., 2017, 7, 37015–37020 RSC.
- H. J. Hua and X. Luo, Pressure induced electronic and optical responses of vacancy-ordered double perovskites Cs2BX6 (B = Zr, Pd, Sn; X = Cl, Br, I), Phys. Scr., 2023, 98, 115520 CrossRef.
- P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. H. Madsen and L. D. Marks, WIEN2k: an APW + lo program for calculating the properties of solids, J. Chem. Phys., 2020, 152, 074101 CrossRef CAS PubMed.
- S. Saha, T. P. Sinha and A. Mookerjee, Electronic structure, chemical bonding, and optical properties of paraelectric BaTiO3, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8828–8834 CrossRef CAS.
- Y. Nishigaki, A. Matsushita, A. Tejada, T. Matsui and H. Fujiwara, Hybrid Perovskite Solar Cells, John Wiley Sons, Ltd, 2021, pp. 541–562 Search PubMed.
- M. R. Filip, C. Verdi and F. Giustino, GW Band Structures and Carrier Effective Masses of CH3NH3PbI3 and Hypothetical Perovskites of the Type APbI3: A = NH4, PH4, AsH4, and SbH4, J. Phys. Chem. C, 2015, 119, 25209–25219 CrossRef CAS.
- B. Djamel, E.-A. Haidar, C. Stampfl, C. Naouel, M. Ali and M. Sahnoun, Strain Engineering of the Pentagonal PtSiTe Monolayer for Enhanced Photovoltaic and Thermoelectric Efficiency: A First-Principles Investigation, ACS Appl. Nano Mater., 2024, 7, 142–152 CrossRef CAS.
- H. J. Snaith, Estimating the Maximum Attainable Efficiency in Dye-Sensitized Solar Cells, Adv. Funct. Mater., 2010, 20, 13–19 CrossRef CAS.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- Reference Solar Spectral Irradiance: Air Mass 1.5. https://www.nrel.gov/grid/solar-resource/spectra-am1.5.html, [accessed: April 2024].
- W. Nie, H. Tsai, R. Asadpour, J.-C. Blancon, A. J. Neukirch, G. Gupta, J. J. Crochet, M. Chhowalla, S. Tretiak, M. A. Alam, H. lin Wang and A. D. Mohite, High-efficiency solution-processed perovskite solar cells with millimeter-scale grains, Science, 2015, 347, 522–525 CrossRef CAS PubMed.
- Y. Takahashi, R. Obara, Z.-Z. Lin, Y. Takahashi, T. Naito, T. Inabe, S. Ishibashi and K. Terakura, Charge-transport in tin-iodide perovskite CH3NH3SnI3: origin of high conductivity, Dalton Trans., 2011, 40, 5563–5568 RSC.
- M. Coduri, T. A. Strobel, M. Szafranski, A. Katrusiak, A. Mahata, F. Cova, S. Bonomi, E. Mosconi, F. De Angelis and L. Malavasi, Band Gap Engineering in MASnBr3 and CsSnBr3 Perovskites: Mechanistic Insights through the Application of Pressure, J. Phys. Chem. Lett., 2019, 10, 7398–7405 CrossRef CAS PubMed.
- S. X. Tao, X. Cao and P. A. Bobbert, Accurate and efficient band gap predictions of Metal Halide perovskites using the DFT-1/2 method: GW accuracy with DFT Expense, Sci. Rep., 2017, 7, 14386 CrossRef PubMed.
- H. Zhang, T. Yu, D. Li, A. Yang, X. Lai, C. Liang and Y. Lu, High-Stability and High-Efficiency Photovoltaic Materials Based on Functional Diamino Organic Cation Halide Hybrid Perovskite Superlattice Structures, ACS Appl. Energy Mater., 2021, 4, 8774–8790 CrossRef CAS.
- L. Cheng, B. Xu, X. Li, Y. Zeng and L. Meng, Electronic and Photovoltaic Properties of Superlattices Constructed by Organic–Inorganic Perovskites: a Theoretical Perspective, ACS Appl. Energy Mater., 2022, 5, 2430–2441 CrossRef CAS.
- D.-Y. Hu, X.-H. Zhao, T.-Y. Tang, L. Li, L.-K. Gao and Y.-L. Tang, First-principles calculations to investigate structural, elastic, electronic and optical properties of leadfree perovskite derivatives Cs2SeX6 (X = Cl, Br, I), Opt. Mater., 2021, 119, 111316 CrossRef CAS.
- T. Nakajima and K. Sawada, Discovery of Pb-Free Perovskite Solar Cells via High-Throughput Simulation on the K Computer, J. Phys. Chem. Lett., 2017, 8, 4826–4831 CrossRef CAS PubMed.
- M.-G. Ju, J. Dai, L. Ma and X. C. Zeng, Perovskite Chalcogenides with Optimal Bandgap and Desired Optical Absorption for Photovoltaic Devices, Adv. Energy Mater., 2017, 7, 1700216 CrossRef.
- Q. Teng, T. Shi, C. Liao and Y.-J. Zhao, First-principles study of aziridinium tin iodide perovskites for photovoltaics, J. Mater. Chem. C, 2021, 9, 982–990 RSC.
- M. Roknuzzaman, C. Zhang, K. K. Ostrikov, A. Du, H. Wang, L. Wang and T. Tesfamichael, Electronic and optical properties of lead-free hybrid double perovskites for photovoltaic and optoelectronic applications, Sci. Rep., 2019, 9, 718 CrossRef PubMed.
- M. Roknuzzaman, J. A. Alarco, H. Wang and K. K. Ostrikov, Structural, electronic and optical properties of lead-free antimony-copper based hybrid double perovskites for photovoltaics and optoelectronics by first principles calculations, Comput. Mater. Sci., 2021, 186, 110009 CrossRef CAS.
- P. Umari, E. Mosconi, F. de Angelis and G. W. Relativistic, calculations on CH3NH3PbI3 and CH3NH3SnI3 Perovskites for Solar Cell Applications, Sci. Rep., 2014, 4, 4467 CrossRef PubMed.
- U. Ayaz Khan, Abdullah, M. R. Sarker, N. U. Khan, S. Khan, J. Y. Al-Humaidi, V. Tirth, M. S. Refat, A. Zaman, A. Algahtani, A. M. Alsuhaibani and F. Ullah, Investigation of structural, opto-electronic, mechanical and thermoelectric properties of Rb-based fluoro-perovskites RbXF3 (X = Rh, Os, Ir) via first-principles calculations, J. Saudi Chem. Soc., 2023, 27, 101627 CrossRef CAS.
- L. Peng and W. Xie, Theoretical and experimental investigations on the bulk photovoltaic effect in lead-free perovskites MASnI3 and FASnI3, RSC Adv., 2020, 10, 14679–14688 RSC.
- D. Saikia, M. Alam, J. Bera, A. Betal, A. N. Gandi and S. Sahu, A First-Principles Study on ABBr3 (A = Cs, Rb, K, Na; B = Ge, Sn) Halide Perovskites for Photovoltaic Applications, Adv. Theory Simul., 2022, 5, 2200511 CrossRef CAS.
- S. R. Kumavat, Y. Sonvane and S. K. Gupta, Structural, optical, transport, and solar cell properties of 2D halide perovskite MAZX3 (Z = Pb, Sn, and X = Cl, Br, I), J. Appl. Phys., 2020, 128, 114304 CrossRef CAS.
- S. Nations, T. Jia, S. Wang and Y. Duan, Electronic and optical properties of orthorhombic (CH3NH3)BX3 (B = Sn, Pb; X = F, Cl, Br, I) perovskites: a first-principles investigation, RSC Adv., 2021, 11, 22264–22272 RSC.
- Z. Xiao, C. Bi, Y. Shao, Q. Dong, Q. Wang, Y. Yuan, C. Wang, Y. Gao and J. Huang, Efficient, high yield perovskite photovoltaic devices grown by interdiffusion of solutionprocessed precursor stacking layers, Energy Environ. Sci., 2014, 7, 2619–2623 RSC.
- D. Liu and T. L. Kelly, Perovskite solar cells with a planar heterojunction structure prepared using room-temperature solution processing techniques, Nat. Photonics, 2014, 8, 133–138 CrossRef CAS.
- J. Jiang, C. K. Onwudinanti, R. A. Hatton, P. A. Bobbert and S. Tao, Stabilizing Lead-Free All-Inorganic Tin Halide Perovskites by Ion Exchange, J. Phys. Chem. C, 2018, 122, 17660–17667 CrossRef CAS PubMed.
- S. Gupta, T. Bendikov, G. Hodes, D. Cahen and A. CsSnBr3, Lead-Free Halide Perovskite for Long-Term Solar Cell Application: Insights on SnF2 Addition, ACS Energy Lett., 2016, 1, 1028–1033 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |