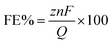Open Access Article
Open Access ArticleAdvanced morphological control over Cu nanowires through a design of experiments approach†
Andrea
Conte
 ,
Antonella
Rosati
,
Antonella
Rosati
 ,
Marco
Fantin
,
Marco
Fantin
 ,
Alessandro
Aliprandi
,
Alessandro
Aliprandi
 ,
Marco
Baron
,
Marco
Baron
 ,
Sara
Bonacchi
,
Sara
Bonacchi
 and
Sabrina
Antonello
and
Sabrina
Antonello
 *
*
Department of Chemical Sciences, University of Padova, Via F. Marzolo 1, 35131, Padova, Italy. E-mail: sabrina.antonello@unipd.it
First published on 30th September 2024
Abstract
Copper nanowires (CuNWs), featuring anisotropic highly conductive crystalline facets, represent an ideal nanostructure to fabricate on-demand materials as transparent electrodes and efficient electrocatalysts. The development of reliable and robust CuNWs requires achieving a full control over their synthesis and morphology growth, a challenge that continues to puzzle materials scientists. In this study, we systematically investigated the correlation between the critical synthetic parameters and the structural properties of nanowires using a design of experiments (DOE) approach. Multiparametric variation of experimental reaction conditions combined with orthogonal technical analysis allowed us to develop a sound predictive model that provides guidelines for designing CuNWs with controlled morphology and reaction yield. Beyond these synthetic achievements, voltammetric and electrocatalytic experiments were used to correlate the CuNWs morphology and structure to their catalytic activity and selectivity toward CO2 electroreduction, thus opening new avenues for further intersectoral actions.
1. Introduction
Since the emergence of nanotechnology, the miniaturization of materials to a scale where size-, shape-, surface-, and defect-dependent effects operate has opened ambitious challenges not only from a technological perspective but also from a visionary perspective. The innovative opportunity conferred to the elements of the periodic table within the nanostructured materials has highlighted plenty of unexpected distinct properties and functions.1 In this framework, copper stands as one of the most pivotal elements that has been exploited to demonstrate the effect of size and structure modification in order to enhance its inherent bulk properties, such as its high electrical conductivity, towards a wider range of emerging applications.2–11One-dimensional copper nanowires (CuNWs), featuring a high aspect ratio (AR > 100) due to their nanometer-size diameter and hundreds of micrometers length,5,12 have been recently investigated to obtain insights into the strong correlations among composition, shape, and surface properties13–16 for developing highly transparent conductive electrodes for application in electronic devices, such as touch screens17 or solar cells,18 as well as in flexible transistors19 and biosensors.20,21 More recently, enhanced electrocatalytic properties towards the production of renewable energy sources such as hydrogen and green carbon-based fuels5,22 have been attributed to the sophisticated manipulations of different crystalline facets within the wires.6,23 Since then, multidisciplinary methods, such as chemical reduction,24,25 physical vapor deposition,26 and electrochemical deposition,27 have been engineered for the synthesis of tailored CuNWs. In particular, the hydrothermal approach, which is based on the reduction of a Cu(II)–complex in aqueous solutions in the presence of surfactants at room temperature,6,28 stands out for its cost, mild conditions, environmental impact, and promising scalability. Despite significant improvements, the ultimate control over the CuNWs morphology and crystallinity has not been achieved yet, suggesting the need for a more comprehensive investigation of the interconnected synthetic parameters, such as copper source, temperature, reaction time, and pH as well as, the type and amount of surfactant and reducing agent to ultimately regulate the final outcome and performances.6,23,29–35
The design of experiments (DOE) method is a well-established method to study the relationship between multiple input variables and key output variables.36,37 In recent years, DOE has attracted much attention from the community of nanomaterials scientists and engineers to progress in the elucidation of the synthetic parameters governing the size and structure of nanoparticles.37–43 This method enables the formulation of predictive models with limited experimental effort and facilitates the detection of interactions between different experimental conditions, which would be challenging to recognize using a one-factor-at-a-time approach. The current main challenge in data-driven material optimization arises from the scarcity and quality of input data.44 In situations where comparable data are lacking, DOE sampling techniques can be invaluable in generating datasets well-suited for modeling.45 Here, we demonstrate how both morphological structures, such as the thickness and aspect ratio, and the reaction yield of CuNWs can be controlled and rationalized by enrolling only four simple parameters in hydrothermal synthesis such as the reaction time, temperature, and type and concentration of reducing agent within a multivariate DOE approach. In particular, we implement the utility of DOE to extract the maximum information from straightforward experiments and to yield statistically robust results while minimizing the synthetic efforts in terms of time and materials. Beyond these synthetic achievements, we also lay the foundation for a complete understanding of the pivotal role played by the CuNWs’ morphologies and regulated features towards highly selective electrocatalyst materials for CO2 reduction.
2. Results and discussion
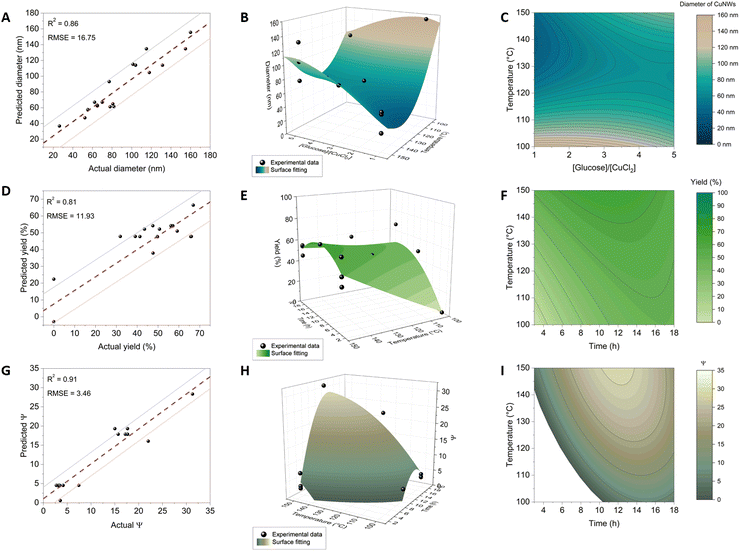
CuNWs were synthesized according to a hydrothermal method, as previously reported30 with some modifications detailed in the Experimental section. In particular, CuCl2⋅2H2O was used as the copper source and 1-octadecylamine (ODA) (4 equivalents) was used as the capping agent in all the performed syntheses. As reported,23,31,46 the presence of ODA guarantees the anisotropic growth of the Cu seed crystals by selectively bonding to the (100) facet and leaving the (111) facet free. This configuration results in a five-fold twinned structure with five (100) side surfaces along the [110] direction. Alkylamines with chains longer than sixteen carbon atoms are needed to obtain CuNWs of good quality.6,47 Besides guaranteeing the anisotropic growth of the CuNWs, the use of alkylamines is instrumental in protecting their surface from oxidation. Indeed, CuNWs synthesized under these conditions are stable for months when dispersed in ethanol solution, in contrast to CuNWs synthesized without capping agents.48 Here, we explore the variables, reaction time, temperature, and type and concentration of the reducing agent to map the chemical reaction space. In particular, we selected glucose and sodium ascorbate as reducing agents because they are environmentally friendly, non-toxic and low-cost reagents. Fig. 1 outlines our workflow for investigating how CuNWs’ yield and morphology are influenced by synthetic parameters. The framework mirrors classical DOE procedures, starting with a screening design phase to identify key parameters impacting CuNWs’ characteristics. Subsequently, our approach utilized “definitive screening design” (DSD) to delve deeper into selected variables, elucidating their relationships and directing their effects toward achieving the desired CuNW morphology. Quantitative measurements of the CuNW structure included the diameter (obtained from SEM images) and the parameter Ψ, defined as the ratio of the maximum intensity of two XRD signals (111)/(200) in the diffractogram, which is known to be correlated with the aspect ratio of CuNWs.49 Additionally, the yield of the reactions was analyzed as a screening output of the synthesis conditions. SAS JMP Pro software was used to perform the experimental design, randomize the order of the experiments, evaluate the model, and obtain the effects of each reaction parameter and their interactions.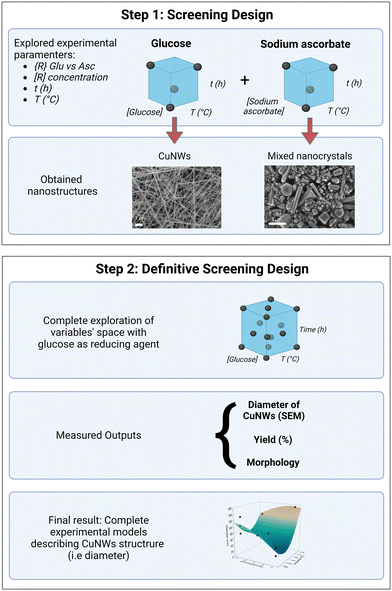 | ||
| Fig. 1 Workflow to establish the relationship between the synthesis parameters and the morphology of CuNWs, based on a sequential DOE approach. | ||
2.1. Screening design
In the screening phase of the DOE method, we selected four variables known to affect the morphology of the CuNWs, such as the reaction temperature (T), reaction time (t), and type {R} and quantity [R] of reducing agent. These parameters were divided into two levels, resulting in a 24 factorial design, comprising a total of 16 experiments: 8 using glucose (Aglu–Hglu) and 8 using sodium ascorbate as the reducing agent (Aasc–Hasc). Therefore, there are four parameters, each assuming two levels. The values of the experimental parameters for the two levels are collected in Table 1.| Factor | Symbol | Level (−) | Level (+) |
|---|---|---|---|
| Time (h) | t | 3 | 18 |
| Temperature (°C) | T | 100 | 150 |
| Equivalents of reducing agent (CR/CCuCl2) | [R] | 1 | 5 |
| Type of reducing agent | {R} | Asc | Glu |
To assess the average size and shapes of the obtained Cu nanostructures, SEM analysis was carried out and the images collected for each synthesis are presented in Fig. S1 and S2 (ESI†). Under the explored synthesis conditions, the type of reducing agent emerged as the parameter with the most significant impact on the morphology of CuNWs, as evidenced by representative SEM images in Fig. 2 (top row: glucose and bottom row: ascorbate). Glucose synthesis consistently produced long CuNWs with well-defined diameters ranging from 26 to 155 nm and a polydispersity index (PDI) ≤0.1. In contrast, sodium ascorbate synthesis yielded mixed structures, including nanoparticles and short, thick CuNWs with an aspect ratio <100 and PDI <0.35.
 | ||
| Fig. 2 Representative SEM images from the glucose synthesis route, Gglu, Iglu, and Nglu, and from the sodium ascorbate synthesis route, Casc, Easc, and Gasc. | ||
The screening design highlighted glucose's consistency in producing nanowires with varying diameters and yields (0–66.9%), prompting further exploration to quantify the relationship between synthesis parameters (t, T, and [R]) and morphology via the glucose route.
2.2. Definitive screening design
A definitive screening design (DSD) was employed to create a quantitative model linking synthesis parameters to measured outputs, considering linear effects (t, T, and [R]) and second-order effects, which include both quadratic (t2, T2, and [R]2) and interaction terms (t × T, t × [R], and T × [R]).50 To include all these additional effects, the DSD expanded on the initial 8 experiments conducted with glucose as the reducing agent, including 10 supplementary experiments at three factor levels according to the experimental design in Table 2, resulting in a total of 18 runs with glucose as the reducing agent. The results are presented in Table 3 that summarizes the average dimensions of the Cu nanostructures for each reaction, the standard deviation, and the PDI. Entries Aglu–Hasc are related to the preliminary screening phase, while entries Iglu–Rglu pertain to the definite screening. The DSD generated precise models that effectively described the diameter, aspect ratio, and reaction yield of CuNWs, as detailed in the following paragraphs.| Factor | Symbol | Level (−) | Level (o) | Level (+) |
|---|---|---|---|---|
| Time | T | 3 | 10.5 | 18 |
| Temperature | T | 100 | 125 | 150 |
| Equivalents of reducing agent (CR/CCuCl2) | [R] | 1 | 3 | 5 |
| Entry | Experimental factors | Measured outputs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| {R} | [R] | T (°C) | t (h) | Structure | Yield (%) | d (nm) | σ of db (nm) | PDI (σ/d)2 | d of NPsa (nm) | σ of NPs db (nm) | PDI (σ/d)2 | Ψ | |
| a d is the average diameter of CuNWs or CuNRODs estimate by SEM. b σ is the standard deviation of d. | |||||||||||||
| Aglu | Glu | 1 | 150 | 3 | NWs | 65.7 | 55 | 17 | 0.095 | — | — | — | 2.73 |
| Aasc | Asc | 1 | 100 | 3 | NWs | 95.8 | 215 | 76 | 0.125 | — | — | — | 2.28 |
| Basc | Asc | 1 | 100 | 3 | NWs | 96.0 | 170 | 58 | 0.116 | — | — | — | 2.75 |
| Bglu | Glu | 1 | 150 | 18 | NWs | 57.1 | 26 | 7 | 0.072 | — | — | — | 17.21 |
| Casc | Asc | 5 | 150 | 3 | NPs + NRODs | 97.4 | 445 | 120 | 0.072 | 200 | 66 | 0.107 | 2.02 |
| Cglu | Glu | 3 | 125 | 10.5 | NWs | 50.7 | 69 | 21 | 0.093 | — | — | — | 17.66 |
| Dasc | Asc | 1 | 150 | 3 | NWs | 96.2 | 302 | 86 | 0.081 | 267 | 48 | 0.032 | 2.24 |
| Easc | Asc | 5 | 150 | 18 | NPs + NRODs | 88.6 | 674 | 230 | 0.116 | 406 | 238 | 0.344 | 2.56 |
| Dglu | Glu | 5 | 100 | 3 | — | 0 | — | — | — | — | — | — | — |
| Fasc | Asc | 5 | 150 | 3 | NPs + NRODs | 99.3 | 400 | 229 | 0.328 | 324 | 92 | 0.081 | 1.52 |
| Eglu | Glu | 1 | 100 | 18 | NWs | 31.9 | 155 | 38 | 0.060 | — | — | — | 3.15 |
| Fglu | Glu | 5 | 100 | 3 | — | 0 | — | — | — | — | — | — | — |
| Gglu | Glu | 5 | 150 | 18 | NWs | 47.5 | 77 | 26 | 0.114 | — | — | — | 17.67 |
| Gasc | Asc | 1 | 100 | 18 | NPs + NWs | 99.0 | 327 | 192 | 0.345 | 466 | 112 | 0.058 | 1.62 |
| Hglu | Glu | 3 | 125 | 10.5 | NWs | 43.5 | 62 | 22 | 0.126 | — | — | — | 13.90 |
| Hasc | Asc | 5 | 100 | 18 | NPs + NRODs | 60.2 | 559 | 163 | 0.085 | 264 | 69 | 0.068 | 0.44 |
| Iglu | Glu | 1 | 100 | 18 | NWs | 66.0 | 115 | 41 | 0.127 | — | — | — | 3.56 |
| Jglu | Glu | 5 | 150 | 3 | NWs | 49.7 | 131 | 29 | 0.049 | — | — | — | 7.43 |
| Kglu | Glu | 1 | 125 | 3 | — | 0 | — | — | — | — | — | — | — |
| Lglu | Glu | 3 | 150 | 18 | NWs | 56.2 | 81 | 18 | 0.049 | — | — | — | 15.70 |
| Mglu | Glu | 3 | 100 | 3 | — | 0 | — | — | — | — | — | — | — |
| Nglu | Glu | 5 | 150 | 3 | NWs | 41.3 | 104 | 17 | 0.027 | — | — | — | 3.43 |
| Oglu | Glu | 5 | 100 | 18 | NWs | 39.1 | 118 | 18 | 0.023 | — | — | — | 4.15 |
| Pglu | Glu | 1 | 150 | 10.5 | NWs | 66.9 | 52 | 13 | 0.063 | — | — | — | 31.30 |
| Qglu | Glu | 5 | 100 | 10.5 | NWs | 47.6 | 101 | 23 | 0.052 | — | — | — | 3.54 |
| Rglu | Glu | 5 | 125 | 18 | NWs | 59.2 | 65 | 16 | 0.061 | — | — | — | 22.01 |
Notably, the model displays a curved surface, with a minimum diameter occurring at approximately 140 °C and 1 equivalent of glucose. Within the central flat surface region (135–115 °C and 3–5 eq. of glucose), a saddle point is present, where the diameter remains almost constant.
Moving up from the saddle point, two distinct regions of the experimental surface are noticeable where large diameters are obtained: one at low equivalents of the reducing agent and low temperatures, and the other at high equivalents of the reducing agent and high temperatures. We posit that the curvature of the surface may arise from the coexistence of two mechanisms of Cu(II) reduction mediated by reductones or amines, respectively, both resulting in thick CuNWs. As described by Sue and co-workers, at higher temperature and with a low amount of glucose, the Cu(I)-alkylamine mediated mechanism prevails, whereas at lower temperature and with a higher amount of glucose, the Maillard mediated mechanism does.49
The combination of conditions affects mostly the absorption equilibrium of amines on CuNW facets, particularly the (100) and (111) facets which undergo continuous modification during synthesis. Furthermore, the temperature can deeply affect the kinetics of the process.42 We observed a highly statistically significant interaction between T and [R] (p-value = 0.003, Table S1, ESI†), indicating an interplay between the two variables. Specifically, at a low temperature of 100 °C, the diameter of CuNWs decreased with an increasing glucose concentration, whereas at a high temperature of 150 °C, the diameter increased with the quantity of glucose. These interaction effects have clear implications for optimizing the morphology of CuNWs and are typically only observed and quantified through structured DOE approaches.
| Diameter [nm] = 115.56 + 5.60[R] − 0.42T − 1.39t + 0.43(T − 130.40)([R] −3.14) + 0.057(T − 130.40)2 | (1) |
| % yield = −39.21 + 0.57 T + 1.91t − 0.059(T − 125.00)(t − 10.50) − 0.28(t − 10.50)2 | (2) |
| Ψ = −30.85 + 0.39T + 0.34t − 0.038(T − 130.36)(t − 12.64) −0.30(t − 12.64)2 −0.0078(T − 130.35)2 | (3) |
The reaction time had a minor impact on the thickness of CuNWs, accounting for only 12% of the diameter variation under the explored synthesis conditions (see Table S1, ESI† that lists the percent contribution of each factor to the model). With longer reaction times, the diameter gradually decreased, possibly due to slow corrosion or surface dissolution. Fig. S5 (ESI†) shows the effect of time on the reaction output.
Overall, both the value of Ψ and the reaction yield depended on the same factors (t and T), and their contour plots had similar shapes (in other terms, Ψ and the reaction yield are highly intercorrelated). This can be explained by considering that higher yields promote the growth of longer CuNW crystals, which develop along their long axis. The constancy of the measured diameter values over the reaction time confirms that, after seed formation, the growth of the crystal proceeds in a unique direction. The plots in Fig. 3H and I show that, at any temperature, the NW length increases reaching a maximum after about 12–15 hours, and then decreases with longer reaction times. Since the diameter remains relatively constant, further insight into the effect of the etching process on the wire length has been disclosed. In our opinion, this correlation analysis, rooted in XRD-derived structural insights, furnishes a quantitative framework for tailoring and optimizing synthesis protocols, thereby advancing the precision and efficacy of nanomaterial fabrication processes.
| Optimized parameters | Optimized conditions | Potential applications | ||||
|---|---|---|---|---|---|---|
| Diametera (nm) | Ψ | Yielda (%) | T (°C) | T (h) | [R] (glucose) | |
| a The arrows indicate the desired direction for the parameter (i.e., maximize or minimize), while the value in parenthesis indicates the predicted value for the optimized reaction conditions. | ||||||
| ↓(43) | ↑(28) | ↑(65) | 150 | 13 | 1 | TCEs (displays) |
| ↑(103) | ↑(28) | ↑(66) | 150 | 11 | 5 | Catalysis (HER, CO2RR, NO3RR, and cross-coupling) |
| ↓(43) | Not relevant | ↑(66) | 150 | 13 | 1 | Nanoelectronics (thin film transistors and interconnects in integrated circuits) |
| ↑(138) | Not relevant | ↑(48) | 100 | 15 | 1 | Energy storage devices (supercapacitors and batteries) |
2.3. Insights into the sodium ascorbate synthesis route
After developing quantitative models for the glucose synthesis route, we present here some insights regarding the syntheses performed employing sodium ascorbate, with which we observed a markedly different pattern in the distribution of nanostructures. Indeed, most of the synthesis yielded Cu nanoparticles (CuNPs) in combination with Cu nanorods, with only the Aasc, Basc, and Dasc syntheses providing CuNWs as the main products. Under the same conditions, using glucose resulted in CuNWs with a diameter of 55 nm. This effect of the reducing agent emerged from different reduction mechanisms that Cu(II) undergoes when using glucose or sodium ascorbate. Sodium ascorbate is a relatively strong reducing agent. In contrast, glucose is a milder reducing agent. Before becoming active, glucose must react with amines to generate the effective reducing species, the reductone.6 Syntheses performed employing sodium ascorbate, generally resulted in higher yields (>60%) compared to those using glucose, although with a mixture of morphologies. A further difference to evaluate concerns the nature of the reducing agent in terms of electronic equivalents provided to the metal cation. Ascorbate acts as a bi-electronic reducing agent,56 meaning that 1 chemical (molar) equivalent of ascorbate counts for 2 electronic equivalents. To understand the role of the reducing agent, we performed a synthesis under the same conditions of Fasc (nomenclature refers to Table 2) but employing 0.5 mol eq. of sodium ascorbate. The result of this synthesis is reported in Fig. S13 (ESI†). By using only 0.5 mol eq. of sodium ascorbate, we found that long CuNWs formed (with average diameter equal to 61 nm, yield = 61.3%). There were also some similarities between the two reducing agents. SEM analysis revealed that all the CuNWs exhibited a penta-twinned structure, indicating that the aggregation process of Cu remained consistent across the two reducing agents. This finding agrees with the work of F. Silly et al., which showed that the more stable Cu seed is the penta-twinned one within the temperature range investigated, namely 100–150 °C.59 For both reducing agents, significant factors such as temperature and concentration of the reducing agent could accelerate the growth of CuNWs and thereby modify their final aspect ratio, Ψ. This parameter was found to be extremely sensitive to the synthesis temperature. Concerning the syntheses carried out employing a high quantity of sodium ascorbate, a common pattern can be observed. Upon inspecting the SEM images in Fig. S2C, E, F, and H (ESI†), it becomes apparent that hollow Cu nanostructures are present. This outcome was achieved when a high concentration (5 eq.) of ascorbate was used. Under these conditions, ascorbate can act as the capping agent and compete with the ODA for the coordination of Cu, thereby significantly affecting the morphology. Moreover, high concentrations of Na+ ions can also affect the absorption dynamics of the capping agent and thus the growth dynamic of the nanocrystals, resulting in the complete lack of their anisotropic growth. In summary, we have demonstrated that the optimal quantity of sodium ascorbate is crucial for the formation of CuNWs, with 1 eq. or, preferably, 0.5 eq. resulting in the production of thin CuNWs.2.4. CuNWs-based electrodes preparation, characterization and test in the CO2RR
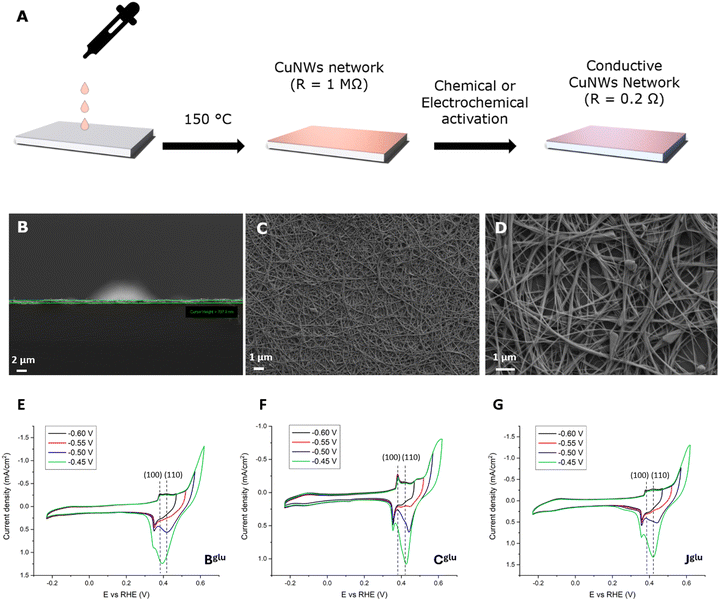
Copper-based nanostructures can potentially play a pivotal role in many fields as we highlighted in Table 4 where we correlated the optimized synthetic parameters with the specific range of applications. Among others, here, we describe how our CuNWs spontaneously form a conductive network that we successfully used as electrodes for activating the electrocatalysis of CO2 reduction. Our approach to employ CuNWs as affective catalysts and electron carriers is illustrated in Fig. 4. We covered an electrochemical inert glass slide with a drop-cast 1 mg mL−1 CuNW ethanol solution to obtain an approximately 1 μm thick CuNW film. The evaporation of the solvent and the consequential attachment of the wires to the glass were favored by heating the plate at 150 °C. The drop-casting method yielded CuNW electrodes with an initially high intrinsic resistance, primarily attributed to the native copper oxide layer and to the presence of the capping agent monolayer provided by ODA. Therefore, to establish a percolative charge network among the CuNWs enabling a guaranteed efficient electron transfer, we exploited both chemical and electrochemical treatments by immersing the NWs in a 3 mg mL−1 NaBH4 solution for 30 minutes or by applying a constant potential of −1.3 V versus RHE for 60 seconds in 1 M KHCO3 solution. From a catalytic point of view, it has been recently pointed out that different copper crystal facets exhibit unique electrocatalytic behaviors within the CO2 reduction reaction (CO2RR),6,60,61 where (111) facets tend to favor methane production, while extended (100) terraces are more selective for ethylene.62–65 To gain insight into the crystalline structure and defects of the surface of our CuNWs, cyclic voltammetry (CV) characterization studies were carried out in a 1 M NaOH solution to observe the peaks related to the adsorption and desorption of OH− ions onto the particular crystallographic facets of the CuNWs which serve as fingerprints for each.65 CV was performed on three NWs selected for their different diameter's sizes: Bglu (![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 26 nm), Cglu (
= 26 nm), Cglu (![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 69 nm), and Jglu (
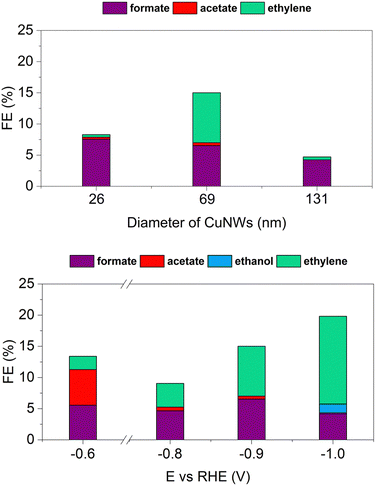
= 69 nm), and Jglu (![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 131 nm). Fig. 4E–G show the CVs’ peaks at +0.37 V and +0.41 V vs. RHE that can be attributed to (100) and (110) facets peculiar surface defects, respectively. Additionally, the signal between −0.05 and −0.1 V vs. RHE can be assigned to a larger exposed (100) surface. These observations are consistent with previous literature reports.65–67 Interestingly, the characteristic peak associated with adsorption/desorption on the (111) facet expected at +0.47 V is not clearly detectable in agreement with the small number of exposed boundaries’ facets within the wires. Although similar peaks have been observed for the three selected CuNWs, different relative heights can be conferred to each of them with the smaller and larger wires being quite similar, whereas the intermediate exhibits a more pronounced (100) signal. Electrocatalytic investigations were then performed by applying constant potential electrolysis experiments in 1 M KHCO3. Fig. 5A illustrates the relative amount of the detected products other than hydrogen that accounted for the remaining FE not represented. The histograms clearly demonstrate that the three nanowires exhibit different catalytic behaviors. As the diameter increases from B to J, the FE of formate and acetate decreases, indicating reduced selectivity for these products. Conversely, the FE of ethylene follows a distinct pattern: both the smallest (Bglu: 26 nm) and the largest (Jglu: 131 nm) nanowires produce ethylene with a low FE of approximately 0.5% while the intermediate sample (Cglu: 69 nm) shows a 16 times better FE in ethylene formation. This relative superior performance of the Cglu CuNWs in terms of efficient electrocatalysts for ethylene production is in agreement with the literature reflecting the presence of the larger response in terms of available (100) active sites compared to the other wires as described above. Vice versa, the lower activity of the 26 nm thick Bglu wire may also be attributed to mechanical fragility due to their small diameter, resulting in an unstable conductive network during experiments. CuNWs Cglu were further tested under varying potentials as described in Fig. 5B. A peculiar trend was detected: while the formate production remains relatively constant across all the tested potentials, the acetate production reaches its maximum at −0.6 V vs. RHE with a FE of 5.5%. Ethylene production, on the other hand, nicely increases as the potential becomes more negative, with FE reaching a value of 14% at −1.0 V vs. RHE.
= 131 nm). Fig. 4E–G show the CVs’ peaks at +0.37 V and +0.41 V vs. RHE that can be attributed to (100) and (110) facets peculiar surface defects, respectively. Additionally, the signal between −0.05 and −0.1 V vs. RHE can be assigned to a larger exposed (100) surface. These observations are consistent with previous literature reports.65–67 Interestingly, the characteristic peak associated with adsorption/desorption on the (111) facet expected at +0.47 V is not clearly detectable in agreement with the small number of exposed boundaries’ facets within the wires. Although similar peaks have been observed for the three selected CuNWs, different relative heights can be conferred to each of them with the smaller and larger wires being quite similar, whereas the intermediate exhibits a more pronounced (100) signal. Electrocatalytic investigations were then performed by applying constant potential electrolysis experiments in 1 M KHCO3. Fig. 5A illustrates the relative amount of the detected products other than hydrogen that accounted for the remaining FE not represented. The histograms clearly demonstrate that the three nanowires exhibit different catalytic behaviors. As the diameter increases from B to J, the FE of formate and acetate decreases, indicating reduced selectivity for these products. Conversely, the FE of ethylene follows a distinct pattern: both the smallest (Bglu: 26 nm) and the largest (Jglu: 131 nm) nanowires produce ethylene with a low FE of approximately 0.5% while the intermediate sample (Cglu: 69 nm) shows a 16 times better FE in ethylene formation. This relative superior performance of the Cglu CuNWs in terms of efficient electrocatalysts for ethylene production is in agreement with the literature reflecting the presence of the larger response in terms of available (100) active sites compared to the other wires as described above. Vice versa, the lower activity of the 26 nm thick Bglu wire may also be attributed to mechanical fragility due to their small diameter, resulting in an unstable conductive network during experiments. CuNWs Cglu were further tested under varying potentials as described in Fig. 5B. A peculiar trend was detected: while the formate production remains relatively constant across all the tested potentials, the acetate production reaches its maximum at −0.6 V vs. RHE with a FE of 5.5%. Ethylene production, on the other hand, nicely increases as the potential becomes more negative, with FE reaching a value of 14% at −1.0 V vs. RHE.
3. Experimental
3.1. Reagents
All manipulations were carried out in air using standard laboratory equipment. All the reagents and the solvents were obtained from commercial suppliers and used as received without further purification.Copper dichloride dihydrated (CuCl2·2H2O, > 99.0% from Merck), 1-octadecyl amine (ODA, from Merck), glucose (>99.5%, from Merck), sodium ascorbate (>98%, from Merck), ethanol (>99.5%, from Merck), isopropanol (>99.8%, from Merck), NaOH (>99% from Merck), and KHCO3 (99.7% from Merck) were used.
3.2. Preparation of CuNWs
The syntheses of CuNWs were performed in a 500 mL flask, closed by a screw cap. A thermostatic oil bath was employed to heat the reaction mixture. Typically, 0.400 g of CuCl2·2H2O and 2.529 g of 1-octadecylamine (ODA) were added to 200 mL of distilled water. The mixture was mixed and sonicated for 40 minutes at 40 °C. Afterward, x equivalents (x = 1, 3 or 5) of glucose (or sodium ascorbate) with respect to CuCl2·2H2O were added to the reaction flask, mixed, and heated for x h (x = 3, 10.5 or 18 h) at x °C (x = 100, 125 or 150 °C), without stirring the solution. The reaction conditions and equivalents of reagents employed for the other synthesis are outlined in Table 3. The reaction flask was cooled at room temperature. A red-brownish slurry was formed. Dark red CuNWs precipitated and accumulated in the bottom of the reaction flask. The product was centrifuged at 4000 rpm for 5 minutes using 100 mL of deionized water. This procedure was repeated ten times. Further ten centrifugations were carried out using 50 mL of an absolute ethanol solvent for each wash. The purification process was focused on removing excess reagents and oxidation byproducts of the organic reducing agents, with a minimal loss of copper nanomaterials. The obtained CuNWs were stored at 20 °C in absolute ethanol or isopropanol under an argon-saturated atmosphere. By implementing these storage protocols, we were able to maintain the structural integrity and functionality of the CuNWs over extended periods (6–9 months). To determine the percentage yield, CuNWs were dried, after the purification protocol, employing rotavapor equipment, and weighted accurately. The weight of CuNWs was converted to the percentage yield.3.3. Materials characterization
Electrocatalytic tests were carried out using an H-cell using the CuNW-based electrode as the working and the SCE as the reference electrode in the cathodic chamber. The counter electrode was located on the anodic chamber, and it was constituted using a platinum plate at which the oxygen evolution reaction (OER) occurred. In each compartment, a 50 mL solution of 1 M KHCO3 was present. The electrical communication between the chambers was ensured using a Nafion membrane. The employed potentiostat was a CHI660c workstation (CHInstruments). The liquid and gaseous products obtained from the electrocatalytic experiments were characterized with nuclear magnetic resonance (NMR) and gas chromatography (GC), respectively, and quantified as described in the ESI.† The measurement of the selectivity is expressed in terms of faradaic efficiency, which defines the number of electrons that were consumed to produce a certain product.21 FE is calculated according to the equation:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1) and Q is the total charge consumed during electrolysis. Electrolyses were conducted for 90 minutes.
485 C mol−1) and Q is the total charge consumed during electrolysis. Electrolyses were conducted for 90 minutes.
4. Conclusions
We demonstrated that a multiparametric DOE approach can be effectively exploited to foresee the reaction yield and the morphological properties of CuNWs, enabling a sound control over their hydrothermal synthesis. For the first time, to our knowledge, the effects of four straightforward synthetic parameters such as the temperature, reaction time, and type and quantity of reducing agents were elucidated by establishing a correlation between the CuNWs’ dimensions and physicochemical properties.Notably, our methodology allows the production of nanostructures with a wide range of diameters and aspect ratios without severe modification of the synthetic setup. As proved by SEM and XRD analyses, the use of sodium ascorbate as the reducing agent induces the formation of thicker and shorter CuNWs compared to those produced with glucose, while an extended reaction time allows longer CuNWs to be synthesized up to hundred microns. In this scenario, our DOE procedure guarantees the CuNWs’ morphological control over a virtual infinitive possibility, thus offering a roadmap for leveraging Cu based materials as robust nanostructures suitable for further surface chemical and physical engineering. The employed hydrothermal method has already been upscaled with success68 and along with the manageable temperature range employed and the use of inexpensive and environmentally friendly reagents, the overall process appears promising for industrial developments. Beyond these successful synthetic results based on the DOE approach, we also drove our Cu-based nanostructures towards industrial developments exploiting their functionality as electrocatalysts. We not only highlighted that CuNWs are easy-to-operate electrodes forming a highly conductive network able to effectively work on inert supports but also that they can be further improved as electrocatalysts for CO2 reduction. The intrinsic permeability and flexibility of CuNWs make them well-suited as gas diffusion electrodes in flow setups enabling the overcoming of the slow diffusion kinetics of reagents and increasing catalyst efficiency, thus paving the way for the realization of environmentally conscious and resource-efficient technologies.
Data availability
The data supporting the findings of this study are available within the article main text and the ESI† in the form of tables, figures, images and equations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to the financial support from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement no. 949087) (A. A.), the Department of Chemical Sciences of the University of Padova [P-DiSC#01BIRD2019-UNIPD] (M. B.), the University of Padova – Supporting Talent in Research – STARS 2019 “TimeForResponse” grant 166081 (S. B.), and the Basell Poliolefine Italia S.r.l. (A. C.). The authors thank Dr Andrea Basagni (University of Padova) for technical support in taking SEM images and profitable discussion on XRD data.Notes and references
- L. Cademartini, G. A. Ozin and J. M. Lehn, Concept of Nanochemistry, Wiley, 2009 Search PubMed.
- Z. Lyu, Y. Shang and Y. Xia, Acc. Mater. Res., 2022, 3, 1137–1148 CrossRef CAS.
- C. Choi, J. Cai, C. Lee, H. M. Lee, M. Xu and Y. Huang, Nano Res., 2021, 14, 3497–3501 CrossRef CAS.
- O. Baranov, K. Bazaka, T. Belmonte, C. Riccardi, H. E. Roman, M. Mohandas, S. Xu, U. Cvelbar and I. Levchenko, Nanoscale Horiz., 2023, 8, 568–602 RSC.
- M. S. Xie, B. Y. Xia, Y. Li, Y. Yan, Y. Yang, Q. Sun, S. H. Chan, A. Fisher and X. Wang, Energy Environ. Sci., 2016, 9, 1687–1695 RSC.
- A. Conte, M. Baron, S. Bonacchi, S. Antonello and A. Aliprandi, Nanoscale, 2023, 15, 3693–3703 RSC.
- K. Rossi and R. Buonsanti, Acc. Chem. Res., 2022, 55, 629–637 CrossRef CAS.
- J. Zhang, W. Luo and A. Zuttel, J. Mater. Chem. A, 2019, 7, 26285–26292 RSC.
- M. Strach, V. Mantella, J. R. Pankhurst, P. Iyengar, A. Loiudice, S. Das, C. Corminboeuf, W. V. Beek and R. Buonsanti, J. Am. Chem. Soc., 2019, 141, 16312–16322 CrossRef CAS.
- G. Zhang, Z.-J. Zhao, D. Cheng, H. Li, J. Yu, Q. Wang, H. Gao, J. Guo, H. Wang, G. A. Ozin, T. Wang and J. Gong, Nat. Commun., 2021, 12, 5745 CrossRef CAS.
- Z. Han, D. Han, Z. Chen, J. Gao, G. Jiang, X. Wang, S. Lyu, Y. Guo, C. Geng, L. Yin, Z. Wenig and Q.-H. Yang, Nat. Commun., 2022, 13, 3158 CrossRef CAS.
- H. Guo, N. Lin, Y. Chen, Z. Wang, Q. Xie, T. Zheng, N. Gao, S. Li, J. Kang, D. Cai and D. L. Peng, Sci. Rep., 2013, 3, 2323 CrossRef.
- J. Gao, A. Bahmanpour, O. Kröcher, S. M. Zakeeruddin, D. Ren and M. Grätzel, Nat. Chem., 2023, 15, 705–713 CrossRef CAS.
- Y. Zhang, Z. Si, H. Du, Y. Deng, Q. Zhang, Z. Wang, Q. Yu and H. Xu, Inorg. Chem., 2022, 61, 20666–20673 CrossRef CAS.
- K. Shi, M. D. Willis, Z. Ren and X. Feng, J. Phys. Chem. C, 2023, 127, 20710–20717 CrossRef CAS.
- S. R. Waldvogel, S. Lips, M. Selt, B. Riehl and C. J. Kampf, Chem. Rev., 2018, 118, 6706–6765 CrossRef CAS.
- H. Guo, N. Lin, Y. Chen, Z. Wang, Q. Xie, T. Zheng, N. Gao, S. Li, J. Kang, D. Cai and D. L. Peng, Sci. Rep., 2013, 3, 2323 CrossRef.
- O. Ohiienko and Y. J. Oh, Mater. Chem. Phys., 2020, 246, 122783 CrossRef CAS.
- T. H. Duong and H. C. Kim, Ind. Eng. Chem. Res., 2018, 57, 3076–3082 CrossRef CAS.
- Y. Zhao, L. Fan, Y. Zhang, H. Zhao, X. Li, Y. Li, L. Wen, Z. Yan and Z. Huo, ACS Appl. Mater. Interfaces, 2015, 7, 16802–16812 CrossRef CAS.
- Q. Li, S. Fu, X. Wang, L. Wang, X. Liu, Y. Gao, Q. Li and W. Wang, ACS Appl. Mater. Interfaces, 2022, 14, 57471–57480 CrossRef CAS.
- C. Choi, S. Kwon, T. Cheng, M. Xu, P. Tieu, C. Lee, J. Cai, H. M. Lee, X. Pan, X. Duan, W. A. Goddard and Y. Huang, Nat. Catal., 2020, 3, 804–812 CrossRef CAS.
- S. Zhao, F. Han, J. Li, X. Meng, W. Huang, D. Cao, G. Zhang, R. Sun and C.-P. Wong, Small, 2018, 14, 1800047 CrossRef.
- J. C. Yu, F. G. Zhao, W. Shao, C. W. Geb and W. S. Li, Nanoscale, 2015, 7, 8811–8818 RSC.
- M. Mohl, P. Pusztai, A. Kukovecz and Z. Konya, Langmuir, 2010, 26, 16496–16502 CrossRef CAS.
- C. Kim, W. Gu, M. Briceno, I. M. Robertson, H. Choi and K. Kim, Adv. Mater., 2008, 20, 1858–1863 Search PubMed.
- N. Ulrich, M. Schäfer, M. Römer, S. D. Straub, S. Zhang, J. Brötz, C. Trautmann, C. Scheu, B. J. M. Etzold and M. E. T. Molares, ACS Appl. Nano Mater., 2023, 6, 4190–4200 CrossRef CAS.
- Z. Liu, Y. Yang, J. Liang, Z. Hu, S. Li, S. Peng and Y. Qian, J. Phys. Chem. B, 2003, 107, 12658–12661 CrossRef CAS.
- S. Li, Y. Chen, L. Huang and D. Pan, Inorg. Chem., 2014, 53, 4440–4444 CrossRef CAS.
- M. Kevin, G. Y. R. Lim and G. W. Ho, Green Chem., 2015, 17, 1120–1126 RSC.
- S. Bhanushali, P. Ghosh, A. Ganesh and W. Cheng, Small, 2015, 11, 1232–1252 CrossRef CAS.
- Z. Tang, H. Kwon, M. Yi, K. Kim, J. W. Han, W. S. Kim and T. Yu, ChemistrySelect, 2017, 2, 4655–4661 CrossRef CAS.
- C. Hwang, J. An, B. Doo Choi, K. Kim, S.-W. Jung, K. J. Baeg, M.-G. Kim, K. M. Ok and J. Hong, J. Mater. Chem. C, 2016, 4, 1441–1447 RSC.
- S. Xu, X. Sun, H. Ye, T. You, X. Song and S. Sun, Mater. Chem. Phys., 2010, 120, 1–5 CrossRef CAS.
- J. Chen, F. Jiang and Y. Yin, Acc. Chem. Res., 2021, 54(5), 1168–1177 CrossRef CAS.
- R. Leardi, Anal. Chim. Acta, 2009, 652, 161–172 CrossRef CAS.
- E. M. Williamson, Z. Sun, L. M.-Tamez and R. L. Brutchey, Chem. Mater., 2022, 34, 9823–9835 CrossRef CAS.
- R. S. Fernandes, I. M. Raimundo and M. F. Pimentel, Colloids Surf., A, 2019, 577, 1–7 CrossRef CAS.
- E. M. Williamson, B. A. Tappan, L. Mora-Tamez, G. Barim and R. L. Brutchey, ACS Nano, 2021, 15, 9422–9433 CrossRef CAS.
- T. Pretto, F. Baum, G. F. S. Andradeb and M. J. L. Santos, CrystEngComm, 2021, 23, 397–403 RSC.
- F. Baum, T. Pretto, R. A. Gouvea and M. J. L. Santos, Cryst. Growth Des., 2022, 22, 3669–3679 CrossRef CAS.
- J. C. de la Rosa and M. Segarra, ACS Omega, 2019, 4, 18289–18298 CrossRef.
- E. M. Williamson and R. L. Brutchey, Inorg. Chem., 2023, 62, 16251–16262 CrossRef CAS.
- H. Tao, T. Wu, M. Aldeghi, T. C. Wu, A. A. Guzik and E. Kumacheva, Nat. Rev. Mater., 2021, 6, 701–716 CrossRef.
- E. J. Braham, R. D. Davidson, M. Al-Hashimi, R. Arroyave and S. Banerjee, Dalton Trans., 2020, 49, 11480–11488 RSC.
- H. J. Yang, S. Y. He and H. Y. Tuan, Langmuir, 2014, 30, 602–610 CrossRef CAS.
- T. Zhang, W. Y. Hsieh, F. Daneshvar, C. Liu, S. P. Rwei and H. J. Sue, Nanoscale, 2020, 12, 17437–17449 RSC.
- J. Cure, A. Glaria, V. Collière, P. F. Fazzini, A. Mlayah, B. Chaudret and P. Fau, J. Phys. Chem. C, 2017, 121, 5253–5260 CrossRef CAS.
- H. Yoon, D. S. Shin, B. Babu, T. G. Kim, K. M. Song and J. Park, Mater. Des., 2017, 132, 66–71 CrossRef CAS.
- B. J. Jones and C. Nachtsheim, J. Qual. Technol., 2011, 43, 1–15 CrossRef.
- Y. Zheng, J. Liang, Y. Chen and Z. Liu, RSC Adv., 2014, 4, 41683–41689 RSC.
- H. Guo, N. Lin, Y. Chen, Z. Wang, Q. Xie, T. Zheng, N. Gao, S. Li, J. Kang, D. Cai and D. L. Peng, Sci. Rep., 2013, 3, 2323 CrossRef.
- D. V. R. Kumar, A. M. Koshy, N. Sharma, N. Thomas and P. Swaminathan, ACS Omega, 2023, 8, 21107–21112 CrossRef CAS.
- Y. Zhang, Z. Si, H. Du, Y. Deng, Q. Zhang, Z. Wang, Q. Yu and H. Xu, Inorg. Chem., 2022, 61, 20666–20673 CrossRef CAS.
- C. S. Lewis, L. Wang, H. Liu, J. Han and S. S. Wong, Cryst. Growth Des., 2014, 14, 3825–3838 CrossRef CAS.
- J. Y. Lin, Y.-L. Hsueh and J. J. Huang, J. Solid State Chem., 2014, 214, 2–6 CrossRef CAS.
- D. V. R. Kumar, I. Kim, Z. Zhong, K. Kim, D. Lee and J. Moon, Phys. Chem. Chem. Phys., 2014, 16, 22107–22115 RSC.
- Y. Tu, D. Njus and H. B. Schlege, Org. Biomol. Chem., 2017, 15, 4417–4431 RSC.
- F. Silly and M. R. Castell, ACS Nano, 2009, 3, 901–906 CrossRef CAS.
- J. M. Chiu, I. Wahdini, Y. N. Shen, C. Y. Tseng, J. Sharma and Y. Tai, ACS Appl. Energy Mater., 2023, 6, 5058–5066 CrossRef CAS.
- S. Jeong, C. Huang, Z. Levell, R. X. Skalla, W. Hong, N. J. Escorcia, Y. Losovyj, B. Zhu, A. N. B. Griffith, Y. Liu, C. W. Li, D. R. Hickey, Y. Liu and X. Ye, J. Am. Chem. Soc., 2024, 146(7), 4508–4520 CrossRef CAS.
- Y. Hori, I. Takahashi, O. Koga and N. Hoshi, J. Mol. Catal. A: Chem., 2003, 199, 39–47 CrossRef CAS.
- Y. C. Zhang, X. L. Zhang, Z. Z. Wu, Z. Z. Niu, L. P. Chi, F. Y. Gao, P. P. Yang, Y. H. Wang, P. C. Yu, J. W. Duanmu, S. P. Sun and M. R. Gao, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2400546121 CrossRef CAS.
- G. Zhang, Z. J. Zhao, D. Cheng, H. Li, J. Yu, Q. Wang, H. Gao, J. Guo, H. Wang, G. A. Ozin, T. Wang and J. Gong, Nat. Commun., 2021, 12, 5745 CrossRef CAS.
- A. K. Engstfeld, T. Maagaard, S. Horch, I. Chorkendorff and I. E. L. Stephens, Chem. – Eur. J., 2018, 24, 17743–17755 CrossRef CAS.
- A. Tiwari, H. H. Heenen, A. S. Bjørnlund, T. Maagaard, E. Cho, I. Chorkendorff, H. H. Kristoffersen, K. Chan and S. Horch, J. Phys. Chem. Lett., 2020, 11, 1450–1455 CrossRef CAS.
- S. Liu, Y. Li, D. Wang, S. Xi, H. Xu, Y. Wang, X. Li, W. Zang, W. Liu, M. Su, K. Yan, A. C. Nielander, A. B. Wong, J. Lu, T. F. Jaramillo, L. Wang, P. Canepa and Q. He, Nat. Commun., 2024, 15, 5080 CrossRef CAS.
- Q. Q. Fu, Y. D. Li, H. H. Li, L. Xu, Z. H. Wang and S. H. Yu, Langmuir, 2019, 35, 4364–4369 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00402g |
| This journal is © The Royal Society of Chemistry 2024 |