The effect of aliovalent dopants on the structural and transport properties of Li₆La₂BaTa₂O₁₂ garnet Li-ion solid electrolytes

Abstract

Li-rich garnet solid electrolytes are promising candidates for all-solid-state batteries, allowing for increased energy densities, compatibility with Li-metal anodes and improved safety by replacing flammable organic-based liquid electrolytes. Li-stuffed garnets typically require aliovalent doping to stabilise the highly ionic conductive Ia3̄d cubic phase. The role of dopants and their location within the garnet framework can greatly affect the conduction properties of these garnets, yet their impact on the structure and resulting ion transport is not fully understood. Here, we evaluate the effect of aliovalent doping with Al³⁺, Ga³⁺ and Zn²⁺ in the Li₆BaLa₂Ta₂O₁₂ (LBLTO) garnet material. A combination of PXRD and XAS reveals a linear cell parameter contraction with an increase in doping and the preference of the 24d Li⁺ sites for Al³⁺ and Zn²⁺ dopants, with Ga³⁺ occupying both the 24d and 48g Li⁺ sites. Macroscopic ionic conductivity analyses by EIS demonstrate an enhancement of the transport properties where addition of small amounts of Al³⁺ decreases the activation energy to Li⁺ diffusion to 0.35(4) eV. A detrimental effect on ionic conductivities is observed when dopants were introduced in Li⁺ pathways and upon decreasing the Li⁺ concentration. Insights into this behaviour are gleaned from microscopic diffusion studies by muon spin relaxation (μ⁺SR) spectroscopy, which reveals a low activation energy barrier for Li⁺ diffusion of 0.16(1) eV and a diffusion coefficient comparable to those of Li₇La₃Zr₂O₁₂ (LLZO) benchmark garnet materials.

---

A. Introduction

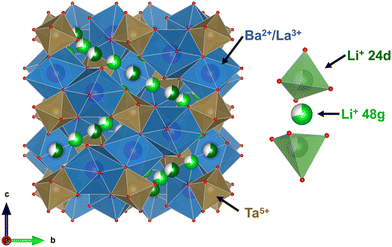
Flammable solvents employed to dissolve electrolyte salts in current Li-ion batteries (LIBs) exhibit inherent safety concerns and limit the energy density and power capabilities accessible due to potential dendrite growth with Li-metal anodes. All-solid-state batteries are positioned as a promising next-generation battery technology, where replacing the liquid electrolyte with a solid-state Li-ion electrolyte may permit increased safety and energy density, together with the compatibility with Li-metal anodes and high-voltage cathodes. With several families of Li⁺ conductors as candidate solid-state electrolytes, including NASICON, thio-LISICON, (anti)perovskites, Li₁₀GeP₂S₁₂, argyrodite or recent thio-phosphates,¹ Li-rich garnet electrolytes represent an outstanding candidate with high electrochemical stability with Li metal and high voltages beyond 6 V and ionic conductivities in the mS cm⁻¹ range.²

The Li garnet crystal structure is derived from that of the garnet mineral which can be described using the formula A₃B₃C₂O₁₂, where A cations are located in an oxygen-tetrahedral environment, B cations are surrounded by 8 oxygen anions and C cations are accommodated in oxygen-octahedral sites. For Li-stuffed garnets, Li⁺ sit on the A sites with the B sites typically occupied by a rare earth metal or a large alkaline earth metal and the C sites can be occupied by a wide range of metal cations with oxidation states usually ranging from 4+ to 6+. Conventional Li₃Ln₃M₂O₁₂ garnets crystallise in a body centred cubic structure with the Ia3̄d space group, where Li⁺ ions occupy the tetrahedral 24d positions, Ln³⁺ ions are located in the 8-fold 24c positions and M⁶⁺ cations are located in the octahedral 16a positions with the O²⁻ sitting on the 96h positions making up the anionic framework. Replacing B-site or/and C-site cations with lower oxidation state elements can increase the number of Li⁺ ions per formula unit of the garnet material, with Li⁺ then occupying partially filled 24d tetrahedral sites and distorted octahedral 48g interstitial positions, which can split into two 96h sites.³ Thangadurai and Weppner reported the Li₆BaLa₂Ta₂O₁₂ (LBLTO) Li-rich garnet in 2005 (Fig. 1) with conductivities topping 10⁻⁵ S cm⁻¹.⁴ A benchmark Li₇La₃Zr₂O₁₂ garnet was also reported by Thangadurai's team with a conductivity of up to 10⁻⁴ S cm⁻¹.⁵ Theoretically, an upper limit of Li = 7.5 could be accessed when taking into account the high electrostatic repulsions occurring between Li⁺ occupying the octahedral positions and the tetrahedral sites if the two adjacent tetrahedral positions are also occupied.⁶ Experimentally, only compositions of up to Li ≈ 7 have been realised.^6,7 Furthermore, Li = 7 garnets are thermodynamically stable in a tetragonal phase with the space group I4/acd resulting from Li⁺ ordering into fully occupied sites, as in the case of undoped Li₇La₃Zr₂O₁₂ and Li₇La₃Sn₂O₁₂ garnets.^8,9 This Li⁺ ordering, phase transformation, and full occupancy of the Li⁺ sites lead to a dramatic decrease in the conduction properties of the garnet down to 10⁻⁶ S cm⁻¹. Aliovalent doping of the Li = 7 compositions is required to avoid the phase transformation from the highly conducting Ia3̄d cubic phase to the low ionic conducting I4/acd tetragonal phase via a vacancy-creation mechanism that stabilises the cubic phase.¹⁰

Fig. 1 Crystallographic representation of the unit cell for the Li₆BaLa₂Ta₂O₁₂ garnet structure with Ia3̄d cubic symmetry where Ba²⁺ and La³⁺ cations are enclosed in blue polyhedra, Ta⁵⁺ in brown polyhedra with Li⁺ ions; 3D chains are presented showing Li⁺ in tetrahedral 24d sites in bright green and Li⁺ in 48g distorted octahedra in dark green. Li⁺ dimers are shown separately for clarity where one 48g octahedral site is surrounded by two 24d tetrahedral sites.

While doping strategies have proven an efficient method for improving ionic conductivities and electrochemical performance in LLZO garnets,^11–14 studies focussing on the dopant effect on the LBLTO family of garnets are limited, which is the subject of the current study. Li-rich garnets with Li⁺ integer compositions, such as in Li₆La₂BaTa₂O₁₂ (LBLTO), can present ordered ground-state crystal structures that lower Li⁺ mobility stemming from reduced Li–Li interactions within these ordered phases.¹⁵ The study of doped LBLTO is therefore desirable, since suitable dopants may stabilise the cubic phase and simultaneously influence the Li⁺ diffusion dynamics. For example, the introduction of additional repulsive forces between dopant and Li⁺ ions¹⁶ or the reduction of grain boundary resistances with better particle sintering may both work to improve ionic conductivity.^17–20 Furthermore, doping with Al³⁺ has been shown to prevent Li loss at high sintering temperatures, when residing at the grain boundaries.²¹ Thus, introduction of additional Li⁺ vacancies in the LBLTO garnet structure via aliovalent doping is expected to influence the transport properties of these materials. However, reports of the local structural and dynamic behaviour in doped LBLTO remain scarce. Here, we examine a series of doped LBLTO garnet materials with the goal of studying the impact of these dopants on the local structure and the resulting ion transport properties.

The location of the dopant within the garnet framework has significant implications on the resulting transport properties and remains a topic of debate. For example, in the case of Al- or Ga-doped LLZO garnets, there are discrepancies as to where the dopant is located depending on the characterisation technique or synthetic methodology employed. Rettenwander et al. proposed Al and Ga dopants to reside with similar populations in both the 24d and 96h sites within the garnet structure.^22,23 Karasulu et al., however, have challenged this, proposing the 24d site as the preferential location for Al or Ga dopants in the LLZO garnet.²⁴ Differences can be ascribed to the choice of synthetic conditions employed. To further complete this picture, Li et al. reported the dopant to be sitting at the octahedral 48g sites, the centre position between two 96h sites, by neutron powder diffraction (NPD) studies.²⁵ An intermediate route has also been reported for Ga-doped LLZO, with 24d sites being initially occupied followed by the occupation of 96h sites.⁵ It has also been found that Ga-doping can lead to a change in the space group from centrosymmetric Ia3̄d to a non-centrosymmetric I4̄3d, due to the preferential occupation of 24d sites in the LLZO garnet.²⁶ A similar story occurs in the case of Ge-doped LLZO, where Ge⁴⁺ was initially found to be more likely sitting at the 96h sites by XANES analyses,²⁷ but later reported to be present in the 24d positions as observed by NPD measurements.²⁸

In this work, we present the microwave-assisted solid-state synthesis of undoped and Al³⁺-, Ga³⁺- and Zn²⁺-doped Li₆BaLa₂Ta₂O₁₂ garnet materials. The use of microwave-assisted solid-state synthesis reduces the required reaction temperatures and synthesis times which can lower the risk of lithium evaporation and contamination from crucibles, affording more precise stoichiometries. Structural changes have been evaluated by PXRD and XAS measurements to identify the most likely atomic position for the dopants within the garnet framework. Variable temperature EIS studies of the synthesised materials have been employed to study the interrelation between the aliovalent substitutions of Li⁺ and the ionic transport properties of the resultant materials. With the dopant influencing the structural and transport properties of the garnet materials, we also wish to understand the origin of the conductivity difference between Li = 6 and Li = 7 families beyond the macroscopic effect of doping. To this end, we have also carried out muon spin relaxation spectroscopy experiments on the undoped LBLTO material to explore the microscopic conduction properties of the material and compare these with our previous results on the LLZO garnet,²⁹ where the required synthetic temperatures and times are different, which could result in differences in the total conductivity due to different grain boundaries and grain sizes contributing to the macroscopic ionic conduction as typically reported in EIS measurements.

B. Results and discussion

Synthesis, and structural and morphological studies

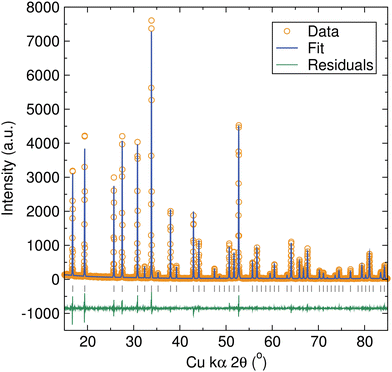
Al-, Ga-, and Zn-doped LBLTO garnet materials were synthesised by a microwave-assisted solid-state approach. The use of this microwave method allows for higher energy efficiency compared with conventional heating methods. Our previous work has demonstrated that this can lead to shorter reaction times and lower synthetic temperatures to obtain phase pure cubic garnet materials.²⁹ In the case of this LBLTO garnet material, the use of this microwave-assisted method led to a reduction in the reaction times and temperatures required to obtain phase pure materials compared with the original synthesis reported by Thangadurai and Weppner.⁴ The reaction temperature was lowered by 100 °C and the time required to obtain phase pure materials reduced from 24 hours to 6 hours.

PXRD data of the parent compound LBLTO were indexed successfully to the Ia3̄d cubic space group with narrow Bragg peaks, indicating the high crystallinity of the synthesised material (Fig. 2). The refined unit cell parameter value was 13.0018(1) Å, in good agreement with the reported value of 13.00 Å for undoped LBLTO.^4,30 Additional details on atom positions, fractional occupancies, thermal energies and cell parameters calculated from Rietveld refinements can be found in Table S1 (ESI†).

Fig. 2 Rietveld refinements of PXRD data for the Li₆BaLa₂Ta₂O₁₂ material. Bragg peak positions for the cubic Li₆BaLa₂Ta₂O₁₂ garnet structure are indicated by vertical grey tick marks. Fit was in good agreement with the cubic space group Ia3̄d with the following cell parameters: a = 13.0018(1) Å and V = 2197.89(3) ų. R_wp = 0.1381, R_p = 0.1002, R_F2 = 0.0344 and χ² = 2.055.

Stoichiometries for the doped LBLTO garnets were tailored in a manner such that the dopant cations are inserted into the Li⁺ ionic sublattice, replacing the Li⁺ ions in the garnet structure. The selection of the aliovalent dopant replacing the Li⁺ was rationalised in terms of atomic size, charge compensation and site geometry. Li⁺ ions have a cation size of 59 pm in a tetrahedral environment and an increased size of 74 pm if the coordination environment is octahedral.²⁸ Al³⁺, Ga³⁺ and Zn²⁺ have cation sizes of 39, 47 and 60 pm respectively in tetrahedral coordination, while their cation sizes increase to 53, 62 and 75 pm in octahedral coordination, respectively.³¹ In addition to this, La³⁺ and Ba²⁺ have far larger cation sizes (>100 pm on their 8-fold coordination)³¹ and the relatively low valence of Zn²⁺ compared to the Ta⁵⁺ cations makes it unlikely for Zn²⁺ to replace Ta⁵⁺ in the garnet structure since this position is occupied predominantly by M^>4+ cations.⁷ The relatively close ionic sizes and charges between the dopants and the Li⁺ ions indicate that doping into the Li⁺ positions is a plausible route for the insertion of the dopants into the LBLTO garnet structure. Computational studies over a wide range of dopants for the garnet structure have shown that Al³⁺, Ga³⁺ and Zn²⁺ display a preference for the Li⁺ positions.³² Moreover, similar substitution routes have been experimentally explored for the LLZO garnet family, also demonstrating the preference of Al³⁺, Ga³⁺ and Zn²⁺ towards the Li⁺ positions.^{16–18,33,34} The dopant concentrations were chosen to allow for direct comparison between various doped materials in terms of the Li⁺ carrier concentrations on the ionic conductivity analyses. The Li⁺ concentration was set at two values to generate two comparable material groups: one with a Li⁺ content of 5.25 moles per formula unit and the other at 5.7 moles per formula unit.

The PXRD profiles of the different doped LBLTO garnets (Fig. S1, ESI†) display sharp peaks, indicative of the high crystallinity of the microwave synthesised materials with no other discernible Bragg reflections from impurities detected. The dotted line corresponding to the (402) reflection is used as a guide for the eye to follow the small displacement of the peak towards higher diffraction angles indicating lattice contraction with progressive doping.³⁵

Fig. 3 shows the variation of the unit cell parameter with respect to the dopant concentration on the LBLTO material. Since the three different dopants have a smaller or similar size to the substituted Li⁺ ions, the cell parameter experienced a linear decrease with increasing concentration of the dopant as expected. Attempts were made to prepare materials with higher dopant concentrations, for example, Li_4.5Al_0.5BaLa₂Ta₂O₁₂. However, as the solubility limits of the dopant were surpassed, these attempts resulted in materials with high impurity content. The cell parameter variation is in good agreement with Vegard's law, confirming the effective formation of a solid-solution and dopant inclusion into the garnet framework.³⁶

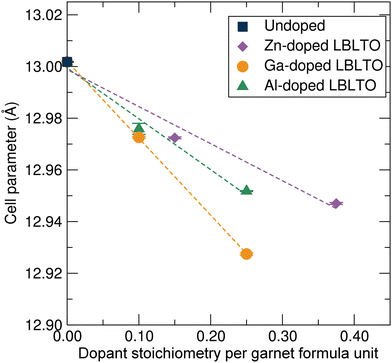Fig. 3 Unit cell parameter evolution following Vegard's law for the cubic Ia3̄d garnet crystal structure with an increase in Al³⁺, Ga³⁺ and Zn²⁺ dopant concentrations.

Zn²⁺ ions have a similar ionic radius to Li⁺, thus displaying the lowest gradient in the Vegard fit. The larger cationic charge on Zn²⁺ ions results in stronger bonding to the surrounding oxygen anions leading to a smaller cell parameter to compensate for the higher oxidation state of the Zn²⁺ cation. In the case of Al³⁺, despite possessing the largest difference in atomic size compared with Li⁺, the slope of the Vegard fit for the Al³⁺ doped samples is smaller than that for the Ga³⁺ dopant, with a smaller ionic size difference with Li⁺. This could be indicative of Ga³⁺ cations occupying the larger 48h octahedral positions, where Ga³⁺ can be accommodated, allowing the crystal cell to further contract.

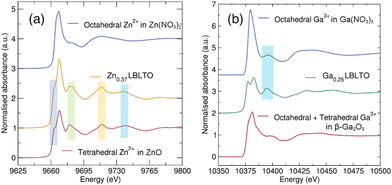
To analyse the local coordination environment of the dopants in the garnet structure, XAS measurements were carried out on Ga and Zn K-edges (10.37 and 9.66 keV respectively) (Fig. 4). Measurements on the Al K-edge (1.56 eV) were not possible as this edge falls outside the energy range available. The presence of strong absorption edges from the Ta L_II (11.14 keV) and L_III (9.89 keV) edges precluded a detailed EXAFS analysis of the local coordination shells of the dopant, limiting to qualitative assessments of the XANES region of the dopant against standards with known coordination environments.

Fig. 4 (a) XANES region of the XAS data measured on the Zn K-edge for Li_5.25Zn_0.37BaLa₂Ta₂O₁₂, and Zn(NO₃)₂·6H₂O and ZnO standards. (b) XANES region of the XAS data measured on the Ga K-edge for Li_5.25Ga_0.25BaLa₂Ta₂O₁₂ and, Ga(NO₃)₃·9H₂O and Ga₂O₃ standards. Coloured boxes indicate common features in the XANES profiles between the different materials analysed.

ZnO and Zn(NO₃)₂·6H₂O were chosen as standards for Zn K-edge analyses. ZnO crystallises in the wurtzite structure under ambient conditions with a P6₃mc group space symmetry.³⁷ In this crystal structure, Zn²⁺ cations are tetrahedrally coordinated to four O²⁻ anions. In the case of Zn(NO₃)₂·H₂O₆, the compound crystallises in the orthorhombic space group Pnma, where the Zn²⁺ cations are coordinated to six O²⁻ anions forming an octahedron.³⁸Fig. 4(a) shows the Zn K-edge XANES data of the Zn-doped Li_5.25Zn_0.37BaLa₂Ta₂O₁₂ garnet material together with the ZnO and Zn(NO₃)₂·6H₂O standards. The profile of the Li_5.25Zn_0.37BaLa₂Ta₂O₁₂ garnet spectrum shares almost identical features with the ZnO standards, where Zn²⁺ forms oxygen-coordinated tetrahedra. The absorption intensity of the Zn K-edge is induced by electronic transitions from Zn 1s orbital to empty Zn 4p orbitals. The absence of empty 3d orbitals in Zn²⁺ cations precludes the easy differentiation between tetrahedral and octahedral coordination due to the lack of a pre-edge feature in the Zn K-edge spectra. In the former, a pre-edge feature could appear from s to d transitions while in the latter the centrosymmetry of the octahedral environment would forbid this transition. In the case of Zn²⁺ in an octahedral environment, a single strong peak is observed. When the local environment is changed to a tetrahedral coordination, a split on the main peak is produced with a shoulder noted. A similar profile is noted for the Li_5.25Zn_0.37BaLa₂Ta₂O₁₂ material. This indicates that the Zn²⁺ cations in the garnet structure tend to occupy the tetrahedral Li⁺ 24d positions.

Analogous analyses were carried out for the Li_5.25Ga_0.25BaLa₂Ta₂O₁₂ garnet material. Fig. 4b shows the XANES region of the XAS data on the Ga K-edge for the Li_5.25Ga_0.25BaLa₂Ta₂O₁₂ material, together with β-Ga₂O₃ and Ga(NO₃)₃·9H₂O standards. Ga(NO₃)₃·9H₂O crystallises in a monoclinic structure with space group P21/c where the Ga³⁺ cations occupy the centre of an octahedron.³⁹ The β-Ga₂O₃ standard crystallises in a monoclinic structure with point symmetry C2/m, where Ga³⁺ cations are distributed in both octahedral and tetrahedral oxide coordination sites.⁴⁰ Again, as Ga³⁺ is isoelectronic with Zn²⁺ and possesses full 3d orbitals, this precludes a simple confirmation of tetrahedral or octahedral coordination from the presence/absence of pre-edge features. In the Li_5.25Ga_0.25BaLa₂Ta₂O₁₂ XANES data, the peak splitting observed on the main edge (not evident for the octahedral Ga reference) indicates there is not an exclusive octahedral coordination around the Ga³⁺ cations. This suggests that the Ga³⁺ ions are also occupying tetrahedral Li⁺ 24d positions in the garnet structure, similar to the Zn-doped analogue. However, this does not exclude Ga³⁺ ions being located on octahedral coordination sites. In fact, a similar feature between the Li_5.25Ga_0.25BaLa₂Ta₂O₁₂ garnet material and the Ga(NO₃)₃·9H₂O standard could indicate that Ga³⁺ ions occupy octahedral as well as tetrahedral Li⁺ positions in the garnet structure. This observation is in agreement with studies by Rettenwander et al. where Ga³⁺ has been found to be located on both Li⁺ 24d and 48g positions by NMR studies.⁴¹

SEM micrographs (Fig. S2, ESI†) revealed inhomogeneous particles with non-regular shapes with sizes ranging from ≈1 to 10 micrometres. The particle sizes and morphologies had no apparent variations with the insertion of the dopant into the garnet structure. EDX analyses (Table S2, ESI†) were also performed for the highest doped LBLTO garnets to analyse the stoichiometry of the compositions studied. Atomic concentrations from EDX measurements were all within the standard deviations, in agreement with the nominal stoichiometries of the synthesised materials. The atomic concentrations were normalised to the Ta⁵⁺ concentration, as this element is fully occupying its site within the garnet structure and has negligible volatility compared to other elements present in the materials. All pelletised samples had a similar relative geometric density of ≈80%, with no variation within the uncertainty of the density measurements.

Ionic transport properties

LBLTO garnets are reported to be one of the best performing garnet compositions in terms of transport properties. The LBLTO intra-grain ionic conductivity is on the order of 10⁻⁵ S cm⁻¹ at room temperature, with reported activation energies as low as 0.4 eV.⁴ Most studies have focussed on modifying the transport properties of the LBLTO material by varying the Ba²⁺/La³⁺ ratios or by Ta⁵⁺ substitutions with other elements.^42,43 Microstructural engineering has also been explored to reduce inter-grain resistances.^44,45 Doping on the Li⁺ positions, however, has remained broadly unexplored for this particular garnet composition.

EIS measurements were carried out to evaluate the impact of doping into the Li⁺ positions on the macroscopic transport properties. Room temperature Nyquist plots of the EIS measurement (Fig. S3, ESI†) for the undoped LBLTO material and the Al-, Ga- and Zn-doped Li = 5.7 garnet compositions reveal a semicircle feature followed by the presence of a tail at low frequencies where Pt-blocking electrodes are applied, indicating the ionic character of conduction in these garnet materials.⁴⁶ Unlike other ionic conductors where intragrain and inter-grain contributions to the total ionic resistance can be separated, this is not always a trivial task in the case of the garnets, where the total resistance (sum of intra- and inter-grain resistance) is often reported since the separation of the two contributions cannot always be resolved at higher temperatures.^47,48 There are some exceptions to this, as in the case of hot-pressed garnet materials where both contributions to the total resistance can be resolved.⁴⁹

The total resistance for the LBLTO materials was fitted to an external electrical circuit composed of resistance with a parallel constant phase element. The constant phase element models double-layer capacitance behaviour between the electrode and the garnet material, and accounts for any nonideal behaviour and dispersion in the time constant.⁵⁰

The ionic conductivity of the material is calculated from the resistance obtained in the fitted models by applying Pouillet's law. The calculated room temperature ionic conductivities for all synthesised materials are given in Table S3 (ESI†) and presented in Fig. 5(a). The room temperature ionic conductivity of the undoped LBLTO material is 3.7 × 10⁻⁶ S cm⁻¹, approximately an order of magnitude lower compared to the original report for this material.⁴ This difference may be caused by the lower temperature and shorter times employed during the microwave-assisted synthesis which may result in lower grain sintering leading to a higher inter-grain resistance of the material. A review of the literature reveals that a wide range of ionic conductivity values are reported for the same type of garnet material depending on different factors.⁷ EIS measurements are sensitive to changes in synthetic and sintering conditions which can interfere with the analyses, often hampering a direct comparison of conductivity values in the literature.

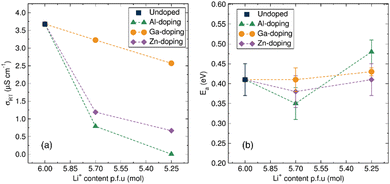Fig. 5 (a) Calculated total ionic conductivity from EIS measurements at room temperature of the undoped and Al-, Ga-, Zn-doped Li₆BaLa₂Ta₂O₁₂ materials with decreasing Li⁺ content. (b) Activation energy evolution for the total ionic conduction of the undoped and Al³⁺, Ga³⁺, Zn²⁺ doped Li₆BaLa₂Ta₂O₁₂ materials from calculated from Arrhenius plots of conductivity data from EIS measurements (Fig. S4 and Table S4, ESI†).

From room temperature conductivity measurements, it is clear that Al-doping had a detrimental impact on the ionic conductivity of the materials, decreasing progressively to 7.9 × 10⁻⁷ S cm⁻¹ for the Li_5.70Al_0.10BaLa₂Ta₂O₁₂ material and a further decrease of two orders of magnitude for the Li_5.25Al_0.25BaLa₂Ta₂O₁₂ garnet to a value of 2.8 × 10⁻⁹ S cm⁻¹. A similar effect, albeit less pronounced, was observed upon the introduction of the Zn dopant to the garnet framework. The room temperature ionic conductivity decreased to a value of 1.2 × 10⁻⁶ S cm⁻¹ for the Li_5.70Zn_0.15BaLa₂Ta₂O₁₂ material with a further decrease to 6.6 × 10⁻⁷ S cm⁻¹ noted for the higher doped Li_5.25Zn_0.37BaLa₂Ta₂O₁₂. In the case of Ga-doped LBLTO materials, the room temperature ionic conductivity remained within the same order of magnitude, only experiencing a small decrease of the conductivity to 3.2 × 10⁻⁶ S cm⁻¹ and 2.6 × 10⁻⁶ S cm⁻¹ for the Li_5.70Ga_0.10BaLa₂Ta₂O₁₂ and Li_5.25Ga_0.25BaLa₂Ta₂O₁₂ garnet materials, respectively. This difference in behaviour between Al³⁺ and, Ga³⁺ and Zn²⁺ dopants again points to the possibility of Ga³⁺ occupying the octahedral Li⁺ 48g positions in the garnet structure, in agreement with our XANES observations. The presence of dopant ions on the Li⁺ 24d positions has been reported to have a detrimental effect on the conductivity of the materials while displacing the dopant towards 48g positions can alleviate this effect.⁵¹ This is essentially due to the 24d sites dominating the ionic conductivity, as they act as nodes between the transport pathways of four Li⁺ located on the neighbouring 48g sites, while the 48g positions act as connection points only between the transport of two Li⁺ located on the 24d positions.^52,53 Additionally, the higher amount of Zn to achieve the same level of Li⁺ concentration could result in a higher number of neighbouring vacancies being deactivated for Li⁺ diffusion.⁵⁴

To further understand the effects of the dopant on the macroscopic transport properties of these garnet materials, temperature variable EIS measurements were also carried out. This allowed analysis of the Arrhenius behaviour of the ionic conductivity (Fig. S4, ESI†) and calculation of activation energies for the total ionic diffusion (Table S4, ESI†). Fig. 5(b) shows the variation of activation energy for the different concentrations of the aliovalent dopants. The activation energy for the undoped LBLTO garnet materials has a calculated value of 0.41(4) eV which is within the 0.40–0.44 eV range of values reported for this material by other authors.^4,42,55 For the Al³⁺ doping, the low concentration of the dopant had a positive effect on the activation energy for total conductivity, lowering this from 0.41(4) eV for the undoped material to a value of 0.35(4) for the Li = 5.7 material. This demonstrates the potentially beneficial effect, in agreement with previous studies, where a Li–Al–O amorphous layer is reportedly formed between the grains for which a 0.10 mol of Al³⁺ per formula unit of garnet reduced the porosity of the pelletised material from 11% to a value close to 1%.⁵⁶ This amorphous Li–Al–O layer has also been reported to enhance the particle contact in garnet materials, lowering the energy requirement for Li⁺ to cross grain boundaries.⁵⁷ Surpassing the Li_5.70Al_0.10BaLa₂Ta₂O₁₂ doping to the higher Li_5.25Al_0.25BaLa₂Ta₂O₁₂ values, however, leads to an increase in the activation energy to 0.48(3) eV, indicating that the beneficial effect of a possible Li–Al–O layer then can be overshadowed by detrimental effects on the intra-grain conductivity as a consequence of lower carrier concentration and blockage of the 24d sites.⁵⁸ Ga and Zn doping have a limited effect on the activation energy, with only a timid decrease in activation energy for low doping with Zn, remaining almost invariant in the case of Ga doping. This points out a trade-off between beneficial vacancy creation and site deactivation by occupation of both the highly mobile 48g/96h and the 24d node sites.⁵⁴

Local lithium diffusion studies by μ⁺-SR

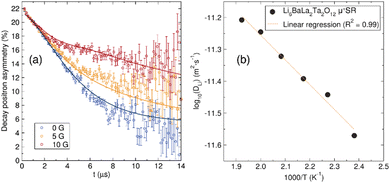
To understand the Li⁺ diffusion properties of the undoped LBLTO garnet material at the local microscopic scale, μ⁺SR studies were performed. μ⁺SR allows to study of the ionic diffusion dynamics at the local scale, without large contribution from interferences at macroscopic, such as grain boundaries or porosity, which typically contribute to EIS measurements.⁵⁹ The temporal evolution of the implanted positron decay asymmetry collected at zero field and two different longitudinal applied magnetic fields is shown in Fig. 6(a). By applying different longitudinal magnetic fields, interactions between the muons and any local nuclear magnetic field distribution can be decoupled, separating these from the stronger electronic contributions that can arise from paramagnetic ions in the material, if any.⁶⁰ The evolution of the asymmetry of the positron decay with increasing applied longitudinal magnetic field shows a slower decrease of the positron decay asymmetry as a result of the forced realignment of the muon spins with the parallel longitudinal magnetic field.

Fig. 6 (a) μ⁺SR raw data collected at room temperature at zero field (blue) and applied fields of 5 G (yellow) and 10 G (red) and fit the data using the Keren function (solid line) for the undoped Li₆BaLa₂Ta₂O₁₂ garnet material. (b) Arrhenius plot of the diffusion coefficient calculated from μ⁺SR for the undoped Li₆BaLa₂Ta₂O₁₂ garnet. The calculated activation energy from it is 0.16(1) eV.

The decay in the positron asymmetry experiences a moderate relaxation at short times, indicating the absence of any fast depolarisation of the muon spin due to any magnetic field in the sample which would have resulted in a more acute decay of the positron asymmetry.⁶⁰ This is expected for the undoped LBLTO garnet, where all the elements forming the material are diamagnetic in their present oxidation states. The positron asymmetry decay at longer times follows a slower relaxation due to muon interactions with nuclear magnetic fields of elements in the samples with positive spins that can interact with the muon's spin. These active nuclei interacting with the muons are both of ⁶Li and ⁷Li with spins = 1 and 3/2 respectively, ¹³⁹La and ¹⁸¹Ta with spins = 7/2 and ¹³⁵Ba with spin = 3/2.

The acquired data were fitted to the Keren analytical expression for the Abragam function which describes the temporal evolution of the positron asymmetry decay in terms of the fluctuation of the muon (ν), the nuclear field width distribution (Δ) and any additional relaxation due to electronic magnetic field contributions.⁶¹ The Keren function is given in eqn (1), where ν is the fluctuation rate of the muon spin due to Li⁺ diffusion, Δ is the field width distribution around the muon stopping site, ω is the Larmor precession frequency in the applied magnetic field and λ accounts for temperature-independent fluctuations associated with electronic magnetic fields. From the fits, ν and Δ parameters related to Li⁺ diffusion were extracted. For the garnet materials, the λ contribution is negligible, simplifying the analyses.

P_z(t) = exp[−Γ(Δ, ν, ω_L, t)t]exp(−λt) (1)

Temperature variable measurements were carried out to study the temperature dependence of the Li⁺ diffusion on the undoped LBLTO material. The fluctuation rate (Fig. S5a, ESI†) presents a flat region at low temperatures, followed by a thermally activated region above 225 K, where ν experiences an exponential increase with temperature due to lithium diffusion. The presence of a small initial increase of fluctuation rate around 350 K indicates the increased dynamics of Li⁺ within the 96h/48g sites. The field width parameter Δ (Fig. S5b, ESI†) remains constant across the range of temperatures measured with a value close to 0.25 MHz, indicative of the static behaviour of the implanted muon within the garnet framework. This Δ value is in line with other oxide materials, where the muon stopping site is at ca. 1 Å distance from the oxygen anions.⁶⁰ Specifically for garnet materials, similar values in the range of 0.2 to 0.3 MHz have been previously reported.^29,62

Li⁺ diffusion coefficients were obtained by applying eqn (2), which relates the diffusion coefficient with the fluctuation rate and the crystal structure of the material in the solid state.⁶³ The term N_i refers to the number of accessible Li⁺ sites in the ith path, Z_v,i is the vacancy fraction of the destination sites, s_i is the jump distance between Li⁺ sites, and ν the calculated fluctuation rate from the μ⁺SR measurements at each temperature. By considering the garnet crystal structure, it is commonly agreed that for Li-rich garnets there are two main accessible pathways for Li⁺ diffusion to occur. These two hopping pathways involve the Li⁺ hopping from the tetrahedral 24d site to one of the four 48g neighbouring octahedral sites or from one octahedral 48g site to either of the two surrounding 24d neighbouring tetrahedral sites (Fig. S6, ESI†),^52,53 with a hopping distance between 24d and 48g sites of 1.99 Å for the LBLTO garnet.⁵⁵

The calculated room temperature Li⁺ diffusion coefficient is 3.35 × 10⁻¹¹ cm² s⁻¹. This value is similar to that reported for the Li₆La₃ZrNbO₁₂ related garnet material⁶² and slightly lower than the value reported for the Al-doped LLZO garnet material of 4.9 × 10⁻¹¹ cm² s⁻¹ obtained by the same technique.²⁹ These Li⁺ diffusion coefficients are all on the same order of magnitude and the observed decrease of this value in the Li = 6 material compared to the Li = 6.5 Al-doped LLZO garnet could be related to the lower carrier concentration and higher occupancy of the less mobile 24d sites, which limits Li⁺ diffusion in the garnet crystal structure.⁵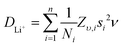²

The diffusion coefficient at different temperatures fits an Arrhenius behaviour and activation energy for local Li⁺ diffusion of 0.16(1) eV was obtained from the linear fit (Fig. 6(b)). This value is similar to other activation energies reported by μ⁺SR in garnet materials of ca. 0.2 eV.^29,62 The value for the undoped LBLTO material studied here is slightly lower compared to the reported value for the Al-doped LLZO material.²⁹ This difference can be attributed to the larger cell parameter of the LBLTO garnet allowing for larger Li⁺ diffusion pathways and less constraining bottlenecks, as well as the lack of Al³⁺ ions on the 24d, which could force some of the Li⁺ located in the 48g/96h positions to jump to neighbouring 48g/96h positions without passing through a neighbouring 24d site, with the consequent increase in the energy required to achieve this. Nevertheless, the activation energies are reasonably close when taking into account their standard deviations (∼10%) to conclude that the energy required for lithium diffusion in both related materials is very similar, with Li⁺ carrier concentration and the balance between the 24d and 48g positions which regulates the diffusion coefficient and conductivity of the material.

The Li⁺ coefficient value reported here is also in line with current cathode materials used in commercial batteries such as the LiFePO₄⁶⁴ or the high energy density NMC family,⁶⁵ indicating that grain boundary engineering could reduce resistance in these materials to a minimum.

C. Experimental

All chemicals employed were used as supplied without further purification unless otherwise indicated. LiOH·H₂O (98%) and La₂O₃ (99%) were purchased from Sigma-Aldrich. Al(NO₃)₃·9H₂O (98–102%), Ga₂O₃ (99.99%), Ga(NO₃)₃·9H₂O (99.999%), ZnO (99.99%), Zn(NO₃)₂·6H₂O (99%), Ta₂O₅ (99.993%) and BaCO₃ (99.997%) were purchased from Alfa Aesar.

For the preparation of the Li_6−3x(Al/Ga)_xBaLa₂Ta₂O₁₂ and Li_6−2xZn_xBaLa₂Ta₂O₁₂ garnet materials, stoichiometric quantities of La₂O₃ (previously dried at 900 °C for 24 h), Ta₂O₅, BaCO₃, Al(NO₃)₃·9H₂O, Ga(NO₃)₃·9H₂O, Zn(NO₃)₂·6H₂O and a 10% excess of LiOH·H₂O were weighed and ball milled for 20 min at a vibrational frequency of 20 Hz in a stainless steel jar. Subsequently, the fine powder was pelletised at 3 tons under uniaxial pressure. The pelletised material was fired at 700 °C for 6 hours to decompose the starting materials. The main heat treatment was carried out in a 2.45 GHz CEM Phoenix hybrid microwave furnace composed of three silicon carbide walls which are heated by microwave irradiation surrounding the sample cavity. This main heat treatment was performed for 6 hours at 800 °C in an open atmosphere. In both cases, the bottom of the alumina crucibles was covered with mother powder in order to avoid any accidental Al contamination and the heating rate was 2 °C min⁻¹.

PXRD measurements were carried out in a PANalytical X’Pert PRO diffractometer using Cu-Kα radiation in the 15–85° 2Θ range with a step size of 0.016° and a nominal scan rate of 53.975 seconds per step. Rietveld refinements of the diffraction data were performed with the generalised structure analysis system (GSAS),⁶⁶ along with the graphical user interface EXPGUI,⁶⁷ by means of a least squares approach.

SEM images were acquired with a Phillips XL30 ESEM microscope. All samples were ground and a tiny amount of the fine powder was deposited over a carbon-taped sample holder. Subsequently, the samples were Au-coated to enhance their surface conductivity and avoid overcharging from irradiation by the electron beam.

Energy-Dispersive X-ray (EDX) spectra were acquired using an Oxford Instruments Energy 250 energy dispersive spectrometer system attached to a Phillips XL30 ESEM microscope. Copper tape was employed as a standard for calibration and the voltage of the incident electron beam was 25 keV.

The AC EIS measurements of the lithium-containing materials synthesised were carried out on a Solatron 1260 impedance analyser in the frequency range of 1 to 7 × 10⁶ Hz with 20 mV perturbation in the temperature range between RT and 200 °C.

XAS spectra were collected in the B18 beamline at the Diamond Source of Light synchrotron. For data acquisition, a few milligrams (between 10 and 100 mg) of the as-synthesised materials were mixed with cellulose fibre (ca. 100 mg) and compacted into a 10 mm diameter thin pellet. The thin pellet was mounted into a holder and exposed to synchrotron X-ray radiation emitted by a bending magnet source which is monochromatised and focused by a vertically collimating Si mirror, a water-cooled Si(111) and Si(311) double crystal monochromator and a focusing double toroidal mirror. The data were collected in the transmission mode using three ionisation chambers mounted in series for simultaneous measurements on the sample and a tungsten foil as the reference. Scans for ca. 3 to 5 minutes were obtained over the desired energy range and merging of three consecutive scans was performed to obtain precise data sets. The data were processed and normalised using the Athena software package using edge step normalisation.

μ⁺SR studies were performed using the EMU instrument at the ISIS pulsed muon facility.⁶⁸ The powdered sample, ca. 1.5 g, was packed into a disk of 30 mm diameter and 1.5 mm thickness and sealed in a titanium sample holder where the front window was made of 25 mm thickness titanium foil. 3.2 MeV spin-polarised positive muons were implanted into the sample and the outcoming positrons were detected by 96 scintillator segments grouped in two circular arrays. The temperature was controlled from 100 K up to a maximum of 600 K by a hot stage attached to a closed cycle refrigerator and the measurements were acquired at three different applied longitudinal magnetic fields (0, 5 and 10 G). A 20 G transverse magnetic field was also applied for the initial asymmetry calibration. Data fits were performed using the WiMDA data analysis program.⁶⁹

D. Conclusions

In this work, the synthesis, structural characterisation and study of the transport properties of Al-, Ga- and Zn-doped LBLTO garnet materials have been carried out. The aliovalent doping of the garnet material was analysed by PXRD, showing a decrease in the unit cell parameter confirming the introduction of the dopant within the garnet framework. XANES analyses on the Zn and Ga K-edge indicated that the Zn²⁺ cations are located on the tetrahedral 24d sites, whereas Ga³⁺ cations are found on both tetrahedral 24d and octahedral 48g sites. The effect of the dopant on the macroscopic ionic conductivity of the materials was analysed by EIS, demonstrating that low concentrations of Al³⁺ doping can have a positive effect on the energy requirements for Li⁺ transport by decreasing the activation energy for total ionic conductivity from 0.41(4) to 0.35(4) eV. In all the cases, a decrease in the room temperature conductivity was found, attributed to the lower Li⁺ concentration and vacancy deactivation by the presence of the dopant in the Li⁺ sublattice. μ⁺SR measurements were carried out on the parent LBLTO garnet material to analyse the local Li⁺ diffusion properties of the material. A low activation energy of 0.16(1) eV for Li⁺ diffusion at the local scale was calculated from variable temperature measurements and a diffusion coefficient of 3.35 × 10⁻¹¹ cm² s⁻¹ was obtained at room temperature, indicating the good intra-grain transport properties of this LBLTO material, comparable with the LLZO benchmark garnet material. The insights gleaned from this comprehensive analysis highlight the importance of dopant selection for Li-rich garnet materials, where the location and charge of the dopant can greatly impact the structure of the garnet framework and the Li⁺ dynamics of the solid-state electrolyte. Insights from this work would suggest that the selection of dopants suitable for the Ta⁵⁺ site may increase the Li⁺ concentration and cell lattice parameter for improved Li⁺ transport properties. A similar approach was used by Thangadurai and coworkers for the Li_6.5La_2.9A_0.1Zr_1.4Ta_0.6O₁₂ garnet, where A = Ca, Sr or Ba.⁷⁰ The good transport properties of the LBLTO material at the local scale, as demonstrated by μ⁺SR, indicate that further macrostructure engineering work is possible to realize the maximum performance of this Li⁺ solid-state electrolyte garnet material.

Author contributions

M. Amores prepared and characterised the garnet materials. E. J. Cussen and S. A. Cussen supervised this work. All authors conducted formal analysis of experimental results, including applying for beamtime support for this project. All authors wrote, reviewed and edited the manuscript. P. Baker assisted with μSR data collection and analysis.

Data availability

Data for this article, including diffraction patterns, X-ray absorption datasets, impedance analysis and raw muon spectroscopy datasets, are available from the UCD Research Data Zenodo Community at https://doi.org/10.5281/zenodo.12657456.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge technical support from Michael Beglan and Dr Peter Chung at the University of Glasgow. The authors also thank the EPSRC for grant funding (SUPERGEN Challenge grant on “Design and high throughput microwave synthesis of Li-ion battery materials”, EP/N001982/2); the STFC for beamtime allocation through the EMU beamline and the Diamond Light Source for XAS beamtime with the assistance of Dr Stephen Parry (B18 instrument, proposal SP11874); and the School of Chemistry at Glasgow for PhD studentship funding.

References

1. Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier, M. Armand and L. Chen, Energy Environ. Sci., 2018, 11, 1945.
2. C. Wang, K. Fu, S. P. Kammampata, D. W. McOwen, A. J. Samson, L. Zhang, G. T. Hitz, A. M. Nolan, E. D. Wachsman, Y. Mo, V. Thangadurai and L. Hu, Chem. Rev., 2020, 120, 4257.
3. E. J. Cussen, Chem. Commun., 2006, 412.
4. V. Thangadurai and W. Weppner, Adv. Funct. Mater., 2005, 15, 107.
5. L. Buannic, B. Orayech, J. M. López Del Amo, J. Carrasco, N. A. Katcho, F. Aguesse, W. Manalastas, W. Zhang, J. Kilner and A. Llordés, Chem. Mater., 2017, 29, 1769.
6. W. G. Zeier, Dalton Trans., 2014, 43, 16133.
7. V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Soc. Rev., 2014, 43, 4714.
8. M. Pasta, D. Armstrong, Z. L. Brown, J. Bu, M. R. Castell, P. Chen, A. Cocks, S. A. Corr, E. J. Cussen, E. Darnbrough, V. Deshpande, C. Doerrer, M. S. Dyer, H. El-Shinawi, N. Fleck, P. Grant, G. L. Gregory, C. Grovenor, L. J. Hardwick, J. T. S. Irvine, H. Jeong Lee, G. Li, E. Liberti, I. McClelland, C. Monroe, P. D. Nellist, P. R. Shearing, E. Shoko, W. Song, D. S. Jolly, C. I. Thomas, S. J. Turrell, M. Vestli, C. K. Williams, Y. Zhou and P. G. Bruce, JPhys Energy, 2020, 2, 032008.
9. J. Awaka, N. Kijima, H. Hayakawa and J. Akimoto, J. Solid State Chem., 2009, 182, 2046.
10. E. J. Cussen, J. Mater. Chem., 2010, 20, 5167.
11. T. Yang, Y. Li, W. Wu, Z. Cao, W. He, Y. Gao, J. Liu and G. Li, Ceram. Int., 2018, 44, 1538.
12. Y. Meesala, Y. K. Liao, A. Jena, N. H. Yang, W. K. Pang, S. F. Hu, H. Chang, C. E. Liu, S. C. Liao, J. M. Chen, X. Guo and R. S. Liu, J. Mater. Chem. A, 2019, 7, 8589.
13. S. Sarkar, C. Santos, J. Glenneberg, I. Bardenhagen, J. Schwenzel and V. Thangadurai, Chem. Mater., 2024, 36, 2685.
14. K. Ma, B. Chen, C.-X. Li and V. Thangadurai, Adv. Sustainable Syst., 2024, 8, 2300656.
15. B. Kozinsky, S. A. Akhade, P. Hirel, A. Hashibon, C. Elsässer, P. Mehta, A. Logeat and U. Eisele, Phys. Rev. Lett., 2016, 116, 55901.
16. R. Jalem, T. Kasuga, W. Manalastas, J. A. Kilner, R. W. Grimes, M. J. D. Rushton and M. Nakayama, Chem. Mater., 2015, 27, 2821.
17. H. El Shinawi and J. Janek, J. Power Sources, 2013, 225, 13.
18. E. Hanc, W. Zając, L. Lu, B. Yan, M. Kotobuki, M. Ziąbka and J. Molenda, J. Solid State Chem., 2017, 248, 51.
19. S. Ohta, J. Seki, Y. Yagi, Y. Kihira, T. Tani and T. Asaoka, J. Power Sources, 2014, 265, 40.
20. M. Amores, S. A. Corr and E. J. Cussen, J. Electrochem. Soc., 2017, 164, A6395.
21. Y. Li, J. T. Han, C. A. Wang, H. Xie and J. B. Goodenough, J. Mater. Chem., 2012, 22, 15357.
22. D. Rettenwander, J. Langer, W. Schmidt, C. Arrer, K. J. Harris, V. Terskikh, G. R. Goward, M. Wilkening and G. Amthauer, Chem. Mater., 2015, 27, 3135.
23. D. Rettenwander, C. A. Geiger, M. Tribus, P. Tropper and G. A. Amthauer, Inorg. Chem., 2014, 53, 6264.
24. B. Karasulu, S. P. Emge, M. F. Groh, C. P. Grey and A. J. Morris, J. Am. Chem. Soc., 2020, 142, 3132.
25. Y. Li, J. T. Han, C. A. Wang, S. C. Vogel, H. Xie, M. Xu and J. B. Goodenough, J. Power Sources, 2012, 209, 278.
26. R. Wagner, G. J. Redhammer, D. Rettenwander, A. Senyshyn, W. Schmidt, M. Wilkening and G. Amthauer, Chem. Mater., 2016, 28, 1861.
27. M. Huang, W. Xu, Y. Shen, Y. H. Lin and C. W. Nan, Electrochim. Acta, 2014, 115, 581.
28. R. H. Brugge, J. A. Kilner and A. Aguadero, Solid State Ionics, 2019, 337, 154.
29. M. Amores, T. E. Ashton, P. J. Baker, E. J. Cussen and S. A. Corr, J. Mater. Chem. A, 2016, 4, 1729.
30. M. O’Callaghan and E. J. Cussen, Chem. Commun., 2007, 2048.
31. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751.
32. L. J. Miara, W. D. Richards, Y. E. Wang and G. Ceder, Chem. Mater., 2015, 27, 4040.
33. D. Rettenwander, G. Redhammer, F. Preishuber-Pflügl, L. Cheng, L. Miara, R. Wagner, A. Welzl, E. Suard, M. Doeff, M. Wilkening, J. Fleig and G. Amthauer, Chem. Mater., 2016, 28, 2384.
34. W. Gu, M. Ezbiri, R. Prasada Rao, M. Avdeev and S. Adams, Solid State Ionics, 2015, 274, 100.
35. W. L. Bragg, Proc. Cambridge Philos. Soc., 1913, 17, 43.
36. L. Vegard, Z. Med. Phys., 1921, 5, 17.
37. S. C. Abrahams and J. L. Bernstein, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 1233.
38. A. Ferrari, A. Braibanti, A. M. M. Lanfredi and A. Tiripicchio, Acta Crystallogr., 1967, 22, 240.
39. A. D. Hendsbee, C. C. Pye and J. D. Masuda, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2009, 65, i65.
40. S. Geller, J. Chem. Phys., 1960, 33, 676.
41. D. Rettenwander, J. Langer, W. Schmidt, C. Arrer, K. J. Harris, V. Terskikh, G. R. Goward, M. Wilkening and G. Amthauer, Chem. Mater., 2015, 27, 3135.
42. R. Murugan, V. Thangadurai and W. Weppner, J. Electrochem. Soc., 2007, 155, A90.
43. Y. Zhong, Q. Zhou, Y. Guo, Z. Li and Y. Qiang, Ionics, 2013, 19, 697.
44. I. Kokal, K. V. Ramanujachary, P. H. L. Notten and H. T. Hintzen, Mater. Res. Bull., 2012, 47, 1932.
45. J. Reinacher, S. Berendts and J. Janek, Solid State Ionics, 2014, 258, 1.
46. Y. Li, C. A. Wang, H. Xie, J. Cheng and J. B. Goodenough, Electrochem. Commun., 2011, 13, 1289.
47. E. J. Cussen, T. W. S. Yip, G. O’Neill and M. P. O’Callaghan, J. Solid State Chem., 2011, 184, 470.
48. V. Thangadurai, H. Kaack and W. J. F. Weppner, J. Am. Ceram. Soc., 2009, 86, 437.
49. W. E. Tenhaeff, J. Wolfenstine, A. P. Sokolov, N. J. Dudney, Y. Wang, J. Sakamoto and E. Rangasamy, ChemElectroChem, 2013, 1, 375.
50. R. A. Huggins, Ionics, 2002, 8, 300.
51. J.-F. Wu, E.-Y. Chen, Y. Yu, L. Liu, Y. Wu, W. K. Pang, V. K. Peterson and X. Guo, ACS Appl. Mater. Interfaces, 2017, 9, 1542.
52. M. Xu, M. S. Park, J. M. Lee, T. Y. Kim, Y. S. Park and E. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 52301.
53. D. Wang, G. Zhong, W. K. Pang, Z. Guo, Y. Li, M. J. McDonald, R. Fu, J. X. Mi and Y. Yang, Chem. Mater., 2015, 27, 6650.
54. Y. Chen, E. Rangasamy, C. Liang and K. An, Chem. Mater., 2015, 27, 5491.
55. J. Awaka, N. Kijima, Y. Takahashi, H. Hayakawa and J. Akimoto, Solid State Ionics, 2009, 180, 602.
56. Y. Wang, P. Yan, J. Xiao, X. Lu, J.-G. Zhang and V. L. Sprenkle, Solid State Ionics, 2016, 294, 108.
57. H. El-Shinawi, G. W. Paterson, D. A. MacLaren, E. J. Cussen and S. A. Corr, J. Mater. Chem. A, 2017, 5, 319.
58. D. O. Shin, K. Oh, K. M. Kim, K.-Y. Y. Park, B. Lee, Y.-G. G. Lee and K. Kang, Sci. Rep., 2015, 5, 18053.
59. I. McClelland, B. Johnston, P. J. Baker, M. Amores, E. J. Cussen and S. A. Corr, Annu. Rev. Mater. Res., 2020, 50, 371.
60. M. Månsson and J. Sugiyama, Phys. Scr., 2013, 88, 068509.
61. A. Keren, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 10039.
62. H. Nozaki, M. Harada, S. Ohta, I. Watanabe, Y. Miyake, Y. Ikedo, N. H. Jalarvo, E. Mamontov and J. Sugiyama, Solid State Ionics, 2014, 262, 585.
63. R. J. Borg and G. J. Dienes, An Introduction to Solid State Diffusion, Elsevier, 1988.
64. T. E. Ashton, J. V. Laveda, D. A. Maclaren, P. J. Baker, A. Porch, M. O. Jones and S. A. Corr, J. Mater. Chem. A, 2014, 2, 6238.
65. I. McClelland, S. G. Booth, N. N. Anthonisamy, L. A. Middlemiss, G. E. Perez, E. J. Cussen, P. J. Baker and S. A. Cussen, Chem. Mater., 2023, 35, 4149.
66. A. C. Larson and R. B. Von Dreele, GSAS: General Structure Analysis System, LAUR, 1994, pp. 86–748.
67. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210.
68. S. A. Corr, E. J. Cussen, B. Johnston, P. J. Baker and M. Amores, Li-Ion Diffusion Studies in Complex Oxides for Li-Ion Battery Applications, STFC ISIS Neutron and Muon Source, 2017 DOI:10.5286/ISIS.E.RB1620255.
69. F. L. Pratt, Phys. B, 2000, 289–290, 710.
70. S. P. Kammampata, H. Yamada, T. Ito, R. Paul and V. Thangadurai, J. Mater. Chem. A, 2020, 8, 2581.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00679h

---