Open Access Article
Open Access ArticleAb initio insight into furan conversion to levulinate ester in reaction with methylal and methanol†
Yun-Sim
Kim
,
Ryong-Wan
Ham
,
Yong-Chol
Pak
,
Man-Sok
O
and
Chol-Jun
Yu
 *
*
Computational Materials Design, Faculty of Materials Science, Kim Il Sung University, Ryongnam-Dong, Taesong District, Pyongyang, People's Republic of Korea. E-mail: cj.yu@ryongnamsan.edu.kp
First published on 5th June 2024
Abstract
Recently, methyl levulinate (MLA) has attracted remarkable attention as a promising fuel additive and its synthesis route from furan and dimethoxymethane (DMM or methylal) has been exploited, but the reaction pathway remains indistinct. In this work, we study the conversion of furan into MLA in reaction with DMM and methanol using ab initio calculations with double-ζ polarization basis sets plus supercell method and B3LYP/6-311+G* basis sets plus cluster method. Our calculations reveal that the reaction of furan + DMM to 2-methoxymethyl-furan (MMF) + methanol is endothermic in vacuum but exothermic in methanol solvent, while the reaction of MMF + water to MLA is exothermic both in vacuum and methanol solvent environments. Moreover, we identify the reaction sites of the individual reactant molecules by analyzing their Fukui functions and verify the Brønsted acid–base reaction fashions for these reactions. Finally, we determine the activation energies for the reactions without and with a protonated methanol molecule, together with the detailed geometries of the intermediates.
1 Introduction
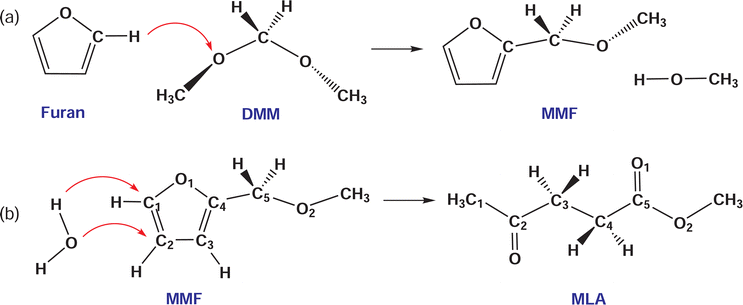
Due to dwindling fossil reserves and increasing environmental concerns, the extensive search and efficient utilization of renewable resources have drawn enormous attention.1,2 Deriving from plant photosynthesis, biomass is a promising source of cheap and renewable energy, and has been widely used for producing high value-added bio-fuels and chemicals.3–5 Recently, a significant research interest has been focused on efficient conversion of biomass or biomass-derived educts into value-added chemicals such as 5-hydroxymethylfurfural (HMF),6–9 levulinic acid (LA),10,11 and levulinate esters.12,13 Among them, levulinate esters including alkyl (methyl, ethyl, propyl, butyl) levulinates are particularly important due to their wide applications in medicine, flavoring and fragrance industries as well as their use as fuel additives for improving properties of petroleum and diesel.14Alkyl levulinates can be produced from various biomass-derived products such as sugars (glucose,13,15 fructose,12 xylose16), cellulose,1,17 furfural,16,18 furfuryl alcohol,19 furan,20 and raw biomass itself.21–23 The direct synthesis of methyl levulinate (MLA) from sugars or cellulose has shown the problems of low yield and very demanding conditions. For example, the one-pot conversion of xylose to MLA with the co-catalysts of Pd/Al2O3 and amberlyst at 7.0 MPa H2 pressure had a yield of 25%.24 Hu et al.16 have reported 52.5 and 37.7% yields of MLA from glucose and xylose at 160 °C. On the other hand, the furfural and furfuryl alcohol are commercially produced from sugars with a high cost of industrial production due to the complicated purification and separation processes. To address these drawbacks, some works reported the synthesis of MLA from furan, which is an important product by catalytic pyrolysis of biomass and used for producing value-added chemical of tetrahydrofuran.25,26 However, the acid-catalyzed conversion of furan has produced benzofuran but not MLA or levulinic acid.27 The structural difference between furfuryl alcohol and furan is the additional hydroxymethyl group in furfuryl alcohol. To solve the problem, Zhang et al.20 developed a new reaction route to produce MLA, in which furan reacts with dimethoxymethane (DMM or methylal) to form 2-methoxymethyl-furan (MMF) as the reactive intermediate and then MMF was converted to MLA via acid catalysis with a co-solvent/reactant of methanol (see Scheme 1). Using the acid-catalyzed conversion to MLA in DMM/methanol solvent, they achieved a higher yield of 67.9% at 170 °C from furan. In this reaction, DMM is the most important reactant that enables furan to convert into MLA. As the smallest member of oxygenated methyl ethers, which are attractive additives for diesel fuels,28–30 DMM itself has been used as a fuel and can be produced from biomass and feedstock.
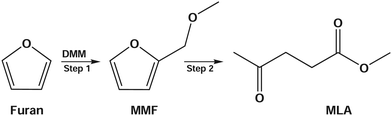 | ||
| Scheme 1 Reaction pathway for producing methyl levulinate (MLA) from furan in DMM/methanol medium.20 | ||
To understand the reaction mechanism of furan conversion to MLA in reaction with DMM/methanol, ab initio study based on quantum theory such as density functional theory (DFT) or Hartree–Fock (HF) theory is necessary. For furan, many theoretical works have been reported for its structural and vibrational properties31,32 and reactivity with small molecules.33,34 For the case of DMM, we found the ab initio works for the different conformations35 and the pyrolysis/combustion.36,37 The conformational equilibrium of the alkyl levulinates has been studied by using the force field method (MMFF94),38 and the thermochemical studies of levulinic acid esters have been performed.39,40 However, no theoretical work for furan conversion to MLA is yet performed, remaining its atomistic understanding indistinct.
In this work, we performed ab initio calculations within the DFT framework to get an atomistic insight into the reaction pathway of furan conversion to MLA. The supercell and cluster modelings were used for the isolated molecules of furan, DMM, MMF and MLA. The solvent effect was considered explicitly by including certain numbers of solvent (methanol) molecules in the supercell and implicitly by using the conductor-like screening model (COSMO). The reaction energies and activation barriers were estimated, together with the detailed structures of intermediates. In the following, Section 2 describes the computational methods, Section 3 explains the results, and Section 4 gives the conclusions.
2 Computational methods
2.1 Supercell and cluster modeling
In this work, we made modeling of isolated molecules using both supercell and cluster models to have confidence in the calculation. For the supercell models, we constructed the three-dimensional (3D) periodic cubic supercells with a lattice constant of 30 Å, which can provide a long distance enough for artificial interaction between the periodic molecular images to be negligible. The isolated molecules in this work include furan (C4H4O), DMM (C3H8O), methanol (CH3OH), MMF (C6H8O2), water (H2O) and MLA (C6H10O3). In fact, according to the reaction route for furan conversion to MLA developed by Zhang et al.,20 the chemical reactions can be expressed as follows,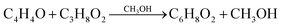 | (1) |
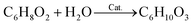 | (2) |
For the cluster modeling, which is more appropriate for molecules with higher accuracy and lower computational cost than the supercell modeling, there is no need to use the 3D periodic supercell. The solvent effect was implicitly considered by using COSMO approach41 with the experimental value of dielectric constant of methanol (32.642).
2.2 Pseudopotential PAO calculations for supercell models
For the supercell models, we applied the pseudopotential and pseudo atomic orbital (PAO) basis sets method as implemented in the SIESTA (version 4.1) package.43 For the electrostatic interaction between the ionic cores and valence electrons, we constructed the non-relativistic Troullier–Martins-type norm-conserving pseudopotentials44 by using the ATOM code provided in the package with the valence configurations of C-2s22p2, O-2s22p4 and H-1s1. For the exchange–correlation (XC) interaction between the valence electrons, we tested different types of functionals such as Perdew–Zunger (PZ) formalism within the local density approximation (LDA)45 and Perdew–Burke–Ernzerhof (PBE) formalism46 and Becke–Lee–Yang–Parr (BLYP)47,48 formalism within the generalized gradient approximation (GGA). To take into account the van der Waals (vdW) interaction, which is important in molecules, we adopted the semi-empirical approach developed by Grimme.49 For PAOs, we used the standard double-ζ plus polarization (DZP) basis sets for all the atoms, generated with an energy shift of 300 meV for orbital-confining cutoff radii and a split norm of 0.25 for split valence of basis. All the calculations were carried out with the plane-wave cutoff energy of 300 Ry and only Γ-point in the first Brillouin zone. All the atoms were relaxed until the forces on atoms became less than 0.01 eV Å−1.For an isolated molecule in vacuum, the lowest energy conformation was derived by performing the conformational search, in which the stochastic search approach was adopted. The molecular structures of the resultant conformations were then optimized using the conjugate gradient (CG) method. To get the equilibrium states for the explicit methanol-solvent models, we performed ab initio molecular dynamics (AIMD) simulations at room temperature (300 K) controlled by means of a Nosé thermostat, a time step of 1 fs and duration of 1 ps. Then, the resultant structures were re-optimized using the CG method.
The activation energies were estimated for the chemical reactions described by eqn (1) and (2). To this end, we simulated the two-molecular systems of furan + DMM, MMF + methanol and MLA + water. For the reaction (1), the two-molecular systems of furan + DMM and MMF + methanol included in the supercells with vacuum (lattice constant 30 Å) and 25 and 40 methanol molecules (lattice constants 12, 14 Å) were optimized, whereas only the vacuum supercell was used for the reaction (2). To calculate the activation energy with the acceptable reaction pathway, the nudged elastic band (NEB) method50 was applied by using our own python script in connection with the SIESTA package, as employed in our previous works.51–53 The number of NEB images was set to be 11 or 15. During the NEB run, all the atomic positions were relaxed and the convergence threshold was set to be 0.05 eV Å−1.
2.3 All-electron AO calculations for cluster models
For the cluster models, we adopted the all-electron Gaussian-type atomic orbital (AO) method as implemented in the NWChem (version 6.6) package.54 The geometry optimizations and frequency calculations of all the reactants, products and transitions states (TS) were performed with the B3LYP48,55/6-311+G* level. Different basis sets of cc-pVTZ and XC functionals of M06-2X56 and PBE were also tested in the geometry optimization of furan. The zero-point correction (ZPC) and thermal correction (TC) to the total energy were considered. The methanol solvent effect was considered implicitly by applying the COSMO method with usage of refinement and parametrization of COSMO for real solvent (COSMO-RS)57 and the experimental dielectric constant of methanol (32.6) as implemented in the NWChem package. In the geometry optimizations, we used the DRIVER module, which is based on the algorithm of quasi-Newton optimization with line searches and approximate energy Hessian updates. Here, the convergence criteria was set to be “tight”, which can provide the highest accuracy for geometry optimization among the possible selections in the package. The activation energies and reaction pathways were also estimated by using the NEB method with 10 beads, which was continued by running the zero-temperature string calculation with 10 beads.3 Results and discussion
3.1 Assessment of XC functionals
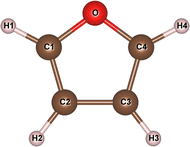
Firstly, the geometry of furan was optimized using different XC functionals and basis sets with supercell and cluster modelings. Table 1 shows the bond lengths, bond angles and dipole moment of furan determined in this work. In the PAO-DZP calculations with SIESTA for the supercell models, the PZ, BLYP and PBE functionals were tested using the cubic supercell with a lattice constant of 30 Å, which contained only one furan molecule. It was found that the PZ functional within LDA underestimated the C–O bond length with a relative error of −0.19% but overestimated the C–H bond length with a relative error of 0.32%, when compared with the experimental values.58 On the contrary, the BLYP and PBE functionals within GGA overestimated the C–O bond length with relative errors of 0.93% and 0.32% while underestimated the C–H bond length with relative errors of −0.46% and −0.07%, respectively. For the C–C bond lengths, the three XC functionals gave the underestimation compared with the experimental value.58 On the whole, the PBE functional can be regarded to give the most reasonable geometry of furan. Therefore, we used the PBE functional for further supercell calculations.| PAO-DZP | B3LYP/6-311+G* | M06-2X/cc-PVTZ | Molecular structure | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PZ | BLYP | PBE | Met-25 | Met-40 | Vac. | Met. | Vac. | Met. | Exp.a | ||
| a Ref. 50. | |||||||||||
| Bond length (Å) |
|
||||||||||
| O–C1 | 1.359 | 1.375 | 1.366 | 1.376 | 1.372 | 1.363 | 1.368 | 1.352 | 1.357 | 1.362 | |
| C1–C2 | 1.355 | 1.354 | 1.354 | 1.360 | 1.360 | 1.358 | 1.359 | 1.351 | 1.352 | 1.361 | |
| C2–C3 | 1.410 | 1.418 | 1.414 | 1.433 | 1.426 | 1.436 | 1.439 | 1.432 | 1.436 | 1.431 | |
| C1–H1 | 1.078 | 1.070 | 1.074 | 1.082 | 1.081 | 1.078 | 1.078 | 1.075 | 1.076 | 1.075 | |
| C2–H2 | 1.076 | 1.069 | 1.071 | 1.086 | 1.083 | 1.080 | 1.080 | 1.075 | 1.076 | 1.077 | |
| Bond angle (degree) | |||||||||||
| C1–O– C1 | 105.5 | 105.2 | 105.4 | 106.7 | 107.7 | 106.9 | 107.0 | 107.0 | 107.2 | 106.7 | |
| C1–C2–C3 | 106.2 | 106.5 | 106.3 | 106.5 | 106.3 | 106.1 | 106.3 | 105.9 | 106.1 | 106.0 | |
| O–C1–C2 | 111.1 | 110.9 | 111.0 | 110.1 | 110.9 | 110.4 | 110.2 | 110.6 | 110.4 | 110.7 | |
| O–C1–H1 | 121.0 | 120.4 | 120.7 | 116.9 | 119.1 | 115.7 | 115.8 | 116.1 | 116.1 | 115.9 | |
| C1–C2–H2 | 124.5 | 124.3 | 124.4 | 123.4 | 123.7 | 126.5 | 126.3 | 126.5 | 126.3 | 126.1 | |
| Dipole moment (Debye) | 0.76 | 0.59 | 0.66 | ||||||||
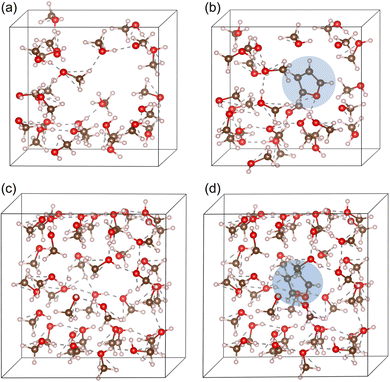
To consider the solvent effect, we treated the supercells containing 25 and 40 methanol molecules with lattice constants of 12 and 14 Å, respectively, giving the mass densities close to the experimental value of 0.791 g cm−3. These molecular systems were denoted as Met-25 and Met-40. We kept a cavity with certain size around the centre of supercells to include the solute molecule later. The molecular systems were equilibrated at 300 K by performing AIMD NVT simulations during 1 ps with a time step of 1 fs and then optimized by performing atomic relaxations. Then, one furan molecule was included into the cavity of the supercells and the furan plus methanol molecular systems were again equilibrated at 300 K using 1 ps AIMD NVT simulations (see Fig. S1, ESI†). After the equilibrations, the resultant molecular systems were optimized by performing atomic relaxations with the PBE XC functional. Fig. 1 shows the obtained configurations of Met-25 and Met-40 systems without and with a furan molecule. Table 1 lists the optimized bond lengths and bond angles of furan. The bond lengths were found to be enlarged by interaction with methanol solvent molecules compared with those in vacuum.
In the AO calculations with cluster modeling, we tested two different XC functionals, such as B3LYP hybrid functional and M06-2X, and two different basis sets, such as Gaussian-type 6-311+G* and numerical cc-PVTZ. The methanol solvent effect was considered implicitly using the COSMO approach. As listed in Table 1, the B3LYP/6-311+G* method gave more reasonable bond lengths and bond angles of furan than the M06-2X/cc-PVTZ method. Our results obtained with the B3LYP/6-311+G* method were well agreed with the previous DFT works employing the UB3LYP/6-311+G* method31 and MP2/cc-PVTZ method.32 Therefore, we chose the B3LYP/6-311+G* method for further calculations, although some reports indicated that B3LYP was less reasonable than M06-2X for dispersion interactions.59 When including the solvent effect, the bond lengths were also found to be slightly enlarged for both methods, being similar to the supercell calculations mentioned above. For the dipole moment, the B3LYP/6-311+G* level gave the overestimated value of 0.76 D, while the M06-2X/cc-PVTZ level yielded the underestimated value of 0.59 D, compared with the experimental value of 0.66 D. Again, the dipole moment was found to be enlarged when including the solvent effect. In addition, the PBE/6-311+G* method was found to produce relatively larger bond lengths than the experimental values (see Table S3, ESI†). We also calculated the frontier molecular orbitals of furan, such as the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), which were −6.50 and −0.12 eV respectively (see Fig. S2, ESI†). Accordingly, the HOMO–LUMO gap was found to be 6.38 eV in good agreement with the previous DFT calculations of 6.37 eV with B3LYP/6-311G(2d,p)60 and 6.00 eV with B3LYP/TZVPP.61 We calculated the harmonic frequencies of furan in good agreement with the previous calculation and experiment (see Fig. S8, ESI†). No imaginary frequencies were obtained, indicating that the optimized geometry (see Fig. S10, ESI†) is acceptable.
3.2 Geometrical features
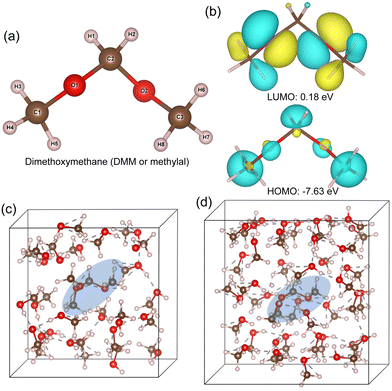
Then, we optimized the geometries of other relevant molecules under study, such as DMM, MMF, MLA, methanol and water, using the PBE functional for the supercell models and B3LYP/6-311+G* method for the cluster models. For the case of DMM, among several conformations including TT, TG and GG (T and G mean trans and gauche), the GG conformation was found to have the lowest energy.35 Therefore, the GG conformation was used for DMM molecule in this work. Fig. 2 shows the optimized geometry of DMM in GG conformation and the HOMO and LUMO calculated with B3LYP/6-311+G*. The HOMO–LUMO gap was calculated to be 7.81 eV (see Fig. 2(b)). The bond lengths and bond angles of DMM calculated with different methods are listed in Table 2.| PBE/DZP | B3LYP/6-311+G* | Prev.a | ||||
|---|---|---|---|---|---|---|
| Vac. | Met-25 | Met-40 | Vac. | Met. | Vac. | |
| a B3LYP/6-31++G** calculation.35 | ||||||
| C1–O1 | 1.433 | 1.439 | 1.430 | 1.423 | 1.431 | 1.426 |
| C2–O1 | 1.410 | 1.402 | 1.416 | 1.404 | 1.409 | 1.406 |
| C2–O2 | 1.413 | 1.402 | 1.417 | 1.404 | 1.409 | 1.407 |
| C3–O2 | 1.428 | 1.439 | 1.429 | 1.423 | 1.431 | 1.426 |
| C1–H3 | 1.138 | 1.094 | 1.126 | 1.098 | 1.096 | 1.100 |
| C1–H4 | 1.129 | 1.094 | 1.107 | 1.094 | 1.093 | 1.096 |
| C1–H5 | 1.112 | 1.093 | 1.109 | 1.089 | 1.089 | 1.092 |
| C2–H1 | 1.116 | 1.097 | 1.111 | 1.096 | 1.094 | 1.098 |
| C2–H2 | 1.123 | 1.118 | 1.108 | 1.096 | 1.094 | 1.098 |
| C3–H6 | 1.111 | 1.103 | 1.156 | 1.098 | 1.096 | 1.100 |
| C3–H7 | 1.098 | 1.088 | 1.101 | 1.089 | 1.089 | 1.092 |
| C3–H8 | 1.114 | 1.104 | 1.127 | 1.094 | 1.093 | 1.096 |
| C1–O1–C2 | 112.0 | 111.7 | 111.3 | 113.9 | 114.0 | 113.9 |
| O1–C2–O2 | 111.8 | 113.2 | 112.6 | 114.1 | 113.8 | 114.1 |
| C3–O2–C2 | 111.3 | 110.9 | 110.1 | 113.9 | 114.0 | 113.9 |
| H1–C2–O2 | 107.5 | 107.3 | 107.5 | 105.2 | 105.6 | 105.2 |
| H2–C2–O2 | 110.2 | 107.0 | 107.0 | 110.9 | 110.5 | 110.9 |
| H6–C3–O2 | 109.6 | 108.4 | 111.9 | 110.8 | 110.5 | 110.8 |
| H7–C3–O2 | 109.7 | 104.7 | 107.0 | 106.7 | 106.8 | 106.6 |
| H8–C3–O2 | 111.8 | 114.7 | 112.9 | 111.6 | 111.4 | 111.6 |
| H3–C1–O1 | 108.7 | 110.4 | 109.6 | 110.8 | 110.5 | 110.8 |
| H4–C1–O1 | 111.6 | 111.0 | 111.3 | 111.6 | 111.4 | 111.6 |
| H5–C1–O1 | 106.9 | 107.8 | 109.1 | 106.7 | 106.8 | 106.6 |
| μ (D) | 0.22 | 0.16 | 0.26 | |||
For all the methods, the C1–O1 and C3–O2 bond lengths at the edge were found to be larger than the C2–O1 and C2–O2 bond lengths at the centre of DMM, in agreement with the previous calculation.35 This can be attributed to the 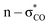 anomeric interaction for the interior C–O bond, originated from the delocalization of oxygen lone pair into a low lying anti-bonding
anomeric interaction for the interior C–O bond, originated from the delocalization of oxygen lone pair into a low lying anti-bonding 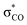 orbital.35 For the PBE/DZP calculations, the inclusion of solvent methanol molecules into the supercell (Met-25 and Met-40) was found to symmetrize the molecular structure around the C2 central carbon atom, like the B3LYP/6-311+G* cluster calculations. Also, the C–O bond lengths were enlarged when considering the solvent effect implicitly for the cluster calculations.
orbital.35 For the PBE/DZP calculations, the inclusion of solvent methanol molecules into the supercell (Met-25 and Met-40) was found to symmetrize the molecular structure around the C2 central carbon atom, like the B3LYP/6-311+G* cluster calculations. Also, the C–O bond lengths were enlarged when considering the solvent effect implicitly for the cluster calculations.
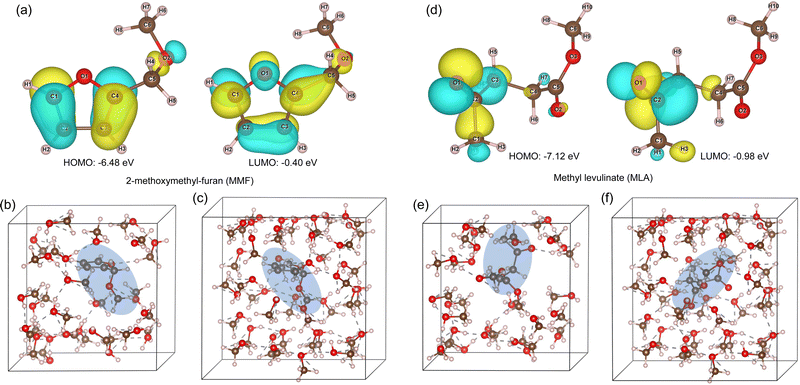
For the MMF and MLA molecules, we performed the conformational searches to find their lowest energy conformations by applying the stochastic search algorithm that uses random generation of conformational parameters. Then, geometry optimizations were performed for the vacuum supercell models and the cluster models. For the explicit methanol solvent supercell models, the NVT equilibrations at 300 K and subsequent optimizations were performed as well. Fig. 3 shows the results for MMF and MLA (see Tables S1 and S2 for their bond lengths, bond angles and dipole moments, ESI†). The HOMO–LUMO gaps were found to be 6.08 and 6.14 eV for MMF and MLA, respectively, with the B3LYP/6-311+G* calculations. The dipole moments were calculated to be 1.29 and 1.27 D for MMF, and 5.68 and 6.51 D for MLA, in vacuum and methanol solvent environments, respectively. We also calculated the harmonic frequencies of DMM, MMF and MLA, confirming no imaginary frequencies (see Fig. S9 and S10, ESI†)). For the methanol and water molecules, the same procedure was carried out (see Fig. S3 and Tables S3, S4, ESI†).
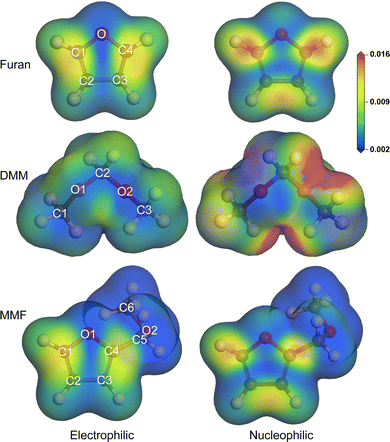
In order to identify the reactivity species in the individual molecules, we calculated the Fukui functions describing the sensitivity of charge density with respect to the electron loss or gain. The B3LYP/6-311+G* method was used for this aim, together with the cluster models in vacuum. Fig. 4 depicts the isodensity surface view of Fukui functions mapped on the isosurface of total electron density at the value of 0.2|e| Å−3, representing the chemical reactivity sites with respect to electrophilic and nucleophilic attacks for the major reactant molecules of furan, DMM and MMF (see Fig. S4 for methanol and water molecules, ESI†). According to the Fukui theory, an electrophile (nucleophile) accepts (donates) a pair of electrons, forming a new chemical bond. In the case of furan, the C atoms bonded to oxygen atom (C1 and C4) were found to be reactive species as their Fukui indices for electrophilic and nucleophilic attacks had the greatest values (0.204 and 0.226 for C1 atom) among the atoms (see Table S6, ESI†). The Fukui indices for electrophilic attack (f−) of C2 were obtained to be 0.10 and 0.13 from the Mulliken and Hirshfeld population analysis, being close to the value of 0.14 in the previous work.62 For the case of DMM, the O2 atom has the greatest value of Fukui index for electrophilic attack (0.215) among the atoms and the C2 central carbon atom has the higher value than those of the edge carbon atoms, indicating that the O2 and C2 atoms should be reactive species. In the MMF molecule, the carbon atoms of the furan heterocycle (C1–C4 atoms) show larger Fukui indices than the branch carbon atoms (C5 and C6 atoms), and the C6 atom of the methyl group has the negative Fukui index, indicating that the main reaction should occur in the furan heterocycle.
3.3 Reaction energetics
We then calculated the DFT total energies of the relevant reactant and product molecules under study in this work to evaluate the reaction energies (see Table S7, ESI†). Table 3 lists the reaction energies evaluated by the total energy differences between the reactant and product molecules with different modelings and simulation methods. For the reaction (1), the reaction energy was calculated to be positive in vacuum as being 0.22 and 0.02 eV with PBE/DZP supercell and B3LYP/6-311+G* cluster methods, indicating that the reaction is endothermic in vacuum. However, when considering the methanol solvent effect either explicitly or implicitly, the reaction became exothermic as the reaction energies became negative both in the explicit supercell and implicit cluster calculations. In the supercell calculations, the reaction energy with Met-40 models (−0.04 eV) was found to be smaller in magnitude than that with Met-25 models (−0.28 eV). This is possibly due to the stronger interaction between the neighbouring furan molecules at the shorter distance (12 Å) in the latter case. We note that the value of −0.04 eV in the Met-40 case is close to the value of −0.07 eV obtained by cluster calculations without zero-point and thermal corrections, implying that the explicit method with the 40 methanol molecules might give more reliable result in agreement with the implicit cluster method. For the reaction (2), the reaction energies were found to be negative by all the different methods, indicating the exothermicity of this reaction. In contrast to the reaction (1), the methanol solvent barely affects the reaction energy for the B3LYP/6-311+G* cluster calculations. However, the reaction energy could be lowered by methanol solvent, except for the case of Met-40 model.| PBE/DZP | B3LYP/6-311+G* | ||||
|---|---|---|---|---|---|
| Vac. | Met-25 | Met-40 | Vac. | Met. | |
| Reaction (1) | 0.22 | −0.28 | −0.04 | 0.02 | −0.11 |
| Reaction (2) | −1.62 | −3.10 | −1.11 | −1.35 | −1.36 |
Then, we determined the activation barriers for these reactions by applying the NEB method. To do this, the reaction pathways were presumed previously. For the initial state (IS) and final state (FS) of the reactions, we prepared the bimolecular systems of furan + DMM, MMF + methanol and MMF + water molecules. In each bimolecular system, the two molecules were placed at a long distance over 2.5 Å with proper orientations according to the reactivity sites identified by Fukui functions (see Fig. 4) and the geometry optimization was performed. For the supercell modeling, the AIMD simulations were performed to equilibrate the systems at 300 K and subsequently atomic relaxations were performed. Also, the breaking chemical bonds of the reactant molecules and the newly formed chemical bonds of the product molecules were suggested by considering the Fukui functions. Scheme 6 shows the chemical reactions schematically with the movement direction of the principal atoms of the reactants (red-coloured arrow). In the reaction (1), the hydrogen cation (proton) attached to the C1 atom adjacent to the O atom in furan is firstly dissociated and then reacted with the oxygen atom of DMM to create MMF, while forming a methanol molecule by bonding the proton with the CH3–O– residue group, as depicted in Scheme 2(a). For the second reaction (2), the oxygen atom of water is reacted with the C2 atom of MMF and the hydrogen atoms of water are bonded to the C1 atom, leading to breaking and creation of several chemical bonds to form a MLA molecule, as depicted in Scheme 2(b).
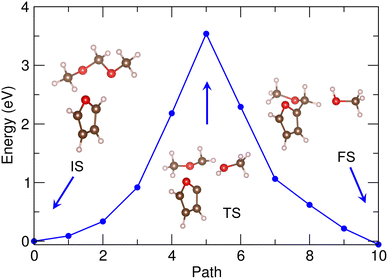
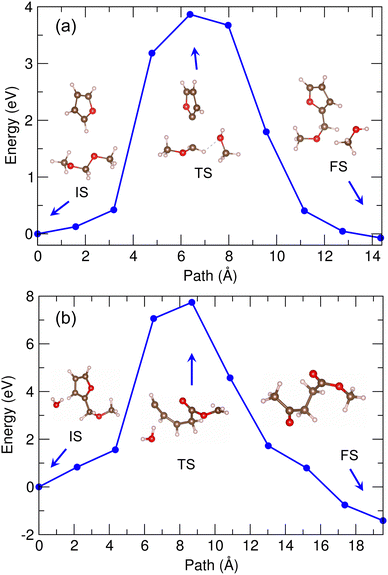
With these expected reaction pathways, we performed the NEB simulations to evaluate the reaction barriers. Fig. 5 shows the energy profile for reaction of furan + DMM into MMF + methanol with the geometries of the bimolecular system corresponding to IS, transition state (TS) and FS, calculated by using PBE/DZP method and the 30 Å supercell in vacuum. Through the geometry analysis during NEB run (see Fig. S5, ESI†), it was confirmed that as the furan molecule approached the DMM molecule, the H atom of C1–H bond in furan was firstly dissociated and bonded to the O2 atom of DMM, leading to the dissociation of DMM into CH3–O1–CH2– and CH3–O2H (methanol). This indicates that in this reaction the furan and DMM act as Brønsted acid and base as they donate and receive the proton (H+), respectively. Then, the furan anion (C4H3O−) was combined with the remaining CH3–O1–CH2– group by forming a new chemical bond between C1 of furan and C2 of DMM to form a MMF molecule as expected before. The activation barrier for this reaction was calculated to be as high as 3.5 eV, as shown in Fig. 5.
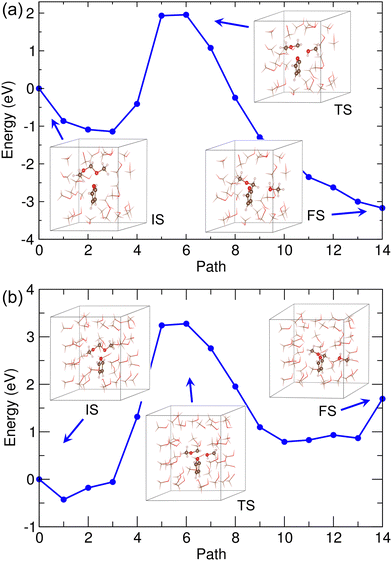
For this reaction, we considered the methanol solvent effect explicitly using both the Met-25 and Met-40 models. The same reaction pathway was suggested. Fig. 6 shows the calculated energy profiles with the revealed supercell structures corresponding to IS, TS and FS (see Fig. S6, ESI†). Although some interacting methanol molecules existed around the reactant molecules, the reaction pathway and geometries were found not to be quite different from those in vacuum mentioned above. The activation barriers were also somewhat similar to that in vacuum as being about 3.3 and 3.7 eV in the Met-20 and Met-40 models, respectively. It should be noted that in these models the ISs were not the lowest energy states, which were found at the third and first NEB images for the Met-20 and Met-40 models, respectively. Also, the energy profiles resembled each other in overall shape as being mount-like, although being sharper in vacuum and wider bases in methanol solvents. This indicates that the methanol solvent barely affects the reaction pathway, and therefore only the results in vacuum will be considered hereafter.
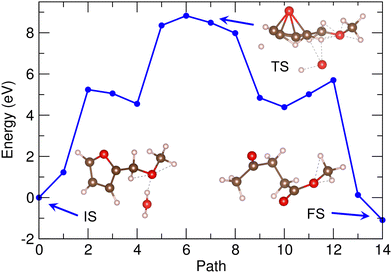
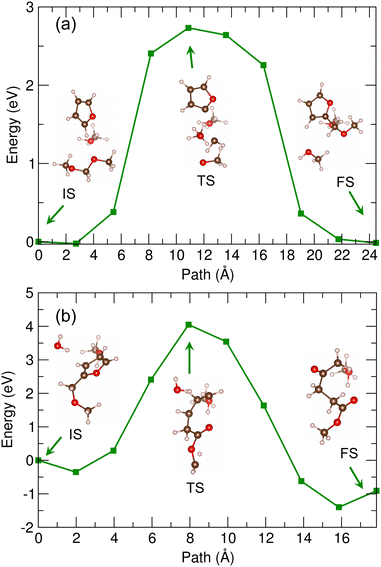
Fig. 7 shows the energy profile for the second reaction (2) of MMF + water to MLA, calculated by using the PBE/DZP method and the 30 Å supercell in vacuum. The geometries of the molecules corresponding to IS, TS and FS are shown together (see Fig. S7, ESI†). In this reaction, water and MMF molecules could also act as Brønsted acid and base as they donate and receive two protons, respectively. When compared with the first reaction, many chemical bonds can be expected to be broken including the dissociation of furan heterocycle in MMF, while many chemical bonds can also be newly formed. Therefore, the activation energy might be higher. As shown in Fig. 7, the activation energy for this reaction was calculated to be 8.4 eV, being over twice higher than that for the first reaction. To make the reaction realistic, therefore, a certain catalyst is needed as the solid acidic resin catalyst of D008 was used in the real experiments.20
Then, the B3LYP/6-311+G* method was applied to the cluster models in vacuum for determining the activation energies and reaction pathways for the two reactions. In these calculations, the number of NEB images was set to be 10. Fig. 8 shows the calculated energy profiles for the reactions (1) and (2). The real path distances were measured in the angstrom unit. We found that the reaction pathways and geometries of the molecules during the NEB runs were similar to those obtained by supercell calculations (see Fig. S8 and S9, ESI†). As shown in Fig. 8(a), the activation energy for the first reaction was calculated to be about 3.9 eV, which was slightly higher than that obtained with the Met-40 supercell calculation (3.8 eV). The mount-like shape of energy profile was also similar to those in the supercell calculation. For the second reaction, the activation energy was found to be about 7.9 eV, being similar to the case of the supercell calculation (see Fig. 8(b)). We note that the reason for such slight differences in activation energies might be slight differences in the optimized geometries of the molecules corresponding to IS, TS and FS. We performed the frequency analysis of TS. For the reaction (1), TS has only one imaginary frequency of −137 cm−1, while for the reaction (2) TS exhibits an imaginary frequency of −230 cm−1. To estimate the effect of different XC functional on the barrier height, we also applied the PBE/6-311+G* method to the NEB simulations for the reactions (1) and (2) (see Fig. S10, ESI†), confirming the almost agreement with those obtained with the DZP/PBE supercell as well as the B3LYP/6-311+G* method.
To consider the effect of solid acidic resin catalyst on the reaction barriers, we added a protonated methanol molecule into the original reaction systems62 and again performed NEB simulations. The protonated methanol molecule was located at the proper position between the reactant molecules with a certain distance over 3 Å and fixed during the NEB simulations. Fig. 9 shows the calculated energy profiles for the reactions, together with the optimized geometries of molecules corresponding to IS, TS and FS (see Fig. S11 and S12 for all the NEB images, ESI†). The activation energies were found to be lowered as 2.8 and 4.1 eV for the reactions (1) and (2) respectively, compared with those obtained without a protonated methanol molecule. This indicates the positive role of the acidic resin catalyst in promoting the furan conversion into MLA.
4 Conclusions
In this work, we have studied the conversion of furan into methyl levulinate using ab initio calculations within the DFT framework. For modeling and simulation, we adopted two different ways of PAO-DZP basis sets with supercell modeling and 6-311+G* basis sets with cluster modeling. The methanol solvent effect was considered explicitly by including 25 and 40 methanol molecules in the supercells with lattice constants of 12 and 14 Å for the supercell modeling and implicitly by using the COSMO approach for the cluster modeling. The geometrical features of individual molecules of furan, DMM, MMF and MLA were analyzed with comparison between those by different methods and models. Through the analysis of the Fukui functions, we identifies the reactive sites in the individual molecules, being necessary for predicting the reaction pathways, and verify the Brønsted acid–base reaction fashions for these reactions. With the calculated DFT total energies, corrected by the zero-point and thermal energies for the cases of B3LYP/6-311+G* cluster calculations, we determined the reaction energies for the reactions of furan + DMM to MMF + methanol and MMF + water to MLA. It was revealed that the first reaction was endothermic in vacuum but became exothermic in methanol solvent, while the second reaction was exothermic in both vacuum and solvent environments. Using the predicted reaction pathways, we carried out the NEB simulations to clarify the real reaction pathways and determine the activation energies for these two reactions without and with a protonated methanol molecule. Our calculations provide the atomistic insight into conversion of biomass-derived furan to MLA used as fuel additive with the detailed geometries and frequencies of the intermediates.Author contributions
Ryong-Wan Ham and Chol-Jun Yu developed the original project. Yun-Sim Kim and Chol-Jun Yu performed the calculations and drafted the first manuscript. Yong-Chol Pak, and Man-Sok O assisted with the post-processing of calculation results, and contributed to useful discussions. Chol-Jun Yu supervised the work. All authors reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported as part of the basic research project “Design of New Energy Materials” (no. 2021-12) funded by the State Commission of Science and Technology, DPR Korea. Computations have been performed on the HP Blade System C7000 managed by Faculty of Materials Science, Kim Il Sung University.References
- G. P. Robertson, S. K. Hamilton, B. L. Barham, B. E. Dale, R. C. Izaurralde, R. D. Jackson, D. A. Landis, S. M. Swinton, K. D. Thelen and J. M. Tiedje, Science, 2017, 356, 6345 CrossRef PubMed.
- F. Qureshi, M. Yusuf, H. Kamyab, D.-V. N. Vo, S. Chelliapan, S.-W. Joo and Y. Vasseghian, Renewable Sustainable Energy Rev., 2022, 168, 112916 CrossRef CAS.
- E. I. García-López, L. Palmisano and G. Marcí, Chem. Eng., 2023, 7, 11 Search PubMed.
- X. Cao, S. Sun and R. Sun, RSC Adv., 2017, 7, 48793–48805 RSC.
- S. D. Stefanidis, E. Heracleous, D. T. Patiaka, K. G. Kalogiannis, C. M. Michailof and A. A. Lappas, Biomass Bioenergy, 2015, 83, 105–115 CrossRef CAS.
- Y. Liu, Y. Chen, W. Guan, Y. Cao, F. Wang and Y. Zhang, Catalysts, 2023, 13, 435 CrossRef CAS.
- X. Li, Y. Wang, X. Xie, C. Huang and S. Yang, RSC Adv., 2019, 9, 9041–9048 RSC.
- S. Zhao, M. Cheng, J. Li, J. Tian and X. Wang, Chem. Commun., 2011, 47, 2176–2178 RSC.
- H. Zhao, J. E. Holladay, H. Brown and Z. C. Zhang, Science, 2007, 316, 1597–1600 CrossRef CAS PubMed.
- N. Kumari, T. Chhabra, S. Kumar and V. Krishnan, Catal. Commun., 2022, 168, 106467 CrossRef CAS.
- K. C. Badgujar, L. D. Wilson and B. M. Bhanage, Renewable Sustainable Energy Rev., 2019, 102, 266–284 CrossRef CAS.
- T. Flannelly, S. Dooley and J. J. Leahy, Energy Fuels, 2015, 29, 7554–7565 CrossRef CAS.
- M. S. Holm, S. Saravanamurugan and E. Taarning, Science, 2010, 328, 602–605 CrossRef CAS PubMed.
- A. Demolis, N. Essayem and F. Rataboul, ACS Sustainable Chem. Eng., 2014, 2, 1338–1352 CrossRef CAS.
- J. Liu, X.-Q. Wang, B.-B. Yang, C.-L. Liu, C.-L. Xu and W.-S. Dong, Renewable Energy, 2018, 120, 231–240 CrossRef CAS.
- X. Hu, S. Jiang, L. Wu, S. Wang and C.-Z. Li, Chem. Commun., 2017, 53, 2938–2941 RSC.
- G. Xu, C. Chang, S. Fang and X. Ma, Renewable Energy, 2015, 78, 583–589 CrossRef CAS.
- H. Chen, H. Ruan, X. Lu, J. Fu, T. Langrish and X. Lu, Chem. Eng. J., 2018, 333, 434–442 CrossRef CAS.
- G. Wang, Z. Zhang and L. Song, Green Chem., 2014, 16, 1436–1443 RSC.
- Z. Zhang, X. Hu, S. Zhang, Q. Liu, S. Hu, J. Xiang, Y. Wang and Y. Lu, Fuel, 2019, 237, 263–275 CrossRef CAS.
- Z. Chen, X. Ma, L. Xu, Y. Wang and J. Long, Bioresour. Technol., 2018, 268, 488–495 CrossRef CAS PubMed.
- C. Chang, L. Deng and G. Xu, Ind. Crops Prod., 2018, 117, 197–204 CrossRef CAS.
- J. Feng, J. Jiang, J. Xu, Z. Yang, K. Wang, Q. Guan and S. Chen, Appl. Energy, 2015, 154, 520–527 CrossRef CAS.
- X. Hu, Y. Song, L. Wu, M. Gholizadeh and C.-Z. Li, ACS Sustainable Chem. Eng., 2013, 1, 1593–1599 CrossRef CAS.
- F. Müller, V. Hermann-Ene, I. Schmidpeter, T. Hammerschick and W. Vetter, J. Agric. Food Chem., 2022, 70, 12620–12628 CrossRef PubMed.
- S. Vaitheeswaran, S. K. Green, P. Dauenhauer and S. M. Auerbach, ACS Catal., 2013, 3, 2012–2019 CrossRef CAS.
- X. Hu, S. Jiang, S. Kadarwati, D. H. Dong and C.-Z. Li, RSC Adv., 2016, 6, 40489–40501 RSC.
- H. Zhao, H. Gao, G. Yu, Q. Li and Z. Lei, Fuel, 2019, 241, 704–714 CrossRef CAS.
- Y. Dong, C. Dai and Z. Lei, Fuel, 2018, 216, 503–512 CrossRef CAS.
- B. Wang, X.-M. Liu, X.-N. Fu, Y.-L. Li, P.-X. Huang, Q. Zhang, W.-G. Li, L. Ma, F. Lai and P.-F. Wang, Fuel, 2018, 234, 207–217 CrossRef CAS.
- S. Yan, Y. Bu and L. Sun, J. Mol. Struct., 2004, 671, 161–172 CrossRef CAS.
- A. Mellouki, J. Liévin and M. Herman, Chem. Phys., 2001, 271, 239–266 CrossRef CAS.
- K. Sendt, G. B. Bacskay and J. C. Mackie, J. Phys. Chem. A, 2000, 104, 1861–1875 CrossRef CAS.
- E. Sánchez-García, A. Mardyukov, A. Tekin, R. Crespo-Otero, L. A. Montero, W. Sander and G. Jansen, Chem. Phys., 2008, 343, 168–185 CrossRef.
- V. Venkatesan, K. Sundararajan, K. Sankaran and K. S. Viswanathan, Spectrochim. Acta, Part A, 2002, 58, 467–478 CrossRef CAS PubMed.
- W. A. Kopp, L. C. Kröger, M. Döntgen, S. Jacobs, U. Burke, H. J. Curran, K. A. Heufer and K. Leonhard, Combust. Flame, 2018, 179, 433–442 CrossRef.
- F. H. Vermeire, H.-H. Carstensen, O. Herbinet, F. Battin-Leclerc, G. B. Marin and K. M. Van Geem, Combust. Flame, 2018, 190, 270–283 CrossRef CAS.
- T. A. Halgren, J. Am. Chem. Soc., 1992, 114, 7827–7843 CrossRef CAS.
- V. N. Emelyanenko, E. Altuntepe, C. Held, A. A. Pimerzin and S. P. Verevkin, Thermochim. Acta, 2018, 659, 213–221 CrossRef CAS.
- R. S. Assary, P. C. Redfern, J. R. Hammond, J. Greeley and L. A. Curtiss, J. Phys. Chem. B, 2010, 114, 9002–9009 CrossRef CAS PubMed.
- A. Klamt and G. Schürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- CRC Handbook of Chemistry and Physics, ed. D. R. Lide, C. R. C. Press, Boca Raton, FL, 2005, https://www.hbcpnetbase.com Search PubMed.
- E. Artacho, E. Anglada, O. Diéguez, J. D. Gale, A. García, J. Junquera, R. M. Martin, P. Ordejón, J. M. Pruneda, D. Sánchez-Portal and J. M. Soler, J. Phys: Condens. Matter, 2008, 20, 064208 CrossRef PubMed.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS PubMed.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 3098–3100 CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- C.-J. Yu, Y.-H. Kye, U.-G. Jong, K.-C. Ri, S.-H. Choe, J.-S. Kim, S.-G. Ko, G.-I. Ryu and B. Kim, ACS Appl. Mater. Interfaces, 2020, 12, 1858–1866 CrossRef CAS PubMed.
- Y.-S. Kim, C.-H. Ri, Y.-H. Kye, U.-G. Jong, X. Wang, Y. Zhang, X. Niu and C.-J. Yu, J. Phys. Chem. C, 2022, 126, 3671–3680 CrossRef CAS.
- S.-A. Kim, Y.-C. Jong, M.-S. Kang and C.-J. Yu, J. Mol. Model., 2022, 22, 287 CrossRef PubMed.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- A. Klamt, V. Jonas, T. Brüger and J. C. W. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085 CrossRef CAS.
- L. A. Montero, R. Gonzalez-Jonte, L. A. Diaz and J. R. Alvarez-Idaboy, J. Phys. Chem., 1994, 98, 5607 CrossRef CAS.
- A. Jiao, H. Zhang, J. Liu and X. Jiang, Combust. Flame, 2018, 196, 377–385 CrossRef CAS.
- R. Salcedo, A. Martínez and L. E. Sansores, Tetrahedron, 2001, 57, 8759–8765 CrossRef CAS.
- N. Gavrilov, S. Salzmann and C. M. Marian, Chem. Phys., 2008, 349, 269–277 CrossRef CAS.
- N. Nikbin, S. Caratzoulas and D. G. Vlachos, ChemSusChem, 2013, 6, 2066–2068 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Tables for bond lengths, bond angles and dipole moment of MMF, MLA, methanol and water molecules, for Fukui indices of molecules and for DFT total energies of reactants and products, and figures for temperature fluctuation during AIMD equilibration, configurations of 26 and 41 methanol molecules, isodensity surface of Fukui functions in methanol and water, and detailed geometries of intermediates during NEB runs. See DOI: https://doi.org/10.1039/d4ma00446a |
| This journal is © The Royal Society of Chemistry 2024 |