Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High-throughput screening of single atom co-catalysts in ZnIn2S4 for photocatalysis†
Md Habibur
Rahman
 a,
Yujie
Sun
b and
Arun
Mannodi-Kanakkithodi
a,
Yujie
Sun
b and
Arun
Mannodi-Kanakkithodi
 *a
*a
aSchool of Materials Engineering, Purdue University, West Lafayette, IN 47907, USA. E-mail: amannodi@purdue.edu
bDepartment of Chemistry, University of Cincinnati, Cincinnati, OH 45221, USA
First published on 15th October 2024
Abstract
In recent years, ZnIn2S4 (ZIS) has garnered attention as a promising photocatalyst due to its attractive properties. However, its performance is hindered by its restricted range of visible light absorption and the rapid recombination of photoinduced holes and electrons. Single-atom co-catalysts (SACs) can improve photocatalytic activity by providing highly active sites for reactions, enhancing charge separation efficiency, and reducing the recombination rate of photo-generated carriers. In this work, we perform high-throughput density functional theory (DFT) computations to search for SACs in ZIS encompassing 3d, 4d, and 5d transition metals as well as lanthanides, considering both substitutional and interstitial sites. For a total of 172 SACs, defect formation energy (DFE) is computed as a function of chemical potential, charge, and Fermi level (EF), leading to the identification of low energy dopants and their corresponding shallow or deep defect levels. Statistical data analysis shows that DFE is highly correlated with the difference in electron affinity between the host (Zn/In/S) atom and the SAC, followed by the electronegativity and boiling point. Among the 60 lowest energy SACs, CoIn, Ybi, TcZn, AuS, Lai, Eui, Aui, TaIn, HfIn, ZrIn, and NiZn lead to a lowering of the Gibbs free energy for hydrogen evolution reaction, improving upon previous ZIS results. The computational dataset and insights from this work promise to accelerate the experimental design of novel dopants in ZIS with optimized properties for photocatalysis and environmental remediation.
1 Introduction
The depletion of energy supplies and the discharge of harmful substances into the environment have become critical issues for long-term human survival due to the rapid expansion of the global population and industrialization. Consequently, discovering sustainable and environmentally friendly solutions to these problems is becoming increasingly important. Heterogeneous photocatalytic systems, which make use of semiconducting materials, have become a promising solution in this context.1–4 The photocatalytic process has the potential to efficiently harness solar energy and produce a range of valuable chemical fuels, such as hydrocarbons through CO2 conversion and H2 and O2via photocatalytic H2O splitting.5,6 Additionally, by efficiently decomposing dangerous and toxic substances, they provide the potential to reduce environmental contamination.7,8 In particular, these semiconducting materials exhibit appealing photocatalytic activity, strong exciton binding energy, non-toxicity, and exceptional photosensitivity.Wide bandgap materials like ZnO and TiO2 have a limitation when it comes to photocatalytic applications since they primarily absorb ultraviolet (UV) light, which limits the effective utilization of the solar spectrum.9 Compared to ZnO and TiO2, ultrathin ZnIn2S4 (ZIS) shows a smaller bandgap which enables higher absorption in the solar spectrum, including visible light.10,11 Additionally, the layered structure of ZIS creates a large surface area and a higher number of active sites for catalytic processes, which makes it easier to adsorb and activate reactant species.6,10 It is also possible to alter the electronic structure and surface properties of ZIS by doping or alloying at the Zn or In sites.12,13 Furthermore, ZIS possesses appealing chemical stability, which is necessary for long-lasting and robust photocatalytic application.14,15 However, the limited visible light absorption and relatively high rate of recombination of photogenerated charge carriers limit the photocatalytic performance of ZIS.16,17 Consequently, to tune the photocatalytic activity of ZIS, several strategies have been proposed including methods like van der Waals (vdW) heterostructure configuration, metal doping, vacancy engineering, metal deposition, and so on.18,19
Defect engineering is a widely utilized approach for altering the optoelectronic properties of semiconductors.18,20 During semiconductor fabrication, defects are unavoidable and can significantly influence the performance of photocatalysts.21,22 Different types of defects, including vacancies, anti-sites, substitutions, interstitials, grain boundaries, and surface states, have been shown to greatly affect the optoelectronic characteristics of photocatalysts.18,20 For instance, creating vacancies is an effective strategy to increase the visible light absorption by introducing impurity states near the Fermi level (EF), thereby facilitating the transfer of electrons from the valence band (VB) to the conduction band (CB).23,24 However, these vacancies can also increase the number of electron traps, which can decrease the mobility and stability of photogenerated carriers, ultimately lowering the photocatalytic efficiency.25,26
Single-atom catalysts (SACs) are atomically scattered metal atoms on a substrate that have become a well-established method for guaranteeing the optimal utilization of catalytically active atoms in heterogeneous catalysis.27,28 Due to their clearly defined and segregated active regions, SACs have distinct benefits over conventional bulk catalysts in terms of selectivity.29,30 SACs lead to larger surface area than bulk catalysts, allowing for more effective exposure of active sites to reactants thus promoting better catalytic activity.29,31 Furthermore, SACs can be designed to have customized electronic and optical characteristics, enabling efficient absorption of a wider range of photons, including visible light.30,32 This eventually broadens the range of visible light that can be absorbed and makes it possible to use solar energy more effectively.33,34 The presence of single atoms on a catalyst surface speeds up charge transfer processes, reduces charge carrier recombination, and enhances the separation and migration of photogenerated electrons and holes, all of which are necessary for fostering photocatalytic reactions.27,28 SACs also have the benefit of having tunable catalytic sites which enable precise atomic-level control, improving the catalytic activity for certain reactions.29,31 Due to their distinct active site topologies, SACs also show better selectivity towards target products, allowing for control over reaction pathways and the suppression of undesirable side effects.30,32
Additionally, SACs have been used to increase the effectiveness of oxygen evolution reaction (OER) and hydrogen evolution reaction (HER) in the context of H2O splitting. The electrochemical processes involved in H2O splitting are made easier by utilizing the active sites in transition metal (TM) SACs, such as Pt, Ni, and Co, which could potentially boost the overall photocatalytic process as well as the production of H2 gas.13,35 For example, a study by Shi et al.36 demonstrated that single Pt atoms on ZIS significantly enhance photocatalytic performance by improving charge separation and minimizing electron–hole pair recombination. Additionally, it could potentially induce a tipping effect that optimizes H adsorption and desorption by promoting efficient proton transfer, which synergistically enhances the thermodynamics and kinetics of the reaction. The reduction of CO2 to CO or other hydrocarbon products has also shown improved catalytic activity in metal-based SACs like Cu and Ag.27,28 Additionally, SACs have been used in photocatalytic reactions to degrade organic contaminants. For instance, Pd and Au-based SACs have shown notable effectiveness and selectivity towards the breakdown of colors, insecticides, and medications.30,32 Metal-based SACs, such as those made of Ni, Fe, or Co, hold great promise to enable very effective and long-lasting overall H2O splitting processes.29,31
Although the formation of native point defects in ZIS and their impact on photocatalytic activity have been well examined, very little is known about the energetics of dopants such as TM-based SACs and how they would affect photocatalytic performance.37,38 When dopants are more stable than native point defects within the semiconductor bandgap, they will modify the equilibrium EF, type of conductivity (p-type, n-type, or intrinsic), as well as the behavior of charge carriers.21,22 To achieve the best optoelectronic performance, it is crucial to accurately estimate the electronic levels that may be introduced by dopants. Deep defect levels can influence charge carrier recombination in multiple ways, unlike shallow donor or acceptor levels located near the band edges.20,23 For instance, deep-level dopants may function as non-radiative recombination centers (i.e., recombination without photon emission) for minority charge carriers, which can decrease carrier lifetime, hinder carrier collection, and reduce optoelectronic efficiency.25,26 Additionally, dopants can either enhance or inhibit the surface adsorption of organic/inorganic species, thereby influencing the semiconductor's photocatalytic capabilities.18,24 Hence, it is essential to comprehensively assess the stability of dopants in ZIS, their electronic levels, and the resulting equilibrium conductivity. Techniques such as photoluminescence (PL), deep-level transient spectroscopy (DLTS), and cathodoluminescence (CL) can be employed to detect, characterize, and locate impurities in semiconductors.22,25 However, the difficulty in introducing specific impurities or dopants and linking measured levels to particular defects means experimental methods often fall short of providing a complete picture of point defects in semiconductors.21,26 On the other hand, density functional theory (DFT) is a powerful tool for simulating point defects and has been widely used to calculate defect formation energies (DFEs) and associated charge transition levels (CTLs) in various crystalline materials.39–44
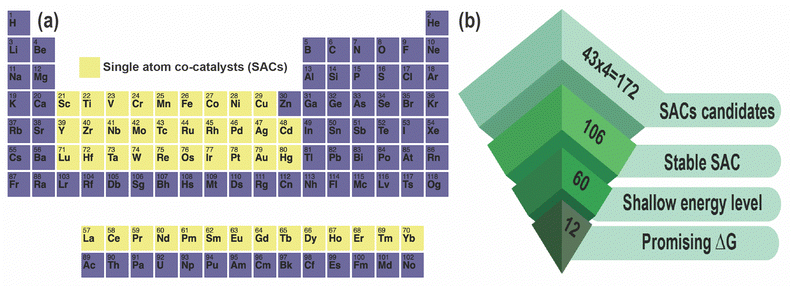
In this article, we present a comprehensive high-throughput DFT study of potential SACs for ZIS. Our investigation encompasses the entire 3d, 4d, and 5d TM series, as well as the lanthanide series, totaling 43 candidates. We examine the energetics of these 43 SACs, focusing on four distinct sites: MZn, MIn, MS, and Mi, where M refers to the specific metal dopant and the subscript is the doping site (Zn, In, S, or interstitial). This approach results in an analysis of 43 × 4 = 172 SACs, considering their DFE as a function of EF in 5 different charge states under three different growth conditions, namely S-rich (anion), In-rich (cation), and moderate (between anion and cation rich conditions). These calculations help us identify the relative stabilities of these SACs as well as their shallow/deep nature in the bandgap, following which we simulate their HER-related Gibbs free energies and determine suitable candidates for improved catalytic performance in ZIS. Although our work is mainly concerned with the photocatalytic activity of ZIS, it is important to note that photo-corrosion of ZIS, especially photo-oxidation and metal leaching, is a concern under real-world conditions. SACs may help to prevent photo-oxidation by blocking the active sites on the ZIS surface that can lead to S2− oxidation and degradation of the ZIS.45 SACs can also immobilize the Zn2+ and In3+ ions in the ZIS lattice and prevent metal leaching, which is a common problem under oxidation. This kind of stabilization is very important for the structural reinforcement and durability of ZIS in photocatalytic processes.
2 Methodology
All DFT calculations were performed using a 3 × 3 × 1 monoclinic supercell of ZIS with 126 atoms (18 Zn, 36 In, and 72 S), with lattice constants of a = 20.03 Å, b = 11.60 Å, and c = 25.00 Å. SACs including 3d, 4d, 5d, and lanthanide series elements as pictured in Fig. 1, were introduced in the optimized supercell and geometry optimization was performed considering 5 distinct charge states (q = −2, −1, 0, +1, +2) while keeping the size and shape of the supercell fixed.37 This results in a total of 43 × 4 (number of defect sites) × 5 = 860 dopant calculations, in addition to which we simulated a total of 12 native defects, leading to 860 + 12 × 5 = 920 total DFT calculations. Spin-polarized DFT was performed using the Vienna ab initio Simulation Package (VASP) and projector augmented wave (PAW) pseudopotentials, with the exchange–correlation energy defined using the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA).39–41 A kinetic energy cutoff of 500 eV was set for the plane-wave basis, and ionic relaxation was performed until the forces on each ion were less than 0.05 eV Å−1.37,46To take into account the impact of on-site Coulomb interactions stemming from the In and Zn atoms, the Hubbard +U correction was applied, with U values of 5 eV and 4.5 eV for In and Zn respectively, following our previous work.46 For GGA+U, the Brillouin zone was sampled using a 1 × 2 × 1 Monkhorst–Pack mesh centered at the Gamma point.37 Furthermore, to prevent interactions between the ZIS surface and its periodic image, a vacuum region of 1 nm was included.37 To achieve accurate predictions of defect levels within the bandgap, the GGA+U relaxed structure is used as input to a single-shot hybrid (mixing the Hartree–Fock and Kohn–Sham theories) HSE06 functional. The DFE (or Ef) and CTL (ε(q1/q2), where a defect transitions from one charge state to another) were calculated using the following equations:37
| Ef(Dq,EF) = E(Dq,ZIS) − E(ZIS) + μ + q(EF + EVBM) + Ecorr | (1) |
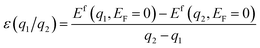 | (2) |
Here, E(ZIS) represents the DFT energy of a ZIS supercell without any defects, E(Dq,ZIS) represents the DFT energy of the ZIS supercell containing a defect D in a charge state q, EVBM is the valence band maximum (VBM) of bulk ZIS, μ represents the chemical potential associated with the creation of the defect, and Ecorr is the charge correction energy which accounts for the interaction between the charged defect and its periodic image, calculated using the scheme developed by Freysoldt et al.37,47 The Ef is dependent on EF in such a way that the slope of the Efversus EF plot is equal to the charge q.38 For each defect in the ZIS compound, the chemical potentials of all atoms are referenced to the lowest energy elemental standard state of each species. The defect CTLs (ε(q1/q2)) correspond to specific EF values where the defect becomes more stable in charge state q2 than q1, independent of μ. In this work, we calculated four different defect levels for each SAC, namely +2/+1, +1/0, 0/−1, −1/−2. The EF takes a range of values corresponding to the HSE06-computed band gap of 3 eV. The procedure to simulate the HER process on a catalyst surface and calculate the Gibbs free energy is described in Section 3.3 along with a discussion of the associated results.
We note that Freysoldt's image-charge correction method47 is the most appropriate for our system as it includes the long-range Coulombic and finite-size effects of the defect supercell, which means no additional dipole or quadrupole (Q) corrections are required. In practice, Q cannot be derived directly from the defect charge distribution as the defects could potentially exist in various forms; their wavefunctions can either be localized or delocalized and they are always accompanied by the screening charges of the host material. To overcome the limitation of periodic boundary conditions and to obtain a rather accurate DFE, we employed a large supercell and applied the Freysoldt correction.47 This approach aligns with best practices in the field, as demonstrated by other studies,48 which have shown that this correction effectively addresses the issues without the need for further corrections.
3 Results and discussion
3.1 Calculating chemical potentials
Prior to computing the energy of SAC doping, we first evaluated the chemical potential limits for ZIS. In thermodynamic equilibrium, the chemical potentials of all native species in ZIS should satisfy the following equations:37| ΔμZn + 2ΔμIn + 4ΔμS = ΔH(ZIS), |
| ΔμZn + ΔμS ≤ ΔH(ZnS), |
| ΔμIn + ΔμS ≤ ΔH(InS), |
| 2ΔμIn + 3ΔμS ≤ ΔH(In2S3), |
| ΔμZn ≤ 0, |
| ΔμIn ≤ 0, |
| ΔμS ≤ 0. |
These conditions are necessary to prevent the decomposition of ZIS into elemental Zn (hexagonal), In (trigonal), and S (monoclinic), or to binary compounds like ZnS (trigonal), InS (orthorhombic) and In2S3 (tetragonal). The formation energy of ZIS, denoted as ΔH(ZIS), is defined as:
| ΔH(ZIS) = E(ZIS) − E(Zn) − 2E(In) − 4E(S), |
| ΔH(ZnS) = E(ZnS) − E(Zn) − E(S), |
| ΔH(InS) = E(ZnS) − E(In) − E(S), |
| ΔH(In2S3) = E(In2S3) − 2E(In) − 3E(S). |
Here, E(system) represents the total DFT energy per formula unit (p.f.u.) of the given system. The chemical potentials of Zn, In, and S are referenced against their respective elemental standard states, such that:
| μZn = ΔμZn + E(Zn), |
| μIn = ΔμIn + E(In), |
| μS = ΔμS + E(S). |
3.2 Defect formation energies
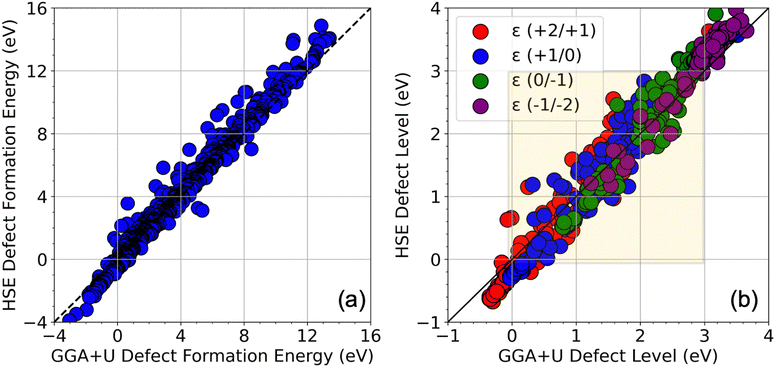
We performed high-throughput DFT computations to investigate the charge-dependent energetics of 43 possible SAC candidates at 4 possible defect sites in ZIS. In our analysis, any defect transition level that occurs within 25% to 75% of the bandgap is categorized as deep, and all other levels are classified as shallow. We first computed the DFE as a function of the EF (where EF extends from the VBM to the CBM) using only the GGA+U energies. Fig. S1 (ESI†) shows a visualization of the entire dataset of GGA+U-computed native defects and SAC dopants, in terms of the neutral state DFE values at In-rich and S-rich conditions, and in terms of all the transition levels, namely ε (+2/+1), ε (+1/0), ε (0/−1), and ε (−1/−2). Furthermore, to assess the extent of DFT optimization on the defect properties, we plotted a DFT-unoptimized (single-shot energy from pristine defect structure) vs. DFT-optimized energy in Fig. S2 (ESI†). It can be seen that the extent of geometry optimization (difference in optimized vs. unoptimized energy) is minimal for vacancies and most interstitials, but significant for some substitutional defects.The GGA+U calculations included previously established U values for Zn and In,46 but we chose not to initialize any U values for the SAC dopants, owing to the difficulty in determining suitable values for each via empirical fitting or self-determination methods, such as the linear response theory.50 To assess the impact of the U parameter on our results, we performed geometry optimization for ZIS with and without a +U correction. This comparative analysis yielded lattice parameters (a = 6.70 Å vs. 6.71 Å, b = 3.87 Å vs. 3.88 Å, c = 12.48 Å vs. 12.50 Å) and bond lengths for Zn–S (2.35 Å vs. 2.34 Å) and In–S (4.62 Å vs. 4.63 Å) from GGA+U vs. GGA, indicating that the geometry inputs for the HSE06 calculations were largely unaffected by the choice of U parameters. This observation underscores the reliability of our crystalline structures against the variability introduced by U values; rather, it's the Kohn–Sham eigenvalues and the energy levels that are highly dependent on the choice of U.
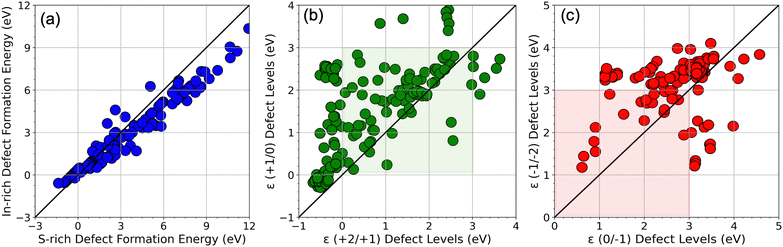
Fig. 2 shows a complete visualization of the HSE06-computed defect properties. We find that the DFEs show a wide range of values from ∼−1 eV to nearly 12 eV with S-rich DFE typically higher than In-rich DFE. While a few (0/−1) and ε (−1/−2) transitions occur within the bandgap (0 to 3 eV), almost every ε (+2/+1) and ε (+1/0) level seems to appear in the bandgap, meaning these transitions may be the primary source of mid-gap levels arising from the SACs. A critical aspect of our findings is illustrated in Fig. 3 in terms of a parity plot between the DFE for all 5 charge states (taken at the VBM, i.e., at EF = 0 eV) and defect levels calculated using GGA+U and HSE06. Remarkably, the data reveals a strong correlation with a few notable exceptions, underscoring the reliability of GGA+U in predicting trends that are consistent with the more rigorous HSE06 calculations. This correlation not only validates our computational strategy but also reinforces the utility of GGA+U for preliminary analyses in defect studies.
As an extension to our recent work,37 we first computed the HSE06 DFEs of all native point defects in ZIS, namely vacancies (VZn, VIn, VS), anti-sites (ZnIn, Zns, InZn, Ins, SZn, SIn), and self-interstitials (Zni, Ini, Si). Anti-site defects ZnIn and InZn are found to be the lowest energy acceptor and donor defects respectively, pinning the equilibrium EF slightly to the right of the middle of the bandgap, indicating moderately n-type conductivity; this can be seen from the intersection point of these defects in Fig. 4. While ZnIn creates one shallow acceptor level ε (0/−1) = 0.56 eV, InZn creates one shallow donor level ε (0/−1) = 2.49 eV (both values measured from the VBM). DFE plots showing all native defects simulated from HSE06 are presented in Fig. S3 (ESI†), for S-rich conditions. It should be noted that similar types of cation–cation low energy anti-site substitutional defects have been reported in quaternary chalcogenides in Kesterite and Stannite phases, e.g., CuZn and CuSn in Cu2ZnSnS4.51
Next, we examined the DFEs of all 172 SAC dopants (substitutional and interstitial) in terms of their Efvs. EF behavior, energetic comparison with ZnIn and InZn, and location of defect levels. We performed screening of these SACs as shown in Fig. 1(b), and found that 106 out of the 172 demonstrate higher stability than native defects under either In-rich or S-rich conditions, such that they will “dominate” over native defects and potentially tune the equilibrium conductivity. A few examples of these low-energy SAC dopants are presented in Table 1, along with their lowest DFE values and the nature of defect levels in the bandgap. Out of the 106 dopants, we find that 60 display only shallow levels, i.e., they do not create any potentially harmful states deep within the bandgap. All of these dopants are listed in Table 2 along with their DFEs and relevant +1/0 or 0/−1 levels, as well as the type of charge state shown within the bandgap. A majority of these screened dopants are substitutional in nature rather than interstitials.
| SACs | DFE (eV) | Nature |
|---|---|---|
| LaZn | −1.54 | Shallow |
| TaIn | −1.47 | Shallow |
| VIn | −1.34 | Deep |
| Eui | −1.20 | Shallow |
| NbIn | −1.14 | Deep |
| VZn | −1.05 | Deep |
| LuIn | −0.93 | Shallow |
| ScIn | −0.89 | Shallow |
| FeZn | −0.88 | Deep |
| Ybi | −0.84 | Shallow |
| Defects | DFE (eV) | ε (+1/0) | ε (0/−1) | Type |
|---|---|---|---|---|
| ScIn | −0.89 | — | — | Neutral |
| TiIn | −0.82 | 2.35 | — | Donor |
| CoIn | 1.35 | 0.29 | 2.46 | Amphoteric |
| YIn | −0.61 | — | — | Neutral |
| ZrIn | −2.38 | 2.45 | — | Donor |
| CdIn | 1.55 | — | 0.53 | Acceptor |
| LaIn | −0.07 | — | — | Neutral |
| CeIn | −0.54 | — | — | Neutral |
| PrIn | −0.14 | — | — | Neutral |
| NdIn | −0.2 | — | — | Neutral |
| PmIn | −0.26 | — | — | Neutral |
| SmIn | −0.33 | — | — | Neutral |
| EuIn | 1.55 | — | 0.65 | Acceptor |
| GdIn | −0.46 | — | — | Neutral |
| TbIn | −0.52 | — | — | Neutral |
| DyIn | −0.59 | — | — | Neutral |
| HoIn | −0.66 | — | — | Neutral |
| ErIn | −0.71 | — | — | Neutral |
| TmIn | −0.79 | — | — | Neutral |
| YbIn | 1.55 | — | 0.51 | Acceptor |
| LuIn | −0.93 | — | — | Neutral |
| HfIn | −3.92 | 2.51 | — | Donor |
| TaIn | −1.47 | 2.43 | — | Donor |
| HgIn | 1.4 | — | 0.59 | Acceptor |
| ScZn | −2.3 | 2.47 | — | Donor |
| MnZn | 1.14 | 2.38 | 2.96 | Amphoteric |
| NiZn | 1.08 | 0.21 | 2.3 | Amphoteric |
| YZn | −2.13 | 2.55 | — | Donor |
| TcZn | 0.27 | 2.83 | — | Donor |
| CdZn | −0.22 | — | — | Neutral |
| LaZn | −1.54 | 2.47 | — | Donor |
| CeZn | −0.4 | 2.43 | — | Donor |
| PrZn | −1.68 | 2.55 | — | Donor |
| NdZn | −1.75 | 2.56 | — | Donor |
| PmZn | −1.83 | 2.57 | — | Donor |
| SmZn | −1.74 | 2.43 | — | Donor |
| EuZn | 0.78 | — | — | Neutral |
| GdZn | −1.89 | 2.46 | — | Donor |
| TbZn | −2.01 | 2.53 | — | Donor |
| DyZn | −2.04 | 2.48 | — | Donor |
| HoZn | −2.18 | 2.56 | — | Donor |
| ErZn | −2.17 | 2.5 | — | Donor |
| TmZn | −2.17 | 2.42 | — | Donor |
| YbZn | 0.67 | — | — | Neutral |
| LuZn | −2.38 | 2.51 | — | Donor |
| HgZn | −0.24 | — | — | Neutral |
| AgS | 0.91 | 2.41 | — | Donor |
| AuS | 0.5 | 2.54 | — | Donor |
| Cui | −0.06 | 2.5 | — | Donor |
| Yi | 0.74 | 2.68 | — | Donor |
| Agi | −0.63 | 2.51 | — | Donor |
| Lai | 0.34 | 0.26 | — | Donor |
| Ndi | 0.64 | — | — | Donor |
| Eui | −1.2 | 2.8 | — | Donor |
| Gdi | 0.72 | 2.48 | — | Donor |
| Tmi | 0.61 | 2.77 | 2.57 | Amphoteric |
| Ybi | −0.84 | 2.83 | — | Donor |
| Hfi | 1.4 | 2.55 | — | Donor |
| Aui | 0.17 | 2.27 | — | Donor |
| Hgi | 0 | 0.26 | — | Donor |
Although the CTLs for native defects and dopants in ZIS are not available experimentally for benchmarking our calculated defect levels, it is important to note that our DFT predictions are based on well-established methodologies that have been shown to produce results in good agreement with measured defect levels in similar systems. Numerous studies have demonstrated that DFT calculations, when accompanied by the appropriate corrections (e.g., band edge, charge correction) and level of theories, can produce CTLs that are nearly equivalent to the experimentally obtained CTLs, as pictured in Fig. S4 (ESI†).52,53 We benchmarked defect levels for a variety of well-known binary semiconductors in past work,53 and as shown in Fig. S4(a) (ESI†), the root mean square errors between DFT and experiment are only around 0.2 eV. Fig. S4(b) (ESI†) further shows that computed defect levels for transition metal dichalcogenides match quite well with experiments.52 The approaches used in this work, such as the selection of functionals and corrections, have been well-validated and used to give reasonable defect levels in various semiconductors. This gives us confidence in the accuracy of our CTL predictions for the systems being studied here.
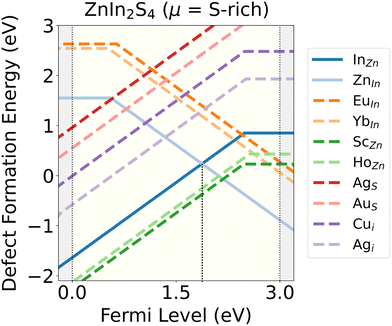
8 out of the 60 promising dopants (EuIn, YbIn, ScZn, HoZn, AgS, AuS, Cui and Aui) are pictured in Fig. 4 in terms of their Ef plotted as a function of EF, and in comparison with the lowest energy native acceptor (ZnIn) and donor (InZn) defects, under S-rich conditions. The reason behind choosing S-rich conditions is that typically, ZIS is synthesized via the solid-state reaction method, which involves reacting stoichiometric quantities of ZnS and In2S3 powders in a S-rich environment to inhibit oxidation under controlled conditions, thereby achieving the desired composition and crystalline structure. We observe that ScZn and HoZn are very low-energy donors and remain stable in p-type conditions while compensating for InZn. EuIn and YbIn are acceptor type defects that become stable in n-type conditions, whereas AgS, AuS, Cui and Agi are donors that are stable in p-type conditions. It should be noted that low energy dopants are determined on the basis of whether they dominate over the native defects under S-rich or In-rich conditions, even though only 2 of the 8 dopants pictured in Fig. 4 are actually dominating under S-rich conditions.
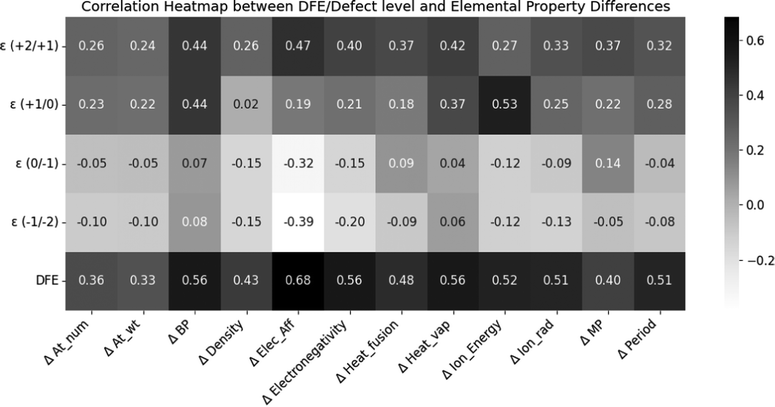
Next, we performed a statistical analysis to understand the correlation between fundamental properties of the SAC cations and the HSE06-computed defect properties, specifically for substitutional dopants. Fig. 5 shows the Pearson coefficients of linear correlation between 5 properties (neutral state DFE, ε (+2/+1), ε (+1/0), ε (0/−1), and ε (−1/−2)) and well-known elemental properties (specifically, the difference between the property of the SAC dopant and the atom it is substituting: Zn, In, or S). These properties include the atomic number, atomic weight, boiling point, density, electron affinity, electronegativity, heat of fusion, heat of vaporization, ionization energy, ionic radius, melting point and period. We find that the DFE is notably positively correlated with ΔElec_Aff, ΔElectronegativity, ΔBP, ΔHeat_vap, ΔIon_Energy, ΔIon_rad, and ΔPeriod. As the electron affinity and electronegativity difference between the host atom and dopant decreases, the DFE also goes down. ε (+2/+1) shows some correlation with ΔElec_Aff and ΔBP, while (+1/0) defect level is highly correlated with ΔIon_Energy, because the ionization energy determines the electron transfer necessary for the +1/0 transition. ε (0/−1) shows some correlation with ΔElec_Aff for the same reasons, while ε (−1/−2) does not show any notable correlations.
The correlations between different elemental descriptors and the computed defect properties help us understand some underlying physical mechanisms driving the behavior of the SACs. For instance, an SAC with a higher electron affinity would be able to collect more of the photogenerated electrons and use these to drive the HER. On the other hand, if the electron affinity of the SAC is too high or too low compared to that of the ZIS matrix, it could either overly stabilize the electrons, preventing their participation in the reaction, or fail to capture them effectively, either of which would reduce catalytic efficiency. The observed positive relationship between DFE and electron affinity (i.e., the difference in electron affinity between the SAC and host site of ZIS such as Zn, In, or S) indicates that the SACs with electron affinities not matching the host site in ZIS are likely to be unstable. This correlation highlights the delicate balance required in choosing SACs that can not only incorporate well in the ZIS structure but also maintain high catalytic activity without compromising stability. Furthermore, the notable correlations between defect CTLs and the ionization energy and electron affinity were noted in our past work,54 as these properties directly determine the ability to accept or donate electrons.
3.3 Photocatalytic hydrogen evolution reaction (HER)
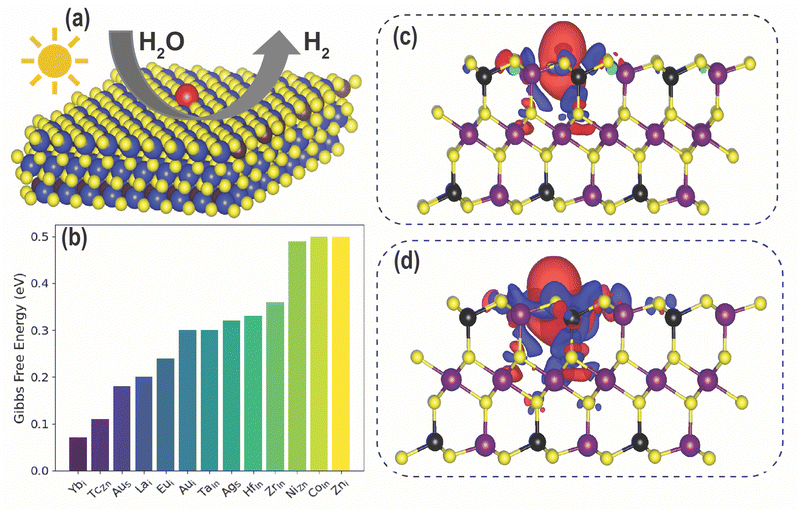
In this section, we explore the effect of the SACs on the photocatalytic HER performance of ZIS-free surfaces; a rough illustration of the process is shown in Fig. 6(a). In an acidic environment, HER typically involves four key steps: the binding of H+ to active sites, the reduction of H+ through electron transfer, the formation of an adsorbed intermediate H*, and the subsequent release of molecular H2. A crucial factor in evaluating the effectiveness of the HER process is the Gibbs free energy difference |ΔG| associated with H adsorption. In this study, we estimate |ΔG| using the following equation: |ΔG| = E(ZIS + H) − E(ZIS) − 0.5H2 + (ΔZPE − TΔS). ZPE is calculated using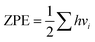 , where vi denotes the vibrational frequency of either free H2 placed in a large simulation box or H species adsorbed on the catalyst. When the vibrational frequency of the adsorbed H species is being computed, the entire catalyst structure (ZIS) is kept fixed, allowing the H atoms to vibrate freely in all directions. The entropy S is calculated using the following equation:
, where vi denotes the vibrational frequency of either free H2 placed in a large simulation box or H species adsorbed on the catalyst. When the vibrational frequency of the adsorbed H species is being computed, the entire catalyst structure (ZIS) is kept fixed, allowing the H atoms to vibrate freely in all directions. The entropy S is calculated using the following equation: 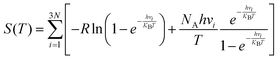 . For a highly efficient HER catalyst, the ideal value of |ΔG| is zero. The HER process faces challenges when |ΔG| is excessively positive or excessively negative. In the former case, the adsorption of H* on the catalyst surface is hindered while in the latter, the desorption of H* from the catalyst surface is impeded.
. For a highly efficient HER catalyst, the ideal value of |ΔG| is zero. The HER process faces challenges when |ΔG| is excessively positive or excessively negative. In the former case, the adsorption of H* on the catalyst surface is hindered while in the latter, the desorption of H* from the catalyst surface is impeded.
We calculated the HER |ΔG| values for the 60 promising SAC candidates identified via DFT screening, which are listed in Table S1 (ESI†). In previous work, our computations showed that a Zni defect in ZIS lowers the HER |ΔG| as compared to pristine ZIS.37 Out of the 60 SACs, we find that CoIn, Ybi, TcZn, AuS, Lai, Eui, Aui, TaIn, HfIn, ZrIn, and NiZn show lower |ΔG| than Zni, as presented in Fig. 6(b). This improvement can be attributed to the modified electronic structure and the creation of localized states within the bandgap due to the introduction of defects. These defect states can potentially increase both the carrier concentration and electronic conductivity. Additionally, defects may introduce new catalytically active sites or enhance the adsorption of reactants, thereby further enhancing photocatalytic performance.
To gain more understanding of the charge transfer mechanism between the catalyst and H atom, we analyzed the charge density difference (CDD) between pure ZIS and H, as well as between Ybi in ZIS and H, as shown in Fig. 6(c) and (d). Due to the introduction of Ybi, the electronic structure is altered and conductivity is bolstered. Consequently, there is more charge transfer between the catalyst and H, which turns into stronger adsorption. These findings highlight the potential of tailored doping strategies for optimizing photocatalytic activity in ZIS. We note that enhancement in photocatalytic activity of Yb-doped TiO2 has been substantiated through experimental investigations,55 which further motivates experimental investigation of Yb-doped ZIS for photocatalysis.
Although ΔG is a key indicator of how efficiently a photocatalyst can facilitate the HER, to understand the practical overall photocatalytic efficiency, several factors must be taken into account. For example, SACs based on noble metals may be expensive and result in increased cost of the photocatalytic system. While SACs could improve HER, they may also open routes for new reaction pathways or interfere with other photocatalytic reactions such as oxygen evolution. This could potentially lower the overall selectivity for hydrogen production and may need to be fine-tuned to optimize these effects. As our calculations of Gibbs free energy suggest, while there is a large potential for improvement of HER activity, translating these theoretical improvements into practical photocatalytic efficiency requires considering the overall system performance, including potential trade-offs. The potential increase in solar-to-hydrogen efficiency and the durability of photocatalysts is encouraging; however, there are other aspects that should also be considered, including cost, synthesis difficulty, and selectivity.
To understand the dynamic stability of the SAC-containing ZIS compounds and to evaluate their performance under conditions close to operating temperatures, we performed ab initio molecular dynamics (AIMD) simulations at 300 K for a chosen SAC, Ybi. During AIMD, the temperature of the system was maintained using a Nosé–Hoover thermostat under the NVT ensemble.37 This simulation was run for a total of 2 ps using a 1 fs time step. The results indicate that ZIS with Ybi maintains its structural integrity throughout the simulation, as depicted in Fig. S5 (ESI†), demonstrating its dynamic stability. The total energy remains roughly constant, and the structure snapshots at different times appear nearly identical. A movie showing the dynamics is included in the ESI† as an MP4 file. We further computed the velocity autocorrelation function (VACF) from the AIMD trajectories, which quantifies how the velocity of an atom at a given time is correlated with its velocity at a later time. Mathematically, it is expressed as:56
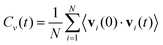 | (3) |
Here, Cv(t) is the velocity autocorrelation function at time t, N is the total number of atoms in the system, vi(0) is the velocity of atom i at time t = 0, vi(t) is the velocity of atom i at time t, and 〈·〉 represents the ensemble average over time or multiple configurations. We then computed the vibrational density of states (VDOS) from the VACF, which represents the distribution of vibrational modes over frequencies in a system. To compute the VDOS from the VACF, we applied the fast Fourier transform (FFT), which transforms the time-domain data (VACF) into the frequency domain. The VDOS, g(ω), is computed as:
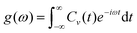 | (4) |
Here, g(ω) is the VDOS at frequency ω, Cv(t) is the velocity autocorrelation function, and e−iωt is the exponential factor in the Fourier transform, which relates time-domain data to frequency-domain data. Peaks in the VDOS correspond to dominant vibrational modes, as pictured in Fig. S5(c) (ESI†), and the absence of significant low-frequency modes suggests dynamic stability since low-frequency or zero-frequency modes often indicate structural instability. This finding reinforces our earlier conclusions regarding the suitability of Ybi as an effective and stable SAC in photocatalytic applications.
Beyond the results discussed so far, it is also important to determine the stability of SACs under operating conditions, particularly during the HER process, especially because single atoms could potentially aggregate into larger particles. To confirm the stability of Ybi on the ZIS surface, we used the nudged elastic band (NEB) method to simulate the migration of Yb on the surface, as shown in Fig. S6(a) (ESI†). As shown in Fig. S6(b) (ESI†), our calculations revealed a very high migration energy barrier for Yb (∼1.01 eV), meaning the Ybi SAC is unlikely to hop or segregate from the ZIS surface. Furthermore, we computed the DFE for an increasing number of Yb atoms on ZIS, going from single Ybi to double, triple, and quadruple defects, as pictured in Fig. S6(c) (ESI†). We found a steady increase in the DFE with Yb atoms, as shown in Fig. S6(d) (ESI†), which indicates that accommodating multiple Ybi is quite energetically unfavorable and that Ybi is stable and non-aggregative, and will remain as discrete single atoms without forming any clusters. This is important in maintaining the catalytic activity of Ybi during HER as it prevents the loss of active sites due to aggregation. However, it should be noted that clusters of atoms (if energetically favorable) could also improve catalytic activity compared to single atoms in some cases.57,58
4 Conclusions
In this study, we performed high-throughput density functional theory (DFT) computations to explore the potential of single-atom co-catalysts (SACs) in improving the photocatalytic performance of ZnIn2S4 (ZIS). Our focus was on transition metals from the 3d, 4d, and 5d series, as well as lanthanides, considering both substitutional and interstitial doping sites. A total of 172 SACs were considered and their defect formation energy (DFE) was computed as a function of chemical potential, charge state, and Fermi level. Our analysis identified 60 SACs with lower DFE than the dominant native defects in ZIS and only shallow defect levels within the bandgap. Notably, SACs such as CoIn, Ybi, TcZn, AuS, Lai, Eui, Aui, TaIn, HfIn, ZrIn, and NiZn demonstrated lower Gibbs free energy for HER compared to previously studied pristine ZIS or ZIS with Zni. This improvement is attributed to the introduction of defect states that enhance carrier concentration and electronic conductivity. The potential of Yb-doped ZIS for photocatalysis is further supported by experimental evidence of enhanced photocatalytic activity in Yb-doped TiO2. Overall, our computational workflow, dataset, and insights provide motivation for the experimental design of novel SACs in ZIS. The identified low-energy SACs offer new avenues for optimizing photocatalytic properties, promising significant advancements in environmental remediation applications.Data availability
All data is available in spreadsheets as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. M. K. acknowledges funding from the National Science Foundation (CHE-1955336) and support from the School of Materials Engineering at Purdue University. Y. S. acknowledges the support of the National Science Foundation (CHE-1955358). This research used resources from the Rosen Center for Advanced Computing (RCAC) clusters at Purdue University.References
- S. Wang, Z. Ding, X. Chang, J. Xu and D.-H. Wang, Catalysts, 2020, 10, 759 CrossRef CAS.
- X. Chang, G. Yu, J. Huang, Z. Li, S. Zhu, P. Yu, C. Cheng, S. Deng and G. Ji, Catal. Today, 2010, 153, 193–199 CrossRef CAS.
- C. Han, G. Han, M. H. Rahman, A. Mannodi-Kanakkithodi and Y. Sun, Chem. – Eur. J., 2023, 29, 202203785 CrossRef PubMed.
- A. Singh, B. Yuan, M. H. Rahman, H. Yang, A. De, J. Y. Park, S. Zhang, L. Huang, A. Mannodi-Kanakkithodi, T. J. Pennycook and L. Dou, J. Am. Chem. Soc., 2023, 145, 19885–19893 CrossRef CAS PubMed.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- X. Shi, L. Mao, P. Yang, H. Zheng, M. Fujitsuka, J. Zhang and T. Majima, Appl. Catal., B, 2020, 265, 118616 CrossRef CAS.
- U. Alam, M. Fleisch, I. Kretschmer, D. Bahnemann and M. Muneer, Appl. Catal., B, 2017, 218, 758–769 CrossRef CAS.
- J. Wang, S. Sun, R. Zhou, Y. Li, Z. He, H. Ding, D. Chen and W. Ao, J. Mater. Sci. Technol., 2021, 78, 1–19 CrossRef CAS.
- J. Low, B. Cheng and J. Yu, Appl. Surf. Sci., 2017, 392, 658–686 CrossRef CAS.
- G. Zhang, H. Wu, D. Chen, N. Li, Q. Xu, H. Li, J. He and J. Lu, Green Energy Environ., 2022, 7, 176–204 CrossRef CAS.
- J. Chen, F. Xin, X. Yin, T. Xiang and Y. Wang, RSC Adv., 2015, 5, 3833–3839 RSC.
- P. Wang, Z. Shen, Y. Xia, H. Wang, L. Zheng, W. Xi and S. Zhan, Adv. Funct. Mater., 2018, 29, 1807013 CrossRef.
- G. Han, X. Liu, Z. Cao and Y. Sun, ACS Catal., 2020, 10, 9346–9355 CrossRef CAS.
- C. Du, Q. Zhang, Z. Lin, B. Yan, C. Xia and G. Yang, Appl. Catal., B, 2019, 248, 193–201 CrossRef CAS.
- Y. Chen, R. Huang, D. Chen, Y. Wang, W. Liu, X. Li and Z. Li, ACS Appl. Mater. Interfaces, 2012, 4, 2273–2279 CrossRef CAS PubMed.
- Y. J. Zhang, H. M. Tang and S.-P. Gao, Phys. Status Solidi B, 2019, 257, 1900485 CrossRef.
- Z. Zafar, S. Yi, J. Li, C. Li, Y. Zhu, A. Zada, W. Yao, Z. Liu and X. Yue, Energy Environ. Mater., 2021, 5, 68–114 CrossRef.
- D. Maarisetty and S. S. Baral, J. Mater. Chem. A, 2020, 8, 18560–18604 RSC.
- W.-K. Chong, B.-J. Ng, C.-C. Er, L.-L. Tan and S.-P. Chai, Sci. Rep., 2022, 12, 1927 CrossRef CAS PubMed.
- H. J. Queisser and E. E. Haller, Science, 1998, 281, 945–950 CrossRef CAS PubMed.
- D. Wang, X.-B. Li, D. Han, W. Q. Tian and H.-B. Sun, Nano Today, 2017, 16, 30–45 CrossRef CAS.
- D. Lee, J.-W. Park, N.-K. Cho, J. Lee and Y. S. Kim, Sci. Rep., 2019, 9, 10323 CrossRef PubMed.
- M. Kumar, P. Basera, S. Saini and S. Bhattacharya, J. Phys. Chem. C, 2020, 124, 10272–10279 CrossRef CAS.
- X. Jing, N. Lu, J. Huang, P. Zhang and Z. Zhang, J. Energy Chem., 2021, 58, 397–407 CrossRef CAS.
- C. Foo, Y. Li, K. Lebedev, T. Chen, S. Day, C. Tang and S. C. E. Tsang, Nat. Commun., 2021, 12, 661 CrossRef CAS PubMed.
- F. G. Sen, A. Mannodi-Kanakkithodi, T. Paulauskas, J. Guo, L. Wang, A. Rockett, M. J. Kim, R. F. Klie and M. K. Chan, Sol. Energy Mater. Sol. Cells, 2021, 232, 111279 CrossRef CAS.
- Y. Niu, C. Yue, S. Li, G. Che, N. Su, H. Dong and C. Li, Carbon Lett., 2023, 33, 957–972 CrossRef.
- Y. Zhang, J. Zhao, H. Wang, B. Xiao, W. Zhang, X. Zhao, T. Lv, M. Thangamuthu, J. Zhang, Y. Guo, J. Ma, L. Lin, J. Tang, R. Huang and Q. Liu, Nat. Commun., 2022, 13, 58 CrossRef CAS PubMed.
- S. Hejazi, M. S. Killian, A. Mazare and S. Mohajernia, Catalysts, 2022, 12, 905 CrossRef CAS.
- C. Li, W. Pan, Z. Zhang, T. Wu and R. Guo, Small, 2023, 19, 2300460 CrossRef CAS PubMed.
- Y. Peng, B. Lu and S. Chen, Adv. Mater., 2018, 30, 1870370 CrossRef.
- Z.-H. Xue, D. Luan, H. Zhang and X. W. (David) Lou, Joule, 2022, 6, 92–133 CrossRef CAS.
- A. Martí, E. Antolí, C. R. Stanley, C. D. Farmer, N. López, P. Díaz, E. Cánovas, P. G. Linares and A. Luque, Phys. Rev. Lett., 2006, 97, 247701 CrossRef PubMed.
- A. Luque and A. Martí, Phys. Rev. Lett., 1997, 78, 5014–5017 CrossRef CAS.
- L. Du, Y. Sun and B. You, Mater. Rep.: Energy, 2021, 1, 100004 CAS.
- X. Shi, C. Dai, X. Wang, J. Hu, J. Zhang, L. Zheng, L. Mao, H. Zheng and M. Zhu, Nat. Commun., 2022, 13, 1287 CrossRef CAS PubMed.
- M. H. Rahman, J. Yang, Y. Sun and A. Mannodi-Kanakkithodi, Surf. Interfaces, 2023, 39, 102960 CrossRef CAS.
- A. Mannodi-Kanakkithodi, J.-S. Park, A. B. F. Martinson and M. K. Y. Chan, J. Phys. Chem. C, 2020, 124, 16729–16738 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- H. T. Mumu, A. Zaman, F. H. Bhuiyan, R. H. Aunkon and A. Sharif, Micro Nanostruct., 2023, 174, 207470 CrossRef CAS.
- A. Zaman, H. T. Mumu, R. H. Aunkon, F. H. Bhuiyan and A. Sharif, J. Phys. Commun., 2022, 6, 105007 CrossRef CAS.
- M. H. Rahman, P. Gollapalli, P. Manganaris, S. K. Yadav, G. Pilania, B. DeCost, K. Choudhary and A. Mannodi-Kanakkithodi, APL Mach. Learn., 2024, 2, 016122 CrossRef.
- J. Zheng, C. Fan, X. Li, Q. Yang, D. Wang, A. Duan, J. Ding, S. Rong, Z. Chen, J. Luo and B. Zhang, Chem. Eng. J., 2022, 446, 137371 CrossRef CAS.
- C. Han, G. Han, S. Yao, L. Yuan, X. Liu, Z. Cao, A. Mannodi-Kanakkithodi and Y. Sun, Adv. Sci., 2021, 9, 2103408 CrossRef PubMed.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van De Walle, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- A. Walsh, npj Comput. Mater., 2021, 7, 72 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W.-W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- S. Yao, B. Anasori and A. Strachan, J. Appl. Phys., 2022, 132(20), 204301 CrossRef CAS.
- J. S. Park, S. Kim, Z. Xie and A. Walsh, Nat. Rev. Mater., 2018, 3, 194–210 CrossRef CAS.
- J. Y. Kim, U. Gelczuk, M. P. Polak, D. Hlushchenko, D. Morgan, R. Kudrawiec and I. Szlufarska, npj 2D Mater. Appl., 2022, 6, 75 CrossRef CAS.
- A. Mannodi-Kanakkithodi, X. Xiang, L. Jacoby, R. Biegaj, S. T. Dunham, D. R. Gamelin and M. K. Chan, Patterns, 2022, 3, 100450 CrossRef CAS PubMed.
- A. Mannodi-Kanakkithodi, M. Y. Toriyama, F. G. Sen, M. J. Davis, R. F. Klie and M. K. Y. Chan, npj Comput. Mater., 2020, 6, 39 CrossRef CAS.
- X. Jiang, C. Li, S. Liu, F. Zhang, F. You and C. Yao, RSC Adv., 2017, 7, 24598–24606 RSC.
- M. S. Islam, I. Mia, A. S. M. J. Islam, C. Stampfl and J. Park, Sci. Rep., 2022, 12, 761 CrossRef CAS PubMed.
- L. Liu, T. Chen and Z. Chen, Adv. Sci., 2024, 11, 2308046 CrossRef CAS PubMed.
- L. Zhang, J. Yang, X. Yang, A. Wang and T. Zhang, Chem Catal., 2023, 3, 100560 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00616j |
| This journal is © The Royal Society of Chemistry 2024 |