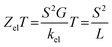DOI:
10.1039/D4MA00646A
(Paper)
Mater. Adv., 2024,
5, 9781-9791
Thermoelectric signature of d-orbitals in tripod-based molecular junctions†
Received
25th June 2024
, Accepted 8th November 2024
First published on 11th November 2024
Abstract
Promoting the thermoelectric properties of single-molecule junctions is a significant goal of a wide range of studies. Herein, the excellent consistency between current theoretical results and the experimental outcomes of previous studies helped establish a robust strategy for incorporating different transition metals into tripod connectors. This strategy proves that the involved dπ–pπ conjugation can not only enhance the electrical conductance, similar to that of conjugated hydrocarbons, but also improve the thermoelectric properties through interactions induced by the metal centre. The incorporation of the metal leads to an unconventional stereoelectronic effect caused by the metal–carbon dπ–pπ hyperconjugation. The odd number of electrons in the d-orbitals of molecular junctions with transition-metal centres presents a clear signature in the enhanced Seebeck coefficient, making them promising candidates for thermoelectric applications.
Introduction
Single-molecule technology is currently considered a technology of the future due to the small size and diversity of molecules, which may lead to the construction of functional devices with unique properties. However, it currently faces challenges related to the small size and diversity of molecules.1,2 In the field of molecular electronics, the design of one-dimensional molecular wires with a single type of anchor group has captured much of the research interest to date.3,4 This motif is simple and could present interesting structure–property relationships and conductance mechanisms without excessive complication.5 However, the difficulty associated with these structures lies in the spatial limitations of the single molecule, which is usually unstable, making junction formation challenging. Therefore, the use of a tripodal structure has been proposed by several groups.6–18 In this context, the number and type of anchor groups are crucial in creating stable junctions.19 M. A. Karimi20 and others21 have reported that the probability of molecular-junction formation increases significantly in the presence of tripod connectors, as these connectors can enhance the stability of the molecular junction. Yutaka Ie et al.22 innovatively prepared a single-molecule junction involving a pyridine-based tripodal anchor unit. The conductance of this structure was 5 ± 1 × 10−4G0, which is considered high compared to other junctions with different anchor groups.23,24 Future thermoelectric and electronic applications of single molecules may not only require high and low conductance, but also a range of modulations to adjust the precise characteristics of the circuit.25,26 The broad palette of ions available in organometallic molecules makes them appropriate candidates for producing a wide range of electrical conductance and thermoelectric capabilities.27–31 At the same time, transition metals exhibit various electronic effects that already play an important role in single-molecule devices,32,33 molecular thermoelectrics,34,35 and molecular spintronic devices,36,37 which rely on redox interactions.38,39 In addition, metals have diverse bonding patterns with light elements through participation of the metal's d-subshell, resulting in secondary interactions.40 For instance, the hyperconjugation impact41,42 could be mediated by the metal centre, leading to dramatic modifications in the reaction mechanism.43,44 Furthermore, the understanding of the secondary interactions could be a useful way to interpret the interactions between the metal and light elements,45,46 which is important in organometallic catalysis.47,48 Although, the influence of secondary interactions is important and can significantly enhance the performance of molecular electronic devices, it has been largely disregarded to date. In this context, the current investigation adopted a new strategy by incorporating d-orbital metals with tripod connectors to explore the electronic and thermoelectric properties of tripod-based molecular junctions.
Results and discussion
A tripodal-molecular platform pictures a perpendicular contact to the electrode, which represents a powerful way to establish a conducting path between two electrodes.49–53Fig. 1(a) shows six of these platforms chosen for study here. They involve with different metals (Mg, Co, Ni, Cu, Zn, and Pt) as a metal centre. The metal is connected to three phenyl rings via three single bonds, and a double bond to the sulfur atom. Each molecule is categorized as a three-dimensional compound consisting of three identical molecular wires linked to methyl sulfide (SMe) anchor groups. The first molecule (M-1) contains magnesium (Mg) atom as a metal centre. Like the other alkaline earth metals, it has a filled s orbital and two valence electrons. Unlike the transition metals, it does not have any partially filled d-orbitals in its atomic structure,54 and it was chosen here for comparison with the transition metals. Cobalt (Co) is the metal centre of molecule M-2, as shown in Fig. 1(a). Cobalt is one of the transition metals and is in the 7th column of the d-block and therefore has 7d electrons. Molecule M-3 possesses the nickel (Ni) atom as a metal centre, with 8 electrons in its d-orbital. Copper (Cu) and zinc (Zn) atoms are the metal centres of molecules M-4 and M-5, respectively, which are classified as transition metals with 10 electrons in their d-orbitals. The d-orbital of the platinum (Pt) atom is partially occupied by 9 electrons for molecule M-6.
 |
| | Fig. 1 (a) Schematic illustration of tripod connectors with six different metal centres; (b) schematic showing the d-orbital shape of some transition metals (Co, Ni, Cu, Zn, and Pt respectively); (c) optimized geometry of all the molecules in a gas phase, and their HOMOs and LUMOs (isosurfaces ±0.02 (e bohr−3)1/2). The blue part is a positive sign, while the red part is a negative sign. aH·aL is the multiplication of the HOMO and LUMO amplitudes. As an example, the HOMO and LUMO for the M-1 molecule possess different signs, and thus the multiplication of the molecular orbitals amplitudes (aH·aL) is a negative sign and the molecule exhibits constructive quantum interference (CQI). | |
Fig. 1(b) depicts the orientations of the d-orbitals for all these molecules with transition-metal centres. The first one (M-2) is dz2, which possesses the shape of a single dumbbell along the Z-axis, with a doughnut-like ring around the nucleus on the x–y plane, while the second one (M-3) is dx2–y2 and is similar to the shape of a clover leaf, but its leaves are oriented along the X and Y axes. The d-orbitals of molecules M-2 and M-6 are characterized by doughnut-like shapes, whereas the d-orbitals of the M-3, M-4, and M-5 molecules are distinguished by a clover-leaf shape. It is worth mentioning that odd numbers of electrons (7 and 9 electrons) belong to the d-orbitals of the M-2 and M-6 molecules, respectively. In contrast, the d-orbitals of molecules M-3, M-4, and M-5 have an even number of electrons (8, 10, and 10 electrons, respectively). In addition, Fig. 1(b) shows that the lowest energies of the LUMO orbitals (0.38 and 0.6 eV) were presented by M-6 and M-2, respectively, while the highest energies (1.12, 0.88, and 0.74 eV) were exhibited by M-5, M-4, and M-3, respectively. These results could be explicated in terms of the crystal field theory (CFT), a bonding model that elucidates many important characteristics of transition-metal complexes, including their structures, stability, and reactivity.55 If the negative charges are distributed uniformly over the surface of a sphere, the d-orbitals of Zn-metal, for example, will remain degenerate, but their energy will be higher due to the repulsive electrostatic interactions between the spherical shell with the negative charge and the electrons in the d-orbitals. The placing of negative charges at the vertices of an octahedron does not change the average energy of the d-orbitals, but it does remove their degeneracy. The five d-orbitals split into two groups (dx2–y2 and dz2), whose energies depend on their orientations, as shown in Fig. 1(b). To obtain a better understanding of the transport behaviour, the electronic properties of all the molecules in a gas phase were investigated using the DFT method (at the B3LYP level of theory56 with a LANL2DZ basis set57,58), as shown in Fig. 1(c). The LUMOs of all complexes, except M-1, displayed a pattern of dπ–pπ interactions along the metal–phenyl axis59 with a large metal character, while the HOMOs exhibited a small metal character. Fig. 1 suggests that the positively charged metal centres (LUMOs) for Co, Ni, Cu, Zn, and Pt atoms can be viewed as excellent electron acceptors, reflecting an interact with the occupied pπ orbital of the carbon atoms. The crystal field theory (CFT) proposes that the positively charged metal centre of molecules could generate an unexpected metal–carbon interaction. These results could be ascribed to the generation of a positively charged metal centre because the protonation occupied a place on the metal carbyne unit of the molecule.
Mülliken population analysis60 of the frontier orbitals of all the molecules indicated that the orbitals make a huge contribution to the LUMO but only a little one to the HOMO, which could be an indication of a LUMO-dominated transport mechanism,25,60–62 which is consistent with the transport behaviour shown in Fig. 2. Herein, orbital analysis was performed to provide further insights into the transport characteristics of the junctions. Lambert et al.63 reported an orbital symmetry rule. The magic ratio theory64 is based on utilizing the exact core Green's function, defined by:
 |
| | Fig. 2 (a) Theoretical model of molecular junctions; (b) transmission coefficient T(E) as a function of electron energy for all molecules. | |
In the literature, various approximations for g(E) are discussed, one of which involves the approximation including only the contributions to the g(E) from the HOMO and LUMO. If the amplitudes of the HOMO on sites a and b are denoted as 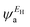 and
and 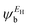 and the amplitudes of the LUMO are
and the amplitudes of the LUMO are 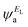 and
and 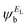 , then if the contributions from all other orbitals are ignored, a crude approximation to the Green's function gba(E) can be given by
, then if the contributions from all other orbitals are ignored, a crude approximation to the Green's function gba(E) can be given by
| | 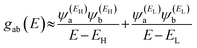 | (2) |
where
EH and
EL are the energies of the HOMO and LUMO respectively. If the HOMO product
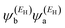
has the same sign as the LUMO product
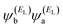
, then the right-hand side of
eqn (2) will vanish at some energy
E in the range
EH ⩽
E ⩽
EL; that is, for some energy
E within the HOMO–LUMO gap. In this case, one can say that the HOMO and the LUMO interfere destructively. On the other hand, if the HOMO and LUMO products have the opposite signs, then the right-hand side of
eqn (2) will not vanish within the HOMO–LUMO gap and one can say that the HOMO and LUMO interfere constructively within the gap (they could have course interfere destructively at some other energy
E outside the gap). When the right-hand side of
eqn (2) vanishes, the main contribution to
gba(
E) comes from all the other orbitals, so in general
eqn (2) could be a poor approximation. One exception to this occurs when the lattice is bipartite, because the Coulson–Rushbrooke (CR) theorem
65 tells us that if a and b are both even or both odd, then the orbital products on the opposite sides of
eqn (3) and (4) have the same sign. Consequently, when the HOMO and LUMO interfere destructively, all the other pairs of orbitals interfere destructively too, leading to the trivial zeros in the magic number table,
64 for which
gba(0) = 0.
The equations of the Coulson–Rushbrooke (CR) theorem are denoted as:65
| | 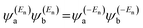 | (3) |
| | 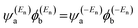 | (4) |
where
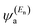
is a vector of amplitudes on even-numbered sites, and
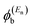
is a vector of amplitudes on odd-numbered sites, ±
En are eigenvalues that come in ± pairs, and the eigenstate belonging to −
En is related to the eigenstate belonging to
En. Obviously, this exact cancellation is a property of bipartite lattices only, but based on its success for bipartite lattices, one might suppose that
eqn (2) is a reasonable approximation for other lattices. Nevertheless, as pointed out by Yoshizawa
et al.,
54,55,59,61 since orbitals such as those in
Fig. 1(c) are often available from DFT calculations, it can be helpful to examine the question of whether or not the HOMO and LUMO (or indeed any other pair of orbitals) interfere destructively or constructively, by examining the colours of orbitals. This can be simplified by writing
eqn (2) in the form below,
| | 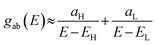 | (5) |
where
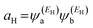
and
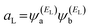
. If the HOMO product a
H has the same sign as the LUMO product
aL, then the right-hand side of
eqn (5) will vanish for some energy
E in the range
EH ⩽
E ⩽
EL. In other words, the HOMO and LUMO will interfere destructively at some energy within the HOMO–LUMO gap. However, this does not mean that the exact
gba(
E) will vanish. Indeed, if the right-hand side of
eqn (5) vanishes, then the contributions from all other orbitals become the dominant terms.
66 Nevertheless, this is an appealing method of identifying QI effects in molecules and describing their qualitative features. Now, based on this analysis, the results in
Fig. 1(c) suggest that the transport behaviour is dominated by a constructive quantum interference phenomenon (CQI), since the product of the HOMO and LUMO amplitudes is the same (negative sign), which means that the HOMOs and LUMOs interfered constructively. These results are interpreting the high values of the transmission coefficient
T(
E) shown in
Table 1 and
Fig. 2.
Table 1 (Γ = ΓM − ΓE) is the number of transferred electrons from molecule to the electrodes; ΓM is the number of electrons on the molecule in a gas phase; ΓE is the number of electrons on the molecule in a junction; Π is number of electrons of the d-orbital; Ω (eV) is the gap between the highest occupied molecular orbitals (HOMO) and the lowest unoccupied molecular orbitals (LUMO); T(E) is the transmission coefficient; LUMO is the lowest unoccupied molecular orbitals of all molecules in a junction
| M |
Metal |
Γ
|
Π
|
Ω (eV) |
T(E) |
| M-1 |
Mg |
1.1 |
— |
3.08 |
5.08 × 10−4 |
| M-2 |
Co |
2.2 |
7 |
2.32 |
29.8 × 10−4 |
| M-3 |
Ni |
1.8 |
8 |
2.27 |
14.8 × 10−4 |
| M-4 |
Cu |
1.5 |
10 |
2.58 |
6.69 × 10−4 |
| M-5 |
Zn |
1.3 |
10 |
2.94 |
6.5 × 10−4 |
| M-6 |
Pt |
2.9 |
9 |
1.96 |
92 × 10−4 |
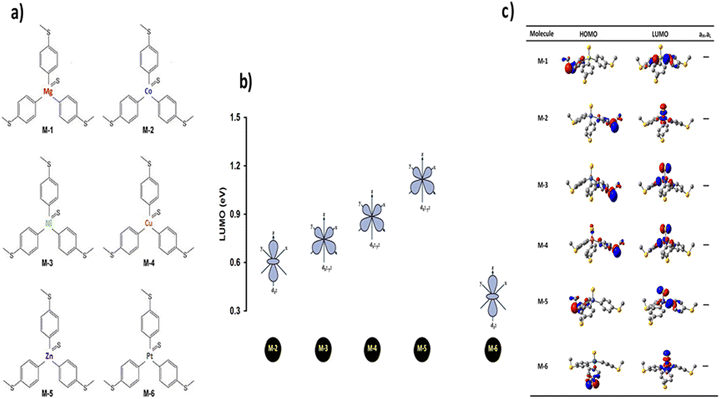
To support the results of the orbital analysis, and to confirm the impact of a constructive quantum interference (CQI), as well as to prove the important role of the different transition metals in improving the electronic and thermoelectric properties of tripod-based molecular junctions, a theoretical model of molecular junctions was constructed. This model was constructed using eight layers of (111)-oriented bulk gold, with each layer consisting of 6 × 6 atoms and a layer spacing of 0.235 nm, which were used to create the molecular junctions, as shown in Fig. 2(a) (see ESI† for all models). These layers were then further repeated to yield infinitely long current-carrying gold electrodes. Each molecule was attached to two (111)-directed gold electrodes; one of these electrodes was pyramidal, representing the scanning tunelling microscopy (STM) tip, while the other was a planar slab representing the electrode formed by the idealized Au(111) substrate in the I(s)-based molecular junction.67–69 The molecules and first layers of the gold atoms within each electrode were then allowed to relax again, to yield the optimal junction geometries, as shown in Fig. 2(a) and Fig. S1 (ESI†). From these model junctions, the transmission coefficient, T(E), was calculated using the GOLLUM code.70
The transmission coefficient according to Landauer–Büttiker71 formalism is given by:
| | | T(E) = Tr{ΓR(E)GR(E)ΓL(E)GR†(E)} | (6) |
where
| | | ΓL,R(E) = i(ΣL,R(E) − Σ†L,R(E)) | (7) |
where
ΓL,R describes the level broadening due to the coupling between the left (L) and right (R) electrodes and the central scattering region, and
ΣL,R(
E) are the retarded self-energies associated with this coupling. Also,
| | | GR = (Eχ − H − ΣL − ΣR)−1 | (8) |
where
GR is the retarded Green's function,
H is the Hamiltonian, and
χ is the overlap matrix. The transport properties can then be calculated using the Landauer formula:
| | 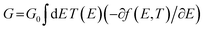 | (9) |
where
G0 = 2
e2/
h is the conductance quantum,
f(
E) = (1 + exp((
E −
EF)/
kBT))
−1 is the Fermi–Dirac distribution function,
T is the temperature, and
kB = 8.6 × 10
−5 eV K
−1 is the Boltzmann's constant.
Fig. 2(a) shows the theoretical model of tripod-based molecular junctions with different metals (Mg, Co, Ni, Cu, Zn, and Pt). All the metals, except Mg, are d-block elements classified as transition metals. It is well known that magnesium does not have a d-orbital, while cobalt, nickel, and platinum atoms possess a partially filled d-orbital. The d-orbital is fully filled for copper and zinc atoms, as shown in Table 1. Regarding the relaxed geometries of the molecular junctions, it is obvious that while the thiolate (RS−) to gold interaction has been studied extensively,72,73 the methylthioether to gold interaction has been less thoroughly explored. Interestingly, all the compounds contact the flat gold surface via three SMe-anchor groups with an Au–S distance of 3.0 Å and an Au–S–Cmethyl angle of 109.5°, as shown in Fig. 2(a). These geometries are comparable with other compounds, such as [Ph3PAuSMe2]–[CF3SO3] (Au–S, 2.323(2) Å; Au–S–Cmethyl 106.7(2), 104.7(2)°),74 and as such the sulfur–gold interaction is well approximated in terms of a coordination-type interaction (chemisorption) between the sulfur donor atom of the thioether and the gold atom. Therefore, it is considered that Fig. 2(a) shows that the methyl thioether contacted compounds are not oriented normal to the idealized, flat electrode surface within the molecular junction. Rather, they are tilted within molecular junctions to accommodate the directionality of the lone pairs of electrons on the sulfur atoms that bind to the gold electrodes,75,76 which forces molecules to take a dome shape and contact the electrodes via all three legs. On the other hand, the thiolate-contacted groups sit close to the apex of each pyramid-shaped model gold electrode, with an Au–S distance of 2.5 Å and an Au–S–Cipso angle of 177.7°.77
Fig. 2(b) shows the transmission coefficient T(E) as a function of the electron energy for all the molecular junctions. All the molecular junctions show a high value of T(E), ranging from the lowest value for molecule M-1 (5.08 × 10−4) to the highest value for molecule M-6 (92 × 10−4), as shown in Table 1. These results are reflective of constructive quantum interference (CQI), consistent with ref. 78–91, and the LUMO states of all molecules are near the theoretical Fermi level (0.0 eV), which suggests a LUMO-transport mechanism, which is in excellent agreement with the predicted outcomes from the orbital analysis calculations. The transmission values obtained from the M-4 and M-5 systems were close to each other, suggesting that the readily synthesized copper and zinc complexes may have an important role to play in the further development of metal complexes for applications in single-molecule electronics. These metal complexes are more conductive than their purely organic analogues of comparable molecular length,5 as shown in Fig. 3. To prove the important role of the d-orbitals in improving the electrical conductance (G/G0), the results shown in Fig. 3 are quoted from our previous study.5Fig. 3 shows a comparison between the calculated G/G0 for organometallic connectors and the measured G/G0 for organic molecules.
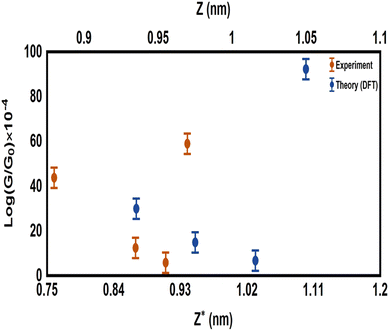 |
| | Fig. 3 Comparison between the calculated electrical conductance (G/G0) of the organometallic molecules in the current investigation, and the measured G/G0 of organic molecules from our previous studies.5 The experimental results have been adapted with permission from ref. 5. Copyright 2018 Royal Society of Chemistry. ExperG/G0 is a function of the experimental break-off distance (Z*), while the theoretical electrical conductance (TheoreG/G0) is a function of the calculated electrode separation in relaxed junctions (Z); Z = dAu–Au − 0.25 nm, where 0.25 nm is the calculated centre-to-centre distance of the apex atoms of the two opposing gold electrodes when the conductance = G0 in the absence of the molecule. | |
It can also be see in Fig. 3 that the experimental break-off distance (Z*) of all the organic-molecular junctions was smaller than the calculated electrode separation (Z) of the organometallic-molecular junctions. However, the values of the (G/G0) of the molecules with transition metals (Theory) were higher than those of the organic molecules (Expermint). These results could be interpreted in terms of the signature of the d-orbitals, which increase the electrical conductance. In addition, these results demonstred that all three-connector molecules (organic and organometallic molecules) had high electrical conductance, which could be ascribed to the high junction-formation probability due to the high binding energy between the three legs and gold electrodes.5
Furthermore, it is well known that the electrical conductance decreases with increasing the tunnelling distance.92 The molecule length of all the molecules was consistent with a dominant contribution from a coherent tunnelling mechanism.93–97 The rectangular tunnel barrier model98 states that the electrical conductance through a single molecule (barrier) decreases exponentially with the length of the barrier, according to the following equation:
where
T(
E) is the transmission coefficient,
β is the electronic decay constant, and
l is the tunnelling distance. Herein, the organometallic molecules (Theory) represented the longest molecules, but they showed the highest value of
T(
E). In contrast, the organic (Experiment) molecules represented the shortest length, but they showed transmission values that were several-fold lower than that of organometallic molecules, as shown in
Fig. 3. Hence, it became clear that there was competition between two parameters, the first one is the tunnelling distance and the second is the presence of the d-orbital effect. These results showed that the existence of the impact of transition metals was dominant, which led to the distinctive difference in the electrical conductance values between the experimental and theoretical results. On the other hand, the partial charge transfer (
Γ), as shown in
Table 1 and
Fig. 4(a), may also be responsible for the high transmission coefficient values presented in
Table 1 and
Fig. 2(b). Thygesen
et al.89 discussed similar situations for C
60-contacted molecular wires and showed that critical molecular orbitals can become pinned close to the Fermi level due to partial charge transfer, leading to a high electrical conductance.
90 In addition,
Fig. 4(a) illustrates the relationship between the number of transffered electrons from the molecule to the gold electrodes (
Γ) and the HOMO–LUMO (H–L) gap (
Ω) eV of the molecules in a junction. Overall, the energy levels moved energetically downwards and the H–L gap shrank for all the molecules with transition metals. The values of the H–L gaps for the M-5, M-4, M-2, and M-3 molecules were 2.94, 2.58, 2.32, and 2.27 eV respectively, as shown in
Table 1. Interestingly,
Fig. 4(a) presents an important result indicating that the molecule offering the highest number of transferred electrons (
Γ) showed the narrowest energy gap, and
vice versa, since molecule M-6 offering the highest number of transferred electrons (2.9 electrons) exhibted the narrowest H–L gap (1.96 eV). In contrast, molecule M-1 introduced the lowest
Γ of 1.1 electrons, and the widest H–L gap of 3.08 eV. Now, we sought to obtain a deep understanding of this finding and to answer the question of what is the relationship between
Γ and
Ω. This work considered the relation between the even and odd numbers of electrons in the d-orbitals (Π). The orientations of these orbitals and the HOMO–LUMO gap (
Ω) for Zn- and Pt-based molelecular junctions were considered as example of even and odd cases, as shown in
Fig. 4(b). The picture of these results could be understood according to the crystal field theory (CFT) concept.
55 Here, the LUMO energies of the two d-orbitals groups (d
x2–y2 and d
z2) for M-5 and M-6, respectively, depend on their orientations. The d
z2 orbital has a dumbbell form with a doughnut-shaped electron cloud in the centre and is symmetrical about the
Z-axis. The value of the HOMO–LUMO (H–L) gap of this orbital is 0.38 eV, which represents the narrowest gap. In contrast, the d
x2–y2 orbital is likewise in the shape of a clover leaf, but its leaves are oriented along the
X and
Y axes. The H–L gap value of this orbital is 2.94 eV, which is wider than that of the d
z2 orbital. This brings us to a predication that an odd number of electrons results in a narrow gap, while an even number leads to a wide one. On the other hand, the quantum-chemical electronic structure analysis shown in
Fig. 4(b) indicates that such a metal–carbon interaction is a positive dπ–pπ hyperconjugation, which in turn increases the conjugation of the Pt-based molecular junction (M-6), resulting in its highest value of
Γ,
59 and the latter increased
T(
E), as shown in
Fig. 4(c). The value of the transmission coefficient
T(
E) of the Zn-based molecular junction (M-5) was lower than that of the Pt-based molecular junction (M-6). The order of
T(
E) for all the molecular junctions is
T(
E)
M-6 >
T(
E)
M-2 >
T(
E)
M-3 >
T(
E)
M-4 >
T(
E)
M-5 >
T(
E)
M-1.
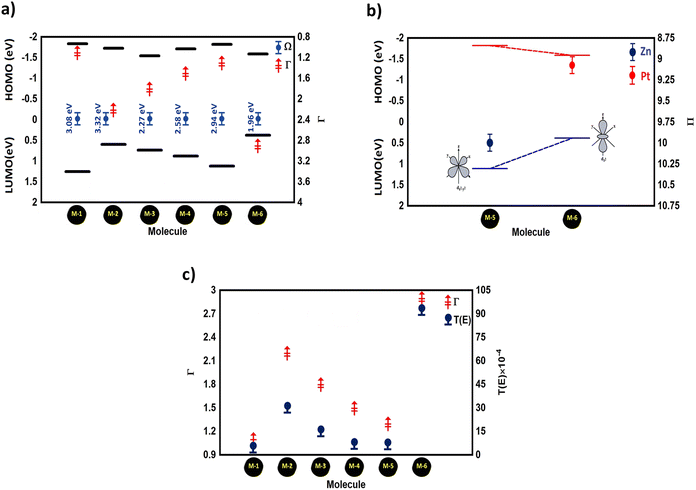 |
| | Fig. 4 (a) HOMO–LUMO gap (Ω) versus the number of transferred electrons (Γ) of the molecular junctions; (b) orbital energies versus the number of electrons in the d-orbital (Π) for M-5 and M-6 molecules, as example system with even and odd numbers of electrons; (c) number of transferred electrons from the molecule to the electrodes (Γ) versus the transmission coefficient T(E) of all the molecular junctions. | |
Exploring the influence of CQI on the transport behaviour, and consequently on the thermoelectric properties was one of the main goals of this work. The slope of T(E) determines the Seebeck coefficient (S), and thus the electronic figure of merit (ZelT). The Seebeck coefficient (S), power factor (P), and (ZelT), are given by:
| | 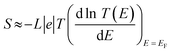 | (11) |
where
L is the Lorenz number
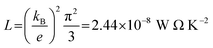
. In other words,
S is proportional to the negative of the slope of ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T
T(
E), evaluated at the Fermi energy (0.0 eV). Based on the Seebeck coefficient, the power factor (
P) is calculated by:
where
T is the temperature
T = 300 K,
G is the electrical conductance and
S is the Seebeck coefficient, and the purely electronic figure of merit (
ZelT) is given by:
91| | 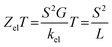 | (13) |
where
kel is the electron thermal conductance. According to previous studies,
91,99 the figure of merit in this work has been calculated only based on a purely electronic contribution. Indeed, it is well known that the performance of thermoelectric materials is characterized by an efficient conversion of an input heat to electricity.
100,101 In this context, the enhancement of the power factor (
P) and electronic figure of merit (
ZelT), which depend on the Seebeck coefficient (
S), are important too.
Fig. 5(a), (b) and Table 2 show that the highest values of S, ZelT, and P (−43.2 μV K−1, 0.068, and 1330.629 W K−1 × 10−15, respectively) were exhibited by molecule M-6. In contrast, molecule M-1 presented the lowest values (−9.9 μV K−1, 0.004, and 0.392 W K−1 × 10−15). For M-2, M-3, M-4, and M-5 molecules, the molecule (M-2) with a Co metal centre possessing an odd number of electrons in its d-orbital showed values of S and ZelT higher than those of the transition metals with an even number of electrons in their d-orbitals, as shown in Table 2. These results could be ascribed to the metal–carbon dπ–pπ hyperconjugation due to the odd number of electrons in the d-orbitals, which modulate the transmission behaviour of single-molecule junctions, as shown in Fig. 6. In addition, the competition between the electrical conductance and Seebeck coefficient according to eqn (12) led to power factors for the molecules in the order of PM-6 > PM-3 > PM-4 > PM-5 > PM-1.
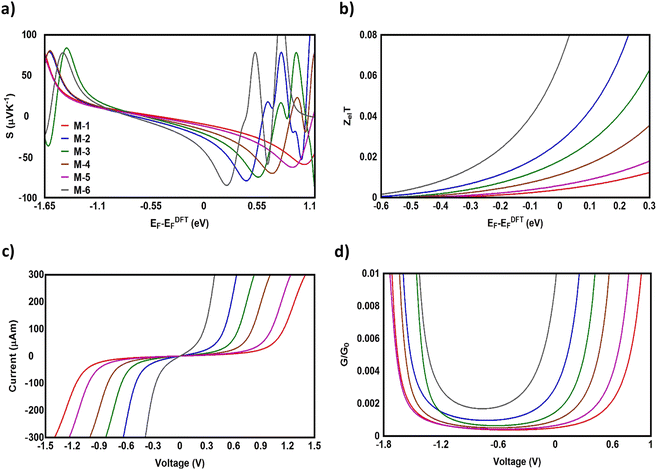 |
| | Fig. 5 (a) Seebeck coefficient (S); (b) electronic figure of merit (ZelT), as a function of the Fermi energy; (c) current–voltage characteristics; (d) electrical conductance (G/G0) as a function of voltage for all the molecular junctions. | |
Table 2 Seebeck coefficient (S); electrical conductance (G); power factor (P); electronic figure of merit (ZelT); and threshold voltage (Vth) of all the molecular junctions
| M |
S (μK V−1) |
G (S × 10−7) |
P (W K−1 × 10−15) |
Z
el
T
|
V
th (V) |
| M-1 |
−9.9 |
0.4 |
0.392 |
0.004 |
0.95 |
| M-2 |
−26.7 |
2.3 |
16.396 |
0.028 |
0.33 |
| M-3 |
−21.5 |
1.14 |
52.696 |
0.018 |
0.45 |
| M-4 |
−16.9 |
0.76 |
21.706 |
0.011 |
0.65 |
| M-5 |
−12.2 |
0.5 |
7.442 |
0.006 |
0.7 |
| M-6 |
−43.2 |
7.13 |
1330.629 |
0.068 |
0.15 |
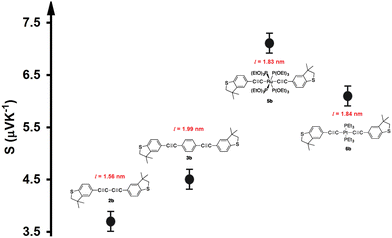 |
| | Fig. 6 Experimental thermopower results for previously studied compounds.34 The data were adapted with permission from ref. 34. Copyright 2015 American Chemical Society. | |
In light of the aforementioned results, it is clear that the transition-metal-based molecules could be considered promising candidates for thermoelectric applications. Obviously, the Seebeck coefficient was negative, which was consistent with the transport behaviour and the orbital analysis indicating that the transport mechanism was LUMO-dominated. Furthermore, Fig. 5(c) and Table 2 present the current–voltage (I–V) characteristics of all the molecular junctions, which were limited to the first and third quadrants of the I–V plane crossing the origin. Therefore, they could be classified as components that consume the electric power, and here the importance of the threshold voltage (Vth) value appears. The values of Vth ranged from 0.15 to 0.95 V. In general, the I–V characteristics of all the molecular junctions exhibited a semiconductor behaviour. Importantly, the values of Vth for molecules M-6, M-2, and M-3 were 0.15, 0.33, and 0.45 V, which are all below 0.5 V, indicating that these molecules are suitable structures for electronic applications.102 These results show a clear message that partially occupied d-orbitals may be an important property in improving the electronic and thermoelectric properties of transition-metal based molecular junctions.103 Moreover, as the voltage increased, the density of electrons also increased, which led to an increase in the number of occupied sub-bands,104 which in turn increased the conductance (in G/G0), as shown in Fig. 5(d). The most prominent result depicted in Fig. 6 is that the values of the thermoelectric properties (S and ZelT) of the transition-metal-based molecular junctions were higher than those based on non-transition metals. On the other hand, Fig. 6 proves that the molecules with metals involved dumbbell-form d-orbitals and had S and ZelT values higher than that of molecules with d-orbitals with a clover-leaf shape. Significantly, these results demonstrate that the existence of the transition metals centre improves the thermoelectric properties of the system.105
To validate and support the predictions of the current investigation regarding the thermoelectric signature of d-orbitals, we adopted some of the experimental results of our previous study.34Fig. 6 shows the Seebeck coefficient of four molecules, two of them (5b and 6b) involved transition metals (Ru and Pt) as metal centres, while the other molecules (2b and 3b) were organic. The data were adapted with permission from ref. 34. Copyright 2015 American Chemical Society. Despite, the length of molecule 2b (1.56 nm) being shorter than that of molecule 5b (1.83 nm), and the lengths of molecules 3b and 6b (1.99 and 1.84 nm respectively) being somewhat identical, Fig. 6 demonstrates that the highest values (7.1 and 6.1 μV K−1) of Seebeck coefficient were exhibited by the organometallic molecules 5b and 6b, respectively. Furthermore, when two points of the conductor are maintained at different temperatures, electrons or holes in the hotter region will move towards the colder region and diffuse. This diffusion stops when the electric field generated due to the migration of charges has established a strong field. For a metal, with carriers being negatively charged electrons, the colder end would become negative, so that the Seebeck coefficient would be negative. In a p-type semiconductor, holes diffuse towards the lower temperature, resulting in a positive Seebeck coefficient. These results leave us with only one explanation, which is that the presence of transition metals significantly improved the thermoelectric properties of the single-molecule junctions.
Conclusions
In summary, this work reports an investigation of the thermoelectric properties of molecular junctions based on tripod connectors terminated by active functional groups (SMe). The considerable and negative values of the Seebeck coefficient established that transport through these molecules took place by tunnelling through the tail of the LUMO resonance near the middle of the HOMO–LUMO gap. The results of this work prove that the tripod template significantly improves the junction-formation probability for increasing the electrical conductance. The excellent consistency between the current theoretical results and experimental outcomes of previous studies demonstrates the important role of transition metals in improving the thermoelectric properties of molecular junctions. In the case of the cobalt and platinum compounds M-2 and M-6, the odd number of electrons in their d-orbitals showed a robust signature in enhancing the Seebeck coefficient, making them to be promising candidates for thermoelectric applications.
Computational methods
Initial optimization of the gas-phase molecules and charges population analysis60 were carried out at the B3LYP level of theory56 with the LANL2DZ basis set.57,58 Geometrical optimization of the gold|molecule|gold configurations under investigation in this work was achieved by implementation of DFT106,107 in the SIESTA106 code, as shown in Fig. S2 (see ESI†). The generalized gradient approximation (GGA) of the exchange and correlation functional was used with a double-ζ polarized (DZP) basis set, a real-space grid defined with an equivalent energy cut-off of 250 Ry. The geometry optimization for each structure was performed for forces smaller than 20 meV Å−1. The mean-field Hamiltonian obtained from the converged DFT calculations was combined with GOLLUM70 code. The quantum transport theory (QTT)45–48,56,57,60,106 implemented in GOLLUM was used to calculate the electronic and thermoelectric properties of all the molecular junctions.
Data availability
The data are available in the manuscript and ESI.†
Conflicts of interest
The authors declare no conflict of interest.
Acknowledgements
O. A. A. and H. N. N. give a deep thanks and appreciation to the University of Babylon for the support. O. A. A.; A. K. O. A.; N. H. A.; M. S. A.; M. H. D. and M. A. A. express their sincere thanks and gratitude to the Al-Zahrawi University College and the University of Karbala for their kind support. A. K. O. A. thanks Al-Qasim Green University for the support.
References
- N. J. Tao, Nat. Nanotechnol., 2006, 1, 173–181 CrossRef CAS PubMed.
- S. S. Alexandre, J. M. Soler, P. J. Sanz Miguel, R. W. Nunes, F. Yndurain, J. Gómez-Herrero and F. Zamora, Appl. Phys. Lett., 2007, 90, 193107 CrossRef.
- W. Hong, D. Z. Manrique, P. Moreno-García, M. Gulcur, A. Mishchenko, C. J. Lambert, M. R. Bryce and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 2292–2304 CrossRef CAS.
- V. Kaliginedi, A. V. Rudnev, P. Moreno-Garcia, M. Baghernejad, C. Huang, W. Hong and T. Wandlowski, Phys. Chem. Chem. Phys., 2014, 16, 23529–23539 RSC.
- R. J. Davidson, D. C. Milan, O. A. Al-Owaedi, A. K. Ismael, R. J. Nichols, S. J. Higgins, C. J. Lambert, D. S. Yufita and A. Beeby, RSC Adv., 2018, 8, 23585–23590 RSC.
- J. K. Whitesell and H. K. Chang, Science, 1993, 261, 73–76 CrossRef CAS PubMed.
- M. A. Fox, J. K. Whitesell and A. J. McKerrow, Langmuir, 1998, 14, 816–820 CrossRef CAS.
- Y. Yao and J. M. Tour, J. Org. Chem., 1999, 64, 1968–1971 CrossRef CAS PubMed.
- W. Guo, E. Galoppini, G. Rydja and G. Pardi, Tetrahedron Lett., 2000, 41, 7419–7421 CrossRef CAS.
- E. Galoppini, W. Guo, P. Qu and G. J. Meyer, J. Am. Chem. Soc., 2001, 123, 4342–4343 CrossRef CAS PubMed.
- E. Galoppini, W. Guo, W. Zhang, P. G. Hoertz, P. Qu and G. J. Meyer, J. Am. Chem. Soc., 2002, 124, 7801–7811 CrossRef CAS.
- X. Deng and C. Cai, Tetrahedron Lett., 2003, 44, 815–817 CrossRef CAS.
- R. S. Loewe, A. Ambroise, K. Muthukumaran, K. Padmaja, A. B. Lysenko, G. Mathur, Q. Li, D. F. Bocian, V. Misra and J. S. Lindsey, J. Org. Chem., 2004, 69, 1453–1460 CrossRef CAS.
- L. Zhu, H. Tang, Y. Harima, K. Yamashita, D. Hirayama, Y. Aso and T. Otsubo, Chem. Commun., 2001, 1830–1831 RSC.
- D. Hirayama, K. Takimiya, Y. Aso, T. Otsubo, T. Hasobe, H. Yamada, H. Imahori, S. Fukuzumi and Y. Sakata, J. Am. Chem. Soc., 2002, 124, 532–533 CrossRef CAS PubMed.
- O. A. Al-Owaedi, RSC Adv., 2024, 14, 14704–14715 RSC.
- L. Wei, K. Padmaja, W. J. Youngblood, A. B. Lysenko, J. S. Lindsey and D. F. Bocian, J. Org. Chem., 2004, 69, 1461–1469 CrossRef CAS PubMed.
- L. Wei, H. Tiznado, G. Liu, K. Padmaja, J. S. Lindsey, F. Zaera and D. F. Roclan, J. Phys. Chem. B, 2005, 109, 23963–23971 CrossRef CAS.
- Y. Ie, T. Hirose, A. Yao, T. Yamada, N. Takagi, M. Kawai and Y. Aso, Phys. Chem. Chem. Phys., 2009, 11, 4949–4951 RSC.
- M. A. Karimi, S. G. Bahoosh, M. Valasek, M. Burkle, M. Mayor, F. Pauly and E. Scheer, Nanoscale, 2016, 8, 10582–10590 RSC.
- B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- M. Valasek, M. Lindner and M. Mayor, Beilstein J. Nanotechnol., 2016, 7, 374–405 CrossRef CAS.
- Y. Ie, T. Hirose, H. Nakamura, M. Kiguchi, N. Takagi, M. Kawai and Y. Aso, J. Am. Chem. Soc., 2011, 133, 3014–3022 CrossRef CAS.
- L. Gerhard, K. Edelmann, J. Homberg, M. Valasek, S. G. Bahoosh, M. Lukas, F. Pauly, M. Mayor and W. Wulfekel, Nat. Commun., 2017, 8, 14672 CrossRef.
- O. A. Al-Owaedi, D. C. Milan, M. Oerthel, S. Bock, D. S. Yufit, J. A. K. Howard, S. J. Higgins, R. J. Nichols, C. J. Lambert, M. R. Bryce and P. J. Low, Organometallics, 2016, 35, 2944–2954 CrossRef CAS.
- O. A. Al-Owaedi, ChemPhysChem, 2024, 25, e202300616 CrossRef CAS PubMed.
- A. A. Al-Jobory and M. D. Noori, J. Electron. Mater., 2020, 49, 5455–5459 CrossRef CAS.
- M. Alsaqer, A. H. S. Daaoub, S. Sangtarash and H. Sadeghi, Nano Lett., 2023, 23, 10719–10724 CrossRef CAS PubMed.
- Z. Liu, T. Liu, C. N. Savory, J. P. Jurado, J. S. Reparaz, J. Li, L. Pan, C. F. J. Faul, I. P. Parkin, G. Sankar, S. Matsuishi, M. Campoy-Quiles, D. O. Scanlon, M. A. Zwijnenburg, O. Fenwick and B. C. Schroeder, Adv. Funct. Mater., 2020, 30, 2003106 CrossRef CAS.
- H. Ozawa, M. Baghernejad, O. A. Al-Owaedi, V. Kaliginedi, T. Nagashima, J. Ferrer, T. Wandlowski, V. M. Garcia-Suarez, P. Broekmann, C. J. Lambert and M. Haga, Chem. – Eur. J., 2016, 22, 12732–12740 CrossRef CAS PubMed.
- S. Bock, O. A. Al-Owaedi, S. G. Eaves, D. C. Milan, M. Lemmer, B. W. Skelton, H. M. Osorio, R. J. Nichols, S. J. Higgins, P. Cea, N. J. Long, T. Albrecht, S. Martin, C. J. Lambert and P. J. Low, Chem. – Eur. J., 2017, 23, 2133–2143 CrossRef CAS PubMed.
- G. Lovat, B. Choi, D. W. Paley, M. L. Steigerwald, L. Venkataraman and X. Roy, Nat. Nanotechnol., 2017, 12, 1050–1054 CrossRef CAS PubMed.
- S. Gunasekaran, D. A. Reed, D. W. Paley, A. K. Bartholomew, L. Venkataraman, M. L. Steigerwald, X. Roy and C. Nuckolls, J. Am. Chem. Soc., 2020, 142, 14924–14932 CrossRef CAS PubMed.
- M. Naher, D. C. Milan, O. A. Al-Owaedi, I. J. Planje, S. Bock, J. Hurtado-Gallego, P. Bastante, Z. M. Abd Dawood, L. RinconGarcia, G. Rubio-Bollinger, S. J. Higgins, N. Agrait, C. J. Lambert, R. J. Nichols and P. J. Low, J. Am. Chem. Soc., 2021, 143, 3817–3829 CrossRef CAS.
- P. Gehring, J. K. Sowa, C. Hsu, J. de Bruijckere, M. van der Star, J. J. Le Roy, L. Bogani, E. M. Gauger and H. S. J. van der Zant, Nat. Nanotechnol., 2021, 16, 426–430 CrossRef CAS.
- F. Schwarz, G. Kastlunger, F. Lissel, C. Egler-Lucas, S. N. Semenov, K. Venkatesan, H. Berke, R. Stadler and E. Lortscher, Nat. Nanotechnol., 2016, 11, 170–176 CrossRef CAS.
- E. Coronado and A. J. Epsetin, J. Mater. Chem., 2009, 19, 1670–1671 RSC.
- T. Albrecht, A. Guckian, J. Ulstrup and J. G. Vos, Nano Lett., 2005, 5, 1451–1455 CrossRef CAS.
- X. Xiao, D. Brune, J. He, S. Lindsay, C. B. Gorman and N. Tao, Chem. Phys., 2006, 326, 138–143 CrossRef CAS.
- S. Mori and M. Shindo, Org. Lett., 2004, 6, 3945–3948 CrossRef CAS PubMed.
- A. G. Davies, J. Chem. Soc., Perkin Trans. 2, 1999, 2461–2467 RSC.
- K. Xiao, Y. Zhao, J. Zhu and L. Zhao, Nat. Commun., 2019, 10, 5639 CrossRef CAS PubMed.
- D. V. Vidhani, M. E. Krafft and I. V. Alabugin, J. Am. Chem. Soc., 2016, 138, 2769–2779 CrossRef CAS.
- J. Yuan, T. Sun, X. He, K. An, J. Zhu and L. Zhao, Nat. Commun., 2016, 7, 11489 CrossRef CAS.
- H. T. Liu, X. G. Xiong, P. Diem Dau, Y.-L. Wang, D.-L. Huang, J. Li and L.-S. Wang, Nat. Commun., 2013, 4, 2223 CrossRef.
- J. Dong, J. R. Robinson, Z.-H. Gao and L.-S. Wang, J. Am. Chem. Soc., 2022, 144, 12501–12509 CrossRef CAS PubMed.
- M. A. Esteruelas, A. M. López and M. Oliván, Chem. Rev., 2016, 116, 8770–8847 CrossRef CAS.
- Q. Zhuo, J. Lin, Y. Hua, X. Zhou, Y. Shao, S. Chen, Z. Chen, J. Zhu, H. Zhang and H. Xia, Nat. Commun., 2017, 8, 1912 CrossRef PubMed.
- M. Lukas, K. Dössel, A. Schramm, O. Fuhr, C. Stroh, M. Mayor, K. Fink and H. V. Löhneysen, ACS Nano, 2013, 7, 6170–6180 CrossRef CAS PubMed.
- S. Katano, Y. Kim, H. Matsubara, T. Kitagawa and M. Kawai, J. Am. Chem. Soc., 2007, 129, 2511–2515 CrossRef CAS PubMed.
- F. L. Otte, S. C. Lemke, S. N. R. Krekiehn, U. J. O. M. Magnussen and R. Herges, J. Am. Chem. Soc., 2014, 136, 11248–11251 CrossRef CAS PubMed.
- Y. Ie, K. Tanaka, A. Tashiro, S. K. Lee, H. R. Testai, R. Yamada, H. Tada and Y. Aso, J. Phys. Chem. Lett., 2015, 6, 3754–3759 CrossRef CAS.
- T. Kitagawa, Y. Idomoto, H. Matsubara, D. Hobara, T. Kakiuchi, T. Okazaki and K. Komatsu, J. Org. Chem., 2006, 71, 1362–1369 CrossRef CAS PubMed.
- J. M. Parr, A. J. P. Whitea and M. R. Crimmin, Chem. Sci., 2022, 13, 6592–6598 RSC.
- H. Bethe, Ann. Phys., 1929, 395, 133–208 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. Al-Laham, W. A. Shirley and J. Mantzaris, A complete basis set model, J. Chem. Phys., 1988, 89, 2193–2198 CrossRef CAS.
- G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090 CrossRef CAS.
- O. A. Al-Owaedi, S. Bock, D. C. Milan, M. Oerthel, M. S. Inkpen, D. S. Yufit, A. N. Sobolev, N. J. Long, T. Albrecht, S. J. Higgins, M. R. Bryce, R. J. Nichols, C. J. Lambert and P. J. Low, Nanoscale, 2017, 9, 9902–9912 RSC.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- T. Albrecht, A. Guckian, A. M. Kuznetsov, J. G. Vos and J. Ulstrup, J. Am. Chem. Soc., 2006, 128, 17132–17138 CrossRef CAS PubMed.
- V. P. Georgiev and J. E. McGrady, J. Am. Chem. Soc., 2011, 133, 12590–12599 CrossRef CAS PubMed.
-
C. J. Lambert, Quantum Transport in Nanostructures and Molecules, IOP Publishing Ltd, 2021 Search PubMed.
- C. J. Lambert and S.-X. Liu, Chem. – Eur. J., 2018, 24, 4193–4201 CrossRef CAS PubMed.
- C. A. Coulson and G. S. Rushbrooke, Math. Proc. Cambridge Philos. Soc., 1940, 36, 193–200 CrossRef CAS.
- M. Camarasa-Gómez, D. Hernangómez-Pérez, M. S. G. Inkpen, E. Lovat, E. Fung, X. Roy, L. Venkataraman and F. Evers, Nano Lett., 2020, 20, 6381–6386 CrossRef PubMed.
- W. Haiss, R. J. Nichols, H. Van Zalinge, S. J. Higgins, D. Bethell and D. J. Schiffrin, Phys. Chem. Chem. Phys., 2004, 6, 4330–4337 RSC.
- W. Haiss, H. Van Zalinge, S. J. Higgins, D. Bethell, H. Hobenreich, D. J. Schiffrin and R. J. Nichols, J. Am. Chem. Soc., 2003, 125, 15294–15295 CrossRef CAS PubMed.
- R. J. Nichols, W. Haiss, S. J. Higgins, E. Leary, S. Martin and D. Bethell, Phys. Chem. Chem. Phys., 2010, 12, 2801–2815 RSC.
- J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Zs Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. W. D. Bailey, K. Gillemot, H. Sadeghi and L. A. Algharagholy, New J. Phys., 2014, 16, 93029 CrossRef.
- M. Büttiker and R. Landauer, Phys. Rev. Lett., 1982, 49, 1739–1742 CrossRef.
- H. Hakkinen, Nat. Chem., 2012, 4, 443–455 CrossRef PubMed.
- C. Herrmann, G. C. Solomon and M. A. Ratner, J. Phys. Chem. C, 2010, 114, 20813–20820 CrossRef CAS.
- J. M. López-De-Luzuriaga, A. Schier and H. Schmidbaur, Chem. Ber. lRecueil, 1997, 130, 647–650 CrossRef.
- B. Capozzi, E. J. Dell, T. C. Berkelbach, D. R. Reichman, L. Venkataraman and L. M. Campos, J. Am. Chem. Soc., 2014, 136, 10486–10492 CrossRef CAS PubMed.
- H. Häkkinen, Nat. Chem., 2012, 4, 443–455 CrossRef PubMed.
- A. S. Mikherdov, M. Jin and H. Ito, Chem. Sci., 2023, 14, 4485–4494 RSC.
- J. Liu, X. Huang, F. Wang and W. Hong, Acc. Chem. Res., 2019, 52, 151–160 CrossRef CAS PubMed.
- C. Nappi, F. Romeo, L. Parlato, F. D. Capua, A. Aloisio and E. Sarnelli, J. Phys. Chem. C, 2018, 122, 11498–11504 CrossRef CAS.
- J. P. Bergfield, G. C. Solomon, C. A. Stafford and M. A. Ratner, Nano Lett., 2011, 11, 2759–2764 CrossRef CAS PubMed.
- O. A. Al-Owaedi, ACS Omega, 2024, 9, 10610–10620 CrossRef CAS PubMed.
- L. Huang, Y. Su and C. Kaun, ACS Omega, 2018, 3, 9191–9195 CrossRef CAS PubMed.
- G. Gryn’ova and C. Corminboeuf, J. Phys. Chem. Lett., 2019, 10, 825–830 CrossRef PubMed.
- D. Z. Manrique, C. Huang, M. Baghernejad, X. Zhao, O. A. Al-Owaedi, H. Sadeghi, V. Kaliginedi, W. Hong, M. Gulcur, T. Wandlowski, R. M. Bryce and C. J. Lambert, Nat. Commun., 2015, 6, 6389 CrossRef CAS PubMed.
- S. Li, H. Yu, K. Schwieter, K. Chen, B. Li, Y. Liu, J. S. Moore and C. M. Schroeder, J. Am. Chem. Soc., 2019, 141, 16079–16084 CrossRef CAS PubMed.
- O. A. Al-Owaedi, T. T. Khalil, S. A. Karim, E. Al-Bermany and D. N. Taha, Syst. Rev. Pharm., 2020, 11, 110–115 CAS.
- H. Ozawa, M. Baghernejad, O. A. Al-Owaedi, V. Kaliginedi, T. Nagashima, J. Ferrer, T. Wandlowski, V. M. García-Suárez, P. Broekmann, C. J. Lambert and M. Haga, Chem. – Eur. J., 2016, 22, 12732–12740 CrossRef CAS PubMed.
- M. A. I. Obayes, E. M. Al-Robayi and O. A. Al-Owaedi, J. Phys.: Conf. Ser., 2021, 1973, 012147 CrossRef.
- T. Markussen, M. Settnes and K. S. Thygesen, J. Chem. Phys., 2011, 135, 144104 CrossRef PubMed.
- N. Cao, W. Bro-Jørgensen, X. Zheng and G. C. Solomon, J. Chem. Phys., 2023, 158, 124305 CrossRef CAS PubMed.
- M. Burkle, T. J. Hellmuth, F. Pauly and Y. Asai, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 165419 CrossRef.
- S. H. Halboos, O. A. Al-Owaedi and E. M. Al-Robayia, Nanoscale Adv., 2024, 6, 5467–5481 RSC.
- F. Jiang, D. I. Trupp, N. Algethami, H. Zheng, W. He, A. Alqorashi, C. Zhu, C. Tang, R. Li, J. Liu, H. Sadeghi, J. Shi, R. Davidson, M. Korb, A. N. Sobolev, M. Naher, S. Sangtarash, P. J. Low, W. Hong and C. J. Lambert, Angew. Chem., Int. Ed., 2019, 58, 18987–18993 CrossRef CAS PubMed.
- M. H. Garner, H. X. Li, Y. Chen, T. A. Su, Z. Shangguan, D. W. Paley, T. F. Liu, F. Ng, H. X. Li, S. X. Xiao, C. Nuckolls, L. Venkataraman and G. C. Solomon, Nature, 2018, 558, 415–419 CrossRef CAS PubMed.
- B. Huang, X. Liu, Y. Yuan, Z. Hong, J. Zheng, L. Pei, Y. Shao, J. Li, X. Zhou, J. Chen, S. Jin and B. Mao, J. Am. Chem. Soc., 2018, 140, 17685–17690 CrossRef CAS PubMed.
- B. Kim, J. M. Beebe, C. Olivier, S. Rigaut, D. Touchard, J. G. Kushmerick, X. Y. Zhu and C. D. Frisbie, J. Phys. Chem. C, 2007, 111, 7521–7526 CrossRef CAS.
- S. M. S. Al-Mohana, H. N. Najeeb, R. M. Al-Utayjawee, F. Babaeia and O. A. Al-Owaedi, RSC Adv., 2024, 14, 23699–23709 RSC.
- Q. Lu, K. Liu, H. M. Zhang, Z. B. Du, X. H. Wang and F. S. Wang, ACS Nano, 2009, 3, 3861–3868 CrossRef CAS PubMed.
- A. Putatunda and D. J. Singh, Mater. Today Phys., 2019, 8, 49–55 CrossRef.
- N. T. Hung, A. R. T. Nugraha and R. Saito, Energies, 2019, 12, 4561 CrossRef CAS.
- B. A. A. Al-Mammory, O. A. Al-Owaedi and E. M. Al-Robayi, J. Phys.: Conf. Ser., 1818, 2021, 012095 Search PubMed.
- R. M. Al-Utayjawee and O. A. Al-Owaedi, J. Phys.: Conf. Ser., 1818, 2021, 012208 Search PubMed.
- A. I. M. Obayes, E. M. Al-Robay and O. A. Al-Owaed, J. Phys.: Conf. Ser., 1973, 2021, 012147 Search PubMed.
- I. A. Shelykh, N. T. Bagraev and L. E. Klyachkin, Semiconductors, 2003, 37, 1390–1399 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef PubMed.
- U. Sivan and Y. Imry, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 551 CrossRef CAS PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminform., 2012, 4, 1–17 CrossRef PubMed.
- H. B. J. Schlegel, S. Binkley and J. A. Pople, J. Chem. Phys., 1984, 80, 1976–1981 CrossRef CAS.
- D. C. Milan, O. A. Al-Owaedi, M. Oerthel, S. Marqués-González, R. J. Brooke, M. R. Bryce, P. Cea, J. Ferrer, S. J. Higgins, C. J. Lambert, P. J. Low, D. Z. Manrique, S. Martin, R. J. Nichols, W. Schwarzacher and V. M. García-Suárez, J. Phys. Chem. C, 2016, 120, 15666–15674 CrossRef CAS.
- R. Davidson, O. A. Al-Owaedi, D. C. Milan, Q. Zeng, J. Tory, F. Hartl, S. J. Higgins, R. J. Nichols, C. J. Lambert and P. J. Low, Inorg. Chem., 2016, 55, 2691–2700 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Involves theories and all details relevant to the computational methods. The author have cited additional references (ref. 108–111). See DOI: 10.1039/d4ma00646a |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Hussein Neama
Najeeb
a,
Ahmed Kareem Obaid
Aldulaimi
bc,
Nathera Hussin
Alwan
b,
Mohammed Shnain
Ali
bd,
Majed H.
Dwech
be and
Muneer A.
AL-Da’amy
f
*ab,
Hussein Neama
Najeeb
a,
Ahmed Kareem Obaid
Aldulaimi
bc,
Nathera Hussin
Alwan
b,
Mohammed Shnain
Ali
bd,
Majed H.
Dwech
be and
Muneer A.
AL-Da’amy
f

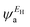 and
and 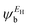 and the amplitudes of the LUMO are
and the amplitudes of the LUMO are 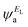 and
and 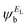 , then if the contributions from all other orbitals are ignored, a crude approximation to the Green's function gba(E) can be given by
, then if the contributions from all other orbitals are ignored, a crude approximation to the Green's function gba(E) can be given by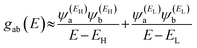
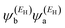 has the same sign as the LUMO product
has the same sign as the LUMO product 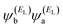 , then the right-hand side of eqn (2) will vanish at some energy E in the range EH ⩽ E ⩽ EL; that is, for some energy E within the HOMO–LUMO gap. In this case, one can say that the HOMO and the LUMO interfere destructively. On the other hand, if the HOMO and LUMO products have the opposite signs, then the right-hand side of eqn (2) will not vanish within the HOMO–LUMO gap and one can say that the HOMO and LUMO interfere constructively within the gap (they could have course interfere destructively at some other energy E outside the gap). When the right-hand side of eqn (2) vanishes, the main contribution to gba(E) comes from all the other orbitals, so in general eqn (2) could be a poor approximation. One exception to this occurs when the lattice is bipartite, because the Coulson–Rushbrooke (CR) theorem65 tells us that if a and b are both even or both odd, then the orbital products on the opposite sides of eqn (3) and (4) have the same sign. Consequently, when the HOMO and LUMO interfere destructively, all the other pairs of orbitals interfere destructively too, leading to the trivial zeros in the magic number table,64 for which gba(0) = 0.
, then the right-hand side of eqn (2) will vanish at some energy E in the range EH ⩽ E ⩽ EL; that is, for some energy E within the HOMO–LUMO gap. In this case, one can say that the HOMO and the LUMO interfere destructively. On the other hand, if the HOMO and LUMO products have the opposite signs, then the right-hand side of eqn (2) will not vanish within the HOMO–LUMO gap and one can say that the HOMO and LUMO interfere constructively within the gap (they could have course interfere destructively at some other energy E outside the gap). When the right-hand side of eqn (2) vanishes, the main contribution to gba(E) comes from all the other orbitals, so in general eqn (2) could be a poor approximation. One exception to this occurs when the lattice is bipartite, because the Coulson–Rushbrooke (CR) theorem65 tells us that if a and b are both even or both odd, then the orbital products on the opposite sides of eqn (3) and (4) have the same sign. Consequently, when the HOMO and LUMO interfere destructively, all the other pairs of orbitals interfere destructively too, leading to the trivial zeros in the magic number table,64 for which gba(0) = 0.
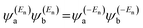
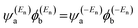
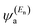 is a vector of amplitudes on even-numbered sites, and
is a vector of amplitudes on even-numbered sites, and 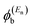 is a vector of amplitudes on odd-numbered sites, ±En are eigenvalues that come in ± pairs, and the eigenstate belonging to −En is related to the eigenstate belonging to En. Obviously, this exact cancellation is a property of bipartite lattices only, but based on its success for bipartite lattices, one might suppose that eqn (2) is a reasonable approximation for other lattices. Nevertheless, as pointed out by Yoshizawa et al.,54,55,59,61 since orbitals such as those in Fig. 1(c) are often available from DFT calculations, it can be helpful to examine the question of whether or not the HOMO and LUMO (or indeed any other pair of orbitals) interfere destructively or constructively, by examining the colours of orbitals. This can be simplified by writing eqn (2) in the form below,
is a vector of amplitudes on odd-numbered sites, ±En are eigenvalues that come in ± pairs, and the eigenstate belonging to −En is related to the eigenstate belonging to En. Obviously, this exact cancellation is a property of bipartite lattices only, but based on its success for bipartite lattices, one might suppose that eqn (2) is a reasonable approximation for other lattices. Nevertheless, as pointed out by Yoshizawa et al.,54,55,59,61 since orbitals such as those in Fig. 1(c) are often available from DFT calculations, it can be helpful to examine the question of whether or not the HOMO and LUMO (or indeed any other pair of orbitals) interfere destructively or constructively, by examining the colours of orbitals. This can be simplified by writing eqn (2) in the form below,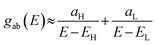
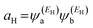 and
and 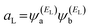 . If the HOMO product aH has the same sign as the LUMO product aL, then the right-hand side of eqn (5) will vanish for some energy E in the range EH ⩽ E ⩽ EL. In other words, the HOMO and LUMO will interfere destructively at some energy within the HOMO–LUMO gap. However, this does not mean that the exact gba(E) will vanish. Indeed, if the right-hand side of eqn (5) vanishes, then the contributions from all other orbitals become the dominant terms.66 Nevertheless, this is an appealing method of identifying QI effects in molecules and describing their qualitative features. Now, based on this analysis, the results in Fig. 1(c) suggest that the transport behaviour is dominated by a constructive quantum interference phenomenon (CQI), since the product of the HOMO and LUMO amplitudes is the same (negative sign), which means that the HOMOs and LUMOs interfered constructively. These results are interpreting the high values of the transmission coefficient T(E) shown in Table 1 and Fig. 2.
. If the HOMO product aH has the same sign as the LUMO product aL, then the right-hand side of eqn (5) will vanish for some energy E in the range EH ⩽ E ⩽ EL. In other words, the HOMO and LUMO will interfere destructively at some energy within the HOMO–LUMO gap. However, this does not mean that the exact gba(E) will vanish. Indeed, if the right-hand side of eqn (5) vanishes, then the contributions from all other orbitals become the dominant terms.66 Nevertheless, this is an appealing method of identifying QI effects in molecules and describing their qualitative features. Now, based on this analysis, the results in Fig. 1(c) suggest that the transport behaviour is dominated by a constructive quantum interference phenomenon (CQI), since the product of the HOMO and LUMO amplitudes is the same (negative sign), which means that the HOMOs and LUMOs interfered constructively. These results are interpreting the high values of the transmission coefficient T(E) shown in Table 1 and Fig. 2.
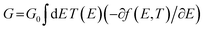

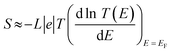
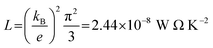 . In other words, S is proportional to the negative of the slope of ln
. In other words, S is proportional to the negative of the slope of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T(E), evaluated at the Fermi energy (0.0 eV). Based on the Seebeck coefficient, the power factor (P) is calculated by:
T(E), evaluated at the Fermi energy (0.0 eV). Based on the Seebeck coefficient, the power factor (P) is calculated by: