Open Access Article
Open Access ArticleCrystal size-dependent framework flexibility of a prototypical metal organic framework is related to metal content: zeolitic imidazolate framework-7†
Akalanka B.
Ekanayake
 ,
Al A.
Tiba
,
Al A.
Tiba
 ,
Leonard R.
MacGillivray
,
Leonard R.
MacGillivray
 and
Alexei V.
Tivanski
and
Alexei V.
Tivanski
 *
*
Department of Chemistry, University of Iowa, Iowa City, IA 52242-1294, USA. E-mail: alexei-tivanski@uiowa.edu
First published on 23rd October 2024
Abstract
Crystal size engineering is an emerging strategy to modulate mechanical and gas adsorption properties of metal–organic frameworks (MOFs). Fundamental principles on how the properties of these materials change with size remain to be understood and explored. Here, supermicron-, micro-, and nano-sized single crystals of a prototypical MOF zeolitic imidazolate framework-7 (ZIF-7) were generated using a solvothermal method. Atomic force microscopy (AFM) imaging revealed that nano- and micro-sized crystals exhibited rounded and prism-like morphologies, respectively. AFM nanoindentation was used to assess the stiffness (Young's modulus) of the rounded and prism-like crystals as a function of crystal size. We demonstrate that the framework flexibility increases (Young's modulus decreases) with crystal size reduction for both morphologies, which can be attributed to a larger number of point defects (missing metal nodes and/or missing linkers) for smaller crystals. Remarkably, scanning electron microscopy (SEM) energy dispersive X-ray spectroscopy measurements on individual prism-like micro-sized crystals of various sizes revealed a decreasing trend in the Zn/C ratio with crystal size reduction. Collectively, the size-dependent SEM and AFM characterization studies suggest that smaller crystals have lower relative metal content via a larger number of missing metal node defects. Our findings highlight how the mechanical properties of MOFs can vary significantly as a function of crystal size likely due to a variable and size-dependent number of missing metal node defects. Such size-dependent behavior especially towards the nanoscale is thus important to consider for the rational design of various functional crystalline materials.
Introduction
Metal–organic frameworks (MOFs) are porous materials generated by facile synthesis methods using a wide range of metal-containing nodes and organic linkers.1 MOFs are now showing great promise for applications in gas storage,2 separation,3 catalysis,4 electronics,5 and sensing,6 but there can be challenges associated with maintaining mechanical integrity when the solids are deployed commercially.7 A unique feature of MOFs is porosity combined with flexibility, which in some cases leads to switchable MOFs, where the frameworks can switch (transform) when exposed to external stimuli (e.g., guest gas pressure and temperature).8,9 Switchable MOFs offer improved gas storage and gas separation characteristics, and currently there is a growing number of applications that utilize such solids for targeted drug delivery and stimuli responsive catalysis applications.2–4,10 The solid–solid phase transition in switchable MOFs can involve gate opening where once a threshold gate opening pressure from a surrounding guest gas molecules is reached, the framework undergoes a solid–solid phase transformation. The transformation involves the linker molecules rearranging in a way to increase porosity while maintaining crystallinity to facilitate gas storage and separation characteristics of switchable MOFs.11Crystal downsizing of MOFs to submicrometer or nanoscale dimensions is beneficial for various applications. Submicrometer- or nano-sized MOFs have higher surface areas and more efficient mass transport characteristics, thus offering improved properties for catalysis.12 Nano-sized switchable MOFs with controlled morphologies and sizes are critical for controlled drug delivery owing to enhanced cellular uptake, uniform drug distribution, and precise, stimuli-responsive release profiles.13,14 A significant number of as-synthesized switchable MOFs are already in the submicrometer- or nano-size range.15 However, previously reported gas adsorption studies of various switchable MOFs at different sizes showed a significant change in gate opening pressure or even complete suppression of gate opening once crystal dimensions are reduced below a certain critical size (typically in the submicrometer size range).13,16,17 While the exact origin of such size-dependent behavior is not known, it is generally assumed to be related to the change in the degree of cooperativity between neighbouring unit cells of a framework, which may change due to a varying number of point defects (e.g., missing linkers or metal nodes) as the crystal size decreases towards the nanoscale.13,18,19 Mechanical studies on various MOFs also show that framework flexibility can change as a result of crystal downsizing to the nanoscale, where the effect was also attributed to changes in the relative number of defects (e.g., missing linkers), where crystals with a larger number of defects are expected to correspond to more disorder and, thus, softer frameworks.20–24 It is worth noting that studies also demonstrate that missing metal node defects can affect the properties of MOFs, such as catalytic activity.19
Recently, we reported how the synthesis of ZIF-8 submicrometer-sized crystals using a modulator (i.e., triethylamine) resulted in a larger number of missing linker defects and a more flexible framework relative to ZIF-8 crystals of similar size generated without the modulator.23 Furthermore, it was observed that crystals with a higher relative number of point defects also exhibited a downward shift in gate opening pressure.23 Thus, defect and size engineering of a switchable MOF can modify mechanical properties and degree of cooperativity between neighbouring unit cells, and in some cases even lead to significant changes or even complete suppression of switchable behavior. Therefore, studies to develop a better understanding of the effects of size reduction of switchable MOFs towards the nanoscale are needed to facilitate the development of submicrometer- and nano-sized switchable MOFs for various applications.
A fundamental understanding of size-dependent effects on the properties of MOFs across various dimensions (e.g., the macroscale, supermicron, submicrometer, and nanoscale) is lacking.25 In this regard, while atomic force microscopy (AFM) nanoindentation can be uniquely employed to directly measure stiffness (Young's modulus) of individual crystals of various sizes, it would be advantageous to identify a method that complements AFM work and provide insight into the compositional origin of flexibilities of MOF materials.24,26–28 Herein, we report the size-dependent mechanical properties of zeolitic imidazolate framework-7 (ZIF-7). ZIF-7 was selected for several reasons. First, reports show successful facile synthesis of ZIF-7 crystals at various morphologies and sizes with high chemical and thermal stability.29,30 Second, ZIF-7 is a switchable MOF with size-dependent gas adsorption characteristics, where previous studies show that the gate opening pressure decreases as the ZIF-7 crystal size decreases towards the nanoscale from the microscale.31–33 In our current study, we show that size reduction of ZIF-7 crystals from the supermicron to nanoscale results in a significant decrease in Young's modulus. While the reduction in Young's modulus is consistent with an increase in the number of defects at the nanoscale, we now reveal using size-dependent scanning electron microscopy (SEM) and energy dispersive X-ray spectroscopy (EDX) single-crystal data that the reduction in mechanical properties is related to relative metal content as crystal size decreases. The data, thus, imply that the changes in mechanical properties can be attributed to the varying number of missing metal nodes. Our use of AFM, SEM, and EDX to identify the type of point defect illustrates the importance of implementing combined techniques to gain insight into behaviours of MOF materials and underscores the importance of understanding size-dependent mechanical properties and links to a varying number of defects in MOFs and gas adsorption properties.
Experimental methods
Materials and synthetic procedures
Benzimidazole and Zn(NO3)2·4H2O were purchased from Acros Organics and Sigma Aldrich, respectively, and used without further purification. ZIF-7 was synthesized solvothermally in dimethylformamide as described previously.29 Briefly, 0.04 M Zn(NO3)2·4H2O and 0.03 M benzimidazole in dimethylformamide (DMF) solutions were prepared and continuously heated at 130 °C for 48 h, followed by cooling to room temperature (∼25 °C). Next, the supernatant was removed, and the resulting solid was washed with chloroform, yielding colourless ZIF-7 crystals, followed by washing with DMF and drying in air.29Powder X-ray diffraction (PXRD) measurements
PXRD data were obtained on a Bruker D500 X-ray diffractometer using Cu Kα1 radiation (λ = 1.54056 Å) (scan type: locked coupled; scan mode: continuous; step size: 0.02°; scan time: 2 s per step). The samples were mounted on glass slides.Atomic force microscopy (AFM) single crystal imaging and nanoindentation measurements
Powdered ZIF-7 crystals were suspended in methanol, HPLC-grade (ca. 10 mg in 10 mL), then drop-cast on a freshly cleaved atomically flat mica substrate (V-1 grade, SPI Supplies, Westchester, PA), and solvent was allowed to evaporate. All AFM studies were conducted using a Molecular Force Probe 3D AFM (Asylum Research, Santa Barbara, CA). AFM images and nanoindentation measurements were performed at room temperature (∼25 °C) and ambient pressure using Si3N4 probes with a hard diamond-like-carbon coating (Mikromasch, San Jose, CA) with a nominal spring constant range of 2–5.4 N m−1 and a tip radius of curvature of 15 nm. Actual spring constants were determined using a built-in thermal noise method.34 Topographic images (height and amplitude) were collected in an intermittent contact mode (AC mode) at a typical scan rate of 1 Hz.AFM nanoindentation experiments were performed by first recording force versus vertical piezo displacement curves (i.e., force curves) of individual substrate-deposited ZIF-7 crystals. The acquisition of force curves and corresponding data analysis was carried out as reported previously.23,24,26,27,35 The force curves were then converted into force versus indentation distance data and then the approach to crystal surface data were fit to the Johnson–Kendall–Roberts (JKR) contact model to determine Young's modulus of the crystal.23,24,26,27 The JKR model was selected due to several reasons. First, the indentation distances were limited to 5 nm (∼3 times less than the tip radius of curvature) and measurements were performed on a relatively flat crystal surface, where the typical area-equivalent diameter of the contact region between the AFM tip and the crystal surface at the maximum indentation distance is at least six times larger than the base size of the smallest crystal studied. These experimental conditions allow us to approximate the AFM nanoindentation experiment as a sphere indenting into a semi-infinite flat surface. Second, the force–indentation data in the contact region display close overlap between the approach and retract from the crystal surface data, confirming that purely elastic nanoindentation and force curves show the presence of adhesion forces between the AFM tip and crystal surface. Collectively, these are consistent with the JKR model assumptions, facilitating its application for this study. Furthermore, previous works have successfully applied this approach model to various solids of different sizes to determine Young's modulus of solids. Typically, 4–6 force curves were collected for each individual crystal at a relatively flat crystal surface region. Images of individual crystals were collected before and after force curve measurements to ensure that there are no apparent changes in the crystal surface. Noteworthily, AFM imaging of individual crystals does not provide direct information on which crystallographic plane is being probed via nanoindentation. Thus, force–indentation measurements are performed at multiple locations across the crystal surface and reported average Young's modulus value for each crystal is assumed to represent an average response from likely several different crystallographic planes.
Scanning electron microscopy (SEM) and energy dispersive X-ray spectroscopy (EDX) measurements
SEM images were collected using a Hitachi S-3400N. Powdered ZIF-7 crystals were deposited onto a Si wafer and imaged at 2 keV and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 magnification with a working distance of 5 mm between the sample and electron source. EDX spectra were collected at 20 keV at an approximate center of each individual crystal.
000 magnification with a working distance of 5 mm between the sample and electron source. EDX spectra were collected at 20 keV at an approximate center of each individual crystal.
Results and discussion
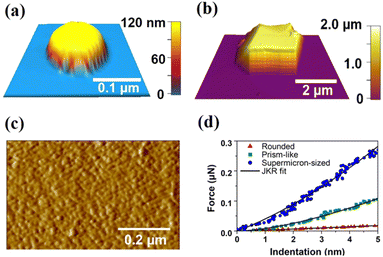
ZIF-7 single crystals were synthesized solvothermally in dimethylformamide following a reported procedure.29 The formation of structurally pure ZIF-7 crystals was confirmed by PXRD measurements, where good agreement was observed between the calculated and experimental patterns (Fig. 1). Additionally, thermogravimetric analysis of the solid (Fig. S1, ESI†) and solution 1H nuclear magnetic resonance measurements (Fig. S2, ESI†) were performed to further confirm the formation of ZIF-7 crystals. AFM imaging of the substrate-deposited ZIF-7 sample revealed the presence of individual ZIF-7 crystals with various morphologies and sizes. The crystal size (base size) was defined as a geometric mean of the length of the longest crystal axis and the width perpendicular to the longest crystal axis, where the length, width, and crystal height were determined from AFM single crystal height images. Nano-sized crystals had rounded morphologies (Fig. 2a) with crystal size ranges of 125–500 nm and crystal heights of 20–300 nm. Micro-sized prism-like crystals (Fig. 2b) were observed with crystal size ranges of 1–7.5 μm and crystal heights of 0.5–4 μm. Supermicron-sized crystals were also present with sizes and heights of tens of micrometres. AFM imaging of the top surface of a typical supermicron-sized crystal revealed a relatively smooth surface (Fig. 2c). Our observations on morphologies and corresponding size ranges are consistent with previous reports.31–33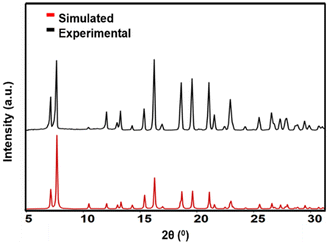 | ||
| Fig. 1 Comparison of ZIF-7 PXRD patterns: simulated pattern from single crystal X-ray diffraction data31 (red) and experimental pattern (black). | ||
AFM nanoindentation experiments were performed by collecting force–indentation curves on multiple individual ZIF-7 crystals of various morphologies and sizes, with representative force–indentation curves for nano-sized rounded, micro-sized prism-like, and supermicron-sized individual crystals being determined (Fig. 2d). Typically, 4–6 repeated force–indentation curves at various positions over a relatively flat region on the crystal surface were recorded per individual rounded nanocrystal (total of 16 crystals) and prism-like micro-sized crystal (total of 16 crystals). For supermicron-sized crystals, 25 repeated force–indentation curves at various positions over a typical crystal surface were collected. Nanoindentation studies on supermicron-sized crystals were performed to compare our AFM based mechanical characterization results with previously published mechanical studies on macro-sized ZIF-7 crystals.7 Each force–indentation curve was fit using the Johnson–Kendall–Roberts elastic contact model36 to determine the average Young's modulus of each crystal following a reported approach.23,24,26,27,35 Young's modulus for a typical supermicron-sized crystal (base size of ∼40 μm and height of ∼20 μm) was determined to be 5.9 ± 1.5 GPa, which closely overlaps with the indenter measurements on macro-sized ZIF-7 crystals reported in the literature (∼6.2 GPa for (101) crystallographic plane),25 confirming applicability of AFM nanoindentation to accurately determine the mechanical properties of individual ZIF-7 crystals.
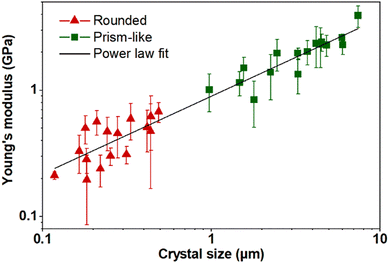
The average Young's moduli of individual crystals vary as a function of corresponding crystal size (log–log axis) for nano-sized rounded (red triangles) and micro-sized prism-like (green squares) crystals (Fig. 3). Young's moduli of both nano- and micro-sized crystals exhibit a clear size-dependent behaviour, where crystals continuously become softer (lower Young's modulus) as the size decreases. In particular, the crystal size reduction (from ∼7.2 μm to ∼110 nm) results in over one order of magnitude decrease in Young's modulus (from 3.9 ± 0.8 GPa to 0.21 ± 0.02 GPa), which implies a remarkable increase in framework flexibility at the nanoscale. Error bars in Fig. 3 represent one standard deviation, calculated from Young's moduli obtained through 4–6 individual force–indentation measurements taken at several different positions on the crystal surface. The dependence of Young's modulus versus crystal size is clearly linear (Fig. 3) in the log–log axis across the entire studied crystal size range; thus, the mechanical data were fit to a power law function (shown as a black solid line in Fig. 3), yielding the following relationship between the size-dependent Young's modulus (E, in GPa) and crystal size (D, in micrometres): E = (0.90 ± 0.07 GPa)D0.61 ± 0.05, with R2 = 0.993. There is no current explanation for the apparent power law dependence and more studies over a wider range of switchable MOFs, which we believe is beyond the scope of the present work, are needed to elucidate if the observed trend is general or uniquely specific to ZIF-7. Noteworthily, the size-dependent Young's modulus variability appears to be similar for both rounded and prism-like morphologies, suggesting that the size-dependent response is largely governed by size rather than the morphological differences. While the exact origin of such a size-dependent mechanical behavior of ZIF-7 crystals is unknown, we hypothesize that it is likely due to a size-dependent number of defects, as will be discussed below.
The observed size-dependent Young's modulus response is consistent with our previous studies where we reported a similar phenomenon with ZIF-8, and crystal downsizing to the nanoscale (from ca. 100 μm to ca. 100 nm) results in smaller yet significant ∼40% reduction in Young's modulus.24 Furthermore, Tan et al. have also studied size-dependent behaviour in a related MOF system (ZIF-8), where it was shown that smaller nanocrystals formed during the early stages of MOF crystallization appear to have larger concentration of defects relative to larger crystals, similar to our observations described in the present study.21 However, we note that other works reported that smaller crystals were found to be stiffer (less flexible) and thus likely contain fewer defects, thus more studies on other MOFs are needed to gain a better understanding of the factors that control such size-dependent behaviour (e.g., assessing the influence of different metals, organic linkers, and crystal structures).37,38
Previously reported CO2 gas adsorption studies at 0 °C on rounded nano- (sizes of ∼100–200 nm) and prism-like micro- (sizes of ∼2–10 μm) ZIF-7 crystals showed ‘S-shaped’ type IV isotherms, confirming that the gate opening transitions occur at each size range.31,32 However, there were significant differences in the shape of the isotherm and gate opening pressure between these samples. Specifically, the gate opening pressure was found to decrease as crystal sizes decreased from micro- to nano-sized crystals. Additionally, the gas adsorption isotherm showed steeper and stepwise characteristics for micro-sized prism-like crystals relative to more gradual and cooperative gate-opening structural expansion for nano-sized rounded crystals.31–33 These size-dependent gas adsorption differences in similar morphologies and size-ranges of ZIF-7 crystals can be rationalized with the size-dependent mechanical properties determined here. In particular, the lower gate opening pressure for nano- versus micro-sized crystals is consistent with the lower Young's modulus at the nanoscale, which implies reduced resistance of the framework to adsorptive stress caused by rotation of organic linkers during the gate opening transition.24 Furthermore, the extent of cooperative transformations in the framework is likely lower for more flexible nanocrystals with likely a larger number of defects (e.g., missing metal nodes), which can explain more gradual gas adsorption uptake during gate-opening transition observed at the nanoscale.
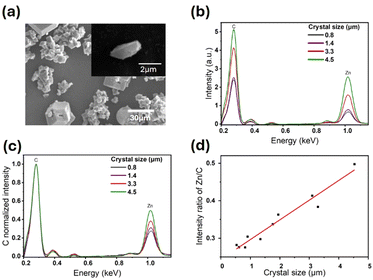
To test if the relative number of defects in ZIF-7 crystals changes as a function of crystal size, single crystal SEM and EDX measurements were performed (Fig. 4). A typical SEM image of prism-like ZIF-7 crystals showed morphologies consistent with the AFM data (Fig. 4a). EDX spectra were collected for 10 different prism-like individual crystals with sizes ranging from ∼0.8 to 4.5 μm. EDX spectra for four selected crystals of various sizes showed a clear decrease in intensities of both the carbon K edge (at 0.27 keV) and the zinc L edge (at 1.02 keV) with crystal size reduction (Fig. 4b). Since the zinc L edge signal is assumed to be directly proportional to the number of metal nodes in the framework, while the carbon K edge signal is reflective of the number of organic linkers, the ratio of Zn to C (i.e., C normalized) is indicative of the relative number of metal nodes to organic linkers. Carbon normalized EDX spectra for the same four selected crystals (Fig. 4c) show that as the crystal size decreases, the zinc L edge signal normalized to C clearly decreases, indicating a lower Zn/C ratio in smaller crystals, which is confirmed for all studied crystals (Fig. 4d). The reduction in the Zn/C ratio with crystal downsizing can be attributed to either a relative decrease in the number of metal nodes (i.e., lower relative zinc L edge signal) or an increase in the relative number of organic linkers (i.e., larger carbon K edge signal). While SEM data alone cannot differentiate between these two possibilities, we note that a possible increase in the relative number of organic linkers with crystal downsizing would correspond to a lower relative number of point defects and, thus, would be expected to yield a more rigid framework (higher Young's modulus) for smaller crystals13 – contrary to the size-dependent mechanical trends that we observe. Therefore, the reduction in the Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio and increase in the framework flexibility at the nanoscale can be attributed to an increase in the relative number of missing metal nodes as the crystal size decreases. Our findings further suggest that Young's modulus measured for individual MOFs could potentially be used to evaluate the relative number of defects in isostructural crystals of varying sizes.
C ratio and increase in the framework flexibility at the nanoscale can be attributed to an increase in the relative number of missing metal nodes as the crystal size decreases. Our findings further suggest that Young's modulus measured for individual MOFs could potentially be used to evaluate the relative number of defects in isostructural crystals of varying sizes.
Conclusions
In summary, we report for the first time how the mechanical properties of individual ZIF-7 crystals vary as a function of crystal size ranging from ∼7.2 μm to 110 nm. The power law dependence between Young's modulus and corresponding crystal size was observed with over one order of magnitude reduction in the crystal stiffness as the crystal size decreases, implying that the framework flexibility dramatically increases at the nanoscale. Single crystal SEM and EDX measurements of ZIF-7 crystals of various sizes revealed a reduction in the Zn/C ratio as the crystal size decreases, which is attributed to an increasing relative number of missing metal node defects. Our studies suggest that measurements of Young's modulus of individual MOFs can be potentially used to assess the relative number of defects in isostructural crystals of different sizes. Future studies can be aimed to expand and probe other types of switchable MOFs to gain further insights into factors that control size-dependent mechanical and gas adsorption properties. Ultimately, such knowledge is expected to facilitate the development of size-specific switchable MOFs with desired functional and mechanical properties for various applications.Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Data availability
All the raw files of the data presented in this manuscript that support the findings of this present work are available from the corresponding author upon request. Please contact the corresponding author via the following e-mail: alexei-tivanski@uiowa.edu.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the National Science Foundation (NSF DMR-2221086) and University of Iowa for financial support.References
- N. Stock and S. Biswas, Chem. Rev., 2012, 112, 933–969 CrossRef CAS PubMed.
- H. Li, L. Li, R.-B. Lin, W. Zhou, Z. Zhang, S. Xiang and B. Chen, EnergyChem, 2019, 1, 100006 CrossRef PubMed.
- T. Rodenas, I. Luz, G. Prieto, B. Seoane, H. Miro, A. Corma, F. Kapteijn, F. X. Llabrés i Xamena and J. Gascon, Nat. Mater., 2015, 14, 48–55 CrossRef CAS PubMed.
- D. D. Díaz, D. Kühbeck and R. J. Koopmans, Chem. Soc. Rev., 2011, 40, 427–448 RSC.
- V. Stavila, A. A. Talin and M. D. Allendorf, Chem. Soc. Rev., 2014, 43, 5994–6010 RSC.
- P. Kumar, A. Deep and K.-H. Kim, TrAC, Trends Anal. Chem., 2015, 73, 39–53 CrossRef CAS.
- J. C. Tan, T. D. Bennett and A. K. Cheetham, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9938–9943 CrossRef CAS PubMed.
- G. Ferey and C. Serre, Chem. Soc. Rev., 2009, 38, 1380–1399 RSC.
- C. Triguero, F.-X. Coudert, A. Boutin, A. H. Fuchs and A. V. Neimark, J. Phys. Chem. Lett., 2011, 2, 2033–2037 CrossRef CAS.
- W. Cai, J. Wang, C. Chu, W. Chen, C. Wu and G. Liu, Adv. Sci., 2019, 6, 1801526 CrossRef PubMed.
- C. Cuadrado-Collados, J. Fernández-Català, F. Fauth, Y. Q. Cheng, L. L. Daemen, A. J. Ramirez-Cuesta and J. Silvestre-Albero, J. Mater. Chem. A, 2017, 5, 20938–20946 RSC.
- A. Herbst, A. Khutia and C. Janiak, Inorg. Chem., 2014, 53, 7319–7333 CrossRef CAS PubMed.
- S. Ehrling, H. Miura, I. Senkovska and S. Kaskel, Trends Chem., 2021, 3, 291–304 CrossRef CAS.
- P. Horcajada, C. Serre, M. Vallet-Regí, M. Sebban, F. Taulelle and G. Férey, Angew. Chem., Int. Ed., 2006, 45, 5974–5978 CrossRef CAS PubMed.
- X. Cai, Z. Xie, D. Li, M. Kassymova, S.-Q. Zang and H.-L. Jiang, Coord. Chem. Rev., 2020, 417, 213366 CrossRef CAS.
- T. Omiya, K. Sasaki, Y. Uchida and N. Nishiyama, ACS Appl. Nano Mater., 2018, 1, 3779–3784 CrossRef CAS.
- S. Krause, V. Bon, I. Senkovska, D. M. Többens, D. Wallacher, R. S. Pillai, G. Maurin and S. Kaskel, Nat. Commun., 2018, 9, 1–8 CrossRef CAS PubMed.
- A. Bratkovsky, E. Salje, S. Marais and V. Heine, Phase Transitions, 1995, 55, 79–126 CrossRef CAS.
- S. Dissegna, P. Vervoorts, C. L. Hobday, T. Duren, D. Daisenberger, A. J. Smith, R. A. Fischer and G. Kieslich, J. Am. Chem. Soc., 2018, 140, 11581–11584 CrossRef CAS PubMed.
- A. K. Cheetham, T. D. Bennett, F.-X. Coudert and A. L. Goodwin, Dalton Trans., 2016, 45, 4113–4126 RSC.
- A. F. Moslein, L. Dona, B. Civalleri and J.-C. Tan, ACS Appl. Nano Mater., 2022, 5, 6398–6409 CrossRef CAS PubMed.
- T. D. Bennett, A. K. Cheetham, A. H. Fuchs and F.-X. Coudert, Nat. Chem., 2017, 9, 11–16 CrossRef CAS PubMed.
- A. A. Tiba, J. A. Perman, L. R. MacGillivray and A. V. Tivanski, J. Mater. Chem. A, 2022, 10, 21053–21060 RSC.
- A. A. Tiba, A. V. Tivanski and L. R. MacGillivray, Nano Lett., 2019, 19, 6140–6143 CrossRef CAS PubMed.
- J. C. Tan and A. K. Cheetham, Chem. Soc. Rev., 2011, 40, 1059–1080 RSC.
- C. Karunatilaka, D.-K. Bučar, L. R. Ditzler, T. Friščić, D. C. Swenson, L. R. MacGillivray and A. V. Tivanski, Angew. Chem., Int. Ed., 2011, 50, 8642–8646 CrossRef CAS PubMed.
- T. P. Rupasinghe, K. M. Hutchins, B. S. Bandaranayake, S. Ghorai, C. Karunatilake, D.-K. Bucar, D. C. Swenson, M. A. Arnold, L. R. MacGillivray and A. V. Tivanski, J. Am. Chem. Soc., 2015, 137, 12768–12771 CrossRef CAS PubMed.
- K. M. Hutchins, T. P. Rupasinghe, S. M. Oburn, K. K. Ray, A. V. Tivanski and L. R. MacGillivray, CrystEngComm, 2019, 21, 2049–2052 RSC.
- K. S. Park, Z. Ni, A. P. Côté, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O’Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10191 CrossRef CAS PubMed.
- T. Xiao and D. Liu, Mater. Today Energy, 2019, 14 Search PubMed.
- W. Cai, T. Lee, M. Lee, W. Cho, D. Y. Han, N. Choi, A. C. Yip and J. Choi, J. Am. Chem. Soc., 2014, 136, 7961–7971 CrossRef CAS PubMed.
- X. Wu, M. Niknam Shahrak, B. Yuan and S. Deng, Microporous Mesoporous Mater., 2014, 190, 189–196 CrossRef CAS.
- A. Arami-Niya, G. Birkett, Z. Zhu and T. E. Rufford, J. Mater. Chem. A, 2017, 5, 21389–21399 RSC.
- J. L. Hutter and J. Bechhoefer, Rev. Sci. Instrum., 1993, 64, 1868–1873 CrossRef CAS.
- T. I. Lansakara, F. Tong, C. J. Bardeen and A. V. Tivanski, Nano Lett., 2020, 20, 6744–6749 CrossRef CAS PubMed.
- K. L. Johnson, K. Kendall and A. Roberts, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313 CAS.
- Y. Xing, L. Luo, Y. Li, D. Wang, D. Hu, T. Li and H. Zhang, J. Am. Chem. Soc., 2022, 144, 4393–4402 CrossRef CAS PubMed.
- A. A. Tiba, M. T. Conway, C. S. Hill, D. C. Swenson, L. R. MacGillivray and A. V. Tivanski, Chem. Commun., 2021, 57, 89–92 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00804a |
| This journal is © The Royal Society of Chemistry 2024 |