Open Access Article
Open Access ArticleFerroelectric-enabled significant carbon dioxide molecular adsorption on BaTiO3(001)†
Alexandru-Cristi
Iancu
ab,
George A.
Lungu
 a,
Cristian A.
Tache
a and
Cristian M.
Teodorescu
a,
Cristian A.
Tache
a and
Cristian M.
Teodorescu
 *a
*a
aNational Institute of Materials Physics, Atomiştilor 405A, 077125 Măgurele, Ilfov, Romania. E-mail: teodorescu@infim.ro
bUniversity of Bucharest, Faculty of Physics, Atomiştilor 405, 077125 Măgurele, Ilfov, Romania
First published on 17th October 2024
Abstract
Carbon dioxide (CO2) is reversibly adsorbed and desorbed from ferroelectric (001) oriented, BaO-terminated barium titanate, as revealed in real time by high resolution and ultrafast photoelectron spectroscopy and certified by low energy electron diffraction. Desorption proceeds when the substrate is heated above its Curie temperature. The amount of CO2 adsorbed is derived to be between one molecule for a surface BaO unit cell (adsorption below room temperature) and one molecule for two unit cells (adsorption above room temperature). The molecule is bound with its carbon to surface oxygen, forming a CO3 structure. The BaTiO3(001) surface is unaffected by repeated cycles of adsorption–desorption. The relatively high amount of CO2 adsorbed and the stability of the substrate after repeated adsorption and desorption processes promotes barium titanate as a promising candidate for decarbonization technologies.
1. Introduction
Decarbonization is clearly an emergency nowadays. Several strategies for direct air capture (DAC) have been constantly proposed,1–3 including aqueous hydroxide sorbents, alkali carbonates, organic–inorganic hybrid sorbents (supported amines and metal–organic-frameworks), gas separation membranes, pressure swing absorption, etc. Despite the fact that ferroelectric materials have been acknowledged for almost two decades as valuable catalysts and photocatalysts,4–7 until recently these materials were not considered systematically for the removal of carbon containing molecules from the atmosphere. Starting with a pioneering work in 1994,8 the interest in using cheap and widely available ferroelectric barium titanate (BaTiO3, BTO in the following) has grown progressively over recent years.9–12 Despite the fact that pure BTO initially showed a low adsorption capacity,9 subsequent studies highlighted its remarkable sorption capacity in the form of nanopowder.10–12 However, to date, quite few surface science studies have been reported on these systems. One possible reason might stem from the difficulty in preparing and maintaining atomically clean surfaces (with no carbon contamination and exhibiting a well-defined crystalline structure, as revealed, for instance, by low energy electron diffraction LEED) before testing different adsorption processes.Once clean surfaces and the controlled dosing setup are available, X-ray photoelectron spectroscopy (XPS), possibly by using soft X-rays generated by synchrotron radiation, is the ideal tool to study such a system. This method is sensitive to tiny quantities of adsorbates (in the range of a few percent of an atomic layer), to reveal their chemical states (charge state, chemical bonds formed) and also to quantify band bending at the surface of ferroelectric materials, then to assess the orientation of the out-of-plane polarization.13–22
It is not surprising that polar molecules are adsorbed on a ferroelectric substrate.15,23–26 The electric field emerging from the surface of a ferroelectric material interacts strongly with the dipole moment of the adsorbate, attracting it to the surface, where chemical bonds are then formed. The first experiments on clean ferroelectric surfaces were performed by testing the adsorption of carbon monoxide (CO) on atomically clean lead zirconate titanate (PZT) with (001) orientation,17 then associating to this surface negatively charged gold nanoparticles.21 The main result was that about half a monolayer (defined in terms of carbon atoms on a surface unit cell) was adsorbed and that most of the CO molecules are dissociated. This was explained later by computing that in the presence of the electric field provided by the ferroelectric substrate, the interaction is strong enough to lead to the dissociation even of a tightly bonded molecule.22 The drawback of such a material with strong polarization is mainly its instability for repeated cycles of adsorption–desorption, since the reduced carbon fixed on the surface is eliminated in the form of CO2, by depleting the oxygen content of the material. In contrast, a ferroelectric with lower polarization, such as BTO(001), may be used for reversible molecular adsorption and desorption of CO22 or ethylene,23 although the former molecule has quite a low initial dipole moment (0.1 D) while the latter has no dipole moment at all. The key process enabling adsorption processes in these experiments is the polarizability of the molecule: when approaching the ferroelectric surface, the electric field of the ferroelectric material polarizes the molecule, and at the end it is attracted and fixed on the surface. Since in this case the interaction energy is quadratic in the electric field, it will also be quadratic in the value of the polarization. Thus, BTO which has a polarization about 4–5 times lower than PZT will develop an interaction energy with the molecule about 20 times lower. As demonstrated in ref. 21 and 22, this interaction energy suffices to fix the molecules on the surface without breaking them. Molecules are desorbed when the substrate is heated above its Curie temperature (120 °C for bulk BTO,27 experimentally around 150–160 °C for a very thin film). And, a very important aspect, the substrate is fully recovered after desorption.
Taking into account the interest in carbon dioxide removal from the atmosphere, the next step, which will be presented in this work, is to apply the same procedure as in ref. 21 and 22 by studying adsorption and desorption of CO2 on BTO(001). Clean surfaces and surfaces after adsorption are characterized by high resolution surface-sensitive XPS using synchrotron radiation, while the crystallinity of the surface is checked by LEED. Desorption processes are followed-up by ultrafast XPS while the substrate temperature is increased progressively. The amount of adsorbate and possibly its adsorption geometry will be derived, the essential role of ferroelectricity in enabling adsorption will also be demonstrated, and the substrate stability upon repeated cycles of adsorption/desorption will be assessed.
2. Experimental
The experiments were performed in the CoSMoS (combined spectroscopy and microscopy on surfaces) end station connected to the SuperESCA beamline at the Elettra (Trieste) synchrotron radiation facility. Most experimental details can be found in ref. 21 and 22. Briefly, for analysis: operating pressure low 10−10 to high 10−11 hPa. Electron energy analyzer: Specs Phoibos 150, acceptance angle ±7°, pass energies 5 eV for C 1s and Ba 4d, measured with 390 eV photon energy, and 10 eV for survey spectra, Ti 2p and O 1s, measured with 650 eV photon energy. Photoelectron take-off angle: 24°, angle between the direction of incoming X-rays and the detected photoelectrons: 90°. Beamline characteristics: resolving power 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, horizontal linearly polarized X-rays, spot size 10 × 100 μm2. The photon energy was calibrated by using a clean Pt(001) crystal28 and recording the Fermi level in exactly the same conditions as for BTO(001). LEED was performed by using a Specs ErLEED 150 with spot size 1.7 mm.29
000, horizontal linearly polarized X-rays, spot size 10 × 100 μm2. The photon energy was calibrated by using a clean Pt(001) crystal28 and recording the Fermi level in exactly the same conditions as for BTO(001). LEED was performed by using a Specs ErLEED 150 with spot size 1.7 mm.29
Sample preparation: BTO(001) thin films are grown by pulsed laser deposition (PLD) on 0.5% Nb-doped SrTiO3(001) (STON) in a setup manufactured by Surface (base pressure 1 × 10−6 hPa), using a KrF laser (248 nm) with a repetition rate of 5 Hz and fluence of 1.5 J cm−2, at 700 °C and partial O2 pressure of 14 Pa. Prior to the deposition, the STON substrate (miscut < 0.3°) was cleaned in hydrofluoric acid buffer solution (NH4–HF) for 15 s, rinsed in deionized water and then annealed in air at 1000 °C for 2 h. This procedure allows the formation of one monolayer step (3.905 Å) terraces with widths of a few hundreds of nm wide.30 After deposition, the sample was cooled down in a rich O2 atmosphere, 0.1 MPa, at a rate of 10 °C min−1. X-ray diffraction revealed a tetragonal crystal structure of BTO(001) with lattice parameters a = 3.905 Å (in plane) and c = 4.121 Å (out-of-plane), see ref. 21. The BTO(001) film thickness, derived by X-ray reflectivity: 12.5 nm. Such samples feature out-of-plane polarization oriented outwards.19 The BTO(001) used in this study was the same as in ref. 21 and 22. Sample cleaning prior to XPS, LEED and adsorption/desorption experiments: heating at 1150 K for 2000 s at an oxygen pressure of 5 × 10−7 hPa, then cooling down in oxygen at 2 × 10−6 hPa. The reason for choosing such a low thickness of BTO(001) was to be sure that the sample exhibits a single domain structure, a phenomenon which occurs quite often in ultrathin ferroelectric films (with thicknesses below 20 nm) and whose origin is the ‘self-doping’ mechanism in order to provide charge carriers for compensating the depolarization field.31 Interfaces or layers of ionized impurities can also play a role in setting up these charge layers.19 In view of a recent theory which proposed a microscopic model for ferroelectricity, these charged layers play the role of ‘stabilization’ of the ferroelectric state in a thin film with uniform polarization.32,33
After cleaning, the samples were characterized by high resolution XPS, then CO2 was dosed (3.4 kL, i.e. 5 × 10−6 hPa during 15 min), again characterization by XPS, then the sample was warmed up at a rate of about 2 °C min−1, with follow-up of C 1s and Ba 4d core level evolution using 390 eV photon energy, or of Ti 2p and O 1s using 650 eV photon energy. After CO2 desorption, the sample was cooled down and again high resolution core level XPS was performed. This procedure was repeated four times, with two CO2 dosings at low temperatures (−191 °C and −46 °C) and two at high temperatures (44 °C and 45 °C). After the last CO2 desorption experiment, the BTO(001) was again dosed with CO2 at room temperature and lower pressure (1.5 × 10−8 hPa) with follow-up of Ba 4d and C 1s core levels (390 eV photon energy). The result was that after about 1 L CO2 dosing, the C 1s signal was already stabilized to its maximum value. Hence, the dose used before (3.4 kL) was largely sufficient to saturate the sample. This last CO2 dosed sample was transferred in another chamber to perform LEED, then it was warmed up following the same procedure as during the fast XPS analysis, and LEED was performed again. The cleanliness of the sample was confirmed afterwards.
3. Results and discussions
3.1. Low energy electron diffraction (LEED)
Fig. 1 shows the LEED patterns obtained at two energies on clean BTO(001) and after dosing 22.5 L CO2 at RT. For the energy of EK = 108.2 eV used, the out-of-plane condition29,34 is satisfied with respect to terraces whose height is c/2, i.e. half of the out-of-plane lattice constant (c = 4.112 Å21), as follows. The LEED pattern obtained at 108.2 eV is of similar intensity as the one obtained at 74.4 eV, where the phase shift has no special value. This suggests a dominant surface termination, BaO or TiO2. Later on, we will argue based on XPS data that the surface termination is BaO. However, the above considerations have to be taken with great care, since the high background and the broad spots of the observed LEED pattern suggest a high degree of structural disorder of the first monolayer. As a comparison, for a cleaved 0.7 at% Nb-doped SrTiO3(001) sample, the LEED spots obtained at a similar electron energy (100 eV) were thinner (about 70 ± 15% from the spots observed in Fig. 1).35 (1 × 1) LEED patterns were observed for the above case although atomically-resolved noncontact atomic force microscopy and scanning tunneling microscopy revealed the formation of SrO and TiO2 terminated domains whose lateral sizes are on the order of 10–100 μm, with Sr vacancies for the former domains and Sr adatoms for the latter.36 Thus, the LEED technique alone cannot grant a full characterization of the surface crystallinity and/or uniform termination. Rather, it is an indication that the surface is close to a crystalline case rather than to a completely disordered case.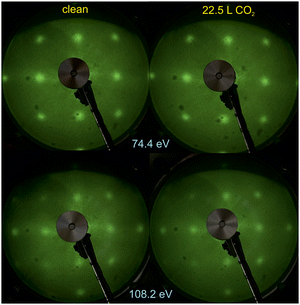 | ||
| Fig. 1 Low energy electron diffraction (LEED) images on clean BaTiO3(001) and after CO2 dosing (22.5 L). The electron energies are indicated on the figure. | ||
There was no sizable modification in the broad LEED pattern observed, nor in the relatively high background, after CO2 dosing. This is a first sign that the substrate structure is not strongly affected by CO2 adsorption. It might also be a sign that the first layers below the surface monolayer are responsible for the observed LEED pattern (also for the sample before dosing), while CO2 adsorption is expected to affect mostly the first monolayer.
3.2. High resolution photoelectron spectroscopy
In the ESI† we present survey spectra (Fig. S1, ESI†), a region of the summed survey spectra to estimate contaminants (Fig. S2, ESI†) and valence band spectra (Fig. S3, ESI†). The survey spectra do not feature noticeable differences between clean and CO2 dosed surfaces. We report from the survey spectra a small Ca contamination, estimated to a maximum Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba ratio as 5.6 ± 0.4% (Fig. S2, ESI†). In the following, we will consider that this Ba>0.95Ca<0.05TiO3(001) sample still has the ferroelectric properties close to ‘normal’ barium titanate. The C 1s signal is barely visible after CO2 dosing, due to its small cross section at 650 eV photon energy.37 The valence band maximum is derived by a linear fit of the main structure from the valence band, and the intercept with the x axis yields the valence band offset 2.46 ± 0.12 eV below the Fermi level. A contribution to this energy difference is assessed to the downwards band bending of the ferroelectric BTO(001),17 which is about 0.4–0.5 eV.21 Hence, in the bulk (away from the region affected by surface band bending) the Fermi level is located at about 2.0–2.1 eV above the valence band maximum (VBM). The bandgap is 3.2 eV, therefore for an intrinsic sample the Fermi level should be at 1.6 eV above the VBM. This suggests that the sample is slightly n doped, and the most probable donor impurities are oxygen vacancies. This should be confirmed later by the compositional analysis, and it was predicted by the ‘self-doping’ mechanism proposed about one decade ago.16 The structure occurring at energies above the VBM are in-gap states, at about 2.0 ± 0.2 eV above the Fermi level. By taking into account the band bending of 0.4 eV (see later), these states are located near the position of the Fermi level for an intrinsic sample.
Ba ratio as 5.6 ± 0.4% (Fig. S2, ESI†). In the following, we will consider that this Ba>0.95Ca<0.05TiO3(001) sample still has the ferroelectric properties close to ‘normal’ barium titanate. The C 1s signal is barely visible after CO2 dosing, due to its small cross section at 650 eV photon energy.37 The valence band maximum is derived by a linear fit of the main structure from the valence band, and the intercept with the x axis yields the valence band offset 2.46 ± 0.12 eV below the Fermi level. A contribution to this energy difference is assessed to the downwards band bending of the ferroelectric BTO(001),17 which is about 0.4–0.5 eV.21 Hence, in the bulk (away from the region affected by surface band bending) the Fermi level is located at about 2.0–2.1 eV above the valence band maximum (VBM). The bandgap is 3.2 eV, therefore for an intrinsic sample the Fermi level should be at 1.6 eV above the VBM. This suggests that the sample is slightly n doped, and the most probable donor impurities are oxygen vacancies. This should be confirmed later by the compositional analysis, and it was predicted by the ‘self-doping’ mechanism proposed about one decade ago.16 The structure occurring at energies above the VBM are in-gap states, at about 2.0 ± 0.2 eV above the Fermi level. By taking into account the band bending of 0.4 eV (see later), these states are located near the position of the Fermi level for an intrinsic sample.
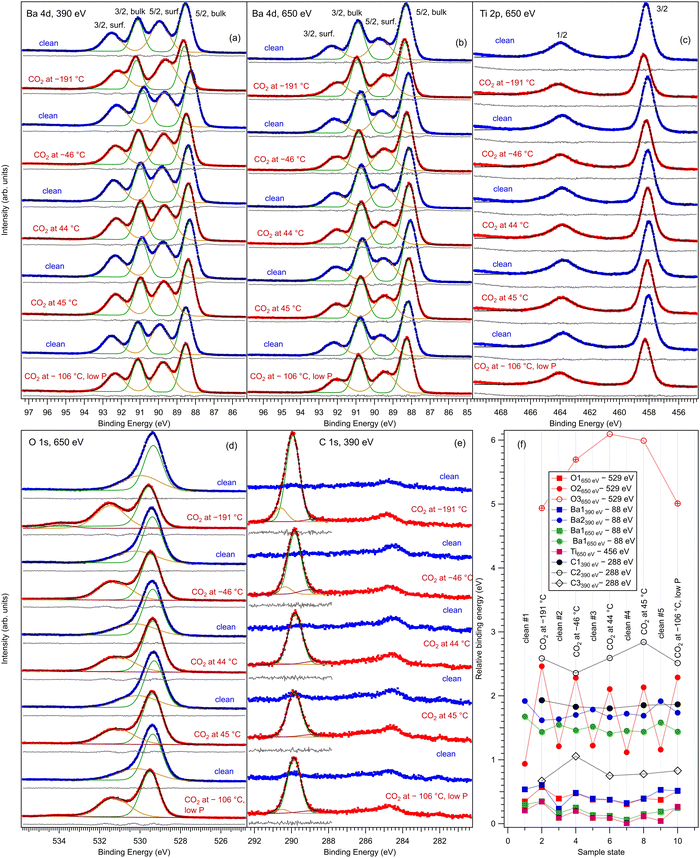
Fig. 2 represents core level spectra with ‘deconvolutions’, for all investigated sample states, in chronological order. Ba 4d spectra are simulated with two Gaussian doublets, since the Lorentzian core level broadening is much lower than the Gaussian experimental resolution.21,22,38 Similarly, the C 1s is simulated with three Gaussian lineshapes, O 1s is simulated with three Voigt lines and Ti 2p with a single Voigt doublet.39 To these lineshapes, integral backgrounds are added for each separate component, thus allowing one to discriminate between the surface and bulk component, since photoelectrons from the surface are not expected to experience inelastic scattering and hence their associated background should be very low.40 As in ref. 21, 22 and 41 the notation of the different chemical states (components) and their attribution are as follows: Ba1 (lower binding energy) represents bulk barium, Ba2 (higher binding energy) represents surface barium from the terminal BaO layer, Ti 2p is fitted with a single component and hence represents bulk titanium, O1 (lower binding energy) represents bulk oxygen, and O2 and O3 with a higher binding energy will be attributed to surface oxygen. The Ba1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba2 ratio increases at 650 eV photon energy with respect to 390 eV, since the kinetic energy and the inelastic mean free path (IMFP) of the electrons increase. Also, the fact that Ba and O feature surface components while Ti does not is a first sign of the BaO termination of the BTO(001).
Ba2 ratio increases at 650 eV photon energy with respect to 390 eV, since the kinetic energy and the inelastic mean free path (IMFP) of the electrons increase. Also, the fact that Ba and O feature surface components while Ti does not is a first sign of the BaO termination of the BTO(001).
The higher binding energy components of the O 1s spectra deserve special attention. In this energy range, quite often the components in question are ascribed to surface hydroxyls.42 However, in the actual case we will attribute this component to surface oxygen from BTO(001). The arguments for this attribution are as follows: (i) from the total pressure in the range of 1 × 10−10 hPa, a maximum of 10% can be attributed to the partial pressure of water in the residual gas. One cannot expect that this water will stick in a significant amount to the surface immediately after having being flashed at temperatures ranging from about 220 °C (in the desorption experiments) to more than 800 °C during the first cleaning procedure in ultrahigh vacuum. Assuming a sticking coefficient of unity, the water dose may be estimated to be at most 3.3 × 10−2 L for about 4400 s, which is the maximum time spent between the cleaning and the first dosing with CO2 (this time was necessary to record XPS spectra for the clean sample). (ii) Immediately after the sample cleaning and while the sample was still hot (160°), the relative amplitude of the high binding component with respect to the main O 1s peak was the same as after about 1200 s with the sample cooled down to about 40 °C by flowing cold nitrogen through the pipes of the manipulator. (iii) As will be discussed in more detail in the following subsection, the O 1s spectra were followed-up by fast XPS during the sample heating after CO2 dosing, and the intensity of the high binding energy peak is stabilized to a constant value which is about one half from its value obtained after CO2 dosing.
For Ba core levels, it is understandable that surface Ba atoms have a higher binding energy, since they are surrounded by a lower amount of oxygen anions whose potential energy should, in principle, increase the electronic levels and yield a decrease in the binding energy with respect to the situation of a free Ba cation. A lower decrease in binding energy is translated into its apparent increase for surface barium. In this hypothesis, the O 1s core levels from surface oxygen should feature an opposite behavior: since these oxygens are surrounded by a lower number of cations, the increase in binding energy due to this surrounding should be lower and therefore the binding energy of surface oxygen should decrease with respect to that of bulk anions. Our attribution that the high binding energy corresponds to surface oxygen contradicts the above mechanism. This puzzle may be solved by supposing that the surface oxygen anions are themselves in a lower negative ionization state, Oδ−, with δ < 2. One reason for this can be attributed to electronic reconstructions necessary to stabilize the (001) surface. In a rough model with Ba2+, Ti4+ and O2− ions, the TiO2 and BaO monolayers are neutral. But the degree of ionicity of Ba–O and Ti–O bonds is not similar, therefore the BTO(001) surface can be framed as being “weakly polar”.43 To avoid a divergence of the total energy due to dipoles formed between BaO and TiO2 layers, one needs to accept ‘electronic reconstruction’, amongst other mechanisms. Atomic reconstructions were not visible by LEED, and extrinsic contributions (e.g. adsorbates) are to be ruled out, in view of the above argumentation. Hence, the surface BaO layer, which should be slightly more negatively charged than a TiO2 layer, will lose some electrons and this electron defect affects mainly the O 1s core levels. A consequence of deviations of the O electronic configuration from 2p6 is also the setting up of a spin polarization of the O 2p related states in the valence band in strontium titanate.41,44 The above considerations were valid by excluding ferroelectricity. The outwards polarization derived for BTO(001) (see ref. 21 and 22 and in the following) implies the formation of ‘static charges’ which should be positive at the outer surface of BTO(001). This positive charging at the surface seems to affect mainly the O 1s levels, but it may also affect in a similar way the Ba 4d levels.
The main fitting parameters are listed in the following, and relevant variations are represented in Tables 1 and 2.
| Preparation | Raw data | Corrected data | ||||
|---|---|---|---|---|---|---|
| O2:Ba2 (O:Basurf) | O1:(Ti + Ba1) O:(Ba+Ti)bulk | Ba1:Ti (Ba:Tibulk) | O:Basurf | O:(Ba+Ti)bulk | Ba:Tibulk | |
| 1 | 1.596 | 0.779 | 1.259 | 1.289 | 1.443 | 0.972 |
| 2 | 1.300 | 0.767 | 1.321 | 0.912 | 1.436 | 1.019 |
| 3 | 1.269 | 0.783 | 1.357 | 0.873 | 1.464 | 1.041 |
| 4 | 1.277 | 0.775 | 1.349 | 0.883 | 1.448 | 1.040 |
| 5 | 1.402 | 0.810 | 1.194 | 1.042 | 1.478 | 0.921 |
| Dosing temperature (°C) | O1:(Ba1 + Ti) (650 eV) | O3:Ba2 (650 eV) | C2:Ba2 (390 eV) | O3:C2 physisorbed | O2:Ba2 (650 eV) | C1:Ba2 (390 eV) | O2:C1 adsorbed |
|---|---|---|---|---|---|---|---|
| −191 | 1.424 | 0.285 | 0.154 | 1.854 | 2.074 | 1.019 | 2.035 |
| −46 | 1.453 | 0.174 | 0.089 | 1.960 | 1.898 | 0.750 | 2.531 |
| 44 | 1.467 | 0.074 | N/R | N/R | 1.444 | 0.592 | 2.440 |
| 45 | 1.461 | 0.065 | N/R | N/R | 1.043 | 0.532 | 1.960 |
| −106 | 1.464 | 0.105 | 0.048 | 2.184 | 1.908 | 0.735 | 2.691 |
(a) Ba 4d, excited with 650 eV photon energy: binding energies (4d5/2) 88.20 ± 0.09 eV and 89.50 ± 0.08 eV, Gaussian full widths at half maximum (FWHMs) 0.81 ± 0.03 eV and 1.26 ± 0.02 eV for components in the order of increasing binding energies, spin–orbit splitting 2.60 ± 0.00 eV and 2.60 ± 0.01 eV for bulk and surface components, respectively, and branching ratios 1.49 ± 0.01 and 1.59 ± 0.01 (surface and bulk).
(b) Ti 2p, excited with 650 eV photon energy: binding energy 458.15 ± 0.11 eV, Lorentzian FWHMs 0.43 ± 0.03 eV and 1.79 ± 0.06 for 2p3/2 and 2p1/2 lines, respectively, Gaussian FWHM 0.74 ± 0.02 eV, spin–orbit splitting 5.75 ± 0.01 eV, branching ratio 1.48 ± 0.03 (see below for more comments).
(c) O 1s, clean sample, excited with 650 eV photon energy: binding energies 529.36 ± 0.03 eV and 530.13 ± 0.12 eV, Lorentzian FWHM 0.02 ± 0.01 eV, Gaussian FWHMs 1.09 ± 0.02 eV and 2.24 ± 0.08 eV for components in order of increasing binding energies.
(d) O 1s, CO2 dosed, excited with 650 eV photon energy: binding energies 529.47 ± 0.08 eV, 531.24 ± 0.14 eV, and 534.55 ± 0.54 eV, Lorentzian FWHM 0.02 ± 0.01 eV, Gaussian FWHMs 1.09 ± 0.03 eV, 1.87 ± 0.12 eV and 1.88 ± 0.51 eV for components in order of increasing binding energies.
(e) Ba 4d, excited with 390 eV photon energy: binding energies (4d5/2) 88.44 ± 0.11 eV and 89.74 ± 0.11 eV, Gaussian FWHMs 0.77 ± 0.04 eV and 1.19 ± 0.06 eV for components in the order of increasing binding energies, spin–orbit splitting 2.60 ± 0.00 eV and 2.60 ± 0.01 eV for bulk and surface components, respectively, branching ratios 1.52 ± 0.02 and 1.65 ± 0.01 (surface and bulk).
(f) C 1s, excited with 390 eV photon energy: binding energies 289.86 ± 0.05 eV, 290.58 ± 0.18 eV, and 288.82 ± 0.15 eV, Gaussian FWHMs 0.88 ± 0.03 eV, 0.76 ± 0.22 eV, and 1.44 ± 0.22 eV.
The following working hypotheses are in order to assess as quantitatively as possible these data.
(a) The Ti 2p signal is under-evaluated since its branching ratio is considerably lower than 2. One possibility is that electrons with large angular momenta are strongly scattered by the O2− anions sitting on top and hence are not detected.21,22 The average branching ratio derived from all fits presented in Fig. 2(c) is 1.48 ± 0.03. Hence, a correction factor of 3/2.48 ≈ 1.35 was introduced in the integral amplitude of the Ti 2p spectra. With this correction, the relevant compositions for the clean surfaces are listed in Table 1, in the first three columns. One notices that the bulk Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti ratio approaches within 20–35% its ideal value of 1, but the oxygen content derived for the sample is far too low, below 50% from its ideal value of 1.5. Also, the O
Ti ratio approaches within 20–35% its ideal value of 1, but the oxygen content derived for the sample is far too low, below 50% from its ideal value of 1.5. Also, the O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba surface composition ratio is too elevated. Therefore, this suggests, as in ref. 21, that some part of the O2 intensity (at higher binding energy) still belongs to bulk oxygen (e.g. from the second TiO2 layer as counted from the surface), and this core level is shifted by the surface band bending due to the outwards polarization of the sample, as demonstrated in ref. 13 and 15 and will be checked in the following with time-resolved fast XPS during the heating of the sample.
Ba surface composition ratio is too elevated. Therefore, this suggests, as in ref. 21, that some part of the O2 intensity (at higher binding energy) still belongs to bulk oxygen (e.g. from the second TiO2 layer as counted from the surface), and this core level is shifted by the surface band bending due to the outwards polarization of the sample, as demonstrated in ref. 13 and 15 and will be checked in the following with time-resolved fast XPS during the heating of the sample.
(b) This suggests a second correction. A factor fO multiplied with the surface Ba intensity (Ba2) will be translated from the surface to bulk oxygen composition. The fact that this factor multiplies the Ba2 (surface) intensity and not the O2 (surface) intensity for the clean samples was a choice dictated by the possibility to apply the same procedure to samples dosed with CO2, where a part of the high binding energy component will be related to adsorbed carbon dioxide.
(c) Still, with only these two correction factors one cannot derive a correct bulk composition ratio. In ref. 21 it was argued that IMFP effects are affecting this composition determination and a sophisticated Monte-Carlo procedure was set to demonstrate that even ideally BaO terminated BaTiO3(001) can yield strong deviations in the composition ratio owing to differences in the photoelectron IMFP from the elements investigated. The procedure proposed in this publication takes into consideration (i) the total composition ratios derived from the survey spectra and (ii) the partial composition ratios derived from the deconvolutions (for surface and bulk components), then it adjusts the IMFPs for each core level in order to obtain the ideal composition of the bulk and the correct ratios for the surface components, through two different Monte-Carlo procedures. Since two average independent ratios are used for each procedure for yielding three IMFPs, in fact a family of solutions is derived in each case. The intersection of the dependence of the IMFP for Ba and O on that of Ti for both procedures yields a unique solution. This procedure could be criticized since it supposes a ‘perfect’ [O:(Ba + Ti)]bulk = 1.5 ratio. From the valence band spectra (see Fig. S2, ESI† and the comments at the beginning of this subsection) one obtains that the clean sample is slightly n doped, some oxygen vacancies should be taken into account, and therefore the ‘perfect’ composition ratio should be modified. In addition, there are effects such as photoelectron diffraction and also the possibility that the theoretical cross sections and asymmetry parameters from ref. 37 are not accurate (in particular, these computations were performed by a non-relativistic Hartree–Fock-Slater method). In the following, we will adapt a more ‘practical’ point of view and introduce some correction factors for the core levels of Ba 4d (bulk and surface, cBa(1) and cBa(2), respectively) and for titanium (bulk only) cTi. Since most composition ratios involve the intensity of oxygen peaks, we will simply assume that the correction factor for oxygen is 1, therefore the above correction factors for barium and titanium are relative to that of oxygen. We will also allow some slight deviations from the ideal bulk composition O1:(Ba1 + Ti) = 1.5 by introducing another parameter Cbulk for the bulk composition. In total, there are 5 parameters to be determined (cBa(1), cBa(2), cTi, fO, and Cbulk) which should give the closest bulk and surface composition to the ‘ideal’ case for all preparations investigated. If Ba1j and Ba2j are the barium integral intensities for the lower and higher binding energies of the preparation, j = 1, …, 5, O1j, O2j and O3j are the integral intensities of the oxygen components in the order of increasing binding energy, and Tij is the integral intensity for titanium (bulk), all of them normalized with respect to cross sections and asymmetry parameters, the following composition ratios will be computed.
(1) Average bulk composition evaluation:
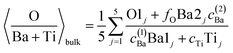 | (1) |
(2) Average surface composition:
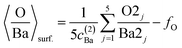 | (2) |
(3) Average bulk Ba to Ti ratio
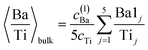 | (3) |
The chi square deciding the best parameters to be kept in the procedure is given by:
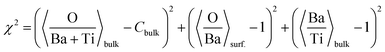 | (4) |
The Monte-Carlo simulation, with progressive restriction of the range allowed for variation of all parameters, yielded: cBa(1) ≈ 0.590; cBa(2) ≈ 0.785; cTi ≈ 0.765; fo ≈ 0.745; Cbulk ≈ 1.454; χ2 ≈ 1.22 × 10−8, with the data from Table 1, the last three columns. The first immediate conclusion is that there are slight variations in the O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Basurf and Ba
Basurf and Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tibulk ratios, and in particular it seems that the first prepared “clean” sample was slightly oxygen enriched at the surface. This deviation is then removed towards some oxygen deficiency for the next three preparations and, again, for the last one, the oxygen content increases again. Such phenomena might be linked to some (uncontrolled) oxygen migration from the bulk, but the figures could also be due to some experimental errors in data acquisition (e.g., beam instabilities) or data analysis. A more systematic deviation is featured by the general oxygen content from the bulk O:(Ba+Ti)bulk, which is slightly below its theoretical value or 1.5. In line with the valence band measurements (see above) this reinforces the hypothesis of the presence of oxygen vacancies near the surface.
Tibulk ratios, and in particular it seems that the first prepared “clean” sample was slightly oxygen enriched at the surface. This deviation is then removed towards some oxygen deficiency for the next three preparations and, again, for the last one, the oxygen content increases again. Such phenomena might be linked to some (uncontrolled) oxygen migration from the bulk, but the figures could also be due to some experimental errors in data acquisition (e.g., beam instabilities) or data analysis. A more systematic deviation is featured by the general oxygen content from the bulk O:(Ba+Ti)bulk, which is slightly below its theoretical value or 1.5. In line with the valence band measurements (see above) this reinforces the hypothesis of the presence of oxygen vacancies near the surface.
In Fig. S4 (ESI†) we present a survey spectrum for a BTO(001) sample heated several times in ultrahigh vacuum (during the preliminary cleaning) and not yet free from carbon contamination; this contamination seems to be graphitic-like (reduced carbon) and it amounts to about 0.6 carbons per formula unit and we may reasonably suppose that it will not affect the sample stoichiometry. The approximate composition derived by using the Wagner sensitivity factors45 ranges between Ba1.20Ti0.80O2.77 and Ba1.10Ti0.90O2.52, depending on whether one considers a correction factor of the Ti 2p signal due to some ‘loss’ of electrons from the 2p3/2 line, which occurs also in the XPS spectra measured in normal emission with a conventional X-ray source.21 The derived oxygen content is lower than the values from Table 1, but one has to note that the spectra of contaminant-free samples analyzed in Table 1 were recorded after annealing in oxygen, thus a recovery of the oxygen stoichiometry can be supposed. The fact that the Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti ratio (total line intensity) is greater than 1 is further proof that the sample is Ba terminated.
Ti ratio (total line intensity) is greater than 1 is further proof that the sample is Ba terminated.
For samples dosed with CO2, the main question, apart for checking the sample composition, is the number of molecules adsorbed. This was the reason for which we measured Ba 4d at both 650 eV and 390 eV. The main figures from this analysis are presented in Table 2. Knowing that the higher binding energy component (Ba2) is attributed to surface Ba from the outermost BaO atomic layer, one can easily derive the amount of carbon atoms with respect to the atomic density of one monolayer of BaO. Then, the ratio between surface oxygen and Ba2 recorded at 650 eV can be used together with the ratio between surface carbon and Ba2 recorded at 390 eV to derive the surface oxygen-to-carbon ratio and hence to infer the surface binding of adsorbates, as performed in ref. 21 and 22. However, the fact that a correction factor cBa(2) was introduced for surface Ba excited with 650 eV doesn’t imply automatically that the same correction factor should be utilized for 390 eV photon energy. The mismatch between the experimental and the theoretical cross sections might be different, and also the photoelectron diffraction effects could be different, since the kinetic energy of the emitted photoelectrons is different. Therefore, another factor cBa(2)′ ≈ 0.332 was used, and this was chosen in a way to obtain the average O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C2 ratio (between the components of highest binding energy of oxygen and carbon) as close as possible to 2, with the implicit assumption that these highest energy components, which manifest mostly when CO2 is adsorbed below room temperature, are due to physisorbed molecules on the cold surface. The factor fO which considers the amount of the O2 component to be removed from the O2
C2 ratio (between the components of highest binding energy of oxygen and carbon) as close as possible to 2, with the implicit assumption that these highest energy components, which manifest mostly when CO2 is adsorbed below room temperature, are due to physisorbed molecules on the cold surface. The factor fO which considers the amount of the O2 component to be removed from the O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba2 (surface) ratio and added to the oxygen intensity in the O1
Ba2 (surface) ratio and added to the oxygen intensity in the O1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (Ba1 + Ti) (bulk) ratio can also be different, since the O2 component for surfaces with CO2 adsorbed already comprise the influence of additional adsorbed oxygen. The factor was adjusted to fo′ ≈ 0.279 in order to obtain a bulk composition similar to that of the clean sample. With these correction factors implemented in eqn (1) and (2), the resulting C1:Ba2 (carbon main peak to surface barium) and O2:C1 (for adsorbates) are represented in the last three columns of Table 2.
(Ba1 + Ti) (bulk) ratio can also be different, since the O2 component for surfaces with CO2 adsorbed already comprise the influence of additional adsorbed oxygen. The factor was adjusted to fo′ ≈ 0.279 in order to obtain a bulk composition similar to that of the clean sample. With these correction factors implemented in eqn (1) and (2), the resulting C1:Ba2 (carbon main peak to surface barium) and O2:C1 (for adsorbates) are represented in the last three columns of Table 2.
The O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C1 ratio ranges between 2 and 3, suggesting the persistence of the CO2 molecule upon adsorption and/or the formation of surface CO3 structures (see below). In fact, if CO3 structures are formed on top oxygen atoms, then it might be expected that the signal from the oxygen which initially was taking part in the surface BaO layer will be attenuated by the molecule adsorbed on top, while the signal from terminal oxygens from the molecule and from carbon will not be attenuated, hence the effective O
C1 ratio ranges between 2 and 3, suggesting the persistence of the CO2 molecule upon adsorption and/or the formation of surface CO3 structures (see below). In fact, if CO3 structures are formed on top oxygen atoms, then it might be expected that the signal from the oxygen which initially was taking part in the surface BaO layer will be attenuated by the molecule adsorbed on top, while the signal from terminal oxygens from the molecule and from carbon will not be attenuated, hence the effective O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C atomic ratio should range between 2 and 3.
C atomic ratio should range between 2 and 3.
In fact, the main peak of C 1s whose binding energy is 289.86 ± 0.05 eV suggests that carbon is taking part in the formation of surface carbonates. Formally, this implies a surface reaction such as BaO + CO2 → BaCO3. Indeed, the C 1s binding energy in BaCO3 was reported at energies such as 290.8 eV46 and 288.9 eV.47,48 Therefore, the binding energy of the main C 1s peak for CO2/BTO(001) frames well between the values previously reported for BaCO3. In particular, the binding energy of this peak might also be affected by the surface band bending of the ferroelectric substrate and possibly also by the interaction of the induced dipole moment of the CO32− radical with the electric field provided by the ferroelectric.
One promising result is the total amount of carbon adsorbed, as related to surface barium (Ba2 component). The C1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba2 ratio is close to 1 when the adsorption proceeds at low temperature, and it is larger than 0.5 (up to 0.6) when the adsorption is performed at temperatures above room temperature. This is several times larger than the amount of carbon adsorbed when CO21 or C2H422 are dosed on BTO(001). The fact that a larger amount of carbon is adsorbed in the case of CO2/BTO(001) than in the case of CO/BTO(001) in quite a similar experiment (same dose, same substrate temperature) is quite visible from the C 1s intensity represented in the ESI,† Fig. S5(d).
Ba2 ratio is close to 1 when the adsorption proceeds at low temperature, and it is larger than 0.5 (up to 0.6) when the adsorption is performed at temperatures above room temperature. This is several times larger than the amount of carbon adsorbed when CO21 or C2H422 are dosed on BTO(001). The fact that a larger amount of carbon is adsorbed in the case of CO2/BTO(001) than in the case of CO/BTO(001) in quite a similar experiment (same dose, same substrate temperature) is quite visible from the C 1s intensity represented in the ESI,† Fig. S5(d).
As for the binding energy variations (Fig. 2(f)), the most important variations are featured by the O2 component (surface oxygen from the BaO terminal layer). This is a first suggestion that this site is the most affected by CO2 adsorption, so probably CO2 is adsorbed on top on this surface oxygen. When CO2 is adsorbed, the O2 binding energy decreases, which means that the surface oxygen becomes more negatively charged than the oxygen from the terminal BaO layer for clean surfaces. This means that partially the negative charges needed to stabilize the outwards polarization of BTO(001)32,33 are located on the adsorbed molecules (“extrinsic compensation” or “extrinsic stabilization”). This situation was commented on to a larger extent in ref. 19 and 20. An interesting aspect is revealed by the comparison of core levels from CO/BTO(001) and CO2/BTO(001) presented in Fig. S5 from the ESI.† Except for C 1s, all binding energies of the bulk components are lower in the case of CO2 dosed, which means that the band bending inside the BTO(001) is lower. This suggests that in the case of CO2/BTO(001) a lower amount of the negative stabilization charge is located inside the ferroelectric substrate, while the remaining charge will be located on the adsorbate.
3.3. Time resolved ultrafast XPS
These data are presented, together with the peak fitting, in Fig. S6–S13 in the ESI.† The binding energy and amplitudes resulting from fitting are shown in Fig. 3 for Ba 4d, Fig. 4 for Ti 2p, Fig. 5 for O 1s, and Fig. 6 for C 1s. For O 1s, only the temperature variation of the binding energies and amplitudes of the most intense components O1 and O2 are represented separately in Fig. 5. The temperature dependence of the integral amplitude and binding energy of O3 is too noisy to extract relevant information. It seems that there was no sizable dependence on the temperature for this component, which is not what we expected initially (a desorption of the physisorbed CO2 when the temperature is still below 0 °C). We may also attribute this result to the limited statistics of the time-resolved O 1s spectra. We could not simply force this component (O3) to vanish at some temperature, since this implies an abusive (and unethical) intervention in the automatic fitting procedure. However, the amplitude of this component is low, such that its consideration in the fitting of the time resolved spectra does not affect the amplitudes of the other two components, which are considerably higher. Note also that the C 1s spectra were fitted with a single component, also due to the limited statistics of the time resolved spectra.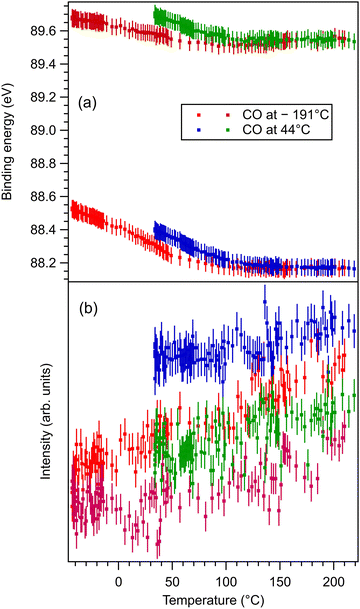 | ||
| Fig. 3 (a) Extracted temperature variations of Ba 4d binding energies for each component from the ‘deconvolutions’ of time-resolved spectra; (b) extracted temperature variation of integral amplitudes for each component, with the same color code as in (a). The spectra and their peak fitting analyses are presented in Fig. S6 and S7 (ESI†). | ||
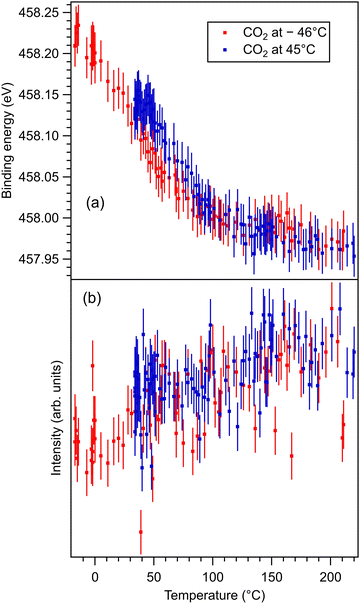 | ||
| Fig. 4 (a) Extracted temperature variations of Ti 2p binding energy from the ‘deconvolutions’ of time-resolved spectra. (b) Extracted temperature variation of the integral amplitude, with the same color code as in (a). The spectra and their peak fitting analyses are presented in Fig. S8 and S9 (ESI†). | ||
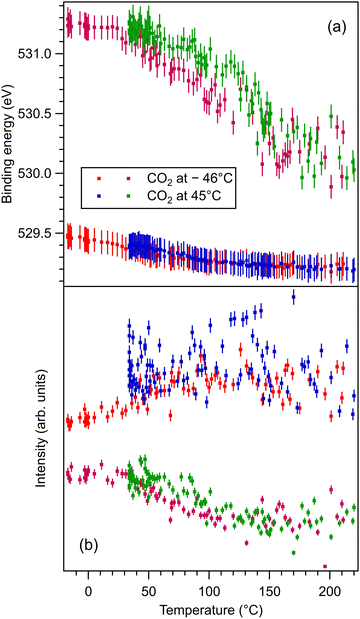 | ||
| Fig. 5 (a) Extracted temperature variations of O 1s binding energy from the ‘deconvolutions’ of time-resolved spectra. (b) Extracted temperature variation of the integral amplitude, with the same color code as in (a). The spectra and their peak fitting analyses are presented in Fig. S10 and S11 (ESI†). | ||
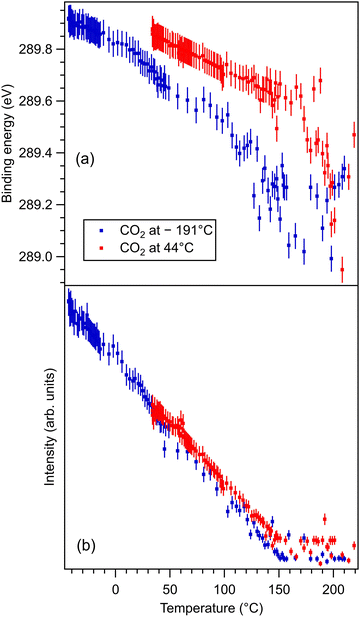 | ||
| Fig. 6 (a) Extracted temperature variations of the binding energy for C 1s spectra; (b) extracted temperature variation of the integral amplitude, with the same color code as in (a). The spectra and their peak fitting analyses are presented in Fig. S12 and S13 (ESI†). | ||
One may identify in all core levels from the substrate a constant decrease in the binding energy when the temperature increases. This is consistent with all previous findings of progressive loss of the polarization as revealed by the band bending towards the surface.17,20–22 It is also clear that the displacements (see Table 3) are lower than in the case of CO/BTO(001), where Ba 4d (bulk) was shifted by 0.41 eV, Ti 2p by 0.56 eV, and O 1s (bulk) by 0.54 eV. Note that, at variance with ref. 17 and 20–22, in this case the decrease in the C 1s intensity seems to feature a ‘universal’ linear dependence on the temperature (see Fig. 6(d)), with practically no dependence (of the entire curve) on the initial adsorption temperature. Hence, a fit with a Langmuir-like dependence, as in ref. 21 and 22, could not be performed in this case. We have no immediate explanation for this so simple linear behavior of the carbon coverage. Note also that this study was performed with a much slower temperature variation and with many more recorded experimental points during the follow-up with fast XPS. Probably, adsorption experiments at temperatures below that of liquid nitrogen might feature deviations from this linear behavior, but to date our setup doesn’t allow such investigations.
| Level sample | Ba1 | Ba2 | Ti | O1 | O2 | C |
|---|---|---|---|---|---|---|
| Dosed at LT | 0.38 | 0.18 | 0.27 | 0.31 | 1.40 | 0.93 |
| Dosed at HT | 0.24 | 0.18 | 0.20 | 0.23 | 1.35 | 0.93 |
The strongest effect is revealed by the core level shift of the O2 (surface) component. This is in line with the strongest variation of this component when CO2 is dosed, as discussed in the previous subsection. This suggests again that the most affected by CO2 adsorption are surface oxygen cations.
With temperature increase, the intensities of core levels from the substrate are increasing, as can be expected from a lower attenuation of outgoing photoelectrons due to adsorbed molecules, see Table 4. However, the increase in the Ti 2p intensity and the O1 intensity, attributed to bulk oxygen, is higher than for barium (both components). This implies that CO2 is sitting on Ti cations, but since the sample is BaO terminated, the hypothesis of CO2 adsorbed on top of oxygen (which, in turn, sits on Ti) is further consolidated. Note that the detection is close to normal emission, i.e. along the [001] direction which connects the subsurface Ti with the surface O.
| Level sample | Ba1 | Ba2 | Ti | O1 | O2 | C |
|---|---|---|---|---|---|---|
| Dosed at LT | 0.131 | 0.095 | 0.180 | 0.205 | −0.528 | −0.936 |
| Dosed at HT | 0.060 | 0.086 | 0.127 | 0.091 | −0.572 | −0.912 |
The fact that O 1s and, to some extent, C 1s have significative shifts towards higher binding energies when the polarization is lost (and CO2 is desorbing) suggests that the adsorbed molecules are negatively charged, as we supposed initially only for the surface cations. Also, the fact that for CO2/BTO(001) the surface oxygen anions are simulated conveniently with a single component O2 (we do not take into account the O3 component, of considerably larger binding energy, attributed to physisorbed CO2) suggests that CO2 forms a bond with a surface oxygen with a local configuration such as CO3 and with similar chemical states on the three oxygens.
3.4. Proposed geometry for adsorption
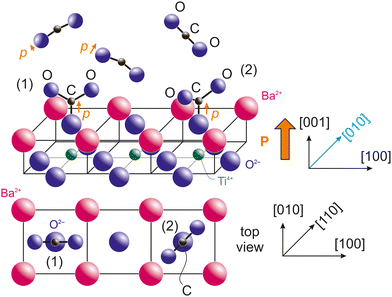
Taking into account the last remarks from the previous subsection, we are able to propose a model for CO2 adsorption on BTO(001). If the molecules are adsorbed on terminal oxygens from the surface, the most natural way for this adsorption is with carbon bound to surface oxygen from BTO(001) and the two oxygens which belonged initially to CO2 oriented outwards and making some angle of 2β between them. The fact that the CO2 molecule deviates from its initial linear configuration is suggested by the progressive polarization by the substrate. CO2 has a molecular polarizability 4πε0αv, with ε0 the vacuum permittivity and αv = 2.911 Å3 the polarizability in volume units.49 Note that this polarizability is larger than that of CO (1.95 Å3) and this might explain the higher number of molecules adsorbed on BTO(001), although detailed surface chemistry should prevail. Secondly, the most reasonable hypothesis from symmetry considerations is that the molecule's plane (together with the surface oxygen initially from BTO(001)) is vertical and its intersection with the (001) surface should be along a high symmetry axis, [100] or [110]. These two configurations are represented in Fig. 7. Some considerations regarding the electrostatic interaction between terminal oxygens from CO3 and the surface barium cations are detailed in the ESI,† see Fig. S14 and S15 and the adjacent text. The first estimate is that configuration (2) with the molecule viewed from the top oriented along the in-plane [110] axis is the most stable. However, the difference in electrostatic energy between both configurations is very low, therefore other chemical effects or even the neighborhood of other adsorbed molecules might affect this adsorption geometry. As in ref. 21 and 22, this proposed adsorption geometry is derived from basic considerations from XPS and guessed using symmetry considerations, but more detailed information might be offered only by structural methods, such as photoelectron diffraction, vibrational spectroscopy and/or ab initio molecular dynamics.In Fig. 7 we also represented the orientation of a supposed dipole moment of the CO3 structure formed on the surface, p. It is obvious that if all three oxygens have similar negative charge and β > 60° the overall dipole moment will be oriented outwards. If the oxygen from the BTO(001) surface is more negative than the outwards oxygens of the molecule, then the overall dipole moment will be oriented outwards even for smaller angles of β. The main problem is what is happening prior to the formation of a chemical bond between the surface oxygen from BTO and CO2. In this case, according to the hypothesis that the dipole moment of the molecule should be parallel to the (outwards oriented) polarization of the ferroelectric, normally the negative oxygens from CO2 should be oriented towards the surface and the positive carbon outwards. At some point, other interactions should manifest to ‘switch’ the orientation of CO2 with its oxygens oriented outwards. This will be discussed in the following.
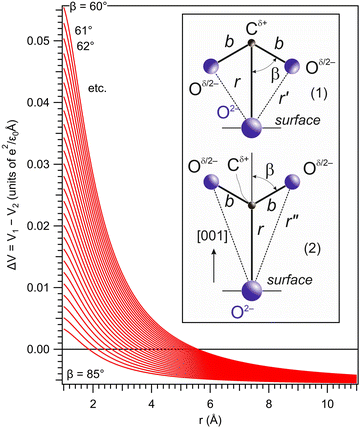
Suppose the C – surface O direction is along the [001] direction. See the insert of Fig. 8. The molecule is approaching the surface with its oxygens oriented towards the BTO, then the dipole moment is oriented parallel to the polarization, and let's call this configuration (1). The attraction energy from the slightly ionized carbon (q being its positive charge) to one surface O2− situated at the distance r is given by:
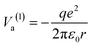 | (5) |
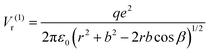 | (6) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond length of the molecule and 2β is the angle between its two C
O bond length of the molecule and 2β is the angle between its two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds. The dipole interaction energy with the electric field oriented outwards is given by
O bonds. The dipole interaction energy with the electric field oriented outwards is given by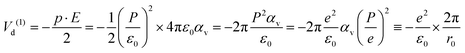 | (7) |
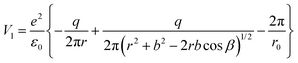 | (8) |
For the configuration with the molecule ‘switched’ with the carbon towards the surface O2− and its oxygens in the opposite direction with respect to the sample surface (configuration (2) in the following, see Fig. S14 and the insert of Fig. 8, ESI†), the interaction energy of the carbon with the surface oxygen will be the same Va(1) = Va(2), and the repulsion energy of oxygens from CO with the surface oxygen anion is given by:
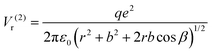 | (9) |
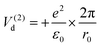 | (10) |
The total interaction energy of this configuration is given by:
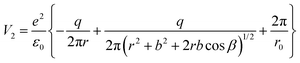 | (11) |
Plotting ΔV = V1 − V2 allows one to determine which configuration is the most stable. Unfortunately, there are too many parameters in this model: the supposed charge of the carbon in CO2q, the bond length b, and the angle β. In Fig. 8 we present a possible variation of ΔV(r) for several values of β, q = 1 and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond length b = 1.16 Å.50 It can be seen that for a distance below a certain limit (about 5.5 Å for β = 60°) the second configuration, with the carbon oriented towards the BTO(001), is the most stable.
O bond length b = 1.16 Å.50 It can be seen that for a distance below a certain limit (about 5.5 Å for β = 60°) the second configuration, with the carbon oriented towards the BTO(001), is the most stable.
This toy model could be refined by taking into account multiple interactions, e.g. also with the Ba atoms from the surface. We are however suspicious whether reliable quantitative results could be obtained by such a simple electrostatic model, taking into account the variety of the parameters that have to be employed and also the fact that at such distances quantum chemistry enters into action to consolidate the surface chemical bonds. The experiments suggest that at higher separation the induced dipole should be more or less parallel to the polarization of the substrate, then the oxygens of CO2 should be oriented towards the BTO(001); while at a certain separation the molecule switches, such that at the end carbon is the closest atom to the surface. Probably a more sophisticated explanation could be offered by molecular dynamics simulations.
4. Conclusion
This experiment was a success in the sense that the amount of CO2 adsorbed was significantly higher than in the case of CO or C2H4 on the same substrate, approaching one molecule per surface unit cell at low temperature. Let us estimate the adsorption capacity for a BaTiO3 powder of 20 nm,51,52 and assume that the powder is formed by cuboidal nanoparticles. Their volume would be 8000 nm3 and their mass would be 4.82 × 10−17 g, by using the density of BaTiO3 of 6.02 g cm−3. The total area of two opposite faces where the polarization is supposed to be oriented out-of-plane is 800 nm2, and it comprises about 5246 surface BaO unit cells. If on each unit cell a CO2 molecule is adsorbed, then the total mass of the adsorbate is estimated at 44 × 1.67 × 10−24 g × 5246 = 3.86 × 10−19 g. Thus, 1 g of BaTiO3 powder might adsorb about 8 mg of CO2. This is below the recommended amount of about 20 mg g−1 for carbon sorbents to be used in decarbonization, but the relative low cost of the barium titanate powder (including its milling to produce nanoparticles) and the simplicity of the process may be seen as compensating this drawback. Note also that desorption could not only be thermally induced, but also by applying an electric field to induce the depolarization of the material. Also, 8 mg g−1 for 20 nm BTO nanoparticles represents almost double the reported adsorption capacity of BTO nanocatalysts with the same average size in ref. 11.In addition to this result, the actual study was a step forward with respect to ref. 21 and 22 in terms of methodology, since the CO2 desorption was followed-up in finer steps and also because the stoichiometry analysis was further developed and simplified. As discussed above, the proposed adsorption geometry should be confirmed by further experimental and theoretical studies. The slight deviations of the stoichiometry from its ideal value is in line with the presence of some oxygen vacancies and with the observed energy difference between the Fermi level and the valence band offset in the valence band spectra.
At the end, let us point out that a separate experiment with N2 adsorption on BTO(001) yielded a negative result, in the sense that no nitrogen was detected on the surface. At the same time, it is reasonable to suppose that no additional oxygen from the atmosphere will be attached on BTO(001), since during the preparation, the sample is supposed to become saturated in oxygen. Thus, from the content of the terrestrial atmosphere, mainly water and carbon containing molecules are supposed to be adsorbed on clean barium titanate.
In conclusion, this fundamental study of carbon dioxide adsorption on atomically clean, (001) oriented barium titanate may be seen as a first encouraging indication to continue towards the industrial feasibility of ferroelectric absorbers for decarbonization.
Author contributions:
Alexandru-Cristi Iancu: investigation, writing – original draft. George A. Lungu: investigation, writing – original draft. Cristian A. Tache: investigation. Cristian M. Teodorescu: conceptualization, supervision, investigation, validation, formal analysis, software, visualization, methodology, writing – original draft, writing – review & editing, funding acquisition, project administration.Data availability
Data is available upon request from the corresponding author. Relevant Igor Pro, MS Excel and CorelDraw files are provided in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge help on the beamline from Dr Monika Schied and from Ms Iulia I. Căprar. This work was funded by the Core Program of the National Institute of Materials Physics, under the project PC1–PN23080101. All experiments were performed using the National Interest Setup “System of complex XPS/ESCA installations and research using synchrotron radiation”.References
- E. S. Sanz-Pérez, C. R. Murdock, S. A. Didas and C. W. Jones, Direct capture of CO2 from ambient air, Chem. Rev., 2016, 116, 11840–11876 CrossRef PubMed.
- D. W. Keith, G. Holmes, D. St. Angelo and K. Heidel, A process for capturing CO2 from the atmosphere, Joule, 2018, 2, 1573–1594 CrossRef CAS.
- O. O. Ayeleru, H. U. Modekwe, O. R. Onisuru, C. R. Ohoro, C. A. Akinnawo and P. A. Olubambi, Adsorbent technologies and applications for carbon capture, and direct air capture in environmental perspective and sustainable climate action, Sust. Chem. Clim. Act., 2023, 3, 100029 Search PubMed.
- K. Garrity, A. M. Kolpak, S. Ismail-Beigi and E. I. Altman, Chemistry of ferroelectric surfaces, Adv. Mater., 2010, 22, 2969–2973 CrossRef CAS PubMed.
- A. Kakekhani and S. Ismail-Beigi, Ferroelectric-based catalysis: Switchable surface chemistry, ACS Catal., 2015, 5, 4537–4545 CrossRef CAS.
- A. Kakekhani, S. Ismail-Beigi and E. I. Altman, Ferroelectrics: A pathway to switchable surface chemistry and catalysis, Surf. Sci., 2016, 650, 302–316 CrossRef CAS.
- W. T. Ding, J. Lu, X. Tang, L. Z. Kou and L. Liu, Ferroelectric materials and their applications in activation of small molecules, ACS Omega, 2023, 8, 6164–6174 CrossRef CAS PubMed.
- A. L. Cabrera, F. Vargas and R. A. Zarate, Adsorption of carbon dioxide by barium titanate: Evidence of adsorption process mediated by dipole-dipole interaction, J. Phys. Chem. Solids, 1994, 55, 1303–1307 CrossRef CAS.
- T. Isobe, S. Saito, T. Oshima, H. Tanaka, K. Yamaura, T. Hoshina, D. Atarashi and O. Sakurai, Carbon dioxide absorption of barium titanate system, J. Soc. Inorg. Mater., Jpn., 2013, 20, 107–110 CAS.
- T. Watanabe, S. Md Khan, H. Kanoh and T. Ohba, Significant CO2 adsorption ability of nanoscale BaTiO3 ceramics fabricated by carbon-template-solvothermal reactions, Phys. Chem.: Indian J., 2017, S1, 101 Search PubMed.
- T. Watanabe and T. Ohba, Temperature-dependent CO2 sorption and thermal-reduction without reactant gases on BaTiO3 nanocatalysts at low temperatures in the range of 300–1000 K, Nanoscale, 2022, 14, 8318–8325 RSC.
- S. Takawane, M. Miyamoto, T. Watanabe and T. Ohba, Pressure-dependent CO2 thermolysis on barium titanate nanocatalysts, RSC Sustainability, 2024, 2, 2218–2224 RSC.
- N. G. Apostol, L. E. Stoflea, G. A. Lungu, C. A. Tache, D. G. Popescu, L. Pintilie and C. M. Teodorescu, Band bending at free Pb(Zr,Ti)O3 surfaces analyzed by X-ray photoelectron spectroscopy, Mater. Sci. Eng., B, 2013, 178, 1317–1322 CrossRef CAS.
- N. G. Apostol, L. E. Stoflea, G. A. Lungu, C. Chirila, L. Trupina, R. F. Negrea, C. Ghica, L. Pintilie and C. M. Teodorescu, Charge transfer and band bending at Au/Pb(Zr,Ti)O3 interfaces investigated by photoelectron spectroscopy, Appl. Surf. Sci., 2013, 273, 415–425 CrossRef CAS.
- L. E. Ştoflea, N. G. Apostol, L. Trupină and C. M. Teodorescu, Selective adsorption of contaminants on Pb(Zr,Ti)O3 surfaces shown by X-ray photoelectron spectroscopy, J. Mater. Chem. A, 2014, 2, 14386–14392 RSC.
- L. Pintilie, C. Ghica, C. M. Teodorescu, I. Pintilie, C. Chirila, I. Pasuk, L. Trupina, L. Hrib, A. G. Boni, N. G. Apostol, L. E. Abramiuc, R. Negrea, M. Stefan and D. Ghica, Polarization induced self-doping in epitaxial Pb(Zr0.20Ti0.80)O3 thin films, Sci. Rep., 2015, 5, 14974 CrossRef CAS.
- L. C. Tănase, N. G. Apostol, L. E. Abramiuc, C. A. Tache, L. Hrib, L. Trupină, L. Pintilie and C. M. Teodorescu, Ferroelectric triggering of carbon monoxide adsorption on lead zirco-titanate (001) surfaces, Sci. Rep., 2016, 6, 35301 CrossRef.
- C. M. Teodorescu, L. Pintilie, N. G. Apostol, R. M. Costescu, G. A. Lungu, L. Hrib, L. Trupină, L. C. Tănase, I. C. Bucur and A. E. Bocîrnea, Low energy electron diffraction from ferroelectric surfaces. Dead layers and surface dipoles in clean Pb(Zr,Ti)O3(001), Phys. Rev. B, 2017, 96, 115438 CrossRef.
- L. C. Tănase, L. E. Abramiuc, D. G. Popescu, A.-M. Trandafir, N. G. Apostol, I. C. Bucur, L. Hrib, L. Pintilie, I. Pasuk, L. Trupină and C. M. Teodorescu, Polarization orientation in lead zirco-titanate (001) thin films driven by the interface with the substrate, Phys. Rev. Appl., 2018, 10, 034020 CrossRef.
- N. G. Apostol, M. A. Husanu, D. Lizzit, I. A. Hristea, C. F. Chirila, L. Trupina and C. M. Teodorescu, CO adsorption, reduction and oxidation on Pb(Zr,Ti)O3(001) surfaces associated with negatively charged gold nanoparticles, Catal. Today, 2021, 366, 141–154 CrossRef CAS.
- A.-C. Iancu, N. G. Apostol, A. Nicolaev, L. E. Abramiuc, C. F. Chirilă, D. G. Popescu and C. M. Teodorescu, Molecular adsorption–desorption of carbon monoxide on ferroelectric BaTiO3(001), Mater. Adv., 2024, 5, 5709–5723 RSC.
- A.-C. Iancu, A. Nicolaev, N. G. Apostol, L. E. Abramiuc and C. M. Teodorescu, Reversible oxidation of ethylene on ferroelectric BaTiO3(001): an X-ray photoelectron spectroscopy study, Heliyon, 2024, 10, e35072 CrossRef CAS PubMed.
- D. Li, M. H. Zhao, J. Garra, A. M. Kolpak, A. M. Rappe, D. A. Bonnell and J. M. Vohs, Direct in situ determination of the polarization dependence of physisorption on ferroelectric surfaces, Nat. Mater., 2008, 7, 473–477 CrossRef CAS.
- M. A. Khan, M. A. Nadeem and H. Idriss, Ferroelectric polarization effect on surface chemistry and photo-catalytic activity: A review, Surf. Sci. Rep., 2016, 71, 1–31 CrossRef CAS.
- N. Domingo, E. Pach, K. Cordero-Edwards, V. Pérez-Dieste, C. Escudero and A. Verdaguer, Water adsorption, dissociation and oxidation on SrTiO3 and ferroelectric surfaces revealed by ambient pressure X-ray photoelectron spectroscopy, Phys. Chem. Chem. Phys., 2019, 21, 4920–4930 RSC.
- L. E. Abramiuc, L. C. Tanase, M. J. Prieto, L. de Souza Caldas, A. Tiwari, N. G. Apostol, M. A. Husanu, C. F. Chirila, T. Schmidt, L. Pintilie and C. M. Teodorescu, Surface charge dynamics on air-exposed ferroelectric Pb(Zr,Ti)O3(001) thin films, Nanoscale, 2023, 15, 13062–13075 RSC.
- K. Sakayori, Y. Matsui, H. Abe, E. Nakamura, M. Kenmoku, T. Hara, D. Ishikawa, A. Kokubu, K. Hirota and T. Ikeda, Curie temperature of BaTiO3, Jpn. J. Appl. Phys., 1995, 34, 5443–5445 CrossRef CAS.
- L. E. Borcan, C. M. Teodorescu, A.-C. Iancu, N. G. Apostol, A. Nicolaev, R. M. Costescu, M. A. Husanu, D. G. Popescu and G. A. Lungu, Surface spin asymmetry in Pt(001)–hex induced by electron accumulation, Heliyon, 2024 DOI:10.2139/ssrn.4696833.
- R. M. Costescu, N. G. Gheorghe, M. A. Husanu, G. A. Lungu, D. Macovei, I. Pintilie, D. G. Popescu and C. M. Teodorescu, Epitaxial ferromagnetic samarium and samarium silicide synthesized on Si(001), J. Mater. Sci., 2012, 47, 7225–7234 CrossRef CAS.
- C. Chirila, A. G. Boni, L. D. Filip, M. Botea, D. Popescu, V. Stancu, L. Trupina, L. Hrib, R. Negrea, I. Pintilie and L. Pintilie, in Epitaxial Ferroelectric Thin Films: Potential for New Applications, Pulsed Laser Processing of Materials, ed. D. F. Yang and K. Gibson, IntechOpen, London, 2024, pp. 84–108 Search PubMed.
- L. Pintilie, C. Ghica, C. M. Teodorescu, I. Pintilie, C. Chirila, I. Pasuk, L. Trupina, L. Hrib, A. G. Boni, N. G. Apostol, L. E. Abramiuc, R. Negrea, M. Stefan and D. Ghica, Polarization induced self-doping in epitaxial Pb(Zr0.20Ti0.80)O3 thin films, Sci. Rep., 2015, 5, 14974 CrossRef CAS PubMed.
- C. M. Teodorescu, Ferroelectricity in thin films driven by charges accumulated at interfaces, Phys. Chem. Chem. Phys., 2021, 23, 4085–4093 RSC.
- C. M. Teodorescu, Self-consistently derived sample permittivity in stabilization of ferroelectricity due to charge accumulated at interfaces, Phys. Chem. Chem. Phys., 2022, 24, 5419–5430 RSC.
- M. Henzler, LEED from epitaxial surfaces, Surf. Sci., 1993, 298, 369–377 CrossRef CAS.
- I. Sokolović, G. Franceschi, Z. C. Wang, J. Xu, J. Pavelec, M. Riva, M. Schmid, U. Diebold and M. Setvín, Quest for a pristine unreconstructed SrTiO3(001) surface: An atomically resolved study via noncontact atomic force microscopy, Phys. Rev. B, 2021, 103, L241406 CrossRef.
- I. Sokolović, M. Schmid, U. Diebold and M. Setvín, Incipient ferroelectricity: A route towards bulk-terminated SrTiO3, Phys. Rev. Mater., 2019, 3, 034407 CrossRef.
- J. J. Yeh and I. Lindau, Atomic subshell photoionization cross sections and asymmetry parameters: 1 ≤ Z ≤ 103, Atomic data and nuclear data tables, 1985, 32, 1–55, https://vuo.elettra.eu/services/elements/WebElements.html.
- M. O. Krause and J. H. Oliver, Natural widths of atomic K and L levels, Ka X-ray lines and several KLL Auger lines, J. Phys. Chem. Ref. Data, 1979, 8, 329–338 CrossRef CAS.
- C. M. Teodorescu, J. M. Esteva, R. C. Karnatak and A. El Afif, An approximation of the Voigt I profile for the fitting of experimental x-ray absorption data, Nucl. Instrum. Methods Phys. Res., Sect. A, 1994, 345, 141–147 CrossRef CAS.
- D. Luca, D. Mardare, F. Iacomi and C. M. Teodorescu, Increased surface hydrophilicity of titania thin films by doping, Appl. Surf. Sci., 2006, 252, 6122–6126 CrossRef CAS.
- D. G. Popescu, A. Nicolaev, R. M. Costescu, L. E. Borcan, G. A. Lungu, C. A. Tache, M. A. Husanu and C. M. Teodorescu, Spin asymmetry of O 2p –related states in SrTiO3(001), Phys. Scr., 2024, 99, 105925 CrossRef.
- I. Spasojevic, G. Sauthier, J. M. Caicedo, A. Verdahuer and N. Domingo, Oxidation processes at the surface of BaTiO3 thin films under environmental conditions, Appl. Surf. Sci., 2021, 565, 150288 CrossRef CAS.
- J. Goniakowski, F. Finocchi and C. Noguera, Polarity of oxide surfaces and nanostructures, Rep. Prog. Phys., 2008, 71, 016501 CrossRef.
- L. E. Borcan, A.-C. Iancu, D. G. Popescu and C. M. Teodorescu, Considerable spin asymmetry of deep valence states induced by partial neutralization of charged SrTiO3(011) surfaces, J. Chem. Phys., 2024 Search PubMed , under review.
- C. D. Wagner, L. E. Zeller, J. A. Taylor, R. H. Raymond and L. H. Gale, Empirical atomic sensitivity factors for quantitative analysis by electron spectroscopy for chemical analysis, Surf. Interface Anal., 1981, 3, 211–225 CrossRef CAS.
- J. A. Th. Verhoeven and H. Van Doveren, An XPS investigation of the interaction of CH4, C2H2, C2H4 and C2H6 with a barium surface, Surf. Sci., 1982, 123, 369–383 CrossRef.
- A. B. Christie, J. Lee, I. Sutherland and J. M. Walls, An XPS study of ion-induced compositional changes with group II and group IV compounds, Appl. Surf. Sci., 1983, 15, 224–237 CrossRef CAS.
- D. Dissanayake, K. C. C. Kharas, J. H. Lunsford and M. P. Rosynek, Catalytic Partial Oxidation of Methane over Ba-Pb, Ba-Bi, and Ba-Sn Perovskites, J. Catal., 1993, 139, 652–663 CrossRef CAS.
- T. M. Miller, in Atomic and molecular polarizabilities, CRC Handbook of Chemistry and Physics, ed. David R. Lide, CRC Press, Boca Raton, FL, USA, 2005, pp. 10–172, https://www.hbcpnetbase.com Search PubMed.
- Bond lengths and angles in gas phase molecules, CRC Handbook of Chemistry and Physics, ed. David R. Lide, CRC Press, Boca Raton, FL, USA, 2005, pp. 9–17, https://www.hbcpnetbase.com Search PubMed.
- A. K. Nath, C. T. Jiten and K. Chandramani Singh, Influence of ball milling parameters on the particle size of barium titanate nanocrystalline powders, Phys. B, 2010, 405, 430–434 CrossRef CAS.
- K. Chandramani Singh and A. K. Nath, Barium titanate nanoparticles produced by planetary ball milling and piezoelectric properties of corresponding ceramics, Mater. Lett., 2011, 65, 970–973 CrossRef . See also https://www.americanelements.com/barium-titanate-nanoparticles-12047-27-7.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00856a |
| This journal is © The Royal Society of Chemistry 2024 |