Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reinforcement of aluminum metal matrix composites through graphene and graphene-like monolayers: a first-principles study
Ellie
Zhang
 * and
Xuan
Luo
* and
Xuan
Luo

National Graphene Research and Development Center, Springfield, Virginia 22151, USA. E-mail: xluo@ngrd.org
First published on 9th November 2024
Abstract
The pursuit of advanced materials with superior properties is a key focus in aerospace engineering, where enhancing the performance of lightweight, high-strength materials like aluminum is crucial. Reinforcing aluminum with strong materials, particularly two-dimensional monolayers such as graphene, silicon carbide, phosphorus-doped graphene, and boron nitride, offers a promising approach for over-coming aluminum's limitations, including susceptibility to fatigue and stress corrosion. This study employs density functional theory (DFT) to calculate the interfacial binding energy, fracture energy, charge transfer, and band structure between aluminum and these 2D monolayers, aiming to optimize the material properties for aerospace applications. Results indicate that silicon carbide and phosphorus-doped graphene would be the most beneficial for industrial use, having both great strength and strong bonds between layers. In contrast, pure graphene and boron nitride demonstrate weaker bonds with aluminum, suggesting limited suitability for applications requiring robust interfacial interactions. Our findings contribute to the fundamental understanding of interactions between reinforcing monolayers and aluminum metal matrix composites, while opening pathways for the design of high-strength, low-weight aluminum-based materials in areas such as aerospace.
1 Introduction
The quest for advanced materials with superior properties has always been at the forefront of aerospace engineering. Aluminum (Al), celebrated for its lightweight properties, high strength-to-weight ratio, and resistance to corrosion, has remained a corner-stone material in this industry for decades.1 However, despite its numerous advantages, aluminum also presents several challenges that must be addressed to optimize its performance in aerospace applications. These challenges include susceptibility to fatigue, stress corrosion cracking, and the ever-present issue of material strength at high temperatures.2–4 To address these issues and push the boundaries of performance, there has been a growing interest in enhancing aluminum's mechanical properties through composite materials.5,6Previously, studies have demonstrated that reinforcing aluminum with monolayers may significantly improve its mechanical properties.7 Researchers have primarily focused on incorporating graphene, a two-dimensional material known for its exceptional strength, lightweightness, and electrical conductivity, into aluminum matrix composites.8,9 These studies demonstrated that the inclusion of graphene monolayers can significantly increase the composite's tensile strength and thermal stability.10–12 For instance, graphene-doped aluminum composites exhibited improved load transfer capabilities and resistance to crack propagation, which are crucial for aerospace applications.13,14 Additionally, there has been exploration into other monolayers, such as boron carbide and titanium diboride, which also showed promise in enhancing aluminum's properties.15–17 These findings suggest potential for monolayer doping to create aluminum-based composites with superior performance characteristics. However, the optimal configurations and interfacial properties for these enhancements are still under investigation.18
In recent years, experimentalists have shown that the combination of graphene and aluminum (Al–Gr) and silicon carbide and aluminum (Al–SiC) have significant effects on the strengthening of aluminum metal matrix composites.19–21 Graphene exhibits extraordinary mechanical strength and electrical conductivity, making it an ideal candidate for reinforcing metals.22,23 Baig et al. was recently able to successfully strengthen aluminum composite through the use of graphene nanoparticles.24 Studies by Bastwros et al. and Raj et al. have shown similar improvements in strength of aluminum through reinforcement using graphene nanosheets and semi-solid processing.25,26 Like graphene, silicon carbide (SiC), a ceramic monolayer known for its hardness and thermal stability, has been explored for its potential to enhance the properties of metal matrix composites.27 Boron nitride (BN) is also a monolayer suggested to improve the strength and other mechanical properties of aluminum metal matrix composites.28 Though there has been experimental research done on these compounds, mechanisms for strengthening their interfacial properties and atomic interactions have not been extensively explored theoretically.29–32
Despite the progress in developing aluminum-based composites, several critical issues remain unresolved. The formation of aluminum carbide (Al4C3) at the interface of aluminum and carbon-based materials poses significant challenges, affecting the composite's overall stability and performance.14,33–35 Aluminum and graphene are also bound together by weak van der Waals forces and have poor lattice mismatch, leading to further weaknesses in the metal matrix composite.36 These problems with combining graphene and aluminum has led to the use of doping or replacing graphene with similar structures to create better stability and stronger bonds.37,38 Most notably, the atomic and electronic structures at the interface between monolayers of SiC and BN with aluminum have not been systematically studied, leaving a gap in understanding the potential benefits and drawbacks of such configurations. Our research aims to solve the issue of weak bonding through studying interfacial binding energy, fracture energy, and electron structure between aluminum, graphene, silicon carbide, and boron nitride. By doing so, we aim to solve existing problems related to the enhancement of aluminum's properties and provide new insights into the potential applications of these advanced composites.
Furthermore, Rohmann et al. indicate that the primary compounds formed at the Al–BN interface, AlN and AlB2, pose significantly fewer issues than Al4C3 formation at Al–Gr interfaces.39,40 Notably, the Al–BN interface demonstrates slower, more controlled reaction-product formation and a stable orientation between Al and AlN crystals, contrasting with the higher reactivity and stability challenges of Al–C systems.41
By employing the density functional theory (DFT)42,43 to study the interfacial interactions of Al–Gr, Al–SiC, doped Al–Gr, and Al–BN composites, we can accurately predict their mechanical behavior and understand the causes for their enhanced properties. This approach not only advances our theoretical understanding but also paves the way for practical applications in aerospace and other industries. The insights gained from this research could lead to the development of new, high-performance materials that meet the standards of modern engineering, ultimately contributing to more efficient, durable, and reliable aerospace structures.
2 Method
2.1 Computational details
We performed first-principle calculations based on the density functional theory (DFT).44,45 These simulations were performed within the generalized gradient approximation (GGA)46 using the Perdew–Burke–Ernzerhof (PBE)47 format implemented in the ABINIT3 package. The projected augmented wave (PAW)48 pseudopotentials were generated using the ATOMPAW code49,50 with the electron configuration and radius cut-off parameters listed in Table 1.| Element | Electron configuration | Radius cut-off (Bohr) | |
|---|---|---|---|
| Aluminum (Al) | 3s2 | 3p2 | 1.90 |
| Carbon (C) | 2s2 | 2p2 | 1.51 |
| Silicon (Si) | 3s2 | 3p2 | 1.91 |
| Phosphorus (P) | 3s2 | 3p3 | 1.91 |
| Boron (B) | 2s2 | 2p1 | 1.70 |
| Nitrogen (N) | 2s2 | 2p3 | 1.20 |
For all materials involved, the vacuum, kinetic energy cut-off, and Monkhorst–Pack k-point grid were converged through self-consistent field (SCF) total energy calculations. SCF iterations were considered converged when the total energy difference was less than 1.0 × 10−10 Hartree twice consecutively. The kinetic energy cut-off, k-point grid, and vacuum height were considered converged when the total energy difference between consecutive datasets was less than 1.0 × 10−4 Hartree twice consecutively.
2.2 Atomic structure
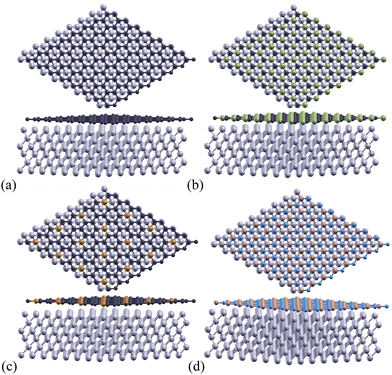
The Al(1 1 1) surface, as shown in Fig. 1, was chosen as our model system for the aluminum metal matrix due to its comparatively low surface and high fracture energies.51,52 Low surface energy is advantageous as it minimizes the number of broken bonds at the surface, thereby enhancing the overall stability of the crystal structure.53 In addition, its high fracture energy ensures that the material can withstand applied forces without breaking easily.54 | ||
| Fig. 1 (a) Top view and (b) side view of Al(1 1 1) surface. A total of 6 layers of Al were used in this calculation. The grey circles represent aluminum atoms. | ||
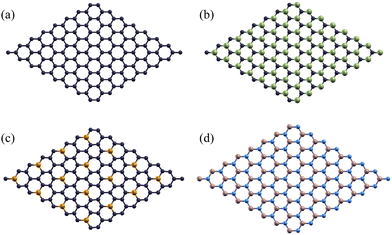
As they have more widely known properties, pristine graphene monolayers were used as a control to test the effectiveness of using silicon carbide, phosphorus-doped graphene, and boron nitride monolayers as a stronger-bonded alternative. One carbon atoms was substituted by phosphorus in each 2 × 2 supercell for the P-doped Gr monolayer. When considering the rotation angle between the aluminum/monolayer interface, we chose a 0° angle to maximize work of adhesion and minimize the formation of Al4C3 by using a clean interface.55 These monolayers are shown below in Fig. 2.
A hexagonal supercell was selected to accommodate the structural characteristics of both the two-dimensional monolayers and the Al(1 1 1) surface. Calculations were performed using a slab model, which provides an accurate representation of the interfaces between the 2D monolayers and the aluminum substrate.
2.3 Binding energy & fracture energy
To measure the strength of various bonds between Al(1 1 1) and layers of Gr, SiC, P-doped Gr, or BN, the four materials were each placed above aluminum to calculate their various total energies. By finding the lowest bonded energies, these were then used to obtain the binding energy of Al with Gr, SiC, P-doped Gr, or BN through the following equation:| Eb = EAl/monolayer − EAl − Emonolayer | (1) |
A negative binding energy would result in a spontaneous exothermic reaction bonding the two materials together. This also indicates that the combined materials are more stable than the separated ones, suggesting a strong and favorable interaction between them. The more negative the binding energy, the stronger the bond indicated is. In contrast, a positive binding energy would indicate that the two materials repel one another.
The fracture energy of the material refers to its likelihood of fracturing under high stress and can be calculated using the equation:
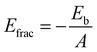 | (2) |
In contrast to binding energy, a higher positive value of fracture energy signifies enhanced resistance to fracture when subjected to high stress, while a lower fracture energy value suggests a material is prone to easy fracturing. Furthermore, there is a direct correlation between binding energy and fracture energy. Stronger binding energy is associated with increased fracture energy, which in turn reflects a material's greater resistance to fracture under applied stress.
2.4 Electronic structure
The electronic structures of these composites were analyzed through charge difference and band structure. Charge density differences were calculated for the Gr/Al, SiC/Al, P-doped Gr/Al, and BN/Al interfaces. To evaluate the interface charge transfer, we computed the difference in charge density between the combined materials and their respective individual constituents. This is represented by the equation| Δρ(r) = ρAl/monolayer(r) − ρAl(r) − ρmonolayer(r), | (3) |
The band structures for Gr/Al, SiC/Al, P-doped Gr/Al, and BN/Al were calculated to further understand the properties of these materials. These were plotted using the high-symmetry k-points Γ (0, 0, 0), M (1/2, 0, 0), K (2/3, 1/3, 0), and Γ (0, 0, 0).
Band structure can also be used to predict the conductivity of a material using the equation
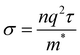 | (4) |
3 Results and discussion
First-principles calculations were conducted to analyze the interfaces of monolayers Gr, SiC, P-doped Gr, and BN over a six-layer Al(1 1 1) substrate. For each configuration, we evaluated the binding energy, fracture energy, charge distribution differences, and band structure.3.1 Atomic structure
A monolayer of 2D Gr, SiC, P-doped Gr, or BN was placed over six layers of Al(1 1 1) to create the complex configurations illustrated in Fig. 3.The total energy of the monolayer/Al system was calculated at various distances between the two for the monolayers Gr, SiC, P-doped Gr, and BN. These energies were plotted to determine the optimal distance between aluminum and each monolayer (Gr, SiC, P-doped Gr, and BN) as shown in Fig. 4. The lowest point on these energy curves corresponds to the optimal interlayer distance. These energetically favorable distances (d) can be found in Table 2.
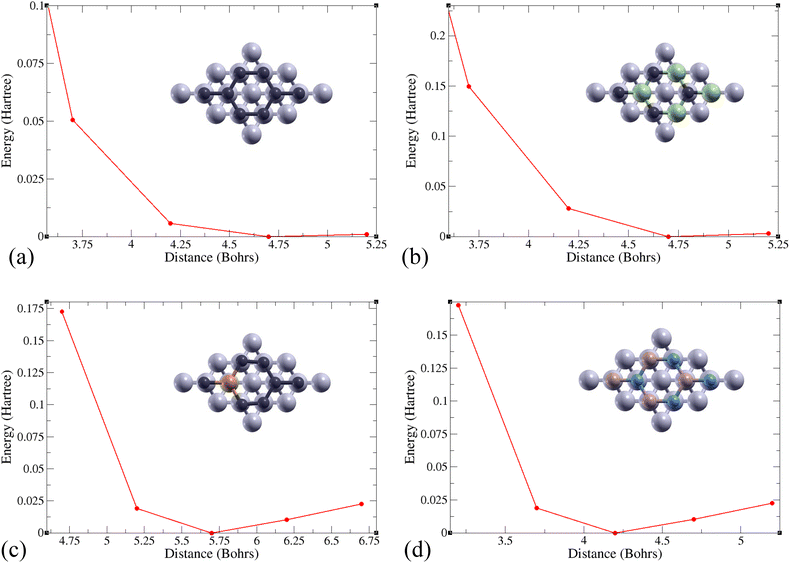 | ||
| Fig. 4 Total energy changes based on distance between the top of 6 layers of aluminum and a 2D monolayer of (a) Gr, (b) SiC, (c) P-doped Gr, or (d) BN. | ||
| Material | d (Bohrs) | E b (Ha) | E frac (Ha per Bohr2) |
|---|---|---|---|
| Gr/Al | 4.7 | −0.0027 | 2.679 × 10−5 |
| SiC/Al | 4.7 | −0.0733 | 7.273 × 10−4 |
| P-doped Gr/Al | 5.7 | −0.0588 | 5.834 × 10−4 |
| BN/Al | 4.2 | −0.0044 | 4.366 × 10−5 |
3.2 Binding energy & fracture energy
The binding energy and fracture energy between aluminum and 2D monolayers of Gr, SiC, P-doped Gr, and BN are shown in Table 2. Each material was analyzed based on its energies when bonded and separated, leading to the calculation of the respective binding energies using eqn (1). The work of adhesion for each material was then calculated using eqn (2).Graphene exhibited a binding energy of −0.0027 Hartree. This indicates a weak interaction between Al and Gr, suggesting limited stability when bonded. This is consistent with previous predictions, due to Gr's inert properties and lattice constant far lower than Al's.
SiC demonstrated a more substantial binding energy of −0.0733 Hartree, indicating a stronger interaction between Al and SiC and highlighting its potential for applications requiring enhanced adhesion.
P-doped Gr showed a binding energy of −0.0588 Hartree. This value reflects a moderate interaction, suggesting that doping the material has a noticeable effect, although it does not surpass that of SiC. This supports the idea that increasing Gr's lattice constant by doping with P effectively allows it to bond better with Al.
The binding energy of −0.0044 Hartree exhibited by BN indicates that similarly to Gr, it has a weak bond with Al. This suggests that BN may not be ideal for applications requiring robust interfacial interactions.
All four calculations also display relatively high fracture energies, shown in Table 2. This implies that Gr/Al, SiC/Al, P-doped Gr/Al, and BN/Al are all able to withstand high-stress situations without fracturing. Notably, SiC/Al and P-doped Gr/Al have higher fracture energies than Gr/Al and BN/Al.
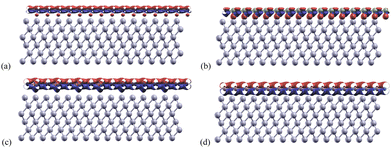
3.3 Charge transfer
Charge transfers refers to the charge difference before and after the monolayers bind to the aluminum layers. These were calculated for each structure using eqn (3) and shown in Fig. 5. The adjusted isosurface values for Al, Gr/Al, SiC/Al, P-doped Gr/Al, and BN/Al were set to be 0.004, 0.005, 0.006, and 0.007 electrons per Bohr3 respectively.In these structures, the charge transfer mechanism between Al(1 1 1) and the monolayers involves the donation of electrons from aluminum to the nanosheets. This is mainly due to the metallic nature of aluminum and its low electronegativity, which enables it to lose electrons readily.
The P-doped Gr/Al and BN/Al structures both show relatively normal charge transfers with the area between the aluminum and monolayer being an electron donor, and the area above the mono-layer being an electron acceptor. Areas of charge transfer for these materials are also much larger than for Gr/Al and SiC/Al. This increased transfer area indicates stronger bonds between the aluminum and monolayer for the materials P-doped Gr/Al and BN/Al.
The phosphorus atoms incorporated into Gr enhance its charge transfer characteristics improving its capacity to accept electrons from Al. This enhancement in bonding capacity is evidenced by the slight protrusions observed below the phosphorus atoms in Fig. 5(c), indicating a greater density of electron donation compared to the surrounding areas. This phenomenon suggests that the presence of phosphorus not only modifies the electronic structure of graphene but also facilitates more effective interactions with aluminum, confirming the important role of dopants in increasing interface strength.
3.4 Band structure
The band structure calculations presented in Fig. 6 provide insight into the effects of integrating non-metal monolayers, specifically Gr, SiC, P-doped Gr, and BN, into Al.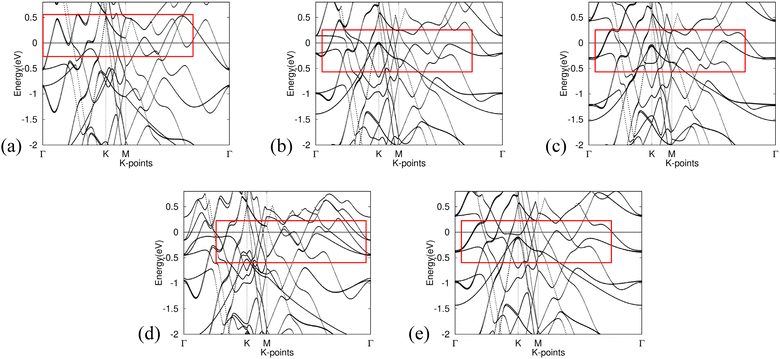 | ||
| Fig. 6 Band structure for (a) Al, (b) Gr/Al, (c) SiC/Al, (d) P-doped Gr/Al, and (e) BN/Al. Fermi level is adjusted for in the calculations. The red boxes highlight areas showing low effective mass. | ||
Despite the incorporation of non-metal elements into the aluminum metal matrix, all calculated composite materials retain the intrinsic metallic characteristics of aluminum. This is evidenced by the presence of bands crossing the Fermi level in all five band structures, as well as the notable similarities observed among them.
The consistency of these band structures indicates that the fundamental electronic properties of aluminum remain largely unaltered by the addition of nonmetal monolayers. Consequently, the resulting compounds are expected to exhibit similar properties, such as malleability.
Furthermore, all band structures calculated exhibit bands with significant curvature near the Fermi level, indicating a small effective mass for the charge carriers. Eqn (4) implies an inverse relationship between effective mass and conductivity. As such, Gr/Al, SiC/Al, P-doped Gr/Al, and BN/Al are all predicted to have good conductivity, an important factor to consider in aerospace engineering.
4 Conclusion
In this study, we have explored the possibility of reinforcing aluminum with various two-dimensional monolayers, specifically graphene, silicon carbide, phosphorus-doped graphene, and boron nitride, using density functional theory (DFT) calculations to assess their material properties and performance.Analysis of electronic structures suggests that silicon carbide and phosphorus-doped graphene are the most promising mono-layers for integration into aluminum, due to the greater amount of charge transferred. It also revealed that the incorporation of phosphorus into graphene can increase the structure's lattice constant as to better fit with the aluminum, thus reinforcing interfacial interactions. Despite the introduction of non-metallic components, the fundamental metallic characteristics of aluminum were preserved within the composites. This preservation bodes well for maintaining desirable mechanical properties such as conductivity and malleability, which are essential components for aerospace applications.
The overall results indicate that silicon carbide and phosphorus-doped graphene are the most promising candidate among the materials studied for applications involving aluminum, due to their relatively high binding energy and fracture energy. Graphene and boron nitride exhibited weaker bonds, indicating lesser suitability for applications requiring adhesion of monolayrs to strengthen aluminum.
Future research is required to determine the relative strengths of SiC and P-doped Gr monolayers when added to Al. Long-term durability and thermal stability tests would also be needed to analyze their value as potential aerospace materials. However, such assessments fall beyond the scope of this paper.
Author contributions
All DFT calculations, data collections, data collection, visualizations and models, and writing – first draft, editing, final draft, and reviewing – were done by Ellie Zhang. Xuan Luo contributed to editing, reviewing, and overall development of the paper.Data availability
Data for this article, including all figures and tables, are available at Open Science Framework at https://doi.org/10.17605/OSF.IO/WUHPY.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
The authors would like to acknowledge and thank Dr Gefei Qian for his valuable insights and technical support.Notes and references
- P. Rambabu, N. Eswara Prasad, V. Kutumbarao and R. Wan-hill, Aerospace materials and material technologies, aerospace materials, 2017, vol. 1, pp. 29–52 Search PubMed.
- P. Dwivedi, A. N. Siddiquee and S. Maheshwari, Russian Journal of Non-Ferrous Metals, 2021, vol. 62, pp. 212–225 Search PubMed.
- X. Zhang, Y. Chen and J. Hu, Prog. Aerosp. Sci., 2018, 97, 22–34 CrossRef.
- F. Czerwinski, Materials, 2020, 13, 3441 CrossRef CAS PubMed.
- S. Y. Karaoglu, S. Karaoglu and I. Ünal, Int. J. Aviation Sci. Technol., 2021, 2, 73–81 Search PubMed.
- A. Tiwary, R. Kumar and J. S. Chohan, Mater. Today: Proc., 2022, 51, 865–870 CAS.
- B. N. Bhat, A. B. Pandey, S. Tamirisakandala, M. V. Nathal, D. L. Ellis, P. B. McGill, J. A. Lee, S. E. Davis, J. Koo and A. Nettleset al., Aerospace Materials Characteristics, American institute of aeronautics and astronautics technical report, 2018 Search PubMed.
- A. Md Ali, M. Z. Omar, H. Hashim, M. S. Salleh and I. F. Mo-hamed, Rev. Adv. Mater. Sci., 2021, 60, 801–817 Search PubMed.
- D. G. Papageorgiou, I. A. Kinloch and R. J. Young, Prog. Mater. Sci., 2017, 90, 75–127 CrossRef CAS.
- P. L. Kumar, A. Lombardi, G. Byczynski, S. N. Murty, B. Murty and L. Bichler, Prog. Mater. Sci., 2022, 128, 100948 CrossRef.
- M. E. Turan and F. Aydin, Mater. Sci. Technol., 2020, 36, 1092–1103 CrossRef CAS.
- J. Liu, J. Shen, Z. Zheng, Y. Wu and L. Zhang, Nanotechnology, 2015, 26, 291003 CrossRef PubMed.
- M. Rashad, F. Pan, A. Tang and M. Asif, Prog. Nat. Sci.: Mater. Int., 2014, 24, 101–108 CrossRef CAS.
- S. F. Bartolucci, J. Paras, M. A. Rafiee, J. Rafiee, S. Lee, D. Kapoor and N. Koratkar, Mater. Sci. Eng., A, 2011, 528, 7933–7937 CrossRef CAS.
- S. Chand, P. Chandrasekhar, R. Sarangi and R. Nayak, Mater. Today: Proc., 2019, 18, 5356–5363 CAS.
- P. Sedigh, A. Zare and A. Montazeri, Comput. Mater. Sci., 2020, 171, 109227 CrossRef CAS.
- S. Yadav, S. Gangwar and S. Singh, Mater. Today: Proc., 2017, 4, 5571–5582 Search PubMed.
- M. Meyyappan, Nanotechnology Aerospace Applications, 2007, pp. 1–2 Search PubMed.
- J. Huang, M. Li, J. Chen, Y. Cheng, Z. Lai, J. Hu, F. Zhou, N. Qu, Y. Liu and J. Zhu, Surf. Interfaces, 2023, 38, 102825 CrossRef CAS.
- H. Nam, S. Jang and W. Lee, J. Nanosci. Nanotechnol., 2014, 14, 7674–7678 CrossRef CAS PubMed.
- H. Zakaria, Ain Shams Eng. J., 2014, 5, 831–838 CrossRef.
- Ö. Güler and N. Bagcı, J. Mater. Res. Technol., 2020, 9, 6808–6833 CrossRef.
- H. P. Kumar and M. A. Xavior, Procedia Eng., 2014, 97, 1033–1040 CrossRef CAS.
- Z. Baig, O. Mamat and M. Mustapha, Crit. Rev. Solid State Mater. Sci., 2018, 43, 1–46 CrossRef CAS.
- M. Bastwros, G.-Y. Kim, K. Zhang and S. Wang, ASME In-ternational Mechanical Engineering Congress and Exposition, 2013, p. V02BT02A030 Search PubMed.
- R. R. Raj, J. Yoganandh, M. S. Saravanan and S. S. Kumar, Carbon Lett., 2021, 31, 125–136 CrossRef.
- K. Parthiban, P. Lakshmanan and A. Gnanavelbabu, Silicon, 2022, 14, 8993–9007 CrossRef CAS.
- Y. Wang, Y. Zhu, R. Li, H. Liu, W. Liu and P. He, J. Alloys Compd., 2022, 906, 164358 CrossRef CAS.
- L. Vargas-Gonzalez, R. F. Speyer and J. Campbell, Int. J. Appl. Ceram. Technol., 2010, 7, 643–651 CrossRef CAS.
- E. H. Chowdhury, M. H. Rahman and S. Hong, Comput. Mater. Sci., 2021, 197, 110580 CrossRef.
- N. Ooi, V. Rajan, J. Gottlieb, Y. Catherine and J. Adams, Mod-elling and Simulation in Materials Science and Engineering, 2006, vol. 14, p. 515 Search PubMed.
- S. N. Monteiro, A. L. D. Skury, M. G. de Azevedo and G. S. Bobrovnitchii, J. Mater. Res. Technol., 2013, 2, 68–74 CrossRef CAS.
- Y. Jiang, Z. Tan, G. Fan, Z. Zhang, D.-B. Xiong, Q. Guo, Z. Li and D. Zhang, Carbon, 2020, 161, 17–24 CrossRef CAS.
- A. Saboori, M. Pavese, C. Badini and P. Fino, Acta Metall. Sin., 2017, 30, 675–687 CrossRef CAS.
- T. Etter, P. Schulz, M. Weber, J. Metz, M. Wimmler, J. F. Löffler and P. Uggowitzer, Mater. Sci. Eng., A, 2007, 448, 1–6 CrossRef.
- D. Zhang, A. F. Fonseca, T. Liang, S. R. Phillpot and S. B. Sinnott, Phys. Rev. Mater., 2019, 3, 114002 CrossRef CAS.
- R. Ranjan and V. Bajpai, Adv. Powder Technol., 2023, 34, 104021 CrossRef CAS.
- M. Li, K. Ma, L. Jiang, H. Yang, E. J. Lavernia, L. Zhang and J. M. Schoenung, Mater. Sci. Eng., A, 2016, 656, 241–248 CrossRef CAS.
- C. Rohmann, V. I. Yamakov, C. Park, C. Fay, M. Hankel and D. J. Searles, J. Phys. Chem. C, 2018, 122, 15226–15240 CrossRef CAS PubMed.
- A. V. Krasheninnikov, N. Berseneva, D. G. Kvashnin, J. Enko-vaara, T. Bjorkman, P. Sorokin, D. Shtansky, R. M. Nieminen and D. Golberg, J. Phys. Chem. C, 2014, 118, 26894–26901 CrossRef CAS.
- D. Lahiri, V. Singh, L. H. Li, T. Xing, S. Seal, Y. Chen and A. Agarwal, J. Mater. Res., 2012, 27, 2760–2770 CrossRef CAS.
- E. K. Gross and R. M. Dreizler, Density functional theory, Springer Science & Business Media, 2013, vol. 337 Search PubMed.
- N. F. Domancich, R. M. Ferullo and N. J. Castellani, J. Theor. Comput. Chem., 2014, 13, 1450055 CrossRef CAS.
- A. H. Romero, D. C. Allan, B. Amadon, G. Antonius, T. App-lencourt, L. Baguet, J. Bieder, F. Bottin, J. Bouchet, E. Bous-quet, F. Bruneval, G. Brunin, D. Caliste, M. Côté, J. Denier, C. Dreyer, P. Ghosez, M. Giantomassi, Y. Gillet, O. Gingras, D. R. Hamann, G. Hautier, F. Jollet, G. Jomard, A. Mar-tin, H. P. C. Miranda, F. Naccarato, G. Petretto, N. A. Pike, V. Planes, S. Prokhorenko, T. Rangel, F. Ricci, G.-M. Rig-nanese, M. Royo, M. Stengel, M. Torrent, M. J. van Setten, B. V. Troeye, M. J. Verstraete, J. Wiktor, J. W. Zwanziger and X. Gonze, J. Chem. Phys., 2020, 152, 124102 CrossRef CAS PubMed.
- X. Gonze, B. Amadon, G. Antonius, F. Arnardi, L. Baguet, J.-M. Beuken, J. Bieder, F. Bottin, J. Bouchet, E. Bousquet, N. Brouwer, F. Bruneval, G. Brunin, T. Cavignac, J.-B. Char-raud, W. Chen, M. Côté, S. Cottenier, J. Denier, G. Gen-este, P. Ghosez, M. Giantomassi, Y. Gillet, O. Gingras, D. R. Hamann, G. Hautier, X. He, N. Helbig, N. Holzwarth, Y. Jia, F. Jollet, W. Lafargue-Dit-Hauret, K. Lejaeghere, M. A. L. Mar-ques, A. Martin, C. Martins, H. P. C. Miranda, F. Naccarato, K. Persson, G. Petretto, V. Planes, Y. Pouillon, S. Prokhorenko, F. Ricci, G.-M. Rignanese, A. H. Romero, M. M. Schmitt, M. Torrent, M. J. van Setten, B. V. Troeye, M. J. Verstraete, G. Zérah and J. W. Zwanziger, Comput. Phys. Commun., 2020, 248, 107042 CrossRef CAS.
- J. P. Perdew, S. Kurth, A. Zupan and P. Blaha, Phys. Rev. Lett., 1999, 82, 2544 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1998, 80, 891 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- N. Holzwarth, A. Tackett and G. Matthews, Comput. Phys. Commun., 2001, 135, 329–347 CrossRef CAS.
- A. Tackett, N. Holzwarth and G. Matthews, Comput. Phys. Commun., 2001, 135, 348–376 CrossRef CAS.
- P. Liu, J. Xie, A. Wang, D. Ma and Z. Mao, Appl. Surf. Sci., 2020, 517, 146040 CrossRef CAS.
- J. Huang, Y. Liu, Z. Lai, J. Hu, F. Zhou and J. Zhu, Vacuum, 2022, 204, 111346 CrossRef CAS.
- R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Sci. Data, 2016, 3, 1–13 Search PubMed.
- T. M. Ozoji, Z.-X. Zhang, A. E. Aladejare, N. Zhang, N. Paaso-vaara and M. R. Arrieta, Eng. Fract. Mech., 2024, 295, 109763 CrossRef.
- S. Zhang, D. He, P. Huang and F. Wang, Mater. Des., 2021, 201, 109509 CrossRef CAS.
- Z. Xu and M. J. Buehler, J. Phys.: Condens. Matter, 2010, 22, 485301 CrossRef PubMed.
- A. Kulkarni, K. H. Schulz, T. Lim and M. Khan, Thin Solid Films, 1999, 345, 273–277 CrossRef.
- S. Yu, H. D. Xiong, K. Eshun, H. Yuan and Q. Li, Appl. Surf. Sci., 2015, 325, 27–32 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |