In situ investigation of controlled polymorphism in mechanochemistry at elevated temperature

Abstract

Mechanochemistry routinely provides solid forms (polymorphs) that are difficult to obtain by conventional solution-based methods, making it an exciting tool for crystal engineering. However, we are far from identifying the full scope of mechanochemical strategies available to access new and potentially useful solid forms. Using the model organic cocrystal system of nicotinamide (NA) and pimelic acid (PA), we demonstrate with variable temperature ball milling that ball milling seemingly decreases the temperature needed to induce polymorph conversion. Whereas Form I of the NA:PA cocrystal transforms into Form II at 90 °C under equilibrium conditions, the same transition occurs as low as 65 °C during ball milling: a ca 25 °C reduction of the transition temperature. Our results indicate that mechanical energy provides a powerful control parameter to access new solid forms under more readily accessible conditions. We expect this ‘thermo-mechanical’ approach for driving polymorphic transformations to become an important tool for polymorph screening and manufacturing.

---

Mechanochemistry has emerged as an environmentally benign alternative to traditional solution-based chemical and materials processing.¹ This sustainable nature owes largely to the absence of solvent necessary for mechanochemical reactions, alongside the commonly higher yields and reduced reaction times that they need.^2–4 Correspondingly, mechanochemical research has risen to the forefront of efforts in green and sustainable chemistry. In addition to its leading role for achieving goals in sustainable chemistry, mechanochemical technologies offer routes to entirely new materials that simply cannot be prepared by other methods. This includes new molecules,⁵ defect-laden materials with altered or enhanced physico-chemical properties,^6–8 new metastable crystal forms,^9–11 or the ability to generate pure bulk powders that by solution chemistry are impure.¹²

The rich variety of benefits offered by mechanochemistry stems from the unique conditions under which these reactions take place. Unlike in solution, the product obtained by solid-state mechanochemical methods results from an interplay between the stress that drives the system away from equilibrium and thermal relaxation that brings the material back to its nascent state.^13,14 Furthermore, the mass transport between solid particles is kinetically hindered, and the thermodynamic state (e.g. pressure and temperature) of the system is transient and spatially localized. Together these conditions often lead to the appearance of kinetically trapped (or metastable) products,^15–17 which are difficult to synthesize by other means.

Though they can appear to be ‘brute force’ methods, a remarkable degree of control is possible over mechanochemical processes. For example, the outcome of a mechanochemical reaction can be tuned to significant degrees by including additives (liquid,^18,19 solids,^20,21 or polymers^16,22) or by changing the material of the milling jar^16,23,24 and ball.^25–28 Though it is a natural analogy to solution chemistry, attempts to fine-tune mechanochemical reactions by either controlling the bulk temperature or by changing the magnitude of the input mechanical energy have been less commonly explored, particularly regarding organic materials. In fact, only a handful of studies have so far reported on controlling organic mechanochemical transformations with milling temperature,^29–32 energy input,^28,33 or their combination: ‘thermo-mechanical’ control.³⁴ However, these early studies do indicate that an interplay between the equilibrium milling temperature and milling intensity can increase the mechanochemical reactivity of the chemical system, and can even facilitate control over very ‘delicate’ physicochemical transformations, such as polymorphic outcome.^29,34 Further studies into the thermo-mechanical control of organic mechanochemical transformations is therefore warranted.

To investigate how temperature and energy input influence a mechanochemical transformation, solid state polymorphic transitions are excellent candidates. These transitions are very sensitive to small changes in experimental conditions, with polymorphs of organic molecules typically differing by < 2–3 kJ mol⁻¹.³⁵ In addition to their academic intrigue, polymorphs have significant importance across industrial sectors, with different crystal forms regularly having notably different physical properties, including solubility/bioavailability,³⁶ hardness,³⁷ tabletability,³⁸ and colour.³⁹ Our ability to control polymorphism through mechanochemical technologies is therefore essential for translating mechanochemical processes from the lab bench to real-world industrial applications.

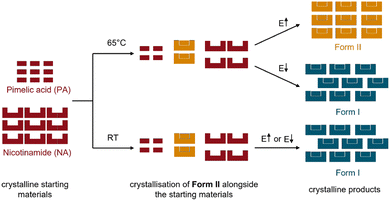
In this regard, we here investigate how the mechanochemical polymorphism of molecular cocrystals can be controlled with thermo-mechanical conditions, i.e. through combinations of milling energy and bulk milling temperature. As a model system we study the 1 : 1 cocrystal of nicotinamide (NA) and pimelic acid (PA), NA:PA, which has two known polymorphic forms, Form I and Form II,^40,41Fig. 1.

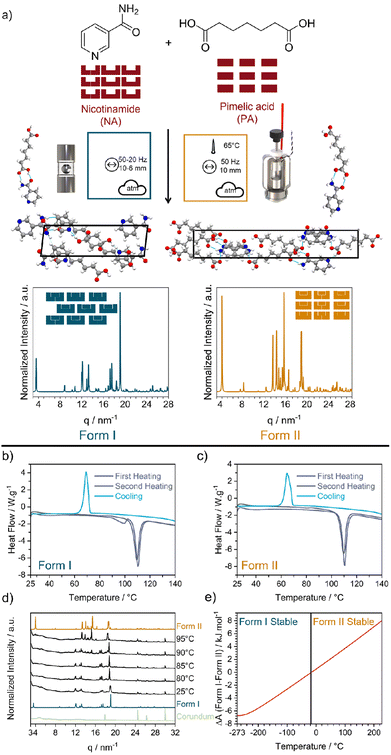Fig. 1 (a) Reaction scheme for the mechanochemical reaction of nicotinamide (NA) and pimelic acid (PA) to form their 1 : 1 cocrystal NA:PA. Mechanochemical reaction nomenclature is taken from ref. 1. The crystal structure of Form I and Form II were obtained from the CCDC database (Form I: NUKYUO01 and Form II: NUKYUO03) atoms are coloured as: H (white), C (grey), O (red) and N (blue). The effect of heating on the polymorphs of the NA:PA cocrystal. DSC measurements of (b) Form I and (c) Form II. Both polymorphs were heated to 147 °C (purple), cooled to 25 °C, and reheated to 147 °C (gray). (d) Variable temperature PXRD patterns of Form I. PXRD patterns for Form I, Form II, and the empty jar are given for comparison. (e) Different of the simulated Helmholtz free energy (A) from Form I and Form II. The change in relative stability, according to our DFT simulations, is marked by a black vertical line at −13 °C.

Form I of NA:PA is reported to be thermodynamically stable under ambient conditions, with Form II becoming the stable form at elevated temperatures.^40,42 Both forms can be prepared by ball milling: Form I is reportedly obtained by neat grinding at ambient temperature⁴⁰ and, as we have found in this work (ESI S2†), Form II is obtained by ball milling at elevated temperatures. Consistent with the literature,⁴⁰ our differential scanning calorimetry (DSC) measurements of Form I, Fig. 1b, show two endotherms. The first endotherm at 90 °C presumably corresponds to the transformation from Form I to Form II, while the second endotherm at 110 °C is consistent with the melting of Form II. Notably, when the melt of Form I was cooled (at either 1, 5, or 10 K min⁻¹) Form II was obtained. Only a single endotherm at 110 °C (i.e. melting) was observed on the second heating. This simpler DSC trace is consistent with that of pure Form II, Fig. 1c and S1.4–1.5,† wherein only a single endotherm for both the first and second heating was observed. Thus, while Form I converts to Form II upon heating, there is no reverse thermal transition. The interpretation of the DSC traces was confirmed by variable-temperature powder X-ray diffraction (VT-PXRD), which revealed a transition from Form I to Form II at ca 90–95 °C, Fig. 1d, without any signs of transitions from Form II to Form I, Fig. S1.6b.†

To further explore the stability of Form I and Form II, slurry and stability test experiments were performed. When a powder of mechanochemically prepared Form II was aged under ambient conditions, traces of Form I appeared within 12 days, although traces of Form II remained even after 61 days (Fig. S1.2†). This slow conversion of Form II → Form I at room temperature has been previously noted.⁴² In full agreement with stability test experiments, slurrying 1 : 1 mixtures of Form I and Form II in a range of solvents also led to formation of pure Form I, ESI S1.3,† lending support to the thermodynamic stability of Form I over Form II at room temperature. Moreover, we note previous high temperature slurry experiments, which indicated that the reverse transformation of Form I → Form II occurs when slurried > 85 °C.⁴⁰ This thermodynamic transition temperature is consistent with our DSC studies.

As a final check of polymorph stability, we investigated the cocrystal forms using DFT simulations. At the PBE-TS level of theory our calculations confirm that Form I is energetically stable at low temperatures. However, when entropic corrections were applied, our simulations do suggest that Form II becomes stable at higher temperatures, Fig. 1e. This is in excellent agreement with our DSC and VT-PXRD measurements, both of which showed a transformation from Form I to Form II upon heating. However, we note that our predicted transition temperature (−13 °C) is significantly lower than that observed experimentally, which is presumably due to our omission of thermal expansion effects. Regardless, our experiments (Fig. 1d) and calculations (Fig. 1e) indicate that Form I and Form II of the NA:PA cocrystals are enantiotropically related, and the expectation of their conversion at elevated temperatures makes them an excellent system to probe thermo-mechanical effects in mechanochemistry.

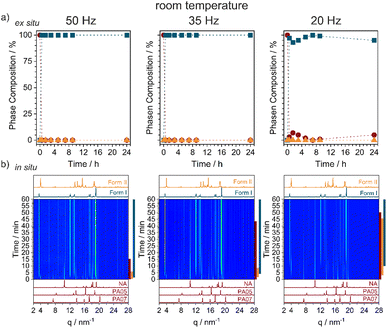
By neat grinding stoichiometric mixtures of NA + PA at ambient conditions we consistently obtained Form I, Fig. 2a and S2.1,† regardless of the milling frequency (50, 35, and 20 Hz) or milling ball size (10, 8, or 6 mm). However, the rate at which Form I appeared depended strongly on the milling conditions. Our highest energy conditions (50 Hz, 10 mm ball) achieved pure Form I after only 15 min of milling, with the lowest energy conditions (20 Hz, 6 mm ball) needing >24 h to convert all of the starting material. Remarkably, time-resolved in situ (TRIS) PXRD revealed a more complex reaction profile, Fig. 2b and S2.2.† Within the first minutes of ball milling at 50 Hz (10 mm ball), transient formation of Form II was observed (see Bragg reflections at q = 3.95 and 18.59 nm⁻¹), though it converted quickly to the final Form I product (see Bragg reflections at q = 3.48 and 18.92 nm⁻¹). By reducing the milling frequency we could extend slightly the lifetime of this transient Form II phase, but it always preceded the emergence of Form I. Form II therefore appears to be a kinetic product under ambient temperature ball milling conditions, with this serving as an excellent example of how TRIS methods help to catch short-lived intermediates in mechanochemical transformations (Fig. 3).⁴³

Fig. 2 Reaction profiles for the ball milling synthesis of NA:PA at ambient temperature using a 10 mm diameter milling ball. (a) Phase composition of the mechanochemically prepared powder, with the composition shown as (red circles) the sum of reagents, (blue squares) Form I, and (orange triangles) Form II. All data were obtained using ex situ PXRD analysis. (b) Time-resolved in situ (TRIS) PXRD measurements of the mechanochemical reaction. The coloured bars on the right-hand side aid visualization of which phases are present throughout the reaction: (red) starting materials, (blue) Form I, and (orange) Form II.

Fig. 3 Schematic representation of the ball milling reaction of the cocrystal NA:PA at ambient temperature (RT) and at 65 °C (sum of the starting materials: red, Form I: blue, and Form II: orange). Note that E indicates a change in milling energy, through either change in milling frequency or the mass of the milling ball.

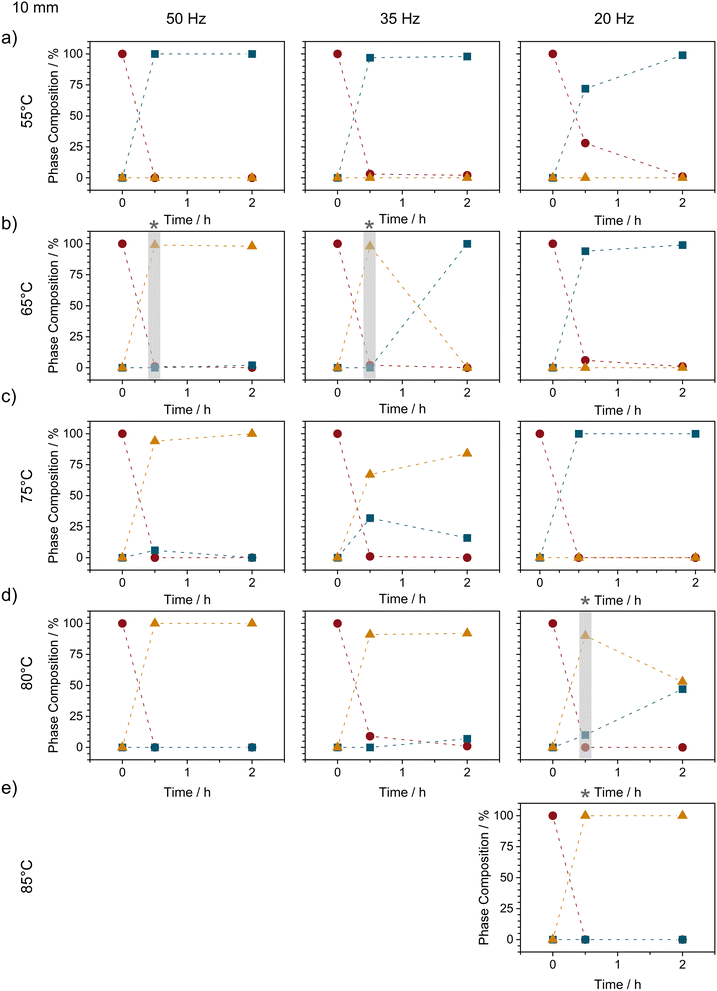
Inspired by our previous findings that thermo-mechanical conditions can reduce polymorph transition temperatures,³⁴ we sought to explore whether–instead of using ball milling energy as a control parameter–the lifetime of Form II could be elongated by ball milling at elevated temperatures. When equimolar mixtures of NA + PA were milled (50 Hz, 10 mm ball) at 45 °C (i.e. slightly above the intrinsic heating associated with milling: ca 35 °C³⁴) we did not observe any notable elongation of the Form II lifetime, see ESI S2.3.† However, when the bulk temperature was increased to 55 °C, our TRIS studies showed that the lifetime of Form II more than doubled, from 3 min to nearly 10 min, Fig. S2.3.† Remarkably, a slight further increase to only 65 °C (still ca. 25 °C below the thermodynamic polymorphic transition temperature, Fig. 1) caused Form II to remain stable for at least 2 h of ball milling, Fig. 4 and S2.4.†

Fig. 4 The ex situ phase composition of variable temperature ball milling experiments of NA + PA at different milling frequencies using a 10 mm stainless steel ball. Compositions are shown at various milling times obtained at temperatures of (a) 55 °C, (b) 65 °C, (c) 75 °C, (d) 80 °C, and (e) 75 °C. Phase compositions are shown as (red circle) the sum of both reagents, (blue squares) Form I, and (orange triangles) Form II. To aid visualization, a grey bar at star are used to indicate when Form II was first observed. Unfortunately, PMMA jars become fragile at elevated temperatures with experiments at 50 and 35 Hz becoming impossible at 85 °C.

As the milling intensity was reduced from 50 to 35 Hz at 65 °C, the overall reaction profiles were elongated (see Fig. S2.4†), as can usually be expected. However, while the reaction slowed, reducing the milling frequency had the opposite effect on the lifetime of Form II, which reduced from >2 h at 50 Hz to only ca 1 h at 35 Hz, and lower still (<30 min) at 20 Hz milling, Fig. 4 and S2.4.†

This apparent correlation between Form II lifetime and the balance of heat and milling intensity points towards a thermo-mechanical energy threshold above which the combined energy provided by heating and mechanical energy is sufficient to stabilise Form II. In this respect we began to further increase the bulk milling temperature with the hopes to increase the lifetime of Form II at lower frequencies. Although little difference was observed (albeit without exceptional temporal resolution) between 65 °C and 75 °C, stark changes in Form II stability were observed when milling was performed at 80 °C, Fig. 4d. Notably, at 80 °C (still ca 10 °C below the equilibrium conversion temperature), Form II remained present in the powder even after 2 h of milling (as a mixture with Form I). With a slight increase in milling temperature to 85 °C (ca 5–7 °C below the equilibrium temperature), we were finally able to stabilise Form II for >2 h of continued ball milling.

In summary, using a temperature-controlled milling setup,³⁴ we investigated polymorphisms in the model stoichiometric organic cocrystal system nicotinamide (NA) and pimelic acid (PA). While ball milling at ambient temperature led to the formation of Form I, Form II was readily prepared by ball milling at 65 °C, 25 °C below the equilibrium thermal transition point observed by variable-temperature powder X-ray diffraction and differential scanning calorimetry. Notably, as the milling energy was reduced, the temperature needed to achieve conversion of Form I to Form II increased, indicating the existence of a thermo-mechanical energy balance in the mechanochemical polymorphism. Our ball milling experiments demonstrate that a high degree of control over mechanochemical polymorphisms can be obtained by a combination of milling temperature and milling energy. It is possible to stabilize the polymorph at a lower temperature than a solid state transformation that can be detected by heating alone (VT-PXRD or DSC). Though we have not yet identified the physical origin of this thermo-mechanical control, we propose that it may involve changes in the ease of crystal comminution at elevated temperatures, making our ability to stabilise metastable phases as nanocrystalline powders more easily at higher temperatures. Such findings would be consistent with recent theories for ball milling polymorph control in organic crystals proposed by Belenguer⁴⁴ and Cruz-Cabeza.⁴⁵ Such detailed investigations will be the subject of a follow-up investigation. Regardless, a better understanding of this feature promises further development toward greener and more sustainable chemistry.

Experimental and computational details

Materials

All chemicals were purchased from commercial suppliers and used without further purification: nicotinamide (SIGMA, >99.5%) and pimelic acid (ROTH, >99%)

Ball milling

A custom-designed three-part milling jar was used for all milling experiments (both ex situ and in situ).⁴⁶ The jars are made of two V2A stainless steel caps and a central cylinder made of polymethylmethacrylate (PMMA) with a wall thickness of 0.7 mm. For the variable temperature ball milling experiments, a temperature-controlled jacket holder was used (for more details see ref. 34). Ball milling experiments were performed with a Pulverisette 23 (Frisch, Germany) vibratory ball mill at 50, 35, or 20 Hz with one stainless steel milling ball of 10 (4.04 ± 0.02 g), 8 (2.07 ± 0.01 g), and 6 mm (0.87 ± 0.01 g) in diameter for 0.5–24 h, as indicated in the text. The 1 : 1 cocrystal of nicotinamide and pimelic acid (NA:PA) was synthesized by co-grinding stoichiometric mixtures of nicotinamide (43 mg, 0.35 mmol) and pimelic acid (57 mg, 0.35 mmol). The cocrystal was obtained as a white crystalline powder after ball milling. The powder was characterized immediately after ball milling by powder X-ray diffraction and thermal analysis.

Ex situ powder X-ray diffraction

All powders were characterized by powder X-ray diffraction (PXRD). Diffraction patterns for powders collected from ball milling experiments were measured using a D8 Discover diffractometer (Bruker, AXS, Germany) with Cu K_α1 (λ = 0.154060 nm) radiation equipped with a Ni K_β filter, over a 2θ range from 4 to 40° using a step size of 0.009° and a step time of 2.5 s. To monitor long-term phase stability, diffraction patterns of Form II were measured daily over a 61 day period to identify changes in phase composition and crystallinity. These long-term experiments were performed using a D8 Advance diffractometer (Bruker, AXS, Germany) with Cu K_α1 (λ = 0.154060 nm) and Cu K_α2 (λ = 0.154440 nm) radiation, over a 2θ range from 4 to 40° using a step size of 0.02° and a step time of 1 s. Variable temperature PXRD measurements (VT-PXRD) were also performed using a D8 Advance diffractometer (Bruker, AXS, Germany) over a range of 4–40° using a step size of 0.02° and a step time of 1.0 s. Form I and Form II powders were heated using a corundum heating plate in the temperature range of 25 °C to 400 K at a rate of 10 °C min⁻¹ with equilibration periods of 3 min per data point. For all PXRD data, Rietveld refinement was performed within the Topas V64 suite by refining the data against literature crystallographic structures, as deposited in the Cambridge Crystallographic Center (CCDC): Form I (NUKYUO01 (ref. 40)), Form II (NUKYUO03 (ref. 41)), nicotinamide (NICOAM⁴⁷), and pimelic acid (PIMELA05,⁴⁸ PIMELA07 (ref. 49)).

Time-resolved in situ (TRIS) powder X-ray diffraction

Time-resolved in situ (TRIS)⁴³ PXRD measurements were performed at the μ-spot beamline⁵⁰ at BESSY-II (Helmholtz-Zentrum Berlin für Material und Energie). Monochromatic radiation with λ = 0.7314 nm (16.95 keV) was used, and each PXRD pattern was obtained by accumulating the scattering intensities for 5 s. The position of the mill was selected so that the X-ray beam passed through the shortest length of the jar to minimize artificial peak broadening.⁴⁶ The obtained diffractograms were reduced using DPDAK v150 (ref. 51) and the background correction was performed in Python using the arPLS method.⁵²

Differential scanning calorimetry (DSC)

DSC measurements were performed using a METTLER Toledo TGA/DSC 3+ instrument. Form I and Form II powders were prepared via mechanochemistry and measured immediately after ball milling. The powders were heated from 27 to 147 °C, cooled from 420 to 27 °C, and heated again from 27 to 147 °C in an open aluminum crucible with nitrogen supplied. The heating and cooling rates were set at the same speed of 10, 5, or 1 °C min⁻¹ as indicated in the text. The measurements were performed with a mass of 4 ± 0.4 mg.

Slurry experiments

Suspensions of 100 mg of 1 : 1 mixture of Form I and Form II were weighted into a glass beaker and 300 μL of varying solvents (cyclohexane, ethanol, or acetonitrile) was added. The suspensions were stirred for three days, before the powder was filtered off, dried, and analysed by powder X-ray diffraction.

Solid state DFT

All simulations were performed within the framework of plane wave Density Functional Theory, as implemented in CASTEP v19.11 (ref. 53). Simulations were performed on experimental crystal structures obtained from the Cambridge Crystallographic Data Centre (CCDC): Form I (NUKYUO01 (ref. 40)) and Form II (NUKYUO03 (ref. 41)). The wave function was expanded in plane waves to a kinetic energy cutoff of 900 eV. The electronic structure was sampled on a Γ-centered k-point grid with a spacing no greater than 0.08 Å⁻¹. For all simulations, the exchange-correlation functional of Perdew–Burke–Ernzerhof (PBE)⁵⁴ was used with the dispersion correction of Tkatchenko–Scheffler (TS).⁵⁵ The core-valence interaction was modeled with a norm-conversing pseudopotential generated on-the-fly as implemented in CASTEP.⁵³ Convergence was accepted when residual atomic forces reached <1 × 10⁻⁵ eV Å⁻¹, with SCF convergence accepted at <1 × 10⁻¹² eV. The simulated unit cell agreed well with the experimentally obtained unit cell, Table 1. As the experiments were performed at elevated temperatures (Form I:−163 °C; Form II: 293 K), whereas the DFT simulations modeled the geometry at 0 K, an underestimation of the experimental unit cell was expected.

Table 1 Comparison of the parameters of the unit cell from Form I and Form II obtained by DFT simulations (sim; by PBE-TS) and with the parameters from experimental results (Exp). The experiments were performed at different temperatures (Form I: −163 °C; Form II: 293 K), while the simulations were done at 0 K. The difference in the volume was calculated with the equation ΔV = (V_calc − V_exp)/V_exp*100

	SG	a Å	b Å	c Å	α Å	β Å	γ Å	V Å^3	ΔV Å %
Form I^exp	P1̄	5.424	7.316	17.917	99.69	94.01	103.93	675.713	−0.09
Form I^calc	P1̄	5.340	7.428	17.851	100.704	93.293	102.685	675.096
Form II^exp	Pna21	8.838	31.514	5.252	—	—	—	1462.791	−4.99
Form II^calc	Pna21	9.725	30.203	4.732	—	—	—	1389.788

---

Phonon frequencies were calculated at the gamma point within the linear response method, as implemented in CASTEP.⁵⁶ Because of the large size of the unit cell, the complete phonon dispersion curves were computationally intractable. However, we calculated the dynamic matrices at the Γ point and on a Γ-centred 2 × 2 × 2 grid, which resulted in minimal changes in the calculated entropy with increasing q-point sampling within a small test range, Fig. S1.7.† Therefore, we believe that the approximate values obtained from our calculations are reasonable.

Author contributions

Experimental and computational investigations were carried out by KL and PCS. AALM and FE conceived, designed, and supervised the project. KL, AALM, and FE prepared the manuscript, which was discussed and agreed by KL, PCS, FE, and AALM.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank BESSY II (Helmholtz Zentrum Berlin) for beam time and BAM IT for computational resource. The computations described in this paper were also performed using the University of Birmingham's BlueBEAR HPC service, which provides a High-Performance Computing service to the University's research community. See http://www.birmingham.ac.uk/bear for more details.

Notes and references

1. A. A. L. Michalchuk, E. V. Boldyreva, A. M. Belenguer, F. Emmerling and V. V. Boldyrev, Front. Chem., 2021, 9, 29.
2. D. Breilly, S. Fadlallah, V. Froidevaux, F. Lamaty, F. Allais and T.-X. Métro, Green Chem., 2022, 24, 7874–7882.
3. J. M. Andersen and H. F. Starbuck, J. Org. Chem., 2021, 86, 13983–13989.
4. N. R. Rightmire, D. L. Bruns, T. P. Hanusa and W. W. Brennessel, Organometallics, 2016, 35, 1698–1706.
5. A. S. McCalmont, A. Ruiz, M. C. Lagunas, W. T. Al-Jamal and D. E. Crawford, ACS Sustainable Chem. Eng., 2020, 8, 15243–15249.
6. R. Kumar and T. C. Alex, Metall. Mater. Trans. B, 2015, 46, 1684–1701.
7. R. Hüttenrauch, S. Fricke and P. Zielke, Pharm. Res., 1985, 02, 302–306.
8. L. L. Driscoll, E. H. Driscoll, B. Dong, F. N. Sayed, J. N. Wilson, C. A. O’Keefe, D. J. Gardner, C. P. Grey, P. K. Allan, A. A. L. Michalchuk and P. R. Slater, Energy Environ. Sci., 2023, 16, 5196–5209.
9. Y. Zhou, F. Guo, C. E. Hughes, D. L. Browne, T. R. Peskett and K. D. M. Harris, Cryst. Growth Des., 2015, 15, 2901–2907.
10. Y. Teoh, G. Ayoub, I. Huskic, H. Titi, C. Nickels, B. Herrmann and T. Friscic, Angew. Chem., Int. Ed., 2022, 61, e202206293.
11. H. Kulla, S. Greiser, S. Benemann, K. Rademann and F. Emmerling, Cryst. Growth Des., 2017, 17, 1190–1196.
12. A. M. Belenguer, T. Friščić, G. M. Day and J. K. M. Sanders, Chem. Sci., 2011, 2, 696.
13. A. A. L. Michalchuk, Mechanochemistry and Emerging Technologies for Sustainable Chemical Manufacturing, CRC Press, Boca Raton, 1st edn, 2023, pp. 59–92.
14. V. V. Boldyrev, Russ. Chem. Rev., 2006, 75, 177–189.
15. P. Kuznetsov, L. Kuznetsova, A. Zhyzhaev, G. Pashkov and V. Boldyrev, Appl. Catal., A, 2002, 227, 299–307.
16. L. S. Germann, M. Arhangelskis, M. Etter, R. E. Dinnebier and T. Friščić, Chem. Sci., 2020, 11, 10092–10100.
17. M. Senna, Trans. Indian Inst. Met., 2023, 1–7.
18. A. M. Belenguer, G. I. Lampronti, N. De Mitri, M. Driver, C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 2018, 140, 17051–17059.
19. K. Kondo, T. Ishiyama, K. Kubota and H. Ito, Chem. Lett., 2023, 52, 333–336.
20. D. Cinčić, I. Brekalo and B. Kaitner, Cryst. Growth Des., 2012, 12, 44–48.
21. D. Zanolla, D. Hasa, M. Arhangelskis, G. Schneider-Rauber, M. R. Chierotti, J. Keiser, D. Voinovich, W. Jones and B. Perissutti, Pharmaceutics, 2020, 12, 289.
22. D. Hasa, G. Schneider-Rauber, D. Voinovich and W. Jones, Angew. Chem., Int. Ed., 2015, 54, 7371–7375.
23. E. Losev, S. Arkhipov, D. Kolybalov, A. Mineev, A. Ogienko, E. Boldyreva and V. Boldyrev, CrystEngComm, 2022, 24, 1700–1703.
24. K. Linberg, F. Emmerling and A. A. L. Michalchuk, Cryst. Growth Des., 2023, 23, 19–23.
25. A. A. L. Michalchuk, I. A. Tumanov and E. V. Boldyreva, CrystEngComm, 2019, 21, 2174–2179.
26. L. Gonnet, A. Chamayou, C. André-Barrès, J.-C. Micheau, B. Guidetti, T. Sato, M. Baron, M. Baltas and R. Calvet, ACS Sustainable Chem. Eng., 2021, 9, 4453–4462.
27. I. C. B. Martins, M. Carta, S. Haferkamp, T. Feiler, F. Delogu, E. Colacino and F. Emmerling, ACS Sustainable Chem. Eng., 2021, 9, 12591–12601.
28. K. Linberg, P. Szymoniak, A. Schönhals, F. Emmerling and A. A. L. Michalchuk, Chem.–Eur. J., 2023, e202302150.
29. G. Félix, N. Fabregue, C. Leroy, T.-X. Métro, C.-H. Chen and D. Laurencin, Phys. Chem. Chem. Phys., 2023, 25, 23435–23447.
30. K. Užarević, V. Štrukil, C. Mottillo, P. A. Julien, A. Puškarić, T. Friščić and I. Halasz, Cryst. Growth Des., 2016, 16, 2342–2347.
31. K. Užarević, N. Ferdelji, T. Mrla, P. A. Julien, B. Halasz, T. Friščić and I. Halasz, Chem. Sci., 2018, 9, 2525–2532.
32. T. Siegrist, C. Besnard, S. Haas, M. Schiltz, P. Pattison, D. Chernyshov, B. Batlogg and C. Kloc, Adv. Mater., 2007, 19, 2079–2082.
33. M. Carta, L. Vugrin, G. Miletić, M. J. Kulcsár, P. C. Ricci, I. Halasz and F. Delogu, Angew. Chem., Int. Ed., 2023, 62, e202308046.
34. K. Linberg, B. Röder, D. Al-Sabbagh, F. Emmerling and A. A. L. Michalchuk, Faraday Discuss., 2023, 241, 178–193.
35. J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165.
36. M. Pudipeddi and A. T. Serajuddin, J. Pharm. Sci., 2005, 94, 929–939.
37. C. M. Reddy, S. Basavoju and G. R. Desiraju, Chem. Commun., 2005, 2439, 3945–3947.
38. P. C. Cruz, F. A. Rocha and A. M. Ferreira, Org. Process Res. Dev., 2019, 23, 2592–2607.
39. L. R. Warren, E. McGowan, M. Renton, C. A. Morrison and N. P. Funnell, Chem. Sci., 2021, 12, 12711–12718.
40. S. Aitipamula, A. B. H. Wong, P. S. Chow and R. B. H. Tan, CrystEngComm, 2012, 14, 8193.
41. A. Lemmerer, D. A. Adsmond, C. Esterhuysen and J. Bernstein, Cryst. Growth Des., 2013, 13, 3935–3952.
42. Y. J. Lee, O. Pahom and B. L. Weeks, Cryst. Growth Des., 2019, 19, 932–941.
43. A. A. L. Michalchuk and F. Emmerling, Angew. Chem., Int. Ed., 2022, 61, 202117270.
44. A. M. Belenguer, G. I. Lampronti, A. J. Cruz-Cabeza, C. A. Hunter and J. K. M. Sanders, Chem. Sci., 2016, 7, 6617–6627.
45. P. Sacchi, S. Wright, P. Neoptolemou, G. I. Lampronti, A. K. Rajagopalan, W. Kras, C. L. Evans, P. Hodgkinson and A. J. Cruz-Cabeza, ChemRxiv, 2023, preprint,  DOI:10.26434/chemrxiv-2023-gz7kb.
46. G. I. Lampronti, A. A. L. Michalchuk, P. P. Mazzeo, A. M. Belenguer, J. K. M. Sanders, A. Bacchi and F. Emmerling, Nat. Commun., 2021, 12, 6134.
47. W. B. Wright and G. S. D. King, Acta Crystallogr., 1954, 7, 283–288.
48. V. R. Thalladi, M. Nüsse and R. Boese, J. Am. Chem. Soc., 2000, 122, 9227–9236.
49. C. A. Mitchell, L. Yu and M. D. Ward, J. Am. Chem. Soc., 2001, 123, 10830–10839.
50. I. Zizak, JLSRF, 2016, 2, A101.
51. G. Benecke, W. Wagermaier, C. Li, M. Schwartzkopf, G. Flucke, R. Hoerth, I. Zizak, M. Burghammer, E. Metwalli, P. Müller-Buschbaum, M. Trebbin, S. Förster, O. Paris, S. V. Roth and P. Fratzl, J. Appl. Crystallogr., 2014, 47, 1797–1803.
52. S.-J. Baek, A. Park, Y.-J. Ahn and J. Choo, Analyst, 2015, 140, 250–257.
53. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr.–Cryst. Mater., 2005, 220.
54. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
55. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
56. K. Refson, P. R. Tulip and S. J. Clark, Phys. Rev. B, 2006, 73, 155114.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mr00019b

---