Open Access Article
Open Access ArticleFirst-principles evaluation of transition metal dichalcogenide–graphene pairs functionalized with oxygen-containing groups for sodium-ion battery anodes†
Wonmyung
Choi
,
Sung Jun
Hong
,
Hoejeong
Jeong
and
Byungchan
Han
 *
*
Department of Chemical and Biomolecular Engineering, Yonsei University, Seoul 03722, Republic of Korea. E-mail: bchan@yonsei.ac.kr
First published on 23rd January 2024
Abstract
Composites of reduced graphene oxides (rGOs) with transition metal dichalcogenides have garnered considerable attention as promising anode materials for sodium-ion batteries (SIBs) because of their superior theoretical capacity and long-term stability compared with pure graphene. However, the underlying mechanism of how the oxygen functional groups improve the functionality of rGO remains unclear. In this study, we investigated the roles of functional groups in rGO-based heterogeneous bilayers using first-principles density functional theory calculations. The thermodynamic affinities to Na atoms, kinetic diffusion, and working potential behaviors of the Na atoms in various models, such as MoS2/graphene (Gr), MoS2/Gr–O, MoS2/Gr–OH, and MoS2/Gr–COOH, were accurately evaluated. It is clearly demonstrated that the noncovalent bonding nature is a predominant descriptor of Na affinity rather than the charge distribution around the intercalated Na atom. The activation barriers for Na atomic diffusion in the MoS2/Gr, MoS2/Gr–O, MoS2/Gr–OH, and MoS2/Gr–COOH models were estimated to be 0.24, 0.27, 0.35, and 0.31 eV, respectively. This indicated that the functional groups slightly delayed the Na motion. Notably, the obtained results demonstrated that the –COOH group not only enhanced the affinity towards Na intercalation but also induced a low working voltage at approximately 1 V. Therefore, the carboxyl functional group exhibits high material stability, making rGO a promising candidate for SIB anode materials.
Introduction
Following the declaration of achieving carbon neutrality by 2050, concerns over the energy crisis and environmental degradation have increased significantly, further accelerating the transition from fossil fuels to renewable energy sources.1,2 It is unsurprising that the demand for electric energy storage devices powering transport vehicles has led to the considerable growth of the rechargeable battery market.3 Presently, lithium-ion batteries (LIBs) are the most widely commercialized rechargeable batteries for electric vehicles owing to their outstanding electrochemical performance, such as thermodynamically high energy density and kinetically fast response to external load.4However, LIBs face several various challenges that need to be addressed, including material and manufacturing costs and limited lithium resources.5 Furthermore, the desire for energy density is far more quickly increasing than that of LIB materials. Over the last decade, sodium-ion batteries (SIBs) have garnered considerable attention as potential solutions to the challenges of LIBs. Sodium (Na) is one of the most abundant elements on Earth, and it is significantly cheaper than Li.6 It is noteworthy that the capacity and long-term stability of SIBs are critically dependent on anodes.7 Searching for suitable anodic materials to host Na is, however, quite challenging and currently still ongoing.8 Graphite was previously considered a potential candidate; however, it was observed that its intercalation capacity was not high owing to insufficient interplanar distance to accommodate Na.9 Graphitic carbon was also problematic because of significantly weak chemical interaction to intercalate Na and considerable material instability.10
Recently, metallic compounds of oxides, sulfides, and phosphides have been studied as alternatives to the carbon-based SIB anodes.11 For instance, TiO2 and Nb5O5 compounds exhibited high rate capability and specific capacity.12 Sn- and Sb-based compounds demonstrated alloying and conversion reaction mechanism over Na intercalation and deintercalation processes in which the capacity reached 847 and 896 mA h g−1, respectively.13 Transition metal dichalcogenides (TMDs) have also garnered considerable attention as anode materials for SIBs owing to their high storage capacity and ionic diffusivity.14–19 In particular, TMDs are able to facilitate a multiple electron transfer reaction through providing relevant active sites for intercalation, conversion, and alloying reactions. Moreover, their large interlayer spacing and high electron concentration make them attractive for use as SIB anodes.20
It was reported, however, that the homogeneous layers of TMDs or metallic compounds are still insufficient for anodes of SIBs because of several flaws: low electronic conductivity and cyclic capability, phase transition, and mechanical degradation over the charging/discharging processes.21 To address these problems, David22 attempted to interface two different two-dimensional (2D) materials of high electric conductivity and mechanical elasticity, resulting in a variety of heterogeneous layers with TMDs (such as MoS2) and carbon or graphene (hard carbon,23 soft carbon,24 carbon fiber,25 carbon nanotube,26 graphene,27 and reduced graphene oxide (rGO)28). In this aspect, bimetallic heterostructures (BMHs) and 2D transition metal carbide and nitride (MXene) were also suggested as SIB anodes.29 For instance, BMHs Sb2S2/FeS2 exhibited a superior rate capability of 537.9 mA h g−1 and cyclic stability with 85.7% capacity retention after 1000 cycles at 5 A g−1.30 There was, however, still a significant decrease in specific capacity after the first cycle, leading to active research on the intercalation mechanism on the interlayer surface.31
Graphene has been widely used as a component for making heterogeneous layers of anodes owing to several excellent chemical, mechanical and electrical properties: (i) significantly large specific area, (ii) outstanding electrical conductivity, and (iii) relatively low volume expansion.32–34 Similarly, rGOs have been intensively studied for their potential as SIB anode materials.35 The rGO sheets were reported to easily form a heterogeneous composite with various transition metals (such as MoS2 and SnS2) through a simple and facile hydrothermal method without physicochemical aggregation of the partner materials.36 Furthermore, unlike the pristine graphene, rGOs play not only the role of a buffer to suppress the volume change of the layered composite but also ensure material durability over long-term electrochemical cycling.37 It was reported that the capacity of a MoS2/rGO layered nanocomposite reached as high as 420 mA h g−1 at a current density of 10 mA g−1, and the cyclic stability and rate capability were still high after 160 cycles.38 Despite its superior rate capability, MoS2/Gr was reported to have a lower capacity than that of MoS2/rGO (370 mA h g−1 at a current density of 8–10 mA g−1), without a clear understanding of the underlying mechanism.39 Previous reports indicate that rGOs provide higher charge capacity to Na but lower rate-capability than pure graphene.
Typically, oxygen-containing functional groups can easily and substantially change the material properties of rGO. Therefore, considerable efforts have been focused on improving the anodic properties of rGOs for SIBs using functional groups. Using first-principles density functional theory (DFT) calculations, we investigated how the oxygen-functional groups (–O–, –OH, and –COOH) on rGO, which form heterogeneous bilayers with MoS2, influence the electrochemical properties of SIB anodes. In addition to the thermodynamic Na affinity and voltage profile, DFT calculations have been extensively applied to MoS2/Gr and MoS2/rGO models to predict the thermodynamically active atomic sites for Na accommodation, charge distribution change over Na adsorption, and kinetic diffusion paths with their energy barriers. The obtained results clearly indicated that the oxygen functional groups significantly affect the Na interaction behavior by modulating the attraction between Na and the heterogeneous bilayers in a non-covalent bonding mode. Considering the thermodynamic and kinetic properties of varying functional groups, we identified the best method to design promising candidates for SIB anodes.
Methods
All calculations were performed using spin-polarized DFT with projector-augmented wave and plane-wave basis set with a cutoff energy of 520 eV, as implemented in the Vienna Ab initio Simulation Package (VASP).40 The exchange–correlation energy was treated using the generalize gradient approximation of Perdew–Burke–Ernzerhof functionals.41 A Γ-centered k-point mesh with dimensions of 5 × 5 × 1 was used for geometric optimizations, and the structures were relaxed until the energy and force converged within 10–5 eV and 0.02 eV Å−1, respectively. To represent the bilayer, we applied a periodic boundary condition to each slab model with 20 Å of vacuum space to the perpendicular direction to avoid undesirable interaction between periodic images. van der Waals (vdW) interactions were considered for all DFT calculations using the DFT-D3 method.42 The Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional was employed to determine the electronic band structure.43 The climbing image nudge elastic band method was used to identify a minimum-energy pathway for Na diffusion.44 Non-covalent interaction (NCI) analysis was performed using the NCI PLOT program, as implemented in CRITIC2.45We defined the formation energy of the heterogeneous bilayer as eqn (1):
| Ef = EHetero − EMoS2 − Emono, | (1) |
The binding energy (Eb) was calculated to estimate the Na-intercalation affinity as expressed in eqn (2):
| Eb = EHetero+Na − EHetero − ENa, | (2) |
The charge density difference was calculated to analyze the charge transfer between the interfaces, as expressed in eqn (3):
| Δρ = ρhetero+Na − ρhetero − ρNa, | (3) |
NCI analysis was conducted to evaluate the effect of oxygen functional groups on the secondary chemical bonding nature of the heterogeneous bilayer. The NCI was defined as expressed in eqn (4).
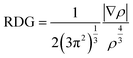 | (4) |
As indicated, the NCI is related to the electron density (ρ) and reduced density gradient (RDG). Noncovalent bonding features were determined using the second eigenvalue of the electron-density Hessian matrix.47
Results and discussion
Model system
Computational models were established to represent the MoS2/Gr and MoS2/rGO bilayer interfaces with the 2H-MoS2 phase, pure graphene, and rGO. To optimize the lattice mismatch and computational cost, we used effective supercell sizes for the heterogeneous layers, as expressed in eqn (5).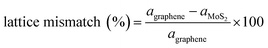 | (5) |
Heterogeneous bilayers are constructed by integrating a (3 × 3) supercell of 2H-MoS2 monolayer with a (4 × 4) supercell of graphene, aligning the periodicities of the two distinct crystalline lattices. The optimized lattice constant of pristine graphene is 9.89, while that of MoS2 is 9.51 Å. The lattice mismatch between the MoS2 and graphene systems was 3.9%, which was considered sufficiently small to avoid altering our main conclusions.48
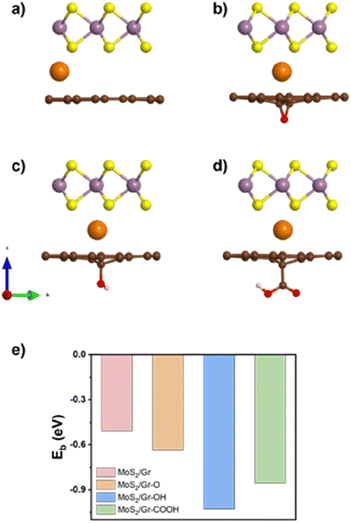
We considered three different oxygen-containing functional groups; –O, –OH, and –COOH, which are frequently used in experimental fabrication.49 Using the groups, we set up four representative heterogeneous bilayers to decouple each influence: (i) MoS2/Gr, (ii) MoS2/Gr–O, (iii) MoS2/Gr–OH, and (iv) MoS2/Gr–COOH. To determine the vertical positions of each oxygen-containing functional group within rGO, we calculated the thermodynamic configuration, as shown in Fig. S1.† The downward chemical bonding of the functional groups was energetically more favorable (Fig. S2a–d†) for all heterogeneous bilayers.
Bilayer interface formation energies were determined as −0.26 (MoS2/Gr), −0.21 (MoS2/Gr–O), −0.22 (MoS2/Gr–OH), and −0.20 eV (MoS2/Gr–COOH). Notably, all the energies were almost equal (Fig. S2e†), indicating that vdW interactions play a similar role in all cases.50 The interlayer distances were 3.51 (MoS2/Gr), 3.44 (MoS2/Gr–O), 3.46 (MoS2/Gr–OH), and 3.40 Å (MoS2/Gr–COOH). These values are well within the suitable range for Na intercalation (generally 3.2–3.5 Å).51
A previous study reported that a single rGO layer with oxygen-containing functional groups exhibited inferior electrical properties compared to pristine graphene.52 We investigated whether the same effect was observed in our heterogeneous bilayers. The band structures of MoS2/Gr and MoS2/rGO, obtained using DFT calculations, are illustrated in Fig. S3.† It is evident that the electronic conductivity of MoS2/Gr is the highest owing to its clear Dirac cone53 crossing the Fermi level at the K-point of the Brillouin zone. In contrast, the band structures of MoS2/rGO with the functional groups are similar to those of a semiconductor, with band gaps at K points 0.58 (MoS2/Gr–O), 0.68 (MoS2/Gr–OH), and 0.61 eV (MoS2/Gr–COOH). Depending on the band gap, the electrical conductivity of the heterogeneous bilayers with oxygen-containing functional groups was the highest for MoS2/Gr–O, followed by MoS2/Gr–COOH and MoS2/Gr–OH. The absence of a Dirac cone in the functionalized MoS2/rGO can be attributed to the hybridization of 2p-orbitals of O with the π-orbitals of the graphene.
We calculated band gaps of MoS2/rGO as the number of oxygen functional groups to understand how the electrical conductivity changes. As represented in Table S5† the band gap increases with the oxygen functional groups. Notably, it was predicted that the trend across the functional groups remained consistent, despite the numbers of oxygen functional groups. It indicates while the oxygen functional groups lead to reduction of the electrical conductivity of the SIB anode, it does not alter the band gap trend of each oxygen functional group. Although the introduction of oxygen functional groups in MoS2/rGO shows a band gap, it has been reported54 that a minimal band gap does not adversely affect the electrical conductivity when applied as an anode material in SIBs. Moreover, in our case, even at maximum concentration of oxygen functional groups the band gap is still suitable for SIB anode.
Na-intercalation affinity
We evaluated the Na intercalation affinity of each bilayer based on the Na binding energy and identified the most plausible thermodynamically active site for Na adsorption. The adsorption sites were classified into six groups according to their local symmetry (Fig. S4 and Table S1†). Two different types of sites were identified in MoS2 (hollow and top), and three in graphene (top, hollow, and edge). The Na binding energies of MoS2/Gr were calculated for the six sites, as shown in Fig. S4 and Table S2.† The obtained results indicated that all the sites were thermodynamically feasible for Na adsorption.In contrast, the Na-adsorption behavior of MoS2/rGO differed considerably from that of MoS2/Gr. The most favorable site was located between the top of MoS2 and the C atoms adjacent to each of the three oxygen-containing functional groups in rGO. Fig. 1e illustrates the Na binding energies in the four heterogeneous bilayer models, highlighting that the rGO layer with three oxygen-containing functional groups exhibits a stronger affinity for Na than pristine graphene.
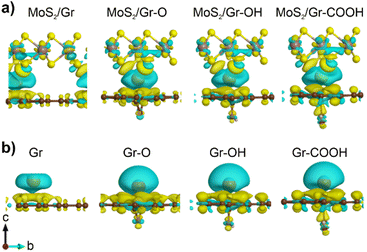
Differences in the charge density with Na adsorption in the heterogeneous bilayers were calculated by varying the three functional groups to analyze the cause of the different chemical affinities toward Na. Fig. 2a illustrates the charge depletion region around the adsorbed Na atom, indicating that most of the Na charges were transferred to neighboring layers. The considerable amount of electron transfer from the adsorbed Na to the adjacent MoS2, graphene, and rGO layers generated a strong coulombic attraction, the greater the depletion, the stronger the ionic interaction. However, distinguishing the charge depletion of Na in heterogeneous bilayers was challenging.
To clarify the effect of each oxygen-containing functional group in rGO on Na charge depletion, we focused on the Na atoms and a single layer of graphene and rGO (Fig. 2b). In these systems, Bader charge analysis was performed to quantify the Na charge depletion in the bilayer and monolayer (Table 1). The results demonstrated that the degree of Na charge depletion in a single layer was linearly correlated with the Na binding energy in the heterogeneous bilayer. This indicated that the Na binding energy in MoS2/rGO was significantly controlled by the rGO side rather than the MoS2 layer. However, it should be noted that Na charge transfer does not exhibit a clear relationship with the Na binding energy in heterogeneous bilayers. Therefore, other mechanisms, such as vdW interactions, influence Na adsorption in heterogeneous bilayers with rGO.
| Heterogeneous bilayers | Q Na | Monolayer | Q Na |
|---|---|---|---|
| MoS2/Gr | +0.84 | Gr | +0.54 |
| MoS2/Gr–O | +0.85 | Gr–O | +0.85 |
| MoS2/Gr–OH | +0.84 | Gr–OH | +0.87 |
| MoS2/Gr–COOH | +0.84 | Gr–COOH | +0.86 |
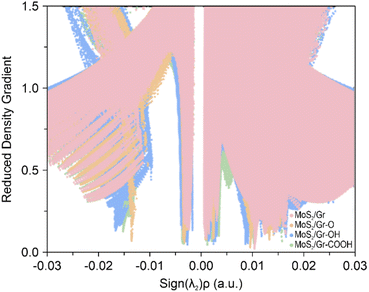
To identify the effect of the vdW interaction on the Na binding energy in MoS2/rGO, we performed NCI analysis, which characterizes noncovalent bonding features, as shown in Fig. 3. The RDG was calculated to identify the non-covalent interaction zones and the sign of the second eigenvalues (λ2) of the Hessian matrix55 was used to distinguish between bonding (λ2 < 0) and non-bonding (λ2 > 0) nature. All four bilayer systems exhibited near-zero region peaks, indicating that vdW interactions play a role in Na intercalation. However, there was a significant variance in the negative-value region. The peaks of MoS2/Gr–O, MoS2/Gr–OH, and MoS2/Gr–COOH appear at approximately −0.015, indicating that all MoS2/rGO bilayers are dominantly under non-covalent interactions, which come from the oxygen-functional groups. The MoS2/Gr–OH exhibited the strongest noncovalent bonding, which was attributed to the formation of a chemical bonding network, followed by MoS2/Gr–O and MoS2/Gr–COOH. In contrast, MoS2/Gr did not exhibit any peak at approximately −0.015. These results indicate that the three functional groups in rGO induce a stronger bonding network between the adsorbed Na and the rGO layer. Furthermore, MoS2/Gr–OH exhibited the strongest chemical interaction with the adsorbed Na, which is consistent with the trend of the Na binding energy.
In summary, our results clearly demonstrate that the dominant factor influencing the Na intercalation affinity in heterogeneous bilayers with oxygen-containing functional groups in rGO is non-covalent interactions.
Na diffusion behavior
The Na atomic diffusion behavior in the bilayer interfaces was studied to determine how the three oxygen-containing functional groups modulate the kinetic properties regarding the rate capability of SIBs. The starting positions for the diffusion were set at the thermodynamically preferred adsorption sites of each system, as predicted by the DFT calculations (Na-intercalation affinity section). To explore the most suitable diffusion route, we doubled the supercell size in the a-direction to commensurate the initial and final points under periodic boundary conditions, as shown in Fig. 4a–d (solid lines). Activation energy barriers for Na diffusion were evaluated as 0.24, 0.27, 0.35, and 0.31 eV in MoS2/Gr, MoS2/Gr–O, MoS2/Gr–OH, and MoS2/Gr–COOH, respectively (Fig. 4e–h). In MoS2/Gr, the rate-determining step (RDS) occurred from the first to the second step. This is ascribed to the fact that the initial point was the most stable for Na adsorption by MoS2/Gr. In contrast, the RDS significantly differs in MoS2/rGO because of the chemical perturbation by the functional groups in rGO. In the MoS2/rGO series, MoS2/Gr–OH exhibited the highest activation energy for Na diffusion, followed by MoS2/Gr–COOH and MoS2/Gr–O. MoS2/rGO generally requires a higher activation energy for Na diffusion than MoS2/Gr because of its stronger Na binding energy. The activation barrier differences can be explained by the Na binding energy of each model, which is determined by the combined non-covalent bonding between Na and the neighboring layers. Therefore, the diffusion barrier of Na in MoS2/rGO was proportional to the strength of the noncovalent bonding of each oxygen-containing functional group.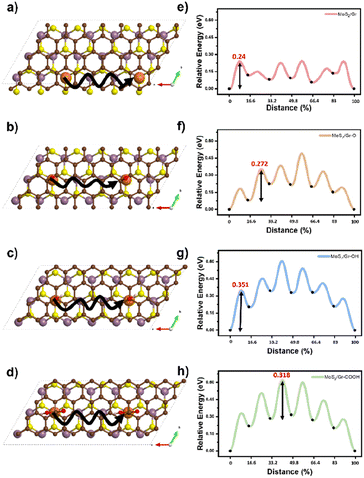 | ||
| Fig. 4 (a–d) Na atom diffusion pathways (solid line) and (e–h) energy profiles for Na diffusion in MoS2/Gr, MoS2/Gr–O, MoS2/Gr–OH, and MoS2/Gr–COOH. | ||
Stability and voltage profiles
We investigated the effect of oxygen-containing functional groups on the stability of the adsorbed Na by varying the coverage of the bilayers. Initially, the energy convex hull was determined using DFT calculations and ab initio thermodynamics of Na-adsorbed graphene and rGO to identify the most thermodynamically stable configuration. A total of 51 symmetrically distinct configurations were generated as functions of Na coverage. Thereafter, the formation energy Ef(x) of the graphene/rGO at Na coverage (x) was determined as expressed in eqn (6).| Ef(x) = Ecal(x) − E0(x), | (6) |
| E0(x) = (1 − x)E(x = 0) + xE(x = 1) | (7) |
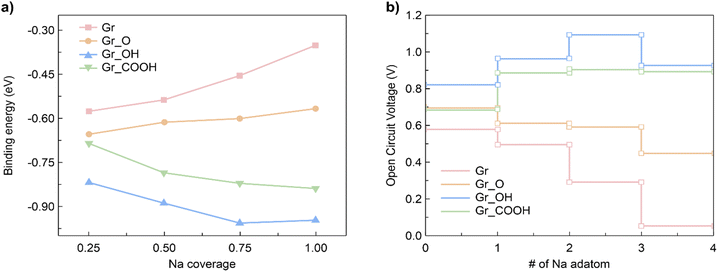
Using the energy convex hull, three stable configurations of graphene were identified, each with Na coverages of 0.16, 0.33, and 0.75, as illustrated in Fig. S6a.† The formation energies with respect to Na coverage in the rGO single layer were also calculated and normalized in accordance with the number of oxygen-containing functional groups (i.e., one oxygen-containing functional group per eight C atoms). The distance between the oxygen-containing functional groups was controlled to maintain commensuration in each configuration. By calculating the formation energy of a single layer using the energy convex hull, it was revealed that a stable configuration was formed at a Na coverage of 0.75, regardless of the specific type of oxygen-containing functional groups.
Subsequently, heterogeneous bilayers were designed by coupling a MoS2 layer with either pure graphene or rGO with functional groups to evaluate the theoretical capacity via the formation energies of the configurations located at the energy convex hull. The Na binding energy was computed in terms of the Na coverage (Fig. 5a). The intercalation energy per Na atom is defined as expressed in eqn (8):
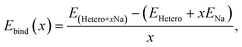 | (8) |
To further understand the Na intercalation properties of the bilayers with oxygen-containing functional groups, we analyzed their thermodynamic voltage profiles. The open-circuit voltage (OCV) at Na coverages ranging from x1 to x2 was evaluated as expressed in eqn (9):56
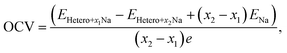 | (9) |
It should be noted that the OCV values are positive in the range of 0.05–1.09 V, indicating structural reconstruction.57 We determined the structural change by calculating interlayer distances into the perpendicular direction of bilayers (Fig. S7†) because we believe that structural modifications were induced by the Na intercalation process. The largest expansion of the interlayer distance was observed for MoS2/Gr–COOH, followed by MoS2/Gr–OH, at the beginning of Na insertion. However, considering the interlayer expansion after Na intercalation (Table S3†), MoS2/Gr–COOH and MoS2/Gr–OH exhibited significantly smaller expansions than MoS2/Gr and MoS2/Gr–O. This indicates that after Na insertion, structural reconstruction occurred in the –OH and –COOH functionalized bilayers. This is consistent with the enhancement of the Na binding energies in MoS2/Gr–OH and MoS2/Gr–COOH with increasing Na adatoms. Therefore, owing to their minimal interlayer expansion, MoS2/Gr–OH and MoS2/Gr–COOH are promising heterogeneous bilayer candidates for stable anodes with a high coverage of Na atoms. In addition, the fact that MoS2/Gr–COOH demonstrates a lower voltage than MoS2/Gr–OH indicates that the –COOH group is a better fit as a functional group for rGO to be used as an SIB anode material. Therefore, the strong Na binding energy, low electrode potential, and high stability after Na intercalation indicate that the –COOH group is optimum for functionalizing rGO in SIB anode applications.
Conclusions
We investigated the role of the oxygen-containing functional groups at the heterogeneous interface (MoS2/rGO) on the electrochemical performance of the anode using DFT calculations. The obtained results demonstrated that the carboxyl functional group satisfies the optimal performance for SIBs anodes considering the Na diffusivity, stability, and voltage perspectives. This study revealed the significance of the role of oxygen-containing functional groups in heterogeneous interface tuning to boost the electrochemical anode performance of SIBs. In addition, the rGO sheet with heterogeneous anodes not only provides insight into the carboxyl-rich functional design of high-quality heterogeneous bilayers but also motivates the development of other rGO composites.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Technology Innovation Program (20011259, Development of Electrostatic Ceramic Heater Including Multizone Capable of Precision Temperature Control) funded by the Ministry of Trade, Industry & Energy (MOTIE, Korea). This work was also supported by the National Research Foundation of Korea (2022M3H4A1A04096482) and funded by the Ministry of Science and ICT. This paper was supported by “Ministry of the Interior and Safety” R&D program (20014778).References
- F. Schreyer, G. Luderer, R. Rodrigues, R. C. Pietzcker, L. Baumstark, M. Sugiyama, R. J. Brecha and F. Ueckerdt, Environ. Res. Lett., 2020, 15, 114016 CrossRef.
- M. S. Whittingham, Science, 1976, 192, 1126–1127 CrossRef CAS PubMed.
- H. Chen, T. N. Cong, W. Yang, C. Tan, Y. Li and Y. Ding, Prog. Nat. Sci., 2009, 19, 291–312 CrossRef CAS.
- M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- J.-M. Tarascon and M. Armand, in Materials for Sustainable Energy: A Collection of Peer-Reviewed Research and Review Articles from Nature Publishing Group, World Scientific, 2011, pp. 171–179 Search PubMed.
- A. Yaroshevsky, Geochem. Int., 2006, 44, 48–55 CrossRef.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS PubMed.
- J. Deng, W. B. Luo, S. L. Chou, H. K. Liu and S. X. Dou, Adv. Energy Mater., 2018, 8, 1701428 CrossRef.
- P. Ge and M. Fouletier, Solid State Ionics, 1988, 28, 1172–1175 CrossRef.
- W. Luo, J. Wan, B. Ozdemir, W. Bao, Y. Chen, J. Dai, H. Lin, Y. Xu, F. Gu and V. Barone, Nano Lett., 2015, 15, 7671–7677 CrossRef CAS PubMed.
- C. Feng, J. Ma, H. Li, R. Zeng, Z. Guo and H. Liu, Mater. Res. Bull., 2009, 44, 1811–1815 CrossRef CAS.
- E. Lim, C. Jo, M. S. Kim, M. H. Kim, J. Chun, H. Kim, J. Park, K. C. Roh, K. Kang and S. Yoon, Adv. Funct. Mater., 2016, 26, 3711–3719 CrossRef CAS.
- M. Lao, Y. Zhang, W. Luo, Q. Yan, W. Sun and S. X. Dou, Adv. Mater., 2017, 29, 1700622 CrossRef PubMed.
- T. Stephenson, Z. Li, B. Olsen and D. Mitlin, Energy Environ. Sci., 2014, 7, 209–231 RSC.
- S. Palchoudhury, K. Ramasamy, J. Han, P. Chen and A. Gupta, Nanoscale Adv., 2023, 5, 2724–2742 RSC.
- Y. Fang, D. Luan, Y. Chen, S. Gao and X. W. Lou, Angew. Chem., 2020, 132, 7245–7250 CrossRef.
- Y. Fang, B. Y. Guan, D. Luan and X. W. Lou, Angew. Chem., Int. Ed., 2019, 58, 7739–7743 CrossRef CAS PubMed.
- Y. Fang, D. Luan and X. W. Lou, Adv. Mater., 2020, 32, 2002976 CrossRef CAS PubMed.
- T. M. Alharbi and C. L. Raston, Nanoscale Adv., 2023, 5, 6405–6409 RSC.
- P. Zhang, F. Qin, L. Zou, M. Wang, K. Zhang, Y. Lai and J. Li, Nanoscale, 2017, 9, 12189–12195 RSC.
- S.-K. Park, J. Lee, S. Bong, B. Jang, K.-d. Seong and Y. Piao, ACS Appl. Mater. Interfaces, 2016, 8, 19456–19465 CrossRef CAS PubMed.
- L. David, R. Bhandavat and G. Singh, ACS Nano, 2014, 8, 1759–1770 CrossRef CAS PubMed.
- X. Chen, Y. Zheng, W. Liu, C. Zhang, S. Li and J. Li, Nanoscale, 2019, 11, 22196–22205 RSC.
- D. Stevens and J. Dahn, J. Electrochem. Soc., 2001, 148, A803 CrossRef CAS.
- L. Fu, K. Tang, K. Song, P. A. van Aken, Y. Yu and J. Maier, Nanoscale, 2014, 6, 1384–1389 RSC.
- M. M. Rahman, I. Sultana, Z. Chen, M. Srikanth, L. H. Li, X. J. Dai and Y. Chen, Nanoscale, 2015, 7, 13088–13095 RSC.
- Y. Lu, Y. Lu, Z. Niu and J. Chen, Adv. Energy Mater., 2018, 8, 1702469 CrossRef.
- Y.-X. Wang, S.-L. Chou, H.-K. Liu and S.-X. Dou, Carbon, 2013, 57, 202–208 CrossRef CAS.
- X. Wu, Z. Wang, M. Yu, L. Xiu and J. Qiu, Adv. Mater., 2017, 29, 1607017 CrossRef PubMed.
- L. Cao, X. Gao, B. Zhang, X. Ou, J. Zhang and W.-B. Luo, ACS Nano, 2020, 14, 3610–3620 CrossRef CAS PubMed.
- M. K. Aslam, T. S. AlGarni, M. S. Javed, S. S. A. Shah, S. Hussain and M. Xu, J. Energy Storage, 2021, 37, 102478 CrossRef.
- L. Ji, P. Meduri, V. Agubra, X. Xiao and M. Alcoutlabi, Adv. Energy Mater., 2016, 6, 1502159 CrossRef.
- R. Raccichini, A. Varzi, S. Passerini and B. Scrosati, Nat. Mater., 2015, 14, 271–279 CrossRef CAS PubMed.
- L. Yu, Y.-H. Lee, X. Ling, E. J. Santos, Y. C. Shin, Y. Lin, M. Dubey, E. Kaxiras, J. Kong and H. Wang, Nano Lett., 2014, 14, 3055–3063 CrossRef CAS PubMed.
- X. Xie, Z. Ao, D. Su, J. Zhang and G. Wang, Adv. Funct. Mater., 2015, 25, 1393–1403 CrossRef CAS.
- B. Qu, C. Ma, G. Ji, C. Xu, J. Xu, Y. S. Meng, T. Wang and J. Y. Lee, Adv. Mater., 2014, 26, 3854–3859 CrossRef CAS PubMed.
- W. Qin, T. Chen, L. Pan, L. Niu, B. Hu, D. Li, J. Li and Z. Sun, Electrochim. Acta, 2015, 153, 55–61 CrossRef CAS.
- W. Zhang, F. Zhang, F. Ming and H. N. Alshareef, EnergyChem, 2019, 1, 100012 CrossRef.
- X. Xu, R. Zhao, W. Ai, B. Chen, H. Du, L. Wu, H. Zhang, W. Huang and T. Yu, Adv. Mater., 2018, 30, 1800658 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 121, 1187–1192 CrossRef CAS PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- A. Otero-de-la-Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018 CrossRef CAS.
- Q. Bai, L. Yang, H. Chen and Y. Mo, Adv. Energy Mater., 2018, 8, 1702998 CrossRef.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- X. Yuan, Z. Chen, B. Huang, Y. He and N. Zhou, J. Phys. Chem. C, 2021, 125, 10226–10234 CrossRef CAS.
- D. R. Dreyer, S. Park, C. W. Bielawski and R. S. Ruoff, Chem. Soc. Rev., 2010, 39, 228–240 RSC.
- N. N. Hieu, H. V. Phuc, V. V. Ilyasov, N. D. Chien, N. A. Poklonski, N. Van Hieu and C. V. Nguyen, J. Appl. Phys., 2017, 122, 104301 CrossRef.
- A. Massaro, A. Pecoraro, A. B. Muñoz-García and M. Pavone, J. Phys. Chem. C, 2021, 125, 2276–2286 CrossRef CAS PubMed.
- H. S. Moon, J. H. Lee, S. Kwon, I. T. Kim and S. G. Lee, Carbon Lett., 2015, 16, 116–120 CrossRef.
- I. N. Yakovkin, Crystals, 2016, 6, 143 CrossRef.
- S. A. Akhade, N. J. Bernstein, M. R. Esopi, M. J. Regula and M. J. Janik, Catal. Today, 2017, 288, 63–73 CrossRef CAS.
- E. Johnson and S. Keinan, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- L. Shi, T. Zhao, A. Xu and J. Xu, J. Mater. Chem. A, 2016, 4, 16377–16382 RSC.
- Q. Li, J. Yang and L. Zhang, J. Phys. Chem. C, 2018, 122, 18294–18303 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00854a |
| This journal is © The Royal Society of Chemistry 2024 |