Dominant higher-order vortex gyromodes in circular magnetic nanodots†
Artem V.
Bondarenko
 *abc,
Sergey A.
Bunyaev
*abc,
Sergey A.
Bunyaev
 a,
Amit K.
Shukla
d,
Arlete
Apolinario
a,
Amit K.
Shukla
d,
Arlete
Apolinario
 a,
Navab
Singh
e,
David
Navas
a,
Navab
Singh
e,
David
Navas
 f,
Konstantin Y.
Guslienko
f,
Konstantin Y.
Guslienko
 gh,
Adekunle O.
Adeyeye
gh,
Adekunle O.
Adeyeye
 *di and
Gleb N.
Kakazei
*di and
Gleb N.
Kakazei
 *a
*a
aInstitute of Physics for Advanced Materials, Nanotechnology and Photonics (IFIMUP), Departamento de Fisica e Astronomia, Faculdade de Ciências, Universidade do Porto, Porto, Portugal. E-mail: gleb.kakazei@fc.up.pt
bKavli Institute of Nanoscience, Delft University of Technology, Delft, The Netherlands. E-mail: a.v.bondarenko@tudelft.nl
cInstitute of Magnetism NASU and MESU, Kyiv, Ukraine
dDepartment of Electrical and Computer Engineering, National University of Singapore, Singapore, Singapore
eInstitute of Microelectronics, A*STAR, Singapore, Singapore
fInstituto de Ciencia de Materiales de Madrid, ICMM-CSIC, Madrid, Spain
gDepartamento de Polímeros y Materiales Avanzados, Universidad del País Vasco, UPV/EHU, San Sebastian, Spain
hIKERBASQUE, the Basque Foundation for Science, Bilbao, Spain
iDepartment of Physics, Durham University, Durham, UK. E-mail: adekunle.o.adeyeye@durham.ac.uk
First published on 19th July 2024
Abstract
The transition to the third dimension enables the creation of spintronic nanodevices with significantly enhanced functionality compared to traditional 2D magnetic applications. In this study, we extend common two-dimensional magnetic vortex configurations, which are known for their efficient dynamical response to external stimuli without a bias magnetic field, into the third dimension. This extension results in a substantial increase in vortex frequency, reaching up to 5 GHz, compared to the typical sub-GHz range observed in planar vortex oscillators. A systematic study reveals a complex pattern of vortex excitation modes, explaining the decrease in the lowest gyrotropic mode frequency, the inversion of vortex mode intensities, and the nontrivial spatial distribution of vortex dynamical magnetization noted in previous research. These phenomena enable the optimization of both oscillation frequency and frequency reproducibility, minimizing the impact of uncontrolled size variations in those magnetic nanodevices.
New conceptsSpin waves are elementary excitation modes in magnetically ordered media, with quantized frequencies in finite-sized samples. Spin eigenmodes can be classified using integer numbers. In two-dimensional systems, higher mode numbers correspond to higher frequencies and more complex spatial distributions. The intensity of a mode, induced by a uniform microwave field, is directly proportional to the square of the mode's volume-averaged magnetization. As mode numbers increase, intensities decrease due to more complex patterns leading to lower magnetization. In our study, we investigated the magnetization dynamics of thick vortex-state permalloy nanodots. We found that extending these systems into the third-dimension results in entirely new effects, surpassing conventional spin wave resonance. Notably, as the thickness of the nanodot increases, the lowest vortex core mode exhibits a reduction in both frequency and intensity until it eventually vanishes. Meanwhile, higher-order modes (with frequencies reaching up to 5 GHz, extending into telecommunication bands) become dominant, positioning the vortex-state thick dot as a potential next-generation microwave nano-oscillator. The observed phenomena can be explained by the significant increase in dipolar energy contributions due to this dimensional extension, along with the varying impact of energy balance alterations on different modes. |
1. Introduction
Ferromagnetic materials have a wide range of novel and exciting applications, including magnetic logic gates,1–3 magnetic memory,4 and a plethora of other magnonic RF components and circuits5,6 that have also been proposed and studied. Further advancements are being achieved with antiferromagnetic materials7 which can host even faster terahertz spin dynamics. Magnetic systems offer numerous convenient ways to interface with existing technology, using spin transfer8,9 and spin–orbit10,11 torque for driving, and a number of techniques like tunneling magnetoresistance12 to read the magnetization out. In this way, a complete ecosystem of magnetic devices is being developed.In magnetic materials, the individual spin angular momenta of the lattice are globally ordered, guided by exchange, dipolar interaction, and other forces. Magnetic vortices are a special type of a magnetization ordering consisting of a global in-plane curl of the spins, and a small localized out-of-plane core.13,14 This type of magnetization is extremely stable throughout a variety of geometries,15 is easily directly observable,13 and is sufficiently malleable16 making it one of the most iconic objects in nanomagnetism. It serves as an extremely useful reference system for probing new physics concepts and experimental techniques.
However, despite the promise of the increased frequency,17 which is important for the development of vortex nano-oscillators,18,19 the exploration of 3D behavior in vortices has been limited to thicknesses up to 100 nm due to technological challenges and the pessimistic outlook provided by initial research.20–25 It has been reported, that at this intermediate scale, the fundamental gyration mode G0 frequency suddenly begins to drop and its amplitude simultaneously decreases.22,25 The mechanism behind this phenomenon remains unclear, despite attempts to explain the frequency drop by including factors such as vortex mass in the model.26
Apart from the lowest frequency vortex gyromode (G0), higher-order gyration modes become observable at intermediate thicknesses. The gyrotropic modes Gn, which are flexure oscillations of the vortex core string with n = 0, 1, 2 … nodes along the dot thickness, can be considered a class of standing spin waves excited in an inhomogeneous magnetic ground state without an external magnetic field. This is similar to the spin wave resonance (standing spin waves) in thin films predicted by Charles Kittel in 195827 and confirmed experimentally soon after.28 Standing spin waves have also been observed in perpendicularly magnetized disks29 and stripes.30 The intensity of a standing spin mode is expected to decrease as the mode number increases due to more complex, inhomogeneous mode profiles and, consequently, lower mode-averaged magnetizations. This behavior has indeed been observed in all the mentioned experiments.
Furthermore, previous works were unable to achieve the resolution necessary to visualize many important details on a microscopic level. However, it was later shown that with thickness increase the lowest mode became strongly localized at the top and bottom faces of the cylindrical dot, and there is no simple vortex core precession with the same amplitude throughout the dot thickness,23,31 unlike the higher-order modes. We will refer to the depth-dependent position of the mz = 1 vortex core a vortex core line (m is the reduced magnetization vector).
In this work, we investigated the magnetization dynamics of thick (up to 350 nm) Ni80Fe20 dome-shaped nanodots, fabricated using nano stencil lithography, through broadband ferromagnetic resonance both experimentally and theoretically. Our results demonstrate that extending nanoelements into the third dimension leads to the emergence of entirely new effects. The behavior of mode frequencies and intensities is drastically different from that of other standing spin waves. As the nanodot thickness increases, the lowest frequency vortex gyromode begins to decrease in both frequency and intensity, eventually disappearing, while higher-order modes become dominant.
Our findings are particularly significant for microwave applications of vortex nano-oscillators. We have clearly demonstrated that the resonance frequency of the dominant mode can be increased directly into telecommunication bands (up to 5 GHz), making vortex-state thick dots a potential next-generation microwave nano-oscillator. This important frequency range is achieved directly, without the need for frequency multiplication, unlike traditional quartz and MEMS oscillator technology. Additionally, the frequency of magnetic oscillators can be rapidly tuned, enabling novel applications such as ultrafast time-resolved spectral analysis.32 Finally, this work clearly shows that extending to 3D leads to the emergence of new and striking effects, as recently demonstrated by Berganza et al. for 3D quasi-skyrmions in dome-shaped structures.33
2. Experimental methods
Periodic arrays of the magnetic dome-shaped nanodots were fabricated over an area (1 mm × 1 mm) on silicon substrates using nanostencil lithography (NSL).34 NSL is a resistless and direct pattern technique where a controlled amount of material is deposited through apertures onto a substrate in a vacuum environment. This technique distinguishes itself from the other nanofabrication techniques by its well-known advantages, such as straightforward fabrication, substrate independence, lack of high-temperature and wet chemical process steps, wafer-scale high throughput and cost-effectiveness due to the reusability of the masks once they are cleaned. The nanostencil masks used in this work contain low-stress silicon nitride membranes. In our sample fabrication process, the nano-sized geometric patterns were transferred onto the membranes using deep UV lithography at an exposure wavelength of 193 nm.35 The apertures were etched using dry etching. To transfer the patterns onto the silicon substrate, permalloy (Ni80Fe20, Py) films of different thicknesses on top of a 5 nm thin Cr adhesive layer were deposited through the corresponding stencil apertures on the substrates by electron beam deposition, operating at a base pressure of 4 × 10−8 torr with an optimized growth rate of 0.2 Å s−1. The dimensions and shapes of the nanodots obtained this way were characterized using atomic force and scanning electron microscopies, and magnetic hysteresis loops were measured using a Quantum Design SQUID-VSM magnetometer at room temperature with the external field applied in the sample plane. The microwave absorption spectra of the dot arrays in their ground state (i.e., without an external magnetic field) and at room temperature were measured using a vector network analyzer. The frequency was swept from 50 MHz to 3 GHz (targeting only the vortex gyrotropic modes) with an input microwave power of 0 dBm and an averaging process repeated 100 times. Samples were placed face down on the coplanar waveguide (CPW), and the normalized microwave absorption was measured. The microwave field with the amplitude below 1 Oersted oscillated in the patterned film plane.The micromagnetic simulations were performed by using the MuMax3 solver.36 The saturation magnetization Ms = 830 × 103 A m−1 and gyromagnetic ratio γ/2π = 2.96 × 1010 s−1 T−1 were directly extracted from ferromagnetic resonance frequency vs. resonance field dependence of the reference Ni80Fe20 continuous film when the exchange stiffness A = 13 pJ m−1 was picked from the literature as the most typical value for permalloy. The Gilbert damping was set at the higher end of the range for permallloy α = 0.02, to decrease the simulation runtime. The cell size and grid size were adjusted dynamically to conserve high performance when the geometric size of the structure is varied. As noted in the accompanying paper of MuMax3, the best performance is achieved for grid sizes, which comes up to the product of the first 7 primes, since the fast Fourier transform library used by MuMax3 is optimized for those. We have constructed a small algorithm that is able to select products 2, 3, and 5, which results in the cell dimensions being from 2.5 nm to 5 nm. For frequency analysis the sinc pulse Bx = Bamp.sinc(2πflimt − φ0) was used, flim sets an upper limit, we used 6 GHz in our case, which is slightly lower than half the sampling 16 GHz frequency to avoid aliasing. In the raw data, we observe that the frequency drops sharply, by as much as 40 dB, at the edge of the excitation pulse as expected. The shift φ0 = 32.31 rad (or roughly 5 periods at flim) was selected such that no matter the flim, 99% of the energy of the excitation pulse is delivered within the simulation time window, which starts at t = 0. The amplitude is selected small enough such that the excitation is in a linear regime.
3. Results and discussion
So far, both experimental and numerical studies of the vortex dynamics in nanodots have been limited to the thickness up to 100 nm. To reveal what happens at higher thicknesses and to obtain a consistent picture of thickness dependencies for different gyrotropic modes, we performed micromagnetic simulations of magnetization dynamics in the cylindrical nanodots (Fig. 1) of varying thickness up to 400 nm with a dimensional resolution much higher than what can be obtained in an experiment. The results of simulations for several representative nanodot diameters 100 nm, 300 nm and 500 nm are presented in Fig. 2.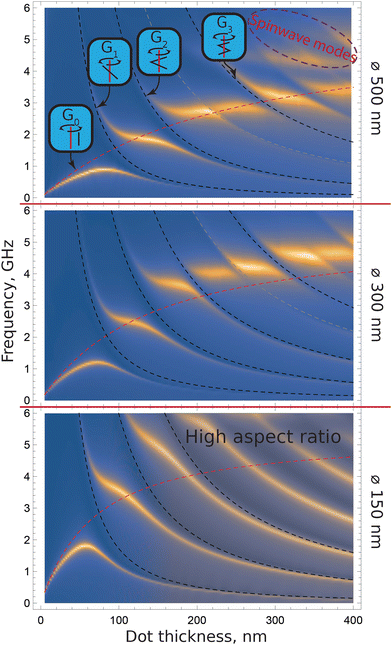 | ||
| Fig. 2 Simulated thickness (l) dependence of the frequencies of the gyrotropic modes for 500 nm, 300 nm, and 150 nm diameter nanodots. Two kinds of approximation curves are used: for a homogenous mode a theoretical dependence17 of the lowest vortex gyrotropic G0 frequency is shown as a red dashed line; dashed black curves represent hyperbolae ∼ l−b fits of the high frequency and high thickness asymptotes of modes. Colour represents the in-plane microwave magnetic field response intensity of the vortex gyromodes. | ||
In numerical simulations, contrary to the experiment, it is easy to explore the depth distribution of the magnetic momenta motion and the resulting motion of the core of a magnetic vortex can be observed directly. This approach immediately allows us to focus exclusively on excitation modes involving the motion of the vortex core (known as gyrotropic modes), distinguishing them from other modes that are typically well localized at the periphery of a nanodot. To introduce similarity with the experiment, all the simulations, presented in Fig. 2, were performed for the square dot arrays with lattice parameters equal to two dot diameters by implying periodic boundary conditions (PBC). To check the influence of dipolar interactions on spin-wave spectra, we performed additional simulations for the representative dot array – diameter D = 500 nm and thickness l = 300 nm – without PBC. In both cases, the excitation spectra exhibited a similar form, with the same number of peaks and their respective intensities. The peak frequencies varied slightly, by less than 0.1 GHz.
To interpret the simulated vortex frequencies shown in Fig. 2, we introduce two easy-to-follow types of gyrotropic model modes consistent with previous analytical descriptions37 by assigning orders to the model modes. Previous studies have shown that with some simplifications, the distinct gyrotropic modes arise differentiated, like in the mechanical string problem, by the number of nodes and depths at which the vortex core is stationary at the axis of the cylindrical nanodot. The initial, 0th order, is distinct from the higher orders because the vortex core stays in almost the same spot along the particle thickness. This makes it so that the homogenous 0th order mode is dipolar, in contrast to the exchange-determined higher order modes, and its frequency rises slowly with the dot thickness increasing, as described by the analytical results.17 Meanwhile, the exchange modes, contrary to the homogenous 0th order, have their frequency decrease in thicker particles. So, even in the simple analytical models, frequency crossings arise between the rising homogenous mode and high-order exchange-determined gyrotropic modes.
It is easy to see that at the points of the crossing of the predicted model modes, a non-accounted interaction produces mode-repulsion behaviour, Fig. 2. The model modes are shown in the figure with dashed lines. The homogeneous mode is plotted against dot thickness (l) using a previously established expression. In contrast, the more complex high-order modes are fitted to the data approximately as ∼l−b, with b being slightly less than 2 (b = 2 corresponds to purely exchange-determined behaviour). Three observations can be made to get the point across further:
(1) The observed frequency curves can be fit well with a linear coupling introduced between the previously mentioned model mode curves with a coupling strength of order g/2π ∼ 500 MHz (the result of a fit of the data in Fig. 2);
(2) Secondly, from a macroscopic perspective, we observe that the amplitudes of the excitations decrease significantly as the mode frequencies diverge from the original homogeneous mode resonance. Therefore, the high-order model modes exhibit zero net magnetization and are excited only indirectly through their coupling with the homogeneous mode.
(3) Microscopically, we observe that the resulting distributions of dynamic magnetization are hybridized, exhibiting the combined motion of several model modes. This hybridization is most clearly seen as a doublet at the point of mode crossing.
Through numerical experiments, we can overcome the challenges of real-world experiments, such as examining thickness variations of the parameters at much higher resolution and extending to much greater end thicknesses. This approach allows us to provide sufficient data to explain previous observations, including mode amplitude inversion and the non-monotonous behavior of the fundamental mode. In addition, the vortex gyration mode crossings at large diameters form geometric dimension intervals where the frequency changes only a little, while the dimension variance can be significant. This provides a good way to produce the structures more repeatably at the expense of needing larger particles to achieve the same frequencies. See the qualitative difference in the lowest diameter particles in Fig. 2.
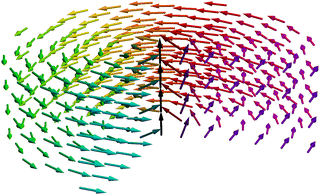
Having gotten through the frequency spectra shown in Fig. 2, we can shift our attention to the calculated mode spatial microscopic distributions of the vortex dynamical magnetization exemplified in Fig. 3. The distributions presented are for a realistic thick nanodot profile, as the one presented in the experimental section of this work. Unlike previous studies, we simultaneously examine the high-order vortex gyrotropic modes (also known as flexure modes20,22,24 of the vortex core string oscillations) in both the time and frequency domains.
The resonance frequencies received with wideband microwave magnetic field excitation were used to excite individual modes with a monochromatic circularly polarized magnetic field. A slightly faster convergence to the stationary state was observed with circular rather than linear polarization as the external magnetic field couples more directly to the magnetization precession. Exciting only selected modes allows us to get the vortex core trajectory directly, without doing pass-filter FFT post-processing, and also slightly refines the quality of the vortex mode spatial distributions.
With the fine resolution of our data, we can attempt to classify the vortex modes of the thick nanodots. The most naïve approach would be to enumerate the resonances by their frequencies. However, as we have already shown, such an approach would make an inter-nanodot comparison impossible because it ignores structural similarities. Although not entirely accurate, the simple flexion gyrotropic mode theory, having been long theorised,20,37 provides a simple picture upon which we can build our interpretation of the spin excitation modes. The main classifying factor in this model is the number of nanodot axis crossings by the vortex core string.
The real behaviour is far more complex, but it is possible to infer several empirical classifying characteristics analogous to the nanodot axis crossings. Firstly, because the vortex core line approaches the dot axis very close, we can extend the idealized model and count close passes instead. This can be achieved by either observing the vortex core position directly or by counting local minima along the axis in spectral distribution. Alternatively, it is also possible to quantify how many turns the core line makes around the axis or how many turns the curve makes on itself. In the simple model, those would increase by half a turn for each successive resonance mode. All three metrics are presented in Table 1 for comparison.
Lower order modes show significant discrepancies in the metrics; for example, the G3 mode, which in the easiest model, should have had close to 1.5 axis turns, even if that would have made it impossible to excite it because there would be two identical lobes and two identical tails opposing each other! We see that this sort of deviation is stronger for high-order vortex modes, making the vortex core line closer to a helix and decreasing the variation of core distance from the nanodot axis.
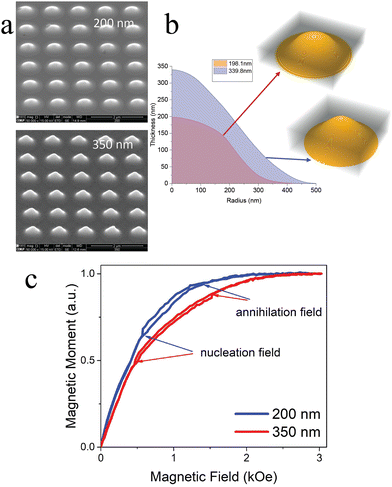
So far, the dot arrays with a maximum thickness of 100 nm have been studied experimentally. To check our findings in numerical simulations reported above, it is necessary to fabricate dots with much higher thickness. Here, nanostencil lithography (NSL) was successfully used for these purposes. Below, the results for two square dot arrays with period 1 μm and thicknesses 200 nm and 350 are presented. The dimensions and shapes of the nanodots were characterized through combined scanning electron and atomic force microscopies, results of which are presented in Fig. 4(a) and (b). Both measurements were taken to get a quantitative description of the resulting structure geometry. The nanodots captured within the field of view of a scanning electron microscope show a good degree of repeatability, with planar size varying by just a couple dozen nanometers over an effective diameter of a nanodot. As one may observe, for both thicknesses, the dots have dome-like shapes with diameters at the bottom larger than the designed 500 nm, which is a known issue of NSL. For a 200 nm thick sample, the edge-to-edge distance at the substrate was found to be 220 nm, and for a 350 nm thick sample – it was only 90 nm. The in-plane magnetization behavior of the fabricated dot arrays is shown in Fig. 4(c). Both hysteresis loops have zero remanence, typical for the dots in the vortex ground state.15 Vortex nucleation and annihilation fields are not as pronounced as in the case of thin cylindrical dots but are still clearly visible. As expected, the thicker dot array has lower susceptibility due to the higher in-plane demagnetizing factor.
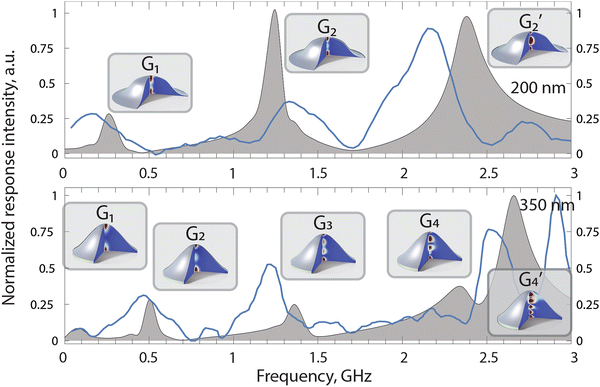
The microwave absorption spectra of the dot arrays in the absence of an external magnetic field are presented in Fig. 5. To identify the observed resonance peaks, the experimental measurements were complemented with MuMax336 micromagnetic calculations of sinc pulse response. It is important to note that the gyrotropic frequencies of the studied dome-shaped dots are similar to the ones of cylindrical dots with the same thickness and 500 nm diameter, which means that properties of the gyrotropic modes are more sensitive to the dot thickness than to lateral shapes. A detailed comparison of the circular and dome-shaped dot geometries is out of the scope of this article; we will focus on those in a separate paper. The simulated spectra were obtained using experimentally determined magnetization and gyromagnetic ratio values, a literature value for exchange stiffness, and nanodot shapes derived from atomic force microscopy data. The MuMax3 software was customized to accommodate arbitrary pre-calculated shape geometries. Dipolar interactions between nanodots were included in the simulations using periodic boundary conditions (PBC), with a center-to-center distance of 1 μm, consistent with the experiment.
It is important to note that for both thicknesses, experimental and simulated spectra contain the same number of peaks: for 200 nm thick dot, three signals are clearly observed, while for 350 nm, the spectrum is richer – there are five of them. Given that the frequencies of the experimental and simulated spectra are quite similar (with the largest difference between corresponding peaks being 250 MHz, or less than 10% at 3 GHz), the experimental modes were identified as G1 and a doublet of G2 gyromodes for the 200 nm sample, and as G1, G2, G3, and a doublet of G4 gyromodes for the 350 nm sample. The only noticeable difference between the simulations and the experiment is the intensity ratio of the doublets. Specifically, for the 350 nm sample, simulations predicted that the intensity of the 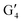 mode would be much higher than that of the G4 mode, whereas the experiment showed their intensities to be almost identical. This effect may be caused by different pinning of the magnetic moments on the bottom and top surfaces of the dots. However, the most important result of this comparison is that it is distinctly observed in the experiment that the most intense peaks shift to higher frequencies with the dot thickness increase, as predicted by micromagnetic simulations.
mode would be much higher than that of the G4 mode, whereas the experiment showed their intensities to be almost identical. This effect may be caused by different pinning of the magnetic moments on the bottom and top surfaces of the dots. However, the most important result of this comparison is that it is distinctly observed in the experiment that the most intense peaks shift to higher frequencies with the dot thickness increase, as predicted by micromagnetic simulations.
The doublets of both the G2 and G4 at corresponding particle thicknesses are a showcase of the hybridization discussed previously in a simulation part. The modes mentioned are the closest ones to the model homogeneous gyration mode in frequency. As a result, they inherit the number of nodes/turns as the high-frequency hybridization partner (refer to Table 1) but have slight differences both in excitation amplitude and mix of the modes.
4. Summary
In summary, a wealth of fascinating magnetic vortex dynamics is revealed in thick nanodots. We observe how the third dimension becomes significant as thickness increases. Initially, the effect is gradual, with the vortex core position remaining consistent throughout the layers. For each higher-order mode, there exists a thickness at which hybridization occurs due to the distinct nature of gyrational modes: the thickness-homogeneous G0 mode, primarily influenced by the demagnetization field, and the higher-order gyromodes, which are mainly affected by exchange interaction. This hybridization eliminates any mode with depth-homogeneous gyration after the first high-order mode G1. We developed a framework for describing and classifying these modes, supported by extensive numerical study. Additionally, we demonstrated the resilience of gyro-modes to the shape imperfections typical of patterned thick films. Practically, this allows for significantly higher excitation frequencies than those expected for magnetic vortices in thin dots, reaching into the telecommunications microwave bands. Furthermore, the new dimension enables engineering the system to minimize the impact of uncontrolled uncertainties by targeting specific frequency crossings.Data availability
All the simulations were performed using MuMax3 – an open-source application for micromagnetic simulation optimized for general-purpose computing on graphic processing unit (GPU). It can be downloaded from https://mumax.github.io/.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Portuguese team acknowledges the support through FCT – Portuguese Foundation for Science and Technology under the projects LA/P/0095/2020 (LaPMET), UIDB/04968/2020, UIDP/04968/2020, 2022.03564.PTDC (DrivenPhonon4Me), 2022.07332.PTDC (H2Flexi-PECs with DOI: 10.54499/2022.07332.PTDC), and contract DL57/2016, Ref. DL 57/2016/CP1454/CT0017 with DOI: 10.54499/DL57/2016/CP1454/CT0017 (A. A.). A. V. B. would like to acknowledge the funding from the European Innovation Council project PALANTIRI. Work at Singapore was supported by the Ministry of Education Singapore Tier 2 funding via grant R-263-000-C61-112. D. N. acknowledges the financial support from the projects CNS2022-135949 and PCI2023-143411 funded by the Spanish Ministry of Science and Innovation, MICINN/10.13039/ 501100011033, and by “ESF Investing in your future”. K. Y. G. acknowledges support by IKERBASQUE (the Basque Foundation for Science). The research of K. Y. G. was funded in part by the Spanish Ministry of Science and Innovation grants PID2019-108075RB-C33/AEI/10.13039/501100011033, PID2022-137567NB-C21/AEI/10.13039/501100011033 and by the Basque Country government under the scheme “Ayuda a Grupos Consolidados” (Ref. IT1670-22). A. O. A. would like to acknowledge the funding from the Wolfson Foundation and the Royal Society.Notes and references
- B. Behin-Aein, D. Datta, S. Salahuddin and S. Datta, Nat. Nanotechnol., 2010, 5, 266–270 CrossRef CAS.
- A. V. Chumak, V. I. Vasyuchka, A. A. Serga and B. Hillebrands, Nat. Phys., 2015, 11, 453–461 Search PubMed.
- S. Mondal, S. Barman and A. Barman, J. Magn. Magn. Mater., 2020, 502, 166520 CrossRef CAS.
- S. Bhatti, R. Sbiaa, A. Hirohata, H. Ohno, S. Fukami and S. Piramanayagam, Mater. Today, 2017, 20, 530–548 CrossRef.
- A. V. Chumak, A. A. Serga and B. Hillebrands, Nat. Commun., 2014, 5, 4700 CrossRef CAS.
- O. V. Dobrovolskiy, R. Sachser, S. A. Bunyaev, D. Navas, V. M. Bevz, M. Zelent, W. Śmigaj, J. Rychły, M. Krawczyk, R. V. Vovk, M. Huth and G. N. Kakazei, ACS Appl. Mater. Interfaces, 2019, 11, 17654–17662 CrossRef CAS PubMed.
- E. V. Gomonay and V. M. Loktev, Low Temp. Phys., 2014, 40, 17–35 CrossRef CAS.
- J. Slonczewski, J. Magn. Magn. Mater., 1996, 159, L1–L7 CrossRef CAS.
- I. N. Krivorotov, N. C. Emley, J. C. Sankey, S. I. Kiselev, D. C. Ralph and R. A. Buhrman, Science, 2005, 307, 228–231 CrossRef CAS PubMed.
- L. Liu, C.-F. Pai, D. C. Ralph and R. A. Buhrman, Phys. Rev. Lett., 2012, 109, 186602 CrossRef PubMed.
- V. E. Demidov, S. Urazhdin, A. Anane, V. Cros and S. O. Demokritov, J. Appl. Phys., 2020, 127, 170901 CrossRef.
- J. Mathon and A. Umerski, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 220403 CrossRef.
- T. Shinjo, T. Okuno, R. Hassdorf, K. Shigeto and T. Ono, Science, 2000, 289, 930–932 CrossRef.
- X. Fu, S. D. Pollard, B. Chen, B.-K. Yoo, H. Yang and Y. Zhu, Sci. Adv., 2018, 4, eaat3077 CrossRef CAS PubMed.
- K. Y. Guslienko, J. Nanosci. Nanotechnol., 2008, 8, 2745–2760 CrossRef CAS.
- L. Ramasubramanian, A. Kákay, C. Fowley, O. Yildirim, P. Matthes, S. Sorokin, A. Titova, D. Hilliard, R. Böttger, R. Hübner, S. Gemming, S. E. Schulz, F. Kronast, D. Makarov, J. Fassbender and A. Deac, ACS Appl. Mater. Interfaces, 2020, 12, 27812–27818 CrossRef CAS.
- V. Novosad, F. Y. Fradin, P. E. Roy, K. S. Buchanan, K. Y. Guslienko and S. D. Bader, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 024455 CrossRef.
- D. Houssameddine, U. Ebels, B. Delaët, B. Rodmacq, I. Firastrau, F. Ponthenier, M. Brunet, C. Thirion, J.-P. Michel, L. Prejbeanu-Buda, M.-C. Cyrille, O. Redon and B. Dieny, Nat. Mater., 2007, 6, 447–453 CrossRef CAS PubMed.
- J.-V. Kim, Chapter Four – Spin-Torque Oscillators, Academic Press, 2012, vol. 63, pp. 217–294 Search PubMed.
- F. Boust and N. Vukadinovic, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 172408 CrossRef.
- M. Yan, R. Hertel and C. M. Schneider, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 094407 CrossRef.
- J. Ding, G. N. Kakazei, X. Liu, K. Y. Guslienko and A. O. Adeyeye, Sci. Rep., 2014, 4, 4796 CrossRef PubMed.
- R. V. Verba, A. Hierro-Rodriguez, D. Navas, J. Ding, X. M. Liu, A. O. Adeyeye, K. Y. Guslienko and G. N. Kakazei, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 214437 CrossRef.
- M. Noske, H. Stoll, M. Fähnle, A. Gangwar, G. Woltersdorf, A. Slavin, M. Weigand, G. Dieterle, J. Förster, C. H. Back and G. Schütz, Phys. Rev. Lett., 2016, 117, 037208 CrossRef PubMed.
- J. Ding, G. N. Kakazei, X. M. Liu, K. Y. Guslienko and A. O. Adeyeye, Appl. Phys. Lett., 2014, 104, 192405 CrossRef.
- K. Y. Guslienko, G. N. Kakazei, J. Ding, X. M. Liu and A. O. Adeyeye, Sci. Rep., 2015, 5, 13881 CrossRef CAS PubMed.
- C. Kittel, Phys. Rev., 1958, 110, 1295–1297 CrossRef.
- M. H. Seavey and P. E. Tannenwald, Phys. Rev. Lett., 1958, 1, 168–169 CrossRef CAS.
- G. N. Kakazei, P. E. Wigen, K. Y. Guslienko, V. Novosad, A. N. Slavin, V. O. Golub, N. A. Lesnik and Y. Otani, Appl. Phys. Lett., 2004, 85, 443–445 CrossRef CAS.
- K. Y. Guslienko, V. Pishko, V. Novosad, K. Buchanan and S. D. Bader, J. Appl. Phys., 2005, 97, 10A709 CrossRef.
- Y. P. Ivanov, A. Chuvilin, L. G. Vivas, J. Kosel, O. Chubykalo-Fesenko and M. Vázquez, Sci. Rep., 2016, 6, 23844 CrossRef CAS.
- A. Litvinenko, V. Iurchuk, P. Sethi, S. Louis, V. Tyberkevych, J. Li, A. Jenkins, R. Ferreira, B. Dieny, A. Slavin and U. Ebels, Nano Lett., 2020, 20, 6104–6111 CrossRef CAS PubMed.
- E. Berganza, J. A. Fernandez-Roldan, M. Jaafar, A. Asenjo, K. Guslienko and O. Chubykalo-Fesenko, Sci. Rep., 2022, 12, 3426 CrossRef CAS.
- O. Vázquez-Mena, G. Villanueva, M. van den Boogaart, V. Savu and J. Brugger, Microelectron. Eng., 2008, 85, 1237–1240 CrossRef.
- A. O. Adeyeye and N. Singh, J. Phys. D: Appl. Phys., 2008, 41, 153001 CrossRef.
- A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen, F. Garcia-Sanchez and B. Van Waeyenberge, AIP Adv., 2014, 4, 107133 CrossRef.
- K. Guslienko, Magnetism, 2022, 2, 239–250 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nh00145a |
| This journal is © The Royal Society of Chemistry 2024 |

![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif)