DOI:
10.1039/D4NH00254G
(Communication)
Nanoscale Horiz., 2024,
9, 1725-1731
Interaction- and phonon-induced topological phase transitions in double helical liquids†
Received
4th June 2024
, Accepted 16th July 2024
First published on 17th July 2024
Abstract
Helical liquids, formed by time-reversal pairs of interacting electrons in topological edge channels, provide a platform for stabilizing topological superconductivity upon introducing local and nonlocal pairings through the proximity effect. Here, we investigate the effects of electron–electron interactions and phonons on the topological superconductivity in two parallel channels of such helical liquids. Interactions between electrons in different channels tend to reduce nonlocal pairing, suppressing the topological regime. Additionally, electron–phonon coupling breaks the self duality in the electronic subsystem and renormalizes the pairing strengths. Notably, while earlier perturbative calculations suggested that longitudinal phonons have no effect on helical liquids themselves to the leading order, our nonperturbative analysis shows that phonons can induce transitions between topological and trivial superconductivity, thereby weakening the stability of topological zero modes. Our findings highlight practical limitations in realizing topological zero modes in various systems hosting helical channels, including quantum spin Hall insulators, higher-order topological insulators, and their fractional counterparts recently observed in twisted bilayer systems.
New concepts
Helical liquids, a quantum state of matter appearing at the edges of time-reversal-invariant topological materials, hold promise for advanced electronics, including low-dissipation devices. When two parallel channels of these helical liquids are in contact with a conventional superconductor, they can stabilize topological zero modes without magnetic fields, providing a foundation for topological quantum computing. However, the robustness of these zero modes face challenges from detrimental effects such as Coulomb interactions and phonons. In this research, we show that both Coulomb interactions between electrons and electron–phonon coupling can lead to new topological phase transitions, weakening the stability of these zero modes. Using a combination of bosonization techniques and renormalization-group analysis, our investigation in the nonperturbative regime reveals new insights into these transitions, reaching a different conclusion from earlier perturbative studies. Since electron–electron interactions and phonons are omnipresent in nature, our findings not only open the door to electrically tunable topological transitions but also highlight significant practical constraints in designing stable devices for topological quantum computing.
|
Helical liquids, appearing at the boundary channels of time-reversal-invariant topological materials,1–22 are promising candidates for advanced electronics such as low-dissipation devices, although the practical application presents certain complexities.23–25 Along with their peculiar transport properties, these helical channels can facilitate Majorana and parafermion zero modes when proximity-induced pairing is introduced,25–34 further extending previous proposals35–39 exploiting nonhelical channels.40–59 Notably, renewed interest in helical liquids has emerged following recent observations of double and triple quantum spin Hall states in twisted bilayer MoTe260 and WSe2,61 as well as dual quantum spin Hall states in monolayer TaIrTe4,62 including findings within the fractional regime.60 There is also theoretical literature exploring fractional helical liquids in interacting systems.29,63–68
While the stability of the helical liquids themselves has been extensively analyzed,5,6,25,69–101 it remains crucial to examine the robustness of the topological zero modes hosted therein against various detrimental effects in realistic settings. Among others, a crucial element in low dimensions is electron–electron interactions. Studies have demonstrated that Majorana zero modes can survive with the interactions102 and, in certain settings, are even stabilized by them.29,31,32,59 Additionally, the resilience of topological phases to phonons can pose challenges for experimental realization. Concerning helical liquids themselves, perturbative analyses have shown that the leading-order effect from longitudinal phonons on charge transport is identically zero.72 Meanwhile, although transverse phonons could affect transport, any resulting corrections are suppressed by a high-power temperature law and vanish at low temperatures.92 The influence of phonons on Majorana zero modes in nonhelical systems has also been studied within the perturbative regime.103
In this work, we explore topological superconductivity in double helical liquids in regimes where both electron–electron interactions and electron–phonon coupling are nonperturbative. When the helical channels are in contact with a superconductor, both local and nonlocal pairing processes take place where the partners of a Cooper pair from the parent superconductor tunnel into one and both of the channels, respectively. Previous works29,32 established that a topological regime is characterized by the dominance of nonlocal pairing over local pairing, a scenario that is feasible with sufficiently strong intrachannel electron–electron interactions. Here, we show that new transitions between topological and trivial phases can be induced by interchannel interactions. Specifically, while intrachannel interaction favors nonlocal pairing, interchannel interaction can suppress it. We further discuss the self duality in the electronic subsystem and the ground state degeneracy protected by parity conservation. Remarkably, we demonstrate that the coupling to phonons can break the self duality and alter the scaling behaviors of both pairing terms, thus triggering further phase transitions. Given the ubiquitous presence of electron–electron interactions and phonons, our findings suggest a practical limitation in realizing topological zero modes in helical channels.
Our setting with two parallel helical channels in proximity to an s-wave superconductor is illustrated in Fig. 1. In addition to configurations using quantum spin Hall insulators29 or higher-order topological insulators32 in the integer regime, we also consider edge channels in twisted bilayer MoTe2,60 which can be operated in either an integer or fractional regime upon adjusting the carrier density. The system can be described by H = Hdh + Hph + Hep + Vloc + Vcap. The first term, Hdh, describes electrons subject to intrachannel and interchannel screened Coulomb interactions. The next two, Hph and Hep, describe the acoustic phonon modes and their coupling to the electrons, respectively. In this work, we treat the three terms nonperturbatively. Finally, we have perturbation terms, Vloc and Vcap, arising from the local and nonlocal pairings, respectively. Below, we first discuss the electronic subsystems described by Hdh + Vloc + Vcap, before analyzing the influence of phonons.
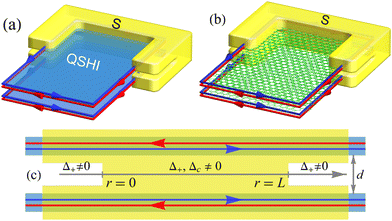 |
| | Fig. 1 Double helical liquids realized using (a) quantum spin Hall insulators (QSHI) or (b) twisted bilayer structures. In both settings, a pair of parallel edge channels, each formed by counter-propagating spin-up (red) and spin-down (blue) electrons, are in contact with an s-wave superconductor (yellow). (c) Side view of the setup in the local coordinate (labeled by r), with an interlayer separation d. The structure induces both local and nonlocal pairings within the segment 0 ≤ r ≤ L, whereas only local pairing occurs for r < 0 and r > L. | |
In our analysis, the electrons are represented by the operator ψ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,n(r) with the spatial coordinate r, the channel index n ∈ {1, 2}, and
,n(r) with the spatial coordinate r, the channel index n ∈ {1, 2}, and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = R (
= R (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = L) for right-moving spin-down (left-moving spin-up) modes, respectively. Within the bosonization scheme,63–65 we have
= L) for right-moving spin-down (left-moving spin-up) modes, respectively. Within the bosonization scheme,63–65 we have
| | 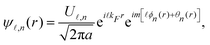 | (1) |
with the Fermi wave number
kF, short-distance cutoff
a =
ħvF/
Δa, bandwidth
Δa and Fermi velocity
vF. Here, the boson fields satisfy
| | 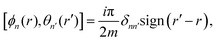 | (2) |
with integer
m. We have the following bosonized expression characterizing double helical liquids with nonuniversal forward scattering interactions,
| | 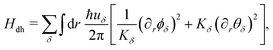 | (3) |
with the index
δ ∈ {
s ≡ +,
a ≡ −} labeling the symmetric/antisymmetric combination of the two channels,
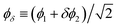
and similarly for
θδ. The velocity
uδ =
vF/
Kδ of the sector
δ is related to the interaction parameter
Kδ = [1 + 2(
Uee +
δVee)/(π
ħvF)]
−1/2 with the intrachannel (interchannel) interaction strength
Uee (
Vee). One obtains compactness in the boson fields,
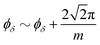
and
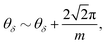
which plays a role when examining the ground state degeneracy below.
The proximity-induced local and nonlocal pairings (characterized by the strengths Δn with n ∈ {1,2} and Δc, respectively) can be expressed as25,29,32
| | 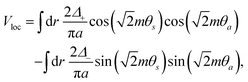 | (4) |
| | 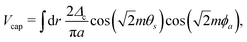 | (5) |
with
Δ± = (
Δ1 ±
Δ2)/2. In the noninteracting limit, the band inversion and topological phase transition occurs when
which gives the criterion for the emergence of Majorana zero modes.
29,32 For simplicity, below we consider the identical pairing setup with
Δ− = 0.
‡ As demonstrated below, in this case, one recovers a self-dual sine-Gordon model;
105 for
m = 2, the model coincides with two-leg ladder systems,
106,107 which host topologically nontrivial pair density wave phases, albeit with distinct realizations. The criterion given in
eqn (6) was derived from the single-particle Hamiltonian.
29,32 To gain more insights into the many-body systems, below we revisit it with the bosonic description.
We now explore the ground state degeneracy determined by the parity conservation, a method shown to be effective in unveiling the topological properties of semiconducting wires108 and spin chains.107,109,110 We note that, owing to the presence of nonlocal pairing, the fermion parity for a single channel here is not conserved. However, since the total fermion parity defined from the total charge remains conserved, we formulate it as 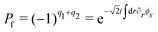 with the fermion number qn for channel n. Utilizing the relation
with the fermion number qn for channel n. Utilizing the relation 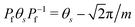 and the compactness of θs, we conclude that the ground states for
and the compactness of θs, we conclude that the ground states for 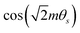 are characterized by eigenstates of Pf, satisfying Pf|e/o〉s = ±|e/o〉s. These states are constructed from even and odd combinations as
are characterized by eigenstates of Pf, satisfying Pf|e/o〉s = ±|e/o〉s. These states are constructed from even and odd combinations as 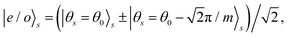 with θ0 being a minimum of the cosine term. Concerning the topological properties, since the θs field appears in both Vloc and Vcap, the total fermion parity does not distinguish between the two terms.
with θ0 being a minimum of the cosine term. Concerning the topological properties, since the θs field appears in both Vloc and Vcap, the total fermion parity does not distinguish between the two terms.
In contrast, since Vloc and Vcap involve different fields, ϕa and θa, in the antisymmetric sector, one can exploit another parity operator to distinguish between the two. Specifically, given the singlet pairing considered here, both local and nonlocal pairings create or annihilate up- and down-spin pairs simultaneously. As a result, the pairings can alter the spin difference between the two channels by either 0 or 2 (in units of ħ/2), thereby preserving a quantity, which we term the “spin difference parity”. This leads to the definition of an operator Psp using the spin quantum number sn for channel n, 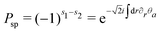 . Again, with
. Again, with 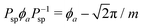 and the compactness of ϕa, we conclude that the ground states for
and the compactness of ϕa, we conclude that the ground states for 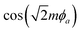 are doubly degenerate and can be written as
are doubly degenerate and can be written as 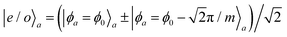 , with eigenvalue ±1 of Psp and a minimum ϕ0. On the other hand, since the spin difference parity operator commutes with θa, the local pairing term exhibits no ground state degeneracy. We thus conclude that the Δc term characterizes a topologically nontrivial phase.§
, with eigenvalue ±1 of Psp and a minimum ϕ0. On the other hand, since the spin difference parity operator commutes with θa, the local pairing term exhibits no ground state degeneracy. We thus conclude that the Δc term characterizes a topologically nontrivial phase.§
Having identified that a dominant Δc term leads to topological superconductivity, we explore its resilience to both intrachannel and interchannel electron–electron interactions. Under these conditions, the criterion in eqn (6) holds upon replacing the pairing strengths to their renormalized values by the interactions.32,102 To proceed, we perform the renormalization-group (RG) analysis and obtain these renormalized strengths; see ESI† for the RG flow equations without phonon contribution (ESI†). In Fig. 2, we present the results for m = 1. The influence of electron–electron interactions is notable. A general trend toward dominant nonlocal pairing requires sufficiently large Uee to preferentially suppress local pairing over nonlocal ones, consistent with earlier findings.32 In contrast, finite interchannel interaction leads to a larger Ka value and reduces the nonlocal pairing. A sufficiently large Vee eventually induces a phase transition toward the trivial superconductivity, suppressing formation of topological zero modes.
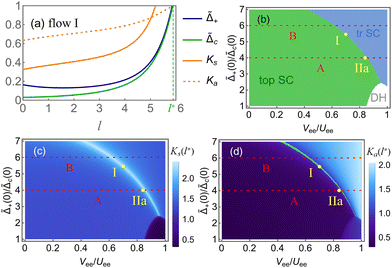 |
| | Fig. 2 RG flow and phase diagrams in the absence of phonons. (a) RG flow for 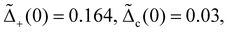 Uee/(πħvF) = 2.5 and Vee/Uee = 0.7. The label l* marks the length scale of the flow end point, where any of the couplings reach unity. (b) Phase diagram determined from the renormalized pairing strengths, with the labels “top SC”, “tr SC” and “DH” denoting topological superconductivity, trivial superconductivity and double helical liquids, respectively. In the last region, none of the pairings reaches unity as the scale l approaches ln(L/a) set by the system size L. (c) and (d) Renormalized interaction parameters, with a highlighted curve where Ka flows to unity. The initial points of the flows in panel (a) and Fig. 3(a) are marked; the line cuts A and B correspond to those in Fig. 4. Uee/(πħvF) = 2.5 and Vee/Uee = 0.7. The label l* marks the length scale of the flow end point, where any of the couplings reach unity. (b) Phase diagram determined from the renormalized pairing strengths, with the labels “top SC”, “tr SC” and “DH” denoting topological superconductivity, trivial superconductivity and double helical liquids, respectively. In the last region, none of the pairings reaches unity as the scale l approaches ln(L/a) set by the system size L. (c) and (d) Renormalized interaction parameters, with a highlighted curve where Ka flows to unity. The initial points of the flows in panel (a) and Fig. 3(a) are marked; the line cuts A and B correspond to those in Fig. 4. | |
Interestingly, both local and nonlocal pairings tend to increase Ks, thereby promoting the ordering of the θs field. Assuming that the θs field is frozen, the low-energy physics is primarily governed by the antisymmetric sector. We can express the pairing terms V = Vloc + Vcap as
| | 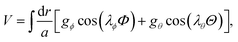 | (7) |
with
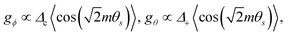
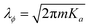
and
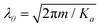
. The new fields
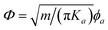
and
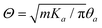
are introduced to match the notations in
ref. 105. We observe that the electronic subsystem characterizes a self-dual sine-Gordon Hamiltonian, with the self-duality point
gϕ =
gθ and
λϕ =
λθ reached when
Ka → 1. Remarkably, for certain initial parameters, such as flow I in
Fig. 2(a), the renormalized value of
Ka converges to unity at the end of the RG flow, accompanied by
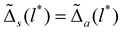
, signifying the arrival at the self-duality point. Moreover, we find that
eqn (7) presents a hierarchy of self-dual sine-Gordon models (ESI
†), where different
m values characterize different classes with
λϕ2 =
λθ2 = 2π
m,
105,111,112 including the
m = 3 model with parafermion modes. Notably, for
m = 2,
eqn (7) can be refermionized using
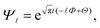
allowing for the introduction of Majorana fields
ξ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
and
η![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
through
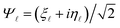
. With the details in the ESI,
† we get
| | 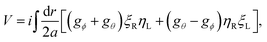 | (8) |
indicating a pair of massive Majorana modes
ξR and
ηL for any
gϕ and
gθ. In contrast, the
ηR and
ξL modes can be massless at a junction where
gθ and
gϕ reverse their relative strength. Translating back to the original notations, this indicates a transition point at which (
Δc −
Δ+) changes its sign and implies topological zero modes at
r = 0,
L in
Fig. 1 with a dominant nonlocal pairing for 0 ≤
r ≤
L, recovering the criterion obtained earlier.
We have examined the robustness of the topological superconductivity in the proximitized double helical liquid, which exhibits self duality in the electronic subsystems and interaction-driven phase transition. However, phonons, generally present in nature, lead to a breakdown of this duality and an additional phase transition, as we discuss below.
To explore the phonon effects, we consider the following term from longitudinal acoustic phonons,
| | 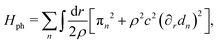 | (9) |
with the phonon velocity
c, the linear mass density
ρ along the channels, the displacement field
dn generated by the phonons and its conjugate field π
n. The coupling between the displacement field and the electron density is described by
| | 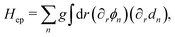 | (10) |
with the electron–phonon coupling strength
g. We remark that isotope engineering can be employed to modify the phonon parameters, as the atomic mass of the lattice can be altered through isotopic substitution, thus affecting the vibrational properties of the lattice. In earlier perturbative analysis,
72 the phonons introduced above are shown to have no leading-order effects on the helical liquids themselves. However, nonperturbative calculation in nonhelical systems
113–116 suggests that phonons can affect the scaling dimensions of pairing operators, which in turn likely affects the phase diagram that we are examining here.
Before proceeding, we comment on optical phonons. With their weakly dispersive energy band near a finite frequency, they have a negligible phonon density of states at low energy compared to acoustic modes,117 leading to reduced contributions at low temperatures. Additionally, these phonons are not expected to produce substantial effects on the scaling dimensions.115 We therefore follow the literature on one-dimensional bosonized models72,113–116 and do not include their contributions here.
From eqn (10), it is evident that phonons couple to the ϕn fields but not to the θn fields, leading to a breakdown of the self duality. Moreover, due to the hybridization of electrons and phonons, the low-energy modes of Hdh + Hph + Hep are characterized by velocities,
| | 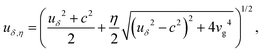 | (11) |
with
η ∈ {+, −} and
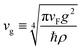
. The modification in velocities from their bare values,
uδ and
c, can be substantial, to the extent that one of the velocities reaches zero, which is referred to as the Wentzel–Bardeen (WB) singularity, known for nonhelical channels.
113–116,118–120 Without pairing terms, the singularity condition is quantified as
| | 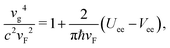 | (12) |
implying that the inclusion of interchannel interaction makes it easier for the system to reach the singularity. The presence of
eqn (4) and (5) results in the renormalization of the interaction parameters and a more complicated condition than
eqn (12); we therefore determine the singularity condition numerically. Crucially, the electron–phonon coupling also modifies the scaling dimensions of the pairing operators, thereby affecting the phase diagrams.
To quantify the effects from phonons, we derive the following RG flow equations,
| | 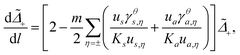 | (13a) |
| | 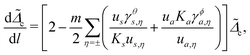 | (13b) |
| | 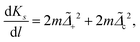 | (13c) |
| | 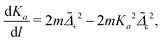 | (13d) |
with d
l = d
a/
a,
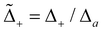
,
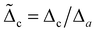
and
| | 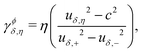 | (14a) |
| | 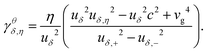 | (14b) |
The equations indicate that the electron–phonon coupling affects the scaling of operators associated with both local and nonlocal pairings. In Fig. 3, we compare the RG flows for scenarios with and without phonon influence. In both instances, Ks is renormalized in a similar manner, supporting both pairing types. The key distinction arises with phonons, where Ka is renormalized towards larger values, favoring local pairing over the nonlocal one. Notably, the RG flows with and without phonons result in the opposite outcomes, despite otherwise identical initial parameter values.
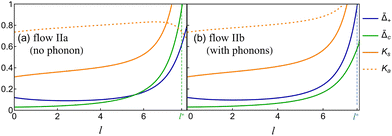 |
| | Fig. 3 Comparison of RG flows without and with phonon influence for 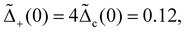 Uee/(πħvF) = 2.5 and Vee/Uee = 0.83. (a) RG flow corresponding to dot IIa in Fig. 2 and 4(a). (b) RG flow with vg2/(cvF) = 0.53, corresponding to dot IIb in Fig. 4(a). Uee/(πħvF) = 2.5 and Vee/Uee = 0.83. (a) RG flow corresponding to dot IIa in Fig. 2 and 4(a). (b) RG flow with vg2/(cvF) = 0.53, corresponding to dot IIb in Fig. 4(a). | |
Next, we deduce phase diagrams by exploring a range of the dimensionless parameters, vg2/(cvF) and Vee/Uee. As illustrated in Fig. 4, the presence of electron–phonon coupling significantly alters the phase diagrams. Specifically, since phonons mediate attractive interactions between electrons within each channel, their presence effectively reduces the strength of Uee. In terms of the RG flow, a nonzero vg increases both the Ks and Ka values, thereby enhancing 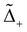 and reducing
and reducing 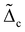 . In consequence, close to the boundary between the two superconducting phases, the electron–phonon coupling can push the system from a topological phase to a trivial phase. Furthermore, the pairing perturbations also influence the boundary approaching the WB singularity. Consequently, the WB singularity is reached for a smaller vg as compared to earlier analysis.113,114 We also note that, for m > 1, a weaker electron–phonon coupling is necessary to induce phase transitions (ESI†), indicating a more fragile topological phase in the fractional regime.
. In consequence, close to the boundary between the two superconducting phases, the electron–phonon coupling can push the system from a topological phase to a trivial phase. Furthermore, the pairing perturbations also influence the boundary approaching the WB singularity. Consequently, the WB singularity is reached for a smaller vg as compared to earlier analysis.113,114 We also note that, for m > 1, a weaker electron–phonon coupling is necessary to induce phase transitions (ESI†), indicating a more fragile topological phase in the fractional regime.
 |
| | Fig. 4 Phase diagrams in the presence of phonons with Uee/(πħvF) = 2.5 for (a) 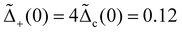 and (b) and (b) 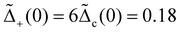 . The label “WB” indicates the regime beyond the WB singularity. The dots IIa and IIb correspond to the flows in Fig. 3(a) and (b), respectively. The line cuts A and B correspond to those marked in Fig. 2. . The label “WB” indicates the regime beyond the WB singularity. The dots IIa and IIb correspond to the flows in Fig. 3(a) and (b), respectively. The line cuts A and B correspond to those marked in Fig. 2. | |
Our results indicate electrically tunable topological phase transitions in proximitized double helical liquids upon varying the strengths of Uee and Vee. As demonstrated in the ESI,† the intrachannel strength Uee can be modulated through the screening effect,32,69,121 which is controlled by either the distance between the channel and a nearby metallic layer or the dielectric material in between. As the interchannel strength Vee additionally depends on the distance d and the dielectric material between the two helical channels,116 they offer extra knobs to adjust the ratio of Vee/Uee through device engineering. In consequence, the electrical tunability of the proposed setups allows one to induce the phase transitions, which are associated with the presence or absence of topological zero modes. The latter feature can be detected through various probes,34 including transport measurements,48,52,122 magnetic field responses,49,51,52 and the parity-controlled 2π-Josephson effect previously proposed.123,124 Given the omnipresence of electron–electron interactions and phonons, even in clean systems, our findings represent practical constraints in utilizing helical channels to realize topological zero modes.
Data availability
All data that support the findings of this work are included within the article and ESI.†
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We thank S.-Y. Chen, M. Hayashi, Y. Kato, T. Kondo, and R. Noguchi for interesting discussions. This work was supported financially by the National Science and Technology Council (NSTC), Taiwan through Grant No. NSTC-112-2112-M-001-025-MY3. We are also grateful to the long-term workshop YITP-T-23-01 held at the Yukawa Institute for Theoretical Physics (YITP), Kyoto University, Japan, where this work was initiated.
Notes and references
- C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2005, 95, 226801 CrossRef CAS PubMed.
- C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2005, 95, 146802 CrossRef CAS PubMed.
- B. A. Bernevig, T. L. Hughes and S.-C. Zhang, Science, 2006, 314, 1757 CrossRef CAS PubMed.
- B. A. Bernevig and S.-C. Zhang, Phys. Rev. Lett., 2006, 96, 106802 CrossRef PubMed.
- C. Wu, B. A. Bernevig and S.-C. Zhang, Phys. Rev. Lett., 2006, 96, 106401 CrossRef PubMed.
- C. Xu and J. E. Moore, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045322 CrossRef.
- M. König, S. Wiedmann, C. Brüne, A. Roth, H. Buhmann, L. W. Molenkamp, X.-L. Qi and S.-C. Zhang, Science, 2007, 318, 766 CrossRef PubMed.
- C. Liu, T. L. Hughes, X.-L. Qi, K. Wang and S.-C. Zhang, Phys. Rev. Lett., 2008, 100, 236601 CrossRef PubMed.
- M. Z. Hasan and C. L. Kane, Rev. Mod. Phys., 2010, 82, 3045 CrossRef CAS.
- I. Knez, R.-R. Du and G. Sullivan, Phys. Rev. Lett., 2011, 107, 136603 CrossRef PubMed.
- J. Maciejko, T. L. Hughes and S.-C. Zhang, Annu. Rev. Condens. Matter Phys., 2011, 2, 31 CrossRef CAS.
- X.-L. Qi and S.-C. Zhang, Rev. Mod. Phys., 2011, 83, 1057 CrossRef CAS.
- X. Qian, J. Liu, L. Fu and J. Li, Science, 2014, 346, 1344 CrossRef CAS PubMed.
- Z. Fei, T. Palomaki, S. Wu, W. Zhao, X. Cai, B. Sun, P. Nguyen, J. Finney, X. Xu and D. H. Cobden, Nat. Phys., 2017, 13, 677 Search PubMed.
- S. Tang, C. Zhang, D. Wong, Z. Pedramrazi, H.-Z. Tsai, C. Jia, B. Moritz, M. Claassen, H. Ryu, S. Kahn, J. Jiang, H. Yan, M. Hashimoto, D. Lu, R. G. Moore, C.-C. Hwang, C. Hwang, Z. Hussain, Y. Chen, M. M. Ugeda, Z. Liu, X. Xie, T. P. Devereaux, M. F. Crommie, S.-K. Mo and Z.-X. Shen, Nat. Phys., 2017, 13, 683 Search PubMed.
- F. Schindler, A. M. Cook, M. G. Vergniory, Z. Wang, S. S. P. Parkin, B. A. Bernevig and T. Neupert, Sci. Adv., 2018, 4, eaat0346 Search PubMed.
- F. Schindler, Z. Wang, M. G. Vergniory, A. M. Cook, A. Murani, S. Sengupta, A. Y. Kasumov, R. Deblock, S. Jeon, I. Drozdov, H. Bouchiat, S. Guéron, A. Yazdani, B. A. Bernevig and T. Neupert, Nat. Phys., 2018, 14, 918 Search PubMed.
- S. Wu, V. Fatemi, Q. D. Gibson, K. Watanabe, T. Taniguchi, R. J. Cava and P. Jarillo-Herrero, Science, 2018, 359, 76 CrossRef CAS PubMed.
- F. Wu, T. Lovorn, E. Tutuc, I. Martin and A. H. MacDonald, Phys. Rev. Lett., 2019, 122, 086402 CrossRef CAS PubMed.
- T. Devakul, V. Crépel, Y. Zhang and L. Fu, Nat. Commun., 2021, 12, 6730 CrossRef CAS PubMed.
- R. Noguchi, M. Kobayashi, Z. Jiang, K. Kuroda, T. Takahashi, Z. Xu, D. Lee, M. Hirayama, M. Ochi, T. Shirasawa, P. Zhang, C. Lin, C. Bareille, S. Sakuragi, H. Tanaka, S. Kunisada, K. Kurokawa, K. Yaji, A. Harasawa, V. Kandyba, A. Giampietri, A. Barinov, T. K. Kim, C. Cacho, M. Hashimoto, D. Lu, S. Shin, R. Arita, K. Lai, T. Sasagawa and T. Kondo, Nat. Mater., 2021, 20, 473 CrossRef CAS PubMed.
- Y.-C. Hung, B. Wang, C.-H. Hsu, A. Bansil and H. Lin, Phys. Rev. B, 2024, 110, 035125 CrossRef.
- G. Gusev, Z. Kvon, E. Olshanetsky and N. Mikhailov, Solid State Commun., 2019, 302, 113701 CrossRef CAS.
- D. Culcer, A. C. Keser, Y. Li and G. Tkachov, 2D Mater., 2020, 7, 022007 CrossRef CAS.
- C.-H. Hsu, P. Stano, J. Klinovaja and D. Loss, Semicond. Sci. Technol., 2021, 36, 123003 CrossRef CAS.
- L. Fu and C. L. Kane, Phys. Rev. Lett., 2008, 100, 096407 CrossRef PubMed.
- L. Fu and C. L. Kane, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 161408(R) CrossRef.
- Y. Tanaka, T. Yokoyama and N. Nagaosa, Phys. Rev. Lett., 2009, 103, 107002 CrossRef PubMed.
- J. Klinovaja, A. Yacoby and D. Loss, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155447 CrossRef.
- C. Schrade, A. A. Zyuzin, J. Klinovaja and D. Loss, Phys. Rev. Lett., 2015, 115, 237001 CrossRef PubMed.
- A. Haim, K. Wölms, E. Berg, Y. Oreg and K. Flensberg, Phys. Rev. B, 2016, 94, 115124 CrossRef.
- C.-H. Hsu, P. Stano, J. Klinovaja and D. Loss, Phys. Rev. Lett., 2018, 121, 196801 CrossRef CAS PubMed.
- Z. Yan, F. Song and Z. Wang, Phys. Rev. Lett., 2018, 121, 096803 CrossRef CAS PubMed.
- A. Haim and Y. Oreg, Phys. Rep., 2019, 825, 1 CrossRef.
- J. Alicea, Rep. Prog. Phys., 2012, 75, 076501 CrossRef PubMed.
- C. Beenakker, Annu. Rev. Condens. Matter Phys., 2013, 4, 113 CrossRef CAS.
- S. Das Sarma, M. Freedman and C. Nayak, npj Quantum Inf., 2015, 1, 15001 CrossRef.
- M. Sato and Y. Ando, Rep. Prog. Phys., 2017, 80, 076501 CrossRef PubMed.
- C. W. J. Beenakker, SciPost Phys. Lect. Notes, 2020, 15 CrossRef.
- A. Y. Kitaev, Phys.-Usp., 2001, 44, 131 CrossRef.
- A. Y. Kitaev, Ann. Phys., 2003, 303, 2 CAS.
- M. Sato, Phys. Lett. B, 2003, 575, 126 CrossRef CAS.
- M. Sato, Y. Takahashi and S. Fujimoto, Phys. Rev. Lett., 2009, 103, 020401 CrossRef PubMed.
- M. Sato and S. Fujimoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 094504 CrossRef.
- R. M. Lutchyn, J. D. Sau and S. Das Sarma, Phys. Rev. Lett., 2010, 105, 077001 CrossRef PubMed.
- Y. Oreg, G. Refael and F. von Oppen, Phys. Rev. Lett., 2010, 105, 177002 CrossRef PubMed.
- J. Klinovaja and D. Loss, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 085408 CrossRef.
- C. L. M. Wong and K. T. Law, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 184516 CrossRef.
- A. Keselman, L. Fu, A. Stern and E. Berg, Phys. Rev. Lett., 2013, 111, 116402 CrossRef PubMed.
- J. Klinovaja, P. Stano, A. Yazdani and D. Loss, Phys. Rev. Lett., 2013, 111, 186805 CrossRef PubMed.
- F. Zhang, C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2013, 111, 056402 CrossRef PubMed.
- A. Haim, A. Keselman, E. Berg and Y. Oreg, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 220504(R) CrossRef.
- E. Gaidamauskas, J. Paaske and K. Flensberg, Phys. Rev. Lett., 2014, 112, 126402 CrossRef PubMed.
- J. Klinovaja and D. Loss, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 045118 CrossRef CAS.
- C.-H. Hsu, P. Stano, J. Klinovaja and D. Loss, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 235435 CrossRef.
- H. Ebisu, B. Lu, J. Klinovaja and Y. Tanaka, Prog. Theor. Exp. Phys., 2016, 2016, 083I01 CrossRef.
- S. Hoffman, J. Klinovaja and D. Loss, Phys. Rev. B, 2016, 93, 165418 CrossRef.
- C. Schrade, M. Thakurathi, C. Reeg, S. Hoffman, J. Klinovaja and D. Loss, Phys. Rev. B, 2017, 96, 035306 CrossRef.
- M. Thakurathi, P. Simon, I. Mandal, J. Klinovaja and D. Loss, Phys. Rev. B, 2018, 97, 045415 CrossRef CAS.
- K. Kang, B. Shen, Y. Qiu, Y. Zeng, Z. Xia, K. Watanabe, T. Taniguchi, J. Shan and K. F. Mak, Nature, 2024, 628, 522 CrossRef CAS PubMed.
-
K. Kang, Y. Qiu, K. Watanabe, T. Taniguchi, J. Shan and K. F. Mak, arXiv, 2024, arXiv:2402.04196 DOI:10.48550/arXiv.2402.04196.
- J. Tang, T. S. Ding, H. Chen, A. Gao, T. Qian, Z. Huang, Z. Sun, X. Han, A. Strasser, J. Li, M. Geiwitz, M. Shehabeldin, V. Belosevich, Z. Wang, Y. Wang, K. Watanabe, T. Taniguchi, D. C. Bell, Z. Wang, L. Fu, Y. Zhang, X. Qian, K. S. Burch, Y. Shi, N. Ni, G. Chang, S.-Y. Xu and Q. Ma, Nature, 2024, 628, 515 CrossRef CAS PubMed.
- M. Levin and A. Stern, Phys. Rev. Lett., 2009, 103, 196803 CrossRef PubMed.
- T. Neupert, L. Santos, S. Ryu, C. Chamon and C. Mudry, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 165107 CrossRef.
- L. Santos, T. Neupert, S. Ryu, C. Chamon and C. Mudry, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 165138 CrossRef.
- A. Stern, Annu. Rev. Condens. Matter Phys., 2016, 7, 349 CrossRef CAS.
- S. Rachel, Rep. Prog. Phys., 2018, 81, 116501 CrossRef PubMed.
- Y.-M. Wu, D. Shaffer, Z. Wu and L. H. Santos, Phys. Rev. B, 2024, 109, 115111 CrossRef CAS.
- J. Maciejko, C. Liu, Y. Oreg, X.-L. Qi, C. Wu and S.-C. Zhang, Phys. Rev. Lett., 2009, 102, 256803 CrossRef PubMed.
- A. Ström, H. Johannesson and G. I. Japaridze, Phys. Rev. Lett., 2010, 104, 256804 CrossRef PubMed.
- Y. Tanaka, A. Furusaki and K. A. Matveev, Phys. Rev. Lett., 2011, 106, 236402 CrossRef PubMed.
- J. C. Budich, F. Dolcini, P. Recher and B. Trauzettel, Phys. Rev. Lett., 2012, 108, 086602 CrossRef PubMed.
- F. Crépin, J. C. Budich, F. Dolcini, P. Recher and B. Trauzettel, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 121106(R) CrossRef.
- E. Eriksson, A. Ström, G. Sharma and H. Johannesson, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 161103(R) CrossRef.
- N. Lezmy, Y. Oreg and M. Berkooz, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235304 CrossRef.
- A. M. Lunde and G. Platero, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 035112 CrossRef.
- T. L. Schmidt, S. Rachel, F. von Oppen and L. I. Glazman, Phys. Rev. Lett., 2012, 108, 156402 CrossRef PubMed.
- B. L. Altshuler, I. L. Aleiner and V. I. Yudson, Phys. Rev. Lett., 2013, 111, 086401 CrossRef CAS PubMed.
- V. Cheianov and L. I. Glazman, Phys. Rev. Lett., 2013, 110, 206803 CrossRef PubMed.
- A. Del Maestro, T. Hyart and B. Rosenow, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165440 CrossRef.
- E. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 235414 CrossRef.
- J. I. Väyrynen, M. Goldstein and L. I. Glazman, Phys. Rev. Lett., 2013, 110, 216402 CrossRef PubMed.
- F. Geissler, F. Crépin and B. Trauzettel, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 235136 CrossRef.
- N. Kainaris, I. V. Gornyi, S. T. Carr and A. D. Mirlin, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 075118 CrossRef CAS.
- J. I. Väyrynen, M. Goldstein, Y. Gefen and L. I. Glazman, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 115309 CrossRef.
- O. M. Yevtushenko, A. Wugalter, V. I. Yudson and B. L. Altshuler, EPL, 2015, 112, 57003 CrossRef.
- L. Kimme, B. Rosenow and A. Brataas, Phys. Rev. B, 2016, 93, 081301(R) CrossRef.
- J. I. Väyrynen, F. Geissler and L. I. Glazman, Phys. Rev. B, 2016, 93, 241301(R) CrossRef.
- C.-H. Hsu, P. Stano, J. Klinovaja and D. Loss, Phys. Rev. B, 2017, 96, 081405(R) CrossRef.
- C.-H. Hsu, P. Stano, J. Klinovaja and D. Loss, Phys. Rev. B, 2018, 97, 125432 CrossRef CAS.
- M. Kharitonov, F. Geissler and B. Trauzettel, Phys. Rev. B, 2017, 96, 155134 CrossRef.
- S. Groenendijk, G. Dolcetto and T. L. Schmidt, Phys. Rev. B, 2018, 97, 241406(R) CrossRef.
- J. I. Väyrynen, D. I. Pikulin and J. Alicea, Phys. Rev. Lett., 2018, 121, 106601 CrossRef PubMed.
- J.-H. Zheng and M. A. Cazalilla, Phys. Rev. B, 2018, 97, 235402 CrossRef CAS.
- A. C. Balram, K. Flensberg, J. Paaske and M. S. Rudner, Phys. Rev. Lett., 2019, 123, 246803 CrossRef CAS PubMed.
- V. D. Kurilovich, P. D. Kurilovich, I. S. Burmistrov and M. Goldstein, Phys. Rev. B, 2019, 99, 085407 CrossRef CAS.
- L. Vannucci, T. Olsen and K. S. Thygesen, Phys. Rev. B, 2020, 101, 155404 CrossRef CAS.
- Y. Vinkler-Aviv, D. May and F. B. Anders, Phys. Rev. B, 2020, 101, 165112 CrossRef CAS.
- O. M. Yevtushenko and V. I. Yudson, New J. Phys., 2022, 24, 023040 CrossRef CAS.
- T. Dietl, Phys. Rev. Lett., 2023, 130, 086202 CrossRef CAS PubMed.
- T. Dietl, Phys. Rev. B, 2023, 107, 085421 CrossRef CAS.
- S. Gangadharaiah, B. Braunecker, P. Simon and D. Loss, Phys. Rev. Lett., 2011, 107, 036801 CrossRef PubMed.
- P. P. Aseev, P. Marra, P. Stano, J. Klinovaja and D. Loss, Phys. Rev. B, 2019, 99, 205435 CrossRef CAS.
- K. Laubscher, D. Chughtai, D. Loss and J. Klinovaja, Phys. Rev. B, 2020, 102, 195401 CrossRef CAS.
- P. Lecheminant, A. O. Gogolin and A. A. Nersesyan, Nucl. Phys. B, 2002, 639, 502 CrossRef.
- A. Jaefari and E. Fradkin, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 035104 CrossRef.
- G. Y. Cho, R. Soto-Garrido and E. Fradkin, Phys. Rev. Lett., 2014, 113, 256405 CrossRef PubMed.
- L. Fidkowski, R. M. Lutchyn, C. Nayak and M. P. A. Fisher, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 195436 CrossRef.
- Y. Fuji, Phys. Rev. B, 2016, 93, 104425 CrossRef.
- N. J. Robinson, A. Altland, R. Egger, N. M. Gergs, W. Li, D. Schuricht, A. M. Tsvelik, A. Weichselbaum and R. M. Konik, Phys. Rev. Lett., 2019, 122, 027201 CrossRef CAS PubMed.
- D. Boyanovsky, J. Phys. A: Math. Gen., 1989, 22, 2601 CrossRef.
- E. Sagi, A. Haim, E. Berg, F. von Oppen and Y. Oreg, Phys. Rev. B, 2017, 96, 235144 CrossRef.
- D. Loss and T. Martin, Phys. Rev. B, 1994, 50, 12160–12163 CrossRef CAS PubMed.
- T. Martin and D. Loss, Int. J. Mod. Phys. B, 1995, 9, 495 CrossRef.
- A. De Martino and R. Egger, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 235418 CrossRef.
- H.-C. Wang and C.-H. Hsu, 2D Mater., 2024, 11, 035007 CrossRef.
-
M. S. Dresselhaus, G. Dresselhaus and A. Jorio, Group Theory: Application to the Physics of Condensed Matter, Springer, Berlin, Heidelberg, 2008 Search PubMed.
- G. Wentzel, Phys. Rev., 1951, 83, 168 CrossRef.
- J. Bardeen, Rev. Mod. Phys., 1951, 23, 261 CrossRef.
- S. Engelsberg and B. B. Varga, Phys. Rev., 1964, 136, A1582 CrossRef.
- P. Stepanov, I. Das, X. Lu, A. Fahimniya, K. Watanabe, T. Taniguchi, F. H. L. Koppens, J. Lischner, L. Levitov and D. K. Efetov, Nature, 2020, 583, 375 CrossRef CAS PubMed.
- J. Li, W. Pan, B. A. Bernevig and R. M. Lutchyn, Phys. Rev. Lett., 2016, 117, 046804 CrossRef PubMed.
- C. Schrade and L. Fu, Phys. Rev. Lett., 2018, 120, 267002 CrossRef CAS PubMed.
- C. Schrade and L. Fu, Phys. Rev. Lett., 2022, 129, 227002 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: The details about the model and the setup, operator product expansion, phonon influence, and additional numerical results of the RG analysis. See DOI: https://doi.org/10.1039/d4nh00254g |
| ‡ To achieve the criterion (6), one can alternatively consider the π-junction setup with Δ+ = 0 but finite Δ−,30,104 which can be mapped back to the same form as the identical pairing setup (ESI†). |
§ Despite a similar form, 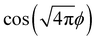 and and 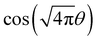 , in ref. 107, the roles of the two cosine terms are reversed: the topological phase is characterized by their current-like θ field, since the parity is related to their density-like ϕ field. , in ref. 107, the roles of the two cosine terms are reversed: the topological phase is characterized by their current-like θ field, since the parity is related to their density-like ϕ field. |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,n(r) with the spatial coordinate r, the channel index n ∈ {1, 2}, and
,n(r) with the spatial coordinate r, the channel index n ∈ {1, 2}, and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = R (
= R (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = L) for right-moving spin-down (left-moving spin-up) modes, respectively. Within the bosonization scheme,63–65 we have
= L) for right-moving spin-down (left-moving spin-up) modes, respectively. Within the bosonization scheme,63–65 we have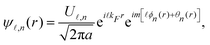
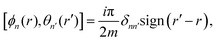
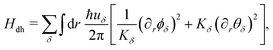
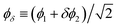 and similarly for θδ. The velocity uδ = vF/Kδ of the sector δ is related to the interaction parameter Kδ = [1 + 2(Uee + δVee)/(πħvF)]−1/2 with the intrachannel (interchannel) interaction strength Uee (Vee). One obtains compactness in the boson fields,
and similarly for θδ. The velocity uδ = vF/Kδ of the sector δ is related to the interaction parameter Kδ = [1 + 2(Uee + δVee)/(πħvF)]−1/2 with the intrachannel (interchannel) interaction strength Uee (Vee). One obtains compactness in the boson fields, 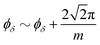 and
and 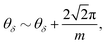 which plays a role when examining the ground state degeneracy below.
which plays a role when examining the ground state degeneracy below.
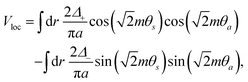
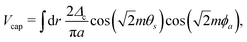
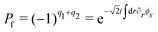 with the fermion number qn for channel n. Utilizing the relation
with the fermion number qn for channel n. Utilizing the relation 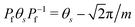 and the compactness of θs, we conclude that the ground states for
and the compactness of θs, we conclude that the ground states for 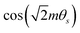 are characterized by eigenstates of Pf, satisfying Pf|e/o〉s = ±|e/o〉s. These states are constructed from even and odd combinations as
are characterized by eigenstates of Pf, satisfying Pf|e/o〉s = ±|e/o〉s. These states are constructed from even and odd combinations as 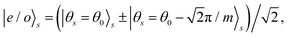 with θ0 being a minimum of the cosine term. Concerning the topological properties, since the θs field appears in both Vloc and Vcap, the total fermion parity does not distinguish between the two terms.
with θ0 being a minimum of the cosine term. Concerning the topological properties, since the θs field appears in both Vloc and Vcap, the total fermion parity does not distinguish between the two terms.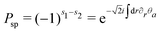 . Again, with
. Again, with 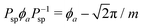 and the compactness of ϕa, we conclude that the ground states for
and the compactness of ϕa, we conclude that the ground states for 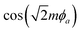 are doubly degenerate and can be written as
are doubly degenerate and can be written as 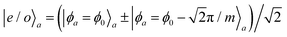 , with eigenvalue ±1 of Psp and a minimum ϕ0. On the other hand, since the spin difference parity operator commutes with θa, the local pairing term exhibits no ground state degeneracy. We thus conclude that the Δc term characterizes a topologically nontrivial phase.§
, with eigenvalue ±1 of Psp and a minimum ϕ0. On the other hand, since the spin difference parity operator commutes with θa, the local pairing term exhibits no ground state degeneracy. We thus conclude that the Δc term characterizes a topologically nontrivial phase.§
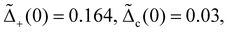 Uee/(πħvF) = 2.5 and Vee/Uee = 0.7. The label l* marks the length scale of the flow end point, where any of the couplings reach unity. (b) Phase diagram determined from the renormalized pairing strengths, with the labels “top SC”, “tr SC” and “DH” denoting topological superconductivity, trivial superconductivity and double helical liquids, respectively. In the last region, none of the pairings reaches unity as the scale l approaches ln(L/a) set by the system size L. (c) and (d) Renormalized interaction parameters, with a highlighted curve where Ka flows to unity. The initial points of the flows in panel (a) and Fig. 3(a) are marked; the line cuts A and B correspond to those in Fig. 4.
Uee/(πħvF) = 2.5 and Vee/Uee = 0.7. The label l* marks the length scale of the flow end point, where any of the couplings reach unity. (b) Phase diagram determined from the renormalized pairing strengths, with the labels “top SC”, “tr SC” and “DH” denoting topological superconductivity, trivial superconductivity and double helical liquids, respectively. In the last region, none of the pairings reaches unity as the scale l approaches ln(L/a) set by the system size L. (c) and (d) Renormalized interaction parameters, with a highlighted curve where Ka flows to unity. The initial points of the flows in panel (a) and Fig. 3(a) are marked; the line cuts A and B correspond to those in Fig. 4.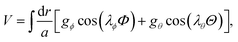
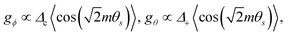
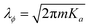 and
and 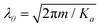 . The new fields
. The new fields 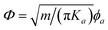 and
and 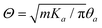 are introduced to match the notations in ref. 105. We observe that the electronic subsystem characterizes a self-dual sine-Gordon Hamiltonian, with the self-duality point gϕ = gθ and λϕ = λθ reached when Ka → 1. Remarkably, for certain initial parameters, such as flow I in Fig. 2(a), the renormalized value of Ka converges to unity at the end of the RG flow, accompanied by
are introduced to match the notations in ref. 105. We observe that the electronic subsystem characterizes a self-dual sine-Gordon Hamiltonian, with the self-duality point gϕ = gθ and λϕ = λθ reached when Ka → 1. Remarkably, for certain initial parameters, such as flow I in Fig. 2(a), the renormalized value of Ka converges to unity at the end of the RG flow, accompanied by 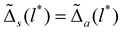 , signifying the arrival at the self-duality point. Moreover, we find that eqn (7) presents a hierarchy of self-dual sine-Gordon models (ESI†), where different m values characterize different classes with λϕ2 = λθ2 = 2πm,105,111,112 including the m = 3 model with parafermion modes. Notably, for m = 2, eqn (7) can be refermionized using
, signifying the arrival at the self-duality point. Moreover, we find that eqn (7) presents a hierarchy of self-dual sine-Gordon models (ESI†), where different m values characterize different classes with λϕ2 = λθ2 = 2πm,105,111,112 including the m = 3 model with parafermion modes. Notably, for m = 2, eqn (7) can be refermionized using 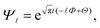 allowing for the introduction of Majorana fields ξ
allowing for the introduction of Majorana fields ξ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and η
and η![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) through
through 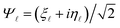 . With the details in the ESI,† we get
. With the details in the ESI,† we get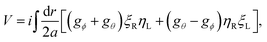
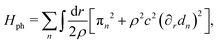
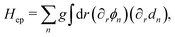
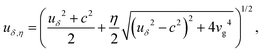
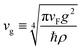 . The modification in velocities from their bare values, uδ and c, can be substantial, to the extent that one of the velocities reaches zero, which is referred to as the Wentzel–Bardeen (WB) singularity, known for nonhelical channels.113–116,118–120 Without pairing terms, the singularity condition is quantified as
. The modification in velocities from their bare values, uδ and c, can be substantial, to the extent that one of the velocities reaches zero, which is referred to as the Wentzel–Bardeen (WB) singularity, known for nonhelical channels.113–116,118–120 Without pairing terms, the singularity condition is quantified as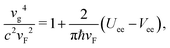
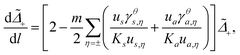
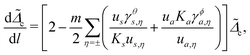
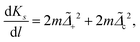
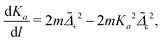
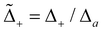 ,
, 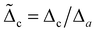 and
and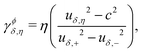
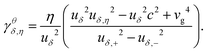

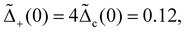 Uee/(πħvF) = 2.5 and Vee/Uee = 0.83. (a) RG flow corresponding to dot IIa in Fig. 2 and 4(a). (b) RG flow with vg2/(cvF) = 0.53, corresponding to dot IIb in Fig. 4(a).
Uee/(πħvF) = 2.5 and Vee/Uee = 0.83. (a) RG flow corresponding to dot IIa in Fig. 2 and 4(a). (b) RG flow with vg2/(cvF) = 0.53, corresponding to dot IIb in Fig. 4(a).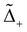 and reducing
and reducing 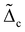 . In consequence, close to the boundary between the two superconducting phases, the electron–phonon coupling can push the system from a topological phase to a trivial phase. Furthermore, the pairing perturbations also influence the boundary approaching the WB singularity. Consequently, the WB singularity is reached for a smaller vg as compared to earlier analysis.113,114 We also note that, for m > 1, a weaker electron–phonon coupling is necessary to induce phase transitions (ESI†), indicating a more fragile topological phase in the fractional regime.
. In consequence, close to the boundary between the two superconducting phases, the electron–phonon coupling can push the system from a topological phase to a trivial phase. Furthermore, the pairing perturbations also influence the boundary approaching the WB singularity. Consequently, the WB singularity is reached for a smaller vg as compared to earlier analysis.113,114 We also note that, for m > 1, a weaker electron–phonon coupling is necessary to induce phase transitions (ESI†), indicating a more fragile topological phase in the fractional regime.
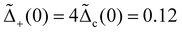 and (b)
and (b) 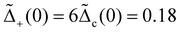 . The label “WB” indicates the regime beyond the WB singularity. The dots IIa and IIb correspond to the flows in Fig. 3(a) and (b), respectively. The line cuts A and B correspond to those marked in Fig. 2.
. The label “WB” indicates the regime beyond the WB singularity. The dots IIa and IIb correspond to the flows in Fig. 3(a) and (b), respectively. The line cuts A and B correspond to those marked in Fig. 2.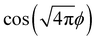 and
and 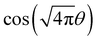 , in ref. 107, the roles of the two cosine terms are reversed: the topological phase is characterized by their current-like θ field, since the parity is related to their density-like ϕ field.
, in ref. 107, the roles of the two cosine terms are reversed: the topological phase is characterized by their current-like θ field, since the parity is related to their density-like ϕ field.
