The thermoelastic properties of monolayer covalent organic frameworks studied by machine-learning molecular dynamics†
Bing
Wang
,
Penghua
Ying‡
 and
Jin
Zhang
and
Jin
Zhang
 *
*
School of Science, Harbin Institute of Technology, Shenzhen 518055, PR China. E-mail: jinzhang@hit.edu.cn
First published on 23rd November 2023
Abstract
Two-dimensional (2D) covalent organic frameworks (COFs) are emerging as promising 2D polymeric materials with broad applications owing to their unique properties, among which the mechanical properties are quite important for various applications. However, the mechanical properties of 2D COFs have not been systematically studied yet. Herein, a machine-learned neuroevolution potential (NEP) was developed to study the elastic properties of two representative monolayer 2D COFs, namely COF-1 and COF-5. The trained NEP enables one to study the elastic properties of 2D COFs in realistic situations (e.g., finite size and temperature) and possesses greatly improved computational efficiency when compared with density functional theory calculations. With the aid of the obtained NEP, molecular dynamics (MD) simulations together with a strain-fluctuation method were employed to evaluate the elastic constants of the considered 2D COFs at different temperatures. The elastic constants of COF-1 and COF-5 monolayers were found to decrease with an increase in the temperature, though they were almost isotropic irrespective of the temperature. The thermally induced softening of 2D COFs below a critical temperature was observed, which is mainly attributed to their inherent ripple configurations at finite temperatures, while above the critical temperature, the damping effect of anharmonic vibrations became the dominant factor. Based on the proposed mechanisms, analytical models were developed for capturing the temperature dependence of elastic constants, which were found to agree with the MD simulation results well. This work provides an in-depth insight into the thermoelastic properties of monolayer COFs, which can guide the development of 2D COF materials with tailored mechanical behaviors for enhancing their performance in various applications.
Introduction
In recent years, covalent organic frameworks (COFs) have emerged as a highly promising class of crystalline porous polymers, which possess unique structures that are composed of a network of dynamic covalent bonds.1 Owing to their unique structures, COFs possess a large void space and a high surface area, which render them the capacity to be used in adsorbing and separating hydrogen, carbon dioxide, methane, and other gases.2–4 Besides, COFs are promising catalytic platforms owing to their abundant and uniform open channels, as well as their excellent insolubility and high stability. These characteristics are crucial for facilitating the mass-transfer process in catalysis.5,6 The highly efficient size selectivity of COFs due to their uniform pores has also led to them being employed as highly efficient and size-selective catalysts.7 Meanwhile, COFs have been designed for use as potential Li-ion solid-state conductors and in flexible electronics, since most of them are flexible and have high conductivities, including thermal conductivity, among the reported crystalline porous materials.8–10Among the different types of COFs, two-dimensional (2D) COFs are currently receiving much attention because of their unique structural properties. Each individual layer in 2D COFs maintains its in-plane stability through strong covalent bonds, while neighboring layer components are connected with each other via weak interlamellar interactions. The inherent structure of 2D COFs allows the precise manipulation and customization of their pores at a nanoscale level.11 As a result, 2D COFs can be designed with multi-level porosity, which makes them possibly exhibit an excellent performance in the applications of adsorption and catalysis and in the manufacture of micro/nanodevices.12,13 Specifically, the most practical applications of 2D COFs strongly rely on their mechanical properties because previous studies indicate that the physical and chemical properties of 2D materials and COFs can be significantly affected by mechanical stimuli.14 Thus, strain engineering is an effective method to modify the size of pores in 2D materials, allowing the separation of different gas mixtures at a specific pore size15 and changes in water permeability for 2D materials.16 Similarly, the thermal conductivity of COFs can be effectively modulated through strain engineering.17,18 Besides, mechanical stimuli are also inevitable in many applications of 2D materials. For instance, in the thermal catalysis applications of 2D materials, such as 2D MXenes, the operational conditions typically encompass elevated temperatures and pressures. The catalytic efficacy is notably contingent upon the thermodynamic and mechanical robustness of 2D MXenes.19 In the manufacture and application of nanosensors, stable mechanical performance of the component 2D films is crucial for the production and reusability of these devices.20 However, even though the mechanical property of 2D COFs is a fundamental intrinsic feature relevant to most of their applications, there are relatively few reports on their mechanical behaviors.
In spite of two very recent experimental reports on the tensile properties of multilayer COFs,21,22 atomistic simulations including density functional theory (DFT) calculations and molecular dynamics (MD) simulations are generally employed to investigate the mechanical properties of 2D COFs. By using DFT calculations, Kapri et al.23 calculated the elastic tensor of some 2D COFs very recently. Although the DFT approach has high accuracy, it is computationally expensive, and it is thus difficult to use DFT for studying COFs with large pores or complex structures. Moreover, it is usually difficult to consider the effects of the crystal size and finite temperature in DFT calculations. To overcome the limitations of DFT calculations, MD simulations are usually treated as a more effective method for theoretically studying the mechanical behaviors of 2D COFs. By exploiting MD simulations, Zhang24 reported a phase transition occurring in 2D COFs due to compression. The phase transition was found to have an effect on the elastic constants, band gap, and thermal conductivity of the studied 2D COFs. Li and Brédas25 reported the elastic properties of COFs using OPLS all-atom force field potentials26 and pointed out that the existence of structural defects will significantly reduce the stiffness of 2D COFs. Very recently, Hao et al.27 revealed that 2D COFs possess a superior impact-resistant capability under high-velocity impacts. Although these initial results reveal some fundamental mechanical characters of 2D COFs, there still exist some limitations in these MD studies. For example, these studies were based on some empirical potentials specifically developed for other materials rather than COFs.25,28 Thus, the accuracy of these empirical potentials in describing 2D COFs may be questionable. Recently, machine-learned potential (MLP) has been shown to be a promising on-demand approach for investigating the mechanical properties of 2D materials.29 For example, machine-learning interatomic potentials (MLIPs) were developed by Mortazavi et al. for studying the mechanical behaviors and properties of various 2D materials.30,31 It was shown that MLIPs could enable the efficient use of classical MD simulations to evaluate the mechanical properties of relatively large 2D material systems with the DFT level of accuracy. Moreover, the MLIPs also enable first-principles multiscale modeling, in which the DFT level of accuracy can be hierarchically bridged to explore the mechanical properties of macroscopic 2D material systems.32 Also, Ying et al. very recently employed MLPs to investigate the mechanical responses of a monolayer quasi-hexagonal-phase fullerene membrane subjected to uniaxial tension.33 Overall, the MLPs developed recently provide a possible avenue for studying the mechanical properties of 2D COFs that possess large pores and abundant elements.
Motivated by these ideas and previous studies, in this work we developed neuroevolution potential (NEP) framework-based MLPs34 for two representative 2D COFs, namely COF-1 and COF-5.1 The obtained NEP was further applied to investigate the elastic properties of the monolayer COFs at different temperatures by using extensive MD simulations together with the strain-fluctuation method.35,36 Here, we considered the monolayers of these 2D COFs because many monolayer COFs have been successfully synthesized recently and have been found to exhibit many unique properties and possess many potential applications.37–39 Moreover, a comprehensive understanding of the elastic property of their component layer is also a necessary first step toward understanding the elastic property of layered 2D COFs. Our results show that the temperature generally has a softening effect on the elasticity of monolayer COFs, although the temperature sensitivity of the elastic constants is different below and above a critical temperature. In particular, the greater softening effect observed below the critical temperature can be majorly attributed to the thermal rippling of monolayer COFs, while the increased nonharmonic forces above the critical temperature can suppress the effect of thermal rippling, resulting in a lower sensitivity of the elastic moduli to temperature. Based on the proposed mechanisms, some analytical models were developed for better capturing the temperature dependence of the elastic constants of monolayer 2D COFs.
Simulation models and methods
Simulation models
In this study, we focused on two typical monolayer COFs, i.e., COF-1 and COF-5, which were assembled through reactions between organic precursors, resulting in strong covalent bonds to afford porous, stable, and crystalline materials. Specifically, as shown in Fig. 1a, COF-1 was composed of the building blocks of benzene-1,3,5-tricarboxylic acid (BTC) and 1,3,5-tris (4-aminophenyl) benzene (TAPB), while COF-5 contained the building blocks of 1,4-benzenedicarboxylic acid (BDC) and 1,2-bis (4-pyridyl) ethylene (BPE). MD simulations were employed to study the elastic behaviors of the aforementioned monolayer 2D COF materials. It is known that the elastic properties, especially the elastic moduli, rely on the size of the structures considered in MD simulations, and the elastic modulus could be wrongly estimated if the size of the simulated system is too small.40 Therefore, to ensure the accuracy of the simulation results, we chose a relatively large size of 40.7 nm × 39.1 nm for COF-1, which consisted of 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 atoms, and a size of 41.8 nm × 39.2 nm for COF-5, which contained 19
500 atoms, and a size of 41.8 nm × 39.2 nm for COF-5, which contained 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 968 atoms. As shown in Fig. S1 in the ESI,† a convergence of the Young's modulus was observed after the length of the COF-1 and COF-5 models was larger than 25 nm, indicating the suitability of the size of 2D COFs selected here. In our simulations, a vacuum spacing of 3 nm was placed in the out-of-plane direction to avoid non-physical interactions between the COF layer and its replicas, while periodic boundaries were employed in the in-plane directions.
968 atoms. As shown in Fig. S1 in the ESI,† a convergence of the Young's modulus was observed after the length of the COF-1 and COF-5 models was larger than 25 nm, indicating the suitability of the size of 2D COFs selected here. In our simulations, a vacuum spacing of 3 nm was placed in the out-of-plane direction to avoid non-physical interactions between the COF layer and its replicas, while periodic boundaries were employed in the in-plane directions.
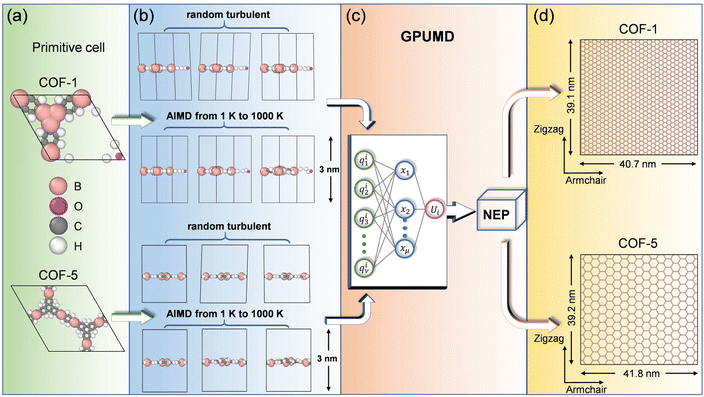 | ||
| Fig. 1 Workflow for training the NEP model for 2D COF monolayers. (a) Primitive cells of COF-1 and COF-5. (b) Construction of the training and testing data sets. (c) Schematic of the NEP frameworks. (d) Supercells of the monolayer COF-1 and COF-5 used to evaluate their elastic properties. The OVITO package was used here for visualization.41 | ||
Acquisition of dataset from first-principles calculations
As illustrated in Fig. 1b, 2400 structures were constructed in total for training and testing the NEP model, which were equally comprised of structures of COF-1 and COF-5. Moreover, 2000 structures were extracted from ab initio molecular dynamics (AIMD) simulations, while the other 400 structures were obtained by manual perturbations. All the structures in the reference dataset were based on the primitive cells of monolayer COF-1 and COF-5. In the AIMD simulations, the structural sampling was performed under the NVT ensemble with a Nosé–Hoover heat bath,42 in which the system temperature was linearly raised from 1 K to 1000 K within 10 ps. Here, the time step was set as 1 fs. The perturbated structures were obtained by randomly adding 5% perturbations to the lattice constants and changing the atomic coordinates with a distance less than 0.2 Å. With the structures of COF-1 and COF-5 established through the aforementioned process, we calculated their energy, virial, and atomic force using single-point DFT calculations. All the DFT calculations and AIMD simulations were implemented by the VASP package43,44 with the Perdew–Burke–Ernzerhof functional.45 The electronic self-consistent loop was set at a threshold of 10−7 eV, while an energy cutoff of 800 eV was utilized. The k-point grid was set as 2 × 2 × 1. The suitability of the energy cutoff and wavevector grid could be verified by the fact that the converged energy of the system was observed at the selected energy cutoff and wavevector grid, as shown in Fig. S2.†Training of the NEP framework for monolayer COFs
The MLP model based on the third-generation NEP framework46 was trained with the aid of using the GPUMD package.47 The workflow is briefly shown in Fig. 1c. Here, we randomly divided the total dataset into a training dataset and a testing dataset in a ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In order to train the NEP potential for the considered monolayer 2D COFs, several hyperparameters needed to be set. The hyperparameters used for testing can be found in the ESI (Table S1†). The impact of various hyperparameters on the accuracy of the NEP model was thoroughly evaluated. Specifically, the cutoff radii for the radial and angular descriptor components were rRc = 10 Å and rAc = 4 Å, respectively. The Chebyshev polynomial expansion orders for the radial and angular descriptor components were nRmax = 6 and nAmax = 4. The suitability of the selected hyperparameters was confirmed by the results shown in Fig. S3.† Moreover, the Legendre polynomial expansion order for the angular descriptor components was lmax = 4. Besides, we employed 100 neurons in the hidden layer of the neural network. The default setting was used for the normalized factors of λ1, λ2, λe, λf, and λv, which were 0.1, 0.1, 1.0, 1.0, and 0.1, respectively. The population size and the number of generations in the algorithm were Npop = 50 and Ngen = 5 × 106, respectively. After determining the aforementioned hyperparameters, we could finally get an NEP function for both the COF-1 and COF-5 monolayers.
1. In order to train the NEP potential for the considered monolayer 2D COFs, several hyperparameters needed to be set. The hyperparameters used for testing can be found in the ESI (Table S1†). The impact of various hyperparameters on the accuracy of the NEP model was thoroughly evaluated. Specifically, the cutoff radii for the radial and angular descriptor components were rRc = 10 Å and rAc = 4 Å, respectively. The Chebyshev polynomial expansion orders for the radial and angular descriptor components were nRmax = 6 and nAmax = 4. The suitability of the selected hyperparameters was confirmed by the results shown in Fig. S3.† Moreover, the Legendre polynomial expansion order for the angular descriptor components was lmax = 4. Besides, we employed 100 neurons in the hidden layer of the neural network. The default setting was used for the normalized factors of λ1, λ2, λe, λf, and λv, which were 0.1, 0.1, 1.0, 1.0, and 0.1, respectively. The population size and the number of generations in the algorithm were Npop = 50 and Ngen = 5 × 106, respectively. After determining the aforementioned hyperparameters, we could finally get an NEP function for both the COF-1 and COF-5 monolayers.
Strain-fluctuation methods
The NEP model obtained above was employed in MD simulations for further evaluating the elastic properties of the monolayer COF-1 and COF-5 at the finite temperature, which was implemented by the strain-fluctuation method.35,36 The strain-fluctuation method calculates the elastic constants by examining strain fluctuations in a thermally equilibrated system without applying any stimuli. Furthermore, all the components of the elastic tensor can be calculated in a single simulation. This method is predicated on the fluctuation-dissipation theorem that relies on the assumption that spontaneous fluctuations and small mechanical stimuli will generate the similar responses of a system in thermodynamic equilibrium.48 Besides the strain-fluctuation method, the stress-fluctuation method is another method based on the fluctuation-dissipation theorem, which also has the capability to calculate the elastic constants of materials at a specific temperature. Nevertheless, the implementation of the stress-fluctuation method is more rigorous and complex, especially for atomic models involving intramolecular interactions.49 Therefore, we chose the strain-fluctuation method here to conduct the thermodynamic statistics tests for the 2D COF structures at a constant temperature and ambient pressure (NPT ensemble), which were further used to calculate the elastic constants for the 2D COFs.To implement the calculations based on the strain-fluctuation method, all the 2D COF structures were relaxed for 1000 ps at 0 GPa in the NPT ensemble by using the stochastic cell rescaling method,50 which makes the structures reach their equilibrium at a certain temperature. In all the simulations, the strain εij was determined from the following equation:35,36
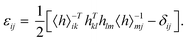 | (1) |
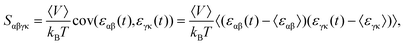 | (2) |
The result in Fig. S4† shows the evolution of the elastic constants with respect to the simulation time, which indicated a convergency of the elastic stiffness tensors after the simulation for 1000 ps. Thus, the unit cell vector was output in another successive simulation with 500 ps, which was further divided into five groups. The average of the compliance tensors of these five groups was treated as the final result, while the standard error of the five groups of data was regarded as the calculation error.
Results and discussion
Validation of the NEP model for COF-1 and COF-5
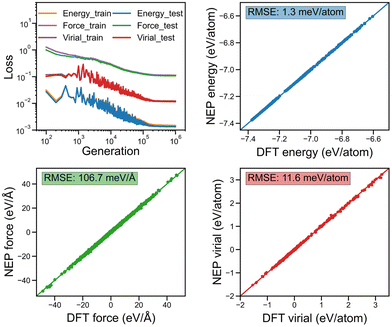
In Fig. 2a and b, we show the evolution of the loss functions for the training dataset of the considered monolayer 2D COFs with respect to the generations. All the loss functions were found to become completely converged when the training was performed after 106 generations. The corresponding energy, force, and virial of the monolayer COFs predicted by NEP were also compared against the corresponding DFT results in Fig. 2. Here, the extremely small values of the root-mean square (RMS) error for the energy, force, and virial indicate that the NEP model trained here was capable of accurately predicting the energy, force, and virial properties of the monolayer COFs considered here.To evaluate the accuracy of the trained NEP model in describing the structures of the 2D COFs considered in the MD simulations, we compared the radial distribution function (RDF) of COF-1 and COF-5 obtained from the NEP-based MD and AIMD simulations at 300 K. As shown in Fig. 3, a good agreement was observed between these two methods, indicating that the NEP model could faithfully capture the structural characteristics of the monolayer COF-1 and COF-5.
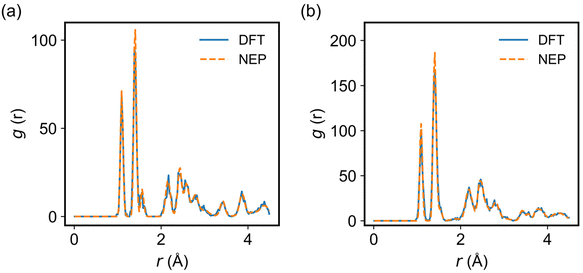 | ||
| Fig. 3 The RDFs of (a) COF-1 and (b) COF-5 calculated by using classical MD simulations at 300 K driven by DFT (solid lines) and NEP (dashed lines). | ||
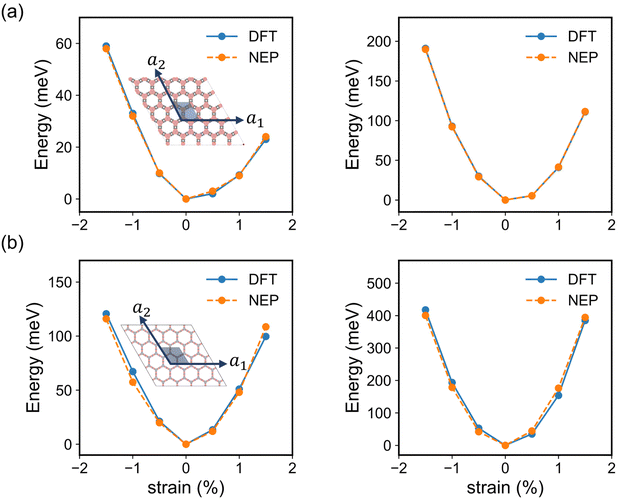
To further validate the precision of NEP in evaluating the elastic properties of the monolayer COF-1 and COF-5, we compared the energy changes in the strained 2D COFs extracted from NEP-based MD simulations and DFT calculations. Here, all the DFT calculation results were based on the primitive cells as shown in the inset of Fig. 4, while all the NEP calculations were based on 5 × 5 × 1 supercells. In addition, the strain was defined as the relative changes of the lattice constants in the strained monolayer.53 As shown in the inset of Fig. 4, the strain was applied along the lattice vector a1 to represent the uniaxial deformation and along both a1 and a2 lattice vectors to represent the biaxial deformation condition to the monolayer COFs. As shown in Fig. 4, the energy changes in both the strained COF-1 and COF-5 monolayers obtained from DFT calculations were identical to the results calculated by the NEP models. We further employed the energy-strain method to calculate the elastic constants of the 2D COFs, which was implemented by VASPKIT.54 In this method, the elastic stiffness tensor is derived from the second-order derivative of the energy change with respect to the applied strain.55 Since the monolayer COF-1 and COF-5 considered here possessed 2D hexagonal structures, only three independent elastic constants, i.e., C11, C12, and C66 were calculated. These independent components of the elastic stiffness tensor calculated from NEP models are summarized in Table 1, in comparison with the corresponding DFT results. As for all elastic constants of monolayer COF-1 and COF-5, the error between the NEP and DFT results was within 1.2%. This good agreement demonstrates the accuracy of the trained NEP model for evaluating the elastic properties of the considered 2D COFs.
| Elastic constant (GPa) | COF-1 | COF-5 | ||
|---|---|---|---|---|
| NEP | DFT | NEP | DFT | |
| C 11 | 81.8 | 82.6 | 57.2 | 57.4 |
| C 12 | 66.0 | 66.0 | 48.6 | 48.7 |
| C 66 | 8.2 | 8.1 | 4.3 | 4.3 |
Thermoelastic properties of monolayer COFs
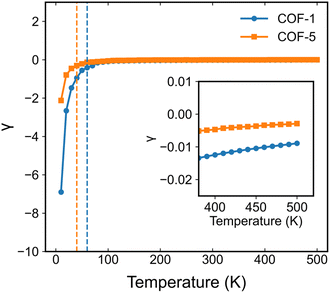
Apart from the high computational cost, DFT calculations usually are only available for calculating the elastic constants of a material at the zero-temperature ground state. Nevertheless, as the temperature increases, the atoms of a material vibrate more vigorously, resulting in thermal expansion and changes in the elastic properties of materials. Therefore, when studying the elastic properties of a material at finite temperatures, it becomes necessary to take into account some additional factors, such as the thermal effect and anharmonic contributions.56,57In this study, we employed the strain-fluctuation method to calculate the elastic constants of monolayer COF-1 and COF-5 over a temperature range from 10 K to 500 K. Here, the interval was 10 K for the temperature increasing from 10 to 100 K, while it was 50 K for the temperature largely growing from 100 to 500 K. The thermodynamical stability of these monolayer COFs at high temperatures could be verified by the stability of their energy during AIMD simulations in the NVT ensemble (Fig. S3†). Fig. 5 illustrates the temperature-dependent variations in the elastic constants C11, C12, and C66. For monolayer COF-1, a significant decrease was observed in both C11 and C12 at temperatures below 60 K. Specifically, as the temperature increased from 0 to 60 K, C11 of COF-1 decreased from 81.8 to 7.3 GPa, while its C12 decreased from 66.0 to −2.27 GPa. In the similar process, a much smaller change was observed in C66, which only declined from 8.2 to 4.2 GPa. However, when the temperature was larger than 60 K, the changes in the elastic constants became much slighter. As shown in Fig. 5a, when the temperature increased from 60 to 500 K, the C11 of COF-1 only decreased from 7.4 to 4.6 GPa, while its C12 and C66 fluctuated within small ranges, which were, respectively, −5.9 to 1.9 GPa and 1.7 to 7.3 GPa.
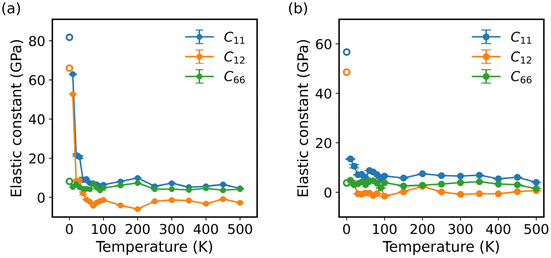 | ||
| Fig. 5 The elastic constants of (a) COF-1 and (b) COF-5 at different temperatures ranging from 0 to 500 K. The hollow circles denote the results at 0 K obtained from DFT calculations. | ||
A similar trend was observed in the elastic constants of COF-5 at different temperatures. As depicted in Fig. 5b, when the temperature increased from 0 to 40 K, C11 and C12 of COF-5 decreased from 57.3 to 7.1 GPa and from 48.6 to −0.6 GPa. In this process, C66 of COF-5 slightly decreased from 3.8 to 3.5 GPa. When the temperature further grew from 40 to 500 K, a decrease with a much smaller rate was observed in C11 of COF-5, which decreased from 7.1 to 4.0 GPa. Now, its C12 and C66 remained relatively stable, fluctuating from −1.6 to 2.4 GPa and from 1.4 to 4.6 GPa, respectively. Based on the above findings, we could conclude that the elastic constants of both COF-1 and COF-5 decreased as the temperature decreased below specific thresholds. However, after the threshold temperature, the sensitivity of all the elastic constants to the temperature change became very different. This result indicates the difference in mechanisms for the thermally induced softening of 2D COFs at small and large temperatures, which will be explained in more detail later.
Based on the obtained elastic constants, we can further calculate the Young's modulus E of the monolayer COFs through the following formula:58
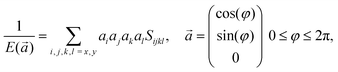 | (3) |
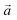 is the direction vector, and φ is the orientation angle in the plane.
is the direction vector, and φ is the orientation angle in the plane.
It is worth noting that, like some other 2D materials with similar hexagonal structures, such as graphene, hexagonal-boron nitride (h-BN), and transition metal-dichalcogenides, the present 2D COFs also possessed two principal directions, i.e., zigzag and armchair directions, as shown in Fig. 1d. In order to study the dependence of the Young's modulus on the crystalline orientation, we specifically evaluated here E in the zigzag and armchair directions by setting φ in eqn (3) as 0 and π/2, respectively. As for both COFs, the values of their E in the zigzag and armchair directions were close to each other, irrespective of the temperature (see Fig. 6). This result, to some extent, indicates the elastic isotropy of the monolayer COFs considered here. In terms of the thermal effect, its effect on the Young's modulus was exactly similar to that on the above elastic constants. Specifically, when the temperature was smaller than the critical value, i.e., 60 K for COF-1 and 40 K for COF-5, the Young's moduli of COF-1 and COF-5 decreased from 28.5 GPa and 15.4 GPa to 6.6 GPa and 7.2 GPa, respectively. However, when the temperature was larger than the critical values, the Young's modulus became less sensitive to the temperature change, though it similarly decreased as the temperature grew. For instance, as the temperature further increased from the critical temperatures to 500 K, the Young's moduli of COF-1 and COF-5 were reduced from 6.6 GPa and 7.2 GPa to 2.9 GPa and 3.8 GPa, respectively.
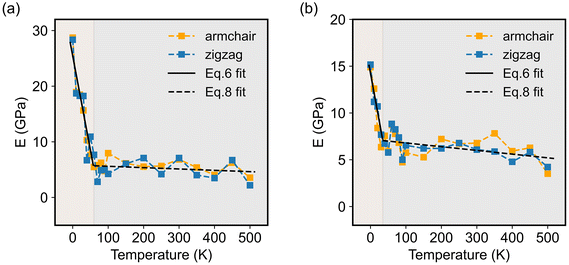 | ||
| Fig. 6 Young's moduli in the armchair and zigzag directions of (a) COF-1 and (b) COF-5 at different temperatures ranging from 0 to 500 K. | ||
A comparison of the Young's modulus of the present 2D COFs to the values of some other representative 2D materials with similar planar structures, such as graphene40 and h-BN,59 is illustrated in Table 2. In line with the method employed here, the Young's moduli of the monolayer graphene and h-BN shown here were similarly extracted from the strain-fluctuation method. As shown in Table 2, whether at the ground state (0 K) or room temperature (300 K), the Young's modulus of the 2D COFs was much lower than that of graphene and h-BN, denoting the high flexibility of the present 2D COFs. Meanwhile, as shown in Table S2,† we compared the Young's moduli of monolayer COF-5 obtained from the present NEP and previous all-atom optimized potentials for liquid simulations (OPLS-AA), which were developed specifically for liquid systems, such as peptides, proteins, nucleic acids, and organic solvents.25,26 Although the accuracy of the Young's moduli in the armchair direction predicted from both potentials were very close to the result from the DFT calculations, the difference between the Young's moduli in the zigzag direction extracted from NEP and DFT calculations was only 2,6%, which was much smaller than the difference (56%) between that calculated from OPLS-AA and DFT calculations. Moreover, the OPLS-AA predicted a strong mechanical anisotropy of COF-5, in contrast to the mechanical isotropy obtained from our NEP and DFT calculations. Thus, the present NEP is expected to provide higher levels of accuracy in estimating the elasticity of 2D COFs. Although the force field of OPLS-AA possesses parameters for a wide range of atoms and functional groups, it also needs to be specifically parameterized in the future for 2D COFs that contain some specific functional groups. The NEP developed here could serve as a benchmark for the future parameterization of the empirical potentials for 2D COFs.
Mechanism of the thermoelastic behaviors
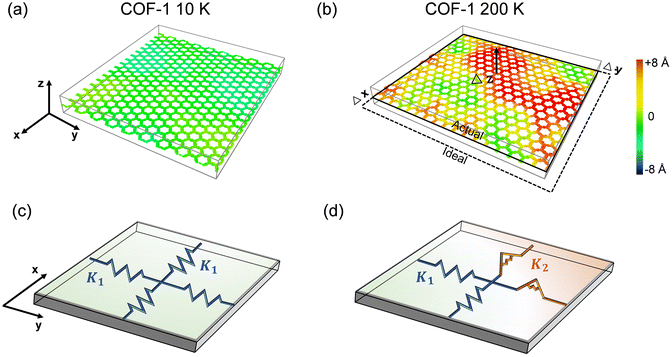
Since the elastic properties of 2D materials are usually related to their configurations, taking monolayer COF-1 as an example, we illustrate its structures at two representative temperatures, i.e., 10 K and 200 K, to explain the significant thermomechanical behaviors observed in monolayer COFs below the critical temperature. Fig. 7a and b show that serious thermal rippling existed in COF-1 at the temperature of 200 K, while COF-1 at the temperature of 10 K almost retained its original flatness configuration. Therefore, as illustrated in Fig. 7c, the expansion of monolayer COFs at relatively low temperatures was primarily resisted by the in-plane tensile stiffness, since it exhibited a planner configuration. However, as the temperature became higher, the de-rippling of the thermally rippled COFs by bending dominated their elongation now (Fig. 7d). As a monolayer material with atomic thickness, the monolayer COF usually possesses an extremely small bending stiffness. Thus, the thermally induced serious thermal rippling at a relatively high temperature was responsible for the reduction in the elastic constants of the monolayer COFs at high temperatures. Actually, many previous MD simulation studies have pointed out that the out-of-plane thermal rippling in 2D materials exerts a notable influence on their elastic moduli.40,60,61To better quantitatively measure the out-of-plane displacement of the monolayer COFs caused by the thermal rippling at different temperatures, we calculated the time-averaged RMS displacement ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) by using the following equation:
by using the following equation:
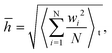 | (4) |
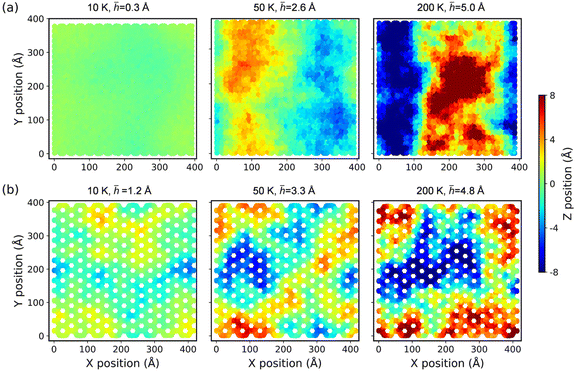 | ||
| Fig. 8 The configurations of (a) COF-1 and (b) COF-5 monolayers at different temperatures. The contour illustrates an out-of-plane deformation of the COFs. | ||
For a better understanding of the thermal rippling, we simplified the monolayer COF as a continuum 2D membrane. At a finite temperature, a membrane without any external forces can be fluctuated with both in-plane and out-of-plane modes. The RMS amplitude of the out-of-plane fluctuation ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) of COFs below the critical temperature can be calculated according to the statistical mechanical analysis, which has the following expression:60
of COFs below the critical temperature can be calculated according to the statistical mechanical analysis, which has the following expression:60
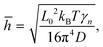 | (5) |
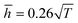 and
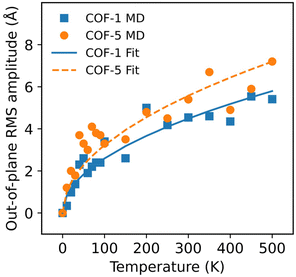
and 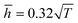 for monolayer COF-1 and COF-5, respectively, indicating a smaller RMS displacement in COF-1. It could be noted that the difference in the fitting coefficients of COF-1 and COF-5 was due to their different bending stiffnesses, since both COFs considered in the MD simulations had similar dimensions. Theoretically, the COF-1 monolayer was expected to have a higher bending stiffness compared to COF-5 monolayer, as the COF-1 monolayer possessed a much denser structure.
for monolayer COF-1 and COF-5, respectively, indicating a smaller RMS displacement in COF-1. It could be noted that the difference in the fitting coefficients of COF-1 and COF-5 was due to their different bending stiffnesses, since both COFs considered in the MD simulations had similar dimensions. Theoretically, the COF-1 monolayer was expected to have a higher bending stiffness compared to COF-5 monolayer, as the COF-1 monolayer possessed a much denser structure.
We further extended the above theories to explain the thermally induced softening of the Young's modulus of the 2D COFs below the critical temperature, since the out-of-plane fluctuation now plays a dominant role in determining the elastic behaviors of monolayer 2D COFs.60,62 According to the statistical mechanics and thermodynamics, the Young's modulus of monolayer COFs below the critical temperature can be expressed by the following formula:
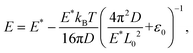 | (6) |
Based on the analyses presented herein, the reduction in the elastic modulus of the 2D COFs at relatively low temperatures could be attributed to the synergistic interplay of the thermal rippling phenomenon and the well-established harmonic vibrations. As the temperature became higher, the impact of the anharmonic coupling between the bending and stretching modes tended to become more significant. As highlighted in an earlier theoretical study, such coupling can effectively mitigate the impact of the out-of-plane thermal fluctuations on the elastic modulus of 2D materials, thereby attenuating the observed softening effect.60,63 In the current study, we conducted a parallel analysis to assess the impact of the anharmonic forces across different temperature regimes. Specifically, we computed the Grüneisen parameter of COF-1 and COF-5, which is a parameter with the ability to provide insights into the underlying anharmonic interactions of 2D COFs.64 The Grüneisen parameter can be mathematically expressed as:65,66
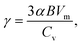 | (7) |
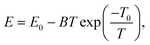 | (8) |
Summary and conclusions
In summary, we developed an NEP model-based MLP for accurately evaluating the thermoelastic properties of two classical monolayer 2D COFs (COF-1 and COF-5). Through comparing with the results obtained from DFT calculations, the MLP trained here was proven to have the capability to enable one to study the elastic behaviors of monolayer COFs, offering greatly improved computational efficiency and high accuracy. Thus, the trained MLP was further employed in MD simulations to calculate the elastic constants of monolayer COFs with relatively large sizes and at high temperatures, as implemented by the strain-fluctuation method. The elasticity of both COF-1 and COF-5 was found to be almost isotropic, irrespective of the temperature. However, the elastic moduli of both monolayer COFs significantly dependent on the temperature, and were found to decrease as the temperature increased. Moreover, the temperature sensitivity of the elastic modulus was found to decrease after a critical temperature, e.g., ∼60 K for COF-1 and ∼40 K for COF-5, because different thermoelastic mechanisms dominated before and after the critical temperature. Specifically, the thermoelastic behavior could be majorly ascribed to the thermal rippling effect before the critical temperature, while the damping effect of anharmonic vibrations became the dominant mechanism after the critical temperature. Based on these mechanisms, two analytical models were also proposed for the temperature dependence of the elastic modulus before and after the critical temperature, which were found to fit the MD simulation results well. The present study not only offers a precise potential for describing the thermoelastic behaviors of monolayer COFs but also provides valuable insights into the elastic properties of 2D COFs in realistic situations.Finally, the following efforts can be made to further extend the application of the NEP in the study of the mechanical properties of 2D COFs. In addition to the monolayer 2D COFs studied here, multilayer structures of 2D COFs also widely exist, which have a wide range of applications.71,72 To develop MLPs for multilayer 2D COFs, the present approach can be further expanded by integrating inter-layer interactions and different stacking methods into the training process of the NEP. Besides, in addition of the elastic property, the fracture property is also of importance for the mechanical performance of 2D COFs. To simulate the fracture behaviors of 2D COFs with large deformations, some representative structures of 2D COFs during the entire tension process need to be added to the current training sets.
Associated content
The training and testing results for the NEP models are freely available at https://github.com/bing93wang/COF-NEP/.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Guangdong Basic and Applied Basic Research Foundation (Grant No. 2022A1515010631) and Shenzhen Science and Technology Program (Grant No. GXWD20220811164345003).References
- A. P. Côté, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170 CrossRef.
- H. Furukawa and O. M. Yaghi, J. Am. Chem. Soc., 2009, 131, 8875–8883 CrossRef CAS.
- J. Fu, S. Das, G. Xing, T. Ben, V. Valtchev and S. Qiu, J. Am. Chem. Soc., 2016, 138, 7673–7680 CrossRef CAS.
- X. Guan, Y. Ma, H. Li, Y. Yusran, M. Xue, Q. Fang, Y. Yan, V. Valtchev and S. Qiu, J. Am. Chem. Soc., 2018, 140, 4494–4498 CrossRef CAS.
- H. Li, Q. Pan, Y. Ma, X. Guan, M. Xue, Q. Fang, Y. Yan, V. Valtchev and S. Qiu, J. Am. Chem. Soc., 2016, 138, 14783–14788 CrossRef CAS.
- S. Yan, X. Guan, H. Li, D. Li, M. Xue, Y. Yan, V. Valtchev, S. Qiu and Q. Fang, J. Am. Chem. Soc., 2019, 141, 2920–2924 CrossRef CAS.
- Q. Fang, S. Gu, J. Zheng, Z. Zhuang, S. Qiu and Y. Yan, Angew. Chem., Int. Ed., 2014, 53, 2878–2882 CrossRef CAS.
- A. M. Evans, A. Giri, V. K. Sangwan, S. Xun, M. Bartnof, C. G. Torres-Castanedo, H. B. Balch, M. S. Rahn, N. P. Bradshaw, E. Vitaku, D. W. Burke, H. Li, M. J. Bedzyk, F. Wang, J.-L. Brédas, J. A. Malen, A. J. H. McGaughey, M. C. Hersam, W. R. Dichtel and P. E. Hopkins, Nat. Mater., 2021, 20, 1142–1148 CrossRef CAS PubMed.
- Y. Zhang, J. Duan, D. Ma, P. Li, S. Li, H. Li, J. Zhou, X. Ma, X. Feng and B. Wang, Angew. Chem., Int. Ed., 2017, 56, 16313–16317 CrossRef CAS PubMed.
- D. A. Vazquez-Molina, G. S. Mohammad-Pour, C. Lee, M. W. Logan, X. Duan, J. K. Harper and F. J. Uribe-Romo, J. Am. Chem. Soc., 2016, 138, 9767–9770 CrossRef CAS PubMed.
- S. Das, P. Heasman, T. Ben and S. Qiu, Chem. Rev., 2017, 117, 1515–1563 CrossRef CAS PubMed.
- R. Liang, S. Jiang, R. A and X. Zhao, Chem. Soc. Rev., 2020, 49, 3920–3951 RSC.
- Y. Jin, Y. Hu and W. Zhang, Nat. Rev. Chem., 2017, 1, 0056 CrossRef.
- A. M. Evans, M. R. Ryder, N. C. Flanders, E. Vitaku, L. X. Chen and W. R. Dichtel, Ind. Eng. Chem. Res., 2019, 58, 9883–9887 CrossRef CAS.
- L. Zhu, Y. Jin, Q. Xue, X. Li, H. Zheng, T. Wu and C. Ling, J. Mater. Chem. A, 2016, 4, 15015–15021 RSC.
- W. Li, Y. Yang, J. K. Weber, G. Zhang and R. Zhou, ACS Nano, 2016, 10, 1829–1835 CrossRef CAS.
- S. Thakur and A. Giri, J. Mater. Chem. A, 2023, 11, 18660–18667 RSC.
- S. Thakur and A. Giri, Mater. Horiz., 2023, 10, 5484–5491 RSC.
- Y. Yang, Y. Xu, Q. Li, Y. Zhang and H. Zhou, J. Mater. Chem. A, 2022, 10, 19444–19465 RSC.
- Z. Wang, Q. Yu, Y. Huang, H. An, Y. Zhao, Y. Feng, X. Li, X. Shi, J. Liang, F. Pan, P. Cheng, Y. Chen, S. Ma and Z. Zhang, ACS Cent. Sci., 2019, 5, 1352–1359 CrossRef CAS.
- Q. Fang, Z. Pang, Q. Ai, Y. Liu, T. Zhai, D. Steinbach, G. Gao, Y. Zhu, T. Li and J. Lou, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2208676120 CrossRef CAS.
- C. Ding, M. Breunig, J. Timm, R. Marschall, J. Senker and S. Agarwal, Adv. Funct. Mater., 2021, 31, 2106507 CrossRef CAS.
- P. Kapri, T. Kawakami and M. Koshino, Comput. Mater. Sci., 2023, 228, 112282 CrossRef CAS.
- J. Zhang, Phys. Chem. Chem. Phys., 2018, 20, 29462–29471 RSC.
- H. Li and J.-L. Brédas, Chem. Mater., 2021, 33, 4529–4540 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- W. Hao, Y. Zhao, L. Miao, G. Cheng, G. Zhao, J. Li, Y. Sang, J. Li, C. Zhao, X. He, C. Sui and C. Wang, Nano Lett., 2023, 23, 1416–1423 CrossRef CAS.
- P. H. H. Duong, Y. K. Shin, V. A. Kuehl, M. M. Afroz, J. O. Hoberg, B. Parkinson, A. C. T. van Duin and K. D. Li-Oakey, ACS Appl. Mater. Interfaces, 2021, 13, 42164–42175 CrossRef CAS.
- B. Mortazavi, X. Zhuang, T. Rabczuk and A. V. Shapeev, Mater. Horiz., 2023, 10, 1956–1968 RSC.
- B. Mortazavi, B. Javvaji, F. Shojaei, T. Rabczuk, A. V. Shapeev and X. Zhuang, Nano Energy, 2021, 82, 105716 CrossRef CAS.
- B. Mortazavi, E. V. Podryabinkin, I. S. Novikov, T. Rabczuk, X. Zhuang and A. V. Shapeev, Comput. Phys. Commun., 2021, 258, 107583 CrossRef CAS.
- B. Mortazavi, M. Silani, E. V. Podryabinkin, T. Rabczuk, X. Zhuang and A. V. Shapeev, Adv. Mater., 2021, 33, 2102807 CrossRef CAS.
- P. Ying, H. Dong, T. Liang, Z. Fan, Z. Zhong and J. Zhang, Extreme Mech. Lett., 2023, 58, 101929 CrossRef.
- Z. Fan, Z. Zeng, C. Zhang, Y. Wang, K. Song, H. Dong, Y. Chen and T. Ala-Nissila, Phys. Rev. B, 2021, 104, 104309 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Chem. Phys., 1982, 76, 2662–2666 CrossRef CAS.
- S. M. J. Rogge, M. Waroquier and V. Van Speybroeck, Acc. Chem. Res., 2018, 51, 138–148 CrossRef CAS.
- X. Li, P. Yadav and K. P. Loh, Chem. Soc. Rev., 2020, 49, 4835–4866 RSC.
- S. Kim and H. C. Choi, ACS Omega, 2020, 5, 948–958 CrossRef CAS.
- J. F. Dienstmaier, A. M. Gigler, A. J. Goetz, P. Knochel, T. Bein, A. Lyapin, S. Reichlmaier, W. M. Heckl and M. Lackinger, ACS Nano, 2011, 5, 9737–9745 CrossRef CAS.
- S. Thomas, K. M. Ajith, S. U. Lee and M. C. Valsakumar, RSC Adv., 2018, 8, 27283–27292 RSC.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- P. H. Hünenberger, in Advanced Computer Simulation, Springer Berlin Heidelberg, Berlin, Heidelberg, 2005, pp. 105–149 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- Z. Fan, Y. Wang, P. Ying, K. Song, J. Wang, Y. Wang, Z. Zeng, K. Xu, E. Lindgren, J. M. Rahm, A. J. Gabourie, J. Liu, H. Dong, J. Wu, Y. Chen, Z. Zhong, J. Sun, P. Erhart, Y. Su and T. Ala-Nissila, J. Chem. Phys., 2022, 157, 114801 CrossRef CAS PubMed.
- Z. Fan, W. Chen, V. Vierimaa and A. Harju, Comput. Phys. Commun., 2017, 218, 10–16 CrossRef CAS.
- J. R. Ray, J. Appl. Phys., 1982, 53, 6441–6443 CrossRef.
- K. Yoshimoto, G. J. Papakonstantopoulos, J. F. Lutsko and J. J. de Pablo, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 184108 CrossRef.
- M. Bernetti and G. Bussi, J. Chem. Phys., 2020, 153, 114107 CrossRef CAS.
- A. Giri and P. E. Hopkins, Nano Lett., 2021, 21, 6188–6193 CrossRef CAS.
- A. Giri, A. M. Evans, M. A. Rahman, A. J. H. McGaughey and P. E. Hopkins, ACS Nano, 2022, 16, 2843–2851 CrossRef CAS.
- T. P. Kaloni, Y. C. Cheng and U. Schwingenschlögl, J. Appl. Phys., 2013, 113, 104305 CrossRef.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS.
- Y. Le Page and P. Saxe, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 174103 CrossRef.
- W. Li, H. Kou, X. Zhang, J. Ma, Y. Li, P. Geng, X. Wu, L. Chen and D. Fang, Mech. Mater., 2019, 139, 103194 CrossRef.
- D. Zakarian, A. Khachatrian and S. Firstov, Met. Powder Rep., 2019, 74, 204–206 CrossRef.
- S. Yalameha, Z. Nourbakhsh and D. Vashaee, Comput. Phys. Commun., 2022, 271, 108195 CrossRef CAS.
- S. Thomas, K. M. Ajith and M. C. Valsakumar, Superlattices Microstruct., 2017, 111, 360–372 CrossRef CAS.
- W. Gao and R. Huang, J. Mech. Phys. Solids, 2014, 66, 42–58 CrossRef CAS.
- H. Li and J.-L. Brédas, J. Phys. Chem. Lett., 2018, 9, 4215–4220 CrossRef CAS PubMed.
- W. Helfrich and R.-M. Servuss, Il Nuovo Cimento D, 1984, 3, 137–151 CrossRef.
- O. L. Anderson, Phys. Rev., 1966, 144, 553–557 CrossRef CAS.
- B. Peng, H. Zhang, H. Shao, Y. Xu, X. Zhang and H. Zhu, RSC Adv., 2016, 6, 5767–5773 RSC.
- G. Grimvall, Thermophysical Properties of Materials, North-Holland, Oxford, England, 2nd edn, 1999 Search PubMed.
- X. Tan, H. Shao, T. Hu, G. Liu, J. Jiang and H. Jiang, Phys. Chem. Chem. Phys., 2015, 17, 22872–22881 RSC.
- P. Anees, M. C. Valsakumar and B. K. Panigrahi, Phys. Chem. Chem. Phys., 2017, 19, 10518–10526 RSC.
- Q. Li, J. Zhou, G. Liu and X. G. Wan, Carbon, 2022, 187, 349–353 CrossRef CAS.
- G. Liu and J. Zhou, J. Phys.: Condens. Matter, 2019, 31, 065302 CrossRef PubMed.
- R. J. Bruls, H. T. Hintzen, G. de With and R. Metselaar, J. Eur. Ceram. Soc., 2001, 21, 263–268 CrossRef CAS.
- S. Chandra, S. Kandambeth, B. P. Biswal, B. Lukose, S. M. Kunjir, M. Chaudhary, R. Babarao, T. Heine and R. Banerjee, J. Am. Chem. Soc., 2013, 135, 17853–17861 CrossRef CAS.
- W. Zhou, M. Wei, X. Zhang, F. Xu and Y. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 16847–16854 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr04509a |
| ‡ Present address: Department of Physical Chemistry, School of Chemistry, Tel Aviv University, Tel Aviv, 6997801, Israel. |
| This journal is © The Royal Society of Chemistry 2024 |