Open Access Article
Open Access ArticlePolymer conformation determination by NMR spectroscopy: comparative diffusion ordered 1H-NMR spectroscopy of poly(2-ethyl-2-oxazoline)s and poly(ethylene glycol) in D2O†
Bryn D.
Monnery
 *ab,
Valentin Victor
Jerca
*ab,
Valentin Victor
Jerca
 c,
Richard
Hoogenboom
c,
Richard
Hoogenboom
 a and
Thomas
Swift
a and
Thomas
Swift
 *d
*d
aSupramolecular Chemistry Group, Centre of Macromolecular Chemistry (CMaC), Department of Organic and Macromolecular Chemistry, Ghent University, Krijgslaan 281 S4, B-9000 Ghent, Belgium. E-mail: bryn.monnery@gmail.com
bDepartment of Biomedical Engineering, University Medical Centre Groningen, University of Groningen, Ant. Deusinglaan 1, 9713 AV Groningen, The Netherlands
cSmart Organic Materials Group, “Costin D. Nenitzescu” Institute of Organic and Supramolecular Chemistry, Romanian Academy, 202B Splaiul Independentei, 060023 Bucharest, Romania
dPolymer and Biomaterials Chemistry Laboratories, University of Bradford, Bradford, West Yorkshire BD 7 1DP, UK. E-mail: t.swift@bradford.ac.uk
First published on 5th July 2024
Abstract
Diffusion ordered 1H-NMR spectroscopy (DOSY) is a useful, non-destructive technique for analysing polymer hydrodynamic size and intrinsic/solution viscosity. However, to date there has been no investigation of DOSY under variable temperature conditions that allow trends in polymer conformation to be determined. Poly(2-ethyl-2-oxazoline) (P(EtOx)) is a hydrophilic polymer that has the potential to replace poly(ethylene glycol) (PEG) in biomedical applications. Applying DOSY to a series of narrow-distribution P(EtOx) revealed that the apparent hydrodynamic radii scaled with molecular weight as expected. By altering the temperature of the solution the trends in Flory-type exponents were determined, enabling the determination of the power laws related to the coil-globule conformation of linear polymers directly from NMR data. These measurements were complicated by the onset of convection currents at higher temperatures, which impose a limit to the effective measurement range of ca. 10–35 °C. It was revealed that P(EtOx) had a more expanded random coil conformation than PEG, and it trended towards θ conditions at the lower critical solution temperature. In comparison, PEG was approximately in θ-conditions at room-temperature. This shows the use, and limitations of DOSY in polymer conformation analysis, and applies it to P(EtOx), a polymer which has not been analysed in this manner before.
1. Introduction
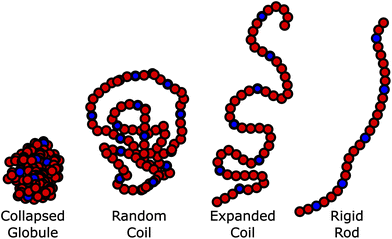
Polymers play an important role in biomedical applications, ranging from polymers for shielding of drug carriers, via polymer excipients to medical devices. For biomedical applications where the polymer is utilized in aqueous solution, the polymer conformation (i.e. its’ degree of swelling and interaction with the environment)1,2 is extremely important. Properties such as renal excretion and tissue penetration are dependent on the hydrodynamic radius of the polymer.3,4 Moreover, the accessibility of the end-group/side-chains is important for targeted prodrug strategies, as the targeting ligand needs to be exposed to the surrounding medium. This of course contrasts directly with the idea of shielding prodrugs with the polymer and has been referred to as the “PEG dilemma” for PEGylation.5–8 It has been reported that with PEG the expanded coil “brush” conformation is far more efficient in shielding nanoparticles than the collapsed “mushroom” conformation.9Therefore, there is a need to improve our understanding of the conformation of applied linear polymers across a variety of temperatures, which is best represented by the Flory-type exponents of the polymer;10 the higher the exponent, the more extended the polymer, and the more available are the end groups and any conjugated drug/active pharmaceutical ingredients (or from a vesicle formed from the polymer). Conversely, as the exponent approaches 0.5 (θ-conditions), the polymer becomes more collapsed and increases shielding from the solvent, this inhibits the activity of the conjugates, by increasing shielding (Fig. 1). For a given formulation, it is likely that a different balance between activity and shielding is needed, but there are contradictory requirements for shielding, and accessibility of the side-chains.
Polymer conformation is commonly measured by viscometry, static light-scattering, dynamic light scattering, and occasionally by osmometry. The literature contains many cases of these techniques being used for P(EtOx)11–14 and PEG.15–20 Solution conformational (solvation induced swelling) is, however, only a factor affecting the volume occupied of a dissolved/miscible polymer in solution. The chain length (degree of polymerisation) is also a critical factor. Variations in production methodologies result in a wide array of size distributions both within and between sample batches. Typically, the gold standard for studying macromolecular molecular weight distributions is based on size exclusion chromatography (SEC). This technique involves fractionating polymers based on their Stokes radius (aka their solvodynamic radius) by filtering the polymer through a crosslinked gel and detecting their elution speed. However, SEC has a number of drawbacks, primarily unintended column interactions leading to a broadening of the distribution.21 DOSY has already been shown as excellent tool for analysing the molecular weights of polymers.22–29 It is non-invasive and requires extremely small amounts of material. It can even be performed on benchtop spectrometers to give rapid and convenient measurements.29 Since DOSY provides a direct measurement of D in a given solvent, it is unaffected by such peak broadening phenomena and will provide an average or peak solvodynamic radii for any specified nuclei environment.
Poly(2-ethyl-2-oxazoline) (P(EtOx)) is an interesting and useful synthetic polymer that has the potential to replace poly(ethylene glycol) (PEG) in biomedical applications.30 It is highly water-soluble, amenable to copolymerisation to give high drug loadings and has not shown any immune response that might limit repeated use as has been observed with PEG.31,32 It has, therefore, been proposed that PEtOx is a useful tool for future nanoparticulate therapy.33 A P(EtOx) based composition for the long term treatment of Parkinson's disease is in clinical trials,34 and a P(EtOx) based, extremely effective, hemostatic sealing patch has been approved for clinical use.35
P(EtOx) is a thermoresponsive polymer, which typically aggregates to induce solution turbidity (TCP – cloud point) at ca. 60 °C at infinite chain length, and thus is extremely soluble in aqueous solutions at 37 °C.36 It is slightly above θ in water at these temperatures.12 Poly(2-alkyl-2-oxazolines) (PAOx) with longer side-chains, and especially poly(2-isopropyl-2-oxazoline) (P(iPrOx)) undergo a conformational change in aqueous media above their TCP, and form crystalline fibres.37–39 X-ray diffraction studies of P(iPrOx) show that at the molecular level the polymer is forming a rigid helix.40 It was previously believed P(EtOx) was completely amorphous, but it has been found to also undergo the same transition, but at a slower rate.41 P(EtOx) has a negative entropy of mixing with water, like PEG. Thus, the miscibility with water is due to the formation of hydrogen bonds with the water. Winnik and coworkers have shown in the closely related poly(2-isopropyl-2-oxazoline) that immiscibility occurs when the polymer adopts a dehydrated fully trans conformation.42 P(EtOx) can theoretically exist in three forms; random coils, helices, and folded helices.43 Bernard predicted with molecular modelling that whilst a helical conformation was possible it was not favoured at 25 °C in water. It has been also shown that P(EtOx) forms a random coil in THF at 25 °C.44
PEG crystallises as helices with 7 repeat units per turn.45 The solution entropy of PEG in water is negative, and quite different to the solution entropy in organic solvents such as chloroform.46 In chloroform the PEG chains exist as random coils, whereas in water ordered structures are seen. PEG is, in fact, solvated by ordered water which bridges oxygens and generates a non-random coil, with a large enthalpic gain. The negative entropy means that as the temperature increases water is excluded and the coil structure begins to reform, up to the point of precipitation when insufficient ordered water remains in the structure for miscibility. However if heating is continued to higher temperatures, eventually the helical structure will break down and the PEG will redissolve.47 Amu showed that salts have a significant effect on the conformation, with salts producing far more random structures, whilst in pure water the structure is reported to be very extended.16
The question of what the conformation of PEG is in aqueous solution is a vexed one, and crucial for some biomedical applications. In binary mixtures of carboxylic acids and water, it is absolutely helical.48 In some conditions, PEG has been observed to form helices in water.49–52 There are observations of ordered structures being formed in aqueous solution,53 being caused by self-association competing with water association.54 The trans and gauche conformations should occur in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio if the PEG was a random coil (and a 2
2 ratio if the PEG was a random coil (and a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio for the helix), and the gauche conformation is heavily favoured in aqueous solution, indicating that random coils dominate.53,55–57 As dilution increases and temperature decreases, this ordered form is favoured.58
1 ratio for the helix), and the gauche conformation is heavily favoured in aqueous solution, indicating that random coils dominate.53,55–57 As dilution increases and temperature decreases, this ordered form is favoured.58
This manuscript reports studies on narrow dispersity polymers with symmetrical Cauchy–Lorentz distributions of varying chain length. It is designed to show the potential of DOSY for disclosing polymer solution properties – however as polymer samples inevitably contain mixtures of molecules with varying chain length, the chain backbone will report on an averaged [1H] of the most common functionality present in the sample. Thus, care should be applied when applying DOSY to samples that are highly disperse, or contain non-symmetrical/multi-modal size distributions as the chain backbone [nuclei] will report on multiple averages depending on the samples population density.
2. Experimental
2.1 Materials
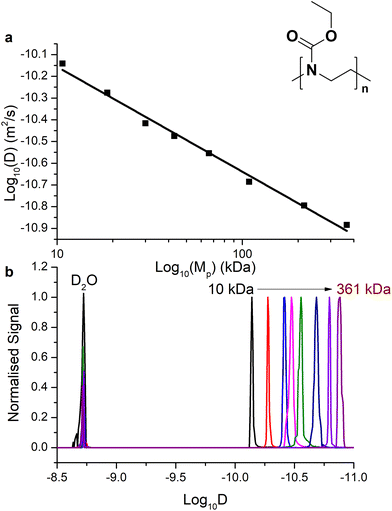
The chemical structures of the polymers used in this study are shown in Fig. 2. The synthesis of the well-defined high molar mass P(EtOx) used in this work has previously been reported.59 PEG with methyl α-terminii and amine ω-terminii were purchased from Sunbright and characterised by size exclusion chromatography. The higher molecular weight polymers were resolved by MALS, and a correction factor for the lower molecular weight materials of 0.565 ± 0.01 (from poly(methyl methacrylate) to PEG) was estimated. The bolded values in Table S1† were used.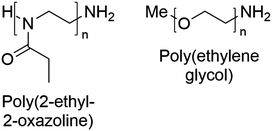 | ||
| Fig. 2 Chemical structures of poly(2-ethyl-2-oxazoline) and poly(ethylene glycol) with the end-groups used in this work. | ||
2.2 Methods
High precision field matched NMR tubes were purchased from Wilmad USA. Deuterated NMR solvents were purchased from Cambridge Isotope Laboratories Inc. USA. Measurements were taken on a Bruker Avance Neo 600 MHz with an iProbe sensor. Calibration of the gradient field strength was performed using a sample of H2O in D2O (1% v/v) doped with GdCl3 (0.1 mg) as a paramagnetic relaxation agent. The instrument was prepared with a Gamma of 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 752 rad, and a DOSY pulse sequence with stimulated echo measurements (to reduce the impact of convection) was employed δ 0.01, Δ 0.04 decays. Gradient strengths were calibrated to provide a diffusion coefficient of 1.91 × 10−9 m−2 s−1 at 298.15 K (gradients operated from 95% to 5% using 16–64 steps across a quadratic decay). Two spoil gradients were applied before each run. The temperature accuracy of the instrument was ensured by initial calibration of the sample temperature to displayed sample control temperature by measurement of the shift between the residual CH3 and OH resonances of methanol (99.8% MeOD). Samples were prepared at 1 mg ml−1 concentration and exactly 0.8 μl of solvent was added to each NMR tube to ensure consistency between results. The spectrometer was controlled using Bruker Topspin 4.3.0 to collect and process NMR data, using the ledbpg2s pulse sequence (ESI Fig. S1†). D was determined using the Bruker Dynamics Centre add-on using the Stejskal–Tanner plots (see ESI Fig. S2† for an example). The volume of a repeat unit was estimated using Vega ZZ software.60
752 rad, and a DOSY pulse sequence with stimulated echo measurements (to reduce the impact of convection) was employed δ 0.01, Δ 0.04 decays. Gradient strengths were calibrated to provide a diffusion coefficient of 1.91 × 10−9 m−2 s−1 at 298.15 K (gradients operated from 95% to 5% using 16–64 steps across a quadratic decay). Two spoil gradients were applied before each run. The temperature accuracy of the instrument was ensured by initial calibration of the sample temperature to displayed sample control temperature by measurement of the shift between the residual CH3 and OH resonances of methanol (99.8% MeOD). Samples were prepared at 1 mg ml−1 concentration and exactly 0.8 μl of solvent was added to each NMR tube to ensure consistency between results. The spectrometer was controlled using Bruker Topspin 4.3.0 to collect and process NMR data, using the ledbpg2s pulse sequence (ESI Fig. S1†). D was determined using the Bruker Dynamics Centre add-on using the Stejskal–Tanner plots (see ESI Fig. S2† for an example). The volume of a repeat unit was estimated using Vega ZZ software.60
Size exclusion chromatography (SEC) was performed with an Agilent 1260 system with a diode array detector and refractive index detector to which was added multi-angle light scattering detector (Wyatt Dawn Heleos II or miniDawn Treos II). The column set was 2× PLGEL MIXED-D (300 × 75 mm) columns and a guard column (50 × 7.5 mm MIXED-D), and the eluent N,N-dimethylacetamide with 50 mM LiCl (flow rate 0.5 mL min−1). Samples were filtered (0.2 μm PTFE filter) before injection. The dn/dc value of PEG was determined by sequential injection of different amounts of polymer. Wyatt ASTRA 7 and Agilent GPC/SEC software were used to process the data.
3. Results and discussion
Johnson and coworkers first noted that D would be related to M as per eqn (1a) This is an application of the Flory scaling law which, when generalised, relates any dimensional property of a polymer (such as intrinsic viscosity, hydrodynamic radius or radius of gyration) to the molecular weight.61,62 Thus, three related equations are in play.| D = cM−b | (1a) |
[η] = Kη![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) av av | (1b) |
| RH = KHMv | (1c) |
wherein the various K constants and α, a and v (generically the exponent) are related but different constants. Eqn (1a) is commonly used in polymer DOSY NMR spectroscopy.21–23,27,62,63Eqn (1a) is the Rouse–Zimm equation, eqn (1b) is the Mark–Houwink equation and eqn (1c) has no formal name, but is directly related to the Stokes–Einstein equation (eqn (2)):15
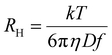 | (2) |
[η] is also related to RHvia hydrodynamic volume, VH, thus:
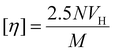 | (3) |
In this case, the exponent in eqn (1c) can be used to determine molecular conformation. In theta conditions, the exponent is 0.5 with the polymer being a perfect random coil. Deviations from this occur at different rates since they are scaled differently, but in all cases a value >0.5 is more extended than perfect, and <0.5 is a compacted globule.
In this work we assume, since the polymers are very narrow, that ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) v can be substituted by
v can be substituted by ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) w (eqn (4)):
w (eqn (4)):
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) v = v = ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) w. w. | (4) |
Although we model polymers as simple hard spheres, in reality they adopt a more solvated form, and the individual polymer chains in solution can adopt many conformations. Conformational analysis is typically carried out using viscometry at varying temperatures.
However, a variety of factors need to be considered, since they can affect the diffusion coefficient. Firstly, there are variations in the solution dynamic viscosity, η, which has been corrected for by Swift and coworkers,63 and Junkers and coworkers,25 and Hiller and Grabe26 using different methodologies. In this work, Swift's method is used, since it actually determines η from information contained within the measurement. Swift's method uses the fact that η of the pure solvent is known, and the D of both pure solvent and the polymer solutions are known, and they are related to η of the solution as per eqn (5).
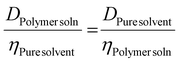 | (5) |
Above a critical concentration, the polymer chains will overlap and restrict free diffusion.27 This will reduce the value of D, and so the concentration of polymers must be sufficiently dilute. We have used 1 mg mL−1, which is regarded as sufficiently dilute.
Finally, since in our experiments we were altering the temperature of the analysed solution, we need to be aware of the potential occurrence of convection currents that could alter the measurements.64 This is pronounced in solvents with low viscosity and lower coefficients of thermal expansion, such as CDCl3 or acetone, but has much less effect in D2O due to the enthalpic resistance to breaking hydrogen bonding networks. However, a limit to the usable temperature range was found as part of this study.
Hiller and Grabe have recently combined the above equations into an elegant equation (eqn (6)), which may be used to determine the Mark–Houwink parameters:26
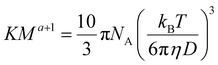 | (6) |
However, they use a value for η of the pure solvent, which fails to correct for self-diffusion. To correct for this, eqn (6) can be used with the value for η of the solution calculated in eqn (5).
3.1 Convection effects
Convection in DOSY can be a serious problem.64 The self-diffusion coefficients of the solvent (water) in standard 5 mm NMR tubes were consistent with literature values.65 However, the self-diffusion coefficient should be linear with temperature due to the first order relationship of D with respect to T in the Stokes–Einstein equation. On examination, this was only true in the range 10–35 °C while at 37 °C and above the D2O peak showed some slight deviation from the linear relation, which increased with increasing temperature. This resulted in nonsensical hydrodynamic radii for the polymers. Whilst the experiments were carried out in standard 5 mm tubes, post-facto the options of 3 mm tubes and 5 mm tubes with inserts were examined. The 3 mm tube was significantly inferior, with a workable range of 10–30 °C, whilst the workable range for a 5 mm tube with an insert was 10–45 °C (ESI Fig. S3†). As a point of comparison, Silva et al. have recently reported using the dstebpgp3s pulse sequence to expand the usable temperature window of the measurement.283.2 Determination of the effect of molar mass on the diffusion coefficient of poly(2-ethyl-2-oxazoline)s
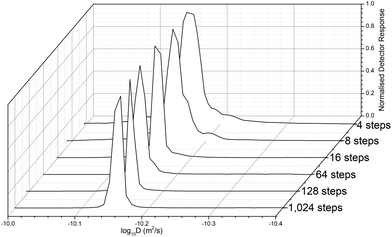
Before determining the molar mass, we investigated the necessary diffusion resolution (from the number of programmed gradient steps of the sample measurement) to estimate D, and the resultant apparent distribution of the polymer diffusion values from across the 1H proton signal peak were captured. The resolution of DOSY is limited by the number of datapoints, but the distribution is free from column interaction effects that broaden the observed molar mass distributions.66 This can be useful in the analysis of polymers, in more realistic conditions that are closer to their true solution properties. It was found that with insufficient resolution <64 steps, the peak appeared band-broadened (Fig. 3). Further testing also showed that the resolution of the DOSY experiments decreases with decreasing D or higher Mw, since the x1 axis is proportion to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D. Thus, sufficient resolution is required to avoid band-broadening artifacts arising from noise. This distribution has, however, no artefacts resulting from band broadening or column interaction effects, which broaden standard SEC measurements without a mass detector, such as MALS. Thus, Đ is low, and typically close to, or less than the value measured by SEC-MALS (Table S2†). For expediency we selected the lowest resolution (64 steps) that produced a sharp peak, to reduce the scan time.
D. Thus, sufficient resolution is required to avoid band-broadening artifacts arising from noise. This distribution has, however, no artefacts resulting from band broadening or column interaction effects, which broaden standard SEC measurements without a mass detector, such as MALS. Thus, Đ is low, and typically close to, or less than the value measured by SEC-MALS (Table S2†). For expediency we selected the lowest resolution (64 steps) that produced a sharp peak, to reduce the scan time.
The relationship of D with the molar mass is expected, for a randomly coiled polymer, to be linearly proportional to the molecular weight. We determined D both using Dynamics Center software (to specify the diffusion at the peak top of 1H proton signal from the polymer backbone) taken as standard (Fig. 4a for P(EtOx) and ESI Fig. S4a† for PEG) and taking the sum diffusion distribution from the software automatically sampling D across the summed 1H signal (Fig. 4b and ESI Fig. 4b†). Using the peak [1H] signal diffusion we found that the expected log–log relationship between Mw and D was found, with the gradient providing the Flory exponent for that temperature (although uncorrected for viscosity, see 3.3). We generated a size calibration curve to estimate Mp (peak molar mass) from these two extrapolation methods (Table 1) and compared this to the molar mass provided by SEC-MALS analysis (see ESI Tables S1 and S2†). Using the size distribution, the relationship of Mw and D in this measurement was slightly different to the peak-top measurements, and thus a calibration derived from the polymers was used. It is essential to keep conditions consistent within the experiment.
| SEC-MALS | DOSY – peak top | DOSY – distribution | ||
|---|---|---|---|---|
| M p (kDa) | M p (kDa) | M p(DOSY)/Mp(SEC) | M p (kDa) | M p(DOSY)/Mp(SEC) |
| 10.7 | 11.1 | 3% | 9.3 | −13% |
| 18.7 | 19.6 | 5% | 17.6 | −6% |
| 30 | 27.6 | −8% | 34.4 | 15% |
| 43 | 45.4 | 6% | 45.5 | 6% |
| 57.9 | 61.0 | 5% | ND | ND |
| 66 | 64.2 | −3% | 66.4 | 1% |
| 108.7 | 92.5 | −15% | 124 | 14% |
| 215.9 | 211.9 | −2% | 208.5 | −3% |
| 366.1 | 408.7 | 12% | 319.5 | −13% |
| Average | 0.33% | 0.13% | ||
The D2O peaks were essentially identical at a given temperature for an experiment, acting as a control. Analysing the data, we discovered a good fit by both methods.
Molar masses and dispersities of P(EtOx) determined from (a) SEC-MALS (previously reported) and (b) DOSY (determined from the data in Fig. 4). The difference in Mp, determined by dividing the Mp(SEC-MALS) by Mp(DOSY) is up to 15% (c), which shows reasonable agreement between the two techniques.
These samples were of narrow dispersity, which is a necessity since broad polymers (Đ > 1.3) often do not follow the expected linear trend with respect to molecular weight.27 A commercial sample of broad dispersity (Aquazol 50) was analysed, and the polymer peak was much broader (ca. 0.5 log units vs. 0.1 for a narrow polymer), and, hence, gave less signal intensity with a peak height less than 1% of the D2O peak height. It also had a much lower than expected diffusion coefficient (see ESI Fig. S5†). This made analysis of molecular weight and dispersity unreliable, which is in agreement with analysis of broadly dispersed polymers by DOSY being limited.27 However, there may be a physical reason for the lower diffusion coefficient, which is discussed in 3.3.
3.3 Power laws for hydrodynamic radius and intrinsic viscosity of poly(2-ethyl-2-oxazoline)
Herein DOSY spectra were interrogated by sampling the [1H] peak-top of the polymer backbone taken as a single point of reference. The hydrodynamic radius was determined by the diffusion coefficient measured in DOSY experiments (eqn (2)) and the viscosity of D2O (eqn (5)).67 Intrinsic viscosity was determined by eqn (3), and the Mark–Houwink parameters by eqn (6).We thus have three different values which can be utilized to determine conformation; diffusion coefficient, intrinsic viscosity and hydrodynamic radius (which is related to radius of gyration), of which the latter two are typically used. The first, as used above and used by Voorter et al.25 fails to account for polymer self-diffusion. The effect is small with low molar mass polymers but increases with molar mass and may become significant when measuring larger polymers. This resulted in an obvious inflection point as the P(EtOx) moved between different self-diffusion regimes (ESI Fig. S6†), although the effect is small. This does give us insight into the behaviour of P(EtOx), with self-entanglement arising above ca. 60 kDa.
The hydrodynamic radius is directly related to the radius of gyration and was related to the molar mass exactly as expected; for each temperature log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RH and log[η] correlated with log
RH and log[η] correlated with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mw (ESI Fig. S7†). The power laws for diffusion coefficient, intrinsic viscosity and hydrodynamic radius could be determined (Table S3†).
Mw (ESI Fig. S7†). The power laws for diffusion coefficient, intrinsic viscosity and hydrodynamic radius could be determined (Table S3†).
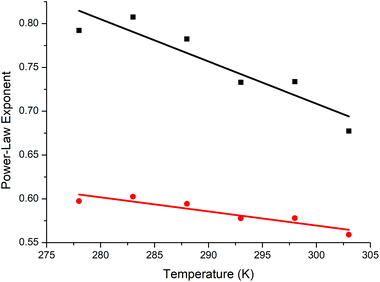
The exponents are decreasing in the manner noted by Gubarev et al., trending towards being in theta conditions at just below ∼60 °C, and intersecting around 60 °C which is just below the lower critical solution temperature (LCST) of high molar-mass P(EtOx) (Fig. 5).14,68 This is consistent with the P(EtOx) being an extended coil at room and body temperature, and contracting with increasing temperatures until being a perfect random coil just below the LCST. Once the temperature is increased above theta, the free energy of mixing will become positive, and the polymer will phase separate.
The intrinsic viscosity data should be compared to analysis of the same polymers by analytical ultracentrifugation in phosphate buffered saline (PBS). The exponents in PBS were lower (at 288 K, 0.63 vs. 0.78), indicating that water (D2O) is a significantly better solvent than saline solutions. The trends, with decreasing exponents with temperature, were the same. Other measurements of intrinsic viscosity have given lower values (α = 0.56) in water at 298 K,12 but with much broader polymers that have significant branching.43,69 As discussed above, their diffusion coefficients and intrinsic viscosities are significantly smaller than the well-defined linear P(EtOx) that we have used, as expected of branched or star-like polymers.70
We know that the hydrodynamic volume of the spherical models compared to the molecular volume of the P(EtOx) (approximated as 110 Å3 per repeat unit) and the polymer coil is typically heavily hydrated. The polymer may be expected to be free-draining at lower temperatures, since the coils hydrodynamic volume is only a few percent polymer (8% for 10 kDa, decreasing with increasing mass to only 0.5% for 361 kDa). As temperature increases, the hydrodynamic volume decreases, and hence the water content of the sphere also decreases (ESI Fig. S8†).
The activation energy of diffusion may be determined by the Arrhenius theory, but there is no trend, with the values scattered randomly between 0.13 and 0.16 J K−1 mol−1, which is per mole of polymer, thus, there is no significant end-group effect with these small end-groups even at ca. 10 kDa (ESI Fig. S9†).
3.4 Comparison of poly(2-ethyl-2-oxazoline) to poly(ethylene glycol)
PEG is the current standard for hydrophilic stealth polymers. For comparison, we analysed commercially available amine terminated PEG, with the same ω-terminii as our P(EtOx). There was significant double molecular weight diol PEG initiated by traces of water in many of the samples leading to a broadening of the dispersity.The power laws were determined as per P(EtOx) (Table S4†). Like P(EtOx), at 308 K convection had taken the exponent off the linear trend, and measurements above 303 K were discarded. At 283 K, the values for 59.2 kDa PEG were very off-trend due to the formation of helices. This datapoint was not included in the linear fits.
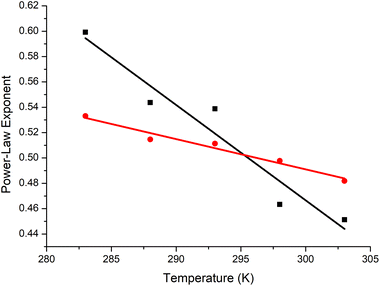
The polymer contracts with increasing temperature, as previously observed by Özdemir and Güner for the range 288–313 K using viscometry.71 PEG was in theta conditions at ∼23 °C, with the trends for the [η] and RH fits crossing over at ≈0.5 (Fig. 6). In the literature, values of α for PEG are inconsistent.63,72 Our observation of near-theta conditions at room temperature is in accord with simulation data,73,74 which are idealised, and some of the experimental data.75 The reason for the scattered exponents is that there are concentration related conformational changes for PEG, and thus the concentration matters. It appears that when measured in very dilute conditions, the theta temperature decreases to values approaching room temperature, whereas semi-dilute or concentrated solutions extrapolated to infinite dilution give much larger values.76,77 This is a topic needing further investigation.
We are comparing PEG to P(EtOx) under the same conditions in the extremely dilute regime at 0.1% (w/v). Under these conditions, PEG was far more compact than P(EtOx). PEG is a random coil at room temperature, whereas P(EtOx) is an expanded coil.
The volume of a PEG repeat unit is half that of a P(EtOx) repeat unit (55 Å3), and the trend with respect to polymer content of the sphere is similar to P(EtOx). However, the PEG sphere contains much less water than P(EtOx) as a result of its’ more collapsed state and hence lower hydrophilicity (ESI Fig. S10†). For the highest MW at the lowest measured temperature (i.e. the one most tending towards helix formation), the value becomes nonsensical, which might be ascribed to the formation of helices or aggregated helices.49–52
With respect to potential biomedical uses, it would appear PEG is more collapsed in solution than P(EtOx), although crowding effects on the surface of (say) nanoparticles will result in a more extended conformation than in high dilution. P(EtOx) of 10 kDa has been observed to effectively shield ligands at the termini, whereas 5 kDa was insufficient.3,4 P(EtOx) would seem to be an excellent choice for prodrug delivery, since the water permeates the structure allowing for release of the drug in a controlled manner.78 P(EtOx) is likely a good substitute for PEG, albeit one that occupies a physically larger volume for a given polymer mass.
4. Conclusions
The effect of temperature on the diffusion coefficient and solution viscosity as determined by DOSY is not an area into which much research has been done. Typically, measurements are done by size-exclusion chromatography and dilute solution viscometry, which are involved techniques requiring special equipment. This is the first example of the determination of the Flory type coefficients using DOSY NMR spectroscopy. The primary drawback of DOSY is that convection becomes an issue outside of a narrow temperature range in 5 mm NMR tubes, but it is sufficient to determine molecular shape, and estimate the theta temperature. Convection increases the motion of the particle and hence the decreases the apparent size.In the convection free zone, the molecular weight, molecular weight distribution, hydrodynamic radius and intrinsic viscosity of P(EtOx) could be determined by DOSY. The power laws for diffusion, intrinsic viscosity and hydrodynamic radius could be determined, and were generally consistent with other methods of measurement. However, the well-defined P(EtOx) that we used was more extended in solution than the partially branched commercial product.
When compared with PEG, P(EtOx) is more extended in aqueous solution, with the hydrated coil having a much greater volume. This indicates that P(EtOx) is likely to interact differently with proteins when used as a stealth polymer.
Author contributions
BDM: conceptualisation, data curation, formal analysis, methodology, visualisation and original writing; VJ: investigation and writing, reviewing & editing; RH: data curation, funding acquisition, project admin, resources, supervision and writing, reviewing & editing; TS: conceptualisation, data curation, formal analysis, investigation, methodology, project admin, resources, supervision and writing, reviewing & editing.Data availability
Data for this article, including raw 1H and DOSY NMR are available at NMRxiv at https://nmrxiv.org/P68.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Royal Society of Chemistry for funding Dr Thomas Swift for a research exchange visit to the University of Ghent (Grant Number: RM1602-1695).References
- D. Dhabal, Z. Jiang, A. Pallath and A. J. Patel, J. Phys. Chem. B, 2021, 125, 5434–5442 CrossRef CAS PubMed.
- Z.-G. Wang, Macromolecules, 2017, 50, 9073–9114 CrossRef CAS.
- M. Glassner, L. Palmieri, B. D. Monnery, T. Verbrugghen, S. Deleye, S. Stroobants, S. Staelens, L. Wyffels and R. Hoogenboom, Biomacromolecules, 2016, 18, 96–102 CrossRef PubMed.
- L. Wyffels, T. Verbrugghen, B. D. Monnery, M. Glassner, S. Stroobants, R. Hoogenboom and S. Staelens, J. Controlled Release, 2016, 235, 63–71 CrossRef CAS PubMed.
- H. Hatakeyama, H. Akita and H. Harashima, Biol. Pharm. Bull., 2013, 36, 892–899 CrossRef CAS.
- Y. Fang, J. Xue, S. Gao, A. Lu, D. Yang, H. Jiang, Y. He and K. Shi, Drug Delivery, 2017, 24, 22–32 CrossRef CAS PubMed.
- T. Liu and B. Thierry, Langmuir, 2012, 28, 15634–15642 CrossRef CAS PubMed.
- H. Hatakeyama, H. Akita and H. Harashima, Adv. Drug Delivery Rev., 2011, 63, 152–160 CrossRef CAS.
- M. Li, S. Jiang, J. Simon, D. Paßlick, M.-L. Frey, M. Wagner, V. Mailänder, D. Crespy and K. Landfester, Nano Lett., 2021, 21, 1591–1598 CrossRef CAS.
- P. J. Flory, J. Chem. Phys., 1949, 17, 303–310 CrossRef CAS.
- F. P. Chen, A. E. Ames and L. D. Taylor, Macromolecules, 1990, 23, 4688–4695 CrossRef CAS.
- T. T. Chiu, B. P. Thill and W. J. Fairchok, in Water-Soluble Polymers, American Chemical Society, 1986, vol. 213, ch. 23, pp. 425–433 Search PubMed.
- C. H. Chen, J. Wilson, W. Chen, R. M. Davis and J. S. Riffle, Polymer, 1994, 35, 3587–3591 CrossRef CAS.
- A. S. Gubarev, B. D. Monnery, A. A. Lezov, O. Sedlacek, N. V. Tsvetkov, R. Hoogenboom and S. K. Filippov, Polym. Chem., 2018, 9, 2232–2237 RSC.
- J. K. Armstrong, R. B. Wenby, H. J. Meiselman and T. C. Fisher, Biophys. J., 2004, 87, 4259–4270 CrossRef CAS PubMed.
- T. C. Amu, Polymer, 1982, 23, 1775–1779 CrossRef CAS.
- S. Kawaguchi, G. Imai, J. Suzuki, A. Miyahara, T. Kitano and K. Ito, Polymer, 1997, 38, 2885–2891 CrossRef CAS.
- D. M. Woodley, C. Dam, H. Lam, M. LeCave, K. Devanand and J. C. Selser, Macromolecules, 1992, 25, 5283–5286 CrossRef CAS.
- S. Kirinčič and C. Klofutar, Fluid Phase Equilib., 1999, 155, 311–325 CrossRef.
- W. F. Polik and W. Burchard, Macromolecules, 1983, 16, 978–982 CrossRef CAS.
- D. Berek, J. Sep. Sci., 2010, 33, 315–335 CrossRef CAS PubMed.
- W. Li, H. Chung, C. Daeffler, J. A. Johnson and R. H. Grubbs, Macromolecules, 2012, 45, 9595–9603 CrossRef CAS PubMed.
- P. Groves, Polym. Chem., 2017, 8, 6700–6708 RSC.
- C. Chamignon, D. Duret, M.-T. Charreyre and A. Favier, Macromol. Chem. Phys., 2016, 217, 2286–2293 CrossRef CAS.
- P.-J. Voorter, A. McKay, J. Dai, O. Paravagna, N. R. Cameron and T. Junkers, Angew. Chem., Int. Ed., 2022, 61, e202114536 CrossRef CAS PubMed.
- W. Hiller and B. Grabe, Anal. Chem., 2023, 95, 18174–18179 CrossRef CAS.
- E. Ruzicka, P. Pellechia and B. C. Benicewicz, Anal. Chem., 2023, 95, 7849–7854 CrossRef CAS PubMed.
- I. W. F. Silva, A. McKay, A. Sokolova and T. Junkers, Polym. Chem., 2024, 15, 1303–1309 RSC.
- O. Tooley, W. Pointer, R. Radmall, M. Hall, V. Beyer, K. Stakem, T. Swift, J. Town, T. Junkers, P. Wilson, D. Lester and D. Haddleton, Macromol. Rapid Commun., 2024, 45, 2300692 CrossRef CAS.
- O. Sedlacek, B. D. Monnery, S. K. Filippov, R. Hoogenboom and M. Hruby, Macromol. Rapid Commun., 2012, 33, 1648–1662 CrossRef CAS.
- P. Zhang, F. Sun, S. Liu and S. Jiang, J. Controlled Release, 2016, 244, 184–193 CrossRef CAS PubMed.
- X. Wan, J. Zhang, W. Yu, L. Shen, S. Ji and T. Hu, Process Biochem., 2017, 52, 183–191 CrossRef CAS.
- R. Luxenhofer, Y. Han, A. Schulz, J. Tong, Z. He, A. V. Kabanov and R. Jordan, Macromol. Rapid Commun., 2012, 33, 1613–1631 CrossRef CAS PubMed.
- C. W. Olanow, D. G. Standaert, K. Kieburtz, T. X. Viegas and R. Moreadith, Mov. Disord., 2020, 35, 1055–1061 CrossRef CAS.
- M. A. Boerman, E. Roozen, M. J. Sánchez-Fernández, A. R. Keereweer, R. P. Félix Lanao, J. C. M. E. Bender, R. Hoogenboom, S. C. Leeuwenburgh, J. A. Jansen, H. Van Goor and J. C. M. Van Hest, Biomacromolecules, 2017, 18, 2529–2538 CrossRef CAS.
- B. D. Monnery and R. Hoogenboom, Polym. Chem., 2019, 10, 3480–3487 RSC.
- M. Litt, F. Rahl and L. G. Roldan, J. Polym. Sci., Part A-2, 1969, 7, 463–473 CrossRef CAS.
- A. L. Demirel, M. Meyer and H. Schlaad, Angew. Chem., Int. Ed., 2007, 46, 8622–8624 CrossRef CAS.
- M. Meyer, M. Antonietti and H. Schlaad, Soft Matter, 2007, 3, 430–431 RSC.
- T. Furuncuoğlu Özaltın, V. Aviyente, C. Atılgan and L. Demirel, Eur. Polym. J., 2017, 88, 594–604 CrossRef.
- P. T. Güner, A. Mikó, F. F. Schweinberger and A. L. Demirel, Polym. Chem., 2012, 3, 322–324 RSC.
- Y. Katsumoto, A. Tsuchiizu, X. Qiu and F. M. Winnik, Macromolecules, 2012, 45, 3531–3541 CrossRef CAS.
- A. M. Bernard, Ph.D. Thesis, Georgia Institute of Technology, 2008.
- J. H. Sung and D. C. Lee, Polymer, 2001, 42, 5771–5779 CrossRef CAS.
- H. Tadokoro, J. Polym. Sci.: Macromol. Rev., 1967, 1, 119–172 CAS.
- S. H. Maron and F. E. Filisko, J. Macromol. Sci., Part B: Phys., 1972, 6, 79–90 CrossRef CAS.
- S. Saeki, N. Kuwahara, M. Nakata and M. Kaneko, Polymer, 1976, 17, 685–689 CrossRef CAS.
- M. L. Alessi, A. I. Norman, S. E. Knowlton, D. L. Ho and S. C. Greer, Macromolecules, 2005, 38, 9333–9340 CrossRef CAS.
- A. Azri, P. Giamarchi, Y. Grohens, R. Olier and M. Privat, J. Colloid Interface Sci., 2012, 379, 14–19 CrossRef CAS.
- F. Oesterhelt, M. Rief and H. Gaub, New J. Phys., 1999, 1, 6 CrossRef.
- B. Hammouda, D. L. Ho and S. Kline, Macromolecules, 2004, 37, 6932–6937 CrossRef CAS.
- K. Tasaki, J. Am. Chem. Soc., 1996, 118, 8459–8469 CrossRef CAS.
- R. Begum and H. Matsuura, J. Chem. Soc., Faraday Trans., 1997, 93, 3839–3848 RSC.
- M. Hishida, R. Kanno and T. Terashima, Macromolecules, 2023, 56, 7587–7596 CrossRef CAS.
- S. Masatoki, M. Takamura, H. Matsuura, K. Kamogawa and T. Kitagawa, Chem. Lett., 1995, 24, 991–992 CrossRef.
- H. Matsuura and T. Sagawa, J. Mol. Liq., 1995, 65–66, 313–316 CrossRef.
- R. Begum, S. Masatoki and H. Matsuura, J. Mol. Struct., 1996, 384, 115–120 CrossRef CAS.
- H. Matsuura and K. Fukuhara, J. Mol. Struct., 1985, 126, 251–260 CrossRef CAS.
- B. D. Monnery, V. V. Jerca, O. Sedlacek, B. Verbraeken, R. Cavill and R. Hoogenboom, Angew. Chem., Int. Ed., 2018, 57, 15400–15404 CrossRef CAS.
- A. Pedretti, A. Mazzolari, S. Gervasoni, L. Fumagalli and G. Vistoli, Bioinformatics, 2021, 37, 1174–1175 CrossRef CAS.
- M. Guettari, R. Gomati and A. Gharbi, J. Macromol. Sci., Part B: Phys., 2012, 51, 153–163 CrossRef CAS.
- A. Chen, D. Wu and C. S. Johnson Jr., J. Am. Chem. Soc., 1995, 117, 7965–7970 CrossRef CAS.
- T. Swift, R. Hoskins, R. Telford, R. Plenderleith, D. Pownall and S. Rimmer, J. Chromatogr., A, 2017, 1508, 16–23 CrossRef CAS.
- I. Swan, M. Reid, P. W. A. Howe, M. A. Connell, M. Nilsson, M. A. Moore and G. A. Morris, J. Magn. Reson., 2015, 252, 120–129 CrossRef CAS PubMed.
- M. Holz, S. R. Heil and A. Sacco, Phys. Chem. Chem. Phys., 2000, 2, 4740–4742 RSC.
- S. T. Popovici, W. T. Kok and P. J. Schoenmakers, J. Chromatogr. A, 2004, 1060, 237–252 CrossRef CAS.
- R. C. Hardy and R. L. Cottington, J. Res. Natl. Bur. Stand., 1949, 42, 573–578 CrossRef CAS.
- P. Lin, C. Clash, E. M. Pearce, T. K. Kwei and M. A. Aponte, J. Polym. Sci., Part B: Polym. Phys., 1988, 26(3), 603–619 CrossRef CAS.
- M. Litt, A. Levy and J. Herz, J. Macromol. Sci., Part A, 1975, 9, 703–727 Search PubMed.
- A. Kowalczuk, J. Kronek, K. Bosowska, B. Trzebicka and A. Dworak, Polym. Int., 2011, 60, 1001–1009 CrossRef CAS.
- C. Özdemir and A. Güner, J. Appl. Polym. Sci., 2006, 101, 203–216 CrossRef.
- C. Ö. Dinç, G. Kibarer and A. Güner, J. Appl. Polym. Sci., 2010, 117, 1100–1119 CrossRef.
- J. Mondal, E. Choi and A. Yethiraj, Macromolecules, 2014, 47, 438–446 CrossRef CAS.
- H. Lee, R. M. Venable, A. D. Mackerell Jr. and R. W. Pastor, Biophys. J., 2008, 95, 1590–1599 CrossRef CAS.
- G. Lancz, M. Avdeev, V. Petrenko, V. Garamus, M. Koneracká and P. Kopčanský, Acta Phys. Pol., A, 2010, 118, 980–982 CrossRef CAS.
- L. Almásy, O. P. Artykulnyi, V. I. Petrenko, O. I. Ivankov, L. A. Bulavin, M. Yan and V. M. Haramus, Molecules, 2022, 27, 2573 CrossRef PubMed.
- V. Petrenko, L. Bulavin, M. Avdeev, V. Garamus, M. Koneracka and P. Kopcansky, Macromol. Symp., 2014, 335, 20–23 CrossRef CAS.
- O. Sedlacek, B. D. Monnery, J. Mattova, J. Kucka, J. Panek, O. Janouskova, A. Hocherl, B. Verbraeken, M. Vergaelen, M. Zadinova, R. Hoogenboom and M. Hruby, Biomaterials, 2017, 146, 1–12 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Tables S1–4; (1) characterisation of PEG used; (2) calculation of molar mass distribution of P(EtOx) from DOSY; (3) power laws for P(EtOx) and (4) power laws for PEG, and 10 figures: (1) the pulse sequence used; (2) example Stejskal–Tanner plot; (3) effect of tube size on convection currents; (4) relationship of D and Mp for PEG at 298 K and the positive projection along the ×1 (diffusion) axis; (5) comparison of commercial Aquazol 50 kDa P(EtOx) with genuine 50 kDa linear P(EtOx); (6) plot of diffusion coefficient of P(EtOx) of various molar masses at various temperatures; (7) relationship of hydrodynamic radius of P(EtOx) of various molar masses at different temperatures; (8) calculation of the volume of the nominal sphere occupied by P(EtOx); (9) plot of the activation energy of diffusion for P(EtOx); and (10) calculation of the volume of a nominal sphere occupied by PEG. See DOI: https://doi.org/10.1039/d4py00505h |
| This journal is © The Royal Society of Chemistry 2024 |