Open Access Article
Open Access ArticleThermodynamic evaluations of the acceptorless dehydrogenation and hydrogenation of pre-aromatic and aromatic N-heterocycles in acetonitrile
Bao-Chen Qiana,
Xiao Wanga,
Qi Wanga,
Xiao-Qing Zhu*b and
Guang-Bin Shen *a
*a
aCollege of Medical Engineering, Jining Medical University, Jining, Shandong 272000, P. R. China. E-mail: gbshen@mail.jnmc.edu.cn
bThe State Key Laboratory of Elemento-Organic Chemistry, Department of Chemistry, Nankai University, Tianjin 300071, China. E-mail: xqzhu@nankai.edu.cn
First published on 2nd January 2024
Abstract
N-heterocycles are important chemical hydrogen-storage materials, and the acceptorless dehydrogenation and hydrogenation of N-heterocycles as organic hydrogen carriers have been widely studied, with the main focus on the catalyst synthesis and design, investigation of the redox mechanisms, and extension of substrate scope. In this work, the Gibbs free energies of the dehydrogenation of pre-aromatic N-heterocycles (YH2) and the hydrogenation of aromatic N-heterocycles (Y), i.e., ΔGH2R(YH2) and ΔGH2A(Y), were derived by constructing thermodynamic cycles using Hess' law. The thermodynamic abilities for the acceptorless dehydrogenation and hydrogenation of 78 pre-aromatic N-heterocycles (YH2) and related 78 aromatic N-heterocycles (Y) were well evaluated and discussed in acetonitrile. Moreover, the applications of the two thermodynamic parameters in identifying pre-aromatic N-heterocycles possessing reversible dehydrogenation and hydrogenation properties and the selection of the pre-aromatic N-heterocyclic hydrogen reductants in catalytic hydrogenation were considered and are discussed in detail. Undoubtedly, this work focuses on two new thermodynamic parameters of pre-aromatic and aromatic N-heterocycles, namely ΔGH2R(YH2) and ΔGH2A(Y), which are important supplements to our previous work to offer precise insights into the chemical hydrogen storage and hydrogenation reactions of pre-aromatic and aromatic N-heterocycles.
1 Introduction
The acceptorless dehydrogenation and hydrogenation of N-heterocycles are key atom-economical and fundamental methods to afford various imine and amine derivatives with potential bioactivities.1–11 Additionally, the two kinds of redox reactions, especially the reversible acceptorless dehydrogenation and hydrogenation of N-heterocycles, involve the release and acceptance of H2, which indicate that N-heterocycles are significant chemical hydrogen-storage materials. In fact, N-heterocycles have already been verified as an important type of chemical hydrogen-storage materials.12–19 The acceptorless dehydrogenation and hydrogenation of N-heterocycles as organic hydrogen carriers have been broadly studied, mainly focusing on the catalyst synthesis and design, investigation of the redox mechanisms, and extension of substrate scope.3–19Since the chemical processes for the acceptorless dehydrogenation and hydrogenation of N-heterocycles involve H2 release and acceptance, therefore, the thermodynamics of the dehydrogenation and hydrogenation of N-heterocycles are important thermodynamic parameters to evaluate the hydrogen-storage abilities and hydrogenation abilities of N-heterocycles, especially for pre-aromatic N-heterocycles possessing reversible dehydrogenation and hydrogenation abilities.3–8 This work follows on from our previous study into the thermodynamics of hydrogen transfer for amines.20 This present work focuses on thermodynamic evaluations of the acceptorless dehydrogenation and hydrogenation of a special category of N-heterocycles, namely, pre-aromatic and aromatic N-heterocycles, in acetonitrile.
In our previous research work, we computed the Gibbs free energies of 84 amines (YH2), including 78 pre-aromatic N-heterocycles and 6 general amines, releasing hydrides and their activation free energies for hydride self-exchange reactions, i.e., ΔGH−R(YH2) and ΔG‡(YH2/YH+), using density functional theory (DFT) calculations in acetonitrile.20a Earlier in 2023, thermodynamic evaluations were conducted of 84 amines releasing two hydrogen ions (H− + H+) and the corresponding 84 imines accepting two hydrogen ions (H− + H+), including ΔGH−PR(YH2) and ΔGH−PA(Y).20b Combined with the above thermodynamic data, in this work, the thermodynamic values upon H2 release and acceptance for the dehydrogenation and hydrogenation of pre-aromatic and aromatic N-heterocycles (Scheme 1) were naturally derived via constructing thermodynamic cycles using Hess' law,21 and the thermodynamic abilities of the pre-aromatic N-heterocycles as chemical hydrogen-storage materials were well evaluated and compared. Moreover, application of the thermodynamic data for identifying pre-aromatic N-heterocycles possessing reversible dehydrogenation and hydrogenation abilities3–8 were investigated and discussed in detail. Undoubtedly, this work focuses on new thermodynamic parameters, which is an important supplement to our previous work to offer precise insights into the chemical hydrogen storage and hydrogenation reactions of pre-aromatic N-heterocycles.1–19
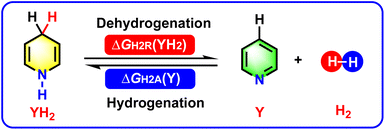 | ||
| Scheme 1 Chemical equations for the acceptorless dehydrogenation and hydrogenation of pre-aromatic and aromatic N-heterocycles. | ||
2 Results and discussion
In this work, 78 various pre-aromatic N-heterocycles (1H2–78H2) were designed to expand the scope of the investigated N-heterocyclic substrates, and 6 general amines (79H2–84H2) were designed for comparison with pre-aromatic N-heterocycles. The chemical structures of 84 amines (YH2), including the 78 pre-aromatic N-heterocycles (1H2–78H2) and 6 general amines (79H2–84H2), are shown in Scheme 2.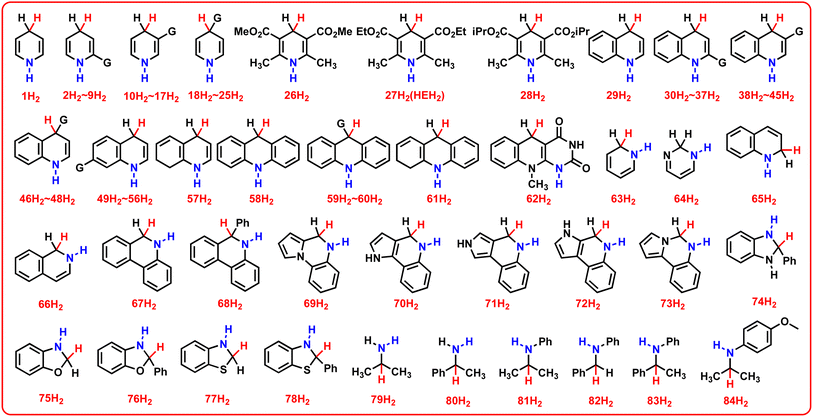 | ||
| Scheme 2 Chemical structures of 84 amines (YH2), including the 78 pre-aromatic N-heterocycles (1H2–78H2) and 6 general amines (79H2–84H2) investigated in this work. | ||
To obtain the Gibbs free energy of YH2 releasing H2, the constructed thermodynamic cycle based on the processes of YH2 releasing two hydrogen ions or H2 in acetonitrile is shown in Scheme 3. As can be seen from Scheme 3, Step 1 is the chemical process of YH2 releasing H2, YH2 → Y + H2, and the thermodynamic driving force of YH2 dehydrogenation could be described by the Gibbs free energy of YH2 releasing H2, ΔGH2R(YH2). Step 2 is the chemical process of YH2 releasing two hydrogen ions, YH2 → Y + H− + H+, and the corresponding thermodynamic driving force was defined as the Gibbs free energy of YH2 releasing two hydrogen ions, ΔGH−PR(YH2).20 Step 3 is the chemical process of H− reacting with H+ to form H2, H− + H+ → H2, and the related thermodynamic driving force was defined as the Gibbs free energy of one molar H− reacting with one molar H+ to generate one molar H2, ΔGPA(H−). The ΔGPA(H−) value was reported as −76.0 kcal mol−1 in acetonitrile.22–24 Therefore, the value of ΔGH2R(YH2) could be calculated using eqn (1) in Table 1 by establishing a thermodynamic cycle according to Hess' law (Scheme 3),21 where ΔGH2R(YH2) = ΔGH−PR(YH2) + ΔGPA(H−) (eqn (1)). For eqn (1), ΔGH−PR(YH2) values are available from our previous work and are displayed in the fourth column of Table 2. Since the ΔGH−R(YH2) values were computed using the DFT method with a precision of 1.1 kcal mol−1 in our previous work,20a and the pKa values of YH+ were predicted using XGBoost with a 0.87 pKa error,20a the ΔGH2R(YH2) values were derived from ΔGH−R(YH2) and pKa(YH+), whereby ΔGH2R(YH2) = ΔGH−R(YH2) + 1.37pKa(YH+), and therefore, the precision of the ΔGH2R(YH2) values could be estimated within 2.3 kcal mol−1, which was a suitable precision to give practical guidance on the chemical hydrogen storage and hydrogenation reactions, etc.
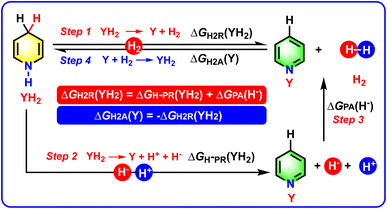 | ||
| Scheme 3 Constructed thermodynamic cycle based on the processes of YH2 releasing two hydrogen ions or H2 in acetonitrile. | ||
| Chemical processes | Thermodynamic parameters | Sources or computed equations | Equation X | |
|---|---|---|---|---|
| Step 1 | YH2 → Y + H2 | ΔGH2R(YH2) | ΔGH2R(YH2) = ΔGH−PR(YH2) + ΔGPA(H−) | 1 |
| Step 2 | YH2 → Y + H− + H+ | ΔGH−PR(YH2) | Ref. 20 | — |
| Step 3 | H− + H+ → H2 | ΔGPA(H−) | −76.0 kcal mol−1 (ref. 22–24) | — |
| Step 4 | Y + H2 → YH2 | ΔGH2A(Y) | ΔGH2A(Y) = −ΔGH2R(YH2) | 2 |
| Compounds | Structures | G | ΔGH−PR(YH2)a | ΔGH2R(YH2)b |
|---|---|---|---|---|
| −ΔGH−PA(Y)a | −ΔGH2A(Y)c | |||
| a ΔGH−PR(YH2) and ΔGH−PA(Y) values are from ref. 20.b ΔGH2R(YH2) = ΔGH−PR(YH2) + ΔGPA(H−).c ΔGH2A(Y) = −ΔGH2R(YH2). | ||||
| 1H2 |  |
— | 68.0 | −8.0 |
| 2H2 | 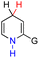 |
CH3 | 68.8 | −7.2 |
| 3H2 | tBu | 70.6 | −5.4 | |
| 4H2 | Ph | 66.5 | −9.5 | |
| 5H2 | NH2 | 63.5 | −12.5 | |
| 6H2 | CHO | 75.6 | −0.4 | |
| 7H2 | CN | 75.2 | −0.8 | |
| 8H2 | NO | 78.9 | 2.9 | |
| 9H2 | NO2 | 71.7 | −4.3 | |
| 10H2 | 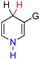 |
CH3 | 69.7 | −6.3 |
| 11H2 | tBu | 71.8 | −4.2 | |
| 12H2 | Ph | 70.2 | −5.8 | |
| 13H2 | NH2 | 67.8 | −8.2 | |
| 14H2 | CHO | 80.6 | 4.6 | |
| 15H2 | CN | 78.7 | 2.7 | |
| 16H2 | NO | 87.3 | 11.3 | |
| 17H2 | NO2 | 85.7 | 9.7 | |
| 18H2 |  |
CH3 | 67.4 | −8.6 |
| 19H2 | tBu | 72.0 | −4.0 | |
| 20H2 | Ph | 64.8 | −11.2 | |
| 21H2 | NH2 | 60.2 | −15.8 | |
| 22H2 | CHO | 72.3 | −3.7 | |
| 23H2 | CN | 74.1 | −1.9 | |
| 24H2 | NO | 76.6 | 0.6 | |
| 25H2 | NO2 | 84.6 | 8.6 | |
| 26H2 | 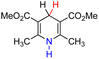 |
— | 83.1 | 7.1 |
| 27H2 | 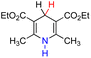 |
— | 83.3 | 7.3 |
| 28H2 | 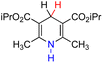 |
— | 83.4 | 7.4 |
| 29H2 | 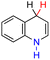 |
— | 77.9 | 1.9 |
| 30H2 | 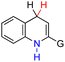 |
CH3 | 75.8 | −0.2 |
| 31H2 | tBu | 79.5 | 3.5 | |
| 32H2 | Ph | 75.9 | −0.1 | |
| 33H2 | NH2 | 69.6 | −6.4 | |
| 34H2 | CHO | 86.0 | 10.0 | |
| 35H2 | CN | 86.4 | 10.4 | |
| 36H2 | NO | 91.0 | 15.0 | |
| 37H2 | NO2 | 81.8 | 5.8 | |
| 38H2 | 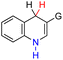 |
CH3 | 76.7 | 0.7 |
| 39H2 | tBu | 81.1 | 5.1 | |
| 40H2 | Ph | 78.8 | 2.8 | |
| 41H2 | NH2 | 76.8 | 0.8 | |
| 42H2 | CHO | 89.4 | 13.4 | |
| 43H2 | CN | 87.3 | 11.3 | |
| 44H2 | NO | 98.0 | 22.0 | |
| 45H2 | NO2 | 93.2 | 17.2 | |
| 46H2 | 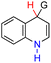 |
CH3 | 73.5 | −2.5 |
| 47H2 | tBu | 84.9 | 8.9 | |
| 48H2 | Ph | 74.9 | −1.1 | |
| 49H2 | 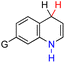 |
CH3 | 76.2 | 0.2 |
| 50H2 | tBu | 80.1 | 4.1 | |
| 51H2 | Ph | 75.9 | −0.1 | |
| 52H2 | NH2 | 74.7 | −1.3 | |
| 53H2 | CHO | 79.0 | 3.0 | |
| 54H2 | CN | 80.6 | 4.6 | |
| 55H2 | NO | 80.4 | 4.4 | |
| 56H2 | NO2 | 81.2 | 5.2 | |
| 57H2 | 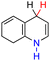 |
— | 67.6 | −8.4 |
| 58H2 | 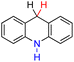 |
H | 87.5 | 11.5 |
| 59H2 | 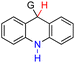 |
CH3 | 87.5 | 11.5 |
| 60H2 | Ph | 87.3 | 11.3 | |
| 61H2 | 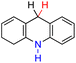 |
— | 76.3 | 0.3 |
| 62H2 | 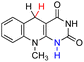 |
— | 87.6 | 11.6 |
| 63H2 | 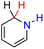 |
— | 64.5 | −11.5 |
| 64H2 | 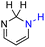 |
— | 73.7 | −2.3 |
| 65H2 | 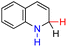 |
— | 74.6 | −1.4 |
| 66H2 | 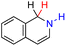 |
— | 77.6 | 1.6 |
| 67H2 | 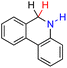 |
— | 79.6 | 3.6 |
| 68H2 | 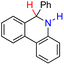 |
— | 78.4 | 2.4 |
| 69H2 | 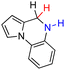 |
— | 84.1 | 8.1 |
| 70H2 | 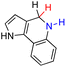 |
— | 76.6 | 0.6 |
| 71H2 | 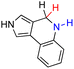 |
— | 80.8 | 4.8 |
| 72H2 | 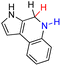 |
77.0 | 1.0 | |
| 73H2 | 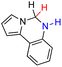 |
— | 84.5 | 8.5 |
| 74H2 | 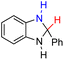 |
— | 68.6 | −7.4 |
| 75H2 | 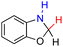 |
— | 85.5 | 9.5 |
| 76H2 | 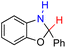 |
— | 78.2 | 2.2 |
| 77H2 | 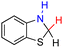 |
— | 82.7 | 6.7 |
| 78H2 | 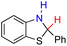 |
— | 76.9 | 0.9 |
| 79H2 | 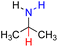 |
— | 86.3 | 10.3 |
| 80H2 | 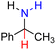 |
— | 87.6 | 11.6 |
| 81H2 | 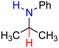 |
— | 91.2 | 15.2 |
| 82H2 | 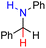 |
— | 93.8 | 17.8 |
| 83H2 | 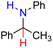 |
— | 93.7 | 17.7 |
| 84H2 |  |
— | 94.3 | 18.3 |
Step 4 in Scheme 2 is the chemical process of Y accepting H2 to offer YH2, Y + H2 → YH2, and the corresponding thermodynamic driving force could be described as the Gibbs free energy of Y accepting H2 to generate YH2, ΔGH2A(Y). Since the Y hydrogenation and YH2 dehydrogenation are reverse chemical reactions, the ΔGH2A(Y) value was the opposite of the ΔGH2R(YH2) value,21 i.e., ΔGH2A(Y) = −ΔGH2R(YH2) (eqn (2) in Table 1). Herein, the chemical processes, thermodynamic parameters, and data sources or computed equations of step 1–step 4 for YH2 dehydrogenation and Y hydrogenation in acetonitrile are presented in Table 1, meanwhile, the ΔGH−PR(YH2), ΔGH−PA(Y), ΔGH2R(YH2), and ΔGH2A(Y) values of the 84 amines (YH2) dehydrogenation and their relevant imines (Y) hydrogenation in acetonitrile are listed in Table 2.
2.1. Thermodynamic abilities of YH2 dehydrogenation as organic hydrogen-storage materials
For better comparing the relationship between the thermodynamic abilities and chemical structures, all 84 amines (YH2) were divided into 4 groups,20 comprising 1,4-dihydropyridine compounds (YIH2, 1H2–62H2), 1,2-dihydropyridines (YIIH2, 63H2–73H2), 1,2-dihydro-3-substituted-indoline analogs (YIIIH, 74H2–78H2), and general amines (YIVH2, 79H2–84H2) (Scheme 4). Among the 4 groups, YIH2, YIIH2, and YIIIH2 were 1,4-dihydro nitric six-member heterocycles, 1,2-dihydro nitric six-member heterocycles, and 1,2-dihydro nitric five-member heterocycles, respectively, which all belong to pre-aromatic N-heterocycles. As pre-aromatic N-heterocycles, the resulting dehydrogenation products Y (YI, YII, and YIII) are aromatic N-heterocycles (Scheme 4) after YH2 releases H2, YH2 → Y + H2.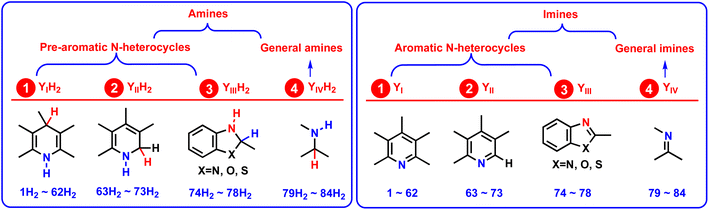 | ||
| Scheme 4 Classifications of the 84 amines (YH2) and imines (Y) and the corresponding 4 groups of YH2 and Y, respectively, considered in this work. | ||
According to the definition of ΔGH2R(YH2), if the ΔGH2R(YH2) value is more negative than 0, ΔGH2R(YH2) < 0, the chemical process of YH2 releasing H2 is thermodynamically favorable, and YH2 is recognized as a thermodynamically excellent H2 donor.21 In contrast, if the ΔGH2R(YH2) value is greater than 0, ΔGH2R(YH2) > 0, the chemical process of YH2 releasing H2 is thermodynamically unfavorable, and YH2 is not a thermodynamically feasible H2 donor.
As can be seen from Table 2, the ΔGH2R(YH2) scale of the 78 pre-aromatic N-heterocycles (1H2–78H2) investigated in this work ranged from −15.8 kcal mol−1 to 22.0 kcal mol−1, which spanned a very wide thermodynamic range of 37.8 kcal mol−1. Moreover, among the 78 pre-aromatic N-heterocycles (1H2–78H2), 21H2 from YIH2 was thermodynamically the best hydrogen donor or carrier (−15.8 kcal mol−1), even better than HCO2H (−5.9 kcal mol−1),25 while 44H2 from YIH2 was thermodynamically the worst hydrogen donor or carrier (22.0 kcal mol−1). For more refined thermodynamic analysis, the distribution of ΔGH2R(YH2) values for the 78 pre-aromatic N-heterocycles (1H2–78H2) in every 5 kcal mol−1 is clearly shown in Fig. 1 with YH2 amounts as the ordinate and ΔGH2R(YH2) ranges as the abscissa.
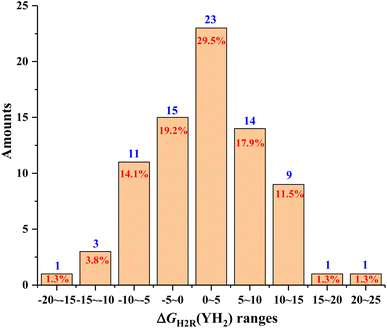 | ||
| Fig. 1 Distributions of ΔGH2R(YH2) ranges for the 78 pre-aromatic N-heterocycles in every 5 kcal mol−1 from −20 kcal mol−1 to 25 kcal mol−1. | ||
From Fig. 1, several interesting conclusions could be drawn as follows. (1) The distribution of YH2 amounts exhibited an excellent normal distribution, and ΔGH2R(YH2) values of pre-aromatic N-heterocycles ranging from 0 to 5 kcal mol−1 were the most common (29.5%). (2) It was found that the ΔGH2R(YH2) values of 30 YH2 were more negative than 0, meaning that 30 YH2 were thermodynamically feasible H2 donors, and belonged to potential chemical hydrogen-storage materials. While the ΔGH2R(YH2) values of 48 YH2 were greater than 0, indicating that the 48 YH2 were thermodynamically unfeasible H2 donors. (3) It was also discovered that 75 ΔGH2R(YH2) values ranged from −15 kcal mol−1 to 15 kcal mol−1, indicating that ∼96% of the thermodynamic driving forces for the pre-aromatic N-heterocycles dehydrogenations were between −15 kcal mol−1 to 15 kcal mol−1, while less than 4% of the thermodynamic driving forces for the pre-aromatic N-heterocycles dehydrogenation were more negative than −15 kcal mol−1 or greater than 15 kcal mol−1. Accordingly, for an unknown pre-aromatic N-heterocycle, the thermodynamic driving force for YH2 dehydrogenation is generally between −15 kcal mol−1 to 15 kcal mol−1 (∼96% possibilities).
To clearly reveal the relationship between the structural features and thermodynamic abilities, the ΔGH2R(YH2) scales of 4 groups of YH2, along with the ΔGH2R(XH2) values of HCO2H, H2, 67H2, 78H2, and HEH2 (Hantzsch ester, 27H2) releasing H2 in acetonitrile are shown in Scheme 5,25–27 because HCO2H,28 H2,29–33 67H2,34,35 78H2,36,37 and HEH2 (27H2)38–40 are the most frequently-used hydrogen reductants (denoted as XH2) used in the hydrogenation reactions.
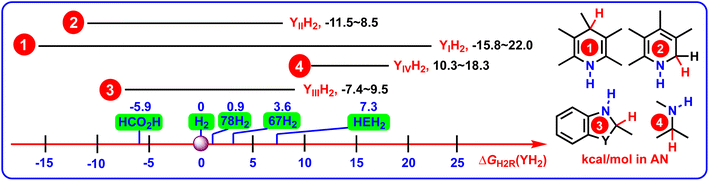 | ||
| Scheme 5 ΔGH2R(YH2) scales of 4 groups of YH2 (YIH2–YIVH2), along with the ΔGH2R(XH2) values of HCO2H, H2, 67H2, 78H2, and HEH2 releasing H2 in acetonitrile (kcal mol−1). | ||
From Scheme 5, the following valuable conclusions could be made: (1) the ΔGH2R(YIH2) scale covered from −15.8 kcal mol−1 to 22.0 kcal mol−1, which spanned the widest thermodynamic range by 37.8 kcal mol−1 among the 4 groups of amines YIH2–YIVH2; (2) according to the ΔGH2R(YH2) scales of YIIH2 (−11.5 to 8.5 kcal mol−1), YIIIH2 (−7.4 to 9.5 kcal mol−1), and YIVH2 (10.3–18.3 kcal mol−1), the dehydrogenation abilities decreased in the order of YIIH2 ≈ YIIIH2 > YIVH2; (3) in view of the relations between sets, it was found that the ΔGH2R(YH2) values displayed the following regular pattern of {ΔGH2R(YIIH2) ∪ ΔGH2R(YIIIH2) ∪ ΔGH2R(YIVH2)} ⊆ ΔGH2R(YIH2); (4) for the pre-aromatic N-heterocycles, the ΔGH2R(YH2) scales ranged from −15.8 to 22.0 kcal mol−1 for YIH2, from −11.5 to 8.5 kcal mol−1 for YIIH2, and from −7.4 to 9.5 kcal mol−1 for YIIIH2, respectively. Since the ΔGH2R(YH2) scales of YIH2, YIIH2, and YIIIH2 crossed negative and positive values (−15.8 to 22.0 kcal mol−1), it was indicated that not all the acceptorless dehydrogenation of pre-aromatic N-heterocycles is a thermodynamically uphill or downhill process under ambient conditions,3–19 and not all pre-aromatic N-heterocycles are thermodynamically feasible to serve as chemical hydrogen-storage materials. ΔGH2R(YH2) is absolutely an important thermodynamic parameter to guide chemists to discover more potentially excellent chemical hydrogen-storage materials.
Initially, we tried to explain the effects of substituents on ΔGH2R(YH2), but we failed to draw a meaningful conclusion. For example, an electron-withdrawing group could decrease the hydride-donating ability of YH2, ΔGH−R(YH2), while it increased the proton-donating ability of YH+, ΔGPR(YH+). Since ΔGH2R(YH2) is derived from ΔGH−R(YH2) and ΔGPR(YH+) essentially, i.e., ΔGH2R(YH2) = ΔGH−R(YH2) + ΔGPR(YH+) + ΔGPA(H−), for YH2 possessing an electron-withdrawing group, whether the ΔGH2R(YH2) value increases or decreases depends on the D-values of ΔGH−R(YH2) decreasing and ΔGPR(YH+) increasing, i.e., ΔΔGH−R(YH2) and ΔΔGPR(YH+). In addition, the steric factors from the substituents will have a significant effect on reaction kinetics, and a slight effect on the reaction thermodynamics.
2.2. Thermodynamic abilities of Y hydrogenation to generate YH2
According to the physical meaning of ΔGH2A(Y), if the ΔGH2A(Y) value is more negative than 0, ΔGH2A(Y) < 0, the Y hydrogenation by H2 is thermodynamically favorable. The more negative the ΔGH2A(Y) value, the larger the thermodynamic driving force of Y hydrogenation by H2. While if the ΔGH2A(Y) value is greater than 0, ΔGH2A(Y) > 0, the Y hydrogenation by H2 is thermodynamically unfavorable, and the larger the ΔGH2A(Y) value, the smaller the thermodynamic driving force of Y hydrogenation by H2. From Table 2, among the 84 imines (Y), aromatic N-heterocycle 44 (−22.0 kcal mol−1) had the largest thermodynamic driving force to accept H2 producing 44H2, while the aromatic N-heterocycle 21 (15.8 kcal mol−1) had the smallest thermodynamic driving force to obtain H2 generating 21H2.As for the ΔGH2A(Y) values, we can safely draw some interesting conclusions to inform the hydrogenation reactions of imines, including aromatic N-heterocycles (1–78) and general imines (79–84), from Scheme 6. Specifically: (1) for aromatic N-heterocycles, the ΔGH2A(Y) scales ranged from −22.0 kcal mol−1 to 15.8 kcal mol−1 for YI, from −8.5 to 11.5 kcal mol−1 for YII, and from −9.5 kcal mol−1 to 7.4 kcal mol−1 for YIII, respectively. The ΔGH2A(Y) scale of aromatic N-heterocycles (YI–YIII) ranged from −22.0 kcal mol−1 to 15.8 kcal mol−1, which covered a very large range of 37.8 kcal mol−1. The ΔGH2A(Y) scales indicated that the H2 (0 kcal mol−1),22–24 even the great hydrogen-reductant HCO2H (−5.9 kcal mol−1),25 could not hydrogenate all the aromatic imines (YI, YII, and YIII) to offer pre-aromatic N-heterocycles (YIH2, YIIH2, and YIIIH2). It also could be deduced that some pre-aromatic N-heterocycles from YIH2, YIIH2, and YIIIH2 were thermodynamically better hydrogen reductants than H2 in hydrogenation reactions. In practice, 27H2 (HEH2),38–40 67H2,34,35 73H2,41 74H2,42 and 78H2 (ref. 36 and 37) have already been extensively researched in hydrogenating various unsaturated compounds, including aldehydes ketones, alkenes, imines, and heterocycles;36–42 (2) in contrast, since YIV were general imines without aromatic structures, all the ΔGH2A(YIV) values (−18.3 to −10.3 kcal mol−1) were all greater than the ΔGH2R(H2) values (0 kcal mol−1), meaning that H2 could hydrogenate the related general imines (YIV) in organic synthesis under suitable catalytic conditions, which has been proved by many published studies in the literature.43–47 Similarly, HCO2H (ΔGH2R(HCO2H) = −5.9 kcal mol−1),28 78H2 (ΔGH2R(78H2) = 0.9 kcal mol−1),36,37 67H2 (ΔGH2R(67H2) = 3.6 kcal mol−1),34,35 and HEH2 (ΔGH2R(HEH2) = 7.3 kcal mol−1)38–40 could be applied to hydrogenate YIV to prepare general amines YIVH2 in organic synthesis from a thermodynamics viewpoint.
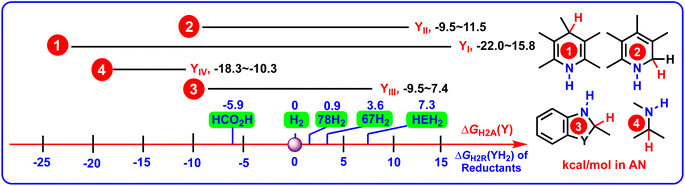 | ||
| Scheme 6 ΔGH2A(Y) scales of 4 groups of Y (YI–YIV), along with the ΔGH2R(XH2) values of HCO2H, H2, 67H2, 78H2, and HEH2 in acetonitrile (kcal mol−1). | ||
2.3. Thermodynamics for the reversible dehydrogenation and hydrogenation of pre-aromatic and aromatic N-heterocycles
Many groups have focused on the reversible dehydrogenation and hydrogenation of pre-aromatic and aromatic N-heterocycles, mainly including discovering better pre-aromatic N-heterocycles carriers and developing novel metal–organic catalysts.1–19 Since we have obtained so much valuable thermodynamic data of pre-aromatic N-heterocycles dehydrogenation and aromatic N-heterocycles hydrogenation, it seemed meaningful to clarify why the reversible dehydrogenation and hydrogenation of pre-aromatic and aromatic N-heterocycles could happen, as well as why they possess the typical thermodynamic feature of the corresponding pre-aromatic N-heterocycles.Theoretically, according to the reaction rule, for the reversible dehydrogenation and hydrogenation of pre-aromatic and aromatic N-heterocycles, if the Gibbs free energy of a YH2 dehydrogenation (YH2 → Y + H2) is more negative than 0, ΔGH2R(YH2) < 0, then the YH2 dehydrogenation reaction is judged as thermodynamically favorable; while if the Gibbs free energy of the corresponding Y hydrogenation reaction (Y + H2 → YH2) is greater than 0, ΔGH2A(Y) > 0, then the hydrogenation reaction of Y is thermodynamically unfavorable. In contrast, if the Gibbs free energy of a YH2 dehydrogenation (YH2 → Y + H2) is greater than 0, ΔGH2R(YH2) > 0, and the dehydrogenation reaction is considered as thermodynamically unfavorable; while if the Gibbs free energy of the corresponding Y hydrogenation (Y + H2 → YH2) is more negative than 0, ΔGH2A(Y) < 0, and the related Y hydrogenation reaction is regarded as thermodynamically favorable. Therefore, it is very curious why the reversible dehydrogenation and hydrogenation of pre-aromatic and aromatic N-heterocycles could happen, even using the same metal–organic catalyst.3–9
Examining the previous literature, it is believed that the H2 plays a very important role in regulating the reversible dehydrogenation and hydrogenation thermodynamics.3–9 In YH2 dehydrogenation, the H2 is released from the reaction system, which greatly affects the dehydrogenation equilibrium.3–9 Therefore, the Gibbs free energy of YH2 dehydrogenation could decrease to make the reaction happen if the ΔGH2R(YH2) value is not too much greater than 0. Furthermore, in Y hydrogenation, the high H2 pressure would prompt more H2 to dissolve in the reaction solvent, which would have a strong influence on the hydrogenation equilibrium.3–9 Consequently, the Gibbs free energy of Y hydrogenation could decrease to make the reaction occur if the ΔGH2A(Y) is not too much greater than 0. Herein, this leads to the other key question: what are the restrictions on the ΔGH2R(YH2) value for the reversible dehydrogenation and hydrogenation of a pre-aromatic and aromatic N-heterocycle?3
Investigating previous work, the Gibbs solvation energy of H2 was estimated as 3.4 kcal mol−1 in acetonitrile.48 That is, the Gibbs free energy of H2 release from acetonitrile solution was −3.4 kcal mol−1, and the H2 release from the dehydrogenation system could decrease the ΔGH2R(YH2) by 3.4 kcal mol−1. Therefore, it is reasonable to deduce that if the ΔGH2R(YH2) value of a pre-aromatic N-heterocycle is greater than −3.5 kcal mol−1 and more negative than 3.5 kcal mol−1, −3.5 kcal mol−1 < ΔGH2R(YH2) < 3.5 kcal mol−1, the pre-aromatic N-heterocycle could be considered as a potentially reversible chemical organic hydrogen material, which could release H2 and be regenerated by H2 too. According to the above judgment criterion, the ΔGH2R(YH2) values of general amines (YIVH2) (10.3–18.3 kcal mol−1) are much greater than 3.5 kcal mol−1, and so YIVH2 could not be designed as reversible dehydrogenation and hydrogenation materials, which is proved by published works.3–9 Moreover, the ΔGH2R(YH2) scale of 28 pre-aromatic N-heterocycles from YIH2, YIIH2, and YIIIH2 ranged from −3.5 kcal mol−1 to 3.5 kcal mol−1, while the corresponding 28 pre-aromatic N-heterocycles were identified as reversible dehydrogenation and hydrogenation materials. The 28 pre-aromatic N-heterocycles included 6H2 (−0.4 kcal mol−1), 7H2 (−0.8 kcal mol−1), 8H2 (2.9 kcal mol−1), 15H2 (2.7 kcal mol−1), 23H2 (−1.9 kcal mol−1), 24H2 (0.6 kcal mol−1), 29H2 (1.9 kcal mol−1), 30H2 (−0.2 kcal mol−1), 31H2 (3.5 kcal mol−1), 32H2 (−0.1 kcal mol−1), 38H2 (0.7 kcal mol−1), 40H2 (2.8 kcal mol−1), 41H2 (0.8 kcal mol−1), 46H2 (−2.5 kcal mol−1), 48H2 (−1.1 kcal mol−1), 49H2 (0.2 kcal mol−1), 51H2 (−0.1 kcal mol−1), 52H2 (−1.3 kcal mol−1), 53H2 (3.0 kcal mol−1), 61H2 (0.3 kcal mol−1), 64H2 (−2.3 kcal mol−1), 65H2 (−1.4 kcal mol−1), 66H2 (1.6 kcal mol−1), 68H2 (2.4 kcal mol−1), 70H2 (0.6 kcal mol−1), 72H2 (1.0 kcal mol−1), 76H2 (2.2 kcal mol−1), and 78H2 (0.9 kcal mol−1), which need further validation and support in experimental work. Examining the chemical structures of the investigated N-heterocycles in previous literature,3–19 they were not exactly the same pre-aromatic N-heterocycle structure, and most cases involved two H2 molecules release and acceptance from N-heterocycles, which could not provide direct experimental data to validate the thermodynamic model.
2.4. Application of thermodynamic parameters to the selection of pre-aromatic N-heterocyclic hydrogen reductants for catalytic hydrogenation reactions
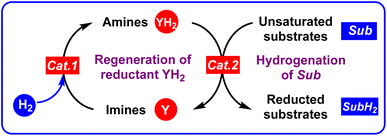
It is well known that H2 is the greenest hydrogenation reagent with 100% atomic economy.43–47 Besides H2, the organic hydrogen molecule reductants, most of which are pre-aromatic N-heterocyclics (such as 27H2, 67H2, 73H2, 74H2, and 78H2),36–42 are irreplaceable hydrogen carriers in hydrogenation reactions. Zhou et al. developed dual hydrogenation strategies and utilized catalytic amounts of Hantzsch ester (HEH2 or 27H2)49 and dihydrophenanthridines (67H2)50 as hydrogen reductants to asymmetrically reduce imines by using H2 as a real reductant for regeneration of the oxidated Hantzsch esters (HE or 27) under a catalyst of metal complexes (Scheme 7). During their work, the reduction of imines, the oxidation of organic hydrogen reductants (pre-aromatic N-heterocycles), as well as the regeneration of oxidated organic hydrogen reductants (aromatic N-heterocycles) all involved H2 transfer. Therefore, the Gibbs free energies for amines dehydrogenation and imines hydrogenation are important thermodynamic parameters to evaluate the reducing abilities of amines and the hydrogenation difficulties of imines, which could help us discover thermodynamically excellent organic hydrogen reductants or chemical hydrogen-storage compounds, choose appropriate hydrogen reductants, especially for catalytic amounts of hydrogen reductants during the hydrogenation of unsaturated substrates.If an unsaturated substrate (Sub) is hydrogenated to a reduced unsaturated substrate (SubH2), Sub + H2 → SubH2, whose thermodynamic driving force is defined as the Gibbs free energy of an unsaturated substrate (Sub) accepting H2 to afford SubH2 (equal to the opposite of Gibbs free energy of SubH2 releasing H2 to give Sub, SubH2 → Sub + H2), ΔGH2A(Sub) = −ΔGH2R(SubH2), then the larger the thermodynamic driving force for the pre-aromatic N-heterocycle reductant dehydrogenation, the more favorable the Sub hydrogenation by YH2, i.e., Sub + YH2 → SubH2 + Y.21
Herein, the applications of thermodynamic parameters on choosing suitable catalytic amounts of pre-aromatic N-heterocycle reductants in hydrogenation reactions are displayed in Scheme 8 to aid a clear discussion.
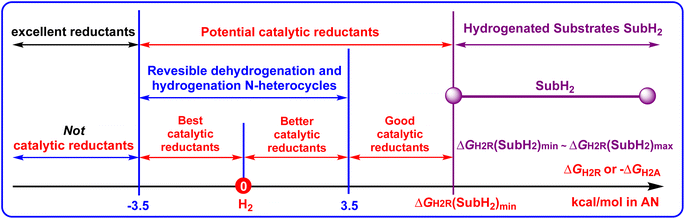 | ||
| Scheme 8 Applications of the thermodynamic parameters on choosing suitable catalytic amounts of N-heterocyclic hydrogen reductants in hydrogenation reactions. | ||
It should be noted that not all unsaturated substrates hydrogenation reactions could be designed as organic hydrogen-reductant catalytic reactions. For unsaturated substrates (Sub), if the ΔGH2R(SubH2) values are more negative than −3.5 kcal mol−1, due to the regeneration of aromatic N-heterocycles being impossible (ΔGH2R(YH2) < −3.5 kcal mol−1), the hydrogenation reactions could not be designed as pre-aromatic N-heterocyclic reductant catalyzed reactions. In contrast, if the ΔGH2R(SubH2) values of unsaturated substrates are greater than 3.5 kcal mol−1, whose thermodynamic driving force scale of SubH2 releasing H2 is denoted as ΔGH2R(SubH2)min ∼ ΔGH2R(SubH2)max, then pre-aromatic N-heterocycles with ΔGH2R(YH2) values more negative than ΔGH2R(SubH2)min and greater than −3.5 kcal mol−1 can be recognized as potential catalytic pre-aromatic N-heterocycle reductants, that is, −3.5 kcal mol−1 < ΔGH2R(YH2) < ΔGH2R(SubH2)min. Specially, if 3.5 kcal mol−1 < ΔGH2R(YH2) < ΔGH2R(SubH2)min, then the corresponding pre-aromatic N-heterocycles could be designed as thermodynamically good catalytic hydrogen reductants. If 0 < ΔGH2R(YH2) < 3.5 kcal mol−1, the corresponding pre-aromatic N-heterocycles could be designed as thermodynamically better catalytic hydrogen reductants. If −3.5 kcal mol−1 < ΔGH2R(YH2) < 0 kcal mol−1, the corresponding pre-aromatic N-heterocycles could be designed as the thermodynamically best catalytic hydrogen reductants. If ΔGH2R(YH2) < −3.5 kcal mol−1, the corresponding pre-aromatic N-heterocycles could be considered thermodynamically very excellent reductants, but they could not be regenerated by H2 and designed as catalytic hydrogen reductants.
Thus, it can be seen that the two new thermodynamic parameters ΔGH2R(YH2) and ΔGH2A(Y) can not only help us evaluate and identify good chemical hydrogen-storage materials, but also choose appropriate hydrogen reductants, especially for catalytic amounts of N-heterocyclic hydrogen reductants during the hydrogenation of unsaturated substrates.
3 Conclusions
In this work, the Gibbs free energies of pre-aromatic N-heterocycles (YH2) dehydrogenation and corresponding aromatic N-heterocycles (Y) hydrogenation, ΔGH2R(YH2) and ΔGH2A(Y), were derived by constructing thermodynamic cycles using Hess' law. The thermodynamic abilities on the acceptorless dehydrogenation and hydrogenation of 78 pre-aromatic N-heterocycles (YH2) and related 78 aromatic N-heterocycles (Y) were well evaluated and discussed in acetonitrile. Several valuable conclusions could be drawn as follows:(1) ΔGH2R(YH2) is an important thermodynamic parameter to guide chemists to discover more potentially excellent hydrogen carriers. Not all pre-aromatic N-heterocycles are thermodynamically feasible chemical hydrogen-storage materials. The ΔGH2R(YH2) scale of the considered 78 pre-aromatic N-heterocycles ranged from −15.8 kcal mol−1 to 22.0 kcal mol−1, with 30 ΔGH2R(YH2) values being more negative than 0, meaning that the related 30 YH2 were identified as thermodynamically feasible H2 donors, and belong to potential chemical hydrogen-storage materials. The ΔGH2R(YIH2) scale (−15.8 to 22.0 kcal mol−1) spanned the widest thermodynamic range by 37.8 kcal mol−1 among YIH2–YIVH2, and the dehydrogenation abilities of YIIH2–YIVH2 decreased in the order of YIIH2 ≈ YIIIH2 > YIVH2.
(2) As for the thermodynamic abilities of Y hydrogenation, the ΔGH2A(Y) data indicated that for H2, even the great hydrogen-reductant HCO2H (−5.9 kcal mol−1), could not hydrogenate all the aromatic imines (YI, YII, and YIII) to form pre-aromatic N-heterocycles. YIV are general imines without aromatic structures, and all their ΔGH2A(YIV) values (−18.3 to −10.3 kcal mol−1) were greater than ΔGH2R(H2) (0 kcal mol−1), meaning that H2 could hydrogenate the related general imines (YIV) in organic synthesis under suitable catalytic conditions.
(3) H2 plays an important role in regulating reversible dehydrogenation and hydrogenation thermodynamics. The thermodynamic features in the reversible dehydrogenation and hydrogenation of pre-aromatic and aromatic N-heterocycles were clarified such that if −3.5 kcal mol−1 < ΔGH2R(YH2) < 3.5 kcal mol−1, the pre-aromatic N-heterocycle is considered as a thermodynamically potential reversible chemical organic hydrogen material, which could release H2 and be regenerated by H2 too.
(4) The application of thermodynamic parameters to the selection of pre-aromatic N-heterocyclic hydrogen reductants in catalytic hydrogenation was exhibited in this work. If the ΔGH2R(SubH2) values of unsaturated substrates (SubH2) are greater than 3.5 kcal mol−1, pre-aromatic N-heterocycles with −3.5 kcal mol−1 < ΔGH2R(YH2) < ΔGH2R(SubH2)min could be recognized as thermodynamically potential catalytic reductants. Specially, if 3.5 kcal mol−1 < ΔGH2R(YH2) < ΔGH2R(SubH2)min, the related pre-aromatic N-heterocycles could be designed as thermodynamically good catalytic hydrogen reductants. If 0 < ΔGH2R(YH2) < 3.5 kcal mol−1, the related pre-aromatic N-heterocycles could be designed as thermodynamically better catalytic hydrogen reductants. If −3.5 kcal mol−1 < ΔGH2R(YH2) < 0 kcal mol−1, the related pre-aromatic N-heterocycles could be designed as the thermodynamically best catalytic hydrogen reductants.
In summary, this work focused on two new thermodynamic parameters, namely ΔGH2R(YH2) and ΔGH2A(Y), which is an important supplement to our previous work to offer precise insights into the chemical hydrogen storage of pre-aromatic N-heterocycles, and hydrogenation reactions.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This study was supported by the College Students' Innovative Training Plan Program of Shandong Province (S202210443003), and the Doctoral Scientific Research Foundation of Jining Medical University.References
- F. Li, L. Lu and P. Liu, Acceptorless Dehydrogenative Coupling of o-Aminobenzamides with the Activation of Methanol as a C1 Source for the Construction of Quinazolinones, Org. Lett., 2016, 18, 2580–2583 CrossRef CAS PubMed
.
- C. Li, S. Zhang, S. Li, Y. Feng and Q.-H. Fan, Ruthenium-Catalyzed Enantioselective Hydrogenation of Quinoxalinones and Quinazolinones, Org. Chem. Front., 2022, 9, 400–406 RSC
.
- R. Xu, S. Chakraborty, H. Yuan and W. D. Jones, Acceptorless, Reversible Dehydrogenation and Hydrogenation of N-Heterocycles with a Cobalt Pincer Catalyst, ACS Catal., 2015, 5, 6350–6354 CrossRef CAS
.
- M. G. Manas, L. S. Sharninghausen, E. Lin and R. H. Crabtree, Iridium Catalyzed Reversible Dehydrogenation-Hydrogenation of Quinoline Derivatives under Mild Conditions, J. Organomet. Chem., 2015, 792, 184–189 CrossRef CAS
.
- R. Yamaguchi, C. Ikeda, Y. Yoshinor Takahashi and K. Fujita, Homogeneous Catalytic System for Reversible Dehydrogenation-Hydrogenation Reactions of Nitrogen Heterocycles with Reversible Interconversion of Catalytic Species, J. Am. Chem. Soc., 2009, 131, 8410–8412 CrossRef CAS PubMed
.
- S. Chakraborty, W. W. Brennessel and W. D. Jones, A Molecular Iron Catalyst for the Acceptorless Dehydrogenation and Hydrogenation of N-Heterocycles, J. Am. Chem. Soc., 2014, 136, 8564–8567 CrossRef CAS PubMed
.
- B. Sawatlon and P. Surawatanawong, Mechanisms for Dehydrogenation and Hydrogenation of N-Heterocycles using PNP-Pincer-Supported Iron Catalysts: A Density Functional Study, Dalton Trans., 2016, 45, 14965–14978 RSC
.
- N. O. Balayeva, Z. Mamiyev, R. Dillert, N. Zheng and D. W. Bahnemann, Rh/TiO2-Photocatalyzed Acceptorless Dehydrogenation of N-Heterocycles upon Visible-Light Illumination, ACS Catal., 2020, 10, 5542–5553 CrossRef CAS
.
- S. Muthaiah and S. H. Hong, Acceptorless and Base-Free Dehydrogenation of Alcohols and Amines using Ruthenium-Hydride Complexes, Adv. Synth. Catal., 2012, 354, 3045–3053 CrossRef CAS
.
- I. Dutta, S. Yadav, A. Sarbajna, S. De, M. Hölscher, W. Leitner and J. K. Bera, Double Dehydrogenation of Primary Amines to Nitriles by a Ruthenium Complex Featuring Pyrazole Functionality, J. Am. Chem. Soc., 2018, 140, 8662–8666 CrossRef CAS PubMed
.
- M. Kannan and S. Muthaiah, Extending the Chemistry of Hexamethylenetetramine in Ruthenium-Catalyzed Amine Oxidation, Organometallics, 2019, 38, 3560–3567 CrossRef CAS
.
- R. H. Crabtree, Hydrogen Storage in Liquid Organic Heterocycles, Energy Environ. Sci., 2008, 1, 134–138 RSC
.
- R. King, A. J. Canty, A. Ariafard, R. A. J. O'Hair and V. Ryzhov, Catalytic Dehydrogenation of Liquid Organic Hydrogen Carrier Model Compounds by CpM+ (M = Fe, Co, Ni) in the Gas Phase, Organometallics, 2022, 41, 3823–3833 CrossRef CAS
.
- O. R. Luca, D. L. Huang, M. K. Takase and R. H. Crabtree, Redox-Active Cyclopentadienyl Ni Complexes with Quinoid N-Heterocyclic Carbene Ligands for the Electrocatalytic Hydrogen Release from Chemical Fuels, New J. Chem., 2013, 37, 3402–3405 RSC
.
- H. Y. Zhao, S. T. Oyama and E. D. Naeemi, Hydrogen Storage Using Heterocyclic Compounds: The Hydrogenation of 2-Methylthiophene, Catal. Today, 2010, 149, 172–184 CrossRef CAS
.
- S. M. Bellows, S. Chakraborty, J. B. Gary, W. D. Jones and T. R. Cundari, An Uncanny Dehydrogenation Mechanism: Polar Bond Control over Stepwise or Concerted Transition States, Inorg. Chem., 2017, 56, 5519–5524 CrossRef CAS PubMed
.
- X. Cui, Y. Li, S. Bachmann, M. Scalone, A.-E. Surkus, K. Junge, C. Topf and M. Beller, Synthesis and Characterization of Iron−Nitrogen-Doped Graphene/Core−Shell Catalysts: Efficient Oxidative Dehydrogenation of N-Heterocycles, J. Am. Chem. Soc., 2015, 137, 10652–10658 CrossRef CAS PubMed
.
- D. Zhang, L.-Z. Wu, L. Zhou, X. Han, Q.-Z. Yang, L.-P. Zhang and C.-H. Tung, Photocatalytic Hydrogen Production from Hantzsch 1,4-Dihydropyridines by Platinum(II) Terpyridyl Complexes in Homogeneous Solution, J. Am. Chem. Soc., 2004, 126, 3440–3441 CrossRef CAS PubMed
.
- A. Moores, M. Poyatos, Y. Luo and R. H. Crabtree, Catalysed Low Temperature H2 Release from Nitrogen Heterocycles, New J. Chem., 2006, 30, 1675–1678 RSC
.
-
(a) Y. Li and X.-Q. Zhu, Theoretical Prediction of Activation Free Energies of Various Hydride Self-Exchange Reactions in Acetonitrile at 298 K, ACS Omega, 2018, 3, 872–885 CrossRef CAS PubMed
; (b) G.-B. Shen, B.-C. Qian, G.-Z. Luo, Y.-H. Fu and X.-Q. Zhu, Thermodynamic Evaluations of Amines as Hydrides or Two Hydrogen Ions Reductants, and Imines as Protons or Two Hydrogen Ions Acceptors, as well as Their Application in Hydrogenation Reactions, ACS Omega, 2023, 8, 31984–31997 CrossRef CAS PubMed
.
- G.-B. Shen, B.-C. Qian, Y.-H. Fu and X.-Q. Zhu, Discovering and Evaluating the Reducing Abilities of Polar Alkanes and Related Family Members as Organic Reductants Using Thermodynamics, J. Org. Chem., 2022, 87, 9357–9374 CrossRef CAS PubMed
.
- E. S. Wiedner, M. B. Chambers, C. L. Pitman, R. M. Bullock, A. J. M. Miller and A. M. Appel, Thermodynamic Hydricity of Transition Metal Hydrides, Chem. Rev., 2016, 116, 8655–8692 CrossRef CAS PubMed
.
- K. R. Brereton, N. E. Smith, N. Hazari and A. J. M. Miller, Thermodynamic and Kinetic Hydricity of Transition Metal Hydrides, Chem. Soc. Rev., 2020, 49, 7929–7948 RSC
.
- R. G. Agarwal, C. F. Wise, J. J. Warren and J. M. Mayer, Correction to Thermochemistry of Proton-Coupled Electron Transfer Reagents and its Implications, Chem. Rev., 2022, 122, 1482 CrossRef CAS PubMed
.
- G.-B. Shen, B.-C. Qian, G.-S. Zhang, G.-Z. Luo, Y.-H. Fu and X.-Q. Zhu, Thermodynamics Regulated Organic Hydride/Acid Pairs as Novel Organic Hydrogen Reductants, Org. Chem. Front., 2022, 9, 6833–6848 RSC
.
- G.-B. Shen, B.-C. Qian, Y.-H. Fu and X.-Q. Zhu, Thermodynamics of the Elementary Steps of Organic Hydride Chemistry Determined in Acetonitrile and their Applications, Org. Chem. Front., 2022, 9, 6001–6062 RSC
.
- G.-B. Shen, Y.-H. Fu and X.-Q. Zhu, Thermodynamic Network Cards of Hantzsch Ester, Benzothiazoline, and Dihydrophenanthridine Releasing Two Hydrogen Atoms or Ions on 20 Elementary Steps, J. Org. Chem., 2020, 85, 12535–12543 CrossRef CAS PubMed
.
- D. Wei and C. Darcel, Iron Catalysis in Reduction and Hydrometalation Reactions, Chem. Rev., 2019, 119, 2550–2610 CrossRef CAS PubMed
.
- H. Wang, J. Wen and X. Zhang, Chiral Tridentate Ligands in Transition Metal-Catalyzed Asymmetric Hydrogenation, Chem. Rev., 2021, 121, 7530–7567 CrossRef CAS PubMed
.
- M. Luneau, J. S. Lim, D. A. Patel, E. C. H. Sykes, C. M. Friend and P. Sautet, Guidelines to Achieving High Selectivity for The Hydrogenation of α,β-Unsaturated Aldehydes with Bimetallic and Dilute Alloy Catalysts: A Review, Chem. Rev., 2020, 120, 12834–12872 CrossRef CAS PubMed
.
- Z. Zhang, N. A. Butt and W. Zhang, Asymmetric Hydrogenation of Nonaromatic Cyclic Substrates, Chem. Rev., 2016, 116, 14769–14827 CrossRef CAS PubMed
.
- F. Meemken and A. Baiker, Recent Progress in Heterogeneous Asymmetric Hydrogenation of C=O and C=C Bonds on Supported Noble Metal Catalysts, Chem. Rev., 2017, 117, 11522–11569 CrossRef CAS PubMed
.
- J.-H. Xie, S.-F. Zhu and Q.-L. Zhou, Recent Advances in Transition Metal-Catalyzed Enantioselective Hydrogenation of Unprotected Enamines, Chem. Soc. Rev., 2012, 41, 4126–4139 RSC
.
- B. Gao, W. Meng, X. Feng and H. Du, Regenerable Dihydrophenanthridine via Borane-Catalyzed Hydrogenation for The Asymmetric Transfer Hydrogenation of Benzoxazinones, Org. Lett., 2022, 24, 3955–3959 CrossRef CAS PubMed
.
- J. Wang, Z.-B. Zhao, Y. Zhao, G. Luo, Z.-H. Zhu, Y. Luo and Y.-G. Zhou, Chiral and Regenerable NAD(P)H Models Enabled Biomimetic Asymmetric Reduction:
Design, Synthesis, Scope, and Mechanistic Studies, J. Org. Chem., 2020, 85, 2355–2368 CrossRef CAS PubMed
.
- C. Zhu, K. Saito, M. Yamanaka and T. Akiyama, Benzothiazoline: Versatile Hydrogen Donor for Organocatalytic Transfer Hydrogenation, Acc. Chem. Res., 2015, 48, 388–398 CrossRef CAS PubMed
.
- H. Osakabe, S. Saito, M. Miyagawa, T. Suga, T. Uchikura and T. Akiyama, Enantioselective Dehydroxyhydrogenation of 3-Indolylmethanols by The Combined Use of Benzothiazoline and Chiral Phosphoric Acid: Construction of A Tertiary Carbon Center, Org. Lett., 2020, 22, 2225–2229 CrossRef CAS PubMed
.
- C. Zheng and S.-L. You, Transfer Hydrogenation with Hantzsch Esters and Related Organic Hydride Donors, Chem. Soc. Rev., 2012, 41, 2498–2518 RSC
.
- S. G. Ouellet, A. M. Walji and D. W. C. Macmillan, Enantioselective Organocatalytic Transfer Hydrogenation Reactions Using Hantzsch Esters, Acc. Chem. Res., 2007, 40, 1327–1339 CrossRef CAS PubMed
.
- M. Rueping, J. Dufour and F. R. Schoepke, Advances in Catalytic Metal-Free Reductions: from Bioinspired Concepts to Applications in the Organocatalytic Synthesis of Pharmaceuticals and Natural Products, Green Chem., 2011, 13, 1084–1105 RSC
.
- Z.-P. Chen, M.-W. Chen, R.-N. Guo and Y.-G. Zhou, 4,5-Dihydropyrrolo[1,2-a]quinoxalines: A Tunable and Regenerable Biomimetic Hydrogen Source, Org. Lett., 2014, 16, 1406–1409 CrossRef CAS PubMed
.
- Y.-S. Feng, C.-Y. Yang, Q. Huang and H.-J. Xu, Study on Comparison of Reducing Ability of Three Organic Hydride Compounds, Tetrahedron, 2012, 68, 5053–5059 CrossRef CAS
.
- A. Cabré, X. Verdaguer and A. Riera, Recent Advances in The Enantioselective Synthesis of Chiral Amines via Transition Metal-Catalyzed Asymmetric Hydrogenation, Chem. Rev., 2022, 122, 269–339 CrossRef PubMed
.
- R. A. A. Abdine, G. Hedouin, F. Colobert and J. Wencel-Delord, Metal-Catalyzed Asymmetric Hydrogenation of C=N Bonds, ACS Catal., 2021, 11, 215–247 CrossRef CAS
.
- D.-S. Wang, Q.-A. Chen, S.-M. Lu and Y.-G. Zhou, Asymmetric Hydrogenation of Heteroarenes and Arenes, Chem. Rev., 2012, 112, 2557–2590 CrossRef CAS PubMed
.
- J.-D. Yang, J. Xue and J.-P. Cheng, Understanding the Role of Thermodynamics in Catalytic Imine Reductions, Chem. Soc. Rev., 2019, 48, 2913–2926 RSC
.
- X. del Corte, E. M. de Marigorta, F. Palacios, J. Vicario and A. Maestro, An Overview of the Applications of Chiral Phosphoric Acid Organocatalysts in Enantioselective Additions to C=O and C=N bonds, Org. Chem. Front., 2022, 9, 6331–6399 RSC
.
- C. A. Kelly and D. R. Rosseinsky, Estimates of Hydride Ion Stability in Condensed Systems: Energy of Formation and Solvation in Aqueous and Polar-Organic Solvents, Phys. Chem. Chem. Phys., 2001, 3, 2086–2090 RSC
.
- Q.-A. Chen, M.-W. Chen, C.-B. Yu, L. Shi, D.-S. Wang, Y. Yang and Y.-G. Zhou, Biomimetic Asymmetric Hydrogenation: In Situ Regenerable Hantzsch Esters for Asymmetric Hydrogenation of Benzoxazinones, J. Am. Chem. Soc., 2011, 133, 16432–16435 CrossRef CAS PubMed
.
- Q.-A. Chen, K. Gao, Y. Duan, Z.-S. Ye, L. Shi, Y. Yang and Y.-G. Zhou, Dihydrophenanthridine: A New and Easily Regenerable NAD(P)H Model for Biomimetic Asymmetric Hydrogenation, J. Am. Chem. Soc., 2012, 134, 2442–2448 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2024 |