Open Access Article
Open Access ArticleThe role of non-covalent interactions in 4-hydroxybenzylamine macrocyclisation: computational and synthetic evidence†
Andrés Gonzalez-Oñate,
Jorge Alí-Torres and
Rodolfo Quevedo
and
Rodolfo Quevedo *
*
Departamento de Química, Facultad de Ciencias, Universidad Nacional de Colombia, Sede Bogotá, Carrera 30 No. 45-03, Bogotá, Colombia. E-mail: arquevedop@unal.edu.co
First published on 23rd January 2024
Abstract
4-hydroxybenzylamine's intermolecular interactions and their possible influence on the course of 4-hydroxybenzylamine's reaction with formaldehyde are analysed in this article. Computational calculations established that 4-hydroxybenzylamine forms dimers in solution by O–H⋯N hydrogen bonds; such dimers are stabilised by π-stacking interactions. These cyclic dimers' formation led to obtaining a 12-atom azacyclophane through 4-hydroxybenzylamine's reaction with formaldehyde.
Introduction
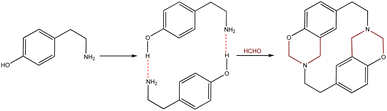
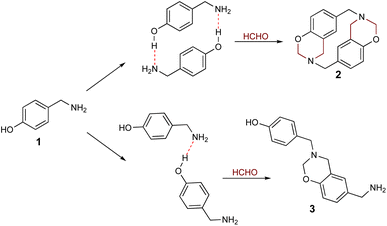
Cyclophanes are macrocyclic compounds containing two or more aromatic rings which are bound to their meta or para positions by short spacers.1 Such compounds are of interest due to their ability to retain ions or molecules within their cavity through non-covalent interactions.2–6 Azacyclophanes are cyclophanes which contain nitrogen atoms in their spacers. These compounds combine cyclophane characteristics with nitrogen's acid–base properties; such combination makes them good candidates for host-guest interaction-related studies.2–7 Their molecular topology, cavity size and solubility depend on the spacer length and the functional groups in the aromatic rings or spacers.4,8–1014-Atom azacyclophane synthesis via 4-hydroxyphenylethylamine reaction with formaldehyde has been reported in the pertinent literature; these azacyclophanes' structure is formed by two 3,4-dihydro-2H-1,3-benzoxazine units joined by ethylene bridges.11,12 It has been proposed that macrocyclisation depends on template formation (cyclic dimers) by hydrogen bonds (O–H⋯N) between phenolic hydroxyls and amino groups having two 4-hydroxyphenylethylamine molecules; this strategy has been called hydrogen bond-assisted macrocyclic synthesis (Scheme 1). Macrocyclisation does not occur when template formation is not promoted by electronic or steric factors; only linear oligomer mixtures are obtained.13–16
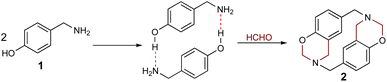
The hydrogen bond-assisted macrocyclic synthesis strategy has only been used for obtaining 14-atom azacyclophanes to date. This article thus describes analysing hydrogen bond-derived template formation using computational calculations; the 4-hydroxybenzylamine (4-(aminomethyl)phenol) 1 and formaldehyde condensation product was isolated and characterised using various solvents for establishing whether 12-atom azacyclophanes could be obtained by 4-hydroxybenzylamine 1 reaction with formaldehyde.
Experimental
General
Commercially available solvents and reagents were used (Alfa Aesar, Panreac). Thin layer chromatography (TLC) was used for monitoring the reactions on silica gel-coated glass plates (Merck Kieselgel 60) until completion; the TLC plates were visualised by staining with iodine vapor. A Mel-Temp digital melting point electrothermal 9100 apparatus was used for determining the melting points, using open capillaries; the reported results have not been corrected. NMR spectra were recorded on a Bruker Avance. Chemical shifts (δ) were reported in parts per million (ppm, from the residual solvent peak). A Chromolith RP-18e column (Merck, Kenilworth, NJ, 50 mm) was used for UPLC analysis, using an Agilent 1200 Liquid Chromatograph (Agilent, Omaha, NE). The products were analysed on a Bruker Impact II LC Q-TOF MS equipped with electrospray ionisation (ESI) in positive mode.Computational details
Computational calculations were carried out using the Gaussian 16 software package,17–20 employing the non-local hybrid functional B3LYP with an empirical Grimme D3BJ dispersion term and the Pople's 6-31+G(d,p) basis set within the density functional theory (DFT) framework.19–21 Interaction energies were corrected on the basis set superposition error (BSSE) to ensure accuracy by applying the counterpoise method.22 This combination of functional and basis set has been proven to provide a proper geometrical and energy description including long-range dispersion contributions.23Furthermore, the implicit and universal SMD solvation model was employed through single-point energy calculations to account for solvent effects on the geometries initially optimized in the gas phase.24
4-Hydroxybenzylamine 1 reaction with formaldehyde
Formaldehyde (37%, 5 mL) was added to a 4-hydroxybenzylamine 1 solution (500 mg, 4 mmol) in 10 mL solvent (ethanol, dioxane, DMF and acetonitrile). The mixture was kept without stirring at room temperature for 24 h; distilled water (15 mL) was then added, and product was extracted with dichloromethane (3 × 5 mL). The organic phase was washed with water (3 × 5 mL), dried with anhydrous sodium sulphate and concentrated. The resulting product was characterised by melting point, ultra-performance liquid chromatography-mass spectrometry (UPLC-MS) and nuclear magnetic resonance (NMR) spectroscopy (1H and 13C). The NMR spectra were obtained from the unpurified reaction products after removing the dichloromethane; the pure products were insoluble. In this article, the spectra of the product obtained from dioxane are analysed. The mass spectrum analysed corresponds to the pure product obtained from dioxane. The yields and melting points reported are those obtained from the pure products.Azacyclophane 2
(13,14,33,34-tetrahydro-12H,32H–1,3(3,6)-bis(1,3-benzoxazine)cyclobutaphane):27 C18H18N2O2. Yellow Solid, m.p. 190–192 °C. 1H-NMR (CDCl3), δ/ppm: 7.27–6.67 (aromatic protons), 4.89–4.75 (benzoxazinic methylenes), 4.01–3.66 (benzylic methylenes). 13C-NMR (CDCl3), δ/ppm: 153.6, 130.5, 130.2, 128.6, 128.4, 120.0, 116.4, 81.9, 55.1, 49.8. ESI-MS (m/z): 271.4143 [M + H-24]+ (Calc. 271.4146), 136.0756 [M + 2H-12]2+ (Calc. 136.0762). Yield: in ethanol: 52% (m.p. 190–192 °C), in dioxane: 55% (m.p. 190–192 °C), in DMF: 61% (m.p. 190–192 °C), in acetonitrile: 59% (m.p. 190–192 °C).Results and discussion
Computational analysis
The formation of azacyclophane 2 from 4-hydroxybenzylamine 1 requires the pre-organisation of molecules into cyclic arrangements that facilitate macrocyclisation. This pre-organisation is achieved through the creation of a template, which is formed by establishing hydrogen bonds between two molecules, as illustrated in Scheme 2. The examined arrangements fall into two categories: linear and cyclic. These arrangements give rise to two distinct types of hydrogen bonds. The first type involves the hydroxyl group as the proton donor and the amino group as the acceptor (O–H⋯N), while the second type reverses these roles, with the amino group acting as the proton donor and the hydroxyl group as the acceptor (N–H⋯O), as depicted in Fig. 1.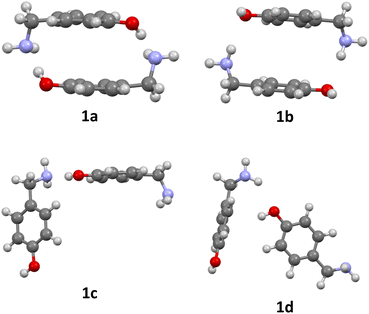 | ||
| Fig. 1 Optimized dimers without dispersion terms of 1: O–H⋯N cyclic dimer (1a), N–H⋯O cyclic dimer (1b), O–H⋯N linear dimer (1c), N–H⋯O linear dimer (1d). | ||
To predict template formation, we calculated the enthalpy (ΔHgpdim) and the free energy of dimerization (ΔGgpdim) in gas phase. These parameters were determined through the following equations:
| ΔHgpdim = Hgpdimer − 2Hgp4−HOBA1 | (1) |
| ΔGgpdim = Ggpdimer − 2Ggp4−HOBA1 | (2) |
| ΔEgpdim = Egpdimer − 2Egp4−HOBA1 | (3) |
We incorporated a single point correction for dispersion interactions (GD3BJ) for the considered arrangements to account for long-range interactions.21 These interactions are relevant in the case of cyclic dimers, where aromatic rings face each other, thereby engaging in π-stacking interactions.
According to the energy changes presented in Table 1, it can be noticed that the dimerization of 1 is only exergonic when dispersive interactions are considered. This indicates that dimerization occurs by hydrogen bonding and is further stabilized by π-stacking. The linear and cyclic arrangements were optimised using dispersion terms to observe their influence on the geometry. The optimised structures are shown in Fig. 2.
| Struct. | B3LYP | ||
|---|---|---|---|
| ΔEgpdim (kcal mol−1) | ΔHgpdim (kcal mol−1) | ΔGgpdim (kcal mol−1) | |
| 1a | −18.6 | −6.5 | 7.1 |
| 1b | −6.6 | 0.5 | 10.3 |
| 1c | −11.9 | −6.8 | 2.2 |
| 1d | −7.1 | −1.6 | 6.2 |
| Struct. | SP B3LYP-D3BJ | ||
|---|---|---|---|
| ΔEgpdim (kcal mol−1) | ΔHgpdim (kcal mol−1) | ΔGgpdim (kcal mol−1) | |
| 1a | −18.6 | −17.0 | −3.8 |
| 1b | −6.6 | −5.3 | 3.9 |
| 1c | −11.9 | −10.1 | −0.1 |
| 1d | −7.1 | −5.7 | 3.1 |
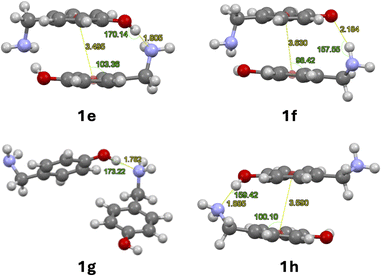 | ||
| Fig. 2 Optimised dimers with dispersion terms of 1: O–H⋯N cyclic dimer (1e), N–H⋯O cyclic dimer (1f), O–H⋯N linear dimer (1g), O–H⋯N linear dimer with stacking (1h). | ||
No significant changes in geometry were observed for structures 1e–g compared to structures 1a–c. The linear arrangement with N–H⋯O hydrogen bond 1d prefers to form a linear dimer with O–H⋯N hydrogen bond, stabilised by π stacking between its aromatic rings 1h. Only the dimerization of 1e and 1g are exergonic according to Table 2.
| Struct. | B3LYP-D3BJ | ||
|---|---|---|---|
| ΔEgpdim (kcal mol−1) | ΔHgpdim (kcal mol−1) | ΔGgpdim (kcal mol−1) | |
| 1e | −19.8 | −18.0 | −3.5 |
| 1f | −8.9 | −7.3 | 4.8 |
| 1g | −12.3 | −10.5 | −0.4 |
| 1h | −11.3 | −9.6 | 2.0 |
The dispersion contribution, π-stacking energies and geometrical parameters for H-bond and π-stacking are detailed in Table 3. Centroid-plane angles were calculated between the plane of the aromatic ring and the centroid of the second aromatic ring using the software Mercury (Fig. 2).25 The dispersion contribution of cyclic dimers was calculated using the following equations:23
| ΔED = ΔEgp,B3LYP-Ddim − ΔEgp,B3LYPdim | (4) |
| ΔHD = ΔHgp,B3LYP-Ddim − ΔHgp,B3LYPdim | (5) |
| ΔGD = ΔGgp,B3LYP-Ddim − ΔGgp,B3LYPdim | (6) |
| ΔEπ-stacking = Egp,Dbenzene dimer − 2Egp,Dbenzene | (7) |
| Struct | ΔED (kcal mol−1) | ΔHD (kcal mol−1) | ΔGD (kcal mol−1) | H-Bond | π−Stacking | |||
|---|---|---|---|---|---|---|---|---|
| H-bond length O–H⋯N (Å) | H-bond angle O–H⋯N (°) | ΔEπ-stacking (kcal mol−1) | Centroid–centroid distance (Å) | Centroid-plane angle (°) | ||||
| 1e | −1.2 | −11.5 | −10.5 | 1.80 | 170.1 | 0.3 | 3.50 | 103.4 |
| 1f | −2.2 | −7.8 | −5.5 | 2.18 | 157.5 | −1.3 | 3.63 | 98.4 |
| 1g | −0.4 | −3.7 | −2.6 | 1.78 | 173.2 | — | — | — |
| 1h | −4.3 | −8.0 | −4.2 | 1.88 | 159.4 | −0.8 | 3.60 | 100.1 |
Shorter H-bonds destabilize π-stacking due to steric repulsion, this effect is compensated by the increase in centroid-plane angles. The cyclic dimer 1e is the most stable due to thermic effects and not due to geometric effects as shown in Table 3.
The significant enthalpic contribution from dispersive interactions, as shown in Table 3, decreases the substantial stabilization that 1g experiences in contrast to 1e due to π stacking between its aromatic rings and formation of two H-bonds. This fact makes the formation of 1e more favoured thermodynamically.
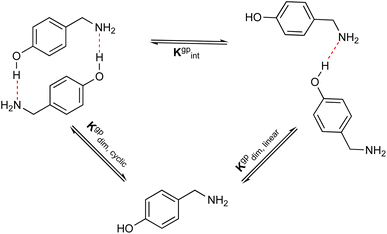
In addition, to examine the relative populations of these two dimers, we have formulated the interconversion constant (Kgpint). This constant is derived from the interplay between the dimerization constants of each process, as outlined in Scheme 3.
According to Scheme 3, the interconversion constant Kgpint was computed at 298.15 K as follows:
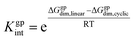 | (8) |
This equation establishes a connection between the equilibrium concentrations of cyclic and linear dimers. For the dimers under consideration, Kgpint was determined to be 1.81 × 102. This value strongly indicates a preference for cyclic dimers over linear ones. Hence, for 1, the formation of cyclic arrangements featuring O–H⋯N hydrogen bonds, and further stabilized by π-stacking interactions between aromatic rings, is highly favoured.
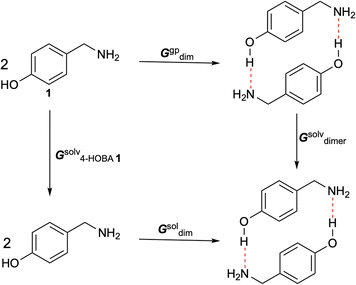
Given the requirement of ethanol as a solvent for hydrogen bond-assisted macrocyclic synthesis, we explored various solvents to optimize the experimental conditions for the reaction of 1 (4-HOBA) with formaldehyde. To assess the thermodynamic feasibility in each solvent, we calculated ΔGsoldim using a thermodynamic cycle, as illustrated in Scheme 4.
The free energy changes in solution were calculated as follows:
| ΔGsoldim = ΔGgpdim − 2ΔGsolv4-HOBA1 + ΔGsolvdimer + ΔGgp→sol | (9) |
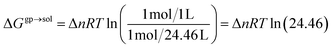 | (10) |
The free energy changes in solution using different solvents are presented in Table 4. In this table the interconversion constants are also presented, to gain insight into the effect of each solvent in the preferences of linear or cyclic arrangements.
| Solvent | Dimeric structure | ΔGsoldim (kcal mol−1) | Ksolint |
|---|---|---|---|
| Water | Cyclic | −2.0 | 2.4 |
| Linear | −1.5 | ||
| DMF | Cyclic | −4.1 | 19.0 |
| Linear | −2.4 | ||
| ACN | Cyclic | −2.9 | 6.0 |
| Linear | −1.8 | ||
| MeOH | Cyclic | −1.8 | 4.2 |
| Linear | −1.0 | ||
| EtOH | Cyclic | −1.7 | 3.4 |
| Linear | −0.1 | ||
| 2-Propanol | Cyclic | −1.7 | 3.4 |
| Linear | −0.1 | ||
| Pyridine | Cyclic | −3.7 | 13.5 |
| Linear | −2.2 | ||
| DCM | Cyclic | −2.2 | 3.5 |
| Linear | −1.4 | ||
| Chloroform | Cyclic | −2.2 | 4.2 |
| Linear | −1.3 | ||
| Toluene | Cyclic | −3.9 | 24.0 |
| Linear | −2.0 | ||
| Dioxane | Cyclic | −5.0 | 88.0 |
| Linear | −2.4 |
Notably, polar aprotic solvents such as dioxane, pyridine, and DMF emerge as strong proponents of cyclic dimer formation due to their limited interference with proton donor atoms. Toluene, a nonpolar solvent devoid of hydrogen bond interactions with the 1 molecule, also favours dimer formation.
In the context of hydrogen bond-assisted macrocyclic synthesis, an essential factor to consider is the solvent's compatibility with a 37% formaldehyde solution, as it affects solvents available for the reaction. While ethanol and acetonitrile exhibit relatively lower Ksolint values compared to other solvents, their ease of removal and low toxicity render them suitable choices for the reaction. Consequently, the solvents employed in the reaction included ethanol, DMF, acetonitrile, and dioxane.
4-Hydroxybenzylamine 1 reaction with formaldehyde
As stated above, it has been proposed that azacyclophane formation by hydrogen bond-assisted macrocyclic synthesis strategy depends on hydrogen bond template formation. Computational calculations have shown that 4-hydroxybenzylamine 1 in solution forms such templates; its reaction with formaldehyde will produce azacyclophane 2, but only a mixture of linear oligomers 3 will be obtained if it forms linear arrangements (Scheme 5).4-hydroxybenzylamine 1 reaction with formaldehyde was carried out using solvents selected by computational calculations. A solid 2 having a high melting point and low solubility was obtained with the four solvents used. Its 1H-NMR spectra had broad signals, thereby hindering the determination of its multiplicity or integrals (Fig. 3); such pattern has been characteristic of previously synthesised 14-atom azacyclophanes.11,12,28 It was observed in this spectrum that the substitution of the aromatic ring changed, and two new signals appeared in the aliphatic region, these signals were assigned to benzylic methylenes at 3.80 ppm and benzoxazinic methylenes at 4.83 ppm.
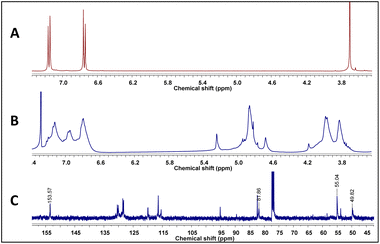 | ||
| Fig. 3 (A) 1H-NMR spectrum of 1, (B) 1H-NMR spectrum of azacyclophane 2, (C) 13C-NMR spectrum of azacyclophane 2. | ||
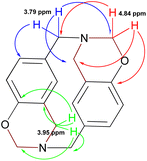
The signals expected for azacyclophane 2 appeared in 13C-NMR spectrum (Fig. 3). Regarding characteristic signals, a signal was observed at 153.5 ppm indicating an aromatic carbon bound to –O–CH2–. Two signals should be observed in this region for linear product 3, one for aromatic carbon bound to hydroxyl and another for aromatic carbon bound to –O–CH2–. Three signals were observed in the aliphatic region; one at 81.9 ppm assigned to benzoxazinic methylenes and another two at 55.1 and 49.8 ppm assigned to benzylic methylenes (four signals should be observed for the linear product). Some low intensity signals were also observed, indicating a small percentage of linear products.
Azacyclophane 2 could not be differentiated from linear product 3 by heteronuclear multiple bond correlation (HMBC) spectrum because they both had the same correlations. Key information was obtained when correlations between benzoxazinic hydrogens (at 4.84 ppm) with the carbon at 153.5 ppm and with the carbons assigned to the benzylic methylenes were observed (Fig. 4). It was also observed that signals at 4.2, 4.6 and 5.2 ppm in 1H-NMR spectra did not correlate with any of the carbons assigned to azacyclophane 2, thereby confirming that they were caused by formaldehyde polymerisation products.
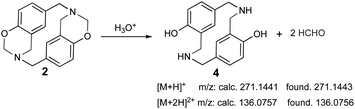
The sample was dissolved in water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) formic acid (0.1%) for UPLC-MS analysis due to poor azacyclophane 2 solubility; the product became partially dissolved in such conditions. Two peaks were observed in the chromatogram, having 0.5- and 0.7 min retention times. The first peak (0.5 min retention time) had two significant ions, the first at 271.1443 m/z [M + H]+ and the second at 136.0756 m/z [M + 2H]2+. These ions did not correspond to azacyclophane 2, they represented azacyclophane 4, which is a product of oxazine ring hydrolysis induced by adding formic acid (Scheme 6). Such hydrolysis is characteristic of the benzoxazines and occurs easily for benzoxazinic azacyclophanes.29,30
formic acid (0.1%) for UPLC-MS analysis due to poor azacyclophane 2 solubility; the product became partially dissolved in such conditions. Two peaks were observed in the chromatogram, having 0.5- and 0.7 min retention times. The first peak (0.5 min retention time) had two significant ions, the first at 271.1443 m/z [M + H]+ and the second at 136.0756 m/z [M + 2H]2+. These ions did not correspond to azacyclophane 2, they represented azacyclophane 4, which is a product of oxazine ring hydrolysis induced by adding formic acid (Scheme 6). Such hydrolysis is characteristic of the benzoxazines and occurs easily for benzoxazinic azacyclophanes.29,30
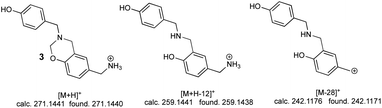
The second peak (0.7 min retention time) had three significant ions; the ion at 271.1440 m/z [M + H]+ corresponding to linear dimer 3 (calc. 271.1441), this structure was confirmed by the ion at 259.1438 m/z [M + H-12]+ (calc. 259.1441) and the ion at 242.1171 m/z [M-28]+ (calc. 242.1176) (Fig. 5).
Mass spectra analysis enabled confirming that 4-hydroxybenzylamine 1 reaction with formaldehyde produced azacyclophane 2 as the major product, along with lower percentage yield of linear dimer 3.
Conclusions
Computational calculations established that 4-hydroxybenzylamine can form dimers (templates) in gas phase and in solution by O–H⋯N hydrogen bonds; such cyclic dimers are stabilised by π-stacking. Cyclic dimer formation led to azacyclophane 2 being obtained via 4-hydroxybenzylamine 1 reaction with formaldehyde. The results demonstrated that hydrogen bond-assisted macrocyclic synthesis is a useful strategy for obtaining both 14- and 12-atom azacyclophane.Author contributions
A. G-O. investigation, computational calculations, writing and original draft preparation. J. A-T. computational calculations supervisor, writing and original draft preparation. R. Q. conceptualization, supervision, writing and reviewing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank the Universidad Nacional de Colombia for providing financial support (Research Project no. 57632).Notes and references
- H. Hopf and R. Gleiter, Modern Cyclophane Chemistry, Wiley-VCH: Federal Republic of Germany, 2004 Search PubMed.
- M. J. Van Eis, F. M. Bickelhaupt, S. Van Loon, M. Lutz, A. L. Spek, W. H. De Wolf, W. J. Van Zeist and F. Bickelhaupt, Tetrahedron, 2008, 64, 11641 CrossRef CAS.
- A. V. Borounov, N. G. Lukyanenko, V. N. Pastushok, K. E. Krakowiak, J. S. Bradshaw, N. K. Dalley and X. Kou, J. Org. Chem., 1995, 60, 4912 CrossRef.
- P. Rajakumar and A. M. A. Rasheed, Tetrahedron, 2005, 61, 5351 CrossRef CAS.
- E. García-Espaňta and S. V. Luis, Supramol. Chem., 1996, 6, 257 CrossRef.
- E. García-España, P. Díaz, J. M. Llinares and A. Bianchi, Coord. Chem. Rev., 2006, 250, 2952 CrossRef.
- M. Arunachalam, I. Ravicumar and P. Ghosh, J. Org. Chem., 2008, 73, 9144 CrossRef CAS PubMed.
- M. Sato, F. Uehara, K. Sato, M. Yamaguchi and C. Kabuto, J. Am. Chem. Soc., 1999, 121, 8270 CrossRef CAS.
- H. Stetter and E. Roos, Chem. Ber., 1955, 88, 1390 CrossRef CAS.
- G. Faust and M. Pallas, J. Prakt. Chem., 1960, 11, 146 CrossRef CAS.
- N. Nuñez-Dallos, A. Reyes and R. Quevedo, Tetrahedron Lett., 2012, 53, 530 CrossRef.
- R. Quevedo and B. Moreno-Murillo, Tetrahedron Lett., 2009, 50, 936 CrossRef CAS.
- C. Díaz-Oviedo and R. Quevedo, J. Mol. Struct., 2020, 1202, 127283 CrossRef.
- C. Díaz-Oviedo and R. Quevedo, Rev. Colomb. Quim., 2018, 47, 5 CrossRef.
- N. Nuñez-Dallos, C. Díaz-Oviedo and R. Quevedo, Tetrahedron Lett., 2014, 55, 4216 CrossRef.
- S. Chaves, M. Macías and R. Quevedo, J. Mol. Struct., 2023, 1298, 137079 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. R. Allouche, J. Comput. Chem., 2011, 32, 174 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- J. Alí-Torres, A. Rimola, C. Rodríguez-Rodríguez, L. Rodríguez-Santiago and M. Sodupe, J. Phys. Chem. B, 2013, 117, 6674 CrossRef PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS PubMed.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 32, 226–235 CrossRef PubMed.
- J. Alí-Torres, L. Rodríguez-Santiago and M. Sodupe, Phys. Chem. Chem. Phys., 2011, 13(17), 7852 RSC.
- K. Hirayama, Tetrahedron Lett., 1972, 13, 2109 CrossRef.
- R. Quevedo, J. Mol. Struct., 2020, 1207, 127777 CrossRef CAS.
- R. Quevedo, M. González and C. Díaz-Oviedo, Tetrahedron Lett., 2012, 53, 1595 CrossRef CAS.
- R. Quevedo, I. Ortiz and A. Reyes, Tetrahedron Lett., 2010, 51, 1216 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra08508b |
| This journal is © The Royal Society of Chemistry 2024 |