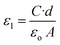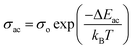Synthesis, structural, spectroscopic and electric/dielectric studies of a nanocrystalline Ni(II) complex based on [(1,3-diphenyl-1H-pyrazol-4-yl)methylene]thiocarbonohydrazide

Abstract

A Ni²⁺ nanocomplex based on a heterocyclic ligand containing a pyrazole moiety was developed in this work, and its electric conductivity and dielectric characteristics were studied. The Ni²⁺ nanocomplex with the general formula [Ni(PyT)₂(H₂O)₂]Cl₂·½H₂O, where PyT = [(1,3-diphenyl-1H-pyrazol-4-yl)methylene]thiocarbonohydrazide, was characterized using various techniques, including elemental and thermal analyses, as well as conductivity, magnetism, TEM, and spectroscopic (FT-IR, UV-Vis and XRD) studies. The results showed that PyT was bonded to the Ni(II) centers via a neutral bidentate ligand, resulting in an octahedral-shaped, thermally stable mononuclear complex. The frequency response of the dielectric properties and ac conductivity was studied in the range from 200 Hz to 6 kHz. Both dielectric constant and dielectric loss decreased with increasing frequency. In addition, the effect of temperature was investigated in the range of 294.1–363.4 K. The ac conductivity increased with increasing temperature in the range of 294.1–333.5 K. The ac conduction is described as correlated barrier hopping between non-intimate valence alternation pairs. Furthermore, the PyT and Ni(PyT) nanocomplex structures were optimized using theoretical calculations and DFT computations.

---

1 Introduction

Thiocarbohydrazide derivatives are an important class of compounds with a wide range of applications in the biochemical, pharmaceutical, and industrial domains.^1,2 The antiviral, antidiabetic, hepatoprotective, antibacterial, and antiproliferative properties of thiocarbohydrazone ligands have been studied.³ Additionally, because of their flexible coordination ability and hybrid soft-hard donor nature, thiocarbohydrazone ligands easily form metal complexes. Both organic molecules and their metal complexes display a wide range of pharmacological functions, including anticancer, antibacterial, and fungistatic actions. The majority of studies mainly report the preparation and identification of thiocarbohydrazones and their coordinated compounds.^4,5

Researchers in the field of electronic materials have been constantly examining and refining particular material features according to their usefulness. However, capacitor dielectrics have long been a focus of research among several electronic materials.⁶

Hydrazones have a variety of qualities that are of interest to scientists and useful in everyday life. Some of these properties include thermal endurance, conductivity, and chelate production. This has sped up the development of novel Schiff bases with unique characteristics and the growth of their applications.^7–9 In recent years, organic semiconductors have gained popularity in electronics and optoelectronic technologies because of their intriguing electrical and optical properties,^10,11 low cost and ease of making films. Additional energy sublevels are formed in organic molecules when transition metal ions are added. These compounds typically exhibit enhanced charge transfer from ligand to metal or metal to ligand, larger electronic transitions, and intramolecular electron delocalization, resulting in increased electrical properties. Using metal complexes to create electrical and photoelectric devices including diodes, transistors, sensors, photodetectors, and solar cells is one of the most fascinating areas of research for chemists and physicists alike. These are seen as alternatives to traditional semiconductor materials because of their possible usage with flexible substrates, ease of production via continuous printing, broad application scope, and considerable environmental and economic benefits.⁹

AC conductivity and dielectric behavior studies of materials are important to discover the charge transport mechanism and explain the origin of dielectric losses, which in turn is helpful to determine the presence of defects in these materials and gain essential knowledge about the transport processes in the localized states of the bandgap.^12–14 In addition, it is important to investigate the dielectric behavior of these materials to design passive devices for integrated circuits.^15,16 In a series of articles, several models have been proposed to explain the electronic structure, ac conduction, and dielectric behavior of materials.^14,17–23

This study reports the synthesis and characterization of a novel Ni(II) nanocomplex based on [(1,3-diphenyl-1H-pyrazol-4-yl)methylene]thiocarbonohydrazide for electronic applications. TGA–DTG, X-ray diffraction, and optical absorption of this new complex were studied. In addition, the temperature and frequency responses of its ac conductivity and dielectric parameters were investigated. Therefore, this study provides new insights into the properties and behavior of the Ni(PyT) complex, which indicate its potential application in various fields such as materials science, optical technology and the determination of complex characteristics, especially conductivity properties, and that they can be developed further for various optical applications in the future.

2 Experimental

2.1. Chemicals and methods

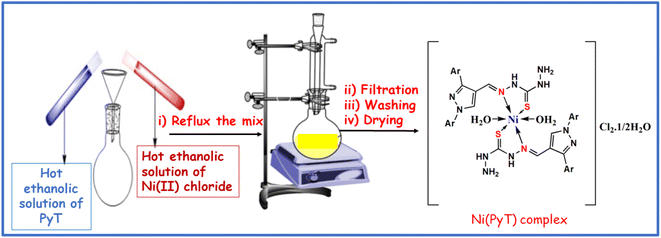
Analytical grading chemicals were used as starting material. Thiocarbohydrazide, pyrazole, and nickel chloride were purchased from BDH, Analar, or Merck chemicals. Spectroscopic grade solvents, including ethanolic solvent and dimethylformamide (DMF), were purchased commercially and used as received.

At Cairo University's Micro-analytical Central Laboratory, the percentage of H, C, N, and S elements was calculated using a Vario EL Element Analyzer. In addition, complexometric titration was used to detect the percentage of the Ni(II) metal. England's Stuart melting point instrument was employed to determine the melting and decomposition points. For molar conductance, a 10⁻³ M solution of the Ni(II) complex was dissolved in DMF using a Corning conductivity meter (NY 14831 model). Moreover, the electronic spectra of PyT and its Ni(II) complex were measured using 10⁻³ M solutions using a JASCO UV-Vis spectrophotometer (V-550). Using an FT-IR Nicolet IS10 spectrometer, FT-IR spectra (4000–400 cm⁻¹) of PyT and its Ni(II) complex were detected. The effective magnetic moment of the Ni(II) complex (μ_eff) was calculated using the relation μ_eff = 2.828 (cm T)^1/2 B.M., where cm is the molar susceptibility corrected for the diamagnetism of all atoms in the compound using Pascal's constants. In addition, a magnetic susceptibility balance from Sherwood Scientific in Cambridge Science Park (England) was used to measure the magnetic susceptibility using the Gouy method. XRD patterns of the produced compounds were captured using a PHILIPS diffractometer with CuK1 radiation (λ = 1.54056 Å, current = 30 mA and accelerating voltage = 40 kV). A transmission electron microscope (TEM, JEM-2100 (JEOL)) working at an accelerating voltage of 200 kV was used for imaging. An RCL Bridge (PM-6304 Fluke & Phillips) was used to measure the loss tangent and capacitance, which were used to determine the dielectric parameters and ac conductivity of the Ni(II) complex sample prepared in the form of a circular disc with a thickness of 0.72 mm. The sample was placed in a furnace using a special holder with two circular electrodes and a temperature controller.

2.2. Synthesis of [(1,3-diphenyl-1H-pyrazol-4-yl)methylene]thiocarbonohydrazide (PyT)

[(1,3-Diphenyl-1H-pyrazol-4-yl)methylene]thiocarbonohydrazide (PyT) was synthesized using a previously reported method.^{24 1}H NMR: 4.82 (br, 2H, NH₂), 7.03–7.88 (m, 10H, Ph–H), 8.16 (s, H, CH=N), 9.24 (s, 1H, H-5_pyrazole), 9.51 (brs, 1H, 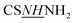), 11.34 (brs, 1H, ).

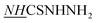2.3. Synthesis of the Ni(PyT) complex

Ethanolic solutions of nickel chloride and PyT were used in a stoichiometric reaction at a molar ratio of 1 : 2 to synthesize the Ni(PyT) complex. For 8 hours, the resulting mixture was heated through a reflux system (pH = 5.5). Then, the colored precipitate was filtered and washed multiple times with a 1 : 1 solution of ethanol and water to remove remnants of unreacted components. The precipitate was finally dried in a suction desiccator, yielding a nearly reddish-brown powder of the Ni(PyT) complex: [Ni(PyT)₂(H₂O)₂]Cl₂·½H₂O; yield: 83%; melting point >300 °C; anal. found (calcd) for C₃₄H₃₇N₁₂O_2.5S₂Cl₂Ni: M. 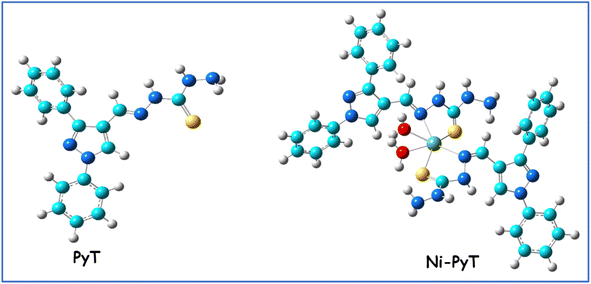wt: (847); %C: 48.41 (48.18); % H: 4.63 (4.40); % N: 20.00 (19.83); % S: 7.61 (7.56); % Ni: 7.11 (6.92); FT-IR (KBr, cm⁻¹): 3410 (νOH), 3102 (νNH₂, νNH), 3054 (νCH_arom), 1597, (νCH=N), 1540, 755 (νC=N_pyrazole), 1156 (νN–N), 1204, 828 (νNH–C=S), 506 (νM–O), 469 (νM–N). Molar conductivity (Λ_m): 107 S mol⁻¹ cm²; UV/Vis (DMF) λ_max (nm): 348, 405, 592, 883. μ_eff (B.M.): 2.7. Scheme 1 provides a representation of the chemical structure of the Ni(PyT) complex.

Scheme 1 Schematic representation of the Ni(PyT) complex.

2.4. DFT calculations

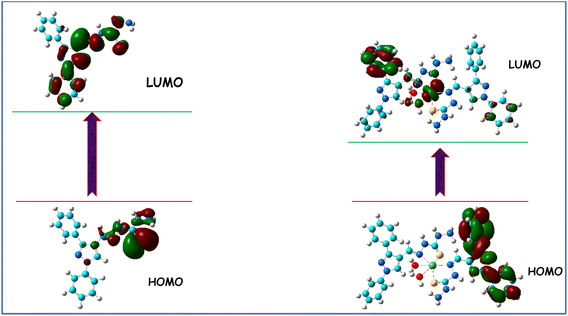
DFT calculations of the PyT structure have been reported in our previous research work.²⁵ Herein, DFT calculations of the Ni(PyT) nanocomplex were carried out using the Gaussian 09 software.²⁶ The standard base set B3LYB/6-311G(p,d) was used to optimize the geometry. Using Gauss View 5.0.9 software, the optimal structure and HOMO–LUMO of the produced compounds were determined.²⁷

3 Results and discussion

3.1. Characterization of the Ni (PyT) nanocomplex

PyT was reacted directly with Ni(II) ions at a molar ratio of 1 : 2, producing a pure reddish-brown precipitate of the Ni(PyT) complex, which has the general formula of [Ni(PyT)₂(H₂O)₂]Cl₂·½H₂O. The powder exhibited no change or decomposition at room temperature, demonstrating excellent stability in the air. However, upon heating to 300 °C, the complex underwent decomposition, which suggests high thermal stability, and as a result, a strong coordination bond between the Ni²⁺ ions and PyT. In organic solvents such as acetone, methanol and ethanol, the Ni(PyT) complex was weakly soluble. However, the Ni(PyT) complex easily dissolved in the solvents DMF and DMSO. The elemental examination supported the predicted structure of Ni(PyT) given in Scheme 1. According to the analytical results, the Ni(PyT) complex was formed when Ni²⁺ and PyT were reacted at a stoichiometric ratio of 1 : 2.

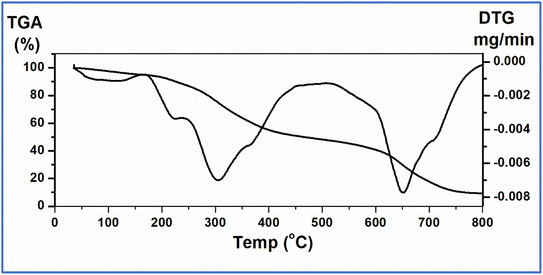
The hypothesized chemical structure of the Ni(PyT) complex is based on analytical data obtained from the thermal gravimetric analysis (TGA). As shown in Fig. 1, the Ni(PyT) complex loses two coordinated water molecules and half a lattice water molecule at 169 °C with an observed weight loss of 5.50% (calcd 5.31%). Then, two molecules of HCl are removed at a higher temperature (250 °C) with a weight loss of 14.00% (calcd 13.91%). The Ni(PyT) complex continues to degrade thereafter from 250 to 433 °C, exhibiting a weight loss of 50.50% (calcd 50.78%), which is attributed to the removal of four molecules of C₆H₆.

Fig. 1 TGA–DTG curve of the Ni(PyT) nanocomplex.

The molar conductance of a 10⁻³ M solution of the Ni(PyT) complex was found to be in a range typical of 1 : 2 electrolytes at ambient temperature, showing that two anions were present as counter ions outside the coordination sphere.^28,29

IR spectral data of PyT and the Ni(PyT) nanocomplex were compared, and some clear and observable spectral changes were found. In addition, the FT-IR data are used to support the chelation modes of PyT with the metal ion. The presence of stretching vibrations of the N–H and C=S groups in the spectrum of Ni(PyT) confirms the coordination of PyT with the metal ion in neutral form. The shift of the ν(NHC=S) of PyT (1235, 843 cm⁻¹) to lower wavenumbers (1205, 828 cm⁻¹) in the spectrum of the complex indicates that thioxo sulfur was chelated with the metal ion.³⁰ In addition, the negative shift of the ν(CH=N) signal from 1617 cm⁻¹ (PyT) to 1597 cm⁻¹ (the Ni(PyT) complex) indicates that the nitrogen of the azomethine group bonded with the metal ion.^24,30 Moreover, the 11 cm⁻¹ shift of the ν(N–N) of PyT to lower wavenumbers in the Ni(PyT) complex spectrum supports the involvement of azomethine nitrogen in coordination.³⁰ The coordination of the azomethine group is further supported by the presence of a non-ligand band at 469 cm⁻¹ assigned to ν(M–N).^31,32 The IR spectrum of the Ni(PyT) complex revealed a new band at 3410 cm⁻¹ corresponding to the ν(OH) group of lattice water.^33,34 The emergence of a band at 506 cm⁻¹ corresponding to ν(M ← O) in the FT-IR spectrum of the Ni(PyT) complex is another evidence in favour of the above hypothesis.^34,35

Therefore, according to the IR analysis, PyT functions as a neutral bidentate ligand with indents at azomethine N and thione S.

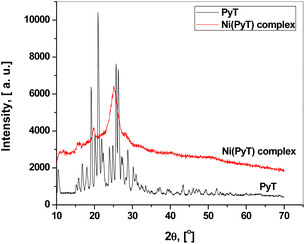
Fig. 2 represents the XRD patterns of the PyT and Ni(PyT) complex powders. PyT has a crystalline form according to the XRD patterns; however, the Ni(PyT) complex has a fine nanocrystalline nature. The crystallite size L of the Ni(PyT) complex was calculated from the main peak using the Scherer equation L = 0.9λ/(β cos θ), where θ is the diffraction angle, and β is the full width at half maximum.³⁶ The calculated crystallite size of the Ni(PyT) complex was about 4.4 nm. The chelation of the metal ion with PyT to form a new complex was confirmed by the differences in diffraction intensity and diffraction angle between PyT and its Ni(PyT) complex.³⁷

Fig. 2 XRD patterns of PyT and the Ni(PyT) complex.

The TEM image of the Ni(PyT) complex showed that the Ni(PyT) complex has a rod shape with an average diameter of 48 nm (Fig. 3).

Fig. 3 TEM image of the Ni(PyT) complex.

The selected area electron diffraction (SAED) patterns of the Ni(PyT) complex showed good diffraction rings, indicating its crystalline nature (Fig. 4).

Fig. 4 Electron diffraction pattern image of the Ni(PyT) complex.

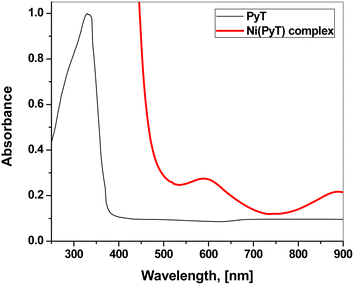
As shown in Fig. 5, the UV-Vis electronic spectra of the DMF solutions of PyT and its Ni(PyT) complex were measured. The absorption spectrum of PyT showed one absorption band at 332 nm due to the n–π* transitions within the C=S and C=N groups. The other band that appeared as a shoulder at 370 nm could be attributed to the π–π* transitions within the aromatic rings.^38,39 In the UV-Vis spectrum of Ni(PyT), the bands of the intra-ligand were shifted to a higher wavelength. This behavior implies that the metal ions coordinate with nitrogen and/or sulfur. Moreover, the absorption spectrum of Ni(PyT) exhibited bands in the visible region. One band appeared at 592 nm, and the other band appeared as a hump at 890 nm. These bands could be assigned to the ³A_2g(F) → ³T_1g(F) and ³A_2g(P) → ³T_1g(P) transitions in the octahedral Ni(II) complex.^40,41 Furthermore, the magnetic moment of the Ni(PyT) complex was measured, and its value was 2.9 B.M. This result is consistent with the octahedral geometry.⁴²

Fig. 5 Absorption spectra of PyT and the Ni(PyT) nanocomplex.

3.2. Dielectric properties

Electrical polarization reduces the electric field inside materials by a factor called complex dielectric permittivity ε*, which is given by the following formula:^43–45

ε* = ε₁ − iε₂

where ε₁ and ε₂ are the dielectric constant and dielectric loss, respectively. ε₁ was calculated from the measured capacitance C using the following equation:^45–47
where A is the effective area, d is the thickness of the sample and ε_o is the permittivity of the vacuum (ε_o = 8.85 × 10⁻¹² F m⁻¹). The response of the dielectric constant to frequency and temperature are shown in Fig. 6(a and b). Clearly, ε₁ decreased with increasing frequency. On the other hand, ε₁ increased with the temperature, reaching its maximum value at 323.5 K at all studied frequencies except for the lowest frequency (200 Hz) for which the maximum value was at 333.5 K. Then, ε₁ decreased with a further increase in temperature.

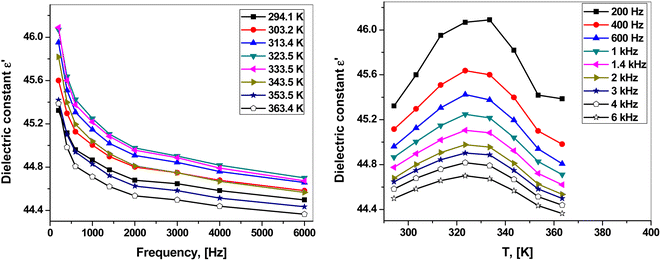Fig. 6 (a) Frequency dependence of the dielectric constant. (b) Temperature dependence of the dielectric constant.

The dielectric constant shows the ability of a material to store electric charge because it refers to the degree of polarization.^42,44 The high dielectric constant ε₁ of the polar material at low frequencies results from different polarization types (interfacial, orientation, ionic and electronic polarization).^42,48 The dielectric constant decreases with increasing frequency because the dipoles are unable to rotate rapidly. This decreases the ionic and orientation contributions.⁴⁹ On the other hand, the first increase in temperature facilitates the orientation of the dipoles, leading to an increase in the dielectric constant. The following decrease in ε₁ at the higher temperature range might result from the change in the structure of the complex and the loss of lattice water (Fig. 1).^44,48

The dielectric loss ε₂, which represents the dissipation of energy, was calculated from the measured loss tangent tan δ as follows:^45,46

ε₂ = ε₁ tan δ

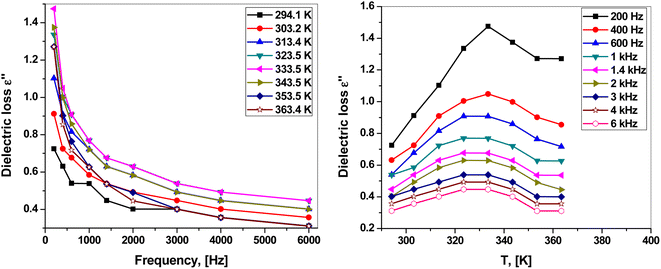
The dependence of dielectric loss ε₂ on the frequency and temperature is presented in Fig. 7(a and b). Clearly, the dielectric loss behaved similarly to the dielectric constant in response to frequency and temperature. Fig. 7(a) shows that ε₂ decreased with increasing frequency. Fig. 7(b) shows that ε₂ increased with increasing temperature, reaching a maximum at around 323.5–333.5 K, and then decreased with a further increase in temperature.

Fig. 7 (a) Frequency dependence of dielectric loss. (b) Temperature dependence of dielectric loss.

At low frequencies, ε₂ has a high value because of different factors such as ion polarization, ion jump, ion vibration, and conduction loss of charge carriers. Some of these sources are lost with increasing frequency, leading to a decrease in dielectric loss.^42,44

When a material is placed in an electric field, electrons hop from the donor to acceptor states, forming a dipole for each pair of these sites.^17,18 The relaxation time τ of each dipole depends on the activation energy attributed to a potential barrier.⁵⁰ This potential barrier results from the coulombic interaction between the neighboring sites of the dipoles.^19–21 The dielectric loss ε₂ is related to the frequency of the applied field as follows:^22,44,51,52

ε₂ = constant × (2πf)^m

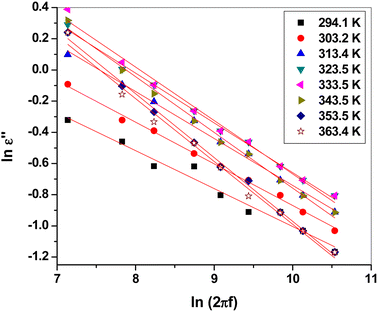
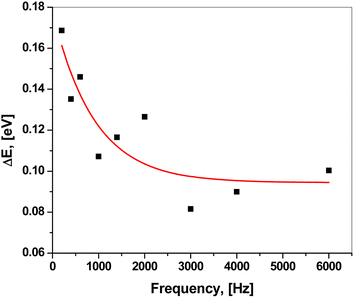
Fig. 8 shows the plot of ln ε₂ versus ln(2πf). Clearly, they could be fitted linearly at all temperatures, obeying the previous equation. The frequency exponent m was determined from the slope of the linear fittings. The barrier height W_m was calculated at each temperature using the following formula:^51,52

W_m = −4k_BT/m

where k_B is the Boltzmann's constant. Table 1 presents the values of barrier height at each temperature. Clearly, W_m decreased with increasing temperature.

Fig. 8 ln ε₂ versus ln(2πf) at different temperatures.

Table 1 Temperature dependence of the potential barrier height

T [K]	Wm [eV]
294.1	0.42
303.2	0.39
313.4	0.36
323.5	0.35
333.5	0.34
343.5	0.33
353.5	0.30
363.4	0.31

---

3.3. AC conductivity

The ac conductivity was determined from the dielectric loss as follows:^53–55

σ_ac = ωε_oε₂

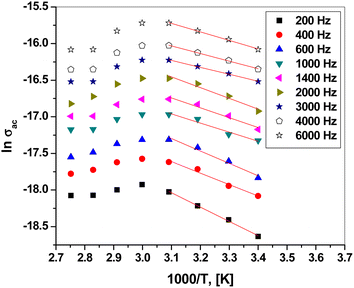
Fig. 9 presents the plot of ln σ_ac versus 1000/T at different frequencies. Clearly, σ_ac increased with increasing temperature up to 323.5 K, obeying the Arrhenius relation:^56–58

where ΔE_ac is the ac activation energy. The increase in σ_ac with increasing temperature could be due to the enhanced thermal activation of the electron drift velocity.^59,60 The values of ΔE_ac were calculated from the slopes of the linear fittings. The frequency dependence plot of ΔE_ac (Fig. 10) revealed enhanced hopping of the charge carriers between the sides of the potential barrier with increasing applied frequency.^59,61

Fig. 9 ln σ_ac versus 1000/T at different frequencies.

Fig. 10 Frequency dependence of the ac activation energy ΔE_ac.

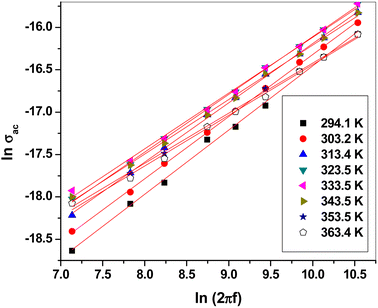
The frequency dependence of ac conductivity σ_ac could be explained by the following equation:^62–64

σ_ac = constant × (2πf)^S

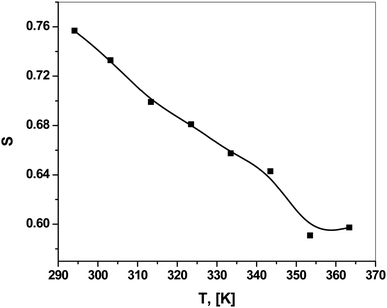
The frequency exponent S refers to the degree of interaction between the ions and their surroundings⁶⁵ and helps in identifying the conduction mechanism. ln σ_ac was plotted versus ln(2πf), as shown in Fig. 11. This relation yielded a linear curve with slope S. Fig. 12 shows the temperature dependence of the frequency exponent S. The S values were less than 1 and decreased with increasing temperature over most of the studied range. Thus, ac conduction can be explained as correlated barrier hopping (CBH) between randomly distributed close pairs of centers (5–10 Å apart).^19,20,65 This mechanism is called correlated barrier hopping between non-intimate valence alternation pairs (CBH-NVAPs) which has been explained in detail by Elliott.^{19,21,55,65,66}

Fig. 11 ln σ_ac versus ln(2πf) at different temperatures.

Fig. 12 Temperature dependence of the frequency exponent S.

3.4. DFT calculations

3.4.1. Geometry optimization. Fig. 13 shows the optimized structures of PyT and the Ni-PyT nanocomplex obtained using the Gaussian algorithm. For PyT and its nickel nanocomplex, the dipole moment values and energy factors were calculated (Table 2). The interaction of the Ni(II) ions with PyT in the Ni(PyT) nanocomplex was defined by two key parameters: the lowest unoccupied molecular orbitals (LUMOs) and the highest occupied molecular orbitals (HOMOs). Fig. 14 displays the HOMO–LOMO structure of the produced compounds. Given the higher HOMO energy of the compound, it appears to have a greater capacity to donate electrons. The larger LUMO energy indicates the increased electron-receiving capacity of the compound.⁶⁷ According to the theoretical calculations, PyT has higher electron donation power than Ni(II) in Ni(PyT) nanocomplex. Furthermore, the Ni(II) ion readily accepts electrons from PyT to create a stable Ni(PyT) nanocomplex.⁶⁷ In addition, there is a significant decrease in the energy gap from 3.797 to 1.038 eV due to the interaction of the Ni(II) ion with PyT. This correlates with the red shift in the absorption edge, as seen in Fig. 5. The energy gap of the Ni(PyT) nanocomplex illustrates its semiconducting behavior in the low-temperature range (294.1–333.5 K) as the ac conductivity increases with increasing temperature. This also illustrates the high value of the dielectric constant. Thus, the optical and dielectric properties of the Ni(PyT) nanocomplex show that it is a promising material for different applications.

Fig. 13 Optimized structure of PyT and its Ni(PyT) nanocomplex.

Table 2 Total energy (au), energy of HOMO (eV), energy of LUMO (eV), energy gap (eV), and dipole moment (Debye) of PyT and its Ni(PyT) nanocomplex

Compound	Total energy (au)	Dipole moment (Debye)	EHOMO (eV)	ELUMO (eV)	Eg (eV)
PyT	−1384	6.712	−5.582	−1.783	3.797
Ni-PyT	−4429	4.940	−3.193	−2.155	1.038

---

Fig. 14 E_g plots of PyT and its Ni(PyT) nanocomplex.

4 Conclusion

The pyrazole thiocarbohydrazide complex of Ni(II) (Ni(PyT) was successfully synthesized. Using the TGA–DTG technique, elemental analysis, molar conductivity, UV-Vis, FT-IR, and XRD spectroscopy, as well as magnetic moment measurements, the synthesized complex was identified and verified. The Ni(PyT) complex has a nanocrystalline structure with a crystallite size of about 4.4 nm. All data reveal that the octahedral geometry of the Ni(PyT) complex is formed via the coordination of the N and S donor sites of the PyT ligand with the Ni(II) metal center. Increasing the frequency of the applied field reduces the dielectric loss and dielectric constant. These values increase with increasing temperature, reaching the maximum at 323.5 K at most of the frequencies tested. Then, they decrease with increasing temperature. These properties can be explained by considering a set of dipoles and the existence of a potential barrier over which the charges must hop. This barrier decreases with increasing temperature. The results suggest that correlated barrier hopping is the mechanism of ac conduction in which hopping happens between non-intimate valence alternation pairs. The energy gap of the Ni(PyT) nanocomplex is 1.038 eV. The interaction of the Ni(II) ions with PyT leads to a redshift and decreases the energy gap from 3.797 to 1.038 eV.

Conflicts of interest

The authors declare that they do not have any conflicts of interest related to this work.

Acknowledgements

The second author extends his appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through a large group Research Project under grant number RGP-2/576/44.

References

1. P. T. Acharya, Z. A. Bhavsar, D. J. Jethava, D. B. Patel and H. D. Patel, A review on development of bio-active thiosemicarbazide derivatives: Recent advances, J. Mol. Struct., 2021, 1226, 129268.
2. F. Kurzer and M. Wilkinson, Chemistry of carbohydrazide and thiocarbohydrazide, Chem. Rev., 1970, 70, 111–149.
3. S. S. Kadam, R. P. Gotarne, M. N. Shinde, V. S. Mane, A. A. Khan and A. A. Kumbhar, Fe(III), Co(II), Ni(II), Cu(II) and Zn(II) complexes of fluorophore-anchored asymmetric thiocarbohydrazone: Synthesis, characterization and biological studies, Inorg. Chim. Acta, 2022, 536, 120887.
4. M. P. Sathisha, U. N. Shetti, V. K. Revankar and K. S. R. Pai, Synthesis and antitumor studies on novel Co(II), Ni(II) and Cu(II) metal complexes of bis(3-acetylcoumarin) thiocarbohydrazone, Eur. J. Med. Chem., 2008, 43, 2338–2346.
5. Z. H. Abd El-Wahab, M. M. Mashaly, A. A. Salman, B. A. El-Shetary and A. A. Faheim, Co(II), Ce(III) and UO2(VI) bis-salicylatothiosemicarbazide complexes: Binary and ternary complexes, thermal studies and antimicrobial activity, Spectrochim. Acta, Part A, 2004, 63, 2861.
6. Y. Lv, J. Zhang, P. Li, T. Deng, Y. Nan, Z. Lei, Y. Li and L. Li, Microstructure and dielectric properties of Na and Ni co-substituted CaCu₃Ti₄O₁₂ ceramics with high dielectric constant and low loss, Mater. Chem. Phys., 2024, 315, 128973.
7. M. E. Alkış, K. Buldurun, N. Turan, Y. Alan, Ü. K. Yılmaz and A. Mantarcı, Synthesis, characterization, antiproliferative of pyrimidine based ligand and its Ni(II) and Pd(II) complexes and effectiveness of electroporation, J. Biomol. Struct. Dyn., 2022, 40, 4073–4083.
8. K. Buldurun, Synthesis, characterization, thermal study and optical property evaluation of Co(II), Pd(II) complexes containing Schiff bases of thiophene-3-carboxylate ligand, J. Electron. Mater., 2020, 49, 1935–1943.
9. N. Turan, H. Seymen, B. Gündüz, K. Buldurun and N. Çolak, Synthesis, characterization of Schiff base and its metal complexes and investigation of their electronic and photonic properties, Opt. Mater., 2024, 148, 114802.
10. N. Turan, K. Buldurun, B. Gündüz and N. Çolak, Synthesis and structures of Fe(II), Zn(II) and Pd(II) complexes with a Schiff base derived from methyl 2-amino-6-methyl-4,5,6,7-tetrahydrothieno[2,3-c]pyridine-3-carboxylate and comparison of their optical constants for different solvents and molarities, J. Nanoelectron.Optoelectron., 2017, 12, 1028–1040.
11. F. A. Almashal, M. Q. Mohammed, Q. M. Ali Hassan, C. A. Emshary, H. A. Sultan and A. M. Dhumad, Spectroscopic and thermal nonlinearity study of a Schiff base compound, Opt. Mater., 2020, 100, 109703.
12. I. Saleem, Qashou, Dielectric relaxation properties, and AC conductivity of Erbium(III)-Tris(8-hydroxyquinolinato) nanostructured films, Phys. B, 2023, 649, 414421.
13. N. Shukla and D. K. Dwivedi, Dielectric relaxation and AC conductivity studies of Se₉₀Cd_10−xIn_x glassy alloys, J. Asian Ceram. Soc., 2016, 4, 178–184.
14. N. Chandel, M. M. A. Imran and N. Mehta, Comprehensive studies of temperature and frequency dependent dielectric and conducting parameters in third generation multi-component glasses, RSC Adv., 2018, 8, 25468.
15. H.-M. Li, C.-H. Ra, G. Zhang, W. J. Yoo and J.-D. LeeK-Wand Kim, J. Korean Phys. Soc., 2009, 54, 1096.
16. S. S. Shenouda, H. Y. Zahran and I. S. Yahia, Facile synthesis and characterization of Co3O4 nanoplates coated with small nanorods, Mater. Res. Express, 2019, 6, 105042.
17. N. F. Mott, E. A. Davis and R. A. Street, States in the gap and recombination in amorphous semiconductors, Phil. Mag., 1975, 32, 961.
18. R. A. Street and N. F. Mott, States in the Gap in Glassy Semiconductors, Phys. Rev. Lett., 1975, 35, 1293.
19. S. R. Elliot, A theory of a.c. conduction in chalcogenide glasses, Philos. Mag. B, 1977, 36, 1291.
20. S. R. Elliott, Temperature dependence of a.c. conductivity of chalcogenide glasses, Philos. Mag. B, 1978, 37, 135.
21. S. R. Elliot, AC conductivity due to intimate pairs of charged defect centres, Solid State Commun., 1978, 27, 749.
22. J. C. Giuntini, J. V. Zanchetta, D. Jullien, R. Eholie and P. Houenou, Temperature dependence of dielectric losses in chalcogenide glasses, J. Non-Cryst. Solids, 1981, 45, 57.
23. N. F. Mott, Conduction in Non-crystalline Materials, Clarendon Press, Oxford, 2nd edn, 1993.
24. S. R. A. Allah, W. S. I. A. Elmagd, K. A. A. Kandeel, M. M. Hemdan, D. S. A. Haneen and A. S. A. Youssef, Synthesis and antimicrobial activity evaluation of some novel hydrazone, pyrazolone, chromenone, 2-pyridone and 2-pyrone derivatives, J. Chem. Res., 2017, 61, 617–623.
25. R. Fouad, T. E. Ali, M. A. Assiri and S. S. Shenouda, Novel Co(II) complex containing N-phenyl-1H-pyrazole moiety: Synthesis, characterization, and dielectric/electrical studies, Inorg. Chem. Commun., 2024, 162, 112195.
26. M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin,V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian Inc., Wallingford, CT, 2009.
27. R. Dennington, T. Keith and J. Millam, GaussView, Version 5, Semichem Inc., Shawnee Mission KS, 2009.
28. W. J. Geary, The use of conductivity measurements in organic solvents for the characterisation of coordination compounds, Coord. Chem. Rev., 1971, 7, 81.
29. S. A. AbouEl-Enein, S. M. Emam, R. M. Wagdy and F. I. Abouzayed, Spectral and thermal investigation of novel biologically active (N-(1dimethyl-3-oxo-2-phenyl-2,3-dihydro-1H-pyrazol-4-yl)-2-(1,5dimethyl-3-oxo-2-phenyl-2,3-dihydro-1H-pyrazol-4-yl-amino)-2oxo-cetimidic acid) ligand and its metal complexes, J. Mol. Struct., 2020, 1215, 128230.
30. T. A. Yousef, G. M. Abu El-Reash, M. Al-Jahdali and E.-B. R. El-Rakhawy, Synthesis, spectral characterization and biological evaluation of Mn(II), Co(II), Ni(II), Cu(II), Zn(II) and Cd(II) complexes with thiosemicarbazone ending by pyrazole and pyridyl rings, Spectrochim. Acta, Part A, 2014, 129, 163–172.
31. M. Shebl, Synthesis and spectroscopic studies of binuclear metal complexes of a tetradentate N₂O₂ Schiff base ligand derived from 4,6-diacetyl resorcinol and benzylamine, Spectrochim. Acta, Part A, 2008, 70, 850.
32. O. M. I. Adly and A. Taha, Coordination diversity of new mononuclear ONS hydrazone with transition metals: Synthesis, characterization, molecular modeling and antimicrobial studies, J. Mol. Struct., 2013, 1038, 250.
33. U. P. S. Prabhakar, Synthesis, structural elucidation of metal nanoparticles prepared from metal complexes via thermal decomposition method, Appl. Surf. Sci. Adv., 2023, 13, 100357.
34. M. Saif, M. M. Mashaly, M. F. Eid and R. Fouad, Synthesis and thermal studies of tetraaza macrocylic ligand and its transition metal complexes. DNA binding affinity of copper complex, Spectrochim. Acta, Part A, 2011, 79, 1849.
35. M. Saif, M. M. Mashaly, M. F. Eid and R. Fouad, Synthesis, characterization and thermal studies of binary and/or mixed ligand complexes of Cd(II), Cu(II), Ni(II) and Co(III) based on 2-(Hydroxybenzylidene) thiosemicarbazone: DNA binding affinity of binary Cu(II) complex, Spectrochim. Acta, Part A, 2012, 92, 347.
36. B. D. Cullity, Elements of X-Ray Diffraction, Addison-Wesley Publishing Co., Reading MA, 2nd edn, 1978.
37. R. Fouad and O. M. I. Adly, Novel Cu(II), Zn(II) Nanocomplexes Drug Based on Hydrazone Ligand Bearings Chromone & Triazine moiety: Structural, Spectral, DFT, Molecular Docking and Cytotoxic Studies, J. Mol. Struct., 2021, 1225, 129158.
38. R. Fouad and A. A. M. Ali, Novel electrospun fibers as carriers for delivering a biocompatible Sm(III) nanodrug for cancer therapy: fabrication, characterization, cytotoxicity and toxicity, RSC Adv., 2023, 13, 1883–1891.
39. B. I. Ceylan, Y. Kurt, O. Bolukbasi, A. Yilmaz, K. Kaya and B. Ülküseven, Synthesis, spectroscopic characterization and quantum chemical studies of a dioxomolybdenum(VI) complex with an N,Ssubstituted pyridoxal thiosemicarbazone, Polyhedron, 2020, 193, 114884.
40. M. Saif, H. F. El-Shafiy, M. M. Mashaly, M. F. Eid, A. I. Nabeel and R. Fouad, Synthesis, characterization, and antioxidant/cytotoxic activity of new chromone Schiff base nanocomplexes of Zn(II), Cu(II), Ni(II) and Co(II), J. Mol. Struct., 2016, 1118, 75–82.
41. A. Cotton and G. Wilkinson, Advanced Inorganic Chemistry, A Comprehensive Text, John Wiley & Sons, New York, 4th edn, 1986.
42. R. Fouad, I. A. Shaaban, T. E. Ali, M. A. Assiri and S. S. Shenouda, Co(II), Ni(II), Cu(II) and Cd(II)-thiocarbonohydrazone complexes: spectroscopic, DFT, thermal, and electrical conductivity studies, RSC Adv., 2021, 11, 37726–37743.
43. A. Singh, H. P. Gogoi and P. Barman, Synthesis of metal oxide nanoparticles by facile thermal decomposition of new Co(II), Ni(II), and Zn(II) Schiff base complexes- optical properties and photocatalytic degradation of methylene blue dye, Inorg. Chim. Acta, 2023, 546, 121292.
44. N. A. El-Ghamaz, A. Z. El-Sonbati, M. A. Diab, A. A. El-Bindary, G. G. Mohamed and Sh. M. Morgan, Correlation between ionic radii of metal azodye complexes and electrical Conductivity, Spectrochim. Acta, Part A, 2015, 147, 200–211.
45. A. Nitika and A. Rana, Study of anneal-tuned dielectric properties, AC conductivity, complex impedance, and modulus of cobalt ferrite nanoparticles, Mater. Today: Proc., 2021, 45, 5444–5448.
46. H. Y. Zahran, S. S. Shneouda, I. S. Yahia and F. El-Tantawy, Facile and rapid synthesis of nanoplates Mg(OH)₂ and MgO via Microwave technique from metal source: structural, optical and dielectric properties, J. Sol-Gel Sci. Technol., 2018, 86, 104–111.
47. P. Priyadarshini, S. Senapati, S. Bisoyi, S. Samal and R. Naik, J. Alloys Compd., 2023, 945, 169222.
48. B. Tareev, Physics of Dielectric Material, Mir Publishers, Moscow, 1975.
49. A. H. Ahmed and M. G. Moustafa, Spectroscopic, morphology and electrical conductivity studies on Co(II), Ni(II), Cu(II) and Mn(II)-oxaloyldihydrazone complexes, J. Saudi Chem. Soc., 2020, 24, 381–392.
50. M. Pollak and G. E. Pike, ac conductivity of glasses, Phys. Rev. Lett., 1972, 28, 1449.
51. P. N. Musfir, S. Mathew, V. P. N. Nampoori and S. Thomas, Investigations on frequency and temperature dependence of AC conductivity and dielectric parameters in Ge₂₀Ga₅Sb₁₀S₆₅ quaternary chalcogenide glass, Optik, 2019, 182, 1244–1251.
52. A. E. Bekheet, Ac conductivity and dielectric properties of Ga₂S₃–Ga₂Se₃ films, Phys. B, 2008, 403, 4342–4346.
53. A. Ullah, I. U. Khan, M. Aljohani, K. Althubeiti, N. Rahman, M. Sohail, S. S. Abdullaev, A. Khan and R. Khan, Effect of yttrium on the structural, dielectric, and magnetic properties of Co-doped ZnO magnetic nanorods for potential spintronic applications, J. Mater. Sci.: Mater. Electron., 2023, 34, 1252.
54. A. El-ghandour, N. A. El-Ghamaza, M. M. El-Nahass and H. M. Zeyada, Temperature and frequency dependence outline of DC electrical conductivity, dielectric constants, and AC electrical conductivity in nanostructured TlInS₂ thin films, Phys. E, 2019, 105, 13–18.
55. S. R. Elliott, A.C. conduction in amorphous chalcogenide and pnictide semiconductors, Adv. Phys., 1987, 36, 135–217.
56. A. M. Shakra, M. Fadel and S. S. Shenouda, Response of electrical and dielectric parameters of ZnIn₂Te₄ thin films to temperature and frequency, Phys. B, 2020, 586, 412082.
57. R. R. Sahoo and R. N. P. Choudhary, Investigation of structural, dielectric, impedance and leakage current behaviour of green phase of yttrium barium copper oxide:Y₂BaCuO₅, Phys. B, 2022, 640, 414027.
58. N. A. Hegab, M. A. Afifi, H. E. Atyia and A. S. Farid, ac conductivity and dielectric properties of amorphous Se80Te20−xGex chalcogenide glass film compositions, J. Alloys Compd., 2009, 477, 925.
59. S. I. Qashou, Dielectric relaxation properties, and AC conductivity of Erbium(III)-Tris(8-hydroxyquinolinato) nanostructured films, Phys. B, 2023, 649, 414421.
60. M. M. El-Nahass, A. A. Atta, E. F. M. El-Zaidia, A. A. M. Farag and A. H. Ammar, Electrical, conductivity and dielectric measurements of CoMTPP, Mater. Chem. Phys., 2014, 143, 490–494.
61. M. M. El-Nahass, E. F. M. El-Zaidia, A. A. A. Darwish and G. F. Salem, Dielectric relaxation, behavior and AC electrical conductivity study of 2-(1,2-Dihydro-7- Methyl- Oxoquinoline, 5-yl) Malononitrile (DMOQMN), J. Electron. Mater., 2017, 46, 1093–1099.
62. E. A. Davis and N. F. Mott, Conduction in non-crystalline systems V. Conductivity, optical absorption and photoconductivity in amorphous semiconductors, Phil. Mag., 1970, 22, 903–922.
63. O. Amorri, H. Slimi, A. Oueslati, A. Aydi and K. Khirouni, Investigation of the structural, optical, electrical and dielectric proprieties of LiCd_0.5Fe₂O₄ spinel ferrite, Phys. B, 2022, 639, 414005.
64. M. Shoab, Z. Aslam, J. Ali and M. Zulfequar, Investigation of electrical conductivity (AC/DC) and dielectric properties of Se₈₀Te_152xCd₅Bi_x (x = 0, 5, 10) quaternary chalcogenide glass, J. Mater. Sci.: Mater. Electron., 2023, 34, 681.
65. A. Anjali, B. S. Patial, S. Bhardwaj, A. M. Awasthi and N. Thakur, On the AC-conductivity mechanism in nano-crystalline Se_79−xTe₁₅In₆Pb_x (x = 0, 1, 2, 4, 6, 8 and 10) alloys, Phys. B, 2017, 523, 52–61.
66. I. G. Austin and N. F. Mott, Polarons in crystalline and noncrystalline materials, Adv. Phys., 1969, 18, 41.
67. K. M. Ibrahim, R. R. Zaky, H. M. Abou-ElBader and S. M. Abo-Zeid, J. Mol. Struct., 2014, 1075, 71.

---