 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Alchemical approach performance in calculating the ligand-binding free energy†
Son Tung Ngo *ab,
Quynh Mai Thai
*ab,
Quynh Mai Thai ab,
Trung Hai Nguyenab,
Nguyen Ngoc Tuanc,
T. Ngoc Han Phamd,
Huong T. T. Phung
ab,
Trung Hai Nguyenab,
Nguyen Ngoc Tuanc,
T. Ngoc Han Phamd,
Huong T. T. Phung d and
Duong Tuan Quang*e
d and
Duong Tuan Quang*e
aLaboratory of Biophysics, Institute for Advanced Study in Technology, Ton Duc Thang University, Ho Chi Minh City, Vietnam. E-mail: ngosontung@tdtu.edu.vn
bFaculty of Pharmacy, Ton Duc Thang University, Ho Chi Minh City, Vietnam
cFaculty of Applied Sciences, Ton Duc Thang University, Ho Chi Minh City, Vietnam
dNTT Hi-Tech Institute, Nguyen Tat Thanh University, Ho Chi Minh City, Vietnam
eDepartment of Chemistry, Hue University, Hue City, Thua Thien Hue Province, Vietnam. E-mail: dtquang@hueui.edu.vn
First published on 8th May 2024
Abstract
Alchemical binding free energy calculations are one of the most accurate methods for estimating ligand-binding affinity. Assessing the accuracy of the approach over protein targets is one of the most interesting issues. The free energy difference of binding between a protein and a ligand was calculated via the alchemical approach. The alchemical approach exhibits satisfactory accuracy over four targets, including AmpC beta-lactamase (AmpC); glutamate receptor, ionotropic kainate 1 (GluK1); heat shock protein 90 (Hsp90); and severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) main protease (Mpro). In particular, the correlation coefficients between calculated binding free energies and the respective experiments over four targets range from 0.56 to 0.86. The affinity computed via free energy perturbation (FEP) simulations is overestimated over the experimental value. Particularly, the electrostatic interaction free energy rules the binding process of ligands to AmpC and GluK1. However, the van der Waals (vdW) interaction free energy plays an important role in the ligand-binding processes of HSP90 and SARS-CoV-2 Mpro. The obtained results associate with the hydrophilic or hydrophobic properties of the ligands. This observation may enhance computer-aided drug design.
Introduction
Binding processes between biomolecules are crucial in physical chemistry and related fields.1 Fundamental problems are associated with chemical reactions, including the interaction of a gene with another gene,2 of a gene with a protein,3 of a protein with another protein,4 and of a compound with a protein,5 etc. Among these, noncovalent binding free energy, ΔGbind, can be computed via molecular dynamics (MD) simulations.6 The metric is related to the inhibition constant, ki, via the formula ΔGbind = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ki), where T is the absolute temperature and R is the gas constant.
ln(ki), where T is the absolute temperature and R is the gas constant.
In computer-aided drug design (CADD), accurately estimating the value of ΔGbind is a crucial task owing to its association with the protein–ligand binding mechanism.6–10 Moreover, the performance of the estimation of ligand-binding affinity relates to the reduction of therapeutic cost.11,12 Therefore, scientists have developed several computational methods to characterize ligand-binding free energies using physics as well as knowledge-based methods.13–29 Generally, the more accurate and precise the approach, the more the cost of computing resources.30–33 Among these, the free energy perturbation method,34 which is also known as the alchemical approach, is recognized to be one of the most accurate methods for determining ligand-binding affinity till date.1,35 However, the computational approach forms the correlation coefficient, which varies in a large range.36,37 Additionally, assessing the performance of a computational approach across different targets is interesting.28,29,38–40 More details, performance of AutoDock Vina over 800 experimental complexes were benchmarked.39 The SQM/COSMO filter scoring over various protein targets including acetylcholine esterase, TNF-α converting enzyme, aldose reductase, HIV-1 protease, and carbonic anhydrase II was tested.28,29 In these works, the SQM/COSMO filter scoring dominated over various approaches.
Recently, several studies were attempted to enhance the performance of alchemical calculations.40–43 However, overall, all of these schemes require massive costs of computing resources compared with the traditional ones. The combined approaches are less popular than the original FEP method. FEP calculations estimates absolute binding free energy between two biomolecules via two states without reference to a third state.44–46 FEP simulations are also performed to simply calculate the relative binding free energy between two biomolecules upon two states relative to a third state, which is typically the ground state.47–49 In addition, the performance of a computational approach strongly depend on applied targets,28,29,50 FEP performance over considered proteins is required to access.
Herein, the performance of the alchemical approach on 4 protein targets including AmpC beta-lactamase (AmpC), glutamate receptor, ionotropic kainate 1 (GluK1), heat shock protein 90 (Hsp90), and SARS-CoV-2 Mpro was assessed. The targets included AmpC involving 1XGI,51 1XGJ,51 2HDU,52 2PU2,53 2R9W,53 2R9X,53 3GR2,54 4KZ3,55 4KZ5,55 and 4OKP;56 GluK1 involving 1VSO,57 2PBW,57 2ZNS,58 2ZNU,58 3FV1,58 3FV2,58 3FVG,58 3FVK,58 4E0X,59 and 4DLD;60 Hsp90 involving 2QG0,61 2QG2,61 3K97,62 3NMQ,63 3QDD,64 3 R4M,65 4CWF,66 4CWT,66 4NH8,67 and 4O07;68 and SARS-CoV-2 Mpro involving 6M2N,69 6WTT,70 6XBG,71 6XMK,72 7B3E,73 7L8I,74 7LDL,75 7NG3,76 7CBT,77 and 8A4T.78 Alchemical calculations yielded an appropriate result for the three targets including AmpC, GluK1, and Hsp90. Moreover, applying FEP on SARS-CoV-2 Mpro requires additional calibrate.
Material and methods
Protein–ligand complexes
The three-dimensional structure of 40 complexes (cf. Fig. 1 and Table S1 of the ESI†), whose identifies are expressed below, was obtained from the Protein Data Bank. Among these, proteins were parameterized via the Amber99SB-ILDN force field.79 The ligands were topologized by the general Amber force field.80 In particular, the charge of the ligands was achieved via the restrained electrostatic potential scheme81 using the quantum calculation at the B3LYP/6-31G(d,p) level of theory. Notably, the ligand protonation state was estimated via the chemicalize webserver.82 During simulations, the complex and individual ligand were inserted into a solvated box, which water molecule was parameterized via the TIP3P water model.83 Besides, the covalent binding between SARS-CoV-2 Mpro and ligand was not modelled in traditional MD simulations.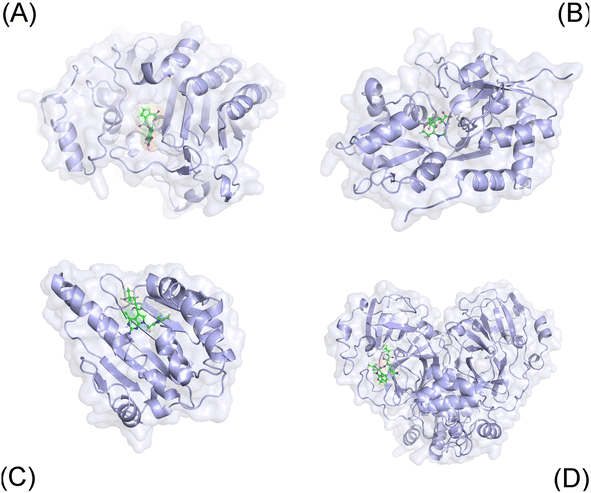 | ||
| Fig. 1 Initial conformation of considered systems including AmpC (A), GluK1 (B), Hsp90 (C), and SARS-CoV-2 Mpro (D). | ||
Alchemical calculations
The perturbation simulations were performed to change the system from state A (bound) to B (unbound).34 In particular, a coupling parameter λ is typically used to conduct the task, and the process is known as perturbation simulations. The free energy change, ΔG, from different states was obtained via several perturbation simulations. Several values of λ, which include two sets of λelec and λvdW changing electrostatic and vdW interactions, respectively, ranging from 0 to 1 can be used to turn the Hamiltonian of the system from state A to B. Thus, ΔG can be computed via formula as follows
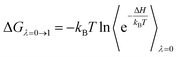 | (1) |
The binding free energy between two biomolecules, ΔGFEP, can thus be calculated as follows
| ΔGFEP = ΔG3 − ΔG1 | (2) |
Molecular dynamics simulations
GROMACS version 2019.6 with the general-purpose graphics processing unit acceleration was performed to simulate the complex and isolated ligand in solution systems.85 During the simulation, the periodic boundary condition was used on both systems. The MD simulation parameters were chosen referring to the previous work. In particular, the time step was selected as 0.002 ps during the Langevin dynamics simulations. The nonbond pair with a cut-off of 0.9 nm was refreshed every 10 steps of each integration. The particle-mesh Ewald method86 was used to present the electrostatic interaction at a cut-off of 0.9 nm. A cut-off scheme with a radius of 0.9 nm was utilized to treat the van der Waals (vdW) interaction.The protein–ligand system in the solution was energy minimized using the steepest descent method. The simulations, which used NVT and NPT ensembles at 310 K with a length of 100 ps each simulation, were subsequently performed to relax the system. The Cα protein atoms were positionally fixed during NVT simulations using a harmonic potential. The solvated protein–ligand complex and free ligand in solution were simulated over 50 and 5 ns of MD simulations, respectively. The final conformations of both systems were used as the initial shape of perturbation simulations. The simulations were repeated two times.
The systemic Hamiltonian was modified over perturbation simulations under constant pressure conditions according to previous works.87 Among these, the electrostatic interaction between an inhibitor and surrounding atoms was changed through eight values of λelec, including 0.00, 0.10, 0.20, 0.35, 0.50, 0.65, 0.80, and 1.00. The vdW interaction was modified via nine values of λvdW concerning 0.00, 0.10, 0.25, 0.35, 0.50, 0.65, 0.75, 0.90, and 1.00. The coupling parameters were chosen referring to the previous work.8,87 Each perturbation simulation had a length of 3.0 ns. The free energy changes, which include ΔG3 and ΔG1, were thus computed via the BAR method.84 The binding free energy of an inhibitor to a receptor was determined according to eqn (2).
Analysis tools
Because ligand protonation states are crucial in the protein–ligand binding process,88 chemicalize webserver, a ChemAxon tool, was employed to predict ligand protonation states. The correlation coefficient error and the root-mean-square error (RMSE) were estimated using 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rounds of the bootstrapping method.89 Sidechain (SC) contact between a ligand and an individual residue of a receptor was counted when the pair between nonhydrogen atoms of two groups is <4.5 Å. The hydrogen bond (HB) contact between a ligand and an individual residue of a receptor was measured when the angle donor–hydrogen–acceptor is >135° and the spacing between donors and acceptors is <3.5 Å. All-atom root-mean-square deviation (RMSD) of the complex and ligand systems was estimated via the GROMACS tools “gmx rms”. The experimental binding free energy, ΔGEXP, was calculated according to the formula
000 rounds of the bootstrapping method.89 Sidechain (SC) contact between a ligand and an individual residue of a receptor was counted when the pair between nonhydrogen atoms of two groups is <4.5 Å. The hydrogen bond (HB) contact between a ligand and an individual residue of a receptor was measured when the angle donor–hydrogen–acceptor is >135° and the spacing between donors and acceptors is <3.5 Å. All-atom root-mean-square deviation (RMSD) of the complex and ligand systems was estimated via the GROMACS tools “gmx rms”. The experimental binding free energy, ΔGEXP, was calculated according to the formula
ΔGEXP = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ki) ln(ki)
| (3) |
ΔGEXP = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(IC50), ln(IC50),
| (4) |
Results and discussion
Assessing the performance of a computational approach is of useful as it may guide the following researchers who will consider the investigated targets.90–94 In particular, the benchmarking of the ability of a method depending on the targets probably has a large influence on the effectiveness and timeliness of the study.95–97 Further, although the alchemical approach is known as one of the most accurate protocols for determining the ligand-binding affinity, the obtained correlation coefficient varies in a large range.36,37 Herein, the accuracy of the alchemical calculation was thus evaluated over six targets included AmpC, GluK1, Hsp90, and SARS-CoV-2 Mpro.Initially, conventional MD simulations were performed to turn the solvated system to stable states. Because the complexed structure was achieved from the experiments, the system rapidly reached equilibrium states (cf. Tables S2–S5 of the ESI†). In particular, the all-atom RMSD of the complex and ligand systems arrives at the stable regions after ca. 25.0 and 2.5 ns of MD simulations, respectively. Two replicas of each system were generated to reduce the error in the computation.
SC and HB contacts between protein–ligand complexes were analyzed over an interval of 25–50 ns of MD simulations, which corresponds to the equilibrium region. Results provide physical insights into the binding process of a ligand to a receptor. The results are shown in Fig. S2–S5 of the ESI.† By counting the residues formed more than rigid SC and HB contacts to inhibitors, the most influential factors controlling the inhibitor binding was clarified. The outcomes are described below.
The final shape of the systems was engaged as an input for free energy calculation via perturbation simulations. As mentioned above, the ligand-binding free energy to the receptor via the FEP approach, ΔGFEP, was calculated using the BAR method.84 Results indicated that FEP simulation is good in characterizing the ligand-binding free energy for the AmpC system. It is a good approach in estimating the ligand-binding affinity of three targets involving GluK1 and Hsp90. FEP calculations yield satisfactory results in the case of SARS-CoV-2. Further, the obtained correlation coefficients are described below. On average, the computed values, 〈ΔGFEP〉 = −14.62 ± 1.66 kcal mol−1, are overestimation compared with the respective experiments, 〈ΔGEXP〉 = −8.40 ± 0.34 kcal mol−1. Notably, 〈ΔGFEP〉 and 〈ΔGEXP〉 are the mean of calculated and experimental binding free energies over all of the considered systems. The overestimation of perturbation simulations is consistent with previous works.33,98,99 The uncorrected simulations of the interaction between ligands and surrounding molecules probably causes the different energy.100,101 Furthermore, the contributions of electrostatic, 〈ΔGcou〉, and vdW, 〈ΔGvdW〉, term to the binding free energy are −7.57 ± 1.85 and −7.06 ± 0.86 kcal mol−1, respectively. In addition, a good correlation coefficient between ΔGFEP and ΔGcou, R = 0.88 ± 0.02, was found, confirming that electrostatic interaction plays an important role in the binding process of the considered systems.
AmpC beta-lactamase
The enzyme clinically associates with the antibiotic resistance of Enterobacteriaceae and other organisms.102 Non-beta-lactam inhibitors of the AmpC have garnered considerable research interest.51 Several inhibitors for the AmpC have been developed.51–53,55,56 Using MD simulations, we gained physical insights into the binding process of these inhibitors to AmpC. Analyzing the equilibrium MD trajectories (cf. Table S2 of the ESI†) of these complexes, it was observed that residues Ser64, Lys67, Tyr150, Asn152, Lys164, Arg204, Ser212, Asn289, Ala318, Asn343, Asn346, and Arg349 are important factors affecting the ligand-binding affinity because they rigidly adopt SC and HB contacts to inhibitors (cf. Fig. 2 and S2 of the ESI†). The outcomes are in good agreement with the previous work,103 especially the activity of Lys67 and Tyr150, which are known as the catalytic residues, and Ser64, which is associated with the enzyme acyl adduct, would be thus inhibited. Therefore, probable mutations at these points could considerably alter the ligand-binding free energy to the AmpC.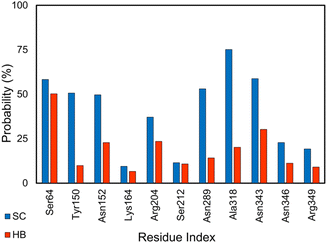 | ||
| Fig. 2 SC and HB contacts between essential residues of AmpC and inhibitors. The values were computed over an interval of 25–50 ns of MD simulations. | ||
The final snapshots of MD simulations were used as the starting shape of perturbation simulations. The work of the ligand decoupling process from the AmpC complexes in solution corresponds to the free energy change ΔG3 (cf. Fig. S1 of the ESI†). Further, the behavior of the ligand in the solution was mimicked. The ΔG1 value (cf. Fig. S1 of the ESI†) was thus calculated by estimating the work of the ligand decoupling process from the solvated ligand system. MD simulations involving the modified Hamiltonian were performed to obtain the work. The values of ΔG3 and ΔG1 were computed using the BAR method84 over an interval of 1–3 ns of the alter-λ simulations with every 100 ps. The obtained results are shown in Table 1. The calculated values of ΔGFEP fall in the range from −0.90 ± 0.13 to −28.43 ± 0.48 kcal mol−1. The metric forms a good agreement with the respective experiments with an of RAmpC = 0.86 ± 0.08 (cf. Fig. 3). It may be argued that FEP is a good approach to be able to rank the ligand-binding affinity for the AmpC target. Moreover, the means of electrostatic and vdW free energy difference of binding are −9.19 ± 3.44 and −2.95 ± 0.44 kcal mol−1, respectively. The outcome suggests that the AmpC inhibitors mostly are hydrophilic compounds. It is consistent with XLogP3 values, whose mean is 1.30 ± 0.51 (cf. Table 1). Furthermore, the average of computed metrics, 〈ΔGFEP〉 = −12.13 ± 3.45 kcal mol−1, is considerably smaller than that obtained via experiments, .e.g., 〈ΔGEXP〉 = −5.15 ± 0.59 kcal mol−1. This means that the computed affinities are overestimated by a large value. The outcomes thus result in the large value of RMSE, which is of 11.67 ± 2.65 kcal mol−1. Although the large value of RMSE was obtained, the approach can be appropriately use for ranking the inhibitory of a ligand.
| No. | PDB ID | XLogP3a | ΔGcou | ΔGvdW | ΔGFEP | ΔGEXPb |
|---|---|---|---|---|---|---|
| a The values were obtained from the PubChem database.104b The experimental binding free energies were computed based on the inhibition constant ki. The computed error was obtained using the bootstrapping method. The unit is kcal mol−1. | ||||||
| 1 | 1XGI51 | 1.8 | −6.11 | −2.97 | −9.08 ± 0.77 | −6.66 (ref. 51) |
| 2 | 1XGJ51 | 1.2 | −23.84 | −3.67 | −27.51 ± 1.23 | −8.24 (ref. 51) |
| 3 | 2HDU52 | 1.2 | −0.19 | −2.82 | −3.01 ± 0.12 | −3.16 (ref. 52) |
| 4 | 2PU2 (ref. 53) | 1.7 | −25.69 | −2.73 | −28.43 ± 0.48 | −6.08 (ref. 53) |
| 5 | 2R9W53 | 3.3 | −17.55 | −0.89 | −18.44 ± 0.87 | −7.00 (ref. 53) |
| 6 | 2R9X53 | 3.2 | −20.63 | −4.40 | −25.03 ± 0.66 | −6.66 (ref. 53) |
| 7 | 3GR2 (ref. 54) | 0.5 | 0.50 | −1.41 | −0.91 ± 2.60 | −3.46 (ref. 54) |
| 8 | 4KZ3 (ref. 55) | 1.0 | −2.53 | −2.98 | −5.51 ± 0.73 | −3.80 (ref. 55) |
| 9 | 4KZ5 (ref. 55) | 1.9 | −0.39 | −2.12 | −2.51 ± 0.48 | −2.75 (ref. 55) |
| 10 | 4OKP (ref. 56) | −2.8 | 4.58 | −5.48 | −0.90 ± 0.13 | −3.70 (ref. 56) |
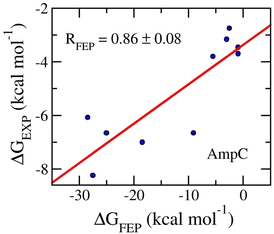 | ||
| Fig. 3 Correlation coefficients between calculated and experimental binding fee energy of AmpC systems. The computed value was obtained via FEP simulations. | ||
Glutamate receptor, ionotropic kainate 1
The GluK1 is a synaptic receptor that forms L-glutamate-gated ion channels and can play essential roles in excitatory neurotransmission of the nervous system.57–60 The GluK1 inhibition may deliver a defense against hyperexcitation.57–60 The ligand-binding domain (LBD) is a clamshell-shaped protein that makes a flexible conformation. LBD connects to the transmembrane domain of the GluK1 via a short linker.105 Ten LBD of the GluK1 + inhibitor systems were relaxed over MD simulations. The binding mechanism of the protein and its ligand is thus illuminated throughout analyzing the free energy difference of binding and SC/HB contacts. The all-atom RMSD of both complexes and ligands in solution systems are described in Table S2 of the ESI.† The residues involving Lys473, Tyr474, Pro501, Thr503, Arg508, Ser674, Thr675, Glu723, Ser726, and Lys747 were found to be able to rigidly adopt SC and HB contacts with GluK1 (cf. Fig. 4 and S3 of the ESI†). Notably, 10 complexes were obtained from Homo sapiens and Rattus norvegicus; however, their sequence is almost identical (cf. the ESI†).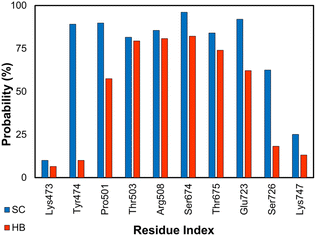 | ||
| Fig. 4 SC and HB contacts between essential residues of GluK1 and inhibitors. The values were computed over an interval of 25–50 ns of MD simulations of all complexes. | ||
Ten ligands were then annihilated from both complexes and ligands in solution systems via perturbation simulations. The BAR method84 was used to assess the free energy change during ligand annihilation. The binding free energy was obtained and is described in Table 2. The obtained results show that ΔGFEP varies in the range from −49.54 ± 4.39 to −3.04 ± 0.32 kcal mol−1. Moreover, the calculated binding free energies procedure a correlation coefficient with the respective experiments by an of RGluK1 = 0.76 ± 0.13 (Fig. 5). The computed errors are RMSEGluK1 = 14.56 ± 4.25 kcal mol−1. Similar to the AmpC systems, the FEP approach is an appropriate protocol to rank the ligand-binding affinity, but the absolute values overestimate the experimental data. The overestimation may be caused by the inaccuracy interaction simulation of the force field as mentioned above.100,101 Furthermore, the means of electrostatic, 〈ΔGcou〉, and vdW, 〈ΔGvdW〉, free energy difference of binding are −16.23 ± 4.08 and −2.54 ± 0.48 kcal mol−1, respectively. The dominance of ΔGcou over ΔGvdW is in good agreement with the circumstance that GluK1 inhibitors are highly hydrophilic substances, 〈XLogP3〉 = −3.29 ± 0.55.
| No. | PDB ID | XLogP3a | ΔGcou | ΔGvdW | ΔGFEP | ΔGEXPb |
|---|---|---|---|---|---|---|
| a The values were obtained from the PubChem database.104b The experimental binding free energies were computed based on the inhibition constant ki. The computed error was obtained using the bootstrapping method. The unit is kcal mol−1. | ||||||
| 1 | 1VSO57 | −2.7 | −3.57 | −3.15 | −6.72 ± 0.95 | −6.48 (ref. 57) |
| 2 | 2PBW57 | −1.3 | −18.56 | −1.74 | −20.3 ± 3.23 | −11.33 (ref. 57) |
| 3 | 2ZNS58 | −3.7 | −15.68 | −0.76 | −16.44 ± 2.74 | −8.97 (ref. 58) |
| 4 | 2ZNU58 | −5.1 | −20.03 | −3.47 | −23.50 ± 0.02 | −11.14 (ref. 58) |
| 5 | 3FV1 (ref. 58) | −7.1 | −45.54 | −4.00 | −49.54 ± 4.39 | −12.77 (ref. 58) |
| 6 | 3FVN58 | −2.8 | −23.25 | −1.51 | −24.76 ± 2.36 | −9.30 (ref. 58) |
| 7 | 3FVG58 | −3.1 | −14.56 | −3.77 | −18.33 ± 0.23 | −9.46 (ref. 58) |
| 8 | 3FVK58 | −4.1 | −12.78 | −4.01 | −16.79 ± 0.74 | −12.11 (ref. 58) |
| 9 | 4E0X59 | −1.8 | −3.05 | −3.51 | −6.56 ± 2.58 | −9.77 (ref. 59) |
| 10 | 4DLD60 | −1.2 | −0.20 | −3.81 | −4.01 ± 0.38 | −7.99 (ref. 60) |
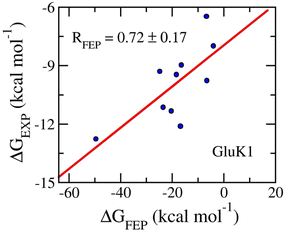 | ||
| Fig. 5 Correlation coefficients between calculated and experimental binding free energy of GluK1 systems. The computed value was obtained via FEP simulations. | ||
Heat shock protein 90
Hsp90 is a highly conserved molecular chaperone protein found in all eukaryotic cells.106 Hsp90 acts as a chaperone for a large number of client proteins, participating in various cellular processes, such as signal transduction, cell cycle regulation, DNA repair, and apoptosis. It is crucial for the folding, maturation, and degradation of proteins. In addition to its normal functions, Hsp90 has been implicated in several disease processes, including cancer, neurodegenerative diseases, and infectious diseases, making it an attractive target for therapeutic intervention.107,108 Over the stable snapshots produced by MD simulations, essential residues considerably contribute to the ligand-binding affinity that can be estimated via contact analyses. Among these, the residues Asn51, Asp93, Gly135, Phe138, Tyr139, and Thr184 form SC and HB contacts to inhibitors more than 50% and 5% of considered snapshots (cf. Fig. 6), respectively. This is in good agreement with previous studies.62,109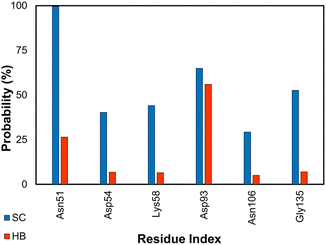 | ||
| Fig. 6 SC and HB contacts between essential residues of GluK1 and inhibitors. The values were computed over an interval of 25–50 ns of MD simulations. | ||
The ligand-binding free energy between Hsp90 and ligands was determined via FEP simulations34 and is shown in Table 3. The calculated binding free energy, ΔGFEP, which adopts in the range from −36.20 ± 1.09 to −5.62 ± 0.16 kcal mol−1, forms a good correlation to the corresponding experiments, RHsp90 = 0.76 ± 0.15 (Fig. 7). The computed error is of RMSEHsp90 = 8.52 ± 3.08 kcal mol−1. The obtained binding affinity overemphasizes the respective experiments, but the approach can be used for ranking ligand-binding affinity. The observation is consistent with previous mention. Moreover, the vdW interaction free energy, 〈ΔGvdW〉 = −13.21 ± 1.57 kcal mol−1, dominates over the electronic ones, 〈ΔGcou〉 = 0.35 ± 2.65 kcal mol−1. The dominant of ΔGvdW is in good agreement with the fact that Hsp90 inhibitors are hydrophobic compounds, 〈XLogP3〉 = 2.56 ± 0.33. It may be argued that the binding mechanism of ligands to Hsp90 is considerably different from those of the AmpC and GluK1 systems.
| No. | PDB ID | XLogP3a | ΔGcou | ΔGvdW | ΔGFEP | ΔGEXPb |
|---|---|---|---|---|---|---|
| a The values were obtained from the PubChem database.104b The experimental binding free energies were computed based on the inhibition constant ki. The computed error was obtained using the bootstrapping method. The unit is kcal mol−1. | ||||||
| 1 | 2QG0 (ref. 61) | 0.8 | −1.80 | −9.97 | −11.78 ± 1.24 | −7.85 (ref. 61) |
| 2 | 2QG2 (ref. 61) | 1.6 | 6.58 | −12.20 | −5.62 ± 0.16 | −7.41 (ref. 61) |
| 3 | 3K97 (ref. 62) | 4.2 | 1.58 | −3.30 | −3.3 ± −1.72 | −10.98 (ref. 62) |
| 4 | 3NMQ63 | 3.1 | −18.04 | −15.95 | −15.95 ± −33.99 | −13.31 (ref. 63) |
| 5 | 3QDD64 | 1.9 | 1.10 | −16.64 | −15.54 ± 0.36 | −12.04 (ref. 64) |
| 6 | 3 R4M65 | 2.1 | −0.57 | −5.13 | −5.70 ± 0.64 | −8.13 (ref. 65) |
| 7 | 4CWF66 | 3.0 | 4.17 | −11.03 | −6.86 ± 0.77 | −6.16 (ref. 66) |
| 8 | 4CWT66 | 2.9 | 7.54 | −14.22 | −6.68 ± 0.40 | −9.26 (ref. 66) |
| 9 | 4NH8 (ref. 67) | 3.2 | −1.63 | −22.18 | −23.80 ± 0.16 | −11.70 (ref. 67) |
| 10 | 4O07 (ref. 68) | 4.1 | 10.80 | −18.85 | −8.05 ± 1.65 | −10.13 (ref. 68) |
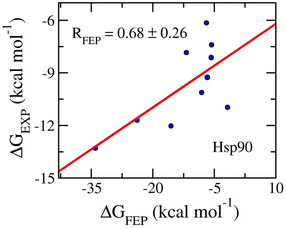 | ||
| Fig. 7 Correlation coefficients between calculated and experimental binding free energy of Hsp90 systems. The computed value was obtained via FEP simulations. | ||
SARS-CoV-2 main protease
SARS-CoV-2 Mpro is an enzyme that plays a crucial role in the replication of SARS-CoV-2, which causes COVID-19.110,111 The main protease is responsible for cleaving large viral polyproteins into functional proteins that are essential for the virus to replicate and infect host cells.112 This makes the main protease an attractive target for drug development as inhibiting its activity could potentially stop the virus from replicating.113 Analyzing the HB and SC contacts between SARS-CoV-2 Mpro and its inhibitors, the residues Thr26, Phe140, Asn142, Gly143, Ser144, Cys145, His163, His164, Met165, Glu166, Arg188, and Gln189 adopts more than 5% and 12% of HB and SC contacts over equilibrium snapshots, respectively (cf. Fig. 8). It is in good agreement with the work on the SARS-CoV-2 Mpro monomer.87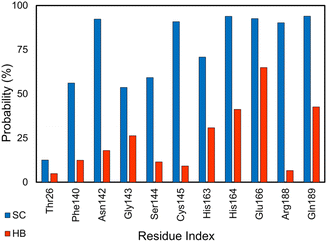 | ||
| Fig. 8 SC and HB contacts between essential residues of SARS-CoV-2 Mpro and inhibitors. The values were computed over an interval of 25–50 ns of MD simulations. | ||
Table 4 shows the FEP binding free energy compared to the respective experiment and the value of the ligand XLogP3. The obtained value of ΔGFEP falls in the range from −22.54 ± 3.52 to −5.69 ± 1.83 kcal mol−1. The calculated results form an appropriate correlation coefficient with the corresponding experiment by a value of RMpro = 0.56 ± 0.26 (Fig. 9). The inaccurate part may be caused by the fact that the conventional MD simulations do not mimic the covalent binding of ligands to the residue Cys145 of SARS-CoV-2 Mpro.114–116 Moreover, in consistency with previous works, the SARS-CoV-2 Mpro inhibitors form an average of XLogP3 = 2.19 ± 0.30. It may be argued that the inhibitors will adopt a stronger vdW interaction free energy to the protease than electrostatic ones. Indeed, the mean of vdW interaction free energy, 〈ΔGvdW〉, is −9.11 ± 0.73 kcal mol−1, which is considerably larger than the mean of electrostatic interaction free energy, 〈ΔGcou〉, is of −4.89 ± 1.72 kcal mol−1. This is in good agreement with the previous study.117
| No. | PDB ID | XLogP3a | ΔGcou | ΔGvdW | ΔGFEP | ΔGEXPc |
|---|---|---|---|---|---|---|
| a The values were obtained from the PubChem database.104b The value was calculated via the XLogP3 server.120c The experimental binding free energies were computed based on the inhibition constant IC50.d The non-covalent binding ligands.e The covalent binding ligands. The computed error was obtained using the bootstrapping method. The unit is kcal mol−1. | ||||||
| 1 | 6M2N69d | 1.7 | −4.36 | −7.61 | −11.97 ± 0.17 | −8.27 (ref. 69) |
| 2 | 6WTT70e | 1.7b | −5.20 | −8.21 | −13.41 ± 1.76 | −9.23 (ref. 111) |
| 3 | 6XBG71e | 1.6b | −10.08 | −12.46 | −22.54 ± 3.52 | −10.08 (ref. 71) |
| 4 | 6XMK72e | 2.3b | −8.16 | −6.18 | −14.34 ± 0.38 | −8.71 (ref. 72) |
| 5 | 7B3E73e | 1.2 | −11.32 | −4.71 | −16.03 ± 2.07 | −9.14 (ref. 118) |
| 6 | 7L8I74d | 3.2 | 2.47 | −10.32 | −7.85 ± 3.23 | −5.72 (ref. 119) |
| 7 | 7LDL75e | 1.9 | −11.02 | −10.03 | −21.05 ± 3.08 | −9.91 (ref. 75) |
| 8 | 7NG3 (ref. 76)e | 4.6 | −3.63 | −9.58 | −13.21 ± 1.96 | −7.42 (ref. 70) |
| 9 | 7LCR75e | 1.7b | −3.68 | −10.18 | −13.86 ± 0.34 | −9.43 (ref. 72) |
| 10 | 8 A4T78e | 2.0 | 6.09 | −11.78 | −5.69 ± 1.83 | −9.50 (ref. 78) |
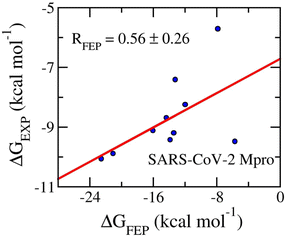 | ||
| Fig. 9 Correlation coefficients between calculated and experimental binding free energy of SARS-CoV-2 Mpro systems. The computed value was obtained via FEP simulations. | ||
Overall, the calculated results are overestimation. The overestimation of perturbation simulations is discussed above as it is probably caused by the uncorrected interaction between ligands and surrounding molecules.100,101 Moreover, the net charge of complex and free inhibitor in solution are not equal to zero, the effects can be large and lead to increase RMSE. A correlation is thus required to be used to fix the overestimation due to the change of systemic net charge.121 Furthermore, four complexes including 1XGJ, 3FV1, 3K97, and 6M2N were randomly selected for FEP calculations (cf. Tables S6 and S7 and Fig. S6 of the ESI†) without consideration of the protonation states of ligands, which may be a hypothesis that it is equivalent to use coupled ions to neutralize the ligand charge. In this case, the average of binding free energy is of −12.02 ± 3.21 kcal mol−1 in comparison with −24.36 ± 1.62 kcal mol−1 of considering protonated ligands. It should be noted that the mean of ΔGEXP is of −10.06 ± 0.96 kcal mol−1. The RMSE of systems with neutralized ligands, RMSE = 5.05 ± 2.47 kcal mol−1, is significantly smaller than the system with protonated ligands, RMSE = 20.88 ± 7.41 kcal mol−1. The calculated value of ΔGFEP, when neutralized ligands were considered, formed a correlation coefficient R = 0.94 compared with the respective experiments. The correlation coefficient, when protonated ligands were investigated, only is of R = 0.56. Absolutely, when neutralized ligands were considered, the correlation coefficient was significantly increased and the RMSE value was rigidly decreased. Further investigation to be able to clarify the issues would be carried out in the future.
Conclusion
Herein, we have demonstrated that FEP calculation is a good approach to characterize the binding free energy of ligands to AmpC, GluK1, Hsp90, and SARS-CoV-2 Mpro.The computed affinity via FEP simulations overestimates the corresponding experimental values. In particular, the electrostatic interaction free energy rules the ligand-binding to AmpC and GluK1. However, the van der Waals (vdW) interaction free energy plays an important role in the ligand-binding processes of HSP90 and SARS-CoV-2 Mpro. The outcomes associate with the hydrophilic or hydrophobic properties of the ligands. Moreover, the important residues controlling the binding process of ligands to four receptors were clarified via SC and HB analyses. The possible mutation at these points may alter the ligand-binding free energy, causing drug resistance. Furthermore, the accuracy of the FEP approach based on conventional MD simulations may be reduced when covalent binding ligands are considered. In addition, the net charge of complex and free inhibitor in solution are not equal to zero, the effects can be large and lead to increase RMSE. A correlation is thus required to be used to fix the overestimation due to the change of systemic net charge.121 A benchmark without consideration of the protonation states of ligands, which may be a hypothesis that it is equivalent to use coupled ions to neutralize the ligand charge, would be performed in the future as well as compared with the other methods such as MM-PBSA or LIE approaches.
Conflicts of interest
There are no conficts to declare.Acknowledgements
This work was supported by Vietnam National Foundation for Science & Technology Development (NAFOSTED) grant #02/2020/ĐX (to DTQ).References
- U. Ryde and P. Soderhjelm, Chem. Rev., 2016, 116, 5520–5566 CrossRef CAS PubMed.
- H. Kang, J. Yoo, B.-K. Sohn, S.-W. Lee, H. S. Lee, W. Ma, J.-M. Kee, A. Aksimentiev and H. Kim, Nucleic Acids Res., 2018, 46, 9401–9413 CrossRef CAS PubMed.
- F. Cozzolino, I. Iacobucci, V. Monaco and M. Monti, J. Proteome Res., 2021, 20, 3018–3030 CrossRef CAS PubMed.
- S. T. Ngo, Comput. Biol. Chem., 2022, 97, 107636 CrossRef CAS PubMed.
- T. H. Nguyen, P.-T. Tran, N. Q. A. Pham, V.-H. Hoang, D. M. Hiep and S. T. Ngo, ACS Omega, 2022, 7, 20673–20682 CrossRef CAS PubMed.
- N. M. Tam, T. H. Nguyen, M. Q. Pham, N. D. Hong, N. T. Tung, V. V. Vu, D. T. Quang and S. T. Ngo, J. Mol. Graphics Modell., 2023, 124, 108535 CrossRef CAS PubMed.
- G. R. Marshall, Annu. Rev. Pharmacol. Toxicol., 1987, 27, 193–213 CrossRef CAS PubMed.
- T. H. Nguyen, N. M. Tam, M. V. Tuan, P. Zhan, V. V. Vu, D. T. Quang and S. T. Ngo, Chem. Phys., 2023, 564, 111709 CrossRef CAS PubMed.
- Y. Sixto-Lopez, M. Bello and J. Correa-Basurto, J. Biomol. Struct. Dyn., 2019, 37, 584–610 CrossRef CAS PubMed.
- P. Sledz and A. Caflisch, Curr. Opin. Struct. Biol., 2018, 48, 93–102 CrossRef CAS PubMed.
- N. Homeyer, F. Stoll, A. Hillisch and H. Gohlke, J. Chem. Theory Comput., 2014, 10, 3331–3344 CrossRef CAS PubMed.
- G. Sliwoski, S. Kothiwale, J. Meiler and E. W. Lowe, Pharmacol. Rev., 2014, 66, 334–395 CrossRef PubMed.
- W. Yu and A. D. MacKerell, in Antibiotics: Methods and Protocols, ed. P. Sass, Springer New York, New York, NY, 2017, pp. 85–106 Search PubMed.
- S. T. Ngo, J. Comput. Chem., 2021, 42, 117–123 CrossRef CAS PubMed.
- G. Subramanian, B. Ramsundar, V. Pande and R. A. Denny, J. Chem. Inf. Model., 2016, 56, 1936–1949 CrossRef CAS PubMed.
- S. Park and K. Schulten, J. Chem. Phys., 2004, 120, 5946–5961 CrossRef CAS PubMed.
- J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300–313 CrossRef CAS.
- G. Leonis, T. Steinbrecher and M. G. Papadopoulos, J. Chem. Inf. Model., 2013, 53, 2141–2153 CrossRef CAS PubMed.
- C. Jarzynski, Phys. Rev. Lett., 1997, 78, 2690–2693 CrossRef CAS.
- C. Jarzynski, Phys. Rev. E, 1997, 56, 5018–5035 CrossRef CAS.
- F. M. Ytreberg, J. Chem. Phys., 2009, 130, 164906 CrossRef PubMed.
- J. D. Holliday, S. S. Ranade and P. Willett, Quant. Struct.-Act. Relat., 1995, 14, 501–506 CrossRef CAS.
- G. M. Morris, R. Huey, W. Lindstrom, M. F. Sanner, R. K. Belew, D. S. Goodsell and A. J. Olson, J. Comput. Chem., 2009, 30, 2785–2791 CrossRef CAS PubMed.
- S. Forli, R. Huey, M. E. Pique, M. F. Sanner, D. S. Goodsell and A. J. Olson, Nat. Protoc., 2016, 11, 905 CrossRef CAS PubMed.
- E. Vrontaki, G. Melagraki, T. Mavromoustakos and A. Afantitis, J. Enzyme Inhib. Med. Chem., 2016, 31, 38–52 CrossRef CAS PubMed.
- T. H. Nguyen, H.-X. Zhou and D. D. L. Minh, J. Comput. Chem., 2018, 39, 621–636 CrossRef CAS PubMed.
- Y. Meng and B. Roux, J. Chem. Theory Comput., 2015, 11, 3523–3529 CrossRef CAS PubMed.
- A. Pecina, R. Meier, J. Fanfrlík, M. Lepšík, J. Řezáč, P. Hobza and C. Baldauf, Chem. Commun., 2016, 52, 3312–3315 RSC.
- A. Pecina, J. Brynda, L. Vrzal, R. Gnanasekaran, M. Hořejší, S. M. Eyrilmez, J. Řezáč, M. Lepšík, P. Řezáčová, P. Hobza, P. Majer, V. Veverka and J. Fanfrlík, ChemPhysChem, 2018, 19, 873–879 CrossRef CAS PubMed.
- D. L. Mobley and M. K. Gilson, Annu. Rev. Biophys., 2017, 46, 531–558 CrossRef CAS PubMed.
- A. Ganesan, M. L. Coote and K. Barakat, Drug Discovery Today, 2017, 22, 249–269 CrossRef CAS PubMed.
- V. Gapsys, L. Perez-Benito, M. Aldeghi, D. Seeliger, H. Van Vlijmen, G. Tresadern and B. L. de Groot, Chem. Sci., 2020, 11, 1140–1152 RSC.
- S. T. Ngo, T. H. Nguyen, N. T. Tung, V. V. Vu, M. Q. Pham and B. K. Mai, Phys. Chem. Chem. Phys., 2022, 24, 29266–29278 RSC.
- R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420–1426 CrossRef CAS.
- É. C. M. Nascimento, M. Oliva, K. Świderek, J. B. L. Martins and J. Andrés, J. Chem. Inf. Model., 2017, 57, 958–976 CrossRef PubMed.
- S. T. Ngo, N. Hung Minh, H. Le Thi Thuy, Q. Pham Minh, T. Vi Khanh, T. Nguyen Thanh and V. Van, RSC Adv., 2020, 10, 40284–40290 RSC.
- Z. Li, X. Li, Y.-Y. Huang, Y. Wu, R. Liu, L. Zhou, Y. Lin, D. Wu, L. Zhang, H. Liu, X. Xu, K. Yu, Y. Zhang, J. Cui, C.-G. Zhan, X. Wang and H.-B. Luo, Proc. Natl. Acad. Sci. U.S.A., 2020, 117, 27381–27387 CrossRef CAS PubMed.
- T. N. H. Pham, T. H. Nguyen, N. M. Tam, T. Y. Vu, N. T. Pham, N. T. Huy, B. K. Mai, N. T. Tung, M. Q. Pham, V. V. Vu and S. T. Ngo, J. Comput. Chem., 2021, 43, 160–169 CrossRef PubMed.
- N. T. Nguyen, T. H. Nguyen, T. N. H. Pham, N. T. Huy, M. V. Bay, M. Q. Pham, P. C. Nam, V. V. Vu and S. T. Ngo, J. Chem. Inf. Model., 2020, 60, 204–211 CrossRef CAS PubMed.
- L. Wang, Y. Wu, Y. Deng, B. Kim, L. Pierce, G. Krilov, D. Lupyan, S. Robinson, M. K. Dahlgren, J. Greenwood, D. L. Romero, C. Masse, J. L. Knight, T. Steinbrecher, T. Beuming, W. Damm, E. Harder, W. Sherman, M. Brewer, R. Wester, M. Murcko, L. Frye, R. Farid, T. Lin, D. L. Mobley, W. L. Jorgensen, B. J. Berne, R. A. Friesner and R. Abel, J. Am. Chem. Soc., 2015, 137, 2695–2703 CrossRef CAS PubMed.
- W. Jiang and B. Roux, J. Chem. Theory Comput., 2010, 6, 2559–2565 CrossRef CAS PubMed.
- Y. Meng, D. Sabri Dashti and A. E. Roitberg, J. Chem. Theory Comput., 2011, 7, 2721–2727 CrossRef CAS PubMed.
- W. Jiang, J. Thirman, S. Jo and B. Roux, J. Phys. Chem. B, 2018, 122, 9435–9442 CrossRef CAS PubMed.
- Y. Khalak, G. Tresadern, M. Aldeghi, H. M. Baumann, D. L. Mobley, B. L. de Groot and V. Gapsys, Chem. Sci., 2021, 12, 13958–13971 RSC.
- L. Liang, H. Liu, G. Xing, C. Deng, Y. Hua, R. Gu, T. Lu, Y. Chen and Y. Zhang, Phys. Chem. Chem. Phys., 2022, 24, 9904–9920 RSC.
- Z. Li, Y. Huang, Y. Wu, J. Chen, D. Wu, C.-G. Zhan and H.-B. Luo, J. Med. Chem., 2019, 62, 2099–2111 CrossRef CAS PubMed.
- S. Azimi, S. Khuttan, J. Z. Wu, R. K. Pal and E. Gallicchio, J. Chem. Inf. Model., 2022, 62, 309–323 CrossRef CAS PubMed.
- A. J. Clark, C. Negron, K. Hauser, M. Sun, L. Wang, R. Abel and R. A. Friesner, J. Mol. Biol., 2019, 431, 1481–1493 CrossRef CAS PubMed.
- A. J. Clark, T. Gindin, B. Zhang, L. Wang, R. Abel, C. S. Murret, F. Xu, A. Bao, N. J. Lu, T. Zhou, P. D. Kwong, L. Shapiro, B. Honig and R. A. Friesner, J. Mol. Biol., 2017, 429, 930–947 CrossRef CAS PubMed.
- B. J. Williams-Noonan, E. Yuriev and D. K. Chalmers, J. Med. Chem., 2018, 61, 638–649 CrossRef CAS PubMed.
- D. Tondi, F. Morandi, R. Bonnet, M. P. Costi and B. K. Shoichet, J. Am. Chem. Soc., 2005, 127, 4632–4639 CrossRef CAS PubMed.
- K. Babaoglu and B. K. Shoichet, Nat. Chem. Biol., 2006, 2, 720–723 CrossRef CAS PubMed.
- K. Babaoglu, A. Simeonov, J. J. Irwin, M. E. Nelson, B. Feng, C. J. Thomas, L. Cancian, M. P. Costi, D. A. Maltby, A. Jadhav, J. Inglese, C. P. Austin and B. K. Shoichet, J. Med. Chem., 2008, 51, 2502–2511 CrossRef CAS PubMed.
- D. G. Teotico, K. Babaoglu, G. J. Rocklin, R. S. Ferreira, A. M. Giannetti and B. K. Shoichet, Proc. Natl. Acad. Sci. U.S.A., 2009, 106, 7455–7460 CrossRef CAS PubMed.
- S. Barelier, O. Eidam, I. Fish, J. Hollander, F. Figaroa, R. Nachane, J. J. Irwin, B. K. Shoichet and G. Siegal, ACS Chem. Biol., 2014, 9, 1528–1535 CrossRef CAS PubMed.
- S. Barelier, J. A. Cummings, A. M. Rauwerdink, D. S. Hitchcock, J. D. Farelli, S. C. Almo, F. M. Raushel, K. N. Allen and B. K. Shoichet, J. Am. Chem. Soc., 2014, 136, 7374–7382 CrossRef CAS PubMed.
- H. Hald, P. Naur, D. S. Pickering, D. Sprogøe, U. Madsen, D. B. Timmermann, P. K. Ahring, T. Liljefors, A. Schousboe, J. Egebjerg, M. Gajhede and J. S. Kastrup, J. Biol. Chem., 2007, 282, 25726–25736 CrossRef CAS PubMed.
- M. Unno, M. Shinohara, K. Takayama, H. Tanaka, K. Teruya, K. Doh-ura, R. Sakai, M. Sasaki and M. Ikeda-Saito, J. Mol. Biol., 2011, 413, 667–683 CrossRef CAS PubMed.
- R. Venskutonytė, K. Frydenvang, H. Hald, A. C. d. Rabassa, M. Gajhede, P. K. Ahring and J. S. Kastrup, Neurochem. Int., 2012, 61, 536–545 CrossRef PubMed.
- R. Venskutonytė, K. Frydenvang, E. A. Valadés, E. Szymańska, T. N. Johansen, J. S. Kastrup and D. S. Pickering, ChemMedChem, 2012, 7, 1793–1798 CrossRef PubMed.
- J. R. Huth, C. Park, A. M. Petros, A. R. Kunzer, M. D. Wendt, X. Wang, C. L. Lynch, J. C. Mack, K. M. Swift, R. A. Judge, J. Chen, P. L. Richardson, S. Jin, S. K. Tahir, E. D. Matayoshi, S. A. Dorwin, U. S. Ladror, J. M. Severin, K. A. Walter, D. M. Bartley, S. W. Fesik, S. W. Elmore and P. J. Hajduk, Chem. Biol. Drug Des., 2007, 70, 1–12 CrossRef CAS PubMed.
- P.-P. Kung, B. Huang, G. Zhang, J. Z. Zhou, J. Wang, J. A. Digits, J. Skaptason, S. Yamazaki, D. Neul, M. Zientek, J. Elleraas, P. Mehta, M.-J. Yin, M. J. Hickey, K. S. Gajiwala, C. Rodgers, J. F. Davies and M. R. Gehring, J. Med. Chem., 2010, 53, 499–503 CrossRef CAS PubMed.
- T. J. Yun, E. K. Harning, K. Giza, D. Rabah, P. Li, J. W. Arndt, D. Luchetti, M. A. Biamonte, J. Shi, K. Lundgren, A. Manning and M. R. Kehry, J. Immunol., 2011, 186, 563–575 CrossRef CAS PubMed.
- J. Shi, R. Van de Water, K. Hong, R. B. Lamer, K. W. Weichert, C. M. Sandoval, S. R. Kasibhatla, M. F. Boehm, J. Chao, K. Lundgren, N. Timple, R. Lough, G. Ibanez, C. Boykin, F. J. Burrows, M. R. Kehry, T. J. Yun, E. K. Harning, C. Ambrose, J. Thompson, S. A. Bixler, A. Dunah, P. Snodgrass-Belt, J. Arndt, I. J. Enyedy, P. Li, V. S. Hong, A. McKenzie and M. A. Biamonte, J. Med. Chem., 2012, 55, 7786–7795 CrossRef CAS PubMed.
- L. Zehnder, M. Bennett, J. Meng, B. Huang, S. Ninkovic, F. Wang, J. Braganza, J. Tatlock, T. Jewell, J. Z. Zhou, B. Burke, J. Wang, K. Maegley, P. P. Mehta, M.-J. Yin, K. S. Gajiwala, M. J. Hickey, S. Yamazaki, E. Smith, P. Kang, A. Sistla, E. Dovalsantos, M. R. Gehring, R. Kania, M. Wythes and P.-P. Kung, J. Med. Chem., 2011, 54, 3368–3385 CrossRef CAS PubMed.
- E. Casale, N. Amboldi, M. G. Brasca, D. Caronni, N. Colombo, C. Dalvit, E. R. Felder, G. Fogliatto, A. Galvani, A. Isacchi, P. Polucci, L. Riceputi, F. Sola, C. Visco, F. Zuccotto and F. Casuscelli, Bioorg. Med. Chem., 2014, 22, 4135–4150 CrossRef CAS PubMed.
- J. T. Ernst, M. Liu, H. Zuccola, T. Neubert, K. Beaumont, A. Turnbull, A. Kallel, B. Vought and D. Stamos, Bioorg. Med. Chem. Lett., 2014, 24, 204–208 CrossRef CAS PubMed.
- J. T. Ernst, T. Neubert, M. Liu, S. Sperry, H. Zuccola, A. Turnbull, B. Fleck, W. Kargo, L. Woody, P. Chiang, D. Tran, W. Chen, P. Snyder, T. Alcacio, A. Nezami, J. Reynolds, K. Alvi, L. Goulet and D. Stamos, J. Med. Chem., 2014, 57, 3382–3400 CrossRef CAS PubMed.
- H.-x. Su, S. Yao, W.-f. Zhao, M.-j. Li, J. Liu, W.-j. Shang, H. Xie, C.-q. Ke, H.-c. Hu, M.-n. Gao, K.-q. Yu, H. Liu, J.-s. Shen, W. Tang, L.-k. Zhang, G.-f. Xiao, L. Ni, D.-w. Wang, J.-p. Zuo, H.-l. Jiang, F. Bai, Y. Wu, Y. Ye and Y.-c. Xu, Acta Pharmacol. Sin., 2020, 41, 1167–1177 CrossRef CAS PubMed.
- C. Ma, M. D. Sacco, B. Hurst, J. A. Townsend, Y. Hu, T. Szeto, X. Zhang, B. Tarbet, M. T. Marty, Y. Chen and J. Wang, Cell Res., 2020, 30, 678–692 CrossRef CAS PubMed.
- M. D. Sacco, C. Ma, P. Lagarias, A. Gao, J. A. Townsend, X. Meng, P. Dube, X. Zhang, Y. Hu, N. Kitamura, B. Hurst, B. Tarbet, M. T. Marty, A. Kolocouris, Y. Xiang, Y. Chen and J. Wang, Sci. Adv., 2020, 6, eabe0751 CrossRef CAS PubMed.
- A. D. Rathnayake, J. Zheng, Y. Kim, K. D. Perera, S. Mackin, D. K. Meyerholz, M. M. Kashipathy, K. P. Battaile, S. Lovell, S. Perlman, W. C. Groutas and K.-O. Chang, Sci. Transl. Med., 2020, 12, eabc5332 CrossRef CAS PubMed.
- M. Kuzikov, E. Costanzi, J. Reinshagen, F. Esposito, L. Vangeel, M. Wolf, B. Ellinger, C. Claussen, G. Geisslinger, A. Corona, D. Iaconis, C. Talarico, C. Manelfi, R. Cannalire, G. Rossetti, J. Gossen, S. Albani, F. Musiani, K. Herzog, Y. Ye, B. Giabbai, N. Demitri, D. Jochmans, S. D. Jonghe, J. Rymenants, V. Summa, E. Tramontano, A. R. Beccari, P. Leyssen, P. Storici, J. Neyts, P. Gribbon and A. Zaliani, ACS Pharmacol. Transl. Sci., 2021, 4, 1096–1110 CrossRef CAS PubMed.
- G. J. Lockbaum, M. Henes, J. M. Lee, J. Timm, E. A. Nalivaika, P. R. Thompson, N. Kurt Yilmaz and C. A. Schiffer, Biochem, 2021, 60, 2925–2931 CrossRef CAS PubMed.
- W. Vuong, C. Fischer, M. B. Khan, M. J. van Belkum, T. Lamer, K. D. Willoughby, J. Lu, E. Arutyunova, M. A. Joyce, H. A. Saffran, J. A. Shields, H. S. Young, J. A. Nieman, D. L. Tyrrell, M. J. Lemieux and J. C. Vederas, Eur. J. Med. Chem., 2021, 222, 113584 CrossRef CAS PubMed.
- E. Costanzi, M. Kuzikov, F. Esposito, S. Albani, N. Demitri, B. Giabbai, M. Camasta, E. Tramontano, G. Rossetti, A. Zaliani and P. Storici, Int. J. Mol. Sci., 2021, 22, 11779 CrossRef CAS PubMed.
- Y. Shi, L. Shuai, Z. Wen, C. Wang, Y. Yan, Z. Jiao, F. Guo, Z. F. Fu, H. Chen, Z. Bu and G. Peng, Emerging Microbes Infect., 2021, 10, 481–492 CrossRef CAS PubMed.
- M. S. Cooper, L. Zhang, M. Ibrahim, K. Zhang, X. Sun, J. Röske, M. Göhl, M. Brönstrup, J. K. Cowell, L. Sauerhering, S. Becker, L. Vangeel, D. Jochmans, J. Neyts, K. Rox, G. P. Marsh, H. J. Maple and R. Hilgenfeld, J. Med. Chem., 2022, 65, 13328–13342 CrossRef CAS PubMed.
- A. E. Aliev, M. Kulke, H. S. Khaneja, V. Chudasama, T. D. Sheppard and R. M. Lanigan, Proteins: Struct., Funct., Bioinf., 2014, 82, 195–215 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- Chemicalize was Used for Prediction of Chemical Properties, https://chemicalize.com/, developed by ChemAxon Search PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- C. H. Bennett, J. Comput. Phys., 1976, 22, 245–268 CrossRef.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- S. T. Ngo, N. M. Tam, M. Q. Pham and T. H. Nguyen, J. Chem. Inf. Model., 2021, 61, 2302–2312 CrossRef CAS PubMed.
- J. A. Henderson, R. C. Harris, C.-C. Tsai and J. Shen, J. Phys. Chem. Lett., 2018, 9, 5440–5444 CrossRef CAS PubMed.
- B. Efron, Ann. Stat., 1979, 7, 1–26 Search PubMed.
- S. D. Wierbowski, B. M. Wingert, J. Zheng and C. J. Camacho, Protein Sci., 2020, 29, 298–305 CrossRef CAS PubMed.
- H. Hwang, T. Vreven, J. Janin and Z. Weng, Proteins: Struct., Funct., Genet., 2010, 78, 3111–3114 CrossRef CAS PubMed.
- I. Alibay, A. Magarkar, D. Seeliger and P. C. Biggin, Commun. Chem., 2022, 5, 105 CrossRef PubMed.
- D. L. Mobley and M. K. Gilson, Annu. Rev. Biophys., 2017, 46, 531–558 CrossRef CAS PubMed.
- H. Zhang, S. Kim and W. Im, J. Chem. Inf. Model., 2022, 62, 6084–6093 CrossRef CAS PubMed.
- S. Zev, K. Raz, R. Schwartz, R. Tarabeh, P. K. Gupta and D. T. Major, J. Chem. Inf. Model., 2021, 61, 2957–2966 CrossRef CAS PubMed.
- C. E. M. Schindler, H. Baumann, A. Blum, D. Böse, H.-P. Buchstaller, L. Burgdorf, D. Cappel, E. Chekler, P. Czodrowski, D. Dorsch, M. K. I. Eguida, B. Follows, T. Fuchß, U. Grädler, J. Gunera, T. Johnson, C. Jorand Lebrun, S. Karra, M. Klein, T. Knehans, L. Koetzner, M. Krier, M. Leiendecker, B. Leuthner, L. Li, I. Mochalkin, D. Musil, C. Neagu, F. Rippmann, K. Schiemann, R. Schulz, T. Steinbrecher, E.-M. Tanzer, A. Unzue Lopez, A. Viacava Follis, A. Wegener and D. Kuhn, J. Chem. Inf. Model., 2020, 60, 5457–5474 CrossRef CAS PubMed.
- S. Wang, X. Sun, W. Cui and S. Yuan, Front. Pharmacol, 2022, 13, 1018351 CrossRef CAS PubMed.
- J. L. Maccallum and D. P. Tieleman, J. Comput. Chem., 2003, 24, 1930–1935 CrossRef CAS PubMed.
- A. Villa and A. E. Mark, J. Comput. Chem., 2002, 23, 548–553 CrossRef CAS PubMed.
- H. Zhang, C. Yin, Y. Jiang and D. van der Spoel, J. Chem. Inf. Model., 2018, 58, 1037–1052 CrossRef CAS PubMed.
- H. Zhang, Y. Jiang, Z. Cui and C. Yin, J. Chem. Inf. Model., 2018, 58, 1669–1681 CrossRef CAS PubMed.
- A. Jacoby George, Clin. Microbiol. Rev., 2009, 22, 161–182 CrossRef CAS PubMed.
- J. C. Vázquez-Ucha, D. Rodríguez, C. Lasarte-Monterrubio, E. Lence, J. Arca-Suarez, M. Maneiro, E. Gato, A. Perez, M. Martínez-Guitián, C. Juan, A. Oliver, G. Bou, C. González-Bello and A. Beceiro, J. Med. Chem., 2021, 64, 6310–6328 CrossRef PubMed.
- S. Kim, P. A. Thiessen, E. E. Bolton, J. Chen, G. Fu, A. Gindulyte, L. Han, J. He, S. He, B. A. Shoemaker, J. Wang, B. Yu, J. Zhang and S. H. Bryant, Nucleic Acids Res., 2016, 44, D1202–D1213 CrossRef CAS PubMed.
- A. Y. Lau and B. Roux, Nat. Struct. Mol. Biol., 2011, 18, 283–287 CrossRef CAS PubMed.
- D. Picard, Cell. Mol. Life Sci., 2002, 59, 1640–1648 CrossRef CAS PubMed.
- L. Neckers and S. P. Ivy, Curr. Opin. Oncol., 2003, 15, 419–424 CrossRef CAS PubMed.
- L. Li, L. Wang, Q.-D. You and X.-L. Xu, J. Med. Chem., 2020, 63, 1798–1822 CrossRef CAS PubMed.
- W. Fiedler, F. Freisleben, J. Wellbrock and K. N. Kirschner, J. Chem. Inf. Model., 2022, 62, 3604–3617 CrossRef CAS PubMed.
- A. Douangamath, D. Fearon, P. Gehrtz, T. Krojer, P. Lukacik, C. D. Owen, E. Resnick, C. Strain-Damerell, A. Aimon, P. Ábrányi-Balogh, J. Brandão-Neto, A. Carbery, G. Davison, A. Dias, T. D. Downes, L. Dunnett, M. Fairhead, J. D. Firth, S. P. Jones, A. Keeley, G. M. Keserü, H. F. Klein, M. P. Martin, M. E. M. Noble, P. O'Brien, A. Powell, R. N. Reddi, R. Skyner, M. Snee, M. J. Waring, C. Wild, N. London, F. von Delft and M. A. Walsh, Nat. Commun., 2020, 11, 5047 CrossRef CAS PubMed.
- W. Vuong, M. B. Khan, C. Fischer, E. Arutyunova, T. Lamer, J. Shields, H. A. Saffran, R. T. McKay, M. J. van Belkum, M. A. Joyce, H. S. Young, D. L. Tyrrell, J. C. Vederas and M. J. Lemieux, Nat. Commun., 2020, 11, 4282 CrossRef CAS PubMed.
- C. B. Jackson, M. Farzan, B. Chen and H. Choe, Nat. Rev. Mol. Cell Biol., 2022, 23, 3–20 CrossRef CAS PubMed.
- S. Ullrich and C. Nitsche, Bioorg. Med. Chem. Lett., 2020, 30, 127377 CrossRef CAS PubMed.
- S. T. Ngo, T. H. Nguyen, N. T. Tung and B. K. Mai, RSC Adv., 2022, 12, 3729–3737 RSC.
- C. A. Ramos-Guzmán, J. J. Ruiz-Pernía and I. Tuñón, Chem. Commun., 2021, 57, 9096–9099 RSC.
- C. A. Ramos-Guzmán, J. J. Ruiz-Pernía and I. Tuñón, Chem. Sci., 2021, 12, 3489–3496 RSC.
- N. M. Tam, P. C. Nam, D. T. Quang, N. T. Tung, V. V. Vu and S. T. Ngo, RSC Adv., 2021, 11, 2926–2934 RSC.
- S. Günther, Y. A. Reinke Patrick, Y. Fernández-García, J. Lieske, J. Lane Thomas, M. Ginn Helen, H. M. Koua Faisal, C. Ehrt, W. Ewert, D. Oberthuer, O. Yefanov, S. Meier, K. Lorenzen, B. Krichel, J.-D. Kopicki, L. Gelisio, W. Brehm, I. Dunkel, B. Seychell, H. Gieseler, B. Norton-Baker, B. Escudero-Pérez, M. Domaracky, S. Saouane, A. Tolstikova, A. White Thomas, A. Hänle, M. Groessler, H. Fleckenstein, F. Trost, M. Galchenkova, Y. Gevorkov, C. Li, S. Awel, A. Peck, M. Barthelmess, F. Schlünzen, P. Lourdu Xavier, N. Werner, H. Andaleeb, N. Ullah, S. Falke, V. Srinivasan, A. França Bruno, M. Schwinzer, H. Brognaro, C. Rogers, D. Melo, J. Zaitseva-Doyle Joanna, J. Knoska, E. Peña-Murillo Gisel, R. Mashhour Aida, V. Hennicke, P. Fischer, J. Hakanpää, J. Meyer, P. Gribbon, B. Ellinger, M. Kuzikov, M. Wolf, R. Beccari Andrea, G. Bourenkov, D. von Stetten, G. Pompidor, I. Bento, S. Panneerselvam, I. Karpics, R. Schneider Thomas, M. Garcia-Alai Maria, S. Niebling, C. Günther, C. Schmidt, R. Schubert, H. Han, J. Boger, C. F. Monteiro Diana, L. Zhang, X. Sun, J. Pletzer-Zelgert, J. Wollenhaupt, G. Feiler Christian, S. Weiss Manfred, E.-C. Schulz, P. Mehrabi, K. Karničar, A. Usenik, J. Loboda, H. Tidow, A. Chari, R. Hilgenfeld, C. Uetrecht, R. Cox, A. Zaliani, T. Beck, M. Rarey, S. Günther, D. Turk, W. Hinrichs, N. Chapman Henry, R. Pearson Arwen, C. Betzel and A. Meents, Science, 2021, 372, 642–646 CrossRef PubMed.
- E. C. Vatansever, K. Yang, K. C. Kratch, A. Drelich, C.-C. Cho, D. M. Mellot, S. Xu, C.-T. K. Tseng and W. R. Liu, Proc. Natl. Acad. Sci. U.S.A., 2021, 118, e2012201118 CrossRef CAS PubMed.
- T. Cheng, Y. Zhao, X. Li, F. Lin, Y. Xu, X. Zhang, Y. Li, R. Wang and L. Lai, J. Chem. Inf. Model., 2007, 47, 2140–2148 CrossRef CAS PubMed.
- G. J. Rocklin, D. L. Mobley, K. A. Dill and P. H. Hünenberger, J. Chem. Phys., 2013, 139, 184103 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The comparison between sequences of Homo sapiens and Rattus norvegicus of glutamate receptor, ionotropic kainate 1; 2D and 3D structure for all ligands of AmpC, GluK1, Hsp90 and SARS-CoV-2 Mpro systems; All-atom RMSD of AmpC + ligand and ligand in solution systems; all-atom RMSD of GluK1 + ligand and ligand in solution systems; all-atom RMSD of Hsp90 + ligand and ligand in solution systems; all-atom RMSD of SARS-CoV-2 Mpro + ligand and ligand in solution systems; calculated versus experimental binding affinities of four systems without consideration of ligand protonation states; all-atom RMSD of four systems without consideration of ligand protonation states; thermodynamics diagram of FEP calculations; intermolecular contacts between AmpC residues and inhibitors; intermolecular contacts between GluK1 residues and inhibitors; intermolecular contacts between Hsp90 residues and inhibitors; intermolecular contacts between SARS-CoV-2 Mpro residues and inhibitors. See DOI: https://doi.org/10.1039/d4ra00692e |
| This journal is © The Royal Society of Chemistry 2024 |
