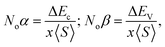DOI:
10.1039/D4RA01759E
(Paper)
RSC Adv., 2024,
14, 16859-16869
Investigation of half metallic properties of Tl2Mo(Cl/Br)6 double perovskites for spintronic devices
Received
7th March 2024
, Accepted 29th April 2024
First published on 24th May 2024
Abstract
The manipulation of electronic device characteristics through electron spin represents a burgeoning frontier in technological advancement. Investigation of magnetic and transport attributes of the Tl2Mo(Cl/Br)6 double perovskite was performed using Wien2k and BoltzTraP code. When the energy states between ferromagnetic and antiferromagnetic conditions are compared, it is evident that the ferromagnetic state exhibits lower energy levels. Overcoming stability challenges within the ferromagnetic state is achieved through the manipulation of negative ΔHf within the cubic state. The analysis of the half metallicity character involves an analysis of band structure (BS) and DOS, elucidating its mechanism through PDOS using double exchange model p–d hybridization. The verification of 100% spin polarization is confirmed through factors such as spin polarization and the integer value of the total magnetic moment. Furthermore, the thermoelectric response, as indicated by the ratios of thermal-electrical conductivity and ZT, underscores the promising applications of these compounds in thermoelectric device applications.
1. Introduction
Spintronics, a new research area at the intersection of physics and electronics, has become particularly interesting owing to its possible influence on the development of novel types of electronic devices based on electron spin (their intrinsic property).1 Unlike in traditional electronics, which mainly rely on electron charges for data handling and storage, spintronics employs the electron's spin degree of freedom, which results in the appearance of electronic devices with novel and enhanced functionalities.2 Spintronics is actually a branch of electronics based on one of the fundamental concepts, namely half metallicity, which is a special property of materials characterized by the fact that they have different conductive properties for electrons with different spin orientations. The interest in half-metallicity lies in its spintronic features, where one spin is conducting while the other spin is insulating.3–5 This property provides completely novel capabilities for controlling and manipulating the magnetic moment of itinerant electrons and opens new avenues for utilizing this spin dependence in various devices. The investigation of half-metallicity in spintronics has opened up new avenues for the fabrication of spin-based electronic devices such as spin valves, magnetic tunnel junctions and spin transistors, which depend on differentiating and manipulating the spin-polarized currents.6 In addition, the design and production of half-metallic materials in spintronics directly affect spin-dependent phenomena such as colossal magneto-resistance and tunnel magneto-resistance, which are limiting factors in high-density magnetic data storage and spintronic memory devices.7 Researchers have targeted the inherent traits of the half metallic substances and intend to outdo the outmoded limitations in electronic devices in terms of power consumption, speed and scalability to ready the juncture for the forthcoming spintronic innovations. Concurrently, the quest for new materials has made this discovery of double perovskites, a very diverse group of compounds famed for their versatile properties.8 In this scenario, the origins of spintronics, half-metallicity, and double perovskites are of great importance, affecting material design and technological innovation.
Besides the emergence of half-metallic materials, the class of compounds known as double perovskite has gained attention because of its unique properties of electronic and magnetic capability due to its complex crystal structure and various cationic configurations. The perovskite structure is characterized by a simplified addressing by the general formula. A2BB′O6 can be regarded as a versatile framework for the investigation of a broad spectrum of physical phenomena and the design of material properties through composition engineering.9 Double perovskites, a subgroup of perovskite materials featuring the simultaneous occupation of two cations at the B site, display various high-order electronic structures with a rich phase space that can lead to numerous electronic transport characteristics. Such engineering would yield a structure with mutable electronic band structures through approaches including, but not limited to, band engineering, strain engineering, and doping. In addition, the functionality of the transition metal nodes of the perovskite lattice leads to significant phase space, and the existence of electronic phenomena, such as colossal magnetoresistance and multiferroicity, is possible. Additionally, the intriguing interplay between phonon properties and electronic states in double perovskite material provides a way to explore novel phenomena that may enhance the properties of the thermoelectric ZT. The essence of the thermoelectric function of double perovskites is the complex relationship between the electronic structure, charge transport, and phonon scattering mechanisms.10 The band engineering possibilities from the dual-cation arrangement ensure that the electronic states can be manipulated, and their mobility is improved, thereby, in the process, boosting the thermoelectric efficiencies.11 Furthermore, particular d-electrons of transition metal ions and conducting oxygen p-orbitals also play a role in the complex electronic behavior of the materials; this means that such compounds have ideal properties for further development of thermoelectric properties.12
Numerous researchers have allocated their findings specifically to studying the double perovskite group due to the intriguing thermoelectric properties of this material. Mahmood et al. studied the ferromagnetic thermoelectric response of K2Z(Cl/Br)6 (Z = Ta, W, Re), which is related to its application in spintronics and energy. Their investigation delivered an in-depth description of the features of these materials when comparing them in terms of their different possible uses in future technological developments. Mahmood et al.'s findings provide a significant impetus for research in materials for spintronic and energy applications.13 Alburaih et al. presented a theoretical investigation, relying thoroughly on DFT calculations, of vacancy-ordered single-crystalline K2TcZ6 (Z = Cl, Br) systems searching owing to their suitable characteristics for spintronic applications. Their work focused on the electronic structure and magnetic response in the studied composition and provided a basis for the development of new spintronic devices and data storage.14 In the research by Mahmood et al. (2022), the impact of 5d electrons on half metallic ferromagnetic behavior and conduction of Cs2Z(Cl/Br)6 (Z = Os, Ir) for devices in spintronics was explored.15 The study featured a comprehensive analysis of the behavior of these materials, which served as the basis for the development of novel spintronic devices. The authors explored the relationship between 5d electrons and their proprieties in detail, providing contributions that can be valuable for materials. Their findings emphasize that the Cs2Z(Cl/Br)6 (Z = Os, Ir) compound might play a key role in the development of spintronics, which again makes them theoretically critical for future science and technology. The molecules Mo and Tl provide remarkably strong spins used in the devices to store and process information using spins. As far as the tunability of Tl and Mo and the possibility of application in devices with the magnetization effect are concerned, magnetronics could be a crucial field. With our calculations, we are confident that Tl2Mo(Cl/Br)6 will definitely be the best composition in spin-based technology. Perovskites with halide composition exhibit applications in several spintronic gadgets, including magnetic memory, spin valves, and spin orbit applications due to the unique magnetic and electrical tunability of the combination. Spintronics has been performing very well, and further advancements in this area will potentially command various possibilities and highly adaptive spintronic device functionalities. The principal objective of the present investigation is to acquire a more comprehensive understanding of the characteristics of Tl2Mo(Cl/Br)6, covering aspects such as structural, electronic, elastic, magnetic, and transport properties.
2. Computational methodology
The stability of a material's structure is crucial because it governs numerous physical attributes. In this study, Tl2Mo(Cl/Br)6 was analyzed using a DFT-based FP-LAPW approach implemented using Wien2k code.16 Ground-state energies were computed using the PBE-sol approximation, with adjustments made to accurately determine bandgaps through the mBJ potential.17 Notably, PBE-sol, a modified version of PBE, incorporates different constraints, offering improved accuracy, particularly for heavy metal systems related to PBE. The TB-mBJ potential, known for its precision akin to HSE06, was employed for electronic BS and DOS computations, alongside consideration of spin–orbit coupling.18,19 To ensure convergence, a K-mesh of 2000 k-points (12 × 12 × 12) was utilized and later increased to 20 × 20 × 20 for thermoelectric calculations. Parameters such as (muffin-tin radius) RMT × Kmax (K-vector), 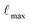 (angular momentum vector) and Gmax (Gaussian factor) were carefully selected for accuracy, with computed results converging to the order of 10−3 mRy. Transport response was estimated utilizing the BoltzTrap code, providing an inclusive analysis of the material's properties.20
(angular momentum vector) and Gmax (Gaussian factor) were carefully selected for accuracy, with computed results converging to the order of 10−3 mRy. Transport response was estimated utilizing the BoltzTrap code, providing an inclusive analysis of the material's properties.20
3. Results and discussion
3.1 Structural analysis
The optimization of energy release from compounds with Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 225) space group in cubic phase and determination of ground-state parameters were conducted using the Birch–Murnaghan equation of states (Table 1).21 Fig. 1 illustrates unit cells in both ball-stick (left) and polyhedral (right) formats, showcasing atomic arrangement and geometric configuration, respectively. Within MoCl/Br6 octahedra, the Tl atom fills vacancies, which exhibit 12-fold coordination with Cl/Br atoms, resulting in individual octahedra being distinct from the others. The Mo atoms occupies the center of the octahedra, encircled by six Cl/Br atoms, while the Mo atoms are also present at the face centers and corners.22 Wyckoff positions for Tl (8c), Mo (4a), and Cl/Br (24e) were utilized for structure generation and optimization. Through the replacement of Cl with Br, atomic radii increase, consequently enlarging the lattice constant in the range of 9.95–10.54 Å and inter-atomic distance, thus reducing material density and solidness, and leading to a decrease in bulk moduli (B) from 43.75–35.95 GPa.23 The same type of variation in the lattice constant has also been observed by Mahmood et al. in Cs2ReCl/Br6 double perovskites.11 The considerable bulk modulus of Tl2MoBr6 suggests greater stiffness compared to Tl2MoCl6. Energy plots against volume in the ferromagnetic (FM) and anti-ferromagnetic (AFM) phases, as displayed in Fig. 2, reveal higher energy release in the FM state, indicating its greater favorability. Furthermore, energy formation was computed to evaluate thermal stability using the following equation:24
m (no. 225) space group in cubic phase and determination of ground-state parameters were conducted using the Birch–Murnaghan equation of states (Table 1).21 Fig. 1 illustrates unit cells in both ball-stick (left) and polyhedral (right) formats, showcasing atomic arrangement and geometric configuration, respectively. Within MoCl/Br6 octahedra, the Tl atom fills vacancies, which exhibit 12-fold coordination with Cl/Br atoms, resulting in individual octahedra being distinct from the others. The Mo atoms occupies the center of the octahedra, encircled by six Cl/Br atoms, while the Mo atoms are also present at the face centers and corners.22 Wyckoff positions for Tl (8c), Mo (4a), and Cl/Br (24e) were utilized for structure generation and optimization. Through the replacement of Cl with Br, atomic radii increase, consequently enlarging the lattice constant in the range of 9.95–10.54 Å and inter-atomic distance, thus reducing material density and solidness, and leading to a decrease in bulk moduli (B) from 43.75–35.95 GPa.23 The same type of variation in the lattice constant has also been observed by Mahmood et al. in Cs2ReCl/Br6 double perovskites.11 The considerable bulk modulus of Tl2MoBr6 suggests greater stiffness compared to Tl2MoCl6. Energy plots against volume in the ferromagnetic (FM) and anti-ferromagnetic (AFM) phases, as displayed in Fig. 2, reveal higher energy release in the FM state, indicating its greater favorability. Furthermore, energy formation was computed to evaluate thermal stability using the following equation:24
| ΔHf = ETotal(TllMom(Cl/Br)n) − lETl − mEMo − nECl/Br, |
where ETotal denotes the total energy of double perovskites; ETl, EMo, and ECl/Br denote energies of Tl, Mo, and Cl/Br, respectively; l denotes the number of Tl; m denotes the number of Mo and n denotes the number of Cl/Br atoms.25 The ΔHf for Tl2MoCl6 is calculated as −1.44 eV. Similarly, for Tl2MoBr6 ΔHf are found to be −1.18 eV for Br. This indicates the thermal stability of the compounds, as evidenced by the negative values of ΔHf in the ferromagnetic state. Another crucial aspect of FM materials in spintronic device applications is the ability to maintain ferromagnetism above RT. To determine Curie temperature (Tc), the Heisenberg model Tc = 2ΔE/3xKB was employed, where x represents the Mo concentration and ΔE = EAFM − EFM, as illustrated in Table 2. The computed Tc for Tl2MoCl6 is 567 K and for Tl2MoBr6 is 533 K, indicating that the FM nature is above room temperature (RT).26
Table 1 Computed lattice parameters, bulk modulus values, ground-state energy differences, Curie temperature (Tc) and formation energy (ΔHf (eV)) of DPs Tl2Mo(Cl/Br)6
| Chalcogenides |
ao (Å) |
B0 (GPa) |
ΔE = EAFM − EFM |
Tc (K) |
ΔHf |
| Tl2MoCl6 |
9.95 |
43.75 |
22.66 |
567 |
−1.44 |
| Tl2MoBr6 |
10.54 |
35.95 |
14.88 |
533 |
−1.18 |
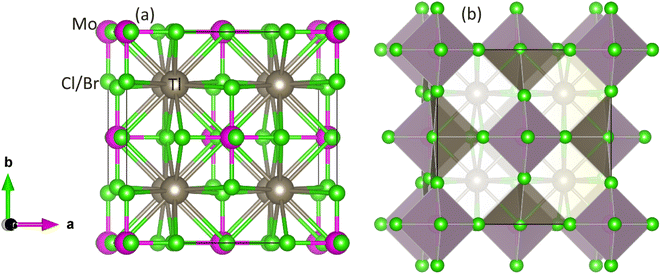 |
| | Fig. 1 Unit cell of DP Tl2Mo(Cl/Br)6: (a) ball-stick and (b) polyhedral model. Gray, pink and green balls show Tl, Mo, and Cl/Br atoms, respectively. | |
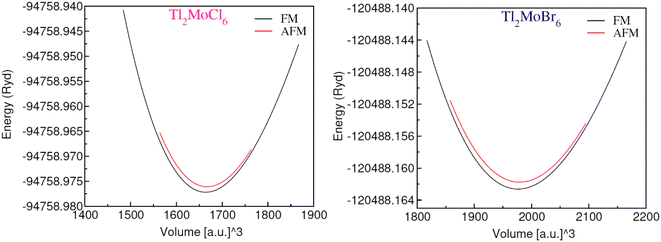 |
| | Fig. 2 Energy against volume plot for Tl2MoCl6 and Tl2MoBr6 in ferromagnetic (FM) and anti-ferromagnetic (AFM) states. | |
Table 2 Computed elastic constants (C11, C12, C44) and computed mechanical parameters for Tl2Mo(Cl/Br)6
| |
C11 |
C12 |
C44 |
B0 |
G |
Y |
B0/G |
υ |
α |
| Tl2MoCl6 |
88.09 |
20.82 |
13.81 |
43.24 |
19.90 |
51.77 |
2.17 |
0.30 |
0.41 |
| Tl2MoBr6 |
71.55 |
16.13 |
14.06 |
34.60 |
18.51 |
47.13 |
1.86 |
0.27 |
0.51 |
3.2 Mechanical properties
The material's performance under stress is defined by elastic constants, ensuring a mechanically stable crystal structure.27 Cubic symmetric properties rely on three elastic constants (C11, C12, and C44), where Born stability conditions (C11 − C12 > 0, C44 > 0, C11 + 2C12 > 0, and C12 < B0 < C11) support mechanical stability, as listed in Table 2.28 The B parameter, calculated as B0 = (C11 + 2C12)/3, elucidates mechanical behavior, indicating that Tl2MoBr6 exhibits lower output compared to Tl2MoCl6, which is consistent with B calculated from optimization.29 Ductility differentiation between materials was determined by controlling Poisson's (ν > 0.26) and Pugh's (B0/G > 1.75) ratio.30 When the component number exceeds the cut-off value, it signifies greater deformability than rigidity. The investigated composition's ductility is presented in Table 2. Anisotropy (A = 2C44/(C11 − C12)) provides additional insight into directional characteristics, where isotropic materials possess a unit value and anisotropic materials exhibit a value less than unity (Table 2).31
3.3 Elastic anisotropy
Elastic anisotropy represents the significant physical characteristics of a material, indicating variations in physical and chemical properties with directional changes.32 Isotropic materials maintain reliable characteristics irrespective of measurement directions, exhibiting identical performance values in all directions. Fig. 3 depicts 3-D surface c representations of Youngs (Y), shear (G) moduli, and Poisson (ν) ratio for Tl2Mo(Cl/Br)6. Isotropic materials manifest spherical 3D surface structures, while deviations from a sphere denote anisotropy, with greater deviations indicating stronger anisotropy.33,34 The 3-D figures for Tl2MoCl6 do not resemble spheres, confirming its anisotropic nature. Further investigation into Tl2Mo(Cl/Br)6 elastic anisotropy involves examining values such as βmax, βmin, Ymax, Ymin, Gmax, Gmin, νmax, and νmin, along with ratios such as βmax/βmin, Ymax/Ymin, Gmax/Gmin, and νmax/νmin (Table 3). For an isotropic material, the ratio of the maximum to minimum elastic modulus is equal to 1,35 whereas anisotropic materials exhibit ratios different from 1, with higher ratios indicating stronger anisotropy. In the case of Tl2MoCl6, βmax/βmin = 1, Ymax/Ymin = 1.841, Gmax/Gmin = 9.742, and νmax/νmin = 0.259, indicating greater anisotropy compared to Tl2MoBr6. Among the studied allotropes, Tl2MoCl6 demonstrates the highest anisotropy.36
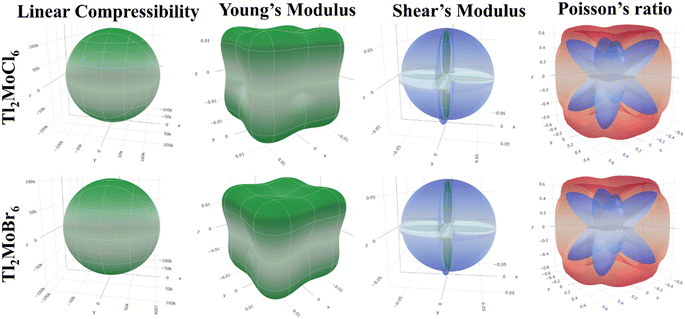 |
| | Fig. 3 Representation of elastic moduli in 3-D. | |
Table 3 Maximum and minimum values of elastic moduli and their anisotropy for Tl2Mo(Cl/Br)6
| Parameters |
Linear compressibility (β) (TPa−1) |
Young's modulus (Y) (GPa) |
Shear modulus (G) (GPa) |
Poisson's ratio (ν) |
| βmin |
βmax |
A |
Ymin |
Ymax |
A |
Gmin |
Gmax |
A |
νmin |
νmax |
A |
| Tl2MoCl6 |
129![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 730 |
129![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 730 |
1 |
0.01135 |
0.0209 |
1.841 |
0.00743 |
0.072411 |
9.742 |
−0.91325 |
−0.23635 |
0.259 |
| Tl2MoBr6 |
103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810 810 |
103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810 810 |
1 |
0.01397 |
0.0255 |
1.821 |
0.00902 |
0.071124 |
7.883 |
−0.87943 |
−0.22544 |
0.256 |
3.4 Electronic properties
To elucidate the electronic behavior of Tl2Mo(Cl/Br6), we generated visual representations of band structures (BS) in Fig. 4, and the density of states (DOS) is depicted in Fig. 5 and 6. The band structures unveil state presence at Fermi level (Ef) within spin-up (↑) configuration, exhibiting characteristics akin to direct bandgap semiconductors. Conversely, within the down (↓) spin channel, the Ef resides in the band-gap, indicating insulating properties.37 This transition of states between the up (↑) and down (↓) configurations underscores the manifestation of the ferromagnetic character. It is imperative to note that achieving complete 100% spin-polarization serves as a fundamental prerequisite for half-metallic FM behavior. Hence, spin-polarization is quantitatively assessed via the equation P = (N↓(EF) − N↑(EF))/(N↓(EF) + N↑(EF)), where N↓(EF) denotes the DOS in the down (↓) spin and N↑(EF) denotes the DOS at Ef in the up (↑) spin configuration. Notably, within the up (↑) spin configuration, states are situated precisely at Ef, whereas in the down (↓) spin configuration, the Ef is notably absent at that position, as depicted in Fig. 5 and 6. Consequently, the investigated halides exhibit complete spin polarization (P = 1).38 Furthermore, to give an inclusive insight into ferromagnetism, the density of states (DOS) is graphically illustrated in Fig. 5 and 6. An analysis of the total density of states (TDOS) reveals that the up (↑) spin channel exhibits characteristics of direct bandgap semiconductors along the Γ symmetry direction, whereas the down (↓) spin channel demonstrates an insulating nature. Consequently, the interplay between semiconductor and insulator responses facilitates electron exchange, thereby inducing ferromagnetic characteristics. The basic driver of ferromagnetism in Tl2MoCl6 and Tl2MoBr6 stems from the individual electronic states of Mo, Tl, and Cl/Br hybridization. Specifically, the d-state of Mo splits into t2g and eg states of Mo upon encountering the octahedral and tetrahedral environments of halide atoms.39 The eg state shifts to low energy levels, whereas the t2g state ascends to high energy levels. Among these, the t2g state, comprising dxy, dyz, and dzx orbitals, exhibits a linear trend and significantly contributes to hybridization, whereas the eg state, comprising dz2 and dx2−y2 orbitals, displays nonlinear behavior and plays a negligible role in ferromagnetism. The distinction between eg and t2g states is quantified as crystal field energy (ΔCF = eg − t2g).40 To promote ferromagnetic behavior, it is imperative to minimize the crystal field energy through direct shifts of Mo d-states. The direct exchange energy Δx(d) = Δ(d↓) − Δ(d↑), representing the energy difference of d states among down (↓) and up (↑) spin configurations, must exceed CF energy (Δx(d) > ΔCF) for ferromagnetism to prevail, as illustrated in Table 4. Additionally, attention is drawn to indirect exchange energy Δx(pd), derived from the VB edge in down-spin (↓), which manifests as negative. This negative (−ve) value signifies the enhanced attractiveness of the down (↓) spin configuration for exchange mechanisms, thereby lowering the system's energy and affirming ferromagnetic stability. Despite the complexity of Mo's electronic configuration, d states of Mo engage in hybridization with the valence states of Tl and the 3p of Cl and 4p state of Br. Particularly, Mo's t2g states exhibit robust hybridization with Cl's 3p state, with negligible influence from Tl's 6s-states, in energy ranges spanning from −0.24 eV to EF and from −4.02 to −4.3 eV in the up (↑) spin configuration. Furthermore, a hybridization zone between the t2g states of Mo and Cl's 3p states emerges in the −2.2 to −4.8 eV energy range although this range is not pertinent to our analysis.41 Notably, significant hybridization is observed between Mo's eg and Cl's 3p states in the vicinity of the CB edge. In the down (↓) spin configuration, hybridization arises among Mo's t2g and Cl's 3p states in VB and CB, respectively. However, the core region witnesses negligible participation in the hybridization process, as shown in Fig. 5. Similarly, robust hybridization is evident between Mo's t2g and 4p states of Br, as illustrated in Fig. 6. Additionally, reasonable hybridization between Mo's eg and Br's 4p states is observed in the conduction band. In the down (↓) spin configuration, hybridization arises among Mo's t2g, Br's 4p states, and Tl's 6s states in VB and CB. We also computed phonon dispersion curves for both investigated materials, revealing that no imaginary mode is observed for Tl2Mo(Cl/Br)6 (see Fig. 7). The positive value of the phonon frequency for both materials indicates that they are dynamically stable in the given temperature range.
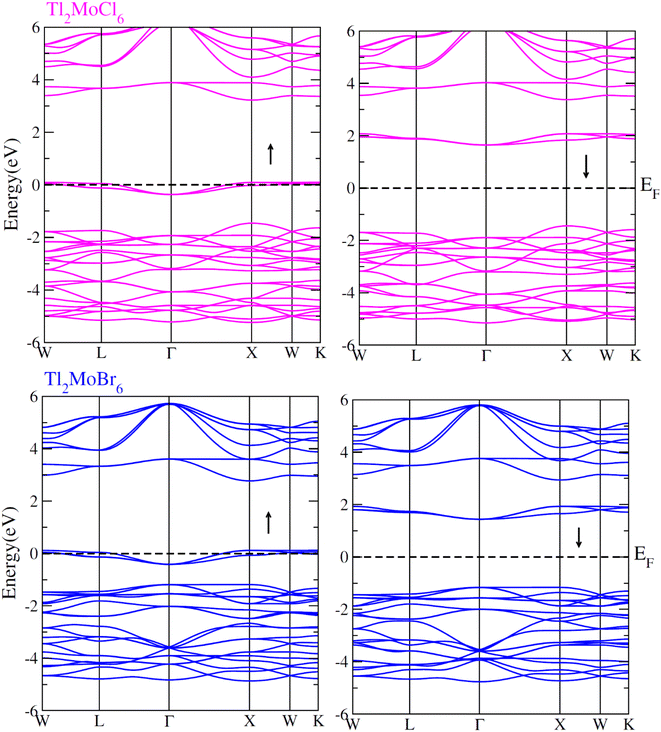 |
| | Fig. 4 Band structures computed for Tl2Mo(Cl/Br)6 for up (↑) and down (↓) spin configurations using mBJ potential. | |
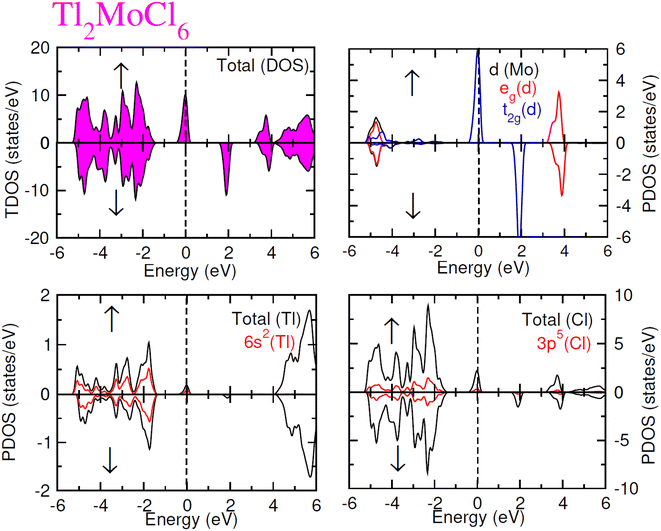 |
| | Fig. 5 Total and partial DOS for Tl2MoCl6 with Tl, Mo and Cl atoms in spin up (↑) and down (↓) spin configurations. | |
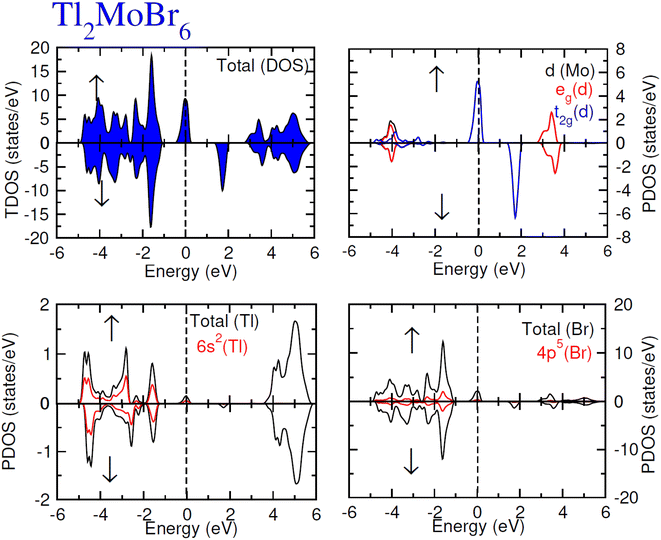 |
| | Fig. 6 Total and partial DOS for Tl2MoBr6 with Tl, Mo and Br atoms in spin up (↑) and down (↓) spin configurations. | |
Table 4 Calculated crystal field (ΔCF) energy, exchange splitting Δx(d), and exchange constants (Noα and Noβ) for Tl2Mo(Cl/Br)6
| |
ΔCF |
Δx(d) |
Δx(pd) |
Noα |
Noβ |
| Tl2MoCl6 |
3.0 |
4.1 |
−1.5 |
0.38 |
−1.92 |
| Tl2MoBr6 |
2.6 |
3.8 |
−1.2 |
0.25 |
−0.93 |
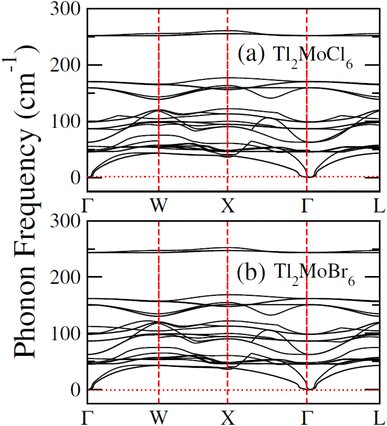 |
| | Fig. 7 Computed phonon dispersion plot for (a) Tl2MoCl6 and (b) Tl2MoBr6. | |
3.5 Magnetic properties
Understanding ferromagnetism relies significantly on the splitting of VB and CB edges, particularly concerning the interactions between s and d orbitals as well as p and d orbitals.42 These orbital interactions, denoted as s–d and p–d couplings, respectively, are delineated based on the average magnetic moments of Mo within the unit cell. The energy discrepancy between the up (↑) and down (↓) spin configurations at the CB edge (denoted as Ec) predominantly reflects the influence of s–d coupling. Conversely, at the valence band edge, this energy difference (denoted as EV) encompasses contributions from p–d coupling. The specifics of these interactions are further expounded through the elucidation of exchange constants as follows:
where x represents the concentration of Mo and 〈S〉 denotes its average magnetic moment.43 The presence of negative values for Noβ indicates high level of attraction towards down (↓) spin configuration within the exchange mechanism, resembling the characteristics of ferromagnetism, akin to exchange energy Δ(pd), as outlined in Table 4. The transition of electrons from the down (↓) spin to up (↑) spin configuration, coupled with robust hybridization between the d states of Mo, 3p state of Cl, and Br 4p-states, introduces both orbital and spin magnetic moments, highlighting their significance in spintronic devices. Detailed magnetic moment data for individual elements Tl, Mo, and Cl/Br, as well as compounds Tl2Mo(Cl/Br)6, are provided in Table 5.44 The presence of magnetic moments on nonmagnetic elements arises from robust hybridization and SOC among the d state of Mo, 3p state of Cl and Br-4p state, underscoring the pivotal contribution of Mo's d state in spintronic applications. Furthermore, Table 5 displays both the total and individual magnetic moments for Tl2Mo(Cl/Br)6. The integral figures of total magnetic moments signify complete spin-polarization of the composition under investigation. The predominant source of magnetic moments stems from the Mo-d state. Strong hybridization particularly results in the transfer of the magnetic moments from the Mo site to Tl and Cl/Br.45
Table 5 Total and local values of magnetic moments for Tl2Mo(Cl/Br)6
| |
MTotal |
MInt. |
MTl |
MMo |
MCl/Br |
| Tl2MoCl6 |
2.000 |
0.3489 |
−0.003 |
1.579 |
0.013 |
| Tl2MoBr6 |
2.000 |
0.3824 |
−0.001 |
1.571 |
0.008 |
3.6 Thermoelectric properties
In recent years, noteworthy attention has been paid to the potential of a thermoelectric material to convert thermal energy into electrical energy across various applications.46 This phenomenon, known as the thermoelectric effect, relies on the transfer of charge movement to generate a heat gradient, thereby creating a potential difference. The thermoelectric properties of Tl2Mo(Cl/Br)6 were examined utilizing the BoltzTraP code with diverse parameters, as presented in Fig. 8(a–f). Within the BoltzTraP simulation, the relaxation time, set at 10−14 s, denotes the average duration between successive collisions within the system. Electrical conduction induced by charge carriers is determined by evaluating σ/τ.47 As depicted in Fig. 8(a), the transition from Cl to Br prompts a rapid escalation in σ/τ, which is attributable to the heightened presence of free electrons transitioning thermally from valence to the conduction band. At 200 K, σ/τ measures 2.5 × 1019 for Tl2MoCl6 and 2.7 × 1019 (Ω m s)−1 for Tl2MoBr6. Analogous trends persist at 800 K. The increase in conductivity following the substitution of Cl with Br can be ascribed to the larger ionic size and the augmented contribution of free carriers. However, as the temperature increases, conductivity decreases potentially due to heightened resistance experienced by free carriers amidst thermal agitation at higher temperatures. Thermal conductivity (κe/τ) represents the carrier's conduction because of heat, with only the electronic component calculated while disregarding lattice contributions. For Tl2MoCl6, thermal conductivity escalates from 1.0 × 1014 at 200 K to 1.42 × 1014 (W m−1 K−1 s−1) at 800 K, and a similar trend is observed for Tl2MoBr6, as illustrated in Fig. 8(c). The optimal performance is indicated by minimizing κe/τ, as observed from κ/σ. The electronic to thermal (κ/σ) conductivity ratio is in the order of 10−6,48 emphasizing their significance for thermoelectric applications due to their lower κ/τ values related to σ/τ. The Seebeck coefficient (S) serves as a crucial gauge of potential gradients and is charted against the temperature. The polarity of S values, negative or positive, delineates whether electrons or holes predominate as charge carriers. For temperatures ranging from 200 to 800 K, Fig. 8(c) illustrates the fluctuation in S. Notably, for Tl2Mo(Cl/Br)6, the S value increases as the temperature increases potentially due to disparities in energy magnitude among the upper VB and Ef,49 as illustrated in Fig. 8(c). The magnetic response of materials is characterized by their susceptibility, typically around 10−9 for semiconductors. At 200 K, Tl2Mo(Cl/Br)6 exhibits susceptibility of 4.4 × 10−9 and 3.6 × 10−9 m3 mol−1, respectively; then, its value decreases at 800 K, which is potentially influenced by thermal effects on electron spin movement, as depicted in Fig. 8(d). In Fig. 8(d), σS2/τ, termed the power factor (PF), representing the thermoelectric potency of materials, is drawn against the temperature. The behavior of σ/τ and PF aligns closely due to the extremely conductive response of a material. As the temperature increases, PF diminishes upon substituting Cl with Br.50 Comparative analysis reveals that PF for Tl2MoCl6 surpasses that of Tl2MoBr6 due to the predominance of n-type carrier contributions over p-type carriers.51 The figure of merit (ZT), illustrated in Fig. 8(f), is expressed by ZT = S2σ/κT. A high ZT value at low-temperature values indicates minimal thermal conductivity alongside a small S and higher σ/τ. The relationship for ZT demonstrates a direct proportional trend between κe/τ and σ/τ against temperature. The curve for Tl2MoBr6 is lower, attributed to slightly greater S and high κe/τ compared to the Tl2MoCl6 curve. The maximum ZT values are 0.33 for Tl2MoCl6 and 0.26 for Tl2MoBr6 at 800 K.52
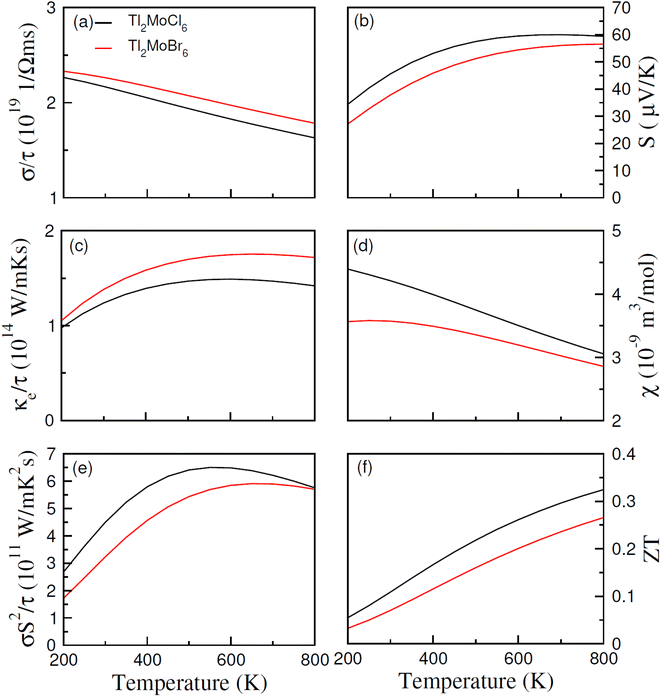 |
| | Fig. 8 Calculated (a) electrical conductivity (σ/τ), (b) thermal conductivity (ke/τ), (c) Seebeck coefficients (S), (d) magnetic susceptibility (χ), (e) power factor and (f) ZT versus temperature for Tl2Mo(Cl/Br)6. | |
4. Conclusion
In the current study, a thorough analysis of the half metallic ferromagnetic and thermoelectric responses of Tl2Mo(Cl/Br)6 double perovskites was conducted to explore their perspectives in spintronics and thermoelectric applications. Initially, structural optimization was performed in the ferromagnetic (FM) and anti-ferromagnetic (AFM) phases, confirming the stability of the FM phase. Additionally, the formation energies of Tl2MoCl6 and Tl2MoBr6 are −1.44 and −1.88 eV, respectively, indicating thermodynamic stability. The 100% spin polarization was confirmed through spin-polarized electronic DOS, revealing underlying hybridization and fractional magnetic moments alongside higher Tc. Exchange energies and valence electron hybridization further confirmed the ferromagnetic response attributed to electron spin instead of clustering. Quantum confinement predominantly influenced negative exchange coefficient values and p–d exchange energy. Moreover, the calculations of S unveiled the existence of p-type semiconducting characteristics in Tl2Mo(Cl/Br)6. The notably higher ZT at 800 K observed as 0.33 and 0.26 for Tl2MoCl6 and Tl2MoBr6, respectively, suggested their comparative suitability for thermoelectric device application.
Data availability
All data presented in this manuscript can be provided by the corresponding author on reasonable demand.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research, King Saud University for funding through the Vice Deanship of Scientific Research Chairs; Research Chair of Prince Sultan Bin Abdulaziz International Prize for Water.
References
- M. Y. Sofi and D. C. Gupta, Scrutinized the inherent spin half-metallicity and thermoelectric response of f-electron-based RbMO3 (M= Np, Pu) perovskites: a computational assessment, Sci. Rep., 2022, 12(1), 19476 CrossRef CAS PubMed.
- Q. L. He, T. L. Hughes, N. P. Armitage, Y. Tokura and K. L. Wang, Topological spintronics and magnetoelectronics, Nat. Mater., 2022, 21(1), 15–23 CrossRef CAS PubMed.
- Y. Zhou, S. Li, W. Zhou, X. Zu and F. Gao, Evidencing the existence of intrinsic half-metallicity and ferromagnetism in zigzag gallium sulfide nanoribbons, Sci. Rep., 2014, 4(1), 5773 CrossRef CAS PubMed.
- P. J. Rajput, S. U. Bhandari and G. Wadhwa, A review on—spintronics an emerging technology, Silicon, 2022, 14(15), 9195–9210 CrossRef CAS.
- B. Dieny, I. L. Prejbeanu, K. Garello, P. Gambardella, P. Freitas, R. Lehndorff and P. Bortolotti, Opportunities and challenges for spintronics in the microelectronics industry, Nat. Electron., 2020, 3(8), 446–459 CrossRef.
- J. Xu, C. Xu, J. B. Liu, L. Bellaiche, H. Xiang, B. X. Liu and B. Huang, Prediction of room-temperature half-metallicity in layered halide double perovskites, npj Comput. Mater., 2019, 5(1), 114 CrossRef CAS.
- S. Niaz, M. A. Khan, N. A. Noor, A. Mahmood, Y. M. Alanazi and S. Mumtaz, Analysis of Structural Stability and Half-Metallic Ferromagnetism of Cs2VX6 (X= Cl, Br) Double-Perovskites for Spintronic Applications: Ab-Initio Simulations, ECS J. Solid State Sci. Technol., 2023, 12(9), 093004 CrossRef.
- S. A. Khandy and D. C. Gupta, New isostructural halide double perovskites Cs2GeNiX6 (X= Cl, Br) for semiconductor spintronics and thermoelectric advancements, J. Solid State Chem., 2021, 300, 122196 CrossRef CAS.
- D. Bendjebbour, T. Seddik, M. W. Mohamed, B. Amrani and K. D. Khodja, Half-metallic ferromagnetism in non-magnetic double perovskite oxides Sr2MSbO6 (M= Al, Ga) doped with C and N, Philos. Mag., 2023, 103(2), 186–201 CrossRef CAS.
- K. Radja, B. L. Farah, A. Ibrahim, D. Lamia, I. Fatima, B. Nabil and A. F. Abd El-Rehim, Investigation of structural, magneto-electronic, elastic, mechanical and thermoelectric properties of novel lead-free halide double perovskite Cs2AgFeCl6: first-principles calcuations, J. Phys. Chem. Solids, 2022, 167, 110795 CrossRef CAS.
- Q. Mahmood, T. Alshahrani, B. Ul Haq, Q. U. A. Gulfam, Y. Tahir, N. A. Kattan and A. Laref, Role of 5d orbital of Re in ferromagnetism and thermoelectric characteristics of Cs2ReCl/Br6 double-perovskites: a density functional theory study, Eur. Phys. J. Plus, 2020, 135(9), 1–13 Search PubMed.
- Q. Mahmood, First-principles calculations to investigate role of 4d electrons spin (Mo/Tc) in half metallic ferromagnetism, and thermoelectric characteristics of Rb2(Tc, Mo) X6 (X= Cl, Br), Ceram. Int., 2023, 49(15), 25121–25129 CrossRef CAS.
- Q. Mahmood, F. Iqbal, T. H. Flemban, E. Algrafy, H. Althib, M. G. B. Ashiq and T. Ghrib, Study of ferromagnetism, and thermoelectric behavior of double perovskites K2Z (Cl/Br)6 (Z= Ta, W, Re) for spintronic, and energy application, J. Phys. Chem. Solids, 2024, 186, 111816 CrossRef CAS.
- H. A. Alburaih, S. Nazir, N. A. Noor and A. Laref, Physical properties of vacancy-ordered double perovskites K2TcZ6 (Z= Cl, Br) for spintronics applications: DFT calculations, RSC Adv., 2024, 14(3), 1822–1832 RSC.
- Q. Mahmood, G. Nazir, A. Rahim, J. Alzahrani, A. I. Aljameel, G. Murtaza and B. U. Haq, Impact of 5d electrons on half metallic ferromagnetism, and thermoelectric properties of Cs2Z(Cl/Br)6 (Z= Os, Ir) for spintronic applications, Mater. Chem. Phys., 2022, 288, 126414 CrossRef CAS.
- J. Doumont, F. Tran and P. Blaha, Implementation of self-consistent MGGA functionals in augmented plane wave based methods, Phys. Rev. B, 2022, 105(19), 195138 CrossRef CAS.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, Accurate and numerically efficient r2SCAN meta-generalized gradient approximation, J. Phys. Chem. Lett., 2020, 11(19), 8208–8215 CrossRef CAS PubMed.
- D. Koller, F. Tran and P. Blaha, Merits and limits of the modified Becke-Johnson exchange potential, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83(19), 195134 CrossRef.
- G. K. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, A(1), 67–71 CrossRef.
- H. R. Aliabad and F. A. Rad, Structural, electronic and thermoelectric properties of bulk and monolayer of Sb2Se3 under high pressure: by GGA and mBJ approaches, Phys. B, 2018, 545, 275–284 CrossRef.
- Z. Xiao, H. Lei, X. Zhang, Y. Zhou, H. Hosono and T. Kamiya, Ligand-hole in [SnI6] unit and origin of band gap in photovoltaic perovskite variant Cs2SnI6, Bull. Chem. Soc. Jpn., 2015, 88(9), 1250–1255 CrossRef CAS.
- A. E. Fedorovskiy, N. A. Drigo and M. K. Nazeeruddin, The role of Goldschmidt's tolerance factor in the formation of A2BX6 double halide perovskites and its optimal range, Small Methods, 2020, 4(5), 1900426 CrossRef CAS.
- Q. Mahmood, M. Hassan, S. H. A. Ahmad, K. C. Bhamu, A. Mahmood and S. M. Ramay, Study of electronic, magnetic and thermoelectric properties of AV2O4 (A= Zn, Cd, Hg) by using DFT approach, J. Phys. Chem. Solids, 2019, 128, 283–290 CrossRef CAS.
- B. Sabir, G. Murtaza, Q. Mahmood, R. Ahmad and K. C. Bhamu, First principles investigations of electronics, magnetic, and thermoelectric properties of rare earth based PrYO3 (Y= Cr, V) perovskites, Curr. Appl. Phys., 2017, 17(11), 1539–1546 CrossRef.
- Q. Mahmood, M. Hassan and N. A. Noor, Systematic study of room-temperature ferromagnetism and the optical response of Zn1− xTMxS/Se (TM= Mn, Fe, Co, Ni) ferromagnets: first-principle approach, J. Phys.: Condens.Matter, 2016, 28(50), 506001 CrossRef CAS PubMed.
- S. A. Mir and D. C. Gupta, Analysis of cage structured halide double perovskites Cs2NaMCl6 (M= Ti, V) by spin polarized calculations, J. Alloys Compd., 2021, 854, 156000 CrossRef CAS.
- X. Du, D. He, H. Mei, Y. Zhong and N. Cheng, Insights on electronic structures, elastic features and optical properties of mixed-valence double perovskites Cs2Au2X6 (X= F, Cl, Br, I), Phys. Lett. A, 2020, 384(8), 126169 CrossRef CAS.
- M. A. Ali, A. A. Alothman, M. Mushab, A. Khan and M. Faizan, DFT insight into structural, electronic, optical and thermoelectric properties of eco-friendly double perovskites Rb2GeSnX6 (X= Cl, Br) for green energy generation, J. Inorg. Organomet. Polym. Mater., 2023, 33(11), 3402–3412 CrossRef CAS.
- S. Maqsood, A. U. Rahman, M. Nawaz, M. A. Ahmad, M. Manzoor, N. A. Noor and S. A. Abdelmohsen, Ab-initio method to investigate organic halide based double perovskites (CH3NH3)2AgMBr6 (M= Sb, Bi) for opto-electronic applications, J. Mater. Res. Technol., 2022, 17, 649–657 CrossRef CAS.
- T. Ouahrani, A. Otero-de-la-Roza, A. H. Reshak, R. Khenata, H. I. Faraoun, B. Amrani and V. Luaña, Elastic properties and bonding of the AgGaSe2 chalcopyrite, Phys. B, 2010, 405(17), 3658–3664 CrossRef CAS.
- N. A. Noor, S. M. Alay-e-Abbas, M. Hassan, I. Mahmood, Z. A. Alahmed and A. H. Reshak, The under-pressure behaviour of mechanical, electronic and optical properties of calcium titanate and its ground state thermoelectric response, Philos. Mag., 2017, 97(22), 1884–1901 CrossRef CAS.
- L. Qiao, Z. Jin, G. Yan, P. Li, L. Hang and L. Li, Density-functional-studying of oP8–, tI16–, and tP4–B2CO physical properties under pressure, J. Solid State Chem., 2019, 270, 642–650 CrossRef CAS.
- Z. Ma, J. Zuo, C. Tang, P. Wang and C. Shi, Physical properties of a novel phase of boron nitride and its potential applications, Mater. Chem. Phys., 2020, 252, 123245 CrossRef CAS.
- X. Li and M. Xing, Novel carbon-rich nitride C3N: a superhard phase in monoclinic symmetry, Comput. Mater. Sci., 2019, 158, 170–177 CrossRef CAS.
- Q. Fan, W. Zhang, S. Yun, J. Xu and Y. Song, III-nitride polymorphs: XN (X= Al, Ga, In) in the Pnma phase, Chem.–Eur. J., 2018, 24(65), 17280–17287 CrossRef CAS PubMed.
- W. Zhang, C. Chai, Q. Fan, Y. Song and Y. Yang, Six novel carbon and silicon allotropes with their potential application in photovoltaic field, J. Phys.: Condens.Matter, 2020, 32(35), 355701 CrossRef CAS PubMed.
- Z. Li, M. Yang, J. S. Park, S. H. Wei, J. J. Berry and K. Zhu, Stabilizing perovskite structures by tuning tolerance factor: formation of formamidinium and cesium lead iodide solid-state alloys, Chem. Mater., 2016, 28(1), 284–292 CrossRef CAS.
- W. Tanveer, Q. Mahmood, I. Mahmood, M. G. B. Ashiq, S. M. Ramay and A. Mahmood, First-principles calculation to investigate half metallic ferromagnetism and thermoelectric properties of Ca0.75Ti0.25X (X= S, Se) alloys, Chem. Phys., 2020, 532, 110690 CrossRef CAS.
- T. H. Flemban, T. Zelai, Q. Mahmood, A. A. S. Devi, M. Sajjad, M. H. Alhossainy and M. A. Amin, Half-metallic ferromagnetism and thermoelectric properties of double perovskites Rb2Z (Cl/Br)6 (Z= Ta, W, Re), J. Alloys Compd., 2022, 894, 162313 CrossRef CAS.
- Y. F. Li, K. C. Zhang and Y. Liu, Spin-orbital coupling and magnetic properties of Ir-based double perovskites with different 5dn (n= 3, 4, 5) states, Phys. Lett. A, 2019, 383(6), 558–565 CrossRef CAS.
- C. W. Zhang and S. S. Yan, First-principles prediction of half-metallic ferromagnetism in Cu-doped ZnS, J. Appl. Phys., 2010, 107(4), 043913 CrossRef.
- A. Bupu, M. A. Majidi and A. Rusydi, Theoretical study on the magnetic moments formation in Ta-doped anatase TiO2, IOP Conf. Ser.: Mater. Sci. Eng., 2017, 188(1), 012009 Search PubMed.
- H. Ishikawa, T. Takayama, R. K. Kremer, J. Nuss, R. Dinnebier, K. Kitagawa and H. Takagi, Ordering of hidden multipoles in spin-orbit entangled 5 d 1 Ta chlorides, Phys. Rev. B, 2019, 100(4), 045142 CrossRef CAS.
- H. T. Jeng and G. Y. Guo, First-principles investigations of orbital magnetic moments and electronic structures of the double perovskites Sr2FeMoO6, Sr2FeReO6, and Sr2CrWO6, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(9), 094438 CrossRef.
- H. Kato, T. Okuda, Y. Okimoto, Y. Tomioka, Y. Takenoya, A. Ohkubo and Y. Tokura, Metallic ordered double-perovskite Sr2CrReO6 with maximal Curie temperature of 635 K, Appl. Phys. Lett., 2002, 81(2), 328–330 CrossRef CAS.
- G. Zhou and D. Wang, Few-quintuple Bi2Te3 nanofilms as potential thermoelectric materials, Sci. Rep., 2015, 5(1), 8099 CrossRef CAS PubMed.
- M. G. B. Ashiq, Q. Mahmood, T. Zelai, O. Hakami, N. A. Kattan, H. Albalawi and K. I. Hussein, The narrow band bap double perovskites X2CuInCl6 (X= K, Rb, Cs) for optoelectronics, and thermoelectric applications, Mater. Sci. Eng. B, 2023, 296, 116690 CrossRef CAS.
- H. C. Wang, P. Pistor, M. A. Marques and S. Botti, Double perovskites as p-type conducting transparent semiconductors: a high-throughput search, J. Mater. Chem. A, 2019, 7(24), 14705–14711 RSC.
- D. Campi, L. Paulatto, G. Fugallo, F. Mauri and M. Bernasconi, First-principles calculation of lattice thermal conductivity in crystalline phase change materials: GeTe, Sb2Te3, and Ge2Sb2Te5, Phys. Rev. B, 2017, 95(2), 024311 CrossRef.
- H. Albalawi, G. Nazir, M. Younas, S. Al-Qaisi, M. G. B. Ashiq, J. Alzahrani and T. Ghrib, Study of lead-free vacancy ordered double perovskites Cs2TeX6 (X= Cl, Br, I) for solar cells, and renewable energy, Phys. Scr., 2022, 97(9), 095801 CrossRef CAS.
- Q. Mahmood, M. H. Alhossainy, M. S. Rashid, T. H. Flemban, H. Althib, T. Alshahrani and A. Laref, First-principles study of lead-free double perovskites Rb2TeX6 (X= Cl, Br, and I) for solar cells and renewable energy, Mater. Sci. Eng. B, 2021, 266, 115064 CrossRef CAS.
- M. Sajjad, N. Singh, S. Sattar, S. De Wolf and U. Schwingenschlögl, Ultralow lattice thermal conductivity and thermoelectric properties of monolayer Tl2O, ACS Appl. Energy Mater., 2019, 2(5), 3004–3008 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b,
Bisma Younasc,
N. A. Noora,
Mehdi Alid,
Sadia Nazir
b,
Bisma Younasc,
N. A. Noora,
Mehdi Alid,
Sadia Nazir *c,
Ahmed Z. Dewidaref and
Hosam O. Elansary*eg
*c,
Ahmed Z. Dewidaref and
Hosam O. Elansary*eg
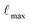 (angular momentum vector) and Gmax (Gaussian factor) were carefully selected for accuracy, with computed results converging to the order of 10−3 mRy. Transport response was estimated utilizing the BoltzTrap code, providing an inclusive analysis of the material's properties.20
(angular momentum vector) and Gmax (Gaussian factor) were carefully selected for accuracy, with computed results converging to the order of 10−3 mRy. Transport response was estimated utilizing the BoltzTrap code, providing an inclusive analysis of the material's properties.20
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 225) space group in cubic phase and determination of ground-state parameters were conducted using the Birch–Murnaghan equation of states (Table 1).21 Fig. 1 illustrates unit cells in both ball-stick (left) and polyhedral (right) formats, showcasing atomic arrangement and geometric configuration, respectively. Within MoCl/Br6 octahedra, the Tl atom fills vacancies, which exhibit 12-fold coordination with Cl/Br atoms, resulting in individual octahedra being distinct from the others. The Mo atoms occupies the center of the octahedra, encircled by six Cl/Br atoms, while the Mo atoms are also present at the face centers and corners.22 Wyckoff positions for Tl (8c), Mo (4a), and Cl/Br (24e) were utilized for structure generation and optimization. Through the replacement of Cl with Br, atomic radii increase, consequently enlarging the lattice constant in the range of 9.95–10.54 Å and inter-atomic distance, thus reducing material density and solidness, and leading to a decrease in bulk moduli (B) from 43.75–35.95 GPa.23 The same type of variation in the lattice constant has also been observed by Mahmood et al. in Cs2ReCl/Br6 double perovskites.11 The considerable bulk modulus of Tl2MoBr6 suggests greater stiffness compared to Tl2MoCl6. Energy plots against volume in the ferromagnetic (FM) and anti-ferromagnetic (AFM) phases, as displayed in Fig. 2, reveal higher energy release in the FM state, indicating its greater favorability. Furthermore, energy formation was computed to evaluate thermal stability using the following equation:24
m (no. 225) space group in cubic phase and determination of ground-state parameters were conducted using the Birch–Murnaghan equation of states (Table 1).21 Fig. 1 illustrates unit cells in both ball-stick (left) and polyhedral (right) formats, showcasing atomic arrangement and geometric configuration, respectively. Within MoCl/Br6 octahedra, the Tl atom fills vacancies, which exhibit 12-fold coordination with Cl/Br atoms, resulting in individual octahedra being distinct from the others. The Mo atoms occupies the center of the octahedra, encircled by six Cl/Br atoms, while the Mo atoms are also present at the face centers and corners.22 Wyckoff positions for Tl (8c), Mo (4a), and Cl/Br (24e) were utilized for structure generation and optimization. Through the replacement of Cl with Br, atomic radii increase, consequently enlarging the lattice constant in the range of 9.95–10.54 Å and inter-atomic distance, thus reducing material density and solidness, and leading to a decrease in bulk moduli (B) from 43.75–35.95 GPa.23 The same type of variation in the lattice constant has also been observed by Mahmood et al. in Cs2ReCl/Br6 double perovskites.11 The considerable bulk modulus of Tl2MoBr6 suggests greater stiffness compared to Tl2MoCl6. Energy plots against volume in the ferromagnetic (FM) and anti-ferromagnetic (AFM) phases, as displayed in Fig. 2, reveal higher energy release in the FM state, indicating its greater favorability. Furthermore, energy formation was computed to evaluate thermal stability using the following equation:24

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730
730![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730
730![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810
810![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810
810