Open Access Article
Open Access ArticleOptimization of the catalytic production of methyl stearate by applying response surface Box–Behnken design: an intensified green option for high-cetane biofuel manufacture†
Federico Manuel Reyes-Cruz a,
Juana Deisy Santamaría-Juáreza,
Manuel Sánchez-Cantú
a,
Juana Deisy Santamaría-Juáreza,
Manuel Sánchez-Cantú *a and
Roberto Quintana-Solórzano
*a and
Roberto Quintana-Solórzano *b
*b
aFacultad de Ingeniería Química, Benemérita Universidad Autónoma de Puebla, Avenida San Claudio y 18 Sur, C.P. 72570 Puebla, Puebla, Mexico. E-mail: manuel.sanchez@correo.buap.mx
bInstituto Mexicano del Petróleo, Eje Central Lázaro Cárdenas Norte 152, Ciudad de México, 07730, Mexico. E-mail: rquintana@imp.mx
First published on 5th June 2024
Abstract
To enhance the efficiency of processes by decreasing the reaction severity and energy consumption, and reducing the equipment size, facilities' space and operation cost, process intensification is an increasingly used option in the chemical industry. Within this framework and in agreement with some of the green chemistry principles (design for energy efficiency and use of renewable feedstocks), this work deals with the implementation of high-shear mixing (HSM) to intensify the homogeneous esterification of stearic acid (SA) with methanol to methyl stearate, a high-cetane number alkyl ester suitable to be added into biofuel streams. The response surface Box–Behnken design (BBD) is applied to quantify the main effects and two-way interactions of four key input reaction factors: methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio (7–16 mol mol−1), catalyst mass (0.25–4.0 wt%), temperature (40–60 °C), time (1–12 min), and to approximate the optimal conditions on the intensified SA esterification. The statistical BBD results indicates that the four linear effects, two of the four possible quadratic effects (catalyst mass and temperature) and only one (catalyst mass–time) of the six existing two-way interactions are statistically relevant at the 95% confidence level. Catalyst mass is the most influencing factor in the reaction, followed by methanol
SA ratio (7–16 mol mol−1), catalyst mass (0.25–4.0 wt%), temperature (40–60 °C), time (1–12 min), and to approximate the optimal conditions on the intensified SA esterification. The statistical BBD results indicates that the four linear effects, two of the four possible quadratic effects (catalyst mass and temperature) and only one (catalyst mass–time) of the six existing two-way interactions are statistically relevant at the 95% confidence level. Catalyst mass is the most influencing factor in the reaction, followed by methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio, temperature, and time. The proposed second-order regression model predicts that the intensified esterification requires only 12 min to practically convert all SA (99% ± 6.8%) running the reaction at 12.4 methanol
SA ratio, temperature, and time. The proposed second-order regression model predicts that the intensified esterification requires only 12 min to practically convert all SA (99% ± 6.8%) running the reaction at 12.4 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio, 4 wt% catalyst mass, 60 °C and 500 rpm, a value experimentally validated (93.2% ± 0.7%). Under these conditions and with the assistance of HSM, the typical reaction length of conventional heterogeneous and homogeneous-phase esterification processes decreases from 5 to 117 and 35 to 90 times, respectively.
SA ratio, 4 wt% catalyst mass, 60 °C and 500 rpm, a value experimentally validated (93.2% ± 0.7%). Under these conditions and with the assistance of HSM, the typical reaction length of conventional heterogeneous and homogeneous-phase esterification processes decreases from 5 to 117 and 35 to 90 times, respectively.
Introduction
Energy consumption worldwide is growing year by year to satisfy the increasing needs of humankind. Although the use of diverse alternative energy forms such as solar, wind, and geothermic are gradually increasing, fossil fuels will still have a relevant role in industrial development worldwide. The key sectors of demand for fossil fuels are well identified and specifically pertain to land, air and maritime transportation as well as to the production of petrochemical compounds, which are gaining importance.1–3 In the context of fuels used for land transportation, particular attention has been paid towards diesel engine motors as they are highly reliable for moving oversized loads in places like cities, country roads and marine regions. Notwithstanding, during diesel combustion in diesel-powered engines, several toxic emissions such as COx, SOx, NOx, particulate matter and unburned hydrocarbons are generated in relatively large amounts.4 From the beginning, biofuels and bioadditives have been decidedly considered alternatives to gradually mitigate the environmental impact caused by the combustion of petroleum-based fuels. Among them, much attention has been centred on biodiesel (BD) due to its similarities to diesel. BD consists of a mixture of alkyl esters that are produced by the transesterification of vegetable oils or animal greases or by the catalytic esterification of fatty acids with a short chain alcohol (generally methanol).5The physicochemical properties of BD are closely related to their quality and, therefore, they can be conveniently adjusted by modifying its native chemical composition. In this respect, the cetane number (CN) of BD, which is a key property for determining diesel's quality, is notably influenced by the nature of the constituent triglyceride or free fatty acids. Giakoumis,6 who reported values of CN for distinct triglyceride sources such as soybean, palm, coconut oil, beef tallow and chicken fat, commented on the effect of the triglyceride profile on the CN values. Yanowitz et al.,7 in turn, published a compilation of 299 CN values for pure chemical compounds. Interestingly, it has been reported that alkyl esters prepared from stearic, palmitic, myristic or lauric acid display the highest CN values. Among them, methyl stearate (MST) exhibited the highest CN ranging from 75.6 to 95.6; therefore, MST production is identified as a reasonable alternative for extensively using this compound as a high CN biofuel or even as a CN bioadditive for low CN fuels.
Concerning MST production, it is well known that this alkyl ester can be synthesized via the esterification of stearic acid (SA) with methanol following homogeneous, heterogeneous, or enzymatic routes; however, the number of reports dealing with the synthesis of MST is scarce contrasting to what is found for other alkyl esters. Regarding the heterogeneous route for MST production, some catalysts including montmorillonite-based clays,8–11 Amberlyst-15,12 Nb2O5,13 tin zirconium oxide,14 amidoximated polyacrylonitrile ion exchange fibres,15 carbon-based catalyst16 and sulfated ZrO2–SiO2 (ref. 17) have been tested. Although the heterogeneous route seems to be the most attractive, it has set disadvantages that are basically ascribed to the required reaction severity, i.e., the relatively high temperature (60–160 °C) and large reaction time (−23 h), the large excess of alcohol related to the fatty acid amount (1–150), the catalyst amount (0.07–30%) and the pretreatment with acids for activation prior to the reaction; all this certainly complicates the route to scale-up. Regarding the enzymatic route, the use of alcohols such as ethanol18,19 and n-butanol19 have been reported in the esterification of SA. Concerning the homogeneous synthesis of MST, two reports were identified in the literature: one using AlCl3 as a catalyst that converted 98% of SA conversion running at 18 h of reaction time, 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio, 5% catalyst and 110 °C,20 and a second one using sulfuric acid as the catalyst in which SA conversion amounted to 97% at 60 °C after 7 h of reaction time, adding 6% catalyst and 60
1 molar ratio, 5% catalyst and 110 °C,20 and a second one using sulfuric acid as the catalyst in which SA conversion amounted to 97% at 60 °C after 7 h of reaction time, adding 6% catalyst and 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mol ratio of alcohol
3 mol ratio of alcohol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fatty acid.17 In homogenous esterification, advantageously, SA conversion was almost complete; nonetheless, a very large reaction time is usually required.
fatty acid.17 In homogenous esterification, advantageously, SA conversion was almost complete; nonetheless, a very large reaction time is usually required.
An attractive alternative to overcome the above-mentioned drawbacks regarding the large reaction time of conventional processes pertains to the incorporation of intensification options.21 Recently, the application of the high-shear mixing (HSM) technology displayed promising results for intensifying the transesterification of triglycerides,22,23 esterification of fatty acids,24 production of azidoesteroids25 and anionic clays,26 respectively. Being little mass transfer restricted and requiring lower reaction severity (temperature, residence time, etc.) to run compared to non-assisted counterparts,27 processes assisted by HSM are expected to be more efficient and require simplified facilities. Thus, it is necessary to perform a quantitative and systematic assessment of the reactor operating variables in the route to scale up and optimize intensified processes. To this end, the application of formal design of experiments (DoE) is a suitable, effective, cheap, and fast option as it provides valuable information through a reasonable number of well-selected set of experimental runs.
Among several studies on MST production are available in the scientific literature, a very small number of publications deal with the application of DoE are found: two report relatively simple 2k factorial designs9,28 and only one applies a Box–Behnken design for a heterogeneous reaction yet is limited to two factors.10 The so-called response surface designs such Central Composite (CCD) and Box–Behnken (BBD) are suitable for investigating processes dealing with more than three factors require a reasonable number of experiments and can be used for optimization.29 BBD includes experimental points positioned in the middle of the edges, thus providing a better description of non-linear effects compared to CCD.29–32 In this context, our publication aims to rigorously quantify, by applying response surface BBD, the concomitant effect of four principal reaction variables (methanol to SA molar ratio, catalyst mass, temperature and time) on the HSM-assisted liquid phase acid-catalysed esterification of SA with methanol to MST.
Material and methods
Chemicals
SA was acquired from Fermont Lab (94.2%), whilst methyl alcohol (95%), isopropyl alcohol (95%), phenolphthalein solution (1%) and sulfuric acid (95%) were purchased from Meyer. Potassium hydroxide in the form of pellets (85%) was procured from Golden Bell and the deuterated chloroform used in the 1H NMR analyses (99.8 atom %D) was acquired from Sigma-Aldrich. All reactants were used without further purification. Deionized water (25 MΩ cm) was supplied by a water deionizing plant installed at the facilities of the BUAP University.Materials characterization
The acid value measurement (AV) was carried out by the titration method reported by Zhang et al.,33 using eqn (1).
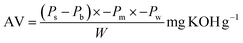 | (1) |
To verify the formation of MST upon the reaction, the product of the esterification of SA with methanol from an experiment carried out at methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio = 11.5, catalyst mass = 2.98 g, temperature = 60 °C and time = 12 min, under stirring at 500 rpm was analysed by proton nuclear magnetic resonance (1H NMR); SA was also characterized by this analytical technique. The reaction products were dissolved in deuterated chloroform and then analysed in a Bruker Avance III 500 MHz NMR spectrometer. The chemical shifts (δ) were expressed in ppm (parts per million).
SA ratio = 11.5, catalyst mass = 2.98 g, temperature = 60 °C and time = 12 min, under stirring at 500 rpm was analysed by proton nuclear magnetic resonance (1H NMR); SA was also characterized by this analytical technique. The reaction products were dissolved in deuterated chloroform and then analysed in a Bruker Avance III 500 MHz NMR spectrometer. The chemical shifts (δ) were expressed in ppm (parts per million).
Esterification reaction of SA
The experimental synthesis of MST was conducted in the batch mode based on the procedure reported previously.24(i) SA was heated at 40 °C, methanol was added, and, afterwards, the resulting mixture was heated to the required reaction temperature.
(ii) Next, sulfuric acid was added to the SA and methanol mixture in the required quantity to catalyse the rection, and.
(iii) The resulting admixture was subsequently dispersed for the defined reaction time at 500 rpm in a ROSS HSM-100 LCI high shear mixer equipped with a slotted stator head dispersion attachment vide Section S1 in the ESI.† The mixing rate was defined through preliminary experiments, which are displayed in detail in the ESI.† Upon the reaction, the unreacted methanol was removed in a rotavapor at reduced pressure. The methanol-free sample was then washed with hot water to eliminate the remaining catalyst (see Section S1 in the ESI†). The aqueous fraction was subsequently removed using a separation funnel, producing a sample consisting of unconverted SA and MST, which was then titrated to determine the AV value.33 Finally, the percentage of SA converted during the esterification reaction was determined according with eqn (2), which is related to the AV, where AVSai is the AV before the reaction) and AVSaf is the AV after the reaction.34
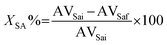 | (2) |
Box–Behnken design
The factors and corresponding operation intervals of the BBD applied to investigate the HSM-assisted liquid phase acid-catalysed esterification of SA with methanol to MST were as follows: methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio (7–16 mol mol−1), catalyst mass (0.25–4.0 g), temperature (40–60 °C), and time (1–12 min). In a similar homogeneous reaction system,24 the incorporation of HSM led to a low stirring speed-sensitive process. Preliminary SA esterification to MST experiments confirmed this behaviour (see Fig. S1 in the ESI†); therefore, the stirring speed was set to 500 rpm and removed from the design experiments, thus leading to a more manageable BBD. The four remaining factors are independent variables influencing the catalyst performance, kinetics and reactor operation, with the respective intervals being defined by combining the state-of-art information, experimental set-up limitations, preliminary experimental results (vide Fig. S2 in ESI†) and chemical equilibrium data.
SA ratio (7–16 mol mol−1), catalyst mass (0.25–4.0 g), temperature (40–60 °C), and time (1–12 min). In a similar homogeneous reaction system,24 the incorporation of HSM led to a low stirring speed-sensitive process. Preliminary SA esterification to MST experiments confirmed this behaviour (see Fig. S1 in the ESI†); therefore, the stirring speed was set to 500 rpm and removed from the design experiments, thus leading to a more manageable BBD. The four remaining factors are independent variables influencing the catalyst performance, kinetics and reactor operation, with the respective intervals being defined by combining the state-of-art information, experimental set-up limitations, preliminary experimental results (vide Fig. S2 in ESI†) and chemical equilibrium data.
Table 1 includes a summary of the four factors of the BBD, the corresponding full and short names for the purposes of this work, and the respective levels in accordance with typical DoE codification wherein the low, central or middle and high levels are denoted by “−1”, “0”, and “+1”, respectively. Notice that three levels per factor are needed. The explicit BBD experimental matrix containing the specific reaction conditions per experiment is displayed in Table S2 in the ESI.† The total number of experimental points (N) is given by 2k (k − 1) + nc, where k = 4 represents the number of factors and nc = 3 denotes the replicates at the middle point. Thus, N amounted to 27, corresponding to the summation of 24 base runs resulting from the combination of the midpoints of edges of the process region and at the centre point, plus 3 replicated runs at the centre point;29–32 which are used to compute the so-called pure error.35,36 Likewise, aimed at finding the set of reaction conditions that maximize SA conversion, response surface methodology was applied fitting the raw experimental data to a full second-order regression model.
| BBD factors coding | BBD factors level | |||
|---|---|---|---|---|
| Full name | Short name | Low | Middle | High |
| −1 | 0 | +1 | ||
Methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio, mol mol−1 SA ratio, mol mol−1 |
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA SA |
7.0 | 11.5 | 16.0 |
| Catalyst mass, wt% | Cat | 0.25 | 2.125 | 4.0 |
| Temperature, °C | Temp | 40 | 50 | 60 |
| Time, min | Time | 1.0 | 6.5 | 12.0 |
Results and discussion
Proton nuclear magnetic resonance (1H NMR) characterization
1H NMR analysis was used to verify the formation of MTS in the esterification reaction between SA and methanol catalized by sulfuric acid. To this end, two samples were analysed, where was SA used as the starting material and the product recovered upon reaction under the following conditions: methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio = 11.5, catalyst mass = 2.98 g, temperature = 60 °C, time = 12 min, and stirring speed = 500 rpm. The corresponding 1H-NMR spectra are shown in Fig. 1. Indicated with number in the SA 1H NMR spectrum in Fig. 1a, the set of observed characteristic chemical shifts, δ (ppm) correspond to 2.37–2.32 (t, 2H, –CH2–) −1, 1.66–1.60 (m, 2H, –CH2–) −2, 1.32–1.25 (m, 28H, –CH2–) −3, 0.89–0.87 (t, 3H, –CH3) −4. The difference between the 1H NMR spectrum of SA and that of MST (see Fig. 1b) is clearly noticed by the signal appearing at 3.67 ppm, which is ascribed to the protons of the methoxy group (s, 3H –OCH3)−1*, thereby evidencing the presence of a methyl ester.15,20
SA ratio = 11.5, catalyst mass = 2.98 g, temperature = 60 °C, time = 12 min, and stirring speed = 500 rpm. The corresponding 1H-NMR spectra are shown in Fig. 1. Indicated with number in the SA 1H NMR spectrum in Fig. 1a, the set of observed characteristic chemical shifts, δ (ppm) correspond to 2.37–2.32 (t, 2H, –CH2–) −1, 1.66–1.60 (m, 2H, –CH2–) −2, 1.32–1.25 (m, 28H, –CH2–) −3, 0.89–0.87 (t, 3H, –CH3) −4. The difference between the 1H NMR spectrum of SA and that of MST (see Fig. 1b) is clearly noticed by the signal appearing at 3.67 ppm, which is ascribed to the protons of the methoxy group (s, 3H –OCH3)−1*, thereby evidencing the presence of a methyl ester.15,20
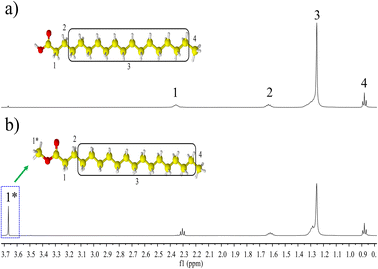 | ||
| Fig. 1 1H NMR spectra: (a) stearic acid (SA) used as a reagent in the esterification reaction, and (b) methyl stearate (MST) produced in the reaction of SA with methanol. | ||
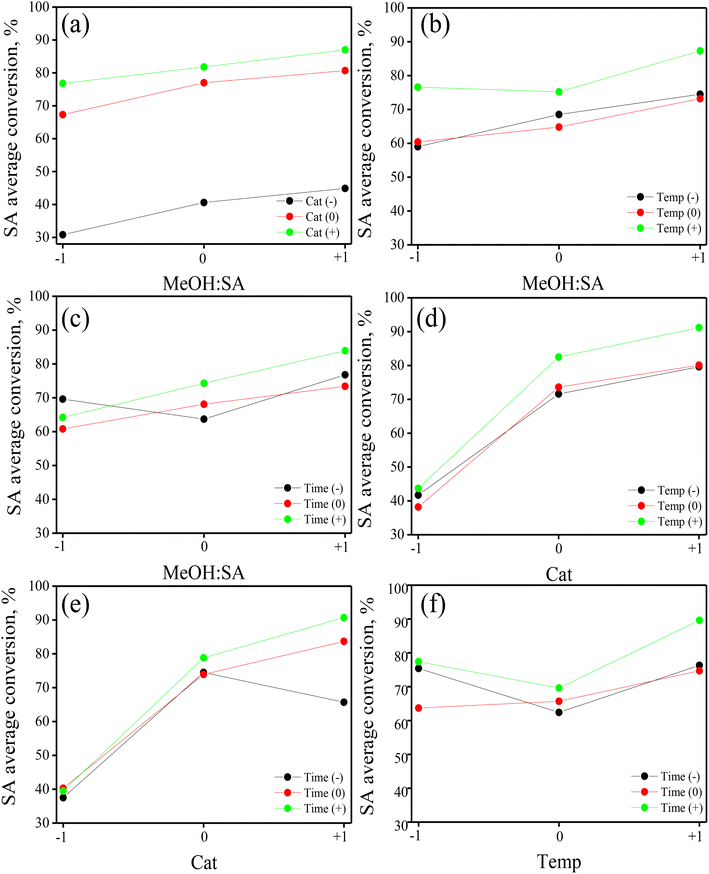
Graphical assessment of the main effects and interactions
A qualitative valuation of the main effects of the individual DoE factors and the possible two-way interactions was done by the visual inspection of the so-called main effect and interaction graphs. Built using the available raw experimental results, these graphs provide valuable information to have an initial view of the relative magnitude and nature of the various treatments in the BBD.37,38 In the case of main effects, they show how the average response value varies as the level of the factor in the BBD gradually increases from level “−1” to “0” and then from level “0” to “+1”. For a multi-factor DoE, the existence of interaction between the pair of factors is common;38 in this sense, the corresponding graphs are useful to visualize whether or not the effect of the first factor is influenced by the level of the second factor.Fig. 2 displays the main effect graphs for the four factors in the BBD. They contain three points comprising the average value of SA conversion of experiments operated at the levels “−1”, “0” and “+1” of a given factor, independent of the level of the other three factors in the DoE.33,34 The shape of the line (straight or curve) joining the three points in the graphs indicates the nature (linear or non-linear) of the main effect, while the slope of the line (positive, neutral, or negative) denotes the direction and intensity of the main effect on the response. From Fig. 2a, it is noted that the main effect of MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio on the response is almost linear and positive and has a moderate intensity. Fig. 2b suggests that the main effect of catalyst mass on SA conversion is positive and non-linear, showing a concave down increasing trend as the response value is more notably affected when augmenting the factor level from “−1” to “0”. Fig. 2c and d are very similar, indicating that both temperature and time have a weak average positive and non-linear effect, displaying a concave up increasing trend.
SA ratio on the response is almost linear and positive and has a moderate intensity. Fig. 2b suggests that the main effect of catalyst mass on SA conversion is positive and non-linear, showing a concave down increasing trend as the response value is more notably affected when augmenting the factor level from “−1” to “0”. Fig. 2c and d are very similar, indicating that both temperature and time have a weak average positive and non-linear effect, displaying a concave up increasing trend.
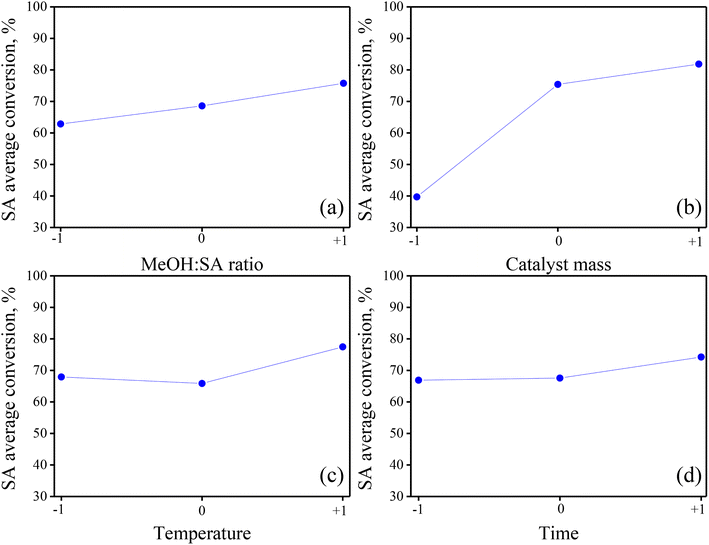 | ||
Fig. 2 Main effects graphs for the four factors accounted for in the BBD: (a) methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio, (b) catalyst mass, (c) temperature and (d) time. SA ratio, (b) catalyst mass, (c) temperature and (d) time. | ||
Based on a comparison of the four main effect graphs in Fig. 2, qualitatively, the catalyst mass appears as the most influencing factor in the process, followed by the MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio, temperature and time. Moreover, as most of the points in the graphs in Fig. 2 do not align to a straight line, quadratic effects (or curvature) are expected to be important in the process with a magnitude that must be quantified through a rigorous formal statistical analysis, as will be presented in further sections.
SA ratio, temperature and time. Moreover, as most of the points in the graphs in Fig. 2 do not align to a straight line, quadratic effects (or curvature) are expected to be important in the process with a magnitude that must be quantified through a rigorous formal statistical analysis, as will be presented in further sections.
Regarding binary interactions, Fig. 3 depicts the six possible two-way interaction graphs of the BBD. These graphs contain three series of average response values of experiments run at the levels “−1”, “0” and “+1” of one of the factors while gradually varying the level of a second factor, irrespective of the level of the two remaining factors.37,38 There is evidence of a binary interaction when the slope of three trendlines changes; in fact, the more different the slopes, the stronger the interaction between the factors. In this sense, the three trendlines in Fig. 3a and d are practically parallel, suggesting that the binary interactions methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio–temperature and catalyst mass – time would not be relevant in the reaction. Conversely, the binary interactions methanol
SA ratio–temperature and catalyst mass – time would not be relevant in the reaction. Conversely, the binary interactions methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio–temperature (Fig. 3b), methanol
SA ratio–temperature (Fig. 3b), methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio–time (Fig. 3c), catalyst mass–time (Fig. 3e), and temperature–time (Fig. 3f) are expected to be relevant as the slope of the three trendlines in the corresponding graphs and even the intercept are different, as occurs in the case of Fig. 3f. The application of formal statistical tools will generate appropriate information to quantify these interactions and determine their statistical significance at a given probability level, vide infra.
SA ratio–time (Fig. 3c), catalyst mass–time (Fig. 3e), and temperature–time (Fig. 3f) are expected to be relevant as the slope of the three trendlines in the corresponding graphs and even the intercept are different, as occurs in the case of Fig. 3f. The application of formal statistical tools will generate appropriate information to quantify these interactions and determine their statistical significance at a given probability level, vide infra.
Fitting the BBD results with the full regression model
When applying response surface design of experiments such as CCD or BBD, a mathematical equation is used to predict the experimental response values as a function of the factors of the DoE.38 As the visual inspection of the main effects and binary interaction graphs (see Fig. 2 and 3) suggests that curvature may be important for some of the BBD factors, a second-order polynomial was incorporated. Notice that this mathematical expression, which is generally represented by eqn (3), explicitly includes linear and quadratic effects and two-way interactions. In eqn (3), Ŷ represents the value response, xi and xj are the factors or independent variables with i (or j) = 1, 2,…, k.37,38 The parameter βo is defined as the intercept with the ordinate axis, and the parameters βi, βii and βij symbolize, accordingly, the regression parameters ascribed to linear, quadratic and two-way interaction effects.
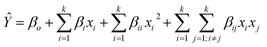 | (3) |
The BBD used in this work contains four factors (i.e., k = 4) and, therefore, the explicit form of the full second-order polynomial model of eqn (3) contains 15 adjustable parameters (β0, β1,…, β4, β11,…, β44, β12,…, β34), whilst the independent variables in eqn (3) correspond to x1, x2, x3 and x4 and denote the factors methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio, catalyst mass, temperature, and time, respectively. The model parameters were numerically estimated via regression with the software Data Fit 7.1 using the 27 experimental SA conversion values as input (see ESI Table S1†). The main values of the parameters in the full regression model are displayed in Table 2, which also includes, as a footnote, the relevant statistical information to assess the quality of the numerical fitting and model adequacy. Notice that the multiple determination coefficient (R2) was as high as 0.9768, indicating that 98% of the data variability is explained by the model, while for the F-test: F0,reg (=36.21) > Fcrit,reg (=2.5342) and the p-test: p value for lack of fit (=0.000) < 0.05; that said, there is evidence that the full regression model exhibits no lack of fit.39
SA ratio, catalyst mass, temperature, and time, respectively. The model parameters were numerically estimated via regression with the software Data Fit 7.1 using the 27 experimental SA conversion values as input (see ESI Table S1†). The main values of the parameters in the full regression model are displayed in Table 2, which also includes, as a footnote, the relevant statistical information to assess the quality of the numerical fitting and model adequacy. Notice that the multiple determination coefficient (R2) was as high as 0.9768, indicating that 98% of the data variability is explained by the model, while for the F-test: F0,reg (=36.21) > Fcrit,reg (=2.5342) and the p-test: p value for lack of fit (=0.000) < 0.05; that said, there is evidence that the full regression model exhibits no lack of fit.39
| Model parameter | Main value | Model parameter | Main value |
|---|---|---|---|
| a Regression sum of squares (SSReg) = 8046.28; lack-of-fit (LoF) sum of squares (SSLoF) = 189.35; error sum of squares (SSError) = 190.43; multiple determination coefficient (R2) = 0.9768; F0,reg = 36.21 with Fcrit,reg (0.05,14,12) = 2.5342, F0,reg > Fcrit,reg.; p value for LoF = 0.000 (<0.05). | |||
| β0 | 110.364 × 100 | — | — |
| β1 | 3.437 × 100 | β44 | 2.684 × 10−2 |
| β2 | 19.295 × 100 | β12 | −1.146 × 10−1 |
| β3 | −3.823 × 100 | β13 | −2.684 × 10−2 |
| β4 | −4.898 × 100 | β14 | 1.258 × 10−1 |
| β11 | −5.403 × 10−2 | β23 | 1.284 × 10−1 |
| β22 | −3.948 × 100 | β24 | 5.569 × 10−1 |
| β33 | 3.997 × 10−2 | β34 | 5.174 × 10−2 |
To verify graphically the adequacy of the full regression model to simulate the experimental results for SA conversion, the so-called parity and residuals plots were built (see Fig. 4). The parity plot in Fig. 4a shows that the predicted response values matched well with the experimental counterparts as the corresponding points are close and align well to the 45° reference line in the graph. Likewise, the plot in Fig. 4b indicates that the residual values distribution (model-predicted SA conversion minus experimental SA conversion) is random with respect to the model-predicted SA conversion values.
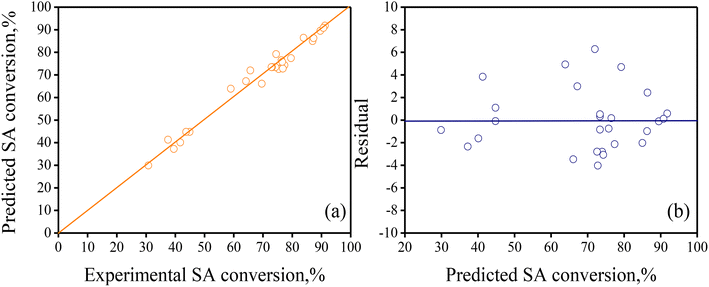 | ||
| Fig. 4 (a) Parity plot contrasting computed SA conversion vs. experimental SA conversion, and (b) residuals as a function of the predicted SA conversion values. The full regression model in eqn (4) with the parameters in Table 2 was used to calculate the response values. | ||
Variance analysis (ANOVA) and individual confidence limits
The application of graphical tools only provided a preliminary understanding of the main effect and interaction of the factors accounted in the BBD; therefore, the implementation of formal statistical tools is required to determine their magnitude and significance at a defined probability level. The ANOVA, which is based on the values of sum of squares (SS) and mean squares (MS) for the different treatments (i.e., main/quadratic effects and interactions),37–39 offers valuable information on their relative magnitude and statistical significance. Notwithstanding, as ANOVA does not offer information about the absolute magnitude and direction of various treatments, it must be complemented with the calculation of the individual confidence limits (ICL), which comprises the estimate of the treatment and its margin of error at the same probability level used in ANOVA.In Table 3, the ANOVA results of the BBD are summarized for the linear and quadratic effects as well as the two-way interactions. To determine the statistical significance of the treatments, the F-test was applied, and the p-values were computed. The F-test incorporates the F value (F0), which is obtained by dividing the MS of the treatment by the MS of the total error. For any treatment and the total error, the MS values are computed by dividing the SS by the degrees of freedom. F0 is next contrasted with the tabulated F-value or F critical (Fcrit), which is obtained at a given probability level (usually 95% or 0.95, or a significance level of 5% or 0.05) and the degrees of freedom of the treatment (ν1) and the total error (ν2). The p-value, in turn, was obtained from F0 and the degrees of freedom ν1 and ν2. The treatment is statistically significant when F0 > Fcrit or p-value < 0.05.
| Treatment | DF | SS | MS | F0 | Fcrit at 95% prob. | p-value | F0 > Fcrit or p-value < 0.05 |
|---|---|---|---|---|---|---|---|
| Full model | 14 | 8046.29 | 574.73 | 36.22 | 2.64 | 0.000 | Sign. |
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA SA |
1 | 500.28 | 500.28 | 31.52 | 4.75 | 0.000 | Sign. |
| Cat | 1 | 5328.98 | 5328.98 | 335.79 | 4.75 | 0.000 | Sign. |
| Temp | 1 | 272.85 | 272.85 | 17.19 | 4.75 | 0.001 | Sign. |
| Time | 1 | 162.07 | 162.07 | 10.21 | 4.75 | 0.008 | Sign. |
(MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA)2 SA)2 |
1 | 6.39 | 6.39 | 0.4 | 4.75 | 0.538 | No sign. |
| (Cat)2 | 1 | 1027.59 | 1027.59 | 64.75 | 4.75 | 0.000 | Sign. |
| (Temp)2 | 1 | 85.23 | 85.23 | 5.37 | 4.75 | 0.039 | Sign. |
| (Time)2 | 1 | 3.52 | 3.52 | 0.22 | 4.75 | 0.646 | No sign. |
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA–cat SA–cat |
1 | 3.74 | 3.74 | 0.24 | 4.75 | 0.636 | No sign. |
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA–temp SA–temp |
1 | 5.77 | 5.77 | 0.36 | 4.75 | 0.558 | No sign. |
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA–time SA–time |
1 | 38.79 | 38.79 | 2.44 | 4.75 | 0.144 | No sign. |
| Cat–temp | 1 | 23.2 | 23.2 | 1.46 | 4.75 | 0.250 | No sign. |
| Cat–time | 1 | 131.93 | 131.93 | 8.31 | 4.75 | 0.014 | Sign. |
| Temp–time | 1 | 32.39 | 32.39 | 2.04 | 4.75 | 0.179 | No sign. |
| Total error | 12 | 190.44 | 15.87 | ||||
| Lack-of-fit | 10 | 189.36 | 18.94 | 35.27 | 4.1028 | 0.028 | |
| Pure error | 2 | 1.07 | 0.54 | ||||
| Total | 26 | 8236.73 |
From what is said above, the information in Table 3 indicates that in the four linear effects (catalyst mass, methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio, temperature and time), two of the four quadratic effects (catalyst mass and temperature) and only one of the six binary interactions (catalyst mass–time) are statistically significant at the 95% probability as their corresponding F0 is greater than the Fcrit counterpart, and the p-values are larger than 0.05. Considering that the magnitude of F0 depends on the impact of the treatment on the response, it is noted that the linear effect of the catalyst mass is, by far, the most influencing variable (F0 = 335.79 vs. Fcrit = 4.75) in the SA esterification reaction. With respect to the two quadratic effects that were statistically significant, the one of the catalyst mass is notably larger (F0 = 64.7 vs. Fcrit = 4.75) than that of temperature (F0 = 5.37 vs. Fcrit = 4.75).
SA ratio, temperature and time), two of the four quadratic effects (catalyst mass and temperature) and only one of the six binary interactions (catalyst mass–time) are statistically significant at the 95% probability as their corresponding F0 is greater than the Fcrit counterpart, and the p-values are larger than 0.05. Considering that the magnitude of F0 depends on the impact of the treatment on the response, it is noted that the linear effect of the catalyst mass is, by far, the most influencing variable (F0 = 335.79 vs. Fcrit = 4.75) in the SA esterification reaction. With respect to the two quadratic effects that were statistically significant, the one of the catalyst mass is notably larger (F0 = 64.7 vs. Fcrit = 4.75) than that of temperature (F0 = 5.37 vs. Fcrit = 4.75).
To determine the absolute magnitude and direction of the treatments in the BBD, the main value of linear effects and quadratic effects as well as two-way interactions with the corresponding t-based ICL at the 95% of probability were computed and are summarized in Table 4. Notice that the ICL involves the t-distribution (or t-student) value and the standard error (SE), the latter computed from the MS of the total error and the sample size. When there is a zero in the ICL of a treatment, one can conclude that it is not statistically significant at the selected probability level.38,40,41 Table 4 also contains the so-called standardized effect designated T-value, which is equal to the main value of the treatment divided by the SE, which provides complementary information to identify if a treatment is statistically significant or not. The T-value was used to obtain the p-values at the probability level indicated before, giving statistical results that are fully consistent to that displayed in Table 3.
| Treatment | ICL (main value ± 2.179 SE)a | T-value | p-value |
|---|---|---|---|
| a The number 2.179 was taken from the t-student distribution at the 95% probability and the degrees of freedom of the total error (=12) in Table 3. | |||
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA SA |
12.92 ± 5.01 | 5.61 | 0.000 |
| Cat | 42.14 ± 5.01 | 18.32 | 0.000 |
| Temp | 9.54 ± 5.01 | 4.15 | 0.001 |
| Time | 7.34 ± 5.01 | 3.20 | 0.008 |
(MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA)2 SA)2 |
−2.18 ± 7.50 | −0.63 | 0.538 |
| (Cat)2 | −27.76 ± 7.50 | −8.05 | 0.000 |
| (Temp)2 | 8.00 ± 7.50 | 2.32 | 0.039 |
| (Time)2 | 1.62 ± 7.50 | 0.47 | 0.646 |
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA–cat SA–cat |
−1.94 ± 8.67 | −0.49 | 0.636 |
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA–temp SA–temp |
−2.40 ± 8.67 | −0.60 | 0.558 |
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA–time SA–time |
6.22 ± 8.67 | 1.56 | 0.144 |
| Cat–temp | 4.82 ± 8.67 | 1.21 | 0.250 |
| Cat–time | 11.48 ± 8.67 | 2.88 | 0.014 |
| Temp–time | 5.70 ± 8.67 | 1.43 | 0.179 |
Notice that the ICL of the four linear effects do not contain any zero and their p-values that are lower than 0.05, which indicate that they are statistically significant. Likewise, these effects are positive, showing that by increasing the level of the factor, the value of the response increases with the catalyst mass being the factor with the most intense linear effect on the response and time corresponding to the factor with the least important impact on the response values. Regarding the quadratic effects, the ones associated with catalyst mass and temperature are statistically significant (no zero in the ICL), in agreement with what was found in the ANOVA, with the former being negative and the latter being positive in accordance with the concavity of the trendline in Fig. 2b and c. Moreover, only the interaction catalyst mass–time is statistically significant and positive, which indicates that the positive effect of catalyst mass on the response is more pronounced as time increases.
Fitting the BBD results with the reduced regression model
From the detailed revision of the ANOVA results in Table 3, combined with the assessment of the ICL values in Table 4, it was found that the quadratic effect of the methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio and time and the binary interactions methanol
SA ratio and time and the binary interactions methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio–catalyst mass, methanol
SA ratio–catalyst mass, methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio–temperature, methanol
SA ratio–temperature, methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio–time, catalyst mass–temperature, and temperature–time were not statistically significant at 95% of probability. Thus, they can be removed out from the full regression model to give a simplified expression, denoted as the reduced regression model.42 In the case of our BBD, this reduced model is represented by eqn (4), which only contains 8 adjustable parameters that were estimated again via regression using the 47 available experimental BBD runs, as was done formerly for the full regression model.
SA ratio–time, catalyst mass–temperature, and temperature–time were not statistically significant at 95% of probability. Thus, they can be removed out from the full regression model to give a simplified expression, denoted as the reduced regression model.42 In the case of our BBD, this reduced model is represented by eqn (4), which only contains 8 adjustable parameters that were estimated again via regression using the 47 available experimental BBD runs, as was done formerly for the full regression model.| Ŷ = βo + β1×1 + β2×2 + β3×3 + β4×4 + β22×22 + β33×32 + β24×2×4 | (4) |
Table 5 presents the main value of the 8 parameters of eqn (4) and includes relevant statistical information as a footnote. Based on this statistical information, R2 = 0.9624, Fc reg (=69.65) > Fcrit (=3.45) and the p-value for LoF = 0.000 (<0.05), along with the parity and residual plots depicted in Fig. 5, it is concluded that the reduced regression model adequately predicts the experimental BBD data and is suitable for updating the ANOVA and ICL values of the statistically significant treatments.
| Parameter | Main value |
|---|---|
| a SSReg = 7927.7, SSLoF = 190.60; SSError = 309.0; F0,reg = 69.65 with Fcrit,reg (0.05,19,7) = 3.45, F0 reg > Fcrit,reg (R2) = 0.9624, p-value for LoF = 0.000 (<0.05). | |
| β0 | 96.318 × 100 |
| β1 | 1.4348 × 100 |
| β2 | 24.313 × 100 |
| β3 | −3.591 × 100 |
| β4 | −5.152 × 10−1 |
| β22 | −3.928 × 100 |
| β33 | 4.068 × 10−2 |
| β24 | 5.569 × 10−1 |
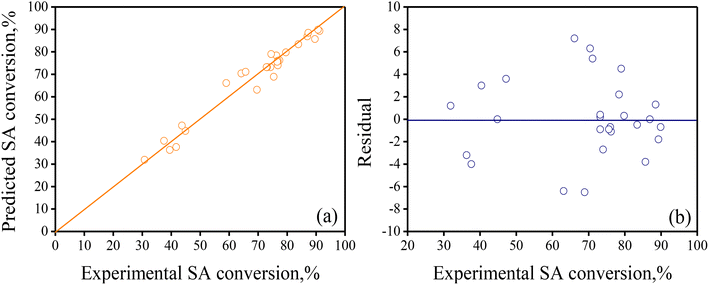 | ||
| Fig. 5 (a) Parity plot contrasting computed SA conversion vs. experimental SA conversion, and (b) residuals as a function of the predicted SA conversion values. The reduced regression model in eqn (5) with the parameters in Table 5 was used to calculate the response values. | ||
Table 6 summarizes the ANOVA results, which were obtained by applying the reduced regression model to adjust the BBD data. As expected, all the treatments, i.e., linear and quadratic effects, as well as binary interactions incorporated to the reduced regression model are statistically significant at the 95% probability level upon fulfilling that F0 > Fcrit. and p-value > 0.05 correspondingly. Table 7, in turn, presents the ICL at the 95% of probability of the treatments retained in the reduced regression model; none of the ICL are zero, indicating that all the treatments are statistically significant, which is consistent with the ANOVA results displayed in Table 6. Summarizing: (i) the four linear effects are positive and that associated with the mass of catalyst is the most influencing on SA conversion, (ii) the quadratic effect of catalyst mass is negative and that of temperature is positive, producing an opposite concavity in the corresponding response surface plots (vide the response surface graphs in the coming section), and (iii) only one interaction (catalyst mass–time) is significant, albeit with a relatively low magnitude based on the narrowness of the ICL.
| Treatment | DF | SS | MS | F0 | Fcrit at 95% prob. | p-value | F0 > Fcrit or p-value < 0.05 |
|---|---|---|---|---|---|---|---|
| Full model | 7 | 7927.72 | 1132.53 | 69.64 | 2.54 | 0.000 | Sign. |
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA SA |
1 | 500.28 | 500.28 | 30.76 | 4.38 | 0.000 | Sign. |
| Cat | 1 | 5328.98 | 5328.98 | 327.66 | 4.38 | 0.000 | Sign. |
| Temp | 1 | 272.85 | 272.85 | 16.78 | 4.38 | 0.001 | Sign. |
| Time | 1 | 162.07 | 162.07 | 9.96 | 4.38 | 0.005 | Sign. |
| (Cat)2 | 1 | 1220.6 | 1220.6 | 75.05 | 4.38 | 0.000 | Sign. |
| (Temp)2 | 1 | 105.92 | 105.92 | 6.51 | 4.38 | 0.019 | Sign. |
| Cat–time | 1 | 131.93 | 131.93 | 8.11 | 4.38 | 0.010 | Sign. |
| Total error | 19 | 309.01 | 16.26 | ||||
| Lack-of-fit | 17 | 307.93 | 18.11 | 33.74 | 19.4 | 0.029 | |
| Pure error | 2 | 1.07 | 0.54 | ||||
| Total | 26 | 8236.73 |
| Treatment | ICL (main value ± 2.093 SE)a | T-value | p-value |
|---|---|---|---|
| a The number 2.093 was taken from the t-test tables at the 95% probability (α = 0.05) and the degrees of freedom of the total error (=19) from Table 6. | |||
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA SA |
12.92 ± 4.86 | 5.55 | 0.000 |
| Cat | 42.14 ± 4.86 | 18.10 | 0.000 |
| Temp | 9.54 ± 4.86 | 4.1 | 0.001 |
| Time | 7.34 ± 4.86 | 3.16 | 0.005 |
| (Cat)2 | −27.62 ± 6.66 | −8.66 | 0.000 |
| (Temp)2 | 8.14 ± 6.66 | 2.55 | 0.019 |
| Cat–time | 11.48 ± 8.46 | 2.85 | 0.010 |
Response surface graphs
The response surface graphs (RSG), which are tridimensional graphs constructed with the corresponding regression models, represent a useful tool to visualize the evolution of the response value in terms of the simultaneous changes in the two factors at a time. The RSG also contain bidimensional contour plots that include lines connecting the points of iso-response values, from which the intensity of the binary interactions can be confirmed.43,44 For a DoE with more than two factors, the factors that are not displayed in the graph are set to a fixed value conventionally to the middle point “0” of the factor interval.39,40 Constructed using the second order reduced regression model (see eqn (4) and Table 5), Fig. 6 shows the complete set of RSG of the BBD, which were graphed using the software Origin 9.0. For the factors not displayed in the RSG, their value was set to at 11.5 mol mol−1, 2.125 wt%, 50 °C, and 6.5 min for methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio, catalyst mass, temperature, and time, respectively, the factors' middle point in the BBD (see Table 1).
SA ratio, catalyst mass, temperature, and time, respectively, the factors' middle point in the BBD (see Table 1).
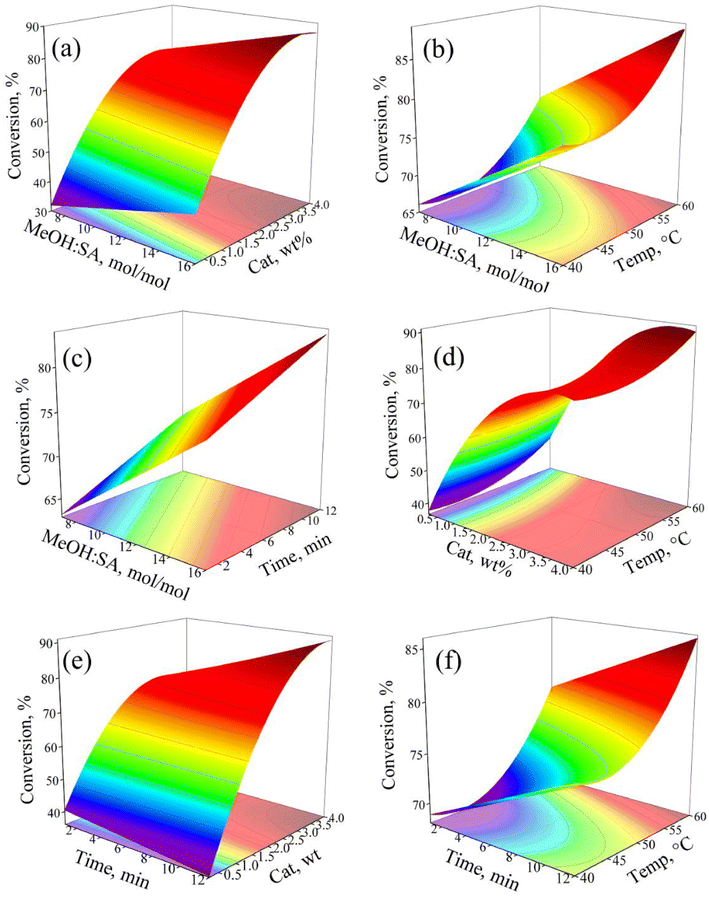 | ||
| Fig. 6 Response surface graphs with contour plots constructed from the reduced regression model (see eqn (5)) that includes the parameters in Table 5. Two factors are included in the graph, and the value of the other two factors was set at the center point “0” in the BBD. | ||
As the regression model in eqn (4) contains linear and two quadratic terms, the shape of the SRP can be pure planar (e.g., Fig. 6c, which includes methanol:SA and time as independent variables) and curve (e.g., Fig. 6a, b and f, which accounts for catalyst mass or temperature and methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA or time as independent variables). Regarding their topology,45 the observed RSG are rising ridge (Fig. 6a and e), planar (Fig. 6c), saddle (Fig. 6d) and falling ridge-like (Fig. 6b and f). It is also noted that the RSG, including catalyst mass and the BBD factor that exhibited a negative quadratic effect, are concave downward (Fig. 6a and e), whereas for those incorporating the temperature, the BBD factor that displayed a positive quadratic effect, are concave upward (Fig. 6b and f). The non-linear effect of the catalyst mass and/or temperature on the response is confirmed by the shape of the contour plots in Fig. 6a, b, d, e and f as their corresponding contour lines are curved. Conversely, the contour lines in the contour plots in Fig. 6c are straight, confirming the linear effect of methanol
SA or time as independent variables). Regarding their topology,45 the observed RSG are rising ridge (Fig. 6a and e), planar (Fig. 6c), saddle (Fig. 6d) and falling ridge-like (Fig. 6b and f). It is also noted that the RSG, including catalyst mass and the BBD factor that exhibited a negative quadratic effect, are concave downward (Fig. 6a and e), whereas for those incorporating the temperature, the BBD factor that displayed a positive quadratic effect, are concave upward (Fig. 6b and f). The non-linear effect of the catalyst mass and/or temperature on the response is confirmed by the shape of the contour plots in Fig. 6a, b, d, e and f as their corresponding contour lines are curved. Conversely, the contour lines in the contour plots in Fig. 6c are straight, confirming the linear effect of methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA and time on the response. An inspection of the iso-response contour lines allows the relative influence of the various factors in the response to be quickly visualized. Thus, in Fig. 6a, d and e, small changes in the catalyst mass make the contour lines move to regions of large response values. Though the response value also increases with augmenting methanol
SA and time on the response. An inspection of the iso-response contour lines allows the relative influence of the various factors in the response to be quickly visualized. Thus, in Fig. 6a, d and e, small changes in the catalyst mass make the contour lines move to regions of large response values. Though the response value also increases with augmenting methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA, temperature and time and the iso-response contour lines displace to higher values, and the positive effect of these three factors is notably lower than the one displayed by the catalyst mass.
SA, temperature and time and the iso-response contour lines displace to higher values, and the positive effect of these three factors is notably lower than the one displayed by the catalyst mass.
In the SRP in Fig. 6, it is also noticed that the operation at the upper limit of the two factors in the plots leads to the largest SA conversion, a behaviour that can be explained in terms of the main effects assessment outlined in the previous sections. For instance, it is observed in Fig. 6a that SA conversion was as high as 87% when running the reaction at 4 wt% of catalyst mass and 16 mol mol−1 of methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio (recall that temperature and time were set to the middle level “0” in the BBD: 50 °C and 6.5 min, vide Table 2). Interestingly, the reaction time required in the HSM-intensified SA esterification with methanol was considerably smaller than the typical reaction time values reported in the literature either for heterogeneous8,13,14,17 or homogeneous17,20 non-intensified processes, as can be verified from the information displayed in Table 8. In fact, the ANOVA (Tables 3 and 6) and the ICL results (see Tables 4 and 7) indicate that time is, among the four factors accounted for in the BBD, the least influencing independent variable in the SA conversion, an issue that appears to be related to the incorporation of HSM into the esterification process. Clearly, by assisting the liquid phase esterification reaction with high shear rotor stator mixer, the reaction less mass-transfer limited the contact between reactants and catalyst is more intimate, and the liquid droplets are smaller and better dispersed, thus ultimately leading to a more efficient process.22–24,46 These results are of great relevance as energy saving can be envisaged by reducing the reaction severity in time (as well as temperature and catalyst amount), which may ultimately positively impact the process economy.
SA ratio (recall that temperature and time were set to the middle level “0” in the BBD: 50 °C and 6.5 min, vide Table 2). Interestingly, the reaction time required in the HSM-intensified SA esterification with methanol was considerably smaller than the typical reaction time values reported in the literature either for heterogeneous8,13,14,17 or homogeneous17,20 non-intensified processes, as can be verified from the information displayed in Table 8. In fact, the ANOVA (Tables 3 and 6) and the ICL results (see Tables 4 and 7) indicate that time is, among the four factors accounted for in the BBD, the least influencing independent variable in the SA conversion, an issue that appears to be related to the incorporation of HSM into the esterification process. Clearly, by assisting the liquid phase esterification reaction with high shear rotor stator mixer, the reaction less mass-transfer limited the contact between reactants and catalyst is more intimate, and the liquid droplets are smaller and better dispersed, thus ultimately leading to a more efficient process.22–24,46 These results are of great relevance as energy saving can be envisaged by reducing the reaction severity in time (as well as temperature and catalyst amount), which may ultimately positively impact the process economy.
| Reaction conditions | Times of reaction severity reduction using the HSM intensified esterification reported in this work | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Type of reaction | Catalyst | Temperature, °C | Time, h | Catalyst mass, wt% | Alcohol : fatty acid, mol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol mol |
SA conversion, % | Temperature | Time | Catalyst mass |
| Heterogeneous | MMT KSF/0 (ref. 8) | 150 | 4 | 10 | 2.06![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
96 | 2.5 | 20 | 2.5 |
| MMT-PO4 (ref. 9) | 160 | 2 | 12 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
96.6 | 2.7 | 10 | 3.0 | |
| MMT K10 (ref. 9) | 160 | 2 | 12 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
94.1 | 2.7 | 10 | 3.0 | |
| Cu2+-MMT K10 (ref. 10) | 80 | 1.03 | 30 | 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
87.05 | 1.3 | 5.15 | 7.5 | |
| Fe-MMT K10 (ref. 11) | 80 | 3 | 30 | 1.06![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
75 | 1.3 | 15 | 7.5 | |
| Amberlyst-15 (ref. 12) | 110 | 5 | 7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Above 50 | 1.8 | 25 | 1.8 | |
| Niobium-oxide12 | 110 | 10 | 7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
50 | 1.8 | 50 | 1.8 | |
| Nb2O5 (ref. 13) | 110 | 23.3 | 5 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
40 | 1.8 | 116.5 | 1.3 | |
| Tin zirconium oxide14 | 120 | 1 | 0.07 | 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
74 | 2.0 | 5 | 0.02 | |
| Amidoximated polyacrylonitrile ion exchange fibres15 | 90 | 3 | 1.5 | 35.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
95.35 | 1.5 | 15 | 0.4 | |
| ZrO2–SiO2 (ref. 17) | 60 | 7 | 6 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
91 | Same | 35 | 1.5 | |
| Homogeneous | AlCl3 (ref. 20) | 110 | 18 | 5 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
98 | 1.8 | 90 | 1.3 |
| Sulfuric acid17 | 60 | 7 | 6 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
97 | Same | 35 | 1.5 | |
For multifactorial response surface DoE, identifying the values of the factors that maximizes the response within the corresponding experiment region is not trivial and requires a numerical approximation. From a ridge max analysis using the reduced regression model as the input, the maximum SA conversion amounted to 99 ± 6.8%, running at 12.4 mol mol−1 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio, 4 g catalyst mass, 60 °C temperature and 12 min time upon stirring at 500 rpm. With the aim to validate this result, three replicated experiments at these reaction conditions were conducted giving, as an average, an SA conversion value of 93.2 ± 0.7%.
SA ratio, 4 g catalyst mass, 60 °C temperature and 12 min time upon stirring at 500 rpm. With the aim to validate this result, three replicated experiments at these reaction conditions were conducted giving, as an average, an SA conversion value of 93.2 ± 0.7%.
Conclusions
The response surface methodology was successfully applied to experimentally/numerically determine the set of conditions that favours the MST production via the liquid phase acid-catalysed esterification of SA acid with methanol. Interestingly, the said homogeneous esterification was intensified by assisting it with high shear mixing (HSM). The use of a four-factor (catalyst mass, methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio, temperature, and time) response surface Box–Behnken design (BBD) allowed us their main effect (linear and quadratic) and two-way interactions on SA conversion to be measured and statistically assessed. In the first stage, the inspection of the constructed main effects and interaction plots was useful for a preliminary view of the relative importance of BBD factors and their nature. By combining numerical and statistical tools (ANOVA and individual confidence limits), the statistically relevant treatments in the BBD (linear and quadratic effect as well as binary interactions) at the 95% probability were identified. The treatments evolved as follows: (i) the four linear effects were positive, (ii) the interaction catalyst mass–time was positive, and (iii) the quadratic effect of catalyst mass and temperature were negative and positive, respectively. The catalyst mass was the most influencing reaction variable, then methanol
SA ratio, temperature, and time) response surface Box–Behnken design (BBD) allowed us their main effect (linear and quadratic) and two-way interactions on SA conversion to be measured and statistically assessed. In the first stage, the inspection of the constructed main effects and interaction plots was useful for a preliminary view of the relative importance of BBD factors and their nature. By combining numerical and statistical tools (ANOVA and individual confidence limits), the statistically relevant treatments in the BBD (linear and quadratic effect as well as binary interactions) at the 95% probability were identified. The treatments evolved as follows: (i) the four linear effects were positive, (ii) the interaction catalyst mass–time was positive, and (iii) the quadratic effect of catalyst mass and temperature were negative and positive, respectively. The catalyst mass was the most influencing reaction variable, then methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio, temperature, and time. The projection of the fitted reduced regression model indicates the intensified process requires only 12 min to almost fully convert SA (99 ± 6.8% conversion) when operating at 12.4 methanol
SA ratio, temperature, and time. The projection of the fitted reduced regression model indicates the intensified process requires only 12 min to almost fully convert SA (99 ± 6.8% conversion) when operating at 12.4 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA ratio, 4 wt% catalyst mass, 60 °C and 500 rpm, a value that was experimentally validated (93.2 ± 0.7%). In comparison with the available state-of-the-art reports, the reaction severity (time in particular) drastically reduced, giving evidence that HSM is a promising option for intensifying green chemistry reactions, visualising noticeable technical, economic, and environmental benefits. As immediate future actions to increase the maturity level of this technology, increasing the scale of the reaction set-up and implementing experiments under more realistic conditions that implies the use of commercial reagents would be two of the key steps.
SA ratio, 4 wt% catalyst mass, 60 °C and 500 rpm, a value that was experimentally validated (93.2 ± 0.7%). In comparison with the available state-of-the-art reports, the reaction severity (time in particular) drastically reduced, giving evidence that HSM is a promising option for intensifying green chemistry reactions, visualising noticeable technical, economic, and environmental benefits. As immediate future actions to increase the maturity level of this technology, increasing the scale of the reaction set-up and implementing experiments under more realistic conditions that implies the use of commercial reagents would be two of the key steps.
Abbreviations
| −1 | Factor's low level in the BBD |
| +1 | Factor's high level in the BBD |
| 0 | Factor's central or middle point in the CCD |
| 1H NMR | Proton nuclear magnetic resonance |
| ANOVA | Analysis of variance |
| AV | Acid value, (mg KOH) g−1 |
| AVSAf | Acid value after reaction, (mg KOH) g−1 |
| AVSAi | Acid value before reaction, (mg KOH) g−1 |
| BD | Biodiesel |
| BBD | Box–Behnken design |
| Cat | Catalyst mass, wt% |
| CI | Confidence interval |
| CN | Cetane number |
| cp | Total number of replicates at the central point |
| DF | Degrees of freedom |
| DoE | Design of experiments |
| Fc | Computed F value in the Fisher's statistical test |
| Fc reg | F value for the regression in the Fisher's statistical test |
| Fcrit | Critical F value in the Fisher's test |
| F-test | Fisher's statistical test |
| F value | Value generated from Fisher's statistical test |
| HSM | High-shear mixing |
| k | Number of factors or independent variables in the DoE |
| LoF | Lack-of-fit |
MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SA SA | Methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) stearic acid molar ratio, mol mol−1 stearic acid molar ratio, mol mol−1 |
| MS | Mean squares |
| MSError | Total error of mean sum of squares |
| MSreg | Mean sum of squares of the regression |
| MST | Methyl stearate |
| N | Total number of experiments in the BBD |
| Pb | Solution required for blank solvent titration, ml |
| Pm | Molarity of the potassium hydroxide solution, mol l−1 |
| Ps | Potassium hydroxide solution, ml |
| Pw | Molecular mass of potassium hydroxide |
| p-value | Probability value used to apply the statistical test |
| R2 | Multiple correlation coefficient in the regression analysis |
| Reg | Regression |
| RSG | Response surface graphs |
| SA | Stearic acid |
| SE | Standard error |
| SS | Sum of squares |
| SSError | Error sum of squares |
| SSLoF | Lack-of-fit sum of squares |
| SSReg | Regression sum of squares |
| Temp | Temperature, °C |
| Time | Time, min |
| W | Mass of titration, g |
| xi, xj | Factor (independent variable) coding in regression model |
| XSA | SA converted during the esterification reaction,% |
| Ŷ | Predicted response value by the regression model |
Greek letters
| α | Significance or probability level used for the F-test and p-value |
| β0 | Intercept parameter in the regression model |
| βi | Parameters related to linear effects in the regression model |
| βii | Parameters related to quadratic effects in the regression model |
| βij | Parameters related to the two-way interactions in the regression model |
Author contributions
Conceptualization: R. Q. S. and M. S. C.; methodology: R. Q. S., M. S. C. and F. M. R. C.; formal analysis: R. Q. S., M. S. C. and F. M. R. C.; investigation: R. Q. S., M. S. C. and F. M. R. C.; data curation: R. Q. S., M. S. C. and F. M. R. C.; 1H NMR analysis: J. D. S. J.; writing—original draft preparation, F. M. R. C., R. Q. S. and M. S. C.; writing—review and editing, F. M. R. C., R. Q. S. and M. S. C.; visualization: R. Q. S. and F. M. R. C.; supervision: R. Q. S. and M. S. C.; project administration: R. Q. S. and M. S. C.; funding acquisition: M. S. C.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Reyes-Cruz F. M. thanks Consejo Nacional de Humanidades Ciencia y Tecnologías (CONAHCYT) for his PhD grant (787223).References
- P. G. Levi and J. M. Cullen, Environ. Sci. Technol., 2018, 52, 1725–1734 CrossRef CAS PubMed.
- E. Işıklı, N. Aydın, L. Bilgili and A. Toprak, J. Cleaner Prod., 2020, 275, 124142 CrossRef.
- E. Khalife, M. Tabatabaei, A. Demirbas and M. Aghbashlo, Prog. Energy Combust. Sci., 2017, 59, 32–78 CrossRef.
- T. Kegl, A. Kovač Kralj, B. Kegl and M. Kegl, Prog. Energy Combust. Sci., 2021, 83, 100897 CrossRef.
- Z. Khan, F. Javed, Z. Shamair, A. Hafeez, T. Fazal, A. Aslam, W. B. Zimmerman and F. Rehman, J. Ind. Eng. Chem., 2021, 103, 80–101 CrossRef CAS.
- E. G. Giakoumis, Renewable energy, 2013, 50, 858–878 CrossRef CAS.
- J. Yanowitz, E. M. A. Ratcliff, R. L. Mccormick, J. D. Taylor and M. J. Murphy Battelle, Compendium of Experimental Cetane Numbers, 2014 Search PubMed.
- S. Bouguerra Neji, M. Trabelsi and M. H. Frikha, Energies, 2009, 2, 1107–1117 CrossRef.
- L. Zatta, E. J. M. Paiva, M. L. Corazza, F. Wypych and L. P. Ramos, Energy Fuels, 2014, 28, 5834–5840 CrossRef CAS.
- E. A. Almadani, F. W. Harun, S. M. Radzi and S. K. Muhamad, Bull. Chem. React. Eng. Catal., 2018, 13, 187–195 CrossRef CAS.
- O. Al, F. W. Harun, E. A. Almadani, S. M. Radzi and F. W. Harun, Int. J. Agric. Crop Sci., 2016, 12, 62–67 Search PubMed.
- M. Banchero and G. Gozzelino, Energies, 2018, 11, 1843 CrossRef.
- M. Banchero and G. Gozzelino, Chem. Eng. Res. Des., 2015, 100, 292–301 CrossRef CAS.
- S. M. Ibrahim, Renewable Energy, 2021, 173, 151–163 CrossRef CAS.
- R. A. Ahmed, S. Rashid and K. Huddersman, J. Ind. Eng. Chem., 2023, 119, 550–573 CrossRef CAS.
- P. Sangsiri, N. Laosiripojana, W. Laosiripojana and P. Daorattanachai, ACS Omega, 2022, 7, 40025–40033 CrossRef CAS PubMed.
- K. Saravanan, B. Tyagi and H. C. Bajaj, J. Porous Mater., 2016, 23, 937–946 CrossRef CAS.
- H. Nakaya, K. Nakamura and O. Miyawaki, J. Am. Oil Chem. Soc., 2002, 79, 23–27 CrossRef CAS.
- G. N. Pereira, J. P. Holz, P. P. Giovannini, J. V. Oliveira, D. de Oliveira and L. A. Lerin, Biocatal. Agric. Biotechnol., 2018, 16, 373–377 CrossRef.
- N. U. Soriano, R. Venditti and D. S. Argyropoulos, Fuel, 2009, 88, 560–565 CrossRef CAS.
- Z. Qian, Q. Chen and I. E. Grossmann, Comput.-Aided Chem. Eng., 2018, 44, 2377–2382 Search PubMed.
- M. Sánchez-Cantú, L. M. Pérez-Díaz, M. Morales-Téllez, I. Martínez-Santamaría, J. C. Hilario-Martínez and J. Sandoval-Ramírez, Fuel, 2017, 189, 436–439 CrossRef.
- M. Sánchez-Cantú, M. Morales Téllez, L. M. Pérez-Díaz, R. Zeferino-Díaz, J. C. Hilario-Martínez and J. Sandoval-Ramírez, Renewable Energy, 2019, 130, 174–181 CrossRef.
- F. M. Reyes-Cruz, R. Quintana-Solórzano and M. Sánchez-Cantú, Int. J. Energy Res., 2022, 46, 19548–19565 CrossRef CAS.
- R. Zeferino-Díaz, J. C. Hilario-Martínez, M. Sánchez-Cantú, M. A. Fernández-Herrera and J. Sandoval-Ramirez, Green Chem., 2019, 21, 1417–1420 RSC.
- J. S. Valente, M. S. Cantu and F. Figueras, Chem. Mater., 2008, 20, 1230–1232 CrossRef CAS.
- B. Ai, J. Guo, S. Zhao, W. Li, M. Zhou and J. Zhang, Ind. Eng. Chem. Res., 2021, 60, 4498–4509 CrossRef CAS.
- J. De Araújo Gonaçalves, A. L. D. Ramos, L. L. L. Rocha, A. K. Domingos, R. S. Monteiro, J. S. Peres, N. C. Furtado, C. A. Taft and D. A. G. Aranda, J. Phys. Org. Chem., 2011, 24, 54–64 CrossRef.
- X. Shen, G. Zhang and B. Bjerg, Energy Build., 2013, 62, 570–580 CrossRef.
- B. Ait-Amir, P. Pougnet and A. El Hami, Embedded Mechatronic Systems, 2015, 2, 151–179 Search PubMed.
- A. Jankovic, G. Chaudhary and F. Goia, Energy Build., 2021, 250, 111298 CrossRef.
- S. L. C. Ferreira, R. E. Bruns, H. S. Ferreira, G. D. Matos, J. M. David, G. C. Brandão, E. G. P. da Silva, L. A. Portugal, P. S. dos Reis, A. S. Souza and W. N. L. dos Santos, Anal. Chim. Acta, 2007, 597, 179–186 CrossRef CAS PubMed.
- J. Zhang, M. Lu, F. Ren, G. Knothe and Q. Tu, J. Am. Oil Chem. Soc., 2019, 96, 1083–1091 CrossRef CAS.
- R. Chakraborty and E. Mandal, J. Taiwan Inst. Chem. Eng., 2015, 50, 93–99 CrossRef CAS.
- I. Miličević, N. Štirmer and D. Bjegović, Optimizing the Concrete Mixture Made with Recycled Aggregate Using Experiment Design, 2011 Search PubMed.
- N. Aslan and Y. Cebeci, Fuel, 2007, 86, 90–97 CrossRef CAS.
- G. E. P. Box and K. B. Wilson, J. R. Stat. Soc. Series B., 1591, 13, 1–45 Search PubMed.
- D. C. Montgomery, Design and analysis of experiments, 2012 Search PubMed.
- P. Qiu, M. Cui, K. Kang, B. Park, Y. Son, E. Khim, M. Jang and J. Khim, Cent. Eur. J. Chem., 2014, 12, 164–172 Search PubMed.
- J. S. Valente, R. Quintana-Solórzano, H. Armendáriz-Herrera, G. Barragán-Rodríguez and J. M. López-Nieto, Ind. Eng. Chem. Res., 2014, 53, 1775–1786 CrossRef CAS.
- G. E. P. Box, J. S. Hunter and W. G. Hunter, Statistics for Experimenters: An Introduction to Design, Data Analysis and Model Building, 1978 Search PubMed.
- E. E. Feistauer, J. F. Dos Santos and S. T. Amancio-Filho, Weld. World., 2020, 64, 1481–1495 CrossRef CAS.
- S. A. Younis, A. Abd-Elaziz and A. I. Hashem, RSC Adv., 2016, 6, 89367–89379 RSC.
- W. Chen, P. Yin, H. Chen and Z. Wang, Ind. Eng. Chem. Res., 2012, 51, 5402–5407 CrossRef CAS.
- R. H. Myers, D. C. Montgomery and C. M. Anderson-Cook, Response Surface Methodology. Process and Product Optimization Using Designed Experiments, 2016 Search PubMed.
- J. Zhang, S. Xu and W. Li, Chem. Eng. Process., 2012, 57–58, 25–41 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra02750g |
| This journal is © The Royal Society of Chemistry 2024 |