Open Access Article
Open Access ArticleHigh precision deep-learning model combined with high-throughput screening to discover fused [5,5] biheterocyclic energetic materials with excellent comprehensive properties†
Youhai Liua,
Fusheng Yang *a,
Wenquan Zhang
*a,
Wenquan Zhang *b,
Honglei Xiab,
Zhen Wua and
Zaoxiao Zhanga
*b,
Honglei Xiab,
Zhen Wua and
Zaoxiao Zhanga
aSchool of Chemical Engineering and Technology, Xi'an Jiaotong University, Xi'an 710049, China. E-mail: yang.fs@mail.xjtu.edu.cn
bResearch Center of Energetic Material Genome Science, Institute of Chemical Materials, China Academy of Engineering Physics (CAEP), Mianyang, 621900, P. R. China. E-mail: zhangwq-cn@caep.cn
First published on 29th July 2024
Abstract
Finding novel energetic materials with good comprehensive performance has always been challenging because of the low efficiency in conventional trial and error experimental procedure. In this paper, we established a deep learning model with high prediction accuracy using embedded features in Directed Message Passing Neural Networks. The model combined with high-throughput screening was shown to facilitate rapid discovery of fused [5,5] biheterocyclic energetic materials with high energy and excellent thermal stability. Density Functional Theory (DFT) calculations proved that the performances of the targeting molecules are consistent with the predicted results from the deep learning model. Furthermore, 6,7-trinitro-3H-pyrrolo[1,2-b][1,2,4]triazo-5-amine with both good detonation properties and thermal stability was screened out, whose crystal structure and intermolecular interactions were also analyzed.
Introduction
Energetic materials are a type of compound or mixture containing explosive groups or oxidants and fuels, which undergo intense redox reactions under specific external energy stimuli, releasing a large amount of energy. Energetic materials are widely used in weapons and equipment, aerospace propulsion, engineering construction, mineral mining and other fields.1–5 Energy and stability are the two most important properties of energetic materials. However, a relationship of mutual contradiction is always present between them. Therefore, the development of energetic materials with high energy and outstanding stability simultaneously remains a great challenge. Recently, fused cyclic energetic materials, which feature a unique conjugated structure consisting of shared atoms and bonds, has been considered as a promising alternative to traditional energetic materials.6 Fused heterocyclic energetic materials exhibit high heat of formation due to their planar fused backbone with multiple nitrogen atoms, meanwhile the presence of π–π interactions between the fused ring endows them with high thermal stability.7–11 Among fused backbones, [5,5]-fused ring is the simplest one for energetic molecules construction.12,13 In recent years, several representative structures of fused [5,5]-bicyclic heterocycle energetic materials were designed and synthesized.13–16 However, these molecules were obtained based on the method of structural design, such as increasing number of N atoms into a fused ring, or substituting explosophoric groups like –NO2, –NHNO2, –C(NO2)2, –NH2 or –C(NO2)3 at certain positions, which heavily relies on the chemical experience (intuition) of researchers, develop through trial-and-error processes, involving long period, high costs and safety risks.17In the past decades, with the advent of the big data era, machine learning (ML) technique has been widely used in almost all the material research fields, such as organic photoelectric materials, perovskite materials, lithium-ion battery materials, photovoltaic materials etc.18–22 The application of machine learning methods in energetic materials has also drawn increasing attention. In order to shorten the development cycle of energetic materials, recent work23–28 presented attempts to use high-throughput screening methods together with ML to target new promising explosives, including insensitive high explosives (IHEs),23 molten castable explosives,24 fluorinated explosives,25 bridged explosive,27 and some positive results were well achieved. However, mostly traditional machine learning models such as KRR,29 SVM30 were used without considering specific characteristics of candidate molecules, resulting in relatively low prediction accuracy for certain crucial properties, e.g. decomposition temperature.
In this work, we present a deep learning model D-MPNN (Directed Message Passing Neural Networks)31 of embedded molecular descriptors combined with high-throughput molecular generation, so as to rapidly screen promising target molecules from 2698 generated fused [5,5]-bicyclic heterocycle structures. After the screening procedure, 2,6,7-trinitro-3H-pyrrolo[1,2-b][1,2,4]triazo-5-amine (ID number:1439), a promising fused [5,5] biheterocyclic backbone-based energetic material was selected. DFT calculation of the properties, along with crystal structure prediction and intermolecular interaction analysis revealed that this new energetic material has outstanding comprehensive properties, including high energy and good thermal stability. These findings demonstrate the great potential of deep learning combining with embedded features in high-performance energetic materials design.
Methods
Workflow
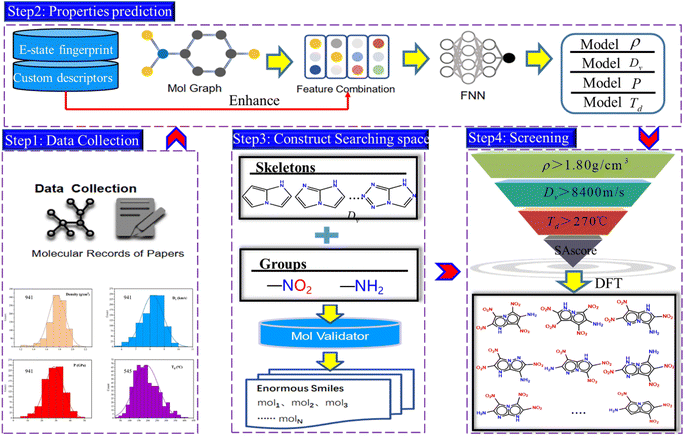
Firstly, the generation of a large number of molecules is implemented and used as search space of fused [5,5] biheterocyclic energetic materials. Subsequently, the high-precision model was obtained by directed Message Passing Neural Networks (D-MPNN) embedded with features, and was used to predict the molecular properties. After that the virtual screening of energetic materials regarding comprehensive performance was carried out. The workflow has been shown in Fig. 1.The work mainly includes four steps, the first step is the data collection. The second step is the prediction of energetic materials properties. With the collected dataset as input and the embedded features as enhancements to the graph structure features, the so-called module b outputs a model for property prediction. The third step involves searching for the spatial construction of energetic materials. The final step is molecule screening, which filters candidates based on the property prediction model developed in step 2 (including density, detonation performance, and decomposition temperature) and the search space constructed in step 3. Step 4 is further divided into two stages. In the first stage, the deep learning model is used to rapidly screen materials with high density, explosive velocity and decomposition temperature, whereas in the second stage, the DFT calculation is applied to evaluate the performance of the selected molecules, thereby assessing the predictive accuracy of this model. It is also utilized for analysing the molecular structures and intermolecular interaction of the candidate molecules.
Dataset
Our dataset consists of two parts. The first part is derived from the reference Song, S. et al.29 After removing data of substances involving halogens and duplicates, we obtained 562 compounds with data for density, detonation velocity and detonation pressure, and 545 compounds for decomposition temperature (see dataset1 in the ESI†). Additionally, 379 publicly available data records for energetic compounds were extracted from Elton et al.30 by also removing data of substances involving halogens and duplicates. In total, 941 data for density, detonation velocity and detonation pressure, and 545 data for decomposition temperature were obtained for training regression models. The dataset covers various structures that have been used as constitute of energetic materials, e.g. aliphatic, aromatic, monocyclic, and polycyclic. Detailed description about the dataset has been provided in Fig. S1 of the ESI.† Essentially the samples in the dataset are divided into three parts: training set, validation set, and testing set. The training set and validation set are used to train the model and perform fine-turning of hyper-parameters, and the testing set is used for the final verification of the model's generalization performance and accuracy.D-MPNN
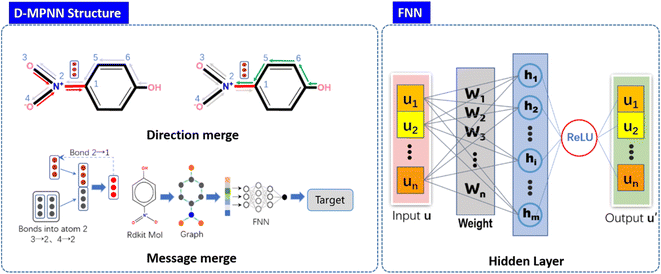
The Message Passing Neural Network (MPNN), that was firstly summarized and proposed by Gilmer et al.,32 is a deep learning model based on graph neural network, operating with atom (node) features and bond (edge) features on an undirected graph G, and has already been used to predict crystal density of energetic materials.33 Based on this, Yang et al.31 made key adjustments to the original messaging neural network framework by adopting messages related to directed bonds and proposed D-MPNN, which has dramatically reduced the noise caused by nodes passing through random paths. D-MPNN consists of two phases: a message passing phase which constructs neural representations of the molecule by transmitting information through the molecule, and a readout phase which generates the final representation of the molecule to predict the properties of materials.The message passing is made up of T steps. On each step t, hidden states hwvand message mvwt(v and w represent the nodes between the bond) are updated using message function Mt and vertex update function Ut.
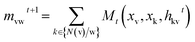 | (1) |
| hvwt+1 = Ut(hvwt, mvwt+1) | (2) |
| ŷ = R({hvT|v ∈ G}) | (3) |
Fig. 2 shows the structure and principle of learning molecular expression of D-MPNN neural network. Module in the left-handed panel of the figure, represents the aggregation of information from two directions on the same bond in the molecule and the process of updating and aggregating information, respectively. The internal structure of the feedforward neural network FNN has been displayed in the right-handed panel of the Fig. 2 u represents the encoded feature vector, w represents the weight update in the training process, h represents the hidden layer, and u′ is the output of the feature vector, which is passed through the activation function. During the training, the D-MPNN networks use the simplified molecular input line entry specification (SMILES) as the molecular input and predict the outputs value through the loss gradient based on the readout phase.
Embedded molecular descriptors
Ideally, the above-described D-MPNN model described above should be able to extract most information about molecules, which is sufficient to complete specific attribute prediction tasks. Nevertheless, there are still limitations to molecular graph features in practice. Firstly, the decomposition temperature dataset is relatively small in size, with only a few hundred molecules. Due to the limited amount of data, D-MPNN could be not able to recognize and extract all the features related to thermal stability. Secondly, the shapes of molecular graphs are rather irregular, and in the message passing process of MPNN, the number of steps is much fewer than the diameter of the molecular graph. Atoms that are farther apart will never receive information from each other. Therefore, for some properties of energetic materials, there are still considerable number of features that cannot be captured simply via the graph convolution process, so it is necessary to add additional features to improve prediction accuracy.In order to effectively combine the additional features, we modified the readout phase of D-MPNN. The feedforward neural network f can be applied to the cascade of the learned molecular feature vector h and the additional input global feature hf. The method for model enhancement is also known as knowledge embedding or feature enhancement. The combination of the graph's feature representation h and the global feature hf can be expressed as the following formula:
| ŷ = f(cat(h,hf) | (4) |
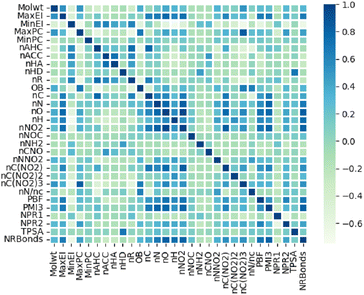
Our embedded molecular features is composed of two parts. The first part includes fingerprints derived from the electro-topological state (E-state) fingerprint, which only involve elements carbon (C), hydrogen (H), oxygen (O), and nitrogen (N) (Table S1 in ESI†), have been widely utilized to construct quantitative relationships between molecular structure and properties.34,35 The second part includes 30 custom molecular descriptors based on molecular electronic states, the number of typical energy groups, molecular composition and three-dimensional shape of molecules (Table S2 in ESI†) obtained from RDKit library. These custom descriptors enhance the description of molecular composition and shape, such as oxygen balance (OB) and normalized principal distance ratio 1 (NPR1), which will help model learn the properties of energetic materials. The heat map in Fig. 3 demonstrates that most of the custom descriptors are not significantly correlated, which is beneficial for model training.
Molecule generation
We have used a homemade script for generating the molecules. The flow chart of the whole generation process is shown in Fig. 4(a), where the yellow part describes the generation of nitrogen-substituted fused ring using the carbon rings as input and the green part illustrates the process of adding the groups to the mother ring skeleton in a manner of permutation and combination.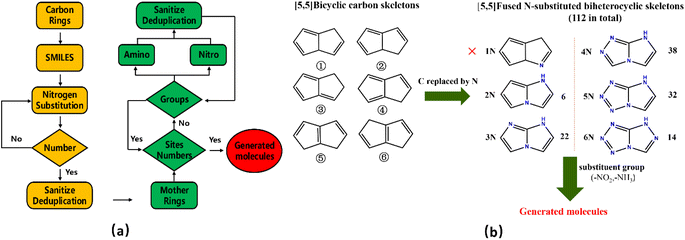 | ||
| Fig. 4 (a) Flow chart for molecular structural generation; (b) generation process of the fused [5,5] biheterocyclic molecules. | ||
Fig. 4(b) shows the generation process of the fused [5,5] biheterocyclic molecules. Initially, the structure of the molecular generation containing six [5,5] bicyclic carbon skeletons, 1N-substitution cannot form fused heterocycle structure, therefore we used the structures (from 2N to 6N) to replace the carbon in the carbon skeleton, by which 112 different fused [5,5] biheterocyclic skeletons were obtained. Collectively, 2698 possible fused [5,5] biheterocyclic were generated via the introduction of nitro (used as energetic group)/amino (group used as balance energy and sensitivity) into 112 fused [5,5] biheterocyclic skeletons.
DFT calculation
In this study, we employ density functional theory (DFT) to investigate the key properties of the selected fused [5,5] bicyclic heterocycle energetic materials. The computational calculations were performed using Gaussian 16 (A.03),36 and the results were analyzed using the wave function analysis software Multiwfn 3.8 (dev),37 more detail is referred to the ESI.†Results and discussion
Molecular screening based on predicted properties
We used our dataset to train and test the model of D-MPNN embedded with molecule features comprising of Estate fingerprints and custom descriptors. In general, the framework of D-MPNN can spontaneously generate their features form molecular graphs through message passing and aggregation algorithms to predict the properties. The initial atom and bond features of the model are list in Table S3 and S4.† All features are calculated using the open-source package RDKit.38 After obtaining hyperparameters via Bayesian Optimization.39 The D-MPNN's depth (number of message-passing steps), hidden size (size of bond message vectors), number of feed-forward network layers, and dropout were set as 5, 1700, 1700, 0.1, respectively. We used a 0.8/0.1/0.1 split for the training, validation, and test sets, and performed 5 folds cross-validation, using ReLU as activation functions, which can extend to act independently on each element of the vector output from the hidden layer, and effectively leverages non-linear activation functions to enhance its capacity for learning and representation of intricate features in the data. Fig. 5 displays the predicted density and detonation velocity before and after the inclusion of embedded features. For density, the R2 increased from 0.846 to 0.917, while the MAE decreased from 0.0365 to 0.026. The trend is similar for detonation velocity, with R2 increasing to 0.879 and MAE decreasing to 0.20. This suggests that the predictive accuracy of the model was improved through the incorporation of embedded features. The same effect was also found in the detonation pressure and decomposition temperature (see Fig S3 in ESI†). Such high accuracy may result from the reasonable features added, which can capture both crystal and molecular characteristics. As for the decomposition temperature, the relatively poor prediction evidenced by R2 of 0.787, may be due to the weaker ability of embedded features in describing intermolecular interactions than the molecular structural characteristics. However, in comparison to the message passing neural network (MPNN) without embedded features, which has an MAE value of 39 °C, the smaller MAE suggests that our model achieves better prediction accuracy.40,41 In a word, considering the potential impact of dataset differences on the model's prediction results, our model shows satisfactory performance in terms of accuracy, effectiveness, and comprehensiveness compared to previous work, as is shown in Table 1.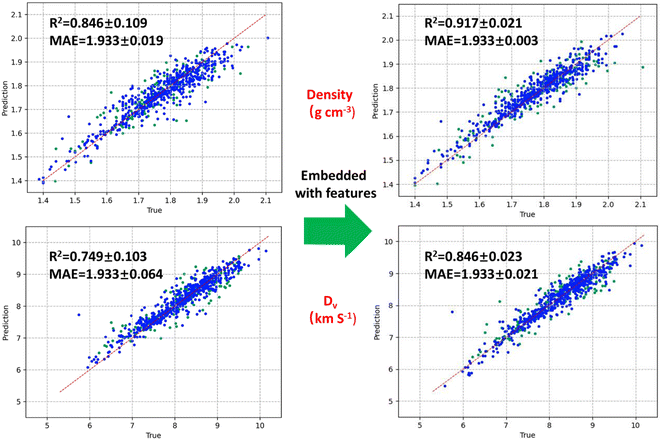 | ||
| Fig. 5 Prediction results before and after the inclusion of embedded features for density and detonation velocity. | ||
| Property | Our models | Song29 | Elton30 | Casey42 | Hou43 | Huang44 | Yang45 | |
|---|---|---|---|---|---|---|---|---|
| Electronic structure calculation | Yes | No | No | Yes | No | Yes | Yes | |
| Density (g cm−3) | Samples | >900 | >1000 | >26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
>400 | — | ||
| MAE | 0.027 | 0.042 | 0.06 | 0.035 | 0.026 | — | 0.040 | |
| Detonation velocity and pressure (km s−1/GPa) | Samples | >900 | >500 | >26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
>400 | >400 | — | |
| MAE | 0.20/1.58 | 0.24/2.38 | 0.31/2.73 | 0.30/1.80 | 0.34/1.49 | 0.235/1.788 (RMSE) | — | |
| Decomposition temperature (oC) | Samples | >500 | >500 | — | — | — | — | |
| MAE | 21.5 | 30.8 | — | — | — | 52.07 (RMSE) | ||
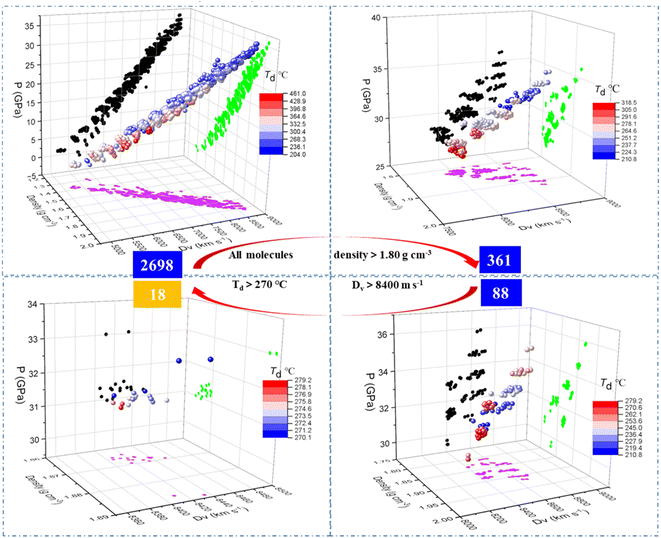
After training the model, the properties including density, Dv, P and Td of the 2698 generated molecules, were predicted by the model (see the ESI data†) and screened through various criteria. The step-by-step screening can be visualized using colour-mapped three dimensional (3D) scatter plots in Fig. 6. As shown in the top left panel, the predicted properties of the 2698 molecules conform to some known common rules of energetic materials, such as a linear correlation between density and Dv/P, and a negative correlation between density and decomposition temperature.40 We used the density of 1,3,5-trinitro-1,3,5-triazinane, (RDX), a typical energetic material, as the first criterion for screening, and only the molecules with density greater than 1.80 g cm−3 were retained, decreasing the number of molecules from 2698 to 361 as indicated in the top right panel of Fig. 6. The 3D scatter plot shows that the molecules with Td (thermal decomposition temperatures) above 270 °C (red dots) were located in areas with relatively low Dv (detonation velocities) values of 8000 m s−1, whereas the molecules with Dv greater than 8800 m s−1 (blue dots) were mostly scattered in areas with relatively low Td of 210 °C. Upon introducing screening criteria on energy (Dv greater than 8400 m s−1) and thermal stability (Td greater than 270 °C) successively, the number of molecules decreased from 361 to 88 (bottom right panel of Fig. 6) at first, and then further decreased to 18 (bottom left panel of Fig. 6).
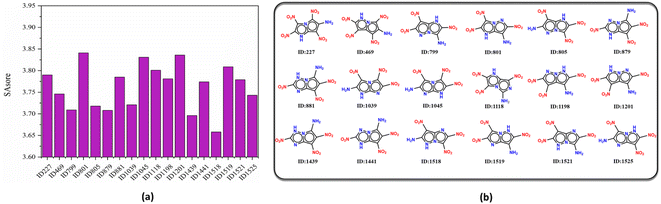
On the other hand, the synthetic accessibility also plays an important role in the application of the targeted molecules. In 2009, Ertl and Schuffenhauer proposed SAscore for estimating the synthesizability of drug molecules46 based on contributions of molecular fragments and complexity, which has been used in the field of energetic materials.26,27 The greater synthesis difficulty corresponds to the larger score. Fig. 7 depicts the SAscore and structures of the 18 screened molecules. Most of the candidate molecules that are easy to synthesize are found to be 3N-substituted molecules. Next, the top 10 molecules (ID number: 1518, 1439, 879, 799, 805, 1039, 1525, 469, 1441 and 1521) with lowest SAscore, were taken for DFT simulation to further evaluate their overall performance, as well as prediction accuracy of the D-MPNN model.
Model evaluation
In this study, we utilized DFT to evaluate the fundamental properties of selected fused [5,5] bicyclic heterocycle energetic materials. We ensure that all optimized structures exhibit local energy minima on the potential energy surface with no imaginary frequencies before performing calculations. For clarity the molecules with the 10 lowest SAscores (ID805, ID799, ID1039, ID1518, ID1525, ID879, ID1439, ID1521, ID1441, ID469) were represented by letter A to J following ascending order, and the ID number alongside the structures of the 10 molecules is show in Table S7 of ESI.†Density
We used the equation proposed by Politzer et al.47 to calculate the density of the selected 10 fused [5,5] biheterocyclic energetic materials. Table 2 shows the calculated results of molecular mass, volumes and related data after all of the structures were optimized (more detail is referred to the ESI†).| Index | M (g mol−1) | V (cm3 mol−1) | ν | σtot2 | ρ (g cm−3) |
|---|---|---|---|---|---|
| A | 257.115 | 140.630 | 0.172 | 192.0087 | 1.816 |
| B | 257.111 | 140.659 | 0.176 | 241.136 | 1.841 |
| C | 257.115 | 139.668 | 0.125 | 521.1232 | 1.917 |
| D | 257.119 | 140.135 | 0.142 | 410.3513 | 1.892 |
| E | 257.119 | 140.517 | 0.178 | 202.3609 | 1.825 |
| F | 257.116 | 140.745 | 0.219 | 325.1201 | 1.886 |
| G | 257.116 | 140.661 | 0.158 | 393.938 | 1.897 |
| H | 257.116 | 141.156 | 0.140 | 354.151 | 1.856 |
| I | 257.106 | 139.686 | 0.208 | 239.494 | 1.874 |
| J | 301.121 | 160.692 | 0.179 | 199.691 | 1.865 |
As shown in Table 2, the densities of the 10 fused [5,5] biheterocyclic molecules are within the ranges of 1.816 g cm−3 to 1.917 g cm−3. Except for molecule J (C6H3O8N7), the remaining molecules share the same molecular formula (C5H3O6N7) and similar structure, which results in the close values of M and V. On the other hand, the scattered values of ν (the balance between positive and negative electrostatic potentials) and σtot2 (the total mean square error of the electrostatic potential), could be responsible for the differences in density. Among the 10 molecules, G and D were found to possess relatively high density.
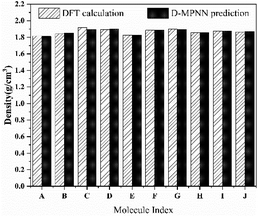
We further evaluated the accuracy of the D-MPNN model by comparing the predicted results with those obtained from rigorous DFT calculation. As shown in Fig. 8, the density predicted by the D-MPNN embedded with features closely approximates that predicted by the DFT method. The largest relative deviation, occurring at molecule C, is 0.01 g cm−3, and the average deviation is 0.006 g cm−3. Moreover, the ordering of results from DFT calculations is consistent with the model, which demonstrates the high prediction model accuracy of the D-MPNN model embedded with additional features.
Heat of formation
We calculated heat of formation (HOF) of the 10 selected molecules based on the designed isodesmic reactions (Table S5 in ESI†). The calculated results are shown in Table 3.| Index | E0 (a.u.) | ZPE (kJ mol−1) | ΔHf,gas (kJ mol−1) | ΔHsub (kJ mol−1) | ΔHf,solid (kJ mol−1) |
|---|---|---|---|---|---|
| A | −1026.851 | 322.850 | 373.797 | 26.526 | 347.271 |
| B | −1026.860 | 322.724 | 341.562 | 26.608 | 314.954 |
| C | −1026.865 | 324.415 | 337.399 | 29.859 | 307.540 |
| D | −1026.843 | 323.112 | 397.907 | 29.525 | 368.381 |
| E | −1026.844 | 322.193 | 403.906 | 26.858 | 377.048 |
| F | −1026.836 | 327.742 | 302.597 | 31.282 | 271.314 |
| G | −1026.824 | 322.986 | 443.610 | 30.125 | 413.484 |
| H | −1026.823 | 323.199 | 453.979 | 29.055 | 424.924 |
| I | −1026.832 | 321.705 | 423.918 | 28.405 | 335.691 |
| J | −1215.340 | 358.095 | 365.684 | 29.994 | 395.512 |
The HOFs of the ten molecules are within the ranges of 271.314 kJ mol−1 to 424.924 kJ mol−1. As energetic materials, their high positive HOF means higher energy contained, which could be attributed to the introduction of nitrogen-rich heterocycles and fused skeletons.
Detonation velocity and detonation pressure
Based on the density and heat of formation calculated by DFT, their detonation heat (Q), detonation velocity (Dv), and detonation pressure (P) of the 10 candidate molecules were obtained using the semi empirical Kamlet–Jacobs formula, which has been proven to be reliable for predicting the detonation performance of high-nitrogen compounds.48 Table 4 shows the calculated results of Q, Dv and P of the 10 molecules.| Index | Q (cal g−1) | D (m s−1) | P (GPa) |
|---|---|---|---|
| A | 1482.992 | 8526.319 | 33.024 |
| B | 1452.951 | 8482.811 | 32.688 |
| C | 1146.060 | 8472.734 | 32.610 |
| D | 1502.613 | 8554.386 | 33.241 |
| E | 1501.669 | 8565.828 | 33.331 |
| F | 1412.388 | 8422.975 | 32.228 |
| G | 1544.537 | 8613.439 | 33.702 |
| H | 1555.171 | 8628.227 | 33.818 |
| I | 1527.832 | 8590.055 | 33.519 |
| J | 1569.385 | 8603.008 | 33.528 |
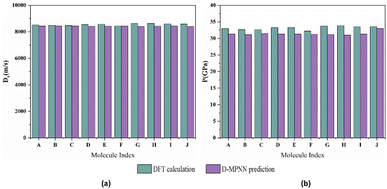
The comparison between the calculated results and the values predicted by the D-MPNN model is depicted in Fig. 9. The average deviations for detonation velocity and detonation pressure is 0.018 km s−1 and 1.202 GPa, respectively, indicating a high level of agreement.
Thermal stability analysis
In this section, we used bond dissociation energy (BDE), HOMO–LUMO energy gap, electrostatic surface potential (ESP) to evaluate the thermal stability of the 10 promising candidates.Bond dissociation energy
The smallest Mayer bond order for all molecules is C–NO2, so we only consider BDE after nitro group dissociation. The calculated results are shown in Table 5. The values of all the molecules are greater than 120 kJ mol−1, meeting the stability criteria for high energy density materials,49 and regional distribution of molecular electrostatic potential in Fig. S4 (ESI)† also provides additional evidence for the stability of concerning molecule. Molecule F and molecule G have high BDE value, implying relatively high stability.| Index | Ea (kJ mol−1) | Eb (kJ mol−1) | E (NO2) (kJ mol−1) | BDE (kJ mol−1) |
|---|---|---|---|---|
| a (Ea and Eb represent the total energy of molecule before and after dissociation, respectively). | ||||
| A | −1026.852 | −821.619 | −205.133 | 261.224 |
| B | −1026.860 | −821.629 | −205.133 | 257.895 |
| C | −1026.865 | −821.632 | −205.133 | 261.214 |
| D | −1026.843 | −821.612 | −205.133 | 255.372 |
| E | −1026.844 | −821.611 | −205.133 | 264.081 |
| F | −1026.880 | −821.630 | −205.133 | 308.446 |
| G | −1026.824 | −821.591 | −205.133 | 264.916 |
| H | −1026.824 | −821.592 | −205.133 | 260.526 |
| I | −1026.832 | −821.601 | −205.133 | 257.396 |
| J | −1215.340 | −1010.111 | −205.133 | 253.172 |
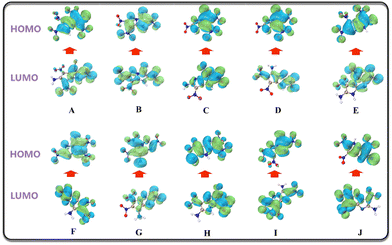
HOMO–LUMO energy gap
HOMO represents the ability of to give electrons, while LOMO represents the ability to receive electrons, hence the HOMO–LUMO energy gap is related to the electronic transition from HOMO to LUMO. A high HOMO–LUMO gap means low sensitivity to external stimuli.50 The HOMO–LUMO diagram and energy gap values of the candidate molecules are shown in Fig. 10 and Table 6, respectively.| Index | HOMO (ev) | LUMO (ev) | GAP (ev) |
|---|---|---|---|
| a From the calculation results, F and G also show superior stability among the 10 molecules. | |||
| A | −7.011 | −4.148 | 2.863 |
| B | −7.130 | −3.914 | 3.216 |
| C | −7.487 | −4.167 | 3.320 |
| D | −7.305 | −3.541 | 3.763 |
| E | −7.150 | −4.072 | 3.078 |
| F | −7.399 | −2.983 | 4.417 |
| G | −7.159 | −3.309 | 3.850 |
| H | −7.027 | −4.099 | 2.927 |
| I | −6.717 | −3.944 | 2.773 |
| J | −6.992 | −4.472 | 2.520 |
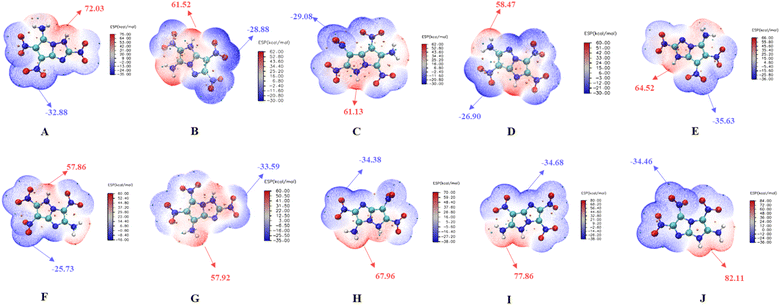
Electrostatic surface potential
The ESP of the 10 molecules is shown in Fig. 11, where the red and blue regions represent the positive and negative charge areas,51 are mainly locating in the electron-withdrawing part (nitro group) or the electron-donating part (amino group). The integral area of the negative region exceeds that of the positive region, indicating that all ten compounds exhibit low mechanical sensitivity (Fig S3 in ESI†). Molecule F and molecule G demonstrate higher stability, as lower ESP values correspond to stronger stability.52,53 The calculated results are consistent with those of BDE and HOM–LUMO energy gap. Among the two notable molecules with high and comparable stability, molecule G exhibits better detonation performance than F, making it a suitable candidate for of fused [5,5] biheterocyclic energetic material.Crystal prediction and intermolecular interaction
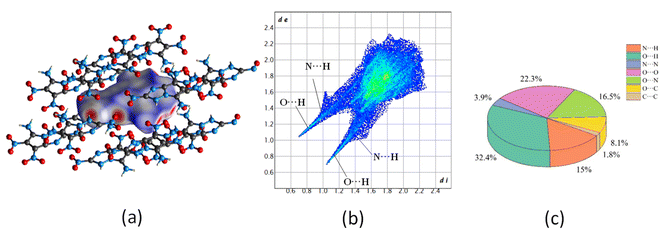
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group, of which the total energy is the lowest among the structures under discussion. Moreover, the corresponding density for P
space group, of which the total energy is the lowest among the structures under discussion. Moreover, the corresponding density for P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group agrees well with the predicted value of molecule G in Table 7, further confirming the conjecture. As shown in Fig. 12(c), molecule G present a layered π–π stacking structure with face-to-face type, which could offset the shortening of the interlayer distance, increase interlayer attraction, and makes the crystal packaging compact. Thereby the generation of hot spots is prevented through interlayer sliding when subject to external stimuli,54 accounting for the superior stability of molecule G.
space group agrees well with the predicted value of molecule G in Table 7, further confirming the conjecture. As shown in Fig. 12(c), molecule G present a layered π–π stacking structure with face-to-face type, which could offset the shortening of the interlayer distance, increase interlayer attraction, and makes the crystal packaging compact. Thereby the generation of hot spots is prevented through interlayer sliding when subject to external stimuli,54 accounting for the superior stability of molecule G.
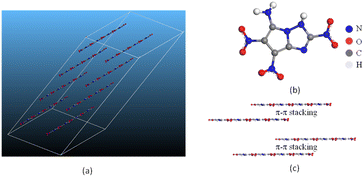 | ||
| Fig. 12 (a) The crystal structure, (b) planar molecular structure and (c) three-dimensional (3D) structure based on π–π stacking of molecule G. | ||
| SG | Etotal (kJ mol−1) | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | ρ (g cm−3) |
|---|---|---|---|---|---|---|---|---|
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
58.859 | 11.314 | 7.812 | 8.178 | 134.667 | 71.509 | 87.218 | 1.898 |
| P21/c | 59.237 | 11.512 | 5.210 | 15.107 | 90.000 | 69.364 | 90.000 | 2.014 |
| C2/C | 59.621 | 14.766 | 5.247 | 28.167 | 90.000 | 53.102 | 90.000 | 1.957 |
| PBCA | 60.516 | 11.369 | 11.369 | 19.611 | 90.000 | 90.000 | 90.000 | 1.944 |
| P212121 | 62.245 | 6.432 | 7.907 | 17.687 | 90.000 | 90.000 | 90.000 | 1.913 |
| PNA21 | 62.389 | 18.170 | 7.832 | 6.272 | 90.000 | 90.000 | 90.000 | 1.913 |
| Cc | 62.339 | 6.012 | 14.895 | 5.433 | 90.000 | 113.473 | 90.000 | 1.913 |
| P21 | 61.269 | 7.813 | 12.261 | 9.566 | 90.000 | 83.585 | 90.000 | 1.875 |
Conclusions
In this work, a high accuracy deep learning model based on D-MPNN embedded with features was established. This model assisted with high-throughput molecular screening was also applied to efficiently explore fused [5,5]-bicyclic heterocycle energetic materials. We rapidly targeted ten promising candidates from 2698 molecular structures. Further DFT calculations demonstrate that 2,6,7-trinitro-3H-pyrrolo[1,2-b][1,2,4]triazo-5-amine exhibited excellent comprehensive performance regarding both detonation properties and thermal stability, which attributes to high value of BDE and HOMO–LUMO energy gap value, low maximal ESP and unique face-to-face crystal structure. This work indicates that the combination of deep learning model embedded with features and high-throughput molecular screening, is a powerful tool for aiding rational design of novel energetic materials.Data availability
The data supporting the findings of this study are available within the article and its ESI files.† Additional data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 22375190).References
- T. M. Klapötke, C. Petermayer, D. G. Piercey and J. Stierstorfer, J. Am. Chem. Soc., 2012, 134, 20827–20836 CrossRef PubMed.
- B. Wang, X. Qi, W. Zhang, K. Wang, W. Li and Q. Zhang, J. Mater. Chem. A, 2017, 5, 20867–20873 RSC.
- D. Fischer, J. L. Gottfried, T. M. Klapötke, K. Karaghiosoff, J. Stierstorfer and T. G. Witkowski, Angew. Chem. Int. Ed., 2016, 55, 16132–16135 CrossRef CAS PubMed.
- D. E. Chavez, M. A. Hiskey and R. D. Gilardi, Angew. Chem. Int. Ed., 2000, 39, 1791–1793 CrossRef CAS PubMed.
- J. Zhang and J. M. Shreeve, J. Am. Chem. Soc., 2014, 136, 4437–4445 CrossRef CAS PubMed.
- Y. Cao, Z. Cai, J. Shi, Q. Zhang, Y. Liu and W. Zhang, Energ. Mater. Front., 2022, 3, 26–31 CrossRef CAS.
- J. Cai, C. Xie, J. Xiong, J. Zhang, P. Yin and S. Pang, Chem. Eng. J., 2022, 433, 134480 CrossRef CAS.
- Y. Tang, C. He, G. H. Imler, D. A. Parrish and J. M. Shreeve, Chem. Commun., 2018, 54, 10566–10569 RSC.
- L. Hu, C. He, G. Zhao, G. H. Imler, D. A. Parrish and J. M. Shreeve, ACS Appl. Energy Mater., 2020, 3, 5510–5516 CrossRef CAS.
- P. Yin, J. Zhang, L. A. Mitchell, D. A. Parrish and J. M. Shreeve, Angew. Chem. Int. Ed., 2016, 55, 12895–12897 CrossRef CAS PubMed.
- Q. Wang, Y. Shao and M. Lu, Chem. Commun., 2019, 55, 6062–6065 RSC.
- Z. Yang, H. Li, X. Zhou, C. Zhang, H. Huang, J. Li and F. Nie, Cryst. Growth Des., 2012, 12, 5155–5158 CrossRef CAS.
- S. A. Shevelev, I. L. Dalinger, T. K. Shkineva, B. I. Ugrak, V. I. Gulevskaya and M. I. Kanishchev, Russ. Chem. Bull., 1993, 42, 1063–1068 CrossRef.
- C. He, J. Zhang, D. A. Parrish and J. M. Shreeve, J. Mater. Chem. A, 2013, 1, 2863 RSC.
- T. M. Klapötke, P. C. Schmid, S. Schnell and J. Stierstorfer, Chem.–Eur. J., 2015, 21, 9219–9228 CrossRef PubMed.
- Y. Tang, C. He and J. M. Shreeve, J. Mater. Chem. A, 2017, 5, 4314–4319 RSC.
- G. H. Gu, J. Noh, I. Kim and Y. Jung, J. Mater. Chem. A, 2019, 7, 17096–17117 RSC.
- F. Ren, L. Ward, T. Williams, K. J. Laws, C. Wolverton, J. Hattrick-Simpers and A. Mehta, Sci. Adv., 2018, 4, eaaq1566 CrossRef PubMed.
- S. Lu, Q. Zhou, Y. Ouyang, Y. Guo, Q. Li and J. Wang, Nat. Commun., 2018, 9, 3405 CrossRef PubMed.
- Y. Zhuo, A. Mansouri Tehrani, A. O. Oliynyk, A. C. Duke and J. Brgoch, Nat. Commun., 2018, 9, 4377 CrossRef PubMed.
- R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D.-G. Ha, T. Wu, G. Markopoulos, S. Jeon, H. Kang, H. Miyazaki, M. Numata, S. Kim, W. Huang, S. I. Hong, M. Baldo, R. P. Adams and A. Aspuru-Guzik, Nat. Mater., 2016, 15, 1120–1127 CrossRef PubMed.
- H. Sahu, F. Yang, X. Ye, J. Ma, W. Fang and H. Ma, J. Mater. Chem. A, 2019, 7, 17480–17488 RSC.
- Y. Wang, Y. Liu, S. Song, Z. Yang, X. Qi, K. Wang, Y. Liu, Q. Zhang and Y. Tian, Nat. Commun., 2018, 9, 2444 CrossRef PubMed.
- S. Song, F. Chen, Y. Wang, K. Wang, M. Yan and Q. Zhang, J. Mater. Chem. A, 2021, 9, 21723–21731 RSC.
- L. Wen, B. Wang, T. Yu, W. Lai, J. Shi, M. Liu and Y. Liu, Fuel, 2022, 310, 122241 CrossRef CAS.
- L. Wen, T. Yu, W. Lai, J. Shi, M. Liu, Y. Liu and B. Wang, J. Phys. Chem. Lett., 2021, 12, 11591–11597 CrossRef CAS PubMed.
- L. Wen, T. Yu, W. Lai, M. Liu, B. Wang, J. Shi and Y. Liu, Fuel, 2022, 324, 124591 CrossRef CAS.
- Z.-J. Lu, Y. Hu, W.-S. Dong, W.-L. Cao, T.-W. Wang, J.-G. Zhang and Q.-Y. Yu, J. Phys. Chem. C, 2023, 127, 18832–18842 CrossRef CAS.
- S. Song, Y. Wang, F. Chen, M. Yan and Q. Zhang, Engineering, 2022, 10, 99–109 CrossRef CAS.
- D. C. Elton, Z. Boukouvalas, M. S. Butrico, M. D. Fuge and P. W. Chung, Sci. Rep., 2018, 8, 9059 CrossRef PubMed.
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley, M. Mathea, A. Palmer, V. Settels, T. Jaakkola, K. Jensen and R. Barzilay, J. Chem. Inf. Model., 2019, 59, 3370–3388 CrossRef CAS PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Proceedings of the 34th International Conference on Machine Learning, 2017, vol. 70, pp. 1263–1272 Search PubMed.
- P. Nguyen, D. Loveland, J. T. Kim, P. Karande, A. M. Hiszpanski and T. Y.-J. Han, J. Chem. Inf. Model., 2021, 61, 2147–2158 CrossRef CAS PubMed.
- L. H. Hall and C. T. Story, J. Chem. Inf. Comput. Sci., 1996, 36, 1004–1014 CrossRef CAS.
- L. H. Hall and L. B. Kier, J. Chem. Inf. Comput. Sci., 1995, 35, 1039–1045 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- G. Landrum, RDKit: Open-source cheminformatics, 2016. http://www.rdkit.org.
- B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. de Freitas, Proc. IEEE, 2016, 104, 148–175 Search PubMed.
- C. Wespiser and D. Mathieu, Propellants, Explos. Pyrotech., 2023, 48, e202200264 CrossRef CAS.
- J. B. Choi, P. C. H. Nguyen, O. Sen, H. S. Udaykumar and S. Baek, Propellants, Explos. Pyrotech., 2023, 48, e202200276 CrossRef CAS.
- A. D. Casey, S. F. Son, I. Bilionis and B. C. Barnes, J. Chem. Inf. Model., 2020, 60, 4457–4473 CrossRef CAS PubMed.
- F. Hou, Y. Ma, Z. Hu, S. Ding, H. Fu, L. Wang, X. Zhang and G. Li, Adv. Theory Simul., 2021, 4, 6 Search PubMed.
- X. Huang, C. Li, K. Tan, Y. Wen, F. Guo, M. Li, Y. Huang, C. Q. Sun, M. Gozin and L. Zhang, iScience, 2021, 24, 102240 CrossRef CAS PubMed.
- C. Yang, J. Chen, R. Wang, M. Zhang, C. Zhang and J. Liu, J. Chem. Inf. Model., 2021, 61, 2582–2593 CrossRef CAS PubMed.
- H.-R. Wang, C. Zhang, B.-C. Hu and X.-H. Ju, J. Mol. Model., 2021, 27, 100 CrossRef CAS PubMed.
- P. Politzer, J. Martinez, J. S. Murray, M. C. Concha and A. Toro-Labbé, Mol. Phys., 2009, 107, 2095–2101 CrossRef CAS.
- M. J. Kamlet and S. J. Jacobs, J. Chem. Phys., 1968, 48, 23–35 CrossRef CAS.
- N. Chandrasekaran, C. Oommen, V. R. S. Kumar, A. N. Lukin, V. S. Abrukov and D. A. Anufrieva, Propellants, Explos. Pyrotech., 2019, 44, 579–587 CrossRef CAS.
- C. Zhi, X. Cheng and F. Zhao, Propellants, Explos. Pyrotech., 2010, 35, 555–560 CrossRef CAS.
- V. Thottempudi, H. Gao and J. M. Shreeve, J. Am. Chem. Soc., 2011, 133, 6464–6471 CrossRef CAS PubMed.
- H. Roohi and S. Khyrkhah, J. Mol. Model., 2015, 21, 1 CrossRef CAS PubMed.
- M. R. Manaa, L. E. Fried and E. J. Reed, J. Comput. Aided Mater. Des., 2003, 10, 75–97 CrossRef CAS.
- Y. Ma, A. Zhang, C. Zhang, D. Jiang, Y. Zhu and C. Zhang, Cryst. Growth Des., 2014, 14, 4703–4713 CrossRef CAS.
- M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392 RSC.
- M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32 RSC.
- W. Hu, G. Zhang, P. Yang, H. Yang and G. Cheng, Chem. Eng. J., 2023, 451, 138640 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra03233k |
| This journal is © The Royal Society of Chemistry 2024 |