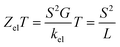DOI:
10.1039/D4RA03574G
(Paper)
RSC Adv., 2024,
14, 23699-23709
Theoretical investigation of thermoelectric properties of methyl blue-based molecular junctions†
Received
15th May 2024
, Accepted 15th July 2024
First published on 29th July 2024
Abstract
Thermoelectric properties of a family of methyl blue-based molecular junctions were theoretically studied using a combination of density functional theory (DFT) methods, and quantum transport theory (QTT). Employing different numbers of amino groups not only proves itself as a powerful strategy for controlling the transport behaviour and lifting the transmission coefficient T(E) from 1.91 × 10−5 to 7.45 × 10−5 with increasing the amino groups from zero to four, but also it enhances the thermoelectric properties of these molecules, since it increases the Seebeck coefficient (S) from 106.8 to 202.4 μV K−1 and the electronic figure of merit (ZelT) has been raised from 0.15 to 0.35, making these molecules promising candidates for thermoelectric applications.
Introduction
The individual and unique structure of single-molecule materials has made them a goal of many studies that investigate the chemical and physical properties of devices based on single molecules over the past century.1–5 One of these materials is methyl blue (MB).6,7 MB is classified as a triaminotriphenylmethane dye, which is usually recorded as an acid blue 93.8,9 This kind of dye has attracted wide interest and many applications, such as in textiles, food, rubber, printing, cosmetics, medicine, plastic, concrete, and the paper industry for multiple purposes.10 In addition, the planarity of sp2-carbon centers,11 which form π-orbitals, has granted the MB molecules an attractive functionality as observed by their unique charge transport properties.12 It is true that the spectroscopy field becomes an attractive source for many researchers13–20 to explore the spectroscopic properties of single molecules. Consequently, the optical and spectroscopic characteristics of MB molecules have been studied widely, and that encourages researchers to expand their investigation and explore the thermoelectric properties21–25 of organic molecules, which significantly improves various applications of single molecule-based molecular junctions ranging from organic electronics26,27 to molecular sensing,28,29 light emitting diodes,30,31 and energy conversion.32 In this context, the potential of computing and measuring thermoelectric properties of MB molecules will provide a considerable body of information to expand their applications. MB molecule is classified as a small molecule of ca. >2 nm, so the coherent electron transport cross the source|MB|drain configuration is depicted as a tunneling process.33 One of the most important phenomena that governing34,35 the tunneling mechanism and consequently the properties of molecular nanojunctions is the quantum interference (QI), phenomenon35 which has been established through a variety of π-conjugated molecules.36–43 Herein, a combination of density functional theory (DFT) methods,44,45 quantum transport theory (QTT),46,47 and an orbital analysis have been used to study the electronic and thermoelectric properties of methyl blue-based molecular junctions. The current work not only explores the effect of number and position of the amine group on thermoelectric properties of MB-based molecular junctions, but also it explores the role of the quantum interference (QI) in determine their transport behaviour.
Computational methods
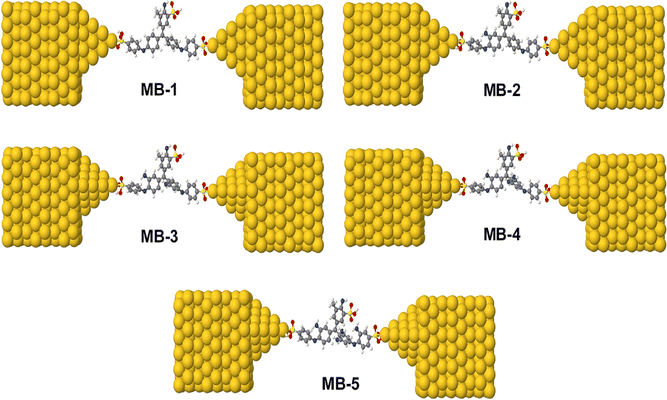
The initial optimization of gas phase molecules and isosurfaces calculations were carried out at the B3LYP level of theory48 with 6-31G** basis set49,50 using density functional theory (DFT) and time-dependent (TD-DFT)51 respectively. The geometrical optimization of all gold|MB|gold configurations under investigation in this work was accomplished by the implementation of DFT45,46 in the SIESTA45 code, as shown in Fig. 4 and S2 (see ESI†). The generalized gradient approximation (GGA) of the exchange and correlation functional is used with a double-ζ polarized (DZP) basis set, a real-space grid defined with an equivalent energy cut-off of 250 Ry. The geometry optimization for each structure is performed to the forces smaller than 20 meV Å−1. The mean-field Hamiltonian obtained from the converged DFT calculations was combined with Gollum52 code. The quantum transport theory (QTT)53,54 implemented in Gollum have been used to calculate the electronic and thermoelectric properties of all molecular junctions. The optimized molecules have been attached two (111)-directed pyramidal gold electrodes. Each electrode constructed of seven layers of (111)-oriented bulk gold with each layer consisting of 6 × 6 atoms and a layer spacing of 0.235 nm were used to create the molecular junctions. These layers were then further repeated to yield infinitely long gold electrodes carrying current, as shown in Fig. 4, (see ESI† for more details).
Results and discussion
Fig. 1 and Table 1, shows that the molecule length (l) of molecule MB-1 equals 1.91 nm, then it decreases to 1.84 nm for molecule MB-2. Molecules MB-3 and MB-4 possess 1.78 and 1.76 nm respectively. The shortest length (1.65 nm) is presented by MB-5. These results could be ascribed to the molecule twisting due to increasing the number of the amino group from 1 to 4. In addition, the HOMO–LUMO gap (H–L gap) of molecules in a gas phase have been fluctuated as well, since it shrinks from 3.5 eV for MB-1 to 2.96 eV for MB-5. The H–L gap of MB-2, MB-3 and MB-4 are 3.47, 3.39 and 3.15 eV respectively.55,56
 |
| | Fig. 1 Schematic illustration of MB molecules. | |
Table 1 Number of amino group (N); molecule length (l); molecular length (d = Au⋯Au); theoretical electrode separation (Z = dAu–Au − 0.25), where 0.25 nm is the calculated centre-to-centre distance of the apex atoms of the two opposing gold electrodes when conductance = G0 in the absence of the molecule, G0 is the conductance quantum; highest occupied molecular orbitals (HOMO); lowest unoccupied molecular orbitals (LUMO); HOMO–LUMO gap (H–L gap); A is the absorption intensity; AλMax is the maximum absorption wavelength; E is the emission intensity; EλMax is the maximum emission wavelength; fem is emission oscillator strength; SS is the Stokes shift
| Molecule |
N |
l (nm) |
d (nm) |
Z (nm) |
HOMO (eV) |
LUMO (eV) |
H–L gap (eV) |
A (a.u.) |
AλMax (nm) |
E (a.u.) |
EλMax (nm) |
fem |
SS (nm) |
| MB-1 |
0 |
1.91 |
2.155 |
1.905 |
5.58 |
2.08 |
3.5 |
65.02 |
816 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 319 319 |
944 |
0.203 |
128 |
| MB-2 |
1 |
1.84 |
2.085 |
1.835 |
5.6 |
2.13 |
3.47 |
54.92 |
800 |
9201 |
900 |
0.217 |
100 |
| MB-3 |
2 |
1.78 |
2.025 |
1.775 |
5.38 |
1.99 |
3.39 |
46.99 |
750 |
8247 |
890 |
0.171 |
140 |
| MB-4 |
3 |
1.76 |
2.005 |
1.755 |
5.05 |
1.9 |
3.15 |
80.56 |
800 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 433 433 |
900 |
0.33 |
100 |
| MB-5 |
4 |
1.65 |
1.895 |
1.645 |
4.94 |
1.98 |
2.96 |
72.06 |
848 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 796 796 |
1016 |
0.37 |
168 |
The orbitals distribution and the electronic structure of molecules were investigated and plots of the optimized structures, the highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO, respectively) are given in Fig. 2. The HOMOs of all molecules display a familiar pattern of π–π interactions along the molecular backbone. The LUMOs are also localized over the molecular backbone and could be described as a π-conjugated system.
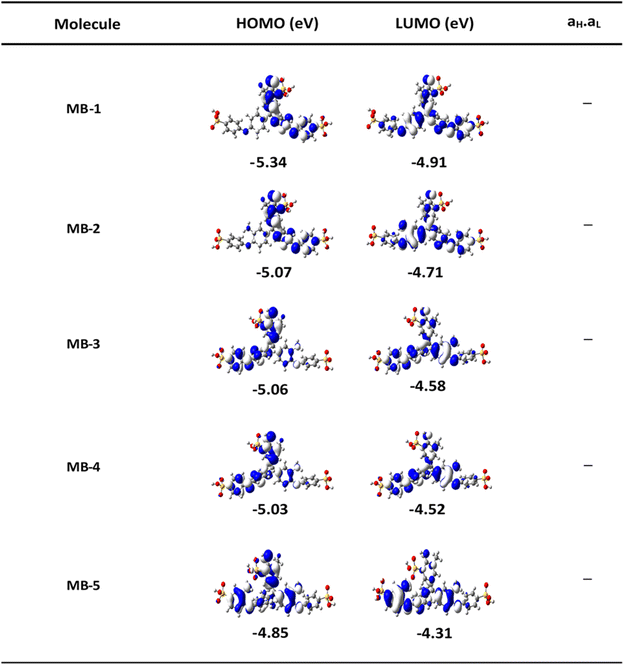 |
| | Fig. 2 The highest occupied and lowest unoccupied molecular orbitals (HOMOs and LUMOs) (isosurfaces ± 0.02 (e bohr−3)1/2), white part is a positive sign, blue part is a negative sign. aH × aL is the multiplication of the HOMO and LUMO amplitudes. As an example, HOMO and LUMO for MB-5 molecule possess different signs, then the multiplication of molecular orbitals amplitudes (aH × aL) is a negative sign and the molecule exhibits a constructive quantum interference (CQI). | |
In order to explore the impact of connectivity type and to prove the existence of QI in MB molecules, the current investigation performed an orbital analysis, and demonstrated that CQI is dominated on the transport of all molecular junctions, as shown in Fig. 2. Lambert et al.57 have reported an orbital symmetry rule. The magic ratio theory58 is based on utilising the exact core Green's function, defined by:
In the literature, various approximations to g(E) are discussed, one of which involves the approximation of including only the contributions to g(E) from the HOMO and LUMO. If the amplitudes of the HOMO on sites a and b are denoted ψaEH and ψbEH and the amplitudes of the LUMO are ψaEL and ψbEL, then if the contributions from all other orbitals are ignored, then, a crude approximation to the Green's function gba(E) is
| |
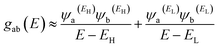 | (2) |
where
EH and
EL are the energies of the HOMO and LUMO respectively. If the HOMO product
ψb(EH)ψa(EH) has the same sign as the LUMO product
ψb(EL)ψa(EL) then the right-hand side of
eqn (2) will vanish at some energy
E in the range
EH ⩽
E ⩽
EL. That is for some energy
E within the HOMO–LUMO gap. In this case, one can say that the HOMO and the LUMO interfere destructively. On the other hand, if the HOMO and LUMO products have opposite signs then the right hand side of
eqn (2) will not vanish within the HOMO–LUMO gap and one can say that the HOMO and LUMO interfere constructively within the gap, (they could of course interfere destructively at some other energy
E outside the gap). When the right-hand side of
eqn (2) vanishes, the main contribution to
gba(
E) comes from all other orbitals, so in general
eqn (2) could be a poor approximation. One exception to this occurs when the lattice is bipartite, because the Coulson–Rushbrooke (CR) theorem
59 tells us that if
a and
b are both even or both odd, then the orbital products on opposite sides of
eqn (3) and
(4) have the same sign. Consequently, the HOMO and LUMO interfere destructively, while all other pairs of orbitals interfere destructively, leading to the trivial zeros in the magic number table,
58 for which
gba(0) = 0.
| | |
ψa(En)ψb(En) = ψa(−En)ψb(−En)
| (3) |
| | |
ϕb(En)ϕb(En) = ϕb(−En)ϕb(−En)
| (4) |
where ±
En are eigenvalues come in ± pairs and the eigenstate belonging to −
En is related to the eigenstate belonging to
En. Obviously, this exact cancellation is a property of bipartite lattices only, but based on its success for bipartite lattices, one might suppose that
eqn (2) is a reasonable approximation, for other lattices. Nevertheless, as pointed out by Yoshizawa
et al.,
60–63 since orbitals such as those in
Fig. 2 are often available from DFT calculations, it can be helpful to examine the question of whether or not the HOMO and LUMO (or indeed any other pair of orbitals) interfere destructively or constructively, by examining the colours of orbitals. This is simplified by writing
eqn (2) in the form
| |
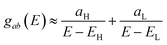 | (5) |
where
aH =
ψa(EH)ψb(EH) and
aL =
ψa(EL)ψb(EL). If the HOMO product
aH has the same sign as the LUMO product
aL then the right-hand side of
eqn (5) will vanish for some energy
E in the range
EH ⩽
E ⩽
EL. In other words, the HOMO and LUMO will interfere destructively at some energy within the HOMO–LUMO gap. However this does not mean that the exact
gba(
E) will vanish. Indeed, if the right hand side of
(5) vanishes, then the contributions from all other orbitals become the dominant terms.
64 Nevertheless, this is an appealing method of identifying QI effects in molecules and describing their qualitative features.
65
The distinctive properties of MB molecules including for example their spectroscopic properties, especially the absorption and emission spectra, have become the subject of the increased interest for many studies.66 Interestingly, the UV/visible absorption and emission spectra showed asymmetric peaks, since the range of the absorption spectra is extend from 750 to 848 nm, as shown in Table 1, and the emission spectra is ranging from 890 to 1016 nm. These results could be interpreted in terms of strain and twisting effects, which are critical qualities that endows molecules atypical spectroscopic properties and reactivity. The inherent strain of the molecule increases with increasing of the amino group number and consequently leads to twisting, which in turn changes the structural and spectroscopic properties. The methyl blue molecule (MB-1) do not possess an amino group. Thus, this molecule is expect to exhibit a largest HOMO–LUMO gap, as shown in Table 1. These results are consistent with the results of references.67,68 Furthermore, Fig. 3 and Table 1 show that the Stokes shift of these molecules is ranging from 100 to 168 nm. Therefore, these results may introduce MB molecules as promising candidates for the encryption and medical applications.69,70 On the other hand, the most important parameters in optoelectronics applications is the emission oscillator strength (fem).71 Theoretically, for a given PL material, fem is directly proportional to the emission cross section (σem) and it is given by:72
| |
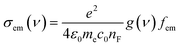 | (6) |
where
e is the electron charge,
ε0 is the vacuum permittivity,
me is the mass of electron,
c0 is the speed of light,
nF is the refractive index of the gain material,
ν is the frequency of the corresponding emission, and g(
ν) is the normalized line shape function with
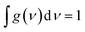
. The emission oscillator strength (
fem) of MB molecules is ranging from 0.17 to 0.37, as shown in
Table 1.
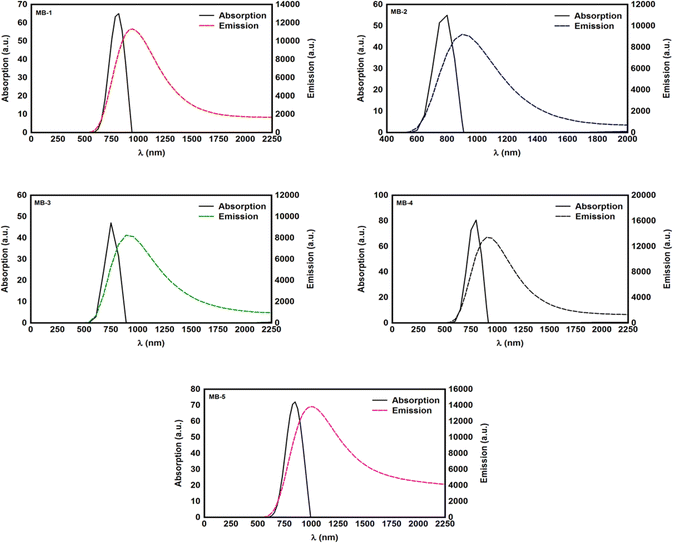 |
| | Fig. 3 UV/Vis absorption spectra (solid curves) and emission spectra (dashed curves) for all molecules. | |
In this work T(E) has been calculated by attach the optimized molecules with two (111)-directed gold electrodes, as shown in Fig. 4. From these molecular junctions the electronic and thermoelectric properties were calculated using Gollum code.52 The transmission coefficient according to Landauer–Büttiker73 formalism is given by:
| | |
T(E) = Tr{ΓR(E)GR(E)ΓL(E)GR†(E)}
| (7) |
where
| | |
ΓL,R(E) = i(ΣL,R(E) − Σ†L,R(E))
| (8) |
where
ΓL,R describes the level broadening due to the coupling between left (L) and right (R) electrodes and the central scattering region,
ΣL,R(
E) are the retarded self-energies associated with this coupling.
| | |
GR = (EX − Ĥ − ΣL − ΣR)−1
| (9) |
where
GR is the retarded Green's function,
Ĥ is the Hamiltonian and
X is the overlap matrix. The transport properties is then calculated using the Landauer formula:
| |
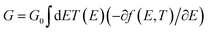 | (10) |
where
G0 = 2
e2/
h is the conductance quantum,
f(
E) = (1 + exp((
E −
EF)/
kBT))
−1 is the Fermi–Dirac distribution function,
T is the temperature and
kB = 8.6 × 10
−5 eV K
−1 is Boltzmann
's constant.
 |
| | Fig. 4 Theoretical models of optimized molecular junctions. | |
Fig. 4 and 5 show that the molecules bind to gold electrodes through sulfonyl groups as anchor groups. It is true that the binding between sulfonyl groups and electrodes is uncommon due to the formation of hypervalent five-coordinate sulfur atoms. However, the results of Fig. 5 suggest considerable values of the binding energy, which are consistent with the outcomes of H. Quan et al.,74 since they reported that the presence of strong electron-withdrawing groups on benzene sulfonyl 5-FU greatly enhanced the binding selectivity.75,76 To perform accurate calculations of the transmission coefficient for the molecular junctions with sulfonyl-anchor groups, the binding energies were computed using eqn (11), for a range of diverse molecular direction within the junction (know by the angle Θ, ∠Cipso–S–Au) as shown in Fig. 5. The maximum binding energies arranged between −0.73 and −0.74 eV for the angles from 140° to 180°, as shown in Fig. 5a. Allowing for room-temperature thermal fluctuations of (∼25 meV), this proposes that the optimal conformation is within the angle Θ equals 180°.
| | |
ΔE(ab) = Eab − (Eaab + Ebab)
| (11) |
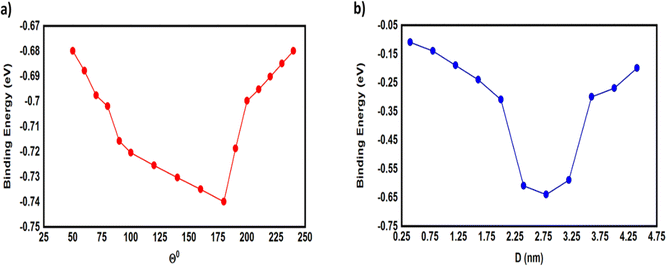 |
| | Fig. 5 (a) The binding energy as a function of the angle (Θ) between anchor group and gold electrode; (b) the binding energy as a function of the molecular junction displacement (D). | |
The molecular systems are denoted a and b. The total energy of the combined a and b systems is Eab, while the total energies of isolated systems a and b are Ea and Eb respectively with keeping identical basis sets for the three energies. ΔEab is the binding energy (BE) between anchor groups and gold electrode.
To gain further insight into the evolution of the binding energy (BE) upon stretching, and to obtain a robust value of the BE between anchor group and gold electrode, we calculated the most probable energies at each relative displacement position. The most-probable absolute displacements (D) in an experimental molecular junction formed between a gold STM tip and an Au(111) surface are obtained by adding the snapback distance ΔDcorr = (0.5 ± 0.1 nm)77–79 to the relative displacement D = ΔD + ΔDcorr. Fig. 5b shows that the highest values of BE ranging between −0.59 and −0.64 eV for the displacements 2.4, 2.8 and 3.2 nm, and the maximum binding energy (−0.64 eV) for the displacement of 2.8 nm.
Fig. 6 shows the transmission coefficient T(E),80 of source|molecule|drain molecular junctions. The signature of a constructive quantum interference (CQI) is clear for all molecules, which leads to high T(E) values, as shown in Fig. 6 and Table 2. These outcomes are ascribed to the para connectivity81–86 between phenyl rings. The order of T(E) is TMB-5 > TMB-4 > TMB-3 > TMB-2 > TMB-1, as shown in Table 2. For all cases, the Fermi level (EF–EDFTF) lies within the HOMO–LUMO gap towards the HOMO resonance, which remarks a HOMO-dominated transport mechanism.
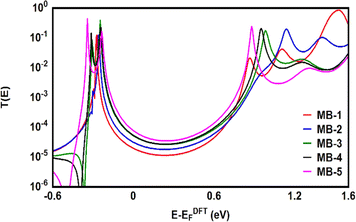 |
| | Fig. 6 Transmission coefficient T(E) as a function of electrons energy for all molecules. | |
Table 2 Number of transfer electrons (Γ = eM − eJ), where eM is the number of electrons on the molecule in a gas phase, eJ is the number of electrons on the molecule in a junction; transmission coefficient T(E); molecule length (l = SS); highest occupied molecular orbitals of the molecules in a junction (JHOMO); lowest unoccupied molecular orbitals of the molecules in a junction (JLUMO); HOMO–LUMO gap (JH–L gap) of the molecules in a junction
| Molecule |
Γ |
T(E) |
JHOMO (eV) |
JLUMO (eV) |
JH–L gap (eV) |
| MB-1 |
1.3 |
1.91 × 10−5 |
0.27 |
0.86 |
1.13 |
| MB-2 |
1.7 |
3.06 × 10−5 |
0.26 |
1.13 |
1.39 |
| MB-3 |
2.1 |
5.02 × 10−5 |
0.25 |
0.98 |
1.23 |
| MB-4 |
2.3 |
5.17 × 10−5 |
0.31 |
0.95 |
1.26 |
| MB-5 |
2.6 |
7.45 × 10−5 |
0.34 |
0.88 |
1.22 |
These consequences are consistent with the results of references.87,88 The results could be understood in terms of the inherent strain, which resulted to the molecular twisting which in turn decreased the tunnelling distance (l) and consequently increasing T(E), according to eqn (12).
where,
T(
E) is the transmission coefficient,
β is the electronic decay constant and
l is the tunnelling distance. In addition, the molecule length of all molecules is smaller than 2 nm, which is consistent with a dominant contribution from coherent tunneling mechanism.
89–93 The rectangular tunnel barrier model
94 states that the electrical conductance through a single molecule (barrier) decreases exponentially with the length of the barrier, according to
eqn (12).
To gain more knowledge of electronic transitions, and the effect of different numbers of an amino group on electron transport, Mulliken population95 was computed to characterize the electronic charge distribution, and the number of electrons transferred from the molecule to the electrodes, as shown in Fig. 7 and Table 2. There is an important result, which is the number of calculated electrons transfer from molecule to the electrodes (Γ) ranges from ca. 1.3 electron for MB-1 molecule to 2.6 electron for MB-5. A partial charge transfer has been observed,96 which is consistent with the energetic location of frontier molecular orbitals as discussed by Thygesen et al.97 Now, by comparing the number of Γ from molecule MB-1 relative to that of molecule MB-5. An increase of the number of amino groups from zero to four increases the electron donor atoms (nitrogen atoms), which rises Γ from 1.3 to 2.6 electron. In addition, the effects of the inherent strain and molecular twisting decrease the molecule length from 1.91 nm for MB-1 to 1.65 nm for MB-5. The latter contributes with CQI in lifting the transmission coefficient from 1.91 × 10−5 to 7.45 × 10−5 for MB-1 and MB-5 respectively, as shown in Fig. 7.
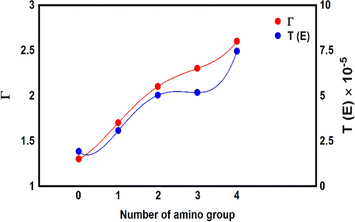 |
| | Fig. 7 The number of transferred electrons from molecule to electrodes (Γ) for all molecules. | |
The slope of T(E) determines the Seebeck coefficient (S) and electronic figure of merit (ZelT), which are given by:
| |
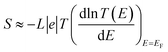 | (13) |
where
L is the Lorenz number
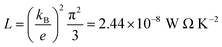
. In other words,
S is proportional to the negative of the slope of ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T
T(
E), evaluated at the Fermi energy. Based on Seebeck coefficient, the power factor was calculated by:
where
T is the temperature
T = 300 K,
G is the electrical conductance and
S is the Seebeck coefficient. The purely electronic figure of merit (
ZelT) is given by:
98,99| |
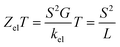 | (15) |
where
kel is the electron thermal conductance. According to previous studies,
98,99 the figure of merit in this work has been calculated only based on a purely electronic contribution, as shown in
eqn (15).
It is well known that the performance of thermoelectric materials is characterized by an efficient conversion of an input heat to the electricity.100,101 In this context, the enhancement of power factor (P) and electronic figure of merit (ZelT), which are depend on the Seebeck coefficient (S) is important. Fig. 8a and b and Table 3 show the highest values of S and ZelT (202.4 μV K−1 and 0.36 respectively) have been exhibited by molecule MB-3. In contrast, molecule MB-1 presented the lowest values of these parameters (106.8 μV K−1, and 0.15). In addition, molecules MB-4 and MB-5 introduce high S and ZelT, as shown in Table 3. These results not only demonstrated the important role of the existence and number of amino group in improvement S and ZelT, but also established a crucial role of the inherent strain in MB molecules, which controls the transport behaviour and improves the thermoelectric properties of these molecules. Furthermore, the competition between electrical conductance and Seebeck coefficient according to eqn (14) led to the power factor order of PMB-5 > PMB-3 > PMB-4 > PMB-2 > PMB-1. In light of the aforementioned results, these molecules could be considered as promise candidates for thermoelectric applications.
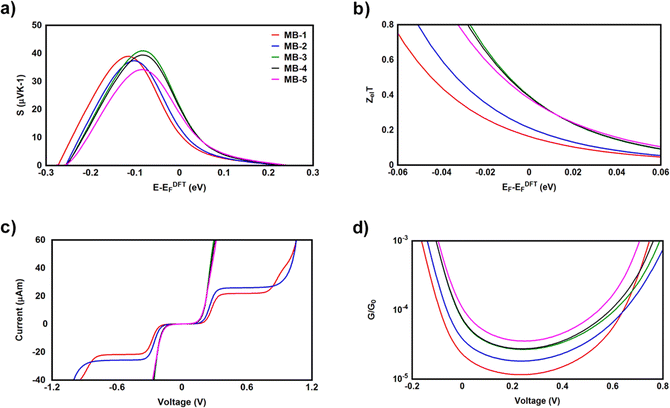 |
| | Fig. 8 (a) Seebeck coefficient (S); (b) electronic figure of merit (ZelT); (c) current–voltage characteristics; (d) electrical conductance (G/G0) as a function of applied voltage for all molecular junctions. | |
Table 3 Seebeck coefficient (S); electronic figure of merit (ZelT); power factor (P); threshold voltage (Vth); Peltier coefficient (Π) for all molecular junctions
| Molecule |
S (μV K−1) |
P (W K−1 × 10−18) |
ZelT |
Vth (V) |
Π (J C−1) |
| MB-1 |
106.8 |
16.9 |
0.15 |
0.23 |
0.034 |
| MB-2 |
127.6 |
38.6 |
0.19 |
0.22 |
0.040 |
| MB-3 |
202.4 |
159.5 |
0.36 |
0.18 |
0.064 |
| MB-4 |
196.9 |
155.6 |
0.36 |
0.19 |
0.062 |
| MB-5 |
178.3 |
183 |
0.35 |
0.18 |
0.056 |
The values of the transmission coefficient T(E), Seebeck coefficient (S) and electronic figure of merit (ZelT) are found to be higher when the contact Fermi energies are close to the middle of the HOMO–LUMO gap and increases as Fermi energies approach resonance with the highest occupied molecular orbitals (HOMO). In somewhat, these results are consistent with an investigation of David C. Milan et al.,93 since they reported that the existent of different solvent environments affect both the molecular junction conductance and the attenuation factors. These properties are depend in a very sensitive manner on the position of the contact Fermi energies within in the HOMO–LUMO gap.
Fang Chen et al.102 have studied the effect of different anchoring groups on the conductance of single molecules using alkanes terminated with dithiol, diamine, and dicarboxylic-acid groups as a model system. They observed that the conductance is highly sensitive to the anchoring group type. They interpreted these observations in terms of the different electronic couplings between the molecules and the electrodes and alignments of the molecular energy levels relative to the Fermi energy level of the electrodes introduced by different anchoring groups. Moreover, they mentioned that the conductance of molecules terminated with diamine and dicarboxylic-acid groups, is sensitive to pH due to protonation and deprotonation of the anchoring groups.
Fig. 8c and d and Table 3 present the current–voltage (I–V) characteristics of all molecular junctions, which are limited to the first and third quadrants of the I–V plane crossing the origin. Therefore, they are classified as components consume the electric power, and here the importance of the threshold voltage (Vth) value appears. The values of Vth are ranging from 0.18 to 0.23 V, which makes these molecules promising candidates for the electronic applications. Moreover, I–V characteristics of MB-3, MB-4 and MB-5 molecular junctions exhibited a semiconductor behaviour, while MB-1 and MB-2 show a quantum staircase structure in the conductance. Obviously, as the voltage increases, the density of electrons also increases, which leads to an increase in the number of occupied subbands. The dependence conductance in this case is a set of plateaus separated by steps of height 2e2/h: a stepwise change in the conductance of MB-1 and MB-2 molecules channels occurs each time the Fermi level coincides with one of the subbands. Hence, the quantum staircase behaviour could be attributed to the adiabatic transparency of spin-nondegenerate subbands of these molecules.65,103
The Peltier coefficient refers to the reversible absorption or liberation of heat at the junction of two materials depending on the direction of a current, I, flowing through the junction. One main component of the heat exchange at the junction of two materials is the irreversible heat dissipation (Joule heating) which has the form QJ = IR2, where R is the junction resistance.104 Joule heating has been recently observed down to atomic-scale.105 Another component is the reversible heat exchange due to Peltier effect which has the form QP = ΠI, where Π is the Peltier coefficient. One important aspect of the Peltier effect is that the direction of the heat exchange at the junction (that is, heating or cooling) can be controlled via switching the current direction. Herein, Fig. 9 and Table 3 show that Peltier values are impalpable at low temperatures, and then begin to increase gradually as temperatures rise. Over a wide range of temperatures, starting from the room temperature (300 K) upwards, Peltier values were steadily increasing. This result is consistent with the current–voltage characteristic results in Fig. 8. Remarkably, molecule MB-3 presented the highest value (0.064 JC−1), while molecule MB-1 shows the lowest Peltier value (0.034 J C−1). The overall order of values was ΠMB-3 > ΠMB-4 > ΠMB-5 > ΠMB-2 > ΠMB-1.
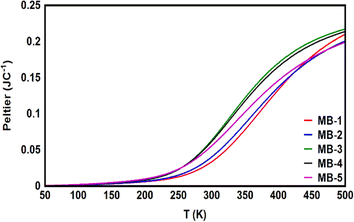 |
| | Fig. 9 Peltier coefficient as a function of the temperature for all molecules. | |
Conclusions
In conclusions, the existent of amino groups leads to increase the inherent strain, and molecular twisting which decreases the molecule length, and the latter along with the effect of CQI rises T(E). The high calculated values of S predicate that MB molecules could be promise candidates for thermoelectric applications. The semiconductor and the quantum staircase behaviors as well as the low threshold voltages of MB molecules suggest that these structures could be suitable compounds for electronic applications. Furthermore, the values of Stokes shift (SS) predicate that MB molecules could be appropriate structures for encryption and medical applications. Please refer to the ESI† for the theories and all details relevant to the computational methods.106–115
Data availability
The data is available at the manuscript and ESI.†
Author contributions
Sarah M. S. Al-Mohana: conceptualization, validation, formal, analysis, investigation, writing – original draft, visualization, Hussein N. Najeeb: software, formal analysis. Rasool M. Al-Utayjawee: investigation. Ferydon Babaei: supervision, investigation, analysis, conceptualization, writing – review & editing. Oday A. Al-Owaedi: software, formal analysis, writing – review & editing.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
S. M. S. M. and F. B. introduce a deep thank and appreciation to the University of Qom for the kind support. O. A. A. and H. N. N. thank the University of Babylon and Al-Zahrawi University College for their support.
Notes and references
- L. Jacob, G. Alessio, P. Alessandro and S. C. Gemma, ACS Nano, 2013, 7, 9183–9194 CrossRef PubMed.
- A. Q. David, S. C. Gemma, G. H. Randall, H. Thorsten, W. R. Michael, V. P. Richard and R. A. Mark, J. Phys. Chem. C, 2008, 112, 16991–16998 CrossRef.
- H. Bing, L. Xu, Y. Ying, H. Ze-Wen, Z. Ju-Fang, P. Lin-Qi, S. Yong, L. Jian-Feng, Z. Xiao-Shun, C. Jing-Zhe, J. Shan and M. Bing-Wei, J. Am. Chem. Soc., 2018, 140, 17685–17690 CrossRef PubMed.
- A. Renad, H. Songjun, W. Qingqing, L. Zitong, H. Wenjing and C. J. Lambert, ACS Sens., 2021, 6, 470–476 CrossRef PubMed.
- O. A. Al-Owaedi, S. Bock, D. C. Milan, M. Oerthel, M. S. Inkpen, D. S. Yufit, A. N. Sobolev, N. J. Long, T. Albrecht, S. J. Higgins, M. R. Bryce, R. J. Nichols, C. J. Lambert and P. J. Low, Nanoscale, 2017, 9, 9902–9912 RSC.
- A. Fernández-Pérez and G. Marbán, ACS Omega, 2020, 5, 29801–29815 CrossRef PubMed.
- T. B. de Queiroz, E. R. de Figueroa, M. D. Coutinho-Neto, C. D. Maciel, E. Tapavicza, Z. Hashemi and L. Leppert, J. Chem. Phys., 2021, 154, 044106 CrossRef CAS PubMed.
- K. A. S. Schulte, H. J and J. K. Sugden, Dyes Pigm., 1997, 34, 159–167 CrossRef.
- Y. Feng, Y. Li, M. Xu, S. Liua and J. Yao, RSC Adv., 2016, 6, 109608 RSC.
- M. Hassan, M. D. Al-Ahmadi and M. Mosaid, Arabian J. Chem., 2015, 8, 72–77 CrossRef CAS.
- Y. Shigeru and K. Eiichi, J. Synth. Org. Chem., Jpn., 2019, 77, 1147–1158 CrossRef.
- S. S. Hemdan, J. Fluoresc., 2023, 33, 2489–2502 CrossRef CAS PubMed.
- W. E. Moerner and T. Basché, Angew. Chem., Int. Ed., 1993, 54, 105–537 Search PubMed.
- W. E. Moerner, Science, 1994, 265, 46–53 CrossRef CAS PubMed.
- M. Orrit, J. Bernard, R. Brown and B. Lounis, Prog. Opt., 1996, 35, 61–144 Search PubMed.
- T. Plakhotnik, E. A. Donley and U. P. Wild, Annu. Rev. Phys. Chem., 1997, 48, 181–212 CrossRef CAS PubMed.
- S. Nie and R. N. Zare, Annu. Rev. Biophys. Biomol. Struct., 1997, 26, 567–596 CrossRef CAS PubMed.
- W. E. Moerner, Science, 1999, 283, 1670–1676 CrossRef CAS PubMed.
- P. Tinnefeld and M. Sauer, Angew. Chem., Int. Ed., 2005, 44, 2642–2671 CrossRef CAS PubMed.
- P. V. Cornish and T. Ha, ACS Chem. Biol., 2007, 2, 53–61 CrossRef CAS PubMed.
- L. Fan, X. Su, H. Zhu, H. Liu, S. Lou, Y. Shi and S. Yan, Adv. Mater. Interfaces, 2023, 10, 2202207 CrossRef CAS.
- O. A. Al-Owaedi, D. C. Milan, M. Oerthel, S. Bock, D. S. Yufit, J. A. K. Howard, S. J. Higgins, R. J. Nichols, C. J. Lambert, M. R. Bryce and P. J. Low, Organometallics, 2016, 35, 2944–2954 CrossRef CAS.
- R. S. Akbarabadi, R. H. Soleimani and B. M. Tagani, Sci. Rep., 2021, 11, 8958 CrossRef PubMed.
- S. V. Aradhya and L. Venkataraman, Nanotechnology, 2013, 8, 399–410 CAS.
- G. Sedghi, L. J. Esdaile, H. L. Anderson, V. M. García-Suárez, C. J. Lambert, S. Martin, D. Bethell, S. J. Higgins and R. J. Nichols, Nat. Nanotechnol., 2011, 6, 517–523 CrossRef CAS PubMed.
- M. Ball, Y. Zhong, B. Fowler, B. Zhang, P. Li, G. Etkin, D. W. Paley, J. Decatur, A. K. Dalsania, H. Li, S. Xiao, F. Ng, M. L. Steigerwald and C. Nuckolls, J. Am. Chem. Soc., 2016, 138, 12861–12867 CrossRef CAS PubMed.
- E. Kayahara, L. Sun, H. Onishi, K. Suzuki, T. Fukushima, A. Sawada, H. Kaji and S. Yamago, J. Am. Chem. Soc., 2017, 139, 18480–18483 CrossRef CAS PubMed.
- T. Iwamoto, Y. Watanabe, T. Sadahiro, T. Haino and S. Yamago, Angew. Chem., Int. Ed., 2011, 50, 8342–8344 CrossRef CAS PubMed.
- P. Li, T. J. Sisto, E. R. Darzi and R. Jasti, Org. Lett., 2014, 16, 182–185 CrossRef CAS PubMed.
- M. Naher, D. C. Milan, O. A. Al-Owaedi, I. J. Planje, S. Bock, J. Hurtado-Gallego, P. Bastante, Z. M. A. Dawood, L. Rincón-García, G. Rubio-Bollinger, S. J. Higgins, N. Agraït, C. J. Lambert, R. J. Nichols and P. J. Low, J. Am. Chem. Soc., 2021, 143(10), 3817–3829 CrossRef CAS PubMed.
- D. Z. Manrique, C. Huang, M. Baghernejad, X. Zhao, O. A. Al-Owaedi, H. Sadeghi, V. Kaliginedi, W. Hong, M. Gulcur, T. Wandlowski, M. R. Bryce and C. J. Lambert, Nat. Commun., 2015, 6, 6389 CrossRef CAS PubMed.
- H. Kirchberg and A. Nitzan, J. Chem. Phys., 2022, 156, 094306 CrossRef CAS PubMed.
- T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 16002 CrossRef CAS.
- M. Baghernejad, Y. Yang, O. A. Al-Owaedi, Y. Aeschi, B. Zeng, Z. M. Dawood, X. Li, J. Liu, J. Shi, D. Silvio, S. Liu, W. Hong and C. J. Lambert, Chem.–Eur. J., 2020, 26, 5264–5269 CrossRef CAS PubMed.
- P. Sautet and C. Joachim, Chem. Phys. Lett., 1988, 153, 511–516 CrossRef CAS.
- M. Mayor, H. B. Weber, J. Reichert, M. Elbing, C. von Hänisch, D. Beckmann and M. Fischer, Angew. Chem., Int. Ed., 2003, 42, 5834–5838 CrossRef CAS PubMed.
- M. Taniguchi, M. Tsutsui, R. Mogi, T. Sugawara, Y. Tsuji, K. Yoshizawa and T. Kawai, J. Am. Chem. Soc., 2011, 133, 11426–11429 CrossRef CAS PubMed.
- C. M. Guédon, H. Valkenier, T. Markussen, K. S. Thygesen, J. C. Hummelen and S. J. van der Molen, Nat. Nanotechnol., 2012, 7, 305 CrossRef PubMed.
- S. V. Aradhya, J. S. Meisner, M. Krikorian, S. Ahn, R. Parameswaran, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Nano Lett., 2012, 12, 1643–1647 CrossRef CAS PubMed.
- C. R. Arroyo, S. Tarkuc, R. Frisenda, J. S. Seldenthuis, C. H. M. Woerde, R. Eelkema, F. C. Grozema and H. S. J. van der Zant, Angew. Chem., Int. Ed., 2013, 52, 3152–3155 CrossRef CAS PubMed.
- Y. Zhang, G. Ye, S. Soni, X. Qiu, T. L. Krijger, H. T. Jonkman, M. Carlotti, E. Sauter, M. Zharnikov and R. C. Chiechi, Chem. Sci., 2018, 9, 4414–4423 RSC.
- V. Rabache, J. Chaste, P. Petit, M. L. Della Rocca, P. Martin, J. Lacroix, R. L. McCreery and P. Lafarge, J. Am. Chem. Soc., 2013, 135, 10218–10221 CrossRef CAS PubMed.
- R. Frisenda, V. A. E. C. Janssen, F. C. Grozema, H. S. J. van der Zant and N. Renaud, Nat. Chem., 2016, 8, 1099 CrossRef CAS PubMed.
- A. Kumar, N. Safdar, S. Kethireddy and D. Chateau, Crit. Care Med., 2010, 8, 1651–1664 CrossRef PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- C. J. Judd, A. S. Nizovtsev, R. Plougmann, D. V. Kondratuk, H. L. Anderson, E. Besley and A. Saywell, Phys. Rev. Lett., 2020, 125, 206803 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2198 CrossRef CAS.
- G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090 CrossRef CAS.
- R. Erich and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef.
- J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Zs Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. W. D. Bailey, K. Gillemot, H. Sadeghi and L. A. Algharagholy, New J. Phys., 2014, 16, 93029 CrossRef.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef PubMed.
- E. Leary, B. Limburg, S. Sangtarash, A. Alanazy, I. Grace, K. Swada, L. J. Esdaile, M. M. Noori, T. González, G. Rubio-Bollinger, H. Sadeghi, N. Agrait, A. Hodgson, S. J. Higgins, C. J. Lambert, H. L. Anderson and R. Nichols, J. Am. Chem. Soc., 2018, 140, 12877–12883 CrossRef CAS PubMed.
- D. Zamel and A. U. Khan, Inorg. Chem. Commun., 2021, 131, 108766 CrossRef CAS.
- H. Kahlert, G. Meyer and A. Albrecht, ChemTexts, 2016, 2, 1–28 CrossRef CAS.
- C. J. Lambert, Quantum Transport in Nanostructures and Molecules, IOP Publishing, Inc., Bristol, 2021, pp. 15–3 Search PubMed.
- C. J. Lambert and S. Liu, Chem.–Eur. J., 2018, 24, 4193–4201 CrossRef CAS PubMed.
- C. A. Coulson and G. S. Rushbrooke, Math. Proc. Cambridge Philos. Soc., 1940, 36, 193 CrossRef CAS.
- K. Yoshizawa, Acc. Chem. Res., 2012, 45, 1612–1621 CrossRef CAS PubMed.
- T. Tada and K. Yoshizawa, Phys. Chem. Chem. Phys., 2015, 17, 32099–32110 RSC.
- Y. Tsuji and K. Yoshizawa, J. Phys. Chem. C, 2017, 121, 9621–9626 CrossRef CAS.
- K. Okazawa, Y. Y. Tsuji and K. Yoshizawa, J. Phys. Chem. C, 2020, 124, 3322–3331 CrossRef CAS.
- M. Camarasa-Gómez, D. Hernangómez-Pérez, M. S. G. Inkpen, E. Lovat, E. Fung, X. Roy, L. Venkataraman and F. Evers, Nano Lett., 2020, 20, 6381–6386 CrossRef PubMed.
- O. A. Al-Owaedi, ChemPhysChem, 2024, 25(1–12), e202300616 CrossRef CAS PubMed.
- A. Mochida, R. Nitta, A. Hashimoto and K. Matsui, J. Jpn. Soc. Colour Mater., 2017, 90, 97–101 CrossRef CAS.
- Z. Liu and T. Lu, J. Phys. Chem. C, 2020, 124, 7353–7360 CrossRef CAS.
- H. A. Majeed and A. B. Sharba, AIP Conf. Proc., 2022, 2547, 030006 CrossRef CAS.
- G. Yang, J. Li, X. Deng, X. Song, M. Lu, Y. Zhu, Z. Yu, B. Xu, M. Li and L. Dang, J. Phys. Chem. Lett., 2023, 14, 6927–6934 CrossRef CAS PubMed.
- O. A. Al-Owaedi, RSC Adv., 2024, 14, 14704–14715 RSC.
- O. Qi, P. Qian and S. Zhigang, Nat. Commun., 2020, 11, 4485 CrossRef PubMed.
- A. V. Deshpande, A. Beidoun, A. Penzkofer and G. Wagenblast, Chem. Phys., 1990, 142, 123–131 CrossRef CAS.
- M. Büttiker and R. Landauer, Phys. Rev. Lett., 1982, 49, 1739–1742 CrossRef.
- H. Quan, Z. KeJun, J. HuiLe, C. XiAn, H. MaoLin and W. Shun, Sci. China: Chem., 2012, 55, 1345–1350 Search PubMed.
- K. B. Male, E. Lam, J. Montes and J. H. T. Luong, ACS Appl. Mater. Interfaces, 2012, 4, 3643–3649 CrossRef CAS PubMed.
- R. M. Al-Utayjawee and O. A. Al-Owaedi, J. Phys.: Conf. Ser., 2021, 1818, 12208 CrossRef CAS.
- M. Kamenetska, S. Y. Quek, A. C. Whalley, M. L. Steigerwald, H. J. Choi, S. G. Louie, C. Nuckolls, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, J. Am. Chem. Soc., 2010, 132, 6817–6821 CrossRef CAS PubMed.
- S. Y. Quek, M. Kamenetska, M. L. Steigerwald, H. J. Choi, S. G. Louie, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, Nat. Nanotechnol., 2009, 4, 230–234 CrossRef CAS PubMed.
- A. I. Yanson, G. R. Bollinger, H. E. van den Brom, N. Agrait and J. M. van Ruitenbeek, Nature, 1998, 395, 783–785 CrossRef CAS.
- D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Chem. Rev., 2016, 116, 4318–4440 CrossRef CAS PubMed.
- O. A. Al-Owaedi, T. T. Khalil, S. A. Karim, M. H. Said, E. Al-Bermany and D. N. Taha, Syst. Rev. Pharm., 2020, 11, 111–115 Search PubMed.
- R. Chen, I. Sharony and A. Nitzan, J. Phys. Chem. Lett., 2020, 11, 4261–4268 CrossRef CAS PubMed.
- C. Wu, D. Bates, S. Sangtarash, N. Ferri, A. Thomas, S. J. Higgins, C. M. Robertson, R. J. Nichols, H. Sadeghi and A. Vezzoli, Nano Lett., 2020, 20, 7980–7986 CrossRef CAS PubMed.
- R. Miao, H. Xu, M. Skripnik, L. Cui, K. Wang, K. G. L. Pedersen, M. Leijnse, F. Pauly, K. Wärnmark, E. Meyhofer, P. Reddy and H. Linke, Nano Lett., 2018, 18, 5666–5672 CrossRef CAS PubMed.
- D. Stefani, K. J. Weiland, M. Skripnik, C. Hsu, M. L. Perrin, M. Mayor, F. Pauly and H. S. J. van der Zant, Nano Lett., 2018, 18, 5981–5988 CrossRef CAS PubMed.
- L. O. Jones, M. A. Mosquera, B. Fu, G. C. Schatz, T. J. Marks and M. A. Ratner, Nano Lett., 2019, 19, 8956–8963 CrossRef CAS PubMed.
- J. R. Quinn, F. W. Foss, L. Venkataraman and R. Breslow, J. Am. Chem. Soc., 2007, 129, 12376–12377 CrossRef CAS PubMed.
- M. Taniguchi, M. Tsutsui, R. Mogi, T. Sugawara, Y. Tsuji, K. Yoshizawa and T. Kawai, J. Am. Chem. Soc., 2011, 133, 11426–11429 CrossRef CAS PubMed.
- B. Huang, X. Liu, Y. Yuan, Z. Hong, J. Zheng, L. Pei, Y. Shao, J. Li, X. Zhou, J. Chen, S. Jin and B. Mao, J. Am. Chem. Soc., 2018, 140, 17685–17690 CrossRef CAS PubMed.
- P. Moreno-Garcia, M. Gulcur, D. Z. Manrique, T. Pope, W. J. Hong, V. Kaliginedi, C. C. Huang, A. S. Batsanov, M. R. Bryce, C. J. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2013, 135, 12228–12240 CrossRef CAS PubMed.
- B. Kim, J. M. Beebe, C. Olivier, S. Rigaut, D. Touchard, J. G. Kushmerick, X. Y. Zhu and C. D. Frisbie, J. Phys. Chem. C, 2007, 111, 7521–7526 CrossRef CAS.
- Q. Lu, K. Liu, H. M. Zhang, Z. B. Du, X. H. Wang and F. S. Wang, ACS Nano, 2009, 3, 3861–3868 CrossRef CAS PubMed.
- D. C. Milan, O. A. Al-Owaedi, M. Oerthel, S. Marqués-González, R. J. Brooke, M. R. Bryce, P. Cea, J. Ferrer, S. J. Higgins, C. J. Lambert, P. J. Low, D. Z. Manrique, S. Martin, R. J. Nichols, W. Schwarzacher and V. M. García-Suárez, J. Phys. Chem. C, 2016, 120, 15666–15674 CrossRef CAS.
- M. H. Garner, H. X. Li, Y. Chen, T. A. Su, Z. Shangguan, D. W. Paley, T. F. Liu, F. Ng, H. X. Li, S. X. Xiao, C. Nuckolls, L. Venkataraman and G. C. Solomon, Nature, 2018, 558, 415–419 CrossRef CAS PubMed.
- R. S. I. Mulliken, J. Chem. Phys., 1955, 23(35), 1833–1840 CrossRef CAS.
- B. A. A. Al-Mammory, O. A. Al-Owaedi and E. M. Al-Robayi, J. Phys.: Conf. Ser., 2021, 1818, 12095 CrossRef CAS.
- T. Markussen, M. Settness and K. S. Thygesen, J. Chem. Phys., 2011, 135, 144104 CrossRef PubMed.
- M. Burkle, T. J. Hellmuth, F. Pauly and Y. Asai, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 165419 CrossRef.
- A. Putatunda and D. J. Singh, Mater. Today Phys., 2019, 8, 49–55 CrossRef.
- N. T. Hung, A. R. T. Nugraha and R. Saito, Energies, 2019, 12, 4561 CrossRef CAS.
- H. Ozawa, M. Baghernejad, O. A. Al-Owaedi, V. Kaliginedi, T. Nagashima, J. Ferrer, T. Wandlowski, V. M. García-Suárez, P. Broekmann, C. J. Lambert and M. Haga, Chem.–Eur. J., 2016, 22, 12732–12740 CrossRef CAS PubMed.
- F. Chen, X. Li, J. Hihath, Z. Huang and N. Tao, J. Am. Chem. Soc., 2006, 128, 15874–15881 CrossRef CAS PubMed.
- I. A. Shelykh, N. T. Bagraev and L. E. Klyachkin, Semiconductors, 2003, 37, 1390–1399 CrossRef CAS.
- L. Cui, R. Miao, K. Wang, D. Thompson, L. A. Zotti, J. C. Cuevas, E. Meyhofer and P. Reddy, Nat. Nanotechnol., 2018, 13, 122–127 CrossRef CAS PubMed.
- W. Lee, K. Kim, W. Jeong, L. A. Zotti, F. Pauly, J. C. Cuevas and P. Reddy, Nature, 2013, 498, 209–212 CrossRef CAS PubMed.
- H. B. Schlegel, J. S. Binkley and J. A. Pople, J. Chem. Phys., 1984, 80, 1976–1981 CrossRef CAS.
- C. J. Lambert, Chem. Soc. Rev., 2015, 44, 875–888 RSC.
- B. Marius, J. H. Thomas, P. Fabian and A. Yoshihiro, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 165419 CrossRef.
- U. Sivan and Y. Imry, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 551 CrossRef CAS PubMed.
- K. Esfarjani, M. Zebarjadi and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 085406 CrossRef.
- K. Müller, J. Chem. Phys., 2008, 129, 044708 CrossRef PubMed.
- O. A. Al-Owaedi, ACS Omega, 2024, 9, 10610–10620 CrossRef CAS PubMed.
- R. Davidson, O. A. Al-Owaedi, D. C. Milan, Q. Zeng, J. Tory, F. Hartl, S. J. Higgins, R. J. Nichols, C. J. Lambert and P. J. Low, Inorg. Chem., 2016, 55, 2691–2700 CrossRef CAS PubMed.
- R. J. Davidson, D. C. Milan, O. A. Al-Owaedi, A. K. Ismael, R. J. Nichols, S. J. Higgins, C. J. Lambert, D. S. Yufita and A. Beeby, RSC Adv., 2018, 8, 23585–23590 RSC.
- S. Bock, O. A. Al-Owaedi, S. Eaves, D. C. Milan, M. Lemmer, B. Skelton, H. Osorio, R. Nichols, S. Higgins, P. Cea, N. Long, T. Albrecht, S. Martín, C. J. Lambert and P. J. Low, Chem.–Eur. J., 2017, 23, 2133–2143 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The theories and all details relevant to the computational methods, as well as it contains the theoretical models of all source|molecule|drain configurations. See DOI: https://doi.org/10.1039/d4ra03574g |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ce
*ce
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 319
319![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 433
433![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 796
796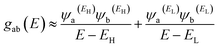
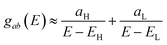
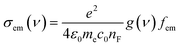
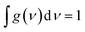 . The emission oscillator strength (fem) of MB molecules is ranging from 0.17 to 0.37, as shown in Table 1.
. The emission oscillator strength (fem) of MB molecules is ranging from 0.17 to 0.37, as shown in Table 1.

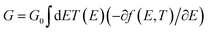

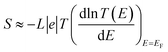
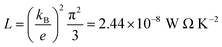 . In other words, S is proportional to the negative of the slope of ln
. In other words, S is proportional to the negative of the slope of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T(E), evaluated at the Fermi energy. Based on Seebeck coefficient, the power factor was calculated by:
T(E), evaluated at the Fermi energy. Based on Seebeck coefficient, the power factor was calculated by: