Exploring the photovoltaic properties of naphthalene-1,5-diamine-based functionalized materials in aprotic polar medium: a combined experimental and DFT approach

Abstract

In this study, a series of naphthalene-1,5-diamine-based donor chromophores (ND1–ND9) with A–D–A architecture was synthesized through a condensation reaction between amines and substituted aldehydes. Various spectroscopic techniques i.e., FTIR, UV-Vis, ¹HNMR and ¹³CNMR were performed for structural elucidation of naphthalene-1,5-diamine-based chromophores. Accompanying the synthesis, quantum chemical calculations were also accomplished at MPW1PW91/6-311G (d,p) functional of DFT/TD-DFT approaches to explore the photovoltaic properties of ND1–ND9 compounds. A comparative study between experimental and DFT results of vibrational and UV-Vis analyses showed a good harmony. All compounds showed band gaps in the range of 3.804–3.900 eV with absorption spectra in the UV region (397.169–408.822 nm). Frontier molecular orbital (FMO) findings revealed an efficient intramolecular charge transfer (ICT) from the central naphthalene-1,5-diamine-based donor core towards terminal acceptors. This significant charge transfer was also supported by the density of states (DOS) and transition density matrix (TDM) maps. All synthesized chromophores showed lower exciton binding energy values (E_b = 0.670–0.785 eV), illustrating higher exciton dissociation rates with greater charge transfer in the studied chromophores. A reasonable harmony was obtained by comparative investigations of a standard hole transport material (HTM), Spiro-OMe TAD, with ND1–ND9 compounds, which illustrated that these synthesized chromophores might be considered as good HTMs. Therefore, all analyses indicated that the naphthalene-1,5-diamine-based chromophores might be utilized as efficient photovoltaic materials.

---

Introduction

Over the last few decades, organic photovoltaic systems have earned remarkable attention in the solar cell industry owing to their low fabrication cost, light molecular weight, high flexibility and easy manufacturing process. Moreover, the photovoltaic world is enriched with other very interesting materials such as organic solar cell fullerene derivatives including PC₆₁BM, PC₇₁BM, and ICBA. Organic solar cells (OSCs) have various points of interest such as tunable energy levels, light weight, simple processing, mechanical flexibility, large area of fabrication and ease of utilizing them as significant photovoltaics tools.^1–3 Nevertheless, owing to certain drawbacks on a large scale, notably their expensive production, low absorption properties and poor V_oc, the OSC community are shifting their focus towards perovskite materials.^3–5 Perovskite solar cells (PSCs) have emerged as the most promising technology in photovoltaics, exhibiting remarkable efficiency, low production cost and versatile application potential.⁶ This class of materials is named after the crystal structure shared with the mineral perovskite (CaTiO₃), and its typical composition is a hybrid organic–inorganic lead or tin halide-based compound. The perovskite material has a general formula of ABX₃, where A is a cation, B is a metal cation and X is a halide anion.⁷ Booming since 2009, its promise in photovoltaic applications was shown by Kojima et al. by obtaining a power conversion efficiency (PCE) of 3.8% through the use of CH₃NH₃PbX₃ as part of the light absorbing layer.⁸ Subsequently, breakthroughs have rapidly followed, and current PSCs are now over 25% efficient, which meets the efficiency of traditional silicon-based solar cells.⁹ The most widely utilized HTM is spiro-OMeTAD (2′,7,7′-tetrakis(N,N-di-p-methoxyphenylamine)-9,9′-spirobifluorene), which demonstrated greater efficiency when doped with additives to enhance its conductivity. Besides this, it has some drawbacks such as moisture sensitivity, high cost, and complex doping procedures to obtain optimal performance.^10,11 As a result, the quest for cheaper and manufactural HTMs with scalability has increased. These include: (1) inorganic materials such as copper thiocyanate and nickel oxide, which are low-cost and easy to synthesize¹² but still have interface recombination losses as well as processing limitations;^13,14 (2) carbon-based materials such as graphene or carbon nanotubes with highly conductive behavior and potentially scalable production methods;¹⁵ (3) organic semiconductors that can be tuned for specific application requirements so long as no environmental factors affect the structure of the molecular design.¹⁶ A planar conjugated backbone, with higher conjugation along the planar fused aromatic units is preferred over most of these options because π-conjugated regions span uniformly towards the end to improve their natural structure.¹⁷ The literature is replete with many examples in which the organic compound consists of a central donor core unit such as benzothiophene (BT),^18–20 perylene diimide (PDI),^21,22 indacenodithiophene (IDT)^23,24 and naphthalene diamine (NDI),²⁵ exhibiting significant photovoltaic characteristics as HTMs. Literature studies have exploited the naphthalene diamine-based chromophores, exhibiting notable photovoltaic properties in PSCs due to their unique molecular structure and electronic characteristics such as amorphous nature, good chemical stability, high purity, good thermal stability, high electron mobility, adequate solubility and well aligned HOMO/LUMO levels.²⁶ The NDI-based chromophores possess a conjugated system composed of alternating single and double bonds, which allows for efficient absorption of photons across a broad spectrum of wavelengths, including visible and near-infrared light.²⁷ Their planar structure supports efficient π–π stacking, which is beneficial for charge mobility in photovoltaic devices. The chemical stability of these compounds is essential for the longevity and durability of solar cells, enhancing their commercial viability.²⁸ The electron-donating and electron-withdrawing groups attached to the naphthalene diamine core facilitate charge separation upon photon absorption, leading to the generation of free charge carriers.^29,30 The structure of naphthalene diamine allows for a variety of functionalization, which enables the optimization of their electronic properties for different photovoltaic applications. Moreover, their tunable energy levels and molecular engineering capabilities enable the optimization of electronic properties, such as the reduction of energy loss via non-radiative recombination. This combination of factors results in enhanced charge transport, and ultimately, higher power conversion efficiencies in photovoltaic devices employing naphthalene diamine-based chromophores.³¹ The synthetic control and structure processing of these materials offer the opportunity to fine-tune their optoelectronic properties by optimizing energetic alignment at the perovskite/HTM interface as well as energy loss minimization, which is very necessary for improving PSCs.³² Furthermore, rigid aromatic structures of naphthalene-based materials effectively stabilize the performance of PSCs in various operational circumstances including moisture, heat and light stability.³³

By inspiring the above-mentioned features of NDI-based chromophores, currently, a series of novel naphthalene-1,5-diamine-based donor chromophores (ND1–ND9) with A–D–A architecture was synthesized for utilization as HTMs in PSCs. To the best of our knowledge, the utilization of naphthalene-1,5-diamine-based compounds for PSC application has not been reported yet. After their structure confirmation through various spectroscopic techniques, the photovoltaic characteristics of ND1–ND9 have been explored through DFT/TD-DFT approaches. It is anticipated that newly synthesized naphthalene-1,5-diamine-based derivatives might be utilized as HTMs for improving the photovoltaic characteristics in PSCs.

Methodology

Designing of naphthalene-1,5-diamine-based chromophores (ND1–ND9)

Herein, a series of naphthalene-1,5-diamine-based donor compounds (ND1–ND9) with A–D–A architecture were designed and synthesized and their photovoltaic properties were explored via the DFT/TD-DFT approach. The main focus of this study was to develop naphthalene diamine-based hole transport materials for perovskite photovoltaic materials. The synthesized compounds consist of two parts, (i) a central donor naphthalene-1,5-diamine core and (ii) terminal acceptors, as shown in Fig. S36.† Two types of acceptors were utilized in the current study: (i) a benzene ring having various electron-withdrawing groups (A1–A5) and (ii) indolyl-based (A6–A9), as illustrated in Scheme 1. The ChemDraw structures of ND1–ND9 compounds and their utilized acceptors (A1–A9) are displayed in Fig. S36 and S37.†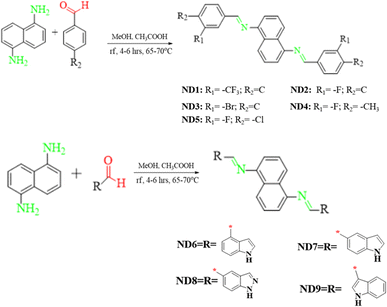

Scheme 1 Syntheses of naphthalene-1,5-diamine-based functional materials using different approaches.

The FMO analysis is associated with the electronic properties of a molecule in terms of molecular interactions, chemical reactivity and stability via molecular orbital energies as well as band gaps. The band gap (ΔE) is a crucial parameter that indicates the energy difference between the valence band (HOMO) and the conduction band (LUMO). The energy difference influences the electrical conductivity, optical properties and molecular stability of the compound. The presence of a narrow band gap makes the photo-excitation process easier and enhances the intramolecular charge transfer within molecules.³⁴ The DOS analysis is performed to examine the importance of individual elements in comparison with a greater molecular system, which demonstrates a distinct number of electronic levels. It not only determines the electron distribution pattern from the HOMO to the LUMO but also confirms the charge distribution through the corresponding DOS percentages on the HOMO–LUMO.³⁵ Binding energy (E_b) is the highest possible amount of energy utilized to determine how excitons unbind and to investigate the coulombic force of interaction between electrons and holes inside molecules. It correlates directly with the electrostatic force of interaction between the electron and hole within a molecular system though inversely correlated to dissociation in the excited state.³⁶ Reorganization energy (RE) is an essential component that decides the charge transfer properties of the molecular system. The performance of PSCs crucially depends on the reorganization energy, which directly dictates transport properties regarding electrons and holes in different materials.³⁷ Excitation energy (E_x) is considered to be another basic factor for the exploration of photoelectric properties in photovoltaic (PV) devices. It is the energy needed for electronic transition from the ground state to the excited state. It plays a very important role in the initiation of charge generation throughout the molecular structure of organic solar cells. After the synthesis and structure confirmation, quantum chemical calculations, such as density of states (DOS) and reorganization energy (RE) analyses were performed utilizing the DFT technique. Furthermore, other analyses including transition density matrix (TDM), frontier molecular orbitals (FMOs), open circuit voltage (V_oc) and UV-Vis were conducted using the TD-DFT approach to investigate electronic and photovoltaic properties.

Synthesis of naphthalene-1,5-diamine based derivatives (ND1–ND9)

The naphthalene-1,5-diamine-based derivatives were synthesized by a condensation reaction between amine and substituted aldehyde. The Schiff base derivatives were synthesized via a modification to the simple condensation reaction.³¹ The reaction involves a typical condensation reaction of the NH₂– moiety of naphthalene and C=O of aldehyde to make a new imine (C=N) bond. In a typical reaction, substituted aldehyde (2 mmol) was dissolved in MeOH (10 ml) and 2–3 drops of CH₃COOH were added as a catalyst. For optimizing the reaction conditions, the reaction of naphthalene-1,5-diamine (1) and aldehyde (2c) was performed in the ratio of 1 : 2 and the polarity of the solvent was switched from polar to non-polar i.e., DMSO, DCM, methanol, ethanol and THF. To set the most favorable situation, methanol was used as a solvent accompanied by glacial acetic acid in catalytic amounts. The reaction was refluxed and as all the reactant dissolved, a solution of naphthalene-1,5-diamine (1 mmol) was added to it and the reaction was refluxed at 65–70 °C for 4–6 hours (Scheme 1) with continuous stirring until precipitates of the product were formed in the flask. The progress of the reaction was observed at regular intervals of time. Subsequently, the resulting product underwent filtration, followed by multiple washes with absolute ethyl alcohol. Afterward, it was dried and weighed. The targeted hydrazones (ND1–ND9) were obtained in good yield (70–85%) and were characterized by UV-Vis, FTIR, ¹HNMR and ¹³CNMR techniques.

(N1E,N5E)-N1,N5-Bis(3-(trifluoromethyl)benzylidene)naphthalene-1,5-diamine (ND1). Yield 89%; IR (KBr) ν cm⁻¹: 3286 (N–H), 1207 (C=S), 1590 (C=N), UV-Vis (acetonitrile): λ_max 368 nm. ¹H-NMR, δ (ppm): (600 MHz, CDCl₃) 8.60 (2H, s), 8.30 (2H, s), 8.25 (2H, d, J = 8.5 Hz), 8.18 (2H, d, J = 7.7 Hz), 7.77 (2H, d, J = 7.8 Hz), 7.64 (2H, t, J = 7.7 Hz), 7.54–7.48 (2H, m), 7.12 (2H, d, J = 7.1 Hz). ¹³C NMR (151 MHz, CDCl₃) δ 158.59, 148.38, 137.04, 132.08, 131.55, 131.34, 129.38, 129.30, 127.85 (t), 126.0, 125.51 (q), 122.36, 113.42.

(N1E,N5E)-N1,N5-Bis(3-fluorobenzylidene)naphthalene-1,5-diamine (ND2). Yield 81%; IR (KBr) ν cm⁻¹: 3286 (N–H), 1207 (C=S), 1590 (C=N), UV-Vis (acetonitrile): λ_max 364 nm. ¹H-NMR, δ (ppm): (600 MHz, DMSO) 8.76 (2H, s), 8.21 (2H, d, J = 8.4 Hz), 7.95–7.83 (4H, m), 7.62 (2H, td, J = 7.9, 6.0 Hz), 7.59–7.55 (2H, m), 7.43 (2H, td, J = 8.4, 2.3 Hz), 7.31 (2H, d, J = 7.1 Hz). ¹³C NMR (151 MHz, DMSO) δ 163.44–161.82 (J_C–F¹ = 244.5 Hz), 160.04 (J_C–F⁴ = 2.3 Hz), 147.89, 138.77, 131.22 (J_C–F⁵ = 7.9 Hz), 129.07, 126.38, 125.52 (J_C–F⁴ = 2.6 Hz), 121.88, 118.6 (J_C–F² = 21.7 Hz), 114.82 (J_C–F² = 22.1 Hz), 113.90.

(N1E,N5E-N1,N5)-Bis(3-bromobenzylidene)naphthalene-1,5-diamine (ND3). Yield 79%; IR (KBr) ν cm⁻¹: 3286 (N–H), 1207 (C=S), 1590 (C=N), UV-Vis (acetonitrile): λ_max 364 nm. ¹H-NMR, δ (ppm): (600 MHz, DMSO) 8.74 (2H, s), 8.26 (2H, s), 8.21 (2H, d, J = 8.4 Hz), 8.08 (2H, d, J = 7.6 Hz), 7.78 (2H, d, J = 8.0 Hz), 7.61–7.52 (4H, m), 7.31 (2H, d, J = 7.1 Hz). ¹³C NMR (151 MHz, DMSO) δ 159.86, 147.89, 147.08, 138.57, 134.36, 131.29, 129.05, 128.06, 126.42, 122.41, 121.90, 113.96, 40.24, 40.09, 33.21.

(N1E,N5E)-N1,N5-Bis(3-fluoro-4-methylbenzylidene)naphthalene-1,5-diamine (ND4). Yield 82%; IR (KBr) ν cm⁻¹: 3286 (N–H), 1207 (C=S), 1590 (C=N), UV-Vis (acetonitrile): λ_max 362 nm. δ_H (500 MHz, DMSO-d₆) 8.71 (2H, d, J = 1.2 Hz), 8.19 (2H, d, J = 8.4 Hz), 7.88–7.76 (4H, m), 7.55 (2H, dd, J = 8.5, 7.2 Hz), 7.50 (2H, t, J = 7.8 Hz), 7.28 (2H, dd, J = 7.2, 1.0 Hz), 2.34 (6H, s). ¹³C NMR (126 MHz, DMSO) δ 159.86, 132.26, 129.05, 128.48, 128.34, 126.26, 125.19, 123.23, 123.21, 121.64, 114.42, 114.24, 113.74, 14.49.

(N1E,N5E)-N1,N5-Bis(4-chloro-3-fluorobenzylidene)naphthalene-1,5-diamine (ND5). Yield 70%; IR (KBr) ν cm⁻¹: 3286 (N–H), 1207 (C=S), 1590 (C=N), UV-Vis (acetonitrile): λ_max 368 nm. ¹H-NMR, δ (ppm): (500 MHz, DMSO) 8.77 (2H, d, J = 1.2 Hz), 8.23 (2H, d, J = 8.5 Hz), 8.08 (2H, dd, J = 10.0, 1.9 Hz), 7.94 (2H, dd, J = 8.2, 1.8 Hz), 7.85–7.77 (2H, m), 7.58 (2H, dd, J = 8.4, 7.2 Hz), 7.33 (2H, dd, J = 7.3, 1.0 Hz).

(N1E,N5E)-N1,N5-Bis((1H-indol-4-yl)methylene)naphthalene-1,5-diamine (ND6). Yield 88%; IR (KBr) ν cm⁻¹: 3286 (N–H), 1207 (C=S), 1590 (C=N), UV-Vis (acetonitrile): λ_max 378 nm. ¹H-NMR, δ (ppm): (600 MHz, DMSO-d₆) 11.48 (1H, s), 8.95 (1H, s), 8.30 (1H, d, J = 8.4 Hz), 7.65 (2H, ddd, J = 10.0, 7.3, 0.9 Hz), 7.62–7.58 (2H, m), 7.48–7.45 (1H, m), 7.32 (1H, dd, J = 7.2, 1.0 Hz), 7.30–7.26 (1H, m); ¹³C NMR (151 MHz, DMSO) δ 162.00, 149.45, 136.77, 129.39, 127.77, 127.68, 126.42, 125.75, 124.63, 121.15, 120.86, 115.49, 113.37, 102.32.

(N1E,N5E)-N1,N5-Bis((1H-indol-5-yl)methylene)naphthalene-1,5-diamine (ND7). Yield 87%; IR (KBr) ν cm⁻¹: 3286 (N–H), 1207 (C=S), 1590 (C=N), UV-Vis (acetonitrile): λ_max 364 nm. ¹H-NMR, δ (ppm): (600 MHz, DMSO-d₆) 11.43 (2H, s), 8.73 (2H, s), 8.20 (4H, s), 7.95 (2H, s), 7.65–7.37 (6H, m), 7.23 (2H, s), 6.60 (2H, s); ¹³C NMR (151 MHz, DMSO) δ 162.04, 149.16, 138.09, 129.33, 128.16, 127.82, 126.92, 126.14, 123.73, 121.17, 120.89, 113.47, 112.16, 102.57.

(N1E,N5E)-N1,N5-Bis((1H-indazol-5-yl)methylene)naphthalene-1,5-diamine (MK-21, ND8). Yield 80%; IR (KBr) ν cm⁻¹: 3286 (N–H), 1207 (C=S), 1590 (C=N), UV-Vis (acetonitrile): λ_max 360 nm. ¹H-NMR, δ (ppm): (600 MHz, DMSO-d₆) 13.37 (2H, s), 8.80 (2H, s), 8.38 (2H, d, J = 1.4 Hz), 8.26 (2H, s), 8.24–8.20 (4H, m), 7.71 (2H, d, J = 8.7 Hz), 7.55 (2H, dd, J = 8.4, 7.2 Hz), 7.27 (2H, dd, J = 7.2, 1.0 Hz); ¹³C NMR (151 MHz, DMSO) δ 161.32, 148.73, 141.46, 135.21, 129.57, 129.26, 126.24, 125.31, 124.71, 123.11, 121.21, 113.65, 111.01.

(N1E,N5E)-N1,N5-Bis((6-chloro-1H-indol-3-yl)methylene)naphthalene-1,5-diamine (ND9). Yield 76%; IR (KBr) ν cm⁻¹: 3286 (N–H), 1207 (C=S), 1590 (C=N), UV-Vis (acetonitrile): λ_max 362 nm. ¹H-NMR, δ (ppm): (600 MHz, DMSO-d₆) 11.91 (2H, s), 8.80 (2H, s), 8.52 (2H, d, J = 8.4 Hz), 8.24 (2H, d, J = 8.4 Hz), 8.12 (2H, s), 7.58 (2H, d, J = 1.9 Hz), 7.54 (2H, t, J = 7.8 Hz), 7.29 (2H, dd, J = 8.4, 1.9 Hz), 7.20 (2H, d, J = 7.2 Hz); ¹³C NMR (151 MHz, DMSO) δ 155.42, 149.94, 137.85, 134.94, 129.46, 127.65, 126.18, 123.83, 123.24, 121.67, 120.52, 115.60, 113.10, 112.03.

Spectra statistics i.e., FT-IR, ¹HNMR and ¹³CNMR spectroscopic techniques were employed for rationalizing the structure of ND1–ND9. The C=N band in FTIR for different products appeared in the span of 1474–1615 cm⁻¹. In ¹H NMR, due to the symmetry of the structure, mostly the aromatic phenyl and naphthalene ring protons appeared in the range between 7.0–8.5 ppm and C=N appeared at 8.5–9.0 ppm, as shown in Fig. S1–S17.† In the case of ND4, where we used a methyl-substituted aldehyde, the appearance of the peak as a triplet at 1.13 ppm confirms the presence of a methyl group. For positioning and numbering of aliphatic and aromatic protons, it was found that spectral data was in congruence with the proposed structures (Fig. S1–S9†).

Computational analysis

After the structure confirmation of ND1–ND9 through spectroscopic techniques, all the quantum chemical calculations were performed with the aid of the Gaussian 09 program³⁸ and input files were reviewed using Gauss View 5.0.³⁹ In order to select the suitable functional, a benchmark study was performed between the experimental λ_max (368 nm) and various functionals of DFT i.e. M06 (ref. 40) (401.90 nm), B3LYP (419.24 nm), MPW1PW91 (399.11 nm), B3PW91 (418.00 nm) and wb97Xd (418.00 nm) along with triple zeta (6-311G (d,p)) basis set for compound ND1. A close harmony between experimental and simulated values of λ_max of ND1 was investigated at the MPW1PW91 functional. Moreover, literature data revealed that the MPW1PW91 functional along with the triple zeta basis set was widely utilized to calculate the spectroscopic properties such as vibrational analysis, NMR, and UV-Vis spectra, energy calculations and photovoltaic properties.^41–43 The triple-zeta basis set is known for high accuracy, and performs exceptionally well, although it incurs a higher computational cost compared to the double-zeta and minimum basis sets. In this research, scientific insights with high accuracy were prioritized, and thus, the increased computational expense was accepted as a necessary trade-off.⁴⁴ For ND6–ND9 compounds having an indolyl-based terminal units (A6–A9), benchmark study was also accomplished between the experimental λ_max (378 nm) and different functionals: M06 (408.90 nm), B3LYP (424.03 nm), MPW1PW91 (405.320 nm), and CAM-B3LYP (347.04 nm) at the 6-311G(d,p) basis set for ND6. The data also showed close harmony at the MPW1PW91 functional. Therefore, this functional was utilized to perform all other calculations. At first geometrical optimization and frequency analyses were carried out to obtain the true minima geometries of the synthesized compounds. The absence of negative eigen values in all calculated frequencies confirmed that the optimized geometries represent true minima on the potential energy surfaces. Further quantum chemical calculations, such as density of states (DOS) and reorganization energy (RE) analyses were performed utilizing the DFT technique. Additionally, other analyses including transition density matrix (TDM), frontier molecular orbitals (FMOs), and UV-Vis were conducted using the TD-DFT approach at the abovementioned level. Various software tools including PyMOlyze,⁴⁵ Gauss View, Avogadro⁴⁶ and Origin⁴⁷ were used to interpret data from the output files.

Results and discussion

The synthesized compounds (ND1–ND9) consist of two parts, (i) a central donor naphthalene-1,5-diamine core and (ii) terminal acceptors, as shown in Fig. S36.† Two types of acceptors are utilized for the current study: (i) a benzene ring having various electron-withdrawing groups (A1–A5) and (ii) indolyl-based moieties (A6–A9) as illustrated in Scheme 1. Among MD6–MD9 compounds, A6 and A7 are actually the same acceptors (1H-indole moiety) and vary due to attachment with naphthalene-1,5-diamine core. In MD6, the 1H-indole group (consisting of benzene and pyrrole rings) is attached to the carbon of the benzene ring adjacent to the pyrrole ring. In contrast, in MD7, the attachment of the 1H-indole group is at the second carbon of the benzene ring adjacent to the pyrrole ring. The A9 acceptor is also the 1H-indole group with the electronegative chloro group attached to the benzene ring and MD8 has the A8 acceptor which is the 1H-indazole moiety as illustrated in Fig. S37.† The presence of an indolyl-based group in MD6–MD9 might exhibit non-covalent interactions, especially hydrogen bonding. Therefore, the quantum theory of atoms in molecules (QTAIM)^48,49 was conducted to calculate the influence of intra- and intermolecular interactions, specifically hydrogen bonding in MD6 chromophores, as shown in Table S13 and Fig. S41.† The AIM analysis revealed that this molecule is stabilized through intra-molecular interactions, which is evidented from the presence of dashed bond paths (BPs) between the atoms. For MD6 structure, the intra-molecular hydrogen bonds are the most important interactions, especially N17–H44 and N18–H51 showing low electron density (ρ) and high positive Laplacian (∇²ρ = +0.035922) and (∇²ρ = +0.035921) suggest that these are weak interactions, likely hydrogen bonds, as can be observed in Table S13 and Fig. S41.† The presence of a high ellipticity (ε) suggests that these interactions deviate from a spherical shape, which is a characteristic feature of hydrogen bonds. The interactions in N40–H43 and N47–H50 exhibit high electron density and negative Laplacian (∇²ρ = −1.794849) and (∇²ρ = −1.794845), suggesting the presence of strong interactions. The little ellipticity indicates a density distribution that is closer to a sphere, which is characteristic of more traditional hydrogen bonding. In N40–C42 and N47–C49, the interactions exhibit moderate electron density and a slightly negative Laplacian (∇²ρ = −0.647432) and (∇²ρ = −0.647431), indicating that they could be either strong covalent interactions or significant non-covalent interactions. The low ellipticity suggests a distribution that is more spherical in shape as can be observed in Table S13 and Fig. S41.†

Vibrational analysis

A comparison between simulated and experimental vibrational modes of the studied compounds was accomplished as illustrated in Tables S1–S9 and Fig. S18–26.† The simulated absorption frequencies for stretching vibration of C–H in ND1 to ND9 are located at 3239–3041, 3238–3233, 3239–3236, 3235–3214, 3239–3236, 3231–3043, 3231–3045, 3232–3052 and 3232–3087 cm⁻¹, respectively. Both symmetric and asymmetric calculated vibrational frequencies of C–H bond are found in the range of 3236–3212 cm⁻¹ for ND1, 3216–3212 cm⁻¹ for ND2, 3213–3212 cm⁻¹ for ND3, 3153 and 3120 cm⁻¹, for ND4, 3216–3197 cm⁻¹ for ND5, 3212–3209 cm⁻¹ for ND6 and ND7, 3213–3206 cm⁻¹ for ND8 and 3213–3205 cm⁻¹ for compound ND9. Both the scissoring and rocking vibrations for C–H are located in the range of 1678–1367, 1632–1558, 1641–1453, 1660–1470, 1686–1564, 1672–1562, 1636–1543, 1677–1556, and 1713–1637 cm⁻¹ in ND1–ND9. Wagging vibrations in ND1 are found at 822, 812 and 717 cm⁻¹, at 823, 805, 701 and 692 cm⁻¹ in ND2, at 810, 802, 695, 799 and 695 cm⁻¹ in ND3, at 850, 807, 754 and 641 cm⁻¹ in ND4 and at 850, 849, 755 and 641 cm⁻¹ in ND5. Similarly, the wagging vibrations for ND6–ND9 were found at the range of 810–743, 846–806, 841–803 and 829–799 cm⁻¹ showing a good agreement with experimental data (Tables 1 and S6†). The simulated twisting vibrations of C–H were located at 1015–1014 cm⁻¹ for ND1, 1011–999 cm⁻¹ for ND2, 1013–1012 cm⁻¹ for ND3, 978–800 cm⁻¹ for ND4, 800 cm⁻¹ for ND5, 1015–1014 cm⁻¹ for ND6, 923–916 cm⁻¹ for ND7, 926–923 cm⁻¹ for ND8, and at 828 and 774 cm⁻¹ for ND9 showing good agreement with the experimental results (Tables 1 and S6†). On the other hand, out plane bending vibrations were located in the range of 1015–967, 1012–930, 1011–910, 935–803, 955–884, 886–885, 1015–915, 1019–923, 1022–972 and 996–962 cm⁻¹ for compounds ND1–ND9 correlating with the experimental data (Tables 1 and S6†). In ND1–ND9, the C–C stretching vibrations in benzene ring were located at 1632–1407, 1721–1098, 1721–1012, 1686–1505, 1717–1444, 1675–1560, 1777–1527, 1713–1444 and 1691–1489 cm⁻¹, respectively. The DFT values have a good agreement with the experimental values (Tables 1 and S4†). In ND1–ND5 the C–N stretching vibrations were located at 1723–1719 and 1710–1704, 1721–1641 and 1721–1716, 1722–1719 and 1721–1717, 1700–1995 and 1708–1701, 1713–1706 and 1695–1690 cm⁻¹, respectively. Compounds ND6 to ND9 having the pyrrole group showed the C–N vibration in the range of 1304–1264, 1389–1362, 1345–1316 and 1418–1396 cm⁻¹, which are in harmony with their experimental results (Tables S1–S6†). The compound ND1 with the –CF₃ group attached to the benzene ring showed the simulated vibrations at the range of 1357–1123 cm⁻¹. On the other hand, the compounds ND2 and ND5 with the –C–Cl group attached to the benzene ring showed absorption bands in the range of 823–791 and 843–811 cm⁻¹. Moreover, the compound ND3 having –C–Br as the benzene functional group showed vibration in the range of 710–681 cm⁻¹. The compound ND4 with the attached –C–F group showed simulated vibrational modes in the range of 1139–1136 cm⁻¹ showing harmony with experimental data (1113 cm⁻¹). The compounds ND6 to ND9 with the N–H group showed vibrations at the 3696, 3693, 3690 and 3683 cm⁻¹, respectively.

Table 1 Wavelength (λ_max), excitation energy (E), oscillator strength (f_os) and nature of the molecular orbital contributions of the title compounds in acetonitrile^a

Compounds	DFT λmax (nm)	Exp λmax (nm)	E (eV)	fos	MO contributions
a MO = molecular orbital, H = HOMO, L = LUMO.
ND1	399.112	368	3.107	0.686	H → L (97%)
ND2	396.052	364	3.131	0.690	H → L (97%)
ND3	398.253	364	3.113	0.711	H → L (97%)
ND4	392.367	362	3.160	0.799	H → L (97%)
ND5	403.686	368	3.071	0.784	H → L (97%)
ND6	405.323	378	3.059	0.949	H → L (95%)
ND7	383.140	320	3.236	1.005	H → L (96%)
ND8	388.057	360	3.195	0.866	H → L (96%)
ND9	411.115	362	3.016	1.350	H → L (96%)

---

Frontier molecular orbitals (FMOs)

The FMO analysis describes the various parameters associated with the electronic properties of a molecule such as molecular interactions, chemical reactivity and stability through the molecular orbital energies and their band gaps. The HOMO is the electron-rich site with maximum electron donating aptitude while the LUMO is the electron-deficient region of the molecule having electron-accepting ability.⁵⁰ Band gap (ΔE) is a crucial parameter that signifies the energy difference between the valence band (HOMO) and conduction band (LUMO). This energy difference influences the electrical conductivity, optical characteristics, and kinetic stability of molecules. A narrow band gap makes the photo-excitation process easier and facilitates significant intramolecular charge transfer within the molecules. Conversely, a larger band gap resulted in a higher energy barrier for electron movement between the HOMO and LUMO, leading to minimal charge transfer. For the currently studied compounds, the FMO findings for HOMO/LUMO energies are tabulated in Table S10,† while the energies of HOMO−1/LUMO+1 and HOMO−2/LUMO+2 are presented in Fig. S38 and S39.†

The FMO data showed that the E_HOMO/E_LUMO values for ND1–ND9 compounds were found as −6.070/−2.232, −6.042/−2.175, −6.060/−2.208, −5.994/−2.094, −6.071/−2.267, −5.783/−2.003, −5.811/−1.830, −5.904/−1.970 and −5.836/−2.133 eV, respectively. The HOMO energies of title compounds are closely related to standard HTMs such as Spiro-OMeTAD^16,51 except for ND1–ND3, which indicated that they are good HTMs for perovskite, similarly, ΔE values of the aforementioned compounds are calculated as 3.838, 3.867, 3.852, 3.900, 3.804, 3.780, 3.981, 3.934 and 3.703 eV, respectively, which are also comparable with standard HTMs such as Spiro-OMeTAD (3.17 eV).^16,52 All the synthesized chromophores showed comparable band gaps, nevertheless, the compound ND9 with indolyl-based acceptors illustrated a slightly smaller band gap (3.703 eV) than that of the others. This reduction in band gap might be due to the presence of the chloro (–Cl) group at the 1H-indole acceptor (A9), which effectively improves the conjugation, probably due to positive resonance (−R).^53,54 A slight increase in the energy gap was seen in ND6 (3.780 eV) as compared to that in ND9 due to the presence of the A6 acceptor. The presence of more resonatic structures in the ND6 chromophore may lower the energy gap in it as compared to that in ND7. The compounds with the A1–A5 acceptor benzene ring with various electron-withdrawing moieties showed a band gap in the range of 3.804–3.900 eV. Among them, the least band gap was found in ND5 having two strong electron-withdrawing groups i.e. chloro and fluoro that through a synergistic effect improve the electron-withdrawing nature of A5.⁵⁵ In other compounds (ND1–ND4), the HOMO/LUMO band gap varies in the same way as the nature of the groups on the terminal acceptors (A1–A4) changes. Overall, the decreasing order for HOMO/LUMO band gaps in eV is noted as ND7 (3.98) > ND8 (3.93) > ND4 (3.90) > ND2 (3.867) > ND3 (3.852) > ND1 (3.838) > ND5 > (3.804) ND6 (3.780) > ND9 (3.703). Accompanying these E_opt for the title compounds was also calculated from experimental UV-Vis. The E_opt for ND1–ND9 was calculated as 3.850, 3.916, 4.065, 3.936, 3.850, 3.647, 3.815 and 3.792 eV, respectively. These E_opt values showed a close harmony with simulated values of title compounds as shown in Fig. 1.

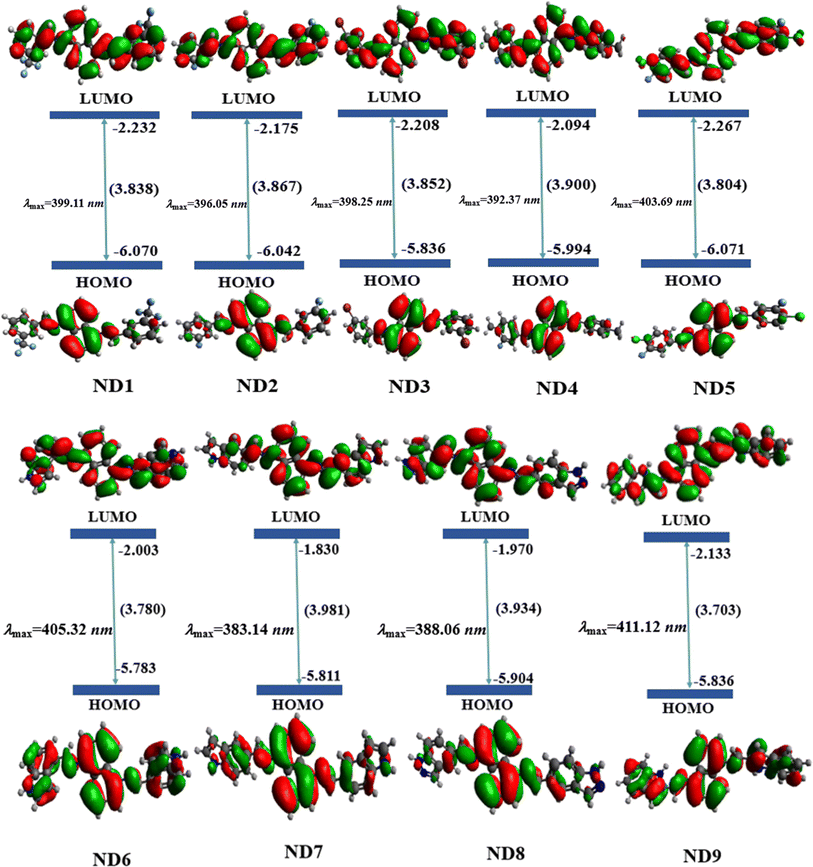Fig. 1 Pictographic representation of charge distribution on HOMO and LUMO along with molecular orbital energies (in eV) of studied molecules.

Besides the molecular orbital (MO) energies, charge transfer between MO was also investigated through FMO counter surfaces as shown inFig. 1, S36 and S37.† The MO surfaces of ND1–ND9 illustrate that the maximum charge density in HOMO is concentrated over the central naphthalene-1,5-diamine donor core except for ND6 and ND9. For these two chromophores, the charge is equally distributed over the entire chromophore in both HOMO and LUMO, which favors the hole transport, since more delocalized molecular orbitals are the faster the charge transport, due to the reduction of the nuclear reorganization energy. For the LUMO, in other chromophores, the electronic cloud is located over the whole molecule. In a nutshell, all synthesized compounds have revealed efficient ICT from the central π-spacer towards terminal acceptors, indicating that charge is substantially transferred from HOMO towards LUMO, which makes them efficient HTMs.

Absorption spectra

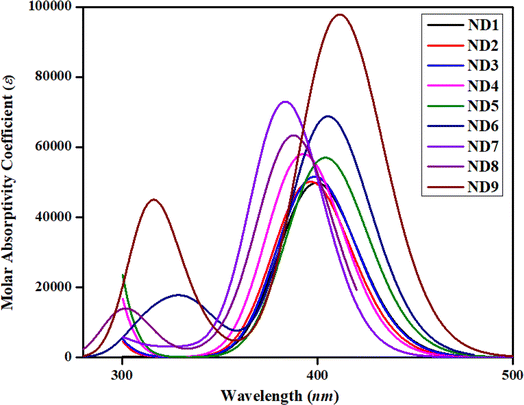
One of the most critical characteristics of HTMs in an inverted perovskite solar cell is their transparency to visible light; specifically, they should not absorb energy within the visible region of the electromagnetic spectrum (400–700 nm).⁵⁶ In order to investigate the absorption spectra of synthesized compounds, UV-Vis investigations were performed in acetonitrile solvent. A comparison between simulated and experimental λ_max (nm) was also accomplished and harmony was noted between the DFT and experimental absorption bands (Table 1 and Fig. S27–S35†). The detailed transitions of ND1–NB9 are tabulated in Table S11.†

The date tabulated in the above-mentioned table showed an inverse pattern of a λ_max with FMOs energies. Among all the synthesized compounds, ND9 chromophore with an A9 acceptor unit showed higher simulated λ_max owing to its lower energy gap. The presence of –Cl over the acceptor A9 might relatively improve the conjugation due to the resonance effect and reduce the band gap and move the absorption spectrum a little bit towards the visible region. Moreover, the conjugation extended due to the A9 acceptor facilitates increased charge transfer from the donor to the acceptor moiety, leading to a bathochromic shift in λ_max values. All compounds showed comparable values of λ_max calculated experimentally. Nevertheless, the higher experimental value of λ_max was observed in ND6. This might be due to the presence of more conjugation and intermolecular non-covalent interactions, especially H-boding (illustrated by QTAIM investigations). The experimental UV-Vis calculations were performed in the bulk form while DFT calculations were accomplished in isolated molecules. Similarly, among A1–A5 acceptors, the chromophore with an A5 acceptor unit having powerful electron-withdrawing moieties (–F and –Cl) exhibited higher λ_max. Nevertheless, the chromophore ND7 in which the 1H-indole group (A7) is attached at the second of the benzene ring adjusted to the pyrrole ring showed a hypsochromic shift among all synthesized chromophores. The attachment of the 1H-indole group at the 2nd carbon atom of the benzene ring showed lower resonatic contribution structures, resulting in reduced conjugation, enhancing the energy gap and diminishing ICT, which moved the absorption spectra towards a lower λ_max. The increasing order of λ_max values for all synthesized chromophores was as follows: ND7 < ND8 < ND4 < ND2 < ND3 < ND1 < ND5 < ND6 < ND9. As shown in Fig. 2, all the compounds exhibited minimal to null absorption in the visible region. Consequently, nearly all these compounds are suitable for use in a perovskite solar cell (PSC), as their absorption spectra do not overlap with those of the perovskite materials. This prevents efficiency loss due to charge recombination.

Fig. 2 Simulated absorption spectra of ND1–ND9 chromophores in acetonitrile.

Excitation energy (E_x) is another fundamental factor of consideration used for the inspection of the photoelectric attributes of photovoltaic (PV) devices. It is the energy required for electronic transition from the ground state to the excited state. It significantly influences the initiation of charge generation within the molecular structure of the photovoltaic materials.⁵⁷ A literature study showed that if the HTM has an appropriate HOMO level relative to the excited state of the perovskite, it can efficiently accept holes, reducing the likelihood of charge recombination. Additionally, HTMs should not absorb significant excitation energy in the visible spectrum to avoid competing with the active layer for photon absorption, which would otherwise decrease the device's efficiency. Therefore, the alignment of excitation energy and HTM energy levels is critical for maximizing charge separation and transport, ultimately enhancing photovoltaic efficiency.^23,58,59 Among all the synthesized chromophores, ND9 exhibits the most minimal excitation energy, leading to the generation of higher charge mobility. This might be due to the pronounced electron-donating nature of the chloro group, which is responsible for the exceptionally low excitation energy in ND9. Table 1 shows that all compounds exhibited excitation energy (E_x) within the range of 3.071–3.236 eV with absorption spectra in the UV region. A comparative study of absorption spectra with standard HTMs materials such as Spiro-OMe TAD^51,52 exhibited close harmony, indicating that the synthesized compounds are good HTMs.

Density of states (DOS) analysis

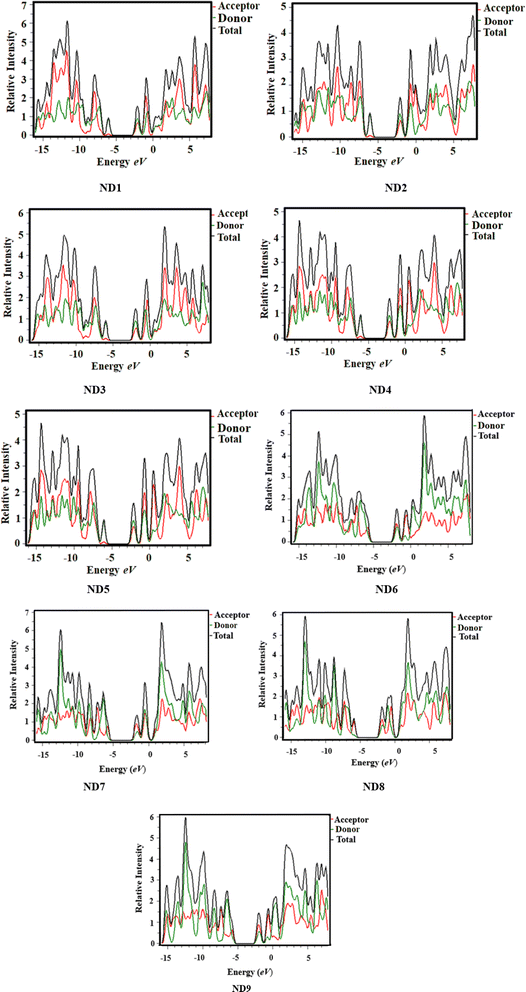
The DOS analysis was conducted to evaluate the significant contributions of each component to the overall molecular system, which demonstrates a distinct number of electronic levels. By changing the terminal acceptor moieties, the electronic charge density is distributed in various patterns over the HOMOs and LUMOs, as represented in Fig. 1. It not only determines the electron distribution pattern from the HOMO to the LUMO but also confirms the charge distribution through the corresponding DOS percentages on HOMO–LUMO.⁶⁰ Along the x-axis, the right-side values in DOS plots show LUMO, while, left-side values denote HOMO and the distance between them indicates the energy gap. To investigate the ICT in currently studied chromophores, these chromophores are divided into two parts: central donor core and terminal acceptor (A) according to Fig. S36,† each represented by a different color (donor with green and A with red lines) as depicted in Fig. 3. In HOMO, the electronic cloud for the naphthalene-1,5-diamine core was investigated as 93.1, 92.5, 92.7, 90.3, 91.6, 70.3, 81.8, 85.9 and 69.0% in ND1–ND9, respectively, whereas, for LUMO, this charge was calculated as 64.0, 66.0, 65.0, 68.2, 63.5, 62.2, 73.7, 67.5 and 67.7%, respectively. Similarly, for the acceptor moieties, the electronic clouds are located as 6.9, 7.5 7.3, 9.7, 8.4, 29.7, 18.2, 14.1 and 31.0% in HOMO, accordingly. While for LUMO, 36.0, 34.0, 35.0, 31.8, 36.5, 37.8, 26.3, 32.5 and 32.3% for ND1–ND9, respectively.

Fig. 3 DOS plots illustrating charge distribution over molecular orbitals in ND1–ND9 chromophores.

Moreover, the DOS maps showed that for HOMO the highest charge density was located over the central donor core, as indicated by a green peak detected at approximately −7.5 eV. Likewise, the charge density for the LUMO was observed near −1.8 to 2 eV by two peaks (red and green) indicating charge transfer from donor towards acceptors. All the DOS percentages and maps uncovered that HOMOs of the electronic cloud for ND1–ND9 predominantly reside on the central core, and in LUMOs; this charge significantly moves towards acceptor units (see Fig. 2 and 4) as supported by FMO counter surfaces. In a nutshell, the DOS investigation exhibits significant charge transference from the donor to the terminal acceptor moieties in all the synthesized compounds, which indicated them as reasonable HTMs in photovoltaic devices.

Fig. 4 The EPM illustrating electron density (isovalue = 0.02) of the title compounds.

Exciton binding energy (E_b) and transition density matrix (TDM) investigations

The binding energy (E_b) represents the maximum amount of energy used to ascertain the degree of exciton dissociation. In order to examine the coulombic force of interaction between electrons and holes within molecules, the binding energy calculations were carried out. It exhibited an inverse relationship with the dissociation in the excited state and a direct correlation with the electrostatic force of the interaction between the electron and the hole within the molecule.⁶¹ A lower E_b value leads to increased exciton dissociation in the S₁ state, attributed to weak coulombic forces between the electron and hole. It is basically the difference between the band gap (E_g) and the excitation energy (E_x) for the electronic transition from the S₀ state to the S₁ state.⁶² Typically, a smaller E_b value is associated with increased charge separation and greater movements of holes and electrons. The calculated E_b values of the ND1–ND9 are determined in the range of 0.751–0.780 eV. Among all the synthesized chromophores, ND9 exhibits the smallest E_b value (0.670 eV), indicating its efficient potential for exciton dissociation and increased ICT. The descending trend of E_b values is determined as follows: ND1 (0.785) > ND8 (0.780) = ND3 (0.780) > ND4 (0.778) > ND7 (0.777) > ND2 (0.776) > ND6 (0.757) > ND5 (0.751) > ND9 (0.670). These lower binding energy values illustrate the greater exciton dissociation with higher ICT. The intermolecular charge transfers were further investigated through the TDM heat maps. TDM elucidates the relationship between donor (D) and acceptor (A) units, manifesting the position of electron–hole pairs within studied compounds, along with the state of electronic excitations.⁶³ The contribution of the hydrogen atoms has been overlooked due to its minimal impact on electronic transitions. The TDM heat maps for all the synthesized compounds are illustrated in Fig. S40.† To perform a TDM investigation, the studied compounds were divided into two parts: central donor core and terminal acceptors. The TDM maps illustrate that the charge majorly consists of the central donor core and then moves towards acceptors as shown in red and blue spots over the dark blue background in Fig. S40.† Notably, this charge transfer occurs without encountering any trapping, demonstrating a coherent and uninterrupted flow as supported by DOS and FMOs investigations. This effective movement of charge transfer within title chromophores supported them as HTMs for PSCs.

Hole–electron reorganization energies and their indices

Reorganization energy (RE) is a critical factor that determines the charge transfer characteristics within molecular structures.⁶⁴ The potential of PSCs heavily relies on reorganization energy, which directly influences the electron and hole transport abilities of different materials. There is an inverse relationship between RE and charge transfer capability, where lower reorganization energy corresponds to higher charge mobilities. The RE consists of two segments (inner-sphere i.e., λ_int. and outer-sphere i.e., λ_ext. reorganization energies).⁶⁴ However, for understanding the charge transfer process in title molecules, we are interested in the calculations of λ_int. The hole reorganization (λ_h) and their indices for ND1–ND9 are calculated and tabulated in Table S12.† The λ_h values for the aforesaid compounds are found as ND1 (0.00101663), ND2 (0.00091249), ND3 (0.00091925), ND4 (0.00061371), ND5 (0.00066893), ND6 (0.00054513), ND7 (0.00028833), ND8 (0.00030848) and ND9 (0.00014392) in eV. This data elucidates that the lower RE values of the hole indicated the greater movement of charge carriers in these compounds. An investigation of the hole–electron index was performed for the ND1–ND9 compounds, specifically focusing on S₀ → S₁ excitations. Table S12† presents a moderate range of excitation energy, specifically from 3.059 to 3.236 eV which indicates the absorption in the UV region. By examining the distribution of holes and electrons, the D indices (a parameter utilized to calculate the spatial distance between electrons and holes) revealed a moderate range of 0.056–1.296 Å, suggesting an optimal separation between the hole and electron distribution. The maximum coulombic attraction energy, E_Coul, is detected in ND2 with a value of 3.9519 eV, while the minimum value has been found in ND9 with a value of 3.4318 eV. The ascending order of E_Coul is as follows: ND2 > ND4 > ND3 > ND1 > ND5 > ND7 > ND8 > ND6 > ND9. The H index (a factor that describes the degree of overlapping between the electrons and hole distributions within a molecule during electron excitation) revealed a broad dispersion of holes and electrons, with elevated values indicating charge distribution. The Sr index (a quantity that describes the spatial extent of separation between electrons and holes) exhibited elevated values (>0.6) in all compounds, indicating the presence of π–π* excitations. All the studied compounds exhibited values in the range of 0.6951 to 0.7504 lower than 1, which indicated the electrons and holes are significantly overlapped and that favours the effective charge transportations in HTMs in PSCs. The negative values of t index (a parameter utilized to measure the spatial separation between the electron and hole in an excited state) suggest a local excitation (LE). The excitation exhibited low and consistent values of heterogeneity of the distribution index (HDI) and entropy of distribution index (EDI) indicating a limited excitation. In a nutshell, the hole reorganization energy and indices of ND1–ND9 elucidated the effective charge transfer in NDI-based chromophores, which supported their utilization as HTMs in PSCs.

Molecular electrostatic potential (MEP) analysis

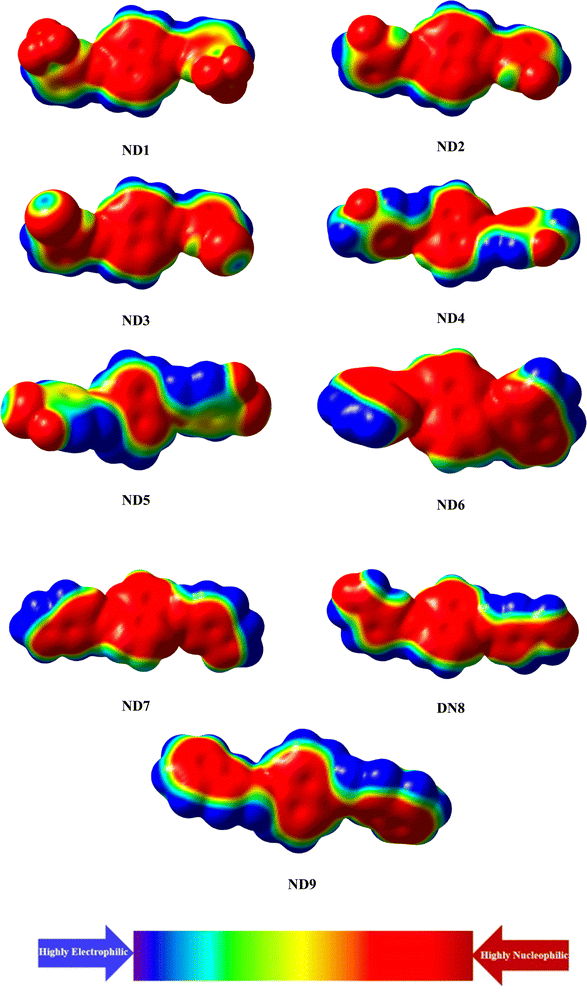
A molecular electrostatic potential (ESP) study helps illustrate a molecule's chemical reactivity by identifying its electron-deficient (electrophilic) and electron-rich (nucleophilic) regions.⁶⁵ The distribution of electrons at these sites is depicted by various colors on the MEP plot of the molecules. Red and yellow colors indicate electron-poor or acceptor regions, blue signifies electron-rich or donor sites, and green represents neutral or zero-potential areas. The electrostatic potential increases in the following order: red > yellow > green > blue.⁶⁶ The MEP plot in Fig. 4 reveals that the primary red areas, centered on highly electronegative atoms such as oxygen, nitrogen, fluoro and chloro atoms, indicate a higher likelihood of the electrophilic attack. Conversely, the blue and green regions, which show a positive potential, are primarily located on the carbon and hydrogen atoms, suggesting that these areas are more prone to nucleophilic reactions.

Conclusions

This study explored the photovoltaic properties of newly synthesized naphthalene-1,5-diamine-based donor chromophores (ND1–ND9) through quantum chemical calculations. The NDI-based chromophores were synthesized through the condensation reaction between amine and substituted aldehyde and further their structural confirmation was accomplished through various spectroscopic techniques. A harmony between experimental and DFT results was investigated through a comparative study between vibrational absorption modes and UV-Vis results. Notably, all synthesized compounds displayed a band gap in the range of 3.703–3.934 eV. Particularly, ND9 exhibited the lowest energy gap of 3.703 eV, attributed to the presence of –Cl with a benzene ring that extended the conjugation of the end-capped acceptor (A9). Similarly, the aforementioned chromophores showed a UV-Vis absorption spectrum from 386.940 to 408.822 nm in acetonitrile solvent. The obtained band gap values, UV-Vis absorption spectra values and comparative study with standard HTM spiro-OMe-TDA supported the utilization of the synthesized compounds as HTMs. A significant charge transfer from the central donor core in HOMO is transferred towards terminal acceptors in LUMO as investigated by FMOs, DOS and TDM analyses. Moreover, ND1–ND9 showed lower binding energy (E_b = 0.670–0.785 eV), which indicated a higher exciton dissociation rate with efficient ICT in title chromophores. The reorganization energies and hole electron indices also showed greater movement of the electronic cloud in NDI-based synthesized chromophores. Among all the synthesized chromophores, ND9 exhibited efficient electronic and photovoltaic properties owing to the presence of the –Cl group on the benzene ring of the terminal acceptor (A9). After that, ND6 also showed good photovoltaic response which might be due to the presence of higher resonance and hydrogen bonding, which stabilized the ND6. These findings elucidate that the synthesized chromophores exhibit good photovoltaic properties and can be utilized as reasonable HTMs for PSC applications.

Data availability

All data generated or analyzed during this study are included in this article and its ESI files.†

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Dr Muhammad Khalid gratefully acknowledges the financial support of HEC Pakistan (project no. 20-14703/NRPU/R&D/HEC/2021). A. A. C. B. acknowledges the financial support of the São Paulo Research Foundation (FAPESP) (Grants 2014/25770-6 and 2015/01491-3), the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) of Brazil for academic support (Grant 309715/2017-2), and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) that partially supported this work (Finance Code 001).

References

1. T. J. Aldrich, M. Matta, W. Zhu, S. M. Swick, C. L. Stern, G. C. Schatz, A. Facchetti, F. S. Melkonyan and T. J. Marks, J. Am. Chem. Soc., 2019, 141, 3274–3287.
2. Y.-J. Cheng, S.-H. Yang and C.-S. Hsu, Chem. Rev., 2009, 109, 5868–5923.
3. Y. Lin, Y. Li and X. Zhan, Chem. Soc. Rev., 2012, 41, 4245–4272.
4. Y. Li, Acc. Chem. Res., 2012, 45, 723–733.
5. A. Anctil, C. W. Babbitt, R. P. Raffaelle and B. J. Landi, Environ. Sci. Technol., 2011, 45, 2353–2359.
6. M. Remec, Š. Tomšič, M. Khenkin, Q. Emery, J. Li, F. Scheler, B. Glažar, M. Jankovec, M. Jošt, E. Unger, S. Albrecht, R. Schlatmann, B. Lipovšek, C. Ulbrich and M. Topič, Adv. Energy Mater., 2024, 14, 2304452.
7. S. Yun, Y. Qin, A. R. Uhl, N. Vlachopoulos, M. Yin, D. Li, X. Han and A. Hagfeldt, Energy Environ. Sci., 2018, 11, 476–526.
8. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051.
9. A. Rajagopal, Z. Yang, S. B. Jo, I. L. Braly, P. Liang, H. W. Hillhouse and A. K. -Y. Jen, Adv. Mater., 2017, 29, 1702140.
10. G. Ren, W. Han, Y. Deng, W. Wu, Z. Li, J. Guo, H. Bao, C. Liu and W. Guo, J. Mater. Chem. A, 2021, 9, 4589–4625.
11. B. Tan, S. R. Raga, A. S. R. Chesman, S. O. Fürer, F. Zheng, D. P. McMeekin, L. Jiang, W. Mao, X. Lin, X. Wen, J. Lu, Y. Cheng and U. Bach, Adv. Energy Mater., 2019, 9, 1901519.
12. Z. Yu and L. Sun, Small Methods, 2018, 2, 1700280.
13. P. Kung, M. Li, P. Lin, Y. Chiang, C. Chan, T. Guo and P. Chen, Adv. Mater. Interfaces, 2018, 5, 1800882.
14. R. Singh, P. K. Singh, B. Bhattacharya and H.-W. Rhee, Appl. Mater. Today, 2019, 14, 175–200.
15. Q.-Q. Chu, B. Ding, J. Peng, H. Shen, X. Li, Y. Liu, C.-X. Li, C.-J. Li, G.-J. Yang and T. P. White, J. Mater. Sci. Technol., 2019, 35, 987–993.
16. L. Calió, S. Kazim, M. Grätzel and S. Ahmad, Angew. Chem., Int. Ed., 2016, 55, 14522–14545.
17. A. F. Latypova, N. A. Emelianov, D. O. Balakirev, P. K. Sukhorukova, N. K. Kalinichenko, P. M. Kuznetsov, Y. N. Luponosov, S. M. Aldoshin, S. A. Ponomarenko, P. A. Troshin and L. A. Frolova, ACS Appl. Energy Mater., 2022, 5, 5395–5403.
18. S. Vegiraju, W. Ke, P. Priyanka, J. Ni, Y. Wu, I. Spanopoulos, S. L. Yau, T. J. Marks, M. Chen and M. G. Kanatzidis, Adv. Funct. Mater., 2019, 29, 1905393.
19. D. Takhellambam, L. A. Castriotta, G. Zanotti, L. Mancini, V. Raglione, G. Mattioli, B. Paci, A. Generosi, M. Guaragno, V. Campanari, G. Ammirati, F. Martelli, E. Calabrò, A. Cricenti, M. Luce, N. Yaghoobi Nia, F. Di Giacomo and A. Di Carlo, Sol. RRL, 2023, 7, 2300658.
20. W. T. Van Gompel, R. Herckens, P.-H. Denis, M. Mertens, M. C. Gélvez-Rueda, K. Van Hecke, B. Ruttens, J. D'Haen, F. C. Grozema and L. Lutsen, J. Mater. Chem. C, 2020, 8, 7181–7188.
21. H. Zhang, L. Xue, J. Han, Y. Q. Fu, Y. Shen, Z. Zhang, Y. Li and M. Wang, J. Mater. Chem. A, 2016, 4, 8724–8733.
22. Q. Guo, Y. Xu, B. Xiao, B. Zhang, E. Zhou, F. Wang, Y. Bai, T. Hayat, A. Alsaedi and Z. Tan, ACS Appl. Mater. Interfaces, 2017, 9, 10983–10991.
23. X. Liu, E. Rezaee, H. Shan, J. Xu, Y. Zhang, Y. Feng, J. Dai, Z.-K. Chen, W. Huang and Z.-X. Xu, J. Mater. Chem. C, 2018, 6, 4706–4713.
24. A. Siddiqui, S. Haseena, K. Narayanaswamy, M. K. Ravva and S. P. Singh, Sol. Energy, 2024, 277, 112732.
25. B. Pashaei, H. Shahroosvand, M. Ameri, E. Mohajerani and M. K. Nazeeruddin, J. Mater. Chem. A, 2019, 7, 21867–21873.
26. M. A. Jameel, T. C.-J. Yang, G. J. Wilson, R. A. Evans, A. Gupta and S. J. Langford, J. Mater. Chem. A, 2021, 9, 27170–27192.
27. P. Cerrada, L. Oriol, M. Piol and J. L. Serrano, J. Polym. Sci., Part A: Polym. Chem., 1996, 34, 2603–2611.
28. T. Jia, C. Sun, R. Xu, Z. Chen, Q. Yin, Y. Jin, H.-L. Yip, F. Huang and Y. Cao, ACS Appl. Mater. Interfaces, 2017, 9, 36070–36081.
29. E. M. Nowak, J. Sanetra, M. Grucela and E. Schab-Balcerzak, Mater. Lett., 2015, 157, 93–98.
30. M. Liu, P. Fan, Q. Hu, T. P. Russell and Y. Liu, Angew. Chem., 2020, 132, 18288–18292.
31. İ. Kaya and F. Z. Yener, Arab. J. Sci. Eng., 2019, 44, 6339–6349.
32. B. Pashaei, RSC Adv., 2024, 14, 19083–19089.
33. R. K. Behera, N. R. Goud, A. J. Matzger, J.-L. Brédas and V. Coropceanu, J. Phys. Chem. C, 2017, 121, 23633–23641.
34. H. Mizuseki, R. V. Belosludov, A. A. Farajian, N. Igarashi, J.-T. Wang, H. Chen, C. Majumder, S. Miura and Y. Kawazoe, Sci. Technol. Adv. Mater., 2003, 4, 377.
35. G. Paasch and S. Scheinert, J. Appl. Phys., 2007, 101, 2.
36. L. Zhu, Z. Wei and Y. Yi, J. Phys. Chem. C, 2022, 126, 14–21.
37. X. Amashukeli, J. R. Winkler, H. B. Gray, N. E. Gruhn and D. L. Lichtenberger, J. Phys. Chem. A, 2002, 106, 7593–7598.
38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, Gaussian 09, Revision A. 02, Gaussian Inc., Wallingford CT, 2016.
39. R. Dennington, T. A. Keith and J. M. Millam, GaussView 5.0, Gaussian Inc., Wallingford, 2008, p. 20.
40. H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544.
41. M. U. Khan, M. Y. Mehboob, R. Hussain, R. Fatima, M. S. Tahir, M. Khalid and A. A. C. Braga, J. Phys. Org. Chem., 2021, 34, e4119.
42. M. N. Arshad, I. Shafiq, M. Khalid, M. Asad, A. M. Asiri, M. M. Alotaibi, A. A. Braga, A. Khan and K. A. Alamry, Polymers, 2023, 15, 1508.
43. R. Hussain, F. Hassan, M. U. Khan, M. Y. Mehboob, R. Fatima, M. Khalid, K. Mahmood, C. J. Tariq and M. N. Akhtar, Opt. Quantum Electron., 2020, 52, 1–20.
44. S. F. Machado, G. G. Camiletti, A. C. Neto, F. E. Jorge and R. S. Jorge, Mol. Phys., 2009, 107, 1713–1727.
45. N. M. O’boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845.
46. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
47. K. J. Stevenson, J. Am. Chem. Soc., 2011, 133, 5621.
48. C. R. Wick and T. Clark, J. Mol. Model., 2018, 24, 1–9.
49. S. J. Grabowski, J. Mol. Model., 2013, 19, 4713–4721.
50. M. I. Nan, E. Lakatos, G.-I. Giurgi, L. Szolga, R. Po, A. Terec, S. Jungsuttiwong, I. Grosu and J. Roncali, Dyes Pigm., 2020, 181, 108527.
51. S. Li, Y.-L. Cao, W.-H. Li and Z.-S. Bo, Rare Met., 2021, 40, 2712–2729.
52. S. Naqvi and A. Patra, Mater. Chem. Phys., 2021, 258, 123863.
53. S. Namuangruk, R. Fukuda, M. Ehara, J. Meeprasert, T. Khanasa, S. Morada, T. Kaewin, S. Jungsuttiwong, T. Sudyoadsuk and V. Promarak, J. Phys. Chem. C, 2012, 116, 25653–25663.
54. W. Rahmalia, J.-F. Fabre, T. Usman and Z. Mouloungui, Spectrochim. Acta, Part A, 2014, 131, 455–460.
55. J. Zhu, Z. Ke, Q. Zhang, J. Wang, S. Dai, Y. Wu, Y. Xu, Y. Lin, W. Ma, W. You and X. Zhan, Adv. Mater., 2018, 30, 1704713.
56. J. D. Quezada-Borja, L. M. Rodríguez-Valdez, J. P. Palomares-Báez, M. A. Chávez-Rojo, L.-L. Landeros-Martinez, M. C. Martínez-Ceniceros, G. Rojas-George, I. A. García-Montoya and N. A. Sánchez-Bojorge, Front. Chem., 2022, 10, 907556.
57. Q. ul Ain, R. A. Shehzad, U. Yaqoob, A. Sharif, Z. Sajid, S. Rafiq, S. Iqbal, M. Khalid and J. Iqbal, Comput. Theor. Chem., 2021, 1200, 113238.
58. Z. H. Bakr, Q. Wali, A. Fakharuddin, L. Schmidt-Mende, T. M. Brown and R. Jose, Nano energy, 2017, 34, 271–305.
59. W.-J. Chi, D.-Y. Zheng, X.-F. Chen and Z.-S. Li, J. Mater. Chem. C, 2017, 5, 10055–10060.
60. P. Goszczycki, K. Stadnicka, M. Z. Brela, J. Grolik and K. Ostrowska, J. Mol. Struct., 2017, 1146, 337–346.
61. A. Sharif, S. Jabeen, S. Iqbal and J. Iqbal, Mater. Sci. Semicond. Process., 2021, 127, 105689.
62. T. M. Clarke and J. R. Durrant, Chem. Rev., 2010, 110, 6736–6767.
63. G. Dennler, M. C. Scharber, T. Ameri, P. Denk, K. Forberich, C. Waldauf and C. J. Brabec, Adv. Mater., 2008, 20, 579–583.
64. E. F. Oliveira and F. C. Lavarda, Polymer, 2016, 99, 105–111.
65. C. H. Suresh, G. S. Remya and P. K. Anjalikrishna, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2022, 12, e1601.
66. S. R. Gadre, C. H. Suresh and N. Mohan, Molecules, 2021, 26, 3289.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra03916e

---