Open Access Article
Open Access ArticleCarbon and boron nitride quantum dots as optical sensor probes for selective detection of toxic metals in drinking water: a quantum chemical prediction through structure- and morphology-dependent electronic and optical properties†
Chedharla Balaji Sarath Kumar a,
Rence Painappallil Reji
a,
Rence Painappallil Reji a,
Yuvaraj Sivalingam
a,
Yuvaraj Sivalingam bc,
Yoshiyuki Kawazoede and
Velappa Jayaraman Surya
bc,
Yoshiyuki Kawazoede and
Velappa Jayaraman Surya *ad
*ad
aNovel, Advanced, and Applied Materials (NAAM) Laboratory, Department of Physics and Nanotechnology, SRM Institute of Science and Technology, Kattankulathur 603203, Tamil Nadu, India. E-mail: suryaj@srmist.edu.in
bLaboratory of Sensors, Energy and Electronic Devices (Lab SEED), Department of Physics and Nanotechnology, SRM Institute of Science and Technology, Kattankulathur 603203, Tamil Nadu, India
cComputer, Electrical and Mathematical Sciences and Engineering Division (CEMSE), King Abdullah University of Science and Technology (KAUST), Thuwal 23955-6900, Kingdom of Saudi Arabia
dNew Industry Creation Hatchery Center, Tohoku University, Aoba-ku, Miyagi, Sendai 980-8579, Japan
eDepartment of Physics and Nanotechnology, SRM Institute of Science and Technology, Kattankulathur 603203, Tamil Nadu, India
First published on 4th September 2024
Abstract
Toxic metals present in drinking water pose a serious threat to the environment and human beings when present in abundance. In this work, we investigated the sensing ability of quantum dots (pristine CQDs, boron/nitrogen/sulphur (B/N/S)-doped CQDs, and BNQDs) of various sizes and morphologies (rectangular, circular, and triangular) towards toxic metals such as arsenic (As), cobalt (Co), nickel (Ni), copper (Cu), and lead (Pb) using quantum chemical density functional theory calculations in both gas and water phases. We probed the structural, electronic, and optical properties of the QDs. All the modelled QDs are energetically stable. Frontier molecular orbital analysis predicted that BNQDs are more chemically stable than all other CQDs. UV-vis absorption and Raman spectra analyses helped to understand the optical properties of all the QDs. Further, adsorption studies revealed that triangular pristine CQDs and sulphur-doped CQDs show higher adsorption affinity towards the toxic metals. The magnitude of adsorption energies follows the trend Ni > Pb > As > Cu > Co in most of the QDs. Several pristine and doped CQDs exhibited chemisorption towards the toxic metals, and hence, they can be used as adsorbents. However, a majority of BNQDs showed physisorption towards the metals, and therefore, they can be used as efficient optical sensors compared to CQDs. Further, the sensing ability of the QDs was explored through optical phenomena such as changes in UV-vis absorption spectra and fluorescence after metal adsorption. When compared to pristine CQDs and B/N/S-doped CQDs, metal complexation caused significant changes in the UV-vis absorbance peak intensities in BNQDs along with peak shifts. Moreover, metal interaction with the QDs increased their fluorescence lifetime with the highest values observed in Co-adsorbed triangular H18C46 (152.30 ns), Pb-adsorbed rectangular H15C30S (21.29 ns), and As-adsorbed circular B27N27H18 (2.99 μs) among pristine CQDs, B/N/S-doped CQDs, and BNQDs, respectively. Overall, we believe that our first-of-its-kind computational prediction of the optical sensing ability of tailor-made zero-dimensional systems such as QDs will be a great aid for experimentalists in designing novel and rapid optical probes to detect toxic metals in drinking water.
1. Introduction
The very existence of life on Earth depends on water, critically. The composition of cells and the transport of nutrients into the cells as well as the metabolism of the body depend on water. Currently, water pollution is one of the serious issues faced by all living forms, including humans and aquatic animals. The availability of limited freshwater resources worldwide has resulted in severe water scarcity, affecting 4 billion people for at least one month annually. Approximately 2.2 billion people lack access to clean drinking water globally.1 According to reports from the World Health Organization (WHO), due to contamination of drinking water, diseases such as diarrhoea kill 485![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 people annually.2 The demand for clean drinking water has increased. However, due to population explosion, urbanization, advancement in technology, and growth of industries, freshwater sources that provide drinking water are under threat. Many toxic elements are released into water without proper drainage/chemical treatment. Major sources that are responsible for the contamination of drinking water are fertilizers, tanning, soldering, electroplating, pesticides, batteries, and pipe manufacturing industries and they accumulate toxic metals in excess concentration.3 Due to this issue, our ecosystem and human health are under serious threat. The accumulation of metals such as copper (Cu), lead (Pb), arsenic (As), cobalt (Co), and nickel (Ni) in drinking water has raised a great concern worldwide as the excess concentration of these metals in water can lead to adverse health effects. Arsenic (As) contamination of water arises from smelting, pesticides, fungicides, and glass production industries.4–6 The most common oxidation states of As ions in water are +3 and +5.7 Long-term exposure to As through water beyond the permissible limit leads to bronchitis, dermatitis, hypopigmentation, hyperkeratosis, and encephalopathy.4,5 The maximum permissible limit of As ions in drinking water set by the WHO is 0.01 mg L−1.5,8 Lead (Pb) is one of the heavy metals arising from automobile emissions, mining sources, lead-based batteries, leaded fuels, and pesticides. The oxidation state of lead ions in water varies from +2 to +4 but the most common oxidation state of lead is +2.9 Prolonged exposure of humans to lead in excess concentrations through water causes damage and malfunctioning of the liver, kidney and reproductive system.8 The maximum contaminant level of Pb ions in drinking water set by the WHO is 0.1 mg L−1.5,6 Copper (Cu) is one of the essential elements for humans and is necessary in trace amounts in our diet to ensure good health. Excessive accumulation of copper in water arises from ore refineries, pesticides, fertilizers, and smelting.5 The Cu ion in water has an oxidation state of +1 and +2.7 Continued exposure to Cu through water leads to gastrointestinal irritation, hemolysis, anaemia, and multiorgan dysfunction syndrome.5,6 The maximum permissible limit of Cu ions in drinking water set by the WHO is 0.1 mg L−1.5,6 Nickel (Ni) is one of the transition metals arising from steel, alloy production, automobile batteries, and surgical instrument industries.4,5 The most common oxidation state of Ni ions in water is +2.7 Prolonged exposure to Ni through water leads to pulmonary fibrosis, dermatitis, gastrointestinal distress, myocarditis, and encephalopathy4,5 The maximum permissible limit of Ni ions in drinking water set by the WHO is 0.2 mg L−1.5 Cobalt (Co) contamination of water arises from hard metal production, diamond, paint, and electronic waste recycling industries.10 The most common oxidation states of Co ions in water are +2 and +3.7 Long-term exposure to Co through water beyond the permissible limit causes damage to the cardiovascular and pulmonary systems.7 The maximum permissible limit of Co ions in drinking water set by the United States Environmental Protection Agency is 100 μg L−1.11
000 people annually.2 The demand for clean drinking water has increased. However, due to population explosion, urbanization, advancement in technology, and growth of industries, freshwater sources that provide drinking water are under threat. Many toxic elements are released into water without proper drainage/chemical treatment. Major sources that are responsible for the contamination of drinking water are fertilizers, tanning, soldering, electroplating, pesticides, batteries, and pipe manufacturing industries and they accumulate toxic metals in excess concentration.3 Due to this issue, our ecosystem and human health are under serious threat. The accumulation of metals such as copper (Cu), lead (Pb), arsenic (As), cobalt (Co), and nickel (Ni) in drinking water has raised a great concern worldwide as the excess concentration of these metals in water can lead to adverse health effects. Arsenic (As) contamination of water arises from smelting, pesticides, fungicides, and glass production industries.4–6 The most common oxidation states of As ions in water are +3 and +5.7 Long-term exposure to As through water beyond the permissible limit leads to bronchitis, dermatitis, hypopigmentation, hyperkeratosis, and encephalopathy.4,5 The maximum permissible limit of As ions in drinking water set by the WHO is 0.01 mg L−1.5,8 Lead (Pb) is one of the heavy metals arising from automobile emissions, mining sources, lead-based batteries, leaded fuels, and pesticides. The oxidation state of lead ions in water varies from +2 to +4 but the most common oxidation state of lead is +2.9 Prolonged exposure of humans to lead in excess concentrations through water causes damage and malfunctioning of the liver, kidney and reproductive system.8 The maximum contaminant level of Pb ions in drinking water set by the WHO is 0.1 mg L−1.5,6 Copper (Cu) is one of the essential elements for humans and is necessary in trace amounts in our diet to ensure good health. Excessive accumulation of copper in water arises from ore refineries, pesticides, fertilizers, and smelting.5 The Cu ion in water has an oxidation state of +1 and +2.7 Continued exposure to Cu through water leads to gastrointestinal irritation, hemolysis, anaemia, and multiorgan dysfunction syndrome.5,6 The maximum permissible limit of Cu ions in drinking water set by the WHO is 0.1 mg L−1.5,6 Nickel (Ni) is one of the transition metals arising from steel, alloy production, automobile batteries, and surgical instrument industries.4,5 The most common oxidation state of Ni ions in water is +2.7 Prolonged exposure to Ni through water leads to pulmonary fibrosis, dermatitis, gastrointestinal distress, myocarditis, and encephalopathy4,5 The maximum permissible limit of Ni ions in drinking water set by the WHO is 0.2 mg L−1.5 Cobalt (Co) contamination of water arises from hard metal production, diamond, paint, and electronic waste recycling industries.10 The most common oxidation states of Co ions in water are +2 and +3.7 Long-term exposure to Co through water beyond the permissible limit causes damage to the cardiovascular and pulmonary systems.7 The maximum permissible limit of Co ions in drinking water set by the United States Environmental Protection Agency is 100 μg L−1.11
Recently, there has been a steady increase in interest in employing quantum dots (QDs) for the detection and removal of toxic metals in drinking water. In this quantum materials era, carbon quantum dots (CQDs) that are zero-dimensional fluorescent nanomaterials with a size range of less than 20 nm have attracted considerable attention in recent years because of their immense potential and use in a wide range of applications such as biosensing,12 bioimaging,13 photodynamic therapy,14 and electrocatalysis.15 CQDs were chosen for the detection of metals because of their distinct properties such as harmless chemical composition (environment friendly), modifiable fluorescence, simple functionalization, tunable optical properties, good fluorescence properties, large surface area, and good physicochemical and photochemical stability.16–22 Heteroatom doping of CQDs with non-metallic elements such as boron (B), nitrogen (N), and sulphur (S) is one of the efficient approaches to alter the chemical composition and to improve the electronic and optical properties of CQDs.19,23,24 Similar to CQDs, BNQDs are metal-free quantum dots, which are made up of non-toxic elements such as B, and N. They are chosen as optical probes for the detection of metals because they are environment-friendly, possess a large surface area, and have polar B–N bonds.25–27 Moreover, they have been continuously explored for various applications such as optoelectronics,28 biomedicine,29 photocatalysis,30 and organic pollutant adsorption due to their unique properties such as good electrical insulation, optical properties, chemical stability, thermal stability, high mechanical strength, and low toxicity.31 The detection of metals using various types of QDs has been investigated in detail by earlier reports using the optical sensing method.32–34 Recently, there have been many reports on the detection of toxic metals such as Pb and Ni in water using carbon nanomaterials.18,35 Moreover, BNQDs have been used for the detection of toxic metals in water. Yao et al., reported the detection of Ni2+ ions in water using BNQDs via a quenching mechanism.36 Liu et al. investigated the detection of Pb2+ and Cu2+ ions in water using BNQDs via a quenching mechanism.37
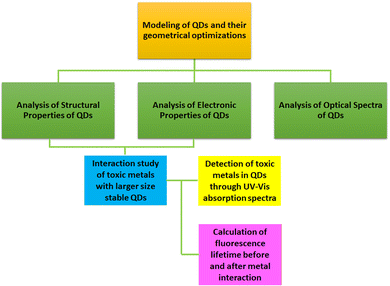
In this work, we investigated the potential of various QDs such as pristine CQD, B/N/S-doped CQDs, and BNQDs of different sizes and morphologies (rectangular, circular, and triangular) to detect toxic elements As, Co, Ni, Cu, and Pb using quantum chemical density functional theory (DFT) calculations. We carried out the structural assessment of the QDs via formation energy analysis. The electronic properties were understood through the highest occupied molecular orbital (HOMO), lowest unoccupied molecular orbital (LUMO), and energy gap analyses. Moreover, optical properties were explored by UV-vis and Raman spectra analyses. The adsorption behaviour of the QDs towards As, Cu, Co, Ni, and Pb in both gas and water phases was investigated. To substantiate the optical sensing ability of the designed QDs, the changes in UV-vis absorption spectra and fluorescence properties were investigated before and after the interaction of toxic elements with them in the water phase. To the best of our knowledge, this is the first report on computational assessment of the detection of toxic elements using QDs of various sizes and morphologies based on the optical transduction mechanism using UV-vis absorption spectra in the water phase. We believe that our computational results obtained through the DFT studies (Scheme 1) will help the experimentalists design engineered QDs as quantum optical sensors for selective detection of toxic elements in drinking water.
2. Computational details
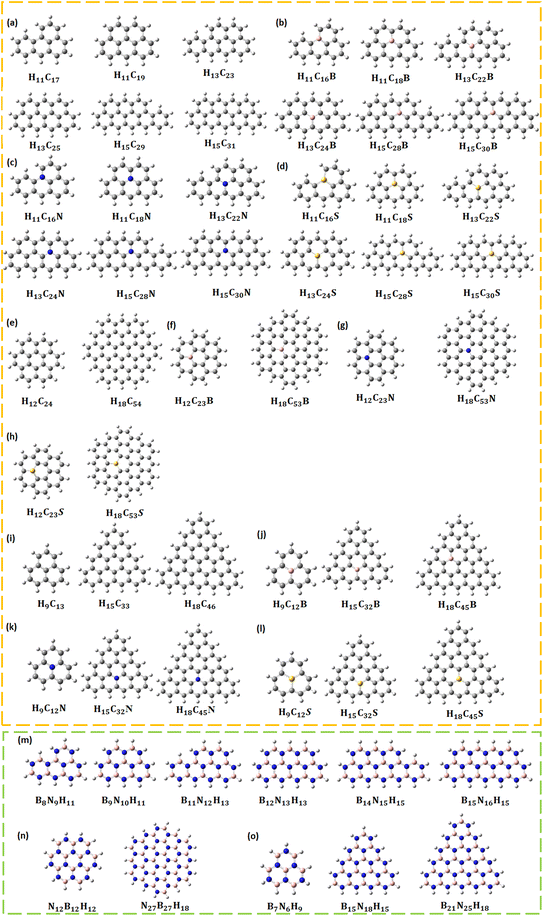
All calculations were carried out using the quantum chemical DFT package Gaussian16 with the Becke-3 parameter-Lee–Yang–Parr (B3LYP) exchange-correlation functional and 6-311G** (d,p)/Los Alamos National Laboratory 2 double-ζ (LANL2DZ) basis sets.38 Pristine, B/N/S CQDs and BNQDs were modelled and optimized to their ground state. All the systems were passivated with hydrogen (H) atoms to account for stability. Table 1 provides the list of 44 different structures along with the number of H, carbon (C), B, N, and S atoms. The optimized structures of all QDs are given in Fig. 1.| CQDs | B/N/S doped CQDs | BNQDs | |||
|---|---|---|---|---|---|
| Systems | Total no. of atoms | Systems | Total no. of atoms | Systems | Total no. of atoms |
| Rectangular | Rectangular | Rectangular | |||
| H11C17 | 28 | H11C16B | 28 | B11N17 | 28 |
| H11C19 | 30 | H11C18B | 30 | B11N19 | 30 |
| H13C23 | 36 | H13C22B | 36 | B13N23 | 36 |
| H13C25 | 38 | H13C24B | 38 | B13N25 | 38 |
| H15C29 | 44 | H15C28B | 44 | B15N29 | 44 |
| H15C31 | 46 | H15C30B | 46 | B15N31 | 46 |
| Circular | H11C16N | 28 | Circular | ||
| H12C24 | 36 | H11C18N | 30 | B12N24 | 36 |
| H18C54 | 72 | H13C22N | 36 | B18N54 | 72 |
| Triangular | H13C24N | 38 | Triangular | ||
| H9C13 | 22 | H15C28N | 44 | B9N13 | 22 |
| H15C33 | 48 | H15C30N | 46 | B15N33 | 48 |
| H18C46 | 64 | H11C16S | 28 | B18N46 | 64 |
| H11C18S | 30 | ||||
| H13C22S | 36 | ||||
| H13C24S | 38 | ||||
| H15C28S | 44 | ||||
| H15C30S | 46 | ||||
The formation energy of a QD was calculated using the following formula:
| Eform = [EQD − (nx × Ex + ny × Ey + nz × Ez)]/N | (1) |
Further, interactions between the QDs and toxic metals (As, Co, Ni, Cu, and Pb) were examined. The adsorption energy of metals with QDs was calculated using the following formula:
| Eadsorption energy = Ecomplex − EQD − Emetal | (2) |
Time-dependent DFT (TD-DFT) calculations were performed for all QDs to obtain UV-vis absorption. Moreover, Raman spectra were recorded for all QDs. Similar calculations were performed during metal interaction studies with selected QDs in both gas and water phases to obtain the UV-vis absorption spectra. The fluorescence lifetime calculation was carried out using the following formula:39
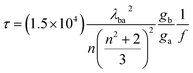 | (3) |
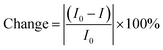 | (4) |
3. Results and discussion
3.1 Structural properties
In N-doped CQDs, the relaxed structures show that the C–C–C and C–N–C bond angles are about 120°, with the increase in size. The optimized C–N bond length is 1.40 Å, and it is similar to N-doped graphenes.42 The optimized bond length of C–C bonds at the inner surface of the N-doped CQD remains the same (1.42 Å) and varies at the edges. In N-doped rectangular CQDs, planarity varies with the size in a lesser magnitude. Their length varies from 7.32 Å to 12.27 Å. In N-doped circular CQDs, the diameter is in the range of 7.32 Å to 12.33 Å. In N-doped triangular CQDs, the optimized bond lengths of C–C bonds at the edges and inner surface of CQDs are 1.38 Å and 1.41 Å, respectively. The size of triangular N-doped CQDs is in the range of 4.86 Å to 12.27 Å.
In S-doped CQDs, due to the larger radius of the S atom, it protrudes out of the plane. In sulphur-doped circular and triangular CQDs, the relaxed structure shows variation in C–C–C (117.64° to 124.82°) and C–S–C (101.67° to 120.33°) bond angles with the increase in size. The optimized bond length of the C–S bond varies from 1.64 to 1.78 Å with the change in the size of S-doped CQDs. The C–S bond length agrees with the previous observations made by Zhao and Ma on sulphur-doped graphenes.43 The length of S-doped rectangular CQDs is in the range of 7.59 to 12.52 Å. The diameter of S-doped circular CQDs is in the range of 7.37 to 12.46 Å. In triangular S-doped CQDs, the optimized bond lengths of carbon C–C at the edges and inner surface of CQDs are 1.39 and 1.41 Å respectively. Their size is in the range of 5.19 to 12.49 Å.
3.1.4.1 Pristine CQDs. The formation energy of pristine CQDs is negative, and it implies that they are energetically stable. A similar kind of observation has been reported by Yamijala et al., for graphene QDs.45 The formation energy of rectangular, circular, and triangular CQDs varies from −6.10 eV to −5.50 eV, −6.80 eV to −6.06 eV, and −6.46 eV to −5.35 eV, respectively. In comparison, it can be understood that circular CQDs are more stable, energetically. Though rectangular H13C23 CQDs and circular H12C24 CQDs have almost the same number of atoms, there is a significant difference in their formation energy (−5.79 and −6.06 eV). At this juncture, one can understand that the morphology of the CQDs determines the stability too. Interestingly, there are many experimental reports on circular CQDs that have been investigated by atomic force microscopy and transmission electron microscopy characterization techniques.46
3.1.4.2 B/N/S-doped CQDs. The formation energy of B-doped rectangular, circular, and triangular CQDs varies in the range of −6.01 eV to −5.36 eV, −6.74 eV to −5.08 eV, and −6.41 to −5.17 eV, respectively. Circular H12C23B CQDs show a maximum change in their formation energy (−0.98 eV) compared to their pristine systems, whereas triangular H18C46B CQDs show a minimum change in their formation energy (−0.05 eV). The formation energy range of N-doped rectangular CQDs is similar to that of B-doped rectangular CQDs (−6.01 eV to −5.41 eV). The range of formation energy of N-doped circular and triangular CQD varies from −6.76 eV to −5.81 eV and −6.44 eV to −5.25 eV, respectively. Circular H12C23N CQDs show a maximum change in their formation energy (−0.25 eV) compared to their pristine forms, whereas triangular H18C45N CQDs show a minimum change in their formation energy (−0.02 eV). The formation energy of rectangular, circular, and triangular S-doped CQDs varies in the range of −5.86 to −5.15 eV, −5.42 to −4.74 eV, and −5.14 to −4.90 eV, respectively. Circular H18C53S shows a maximum change in its formation energy (−1.39 eV) compared to the pristine circular CQD (H18C54) and triangular H9C12S shows a minimum change in its formation energy (−0.46 eV) compared to its pristine counterpart. The formation energy range of all B/N/S-doped CQDs is negative, hence they are stable.
3.1.4.3 BNQDs. Similar to CQDs, the formation energy values of all BNQDs with different morphologies are negative and they are energetically stable. This is in line with the previous report.47 The range of formation energy of rectangular, circular, and triangular BNQDs is −5.36 eV to −4.84 eV, −5.96 eV to −5.27 eV, and −5.79 to −4.58 eV, respectively. Experimentally, Sert et al., have reported on the synthesis of BNQDs with circular morphology.48
3.2 Electronic properties
3.2.2.1 Pristine CQDs. The analysis of frontier molecular orbitals (FMOs) such as HOMO and LUMO followed by the calculated energy gap helps determine the chemical stability of a system. The system having the highest energy gap is more chemically stable. The pictorial illustration of the HOMO–LUMO analysis plots of all QD systems is given in Fig. S2.† Due to the presence of unpaired electrons in some of the QDs, the spin is in a doublet state which causes the FMO to split into alpha and beta molecular orbitals.54,55 In rectangular CQDs, the spin of rectangular CQD is in a doublet state which causes the frontier orbitals to split into alpha and beta molecular orbitals having two different energy gaps. This kind of observation was earlier reported for an organic molecule.56 The energy gap decreases with the increase in the size of rectangular CQDs due to the quantum confinement effect. This observation agrees with the previous report on graphene QDs.57 The energy gap of alpha molecular orbitals varies from 2.29 (H15C31) to 3.24 eV (H11C17). The increasing order of stability of rectangular CQDs for alpha molecular orbitals based on the energy gap is as follows:
| H15C31 < H15C29 < H13C25 < H13C23 < H11C19 < H11C17 |
The energy gap of beta molecular orbitals varies from 2.21 to 3.33 eV. The same trend was observed for beta molecular orbitals too.
The energy gap of circular CQDs decreases with the increase in diameter. A similar observation has been reported by Kateris et al., for polycyclic aromatic hydrocarbons.58 Smaller sized circular CQDs (H12C24) have the highest energy gap of 4.00 eV and larger sized circular CQDs (H18C54) have the lowest energy gap of 2.81 eV. This observation is in line with the previously reported values for similar systems investigated by Masfioui et al., using the B3LYP functional and a 6-31 g (d) basis set.59 In triangular CQDs, the spin of H9C13 and H15C33 is in a doublet state. Hence, the frontier orbitals to split into alpha and beta molecular orbitals have two different energy gaps. Similar to rectangular and circular CQDs, the energy gap decreases with the increase in size in triangular CQDs. The energy gap of triangular CQDs varies from 0.30 (H18C46) to 4.04 (H9C13) eV. The increasing order of stability of triangular CQDs based on the energy gap is as follows:
| H18C46 < H15C33 < H9C13e |
Overall, based on the energy gap, it can be concluded that circular CQDs are more chemically stable than triangular and rectangular CQDs. Interestingly, most of the CQDs which are experimentally synthesized have the circular morphology.13
3.2.2.2 B/N/S-doped CQDs. The doping of B/N/S on the surface of CQDs leads to the creation of additional energy levels between π (bonding) and π* (antibonding) molecular orbitals of the C atom. Hence, the variations in the HOMO and LUMO values are observed. Conversely, the energy gap gets changed too. A similar kind of observation has been made by Feng et al., for B-doped graphene dots.60
3.2.2.2.1 B-doped CQDs. All rectangular, circular, and triangular B-doped CQDs have a lesser energy gap than that of their pristine counterparts. The energy gap of rectangular B-doped CQDs is in the range of 1.25 eV to 1.93 eV. The increasing order of stability based on the energy gap is as follows:
| H13C24B < H15C28B < H15C30B < H13C22B < H11C16B < H11C18B |
| H15C32B < H18C45B < H9C12B |
3.2.2.2.2 N-doped CQDs. The energy gap has decreased in all N-doped rectangular, circular, and triangular CQDs compared to the bare CQDs. The energy gap of N-doped rectangular CQDs varies from 1.36 to 1.99 eV. The increasing order of chemical stability based on the energy gap for N-doped rectangular CQDs is as follows:
| H15C28N < H15C30N < H13C24N < H13C22N < H11C16N < H11C18N |
3.2.2.2.3 S-doped CQD. All S-doped rectangular CQDs are in a doublet state. The energy gap of alpha and beta molecular orbitals varies from 0.34 eV to 2.89 eV and 1.21 eV to 1.70 eV, respectively. Based on the energy gap, the increasing order of stability for alpha molecular orbitals is as follows:
| H11C18S < H15C30S < H15C28S < H13C22S < H13C24S < H11C16S |
Similarly, the increasing order of stability for beta molecular orbitals is as follows:
| H15C28S < H15C30S < H13C24S < H13C22S < H11C16S < H11C18S |
3.2.2.6 BNQDs. In rectangular BNQDs, there is a decrease in the energy gap with the increase in the size of the systems. However, the reduction is very minimal when compared to the CQDs. A similar observation has been highlighted by Guerra et al., for hexagonal BN nanoflakes.62 The energy gap of rectangular BNQDs lies between 6.06 and 6.16 eV. Based on the obtained energy gap, it is understood that the stability of BNQD is very high compared to pristine and B/N/S-doped CQDs. The increasing order of stability for rectangular BNQDs based on the energy gap is as follows:
| B14N15H15 < B15N16H15 < B11N12H13 < B12N13H13 < B8N9H11 < B9N10H11 |
A similar trend is exhibited by circular BNQDs with the increase in size. It is in line with the observations of Shayeganfar et al., on functionalized BNQDs having circular shapes.63 The energy gap of circular BNQDs varies from 6.27 eV to 6.64 eV. B12N12H12 and B27N27H18 have the highest and lowest energy gaps, respectively. In triangular BNQDs too, a decrease in the energy gap due to the increase in the number of atoms and size of BNQD is observed. The energy gap of triangular BNQDs varies from 5.77 eV to 7.11 eV. The increasing order of stability for triangular BNQDs based on energy gap is as follows:
| B21N25H18 < B15N18H15 < B7N6H9 |
Viana et al., have observed similar results for BN nanoflakes having different morphologies.64 Overall, BNQDs are more stable than their corresponding CQDs of any morphology.
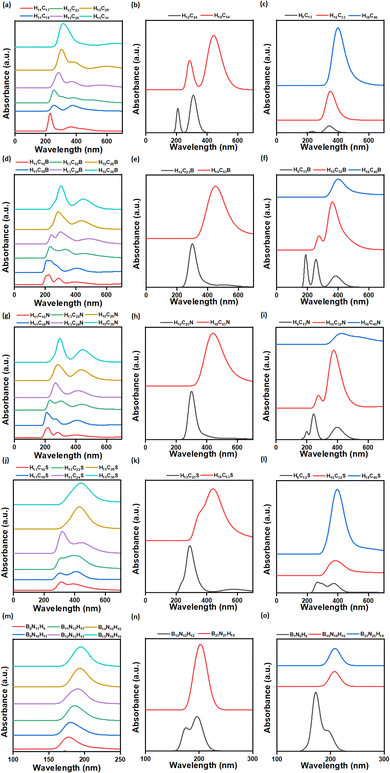
3.3 Optical properties
3.3.1.1 Pristine CQDs. Two characteristic peaks have been observed in CQDs (rectangular, circular and triangular). They occur due to π (bonding orbital)-to-π* (antibonding orbital) and n (non-bonding orbital)-to-π* transition, as reported by Zhang et al., for graphene QDs.66 The π-to-π* transition occurs in the wavelength range of 228–312 nm, 211–284 nm, and 232–408 nm for rectangular, circular and triangular CQDs, respectively. This transition is due to the presence of aromatic sp2 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) domains.67 Similarly, n-to-π* transition is observed in the wavelength range of 358–391 nm, 312–447 nm, and 343–408 nm for rectangular, circular and triangular CQDs, respectively.
C) domains.67 Similarly, n-to-π* transition is observed in the wavelength range of 358–391 nm, 312–447 nm, and 343–408 nm for rectangular, circular and triangular CQDs, respectively.
3.3.1.2 B/N/S-doped CQDs.
3.3.1.2.1 B-doped CQDs. In B-doped rectangular CQDs, we notice three characteristic peaks. One of the peaks is due to π-to-π* transition and the other two peaks are due to n-to-π* transition. This observation matches with the report of Fan et al., on B-doped graphene quantum dots.68 The π-to-π* transition in the wavelength range of 222–308 nm is due to the presence of aromatic sp2 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) domains. The n-to-π* transition in the wavelength range of 290–500 nm is due to the C–B bonds.69 In B-doped circular CQDs, there is only one characteristic peak in the wavelength range of 299–455 nm. The wavelength shift is more in B-doped circular CQDs than in pristine circular CQDs. Saha and Bhattacharyya have made a similar observation in B-doped coronene.70 Two characteristic peaks except for H18C45B are detected in the wavelength range of 191–403 nm. As noted in other QDs, the π-to-π* transition in the wavelength range of 191–284 nm is due to the presence of aromatic sp2 (C
C) domains. The n-to-π* transition in the wavelength range of 290–500 nm is due to the C–B bonds.69 In B-doped circular CQDs, there is only one characteristic peak in the wavelength range of 299–455 nm. The wavelength shift is more in B-doped circular CQDs than in pristine circular CQDs. Saha and Bhattacharyya have made a similar observation in B-doped coronene.70 Two characteristic peaks except for H18C45B are detected in the wavelength range of 191–403 nm. As noted in other QDs, the π-to-π* transition in the wavelength range of 191–284 nm is due to the presence of aromatic sp2 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) domains. Moreover, the n-to-π* transition has occurred in the wavelength range of 357–404 nm due to the C–B bonds.
C) domains. Moreover, the n-to-π* transition has occurred in the wavelength range of 357–404 nm due to the C–B bonds.
3.3.1.2.2 N-doped CQDs. The N doping in rectangular CQDs gives rise to 2 important characteristic peaks. They are due to π-to-π* and n-to-π* transitions. A similar kind of remark has been made by Hasibuan et al., in their research work on N-doped carbon dots.71 Here too, the π-to-π* transition occurs in the wavelength range of 214–296 nm due to the presence of aromatic sp2 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) domains. The n-to-π* transition is observed in the wavelength region below 500 nm, and this is due to the transition between the non-bonding orbital of C
C) domains. The n-to-π* transition is observed in the wavelength region below 500 nm, and this is due to the transition between the non-bonding orbital of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and the antibonding orbital (π*) of carbon. In N-doped circular CQDs, only one characteristic peak in the wavelength range of 302 to 442 nm, corresponding to the n-to-π* transition, is observed. This is because of the n-to-π* transition between the non-bonding orbital of C
N and the antibonding orbital (π*) of carbon. In N-doped circular CQDs, only one characteristic peak in the wavelength range of 302 to 442 nm, corresponding to the n-to-π* transition, is observed. This is because of the n-to-π* transition between the non-bonding orbital of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and the antibonding orbital (π*) of carbon. In triangular N-doped CQDs, two characteristic peaks except for H18C45N have been noticed. Similar to previous cases, the π-to-π* transition happens in the wavelength range of 204–273 nm, because of the presence of aromatic sp2 (C
N and the antibonding orbital (π*) of carbon. In triangular N-doped CQDs, two characteristic peaks except for H18C45N have been noticed. Similar to previous cases, the π-to-π* transition happens in the wavelength range of 204–273 nm, because of the presence of aromatic sp2 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) domains. Parallelly, the n-to-π* transition occurs in the wavelength region (382 to 423 nm) below 500 nm due to the non-bonding orbital of C
C) domains. Parallelly, the n-to-π* transition occurs in the wavelength region (382 to 423 nm) below 500 nm due to the non-bonding orbital of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and the antibonding orbital (π*) of the C atom.
N and the antibonding orbital (π*) of the C atom.
3.3.1.2.3 S-doped CQDs. The UV-vis absorption spectrum of S-doped rectangular CQDs in water gives rise to characteristic peaks, which are due to π-to-π* and n-to-π* transitions. A similar kind of observation was reported by Wu et al., for S-doped CQDs.72 The occurrence of π-to-π* transition was observed in the wavelength range of 304–320 nm, which is due to the presence of aromatic sp2 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) domains. The occurrence of n-to-π* transition was observed in the wavelength region below 500 nm. With the increase in the size of rectangular S-doped CQDs, the red shift was observed in the UV absorption spectrum as the absorption peaks shifted towards a higher wavelength.65 S-doped circular CQDs give rise to characteristic peaks due to π-to-π* and n-to-π* transitions, as highlighted by Wu et al., in S-doped CQDs.72 The π-to-π* transition was observed for H12C23S at a wavelength below 300 nm and it is due to the presence of aromatic sp2 (C
C) domains. The occurrence of n-to-π* transition was observed in the wavelength region below 500 nm. With the increase in the size of rectangular S-doped CQDs, the red shift was observed in the UV absorption spectrum as the absorption peaks shifted towards a higher wavelength.65 S-doped circular CQDs give rise to characteristic peaks due to π-to-π* and n-to-π* transitions, as highlighted by Wu et al., in S-doped CQDs.72 The π-to-π* transition was observed for H12C23S at a wavelength below 300 nm and it is due to the presence of aromatic sp2 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) domains. Here, n-to-π* transition is observed for all circular S-doped CQDs in the wavelength region below 500 nm. With the increase in the size of circular S-doped CQDs, the red shift is observed in the UV absorption spectrum. In triangular S-doped CQDs, two characteristic peaks were obtained in the wavelength range of 268–400 nm. The π-to-π* transition was observed for H9C12S at a wavelength below 300 nm due to the presence of aromatic sp2 (C
C) domains. Here, n-to-π* transition is observed for all circular S-doped CQDs in the wavelength region below 500 nm. With the increase in the size of circular S-doped CQDs, the red shift is observed in the UV absorption spectrum. In triangular S-doped CQDs, two characteristic peaks were obtained in the wavelength range of 268–400 nm. The π-to-π* transition was observed for H9C12S at a wavelength below 300 nm due to the presence of aromatic sp2 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) domains. The n-to-π* transition was observed for all triangular S-doped CQDs in the wavelength region below 400 nm. Similar to S-doped circular CQDs, the red shift is observed in S-doped triangular CQDs with the increase in size.
C) domains. The n-to-π* transition was observed for all triangular S-doped CQDs in the wavelength region below 400 nm. Similar to S-doped circular CQDs, the red shift is observed in S-doped triangular CQDs with the increase in size.
3.3.1.3 BNQDs. In the UV-vis absorption spectra of all rectangular, circular, and triangular BNQDs, a single absorption peak is observed in the wavelength ranges of 178–196 nm, 176 to 202 nm, and 174 to 210 nm, respectively. A similar kind of observation was made by Sert et al., for BNQDs.48
3.3.2.1 Pristine CQDs. Raman spectroscopy is a non-destructive tool used to investigate the degree of structural disorder in the carbon matrix occurring due to doping, vacancy, and point defects, both quantitatively and qualitatively.73 Raman spectrum is classified into two zones: one of them corresponds to the spectral range of 900–1900 cm−1 (first-order spectrum) and the other zone to 2500–3300 cm−1 (second-order spectrum).74 The typical features of Raman spectra of carbonaceous materials are the D (disorder) band, which arises due to the presence of defects in carbon, the G (graphitic order) band arising from the stretching of the C–C bond, the 2D (D peak overtone) band arising due to in-plane vibrations, D + G band arising due to the combination of overtone, D′ which is a phonon mode arising due to defects, and 2G which is a second-order mode appearing at higher frequencies.68
In the Raman spectra of pristine CQDs with various morphologies such as rectangular, circular, and triangular, the spectral range from 0 to 3500 cm−1 is considered (Fig. S3†). As the size of CQD increases, the intensity of the bands lying in the spectral range from 1300 to 1600 cm−1 and beyond 3100 cm−1 also increases. The Raman spectra of pristine CQDs show second-order modes (2G) around 3178–3185 cm−1. This arises due to the C–H vibrations of CQD. The intensity of the 2G band increases and becomes well defined with the increase in the size of the CQDs. Dervishi et al., have reported a similar observation in graphene QDs.75 The D and G characteristic bands appear in the wavelength range of 1344 to 1371 cm−1 and 1571 to 1651 cm−1, respectively. The presence of D and G bands in circular CQDs (C24H12, and C54H18), agrees with the previous observation made by Shtepliuk et al., for graphene QDs (C24H12).76
3.3.2.2 B-doped CQDs. In the B-doped CQDs too, with the increase in the size, the intensity of bands lying in the wavelength region of 1000 to 1600 cm−1 and beyond 3100 cm−1 increases. There is an appearance of second-order modes (2G) in the wavelength range of 3000 to 3200 cm−1, as highlighted by Venkatesan et al., for B-doped graphenes.77 The intensity of 2G bands becomes well defined with the increase in the size of B-doped CQDs.
In B-doped rectangular CQDs, the D and G bands appear in the spectral range of 1365–1386 cm−1 and 1575–1603 cm−1, respectively. These are in line with previously reported observations.78–80 In H11C16B, H13C24B, and H15C28B systems, the intensity of the peak appearing at 1638 cm−1 increases. In all B-doped rectangular CQDs, intense peaks were obtained between 1300 and 1600 cm−1. This is in line with the report of Zhang et al., on B-doped graphene QDs.81 The appearance of new bands was observed in all B-doped rectangular CQDs in the spectral range of 2947 to 2989 cm−1 and at 1806 cm−1. However, the intensity of the bands is low. A similar observation was reported by Kim et al., for B-doped graphenes for the band appearing at 2950 cm−1. This band arises due to a defect and it is attributed to the defect-induced double resonance (D + D′). They originate due to B doping in the CQD.82 The disappearance of peaks in the spectral range from 1785 to 1799 cm−1, 3360 to 3367 cm−1, and 1806 to 1813 cm−1 was observed in H11C18B, H13C22B, and H13C24B, respectively.
In B-doped circular CQDs, the D band appears at 1372 cm−1 and the G band appears in the wavelength range of 1533–1582 cm−1, respectively. The appearance of new peaks in the spectral range of 2986 to 2989 cm−1 was observed in the Raman spectrum of H12C23B, and H18C53B. The disappearance of peaks in the spectral range of 1813 to 1820 cm−1 was observed in H18C53B compared to the Raman spectrum of H18C54 and also at 1806 cm−1 for H12C23B when compared to the Raman spectrum of H12C24.
In B-doped triangular CQDs, the D and G bands appear in the spectral range of 1302–1386 cm−1 and 1547–1596 cm−1, respectively. These are in line with the earlier observations.78,79 The appearance of new peaks in the spectral range from 2954 to 2996 cm−1 was observed in the Raman spectrum of H9C12B, and H15C32B. These peaks correspond to D + D′ bands, and a similar observation was made by Chesnokov et al., in B-doped graphenes.80 The disappearance of peaks in the spectral range of 1771 to 1778 cm−1 was observed in H18C45B compared to the pristine CQD, H18C46.
3.3.2.3 N-doped CQDs. In N-doped CQDs, there is an appearance of second-order modes (2G) in the wavelength range of 3000 to 3200 cm−1. A similar observation was reported by Atchudan et al., for nitrogen-doped CQDs.83
In the N-doped rectangular CQDs, the D and G bands appear in the wavelength range of 1372–1393 cm−1 and 1610–1652 cm−1 respectively. These are in line with the earlier observations made by Liu et al., for N-doped CQDs.84 The presence of the D′ band at 1624 cm−1 in N-doped rectangular CQDs was reported by Zafar et al., for N-doped graphenes too.85 In all N-doped rectangular CQDs, the band's intensity appearing between 1650 and 1675 cm−1 increases. In N-doped rectangular CQDs, there is an appearance of new bands in the spectral range of 1806 to 1827 cm−1 and 3300 to 3500 cm−1. The bands at 2996 cm−1 in H13C24N and H15C30N have disappeared.
In the Raman spectra of N-doped circular CQDs having various sizes, the D and G bands appear in the spectral range of 1351–1379 cm−1 and 1617–1638 cm−1, respectively. A similar observation is made by Ayiania et al., for N-doped coronene.86 The appearance of new peaks at 1813 cm−1 and also in the spectral range of 3339 to 3353 cm−1 was observed in the Raman spectrum of H12C23N. Similarly, a new peak at 3339 cm−1 was observed for H18C53N. The peak at 2996 cm−1 in H12C23N vanished when compared to the pristine H12C24.
In the Raman spectra of N-doped triangular CQDs, the D and G bands appear in the spectral range of 1309–1365 cm−1 and 1561–1582 cm−1, respectively. New peaks appeared in the spectral range of 1750 to 1813 cm−1 and at 3346 and 3367 cm−1. The peaks at wavelengths 3003 and 3010 cm−1 in H9C12N disappeared when compared to the Raman spectrum of H9C13. Similarly, the appearance of new peaks at wavelengths 1778, 1785, 3346, and 3353 cm−1 was observed in the Raman spectrum of H15C32N compared to the Raman spectrum of H15C33. The appearance of new peaks in the spectral range of 1785 to 1869 cm−1 and at wavelength 3346 cm−1 was observed in the Raman spectrum of H18C45N when compared to pristine H18C46.
3.3.2.4 S-doped CQDs. The Raman spectra of the S-doped rectangular CQDs were observed in the spectral range from 0 to 3500 cm−1. The characteristic bands, D and G, appear in the wavelength range of 1344–1358 cm−1 and 1533–1624 cm−1, respectively. This agrees with the earlier observations made by Kadian et al., for S-doped graphene QDs.51 As the size of CQDs increases, the intensity of the bands lying in the spectral range of 300–1800 cm−1 and beyond 3100 cm−1 also becomes more intense, and the second-order modes (2G) appear in the spectral range of 3178–3192 cm−1. The disappearance of peaks in the wavelength range from 1771 to 1813 cm−1 was observed in the Raman spectrum of H11C16S, H15C28S, and H15C30S and also in the wavelength range of 3360 to 3353 cm−1 was observed in the Raman spectrum of H13C22S, H13C24S, and H15C28S. The appearance of peaks in the wavelength range 3367 to 3430 cm−1 was observed in the Raman spectrum of H11C16S, H13C22S and also at wavelength 2996 cm−1 for H11C16S, H13C24S.
3.3.2.5 BNQDs. In the Raman spectra of BNQDs with various morphologies such as rectangular, circular, and triangular, the spectral range was considered from 200 to 2000 cm−1. In all BNQDs, when the size is increased, the intensity of the bands lying in the spectral range of 1000–1600 cm−1 also increases. In all BNQDs of various sizes and morphologies, a characteristic peak with low intensity appears in the wavelength range of 1344 to 1379 cm cm−1. This peak corresponds to the E2g vibration mode due to the stretching of the B–N bond in h-BN, this agrees with the previous observation reported by Ahmad et al., for h-BNQDs.87
3.4 Interaction studies of toxic metals with QDs
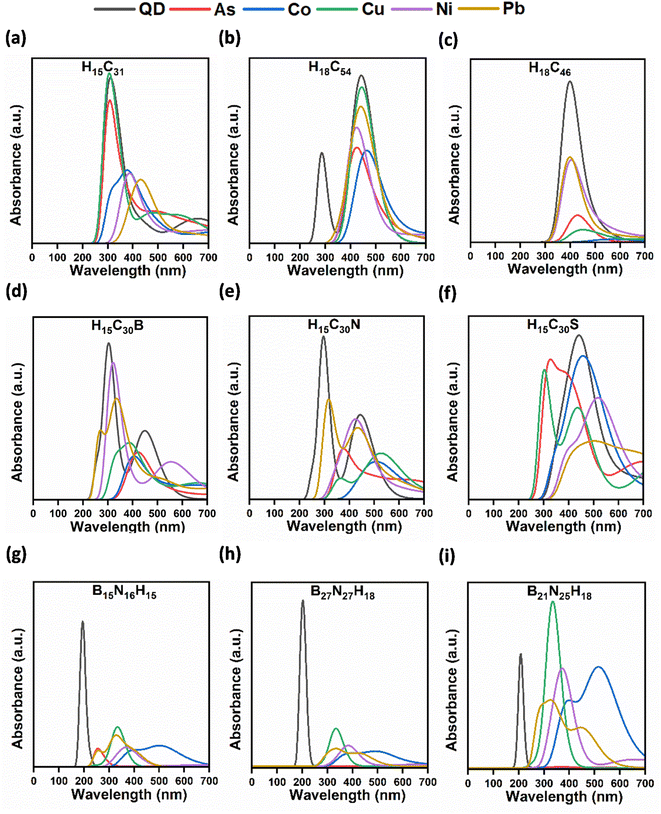
Larger sized QDs (rectangular H15C31, circular H18C54, triangular H18C46, rectangular H15C30B/N/S, rectangular B15N16H15, circular B27N27H18, and triangular B21N25H18) are taken for the toxic metal interaction studies due to their enhanced structural stability. The investigations were carried out in both gas and water phases. After metal adsorption, we can observe changes in the bond lengths, bond angles and planarity in a few of the CQDs and B/N/S-doped CQDs. However, negligible changes are noted in B–N, B–H, and N–H bond lengths, and N–B–N and B–N–B bond angles after metal complexation in BNQDs. Hence, their planarity is preserved even after the metal adsorption. Fig. 3 represents the QD + metal complexes having higher interactions with each other and the rest of them are given in Fig. S4.† The calculated formation energy of metal-adsorbed QDs was found to be negative, implying the formation of structurally stable complexes (Table S1†).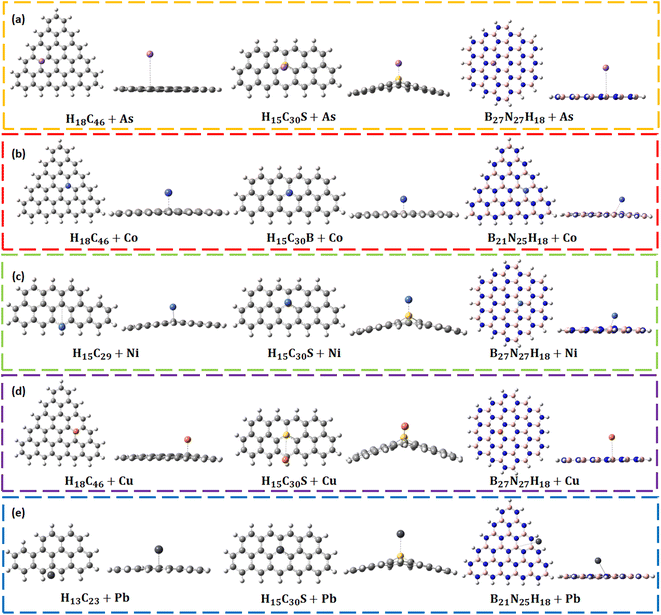 | ||
| Fig. 3 Optimized structures of QD + metals: (a) As, (b) Co, (c) Ni, (d) Cu, and (e) Pb complexes having higher adsorption energies. | ||
The As adsorption energies in B/N/S doped CQDs are in the range of −1.27 eV to −3.16 eV, which confirms the chemisorption of As on these systems. The obtained adsorption energy values with H15C30B, and H15C30N agree with the previous reports.89,90 H15C30S has the highest adsorption energy towards As (−3.16 eV) among all other QDs. Due to the strong interaction, the C–S–C bond angle has changed about 20.72°. The planarity of H15C30S + As gets distorted by 38.12°. The interaction distance between As and S (2.20 Å) closely agrees with the bond length As–S bond of Arsenopyrite.91 In all BNQDs, the As adsorption energies are nearly the same (−1.03 to −1.06 eV) suggesting chemisorption. The planarity of B15N16H15 + As gets reduced on As interaction and the highest change occurs by about 6.90°.
The interaction of Co with B/N/S-doped rectangular CQDs causes no appreciable change in the C–C–C bond angle and C–(B/N)–C bond angle, except C–S–C. The C–S–C bond angle has changed by 14.46°. The planarity gets disturbed on this interaction, and the planarity of H15C30S + Co (35.32°) gets affected more. The Co-metal shows good bond formation with S of H15C30S at an interaction distance of 2.04 Å, which matches the bond length of the cobalt–sulphide system.93 Similarly, the diameter of H15C30S + Co has varied (0.35 Å) much from its pristine system. H15C30B + Co has the highest adsorption energy (−1.86 eV) among all other B/N/S-doped CQDs. Interestingly, rectangular H15C30N + Co has an adsorption energy (−1.04 eV) larger than that of H15C31 + Co (0.39 eV). A similar observation was made by Jin et al., for the adsorption of Co on graphenes.94 The adsorption energy (−0.27 to −0.31 eV) and interaction distance (2.34 to 2.83 Å) of BNQDs on Co interaction suggest that Co is physisorbed on these BNQDs with different morphologies and the adsorption energy range is modest. The planarity gets reduced on Co interaction and the highest change occurs for N16B15H15 + Co.
After the interaction of Ni with B/N/S-doped rectangular CQDs, there is no appreciable change in the C–C–C bond angles and C-(B/N)–C bond angle, except C–S–C. The C–S–C bond angle has changed by 19.84°. The planarity gets disturbed on this interaction, and the planarity of rectangular H15C30S + Ni (35.62°) gets affected more. The adsorption energy of Ni on these systems (−1.38 to −4.22 eV) suggests that it gets chemisorbed. Ni metal shows good bond formation with S of H15C30S during interaction, an interaction distance of 2.00 Å matches the bond length of the NiS system.96 H15C30S + Ni has the highest adsorption energy (−4.21 eV) among all other QDs. The interaction between Ni and B/N doped CQD is due to the hybridization between 3 d orbitals of Ni and 2p orbitals of B/N atoms of CQD, a similar observation was made by Zhou et al., for B/N-doped graphenes.97
The adsorption energy values (−1.44 to −1.47 eV) are nearly the same for all BNQDs with Ni and the interaction distance (2.42 to 2.45 Å) between BNQDs and Ni suggests the chemisorption between the two entities. A negligible change in the diameter is observed in Ni interaction with BNQDs because of very little distortion and stability of BNQDs. The interaction of Ni with circular BNQDs (N27B27H18) is the highest (−1.47 eV).
The adsorption energies of Cu on B/N/S-doped rectangular CQDs are from −0.84 to −3.72 eV. The adsorption energy (−0.84 eV) and interaction distance of 3.92 Å were observed when Cu interacts with H15C30N, which suggests that Cu is physisorbed. Cu interaction with H15C30S and H15C30B shows chemisorption with adsorption energies of −3.72 eV and −1.44 eV, respectively with the former having the highest adsorption energy. Due to the strong interaction, the C–S–C bond angle has changed by 19.10°. The planarity gets disturbed more with an out-of-plane projection of about 42.50° in H15C30S + Cu. Similarly, the diameter of H15C30S + Cu varied (0.61 Å) much from its pristine system. For systems H15C30S + Cu and H15C30N + Cu, the diameter gets reduced on Cu interaction. The chemical bonding between Cu and B/N-doped CQD is due to the interaction between the 2p orbitals of C and B/N and the d orbitals of the Cu atom. A similar observation was made by An and Turner on the interaction study of Cu with B/N-doped single-walled carbon nanotubes.99
The adsorption energies (−0.23 to −0.25 eV) and interaction distance (3.22 to 3.35 Å) of BNQDs + Cu complexes suggest that Cu is physisorbed on these BNQDs. It suggests weak interaction between Cu and BNQDs and our observations are in line with Liu et al.100 The N–B–N and B–N–B bond angles have changed by 0.83° and 0.38°, respectively in B15N16H15 + Cu. The planarity gets reduced on Cu interaction and the highest change occurs for B15N16H15 + Cu by about 1.26°.
The adsorption energies of Pb on B/N/S-doped CQDs (−0.79 to −3.32 eV) suggest that it gets chemisorbed. An adsorption energy of −0.79 eV and an interaction distance of 3.88 Å were observed when Pb interacted with H15C30N. A similar observation was made by Srivastava et al., for Pb with B and N-doped graphenes, which has occurred due to the nucleophilic behaviour of the N-doped CQD.102 H15C30S + Pb has the highest adsorption energy (−3.32 eV) among all other QDs. The C–S–C bond angle changed by 18.69°. The planarity gets disturbed on this interaction, and the planarity of H15C30S + Pb (35.62°) gets affected more. The Pb metal shows good bond formation with S of H15C30S during the interaction. The interaction distance of 2.85 Å matches the bond length of the Galena (PbS) system.103
The adsorption energies (−0.15 to −0.47 eV) and interaction distance (3.26 to 4.71 Å) of Pb-adsorbed BNQDs suggest that Pb is physisorbed on the latter. The interaction of Pb with circular BNQDs (B27N27H18) is the lowest. This may be due to the high stability of circular BNQDs.
In summary, pristine rectangular H15C31 and circular H18C54 CQDs showed the highest adsorption towards Ni. Meanwhile, triangular H18C46 CQDs showed the highest adsorption towards As. Both B/N-doped CQDs showed more affinity toward Pb. Furthermore, S-doped CQDs showed the highest interaction with Cu. Interestingly, BNQDs of all morphologies showed the highest interaction with As. More importantly, pristine triangular and S-doped CQDs showed a larger affinity towards all toxic metals. We propose the following facts based on the nature of interaction and the magnitude of the obtained adsorption energies of metals with the considered QDs. Most of the metals interact with the pristine and B/N/S-doped CQDs with higher adsorption energies ensuring chemisorption. Such QDs can also be used as adsorbents or filters in the process of obtaining clean drinking water.101,104 Furthermore, the BNQDs have shown physisorption towards all toxic metals enabling them to be reused. Hence, BNQDs can be more efficient optical sensors than CQDs.
3.5 Interaction studies of toxic metals with QDs in water phase
PCM was employed to include the effect of solvent, i.e. water. The PCM uses continuous solvent distribution to describe the interaction between the solute and the solvent. In this section, the changes in the adsorption energy, formation energy and dipole moment after metal complexation with QDs in the water phase were analyzed. The calculated formation energies of QD + metal complexes are negative, confirming their complexation stability in the water phase (Table S1†). We can observe a large change in the dipole moments in all QDs after the interaction with toxic metals (Table S2†). An increase in the dipole moment of the complex was observed due to a change in the charge distribution due to the effect of water.1053.6 Detection of toxic metals using UV-vis absorption spectra in the water phase
The UV-vis absorption spectra of QDs with metals (As, Co, Ni, Cu, Ni, and Pb) in the water phase were recorded (Fig. 4). After the interaction of metals with QDs, there is either a decrease or an increase in the absorbance peaks when compared to the absorption spectra of bare QDs (Table 2). This percentage of change is quantified based on the intensity variation of the absorption peaks before and after interaction with metals.| Morphology/QD | Calculated percentage of absorbance reduction/increment (%) | ||||
|---|---|---|---|---|---|
| As | Co | Ni | Cu | Pb | |
| a % increment in the absorbance peak intensity. | |||||
| Rectangular H15C31 | 13.19 | 55.42 | 57.48 | 3.56a | 61.31 |
| Circular H18C54 | 42.81 | 44.61 | 30.88 | 6.88 | 18.60 |
| Triangular H18C46 | 83.20 | 98.17 | 47.89 | 92.22 | 46.96 |
| Rectangular H15C30B | 69.57 | 72.29 | 12.20 | 63.98 | 34.95 |
| Rectangular H15C30N | 68.16 | 77.11 | 50.11 | 71.33 | 38.04 |
| Rectangular H15C30S | 14.66 | 12.58 | 38.02 | 21.24 | 63.64 |
| Rectangular B15N16H15 | 87.72 | 85.34 | 86.45 | 72.85 | 78.10 |
| Circular B27N27H18 | 99.96 | 90.90 | 87.54 | 77.30 | 89.31 |
| Triangular B21N25H18 | 99.16 | 11.32 | 12.89 | 44.94a | 40.41 |
Upon interaction of metals with triangular H18C46 CQDs, the absorption peak intensity reduction was observed. A maximum decrease in the absorbance was observed for triangular H18C46 + Co. The percentage of absorption reduction for metals with triangular CQDs ranges from 46.96 to 98.17%. The highest percentage of intensity diminution was observed for Co with H18C46 (98.17%). The interaction of triangular CQDs with metals results in a redshift with the absorption peaks shifting from 400 to 573 nm. Our findings on the absorption reduction of Cu, Co, and Pb using circular and triangular CQDs are in line with the previously reported observations on quenching and decrease in the intensity of emission/fluorescence spectra upon the addition of metals to CQDs in water.113–115
The percentage of absorbance reduction for metals with rectangular N-doped CQDs ranges from 38.04 to 77.11%. The highest percentage of quenching is observed for Co with H15C30N (77.11%). The quenching of metals (Cu, Pb, and Co) such as using N-doped CQDs in line with previously reported observations based on photoluminescence emission and fluorescence spectra.117–119 This decrement has occurred due to charge and energy transfer between metal and rectangular N-doped CQDs. Fluorescence quenching was observed by Wu et al. during the detection of Cu2+ ions using N-doped CQDs.120 The interaction of rectangular N-doped CQDs with metals resulted in a redshift of peaks from 299 to 530 nm.
The percentage of absorbance abatement for metals with rectangular S-doped CQDs ranges from 12.58 to 63.64%. The highest percentage of quenching is achieved for Pb with H15C30S (63.64%). A significant amount of reduction agrees well with the interaction energy of rectangular S-doped CQDs with Pb, as it shows a higher interaction energy. The decrement occurs due to charge and energy transfer between metal and rectangular S-doped CQDs, due to the higher binding affinity of S towards metals.121 The absorbance peak reduction in Pb-adsorbed S-doped CQDs matches with the observations of Bian et al. on the detection of Pb2+ ions using S-doped graphene QDs in fluorescence spectra.121 The interaction of metals with rectangular S-doped CQD resulted in a redshift of the peaks from 305 to 510 nm.
3.7 Lifetime of QDs in water phase
Lifetime is one of the important characteristics of QDs. This depends on many internal factors such as the structure of fluorophore (QDs), and also external factors such as temperature, polarity, and the presence of quenchers (metals). When the timescale is in several nanoseconds, it is called fluorescence.122 Here, we calculated the lifetime of all QDs before and after metal adsorption in the water phase. The obtained lifetime range suggests fluorescence in all QDs. Moreover, we can observe that the lifetime values change concerning the size and morphology of the QDs.3.8 Lifetime of QDs with toxic metals in water phase
| Morphology/QD | Lifetime (ns) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Calculated lifetime | Experimentally observed lifetime | References | |||||||||
| As | Co | Ni | Cu | Pb | As | Co | Ni | Cu | Pb | ||
| Rectangular H15C31 | 0.79 | 5.54 | 2.16 | 0.60 | 4.77 | — | — | — | 5.40 | 3.35 to 3.58 | 109 and 127 |
| Circular H18C54 | 1.76 | 2.79 | 2.79 | 1.14 | 1.65 | — | — | — | 5.40 | 3.35 to 3.58 | 109 and 127 |
| Triangular H18C46 | 4.63 | 152.30 | 1.63 | 20.14 | 1.29 | — | — | — | 5.40 | 3.35 to 3.58 | 109 and 127 |
| Rectangular H15C30B | 3.85 | 4.86 | 1.50 | 2.31 | 1.94 | — | — | — | 1.92 to 5.11 | 1.92 to 4.80 | 116 |
| Rectangular H15C30N | 2.14 | 6.77 | 2.82 | 4.76 | 0.81 | — | — | — | 5.54 | — | 128 |
| Rectangular H15C30S | 1.39 | 6.73 | 4.16 | 1.76 | 21.29 | — | — | — | — | — | — |
| Rectangular B15N16H15 | 4.55 | 17.53 | 9.94 | 2.86 | 6.67 | — | — | Very small | — | — | 36 |
| Circular B27N27H18 | 2992.39 | 19.99 | 8.84 | 3.03 | 15.35 | — | — | Very small | — | — | 36 |
| Triangular B21N25H18 | 1198.77 | 14.69 | 9.73 | 3.23 | 10.87 | — | — | Very small | — | — | 36 |
4. Conclusion
We have investigated the toxic metal (As, Co, Ni, Cu, and Pb) detection capability of QDs (CQDs, B/N/S-doped CQDs, and BNQDs) of various sizes and morphologies (rectangular, circular, and triangular) as potential optical receptors using quantum chemical DFT calculations. Structurally, the circular QDs are very stable. Energy gap analysis has revealed that BNQDs are more stable than CQDs. All toxic metals in the gas phase and water phase get adsorbed in the energy range of −0.02 to −4.21 eV and −0.008 to −4.81 eV, respectively. Among all QDs, pristine triangular CQDs and S-doped CQDs exhibit higher adsorption affinity towards the toxic metals. Most of the QDs show higher interaction with Ni followed by Pb, As, Cu and Co. Moreover, most of the metals are chemisorbed in CQDs and B/N/S-doped CQDs, suggesting such systems to be used as adsorbents. Interestingly, the majority of BNQDs have exhibited physisorption towards the toxic metals. The UV-vis absorption spectra of all QDs indicate the redshift of the absorbance peaks with the increase in the size of the QDs. Raman spectra have confirmed the structural integrity of the modelled QDs. The detection of metals using QDs in the water phase has been understood through absorption peak intensity modulation as observed in the UV-vis absorption spectra. It is noted that BNQDs show the highest percentage of intensity reduction in the UV-vis absorption spectra compared to other QDs after metal adsorption. Reasonably, considerable fluorescence lifetime is obtained for Co with triangular H18C46 (152.30 ns) in CQDs, Pb with rectangular H15C30S (21.29 ns) in B/N/S-doped CQDs, and As with circular B27N27H18 (2.99 μs) in BNQDs. The nature of interaction of toxic metals as well as the highest degree of absorption peak intensity changes in BNQDs suggests that they can be more efficient than CQDs in the optical sensing of toxic metals. In summary, our extensive DFT studies have demonstrated QDs as optical sensor receptors and the findings will help the experimentalists in designing such environment-friendly probes for the detection of toxic metals in drinking water.Author contributions
The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors would like to express their sincere thanks to the crew of the Center for Computational Materials Science of the Institute for Materials Research, Tohoku University, for their continuous support towards supercomputing facilities. Also, the authors thank SRM-HPCC for availing the supercomputer for computations. The authors Y. S. and V. J. S. acknowledge the financial support from DST-SERB under the Core Research Grant (CRG/2021/006647). C. B. S. thanks SRMIST for the fellowship to carry out the research.References
- M. Salehi, Environ. Int., 2022, 158, 106936 CrossRef PubMed.
- Y. Zhang, J. Deng, B. Qin, G. Zhu, Y. Zhang, E. Jeppesen and Y. Tong, Fundam. Res., 2023, 3, 265–273 CrossRef CAS PubMed.
- R. Kumar, M. Qureshi, D. Kumar and N. Al-ansari, Case Stud. Chem. Environ. Eng., 2022, 6, 100219 CrossRef CAS.
- N. A. A. Qasem, R. H. Mohammed and D. U. Lawal, npj Clean Water, 2021, 4, 1–15 CrossRef.
- N. Verma and R. Sharma, Recent Pat. Biotechnol., 2017, 11, 171–187 CAS.
- S. Fahimirad and M. Hatami, Med. Plants Environ. Challenges, 2017, pp. 189–214 Search PubMed.
- A. Lace and J. Cleary, Chemosensors, 2021, 9, 60 CrossRef CAS.
- H. N. M. Ekramul Mahmud, A. K. Obidul Huq and R. B. Yahya, RSC Adv., 2016, 6, 14778–14791 RSC.
- M. N. Nadagouda, C. White and D. Lytle, Microsc. Microanal., 2011, 17, 284–291 CrossRef CAS PubMed.
- L. Leyssens, B. Vinck, C. Van Der Straeten, F. Wuyts and L. Maes, Toxicology, 2017, 387, 43–56 CrossRef CAS PubMed.
- Z. Haftu and P. Sathishkumar, Chem. Afr., 2020, 3, 419–426 CrossRef CAS.
- W. E. Omer, M. F. Abdelbar, N. M. El-Kemary, N. Fukata and M. A. El-Kemary, RSC Adv., 2021, 11, 31047–31057 RSC.
- C. Huang, H. Dong, Y. Su, Y. Wu, R. Narron and Q. Yong, Nanomaterials, 2019, 9, 387 CrossRef CAS PubMed.
- X. Li, K. Vinothini, T. Ramesh and M. Rajan, Drug Delivery, 2020, 27, 791–804 CrossRef CAS PubMed.
- W. Chen, Z. Qin, B. McElhenny, F. Zhang, S. Chen, J. Bao, Z. M. Wang, H.-Z. Song and Z. Ren, J. Mater. Chem. A, 2019, 7, 21488–21495 RSC.
- P. Devi, P. Rajput, A. Thakur and K. Kim, Trends Anal. Chem., 2019, 114, 171–195 CrossRef CAS.
- S. Y. Lim, W. Shen and Z. Gao, Chem. Soc. Rev., 2015, 44, 362–381 RSC.
- T. Vyas and A. Joshi, Analyst, 2024, 149, 1297–1309 RSC.
- F. Wang, Q. Hao, Y. Zhang, Y. Xu and W. Lei, Microchim. Acta, 2016, 183, 273–279 CrossRef CAS.
- U. Abd Rani, L. Y. Ng, C. Y. Ng and E. Mahmoudi, Adv. Colloid Interface Sci., 2020, 278, 102124 CrossRef CAS PubMed.
- J. Dhariwal, G. K. Rao and D. Vaya, RSC Sustainability, 2024, 2, 11–36 RSC.
- S. D. T. Landa, N. K. R. Bogireddy, I. Kaur, V. Batra and V. Agarwal, Iscience, 2022, 25, 103816 CrossRef PubMed.
- Q. Yang, J. Duan, W. Yang, X. Li, J. Mo, P. Yang and Q. Tang, Appl. Surf. Sci., 2018, 434, 1079–1085 CrossRef CAS.
- Y. Hu, J. Yang, J. Tian, L. Jia and J.-S. Yu, Carbon, 2014, 77, 775–782 CrossRef CAS.
- P. M. Revabhai, R. K. Singhal, H. Basu and S. K. Kailasa, J. Nanostruct. Chem., 2023, 13, 1–41 CrossRef CAS.
- J. Rawat, D. Sajwan, S. V. Garimella, H. Sharma and C. Dwivedi, NanoTrends, 2023, 2, 100008 Search PubMed.
- X. Zhang, L. An, C. Bai, L. Chen and Y. Yu, Mater. Today Chem., 2021, 20, 100425 CrossRef CAS.
- Y. Ding, P. He, S. Li, B. Chang, S. Zhang, Z. Wang, J. Chen, J. Yu, S. Wu and H. Zeng, ACS Nano, 2021, 15, 14610–14617 CrossRef CAS PubMed.
- S. Umrao, A. K. Maurya, V. Shukla, A. Grigoriev, R. Ahuja, M. Vinayak, R. R. Srivastava, P. S. Saxena, I. K. Oh and A. Srivastava, Mater. Today Bio, 2019, 1, 100001 CrossRef CAS PubMed.
- W. Guo, Y. Yang, Q. Jin, H. Zhao, R. Zhang and Y. Zhai, J. Mater. Sci. Mater. Electron., 2021, 32, 9946–9955 CrossRef CAS.
- L. Chen, X. Zhang, Z. Zhao, F. Wang, Y. Huang, C. Bai, L. An and Y. Yu, Colloids Surf., A, 2021, 614, 126181 CrossRef CAS.
- X. Wang, L. Kong, S. Zhou, C. Ma, W. Lin, X. Sun, D. Kirsanov, A. Legin, H. Wan and P. Wang, Talanta, 2022, 239, 122903 CrossRef CAS PubMed.
- Z. Wang, B. Yao, Y. Xiao, X. Tian and Y. Wang, Chemosensors, 2023, 11, 405 CrossRef CAS.
- V. R. Nair, M. Shanthil, K. Sandeep, K. U. Savitha, A. Archana, V. Deepamol, C. Swetha and P. V. Vaishag, ACS Omega, 2023, 8, 29468–29474 CrossRef CAS PubMed.
- L. Gontrani, O. Pulci, M. Carbone, R. Pizzoferrato and P. Prosposito, Molecules, 2021, 26, 5519 CrossRef CAS PubMed.
- Q. Yao, Y. Feng, M. Rong, S. He and X. Chen, Microchim. Acta, 2017, 184, 4217–4223 CrossRef CAS.
- B. Liu, S. Yan, Z. Song, M. Liu, X. Ji, W. Yang and J. Liu, Chem. Eur J., 2016, 22, 18899–18907 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- H. Riesen, C. Wiebeler and S. Schumacher, J. Phys. Chem. A, 2014, 118, 5189–5195 CrossRef CAS PubMed.
- M. Javan, R. Jorjani and A. R. Soltani, J. Mol. Model., 2020, 26, 1–10 CrossRef PubMed.
- R. E. Ambrusi, C. R. Luna, A. Juan and M. E. Pronsato, RSC Adv., 2016, 6, 83926–83941 RSC.
- K. Li, N. Li, N. Yan, T. Wang, Y. Zhang, Q. Song and H. Li, Appl. Surf. Sci., 2020, 515, 146028 CrossRef CAS.
- J. Zhao and J. Ma, J. Phys. Chem. C, 2016, 120, 25131–25141 CrossRef CAS.
- M. Maruyama and S. Okada, Sci. Rep., 2018, 8, 16657 CrossRef PubMed.
- S. S. Yamijala, M. Mukhopadhyay and S. K. Pati, J. Phys. Chem. C, 2015, 119, 12079–12087 CrossRef CAS.
- L. Mishra, R. K. Behera, S. Mondal, S. Kumar, A. Panigrahi and M. K. Sarangi, Carbon, 2021, 178, 594–605 CrossRef CAS.
- S. S. Yamijala, A. Bandyopadhyay and S. K. Pati, J. Phys. Chem. C, 2013, 117, 23295–23304 CrossRef CAS.
- B. Sert, S. Gonca, Y. Ozay, E. Harputlu, S. Ozdemir, K. Ocakoglu and N. Dizge, Colloids Surf., B, 2021, 205, 111867 CrossRef CAS PubMed.
- H. R. Jiang, T. S. Zhao, L. Shi, P. Tan and L. An, J. Phys. Chem. C, 2016, 120, 6612–6618 CrossRef CAS.
- A. El Hadki, K. Ulucan-altuntas, H. El Hadki, C.B. Ustundag, O. K. Kabbaj, A. Dahchour, N. Komiha, A. Zrineh and E. Debik, FlatChem, 2021, 27, 100238 CrossRef.
- S. Kadian, N. K. Tailor, N. Chaulagain, K. Shankar, S. Satapathi and G. Manik, J. Mater. Sci. Mater. Electron., 2021, 32, 17406–17417 CrossRef CAS.
- S. N. Ema, M. A. Khaleque, A. Ghosh, A. A. Piya, U. Habiba and S. U. D. Shamim, RSC Adv., 2021, 11, 36866–36883 RSC.
- R. Talaei, B. Khalili and M. Mokhtary, J. Mol. Liq., 2020, 304, 112696 CrossRef CAS.
- M. M. El-Nahass, M. A. Kamel, A. F. El-Deeb, A. A. Atta and S. Y. Huthaily, Spectrochim. Acta, Part A, 2011, 79, 1499–1504 CrossRef CAS PubMed.
- C.-G. Liu, Z.-M. Su, X.-H. Guan and S. Muhammad, J. Phys. Chem. C, 2011, 115, 23946–23954 CrossRef CAS.
- M. Ahmed, M. El-Mansy, M. Hassan, M. A. Mostafa, M. A. M. El-Mansy, H. M. Hassanin and M. A. Mostafa, Org. Optoelectron., 2015, 1, 1 Search PubMed.
- B. Mandal, S. Sarkar and P. Sarkar, J. Nanopart. Res., 2012, 14, 1–8 CrossRef.
- N. Kateris, A. S. Jayaraman and H. Wang, Proc. Combust. Inst., 2023, 39, 1069–1077 CrossRef.
- M. El Masfioui, S. Bahsine, A. Elbiyaali and F. Allali, in E3S Web of Conferences, EDP Sciences, 2022, vol. 336, pp. 48 Search PubMed.
- J. Feng, H. Dong, B. Pang, F. Shao, C. Zhang, L. Yu and L. Dong, Phys. Chem. Chem. Phys., 2018, 20, 15244–15252 RSC.
- W. Sun, C. Chen, C. Li, D. Wu, J. Kang, Y. Li and Z. Li, ChemPhysChem, 2018, 19, 2518–2524 CrossRef CAS PubMed.
- T. Guerra, L. R. S. Araújo and S. Azevedo, J. Phys. Chem. Solids, 2019, 135, 109085 CrossRef CAS.
- F. Shayeganfar, M. R. R. Tabar, A. Simchi and J. Beheshtian, Phys. Rev. B, 2017, 96, 165307 CrossRef.
- G. E. D. Viana, A. M. Silva, F. U. da C. Barros, F. da Silva, E. W. S. Caetano, J. J. S. Melo and A. Macedo-Filho, J. Mol. Model., 2020, 26, 1–11 CrossRef PubMed.
- F. Zhang, F. Liu, C. Wang, X. Xin, J. Liu, S. Guo and J. Zhang, ACS Appl. Mater. Interfaces, 2016, 8, 2104–2110 CrossRef CAS PubMed.
- M. Zhang, L. Bai, W. Shang, W. Xie, H. Ma, Y. Fu, D. Fang, H. Sun, L. Fan and M. Han, J. Mater. Chem., 2012, 22, 7461–7467 RSC.
- A. Ananthanarayanan, X. Wang, P. Routh, B. Sana, S. Lim, D. Kim, K. Lim, J. Li and P. Chen, Adv. Funct. Mater., 2014, 24, 3021–3026 CrossRef CAS.
- Z. Fan, Y. Li, X. Li, L. Fan, D. Fang and S. Yang, Carbon, 2014, 70, 149–156 CrossRef CAS.
- Y. Ma, A. Y. Chen, Y. Y. Huang, X. He, X. F. Xie, B. He, J. H. Yang and X. Y. Wang, Carbon, 2020, 162, 234–244 CrossRef CAS.
- B. Saha and P. K. Bhattacharyya, ACS Omega, 2018, 3, 16753–16768 CrossRef CAS PubMed.
- P. A. Z. Hasibuan, M. Tanjung, W. Lianto, S. Gea, A. Piliang and S. A. Situmorang, Case Stud. Chem. Environ. Eng., 2023, 8, 100455 CrossRef.
- F. Wu, M. Yang, H. Zhang, S. Zhu, X. Zhu and K. Wang, Opt. Mater., 2018, 77, 258–263 CrossRef CAS.
- S. Sangam, A. Gupta, A. Shakeel, R. Bhattacharya, A. K. Sharma, D. Suhag, S. Chakrabarti, S. K. Garg, S. Chattopadhyay and B. Basu, Green Chem., 2018, 20, 4245–4259 RSC.
- A. Cuesta, P. Dhamelincourt, J. Laureyns, A. Martinez-Alonso and J. M. D. Tascón, Carbon, 1994, 32, 1523–1532 CrossRef CAS.
- E. Dervishi, Z. Ji, H. Htoon, M. Sykora and S. K. Doorn, Nanoscale, 2019, 11, 16571–16581 RSC.
- I. Shtepliuk, N. M. Caffrey, T. Iakimov, V. Khranovskyy, I. A. Abrikosov and R. Yakimova, Sci. Rep., 2017, 7, 3934 CrossRef PubMed.
- N. Venkatesan, K. S. Archana, S. Suresh, R. Aswathy, M. Ulaganthan, P. Periasamy and P. Ragupathy, ChemElectroChem, 2019, 6, 1107–1114 CrossRef CAS.
- M. P. Kumar, C. Takahashi, S. Kundu, T. N. Narayanan and D. K. Pattanayak, New J. Chem., 2019, 43, 14313–14319 RSC.
- C. Hsu, L. Laysandra, Y. Chiu and W. Liu, Chem. Eng. J., 2023, 473, 145469 CrossRef CAS.
- V. V. Chesnokov, I. P. Prosvirin, E. Y. Gerasimov and A. S. Chichkan, Materials, 2023, 16, 1986 CrossRef CAS PubMed.
- L. Zhang, Z.-Y. Zhang, R.-P. Liang, Y.-H. Li and J.-D. Qiu, Anal. Chem., 2014, 86, 4423–4430 CrossRef CAS PubMed.
- Y. A. Kim, K. Fujisawa, H. Muramatsu, T. Hayashi, M. Endo, T. Fujimori, K. Kaneko, M. Terrones, J. Behrends and A. Eckmann, ACS Nano, 2012, 6, 6293–6300 CrossRef CAS PubMed.
- R. Atchudan, T. N. J. I. Edison, S. Perumal, N. C. S. Selvam and Y. R. Lee, J. Photochem. Photobiol., A, 2019, 372, 99–107 CrossRef CAS.
- Y. Liu, L. Jiang, B. Li, X. Fan, W. Wang, P. Liu, S. Xu and X. Luo, J. Mater. Chem. B, 2019, 7, 3053–3058 RSC.
- Z. Zafar and Z. H. Ni, Carbon, 2013, 61, 57–62 CrossRef CAS.
- M. Ayiania, E. Weiss-Hortala, M. Smith, J.-S. McEwen and M. Garcia-Perez, Carbon, 2020, 167, 559–574 CrossRef CAS.
- P. Ahmad, M. U. Khandaker, F. Rehman, N. Muhammad, M. R. I. Faruque, Z. Ullah, M. A. R. Khan, G. Khan, M. I. Khan and H. Ali, et al.,, Ceram. Int., 2021, 11, 222 CAS.
- M. Srivastava, A. Srivastava and S. K. Pandey, Appl. Surf. Sci., 2020, 146021 CrossRef CAS.
- M. Srivastava and A. Srivastava, Mater. Today: Proc., 2022, 48, 661–665 CAS.
- S. S. Meshkat, S. Hoseinzadeh, Z. Hosseini-dastgerdi, R. Mehrabi, E. Ghasemy and M. Esrafili, Int. J. Environ. Sci. Technol., 2023, 20, 8287–8302 CrossRef CAS.
- H. Fuess, T. Kratz, J. Töpel-Schadt and G. Miehe, Z. Kristallogr. Krist., 1987, 179, 335–346 CrossRef CAS.
- A. N. Rudenko, F. J. Keil, M. I. Katsnelson and A. I. Lichtenstein, Phys. Rev. B, 2012, 86, 75422 CrossRef.
- E. L. Uzunova, Phys. Chem. Chem. Phys., 2022, 24, 20228–20238 RSC.
- C. Jin, L. Cheng, G. Feng, R. Ye, Z.-H. Lu, R. Zhang and X. Yu, Langmuir, 2022, 38, 3694–3710 CrossRef CAS PubMed.
- C. Gong, G. Lee, B. Shan, E. M. Vogel, R. M. Wallace and K. Cho, J. Appl. Phys., 2010, 108, 123711 CrossRef.
- K. Sharkas, L. Gagliardi and D. G. Truhlar, J. Phys. Chem. A, 2017, 121, 9392–9400 CrossRef CAS PubMed.
- X. Zhou, W. Chu, W. Sun, Y. Zhou and Y. Xue, Comput. Theor. Chem., 2017, 1120, 8–16 CrossRef CAS.
- K. Nakada and A. Ishii, Graphene Simul., 2011, pp. 1–19 Search PubMed.
- W. An and C. H. Turner, J. Phys. Chem. C, 2009, 113, 7069–7078 CrossRef CAS.
- X. Liu, T. Duan, Y. Sui, C. Meng and Y. Han, RSC Adv., 2014, 4, 38750–38760 RSC.
- S. M. Elgengehi, S. El-taher, M. A. A. Ibrahim, K. Jacques and K. E. El-kelany, Appl. Surf. Sci., 2019, 145038 Search PubMed.
- M. Srivastava and A. Srivastava, Mater. Sci. Eng., B, 2021, 269, 115165 CrossRef CAS.
- J. Chen, X. Long and Y. Chen, J. Phys. Chem. C, 2014, 118, 11657–11665 CrossRef CAS.
- M. K. Hossain, D. Roy and F. Ahmed, J. Mol. Struct., 2021, 1237, 130302 CrossRef.
- L. Guo, S. Kaya, I. B. Obot, X. Zheng and Y. Qiang, J. Colloid Interface Sci., 2017, 506, 478–485 CrossRef CAS PubMed.
- M. H. Miah, M. R. Hossain, M. S. Islam, T. Ferdous and F. Ahmed, RSC Adv., 2021, 11, 38457–38472 RSC.
- H. Abdelsalam, N. H. Teleb, I. S. Yahia, H. Y. Zahran, H. Elhaes and M. A. Ibrahim, J. Phys. Chem. Solids, 2019, 130, 32–40 CrossRef CAS.
- D. Kong, F. Yan, Z. Han, J. Xu, X. Guo and L. Chen, RSC Adv., 2016, 6, 67481–67487 RSC.
- Z. Sun, Y. Zhou, W. Zhou, J. Luo, R. Liu, X. Zhang, L. Zhou and Q. Pang, Nanoscale, 2021, 13, 2472–2480 RSC.
- F. Noun, E. A. Jury and R. Naccache, Sensors, 2021, 21, 1391 CrossRef CAS PubMed.
- Y. Liu, Q. Zhou, J. Li, M. Lei and X. Yan, Sens. Actuators, B, 2016, 237, 597–604 CrossRef CAS.
- I. Shtepliuk and R. Yakimova, Materials, 2018, 11, 1217 CrossRef PubMed.
- B. Rooj, A. Dutta, S. Islam and U. Mandal, J. Fluoresc., 2018, 28, 1261–1267 CrossRef CAS PubMed.
- C.-L. Li, C.-C. Huang, A. P. Periasamy, P. Roy, W.-C. Wu, C.-L. Hsu and H.-T. Chang, RSC Adv., 2015, 5, 2285–2291 RSC.
- T. Ghosh, R. Sahoo, S. K. Ghosh, P. Banerji and N. C. Das, Front. Chem. Sci. Eng., 2023, 17, 536–547 CrossRef CAS.
- Z.-X. Wang, X.-H. Yu, F. Li, F.-Y. Kong, W.-X. Lv, D.-H. Fan and W. Wang, Microchim. Acta, 2017, 184, 4775–4783 CrossRef CAS.
- V. Singh, V. Kumar, U. Yadav, R. Kr and J. ISSS, Micro Smart Syst., 2017, 6, 109–117 CrossRef.
- R. Bandi, R. Dadigala and B. Reddy, J. Photochem. Photobiol., B, 2018, 178, 330–338 CrossRef CAS PubMed.
- D. Bano, V. Kumar, S. Chandra, V. K. Singh, S. Mohan, D. K. Singh, M. Talat and S. H. Hasan, Opt. Mater., 2019, 92, 311–318 CrossRef CAS.
- X. Wu, L. Wu, X. Cao, Y. Li, A. Liu and S. Liu, RSC Adv., 2018, 8, 20000–20006 RSC.
- S. Bian, C. Shen, H. Hua, L. Zhou, H. Zhu, F. Xi, J. Liu and X. Dong, RSC Adv., 2016, 6, 69977–69983 RSC.
- A. Jain, C. Blum and V. Subramaniam, Advances in Biomedical Engineering, Elsevier, 2009, pp. 147–176 Search PubMed.
- M. Röding, S. J. Bradley, M. Nydén and T. Nann, J. Phys. Chem. C, 2014, 118, 30282–30290 CrossRef.
- W. Kwon, J. Lim, J. Lee, T. Park and S.-W. Rhee, J. Mater. Chem. C, 2013, 1, 2002–2008 RSC.
- A. B. Bourlinos, G. Trivizas, M. A. Karakassides, M. Baikousi, A. Kouloumpis, D. Gournis, A. Bakandritsos, K. Hola, O. Kozak and R. Zboril, Carbon, 2015, 83, 173–179 CrossRef CAS.
- Z. Qian, J. Ma, X. Shan, H. Feng, L. Shao and J. Chen, Chem. Eur J., 2014, 20, 2254–2263 CrossRef CAS PubMed.
- F. Wang, Z. Gu, W. Lei, W. Wang, X. Xia and Q. Hao, Sens. Actuators, B, 2014, 190, 516–522 CrossRef CAS.
- L. Zhao, H. Li, Y. Xu, H. Liu, T. Zhou, N. Huang, Y. Li and L. Ding, Anal. Bioanal. Chem., 2018, 410, 4301–4309 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: ESP plots of all QDs, HOMO–LUMO plots of rectangular QDs, Raman spectra of all QDs, Optimized structures of QDs + metal complexes, Formation energies of Metal–QD complexes in gas and water phases, dipole moments of all QDs before and after metal interaction. See DOI: https://doi.org/10.1039/d4ra04843a |
| This journal is © The Royal Society of Chemistry 2024 |