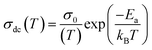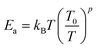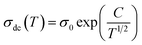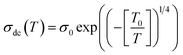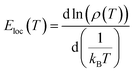Investigation of the structural, magnetic, and electrical characteristics of the La_0.7Sr_0.25Na_0.05Mn_0.8Ti_0.2O₃

Abstract

This article reveals the crucial structural, magnetic, and electrical properties of La_0.7Sr_0.25Na_0.05Mn_0.8Ti_0.2O₃ (LSNMTO) manganite, highlighting the significance of this material in the field of materials science. Gain a deeper understanding of the promising properties of LSNMTO and its potential for technological advancement by delving into this informative article. The X-ray diffraction data of the LSNMTO indicate that this ceramic solid solution crystallizes in the R3̄c rhombohedral structure. The magnetic results confidently demonstrate that the LSNMTO ceramic undergoes a transition from paramagnetic to ferromagnetic phases around 125 K. This significant finding could pave the way for further progress in the field of materials science. The DC conductivity response confirms the semiconductor nature of the elaborated compound over the studied temperature domain. Such behavior is linked to the contribution of the small polaron hopping mechanism at elevated temperatures and the Shklovskii Efros variable range hopping process at low temperatures. In the limit of the AC regime, the temperature-dependent AC conductivity confirms the appearance of a metal–semiconductor behavior at T_M–S = 120 K that confirms the strong correlations between the transport and the magnetic properties of the sample. Over the explored temperature domain, the conductivity spectra follow a power law-like behavior. The scaled conductivity curve of LSNMTO is not superimposed on the particle grains' restricted reaction area. The Summerfield scaling of the electrical conductivity confirms with confidence the significant contribution of carrier concentration to the overall conduction of the material.

---

1. Introduction

Because of its many uses, rare earth-doped manganite structures, with the general formula R_1−xA_xMnO₃ (where R stands for rare earth and A for divalent ion), have been the focal point of advanced materials research for almost 50 years.^1–3 The chemical flexibility of these materials^4–6 makes it easier to use them for multiple purposes. According to the literature, the physical characteristics and the crystallographic structure of manganites can be intentionally controlled by substituting a divalent ion for a portion of the rare earth.^7–10 The interaction between their special qualities, such as magnetocaloric effects and colossal magnetoresistance (CMR), makes them advantageous for potential applications.^11,12 The metal–insulator and ferromagnetic–paramagnetic transitions that are governed by double-exchange (DE) interactions (DE), characteristically accompany the appearance of the CMR effect.^11–14 For manganite structures, the intimate interaction between electric and magnetic properties is largely explained by the DE transport mechanism, which regulates the amount of Mn³⁺/Mn⁴⁺ ratio.^11,15 It has been confirmed that the creation of the mixed valence state in LaMnO₃ can be achieved when bivalent strontium ions substitute the La-site of the material.^10,16,17 For the Sr-doped LaMnO₃ (LSMO) systems, it has been observed that the physical properties are governed by the strong impact of both structural distortions and charge carrier motions between the Mn³⁺ and Mn⁴⁺ ion states.^10,16,17 The hopping motions between Mn³⁺ and Mn⁴⁺ ions consist of ferroelectricity and magnetism simultaneously emerging into the structure by the resulting coupling between electric dipoles and spins. Recently, the LSMO structure has attracted great interest in multiferroic applications due to its CMR effects, its broad range of stable structures, and greater flexibility characteristics.^10,16,17 The physical properties of this material family are directly related to the Mn⁴⁺/Mn³⁺ mixed-valence states that depend in turn on the synthesis method and the inhomogeneous composition within the microstructure. In this context, it has been found that doped La_1−xSr_xMnO₃ (LSMO) compounds are regrouped as materials that exhibit a range of fascinating physical characteristics, mostly when the trivalent La ions are doped with the Sr bivalent element at various concentration levels.^10,16,17 Accordingly, substituting the La trivalent with Sr bivalent ions induces a cationic disorder in the A-site of the manganite lattice, affecting the bandwidth, structural properties, and electronic interactions. This influences in turn the electronic structure, the magnetic behavior, and the dynamics of the charge carriers in manganites. Under certain doping and temperature conditions, the increase of the Sr level leads to the appearance of structural phase transitions. Moreover, the increase of the Sr level in the LSMO perovskite structure can imply the variation of the metal–insulator transition temperature. Furthermore, the increase of the Sr level affects the electrical conductivity. Early investigation on the magnetic properties of the manganite materials has shown that the variation of the Sr level affects strongly the ferromagnetism of the LSMO perovskites.^10,16,17 Accordingly, it is found that the Curie temperature (T_C) attains its maximum value of T_C = 370 K when the Sr level attains a concentration of x = 0.3. In the same context, it is concluded that LSMO manganites exhibit a CMR that is more pronounced at around the transition temperature. Depending on the Sr doping level and temperature, it is found that the LSMO systems can show various types of magnetic ordering, like the ferromagnetic, antiferromagnetic, or even mixed-phase regions. Due to lattice mismatch between the La and the Sr ions, it has been found that the variation of the Sr doping concentration modifies mainly the strain that significantly affects the magnetic and electrical properties of the materials. Versus the increase of the Sr concentration level, it is found that the material behavior shifts from the insulating antiferromagnetic state (low Sr content level) to the ferromagnetic metallic state (around x = 0.3). Additional rises in the Sr concentration can lead to the reemergence of insulating behavior due to the presence of both disorder and phase separation effects. The LSMO is suitable for storage energy systems because it has a high conductivity compared to pure silicon and a significant permittivity value of up to 10⁵ F m⁻¹.^10,16,17 Typically, the coupling of the spin-phonon and the DE phenomena, connected directly to dynamic Jahn–Teller distortions produced from the coupling of a strong electron–phonon, have been employed to clarify the origin of the rare phenomena of manganite structures.^11–15 Based on the aforementioned discussion, we can assume that sample substitution of manganites in A and/or B sites affects mainly the electrical and magnetic properties of various systems, which are strongly dependent on the structural and microstructural characteristics of those compounds. The substitution process is an effective conservative factor for improving the physicochemical properties and the magnetic features of manganites.^1,2 It changes the Mn–O distances and the Mn–O–Mn angles of materials.^1,2 In addition, the substitution process changes the internal chemical pressure that is the main intrinsic characteristic of a material and the DE interaction talent in manganites. For the LSMO system, the crystallographic structure is characteristically orthorhombic or rhombohedral, depending on the precise doping stoichiometry and elaboration conditions. Mainly, the substitution of a manganite with Ti ions tends to distort its lattice structure. The increase of the Ti doping level can affect the material's structure, with possible phase transitions. In addition, such kind of substitutions affects mainly the electrical conductivity order. Accordingly, the electrical conductivity of the LaSrMn_1−xTi_xO₃ system changes mainly with the Ti doping level. At low Ti doping levels, the manganite typically reveals a metallic behavior due to the existence of Mn mixed-valence states. Nevertheless, raising the Ti level can imply a conductivity decrease due to the substitution of Mn³⁺ or Mn⁴⁺ ions with Ti⁴⁺, which disrupts the electron hopping mechanism. For materials with metal–insulator transition, the variation of the Ti concentration level affects the transition temperature value. In addition, the substitution with Ti usually suppresses the ferromagnetic ordering because Ti ions do not participate in the DE mechanism that is responsible for ferromagnetism in manganites. In addition, this kind of substitution reduces the T_C value. In recent decades, there have been numerous investigations aimed at improving the transport performance of manganite oxides.^1,2 For various ceramic manganites, the transport characteristics of this material family are mainly linked to the microstructure that contains conductive grain size separated by more resistive grain boundary zones.^1,2 The electrical conductivity of the manganites is dependent on charge type (electron, bi-polaron, and polaron), carrier mobility and density, and porosity of the material. To investigate the origin of the charge carrier displacement and the transport phenomenon within manganites, various electrical models have been employed based on Mott's theory.^18–20 Among the most employed conduction mechanisms in the limit of the DC regime, we cite the variable range hopping process that describes the electrical semiconductor property at low temperatures. Moreover, we mention the small polaron hopping conduction process that describes the transport phenomena’ origins at high temperatures. In addition, in the limit of the AC regime, the conductivity dispersion response of the manganite compounds has usually been explained via hopping, tunneling, and jumping conduction processes.^21–23 Mainly, the conductivity spectra reveal single and double Jonscher power law responses or metallic variation.^21–23 For materials with dispersive conductivity variation, the scaling models are important for developing and optimizing materials for applications like solid oxide fuel cells, oxygen sensors, and other devices that rely on oxide perovskites. Understanding the electrical conductivity in manganites allows for better design and improvement of materials with motivating electrical conductivity. In this context, the scaling models are fundamental tools in the field of materials science, providing insights into the complex behaviors of various materials like the disordered ionic conductors and the oxide perovskites.

Alterations to the electronic structure and the distribution of charges have the potential to influence the electrical and magnetic behaviors of manganites. In this work, structural, microstructural, magnetic, and complex impedance analyses are adopted to get information about the strong correlations between the electrical and magnetic properties of LSNMTO. The magnetic and AC conductivity results confidently demonstrate that LSNMTO undergoes a transition from paramagnetic to ferromagnetic phases and from metallic to semiconductor behaviors at around 125 K. This confirms the strong relationships between the electrical and magnetic characteristics of LSNMTO and makes this material a candidate for future low-temperature applications. AC and DC conductivity analyses are used to release a complete study of the charge carriers' dynamics and the material's complex behaviors (multiple conduction mechanisms). The Summerfield scaling model is proposed to get detailed evidence about the dynamics of the charge carriers in LSNMTO and interactions within the ceramic. In addition, this model provides a deeper understanding of the material properties and aids in developing new materials with tailored electronic and magnetic properties. A comparison of the obtained structural, electrical, and magnetic results with some previous investigations is conducted to search for the possible applications of LSNMTO.

2. Experimental part

We used a solid-state process to elaborate the LSNMTO ceramic system's solid solution. Accordingly, La₂O₃, SrCO₃, Na₂O₃, MnO₂, and TiO₂ precursors have been suggested as the starting materials. Fine powders are obtained by mixing the aforementioned powders according to the proposed stoichiometry and milling them in an agate mortar. Subsequently, the attained material has been imperiled to a calcination step, via a programmable muffle furnace. In the same context, to achieve the formation of the proposed ceramic structure, the material is pressed into a circular pellet form via a hydraulic press. After that, the pressed powder is sintered for 48 hours at a temperature of 1350 °C in the air. Both phase purity and crystal structure of the prepared ceramic manganite have been observed via the well-known X-ray diffraction (XRD) characterization and using the theoretical Rietveld analysis. The room temperature XRD experimental data are obtained through an XPERT-PRO diffractometer that exhibits a radiation CuK_α with λ_CuKα = 1.5406 Å. The achievement of the results is recorded in the 2θ angular region that varies between 15 and 100° with an acquisition time of 18 s. The electrical data are obtained using an Agilent 4294 A analyzer. Each measurement is conducted under darkness and vacuum. The conductivity characterization is achieved in the angular frequency domain between 251 rad s⁻¹ and 7 × 10⁶ rad s⁻¹ and for a temperature range between 80 K and 360 K. The magnetic measurements are performed in field-cooled circumstances (under an applied magnetic field of (H = 500 Oe.)) using a BS1 magnetometer developed in Louis Néel Laboratory at Grenoble. In this study, we measured the magnetization versus the temperature near the Curie temperature T_C and in the temperature range between 10 K and 330 K.

3. Results and discussions

3.1 Structural and microstructural investigation

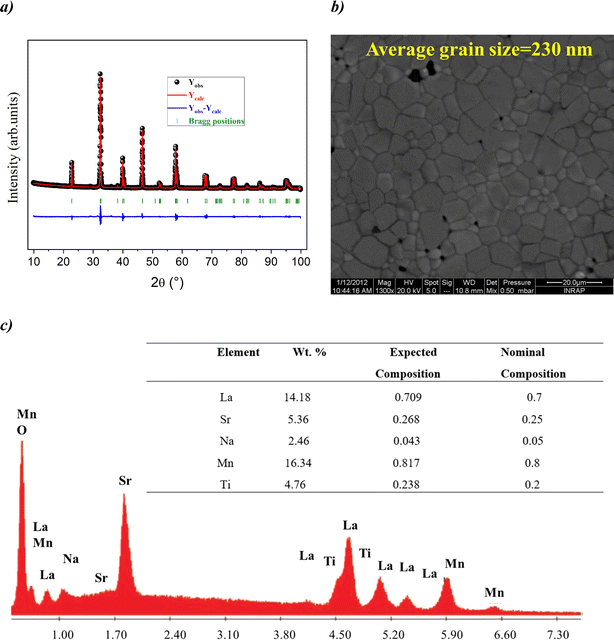
Fig. 1(a) reveals the X-ray diffraction pattern (Y_obs) that is conducted at room temperature for the studied LSNMTO system. The calculated X-ray data (Y_cal), using the Rietveld refinement and the difference between the observed and the calculated results (Y_obs − Y_cal) that are shown in Fig. 1 indicate that the elaborated ceramic reveals a perovskite structure. The studied LSNMTO perovskite crystallizes in a rhombohedral R3̄c structure. The attendance of fine and intense peaks reflects the good crystallization of the prepared powder. Using the Rietveld refinement results, the deduced structural parameters are illustrated in Table 1. The simulated diffraction refinement and the difference between the experimental and the theoretical data indicate a good structural adjustment (χ² = 4.83, R_F = 6.55%, R_p = 4.9% and R_wp = 7.6%). The calculated structural lattice parameters are a = b = 5.531 (2) Å, c = 13.416 (1) Å, and the cell volume V = 355.56 (1) ų. The deduced bond angles and bond distances values are respectively θ_{Mn/Ti–O–Mn/Ti} = 165.13° and d_Mn/Ti–O = 1.965 Å. For our case, the substitution in the Mn site by diamagnetic Ti ions raises the lattice structural parameters. This result is mainly accompanied by the distortion of the hexagonal structure due to the appearance of elongation along both the ‘a’ and ‘c’ axes (raising the cell volume).² As compared with the La_0.7Sr_0.25Na_0.05MnO₃ system,^2,12 we found from Table 1 that the substitution of the material with a concentration of x = 0.2 has affected the average cationic radius (〈r_B>〉 = 0.629 Å), the tolerance factor t_G = 0.941, and the parameter W = 9.32 × 10⁻² that control mainly the hopping conductivity and the electrical behavior of the material. To gain more insight into the microstructural response of LSNMTO, scanning electron microscopy (SEM) characterization combined with energy dispersive analysis of X-rays (EDAX) is conducted to study the microstructures and the chemical composition of the material. From Fig. 1(b), the obtained SEM photograph indicates that a dense microstructure with large grains and clear grain boundary regions characterize the sample. Besides, the estimated average grain size for LSNMTO is around 230 nm. From Fig. 1(c) (expected chemical composition of the used elements), the measurements confirm the correspondence between the expected and the nominal cationic compositions for LSNMTO. Therefore, it is reasonable to assume that the Ti element is substituted for Mn in the studied sample.

Fig. 1 X-ray diffraction results of the elaborated manganite structure (a). The scanning electron microscopy (SEM) image of the studied material (b). Results of EDAX analysis of La_0.7Sr_0.25Na_0.05Mn_0.8Ti_0.2O₃ manganite (c).

Table 1 Rietveld refinements results for LSNMTO compound

a (Å)	5.531 (2)
c (Å)	13.416 (1)
Cell volume (Å^3)	355.56 (1)
B(La/Sr/Na) (Å^2)	0.604 (3)
B(Mn/Ti) (Å^2)	0.218 (2)
B(O) (Å^2)	1.489 (5)
dMn/Ti–O (Å)	1.965
θMn/Ti–O–Mn/Ti (°)	165.13
〈rB>〉 (Å)	0.629
tG	0.941
W (10^−2)	9.32
Rwp (%)	7.6
Rp (%)	4.9
RF (%)	6.55
χ^2	4.83

---

3.2 Magnetic investigation

To evaluate the characteristic Curie temperature T_C of LSNMTO, the evolution of the magnetization M(T) as a function of the temperature is measured over a large temperature range from 10 K to 330 K. In the present work, the curve of M(T) is demonstrated in Fig. 2. We found that LSNMTO displays only one magnetic transition from the ferromagnetic (FM) to the paramagnetic (PM) states. A sharp increase in the magnetization is detected near T_C that can be attributed to the alignment of spins to FM order. To estimate the value of T_C, the evolution of dM/dT versus the temperature has been shown in Fig. 2. Accordingly, the plotted curve shows that the Curie temperature, which is defined as the inflection point of the dM/dT curve, is in the order of T_C = 125 K. For LSNMTO, the low value of T_C can be attributed to the decrease of the Ti⁴⁺ content, and the ensuing Mn³⁺–O–Mn⁴⁺ DE-FM interaction decrease. As a result, the Mn⁴⁺–O²⁻–Mn⁴⁺ super-exchange (SE) interaction effect in LSNMTO is improved after the substitution of Mn by Ti cations. The presence of Ti in LSNMTO reduces the number of available hopping sites and modifies the Mn³⁺/Mn⁴⁺ ratio. Because the Ti⁴⁺ cations are non-magnetic ions, there are no exchange interactions between Ti⁴⁺–O–Mn^4+/3+. This favors the SE interactions via oxygen 2p orbital. In this case, we can conclude that introducing a transition metal element in the Mn-site gives a negative contribution to the DE mechanism and reduces T_C. Mainly, the value of T_C is an essential factor in defining the potential applications of manganites, essentially in magnetic and electronic devices. For the LSNMTO, the obtained T_C of around 125 K (approximately −148 °C) has practical advantages and implications. Accordingly, a T_C = 125 K recommends that LSNMTO maintain its FM properties at relatively low temperatures, which makes it suitable for applications requiring operation in cryogenic environments (space technologies or other low-temperature environments). Generally, in manganite compounds a T_C = 125 K is beneficial for applications that necessitate low-temperature operation, important magnetoresistance effects, and the potential integration with superconducting materials. These characteristics make the LSNMTO manganite valuable in fields like cryogenics, spintronics, and advanced magnetic storage technologies.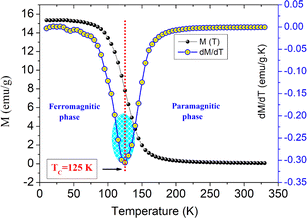

Fig. 2 Evolution of the magnetization M(T) and its derivate dM/dT versus the temperature for the studied system.

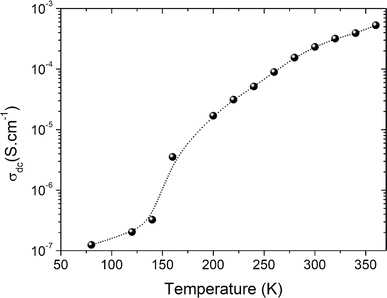
3.3 Electrical investigation

3.3.1 Direct current conductivity regime. To understand the transport characteristics of the elaborated LSNMTO substituted manganite, it is necessary to study the evolution of the electrical DC conductivity versus the temperature. Over the investigated temperature domain, the obtained results in Fig. 3 show that the conductivity σ_dc has increased versus the temperature increase, which confirms that the prepared material exhibits a semi-conductor nature over a large temperature domain (between 80 K and 360 K). Due to the strong correlation between the current transport mechanisms in the studied temperature domain, the electrical conductivity is constantly increasing.^1,2 Therefore, according to the literature, the DC electrical conductivity response and the appearance of semiconductor behavior in ceramics-type manganite are mainly related to the effects of the cationic disorder at low temperatures. In addition and based on Mott's theory, the electrical conductivity responses of the ceramics-type oxides originate from the contribution of the small polaron hopping conduction mechanism at elevated temperature values. According to Mott et al. works,^18,19 the presence of hopping mechanisms like the motion of small polarons to nearest neighboring sites (SPH) and variable range states (VRH) may be considered as the principal origin for the occurrence of a semiconductor nature in the materials. For numerous perovskite systems like the Lantanium manganites, that exhibit a general formula LaCaMnO₃, the activation of the small polaron hopping conduction processes has been confirmed beyond a certain characteristic temperature value named the half of the Debye temperature (θ_D/2). In this context, the formation of polaron charges with small size arises through the link of the disorder (E_D/2) and the binding energy values (E_P/2). Moreover, the remarkable effect of the cationic disorder contributes mainly to the activation of the variable range hopping conduction mechanism below θ_D/4, in which only a small amount of electrons exist around the Fermi level. As suggested by Mott et al.^18,19 and according to previous experimental investigations, the contribution of the SPH conduction process to the enhancement of the electrical conductivity behavior can be confirmed by plotting the variation of ln(σ_dcT) versus 1/(k_BT). In this case, the evolution of the electrical conductivity follows the relation below:^18,19
T is the absolute temperature, the factor σ₀ is a pre-exponential index, the parameter k_B represents the Boltzmann constant, E_a is the activation energy needed by each conduction process to be activated. The following relation gives the temperature dependence of such energy:²⁴
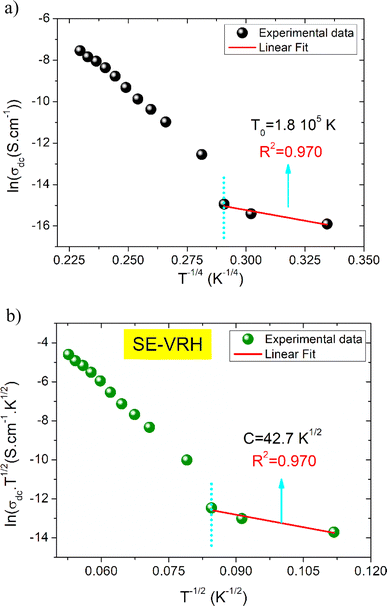
T₀ is a characteristic temperature proposed by Mott to get an idea about the density of states around the Fermi level.^18,19 The parameter p is a temperature exponent that gives information about the nature of the activated conduction process in the material. When the electrical conductivity is governed by the hopping over the nearest sites (NSH) the exponent p is nearly equal to one (p = 1). Therefore, the activation energy can be defined by the relation E_a = k_BT₀. However, when the electrical conductivity is governed by the Mott-VRH regime the exponent is equal to p = 1/4. This exponent is equal to p = 0.5 for the SE-VRH regime. For the under-investigated solid solution, the variation of ln(σ_dcT) as a function of 1/(k_BT) is shown in Fig. 4. The obtained curve displays the presence of two linear slopes at two different temperature domains. This kind of behavior indicates the activation of two main conduction mechanisms at two different temperature regions. The observed result for the studied system is similarly reported for another manganite system like the Pr_0.7Ca_0.3Mn_0.95Fe_0.05O₃ ceramic.²⁴ For our case, the observed linearity at high temperatures (region I) confirms the activation of the small polaron hopping conduction process via an activation energy E_a1 = 162 meV. In this case, the deduced value of the energy E_a1 is defined by the expression E_a1 = E_H + E_D/2. The deduced energy E_a2 = 22 meV is attributed to the activation of the variable range hopping conduction mechanism below a certain characteristic temperature value. At low temperatures and below θ_D/4 it has been reported that various types of mixed valence systems like the manganite oxides reveal a negligible hopping and binding energy value, as compared to the significant disorder energy that is related to the presence of cationic disorder in the material. Therefore, we can assume that the conduction properties of the materials, according to Mott's theory, are appropriately clarified via the cationic disorder ensuing from the difference in the local ions arrangement in the compounds.^18,19 As a result, we can propose the variable range hopping conduction process to examine the origin of the charge carrier displacement in the compound under investigation. In Fig. 5(a and b), we can conclude from the linear variation of ln(σ_dc) versus T^−1/4 that the variable range hopping transport process governs the electrical conduction of the studied ceramic solution. Two kinds of variable range hopping models are used in the literature to explain the behavior of the hopping of charge carriers in mixed-valence systems. For the case of the manganite, oxides both Mott-VRH¹⁸ and Shklovskii Efros-VRH models are used to interpret the electrical conductivity response below θ_D/2. The relations below respectively describe the DC conductivity below θ_D/2 for the Mott-VRH and the SE-VRH models:^18–20

The parameter σ₀ is a pre-exponential factor. C and T₀ are the SE-VRH and the Mott-VRH characteristic factors. In the case of the SE-VRH model, the Coulomb interaction between charges becomes important, which is not the case for the Mott-VRH model. In the literature, to estimate the exact nature of the VRH process below the temperature θ_D/2, it is necessary to plot the evolution of ln(σ_dc) versus T^−1/4 and ln(σ_dcT^1/2) versus T^−1/2. After that, it is important to compare the quality R² of the linear fitting slopes. According to the obtained results, we found that the application of both Mott-VRH¹⁸ and SE-VRH¹⁹ models gives the same linear slope quality of R² = 0.97. For similar curves (the same R²), it is essential to investigate the evolution of the local energy (E_loc(T)) versus the temperature. The determination of the temperature dependence of this energy can be effectuated using the following equation:
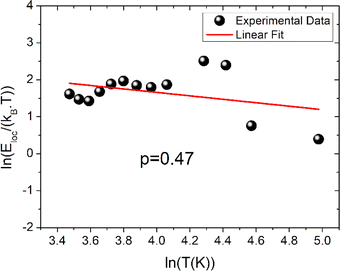
The function ρ(T) is the electrical resistivity. For our case, the exact nature of the VRH hopping process is determined from the linear slope of the local energy ln(E_loc(T)/k_BT) versus ln(T), which is plotted in Fig. 6. We found that the curve exhibits a linearity with a slope of p = 0.47 and an error of 0.03. Such result demonstrates the evidence of the contribution of the SE-VRH regime in the conductivity variation of the prepared sample below θ_D/2.

Fig. 3 Thermal evolution of the DC electrical conductivity of the compound from 80 K to 360 K.

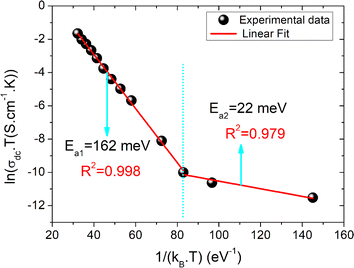Fig. 4 The evolution of the logarithm of the conductivity versus the inverse of the temperature and the deduced activation energy values.

Fig. 5 Evolution of ln(σ_dc) as a function of T^−1/4 and ln(σ_dcT^1/2) versus T^−1/2.

Fig. 6 Temperature dependence of the local energy.

3.3.2 Investigation of the conductivity spectra at various temperatures. On a variety of ceramic materials, the electrical conductivity spectra at numerous temperatures show characteristic evolutions characterized by universal power laws. The attendance of a dynamic electrical conduction domain in various material types, in which the conductivity increases versus the frequency can be, investigated through the Bruce and the Jonscher power laws.^21–23

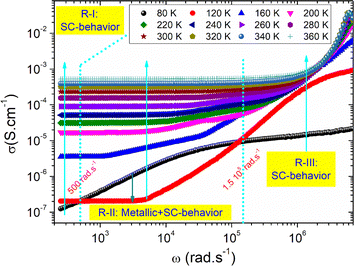
Fig. 7 shows the AC-conductivity spectra of the under-investigated sample in a large angular frequency domain from 251 rad s⁻¹ to 7 × 10⁶ rad s⁻¹ and for a temperature range between 80 K and 360 K. According to the obtained results, all the plotted spectra are characterized by the occurrence of a frequency dispersion domain and a DC conductivity plateau at low frequencies. Unusual behavior is observed at T = 80 K, in which we found the absence of the DC plateau. This kind of variation could be attributed to the presence of the electrode contribution at a low-frequency range. As a function of the frequency increase, the occurrence of a crossover from the low frequency-independent conductivity variation to the high frequency-dependent spectra shows the presence of a conductivity relaxation phenomenon, which moves towards higher frequency domains with increasing temperature. The material has uneven distribution, resulting in a remarkable conductivity dispersion. Mainly, the frequency dependence of the electrical conductivity can be investigated using the following power laws of Bruce and Jonscher:^21,23

σ(ω,T) = σ_dc(T) + A₁(T)ω^s₁ + A₂(T)ω^s₂

σ(ω,T) = σ_dc(T) + A₂(T)ω^s₂

A₁ and A₂ are two temperature-dependent factors. Parameters “s₁” and “s₂” are temperature-dependent frequency exponents. In our case, the occurrence of double Jonscher evolution has been reported for temperatures below 200 K. After that, the electrical conductivity spectra exhibit only a large conductivity plateau (σ_dc) and a superlinear-linear dynamic domain with only one power law variation. In this case, the electrical conductivity can be investigated using the Jump relaxation model. Therefore, the AC-conductivity spectra establish a considerable increase with the frequency increase, which is related to the short-range motion of free charge carriers in the studied sample.

Fig. 7 Electrical conductivity spectra at various temperatures for the prepared compound.

3.3.3 Investigation of the evolution of the AC conductivity versus temperature. Fig. 8 shows the variation of the AC conductivity of the material versus the temperature and at selected frequency values from 251 to 5 × 10⁵ rad s⁻¹. It is appreciated that the electrical AC conductivity at ω = 251 rad s⁻¹ rises as the temperature increases, confirming the semiconductor behavior of the material at very low frequencies. By increasing the frequency, we found that the electrical conductivity is improved over the explored temperature range, especially at low temperatures. The impact of the frequency variation is less pronounced at high temperatures. On this temperature side, the consequence of the frequency variation on the electrical conductivity is determined by the effect of the SPH conduction process. As a second effect, the frequency increase leads to the appearance of a meal–semiconductor transition at low temperatures and 120 K. This temperature value is very close to the deduced Curie temperature T_C from the magnetic results. Since the electrical conductivity of LSNMTO can switch between metallic and insulating states based on temperature, this property can be exploited in resistive switching devices and memory elements, providing non-volatile memory solutions. In correlation with the magnetic characteristics of manganites, the low T_C = 125 K for LSNMTO makes this compound ideal for temperature-sensing applications. As the material transitions from FM to paramagnetic at T_C = 125 K, the change in electrical conductivity can be used to detect temperature variations precisely. In this work, the increase of the electrical conductivity versus the frequency increase can be attributed to the increase in the density of hopping sites. At high temperatures and for ω < 5 × 10⁵ rad s⁻¹, the electrical AC conductivity is frequency independent. The frequency variation mainly affects the material's electrical response, especially at low temperatures.^25,26

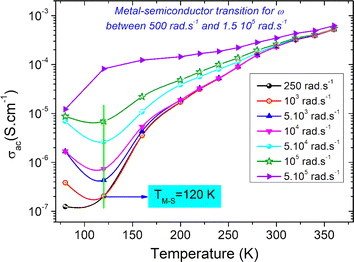Fig. 8 Thermal evolution of the AC electrical conductivity of the compound at various frequency values.

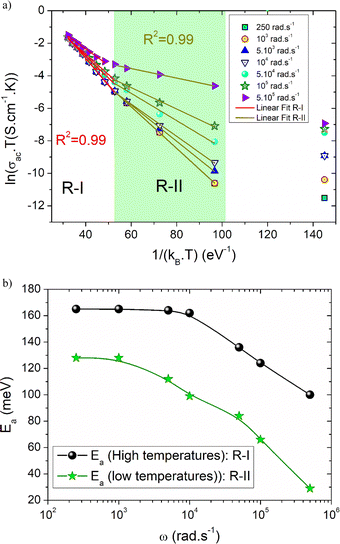
Fig. 9(a) shows the variation of ln(σ_acT) with temperature at various angular frequencies for the studied system. The resulting curves are used to determine the contribution of the SPH process to the electrical conductivity over the explored frequency range and to compare the disorder energy at low temperatures and the activation energy at high temperatures for each angular frequency value. It should be noted that the plotted curves at various frequencies reveal linear slopes that confirm the thermal activation of the SPH process at high temperatures. Via the frequency increase, we found that the slope of all curves does not mainly change. However, a remarkable change in the linear slope is observed in the second temperature region (R-II). For the studied compound, the deduced energy values at low and high temperatures (R-I, and R-II) at various frequencies are shown in Fig. 9(b). From the reported curves, we found that the frequency increase affects mainly the energy at low temperatures (disorder energy). Accordingly, E_a (low) has decreased from 128 meV at ω = 251 rad s⁻¹ to reach 29 meV at ω = 5 × 10⁵ rad s⁻¹. In the literature and according to Miller-Abraham's theory,²⁷ the observed variation in the energy can be attributed to changes in the mean separation path between the hop centers.

Fig. 9 Dependence of the AC conductivity on the inverse of the temperature at various frequency values (a); evolution of the activation energy versus the angular frequency (b).

3.4 Application of the Summerfield scaling approach on the electrical conductivity spectra

To characterize the grain relaxation mechanisms and grain boundaries in frequency-dependent behavior, we analyzed a growth model based on AC conduction data at low temperatures.

Fig. 10 demonstrates the scaled conductivity spectra of the LSNMTO compound from 200 to 360 K. The conductivity spectrum appears to be different from the single master curve. Deviation from Summerfield scaling confirms that the concentration of carriers is not constant and the relaxation mechanism is temperature dependent in the studied temperature range.^28–33 The same behavior is observed in other manganite compounds like the doped La-manganites. In the literature, Moualhi et al.^25,28,33 attributed the observed deviation of the electrical conductivity at high frequencies to changes in the number of carriers and changes in the number of available heat transfer channels.

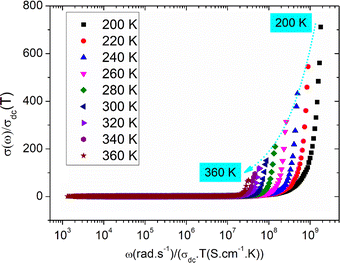Fig. 10 Summerfield scaling of the electrical conductivity between 200 and 360 K for the studied system.

3.5 Correlation of the physical properties of LSNMTO with some works of literature

In the literature,^2,6,28 it has been found that controlling the physical properties of manganites is crucial for optimizing their performance in various applications, especially where magnetoresistance, spin-dependent transport, and phase stability. This material family exhibits a wide domain of attractive physical characteristics, like CMR, charge ordering, and metal–insulator transitions, which make them candidates for numerous technological applications. As reported in Table 2, it is found that the physical properties of manganites are influenced by various factors like the substitution level, site, and the nature of the doping element. In this context, we can assume that the aforementioned factors control mainly the lattice, the space group, the Mn–O distance, the Mn–O–Mn angle, the A-site cation size, the cationic disorder, and the Mn³⁺/Mn⁴⁺ ratio. All those parameters are the main keys for designing materials with specific characteristics. Based on the results of Table 2, we can find that the ionic radii of the A-site cations affect the lattice parameters and the distortion degree in the Mn–O bond angles and lengths. This distortion modifies the bandwidth and electronic structure, affecting the electrical properties like the metal–insulator transition temperature. From Table 2, it is found that the nature of the existing cations in the A-site of manganites controls the space group. For LSNMTO, this material crystallizes in the rhombohedral structure with an R3̄c space group. As compared with the reported investigation by El. Kossi et al.¹² it is found that the substitution of the La_0.7Sr_0.25Na_0.05MnO₃ manganite by the Ti cation does not affect the space group of LSNMTO. Nevertheless, it modifies strongly the lattice and the structural characteristics of this compound. Accordingly, previous investigations confirm that the substitution with the Ti cations increases the lattice parameters.^2,12 As compared with La_0.7Sr_0.25Na_0.05MnO₃, our results indicate that the presence of Ti affects mainly the structural parameters (Mn–O–Mn angle (°) and Mn–O distance). Since the Ti⁴⁺ ionic radius is higher than that of Mn⁴⁺, the substitution of Ti⁴⁺ for Mn⁴⁺ distorts the hexagonal structure by an elongation along both the a and c axes, and therefore the presence of this element increases the cell volume. This increase is induced by the increase of the Mn–O bond length (Mn–O = 1.953 Å for La_0.7Sr_0.25Na_0.05MnO₃ and Mn–O = 1.965 Å for LSNMTO). Based on Table 2, it is observed that the material space group can change when we replace the Sr with the calcium Ca (migration from the R3̄c to the Pnma). When the Samarium Sm replaces the trivalent La, the crystallographic space group of manganites that contain the Sr element migrate from the R3̄c to the Pbnm space group. The aforementioned variations are due to the change in the distortion degree that depends in turn on the ionic radii of the A-site elements. The variation of the crystallographic space group is mainly accompanied by a strong variation in the electrical and magnetic properties of the manganite systems. Accordingly, introducing x = 0.2 of Ti in La_0.7Sr_0.25Na_0.05MnO₃ decreases T_C from 363 K to 125 K. More increases in Ti content x = 0.3 remain T_C in the order of 65 K, which makes this material family a candidate for cryogenic temperature sensing applications. In the same context, Table 2 shows that the Ti doping level increase affects the manganite behavior and the activation energy value. In the limit of the DC limit, LSNMTO exhibits a semiconductor behavior. As compared with other compounds like the La_0.7Sr_0.25Na_0.05Mn_0.8Ti_0.3O₃, we found that the variation of the Ti level favors the appearance of a metal–semiconductor transition at 415 K. For all the mentioned compounds in Table 2, we can found that the doping level in both La and Mn sites controls the Mn³⁺/Mn⁴⁺ ratio, influencing the electronic structure, the balance between the Mn–Mn, Mn–O–Mn interactions and the different magnetic interactions (FM, antiferromagnetic). This affects the activation energy needed by the small polaron charges to move between the nearest neighboring sites. Therefore, we can conclude from Table 2 that varying the nature, the site, and the level of the substitution alters the electronic bandwidth and hopping probability, affecting the manganite conductivity, including transitions between metallic and insulating states and the activation energy value. In this case, the conduction mechanism may shift from band-like conduction in the metallic phase to small polaron hopping or variable-range hopping in the insulating phase at higher Ti concentrations. The unique combination of tunable magnetic and electrical properties in doped manganites, especially with a low T_C, positions the manganites as promising candidates for a large range of future applications. From spintronic and energy-efficient sensor devices to advanced memory technologies, these oxides offer a versatile platform for innovation in both current and emerging technologies.

Table 2 Comparison of the physical results (structural, electrical, magnetic, activation energy, etc.) of the prepared material with results from the literature

Material	Structural properties			Magnetic properties		Electrical behavior			References
	Space group	Mn–O–Mn angle (°)	Mn–O distance (Å)	TC (K)	Magnetic behaviors (below TC)	Electrical behavior	TM–S (K)	Ea (meV)
La0.7Sr0.25Na0.05Mn0.8Ti0.2O3	R3̄c	165.13	1.965	125	FM	SC beyond 120 K	120 K (AC limit)	162	This work
La0.7Sr0.25Na0.05Mn0.8Ti0.3O3	R3̄c	164.24 (3)	1.97 (1)	65	FM	SC below 415 K	415	147	2
La0.7Sr0.25Na0.05MnO3	R3̄c	166.67	1.953	363	FM	—	—	—	12
La0.5Ca0.5MnO3	Pnma	161.16 (2)	1.937 (6)	222	FM + AFM	SC	—	153	6
La0.5Ca0.3Ag0.2MnO3	Pnma	160.59 (8)	1.951 (1)	264	FM	SC	—	54	28
La0.5CaMn0.8Nb0.2O3	Pnma	157.0847 (2)	1.9576 (6)	232 ± 5 K	FM	SC	—	249	34 and 35
Sm0.45Pr0.1Sr0.45MnO3	Pbnm	159	1.954	132	FM	SC below 140 K	140 K	168	36
La0.7Sr0.25Ka0.05MnO3	R3̄c	—	—	332	FM	SC	260 K	120	37 and 38
La0.7Sr0.25Na0.05Mn0.85Ti0.10O3	R3̄c	165.87	1.964	155	FM	SC	—	190	39

---

4. Conclusion

To summarize, we conduct a comprehensive examination of the structural, magnetic, and electrical characteristics of LSNMTO manganite derived from a solid-state reaction. The magnetic results indicate that the elaborated ceramic reveals a magnetic transition from the paramagnetic to ferromagnetic transition at T_C = 125 K. The conductivity isotherms are found to obey the double Jonscher power law. The DC-conductivity investigation shows the semiconductor nature of the studied system. The aforementioned behavior is investigated based on the small polaron hopping and the Shklovskii Efros variable range hopping models. The impact of the frequency variation on the activation energies is more pronounced at low temperatures. Deviations from the Summerfield scale confirm that the investigated solid solution has higher conductivity at high temperatures and frequencies. This is not only due to the increase in ion mobility but is closely related to a significant increase in carrier concentration.

Data availability

The data included in this manuscript are available and can be discussed (or shared), on request from the corresponding author.

Conflicts of interest

The authors declare that they have no known competing fnancial interests or personal relationships that could have appeared to infuence the work reported in this paper.

Acknowledgements

The authors are thankful to the Deanship of Graduate Studies and Scientific Research at Najran University for funding this work under the Growth Funding Program grant code (NU/GP/SERC/13/273-1).

References

1. Y. Moualhi, M. Smari, H. Nasri and H. Rahmouni, Combined transport and dielectric models and experimental characterization based on impedance spectroscopy for studying the microstructural and transport properties of electro-ceramic perovskites, Mater. Today Commun., 2024, 38, 108529.
2. Y. Moualhi, M. A. Alamri, A. Jbeli, N. A. Althumairi, S. El Kossi, R. B. Brahem and H. Rahmouni, Elaboration of La(Sr/Na) Mn(Ti)O₃ ceramic, structural, and morphological investigations, and contribution of direct and indirect interactions on transport properties, Ceram. Int., 2024, 50(9), 16587–16597.
3. P. Jena and P. K. Patro, Perovskite manganite materials: recent advancements and challenges as cathode for solid oxide fuel cell applications, Energy Mater. Struct. Prop. Appl., 2023, 163–183.
4. A. López, J. Tornos, A. Peralta, I. Barbero, F. Fernandez-Canizares, G. Sanchez-Santolino, M. Varela, A. Rivera, J. Camarero, C. León and J. Santamaría, Miguel romera, electrolyte gated synaptic transistor based on an ultra-thin film of La_0.7Sr_0.3MnO₃, Adv. Electron. Mater., 2023, 9(7), 2300007.
5. B. Zhang, P. Yang, J. Ding, J. Chen and G. Moog Chow, Anisotropic melting path of charge-ordering insulator in LSMO/STO superlattice, Adv. Sci., 2023, 10(4), 2203933.
6. Y. Moualhi, M. Smari, H. Rahmouni and K. Khirouni, Fundamental behaviors, and contributions of hopping and tunneling mechanisms to the transport characteristics of the La_0.5Ca_0.5MnO₃ phase separated perovskite, ACS Appl. Electron. Mater., 2020, 4, 4893–4902.
7. H. Belmabrouk and T. Alharbi, Dielectric properties and conduction mechanism of La_0.7Sr_0.25Na_0.05Mn_0.95Al_0.05O₃ perovskite manganite, J. Taibah. Univ. Sci., 2023, 17, 2204809.
8. Y. Moualhi, A. Mleiki, H. Rahmouni, K. Khirouni and A. Cheikhrouhou, Temperature, frequency and bias voltage effects on the electrical transport properties of (Sm-Pr-Sr) MnO₃ perovskite, Mater. Res. Bull., 2022, 155, 111976.
9. D. T. Bui, T. A. Ho, N. N. Hoang, T. L. Phan, B. W. Lee, N. T. Dang, D. T. Khan, L. V. Truong-Son, D. N. Petrov, B. T. Huy and D. S. Yang, Instability of the crystal and electronic structures due to hydrogenation influenced the magnetic properties of a La_2/3Ca_1/3MnO₃ manganite, Mater. Trans., 2023, 64(9), 2070–2076.
10. J. Lloyd-Hughes, C. D. W. Mosley, S. P. P. Jones, M. R. Lees, A. Chen, Q. X. Jia, E.-M. Choi and J. L. MacManus-Driscoll, Colossal terahertz magnetoresistance at room temperature in epitaxial La_0.7Sr_0.3MnO₃ nanocomposites and single-phase thin films, Nano Lett., 2017, 17, 2506–2511.
11. Y. Moualhi, R. M'nassri, M. M. Nofal, H. Rahmouni, A. Selmi, M. Gassoumi, N. Chniba- Boudjada, K. Khirouni and A. Cheikrouhou, Magnetic properties and impedance spectroscopic analysis in Pr_0.7Ca_0.3Mn_0.95Fe_0.05O₃ perovskite ceramic, J. Mater. Sci.: Mater. Electron., 2020, 31, 21046–21058.
12. S. E. Kossi, S. Mnefgui, J. Dhahri and E. K. Hlil, Critical behavior and its correlation with magnetocaloric effect in La_0.7Sr_0.25Na_0.05Mn_(1−x)Ti_xO₃ (0 ≤ x ≤ 0.1) manganite oxide, Ceram. Int., 2015, 41, 8331–8340.
13. A. Millis, Cooperative Jahn–Teller effect and electron-phonon coupling in La_1−xA_xMnO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 8434.
14. C. Zener, Interaction between the d-shells in the transition metals. II. Ferromagnetic compounds of manganese with perovskite structure, Phys. Rev. B: Condens. Matter Mater. Phys., 1951, 82, 403.
15. Y. Moualhi, R. M'nassri, M. M. Nofal, H. Rahmouni, A. Selmi, M. Gassoumi, N. Chniba-Boudjada, K. Khirouni and A. Cheikrouhou, Influence of Fe doping on physical properties of charge ordered praseodymium-calcium-manganite material, Eur. Phys. J. Plus, 2020, 135, 1–23.
16. J. E. R. Rocha, D. M. L. Calzonci, C. L. G. Soto, J. A. L. Gámez, J. S. J. Ferrer and S. G. Granados, Preparation and characterization of binder-free electrodes based on PEDOT and perovskites type La_(1−x) Sr_xMnO₃ for use in supercapacitors, J. Solid State Electrochem., 2023, 27, 3149–3162.
17. N. Paul, S. Vadnala, S. Bonam, A. Agrawal, S. R. K. Vanjari and S. G. Singh, Fabrication and characterization of suspended La_0.7Sr_0.3MnO₃ nanofibers for high-sensitive and fast-responsive infrared bolometer, J. Manuf. Syst., 2023, 33, 125008.
18. N. F. Mott, Conduction in non-crystalline systems: IV. Anderson localization in a disordered lattice, Philos. Mag., 1970, 22, 7–29.
19. N. F. Mott, Conduction in glasses containing transition metal ions, J. Non-Cryst. Solids, 1968, 1, 1–17.
20. A. L. Efros and B. I. Shklovskii, Coulomb interaction in disordered systems with localized electronic states, Mod. Prob. Cond. Matter Sci., 1985, 10, 409–482.
21. P. Bruce, High and low frequency Jonscher behavior of an ionically conducting glass, Solid State Ionics, 1985, 15(3), 247–251.
22. Y. Moualhi, M. Smari, H. Rahmouni, K. Khirouni and E. Dhahri, Superlinear dependence of the conductivity, double/single Jonscher variations and the contribution of various conduction mechanisms in transport properties of La_0.5Ca_0.2Ag_0.3MnO₃ manganite, J. Alloys Comp., 2022, 898, 162866.
23. A. K. Jonscher and M. S. Frost, Weakly frequency-dependent electrical conductivity in a chalcogenide glass, Thin Solid Films, 1976, 37(2), 267–273.
24. Y. Moualhi, M. M. Nofal, R. M’nassri, H. Rahmouni, A. Selmi, M. Gassoumi, K. Khirouni and A. Cheikrouhou, Double Jonscher response and contribution of multiple mechanisms in electrical conductivity processes of Fe-PrCaMnO ceramic, Ceram. Int., 2020, 46, 1601–1608.
25. Y. Moualhi, H. Rahmouni and K. Khirouni, Dynamics of charge carriers in doped manganite based on conductivity measurements and theoretical models, Phys. B: Condens. Matter., 2021, 616, 413129.
26. Y. Moualhi, H. Rahmouni and K. Khirouni, Usefulness of theoretical approaches and experiential conductivity measurements for understanding manganite-transport mechanisms, Results Phys., 2020, 19, 103570.
27. A. Miller and E. Abrahams, Impurity conduction at low concentrations, Phys. Rev., 1960, 120, 745.
28. Y. Moualhi, H. Rahmouni, M. Gassoumi and K. Khirouni, Summerfield scaling model and conduction processes defining the transport properties of silver substituted half doped (La–Ca) MnO₃ ceramic, Ceram. Int., 2020, 46, 24710–24717.
29. S. Murugavel and B. Roling, ac conductivity spectra of alkali tellurite glasses: composition-dependent deviations from the summerfield scaling, Phys. Rev. Lett., 2002, 89, 195902.
30. D. L. Sidebottom, Universal approach for scaling the ac conductivity in ionic glasses, Phys. Rev. Lett., 1999, 82, 3653.
31. B. Roling, Scaling properties of the conductivity spectra of glasses and super cooled melts, Solid State Ionics, 1998, 105, 185–193.
32. B. Roling, A. Happe, K. Funke and M. D. Ingram, Carrier concentrations and relaxation spectroscopy: new information from scaling properties of conductivity spectra in ionically conducting glasses, Phys. Rev. Lett., 1997, 78, 2160.
33. M. Smari, Y. Moualhi, R. Hamdi, H. Rahmouni and Y. Haik, Charge carrier motion and Mn-spin coupling defining the transport behaviors and the magnetic order at DySrCaMnO₃ polycrystalline ceramic, Mat. Sci. Semicon. Proc., 2024, 181, 108608.
34. Y. Moualhi, M. Smari and H. Rahmouni, Understanding the charge carriers dynamics in the La_0.55Ca_0.45Mn_0.8Nb_0.2O₃ perovskite: scaling of electrical conductivity spectra, RSC Adv., 2023, 13, 30010–30021.
35. M. Smari, Y. Moualhi, Y. Tong, S. Mansour and H. Rahmouni, Magnetic effect and chemical distribution study of LCMNO₃ perovskite by photoelectron spectroscopy, Phys. Scr., 2024, 99, 025907.
36. Y. Moualhi, A. Mleiki, H. Rahmouni and K. Khirouni, Investigation of the dielectric response and the transport properties of samarium and strontium-based manganite, Eur. Phys. J. Plus, 2022, 137, 406.
37. S. El Kossi, J. Dhahri and E. K. Hlil, Structural, magnetic and theoretical investigations on the magnetocaloric properties of La_0.7Sr_0.25K_0.05MnO₃ perovskite, RSC Adv., 2016, 6, 63497–63507.
38. M. Selmi, A. Smida and S. El Kossi, Effect of polaron formation in conduction and dielectric behavior in La_0.7Sr_0.25K_0.05MnO₃ oxide, J. Mater. Sci.: Mater. Electron., 2021, 32, 6014–6027.
39. S. El Kossi, F. I. H. Rhouma, J. Dhahri and K. Khirouni, Structural and electric properties of La_0.7Sr_0.25Na_0.05Mn_0.9Ti_0.1O₃ ceramics, Phys. B, 2014, 440, 118–123.

---