First principles approach and experimental exploration of a new double perovskite phase Sr₂(In_0.33 Sn_0.33Sb_0.33)₂O₆: evaluation of structural, optical, and dielectric properties

Abstract

A new double perovskite phase, Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆, was successfully synthesized via a solid-state reaction and comprehensively characterized using both experimental and theoretical techniques. Powder X-ray diffraction was used to determine the crystal structure, while scanning electron microscopy (SEM) revealed a high degree of densification and uniform grain distribution across the ceramic. Raman and Fourier-transform infrared (FTIR) absorption spectra of the powder present broad bands predominantly due to different stretching modes of the various SnO₃²⁻, InO₃²⁻ and SbO₃²⁻ octahedra in the region ν = 400–800 cm⁻¹. An analysis of the UV-Vis diffuse reflectance spectrum shows excellent optical transparency and gives an estimation of an optical gap E_g ∼ 3.6 eV on bulk Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆, making this material a promising candidate for optoelectronic devices. Density Functional Theory calculations further validated the experimental findings, confirming the crystal structure and providing insight into the electronic and vibrational properties. Impedance spectroscopy revealed non-Debye dielectric relaxation and confirmed typical negative temperature coefficient of resistance (NTCR) behavior, underscoring the material's potential for temperature-sensing applications. The primary conduction mechanism, modeled as correlated barrier-hopping (CBH), was complemented by an Arrhenius-type process with activation energies of 0.33 eV and 0.9 eV across two distinct temperature ranges.

---

1. Introduction

Stannate's derivatives with an ABO₃ perovskite-like structure continue to attract significant attention due to their exceptional electronic, optical and magnetic properties.^1–5 They are increasingly finding practical applications in many areas, including solar cells, LEDs, sensors and catalysts. With a bandgap ranging from 3.8 to 4.1 eV,³ the orthorhombic phase SrSnO₃ (SSO) meets the criteria for an ideal transparent conductive oxide (TCO) and could be considered as a serious contender to match the electro-optical properties of indium tin oxide (ITO).^6,7 Many attempts have been made over the past decades to address this challenge by introducing relevant dopants or substituents at metal sites. SSO doped with metals like Er, Sb, Nd, Fe, Cr, and Ta, behaves as an n-type semiconductor, displaying impressive electrical conductivity and high optical transmittance, exceeding 90% in the visible spectrum.^6–10 Conversely, when transition metals like La, Ni, and Co are incorporated, it exhibits p-type semiconducting behavior.¹¹ Notably, recent work has demonstrated that substituting a metalloid like Al at the B-site is not only feasible but also results in high-performing p-type TCO materials.¹²

The exploration of co-doping to create double or triple perovskite becomes a compelling option. Double perovskites have been the subject of extensive research due to their potential in various technological applications, owing to their intriguing blend of physical and chemical stability, alongside their noteworthy optical, electrical, and magnetic attributes.^13–15 These characteristics are intimately connected with their structural aspects, encompassing the ionic radii of cations, their oxidation states, and the degree of organization of cations within octahedral sites. Another research, which led to the development of the monoclinic double perovskites Sr₂Sn_0.8In_0.8W_0.4O₆ and Sr₂Sn_1.6In_0.2Cu_0.2O_6−δ.¹⁵ shows mixed electronic and ionic conduction characters. Theoretical study of Sr₂Sn_0.8In_0.8W_0.4O₆ suggests that it belongs to the category of semimetals.¹⁶ Notably, double perovskite antimonate such as co-substituted/doped A₂InSbO₆ (where A represents Sr or Ba) are attracting due to their interesting properties and their applications in the optical field as well as emerging materials in the realm of renewable energy.¹⁴ Furthermore, the proposal to use Sr₂SbInO₆ doped with Eu³⁺, Mn⁴⁺, Cr³⁺, and Fe³⁺ as a phosphor alongside commercially available phosphors for applications in white LEDs or optical temperature sensors has been made, focusing on their sensitivity in detection.^17–20 Given the industrial importance of developing innovative and more efficient materials in the field of optoelectronics, we have chosen to act on the chemical flexibility of SrSnO₃ and Sr₂SbInO₆ by co-doping Sn, Sb and In order to synthesize a new phase Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆. We aimed by the way to enhance the visible light transparency, phosphorus-hosting capacity, and thermal stability of a high-temperature dielectric and thermistor ceramic. Besides analytical and experimental approaches, ab initio simulations have emerged as an effective tool to search and analyze a diverse range of new materials, for their general physical properties.^21–23 An extensive combined experimental and theoretical study is undertaken to understand the material's vibrational and electronic characteristics, using both IR and Raman spectroscopy and UV-visible diffuse reflectance along with Density Functional Theory (DFT) calculations.

2. Experimental and computational details

2.1. Measurements of material and physical properties

Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ was synthesized by a solid-state interaction method. The precursor materials, including SrCO₃, SnO₂, In₂O₃, and Sb₂O₃, were mixed and pulverized into powder. Hexane was introduced and mixing was undertaken for one hour in an agate mortar and pestle. The mixture was calcined at 900 °C for 12 h. The resulting powder was pressed into pellets and sintered with intermittent grinding at multiple temperatures up to 1300 °C for 18 h, and then cooled to room temperature. The light gray polycrystalline solid product was subjected to X-ray diffraction (XRD) analysis using an X'Pert3 powder PANalytical diffractometer with a CuKα radiation source (λ = 1.54056 Å). The XRD data were first analyzed through profile fits using the Le Bail method, and the refinement realized in monoclinic P2₁/c space group presents satisfactory agreement factors. Whereas, the structural refinement was done by Rietveld method using Sr₂SbInO₆ structure model with the FullProf program. The XRD data were collected in continuous scan mode, with 2θ ranging from 15° to 110° and a step of 0.01° per 30 seconds. The infrared (IR) spectrum of the perovskite was recorded using a Bruker FTIR spectrophotometer Tensor 27 with the KBr pellet technique over a range of 4000–400 cm⁻¹ and a resolution of 4.0 cm⁻¹. UV-Vis-NIR diffuse reflectance data was acquired with a Shimadzu UV-3101 PC spectrophotometer covering the range from 300 to 2500 nm. Morphological investigations of the sample were conducted using a Jeol JSM IT-100 Scanning Electron Microscope. A room temperature Raman spectroscopy study was carried out using a Horiba Labram HR 800 monochromator. A Solartron SI 1260 impedance analyzer was used to perform impedance spectroscopy measurements covering a frequency range from 100 to 5 MHz, over a temperature range of 393 K to 673 K. Silver electrodes were deposited on both sides of a cylindrical pellet with a diameter of 8 mm and a thickness of 1.2 mm. The latter is placed in a temperature control system for measurements.

2.2. Computational details

First-principles Density Functional Theory (DFT)^24,25 calculations were conducted on Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ utilizing the Generalized Gradient Approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE)²⁶ functional for exchange and correlation energies, as implemented in the CRYSTAL23 software.²⁷ The all electron wave-functions were described using a Gaussian basis set, specifically a 6-31d1G for oxygen, a 97-63111d631G for antimony and tin, a 97-641d51 for strontium and a 97-631111d631G for indium.²⁸ A thorough optimization of all atomic coordinates and lattice parameters was achieved via conjugate gradient energy minimization, with a force tolerance threshold of 10⁻⁴ eV Å⁻¹ for structural relaxation. To thoroughly assess the thermodynamic properties of this novel phase, we constructed several structural models reflecting varied Sn/Sb and Sn/In configurations. These calculations were executed in an adequately sized super-cell, designed to capture the statistical distribution of different Sn/Sb and Sn/In metal sites. The vibrational properties were then performed at 0 K and at the Γ point within the harmonic approximation using the analytic Coupled Perturbed Kohn–Sham (CPKS) method.^29–31

3. Results and discussion

3.1. Structural and morphological properties

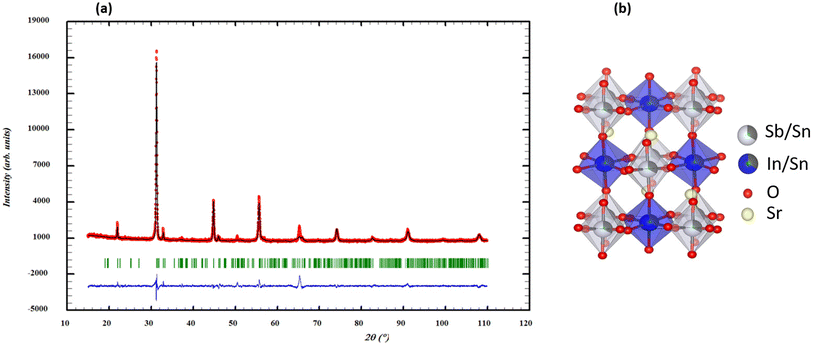
The stability of the crystal structure in Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ was first evaluated by calculating the Goldschmidt tolerance factor (t) using the Shanon radius of the different elements (r_Sn⁴⁺ = 0.69 Å, r_In³⁺ = 0.80 Å, and r_Sb⁵⁺ = 0.60 Å).³² The calculated value of t = 0.958 suggests a possible reduction in symmetry.³³ The reduced monoclinic symmetry (P2₁/c) results from the deformation of the ideal cubic perovskite, following a modification of the crystal structure by co-doping of Sn, In an Sb in Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆.³³ The auto-indexing of the PXRD pattern of the sample using the DICVOL software from the FullProf suite³⁴ reveals monoclinic symmetry with the following unit cell parameters: a = 5.450 Å, b = 5.720 Å, c = 9.700 Å and β = 123.53° as the best proposal. The search-match analysis using the ICDD PDF4+ database³⁵ indicates that the double perovskite Sr₂SbInO₆ is the most suitable structural model for our compound, exhibiting monoclinic P2₁/c symmetry and lattice parameters consistent with those previously suggested by the DICVOL program, in agreement with the calculated t value of 0.958.^34–36 During the Rietveld refinement, structural disorder within the octahedral sites was evidenced due to small variations in the radii of the cations within those sites (Fig. 1a). Consequently, a scenario was adopted for the distribution of Sb, In, and Sn cations, i.e. Sr₂(In_0.666Sn_0.334) (Sb_0.666Sn_0.334)O₆, considering a 1 : 1 pseudo-ordering of the B cations in the Wyckoff sites 2a and 2d of P2₁/c (Fig. 1b). The results of the refinement in a monoclinic unit cell indicate a good agreement between calculated and observed patterns and the double perovskite structure is confirmed with good reliability factors (Table 1). The analysis of bond lengths in Table 2 shows that (Sn/Sb)–O distances, ranging from 1.94 to 1.98 Å, are more consistent with Sb⁵⁺ cation distances reported by Gagné, rather than Sb³⁺.³⁷ However, our measured Sn/In–O distances are shorter, leading to BO₃²⁻ octahedra. Co-substitution with Sn, In and Sb in the B sites results in distorted (Sn/Sb)O₆ and (Sn/In)O₆ octahedra, causing crystal deformation, structural defects and changes in electronic and conduction properties.

Fig. 1 (a) Rietveld refinement of XRD pattern of Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ double perovskite (the black line corresponds to the experimental value, the red solid line is the fitted value, and the blue solid line is the difference between the experimental value and the fitted value). (b) The crystal structure of Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ double perovskite.

Table 1 Crystal data, structure refinement details and atomic positions determined through Rietveld refinement for new phase Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆

Atom	Sites	x	y	z	Uiso
Sr	4e	0.24100	0.47400	0.24000	0.1051
0.334Sn/0.666Sb	2a	0.0	0.0	0.0	0.0555
0.334Sn/0.666In	2d	0.5	0.0	0.5	0.0941
O1	4e	0.17600	0.01060	0.23900	0.4618
O2	4e	0.31100	0.20110	0.02800	0.251
O3	4e	0.26170	0.73220	0.04000	0.1225
Lattice parameters: a = 5.4502(3) Å, b = 5.72056(7) Å, c = 9.7006(7) Å and β = 123.53(1)°, RB(I) = 4.4886, χ^2 = 2.0868

---

Table 2 Experimental and modeled M–O distances as well as relative errors in %

Distances	Exp. (Å)	Mean calc. (Å)	Relative error (%)
(Sn/In)–O1	2 × 2.1430(3)	2.169	1.2
(Sn/In)–O3	2 × 2.0393(1)	2.145	4.1
(Sn/In)–O2	2 × 2.0899(1)	2.123	2.9
(Sn/Sb)–O2	2 × 1.9395(2)	2.046	7.1
(Sn/Sb)–O1	2 × 1.9600(2)	2.077	4.4
(Sn/Sb)–O3	2 × 1.9800(1)	2.068	4.5

---

To better understand the electronic structure of this new phase and confirm its structural properties, we decided to conduct further investigations using theoretical calculations with the GGA-PBE functional, along with all-electron Gaussian wave functions, implemented in the CRYSTAL23 software,²⁷ as specified in the computational details section. To accurately replicate the experimental structure, we created a series of supercell models based on the most likely experimental model, the double perovskite P2₁/c. We also explored a triple perovskite model, also with P2₁/c symmetry, using the XRD data provided in Table S1.† Further details on the construction of these models and the results of structural relaxations can be found in the ESI (Table S1 and Fig. S1†). Table S1† shows that the double perovskite (O6) models exhibit greater stability compared to the triple perovskites (O9), with a small energy difference of 94 meV. We also note that the energies of all the considered double perovskite models are well below the thermal activation energy threshold of 25 meV. Although the possibility of polymorphism exists, it appears to be contrary to the potential for stabilization at high temperatures. The formation free energy calculations as a function of temperature, based on the double perovskite model and the reaction: SrSnO₃ + Sr₂SbInO₆ → 3/2 Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆, clearly demonstrate that synthesis becomes feasible above 500 K (Fig. S2†). This strong correlation reinforces the validity of the experimentally proposed structural model and the statistical distribution of Sn/In and Sn/Sb across the 2d and 2a sites, emphasizing the significant configurational entropy at the B-sites. These findings provide solid evidence in support of the high-temperature stability of the new double perovskite phase.

Table S1† offers a comparative analysis of the experimental and theoretical average lattice parameters, including their relative errors. The results exhibit excellent congruence for the b, c, and β cell parameters, with discrepancies below 3.6%. However, the reproduction of the a parameter shows a larger deviation of 6%. To investigate this discrepancy, Table 2 contrasts the mean Sn/In–O and Sn/Sb–O bond lengths from the models with the experimental data. A general overestimation in the modeled distances compared to experimental predictions, possibly due to the functional employed is observed. A quite good alignment is seen for all Sn/In–O bonds, Sn/Sb–O1, and Sn/Sb–O3, with errors within 4.5%. Yet, the Sn/Sb–O2 bond length is notably overestimated (by 7%) in the calculations. This may be ascribed to the inherently challenging accurate positioning of oxygen atoms in Rietveld refinement, as oxygen's lighter atomic weight compared to elements like Sn, Sb, In, and Sr impacts the precision of their determined positions especially when defects or impurities are observed. The latter point will be further discussed below.

3.2. Crystallite size and microstrain

The Williamson–Hall method was employed to estimate the size of crystallites and lattice strain in the bulk. This method is expressed by the equation: β cosθ = K × λ/D + 4ε sinθ, where β represents the full width at half maximum (FWHM) in radians, θ denotes the diffraction angle, λ stands for the X-ray wavelength, K is a shape constant (0.9), D indicates the crystallite size, and ε represents the micro-strain. In calculating the crystallite size, instrumental broadening was considered. An empirical linear equation was then applied to the experimental data. Utilizing the intercept and slope of this linear plot, the average crystallite size and micro-strain were determined in the annealed sample. The crystallite size was calculated to be 46 nm, and the lattice strain was measured at 1.15 10⁻³ (Fig. S3†). Interestingly, the micro-strain increased from 1.74 10⁻³ in SrSnO₃ to 2.61 10⁻³ following the doping of Sn (+IV) with 5% In (+III)³⁸ and subsequently decreased to 1.15 10⁻³ upon co-doping with In (+III) and Sb (+V) in Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆. These variations in strain values arise from differences in the ionic radii of the elements involved. Furthermore, an analysis of the scanning electron microscope (SEM) image (Fig. 2a) reveals the presence of a wide distribution of grains. This is due to agglomeration, which is the result of high sintering temperatures. The relative particle size histogram of the Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ sample annealed at 1300 °C is displayed in Fig. 2a. To obtain statistics on grain sizes, Image J software was employed,³⁹ and measurements were taken for at least 30 grains with size varying from 50 to 120 nm. The average grain size within the sample was estimated to be approximately 70 nm, a value somewhat higher than that determined by XRD analysis (46 nm). This discrepancy is attributed to the fact that the former reflects the size of aggregates, while the latter pertains to the size of coherent domains within the particles.⁴⁰ By applying the relationship N = r_SEM/r_X-ray, we calculate the number of coherent diffraction domains within a particle. The results indicate that, on average, a particle comprises no more than 1.52 coherent diffraction domains. Table S2† presenting the EDX analysis results, reveals that the chemical composition of the compound closely aligns with the expected atomic percentages (Fig. 2b). The presence of carbon during the experimental analysis is likely due to the propensity of stannates to develop carbonates on their surfaces.⁴¹

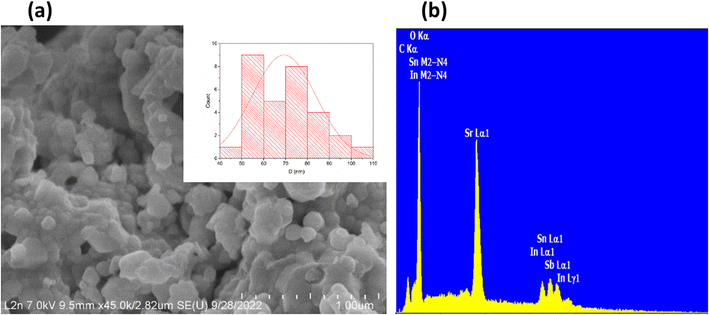Fig. 2 (a) SEM image (b) EDS spectrum of the Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ perovskite, In insert particle size histogram (b) EDX spectra.

3.3. FTIR and Raman spectroscopies

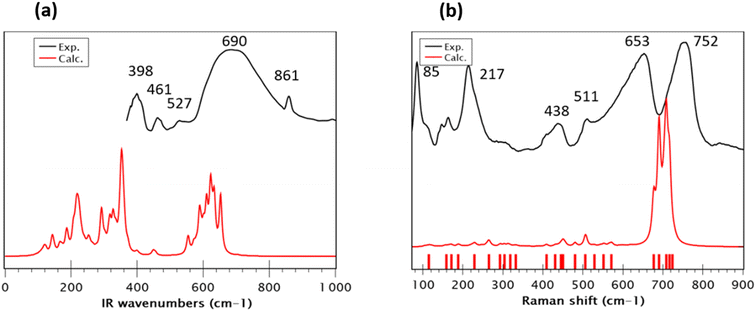
The FT-Infrared spectrum of Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ was recorded at room temperature, covering the wavenumber range of 400–4000 cm⁻¹. The modeling of the vibrational spectra (IR and Raman) of the new phase Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆, indicates that all its internal normal modes are located below 800 cm⁻¹. For better clarity and to facilitate an effective comparison between theory and experiment, we limited the frequencies range in Fig. 3a. In the 550–750 cm⁻¹ region of experimental spectrum, a broad absorption band is predominantly assigned to the antisymmetric stretching modes of the various BO₃²⁻ octahedra (SnO₃²⁻, InO₃²⁻ and SbO₃²⁻) in agreement with previously published findings.^16,42,43 Moreover, both spectra exhibit similarities with those reported in the literature for SrSnO₃.⁴⁴ Experimental peaks at around ∼450 and ∼400 cm⁻¹ reasonably correspond to the theoretical calculations at ∼450 and 325 cm⁻¹, respectively. These normal modes are related to the bending of the O–B–O bonds. Interestingly, the calculated wavenumbers show a redshift compared to the experimentally observed frequencies, diverging from the usual overestimation typically seen when employing a harmonic potential. This discrepancy can be initially attributed to the previously noted overall overestimation of the B–O bond distances and, secondly, to the fact that the vibrational calculations were performed only at the Brillouin zone center, neglecting the dispersion effects near this point, even though supercell calculations somewhat account for disorder. The disordered metallic nature of the compound and the nanoscale crystallite size suggest significant dispersion impacting the broadness of the peaks. Furthermore, not accounting for the longitudinal-optical (LO) and transverse-optical (TO) splitting, which results from long-range coulombic interactions in the calculations, might contribute to these underestimated frequencies. Other perovskite variants like BaTiO₃ and SrTiO₃ often exhibit this phenomenon, which could account for the observed differences in our study.⁴⁵ The experimental IR spectrum shows vibrations at 527, 859, 1070, 1468 and 1772 cm⁻¹ (Fig. S4†), are likely due to the formation of carbonate groups during the calcination of SrCO₃, as previously reported by Hong et al.⁴⁶ The Raman spectral analysis of the Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ compound (excitation wavelength 633 nm), depicted in Fig. 3b, provides critical insights into the perovskite's local structure.⁴⁷ However, accurately assigning all vibrational modes in bulk samples remains a complex task. The Raman spectrum, recorded at room temperature alongside the calculated spectrum, reveals significant findings. In the high wavenumber region (>500 cm⁻¹), two broad experimental bands at approximately 653 and 752 cm⁻¹ correspond to theoretical modes at 717, 708, 703, 690, and 677 cm⁻¹. This region is correlated with the breathing modes of the BO₆ octahedra. The higher wavenumber modes (>700 cm⁻¹) are primarily associated with the stretching of B–O bonds within the BO₆ octahedra, particularly a main mix of Sn–O and In–O bonds. Modes in the range of 700–650 cm⁻¹ are assigned to the stretching of Sb–O and Sn–O bonds. These modes are illustrated in Fig. S5.† The sequence of symmetric stretching modes appears to be more influenced by differences in effective mass than by bond length. Nevertheless, the comparison of this Raman spectrum with that of SrSnO₃, as reported in the literature, which exhibits weak intensities in this region, suggests that the strong polarizability variations observed for this new phase are due to In–O and Sb–O bonds rather than Sn–O bonds.^41,44 The mid-range frequencies (500–400 cm⁻¹) combine stretching and bending motions, aligning with findings in related research.⁴⁸ In the lower wavenumber region (<300 cm⁻¹), the Raman spectrum displays long-range structural modes, with two prominent peaks at 217 and 85 cm⁻¹, which are absent in the calculated spectrum. These low-frequency modes, as pronounced as the higher-frequency ones, bear resemblance to those seen in double rock salt perovskites.^49,50 According to M. G. Masud et al.,⁵¹ these bands are indicative of the characteristic band patterns of the partially disordered monoclinic double perovskite structure. The experimental observation of these intense soft modes contrasts with their relatively muted presence in theoretical predictions. This discrepancy can be explained by the high polarizability calculated for Sb–O and In–O bonds, amplifying the intensity of harder modes and overshadowing the softer ones. The attribution of these modes to the presence of disorder is consistent with the fact that the Raman spectrum of a perfectly ordered model (model 8, Fig. S5†) also lacks these modes. It should also be noted that this model only exhibits just two intense hard modes, further confirming the synthesis of a disordered O6 model. Additionally, the nanometric particle size (40–70 nm), differing from the perfect crystal model in calculations, might introduce unaccounted surface effects, suggesting the need for a larger computational model for accurate depiction a task that is currently prohibitively expensive and challenging. Finally, the nanoscale particle size, in tandem with the presence of defects and metallic disorder, restricts phonon propagation, leading to broader Raman spectral bands. This is evidenced by an increased FWHM of these bands, similar to the phenomena observed in IR investigations. This analysis highlights the complex interplay between particle size, structural disorder and defect and their impact on the interpretations of the vibrational properties.

Fig. 3 Comparison between experimental and theoretical (a) infrared and (b) Raman spectra of Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆. The precise positions of the calculated frequencies are depicted as sticks for clarity and precision.

3.4. UV-visible diffuse reflectance spectroscopy

The Kubelka–Munk function, denoted as F(R) and calculated from the diffuse reflectance data, is expressed as F(R) = (1 − R)²/2R ≈ K/S, where R represents the diffuse reflectance, and S and K stand for the scattering and absorption coefficients, respectively. The determination of the optical band gap (E_g) of Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ was carried out using the Tauc model: (F(R) × hν)^p = A(hν − E_g), with E_g representing the band gap energy, A being a constant, and the exponent p specifying the type of transition, which is 2 for a direct transition and 1/2 for an indirect transition. The band structure, as delineated in PBE (Fig. 4a), reveals a direct energy gap of 1.8 eV, consistent with the semiconductor characteristics of this phase. Additionally, according to the band structure, an indirect gap transitioning from X → Γ and occurs at 2.0 eV, approximately 200 meV higher. The density of state projection curves indicate electronic transitions predominantly from O²⁻(2p) to the unoccupied states of metals In, Sn, and Sb (Fig. 4b). These metals contribute comparably at the bottom of the conduction band. It is also observed that the M–O bonds exhibit a degree of covalence, evidenced by the presence of metal states in the valence band, along with a significant influence of indium states mingling with the oxygen band (Fig. 4b).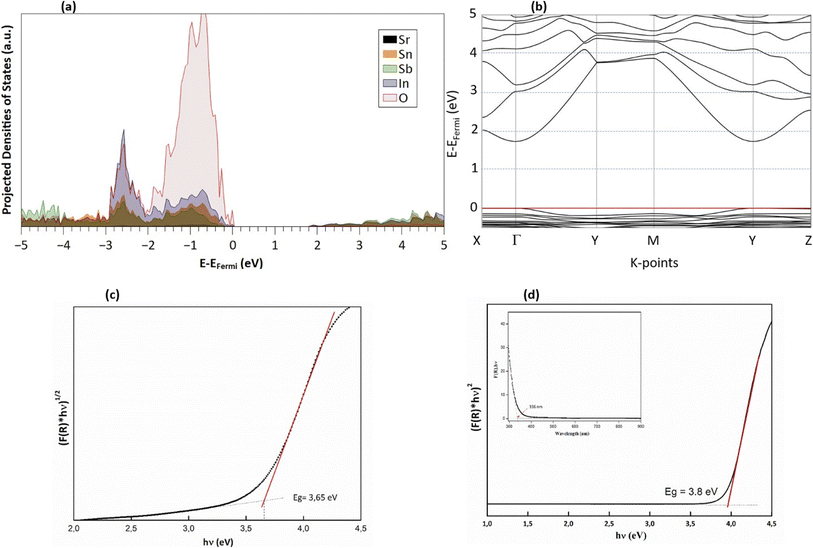

Fig. 4 (a) Calculated band structure, (b) projected densities of states (PDOS), (c) Tauc plot for the indirect band gap and (d) direct band gap estimation from experimental reflectance data.

The band gap energy (E_g) of Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ is obtained through the extrapolation of the linear section of the [F(R) × hν]^p plot. This analysis yields an optical band gap of 3.65 for indirect transition (Fig. 4c) and 3.8 eV for direct transition, which aligns with the E_opt value that calculated using the absorption edge's wavelength (Fig. 4d).⁵² The discrepancy between modeled and measured band gap is primarily due to the PBE-GGA functional, which is known to underestimate the measured optical gaps due to its poor treatment of exchange and correlation interactions.^44,53 Nevertheless, regardless of the absolute value of the gap, and as noted earlier, the direct and indirect gaps in DFT are relatively close, with a difference of only ∼200 meV. This proximity may explain why UV measurements can be fitted to both direct and indirect gaps, with an observed difference of approximately 300 meV. Although DFT may underestimate the absolute value of the band gap, it accurately describes the relationship between the two types of gaps, offering valuable insights into the material's electronic structure. In light of these results, one can conclude that this property makes it a promising candidate for technological applications, given its classification as a wide-gap non-magnetic insulator.

3.5. Complex impedance analysis

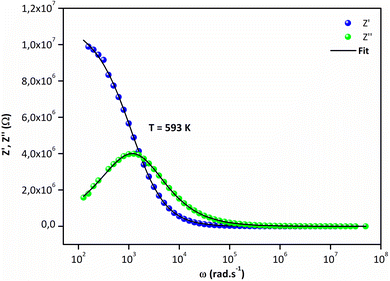
Fig. 5a and (b) report the frequency dependence of real Z′ and imaginary Z′′ impedance plots at various temperatures. It is observed in Fig. 5a that Z′ diminishes with enhancing temperature at lower frequencies, indicating an increase in the alternating current (AC) conductivity and the NTCR behavior.⁵⁴ At higher frequencies (f > 10⁴ kHz), the values of Z′ merge for all temperatures. Z′ is temperature-independent, which signifies the release of space charges in the material.⁵⁵ The dependence of the imaginary impedance (Z′′) as the function of frequency for different temperatures well illustrates the charge transport mechanism and the relaxation mode in Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ at different temperatures (Fig. 5b). The relaxation process appears to be influenced by immobile charge carriers at low temperatures and defects/vacancies at high temperatures. As the temperature increases, a shift of the relaxation peak occurs towards higher frequencies indicating a thermally dependent relaxation mechanism. Furthermore, the magnitude of this peak decreases consequently, suggesting a decrease in grain resistance with temperature. The width of the relaxation peak in Z′′ indicates the possibility of a distribution of relaxation times (Fig. 6).⁵⁶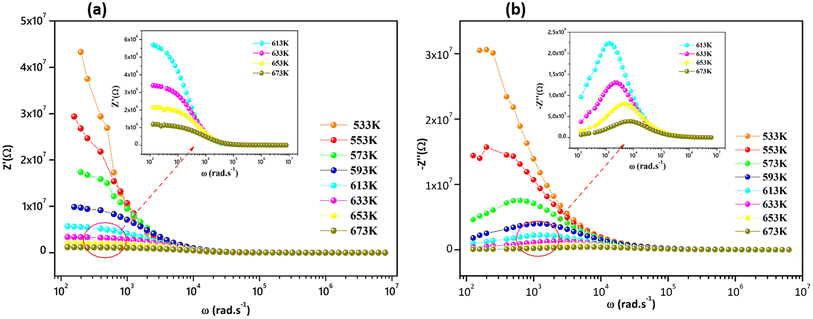

Fig. 5 (a) Variation of real part, and (b) variation of imaginary part of impedance with angular frequency at several temperatures.

Fig. 6 Frequency dependence of (a) Z′ and (b) Z′′ at 593 K.

Fig. 7 displays the Cole–Cole plots (Z′′ vs. Z′) at various temperatures. A semicircular arc with a center below the Z′ axis is displayed in every plot. The temperature-dependent poly-dispersive character of dielectric relaxation in non-Debye behavior in Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ is confirmed by the tilt parameter α in the Cole–Cole diagram, which quantifies the distribution of relaxation durations, being non-zero. The majority of relaxors are complex perovskite structures with two or more ions in the A- and B-sub-lattices having complete or partial abnormalities.⁵⁷ The material contribution coming from a parallel combination of grain capacitance (C_g), constant phase element (CPE1), and resistance (R) to grain can be responsible for high-frequency semicircular arcs. Values (R, C_g, Q, and α) obtained from an experimental fit of the data are displayed in Table S3.† Fig. 7 depicts the corresponding electrical circuit. The insert's graphical depiction demonstrates how resistance R drops as temperature rises, this behavior is characteristic with negative temperature coefficient of resistance (NTCR) compounds widely used as thermistors, i.e. temperature sensors in industrial and medical domains because of their high-temperature sensitivity, durability, and cheap.^58,59

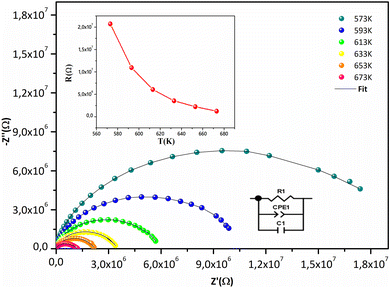Fig. 7 Nyquist plot of Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ at different temperatures and equivalent circuit of fitting data for the system. The resistance plot as a function of temperature in inset.

3.6. AC conductivity study

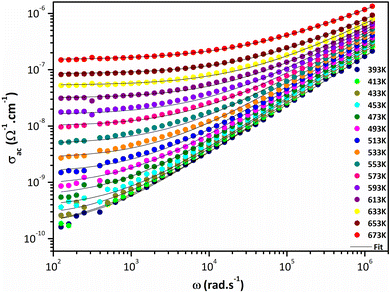
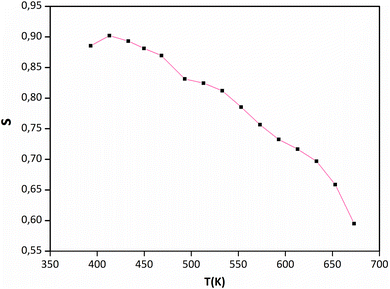
Fig. 8 shows temperature and frequency variations of the sample's conductivity. AC conductivity corresponds to the frequency dispersion zone, which is shifts to higher frequencies and at higher temperature, corresponds to the DC conductivity.⁵⁶ As the temperature increases, the DC conductivity value increases, indicating that the sample exhibits semiconductive behavior (Fig. 8).

Fig. 8 Variation of AC conductivity as a function of frequency at several temperatures.

Jonscher's universal power law explained by σ_ac(ω) = σ_dc + Aω^S is a useful model for describing the conduction process in dielectric materials, especially in terms of their alternating current conductivity. A is a constant influenced by temperature, ω represents angular frequency, “s” signifies the level of interaction among mobile charge carriers and their environment, and σ_dc refers to direct current conductivity. Fig. 9 portrays the connection between the temperature and the frequency exponent “s”. Within the temperature range of 400 to 473 K, the exponent remains consistently around 0.9. This pattern is indicative of conduction through tunneling without the need of thermal activation. The value of “s” remains stable during this period and then gradually decreases before experiencing a more pronounced decline. This reduction occurs in two phases: a subtle one between 473 and 593 K, followed by a more substantial drop between 593 and 673 °C. This suggests that in this material, the grain conduction phenomenon aligns with the correlated barrier hopping (CBH) behavior.⁶⁰

Fig. 9 Temperature dependence of “s” for Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆.

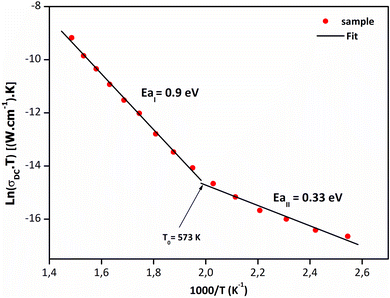
The DC conductivity of the sample was related to temperature by the transformed equation: Lnσ_dc = Lnσ₀ + [−E_a/(1000/T)]. Fig. 10 indicates an Arrhenius-type conduction in the temperature range 393–673 K. As shown in the Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆, the temperature dependency indicates two conduction mechanisms that are active in the sample. The activation energy is 0.33 eV at low temperature and 0.9 eV at high temperature. As above mentioned in the electrical study section, the dielectric loss factor reaches its maximum at this same critical temperature when the transition from one section to the next is noticed. Such a low activation energy value results from the connection between the polarons breaking and migrating freely as the temperature rises more. A shift in the charge carrier from a single to a double polaron, or from a small to a large one can account for the change in the slope at 573 K.

Fig. 10 Arrhenius plot of Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆.

3.7. Modulus analysis

Fig. 11, displays how the angular frequency affects the real part of the electrical modulus (M′) and the imaginary part (M′′) at various temperatures. At lower temperatures, M′(ω) follows a less dispersed pattern, almost appearing linear.⁶¹ However, as the temperature increases, M′(ω) starts to display a dispersive behavior, where the value of M′ increases and reaches a maximum saturation point at different temperatures (Fig. 11a and b). When looking at lower frequencies, the low values of M′ indicate the absence of electrode and/or ionic polarization effects and suggest the migration of polarons over longer distances due to the slow reversal of the electrical field. From 593 K onwards, the behavior of M′′ displays a broad peak. The shape of the M′′(ω) curves implies a relaxation process with a shift towards higher frequencies with increasing temperature, indicating the thermally activated nature of the relaxation time.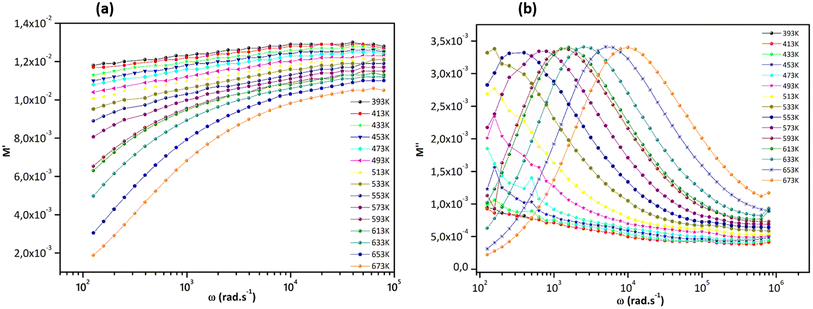

Fig. 11 (a) Dependence of M′ and (b) M′′ of Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆ versus frequency at different temperatures.

4. Conclusion

A transparent semiconductor perovskite oxide, Sr₂(Sn_0.33Sb_0.33In_0.33)₂O₆, was synthesized via solid-state reaction and subjected to comprehensive experimental and theoretical analyses to assess its structural, microstructural, optical, vibrational, electronic, and dielectric properties. XRD and EDX results confirmed the excellent crystalline quality and accurate elemental composition of the prepared sample. DFT–PBE calculations, through extensive structural, thermodynamic, and vibrational studies, validated the synthesis and structural refinement of this new phase, classifying it as a double perovskite crystallizing in the P2₁/c space group. Experimental UV-visible measurements demonstrated high optical transparency across a broad spectral range, with an indirect bandgap of 3.65 eV, supported by theoretical calculations.

According to DOS curves, electronic transitions predominantly occur from O²⁻ (2p) to the unoccupied states of In, Sn, and Sb, indicating the material's potential for optoelectronic applications. Further insight into the conduction mechanism was gained by analysing the frequency-dependent behaviour of σ_ac for grain response, using Jonscher's universal power law at different temperatures. This analysis revealed that correlated barrier hopping is the predominant conduction mechanism. The temperature dependence of DC conductivity indicated two distinct conduction mechanisms, with activation energies of 0.33 eV and 0.9 eV below and above T = 573 K, respectively. Finally, electric modulus analysis confirmed the presence of dielectric relaxation. The observed decrease in resistance with increasing temperature aligns with the overall findings, suggesting that this material could be a promising candidate for high-temperature thermistor applications, relying on the NTCR (Negative Temperature Coefficient of Resistance) effect.

Data availability

The data that support the findings of this study are available on request from the corresponding author, Besma BELGACEM upon reasonable request.

Author contributions

Besma Belgacem: carried out material preparation, collection and data analysis and paper draft. Nabil Nasri: carried out the preparation of the material, and data optical analysis. Mouna Ben Yahia: drafted the theoretical section, participated in discussions, results interpretation, and manuscript revision. Abderrazek Ouslati: participated in impedance measurements, results' discussion and manuscript revision. Rached Ben Hassen: was responsible for the methodology, data curation, writing, visualization, validation and supervision. All authors have read and approved the final manuscript.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

Financial support from the Ministry of Higher Education and Scientific Research of Tunisia is gratefully acknowledged. The authors gratefully acknowledge the ICDD for financial support (Grant number: 09–04). The authors thank Dr Akram Alhussein, Université de Technologie de Troyes, Pole Technologique Sud Champagne, France for scanning electron microscope (SEM) measurements, energy dispersive X-ray (EDX) measurements. The authors thank Pr. Hammadi Khemekhem, University of Sfax, Faculty of Science of Sfax for the Raman measurements. The authors appreciate Ms. Hajer REBAI for linguistic editing and proofreading of the manuscript.

References

1. A. R. F. A. Teixeira, A. de Meireles Neris, E. Longo, J. R. de Carvalho Filho, A. Hakki and D. Macphee, et al., SrSnO₃ perovskite obtained by the modified Pechini method—Insights about its photocatalytic activity, J. Photochem. Photobiol., A, 2019, 369, 181–188.
2. L. Chantelle, A. L. Menezes de Oliveira, B. J. Kennedy, J. Maul, M. R. S. da Silva and T. M. Duarte, et al., Probing the Site-Selective Doping in SrSnO₃: Eu Oxides and Its Impact on the Crystal and Electronic Structures Using Synchrotron Radiation and DFT Simulations, Inorg. Chem., 2020, 59(11), 7666–7680.
3. B. Hadjarab, A. Bouguelia and M. Trari, Synthesis, physical and photo electrochemical characterization of La-doped SrSnO₃, J. Phys. Chem. Solids, 2007, 68(8), 1491–1499.
4. H. He, Z. Yang, Y. Xu, A. T. Smith, G. Yang and L. Sun, Perovskite oxides as transparent semiconductors: a review, Nano Convergence, 2020, 7(1), 32.
5. S. Barouni, A. Brahmia, H. Chaker, M. M. Maslov, A. Alhussein and R. B. Hassen, First-principles prediction of half metallic-ferromagnetism in La_0.25Sr_0.75Sn_0.4In_0.25Ru_0.35O₃ and enhanced experimental electrical and magnetic behaviours, Phys. Chem. Chem. Phys., 2024, 26(26), 18102–18112.
6. Q. Liu, J. Dai, X. Zhang, G. Zhu, Z. Liu and G. Ding, Perovskite-type transparent and conductive oxide films: Sb- and Nd-doped SrSnO₃, Thin Solid Films, 2011, 519(18), 6059–6063.
7. Q. Liu, F. Jin, G. Gao and W. Wang, Ta doped SrSnO₃ epitaxial films as transparent conductive oxide, J. Alloys Compd., 2017, 717, 62–68.
8. J. Kim, H. Yun, J. Seo, J. H. Kim, J. H. Kim and K. A. Mkhoyan, et al., Deep-UV Transparent Conducting Oxide La-Doped SrSnO₃ with a High Figure of Merit, ACS Appl. Electron. Mater., 2022, 26(7), 3623–3631.
9. M. Kumar Mahapatra, P. Singh, D. Kumar and O. Parkash, Synthesis, crystal structure, microstructure and electrical behaviour of systems Sr_1−x La_x SnO₃ and SrSn_1−x Ni_x O₃ (X ≤ 0·10), Adv. Appl. Ceram., 2006, 105(6), 280–284.
10. M. A. Sattar, M. Benkraouda and N. Amrane, First-principles investigation on the structural, electronic, vibrational and magnetic properties of the Co-substituted orthorhombic SrSnO₃, Phys. B, 2020, 590, 412216.
11. B. Raveau, The Perovskite History More than 60 Years of Research from the Discovery of Ferroelectricity to Colossal Magnetoresistance via High TC Superconductivity, Solid State Chem., 2007, 35, 171–173.
12. A. L. Ben, B. Belgacem, J. S. Filhol, M. L. Doublet, M. B. Yahia and R. Ben Hassen, New p-type Al-substituted SrSnO₃ perovskites for TCO applications?, Chem. Commun., 2020, 56(17), 2566–2569.
13. K. I. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Room-temperature magnetoresistance in an oxide material with an ordered double-perovskite structure, Nature, 1998, 395(6703), 677–680.
14. M. A. Amin, G. Nazir, Q. Mahmood, J. Alzahrani, N. A. Kattan and A. Mera, et al., Study of double perovskites X₂InSbO₆ (X = Sr, Ba) for renewable energy; alternative of organic-inorganic perovskites, J. Mater. Res. Technol., 2022, 18, 4403–4412.
15. A. Zouaghi, B. Belgacem, A. Alhussein, A. Brahmia and R. Ben Hassen, Study of the structural, optical, and electrical characteristics of Sr₂Sn_1.6In_0.2Cu_0.2O_6−δ mixed ionic-electronic conductor, J. Solid State Chem., 2023, 328, 124303.
16. B. Belgacem, M. M. Maslov, S. Kaya, I. H. Ali and R. Ben Hassen, Crystal chemistry, DFT calculation and optical properties of the double perovskite stannate Sr₂Sn_0.8In_0.8W_0.4O₆, J. Mol. Struct., 2022, 1259, 132716.
17. L. Li, X. Li, W. Xia, Y. Wang, F. Ling and S. Jiang, et al., Investigation on the optical sensing behaviors in single Eu³⁺-activated Sr₂InSbO₆ phosphors under green light excitation, J. Alloys Compd., 2022, 906, 164322.
18. Y. Xie, X. Geng, J. Guo, W. Shi, Q. Lv and J. Kong, et al., Luminescence of a novel double-perovskite Sr₂InSbO₆: Eu³⁺ orange-red-emitting phosphor for white LEDs and visualization of latent fingerprints, Mater. Res. Bull., 2022, 146, 111574.
19. M. Zhao, S. Liu, F. Zhao, H. Cai, Z. Song and Q. Liu, Cr³⁺-doped double perovskite antimonate, efficient and tunable phosphors from NIR-I to NIR-II, Inorg. Chem. Front., 2022, 9, 4602–4607.
20. D. Liu, G. Li, P. Dang, Q. Zhang, Y. Wei and L. Qiu, et al., Highly efficient Fe³⁺-doped A₂BB′O₆ (A = Sr²⁺, Ca²⁺; B, B′ = In³⁺, Sb⁵⁺, Sn⁴⁺) broadband near-infrared-emitting phosphors for spectroscopic analysis, Light: Sci. Appl., 2022, 27(1), 112.
21. M. Y. Sofi and D. C. Gupta, Scrutinized the inherent spin half-metallicity and thermoelectric response of f-electron-based RbMO₃ (M = Np, Pu) perovskites: a computational assessment, Sci. Rep., 2022, 12, 19476.
22. M. Y. Sofi, M. S. Khan and J. Ali, et al., Exploring the lead-free halide Cs₂MGaBr₆ (M = Li, Na) double perovskites for sustainable energy applications, Sci. Rep., 2024, 14, 5520.
23. M. Y. Sofi, M. S. Khan and J. Ali, et al., Unlocking the role of 3d electrons on ferromagnetism and spin-dependent transport properties in K₂GeNiX₆ (X = Br, I) for spintronics and thermoelectric applications, J. Phys. Chem. Solids, 2024, 112022.
24. P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136(3B), B864–B871.
25. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140(4A), A1133–A1138.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 28(18), 3865–3868.
27. A. Erba, J. K. Desmarais, S. Casassa, B. Civalleri, L. Donà and I. J. Bush, et al., CRYSTAL23: A Program for Computational Solid State Physics and Chemistry, J. Chem. Theory Comput., 2023, 24(20), 6891–6932.
28. J. Grant Hill, Int. J. Quantum Chem., 2013, 113, 21–34.
29. M. Ferrero, M. Rérat, R. Orlando and R. Dovesi, The calculation of static polarizabilities of 1-3D periodic compounds. the implementation in the crystal code, J. Comput. Chem., 2008, 29(9), 1450–1459.
30. M. Ferrero, M. Rérat, R. Orlando and R. Dovesi, Coupled perturbed Hartree–Fock for periodic systems: the role of symmetry and related computational aspects, J. Chem. Phys., 2008, 7(1), 014110.
31. M. Ferrero, M. Rérat, B. Kirtman and R. Dovesi, Calculation of first and second static hyperpolarizabilities of one- to three-dimensional periodic compounds. Implementation in the CRYSTAL code, J. Chem. Phys., 2008, 28(24), 244110.
32. R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32(5), 751–767.
33. B. E. Day, N. D. Bley, H. R. Jones, R. M. McCullough, H. W. Eng and S. H. Porter, et al., Structures of ordered tungsten- or molybdenum-containing quaternary perovskite oxides, J. Solid State Chem., 2012, 185, 107–116.
34. J. Rodriguez-Carvajal. FULLPROF: a program for Rietveld refinement and pattern matching analysis, in Satellite Meeting on Powder Diffraction of the XV Congress of the IUCr, Toulouse, France, 1990.
35. S. N. Kabekkodu, J. Faber and T. Fawcett, New Powder Diffraction File (PDF-4) in relational database format: advantages and data-mining capabilities, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2002, 58(Pt 3 Pt 1), 333–337.
36. W. T. Fu and D. J. W. IJdo, X-ray and neutron powder diffraction study of the monoclinic perovskites Sr₂MSbO₆ (M = In, Y), Solid State Commun., 2005, 134(3), 177–181.
37. O. C. Gagné and F. C. Hawthorne, Bond-length distributions for ions bonded to oxygen: metalloids and post-transition metals, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2018, 1(1), 63–78.
38. T. Mohan, S. Kuppusamy and R. J. V. Michael, Tuning of Structural and Magnetic Properties of SrSnO₃ Nanorods in Fabrication of Blocking Layers for Enhanced Performance of Dye-Sensitized Solar Cells, ACS Omega, 2022, 7(22), 18531–18541.
39. C. A. Schneider, W. S. Rasband and K. W. Eliceiri, NIH Image to ImageJ: 25 years of image analysis, Nat. Methods, 2012, 9(7), 671–675.
40. M. Sukumar, L. John Kennedy, J. Judith Vijaya, B. Al-Najar and M. Bououdina, Facile microwave assisted combustion synthesis, structural, optical and magnetic properties of La_2−xSr_xCuO₄ (0 ≤ x ≤ 0.5) perovskite nanostructures, J. Magn. Magn. Mater., 2018, 465, 48–57.
41. M. C. F. Alves, M. R. Nascimento, S. J. G. Lima, P. S. Pizani, J. W. M. Espinosa and E. Longo, et al., Influence of synthesis conditions on carbonate entrapment in perovskite SrSnO₃, Mater. Lett., 2009, 63(1), 118–120.
42. S. Ouni, S. Nouri, H. Khemakhem and R. Ben Hassen, Phase transitions, dielectric properties, and vibrational study of stannates perovskites Sr_1−xEr_xSnO_3−δ, Mater. Res. Bull., 2014, 51, 136–140.
43. C. Bharti and T. P. Sinha, Dielectric properties of rare earth double perovskite oxide Sr₂CeSbO₆, Solid State Sci., 2010, 4, 498.
44. E. Moreira, J. M. Henriques, D. L. Azevedo, E. W. S. Caetano, V. N. Freire and E. L. Albuquerque, Structural, optoelectronic, infrared and Raman spectra of orthorhombic SrSnO₃ from DFT calculations, J. Solid State Chem., 2011, 1(4), 921–928.
45. L. L. Rusevich, G. Zvejnieks, E. A. Kotomin, M. M. Kržmanc, A. Meden and Š. Kunej, et al., Theoretical and Experimental Study of (Ba, Sr)TiO₃ Perovskite Solid Solutions and BaTiO₃/SrTiO₃ Heterostructures, J. Phys. Chem. C, 2019, 31(4), 2031–2036.
46. J. Hong, S. J. Heo and P. Singh, Water mediated growth of oriented single crystalline SrCO₃ nanorod arrays on strontium compounds, Sci. Rep., 2021, 9(1), 3368.
47. A. P. Ayala, I. Guedes, E. N. Silva, M. S. Augsburger, C. del, M. Viola and J. C. Pedregosa, Raman investigation of A₂CoBO₆ (A = Sr and Ca, B = Te and W) double perovskites, J. Appl. Phys., 2007, 15(12), 101.
48. V. L. Vilesh and G. Subodh, Crystal structure and dielectric properties of BaANaTeO₆ (A = Bi, La) double perovskites, Ceram. Int., 2017, 15(15), 12718–12723.
49. S. A. Prosandeev, U. Waghmare, I. Levin and J. Maslar, First-order Raman spectra of First-order Raman spectra of AB′1/2B′′1/2O3 double perovskites, Phys. Rev. B, 2005, 71(21), 214307.
50. A. Dias, G. Subodh, M. T. Sebastian, M. M. Lage and R. L. Moreira, Vibrational Studies and Microwave Dielectric Properties of A-Site-Substituted Tellurium-Based Double Perovskites, Chem. Mater., 2008, 8(13), 4347–4355.
51. M. G. Masud, H. Sakata, A. K. Biswal, P. N. Vishwakarma and B. K. Chaudhuri, Structural, ac conductivity scaling and magnetodielectric behaviour of a partially disordered insulating ferromagnetic double perovskite Eu₂NiMnO₆, J. Phys. D: Appl. Phys., 2015, 48(37), 375504.
52. M. Z. M. Halizan, Z. Mohamed and A. K. Yahya, Understanding the structural, optical, and dielectric characteristics of SrLaLiTe_1−xMn_xO₆ perovskites, Sci. Rep., 2021, 7(1), 9744.
53. P. Borlido, et al., Exchange-correlation functionals for band gaps of solids: benchmark, reparametrization and machine learning, npj Comput. Mater., 2020, 6, 96.
54. R. Das and R. N. P. Choudhary, Dielectric relaxation and magneto-electric characteristics of lead-free double perovskite: Sm₂NiMnO₆, J. Adv. Ceram., 2019, 1(2), 174–185.
55. O. Bidault, P. Goux, M. Kchikech, M. Belkaoumi and M. Maglione, Space-charge relaxation in perovskites, Phys. Rev. B, 1994, 15(12), 7868–7873.
56. D. K. Mahato, A. Dutta and T. P. Sinha, relaxation and ac conductivity of double perovskite oxide Ho₂ZnZrO₆ Dielectric, Phys. B, 2011, 1(13), 2703–2708.
57. A. K. Singh, S. K. Barik, R. N. P. Choudhary and P. K. Mahapatra, Ac conductivity and relaxation mechanism in Ba_0.9Sr_0.1TiO₃, J. Alloys Compd., 2009, 24(1), 39–42.
58. A. Feteira, Negative Temperature Coefficient Resistance (NTCR) Ceramic Thermistors: An Industrial Perspective, J. Am. Ceram. Soc., 2009, 92(5), 967–983.
59. B. K. Das, T. Das, K. Parashar, S. K. S. Parashar, R. Kumar and H. K. Choudhary, et al., Investigation of structural, morphological and NTCR behaviour of Cu-doped ZnO nanoceramics synthesized by high energy ball milling, Mater. Chem. Phys., 2019, 1, 419–429.
60. R. Mukherjee, S. Saha, A. Dutta and T. P. Sinha, Dielectric and Raman spectroscopic studies of A₂ErSbO₆ (A = Ba, Sr and Ca), J. Alloys Compd., 2015, 5, 222–229.
61. I. M. Hodge, M. D. Ingram and A. R. West, Impedance and modulus spectroscopy of polycrystalline solid electrolytes, J. Electroanal. Chem. Interfacial Electrochem., 1976, 74, 125–143.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra05308g

---