Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reaction of methylene blue with OH radicals in the aqueous environment: mechanism, kinetics, products and risk assessment†
Quan V. Vo *a,
Luu Thi Thu Thaob,
Tran Duc Manhb,
Mai Van Bayb,
Bich-Tram Truong-Lec,
Nguyen Thi Hoaa and
Adam Mechler
*a,
Luu Thi Thu Thaob,
Tran Duc Manhb,
Mai Van Bayb,
Bich-Tram Truong-Lec,
Nguyen Thi Hoaa and
Adam Mechler d
d
aThe University of Danang – University of Technology and Education, Danang 550000, Vietnam. E-mail: vvquan@ute.udn.vn
bThe University of Danang – University of Sciences and Education, Danang 550000, Vietnam
cDepartment of Science and International Cooperation, The University of Danang, Danang 550000, Vietnam
dDepartment of Biochemistry and Chemistry, La Trobe University, Victoria 3086, Australia
First published on 27th August 2024
Abstract
Methylene Blue (MB) is an industrial chemical used in a broad range of applications, and hence its discharge is a concern. Yet, the environmental effects of its degradation by HO˙ radicals have not been fully studied yet. This study employs quantum chemical calculations to investigate the two-step degradation of MB by HO˙ radicals in aqueous environments. It was found that MB undergoes a rapid reaction with the HO˙ radical, with an overall rate constant of 5.51 × 109 to 2.38 × 1010 M−1 s−1 and has a rather broad lifetime range of 11.66 hours to 5.76 years in water at 273–383 K. The calculated rate constants are in good agreement with the experimental values (kcalculation/kexperimental = 2.62, pH > 2, 298 K) attesting to the accuracy of the calculation method. The HO˙ + MB reaction in water followed the formal hydrogen transfer and radical adduct formation mechanisms, yielding various intermediates and products. Based on standard tests these intermediates and some of the products can pose a threat to aquatic organisms, including fish, daphnia, and green algae, they have poor biodegradability and have the potential to induce developmental toxicity. Hence MB in the environment is of moderate concern depending on the ratio of safe to harmful breakdown products.
1. Introduction
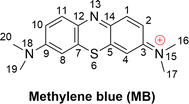
Methylene blue (MB, Fig. 1) is an aromatic heterocyclic dye that is extensively used in industry, especially for coloring silk, cotton, wool, paper, and similar materials.1–3 MB is a cationic dye that is difficult to degrade in natural processes;4,5 therefore, it has the potential to disrupt ecological systems and in an uncontrolled release to cause a variety of health hazards to humans,2,3 albeit it also has well-established clinical uses.6–8 Consistently, the elimination of MB from drinking water is a critical concern.9–14Several techniques such as UV-based advanced oxidation processes (AOPs), photocatalytic methods, and ultra-sonic treatments are in use for the decomposition of toxic chemicals including MB from waste water.1,11,15–20 The pulsed power technique can entirely remove MB in alkaline solutions within 6–8 minutes.11 MB degradation can be greatly enhanced by using the vacuum-ultraviolet/ultraviolet/persulfate process in comparison to the conventional ultraviolet/persulfate process.15 The degradation of MB in water treatment can also be enhanced by using photocatalysts such as TiO2 and ZnO; ultrasonic irradiation is also an efficient method.1,17,20–22 Arguably the simplest approach is supplementing naturally occurring reactive oxygen species (ROS, including HO˙, SO4˙−, Cl˙, ClO˙, HOO˙ and O2˙−) for the AOPs technique. Of these, HO˙ radicals are known to be the primary active substances for MB oxidation.16,19
HO˙ radicals are key natural oxidizing species in natural aquifers due to their strong reactivity towards organic substrates,23,24 playing a substantial role in defining the environmental fate of industrial chemicals despite their low steady-state concentrations ranging from 10−18 to 10−15 M.25–27 Therefore, principal photo-oxidation products are expected to form with the involvement of HO˙ in the self-cleaning process of water in nature. Multiple empirical studies have been carried out to determine the rate of the MB + ˙OH reaction and to identify the products of MB oxidation that occur in an aqueous solution through the introduction of ˙OH.9,10,15,16,28–30 The rate constant for the interaction of MB with ˙OH at ambient temperature was determined to be 3.8 × 109 M−1 s−1.15 This indicates that MB reacts quickly with HO˙ in water. In spite of the promising results, no further studies have been performed on the kinetics of the process.
The HO˙ + MB reaction proceeds principally through the radical adduct formation (RAF) mechanism of HO˙ radicals into the aromatic ring. Therefore the predominant intermediates of the HO˙ + MB reaction are the adduct cations detected by mass spectrometry at m/z = 300,28 whereas a two-step reaction of MB with HO˙ radicals yields products at m/z = 316.10,11,28 To explain the mass spectrometry results the addition of HO˙ radicals into the C1 and C11 positions was proposed.2,10,11 However, there is no evidence supporting this mechanism. Furthermore, it was noted that the degradation of MB occurs slowly in the natural environment and thus the formation of intermediates that may cause toxicity for organic molecules cannot be neglected. Yet the safety of these intermediates has not attracted any attention thus far.
Quantum chemical calculations are well established as a reliable method for determining thermodynamic and kinetic properties of chemical reactions, including radical reactions.31–35 Here we present a computational study of the thermodynamic and kinetic properties of the hydroxyl radical reactions that involve MB and related compounds, as well as the intermediate product reactions that take place within the specified environmental conditions. The toxicity, developmental toxicity, mutagenicity, bioconcentration, and biodegradability of MB and its degradation products were also evaluated.
2. Computational methods
Kinetic calculations were performed using the Quantum Mechanics-based Overall Free Radical Scavenging Activity (QM-ORSA) protocol31 which is directly applicable in this case.36,37 Eqn (1) was the basis of calculating the rate constant (k) by the application of transition state theory (TST) under standard conditions of 1 M at varying ambient temperatures (253–323 K for the gas phase and 283–323 K for water).38–44
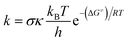 | (1) |
The reaction symmetry number is denoted by σ.45,46 Tunneling corrections are represented by κ and were calculated using the Eckart barrier,47 kB represents the Boltzmann constant, h is the Planck constant, and ΔG≠ is the Gibbs free energy of activation. The Marcus theory was used to determine the reaction barriers of single electron transfer (SET) reactions in the solvent.48,49 Eqn (2) and (3) were used to calculate the ΔG≠ for the SET reaction.
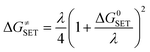 | (2) |
| λ ≈ ΔESET − ΔG0SET | (3) |
For SET reaction, the nonadiabatic energy difference between the reactants and the products is represented by ΔESET, while the conventional Gibbs free energy change of the reaction is denoted by ΔG0SET.50,51 An adjustment was made for rate constants around the diffusion limit.47 The steady-state Smoluchowski rate constant (kD) was estimated from the literature, and the apparent rate constants (kapp) for an irreversible bimolecular diffusion-controlled process in solvents52 were computed using Collins–Kimball theory.50,53
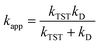 | (4) |
| kD = 4πRABDABNA | (5) |
DAB = DA + DB (denotes the mutual diffusion coefficient of A and B),52,54 where DA or DB is obtained using the Stokes–Einstein formulation (6).55,56
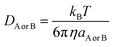 | (6) |
Energy minimization was applied to all conformers of species with multiple conformers; the conformer with the lowest electronic energy was used in the study.57 Each transition stage was characterized by the exclusive existence of a single imaginary frequency. Calculations of intrinsic coordinates were conducted in order to verify the accurate connection between each transition state and the pre- and post-complexes. In addition, the pre- and post-complexes were incorporated into the kinetic calculations.32,58
The calculations for this work were conducted using the Gaussian 16 software package59 at the M06-2X/6-311++G(d,p) level of theory, known for providing precise thermodynamics and kinetics results given the current computational resources.37,60,61 The SMD methodology was employed to simulate the solvent effects of water,60 a typical method for assessing the radical scavenging properties of antioxidants. The calculated values showed moderate differences compared to the experimental results, with a kcalc/kexp ratio ranging from 0.3 to 2.9.32,37,43,62–66
The ecotoxicity assessment was carried out using the Ecological Structure-Activity Relationship Model (ECOSAR V2.0), which has a proven efficacy in assessing the ecotoxicity of organic contaminants.33,67–70 The developmental toxicity and mutagenicity of MB and its transformed products were evaluated through toxicological analysis utilizing the T.E.S.T. (Toxicity Estimation Software Tool) toxicity assessment software.71 Utilizing the BCFBAF module of EPISUITE, the biological concentration factors (BCFs) produced by the conversion products of MB degradation were calculated. Utilizing the BIOWIN 3 & 4 model integrated into the EPISUITE software,72 an assessment was made of the biodegradability of MB and its degradation products.
3. Results and discussion
3.1. Reaction of hydroxyl radical with MB in water
The reaction between MB and HO˙ can occur via the radical adduct formation (RAF), formal hydrogen transfer (FHT), or SET, as per eqn (7)–(9):33,36,37,75
| RAF: MB–H + HO˙ → [HO–MB–H]˙ | (7) |
| FHT: MB–H + HO˙ → MB˙ + H2O | (8) |
| SET: MB–H + HO˙ → [MB–H]˙+ + HO− | (9) |
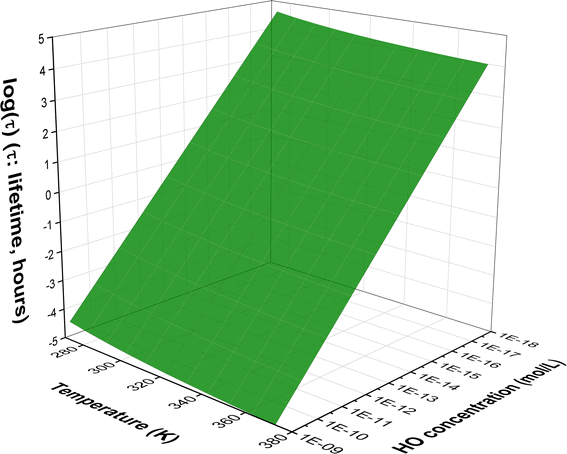
The kinetics of these reactions were calculated and are presented in Table 1, whereas the effect of temperature on the degradation of MB is shown in Fig. 2. We found that the reaction between MB and HO˙ radicals had an overall rate constant (koverall) of 1.02 × 1010 M−1 s−1. This is consistent with the observed experimental rate constant (kexp = 3.8 × 109 M−1 s−1).15 The FHT reactions at C16/17–H accounted for approximately 35.7% of the total rate constant, while the SET reaction had no contribution (Γ = 0%) to the MB + HO˙ reaction. The MB + HO˙ reaction was predominantly taking place via the RAF reactions, which represented 64.2% of the reaction. The RAF (C2, C4, and C14) took place rapidly with a rate constant similar to the rate of diffusion (k ≈ 109 M−1 s−1) and formed the cations [MB–OH]+ (m/z = 300) that were also observed in the experimental studies.11,28 On the other hand, the RAF reaction at the C1, C3, and C5 sites had moderate reaction rates (k = 105 to 107 M−1 s−1) and did not have any impact on the overall reaction. Therefore, the formation of cations [MB–OH]+ (m/z = 300) can occur by introducing HO˙ radicals to the C2, C4, or C14 sites (Fig. 3), but not at the C1 position, this is also consistent with prior research.11,28 The likely cause for the preferential adduct formation could be attributed to the presence of the electron-donating group N(CH3)2 in either the ortho- or para-position. This group has the potential to stabilize both the transition states and the resultant radicals.
| Mechanisms | Positions | ΔG≠ | κ | kapp | Γ | Intermediates |
|---|---|---|---|---|---|---|
| a The nuclear reorganization energy (λ, in kcal mol−1). | ||||||
| SET | 10.1 | 0.4a | 2.50 × 105 | 0.0 | ISET | |
| FHT | C16–H | 5.3 | 1.0 | 1.90 × 109 | 18.6 | I16 |
| C17–H | 5.4 | 1.0 | 1.75 × 109 | 17.1 | I17 | |
| RAF | C1 | 8.2 | 1.2 | 1.50 × 107 | 0.1 | I1 |
| C2 | 4.1 | 1.0 | 2.07 × 109 | 20.2 | I2 | |
| C3 | 8.4 | 1.2 | 9.50 × 106 | 0.1 | I3 | |
| C4 | 1.8 | 1.0 | 2.69 × 109 | 26.3 | I4 | |
| C5 | 10.8 | 1.2 | 2.00 × 105 | 0.0 | I5 | |
| C14 | 4.6 | 1.0 | 1.79 × 109 | 17.5 | I14 | |
| N13 | 14.7 | 1.8 | 1.90 × 102 | 0.0 | I13 | |
| koverall | 1.02 × 1010 | |||||
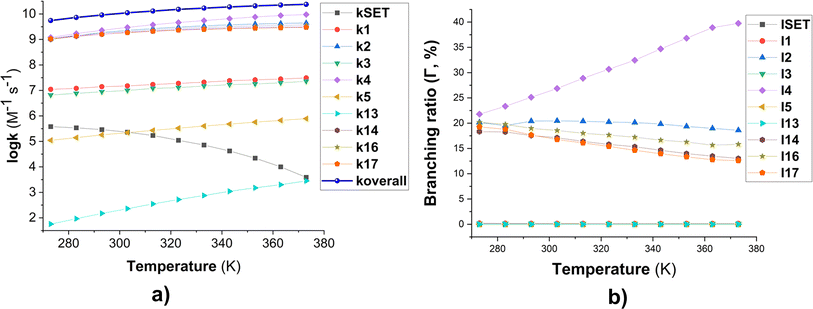 | ||
Fig. 2 Temperature dependence of apparent rate constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k) in water in the range of 273–373 K ((a) the MB + HO˙ reactions; (b) branching ratio (Γ, %) of the MB + HO˙ reactions; ki = 1–17: the rate constants of the positions in Table 1). k) in water in the range of 273–373 K ((a) the MB + HO˙ reactions; (b) branching ratio (Γ, %) of the MB + HO˙ reactions; ki = 1–17: the rate constants of the positions in Table 1). | ||
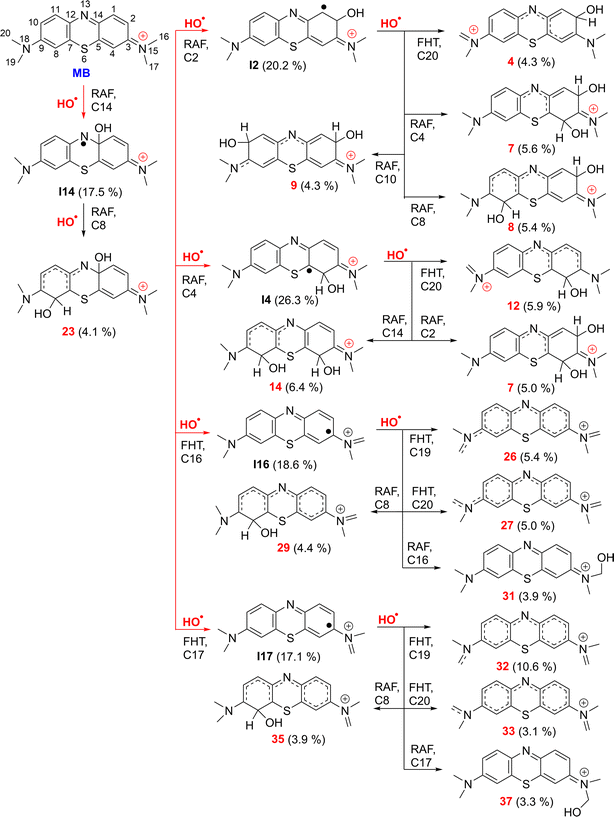 | ||
| Fig. 3 The selected mechanisms and % products (Γ ≥ 3%) of the two steps HO˙ + MB reactions in water at 298.15 K. | ||
The incorporation of HO˙ radicals into the N13 position is expected to be extremely rare with the highest activation energy (ΔG≠ = 14.7 kcal mol−1) and the lowest rate constant (k = 1.90 × 102 M−1 s−1). Therefore, this reaction does not contribute to the destruction of MB by HO˙ radicals. The primary intermediates of the MB + HO˙ reaction were I2 (20.2%), I4 (26.3%), I14 (17.5%), I16 (18.6%), and I17 (17.1%), as indicated in Table 1 and Fig. 3. Therefore, these intermediates were used as a starting point for assessing the kinetics of the subsequent reaction step.
To examine the effect of temperature on the degradation of MB in water, we determined the rate constants for each reaction in the range of 273 to 383 K (Fig. 2). The rate constants for all reactions increase as the temperature rises with the exception of the SET reaction, where the rate decreased from 3.80 × 105 to 3.90 × 103 M−1 s−1. The overall rate constants exhibited a 4.33-fold increase, rising from 5.51 × 109 to 2.38 × 1010 M−1 s−1 (Fig. 2a). The FHT and RAF (C2, C4, and C14) reactions defined the overall rate constants of the MB + HO˙ reaction at all temperatures investigated. However, the RAF reactions at C1, C3, C5, and N13 did not contribute to the degradation of MB by HO˙ radicals.
As the temperature increases, the major intermediates for the MB + HO˙ reaction, shown in Fig. 2b, exhibit varying branching ratios. Specifically, the percentages of I2 change from 20.2% to 18.6%, I4 changes from 21.8% to 39.7%, I14 goes from 18.3% to 13.0%, I16 changes from 20.2% to 15.8%, and I17 from 19.2% to 12.6%. Thus when the temperature climbed, the fraction of intermediate I4 grew, while the amount of all other intermediates decreased. Percentage-wise I4 is the main intermediate in all of the studied temperatures.
| States | Mechanism | ΔG≠ | κ | kapp | kr | Γ | Products | |
|---|---|---|---|---|---|---|---|---|
| kr = r × kapp; koverall (r) = Σkr; koverall (MB + HO˙, step 2) = Σkoverall (r); Γ = kr × 100/koverall (MB + HO˙, step 2); r(I2) = 0.202; r(I4) = 0.263; r(I14) = 0.175; r(I16) = 0.186; r(I17) = 0.171. | ||||||||
| I2 | FHT | C16 | 8.9 | 4.4 | 2.40 × 107 | 4.86 × 106 | 0.1 | 1 |
| C17 | 9.0 | 4.6 | 2.10 × 107 | 4.25 × 106 | 0.1 | 2 | ||
| C19 | 6.4 | 5.1 | 1.10 × 109 | 2.23 × 108 | 2.4 | 3 | ||
| C20 | 5.7 | 4.9 | 2.00 × 109 | 4.05 × 108 | 4.3 | 4 | ||
| RAF | C1 | 5.8 | 1.3 | 3.60 × 108 | 7.29 × 107 | 0.8 | 5 | |
| C3 | 5.6 | 1.2 | 4.50 × 108 | 9.11 × 107 | 1.0 | 6 | ||
| C4 | 2.5 | 1.0 | 2.60 × 109 | 5.26 × 108 | 5.6 | 7 | ||
| C8 | 2.7 | 1.1 | 2.50 × 109 | 5.06 × 108 | 5.4 | 8 | ||
| C10 | 3.7 | 1.1 | 2.00 × 109 | 4.05 × 108 | 4.3 | 9 | ||
| C14 | 5.0 | 1.1 | 9.40 × 108 | 1.90 × 108 | 2.0 | 10 | ||
| koverall (r) (I2 + HO˙) | 2.43 × 109 | 25.9 | ||||||
| I4 | C19 | 6.5 | 1.1 | 3.30 × 108 | 8.68 × 107 | 0.9 | 11 | |
| C20 | 6.2 | 12.3 | 2.10 × 109 | 5.52 × 108 | 5.9 | 12 | ||
| RAF | C1 | 7.1 | 1.2 | 4.50 × 107 | 1.18 × 107 | 0.1 | 13 | |
| C2 | 4.1 | 1.1 | 1.80 × 109 | 4.73 × 108 | 5.0 | 7 | ||
| C8 | 1.8 | 1.0 | 2.30 × 109 | 6.05 × 108 | 6.4 | 14 | ||
| C14 | 7.2 | 1.2 | 4.10 × 107 | 1.08 × 107 | 0.1 | 15 | ||
| koverall (r) (I4 + HO˙) | 1.74 × 109 | 18.6 | ||||||
| I14 | FHT | C16 | 8.6 | 2.6 | 2.50 × 107 | 4.37 × 106 | 0.1 | 17 |
| C19 | 7.5 | 5.4 | 2.70 × 108 | 4.72 × 107 | 0.5 | 18 | ||
| C20 | 7.2 | 5.1 | 4.30 × 108 | 7.51 × 107 | 0.8 | 19 | ||
| RAF | C1 | 7.2 | 1.1 | 3.90 × 107 | 6.81 × 106 | 0.1 | 20 | |
| C2 | 6.0 | 1.2 | 2.70 × 108 | 4.72 × 107 | 0.5 | 10 | ||
| C3 | 4.5 | 1.1 | 1.40 × 109 | 2.45 × 108 | 2.6 | 21 | ||
| C4 | 5.0 | 1.1 | 8.80 × 108 | 1.54 × 108 | 1.6 | 16 | ||
| C5 | 6.9 | 1.2 | 6.30 × 107 | 1.10 × 107 | 0.1 | 22 | ||
| C8 | 3.3 | 1.1 | 2.20 × 109 | 3.84 × 108 | 4.1 | 23 | ||
| C10 | 5.4 | 1.0 | 5.70 × 108 | 9.96 × 107 | 1.1 | 24 | ||
| C11 | 6.6 | 1.2 | 9.80 × 107 | 1.71 × 107 | 0.2 | 25 | ||
| koverall (r) (I14 + HO˙) | 1.09 × 109 | 11.7 | ||||||
| I16 | FHT | C19 | 5.6 | 16.0 | 5.80 × 109 | 9.93 × 108 | 5.4 | 26 |
| C20 | 5.5 | 9.5 | 1.70 × 109 | 2.91 × 108 | 5.0 | 27 | ||
| RAF | C2 | 5.6 | 1.2 | 2.60 × 107 | 4.45 × 106 | 0.9 | 1 | |
| C4 | 6.9 | 1.2 | 2.81 × 108 | 4.81 × 107 | 0.1 | 28 | ||
| C8 | 1.5 | 1.1 | 2.14 × 109 | 3.67 × 108 | 4.4 | 29 | ||
| C10 | 5.2 | 1.0 | 8.70 × 108 | 1.49 × 108 | 1.4 | 30 | ||
| C16 | 3.6 | 1.0 | 1.98 × 109 | 3.68 × 108 | 3.9 | 31 | ||
| koverall (r) (I16 + HO˙) | 1.97 × 109 | 21.0 | ||||||
| I17 | FHT | C19 | 5.8 | 19.0 | 5.80 × 109 | 9.93 × 108 | 10.6 | 32 |
| C20 | 6.4 | 10.5 | 1.70 × 109 | 2.91 × 108 | 3.1 | 33 | ||
| RAF | C2 | 7.4 | 1.2 | 2.60 × 107 | 4.45 × 106 | 0.1 | 2 | |
| C4 | 5.9 | 1.0 | 2.81 × 108 | 4.81 × 107 | 0.5 | 34 | ||
| C8 | 3.1 | 1.0 | 2.14 × 109 | 3.67 × 108 | 3.9 | 35 | ||
| C10 | 5.0 | 1.0 | 8.70 × 108 | 1.49 × 108 | 1.6 | 36 | ||
| C17 | 4.1 | 1 | 6.20 × 109 | 3.05 × 108 | 3.3 | 37 | ||
| koverall (r) (I17 + HO˙) | 2.16 × 109 | 23.0 | ||||||
| koverall (MB + HO˙, step 2) | 9.39 × 109 | |||||||
The results show that the intermediates exhibit high reactivity with the HO˙ radical, with an overall rate constant of the second step koverall (MB + HO˙, step 2) = 9.39 × 109 M−1 s−1. The I2 + ˙OH reaction has the highest rate, with koverall (r) (I2 + HO˙) = 2.43 × 109 M−1 s−1 (Γ = 25.9%). This reaction is 2.2 times faster than the I14 + ˙OH reaction (koverall (r) (I14 + HO˙) = 1.09 × 109 M−1 s−1, Γ = 11.7%). The I4/16/17 + ˙OH reactions have moderate activity with koverall (r) values of 1.74 × 109 (Γ = 18.6%), 1.97 × 109 (Γ = 21.0%) and 2.16 × 109 (Γ = 23.0%), respectively. The rate constant of the second step reaction (koverall (MB + HO˙, step 2) = 9.39 × 109 M−1 s−1) was approximately 1.1 times lower than the rate constant of the first step reaction (koverall (MB + HO˙, step 1) = 1.02 × 1010 M−1 s−1, Table 1).
Fig. 3 illustrates that the two-step reaction between MB and ˙OH in water can potentially take place through five different pathways. The reaction can proceed initially via RAF(C2) followed by FHT(C20), or via RAF(C4/C8 or C10), resulting in the formation of cations 4 (4.3%), 7 (5.6%), 8 (5.4%) and 9 (4.3%). The RAF(C14)–RAF(C8) and RAF(C4)–RAF(C2/C14)/FHT(C20) processes produced the cations 23 (4.1%), 7 (5.0%), 14 (6.4%) and 12 (5.9%), respectively. Conversely, the FHT(C16/17)–FHT(C19/20)/RAF(C8/16/17) pathways could form the cations 26 (5.4%), 27 (5.0%), 29 (4.4%), 31 (3.9%), 32 (10.6%), 33 (3.1%), 35 (3.9%), and 37 (3.3%), respectively. Cation 32 has the largest branching ratio value, reaching 11.6%, while the other products displayed values below 7%. Overall the breakdown of MB by HO˙ radicals through a two-step reaction is intricate and could produce several compounds with low branching ratios (Γ < 11%).
The breakdown of MB by HO radicals leads to the formation of hydroxylated products (7, 8, 9, 14, and 23; m/z = 316) through the addition of two HO˙ groups to the MB molecule. This finding is consistent with prior experimental studies that used ESI-MS to analyze the breakdown of MB by HO˙ radicals.10,11,28 Our calculations also highlighted that the addition reaction can only occur in even positions (C2, C4, C8, C10, or C14), but not in odd positions such as the C1 and C11 positions (Fig. 1) as shown in previous studies.10,11,28 Hence, the computational approach uncovered details of the MB breakdown process that experimental observations failed to reveal.
3.2. Environmental risk assessment
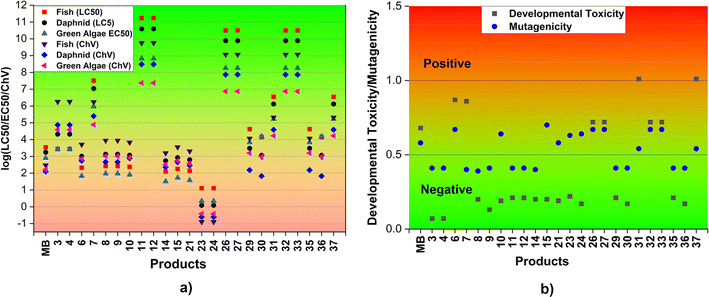 | ||
| Fig. 5 Acute and chronic toxicity (log(LC50/EC50/ChV), mg L−1) (a) and the developmental toxicity and mutagenicity (b) of MB and the main products (F: fish; D: daphnia; GA: green algae). | ||
In order to assess the impact of MB and its breakdown products on living creatures, the developmental toxicity and mutagenicity of these compounds were also determined using T.E.S.T. The corresponding outcomes are illustrated in Fig. 5b and Table S3, ESI.† The results imply that products 6, 7, 26, 27, 31, 32, 33, and 37, along with MB may have developmental toxicity, as indicated by toxicity values for development that are higher than 0.5. These substances have the ability to disrupt the processes of nucleic acid translation and expression, potentially affecting the growth and development of humans.71 Simultaneously, the calculations indicate that the products 6, 10, 15, 21, 23, 24, 26, 27, 31, 32, 33, and 37, as well as MB, may present mutagenic hazards (mutagenicity values ≥ 0.5). The rest of the products, specifically 3, 4, 8, 9, 11, 12, 14, 29, 30, 35, and 36, do not exhibit any developmental toxicity or mutagenicity. This can be explained by the structural change where the addition reaction has the potential to disrupt the aromatic ring of MB which is mostly responsible for its toxicity.
The biodegradability of the reactant MB and its degradation products was assessed using the BIOWIN 3, 4, and 5 models incorporated in the EPISUITE program (Table S3, ESI†).72 The results obtained from the BIOWIN models suggest that degradation products undergo initial biodegradation during a period ranging from a few days to months, while both the MB and degradation products may not be biodegradable. Consequently, the breakdown of MB by HO˙ radicals in the two-step process could result in the formation of non-biodegradable substances. However, these substances may not accumulate in living organisms.
4. Conclusion
A computational analysis was conducted to study the breakdown pathways of MB in the presence of HO˙. An assessment of the thermodynamic and kinetic parameters of possible reaction paths was conducted in order to ascertain the most probable products. It was found that in natural water bodies MB can undergo degradation with lifetimes in the broad range of 11.66 to 5.04 × 104 hours (i.e. 11.66 hours to 5.76 years). The HO˙ + MB reaction in water can take place via either FHT or RAF mechanism. The addition reaction is possible at carbon atoms at most even positions C2, C4, C8, C10, or C14, but not at odd positions. The intermediates and some of the products generated in the process can pose a threat to aquatic organisms, including fish, daphnia, and green algae. Additionally, they have the potential to induce developmental toxicity and have poor biodegradability. However, the introduction of the HO radical to the aromatic ring might lead to the creation of compounds that do not exhibit any developmental toxicity or mutagenicity. Hence, MB poses a moderate environmental risk with a mix of safe and toxic breakdown products.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by the Vietnamese Ministry of Education and Training under project number B2024.DNA.09.References
- M. I. Din, R. Khalid, J. Najeeb and Z. Hussain, J. Cleaner Prod., 2021, 298, 126567 CrossRef CAS.
- M. Rafatullah, O. Sulaiman, R. Hashim and A. Ahmad, J. Hazard. Mater., 2010, 177, 70–80 CrossRef CAS PubMed.
- M. Mohammed, A. Shitu and A. Ibrahim, Res. J. Chem. Sci., 2014, 4, 91–102 Search PubMed.
- W. Subramonian and T. Y. Wu, Water, Air, Soil Pollut., 2014, 225, 1–15 CrossRef CAS.
- T. Liu, Y. Li, Q. Du, J. Sun, Y. Jiao, G. Yang, Z. Wang, Y. Xia, W. Zhang and K. Wang, Colloids Surf., B, 2012, 90, 197–203 CrossRef CAS PubMed.
- A. Sipos and H. Urakawa, Lett. Appl. Microbiol., 2016, 62, 199–206 CrossRef CAS.
- M. Wainwright and K. Crossley, J. Chemother., 2002, 14, 431–443 CrossRef CAS.
- M. Oz, D. E. Lorke and G. A. Petroianu, Biochem. Pharmacol., 2009, 78, 927–932 CrossRef CAS PubMed.
- C.-H. Wu and J.-M. Chern, Ind. Eng. Chem. Res., 2006, 45, 6450–6457 CrossRef CAS.
- C. Luo, S. Wang, D. Wu, X. Cheng and H. Ren, Environ. Technol. Innovation, 2022, 25, 102198 CrossRef CAS.
- R. K. Singh, V. Babu, L. Philip and S. Ramanujam, J. Water Process Eng., 2016, 11, 118–129 CrossRef.
- H. Valdés, R. F. Tardón and C. A. Zaror, Chem. Eng. J., 2012, 211, 388–395 CrossRef.
- A. Syoufian and K. Nakashima, J. Colloid Interface Sci., 2008, 317, 507–512 CrossRef CAS.
- C. Minamoto, N. Fujiwara, Y. Shigekawa, K. Tada, J. Yano, T. Yokoyama, Y. Minamoto and S. Nakayama, Chemosphere, 2021, 263, 128141 CrossRef CAS PubMed.
- D. Wen, W. Li, J. Lv, Z. Qiang and M. Li, J. Hazard. Mater., 2020, 391, 121855 CrossRef CAS PubMed.
- N. T. Hoang, T. D. Manh, V. T. Nguyen, N. T. T. Nga, F. M. Mwazighe, B. D. Nhi, H. Y. Hoang, S. W. Chang, W. J. Chung and D. D. Nguyen, Chemosphere, 2022, 308, 136457 CrossRef CAS PubMed.
- Z. Eren and K. O'Shea, J. Environ. Eng., 2019, 145, 04019070 CrossRef CAS.
- F. Banat, S. Al-Asheh and M. Nusair, Desalination, 2005, 181, 225–232 CrossRef CAS.
- Z. Wang, H. Zhao, H. Qi, X. Liu and Y. Liu, Environ. Technol., 2019, 40, 1138–1145 CrossRef CAS PubMed.
- A. Houas, H. Lachheb, M. Ksibi, E. Elaloui, C. Guillard and J.-M. Herrmann, Appl. Catal., B, 2001, 31, 145–157 CrossRef CAS.
- A. Mills, Appl. Catal., B, 2012, 128, 144–149 CrossRef CAS.
- R. H. Waghchaure, V. A. Adole and B. S. Jagdale, Inorg. Chem. Commun., 2022, 143, 109764 CrossRef CAS.
- P. P. Vaughan and N. V. Blough, Environ. Sci. Technol., 1998, 32, 2947–2953 CrossRef.
- K. Takeda, H. Takedoi, S. Yamaji, K. Ohta and H. Sakugawa, Anal. Sci., 2004, 20, 153–158 CrossRef CAS.
- H. Xu, Y. Li, J. Liu, H. Du, Y. Du, Y. Su and H. Jiang, Water Res., 2020, 176, 115774 CrossRef CAS.
- S. A. Timko, C. Romera-Castillo, R. Jaffé and W. J. Cooper, Environ. Sci.: Processes Impacts, 2014, 16, 866–878 RSC.
- D. Vione, G. Falletti, V. Maurino, C. Minero, E. Pelizzetti, M. Malandrino, R. Ajassa, R.-I. Olariu and C. Arsene, Environ. Sci. Technol., 2006, 40, 3775–3781 CrossRef CAS PubMed.
- K. Sharma, R. K. Vyas and A. K. Dalai, J. Chem. Eng. Data, 2017, 62, 3651–3662 CrossRef CAS.
- D. Kobayashi, C. Honma, H. Matsumoto, T. Takahashi, C. Kuroda, K. Otake and A. Shono, Ultrason. Sonochem., 2014, 21, 1489–1495 CrossRef CAS PubMed.
- I. A. Salem and M. S. El-Maazawi, Chemosphere, 2000, 41, 1173–1180 CrossRef CAS.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2013, 34, 2430–2445 CrossRef CAS PubMed.
- M. E. Alberto, N. Russo, A. Grand and A. Galano, Phys. Chem. Chem. Phys., 2013, 15, 4642–4650 RSC.
- N. T. Hoa and Q. V. Vo, Chemosphere, 2023, 314, 137682 CrossRef CAS PubMed.
- P. A. Denis and F. R. Ornellas, J. Phys. Chem. A, 2009, 113, 499–506 CrossRef CAS.
- P. A. Denis, J. Phys. Chem. A, 2006, 110, 5887–5892 CrossRef CAS.
- A. Galano, G. Mazzone, R. Alvarez-Diduk, T. Marino, J. R. Alvarez-Idaboy and N. Russo, Annu. Rev. Food Sci. Technol., 2016, 7, 335–352 CrossRef CAS PubMed.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2014, 35, 2019–2026 CrossRef CAS PubMed.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- D. G. Truhlar, W. L. Hase and J. T. Hynes, J. Phys. Chem., 1983, 87, 2664–2682 CrossRef CAS.
- T. Furuncuoglu, I. Ugur, I. Degirmenci and V. Aviyente, Macromolecules, 2010, 43, 1823–1835 CrossRef CAS.
- E. Vélez, J. Quijano, R. Notario, E. Pabón, J. Murillo, J. Leal, E. Zapata and G. Alarcón, J. Phys. Org. Chem., 2009, 22, 971–977 CrossRef.
- E. Dzib, J. L. Cabellos, F. Ortíz-Chi, S. Pan, A. Galano and G. Merino, Int. J. Quantum Chem., 2019, 119, e25686 CrossRef.
- E. Dzib, J. L. Cabellos, F. Ortiz-Chi, S. Pan, A. Galano and G. Merino, Eyringpy 1.0.2, Cinvestav, Mérida, Yucatán, 2018 Search PubMed.
- E. Pollak and P. Pechukas, J. Am. Chem. Soc., 1978, 100, 2984–2991 CrossRef CAS.
- A. Fernández-Ramos, B. A. Ellingson, R. Meana-Pañeda, J. M. Marques and D. G. Truhlar, Theor. Chem. Acc., 2007, 118, 813–826 Search PubMed.
- C. Eckart, Phys. Rev., 1930, 35, 1303 CrossRef CAS.
- R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155–196 CrossRef CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599 CrossRef CAS.
- S. F. Nelsen, S. C. Blackstock and Y. Kim, J. Am. Chem. Soc., 1987, 109, 677–682 CrossRef CAS.
- S. F. Nelsen, M. N. Weaver, Y. Luo, J. R. Pladziewicz, L. K. Ausman, T. L. Jentzsch and J. J. O'Konek, J. Phys. Chem. A, 2006, 110, 11665–11676 CrossRef CAS.
- F. C. Collins and G. E. Kimball, J. Colloid Sci., 1949, 4, 425–437 CrossRef CAS.
- M. Von Smoluchowski, Z. Phys. Chem., 1917, 92, 129–168 CAS.
- D. G. Truhlar, J. Chem. Educ., 1985, 62, 104 CrossRef CAS.
- A. Einstein, Ann. Phys., 1905, 17, 549–560 CrossRef CAS.
- G. G. Stokes, Mathematical and Physical Papers, University Press, Cambridge, 1905 Search PubMed.
- S. Benson, The Foundations of Chemical Kinetics, Malabar, Florida, 1982 Search PubMed.
- J. R. Alvarez-Idaboy, L. Reyes and N. Mora-Diez, Org. Biomol. Chem., 2007, 5, 3682–3689 RSC.
- J. R. Alvarez-Idaboy, N. Mora-Diez, R. J. Boyd and A. Vivier-Bunge, J. Am. Chem. Soc., 2001, 123, 2018–2024 CrossRef CAS.
- M. Carreon-Gonzalez, A. Vivier-Bunge and J. R. Alvarez-Idaboy, J. Comput. Chem., 2019, 40, 2103–2110 CrossRef CAS PubMed.
- N. Mora-Diez, J. R. Alvarez-Idaboy and R. J. Boyd, J. Phys. Chem. A, 2001, 105, 9034–9039 CrossRef CAS.
- J. R. l. Alvarez-Idaboy and A. Galano, J. Phys. Chem. B, 2012, 116, 9316–9325 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- Q. V. Vo, M. V. Bay, P. C. Nam, D. T. Quang, M. Flavel, N. T. Hoa and A. Mechler, J. Org. Chem., 2020, 85, 15514–15520 CrossRef CAS PubMed.
- Q. V. Vo, N. T. Hoa and A. Mechler, Polym. Degrad. Stab., 2021, 185, 109483 CrossRef CAS.
- Q. Mei, J. Sun, D. Han, B. Wei, Z. An, X. Wang, J. Xie, J. Zhan and M. He, Chem. Eng. J., 2019, 373, 668–676 CrossRef CAS.
- J. Sun, B. Wei, Q. Mei, Z. An, X. Wang and M. He, Chem. Eng. J., 2019, 358, 456–466 CrossRef CAS.
- S. Luo, Z. Wei, D. D. Dionysiou, R. Spinney, W.-P. Hu, L. Chai, Z. Yang, T. Ye and R. Xiao, Chem. Eng. J., 2017, 327, 1056–1065 CrossRef CAS.
- Y. Gao, Y. Ji, G. Li and T. An, Water Res., 2016, 91, 77–85 CrossRef CAS.
- Toxicity Estimation Software Tool; A Program to Estimate Toxicity from Molecular Structure, U.S. EPA, 2020 Search PubMed.
- R. S. Boethling, D. G. Lynch, J. S. Jaworska, J. L. Tunkel, G. C. Thom and S. Webb, Environ. Toxicol. Chem., 2004, 23, 911–920 CrossRef CAS.
- Q. V. Vo, N. T. Hoa and A. Mechler, New J. Chem., 2021, 45, 17683–17691 RSC.
- O. Impert, A. Katafias, P. Kita, A. Mills, A. Pietkiewicz-Graczyk and G. Wrzeszcz, Dalton Trans., 2003, 348–353 RSC.
- B. N. Ames, M. K. Shigenaga and T. M. Hagen, Proc. Natl. Acad. Sci. U.S.A., 1993, 90, 7915–7922 CrossRef CAS PubMed.
- J. M. Burns, W. J. Cooper, J. L. Ferry, D. W. King, B. P. DiMento, K. McNeill, C. J. Miller, W. L. Miller, B. M. Peake and S. A. Rusak, Aquat. Sci., 2012, 74, 683–734 CrossRef CAS.
- P. Reuschenbach, M. Silvani, M. Dammann, D. Warnecke and T. Knacker, Chemosphere, 2008, 71, 1986–1995 CrossRef CAS PubMed.
- N. Wang, L. He, X. Sun, X. Li and M. Li, J. Hazard. Mater., 2022, 427, 127941 CrossRef CAS PubMed.
- M.-J. He, X.-J. Luo, M.-Y. Chen, Y.-X. Sun, S.-J. Chen and B.-X. Mai, Sci. Total Environ., 2012, 419, 109–115 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra05437g |
| This journal is © The Royal Society of Chemistry 2024 |