Open Access Article
Open Access ArticleAdsorption of molecular hydrogen (H2) on a fullerene (C60) surface: insights from density functional theory and molecular dynamics simulation
Muhammad Tariq Aziza,
Waqas Amber Gillb,
Muhammad Kaleem Khosaa,
Saba Jamilc and
Muhammad Ramzan Saeed Ashraf Janjua *a
*a
aDepartment of Chemistry, Government College University Faisalabad, Faisalabad 38000, Pakistan. E-mail: Janjua@gcuf.edu.pk; Dr_Janjua2010@yahoo.com
bInstitute of Chemistry, University of Sargodha, Sargodha 40100, Pakistan
cDepartment of Chemistry, University of Agriculture, Faisalabad 38000, Pakistan
First published on 15th November 2024
Abstract
Understanding the adsorption behavior of molecular hydrogen (H2) on solid surfaces is essential for a variety of technological applications, including hydrogen storage and catalysis. We examined the adsorption of H2 (∼2800 configurations) molecules on the surface of fullerene (C60) using a combined approach of density functional theory (DFT) and molecular dynamics (MD) simulations with an improved Lennard-Jones (ILJ) potential force field. First, we determined the adsorption energies and geometries of H2 on the C60 surface using DFT calculations. Calculations of the electronic structure help elucidate underlying mechanisms administrating the adsorption process by revealing how H2 molecules interact with the C60 surface. In addition, molecular dynamics simulations were performed to examine the dynamic behavior of H2 molecules on the C60 surface. We accurately depicted the intermolecular interactions between H2 and C60, as well as the collective behavior of adsorbed H2 molecules, using an ILJ potential force field. Our findings indicate that H2 molecules exhibit robust physisorption on the C60 surface, forming stable adsorption structures with favorable adsorption energies. Calculated adsorption energies and binding sites are useful for designing efficient hydrogen storage materials and comprehending the nature of hydrogen's interactions with carbon-based nanostructures. This research provides a comprehensive understanding of H2 adsorption on the C60 surface by combining the theoretical framework of DFT calculations with the dynamical perspective of MD simulations. The outcomes of the present research provide new insights into the fields of hydrogen storage and carbon-based nanomaterials, facilitating the development of efficient hydrogen storage systems and advancing the use of molecular hydrogen in a variety of applications.
1. Introduction
The adsorption of molecular hydrogen (H2) on surfaces has been extensively studied owing to its significance in various scientific and technological fields, including materials science, catalysis, and hydrogen storage.1 Understanding the interaction between H2 and carbon-based surfaces is particularly important. Fullerene molecules, such as C60, possess a unique spherical structure and large surface area, making them intriguing for investigating H2 adsorption.2 Fullerene molecules are spherical carbon cages consisting of a network of fused carbon atoms. C60 fullerene, in particular, is composed of 60 carbon atoms arranged in a highly symmetric structure. This unique structure provides a large surface area and multiple adsorption sites for interactions with other molecules. Physisorption and chemisorption are two fundamental absorption techniques that are responsible for adsorption of H2 on fullerene. The former technique involves van der Waals forces or π–π stacking interactions between molecular H2 and the surface of fullerene. Conversely, the latter one involves the establishment of stronger chemical bonds between the adsorbate and the fullerene surface.3 A comprehensive understanding of fundamental processes and energetics involved in the adsorption of H2 on fullerene surfaces can facilitate the development of advanced materials and efficient hydrogen storage systems.4 Understanding the adsorption behavior on fullerene surfaces is crucial to understand its applications such as the storage of gases, drug delivery, and sensor devices. It allows for the optimization of surface properties, such as surface chemistry and morphology, to enhance adsorption efficiency and selectivity. Additionally, investigating the adsorption behavior of different molecules on fullerene surfaces provides deep insights into the fundamental interactions between molecules and carbon-based materials.In this study, a combination of density functional theory (DFT) and molecular dynamics (MD) simulations is employed to thoroughly understand the adsorption of H2 on the surface of C60. DFT calculations allow for a detailed investigation of the electronic structure and energetics associated with the adsorption process.5 MD simulations provide important information about the movement and dynamics of H2 molecules during the adsorption process.6 By utilizing these computational techniques, we aim to obtain a comprehensive understanding of the adsorption mechanism and the factors influencing the adsorption strength. While previous studies have explored the interaction between H2 and carbon-based surfaces, there is limited research specifically focusing on the adsorption of H2 on fullerene surfaces using DFT and MD simulations.7 Therefore, this study aims to contribute to the existing knowledge and provide deeper insights into the phenomenon of H2 adsorption on fullerene surfaces.
The durability of fullerene (C60) and its potential for effective hydrogen storage have drawn a lot of attention to the study of hydrogen adsorption on C60 surfaces. According to recent research studies, fullerenes have the ability to efficiently physisorb hydrogen molecules, and their binding energies are equivalent to those of other carbon allotropes such as graphene. The current state of research, however, points to a number of difficulties. The most notable one is associated with fullerenes' low accessible surface area, which limits their ability to store hydrogen.8 To improve this capacity, innovations has been made to increase porosity and facilitate hydrogen transportation inside the material.9
Even with these developments, there are still a number of challenges in comprehending the complex mechanics underlying hydrogen adsorption on fullerenes. While theoretical methods, such as molecular dynamics simulations (MD)10 and density functional theory (DFT),11 offer important insights, they are frequently constrained by computational limitations and modeling errors in intricate interactions.12 For example, MD simulations can be hampered by time-scale constraints that make it difficult to capture long-term adsorption patterns, while DFT struggles with self-interaction errors and the selection of exchange–correlation functionals.13 A concentrated effort has been made to resolve these issues in our research work to improve computational models and investigate novel structural alterations to optimize fullerene-based materials for hydrogen storage applications.
This study aims to utilize the improved Lennard-Jones (ILJ) potential for the provision of a set of systematic potentials that can describe the characteristics of H2 adsorption on fullerene. By balancing accuracy with simplicity, these potentials appear to be a helpful tool for molecular simulations. Then, the second virial coefficients are computed using the molecular dynamic simulations to compare the efficacy of the proposed force field. It helps us to deduce the effectuality of the diversified force fields by drawing a comparison between these results and the previously reported experimental results. Additionally, we predict the preferred interaction sites for gas molecules on fullerenes by applying a precise technique, such as density functional theory (DFT), and then find out the optimal orientations of molecular hydrogen on fullerenes. In Section 2, the computational specifics applied in this study are discussed. Section 3 discusses the potential energy surface, with a focus on the analysis for the derivation of PES, while MD simulations are the core study of Section 4. The findings of our study are summarized in the last and final section, with a conclusion for designing hydrogen storage materials and for the development of carbon-based nanomaterials. This work focuses on building a set of force fields that are acceptable to evaluate the van der Waals interactions, specifically to the system of hydrogen in fullerenes, by applying a well-known Improved Lennard-Jones (ILJ) potential.14,15 Furthermore, various charge schemes, such as Hirshfeld,16 CHelpG,17 MBS (Minimum Basis Set),18 MK (Merz–Kollman),19 and NBO (Natural Bonding Orbitals),20 are incorporated to investigate the impact of electrostatic components on the force field parameters to estimate their effectiveness and feasibility.
2. Computational details
To investigate the interaction energies of molecular hydrogen (H2) on the surface of a fullerene molecule (C60), we employed computational methods utilizing the B97D/TZV2P basis set in Gaussian 16 software. Our goal was to generate a diverse set of random conformations of H2 adsorbed on the fullerene surface, and calculate the corresponding interaction energies.We began by implementing density functional theory (DFT) calculations, specifically utilizing the B97D functional,21–24 which accounts for dispersion forces, and the TZV2P basis set, known for its accuracy in carbon-based systems.25–30 These calculations allowed us to perform quantum mechanical simulations and obtain reliable energy values. To generate a representative ensemble of conformations, we utilized molecular dynamics (MD) simulations combined with a randomization algorithm.31–34 Starting from an initial configuration with H2 in proximity to the fullerene surface, the MD simulations allowed for the exploration of different orientations and positions of H2 molecules on the surface. Throughout the simulations, the interatomic interactions between H2 and the fullerene surface were considered using an appropriate force field. During the MD simulations, we sampled a large number of conformations to ensure thorough coverage of the conformational space. Specifically, we generated approximately 2800 random conformations of H2 adsorbed on the fullerene surface. Each conformation represented a unique arrangement and orientation of the H2 molecule relative to the fullerene surface.
Following the generation of these conformations, we performed energy calculations to determine the interaction energies between H2 and the fullerene surface for each conformation. The interaction energy was defined as the energy difference between the H2–fullerene complex and the isolated H2 molecule and pristine fullerene surface. The obtained ensemble of conformations provided valuable insights into the range of possible orientations and arrangements of H2 on the fullerene surface. By analyzing the distribution of interaction energies, we gained a comprehensive understanding of the adsorption behavior and the strengths of the H2–fullerene interactions.
Furthermore, the calculated interaction energies allowed us to identify energetically favorable conformations and investigate the factors influencing the strength of the H2–fullerene interaction. Parameters such as the distance between the H2 molecule and the fullerene surface, as well as the orientation and rotational freedom of the H2 molecule, played crucial roles in determining the interaction energies. To analyze the obtained ensemble of conformations and interaction energies, we performed a comprehensive statistical analysis. We examined the distribution of interaction energies to understand the range and variability of the adsorption strengths. This analysis allowed us to identify trends and patterns in the data, such as the presence of energetically favorable conformations that exhibited stronger H2–fullerene interactions.
Moreover, we conducted a detailed examination of the geometric parameters for each conformation. This involved investigating the distance between the H2 molecule and the fullerene surface, as well as analyzing the orientation and rotational freedom of the H2 molecule with respect to the surface. By correlating these parameters with the corresponding interaction energies, we gained insights into the structural factors influencing the adsorption behavior. The statistical analysis also provided information about the population distribution of different types of conformations. We could identify dominant conformations that represented the most frequently observed orientations or arrangements of H2 on the fullerene surface. This information was valuable for understanding the preferred adsorption configurations and the most stable adsorption sites. To validate the accuracy and reliability of our computational methodology, we compared our calculated interaction energies with available experimental data or theoretical predictions from previous studies. This comparison allowed us to assess the performance of the B97D/TZV2P method in capturing the adsorption behavior of H2 on fullerene surfaces, and to validate the suitability of our generated conformations. Our methodology involved employing DFT calculations with the B97D/TZV2P basis set, combined with MD simulations and a randomization algorithm, to generate a diverse ensemble of approximately 2800 random conformations of H2 on the fullerene surface. The subsequent calculation of the interaction energies provided valuable insights into the adsorption behavior and the factors influencing the H2–fullerene interactions.
3. Results and discussion
3.1. Potential energy surface
There are two major components of potential energy surface, i.e., electrostatic and non-electrostatic forces. The coulombic interactions between charged particles are responsible for the electrostatic component of the potential energy for H2 over fullerene. Meanwhile, the van der Waal interactions between neutral molecules are responsible for the non-electrostatic component of the potential energy surface. If these components are investigated separately, and we assume their separability, then the total energy is calculated by adding the two components. The combination of the two charge schemes helps us to investigate how the two components impact the force field parameters. This presumption streamlines building up a process that makes it straightforward to manage each contribution independently.The potential energy contributions are assumed to be expressed as the sums over the centers of molecules labeled arbitrarily as A and B to make the calculation simple, efficient and easily understandable. Now, totaling the contributions from each center of the two sides, it is easy to describe the interaction between the two molecules by a straightforward and efficient computational manner. An important point is that not all of the molecular systems can be approached by these assumptions. In these cases, the novel methods should necessarily be incorporated according to the specific circumstances:
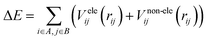 | (1) |
The interactions that occur between molecules can be explained in a variety of ways. These involve the coulombic sums over charges of atoms that are assigned to them. These sums are represented by
 | (2) |
 indicates that the energy is calculated for all pairs of particles from sets A and B.
indicates that the energy is calculated for all pairs of particles from sets A and B.
The PES clearly describes the perceptible contributions of both components, i.e., electrostatic and non-electrostatic forces. The interaction between the charged particles within the molecule is responsible for electrostatic interactions. Meanwhile, the non-electrostatic forces comprise the interactions between the inert particles.
| Vtot(R) = Vnelec(R) + Velec(R) = VILJ(R) + Vcoul(R) | (3) |
The molecular simulation applies the ILJ potential as a model for the characterization of the non-electrostatic part of the PES. Non-electrostatic interactions are usually accredited to the van der Waal interactions. These originate from the distortion produced in the electronic clouds enveloping the atoms or molecules.
 | (4) |
 | (5) |
In Table 1, the “Fitted” column represents the values achieved by fitting the ILJ potential to the H2–fullerene interaction. These fitted values provide information about the interaction energy and can serve as a benchmark for evaluating the performance of different charge models. To determine the “best” charge method, we need to assess how closely the interaction energies obtained using each charge model align with the fitted values. A higher level of agreement indicates a better performance of the charge model in capturing the interaction energy. By comparing the fitted values with the interaction energies calculated using different charge models, we can assess the accuracy and suitability of each method. It is important to note that this comparison should be performed using appropriate statistical measures, such as correlation coefficient (R2), root mean square error (RMSE), or mean absolute error (MAE). For example, if a charge model consistently produces interaction energies that closely match the fitted values, it can be considered more accurate and reliable for the H2–fullerene interaction. Conversely, if a charge model consistently deviates from the fitted values, it indicates a limitation or less favorable performance for this particular system.
| Parameters | Fitted | Hirshfeld | CHelpG | MBS | MK | NBO |
|---|---|---|---|---|---|---|
| qC | 0.446 | 0.482 | 0.493 | 0.445 | 0.472 | 0.466 |
| βHC | 8.452 | 8.726 | 8.596 | 8.497 | 8.871 | 8.982 |
| εHC | 0.379 | 0.419 | 0.399 | 0.385 | 0.486 | 0.392 |
| rHC | 3.345 | 3.375 | 3.463 | 3.591 | 3.388 | 3.395 |
| R-Squared | 0.993422 | 0.99517 | 0.997504 | 0.997953 | 0.997504 | 0.998213 |
| MAES | 0.844685 | 0.788179 | 0.626049 | 0.411928 | 0.436576 | 0.388713 |
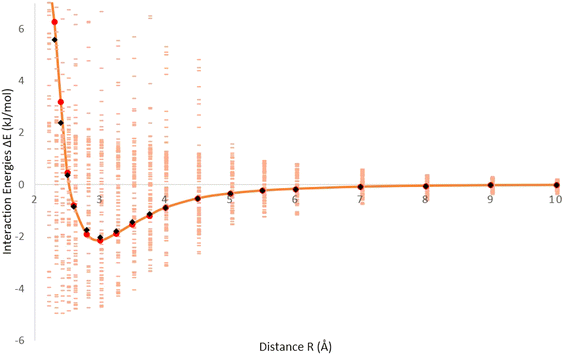
Fig. 1 displays the interaction energies of molecular hydrogen (H2) adsorbed on a fullerene surface. The energies are generated from B97D/TZV2P calculations, and the data points representing the interaction energies are shown in pink. In Fig. 1, there are additional points represented in red, which correspond to the averaged interaction energies. These points are calculated by taking the average of multiple data points to provide a smoother representation of the overall interaction trend. Furthermore, an orange solid line is depicted, which represents the optimized Improved Lennard-Jones (ILJ) potential. This potential is fitted to accurately describe the H2–fullerene interaction energies. The ILJ potential is optimized using the B97D/TZV2P calculations, and provides a mathematical model that captures the interaction behavior between H2 and the fullerene surface. The black data points on the graph represent the Hirshfeld charges, which are obtained from the Hirshfeld charge model. These charges are fitted to the ILJ potential to further refine the accuracy of the potential energy surface. By incorporating the fitted ILJ potential and the Hirshfeld charges, the interaction energies between H2 and the fullerene surface can be more accurately described, providing a better understanding of the H2–fullerene interaction. Fig. 1 represents the relationship between the interaction energies of H2 adsorbed on the fullerene surface, the averaged interaction energies, the optimized ILJ potential, and the incorporation of the Hirshfeld charges. This information allows for a more detailed analysis of the adsorption behavior and the strength of the H2–fullerene interactions.
Fig. 2 represents the electrostatic potential of fullerene (C60),35–38 referring to the distribution of electrostatic forces or charges on the surface of the molecule. It represents the spatial variation of the electric potential generated by the arrangement of electrons within the molecule. ESP provides valuable information about the charge distribution, electron density, and reactivity of fullerene. By analyzing the ESP, one can gain insights into the regions of positive and negative electrostatic potential. Positive regions typically correspond to regions where electrons are relatively depleted, while negative regions indicate areas of electron accumulation. This information can be useful in understanding the interactions and binding sites for other molecules or ions near the fullerene surface. The HOMO of fullerene (C60)39,40 refers to the molecular orbital with the highest energy level that is fully occupied by electrons. It represents the highest energy level among the orbitals containing electrons in the ground state configuration of the molecule. The HOMO plays a crucial role in the chemical reactivity and electronic properties of fullerene. It determines the molecule's ionization potential and is involved in electron transfer processes. The energy and spatial distribution of the HOMO can influence the interaction of fullerene41,42 with other molecules, such as in electron donor–acceptor systems or in chemical reactions. The LUMO of fullerene (C60) refers to the molecular orbital39 with the lowest energy level that is unoccupied by electrons. It represents the lowest unoccupied energy level among the orbitals in the molecule's electronic structure. The LUMO is important for understanding the electronic properties43,44 and reactivity of fullerene.45 It influences the molecule's electron affinity and can participate in electron transfer processes. The energy and spatial distribution of the LUMO are relevant for interactions with electron donors or for involvement in chemical reactions. Both HOMO and LUMO, collectively known as the frontier molecular orbitals, are significant for understanding the electronic structure, chemical reactivity, and optical properties of fullerene (C60). The well-defined HOMO and LUMO values in pristine C60 are evidence of its stability and electrical characteristics. Its electrical characteristics and reactivity are indicated by the energy gap between these orbitals. However, the electrical configuration is changed by the addition of hydrogen. For instance, electron donation from hydrogen to the fullerene via physisorbed hydrogen onto C60 results in a reduction of the energy gap between the HOMO and LUMO levels. As demonstrated by experiments, the binding energies for physisorbed H2 depend on the charge state of the fullerene. This impact is more noticeable when numerous hydrogen molecules are adsorbed. Furthermore, these orbitals can be further stabilized by charge transfer during adsorption, which results in changes in their energy levels. They provide valuable insights into its behavior in various applications, including optoelectronics, photovoltaics, and catalysis. Fig. 2 depicts a comprehensive representation of the electrical characteristics of fullerene. The ESP displays the distribution of charges throughout the molecule. Potential reactivity in chemical interactions is highlighted by the HOMO and LUMO, which provide information about a molecule's capacity to give or take electrons, respectively. The thermodynamic and kinetic characteristics of hydrogen adsorption can be better understood by establishing a correlation between the ESP values and HOMO and LUMO energies. A region has higher adsorption energy if it has the right HOMO/LUMO properties and low ESP values. By using these electronic characteristics as markers, one can anticipate the adsorption behavior of materials based on fullerenes and use that information to inform the development of novel hydrogen storage devices. So, by studying the ESP, HOMO, and LUMO of fullerene,46,47 we can gain a deeper understanding of its charge distribution, electronic structure, and reactivity, enabling the design and development of novel materials and applications based on this unique carbon molecule.
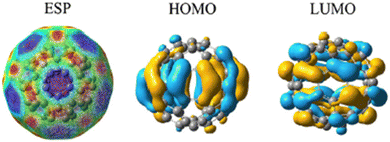 | ||
| Fig. 2 Exploring the electrostatic potential, HOMO, and LUMO of fullerene (C60) and insights into charge distribution and electronic properties. | ||
3.2. Molecular dynamics simulation
Molecular dynamic simulation48,49 is a powerful tool for investigating the adsorption of molecular hydrogen on the surfaces of fullerenes. To apply this method, we first generated virtual models of the fullerene surface50,51 and H2 molecules. Then, mathematical expressions were applied along with a force field to determine the inter-atomic interactions. During the simulation timeframe, the forces acting on atoms and their movements are calculated by simulation. How the molecular hydrogen can approach and interact with the fullerene surface can be studied by molecular dynamics.52,53 This technique is very useful in providing information about the adsorption process, including the distribution of H2 adsorbed on the surface of fullerene, their binding energies and the dynamics of the system. Important information, such as the adsorption energy, points out how strongly the H2 is adsorbed on the fullerene, and can be obtained by analysis of the simulation results. The diffusion of molecules on the fullerene surface54 provides valuable information about the mobility and stability of the adsorbed hydrogen, and can also be investigated by applying the MD simulations. This technique also makes us understand the key mechanism by which adsorption of H2 takes place on the fullerene surface. The simulation successfully evaluated fullerene as an excellent adsorbent material for hydrogen storage55 or other applications.56 This information and direct experimental research offers insightful knowledge regarding the kinetics of the adsorption process57,58 and its thermodynamic studies.For molecular dynamics calculations, we applied DL_POLY.59,60 Periodic boundary conditions were applied in the x, y, and z axes using the microcanonical (NVE) ensemble under standard conditions (273 K and 1 atm). Utilizing a timestep of 1 fs, convergence was demonstrated while monitoring the temperature and energy for a runtime of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps including 3
000 steps including 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 equilibration steps, for a runtime of 5 ns. van der Waals coulombic and coulombic cutoffs were adjusted to 18 Å, and 100H2 molecules were distributed randomly in a cube with 160 Å sides, in order to assure the standard density of H2.
000 equilibration steps, for a runtime of 5 ns. van der Waals coulombic and coulombic cutoffs were adjusted to 18 Å, and 100H2 molecules were distributed randomly in a cube with 160 Å sides, in order to assure the standard density of H2.
The following Einstein equation was applied to compute the diffusion coefficient:
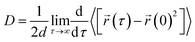 | (6) |
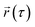 represents the position of the particle of interest at time τ. The term
represents the position of the particle of interest at time τ. The term 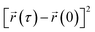 in the equation is the mean-squared-displacement (MSD), which varies linearly over time. To ensure reliable statistics, for each starting configuration, we sampled two million MSD values against time for five specific starting configurations to calculate the diffusion coefficient of H2 gas. By dividing time step 1 to a million, we determined that the diffusion coefficient surpassed one million different time origins. Similarly, timestep 2 was divided to one million and so on. Two different calculation approaches, i.e., density functional theory (DFT) and molecular dynamics (MD) simulations, were selected to investigate the adsorption behavior of H2 on fullerene. Table 2 summarizes the results comprising the distance between hydrogen and the fullerene surface, and the resultant configurational energies (Ecfg) in kilojoules per mole (kJ mol−1).
in the equation is the mean-squared-displacement (MSD), which varies linearly over time. To ensure reliable statistics, for each starting configuration, we sampled two million MSD values against time for five specific starting configurations to calculate the diffusion coefficient of H2 gas. By dividing time step 1 to a million, we determined that the diffusion coefficient surpassed one million different time origins. Similarly, timestep 2 was divided to one million and so on. Two different calculation approaches, i.e., density functional theory (DFT) and molecular dynamics (MD) simulations, were selected to investigate the adsorption behavior of H2 on fullerene. Table 2 summarizes the results comprising the distance between hydrogen and the fullerene surface, and the resultant configurational energies (Ecfg) in kilojoules per mole (kJ mol−1).
| Types of calculation | Distances (Å) | Ecfg (kJ mol−1) |
|---|---|---|
| DFT approach | 2.072 | −33.62 |
| MD (T = 273 K and P = 1 atm) | 2.056 | −32.91 |
In Table 2, the DFT approach predicts a distance of 2.072 Å, while the MD simulation predicts a slightly smaller distance of 2.056 Å. To interact with the carbon atoms surrounding the ring, H2 prefers to adsorb at the hexagonal position. H2 usually has an adsorption geometry parallel to the C60 surface and a weak van der Waals interaction, which results in physisorption. Usually, the H2 molecule and the C60 surface are separated by 2.5–3.5 Å, which denotes weak adsorption. The difference between the two distances is small, indicating reasonably good agreement in terms of the structural aspects of the system. The DFT approach yields a configurational energy of −33.62 kJ mol−1, whereas the MD simulation predicts a value of −32.91 kJ mol−1. The energies obtained from both methods are close, suggesting a relatively good agreement in terms of the energy calculations. Table 2 suggests that there is reasonable agreement between the DFT and MD simulation results. The interatomic distances predicted by the two methods are quite close, indicating consistent structural information. Additionally, the configurational energies obtained from DFT and MD are also in agreement, with relatively small differences. Both DFT and MD simulations have their strengths and limitations. Presenting accurate electronic structure information is the core focus of DFT, but it fails to record the dynamic behavior of atoms. MD simulations can capture the dynamic behavior, but have limitations due to the choice of force fields and simulation parameters.
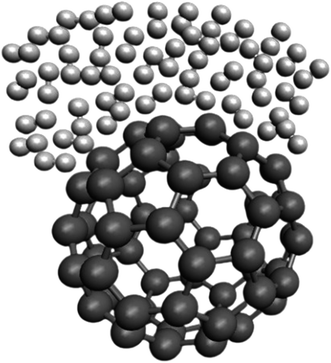
Fig. 3 represents a snapshot of the final configuration of the simulation for the H2/fullerene system at a temperature (T) of 273 K and pressure (P) of 1 atm. The image provides a visual representation of the arrangement of molecules in the system. In Fig. 3, the grey dumbbells represent the carbon surface of the fullerene molecule, which is a cage-like structure composed of carbon atoms. On top of this carbon surface, we see the presence of H2 molecules depicted as random white dumbbells. The white dumbbells represent the H2 molecules, with each dumbbell indicating a hydrogen (H) atom. The color variation within the dumbbells represents different orientations or states of the H2 molecules within the system. By observing this figure, we can visualize the spatial arrangement and distribution of the H2 molecules on the carbon surface of the fullerene. This snapshot provides insights into the relative positions and interactions between the H2 molecules and the carbon surface at the given temperature and pressure conditions.
3.3. Binding energies
According to previous research studies, physisorbed H2 binds to fullerenes like C60 with an energy of about 57 meV for charged complexes and little over 70 meV for neutral complexes. These values are similar to those seen in other carbon-based materials, like carbon nanotubes and graphene, where average physisorption energies are in the range of 50 meV. These adsorption energies can be greatly increased by the insertion of flaws or charges, allowing for the efficient storage of hydrogen at modest pressures.613.4. Influence of structural characteristics
Unlike planar materials like graphene, fullerenes have a unique spherical shape that enables a specific adsorption behavior. For example, fullerenes exhibit less strong corrugation effects than graphene, which result in a more uniform distribution of adsorbed hydrogen molecules over the surface. This feature enable a denser packing of H2 molecules, hence augmenting the total storage capacity.613.5. Adsorption properties
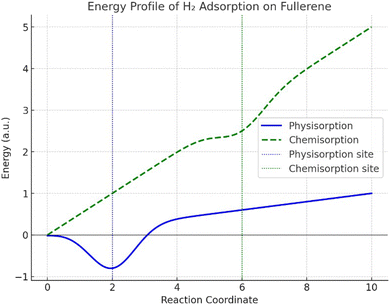
Fig. 4 shows the plot of the total energy (y-axis) as a function of the H2 distance from the fullerene surface (x-axis) after determining the energy at various distances. The x-axis shows the separation between the nearest fullerene carbon atom and the center of mass of H2. A shallow energy well during physisorption (solid blue line) near reaction coordinate 2 indicates a weak interaction between the fullerene and van der Waals forces. Their low energy has been given, which shows that H2 molecules appear to be loosely bonded and readily desorb. The deeper energy well seen during chemisorption (dashed green line) at a higher reaction coordinate (close to 6) suggests a stronger covalent connection between H2 and fullerene. As opposed to physisorption, this process is more persistent because it takes more energy to break the connection. The plot also highlights how the energy profiles of physisorption and chemisorption differ, with chemisorption being a stronger but less reversible process.Fig. 4 shows that the physisorption has a low binding energy, which makes it appropriate for uses requiring the reversible storage of hydrogen. However, chemisorption is more powerful and helpful in situations when fixing hydrogen chemically is required. By adding dopants or defects to fullerene, one can change its energy profile and increase its capacity for adsorption. This procedure shows how fullerene has potential for hydrogen storage applications because of its large surface area and capacity for both types of adsorption. We saw in Fig. 4 how the energy fluctuated with the distance between H2 and fullerene. When H2 approaches fullerene, its energy diminishes, reaching a minimum at approximately 2.5 Å. However, when the molecules approach too closely, repulsive interactions intensify and the energy somewhat rises once again. The energy of the H2–fullerene system at equilibrium distance can be compared to the total of the separate energies of isolated H2 and fullerene to get the adsorption energy, as shown in eqn (7):
| Eads = EH2–fullerene − (EH2 + Efullerene) | (7) |
When H2 is located approximately 2.5 Å away from the fullerene surface, the system is at its most stable configuration. At this moment, the energy is at its lowest and the forces between the molecules are balanced. Another adsorption property is the binding strength. The weak interaction between H2 and fullerene is likely due to the limited adsorption energy. This is to be expected for physisorption, where the binding strength is enough for uses such as reversible hydrogen storage, even though it is less than that of chemical bonding. The adsorption process is probably reversible because physisorption predominates in the contact. Because of this, fullerenes are proven to be helpful in applications requiring hydrogen to be readily adsorbed and desorbed under carefully regulated circumstances.
4. Literature comparison
Using density functional theory (DFT) and molecular dynamics (MD) simulations, another study by Aziz et al. on H2 adsorption on CHA-zeolite reveals the energetic characteristics and binding configurations of H2 inside the zeolite framework. The study highlighted how MD simulations clarify H2 diffusion mechanisms and mobility in porous materials, underscoring the need of comprehending the interaction dynamics to enhance hydrogen storage systems.62In another research study, Hug and Cranford studied the absorption of hydrogen on fullerenes, which is another allotrope that can be compared with that of fullerenes. Fullerenes are sparse structures that resemble fullerenes and have acetylenic substitutions. Because of their higher specific surface area and porosity, fullerenes have been shown to have enhanced hydrogen storage capabilities. Because of their internal architectures, fullerynes allow for enhanced hydrogen diffusivity, while exhibiting nearly equal adsorption energies to fullerenes.62 This implied that in hydrogen storage applications, new carbon allotropes perform better than conventional fullerenes.63
For the diffusion of hydrogen on C60, it is also important to discuss the mechanisms underlying hydrogen's diffusion on fullerene surfaces. On fullerenes, hydrogen can physisorb. However, the curvature and surface topology affect the hydrogen mobility. Research suggests that diffusion occurs more easily in the spherical shape of fullerenes than on flat surfaces such as graphene.63 Faster kinetics in the uptake and release of hydrogen have resulted from this trait.
The potential of fullerenes for storing hydrogen has been supported by recent research. For example, the adsorption behavior in charged fullerene complexes is consistent with earlier experimental findings showing that fullerene surfaces are capable of efficiently stabilizing H2 molecules.61 Furthermore, comparative research indicates that although fullerenes have significant physisorption capacities, they can perform even better if their matrix is modified structurally or contains other components. When contrasting these results with previous research, the energetic parameters for H2 adsorption in various materials consistently show that the adsorption effectiveness was highly dependent on the structural features. The complex nature of the atomic-level interactions is emphasized by diffusion mechanisms, which can occur through metal oxides or zeolites, and vary greatly depending on the composition of the material. Techniques for functionalization, including adding lithium to carbon nanotubes or changing the structure of graphene, have the potential to improve hydrogen storage. In another research by Saha et al., a palladium and ruthenium complex of the C60 fullerene was synthesized by an incipient wetness impregnation method. The resulting complex was characterized with transmission electron microscopy, X-ray diffraction, and Raman spectroscopic analyses. The hydrogen adsorption study was performed at ambient temperature (298 K) and hydrogen pressure up to 300 bar. The hydrogen adsorption experiments allow us to examine the hydrogen storage performance enhancement by the influence of metallic counterparts over fullerene at different pressures, and to elucidate the possible adsorption mechanisms of hydrogen on the metal fullerene complexes.64
The interaction between hydrogen and carbon fullerenes as a function of their curvature was systematically studied in another research study by Vehviläinen et al., with graphene being considered as the limit of zero curvature. Another study found that although hydrogen adsorption on the outer surface was possible, hydrogen accumulation inside fullerenes was unlikely because of a large penetrating barrier. While molecular hydrogen (H2) had been adsorbed if the dissociation activation energy was supplied, atomic hydrogen had been adsorbed in the absence of a barrier. Since fullerene size affects the hydrogen adsorption energy, smaller fullerenes have lower dissociation and adsorption energies. Furthermore, fullerenes adorned with hydrogen can display magnetic characteristics; in fact, a single hydrogen atom induced magnetism, as demonstrated by the 0.85 μB magnetic moment in C32H. This work demonstrated that fullerene magnetization endured with increased hydrogen adsorption, in contrast to previous research that associated magnetism in carbon nanostructures with defects, doping, or high hydrogen coverage.65 Using density functional theory, the properties of Hn@C60 structures, concentrating on the formation energy, C–C bond elongation, and internal hydrogen pressure as functions of the number of hydrogen atoms (n) enclosed in the structure, had been examined by Pupysheva et al. Despite being very endothermic, these structures still correspond to local energy minima when a substantial number of hydrogen atoms were encapsulated. Certain hydrogen atoms had the ability to chemisorb on the inner surface at high values of n, creating covalent C–H bonds. With 58 hydrogen atoms, the maximal metastable structure was formed (H58@C60). Room-temperature ab initio molecular dynamics simulations demonstrated that hydrogen chemisorption weakens C–C bonds, allowing for the opening of nanocages. Furthermore, the study showed the remarkable mechanical properties of fullerene cages, which make them promising candidates for hydrogen storage. A general relationship was derived between the internal pressure and C–C bond elongation in fullerene cages of varying sizes, providing an estimate for the hydrogen storage capacity.66 The findings of our research have been compared with results from previous research work, as shown in Table 3.
| Study | Method | Key findings | Our findings |
|---|---|---|---|
| Hydrogen adsorption on Pd- and Ru-doped C60 fullerene at an ambient temperature64 | Incipient wetness impregnation method | • The hydrogen storage performance enhancement by the influence of metallic counterparts over fullerene at different pressures | • H2 molecules exhibit robust physisorption on the C60 surface, forming stable adsorption structures with favorable adsorption energies |
| • The possible adsorption mechanisms of hydrogen on metal fullerene complexes | • Preferred interaction sites for gas molecules on fullerenes | ||
| Hydrogen interaction with fullerene: from C20 to graphene65 | DFT | • Fullerene magnetization was endured with increased hydrogen adsorption | • Design of hydrogen storage materials contributes to the development of carbon-based nanomaterials |
| Fullerene nanocage capacity for hydrogen storage66 | DFT | • The maximal metastable structure was formed (H58@C60) | • On the C60 surface, H2 molecules showed strong physisorption, generating stable adsorption structures with advantageous adsorption energies |
| • Hydrogen chemisorption weakens C–C bonds, allowed for the opening of nanocages | |||
| • Remarkable mechanical properties of fullerene cages, which make them promising candidates for hydrogen storage |
5. Conclusion
We investigated the adsorption of molecular hydrogen (H2) on the surface of fullerene (C60) by combining density functional theory (DFT) calculations and molecular dynamics (MD) simulations with an improved Lennard-Jones potential force field. Our findings disclose the underlying dynamics and mechanisms of the adsorption process, revealing the interaction between molecular H2 and the C60 surface. We determined the adsorption energies and geometries of H2 on the C60 surface using DFT calculations, uncovering stable adsorption configurations with favorable adsorption energies. Calculations of the electronic structure allowed us to comprehend the nature of the interaction between H2 molecules and the C60 surface, which is crucial for the design of hydrogen storage materials. In addition, our molecular dynamics simulations faithfully captured the intermolecular interactions and dynamic behavior of H2 molecules on the surface of C60. The simulations validated the robust physisorption of H2 and strengthened the stability of the adsorption configurations. These discoveries contribute to our comprehension of hydrogen storage mechanisms and the application of nanomaterials based on carbon. This study provides a comprehensive understanding of H2 adsorption on the C60 surface through a combined DFT and MD simulations approach. The calculated adsorption energies and binding sites provide valuable information for the advancement of hydrogen-related applications and the development of efficient hydrogen storage systems. Future research can investigate the effects of temperature, pressure, and surface modifications on the adsorption behavior of hydrogen on C60. In addition, research on other carbon-based nanostructures and various adsorbates can provide a deeper understanding of the adsorption phenomena, and increase the potential applications of these materials. Our study provides critical insights into the adsorption of H2 on the C60 surface, elucidating the involved mechanisms and dynamics by combining theoretical calculations with simulations. These findings have implications for the design of hydrogen storage materials, and contribute to the development of carbon-based nanomaterials for use in a variety of technological applications.Data availability
Information about the data, software and code supporting the results reported in this published article can be requested via email from the corresponding author.Conflicts of interest
There are no conflicts to declare.References
- M. Nasrollahzadeh, M. S. Sajadi, M. Atarod, M. Sajjadi and Z. Isaabadi, An Introduction to Green Nanotechnology, Academic Press, 2019 Search PubMed.
- C. M. S. Pereira, Computational Study of Ion Selective Separation through Graphene Nanowindows, Universidade do Porto, Portugal, 2019 Search PubMed.
- S. Gadipelli and Z. X. Guo, Graphene-based materials: Synthesis and gas sorption, storage and separation, Prog. Mater. Sci., 2015, 69, 1–60 CrossRef CAS.
- R. Maleki, A. Khoshoei, E. Ghasemy and A. Rashidi, Molecular insight into the smart functionalized TMC-Fullerene nanocarrier in the pH-responsive adsorption and release of anti-cancer drugs, J. Mol. Graphics Modell., 2020, 100, 107660 CrossRef CAS.
- H. Mert, C. U. Deniz and C. Baykasoglu, Monte Carlo simulations of hydrogen adsorption in fullerene pillared graphene nanocomposites, Mol. Simul., 2020, 46(8), 650–659 CrossRef CAS.
- O. Faye, U. Eduok, J. Szpunar, B. Szpunar, A. Samoura and A. Beye, Hydrogen storage on bare Cu atom and Cu-functionalized boron-doped graphene: a first principles study, Int. J. Hydrogen Energy, 2017, 42(7), 4233–4243 CrossRef CAS.
- Y. Zheng, T. J. Slade, L. Hu, X. Y. Tan, Y. Luo, Z. Z. Luo, J. Xu, Q. Yan and M. G. Kanatzidis, Defect engineering in thermoelectric materials: what have we learned?, Chem. Soc. Rev., 2021, 50(16), 9022–9054 RSC.
- J. Joseph, V. S. Sivasankarapillai, S. Nikazar, M. S. Shanawaz, A. Rahdar, H. Lin and G. Z. Kyzas, Borophene and boron fullerene materials in hydrogen storage: opportunities and challenges, ChemSusChem, 2020, 13(15), 3754–3765 CrossRef CAS.
- M. Rampai, C. Mtshali, N. Seroka and L. Khotseng, Hydrogen production, storage, and transportation: recent advances, RSC Adv., 2024, 14(10), 6699–6718 RSC.
- J. Wang, P. R. Arantes, A. Bhattarai, R. V. Hsu, S. Pawnikar, YmM. Huang, G. Palermo and Y. Miao, Gaussian accelerated molecular dynamics: principles and applications, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11(5), e1521 CAS.
- S. E. Marsha Putra, T. D. Kencana Wungu and I. Arif, Ab-Initio Calculation of Chlorophyll-b UV-Vis Absorbance Spectra using Gaussian 09 based Density Functional Theory (DFT), International Journal of Nanoelectronics & Materials, 2021, 14(1), 11–26 Search PubMed.
- M. U. Rahman, S. Khan, H. Khan, A. Ali and F. Sarwar, Computational chemistry unveiled: a critical analysis of theoretical coordination chemistry and nanostructured materials, Chem. Prod. Process Model., 2024, 19(4), 473–515 CrossRef CAS.
- J. Abdul Nasir, A. Munir, N. Ahmad, H. Tu, Z. Khan and Z. Rehman, Photocatalytic Z-Scheme Overall Water Splitting: Recent Advances in Theory and Experiments, Adv. Mater., 2021, 33(52), 2105195 CrossRef CAS PubMed.
- R. M. de Oliveira, L. G. Machado de Macedo, T. F. da Cunha, F. Pirani and R. Gargano, A spectroscopic validation of the improved Lennard-Jones model, Molecules, 2021, 26(13), 3906 CrossRef CAS PubMed.
- R. M. de Oliveira, MdJ. M. B. Neta, J. de Sousa Oliveira, L. G. M. de Macedo, R. F. de Menezes, F. Pirani and R. Gargano, Weakly bound mercury-noble gas adducts: Strength, range and nature of the interaction, spectroscopic and thermodynamical properties, Comput. Theor. Chem., 2024, 1239, 114797 CrossRef CAS.
- H. Liu, G. Qi, Q. Song and H. Wang, Benzene expansion Janus GC base analogues: a detailed theoretical study, J. Photochem. Photobiol., A, 2018, 354, 119–126 CrossRef CAS.
- A. V. Marenich, W. Ding, C. J. Cramer and D. G. Truhlar, Resolution of a challenge for solvation modeling: calculation of dicarboxylic acid dissociation constants using mixed discrete-continuum solvation models, J. Phys. Chem. Lett., 2012, 3(11), 1437–1442 CrossRef CAS PubMed.
- Y. J. Franzke and J. M. Yu, Quasi-relativistic calculation of EPR g tensors with derivatives of the decoupling transformation, gauge-including atomic orbitals, and magnetic balance, J. Chem. Theory Comput., 2022, 18(4), 2246–2266 CrossRef CAS PubMed.
- M. M. Ghahremanpour, P. J. Van Maaren and D. Van Der Spoel, The Alexandria library, a quantum-chemical database of molecular properties for force field development, Sci. Data, 2018, 5(1), 1–10 CrossRef PubMed.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, All-electron scalar relativistic basis sets for third-row transition metal atoms, J. Chem. Theory Comput., 2008, 4(6), 908–919 CrossRef CAS PubMed.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27(15), 1787–1799 CrossRef CAS.
- S. Grimme, Accurate description of van der Waals complexes by density functional theory including empirical corrections, J. Comput. Chem., 2004, 25(12), 1463–1473 CrossRef CAS PubMed.
- C. Peltier, C. Adamo, P. P. Lainé, S. Campagna, F. Puntoriero and I. Ciofini, Theoretical insights into branched and fused expanded pyridiniums by the means of density functional theory, J. Phys. Chem. A, 2010, 114(32), 8434–8443 CrossRef CAS.
- E. R. Johnson, I. D. Mackie and G. A. DiLabio, Dispersion interactions in density-functional theory, J. Phys. Org. Chem., 2009, 22(12), 1127–1135 CrossRef CAS.
- R. Peverati and K. K. Baldridge, Implementation and performance of DFT-D with respect to basis set and functional for study of dispersion interactions in nanoscale aromatic hydrocarbons, J. Chem. Theory Comput., 2008, 4(12), 2030–2048 CrossRef CAS PubMed.
- Y. Cho, W. J. Cho, I. S. Youn, G. Lee, N. J. Singh and K. S. Kim, Density functional theory based study of molecular interactions, recognition, engineering, and quantum transport in π molecular systems, Acc. Chem. Res., 2014, 47(11), 3321–3330 CrossRef CAS.
- S. Mishra, D. Beyer, K. Eimre, S. Kezilebieke, R. Berger, O. Gröning, C. A. Pignedoli, K. Müllen, P. Liljeroth, P. Ruffieux and X. Feng, Topological frustration induces unconventional magnetism in a nanographene, Nat. Nanotechnol., 2020, 15(1), 22–28 CrossRef CAS PubMed.
- S. Mishra, T. G. Lohr, C. A. Pignedoli, J. Liu, R. Berger, J. I. Urgel, K. Müllen, X. Feng, P. Ruffieux and R. Fasel, Tailoring bond topologies in open-shell graphene nanostructures, ACS Nano, 2018, 12(12), 11917–11927 CrossRef CAS.
- S. Mishra, M. Krzeszewski, C. A. Pignedoli, P. Ruffieux, R. Fasel and D. T. Gryko, On-surface synthesis of a nitrogen-embedded buckybowl with inverse Stone–Thrower–Wales topology, Nat. Commun., 2018, 9(1), 1714 CrossRef PubMed.
- K. Low, L. Wylie, D. L. Scarborough and E. I. Izgorodina, Is it possible to control kinetic rates of radical polymerisation in ionic liquids?, Chem. Commun., 2018, 54(80), 11226–11243 RSC.
- J. E. Basconi and M. R. Shirts, Effects of temperature control algorithms on transport properties and kinetics in molecular dynamics simulations, J. Chem. Theory Comput., 2013, 9(7), 2887–2899 CrossRef CAS PubMed.
- L. J. LaBerge and J. C. Tully, A rigorous procedure for combining molecular dynamics and Monte Carlo simulation algorithms, Chem. Phys., 2000, 260(1–2), 183–191 CrossRef CAS.
- D. Hamelberg, J. Mongan and J. A. McCammon, Accelerated molecular dynamics: a promising and efficient simulation method for biomolecules, J. Chem. Phys., 2004, 120(24), 11919–11929 CrossRef CAS PubMed.
- Z. Zhang, J. Wang, Y. Zhang, J. Xu and R. Long, Charge recombination dynamics in a metal halide perovskite simulated by nonadiabatic molecular dynamics combined with machine learning, J. Phys. Chem. Lett., 2022, 13(46), 10734–10740 CrossRef CAS.
- A. M. Bayoumy, Y. O. Osman, H. Elhaes, M. A. Ibrahim and M. A. El-Mansy, Effect of substitutions on the electronic properties of acetylsalicylic acid, Opt. Quantum Electron., 2021, 53, 1–10 CrossRef.
- D.-L. Wang, H.-T. Shen, H.-M. Gu and Y.-C. Zhai, Ab initio studies on the molecular electrostatic potential of C50, J. Mol. Struct.: THEOCHEM, 2006, 776(1–3), 47–51 CrossRef CAS.
- H. Yao, D. Qian, H. Zhang, Y. Qin, B. Xu, Y. Cui, R. Yu, F. Gao and J. Hou, Critical role of molecular electrostatic potential on charge generation in organic solar cells, Chin. J. Chem., 2018, 36(6), 491–494 CrossRef CAS.
- M. Saladina, P. Simón Marqués, A. Markina, S. Karuthedath, C. Wöpke, C. Göhler, Y. Chen, M. Allain, P. Blanchard, C. Cabanetos and D. Andrienko, Charge Photogeneration in Non-Fullerene Organic Solar Cells: Influence of Excess Energy and Electrostatic Interactions, Adv. Funct. Mater., 2021, 31(8), 2007479 CrossRef CAS.
- T. J. Fuhrer, J. Snelgrove, C. A. Corley and S. T. Iacono, Density Functional Theory Investigation of Fulvene-Derivatized Fullerenes as Candidates for Organic Solar Cells, J. Phys. Chem. A, 2020, 124(49), 10324–10329 CrossRef CAS PubMed.
- A. S. Pimenova, A. A. Kozlov, A. A. Goryunkov, V. Y. Markov, P. A. Khavrel, S. M. Avdoshenko, I. N. Ioffe, S. G. Sakharov, S. I. Troyanov and L. N. Sidorov, Synthesis and characterization of difluoromethylene-homo [60] fullerene, C60 (CF 2), Chem. Commun., 2007,(4), 374–376 RSC.
- V. A. Basiuk, Interaction of porphine and its metal complexes with C60 fullerene: a DFT study, J. Phys. Chem. A, 2005, 109(16), 3704–3710 CrossRef CAS.
- S. M. Ryno, M. K. Ravva, X. Chen, H. Li and J. L. Brédas, Molecular understanding of fullerene–electron donor interactions in organic solar cells, Adv. Energy Mater., 2017, 7(10), 1601370 CrossRef.
- A. S. Rad and K. Ayub, Nonlinear optical and electronic properties of Cr-, Ni-, and Ti-substituted C20 fullerenes: a quantum-chemical study, Mater. Res. Bull., 2018, 97, 399–404 CrossRef CAS.
- P. Sood, K. C. Kim and S. S. Jang, Electrochemical and electronic properties of nitrogen doped fullerene and its derivatives for lithium-ion battery applications, J. Energy Chem., 2018, 27(2), 528–534 CrossRef.
- W. Q. Tian, L. V. Liu and Y. A. Wang, Electronic properties and reactivity of Pt-doped carbon nanotubes, Phys. Chem. Chem. Phys., 2006, 8(30), 3528–3539 RSC.
- Q. Zhang, Y. J. Zheng, W. Sun, Z. Ou, O. Odunmbaku, M. Li, S. Chen, Y. Zhou, J. Li, B. Qin and K. Sun, High-efficiency non-fullerene acceptors developed by machine learning and quantum chemistry, Adv. Sci., 2022, 9(6), 2104742 CrossRef CAS PubMed.
- K. Xian, Y. Cui, Y. Xu, T. Zhang, L. Hong, H. Yao, C. An and J. Hou, Efficient Exciton Dissociation Enabled by the End Group Modification in Non-Fullerene Acceptors, J. Phys. Chem. C, 2020, 124(14), 7691–7698 CrossRef CAS.
- M. Rezaian, R. Maleki, M. Dahri Dahroud, A. Alamdari and M. Alimohammadi, pH-sensitive co-adsorption/release of doxorubicin and paclitaxel by carbon nanotube, fullerene, and graphene oxide in combination with N-isopropylacrylamide: a molecular dynamics study, Biomolecules, 2018, 8(4), 127 CrossRef.
- D. Bedrov, G. D. Smith, H. Davande and L. Li, Passive transport of C60 fullerenes through a lipid membrane: a molecular dynamics simulation study, J. Phys. Chem. B, 2008, 112(7), 2078–2084 CrossRef CAS.
- S. Kar, N. Sizochenko, L. Ahmed, V. S. Batista and J. Leszczynski, Quantitative structure-property relationship model leading to virtual screening of fullerene derivatives: exploring structural attributes critical for photoconversion efficiency of polymer solar cell acceptors, Nano Energy, 2016, 26, 677–691 CrossRef CAS.
- H. Li and J. L. Bredas, Comparison of the Impact of Zinc Vacancies on Charge Separation and Charge Transfer at ZnO/Sexithienyl and ZnO/Fullerene Interfaces, Adv. Mater., 2015, 28(20), 3928–3936 CrossRef PubMed.
- M. Murata, S. Maeda, Y. Morinaka, Y. Murata and K. Komatsu, Synthesis and reaction of fullerene C70 encapsulating two molecules of H2, J. Am. Chem. Soc., 2008, 130(47), 15800–15801 CrossRef CAS.
- K. Chandrakumar and S. K. Ghosh, Alkali-metal-induced enhancement of hydrogen adsorption in C60 fullerene: an ab initio study, Nano Lett., 2008, 8(1), 13–19 CrossRef CAS PubMed.
- S. R. Varanasi, O. A. Guskova, A. John and J. U. Sommer, Water around fullerene shape amphiphiles: a molecular dynamics simulation study of hydrophobic hydration, J. Chem. Phys., 2015, 142(22), 206806 CrossRef PubMed.
- M. Yoon, S. Yang, C. Hicke, E. Wang, D. Geohegan and Z. Zhang, Calcium as the Superior Coating Metal in Functionalization of Carbon Fullerenes for High-Capacity Hydrogen Storage, Phys. Rev. Lett., 2008, 100(20), 206806 CrossRef.
- H. Lee, D. G. Park, J. Park, Y. H. Kim and J. K. Kang, Amorphized Defective Fullerene with a Single-Atom Platinum for Room-Temperature Hydrogen Storage, Adv. Energy Mater., 2023, 13(20), 2300041 CrossRef CAS.
- N. A. Elessawy, M. Elnouby, M. H. Gouda, H. A. Hamad, N. A. Taha, M. Gouda and M. S. Eldin, Ciprofloxacin removal using magnetic fullerene nanocomposite obtained from sustainable PET bottle wastes: adsorption process optimization, kinetics, isotherm, regeneration and recycling studies, Chemosphere, 2020, 239, 124728 CrossRef CAS PubMed.
- O. Moradi and K. Zare, Adsorption of Pb (II), Cd (II) and Cu (II) ions in aqueous solution on SWCNTs and SWCNT-COOH surfaces: kinetics studies, Fullerenes, Nanotub. Carbon Nanostruct., 2011, 19(7), 628–652 CrossRef CAS.
- W. Smith, C. Yong and P. Rodger, DL_POLY: application to molecular simulation, Mol. Simul., 2002, 28(5), 385–471 CrossRef CAS.
- W. Smith and I. T. Todorov, A short description of DL_POLY, Mol. Simul., 2006, 32(12–13), 935–943 CrossRef CAS.
- A. Kaiser, C. Leidlmair, P. Bartl, S. Zöttl, S. Denifl, A. Mauracher, M. Probst, P. Scheier and O. Echt, Adsorption of hydrogen on neutral and charged fullerene: Experiment and theory, J. Chem. Phys., 2013, 138(7), 074311 CrossRef CAS.
- M. T. Aziz, S. A. Naqvi, M. R. Janjua, M. Alam and W. A. Gill, Exploring the adsorption behavior of molecular hydrogen on CHA-zeolite by comparing the performance of various force field methods, RSC Adv., 2023, 13(44), 30937–30950 RSC.
- C. Hug and S. W. Cranford, Sparse fulleryne structures enhance potential hydrogen storage and mobility, J. Mater. Chem. A, 2017, 5(40), 21223–21233 RSC.
- D. Saha and S. Deng, Hydrogen adsorption on Pd-and Ru-doped C60 fullerene at an ambient temperature, Langmuir, 2011, 27(11), 6780–6786 CrossRef CAS PubMed.
- T. Vehviläinen, M. Ganchenkova, L. Oikkonen and R. Nieminen, Hydrogen interaction with fullerenes: from C20 to graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(8), 085447 CrossRef.
- O. V. Pupysheva, A. A. Farajian and B. I. Yakobson, Fullerene nanocage capacity for hydrogen storage, Nano Lett., 2008, 8(3), 767–774 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |