Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Positron scattering from interstellar phosphorus-bearing compounds†
Irabati Chakraborty a,
Nafees Uddin
a,
Nafees Uddin b and
Bobby Antony
b and
Bobby Antony *a
*a
aDepartment of Physics, Indian Institute of Technology (Indian School of Mines), Atomic and Molecular Physics Laboratory, Dhanbad – 826004, Jharkhand, India. E-mail: bobby@iitism.ac.in
bApplied Science Department, JIMS Engineering Management Technical Campus, 48/4, Knowledge Park III, Greater Noida, 201308, Uttar Pradesh, India
First published on 10th December 2024
Abstract
This article reports an investigation of positron impact scattering from several phosphorus-bearing compounds detected in the interstellar medium. The targets studied are HCP, CCP, CP, PN, and PO. For our theoretical model, we employed the spherical complex optical potential (SCOP) and complex scattering potential – ionization contribution (CSP-ic) methods. We computed the positron impact integral cross-sections for a wide range of energies, from 1 eV to 5000 eV in a fine energy grid. These cross-sections include positronium formation, direct ionization, total ionization, elastic, differential, and total cross-sections. We compared our newly reported data to molecules with similar structures to assess the quality of the calculated data. These results provide a valuable benchmark for future experimental and theoretical research on these targets.
1 Introduction
Phosphorus is a critical element in the chemistry of life, serving as a foundational component of key biological molecules.1 It is a key component of DNA and RNA, the molecules responsible for storing and transmitting genetic information in all living organisms.2 Phosphorus is also a major part of ATP (adenosine triphosphate), the primary energy carrier in cells, facilitating energy transfer and storage necessary for numerous cellular functions.3 Furthermore, phospholipids contribute to the structure of cell membranes, ensuring cellular integrity and function. The prebiotic importance of phosphorus lies in its ability to facilitate energy transfer and biochemical reactions, making it indispensable for the emergence and sustainability of life.4 The versatility of phosphorus in forming various chemical compounds under prebiotic conditions has led to the hypothesis that it could have been a key element in the early stages of biochemical evolution.5,6 The widespread distribution of phosphorus on Earth reflects its fundamental role in biological and geological processes.7 Recent studies have identified several phosphorus-bearing compounds, such as PO (phosphorus monoxide), PN (phosphorus mononitride), CP (carbon monophosphide), CCP radical, and HCP (phosphaethyne), in the gas phase of circumstellar envelopes around evolved stars.8 Among these, PO and PN have been detected in star-forming regions.9 Therefore, the study of phosphorus in prebiotic chemistry is not only vital for understanding the origin of life on Earth but also for exploring the potential for life elsewhere in the universe.10The first detection of a phosphorus-bearing compound in space began with PN (phosphorus mononitride), which Turner and Bally discovered in 1987 in the Orion Molecular Cloud using millimeter-wave observations.11 Since then, PN has been detected in several star-forming regions and remained the only phosphorus-containing species identified in dense interstellar mediums (ISM) for many years,12–14 until PO (phosphorus monoxide) was discovered by Rivilla et al. in 2016 in massive star-forming regions, along with PN, using the IRAM 30 m telescope.9 Guélin et al. subsequently identified CP (carbon monophosphide) in the circumstellar envelope of the star IRC+10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 216 in 1990.15 Agúndez et al. discovered HCP (phosphaethyne) in the circumstellar envelope of IRC+10
216 in 1990.15 Agúndez et al. discovered HCP (phosphaethyne) in the circumstellar envelope of IRC+10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 216 using millimeter-wave spectroscopy.16 Halfen et al. detected the CCP radical in IRC+10
216 using millimeter-wave spectroscopy.16 Halfen et al. detected the CCP radical in IRC+10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 216 in 2008.17 These discoveries have significantly contributed to our understanding of phosphorus chemistry in space.
216 in 2008.17 These discoveries have significantly contributed to our understanding of phosphorus chemistry in space.
The study of positron scattering with molecules plays a pivotal role in bridging fundamental physics with practical applications across various fields. These studies enhance our understanding of fundamental interactions by resolving how positrons, the anti-particles of electrons, interact with matter. In recent decades, there has been increased interest in positron scattering from various targets, owing to its contributions across several fields, including medical sciences, atomic physics,18,19 astrophysics,20,21 and spectroscopy.22,23 Positron–molecule interaction cross sections are crucial for understanding particle track simulations.24 These cross sections are fundamental inputs for modeling software like GEANT,25 PENELOPE,26 EPOTRAN,27 and LEPTS,28 which use them to estimate radiation-induced damage. Positron Emission Tomography (PET)29,30 is a powerful medical imaging technique used to observe metabolic processes in the body. Oncology, neurology, and cardiology widely use it for diagnosing and monitoring diseases such as cancer, Alzheimer's disease, and heart conditions. In PET imaging, cross-section data is essential for modeling the scattering behavior of positrons, enabling more accurate simulations of their trajectories.31,32 In the past, positron scattering experiments were challenging to conduct, primarily due to limited access to high-resolution positron beams and the complexity involved in distinguishing the different partial cross sections. Thus, theoretical studies of positron scattering cross sections are essential for advancing science, interpreting astronomical data, improving material research, and guiding experimental efforts.
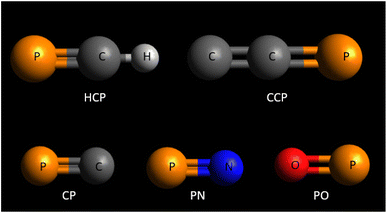
In this work, we focused on the positron impact cross sections for a set of phosphorus-bearing compounds that have been identified in the interstellar medium. The specific compounds examined include HCP, CCP, CP, PN, and PO. The structure of these phosphorus-bearing compounds are given in Fig. 1. To achieve a comprehensive analysis, we utilized well-established theoretical models, the spherical complex optical potential (SCOP), and the CSP-ic (complex scattering potential – ionization contribution) methods. These two methods have been widely used to calculate electron33–37 and positron38–40 scattering cross sections for various atomic and molecular targets across a wide range of energy. Given that there are no previous experimental or theoretical studies available for these specific targets, we compared our findings with those of molecules that possess similar structures and bonding characteristics. This approach allowed us to validate our results against known data, even though direct comparisons for the exact compounds were not possible. The different types of positron impact cross sections that we computed in our study are total cross sections, positronium formation cross sections, direct ionization cross sections, elastic cross sections, total ionization cross sections, and elastic differential cross sections. We conducted these calculations across an extensive energy range, ranging from 1 eV to 5000 eV. This broad energy span ensures that our results cover a significant portion of the relevant physical processes involved in positron interactions with these phosphorus-bearing compounds. The present study aims to provide detailed data that will serve as a benchmark for future experimental and theoretical investigations in the field. By offering a comprehensive set of cross-section data, our findings will aid researchers in validating and refining their models and experiments, ultimately advancing the understanding of positron–molecule interactions in various scientific and practical applications.
2 Theoretical methodology
This study employs a modified version of the well-established optical potential formalism, SCOP, along with the CSP-ic method38–40 to compute various cross-sections. A single-center additivity rule (SCAR) is considered for all the molecules, as these targets are compact in structure. In the SCAR method, the molecular charge density and potential are obtained from the atomic charge densities and potentials by expanding them from the center of mass of the respective target before calculating the cross sections of the molecule. In the SCOP formalism, the positron–target interaction is modeled by a complex potential,| Vopt = VR + iVI = Vst + Vpol + iVabs | (1) |
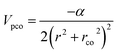 | (2) |
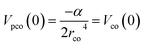 , which makes Vpco(r) and Vco(r) equal at the origin. In the near target region, Vpco(r) approaches Vco(r) and at large r, it takes the asymptotic form −α/2r4. The mathematical form of the correlation potential Vco(r) proposed by Perdew and Zunger is given as,
, which makes Vpco(r) and Vco(r) equal at the origin. In the near target region, Vpco(r) approaches Vco(r) and at large r, it takes the asymptotic form −α/2r4. The mathematical form of the correlation potential Vco(r) proposed by Perdew and Zunger is given as,
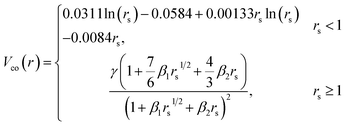 | (3) |
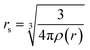 is the density parameter, ρ(r) is the charge density of the target and γ, β1 and β2 are the constants having values −0.1423, 1.0523, and 0.3334 respectively.
is the density parameter, ρ(r) is the charge density of the target and γ, β1 and β2 are the constants having values −0.1423, 1.0523, and 0.3334 respectively.
On the other hand, Vabs is the imaginary part. It takes into account all the inelastic processes and shows how much of the incident flux is lost through all the possible inelastic channels when the positron is scattered by the target. In the present calculation, electronic excitations, positronium (Ps) formation, and direct ionization are the inelastic channels considered. For the absorption potential we have adopted the parametric form proposed by Reid and Wadehra.44 It is given as follows:
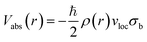 | (4) |
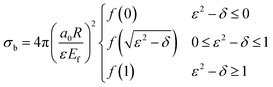 | (5) |
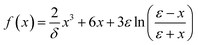 | (6) |
The parameters used in this expression are defined as 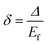 and
and 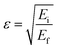 . Here, Δ represents the inelastic threshold, Ei is the incident energy of the projectile, and Ef is the Fermi energy associated with the target charge density.
. Here, Δ represents the inelastic threshold, Ei is the incident energy of the projectile, and Ef is the Fermi energy associated with the target charge density.
The main challenge in the case of positron scattering is defining the inelastic threshold, below which all inelastic processes are prohibited. Reid and Wadehra proposed using the energy (Δp) needed for Ps formation as the absorption threshold (Δ). However, this approach tends to slightly overestimate the total cross-section at higher energies. To address this problem, we modified Chiari's45 exponential form of the threshold by substituting the target's electronic excitation energy with its ionization potential (IP). We made this change because the positronium formation threshold for many targets nearly matches their electronic excitation energy, leading to inaccurate results. This work uses a modified form of the inelastic threshold given by,
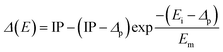 | (7) |
In the above equation, Δp is the energy level at which positronium (Ps) starts to form, and Em is the energy level at which the absorption potential (Vabs) generates the maximum cross section in the absence of Ps formation.
Unlike the electron scattering case, the presence of the Ps formation channel prevents the CSP-ic method from estimating the ionization cross section directly from the inelastic cross section. To overcome this, another inelastic cross section (Qin) is introduced, excluding the Ps formation channel. This new inelastic cross section is employed to calculate the direct ionization cross section (Qiond) using the well-known CSP-ic method. The Ps formation cross section (Qps) is calculated using the equation,
| Qps(Ei) = Qinel(Ei) − Qin(Ei) | (8) |
| Qiont(Ei) = Qiond(Ei) + Qps(Ei) | (9) |
The target properties such as ionization potential (IP), positronium formation threshold (Δp) and polarizability (α) that are used in this work are presented in Table 1. All the target properties of the targets HCP, CP, PN and PO are taken from the CCCBDB database.46 The ionization potential values of these targets provided in the database are experimentally measured. However, since experimentally determined polarizability values are unavailable for all these targets, calculated polarizabilities through Density Functional Theory (wB97X-D) with the aug-cc-pVTZ basis set were used. The target properties of CCP radical are not available in the CCCBDB database. Therefore, the molecular geometry of the CCP was built using Avogadro molecular modelling software48 and optimized using Density Functional Theory (B3LYP)49 method along with basis set def2-QZVPP50 and auxiliary basis set def2/J.51 Geometry optimization along with ionization potential and polarizability calculations were performed using ORCA 5.0.1 (ref. 47) and visualized in Gabedit.52
3 Results
This section presents graphical representations of different cross-sections for positron impact scattering on the selected targets.3.1 Total cross section
Fig. 2 shows the total cross section of HCP and CCP across a wide energy range from 1 eV to 5000 eV. The total cross section trend is similar for both targets, but CCP has a higher magnitude across the entire energy range due to its larger size. For HCP, the total cross section Qtot initially shows a plateau at lower energies until the energy reaches the Ps formation threshold. Beyond this threshold, the cross section increases, peaking at 26.612 Å2 at 13 eV, and then decreases monotonically. Similarly, for CCP, Qtot increases beyond the Ps formation threshold, reaching a maximum value of 45.242 Å2 at 9 eV, before decreasing monotonically at higher energies.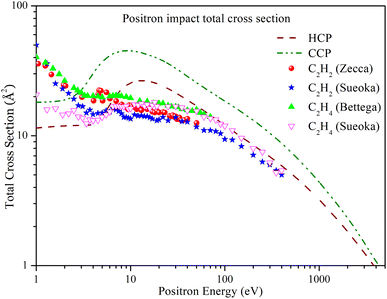 | ||
| Fig. 2 Positron impact total cross section of HCP and CCP compared with experimental Qtot of C2H2 and C2H4. Dashed line: HCP; dashed dot dotted line: CCP; solid spheres: C2H2 measured by Zecca et al.;53 solid stars: C2H2 measured by Sueoka et al.;54 solid triangles: C2H4 measured by Bettega et al.;55 hollow inverted triangles: C2H4 measured by Sueoka et al.56 | ||
In the absence of previous experimental or theoretical studies on these targets, we compared the present results with those of acetylene (C2H2) and ethylene (C2H4) molecules. Acetylene is a linear molecule with a carbon–carbon triple bond, similar to the carbon-phosphorus triple bond in HCP. As a result, we used acetylene to compare HCP's total cross-section. We selected ethylene for comparison with CCP because it has a linear structure and a carbon–carbon double bond similar to CCP's.
Fig. 2 includes experimental total cross-section data for acetylene measured by Zecca et al.53 and Sueoka et al.54 Except at energies below 10 eV, there is qualitative agreement between the cross-section values of acetylene and HCP. In this study, rotational and vibrational cross sections were not considered, which may cause lower cross section values at energies below the Ps formation threshold. Furthermore, the study fails to adjust the experimental values for forward angle scattering, which could result in an overestimation of the cross-section values. In the intermediate energy range from 10 eV to 100 eV, the cross section of HCP is higher than that of acetylene, as expected due to its larger size. As energy increases, the difference in the magnitude of their cross-section decreases. The Qtot measured by Sueoka et al.54 aligns well with the present Qtot of HCP above 100 eV.
The figure also includes experimental total cross-section data for ethylene measured by Bettega et al.55 and Sueoka et al.56 The data reported by Bettega are much higher than the present results at lower energies. In our approach, rotational and vibrational contributions were not included, which may cause an underestimation of the total cross section (TCS) compared to experimental values. Sueoka's data align well with the present results at lower energies below the Ps formation threshold. At higher energies, the larger size of the phosphorus atom in CCP justifies a significantly higher cross section than that of ethylene.
Fig. 3 shows the energy dependence of the total cross section of CP, PN, and PO over a range of 1 eV to 5000 eV. The cross-sections of CP and PN show similar trends. For CP, the total cross section Qtot initially exhibits a plateau at lower energies until it reaches the Ps formation threshold. Beyond this threshold, the cross section increases, peaking at 23.642 Å2 at 12 eV, and then decreases monotonically. Similarly, for PN, Qtot increases beyond the Ps formation threshold, reaching a maximum value of 18.787 Å2 at 18 eV, before decreasing monotonically at higher energies. The cross section of PO increases with energy, peaking at 30.363 Å2 at 6 eV, and then decreases monotonically at higher energies. The graph shows that for all three targets, the Qtot converges at higher energies.
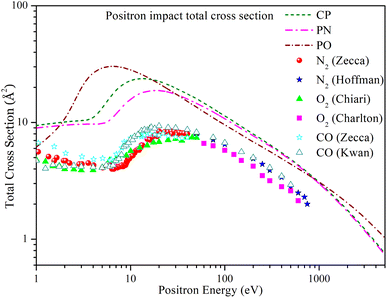 | ||
| Fig. 3 Positron impact total cross section of CP, PN, and PO compared with experimental Qtot of N2, O2 and CO. Short dashed line: CP; dashed dotted line: PN; short dashed dotted line: PO; solid spheres: N2 measured by Zecca et al.;53 solid stars: N2 measured by Hoffman et al.;57 solid triangles: O2 measured by Chiari et al.;45 solid squares: O2 measured by Charlton et al.;58 hollow stars: CO measured by Zecca et al.;53 hollow triangles: CO measured by Kwan et al.59 | ||
In the absence of previous experimental or theoretical studies on these targets, we have chosen CO, N2, and O2 molecules for comparison. The CO molecule has a carbon–oxygen triple bond, similar to the phosphorus–carbon triple bond in CP. We compare the N2 molecule, which has a nitrogen–nitrogen triple bond, with PN, which has a similar phosphorus–nitrogen triple bond. Lastly, we compare the O2 molecule, which has an oxygen–oxygen double bond, to PO, which also has a similar phosphorus–oxygen double bond.
Fig. 3 includes experimental Qtot data for CO measured by Zecca et al.53 and Kwan et al.,59 for N2 measured by Zecca et al.53 and Hoffman et al.,57 and for O2 measured by Chiari et al.45 and Charlton et al.58 The experimental cross sections show a similar trend to the present results, but the present Qtot values have a higher magnitude across the entire energy range. A significant contribution to such differences comes from the positronium formation cross sections.
3.2 Positronium formation cross section
In Fig. 4, the positronium formation cross section (Qps) is plotted as a function of energy for all five targets. For all targets, the general trend of Qps is similar: it starts increasing above the Ps formation threshold, reaches a peak, and then decreases monotonically, fading out beyond 150 eV. According to the figure, Qps for HCP and CP almost overlap up to 7 eV. Beyond 7 eV, Qps for HCP is slightly higher than for CP, but they converge again beyond 30 eV. Qps for HCP reaches its maximum value of 15.704 Å2 at 12 eV, while for CP it peaks at 13.663 Å2 at 11 eV. For CCP and PO, Qps increases with energy, plateaus around 10 eV, and then decreases monotonically. The maximum Qps for CCP is 27.336 Å2 at 9 eV, and for PO it is 19.713 Å2 at 6 eV. For PN, Qps is relatively lower than for the other targets. It increases with energy, peaks at 9.576 Å2 at 14 eV, and then merges with the others beyond 30 eV.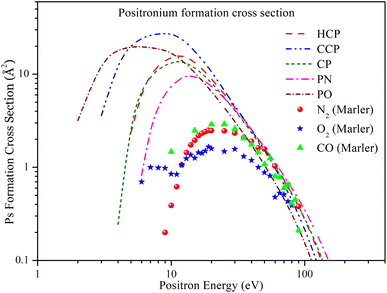 | ||
| Fig. 4 Positron impact Ps formation cross section of all phosphorus-bearing compounds compared with experimental Qps of N2, O2 and CO. Dashed line: HCP; dashed dot dotted line: CCP; short dashed line: CP; dashed dotted line: PN; short dashed dotted line: PO; solid spheres: N2;60 solid stars: O2;60 solid triangles: CO.60 | ||
Since there are no previous theoretical or experimental studies on these targets, we have included experimental Qps data for CO, N2, and O2 reported by Marler et al.60 The figure shows that the experimental Qps values are significantly lower than our results, which can be attributed to the presence of the phosphorus atom in the chosen targets.
3.3 Direct ionization cross section
In Fig. 5, the direct ionization cross section (Qiond) is plotted against energy. The general trend for Qiond is similar for all targets: it increases rapidly above the ionization threshold, reaches a maximum value, and then decreases monotonically. CCP has a higher magnitude of cross section over the entire energy range, with Qiond reaching its peak value of 11.127 Å2 at 40 eV. HCP and CP have almost overlapping cross sections across the entire energy range, although HCP has a slightly higher maximum value of Qiond of 6.612 Å2 at 48 eV, compared to 6.015 Å2 at 50 eV for CP. At lower energies, PN shows a relatively lower magnitude of Qiond, reaching its maximum value of 5.128 Å2 at 60 eV. However, as energy increases above 100 eV, the differences in Qiond diminish, and at higher energies, the values for HCP, CP, PO, and PN align with each other.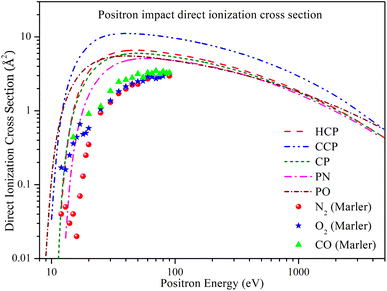 | ||
| Fig. 5 Positron impact direct ionization cross section of all phosphorus-bearing compounds compared with experimental Qiond of N2, O2 and CO. Dashed line: HCP; dashed dot dotted line: CCP; short dashed line: CP; dashed dotted line: PN; short dashed dotted line: PO; solid spheres: N2;60 solid stars: O2;60 solid triangles: CO.60 | ||
Because there were no previous theoretical or experimental studies on the selected targets, we included experimental direct ionization cross-section data for CO, N2, and O2 reported by Marler et al.60 However, these data are only available up to 100 eV. The figure shows that the trend of the experimental data is similar to our results, although the experimental Qiond values are relatively lower. This discrepancy is likely due to the presence of heavier phosphorus atoms in the chosen targets.
3.4 Elastic cross section
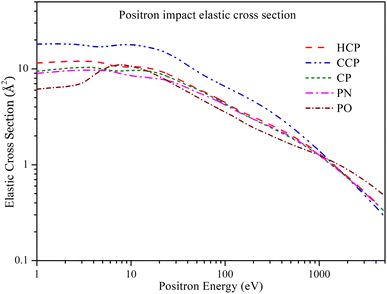
In Fig. 6, the positron impact elastic cross section (Qel) is plotted as a function of energy over a range from 1 eV to 5000 eV. Due to the lack of available data for comparison in the literature, we compared the Qel values of the targets with each other. For all targets, the general trend of Qel is similar. CCP has a higher magnitude of Qel up to 1000 eV, after which Qel for CCP, HCP, CP, and PN align with each other. The PO's Qel is slightly higher than the others above 1000 eV. For PO, Qel exhibits a plateau at lower energies up to 3 eV, then increases to a peak value of 11.01 Å2 at 8 eV, and subsequently decreases to a minimum of 0.472 Å2 at 5000 eV. The other four targets (CCP, HCP, CP, and PN) show a plateau at lower energies up to 10 eV, beyond which Qel starts decreasing. At lower energies, Qel for HCP, CP, and PN have slightly different values, but these differences diminish as energy increases. Above 100 eV, Qel for HCP, CP, and PN overlap with each other.3.5 Total ionization cross section
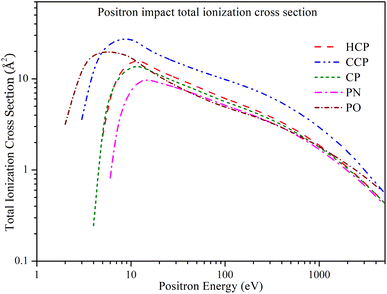
In Fig. 7, we can see how the positron impact total ionization cross section (Qiont) changes with energy from 1 eV to 5000 eV. Due to the absence of comparable data in the literature, we have compared the Qiont values for the targets with each other. The general trend of Qiont is similar across all targets: the cross sections increase above the Ps formation threshold, reach a maximum value, and then decrease as the energy increases. CCP exhibits a higher magnitude of Qiont over the entire energy range, with a peak value of 27.336 Å2 at 9 eV. HCP and CP have overlapping Qiont values at lower energies. However, HCP has a slightly higher maximum value of Qiont than CP. Qiont of HCP achieves its maximum value of 15.753 Å2 at 12 eV, whereas Qiont for CP reaches its peak value of 13.666 Å2 at 11 eV. As the energy increases, the difference between their cross sections decreases. PN shows a relatively lower Qiont at lower energies, reaching a maximum value of 9.679 Å2 at 14 eV. It then decreases and aligns with the Qiont of PO from 40 eV to 400 eV. Beyond 400 eV, the Qiont of PN aligns with that of HCP and CP. For PO, Qiont reaches its maximum value at a lower energy compared to the other targets, peaking at 19.713 Å2 at 6 eV, and then decreases as the energy increases.3.6 Differential cross section
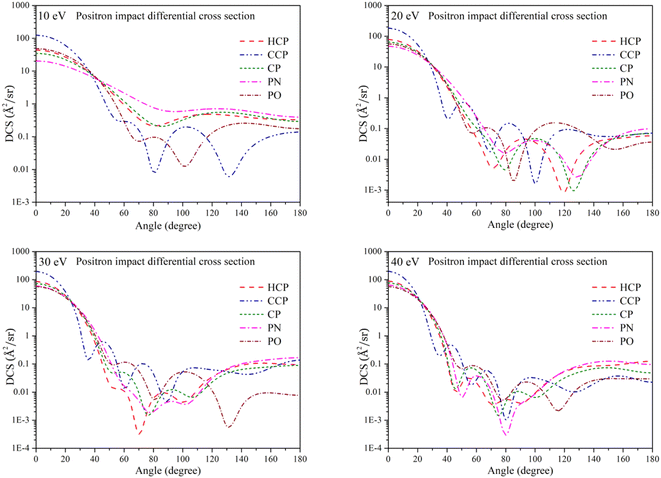
Fig. 8 shows the elastic differential cross section (DCS) as a function of scattering angle at positron impact energies of 10, 20, 30, and 40 eV. The scattering angle is measured relative to the direction of the incident particle approaching the target molecule. Which means, the scattering angle is defined as the angle between the incoming positron's initial trajectory and the direction of the scattered positron after interacting with the target. The differential cross-section data explains the scattering of positrons at different angles during interactions with various compounds. The DCS data helps to model the scattering behavior of positrons, allowing for more accurate simulations of their paths. This modeling improves the precision of image reconstruction algorithms used in positron emission tomography (PET) imaging. At small scattering angles, the DCS curves initially had high values, indicating strong forward scattering. This occurs because of the coulombic interaction, i.e., the long-range part of the potential. As the scattering angle increases, the probability of scattering typically decreases. The diminishing influence of long-range interactions at larger angles is responsible for this decrease. In addition to this decrease, an oscillatory behavior is observed for CCP and PO at 10 eV. As the energy increases, other targets start exhibiting this oscillation as well. This oscillatory nature of the DCS curves arises from the contributions of different partial waves, each associated with a specific angular momentum quantum number. When these partial waves scatter off a target, they interfere constructively or destructively depending on the scattering angle. At certain angles, partial waves interfere constructively, resulting in a peak in the differential cross section. At other angles, they interfere destructively, leading to dips. This interference pattern leads to the observed oscillations in the cross section. The point where the DCS curve reaches its minimum value represents the angle at which the scattering probability is the lowest. The increase in DCS toward 180° suggests a higher probability of backscattering. This can be attributed to polarization effects, in which the positron induces a dipole in the target, increasing scattering at larger angles.4 Conclusion
This research investigates the positron impact cross sections for many phosphorus-containing compounds, such as HCP, CCP, CP, PN, and PO, at a wide energy range. The results provide important information about how positrons interact with these molecules. This helps us to understand their role in the interstellar medium and how they might be used in areas like positron emission tomography (PET) imaging. The total cross-section analysis (Qtot) showed that CCP always has the highest cross-section across all energy ranges. This is due to its larger molecular size compared to other targets. HCP and CP showed similar trends, with HCP having slightly higher cross-section values, while PN displayed relatively lower cross-sections. PO exhibited unique behavior, with an earlier peak and a more rapid decrease, indicating distinct interaction dynamics, possibly due to the presence of a double bond. Additionally, the higher cross section of PO may result from oxygen's higher atomic number compared to carbon and nitrogen. In the absence of previous data on these specific targets, we made comparisons with molecules such as acetylene, ethylene, CO, N2, and O2, which revealed qualitative agreements and highlighted the influence of the phosphorus atom in the observed increased cross-section values. This comparative approach allowed for a better understanding of the molecular similarities and differences in scattering behavior. For all targets, the positronium formation cross section (Qps) and direct ionization cross section (Qiond) data showed similar trends, with clear peaks corresponding to different regions of energies. The presence of phosphorus in the targets significantly affected the Qps and Qiond, leading to higher values compared to the analogous molecules without phosphorus. These results were further supported by the elastic cross section (Qel) and total ionization cross section (Qiont) data, which showed consistent trends across the energy spectrum and among the different targets. Differential cross-section (DCS) analysis at various positron impact energies provided detailed information on the scattering behavior at different angles. At smaller angles, strong forward scattering was observed, reflecting the dominance of coulombic interactions. The oscillatory nature of the DCS curves, with peaks and dips resulting from constructive and destructive interference of partial waves, emphasizes the role of angular momentum in positron–molecule interactions. The variations in DCS across the different targets underscored the role of molecular structure in determining scattering behavior. In conclusion, this study not only fills a critical gap in the literature by providing cross-sectional data for previously unstudied phosphorus-bearing compounds but also underscores the importance of such data in understanding the physical and chemical processes in the interstellar medium. The results highlight the significance of the phosphorus atom in altering scattering dynamics, paving the way for further theoretical and experimental investigations. The present study also holds potential implications for practical applications, particularly in the refinement of imaging techniques in medical diagnostics.Data availability
See the ESI† for numerical cross-section data for the present targets (PDF).Conflicts of interest
There are no conflicts of interest.References
- C. Fernández-García, A. J. Coggins and M. W. Powner, Life, 2017, 7, 31 CrossRef.
- E. Maciá*, M. Hernández and J. Oró, Origins Life, 1997, 27, 459–480 CrossRef.
- J. W. Błaszczyk, Metabolites, 2023, 13, 860 CrossRef.
- O. I. Kolodiazhnyi, Symmetry, 2021, 13, 889 CrossRef CAS.
- Y. Zhao, Y. Liu, X. Gao and P. Xu, Phosphorus Chemistry: the Role of Phosphorus in Prebiotic Chemistry, Walter de Gruyter GmbH & Co KG, 2018 Search PubMed.
- A. W. Schwartz, Philos. Trans. R. Soc., B, 2006, 361, 1743–1749 CrossRef CAS PubMed.
- C. R. Walton, S. Ewens, J. D. Coates, R. E. Blake, N. J. Planavsky, C. Reinhard, P. Ju, J. Hao and M. A. Pasek, Nat. Geosci., 2023, 16, 399–409 CrossRef CAS.
- V. Rivilla, I. Jiménez-Serra, S. Zeng, S. Martín, J. Martín-Pintado, J. Armijos-Abendaño, S. Viti, R. Aladro, D. Riquelme and M. Requena-Torres, et al., Mon. Not. R. Astron. Soc.:Lett., 2018, 475, L30–L34 CrossRef CAS.
- V. Rivilla, F. Fontani, M. Beltrán, A. Vasyunin, P. Caselli, J. Martín-Pintado and R. Cesaroni, Astrophys. J., 2016, 826, 161 CrossRef.
- Z. R. Todd, Life, 2022, 12, 1268 CrossRef CAS PubMed.
- B. Turner and J. Bally, Astrophys. J., 1987, 321, L75–L79 CrossRef CAS.
- L. M. Ziurys, Astrophys. J., 1987, 321, L81–L85 CrossRef CAS.
- B. Turner, T. Tsuji, J. Bally, M. Guelin and J. Cernicharo, Astrophys. J., 1990, 365, 569–585 CrossRef CAS.
- F. Fontani, V. Rivilla, P. Caselli, A. Vasyunin and A. Palau, Astrophys. J., Lett., 2016, 822, L30 CrossRef.
- M. Guélin, J. Cernicharo, G. Paubert and B. Turner, Astron. Astrophys., 1990, 230, L9–L11 Search PubMed.
- M. Agúndez, J. Cernicharo and M. Guélin, Astrophys. J., 2007, 662, L91 CrossRef.
- D. Halfen, D. Clouthier and L. M. Ziurys, Astrophys. J., 2008, 677, L101 CrossRef CAS.
- G. Ryzhikh, J. Mitroy and K. Varga, J. Phys. B: At., Mol. Opt. Phys., 1998, 31, 3965 CrossRef CAS.
- M. Puska, P. Lanki and R. Nieminen, J. Phys.: Condens. Matter, 1989, 1, 6081 CrossRef CAS.
- N. Guessoum, R. Ramaty and R. E. Lingenfelter, Astrophys. J., 1991, 378, 170–180 CrossRef CAS.
- R. Murphy, G. Share, J. Skibo and B. Kozlovsky, Astrophys. J., Suppl. Ser., 2005, 161, 495 CrossRef CAS.
- A. Dupasquier and A. Mills Jr, Positron Spectroscopy of Solids, IOS press, 1995, vol. 125 Search PubMed.
- P. G. Coleman, in Encyclopedia of Applied Spectroscopy, Wiley-VCH, 2009, pp. 115–152 Search PubMed.
- P. Arce, A. Muñoz, M. Moraleda, J. M. Gomez Ros, F. Blanco, J. M. Perez and G. García, Eur. Phys. J. D, 2015, 69, 1–5 CrossRef.
- S. Agostinelli, J. Allison, K. a. Amako, J. Apostolakis, H. Araujo, P. Arce, M. Asai, D. Axen, S. Banerjee and G. Barrand, et al., Nucl. Instrum. Methods Phys. Res., Sect. A, 2003, 506, 250–303 CrossRef CAS.
- J. Baró, J. Sempau, J. Fernández-Varea and F. Salvat, Nucl. Instrum. Methods Phys. Res., Sect. B, 1995, 100, 31–46 CrossRef.
- C. Champion, C. Le Loirec and B. Stosic, Int. J. Radiat. Biol., 2012, 88, 54–61 CrossRef CAS.
- F. Blanco, A. Munoz, D. Almeida, F. Ferreira da Silva, P. Limao-Vieira, M. C. Fuss, A. G. Sanz and G. García, Eur. Phys. J. D, 2013, 67, 1–18 CrossRef.
- M. E. Phelps, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 9226–9233 CrossRef CAS PubMed.
- S. Jan, G. Santin, D. Strul, S. Staelens, K. Assié, D. Autret, S. Avner, R. Barbier, M. Bardiès and P. Bloomfield, et al., Phys. Med. Biol., 2004, 49, 4543 CrossRef CAS PubMed.
- S. Salvador, J. Colin, D. Cussol, C. Divay, J.-M. Fontbonne and M. Labalme, Phys. Rev. C, 2017, 95, 044607 CrossRef.
- R. E. Robson, M. J. Brunger, S. J. Buckman, G. Garcia, Z. L. Petrović and R. D. White, Sci. Rep., 2015, 5, 12674 CrossRef CAS PubMed.
- D. Gupta, R. Naghma, B. Goswami and B. Antony, RSC Adv., 2014, 4, 9197–9204 RSC.
- B. Goswami, R. Naghma and B. Antony, RSC adv., 2014, 4, 63817–63823 RSC.
- J. Kaur, R. Naghma and B. Antony, RSC Adv., 2015, 5, 20090–20097 RSC.
- P. Modak, J. Kaur and B. Antony, Phys. Plasmas, 2017, 24, 083514 CrossRef.
- I. Chakraborty, N. Sinha and B. Antony, Chem. Phys., 2023, 573, 111974 CrossRef CAS.
- S. Singh, S. Dutta, R. Naghma and B. Antony, J. Phys. Chem. A, 2016, 120, 5685–5692 CrossRef CAS.
- S. Singh and B. Antony, Phys. Plasmas, 2018, 25, 053503 CrossRef.
- N. Sinha, A. K. Sahoo and B. Antony, J. Phys. Chem. A, 2020, 124, 5147–5156 CrossRef CAS PubMed.
- H. Cox Jr and R. Bonham, J. Chem. Phys., 1967, 47, 2599–2608 CrossRef.
- X. Zhang, J. Sun and Y. Liu, J. Phys. B: At., Mol. Opt. Phys., 1992, 25, 1893 CrossRef CAS.
- J. P. Perdew and A. Zunger, Phys. Rev. B, 1981, 23, 5048 CrossRef CAS.
- D. D. Reid and J. Wadehra, J. Phys. B: At., Mol. Opt. Phys., 1996, 29, L127 CrossRef CAS.
- L. Chiari, A. Zecca, S. Girardi, E. Trainotti, G. Garcia, F. Blanco, R. McEachran and M. J. Brunger, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 215206 CrossRef.
- Computational Chemistry Comparison and Benchmark Database, https://cccbdb.nist.gov/ Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 1–17 Search PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- A. Allouche, Gabedit, http://gabedit.sourceforge.net/ Search PubMed.
- A. Zecca, L. Chiari, A. Sarkar and M. Brunger, New J. Phys., 2011, 13, 115001 CrossRef.
- O. Sueoka and S. Mori, J. Phys. B: At., Mol. Opt. Phys., 1989, 22, 963 CrossRef CAS.
- M. H. Bettega, S. d’A. Sanchez, M. T. d. N. Varella, M. A. Lima, L. Chiari, A. Zecca, E. Trainotti and M. J. Brunger, Phys. Rev. A:At., Mol., Opt. Phys., 2012, 86, 022709 CrossRef.
- O. Sueoka and S. Mori, J. Phys. B:At., Mol. Opt. Phys., 1986, 19, 4035 CrossRef CAS.
- K. Hoffman, M. Dababneh, Y.-F. Hsieh, W. Kauppila, V. Pol, J. Smart and T. Stein, Phys. Rev. A, 1982, 25, 1393 CrossRef CAS.
- M. Charlton, T. Griffith, G. Heyland and G. Wright, J. Phys. B:At., Mol. Opt. Phys., 1980, 13, L353 CrossRef CAS.
- C. K. Kwan, Y. Hsieh, W. Kauppila, S. J. Smith, T. Stein, M. Uddin and M. Dababneh, Phys. Rev. A, 1983, 27, 1328 CrossRef CAS.
- J. Marler and C. Surko, Phys. Rev. A:At., Mol., Opt. Phys., 2005, 72, 062713 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra06809b |
| This journal is © The Royal Society of Chemistry 2024 |