Open Access Article
Open Access ArticleDesorption of pharmaceutical hydrochlorides from transition metal oxide nanoparticles – investigation by capillary electrophoresis
Eman T. Elmorsi and
Edward P. C. Lai *
*
Ottawa-Carleton Chemistry Institute, Department of Chemistry, Carleton University, Ottawa, ON K1S 5B6, Canada. E-mail: edward.lai@carleton.ca; Fax: +1 (613) 520 3749; Tel: +1 (613) 520 2600 ext. 3835
First published on 19th December 2024
Abstract
The binding affinity of pharmaceutical hydrochlorides onto transition metal oxide nanoparticles (TMONPs) was investigated through a consecutive process of adsorption and desorption. Mexiletine (MEX) was chosen as a model pharmaceutical hydrochloride that bound onto TMONPs' surface through electrostatic interactions and coordination bonding. Response surface methodology was applied for their optimal separation by capillary electrophoresis to achieve accurate quantitation. Linear and quadratic regressions were applied to model peak resolution and migration times. The response surface methodology was next applied to investigate the maximum desorption percentages of mexiletine (MEX) from the surface of TiO2 and Co3O4 nanoparticles. ANOVA indicated a positive correlation between the MEX desorption results with pH, metformin (MET) competitive desorption agent concentration, Na2HPO4 concentration (hence ionic strength), and Na2S2O5 reducing agent concentration. The MEX desorption increased from TiO2 (46 ± 1%) to Co3O4 (63 ± 1%), suggesting a stronger binding interaction between MEX and TiO2 nanoparticles. TiO2 exhibited the order of pH > [MET] > [Na2HPO4] > [Na2S2O5]; Co3O4 exhibited the order [Na2HPO4] > pH > [MET] > [Na2S2O5]. This novel finding demonstrates the potential of TMONPs for use as efficient adsorbents to remove pharmaceutical compounds that accidently enter environmental water sources, with feasible regeneration.
1. Introduction
The widespread use of pharmaceutical active compounds (PACs) has increased research interest because inadvertent exposure to these compounds in environmental water sources is associated with toxicity that can impact ecological and human health.1 Therefore, selective detection and sensitive determination of PAC levels in environmental water testing is crucial.2 Focused monitoring and evaluation of contaminants in the aquatic environment is generally regarded to be necessary for the protection of water quality and hence community health.3 In recent years, advances in nanotechnology have emerged as an important industry for the manufacture of new nanomaterials.4 Consequently, nanoparticles including metal oxide nanoparticles are widely found in a large variety of commercial and household products that are often dumped in landfills or sewage as wastes.5 Titanium dioxide (TiO2) nanoparticles have become a focal point of research due to their widespread daily use.6 Upon irradiation with light, the exceptional band gap characteristic of this nanostructured semiconductor creates electron–hole pairs that result in the waste degradation cascade process.7 These nanoparticles have attracted a substantial amount of attention in photocatalysis for the treatment of wastewater.8 Cobalt tetroxide (Co3O4) nanoparticles play an important role in new energy battery technologies due to their excellent electrochemical stability, high energy density, and specific capacitance.9 Their mass production and widespread use have gradually increased the risk of their environmental presence due to industrial and anthropogenic discharge.10 Upon leaching release into ground and surface water, these nanoparticles with their characteristic high surface area-to-volume ratio exhibit a high adsorption capacity to bind numerous pharmaceutical compounds.11 Furthermore, environmental effects such as pH and ionic strength changes could eventually desorb the compounds from the nanoparticle surface. Notably, the pH dictates the cationic, anionic, and zwitterionic speciation of pharmaceutical compounds as well as the surface charge of nanoparticles, thus affecting their interactions.12 Generally, in a pH-controlled process, anionic compounds can be desorbed with an alkaline solution and cationic compounds can be desorbed with an acidic solution through electrostatic repulsion.13,14 It has previously been reported by Dhiman and Sharma that pH plays a crucial role in ciprofloxacin adsorption onto ZnO nanoparticles.15 It was determined that pH 8 is optimal for maximum adsorption based on the pKa value of 6 for ciprofloxacin and the zero charge of 8.7 for ZnO. Moreover, Attia et al. observed the desorption of acidic pharmaceutical compounds (ibuprofen, naproxen, diclofenac-Na, and gemfibrozil having pKa values around 4.1–4.9) from Fe2O3–zeolite composite surface at high pH levels, where the zeolite composite becomes negatively charged and electrostatic repulsion causes desorption of the pharmaceutical molecules.16Furthermore, the ionic strength of the aqueous solution can enhance or suppress electrostatic interactions. An increase in the ionic strength will enhance adsorption by reducing the electrostatic repulsion between the adsorbent surface and the adsorbate molecules. On the other hand, if electrostatic interactions are attractive, increasing the ionic strength leads to desorption.17 According to Gulley-Stahl et al., this phenomenon can be explained by the increasing density of electrolyte ions at high ionic strengths, which decreases the diffuse layer thickness.18 Furthermore, if electrolyte ions adsorb significantly, there would be an increase in competition for available surface sites, leading to desorption of pharmaceutical molecules. Bui et al. investigated the effect of varying ionic strength on the adsorption of four pharmaceutical compounds (carbamazepine, diclofenac, ibuprofen, and ketoprofen) onto porous silica. Based on the pKa values of the compounds, at pH 5.3 carbamazepine is a neutral compound whereas diclofenac, ibuprofen, and ketoprofen are deprotonated and hence negatively charged. Consequently, carbamazepine adsorption slightly decreased as ionic strength increased from 0 to 50 mM.19 As reported by Claussen et al., dissolution of pharmaceutical compounds in water could be influenced by ionic strength; a higher ionic strength may cause neutral pharmaceuticals to be less soluble while ionizable acidic pharmaceuticals dissolve more readily.20 Gao et al. observed that an increase in ionic strength enhanced the desorption of uncharged sulfamethazine to montmorillonite while the adsorption of anionic sulfamethazine increased.21 Generally, one pharmaceutical compound does not exist alone in the environment but coexists with many other compounds. Competitive adsorption usually occurs between compounds with similar ionic charges for available active sites. Eventually, this competitive process could lead to the desorption of the previously adsorbed compounds.22
Response surface methodology (RSM) has been widely applied as an optimization method in scientific research.23 It consists of several statistical techniques that can be used to model and analyze the effects of a variety of experimental parameters.24 Using RSM, researchers can determine the best combination of parameters (aka factors) to produce optimum results.25 By adopting this statistical approach, the number of experiment runs is reduced and the effects of each factor can be recognized.26 Different studies have applied RSM to optimize electrochemical27 and advanced oxidation28 processes for drinking water treatment. Various process parameters including adsorbent dose, pH, metal ion concentration and reaction time have been successfully optimized for the biosorption of metals29,30 and dyes.31 Alidadi et al. investigated the effect of different parameters for optimizing the extraction of amoxicillin from an aqueous medium by using an emulsion liquid membrane based on the central composite design (CCD) model.32 Another study successfully applied RSM using the Box–Behnken design (BBD) model to optimize fluoride adsorption onto apatite tricalcium phosphate.33 To the best of our knowledge, statistical experimental design techniques have not been previously reported for the investigation of desorption processes. Specifically, the main objective of our present work was to apply RSM using the CCD model to investigate the desorption of a model PAC, mexiletine hydrochloride (MEX), from TiO2 and Co3O4 nanoparticle surfaces. MEX is a well-established sodium channel blocker that acts on cardiac myocytes and neurons. It has long been used to treat some rare cardiopathy, epilepsy, neuromuscular diseases, and pain disorders in children.34 This antiarrhythmic drug is also used to treat acute and chronic ventricular arrhythmias in adults.35 Although mexiletine is extensively metabolized in humans via phase I and phase II reactions, approximately 10% of each mexiletine dose administered is recovered without modifications in urine.36 The need of the current study also arises from inadvertent disposal of mexiletine due to shelf life expiry. While the US EPA – 40 CFR Part 439, Pharmaceutical Manufacturing Point, applies to process wastewater discharges resulting from the research and manufacture of pharmaceutical products,37 environmental discharge through treatment plants cannot ensure minimizing the discharge of pharmaceutical waste completely.38,39 Interesting findings had previously been reported on the binding of MEX with TiO2, Co3O4 and ZnO nanoparticles.40 MEX binding occurred through physical and chemical approaches between the pores of the external surface and within the pores of the internal surface of TMONPs. The Freundlich model showed the best fitting with a high value of R2 and the minimum error values of SSE. It can be concluded that MEX·HCl bonded to heterogenous sites forming mono- and multilayers onto the surface of TMONPs as controlled by physisorption mechanism. The main mechanism was accomplished via electrostatic interaction and hydrogen bonding.
The combined effects of four independent variables, namely pH, metformin (MET) as competitive desorption agent, Na2HPO4 for ionic strength control, and Na2S2O5 as reducing agent, on the desorption response were investigated in the present study. MET was selected as the competitive desorption agent in this study, on the basis of its pKa of 12.4 (ref. 41) which is significantly higher than 9.5 for MEX.
2. Materials and methods
2.1. Preparation of samples and background electrolyte (BGE)
The stock solutions of MEX·HCl, MET·HCl, Na2HPO4, and Na2S2O5 were prepared in deionized water. A calibration curve for MEX·HCl was constructed to determine the concentrations before and after adsorption–desorption experiments. A background electrolyte (BGE) solution was prepared by dissolving sodium phosphate dibasic in deionized water and adjusted with 1 M HCl or 1 M NaOH to the required pH level.2.2. Batch adsorption–desorption experiments
Desorption studies were conducted to investigate the leaching behavior of mexiletine from TiO2 and Co3O4 nanoparticles (adsorbents). Both TiO2 (79.87 g mol−1) nanopowder with particle size <50 nm and Co3O4 (240.80 g mol−1) nanopowder with particle size <50 nm were obtained from Millipore Sigma (Oakville, ON, Canada). Initially, an adsorption process was conducted in 20 mL of 0.02 mM (100 μg mL−1) MEX·HCl containing 1 g L−1 (1 mg mL−1) of the selected nanoparticles for MEX adsorption overnight. Upon completion of the adsorption process in 24 h, the contents were centrifuged at 300 rpm for 5 min. The supernatant was discarded, and the nanoparticles carrying the adsorbed MEX were air-dried overnight. A series of 30 desorption experiments with duplicate trials, as designed by CCD, were conducted with an appropriate amount of the dried nanoparticles carrying adsorbed MEX·HCl. In different bottles, the required volumes of desorbing solutions of MET·HCl (0–0.016 mM), Na2HPO4 (0–100 mM), and Na2S2O5 (0.0–1.0 mM) were added at pH levels ranging from 3 to 11. After stirring for 24 hours to minimize particle–particle aggregation at the high ionic strength provided by Na2HPO4, the supernatant was analyzed using capillary electrophoresis (CE)42 to determine the desorbed amount of MEX.2.3. Determination of mexiletine hydrochloride by CE-UV
The adsorption/desorption samples were analyzed by capillary electrophoresis (G1600AX CE system, Agilent Technologies, Santa Clara, USA) equipped with a fused silica capillary of 28 cm length from the inlet to the detection window. To display the migration time of analytes, a diode array detector (DAD) was set up at three wavelengths of 200, 230 and 254 nm to monitor the UV spectral characteristics of different PACs. The capillary was filled with 75 mM Na2HPO4 BGE adjusted to pH 9.4. The samples were injected hydrodynamically at 20 mbar for 10 s. With an applied voltage of 10 kV, the capillary was equilibrated at a temperature of 20 °C. A calibration curve was constructed for determining the unknown concentrations of MEX after desorption from TiO2 and/or Co3O4. The % desorption was calculated according to:
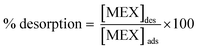 | (1) |
2.4. Experimental design and statistical analysis
Design Expert 22.0.1 statistical software (Stat-Ease, Minneapolis, MN, USA) was used for the initial design of experiments (DOE) and subsequent data analysis. Response surface methodology (RSM) was used with central composite design (CCD) to optimize the variables affecting the % desorption of MEX from the surfaces of both TiO2 and Co3O4 nanoparticles. In order to determine the optimum desorption conditions, four independent variables were considered: pH level, MET as competing desorption agent, Na2HPO4 for ionic strength control, and Na2S2O5 as reducing agent. Optimization experiments were performed on the four factors, each factor taking five different values as shown in Table 1. The CCD consisted of 2n factorial runs, 2n axial runs, as well as nC center runs. The total number of experimental runs (N) conducted was therefore:| N = 2n + 2n + nC | (2) |
| N = 24 + 2(4) + 6 = 30 runs | (3) |
| Variable | Actual values | Coded values | Real values at 5 coded levels | ||||
|---|---|---|---|---|---|---|---|
| −α | −1 | 0 | 1 | +α | |||
| pH | A | A | 3 | 5 | 7 | 9 | 11 |
| MET·HCl concentration | B (μg mL−1) | B | 0 | 25 | 50 | 75 | 100 |
| Na2HPO4 concentration | C (mM) | C | 0 | 25 | 50 | 75 | 100 |
| Na2S2O5 concentration | D (mM) | D | 0.0 | 0.1 | 0.43 | 0.75 | 1.00 |
A total of 30 experiments were conducted in random order to avoid biases. The axial point ensures rotatability, whereas the center point ensures reproducibility and defines experimental errors. Table 1 presents the real values of the four variables at 5 coded levels in the CCD model.
3. Results and discussion
3.1. Central composite design (CCD) model
In analytical separation, challenges may arise from insufficient resolution between adjacent CE peaks for accurate height measurement.43 To address these challenges, the response surface methodology (RSM) can be used to optimize all three experimental parameters. Using this statistical method, the relationships between several explanatory variables and one or more response variables can be explored in the least amount of time. It is possible to screen many parameters simultaneously to determine which ones are significant factors in the separation process.44 A statistical approach of CCD was employed to optimize MEX desorption from both TiO2 and Co3O4 nanoparticles using a combination of thirty experimental runs. The CCD model required 16 factorial runs, 8 axial runs and 6 center runs for optimizing the desorption process. This large number of experiments, encompassing a wide range of conditions, was essential to determining the optimal factors for MEX desorption. Eqn (4) and (5) were used to calculate the % desorptions of MEX, shown as responses in Table 2. The experimental data was also analyzed by CCD to determine if the linear or quadratic model would be better for predicting the maximum desorption percentage. The quadratic model (second-degree polynomial function) showed a high R2 value and a p-value of less than 0.05. The model also showed a low standard deviation and a high F- and regression coefficient values. Thus, the quadratic model was chosen for the calculation of the predicted values of % desorption and its relationship to the independent variables. The validity of the proposed model, as well as the agreement between the experimental and predicted values of % desorption, could then be evaluated using an analysis of variance (ANOVA) next.| Std run | Rand. run | CCD position | Independent design factors | Responses | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| pH | Competitive [MET·HCl] μg mL−1 | Ionic strength [Na2HPO4] mM | Reducing agent [Na2S2O5] mM | Desorption from TiO2 | Desorption from Co3O4 | |||||||
| Des. (%) exp | S. D. | Des. (%) pre | Des. (%) exp | S. D. | Des. (%) pre | |||||||
| 1 | 14 | Factorial | 5 | 25 | 25 | 0.1 | 17.35 | 0.86 | 18.92 | 29.41 | 0.16 | 30.52 |
| 2 | 30 | Factorial | 9 | 25 | 25 | 0.1 | 5.96 | 0.35 | 6.05 | 15.36 | 0.16 | 13.86 |
| 3 | 20 | Factorial | 5 | 75 | 25 | 0.1 | 31.44 | 0.43 | 31.46 | 36.78 | 0.56 | 38.39 |
| 4 | 1 | Factorial | 9 | 75 | 25 | 0.1 | 12.79 | 0.86 | 12.63 | 30.42 | 0.32 | 30.65 |
| 5 | 17 | Factorial | 5 | 25 | 75 | 0.1 | 28.12 | 0.49 | 26.93 | 43.13 | 0.59 | 44.62 |
| 6 | 28 | Factorial | 9 | 25 | 75 | 0.1 | 11.14 | 0.32 | 11.08 | 23.39 | 0.43 | 22.86 |
| 7 | 16 | Factorial | 5 | 75 | 75 | 0.1 | 42.62 | 0.65 | 44.14 | 57.53 | 0.32 | 56.31 |
| 8 | 26 | Factorial | 9 | 75 | 75 | 0.1 | 21.49 | 0.43 | 22.34 | 42.47 | 0.32 | 43.47 |
| 9 | 23 | Factorial | 5 | 25 | 25 | 0.75 | 20.25 | 0.32 | 19.56 | 32.09 | 0.99 | 32.56 |
| 10 | 27 | Factorial | 9 | 25 | 25 | 0.75 | 8.65 | 0.16 | 7.53 | 19.71 | 0.28 | 20.15 |
| 11 | 7 | Factorial | 5 | 75 | 25 | 0.75 | 29.78 | 0.71 | 30.39 | 34.43 | 0.32 | 34.05 |
| 12 | 15 | Factorial | 9 | 75 | 25 | 0.75 | 10.31 | 0.32 | 12.42 | 30.08 | 0.43 | 30.56 |
| 13 | 25 | Factorial | 5 | 25 | 75 | 0.75 | 28.16 | 1.06 | 28.84 | 52.51 | 0.59 | 51.76 |
| 14 | 12 | Factorial | 9 | 25 | 75 | 0.75 | 13.21 | 0.28 | 13.83 | 34.43 | 0.32 | 34.25 |
| 15 | 8 | Factorial | 5 | 75 | 75 | 0.75 | 44.28 | 0.97 | 44.35 | 54.51 | 0.32 | 57.07 |
| 16 | 29 | Factorial | 9 | 75 | 75 | 0.75 | 23.15 | 0.49 | 23.40 | 50.50 | 0.43 | 48.48 |
| 17 | 13 | Axial | 3 | 50 | 50 | 0.425 | 46.41 | 0.71 | 45.95 | 63.22 | 0.59 | 60.96 |
| 18 | 3 | Axial | 11 | 50 | 50 | 0.425 | 12.38 | 0.32 | 12.12 | 34.43 | 0.71 | 35.71 |
| 19 | 19 | Axial | 7 | 0 | 50 | 0.425 | 5.75 | 0.28 | 7.19 | 15.02 | 0.99 | 15.98 |
| 20 | 9 | Axial | 7 | 100 | 50 | 0.425 | 31.44 | 0.99 | 29.29 | 39.12 | 0.65 | 38.08 |
| 21 | 24 | Axial | 7 | 50 | 0 | 0.425 | 17.35 | 0.71 | 17.25 | 21.38 | 0.81 | 20.37 |
| 22 | 4 | Axial | 7 | 50 | 100 | 0.425 | 36.41 | 0.71 | 36.24 | 51.84 | 0.56 | 52.39 |
| 23 | 2 | Axial | 7 | 50 | 50 | 0 | 26.47 | 0.86 | 25.42 | 39.45 | 0.71 | 38.47 |
| 24 | 22 | Axial | 7 | 50 | 50 | 1 | 20.20 | 0.71 | 19.57 | 40.46 | 0.86 | 40.71 |
| 25 | 11 | Center | 7 | 50 | 50 | 0.425 | 35.17 | 0.81 | 34.59 | 45.81 | 1.01 | 44.60 |
| 26 | 21 | Center | 7 | 50 | 50 | 0.425 | 35.58 | 1.23 | 34.59 | 44.14 | 0.86 | 44.60 |
| 27 | 5 | Center | 7 | 50 | 50 | 0.425 | 34.34 | 1.49 | 34.59 | 45.48 | 1.17 | 44.60 |
| 28 | 10 | Center | 7 | 50 | 50 | 0.425 | 33.92 | 1.39 | 34.59 | 42.13 | 1.33 | 44.60 |
| 29 | 6 | Center | 7 | 50 | 50 | 0.425 | 33.09 | 1.41 | 34.59 | 44.81 | 1.01 | 44.60 |
| 30 | 18 | Center | 7 | 50 | 50 | 0.425 | 34.34 | 1.49 | 34.59 | 45.14 | 1.44 | 44.60 |
Calculating the predicted values of % desorption required the determination of the regression coefficients (as predictors) of a quadratic model. By altering the desorption process factors, the CCD analysis normalized the experimental data through multiple regression analysis. A polynomial second order (quadratic) model was then produced by calculating the regression coefficients and subtracting any/all non-significant effects. Using the general quadratic model equation and the regression coefficients determined, two coded models eqn (4) and (5) were generated for MEX desorption from TiO2 and Co3O4 nanoparticles:
| % desorption (TiO2) = −16.98 + 2.73A + 1.01B + 0.50C + 40.22D − 0.03AB − 0.02AC + 0.33AD + 0.002BC − 0.05BD + 0.04CD − 0.35A2 − 0.007B2 − 0.003C2 − 47.71D2 | (4) |
| % desorption (Co3O4) = 33.67 − 8.07A + 0.62B + 0.68C + 13.97D − 0.04AB − 0.03AC + 1.63AD + 0.001BC − 0.12BD + 0.16CD − 0.23A2 − 0.007B2 − 0.003C2 − 21.20D2 | (5) |
By replacing the coded variables with the actual variables studied (pH, MET·HCl concentration, Na2HPO4 concentration, and Na2S2O5 concentration), the following equations were obtained for calculating the predicted values of the % desorption of MEX from TiO2 and Co3O4 nanoparticles:
| % desorption from TiO2 = −16.98 + 2.73 × pH + 1.01 × [MET·HCl] + 0.50 × [Na2HPO4] + 40.22 × [Na2S2O5] −0.03 × pH × [MET·HCl] − 0.02 × pH × [Na2HPO4] + 0.33 × pH × [Na2S2O5] + 0.002 × [MET·HCl] × [Na2HPO4] − 0.05 × [MET·HCl] × [Na2S2O5] + 0.04 × [Na2HPO4] × [Na2S2O5] − 0.35 × pH2 − 0.007 × [MET·HCl]2 − 0.003 × [Na2HPO4]2 − 47.71 × [Na2S2O5]2 | (6) |
| % desorption from Co3O4 = 33.67 − 8.07 × pH + 0.62 × [MET·HCl] + 0.68 × [Na2HPO4] + 13.97 × [Na2S2O5] + 0.04 × pH × [MET·HCl] − 0.03 × pH × [Na2HPO4] + 1.63 × pH × [Na2S2O5] + 0.001 × [MET·HCl] × [Na2HPO4] − 0.12 × [MET·HCl] × [Na2S2O5] + 0.16 × [Na2HPO4] × [Na2S2O5] + 0.23 × pH2 − 0.007 × [MET·HCl]2 − 0.003 × [Na2HPO4]2 − 21.20 × [Na2S2O5]2 | (7) |
These two mathematical quadratic models, eqn (6) and (7) where each concentration is represented by a pair of square brackets, unambiguously identify the individual and interaction impacts of the variables studied. The predicted values calculated from the two models ranged from 6.05% to 45.95% for TiO2 and 13.86% to 60.96% for Co3O4. In comparison, the results in Table 2 indicated that the effect of the four factors on the values of the experimental % desorption of MEX ranged from 5.95% ± 0.35% to 46.41% ± 0.71% for TiO2 nanoparticles, and 15.36% ± 0.16% to 63.22% ± 0.59% for Co3O4 nanoparticles. As expected, the predicted range of values are consistent with the experimental range of results for each TMONP. Overall, the ranges obtained for TiO2 nanoparticles are lower in values than those obtained for Co3O4 nanoparticles. This clear distinction between the two TMONPs can be explained by their different physicochemical properties. For the sake of chemical analysis, it would be more difficult to recover MEX by desorption from TiO2 than Co3O4 nanoparticles, using the four factors studied.
3.2. ANOVA and determination of significant effects
Analysis of variance (ANOVA), contour plots, and response surfaces were used to evaluate the validity of the selected model as well as the agreement between experimental and predicted values. In addition, the effects of factor interactions on the % desorption responses were examined. ANOVA is a hypothesis testing technique based on the F-test, p-values, and lack-of-fit statistical calculations to study the validity of a selected model. Statistical significance is determined by the p-values of the collected results, which should be <0.05 with a 95% confidence level.| Source | Sum of squares (SS) | Mean square | DFa | F-Value | p-Value |
|---|---|---|---|---|---|
| a Degree of freedom (DF) is the number of estimated parameters used to compute the source's sum of squares. The DF for the terms was 1 as the sum of squares equals the mean square (divided by DF = 1). The DF for the model equals 14 as obtained by dividing the sum of squares (3908.4) by the mean square (279.17). | |||||
| Model (quadratic) (predicted value) | 3908.45 | 279.17 | 14 | 144.11 | <0.0001 |
| Corrected total sum of squares (TSS) (actual value) | 3937.51 | 135.77 | 29 | ||
| Lack of fit | 25.28 | 2.53 | 10 | 3.34 | 0.0976 |
| A-pH | 1716.70 | 1716.70 | 1 | 886.19 | <0.0001 |
| B-Competing agent (metformin) | 732.61 | 732.61 | 1 | 378.19 | <0.0001 |
| C-Ionic strength (Na2HPO4) | 540.55 | 540.55 | 1 | 279.04 | <0.0001 |
| D-Reducing agent (Na2S2O5) | 3.61 | 3.61 | 1 | 1.86 | 0.1926 |
| AB | 35.40 | 35.40 | 1 | 18.28 | 0.0007 |
| AC | 8.85 | 8.85 | 1 | 4.57 | 0.0494 |
| BC | 21.86 | 21.86 | 1 | 11.28 | 0.0043 |
| AD | 0.7225 | 0.7225 | 1 | 0.3730 | 0.5505 |
| BD | 2.89 | 2.89 | 1 | 1.49 | 0.2408 |
| CD | 1.63 | 1.63 | 1 | 0.8392 | 0.3741 |
| A2 | 53.91 | 53.91 | 1 | 27.83 | <0.0001 |
| B2 | 466.95 | 466.95 | 1 | 241.05 | <0.0001 |
| C2 | 107.65 | 107.65 | 1 | 55.57 | <0.0001 |
| D2 | 349.56 | 349.56 | 1 | 180.45 | <0.0001 |
| Residual | 29.06 | 1.94 | 15 | ||
| Pure error | 3.78 | 0.7562 | 5 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Predicted R2 = 0.960 | |||||
| Adjusted R2 = 0.986 | |||||
| Adequate precision = 40.55 | |||||
| Source | Sum of squares (SS) | Mean square | DF | F-Value | p-Value |
|---|---|---|---|---|---|
| Model (quadratic) (predicted value) | 4218.07 | 301.29 | 14 | 115.00 | <0.0001 |
| Corrected total sum of squares (TSS) (actual value) | 4257.37 | 146.80 | 29 | ||
| Lack of fit | 33.39 | 3.34 | 10 | 2.82 | 0.1316 |
| A-pH | 956.34 | 956.34 | 1 | 365.02 | <0.0001 |
| B-Competitive (metformin) | 732.61 | 732.61 | 1 | 279.62 | <0.0001 |
| C-Ionic strength (Na2HPO4) | 1537.60 | 1537.60 | 1 | 586.87 | <0.0001 |
| D-Redox (Na2S2O5) | 62.86 | 62.86 | 1 | 23.99 | 0.0002 |
| AB | 79.66 | 79.66 | 1 | 30.40 | <0.0001 |
| AC | 26.01 | 26.01 | 1 | 9.93 | 0.0066 |
| AD | 18.06 | 18.06 | 1 | 6.89 | 0.0191 |
| BC | 14.63 | 14.63 | 1 | 5.58 | 0.0321 |
| BD | 40.64 | 40.64 | 1 | 15.51 | 0.0013 |
| CD | 26.01 | 26.01 | 1 | 9.93 | 0.0066 |
| A2 | 24.27 | 24.27 | 1 | 9.26 | 0.0082 |
| B2 | 539.35 | 539.35 | 1 | 205.86 | <0.0001 |
| C2 | 118.09 | 118.09 | 1 | 45.07 | <0.0001 |
| D2 | 69.06 | 69.06 | 1 | 26.36 | 0.0001 |
| Residual | 39.30 | 2.62 | 15 | ||
| Pure error | 5.91 | 1.18 | 5 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Predicted R2 = 0.982 | |||||
| Adjusted R2 = 0.950 | |||||
| Adequate precision = 41.15 | |||||
As evaluated by the p values, the significance of RSM-CCD results was <0.05 with a 95% confidence level representing a significant correlation between the experimental and predicted values. Nevertheless, the effects of the four individual factors were different for the two adsorbents. TiO2 exhibited the order of pH > MET concentration > Na2HPO4 concentration > Na2S2O5 concentration, as indicated by the F-values of 886, 378, 279, and 1.86, respectively. On the other hand, Co3O4 exhibited the order Na2HPO4 concentration > pH > MET concentration > Na2S2O5 concentration, as indicated by the F-values of 587, 365, 280, and 24. The results indicated that the % desorption of MEX from TiO2 and Co3O4 could be increased by decreasing the pH level from 11 to 3 in water sample pretreatment. Also, as the concentration Na2HPO4 and hence ionic strength increase, electrostatic interactions decrease, resulting in more MEX desorption. Furthermore, MET competition with active sites on TiO2 and Co3O4 surfaces enhances MEX desorption. However, the change in Na2S2O5 concentration had very minimal effect on the % desorption. In conclusion, based on the 46% desorption of mexiletine from TiO2 being less than the 63% desorption from Co3O4, the binding interactions between MEX and TiO2 are stronger than MEX interactions with Co3O4.
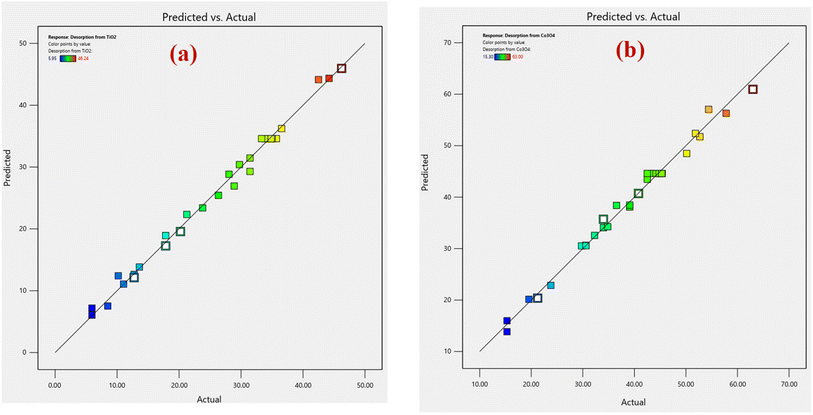 | ||
| Fig. 1 Comparison of predicted versus actual data of RSM-CCD for (a) % desorption from TiO2 nanoparticles, and (b) % desorption from Co3O4 nanoparticles. | ||
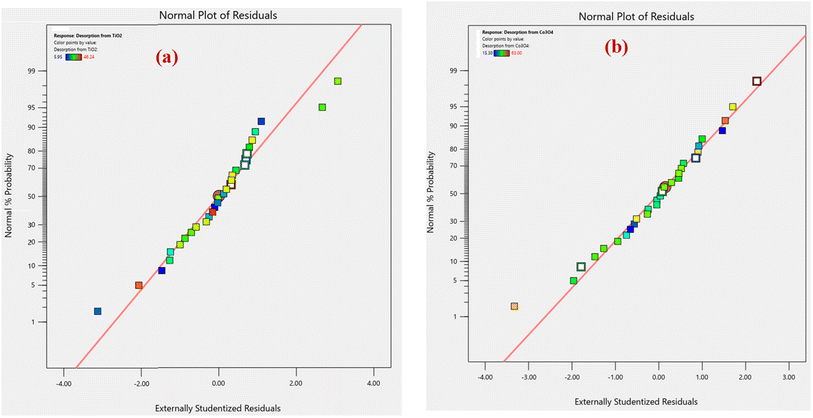
An analysis of normal probability plots was performed to evaluate the normality of the data. Fig. 2(a and b) show the normal probability plot of residuals for % desorption from TiO2 and Co3O4 nanoparticles. Both % desorption plots are linear, which indicates that errors are normally distributed.
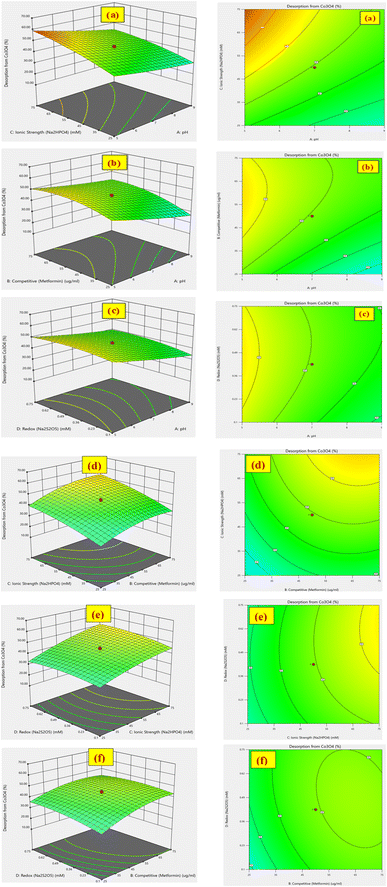
3.3. Desirability function for optimization
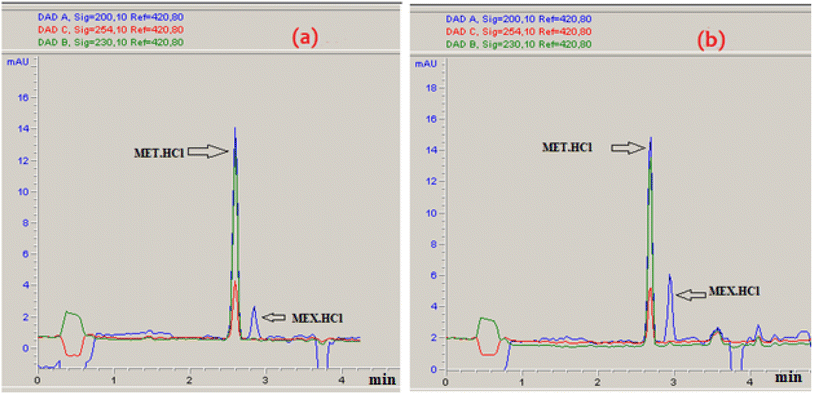
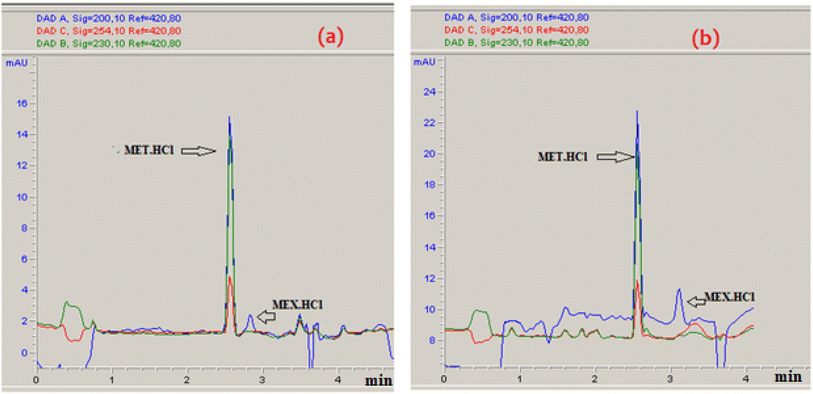
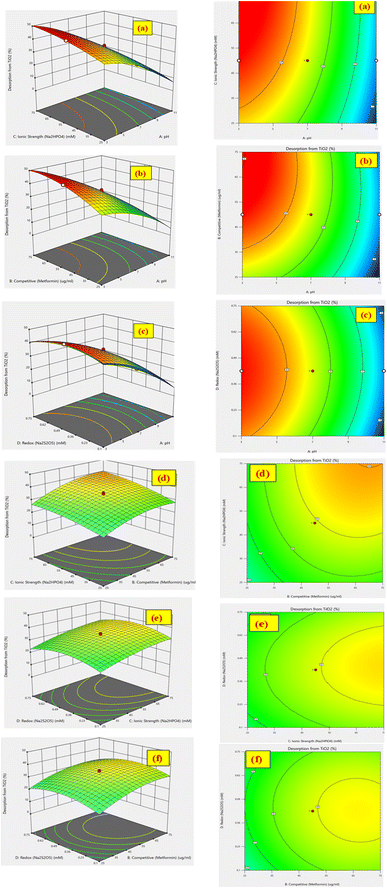
The % desorption goal for TiO2 and Co3O4 nanoparticles was set to attain the optimum point. After validating the model, desirability function was used to determine the conditions that could lead to the optimum response values by optimizing the independent variables. The desirable range is between 0 and 1; zero represents an unacceptable configuration, while 1 represents the ideal configuration for the selected response.45 It was found that at pH 3, 50 mM Na2HPO4, 50 μg mL−1 MET·HCl and 0.425 M Na2S205, desirability was 0.999 for both % desorptions from TiO2 and Co3O4 hence confirming the optimum value for each factor. As illustrated by the 3D and counter plots shown in Fig. 5 and 6, the % desorptions from TiO2 and Co3O4 were optimized to maximum values at 46.41% ± 0.71 and 63.22% ± 0.59 respectively under these conditions. Fig. 3(a and b) illustrates the electropherogram obtained from CE, for maximum % desorptions from TiO2 and Co3O4 respectively. These two pharmaceutical compounds were separated in the migration order of metformin (2.65 min) and mexiletine (2.90 min), with good resolution between the two peaks down to the baseline.Note that the % desorption could not be easily determined by CE-DAD analysis at the PAC concentration levels tested in the present study if microparticles or milliparticles were chosen. Only nanoparticles offered a sufficiently high specific surface area (cm2 mg−1) to result in a measurable change in the high working concentration of MEX required by the relatively low sensitivity of CE-DAD analysis, to yield experimental data of adequate signal-to-noise ratio values for reliable statistical significance evaluation.
3.4. Effect of factors on the responses
The quadratic models represented in eqn (6) and (7) show the effects of four factors (pH, MET·HCl concentration, Na2HPO4 concentration, and Na2S2O5 concentration) on the % desorption of MEX from TiO2 and Co3O4 nanoparticles, respectively. The ANOVA calculation results for % desorption from TiO2 nanoparticles in Table 3 show significant effects of pH, MET·HCl concentration, Na2HPO4 concentration, pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [MET·HCl], and [MET·HCl]
[MET·HCl], and [MET·HCl]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Na2HPO4]. The individual factors descend in the order of pH > MET concentration > Na2HPO4 concentration > Na2S2O5 concentration, as indicated by the F-values of 886, 378, 279, and 1.86. For % desorption of MEX from Co3O4 nanoparticles in Table 4, all the individual factors and their interactions have a significant effect as indicated by p-values <0.05. However, the individual factors descend in a different order as Na2HPO4 concentration > pH > MET concentration > Na2S2O5 concentration as indicated by the F-values of 587, 365, 280, and 24. It was noted that Na2S2O5 concentration has the lowest effect on the % desorption for both types of nanoparticles, as indicated by the low F-values of 1.86 and 24. This suggests that redox interactions between Na2S2O5 and TiO2 or Co3O4 nanoparticles did not play any important role in the MEX desorption.
[Na2HPO4]. The individual factors descend in the order of pH > MET concentration > Na2HPO4 concentration > Na2S2O5 concentration, as indicated by the F-values of 886, 378, 279, and 1.86. For % desorption of MEX from Co3O4 nanoparticles in Table 4, all the individual factors and their interactions have a significant effect as indicated by p-values <0.05. However, the individual factors descend in a different order as Na2HPO4 concentration > pH > MET concentration > Na2S2O5 concentration as indicated by the F-values of 587, 365, 280, and 24. It was noted that Na2S2O5 concentration has the lowest effect on the % desorption for both types of nanoparticles, as indicated by the low F-values of 1.86 and 24. This suggests that redox interactions between Na2S2O5 and TiO2 or Co3O4 nanoparticles did not play any important role in the MEX desorption.
4. Conclusion
In this study, RSM using the CCD model was applied to maximize the desorption percentages of MEX from TiO2 and Co3O4 nanoparticles. All data analysis and design of experiments were performed using Design Expert statistical software. To determine the optimal desorption conditions, four independent factors were studied: pH, concentration of MET as competitive desorption agent, concentration of Na2HPO4 for ionic strength control, and concentration of Na2S2O5 reducing agent. The ANOVA results indicated that the quadratic model was good for estimating the predicted values of % desorption and analyzing the relationship between the independent factors. There was a positive correlation between these four factors and the experimental desorption results obtained for MEX·HCl, ranging from 5.9% to 46.2% for TiO2 nanoparticles and 15.3% to 63.0% for Co3O4 nanoparticles. Using the mathematical quadratic model, the predicted desorption values for TiO2 and Co3O4 ranged from 6.0% to 45.9% for TiO2 and 13.3% to 63.0% for Co3O4. Overall, it would be more difficult to quantitatively recover MEX by desorption from TiO2 than Co3O4 nanoparticles, using the four factors studied. For the most accurate determination of PAC levels in environmental water testing, it would be crucial to consider the existence of various TMONPs and their potential binding with PACs. Further research will be needed to optimize more chemical desorption parameters, in the presence of all major TMONPs as found in environmental water sources. The scope of our future study will explore the dynamic relationship between the pharmaceutical hydrochlorides dissolved in water and those bound on TMONPs. Ultimately, the method of standard additions may prove itself to be the most practical analytical approach towards accurate determination of PAC levels in environmental water especially when mass spectrometry detection is hyphenated with CE. After using TMONPs as adsorbents for the efficient removal of pharmaceuticals in environmental water source remediation, the feasibility of their regeneration under optimal desorption conditions must be fully demonstrated to keep investment costs down.Data availability
The data sets supporting this article will be made available on request.Author contributions
Conceptualization, Edward Lai; data curation, Eman Elmorsi; funding acquisition, Edward Lai; investigation, Eman Elmorsi; methodology: Eman Elmorsi and Edward Lai; project administration, Edward Lai; resources, Edward Lai; supervision, Edward Lai; writing – original draft, Eman Elmorsi; and writing – review & editing, Edward Lai.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge the Natural Sciences and Engineering Research Council of Canada (NSERC) RGPIN-2018-05320 for the financial support of this research.References
- M. R. Letsoalo, T. Sithole, S. Mufamadi, Z. Mazhandu, M. Sillanpaa, A. Kaushik and T. Mashifana, J. Cleaner Prod., 2023, 387, 135798 CrossRef CAS.
- O. Canlı, E. Oktem Olgun, B. Güzel and M. Kaplan, Int. J. Environ. Anal. Chem., 2022, 104, 1778–1804 CrossRef.
- S. Sharma, V. Sharma, A. Mittal, D. K. Das, S. Sethi, S. Yadav, B. Vallamkonda and V. K. Vashistha, Water Environ. Res., 2024, 96(8), 11106 CrossRef PubMed.
- R. A. de Jesus, G. C. de Assis, R. J. de Oliveira, J. A. S. Costa, C. M. P. da Silva, M. Bilal, H. M. N. Iqbal, L. F. R. Ferreira and R. T. Figueiredo, Environ. Technol. Innovation, 2021, 24, 101851 CrossRef CAS.
- A. B. Sengul and E. Asmatulu, Environ. Chem. Lett., 2020, 18, 1659–1683 CrossRef CAS.
- N. Thakur, N. Thakur, A. Kumar, V. K. Thakur, S. Kalia, V. Arya, A. Kumar, S. Kumar and G. Z. Kyzas, Sci. Total Environ., 2024, 914, 169815 CrossRef CAS PubMed.
- K. K. Yadav, M. M. S. Cabral-Pinto, A. Gacem, A. M. Fallatah, B. Ravindran, S. Rezania, J. S. Algethami, L. Bashier Eltayeb, M. Abbas, T. Hassan Al-shareef, V. Vinayak, C. Truong Son, M. Awjan Alreshidi, J. Manuel Rodríguez-Díaz and R. Z. Homod, Mater. Today Chem., 2024, 40, 102226 CrossRef.
- M. Mohadesi, M. Sanavi Fard and A. Shokri, Int. J. Environ. Anal. Chem., 2022, 104, 2571–2592 CrossRef.
- C. R. Babu, A. V. Avani, T. S. Xavier, M. Tomy, S. Shaji and E. I. Anila, J. Energy Storage, 2024, 80, 110382 CrossRef.
- Q. Wang, G. Zhu, Q. Wang, W. Zhao, Y. Li, N. Shakoor, Z. Tan, F. Wang, P. Zhang and Y. Rui, J. Environ. Manage., 2024, 368, 122186 CrossRef CAS PubMed.
- S. Attarilar, J. Yang, M. Ebrahimi, Q. Wang, J. Liu, Y. Tang and J. Yang, Front. Bioeng. Biotechnol., 2020, 8, 822 CrossRef PubMed.
- T. Atugoda, M. Vithanage, H. Wijesekara, N. Bolan, A. K. Sarmah, M. S. Bank, S. You and Y. S. Ok, Environ. Int., 2021, 149, 106367 CrossRef CAS PubMed.
- L. Wang, C. Shi, L. Wang, L. Pan, X. Zhang and J.-J. Zou, Nanoscale, 2020, 12, 4790–4815 RSC.
- P. R. Yaashikaa, P. S. Kumar, A. Saravanan and D.-V. N. Vo, J. Hazard. Mater., 2021, 420, 126596 CrossRef CAS PubMed.
- N. Dhiman and N. Sharma, Environ. Technol. Innovation, 2019, 15, 100392 CrossRef.
- T. M. Salem Attia, X. L. Hu and D. Q. Yin, Chemosphere, 2013, 93, 2076–2085 CrossRef CAS PubMed.
- V. López-Ramón, C. Moreno-Castilla, J. Rivera-Utrilla and L. R. Radovic, Carbon, 2003, 41, 2020–2022 CrossRef.
- H. Gulley-Stahl, P. A. Hogan II, W. L. Schmidt, S. J. Wall, A. Buhrlage and H. A. Bullen, Environ. Sci. Technol., 2010, 44, 4116–4121 CrossRef CAS PubMed.
- T. X. Bui and H. Choi, Chemosphere, 2010, 80, 681–686 CrossRef CAS PubMed.
- F. Claussen, J. Al-Gousous, N. Salehi, M. A. Garcia, G. L. Amidon and P. Langguth, Pharm. Res., 2024, 41, 937–945 CrossRef CAS PubMed.
- J. Gao and J. A. Pedersen, Environ. Sci. Technol., 2005, 39, 9509–9516 CrossRef CAS PubMed.
- F. L. Theiss, M. J. Sear-Hall, S. J. Palmer and R. L. Frost, Desalin. Water Treat., 2012, 39, 166–175 CrossRef CAS.
- S. M. Azcarate, L. Pinto and H. C. Goicoechea, J. Chemom., 2020, 34(12), e3246 CrossRef CAS.
- W. A. Jensen, J. Qual. Technol., 2017, 49, 186–188 CrossRef.
- L. Vera Candioti, M. M. De Zan, M. S. Cámara and H. C. Goicoechea, Talanta, 2014, 124, 123–138 CrossRef CAS PubMed.
- A. Morshedi and M. Akbarian, Indian Journal of Fundamental and Applied Life Sciences, 2014, 4, 2434–2439 Search PubMed.
- K. Rajkumar and M. Muthukumar, Appl. Water Sci., 2015, 7, 637–652 CrossRef.
- L. Yahia Cherif, I. Yahiaoui, F. Aissani-Benissad, K. Madi, N. Benmehdi, F. Fourcade and A. Amrane, Ind. Eng. Chem. Res., 2014, 53, 3813–3819 CrossRef CAS.
- M. Yousefi, R. Nabizadeh, M. Alimohammadi, A. A. Mohammadi and A. H. Mahvi, MethodsX, 2019, 6, 35–42 CrossRef PubMed.
- M. A. Watson, A. Tubić, J. Agbaba, J. Nikić, S. Maletić, J. Molnar Jazić and B. Dalmacija, J. Hazard. Mater., 2016, 312, 150–158 CrossRef CAS PubMed.
- P. Bangaraiah and B. Sarathbabu, Chem. Eng. Commun., 2018, 206, 986–993 CrossRef.
- H. Alidadi, A. Ghorbanian, M. Ghorbanian, E. Rahmanzadeh, N. Nemanifar and M. Mehrabpour, Desalin. Water Treat., 2018, 132, 350–358 CrossRef CAS.
- M. Mourabet, A. El Rhilassi, H. El Boujaady, M. Bennani-Ziatni, R. El Hamri and A. Taitai, Appl. Surf. Sci., 2012, 258, 4402–4410 CrossRef CAS.
- C. Sarret, S. Barrière, G. Remerand, G. Massoullie, A. Chalard, C. Dauphin, B. Pontier and F. Laffargue, J. Pediatr. Neurol., 2024, 22(06), 425–428 CrossRef CAS.
- V. Muppavarapu, G. N. Challa, M. Gande, P. R. Billa, S. Gogineni and S. R. Yarraguntla, Sep. Sci. plus, 2024, 7(8), e202400038 CrossRef CAS.
- A. Catalano, A. Carocci and M. Sinicropi, Curr. Med. Chem., 2015, 22, 1400–1413 CrossRef CAS PubMed.
- CFR Part 439 – Pharmaceutical Manufacturing Point Source Category, https://www.ecfr.gov/current/title-40/chapter-I/subchapter-N/part-439, accessed November 12, 2024 Search PubMed.
- K. Samal, S. Mahapatra and M. Hibzur Ali, Energy Nexus, 2022, 6, 100076 CrossRef CAS.
- E. T. Elmorsi and E. P. C. Lai, Int. J. Plant, Anim. Environ. Sci., 2024, 14, 6–16 Search PubMed.
- E. T. Elmorsi and E. P. C. Lai, Int. J. Plant, Anim. Environ. Sci., 2024, 14, 6–16 Search PubMed.
- A. Flatie Alemu, A. Tegegne and N. Getaw, Drug, Healthcare Patient Saf., 2024, 16, 19–28 CrossRef CAS PubMed.
- F. Krebs, H. Zagst, M. Stein, R. Ratih, R. Minkner, M. Olabi, S. Hartung, C. Scheller, B. H. Lapizco-Encinas, C. Sänger-van de Griend, C. D. García and H. Wätzig, Electrophoresis, 2023, 44, 1279–1341 CrossRef CAS PubMed.
- S. Krait, M. Konjaria and G. K. E. Scriba, Electrophoresis, 2021, 42, 1709–1725 CrossRef CAS PubMed.
- W. A. Jensen, J. Qual. Technol., 2017, 49, 186–188 CrossRef.
- A. Chabbi, M. A. Yallese, I. Meddour, M. Nouioua, T. Mabrouki and F. Girardin, Measurement, 2017, 95, 99–115 CrossRef.
- P. Szabová, D. Varjúová, M. Kováčová, J. Prousek and I. Bodík, Pol. J. Environ. Stud., 2022, 31, 1805–1812 CrossRef PubMed.
- A. F. Pant, D. Özkasikci, S. Fürtauer and M. Reinelt, Front. Chem., 2019, 7, 00680 CrossRef CAS PubMed.
- N. Sivarajasekar, T. Paramasivam, R. Subashini, J. P. Maran and S. Kandasamy, Asian J. Microbiol., Biotechnol. Environ. Sci., 2017, 19, 130 Search PubMed.
- M. Bizi and F. E. El Bachra, Molecules, 2021, 26, 7318 CrossRef CAS PubMed.
- Y. Bian, X. Chen and Z. J. Ren, Environ. Sci. Technol., 2020, 54, 9116–9123 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2024 |