Noticeable characteristics of conventional and nonconventional hydrogen bonds in the binary systems of chalcogenoaldehyde and chalcogenocarboxylic acid derivatives

Abstract

Forty-eight stable structures of complexes formed between XCHZ and RCZOH (with X = H, F; R = H, F, Cl, Br, CH₃, NH₂; Z = O, S, Se, Te) were comprehensively investigated. It was found that the HZ–RZ complexes were more stable than the FZ–RZ ones, and their stability tendency decreased in the following order of Z: O > S > Se > Te. A predominant role of the electrostatic component was observed in XO–RO, while an outstanding contribution of the induction term was estimated in XS–RS, XSe–RSe, and XTe–RTe. A pivotal role of O compared to S, Se, and Te for improving the strength and characteristics of nonconventional C_sp²–H⋯O/S/Se/Te hydrogen bonds was proposed. The O–H⋯Z hydrogen bonds were much more stable than the nonconventional C_sp²–H⋯Z hydrogen bonds. Following complexation, the stretching frequency for C_sp²–H involving nonconventional C_sp²–H⋯Z hydrogen bonds gradually turned from the blue shift to red shift when one O of >C=O in XCHO and RCOOH was substituted by S, Se, and Te, with R varying from the electron-withdrawing to electron-donating groups. A very large red-shift of the O–H⋯Z hydrogen bonds up to −535.4 cm⁻¹ and a C_sp²–H blue-shift of the nonconventional C_sp²–H⋯O hydrogen bonds reaching 86.9 cm⁻¹ were observed in this work. It was noted that the considerable decrease in the intramolecular electron density transfer to the σ*(C_sp²–H) orbitals significantly impacted on the blue-shift of the C_sp²–H bonds involving hydrogen bonds.

---

1. Introduction

Hydrogen bonding is a well-known concept, and many theoretical and experimental studies have been conducted to provide a clear understanding of its formation and characteristics. The importance of hydrogen bonding is owing to its significant role in various fields, including chemistry, biochemistry, catalysis, and crystal packing.^1–3 In particular, hydrogen bonding is one of the factors that contribute to the processes of biomolecular recognition, enzyme catalysis, and building of higher peptide and nucleic acid structures.^4–6 Additionally, hydrogen bonding is considered one of the main factors to evaluate and classify new crystal structures^7–9 so that various kinds of materials with high quality could be created.^10,11 Therefore, the applications of hydrogen bonding has become a major research focus for scientists.

The A–H⋯B hydrogen bond is noncovalent and is formed by the interaction between the proton–donor A–H and the proton–acceptor B. Classical hydrogen bonds, also known as conventional hydrogen bonds, typically involve atoms A and B with high electronegativity, or B may represent a highly negatively charged region. This type of hydrogen bond is characterized by an increase in the A–H bond length and a decrease in its stretching frequency, shifting toward the red wavelength upon complexation, and is thus called a red-shifted hydrogen bond.¹² Another type of hydrogen bond is the nonconventional one, in which either or both A and B have low electronegativity or a lower electron density region compared to that of the conventional hydrogen bond. Nonconventional hydrogen bonds can present characteristics of red-shifting or blue-shifting.^12–14 Therein, the blue-shifting of nonconventional hydrogen bonds is shown through a contraction of the A–H bond length and an enhancement in its stretching frequency.^15,16 Thus, to better understand the application of hydrogen bonds, their characteristics, especially nonconventional hydrogen bonds, should be further clarified.

Over the years, many studies have investigated nonconventional C–H⋯B hydrogen bonds with different hybridization states of the C atom, including sp³,^17–20 sp²,^21–23 and sp.²⁴ Notably, some reports have shown that the blue-shifting of C_sp²–H bonds in these hydrogen bonds is larger than that observed for C_sp³–H bonds.^25,26 Furthermore, the presence of Se and Te as proton acceptors in hydrogen bonds has been increasingly reported in recent times, with their strength being almost comparable to that of hydrogen bonds with O and S proton acceptors.^27–29 Experimental evidence has also indicated the formation and stability of O/N–H⋯Se hydrogen bonds.^30–32 Additionally, C–H⋯Se/Te hydrogen bonds are attracting significant interest among scientists due to their potential applications, including in crystal engineering, superconductivity, and field-effect transistors.²⁹ Accordingly, these findings have opened up new opportunities for further research into nonconventional hydrogen bonds where Se and Te atoms act as proton acceptors.

Some models have been proposed to explain the characteristics of nonconventional hydrogen bonds.^33–36 Each model offers certain advantages and disadvantages, but a common point is their focus on clarifying the characteristics of hydrogen bonding on the basis of complexation, rather than considering the isolated properties of the initial proton donors and proton acceptors, and their relationships. Hence, investigating the nature of hydrogen bonds according to the characteristics of the monomers in complexes may bring incredible results. Following this perspective, our research team pursued an approach to explain the nature of hydrogen bonds based on the polarity of the proton donors and the proton affinity of the proton acceptors.^37–40 We recognized that the large blue-shifting of C_sp²–H⋯O hydrogen bonds can reach 104.5 cm⁻¹ or 109 cm⁻¹ in complexes containing chalcogenoaldehyde derivatives.^41,42 Interestingly, a red-shift in the stretching frequencies of C_sp²–H bonds in nonconventional C_sp²–H⋯Se/Te hydrogen bonds was found in complexes of XCHO and nH₂Z (X = F, Cl, Br, CH₃; Z = O, S, Se, Te; n = 1, 2),⁴³ as well as in RCHZ dimers (R = H, F, Cl, Br, CH₃, NH₂; Z = O, S, Se, Te).⁴⁴ These reports, thus, serve as useful background to expand the research into the effects of various substituents on the characteristics of C_sp²–H⋯Se/Te, and O–H⋯Se/Te hydrogen bonds. In general, the blue-shifting and red-shifting of hydrogen bonds are normally consistent with the polarity of the proton donors and the proton affinity of the proton acceptors, which are reflected through the deprotonation enthalpy (DPE) of the proton donors and the proton affinity (PA) of the proton acceptors. Notably, our previous reports also suggested using the DPE/PA ratio as an index to classify nonconventional hydrogen bonds.^39,45

Therefore, to give a clearer view of the characteristics of hydrogen bonds and establish more theoretical models to explain the nature of hydrogen bonds and to classify them, in the present study we mainly examined the formation and stability of XCHZ⋯RCZOH complexes (X = H, F; R=H, F, Cl, Br, CH₃, NH₂; Z = O, S, Se, Te) and the characteristics of their hydrogen bonds, including C_sp²–H⋯Z, and O–H⋯Z with Z = O, S, Se, Te. By replacing different X, R, and Z substituents, we aimed to evaluate their influences on the strength of the complexes, and on the changes in the properties of the proton donors and proton, acceptors as well as the electron density transfer between the interacting components. It was hoped that the findings could contribute to proposing a comprehensive rule about the characteristics of nonconventional C_sp²–H⋯Z hydrogen bonds, with Z being chalcogen atoms.

2. Computational methods

Geometrical optimization and harmonic vibrational frequency calculations for the complexes and the corresponding monomers were implemented by the second-order perturbation theoretical method (MP2) to resolve the electron correlation effectively.^46,47 The aug-cc-pVTZ basis set, which contains diffuse and polarized valence triple zeta functions, was employed in conjunction with the MP2 method to calculate the multi-electron and highly correlated systems.⁴⁸ However, the aug-cc-pVTZ basis set cannot be used for the heavy atom Te, thus the pseudopotential basis set aug-cc-pVTZ-PP is used exclusively for this element.⁴⁹ These calculations were carried out utilizing the Gaussian 16 suite.⁵⁰ Herein, the DCHZ isotopomers were used to compute the harmonic frequencies for the HCHZ monomers and HCHZ⋯RCZOH complexes in order to avoid vibrational coupling between the –CH₂– stretching modes in HCHZ (Z = O, S, Se, Te). Besides, to evaluate the polarity of the proton donors and proton affinity of the proton acceptors, the DPE of C_sp²/O–H bonds and the PA at the Z sites in the monomers were determined with CCSD(T)/aug-cc-pVTZ-PP for Te and CCSD(T)/aug-cc-pVTZ for the other atoms.

The interaction energies of the complexes were calculated according to following equation:

ΔE* = (E_complex − ∑E_monomers) + (ZPE_complex − ∑ZPE_monomers) + BSSE

In which the single-point energies of the complexes (E_complex) and monomers (E_monomers), and the basis set superposition error (BSSE) correction were computed by CCSD(T) methods. Meanwhile, zero-point energies (ZPEs) were collected from the optimized geometries of the complexes and corresponding monomers with MP2 methods using the aug-cc-pVTZ basis set, or the aug-cc-pVTZ-PP for the Te atom. Additionally, complete basis set (CBS) extrapolations were implemented for some XCHZ⋯RCZOH complexes and their corresponding monomers, with X = H, F, and R = H, F, NH₂, and Z = O to benchmark the interaction energy in the CCSD(T) methods. Herein, the CBS extrapolations were carried out separately for the Hartree–Fock (HF) and CCSD(T) total energies, as well as the CCSD(T) correlation energies. In particular, the HF total energy was fitted with the exponentially extrapolated form⁵¹ at the HF/aug-cc-pVnZ (n = 2, 3, 4) level. Meanwhile, the power form was used to fit the correlation energy for CCSD(T)/aug-cc-pVnZ (n = 2, 3, 4).^52,53

The formation and strength of the hydrogen bonds in the complexes were determined at the MP2/aug-cc-pVTZ-PP level for Te and MP2/aug-cc-pVTZ for the remaining ones through quantum theory of atoms in molecules (QTAIM) analysis^54,55 through the AIMall program.⁵⁶ The results from the AIM analysis can provide evidence for the existence of hydrogen bonds through the bond critical points (BCPs). Besides, some parameters to indicate the strength of hydrogen bonds, such as the electron density [ρ(r)], Laplacian electron density [∇²ρ(r)], and potential energy density [V(r)], at the BCPs were collected. In particular, the V(r) parameter was used to calculate the individual energy of the hydrogen bonds (E_HB) following the formula of Espinosa–Molins–Lecomte: E_HB = 0.5 V(r).⁵⁷ Additionally, a noncovalent interaction plot (NCIPLOT)^58,59 was used to support the appearance of weak noncovalent interactions through the Multiwfn 3.8,⁶⁰ Gnuplot 5.4, and VMD software packages. The relationship and strength of the nonconventional hydrogen bonds could be confirmed through the ratio between the H⋯Z intermolecular distances and their total van der Waals radii (r_H⋯Z/∑r_vdW).⁶¹

Natural bond orbital (NBO) analysis⁶² was implemented by utilizing the NBO 7.0 program⁶³ with the ωB97XD method and with the same basis sets used for the AIM analysis. NBO analysis can point out the intermolecular electron density transfer between proton donors and proton acceptors in hydrogen bonds, and the intramolecular electron density transfer in monomers, as well as show the NBO charges of each atom. In addition, to visualize the distribution of electron density on the surfaces of the monomers and determine the electron-rich centers on them, molecular electrostatic potential (MEP) calculations were carried out.⁶⁴ Moreover, the symmetry-adapted perturbation theory (SAPT)⁶⁵ was used through the Psi4 program,⁶⁶ in order to shed light on the contribution levels of each of the energy components to the stability of the complexes.

3. Results and discussion

3.1. Geometrical structures and AIM analysis

The geometrical structures of the complexes formed between XCHZ and RCZOH with X = H, F; Z = O, S, Se, Te; and R = H, F, Cl, Br, CH₃, NH₂ were optimized at the MP2/aug-cc-pVTZ-PP level for Te atoms, and MP2/aug-cc-pVTZ for the remaining ones. The results showed the existence of 48 optimal geometries, as shown in Fig. S1 of the ESI.† The geometries of the stable complexes are displayed in Fig. 1 and are labeled with the notation XZ–RZ (X = H, F; Z = O, S, Se, Te; R = H, F, Cl, Br, CH₃, NH₂). The obtained structures had flat ring shapes, as reflected through the appearance of ring critical points (RCPs) in the middle of the rings (cf. Fig. S2†). In general, the ring structures of complexes are formed by two interactions, such as C_sp²–H⋯Z and O–H⋯Z (with Z = O, S, Se, or Te). The data in Tables S1a and b,† collected from the AIM analysis, indicate that the interaction distances between H⋯O, H⋯S, H⋯Se, and H⋯Te ranged from 1.70–2.39, to 2.19–2.74, 2.28–2.77, and 2.45–2.93 Å, respectively, being shorter than the sum of the van der Waal radii of interacted atoms (∑r_vdW). This initially predicted the formation of weak interactions for C_sp²–H⋯Z and O–H⋯Z in the investigated complexes.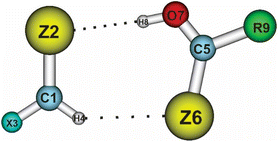

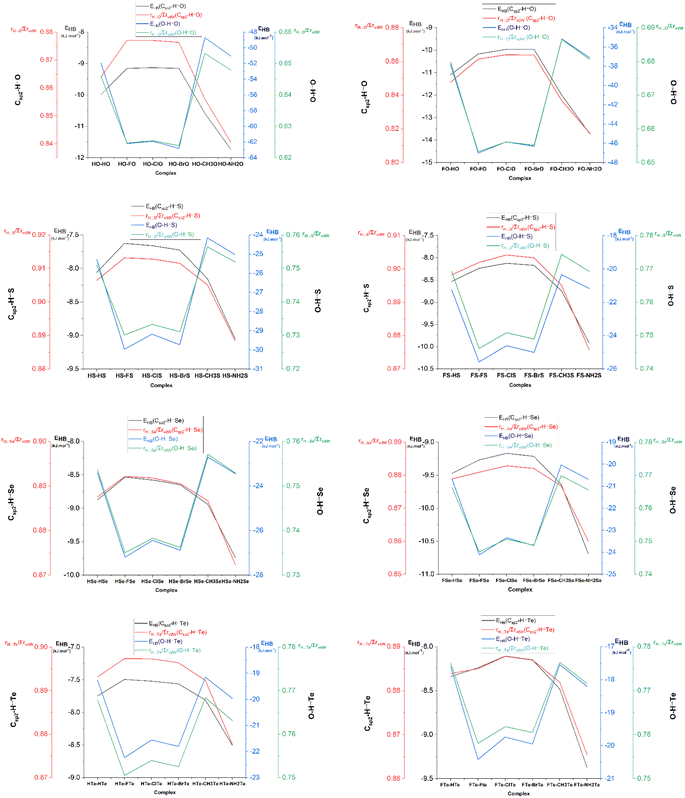
Fig. 1 Optimized structures of XCHZ⋯RCZOH complexes, where X = H, F; R = H, F, Cl, Br, CH₃, NH₂ and Z = O, S, Se, Te.

The bond critical points (BCPs) standing in the lines connecting H and Z atoms immediately confirmed that the C_sp²–H⋯Z and O–H⋯Z interactions were hydrogen bonds (cf. Fig. S2†). Therein, the electron density and Laplacian electron density at the BCPs of the O/C_sp²–H⋯Z hydrogen bonds belong to regions of weak noncovalent interactions.⁶⁷ In particular, the ρ(r) values at the BCPs of the O–H⋯Z and C_sp²–H⋯Z hydrogen bonds were respectively in the ranges of 0.023–0.047 au and 0.011–0.016 au, while the values of ∇²ρ(r) ranged from 0.028 to 0.099 au for the former, and from 0.026 to 0.062 au for the latter. These imply the stronger strength of the O–H⋯Z than the C_sp²–H⋯Z hydrogen bonds, which, in turn, was confirmed by the E_HB values of the O–H⋯Z hydrogen bonds (from −17.6 to −62.8 kJ mol⁻¹) being more negative than those of the C_sp²–H⋯Z ones (from −7.5 to −13.7 kJ mol⁻¹). The r_H⋯Z/∑r_vdW ratios of the H⋯Z interactions were calculated to provide more evidence for the strength of hydrogen bonds, in which, the smaller the r_H⋯Z/∑r_vdW ratio, the stronger the hydrogen bond. The results showed that the r_H⋯Z/∑r_vdW ratios of the O–H⋯Z hydrogen bonds (0.62–0.77) were smaller than those of the C_sp²–H⋯Z hydrogen bonds (0.84–0.91) (cf. Fig. 2), confirming again the greater strength of the O–H⋯Z hydrogen bonds relative to the C_sp²–H⋯Z ones. In addition, the results from the MEP analysis show that the most negative potential sites (presented in red) were associated with the >C=Z regions, which favor connecting with the most positive potential sites (presented in blue) located at the H atoms of the O–H and the C_sp²–H proton donors (cf. Fig. S3†). These observations strongly support the formation of the O–H⋯Z and C_sp²–H⋯Z hydrogen bonds. Notably, the maximum positive potential energies (V_s,max) at the H atom of the O–H bonds ranged from 224.1 to 306.4 kJ mol⁻¹ nearly doubling those of the C_sp²–H bonds, in the range of 111.0–179.0 kJ mol⁻¹ (cf. Table S2†). Therefore, these factors reflect the greater strength of the O–H⋯Z hydrogen bonds than the C_sp²–H⋯Z hydrogen bonds.

Fig. 2 Relationship between the individual hydrogen bond energy (E_HB, kJ mol⁻¹) and r_H⋯Z/∑r_vdW ratio for C_sp²–H⋯Z and O–H⋯Z hydrogen bonds in XZ–RZ complexes with X = H, F; R = H, F, Cl, Br, CH₃, NH₂ and Z = O, S, Se, Te.

For the same X and R substituents, the E_HB values of the O–H⋯Z hydrogen bonds were more negative, following the order O–H⋯Te < O–H⋯Se < O–H⋯S ≪ O–H⋯O. Besides, the r_H⋯Z/∑r_vdW ratios of the O–H⋯Z hydrogen bonds were also enhanced upon changing the Z from O to S to Se, then to Te (cf. Tables S1a and b†), affirming the stability trend of the O–H⋯Z hydrogen bonds as aforementioned. This observation could be explained by the much more negative NBO charge at the O atom in the XCHO monomers compared to those at the S, Se, and Te atoms in XCHS, XCHSe, and XCHTe (cf. Table S3†), along with the decrease in the negative values of V_s,min at the Z atoms upon changing Z from O via S via Se via Te (cf. Table S2†). This was accompanied by a reduction in the electrostatic attraction of H⋯Z as Z goes from O to Te. A superior strength of the O–H⋯O hydrogen bonds compared to the O–H⋯S ones was reported by An et al.⁴¹ Regarding the nonconventional C_sp²–H⋯Z hydrogen bonds, their strength decreased in the sequence: C_sp²–H⋯O > C_sp²–H⋯Se > C_sp²–H⋯S > C_sp²–H⋯Te (cf. Tables S1a and b†), as also observed in XCHO⋯nH₂Z complexes (with X = H, F, Cl, Br, CH₃; Z = O, S, Se, Te; n = 1, 2) by Cuc et al.⁴³ However, the strength of the nonconventional C_sp²–H⋯Z hydrogen bonds in the XZ–RZ complexes (from −7.5 to −13.7 kJ mol⁻¹) was higher than those in the binary systems of XCHO⋯H₂Z (from −3.7 to −10.2 kJ mol⁻¹). This tendency was associated with the increase in the r_H⋯Z/∑r_vdW ratios with Z going from O, to S, Se, and Te, respectively. In addition, the much more negative charge at the O atom (in >C=O) than at the S, Se, and Te atoms also indicated the stronger strength of the C_sp²–H⋯O hydrogen bonds compared to the C_sp²–H⋯S/Se/Te ones. Consequently, these obtained results highlight the crucial role of the O atom relative to the S, Se, and Te atoms in stabilizing the O–H⋯Z and the C_sp²–H⋯Z hydrogen bonds.

For the same X and Z, the strength of the O–H⋯Z hydrogen bonds decreased in the order of R substituents as: F > Br > Cl > H–NH₂ > CH₃ (cf. Fig. 2), which was in line with the descending polarity of the O–H bond in RCZOH as per the following: F/Cl/BrCZOH > HCZOH > NH₂/CH₃CZOH (cf. Table 1). Thus, replacing R with an electron-withdrawing substituent (F, Cl, Br) led to a higher strength of the O–H⋯Z hydrogen bonds, whereas, an opposite result was true for the presence of electron-donating groups (NH₂, CH₃). By contrast, when R went from NH₂ to CH₃ to H to F to Cl to Br, the strength of the C_sp²–H⋯Z hydrogen bonds showed a declining tendency (cf. Fig. 2). Accordingly, when X and Z were fixed, the strength of the C_sp²–H⋯Z hydrogen bonds was enhanced, along with an increase in the proton affinity (PA) at the Z sites in RCZOH monomers. This observation was also supported by the values of V_s,min in RCZOH being increasingly negative in the order: F–Cl–Br < H < CH₃ < NH₂ (cf. Table S2†). A greater influence of electron-donating substituents (CH₃, NH₂) compared to electron-withdrawing ones (F, Cl, Br) on the strength of the C_sp²–H⋯Z hydrogen bonds was also noted recently in the dimers of chalcogenoaldehyde derivatives.⁴⁴ However, the strength of the nonconventional C_sp²–H⋯Z hydrogen bonds in the dimers of the chalcogenoaldehyde derivatives, calculated at the MP2/6-311++G(3df,2pd) level (ranging from −4.7 to −11.0 kJ mol⁻¹) was weaker than that in XZ–RZ complexes (ranging from −7.5 to −13.7 kJ mol⁻¹).

Table 1 Deprotonation enthalpies (DPE, kJ mol⁻¹) of the C_sp²–H bonds (in XCHZ), O–H bonds (in RCZOH), and the proton affinities (PA, kJ mol⁻¹) at the Z sites of XCHZ and RCZOH monomers (X = H or F; R = H, F, Cl, Br, CH₃ or NH₂ and Z = O, S, Se or Te)

	HCHO	HCHS	HCHSe	HCHTe	FCHO	FCHS	FCHSe	FCHTe
DPE (C–H)	1650.6	1613.6	1603.9	1604.9	1502.7	1539.8	1534.9	1539.2
PA (Z)	701.8	754.4	763.2	783.5	646.3	708.4	724.5	751.8

---

	HCOOH	HCSOH	HCSeOH	HCTeOH	FCOOH	FCSOH	FCSeOH	FCTeOH
DPE (O–H)	1428.3	1372.2	1353.1	1335.6	1353.6	1302.3	1283.6	1262.6
PA (Z)	714.3	757.4	768.9	791.6	668.9	730.3	747.8	778.3

---

	ClCOOH	ClCSOH	ClCSeOH	ClCTeOH	BrCOOH	BrCSOH	BrCSeOH	BrCTeOH
DPE (O–H)	1280.3	1265.5	1268.4	1253.4	1253.7	1239.7	1242.9	1241.6
PA (Z)	692.9	750.6	765.2	790.7	699.0	756.3	770.4	794.6

---

	CH3COOH	CH3CSOH	CH3CSeOH	CH3CTeOH	NH2COOH	NH2CSOH	NH2CSeOH	NH2CTeOH
DPE (O–H)	1444.9	1384.7	1364.0	1340.7	1443.5	1386.5	1365.8	1342.8
PA (Z)	760.4	796.4	805.6	825.0	798.8	827.1	836.0	855.2

---

For the same R and Z, the E_HB values of the O–H⋯Z hydrogen bonds in HZ–RZ (from −19.2 to −62.8 kJ mol⁻¹) were more negative than those of FZ–RZ (from −17.6 to −47.0 kJ mol⁻¹), demonstrating a decrease in the strength of the O–H⋯Z hydrogen bonds when replacing one H atom in HCHZ by F. This was likely associated with the greater proton affinity at the Z sites in HCHZ compared to in FCHZ (cf. Table 1). In contrast, the stability of conventional O–H⋯O hydrogen bonds in XCHO⋯YCOOH complexes (where X = H, CH₃, NH₂; Y = H, F, Cl, Br, CH₃, C₂H₅, NH₂), computed at the MP2/6-311++G(2d,2p) level, decreased when X was changes from an electron-donating group to H.⁴⁰ This, therefore, suggests that the stability of conventional O–H⋯Z hydrogen bonds increases when one H atom in HCHZ is replaced with an electron-donating group but decreases when H is substituted by an electron-withdrawing one. On the other hand, the stronger proton donating ability of the C_sp²–H bonds in the FCHZ monomers than in the HCHZ ones (cf. Table 1) agreed well with the higher strength of the nonconventional C_sp²–H⋯Z hydrogen bonds in FZ–RZ over those in HZ–RZ.

3.2. Interaction energy and SAPT2+ analysis

To evaluate the stability of the XZ–RZ complexes, the interaction energies corrected by both the ZPE and BSSE (ΔE*) of the complexes were calculated with the CCSD(T) method with the aug-cc-pVTZ-PP basis set for Te atoms, and aug-cc-pVTZ for the remaining ones.

The collected results, presented in Table 2, displayed negative values for the interaction energies of complexes ranging from −41.1 to −21.6 kJ mol⁻¹. This demonstrates the stability of the XZ–RZ complexes on the potential energy surface. The strengths of the HZ–RZ complexes were stronger than that of the FZ–RZ complexes, with ΔE* values ranging from −41.1 to −22.3 kJ mol⁻¹, and from −35.4 to −21.6 kJ mol⁻¹, respectively. This is consistent with the higher strength of the O–H⋯Z hydrogen bonds in HZ–RZ than those in FZ–RZ. Thus, this observation emphasizes the more predominant role of the O–H⋯Z hydrogen bonds compared to the C_sp²–H⋯Z ones in stabilizing the complexes.

Table 2 Interaction energy corrected by ZPE and BSSE (ΔE*, kJ mol⁻¹) for XZ–RZ complexes with X = H, F; R = H, F, Cl, Br, CH₃, NH₂ and Z = O, S, Se, Te calculated with CCSD(T)/aug-cc-pVTZ-PP//MP2/aug-cc-pVTZ-PP for Te, and CCSD(T)/aug-cc-pVTZ//MP2/aug-cc-pVTZ for the remaining atoms

Complex	ΔE*	Complex	ΔE*	Complex	ΔE*	Complex	ΔE*
HO–HO	−33.0	HS–HS	−25.7	HSe–HSe	−24.9	HTe–HTe	−22.3
HO–FO	−41.1	HS–FS	−32.2	HSe–FSe	−31.7	HTe–FTe	−29.4
HO–ClO	−39.5	HS–ClS	−30.3	HSe–ClSe	−29.4	HTe–ClTe	−26.8
HO–BrO	−39.3	HS–BrS	−30.2	HSe–BrSe	−29.4	HTe–BrTe	−26.7
HO–CH3O	−32.3	HS–CH3S	−25.7	HSe–CH3Se	−24.9	HTe–CH3Te	−22.6
HO–NH2O	−34.7	HS–NH2S	−28.1	HSe–NH2Se	−27.5	HTe–NH2Te	−25.8
FO–HO	−29.9	FS–HS	−22.8	FSe–HSe	−23.1	FTe–HTe	−21.6
FO–FO	−35.4	FS–FS	−27.7	FSe–FSe	−28.6	FTe–FTe	−27.7
FO–ClO	−33.6	FS–ClS	−25.9	FSe–ClSe	−26.5	FTe–ClTe	−25.2
FO–BrO	−33.2	FS–BrS	−25.8	FSe–BrSe	−26.4	FTe–BrTe	−25.1
FO–CH3O	−30.7	FS–CH3S	−23.6	FSe–CH3Se	−23.9	FTe–CH3Te	−22.4
FO–NH2O	−33.2	FS–NH2S	−25.5	FSe–NH2Se	−26.0	FTe–NH2Te	−25.1

---

When fixing X and R, it was found that the strength of the HZ–RZ complexes decreased in the order of HO–RO > HS–RS > HSe–RSe > HTe–RTe. Meanwhile, the ΔE* values of the FZ–RZ complexes were less negative in the sequence: FO–RO > FSe–RSe > FS–RS > FTe–RTe (cf. Table 2). It is clear that the outstanding stability of the O–H⋯O and C_sp²–H⋯O hydrogen bonds was the key factor leading to the greater strength of the XO–RO complex among the other considered complexes in this work. Remarkably, the NBO charges at the Se atoms in HSe–RSe were much more positive than the NBO charges at the S atoms in HS–RS, leading to the weaker electrostatic attraction of H⋯Se compared to H⋯S (cf. Table S3†). Thus, this resulted in a greater strength of HS–RS relative to that of HSe–RSe. In contrast, the FSe–RSe complexes were stronger than the FS–RS ones because the sum of the intermolecular electron density transfer from the n(Se) to σ*(O/C_sp²–H) orbitals was much greater than that from n(S) to σ*(O/C_sp²–H) (cf. Table 4). This influence surpassed the larger electrostatic attraction of H⋯S than that of H⋯Se. Therefore, the intermolecular electron density transfer was more dominant than the electrostatic attraction in stabilizing FSe–RSe and FS–RS.

For the same X and Z, it was found that the stability of the complexes decreased in the order of R substituents as F > Cl–Br > NH₂ > CH₃–H. In general, a higher stability of the XZ–RZ complexes was observed with electron-withdrawing substituents (F, Cl, Br) compared to electron-donating ones (NH₂, CH₃). This is in line with the O–H⋯Z hydrogen bonds in XZ–FZ, XZ–ClZ, and XZ–BrZ being stronger than that in XZ–NH₂Z and XZ–CH₃Z. Additionally, the intermolecular electron density transfer from n(Z2) to σ*(O–H) orbitals in the complexes containing electron-withdrawing substituents (F, Cl, Br) was larger than that in the complexes with electron-donating groups (NH₂, CH₃) (cf. Tables 3 and 4). The greater polarity of the O–H proton donor in the F/Cl/BrCZOH monomers with respect to that in the NH₂/CH₃CZOH ones also supports this observation. Interestingly, Table S2† points out that the positive values of V_s,max at the H atom in the RCZOH monomers increased considerably when R went from electron-donating groups to electron-withdrawing ones. This reflects that the strength of the XZ–RZ complexes was enhanced as there was an increase in the maximum electrostatic potential at the H atom in RCZOH, and vice versa. It is worth noting that the interaction energies of XO–HO, XO–FO, and XO–NH₂O computed with CBS extrapolations were found to be more negative than those calculated with CCSD(T)/aug-cc-pVTZ by about 2–3 kJ mol⁻¹ (cf. Tables S4a and b†). Nevertheless, the strength tendency of the complexes is in the order: XO–FO > XO–NH₂O > XO–HO, and HO–RO > FO–RO, which were similar for both methods. This, therefore, indicates the reliability of the interaction energies calculated with CCSD(T)/aug-cc-pVTZ in this work. In a recent publication, An et al. also reported a decrease in the stability of complexes in the order of HCHO⋯FCOOH > HCHO⋯NH₂COOH > HCHO⋯HCOOH calculated with CCSD(T)/aug-cc-pVTZ//MP2/6-311++G(2d,2p). That observation was also confirmed by CBS extrapolation, with the CBS interaction energies appearing to be more negative than those computed at the CCSD(T)/aug-cc-pVTZ//MP2/6-311++G(2d,2p) level of about 5–6 kJ mol⁻¹.⁴⁰

Next, SAPT2+ was performed with the def2-TZVPD basis set to appraise the contributions of the energy components to the stability of the investigated complexes according to changing the chalcogen substituents. The results presented in Table S5 and Fig. S4a and b† show the strength of the XZ–RZ complexes was mainly dominated by three energy components, namely the electrostatic, induction, and dispersion terms. Therein, while the electrostatic and induction components contributed mostly to the strength of the complexes, with contributions ranging from 33.9% to 53.0%, and from 29.1% to 53.8%, respectively (cf. Table S5†), the contribution from the dispersion term was very low, just being in the range of 0.2–21.2%. In general, the percentage electrostatic components in the XO–RO complexes ranging from 50.0% to 53.0% dominated over their induction terms, in the range of 29.1–33.6%, which could be attributed to the much more negative charge at the O atom compared to the other chalcogen atoms, causing a stronger electrostatic attraction between the monomers in the XO–RO complexes. An opposite result was noted for XS–RS, XSe–RSe, and XTe–RTe, especially for the induction term governing the stability of XTe–RTe, with the percentage being just over 53%. Such a significant contribution of the induction component was also found for RCHTe dimers,⁴⁴ and XCHO···nH₂Te complexes.⁴³

3.3. NBO and NCI analyses

To obtain a clearer view of the intermolecular electron density and the distribution of electron density during the complexation, NBO analysis was implemented with the ωB97XD method and the aug-cc-pVTZ-PP basis set for the Te atoms, and aug-cc-pVTZ for the remaining ones. The obtained results are given in Tables 3 and 4, and show positive values for the total electron density transfer (EDT) of the XCHZ monomers, indicating that the electron density transfer occurred mainly from the XCHZ to RCZOH monomers. This observation agreed with the intermolecular electron density transfer value (E_inter) from the n(Z2) to σ*(O7–H8) orbitals being larger than that from the n(Z6) to σ*(C1–H4) orbitals (or σ*(C_sp²–H) orbitals). Indeed, the E_inter[n(Z2)→ σ*(O7–H8)] and E_inter[n(Z6) → σ*(C1–H4)] values were in the ranges of 63.7–155.5 kJ mol⁻¹ and 6.1–30.6 kJ mol⁻¹, respectively. This affirms again the stronger O–H⋯Z hydrogen bonds compared to the C_sp²–H⋯Z ones. In addition, replacing one H atom in the HCHZ monomers with F resulted in a decrease in the electron density transfer from n(Z2) to σ*(O7–H8), implying the greater strength of the O–H⋯Z hydrogen bonds in the HZ–RZ complexes relative to the FZ–RZ ones. However, the E_inter[n(Z6) → σ*(C1–H4)] values in the HZ–RZ complexes ranged from 6.1 to 20.9 kJ mol⁻¹, which was smaller than in the FZ–RZ complexes, with their figure being in the range of 7.5–30.6 kJ mol⁻¹. This once again shows the greater strength of the C_sp²–H⋯Z hydrogen bonds when X goes from H to F.

Table 3 Data from the NBO analysis of HZ–RZ complexes, with R = H, F, Cl, Br, CH₃, NH₂ and Z = O, S, Se, Te

	HO–HO	HO–FO	HO–ClO	HO–BrO	HO–CH3O	HO–NH2O
EDT (HCHZ)	0.04	0.05	0.05	0.05	0.03	0.03
Einter[n(Z2) → σ*(O7–H8)] (kJ mol^−1)	99.0	123.7	124.2	126.5	91.0	95.3
Einter[n(Z6) → σ*(C1–H4)] (kJ mol^−1)	8.1	6.6	6.1	6.1	8.5	10.2
ΔEintra[n(>C1=Z2/Z2) → σ*(O7–H8)] (kJ mol^−1)	0.0	0.0	−1.9	−1.9	0.6	0.8
ΔEintra[n(>C5=Z6/Z6) → σ*(C1–H4)] (kJ mol^−1)	−23.3	−25.3	−24.6	−24.7	−28.6	−24.6
Δσ*(O–H) (e)	0.040	0.049	0.049	0.049	0.037	0.039
Δσ*(Csp^2–H) (e)	−0.010	−0.012	−0.012	−0.012	−0.010	−0.011

---

	HS–HS	HS–FS	HS–ClS	HS–BrS	HS–CH3S	HS–NH2S
EDT (HCHZ)	0.05	0.07	0.07	0.07	0.05	0.05
Einter[n(Z2) → σ*(O7–H8)] (kJ mol^−1)	103.7	130.6	128.0	131.4	96.7	99.8
Einter[n(Z6) → σ*(C1–H4)] (kJ mol^−1)	15.3	13.4	13.2	13.3	15.2	18.0
ΔEintra[n(>C1=Z2/Z2) → σ*(O7–H8)] (kJ mol^−1)	−0.6	5.9	5.1	5.2	4.0	3.6
ΔEintra[n(>C5=Z6/Z6) → σ*(C1–H4)] (kJ mol^−1)	−9.2	−10.1	−9.5	−9.4	−9.3	−10.3
Δσ*(O–H) (e)	0.062	0.078	0.077	0.073	0.058	0.060
Δσ*(Csp^2–H) (e)	0.003	−0.001	0.000	0.001	0.002	0.002

---

	HSe–HSe	HSe–FSe	HSe–ClSe	HSe–BrSe	HSe–CH3Se	HSe–NH2Se
EDT (HCHZ)	0.06	0.08	0.08	0.08	0.06	0.06
Einter[n(Z2) → σ*(O7–H8)] (kJ mol^−1)	117.5	145.2	142.1	145.6	112.0	115.4
Einter[n(Z6) → σ*(C1–H4)] (kJ mol^−1)	19.7	17.8	17.6	17.8	19.4	22.5
ΔEintra[n(>C1=Z2/Z2) → σ*(O7–H8)] (kJ mol^−1)	4.6	4.6	5.8	6.2	4.9	4.0
ΔEintra[n(>C5=Z6/Z6) → σ*(C1–H4)] (kJ mol^−1)	−7.2	−7.9	−7.3	−7.3	−7.3	−8.3
Δσ*(O–H) (e)	0.073	0.092	0.090	0.092	0.071	0.073
Δσ*(Csp^2–H) (e)	0.007	0.004	0.005	0.005	0.007	0.007

---

	HTe–HTe	HTe–FTe	HTe–ClTe	HTe–BrTe	HTe–CH3Te	HTe–NH2Te
EDT (HCHZ)	0.07	0.10	0.09	0.10	0.07	0.08
Einter[n(Z2) → σ*(O7–H8)] (kJ mol^−1)	125.3	155.5	150.7	153.1	123.5	129.8
Einter[n(Z6) → σ*(C1–H4)] (kJ mol^−1)	18.6	16.7	16.6	16.8	18.1	20.9
ΔEintra[n(>C1=Z2/Z2) → σ*(O7–H8)] (kJ mol^−1)	3.5	5.2	6.5	6.8	3.6	4.5
ΔEintra[n(>C5=Z6/Z6) → σ*(C1–H4)] (kJ mol^−1)	−4.5	−4.9	−4.4	−4.4	−4.6	−5.3
Δσ*(O–H) (e)	0.084	0.108	0.104	0.106	0.084	0.088
Δσ*(Csp^2–H) (e)	0.010	0.007	0.008	0.008	0.009	0.009

---

Table 4 Data from the NBO analysis of FZ–RZ complexes, with R = H, F, Cl, Br, CH₃, NH₂ and Z = O, S, Se, Te

	FO–HO	FO–FO	FO–ClO	FO–BrO	FO–CH3O	FO–NH2O
EDT (FCHZ)	0.02	0.03	0.03	0.03	0.02	0.02
Einter[n(Z2) → σ*(O7–H8)] (kJ mol^−1)	69.6	90.6	89.1	90.2	63.7	67.0
Einter[n(Z6) → σ*(C1–H4)] (kJ mol^−1)	10.2	8.3	7.6	7.5	11.1	13.9
ΔEintra[n(>C1=Z2/Z2) → σ*(O7–H8)] (kJ mol^−1)	−0.2	−0.0	−2.2	−2.2	0.5	0.6
ΔEintra[n(>C5=Z6/Z6) → σ*(C1–H4)] (kJ mol^−1)	−18.1	−18.6	−17.7	−17.5	−18.1	−20.2
Δσ*(O–H) (e)	0.026	0.034	0.033	0.033	0.024	0.026
Δσ*(Csp^2–H) (e)	−0.006	−0.008	−0.007	−0.007	−0.006	−0.006

---

	FS–HS	FS–FS	FS–ClS	FS–BrS	FS–CH3S	FS–NH2S
EDT (FCHZ)	0.03	0.05	0.05	0.05	0.03	0.03
Einter[n(Z2) → σ*(O7–H8)] (kJ mol^−1)	81.9	106.8	102.7	105.2	76.1	79.0
Einter[n(Z6) → σ*(C1–H4)] (kJ mol^−1)	20.2	18.2	17.6	17.7	20.3	24.6
ΔEintra[n(>C1=Z2/Z2) → σ*(O7–H8)] (kJ mol^−1)	3.0	5.4	4.4	4.5	3.4	2.9
ΔEintra[n(>C5=Z6/Z6) → σ*(C1–H4)] (kJ mol^−1)	−10.3	−10.6	−10.0	−9.9	−10.6	−12.3
Δσ*(O–H) (e)	0.047	0.062	0.060	0.061	0.044	0.046
Δσ*(Csp^2–H) (e)	0.005	0.002	0.003	0.003	0.005	0.005

---

	FSe–HSe	FSe–FSe	FSe–ClSe	FSe–BrSe	FSe–CH3Se	FSe–NH2Se
EDT (FCHZ)	0.04	0.06	0.06	0.06	0.04	0.04
Einter[n(Z2) → σ*(O7–H8)] (kJ mol^−1)	98.4	124.4	120.3	123.1	93.4	96.3
Einter[n(Z6) → σ*(C1–H4)] (kJ mol^−1)	26.0	24.1	23.4	23.6	25.9	30.6
ΔEintra[n(>C1=Z2/Z2) → σ*(O7–H8)] (kJ mol^−1)	4.0	4.0	5.1	5.4	4.2	3.3
ΔEintra[n(>C5=Z6/Z6) → σ*(C1–H4)] (kJ mol^−1)	−7.2	−9.6	−8.9	−8.8	−7.5	−8.8
Δσ*(O–H) (e)	0.059	0.077	0.074	0.076	0.057	0.060
Δσ*(Csp^2–H) (e)	0.010	0.006	0.007	0.008	0.009	0.009

---

	FTe–HTe	FTe–FTe	FTe–ClTe	FTe–BrTe	FTe–CH3Te	FTe–NH2Te
EDT (FCHZ)	0.05	0.07	0.07	0.07	0.05	0.05
Einter[n(Z2) → σ*(O7–H8)] (kJ mol^−1)	109.4	138.3	133.1	135.0	107.8	113.0
Einter[n(Z6) → σ*(C1–H4)] (kJ mol^−1)	24.9	23.3	22.4	22.8	24.8	28.8
ΔEintra[n(>C1=Z2/Z2) → σ*(O7–H8)] (kJ mol^−1)	3.1	4.7	6.0	6.3	3.1	4.0
ΔEintra[n(>C5=Z6/Z6) → σ*(C1–H4)] (kJ mol^−1)	−6.7	−6.8	−8.4	−6.3	−7.0	−8.0
Δσ*(O–H) (e)	0.071	0.093	0.089	0.090	0.071	0.074
Δσ*(Csp^2–H) (e)	0.013	0.010	0.011	0.011	0.012	0.013

---

For the same X and R, it was found that the intermolecular electron transfer from the lone pair of Z2 to σ*(O7–H8) orbitals and from Z6 to σ*(C1–H4) orbitals was enhanced in the order of Z substituents: O < S < Se < Te (cf. Tables 3 and 4). Strikingly, although the NBO analysis indicated the intermolecular electron density transfer in the XO–RO complexes was weaker than that in XS–RS, XSe–RSe, and XTe–RTe, the AIM analysis also determined that the O/C_sp²–H⋯O hydrogen bonds were stronger compared to the O/C_sp²–H⋯S/Se/Te ones. This could be explained by the electronegativity and negative charge of the O atom being more significant than those of the S, Se, and Te ones (cf. Table S3†). This led to a stronger Coulomb electrostatic attraction between the proton donor and proton acceptor in the O/C_sp²–H⋯O hydrogen bonds compared to the O/C_sp²–H⋯S/Se/Te ones. Thereby, the strength of the O–H⋯Z and C_sp²–H⋯Z hydrogen bonds in the investigated complexes were primarily driven by electrostatic attraction and electron density transfer. However, a more predominant role was observed for the former than the latter.

When fixing X and Z and changing R, it was found that the intermolecular electron density transfer from n(Z2) to σ*(O7–H8) orbitals descended in the sequence: Br > Cl–F > H > NH₂ > CH₃ (cf. Tables 3 and 4). Besides, when fixing X and Z, a good linear correlation between the intermolecular electron density transfer from n(Z2) to σ*(O7–H8) orbitals and the electron density at the BCPs of O–H⋯Z hydrogen bonds was observed, as shown in Fig. S5.† As opposed to the O–H⋯Z hydrogen bonds, the E_inter[n(Z6) → σ*(C1–H4)] values of the C_sp²–H⋯Z hydrogen bonds experienced a decline with R varying in the order of NH₂ > CH₃ > H > F > Cl > Br. These results highlight the dominant influence of the electron-withdrawing groups on the strength of the O–H⋯Z hydrogen bonds. Meanwhile, an improvement in the strength of the C_sp²–H⋯Z hydrogen bonds was observed in the presence of electron-donating substituents. This was due to the electron-donating groups (NH₂, CH₃) tending to increase the electron density at the Z sites in >C=Z bonds; therefore promoting the electrostatic attraction and electron transfer between the Z atoms in NH₂/CH₃CZOH and the protons in the XCHZ monomers. The larger PA values of the NH₂/CH₃CZOH monomers compared to the F/Cl/BrCZOH ones (cf. Table 1) served as further evidence backing up this observation.

Furthermore, the blue-shifting or red-shifting of the C_sp²–H⋯Z and O–H⋯Z hydrogen bonds could be predicted through considering the change in the electron density at the σ*(C_sp²–H) and σ*(O–H) anti-bonding orbitals in the complexes compared to the corresponding monomers, which can be denoted as Δσ*(C_sp²–H) and Δσ*(O–H), respectively (cf. Tables 3 and 4). In general, the Δσ*(O–H) calculations presented positive values for all the considered complexes, ranging from 0.024 to 0.108 e. The significant intermolecular and intramolecular electron density transfer to the σ*(O–H) orbitals led to an increase in electron density at σ*(O–H) orbitals in XZ–RZ compared to initial RCZOH monomers. Consequently, a lengthening of the O–H bonds was observed. Consequently, O–H⋯Z are considered to be red-shifting hydrogen bonds. Regarding the nonconventional C_sp²–H⋯Z hydrogen bonds, the Δσ*(C_sp²–H) values of the C_sp²–H⋯S/Se/Te hydrogen bonds were found to be positive, except for the C_sp²–H⋯O ones, showing negative values of Δσ*(C_sp²–H) ranging from −0.012 to −0.006 e. Hence, while the C_sp²–H⋯Z (Z = S, Se, Te) hydrogen bonds are red-shifting, the C_sp²–H⋯O ones with the decrease in electron density at σ*(C_sp²–H) orbitals during the complexation can be characterized as blue-shifting. The reason for the difference in the Δσ*(C_sp²–H) values of the C_sp²–H⋯O hydrogen bonds was due to the decrease in the total intramolecular electron density transfer from n(O2) and n(>C1=O2) to σ*(C1–H4) (from −17.5 to −28.6 kJ mol⁻¹), which surpasses the intermolecular electron density transfer from n(O6) to σ*(C1–H4) (from 6.1 to 13.9 kJ mol⁻¹). This causes a rearrangement of the electron density on the RCOOH monomers during the complexation, and a reduction in the occupation at the σ*(C_sp²–H) orbitals in the XO–RO complexes compared to in the initial monomers. By contrast, the large intermolecular electron transfer from n(Se6/Te6) to σ*(C_sp²–H) orbitals exceeded the decrease in the intramolecular electron transfer to the σ*(C_sp²–H), which induced the electron density to increase at the σ*(C_sp²–H) orbitals in XSe–RSe and XTe–RTe. Thus, the intramolecular electron density transfer also contributed considerably to the distribution of electron density on the whole complexes, which also impacted the characteristics of the hydrogen bonds.

In addition, the results from the NCI plot (cf. Fig. S6a and b†) also showed the existence of O–H⋯Z and the C_sp²–H⋯Z hydrogen bonds, as shown by the appearance of two spikes lying on the negative region of sign(λ₂)·ρ(r), ranging from 0.01 to 0.05 au. This reflects the weak attractive interaction in these hydrogen bonds.^58,59 Therein, the spikes for the O–H⋯Z hydrogen bonds colored dark blue fell in the more negative region of sign(λ₂)·ρ(r) (from nearly 0.03 to over 0.05 au) compared to the spikes for the nonconventional C_sp²–H⋯Z hydrogen bonds (from 0.01 to 0.02 au) denoted with a light green color. This reveals the greater attraction of the O–H⋯Z hydrogen bonds compared to the C_sp²–H⋯Z ones. When X was changed from H to F, the negative values of sign(λ₂)·ρ(r) for the C_sp²–H⋯Z hydrogen bonds showed an increase while the values for the O–H⋯Z hydrogen bond spikes showed a decrease. This further confirmed that the strength of the C_sp²–H⋯Z hydrogen bonds in the FZ–RZ complexes were stronger than in the HZ–RZ ones. At the same time, an opposite trend was observed for the strength of the O–H⋯Z hydrogen bonds. Besides, the spikes of O/C_sp²–H⋯Z hydrogen bonds showed a tendency to move to the right of the sign(λ₂)·ρ(r) region with Z going from O to S to Se to Te. Moreover, Fig. S6a and b† also confirmed again the more significant role of electron-withdrawing substituents (F, Cl, Br) than electron-donating ones (NH₂, CH₃) on the strength of O–H⋯Z hydrogen bonds, since their spikes in the XZ–FZ, XZ–ClZ, and XZ–BrZ complexes were located in more negative regions than in XZ–NH₂Z and XZ–CH₃Z. By contrast, the C_sp²–H⋯Z hydrogen bond spikes tended toward the left with R going from Br/Cl/F to H to CH₃/NH₂, verifying the increase in the strength of the C_sp²–H⋯Z hydrogen bonds in the order of R substituents of: F–Cl–Br < H < CH₃ < NH₂. This result well agreed with the AIM analysis above.

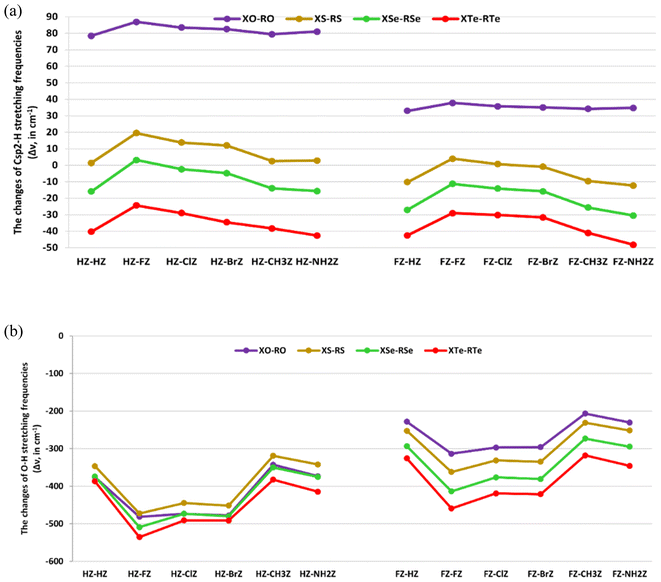
3.4. Changes in the bond lengths and stretching frequencies of the O–H and C_sp²–H bonds

The changes in bond lengths and stretching frequencies of the C_sp²–H, and the O–H proton donors were computed to assess the characteristics of the C_sp²–H⋯Z, and the O–H⋯Z hydrogen bonds in the XZ–RZ complexes. The results are presented in Fig. 3a and b, and Tables S6a and b.†

Fig. 3 (a) Changes in the C_sp²–H stretching frequencies of the C_sp²–H⋯Z hydrogen bonds in XZ–RZ complexes, with X = H, F; R = H, F, Cl, Br, CH₃, NH₂ and Z = O, S, Se, Te. (b) Changes in the O–H stretching frequencies of O–H⋯Z hydrogen bonds in XZ–RZ complexes, with X = H, F; R = H, F, Cl, Br, CH₃, NH₂ and Z = O, S, Se, Te.

Tables S6a and b† show the changes in the O–H bond length (Δr(O–H)) ranged from 0.0102 to 0.0256 Å, accompanied by a decrease in its stretching frequency (Δν(O–H)) in the complexes compared to in the initial monomers, being from −535.4 to −206.5 cm⁻¹. This indicates that there was an elongation of the O–H bond length and a decrease in its stretching frequency during the complexation, revealing the red-shifting of the O–H⋯O, O–H⋯S, O–H⋯Se, and O–H⋯Te hydrogen bonds. This was completely consistent with the prediction about the red-shifting of the O–H⋯Z hydrogen bonds mentioned in NBO analysis above. Such a red-shifting of O–H⋯Z hydrogen bonds has also been pointed out in complexes of XCHZ with YCOOH,⁴⁰ and H₂O.⁴² Interestingly, the red-shifting of O–H bonds in the O–H⋯Z hydrogen bonds in HCHZ⋯H₂O and FCHZ⋯H₂O calculated at the MP2/6-311++G(3df,2pd) level of theory were in the ranges of −147.5 to −121.2 cm⁻¹, and −90.3 to −66.2 cm⁻¹, respectively.⁴² The red-shifting of O–H bonds in the H/FCHZ⋯H₂O complexes was thus smaller than that noted for the XZ–RZ complexes in this work.

The magnitude of O–H red-shifting of the O–H⋯Z hydrogen bonds in the HZ–RZ complexes was stronger than that in FZ–RZ. Indeed, the Δν(O–H) values in HZ–RZ and FZ–RZ ranged from −535.4 to −318.8 cm⁻¹, and from −459.2 to −206.5 cm⁻¹, respectively, in agreement with the larger proton affinity at the Z atoms in HCHZ relative to the FCHZ monomers (cf. Table 1). The O–H red-shifts of the O–H⋯O hydrogen bonds in CH₃CHO⋯YCOOH and NH₂CHO⋯YCOOH computed at the MP2/6-311++G(3d,2p) level by An et al. (from −705.2 to −370.6 cm⁻¹)⁴⁰ were larger than those in the HO–RO and FO–RO complexes in this work (from −481.4 to −206.5 cm⁻¹). This suggests that replacing electron-withdrawing substituents in XCHO monomers with electron-donating ones leads to a stronger red-shifting for the O–H⋯O hydrogen bonds in the XCHO⋯RCOOH complexes. In addition, the O–H red-shifting in the XZ–RZ complexes increased with Z going from O to S to Se to Te (cf. Fig. 3a and b). This was evidenced by the increase in occupation at the σ*(O–H) orbitals in the O–H⋯Z (Z = S, Se, Te) hydrogen bonds surpassing that of the O–H⋯O ones, as mentioned in the NBO analysis. Therefore, the vibrational stretching frequencies of O–H bonds in O–H⋯Z (Z = S, Se, Te) decreased more deeply than those in the O–H⋯O hydrogen bonds. The higher polarity of the O–H bonds in RCSOH, RCSeOH, and RCTeOH compared to in RCOOH was also consistent with the trend of O–H red-shifting above (cf. Table 1). When fixing X and Z and changing R, it was observed that the red-shifting of the O–H⋯Z hydrogen bonds declined in the order: F > Cl > Br > NH₂ > H > CH₃. This was consistent with the larger intermolecular electron density transfer from n(Z2) to σ*(O–H) orbitals in the XZ–FZ, XZ–ClZ, and XZ–BrZ complexes compared to that in the XZ–CH₃Z and XZ–NH₂Z ones (cf. Tables 3 and 4). This result was also stated in the report of An et al. about the O–H⋯O hydrogen bonds in XCHO⋯YCOOH complexes (X = H, CH₃, NH₂; Y = H, F, Cl, Br, CH₃, C₂H₅, NH₂).⁴⁰ However, in our work, this tendency was not only obtained for the conventional O–H⋯O hydrogen bonds but also for the nonconventional O–H⋯S/Se/Te ones. In consequence, these observations suggest a red-shifting of the O–H⋯Z (Z = O, S, Se, Te) hydrogen bonds that was consistent with the increases in both the O–H polarity and proton affinity at the Z atoms, as well as the enhancement of the intermolecular electron density transfer from n(Z2) to σ*(O–H) orbitals.

On the other hand, the C_sp²–H⋯Se/Te hydrogen bonds in the investigated complexes demonstrated a lengthening of the C_sp²–H bond, along with a reduction in its stretching frequency compared to in the corresponding monomers (cf. Tables S6a and b†). This revealed a red-shift of the nonconventional C_sp²–H⋯Se and C_sp²–H⋯Te hydrogen bonds in XSe–RSe and XTe–RTe. Accordingly, the Δν(C_sp²–H) values of the C_sp²–H⋯Se/Te hydrogen bonds in FZ–RZ (Z = Se, Te) (from −48.2 to −11.3 cm⁻¹) were found to be more negative than those in HZ–RZ (Z = Se, Te) (from −42.7 to −2.4 cm⁻¹). Hence, the C_sp²–H red-shifting in the C_sp²–H⋯Se/Te hydrogen bonds increased according to changing the X substituent from H to F. The Δν(C_sp²–H) values of the C_sp²–H⋯Se/Te hydrogen bonds in 2RCHSe/Te dimers computed at the MP2/6-311++G(3df,2dp) level were reported to be from −38.6 to −8.4 cm⁻¹.⁴⁴ For the same X and Z, the Δν(C_sp²–H) values of C_sp²–H bonds in the C_sp²–H⋯Se/Te hydrogen bonds were found to be more negative based on the order of R substituents F < Cl < Br < CH₃ < H < NH₂ (cf. Fig. 3a). This was in line with the descending E_inter[n(Se6/Te6) → σ*(C_sp²–H)] values in the sequence of NH₂ > H > CH₃ > Br > Cl > F (cf. Tables 3 and 4). Simultaneously, the proton affinity at the Se, and Te atoms in the RCZOH monomers (Z = Se, Te) also showed a decrease with R going from NH₂ to CH₃ to H to Br to Cl to F (cf. Table 1). This emphasizes the greater red-shifting of the C_sp²–H⋯Se/Te hydrogen bonds in complexes containing electron-donating groups (NH₂, CH₃) compared to complexes with electron-withdrawing substituents (F, Cl, Br). In addition, the better electron density transfer and proton affinity at the proton acceptors Z also contributed to the larger red-shifting of the C_sp²–H proton donors. Remarkably, the decrease in the red-shifting of the nonconventional C_sp²–H⋯Se/Te hydrogen bonds occurred along with the increase in the red-shifting of the O–H⋯Se/Te hydrogen bonds. The reason for this is that the strong intermolecular electron transfer from the lone pair of Se2, and Te2 atoms in XCHZ to the σ*(O–H) orbitals in RCZOH decreased the intramolecular electron transfer from n(Se2/Te2) to σ*(C_sp²–H). This reduced the electron density at σ*(C_sp²–H) orbitals (cf. Tables 3 and 4).

By contrast, the nonconventional C_sp²–H⋯O and C_sp²–H⋯S hydrogen bonds in most the XO–RO and XS–RS complexes were characterized by a blue-shifting, except for the C_sp²–H⋯S hydrogen bonds in the FS–HS, FS–BrS, FS–CH₃S, and FS–NH₂S complexes which showed red-shifts. The blue-shifting of the C_sp²–H⋯O hydrogen bonds in the HO–RO complexes up to the range of 78.5–86.9 cm⁻¹ was larger than that in FO–RO, with Δν(C_sp²–H) values from 32.9 to 37.8 cm⁻¹. This observation was in agreement with the decrease in occupation at the σ*(C_sp²–H) orbitals in the C_sp²–H⋯O hydrogen bonds during the complexation. Similarly, the stretching frequencies of the C_sp²–H bonds in HS–RS increased more highly than those in FS–FS and FS–ClS (cf. Tables S6a and b†). Therefore, when replacing HCHZ with FCHZ monomers, the magnitude of blue-shifting of the nonconventional C_sp²–H⋯O, and C_sp²–H⋯S hydrogen bonds tended to decrease. This was in line with the weaker polarity of the C_sp²–H bond in HCHZ versus FCHZ.

For the same X and R substituents, the blue-shifting of the C_sp²–H bonds showed a tendency to decrease and even moved gradually to red-shifting when replacing the O substituent in the XO–RO complexes with S, Se, and Te. This trend was consistent with the increasing intermolecular electron density transfer from n(Z6) to σ*(C1–H4), which followed the order: O < S < Se < Te (cf. Tables 3 and 4). This result emphasizes the crucial role of the O atom in the blue-shifting of the nonconventional C_sp²–H⋯O hydrogen bonds. The blue-shifting of the C_sp²–H⋯O hydrogen bonds in the RCHO dimers, at the range of Δν(C_sp²–H) from 21.3 to 52.6 cm⁻¹,⁴⁴ was smaller than the blue-shifting of the C_sp²–H⋯O hydrogen bonds observed in this work. It is remarkable that for the same X and Z, the C_sp²–H blue-shifting of the C_sp²–H⋯O/S hydrogen bonds showed a decline when R was F, Cl, Br, NH₂, CH₃, and H, respectively (cf. Fig. 3a and b). This implies that there was a more considerable contribution of electron-withdrawing substituents than electron-donating ones in RCZOH to the large blue-shifting of the C_sp²–H⋯O/S hydrogen bonds. The explanation for this result is that the electron density transfer from n(O6/S6) to σ*(C1–H4) orbitals in the XZ–FZ, XZ–ClZ, and XZ–BrZ complexes (with Z = O, S) was smaller than that in the XZ–NH₂Z and XZ–CH₃Z ones (with Z = O, S). This led to a stronger decrease in electron density at the σ*(C_sp²–H) orbitals in XZ–FZ, XZ–ClZ, and XZ–BrZ compared to in XZ–NH₂Z and XZ–CH₃Z. The blue-shifting of the C_sp²–H⋯O hydrogen bonds in the CH₃CHO⋯FCOOH being larger than that in the CH₃CHO⋯CH₃COOH complex was also reported.⁴¹ Besides, a relationship between the C_sp²–H blue-shifting and proton affinity at the Z sites in RCZOH was also determined. In particular, the larger blue-shifts of the C_sp²–H⋯O, and C_sp²–H⋯S hydrogen bonds were consistent with the weaker proton affinity at O in RCOOH and S in RCSOH. It is notable that the increase in the blue-shifting of the C_sp²–H⋯O/S hydrogen bonds occurred along with the increase in the red-shifting of the O–H⋯O/S ones (cf. Tables S6a and b†). This, thus, underlines that the strong red-shifting of the O–H⋯O/S hydrogen bonds was closely related to the increase in the C_sp²–H blue-shifting of the nonconventional C_sp²–H⋯O/S hydrogen bonds.

4. Concluding remarks

Forty-eight structures of XZ–RZ (with X = H, F; R = H, F, Cl, Br, CH₃, NH₂, and Z = O, S, Se, Te), which were stabilized by the dominant role of the O–H⋯Z hydrogen bonds along with the C_sp²–H⋯Z hydrogen bonds, were found on the potential energy surface. The obtained results indicated a larger strength of the HZ–RZ complexes versus the FZ–RZ ones and a decreasing trend as Z changed from O to S to Se to Te. The higher stability of the XZ–RZ complexes was observed for R being an electron-withdrawing group. For XO–RO, this was mainly contributed by the electrostatic component, while the dominant role of the induction term compared to the other components most determined the stability of the XS–RS, XSe–RSe, and XTe–RTe complexes.

The strength of the O–H⋯Z hydrogen bonds decreased in the sequence of O–H⋯O ≫ O–H⋯S > O–H⋯Se > O–H⋯Te, indicating the noticeable importance of O compared to S, Se, and Te in stabilizing the complexes. The red-shifting of the O–H bonds was observed for the O–H⋯Z hydrogen bonds. The strength of O–H⋯Z hydrogen bonds and the red-shifts of the O–H stretching frequencies also showed a decrease with X going from H to F, and as R changed from an electron-withdrawing to an electron-donating group. In addition, the O–H red-shifting in the hydrogen bonds was enhanced with Z going from O to S to Se and then to Te. It was found that the very large electron transfer from the n(Z2) to σ*(O–H) orbital caused a considerable elongation of the O–H bond accompanied by a substantial red-shifting of its stretching frequency following complexation.

The C_sp²–H⋯O hydrogen bond is much more stable than the C_sp²–H⋯S/Se/Te ones. An increase in the strength of the nonconventional C_sp²–H⋯Z hydrogen bonds was also observed when R went from electron-withdrawing to electron-donating substituents, and X changed from the H to the F atom. Strikingly, the stretching frequencies of the C_sp²–H bonds gradually turned from blue-shifting to red-shifting when the O of >C=O in XCHO and RCZOH was substituted by S, Se, or Te, and R varied from an electron-withdrawing group to an electron-donating group. The results showed that the lower polarity of the C_sp²–H proton donor and the weaker proton affinity at proton acceptor Z induced a contraction of the C_sp²–H bond length and an increase in its stretching frequency, and vice versa. Besides, the considerable impact of intramolecular electron density transfer on the blue-shifting of the nonconventional C_sp²–H⋯O hydrogen bonds was also investigated in this work. Interestingly, the enhancement of O–H red-shifting in the O–H⋯Z hydrogen bonds was found to be correlated with an increase in the C_sp²–H blue-shifting in the C_sp²–H⋯O hydrogen bonds, but a decrease in C_sp²–H red-shifting of the C_sp²–H⋯S/Se/Te ones.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article and its ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Le Thi Tu Quyen was funded by the Master Scholarship Programme of Vingroup Innovation Foundation (VINIF), code VINIF.2023.ThS.110. This research was funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 104.06-2023.49.

References

1. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond: in Structural Chemistry and Biology, Vol. 9, International Union of Crystal, 2001.
2. R. L. McKiernan, A. M. Heintz, S. L. Hsu, E. D. Atkins, J. Penelle and S. P. Gido, Macromolecules, 2002, 35(18), 6970–6974.
3. J. N. Reek, B. de Bruin, S. Pullen, T. J. Mooibroek, A. M. Kluwer and X. Caumes, Chem. Rev., 2022, 122(14), 12308–12369.
4. V. R. Mundlapati, S. Gautam, D. K. Sahoo, A. Ghosh and H. S. Biswal, J. Phys. Chem. Lett., 2017, 8(18), 4573–4579.
5. D. M. Granum, S. Vyas, S. V. Sambasivarao and C. M. Maupin, J. Phys. Chem. B, 2014, 118(2), 434–448.
6. J. D. Graham, A. M. Buytendyk, D. Wang, K. H. Bowen and K. D. Collins, Biochemistry, 2014, 53(2), 344–349.
7. C. A. Johnson, O. B. Berryman, A. C. Sather, L. N. Zakharov, M. M. Haley and D. W. Johnson, Cryst. Growth Des., 2009, 9(10), 4247–4249.
8. S. Chakraborty, L. Rajput and G. R. Desiraju, Cryst. Growth Des., 2014, 14(5), 2571–2577.
9. H. Qu, J. Zhang, G. Zhang, Z. Li, Y. Liu, S. Wu and J. Gong, Cryst. Growth Des., 2022, 22(2), 1083–1093.
10. D. K. Kumar, A. Das and P. Dastidar, Inorg. Chem., 2007, 46(18), 7351–7361.
11. V. Carpenella, C. Fasolato, D. Di Girolamo, J. Barichello, F. Matteocci, C. Petrillo and A. Nucara, J. Phys. Chem. C, 2023, 127(45), 22097–22104.
12. Grabowski, S. J., Hydrogen Bonding: New Insights, Vol. 3. Dordrecht: Springer, 2006.
13. L. Sobczyk, S. J. Grabowski and T. M. Krygowski, Chem. Rev., 2005, 105(10), 3513–3560.
14. X. Chang, Y. Zhang, X. Weng, P. Su, W. Wu and Y. Mo, J. Phys. Chem. A, 2016, 120(17), 2749–2756.
15. P. Hobza and Z. Havlas, Chem. Rev., 2000, 100(11), 4253–4264.
16. B. J. van der Veken, W. A. Herrebout, R. Szostak, D. N. Shchepkin, Z. Havlas and P. Hobza, J. Am. Chem. Soc., 2001, 123(49), 12290–12293.
17. V. C. C. Wang, S. Maji, P. P. Y. Chen, H. K. Lee, S. S. F. Yu and S. I. Chan, Chem. Rev., 2017, 117(13), 8574–8621.
18. B. Yang, J. F. Cui and M. K. Wong, RSC Adv., 2017, 7(49), 30886–30893.
19. E. Bosch and N. P. Bowling, Cryst. Growth Des., 2020, 20(3), 1565–1571.
20. B. Behera and P. K. Das, J. Phys. Chem. A, 2019, 123(9), 1830–1839.
21. P. N. Khanh and N. Tien Trung, InTech, 2018, 105–121.
22. A. K. Chandra and T. Zeegers-Huyskens, J. Comput. Chem., 2012, 33, 1131–1141.
23. A. Kovács, A. Szabó, D. Nemcsok and I. Hargittai, J. Phys. Chem. A, 2002, 106, 5671–5678.
24. A. Rana, D. Pal and S. Chakraboty, Indian J. Phys., 2024, 1–9.
25. N. T. Trung, P. N. Khanh, A. J. P. Carvalho and M. T. Nguyen, J. Comput. Chem., 2019, 40(13), 1387–1400.
26. A. Karpfen and E. S. Kryachko, J. Phys. Chem. A, 2007, 111(33), 8177–8187.
27. P. Chopra and S. Chakraborty, Chem. Phys., 2018, 500, 54–61.
28. D. K. Sahoo, S. Jena, J. Dutta, A. Rana and H. S. Biswal, J. Phys. Chem. A, 2019, 123(11), 2227–2236.
29. A. Chand and H. S. Biswal, J. Indian Inst. Sci., 2020, 100, 77–100.
30. V. R. Mundlapati, D. K. Sahoo, S. Ghosh, U. K. Purame, S. Pankey, R. Acharya, N. Pal, P. Tiwari and H. S. Biswal, J. Phys. Chem. Lett., 2017, 8, 794–800.
31. K. K. Mishra, S. K. Singh, S. Kumar, G. Singh, B. Sarkar, M. S. Madhusudhan and A. Das, J. Phys. Chem. A, 2019, 123(28), 5995–6002.
32. K. K. Mishra, S. K. Singh, P. Ghosh, D. Ghosh and A. Das, Phys. Chem. Chem. Phys., 2017, 19(35), 24179–24187.
33. X. Chang, Y. Zhang, X. Weng, P. Su, W. Wu and Y. Mo, J. Phys. Chem. A, 2016, 120(17), 2749–2756.
34. Y. Mao and M. Head-Gordon, J. Phys. Chem. Lett., 2019, 10(14), 3899–3905.
35. C. Wang, D. Danovich, S. Shaik and Y. Mo, J. Chem. Theory Comput., 2017, 13(4), 1626–1637.
36. S. Shaik, D. Danovich and R. N. Zare, J. Am. Chem. Soc., 2023, 145(36), 20132–20140.
37. N. Thi Hong Man, P. Le Nhan, V. Vo, D. Tuan Quang and N. Tien Trung, Int. J. Quantum Chem., 2017, 117(6), e25338.
38. N. T. Trung, T. T. Hue, M. T. Nguyen and T. Zeegers-Huyskens, Phys. Chem. Chem. Phys., 2008, 10(33), 5105–5113.
39. N. N. Tri, N. T. H. Man, N. Le Tuan, N. T. T. Trang, D. T. Quang and N. T. Trung, Theor. Chem. Acc., 2017, 136, 1–12.
40. N. T. An, N. V. Thi and N. T. Trung, Phys. Chem. Chem. Phys., 2024, 26(34), 22775–22789.
41. N. T. An, N. T. Duong, N. N. Tri and N. T. Trung, RSC Adv., 2022, 12(54), 35309–35319.
42. N. T. T. Cuc, N. T. An, V. T. Ngan, A. K. Chandra and N. T. Trung, RSC Adv., 2022, 12(4), 1998–2008.
43. N. T. T. Cuc, C. T. D. Phan, N. T. A. Nhung, M. T. Nguyen, N. T. Trung and V. T. Ngan, J. Phys. Chem. A, 2021, 125(48), 10291–10302.
44. L. T. T. Quyen, B. N. Tung, P. N. Thach, N. N. Tri and N. T. Trung, RSC Adv., 2024, 14(20), 14114–14125.
45. P. N. Khanh, V. T. Ngan, N. T. H. Man, N. T. A. Nhung, A. K. Chandra and N. T. Trung, RSC Adv., 2016, 6(108), 106662–106670.
46. M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153(6), 503–506.
47. K. E. Riley, M. Pitonák, P. Jurecka and P. Hobza, Chem. Rev., 2010, 110(9), 5023–5063.
48. K. E. Riley, J. A. Platts, J. Rezac, P. Hobza and J. G. Hill, J. Phys. Chem. A, 2012, 116(16), 4159–4169.
49. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119(21), 11113–11123.
50. M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian 16 Rev. A. 03, Gaussian Inc., Wallingford CT, 2016.
51. A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper and J. Olsen, Chem. Phys. Lett., 1999, 302(5–6), 437–446.
52. T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106(23), 9639–9646.
53. A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286(3–4), 243–252.
54. R. F. Bader, Chem. Rev., 1991, 91(5), 893–928.
55. M. Ziółkowski, S. J. Grabowski and J. Leszczynski, J. Phys. Chem. A, 2006, 110(20), 6514–6521.
56. R. F. Bader, Acc. Chem. Res., 1985, 18(1), 9–15.
57. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285(3–4), 170–173.
58. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7(3), 625–632.
59. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132(18), 6498–6506.
60. T. Lu, J. Chem. Phys., 2024, 161(8), 082503.
61. A. Amonov and S. Scheiner, Phys. Chem. Chem. Phys., 2023, 25(35), 23530–23537.
62. E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2012, 2(1), 1–42.
63. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40(25), 2234–2241.
64. Politzer, P. and Truhlar, D. G. Chemical Applications of Atomic and Molecular Electrostatic Potentials: Reactivity, Structure, Scattering, and Energetics of Organic, Inorganic, and Biological Systems. Springer Science & Business Media, 2013.
65. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94(7), 1887–1930.
66. J. M. Turney, A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. A. Evangelista, J. T. Fermann and T. D. Crawford, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2012, 2(4), 556–565.
67. U. Koch and P. L. Popelier, J. Phys. Chem. A, 1995, 99(24), 9747–9754.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra07498j

---