Open Access Article
Open Access ArticleEvidencing an elusive conical intersection in the dissociative photoionization of methyl iodide
Jesús
González-Vázquez
 ab,
Gustavo A.
García
ab,
Gustavo A.
García
 c,
David V.
Chicharro
c,
David V.
Chicharro
 d,
Luis
Bañares
d,
Luis
Bañares
 de and
Sonia Marggi
Poullain
de and
Sonia Marggi
Poullain
 *d
*d
aDepartamento de Química, Facultad de Ciencias, Universidad Autónoma de Madrid, Spain
bInstitute for Advanced Research in Chemical Sciences (IAdChem), Universidad Autónoma de Madrid, 28049 Madrid, Spain
cSynchrotron SOLEIL, L'Orme des Merisiers, St. Aubin, BP 48, 91192 Gif-sur-Yvette, France
dDepartamento de Química Física, Facultad de Ciencias Químicas, Universidad Complutense de Madrid, 28040 Madrid, Spain. E-mail: smarggi@ucm.es
eInstituto Madrileño de Estudios Avanzados en Nanociencia (IMDEA-Nanoscience), Cantoblanco, 28049 Madrid, Spain
First published on 9th January 2024
Abstract
The valence-shell dissociative photoionization of methyl iodide (CH3I) is studied using double imaging photoelectron photoion coincidence (i2 PEPICO) spectroscopy in combination with highly-tunable synchrotron radiation from synchrotron SOLEIL. The experimental results are complemented by new high-level ab initio calculations of the potential energy curves of the relevant electronic states of the methyl iodide cation (CH3I+). An elusive conical intersection is found to mediate internal conversion from the initially populated first excited state, CH3I+(Ã2A1), into the ground cationic state, leading to the formation of methyl ions (CH3+). The reported threshold photoelectron spectrum for CH3+ reveals that the ν5 scissors vibrational mode promotes the access to this conical intersection and hence, the transfer of population. An intramolecular charge transfer takes place simultaneously, prior to dissociation. Upon photoionization into the second excited cationic state, CH3I+(![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2E), a predissociative mechanism is shown to lead to the formation of atomic I+.
2E), a predissociative mechanism is shown to lead to the formation of atomic I+.
1 Introduction
Radiationless electronic relaxation processes govern the dynamics following absorption of UV light in many isolated molecules.1 In particular, radiationless transitions between electronic states of the same multiplicity, referred to as internal conversion (IC), constitute a universal first step in the photo-induced dynamics of polyatomic systems leading afterwards to a variety of outcomes including dissociation or isomerization. The topology characterizing the potential energy surfaces of the electronic states involved directly determines the efficiency and the associated timescale of this type of process. For instance, IC in prebiotic molecules is often mediated by the presence of conical intersections leading to an efficient fast decay back into the ground state in a sub-picosecond timescale, preventing thus any photodamage (see for instance2,3). Biological systems need indeed a certain flexibility to access conical intersections allowing for a fast decay and thus surviving photodamage, as seen for instance in canonical DNA bases and pairs (see ref. 4 and references therein). In contrast, IC in other molecular systems, such as alkyl radicals, occurs between bound electronic states where no curve crossing is located.5,6 It takes place then through the overlap of the wavefunctions associated with highly-excited vibrational levels of two electronic states. This leads to a remarkably slow transfer of population followed in some cases by a statistical dissociation from vibrationally hot ground state. This type of mechanism is revealed by Boltzmann-type translational energy distributions characterizing the fragment products. In these cases, the long reaction time allows for intramolecular vibrational energy redistribution (IVR), adding further complexity to the associated dynamics. Here, in a joint experimental and theoretical investigation, an elusive conical intersection (CI) is revealed to mediate IC from the first excited state into the ground state of ionic methyl iodide (CH3I+). As evidenced by the threshold photoelectron spectrum measured for the methyl ion (CH3+), and supported by new high-level ab initio calculations, the scissors vibrational mode of the methyl group promotes the access to such CI, facilitating the transfer of population.Methyl iodide photoinduced dynamics has attracted a lot of interest over the years. It has indeed served as a proof-of-concept of experimental techniques such as ion imaging7 and velocity map imaging (VMI).8 A variety of methodologies, including experiments employing nanosecond lasers and slice imaging for dynamics9,10 and stereodynamics,11,12 femtosecond time-resolved experiments,13–16 experiments based on Coulomb explosion imaging17,18 or, more recently, attosecond transient absorption spectroscopy (ATAS),19,20 along with high-level ab initio calculations and semiclassical multidimensional trajectory calculations, including spin–orbit coupling and surface hopping, have been employed to disentangle the photodissociation dynamics upon UV photoexcitation18,21 and even to quantum-control the photodynamics by creating light-induced conical intersections and light induced potentials using intense ultrafast laser pulses.22–24 Although its photoionization and dissociative photoionization have received much less attention, recent experiments on the photodissociation of the methyl iodide cation (CH3I+) from excited states reached by UV two-photon absorption,25 and by XUV one-photon absorption,26 in combination with VMI have been reported, the latter in a time-resolved fashion in the femtosecond timescale involving IR femtosecond laser probe pulses.
Early work on methyl iodide photoionization includes photoelectron photoion coincidence experiments27–29 and time-of-flight spectroscopy,30 as well as the measurement of high-resolution photoelectron spectra.31 The ionization potential of CH3I has been determined to be 9.54150 ± 0.00003 eV,32 which is associated to the photoionization into the low component of the spin–orbit splitted CH3I+(![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2EJ) (J = 3/2, 1/2) ground state. The measured photoelectron spectrum using HeIα radiation features indeed two narrow peaks associated with the photoionization into vibrationally cold CH3I+(
2EJ) (J = 3/2, 1/2) ground state. The measured photoelectron spectrum using HeIα radiation features indeed two narrow peaks associated with the photoionization into vibrationally cold CH3I+(![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E3/2,1/2).31,33 A second band in the 12–13 eV photon energy range is assigned to ionization into CH3I+(Ã2A1). The ro-vibrational structure of this loosely bound state, which has been investigated in detail,31,34–39 is dominated by the C–I stretching mode (ν3), superimposed on the symmetric C–H stretch (ν1) and the umbrella mode (ν2). A third band lying at higher energies between 14.0 and 16.5 eV is observed in the reported photoelectron spectra and assigned to photoionization into the second excited cationic state, CH3I+(
2E3/2,1/2).31,33 A second band in the 12–13 eV photon energy range is assigned to ionization into CH3I+(Ã2A1). The ro-vibrational structure of this loosely bound state, which has been investigated in detail,31,34–39 is dominated by the C–I stretching mode (ν3), superimposed on the symmetric C–H stretch (ν1) and the umbrella mode (ν2). A third band lying at higher energies between 14.0 and 16.5 eV is observed in the reported photoelectron spectra and assigned to photoionization into the second excited cationic state, CH3I+(![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2E). The à cationic state is not stable and yields mainly CH3+ fragments with an appearance threshold of 12.248 ± 0.003 eV.40 This dissociation channel has been proposed to take place through IC into the ground state of the cation.26,28 The dissociation dynamics was later suggested to occur through a loose transition state, lacking a reverse activation barrier, while a long lifetime on the 10−7 s timescale was estimated.30 More recently, Bodi and co-workers discussed, based on high-resolution spectroscopy, the role of Rydberg states in the photoionization in the Franck–Condon gap between the cationic ground and first excited states.40 The appearance thresholds for the I+ fragment and the H-atom loss channel yielding CH2I+, were determined at 12.87 eV and 12.74 eV, respectively.28 Major formation of these two ionic fragments, I+ and CH2I+, occurs upon photoionization into the
2E). The à cationic state is not stable and yields mainly CH3+ fragments with an appearance threshold of 12.248 ± 0.003 eV.40 This dissociation channel has been proposed to take place through IC into the ground state of the cation.26,28 The dissociation dynamics was later suggested to occur through a loose transition state, lacking a reverse activation barrier, while a long lifetime on the 10−7 s timescale was estimated.30 More recently, Bodi and co-workers discussed, based on high-resolution spectroscopy, the role of Rydberg states in the photoionization in the Franck–Condon gap between the cationic ground and first excited states.40 The appearance thresholds for the I+ fragment and the H-atom loss channel yielding CH2I+, were determined at 12.87 eV and 12.74 eV, respectively.28 Major formation of these two ionic fragments, I+ and CH2I+, occurs upon photoionization into the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) excited state manifold. Direct dissociation in this state manifold would lead to the H-atom loss while IC into the à state has been proposed to lead to I+ formation.29,41
excited state manifold. Direct dissociation in this state manifold would lead to the H-atom loss while IC into the à state has been proposed to lead to I+ formation.29,41
Theoretical works include vertical excitation energies associated with the valence-shell photoionization into different excited states, using the outer valence Green function method (OVGF)42 and later using the many-body Green function approach.33 Locht et al.43 carried out complete active space self-consistent field (CASSCF) calculations of vertical excitation energies and partial potential energy curves for the first electronic states of the cation. All these calculations were performed by neglecting the spin–orbit coupling. In a more recent investigation, we have shown how the spin–orbit coupling significantly alters the landscape based on the potential energy curves and thus the expected dynamics.25 A second set of calculations, including full dimension on-the-fly trajectory calculations on the Ã2A1 state have been later reported to explore the role of an IR probe pulse after one-photon XUV absorption.26
The present work reports experimental results using the double imaging photoelectron photoion coincidence (i2 PEPICO) technique upon one-photon ionization by tunable synchrotron radiation along with high-level ab initio calculations. The major formation of CH3+ from the CH3I+(Ã2A1) excited state is shown to occur through an elusive CI mediating the IC into the CH3I+(![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E) ground state. This transfer of population appears to be promoted by the ν5 scissors vibrational mode. In addition, the formation of I+ and CH3+ following ionization into the B band is shown to occur through a predissociative mechanism. Theoretical support in the form of complete active space perturbation theory (CASPT2) calculations taking into account the spin–orbit components and including a larger active space, in comparison with previous calculations,26 are presented to extract insight into the dissociation dynamics upon valence-shell photoionization.
2E) ground state. This transfer of population appears to be promoted by the ν5 scissors vibrational mode. In addition, the formation of I+ and CH3+ following ionization into the B band is shown to occur through a predissociative mechanism. Theoretical support in the form of complete active space perturbation theory (CASPT2) calculations taking into account the spin–orbit components and including a larger active space, in comparison with previous calculations,26 are presented to extract insight into the dissociation dynamics upon valence-shell photoionization.
The manuscript is organized as follows. In Section 2, the experimental and theoretical methods are described, while in Section 3, the experimental and theoretical results including the measured threshold photoelectron spectra and the photoion–photoelectron kinetic energy correlation diagrams are presented along with the computed potential energy curves. The different fragmentation mechanisms are discussed based on the experimental and theoretical results. Finally, the main conclusions of this work are summarized in Section 4.
2 Methods
2.1 Experimental
Experiments were performed at the DESIRS beamline of the French synchrotron SOLEIL,44 on the permanent end-station SAPHIRS,45 employing the double imaging photoelectron photoion coincidence (i2 PEPICO) spectrometer DELICIOUS III.46 Synchrotron photons emitted from an undulator were dispersed by a 6.65 m normal incidence monochromator. A 200 lines per mm−1 grating was used and the monochromator slits were set to provide a photon energy resolution ranging between ∼4 meV at 12.0 eV to 8 meV at 17 eV photon energy with an estimated photon flux of 5 × 1012 photons per s−1. Spectral purity was ensured by means of a gas filter filled with Ar or Ne47 to remove high harmonics emitted from the undulator. The absolute photon energy scale was calibrated separately within an accuracy of 1 meV using the absorption lines of Ar in the gas filter. Methyl iodide (Sigma Aldrich) was placed in a bubbler at −15 °C (no carrier gas used) and expanded through a 50 μm diameter nozzle and collimated by two skimmers (Beam Dynamics, 1.0 mm diameter) to form a continuous molecular beam.The molecular beam crossed the synchrotron light at a right angle in the center of DELICIOUS III, and all electrons and ions produced were extracted and accelerated in opposite directions by an electric field. A velocity map imaging (VMI) and a modified Wiley-McLaren time-of-flight (TOF) imaging spectrometers were employed to detect electrons and ions, respectively. Photoelectron energy spectra (PES) and angular distributions were obtained from the electron VMI image by Abel inversion using the pBasex algorithm48 while the full ion 3D momentum distribution was extracted from the ion time-of-flight (TOF) and the 2D arrival position onto the corresponding position-sensitive detector. The coincidence scheme yielded electron images, and thus a photoelectron spectrum (PES) correlated to a particular ion momentum, which in turn produced the photoelectron and photoion kinetic energy correlation diagram (KECD). The mass resolving power M/ΔM was sufficient to separate the CH2I+ fragment ion (m/z = 141) from the parent ion CH3I+ (m/z = 142).
Measurements at two fixed photon energies, i.e. 14 eV and 15.5 eV, were performed first, and a scan between 12.0 eV and 17.0 eV with steps of 25 meV was then carried out plus an additional scan of the A band with a 2.5 meV step. While the photoelectron and photoion KECDs constitute the main result for a dissociative photoionization measurement at a fixed photon energy, the scan is analyzed to obtain for each ion, the coincident electron signal as a function of the ion and electron kinetic energy, and the photon energy. Such 3D histograms are here condensed to 2D and 1D representations by integration over a limited bandwidth of the electron energy along constant ionic states, reducing the electron energy distribution to threshold photoelectron spectra (TPES), as detailed elsewhere.49 This allows extraction of 2D energy correlation diagrams as a function of ion kinetic and cationic state, as well as 1D TPES by integration over all ion kinetic energies. The photon energy scale has been calibrated with the O2 autoionizations lines50 in the photon energy scans.
2.2 Theoretical
All calculations were performed using the OpenMOLCAS51,52 suite including the extended multi-state complete active space self-consistent field second-order perturbation theory (XMS-CASPT2) analytical gradients.51 The energy of the different electronic states was obtained using a complete active space self-consistent field (CASSCF)/XMS-CASPT2 protocol with an ANO-RCC53 basis set contracted to VTZP with a Douglas Kroll Hamiltonian.54 All valence orbitals were included in the active space, i.e. the two lone pairs of the I and the bonding and antibonding orbitals for both the C–I and the C–H bonds, giving a total of 10 orbitals, CAS(11,10). For the XMS-CASPT2 calculation, an imaginary shift of 0.2 was employed and the ionization-potential-electron-affinity (IPEA) shift was removed. The final energy was obtained including the spin–orbit coupling in an atomic mean field interaction approximation55 with the perturbed modified CASSCF (PM-CASSCF) electronic wavefunctions. Concerning the optimization procedure, the Franck–Condon geometry was calculated using many-body second-order perturbation theory and the rest of the geometries with the XMS-CASPT2 for the spin-free states. One-dimension potential energy curves were calculated along the C–I distance while the rest of the coordinates were relaxed following the gradient of the first doublet at XMS-CASPT2. The present calculations, named hereafter CASPT2(11,10), were compared thoroughly with previous calculations carried out by using the same methodology but a smaller active space, i.e. CAS(5,4), named hereafter CASPT2(5,4),26 and by using multireference configuration interaction (MRCI) with an active space CAS(5,4), hereafter MRCI(5,4).25In order to estimate the semiclassical photoelectron spectrum, several geometries mimicking the harmonic ground state were obtained using a Wigner distribution on the Franck–Condon geometry and the energies and Dyson amplitudes were obtained with the previous protocol. Similarly to the case of the spin–orbit couplings, the Dyson amplitudes were calculated in the frame of perturbed modified CASSCF. Finally, in order to consider the effects of the other degrees of freedom, stationary points were optimized considering the spin–orbit numerical gradients in a modified version of the Atomic Simulation Environment56 with the FIRE optimizer,57 where a new calculator was created. Similarly to the SHARC method58 in a recent implementation,59 the spin–orbit gradient was estimated by averaging the gradient of the different spin-free states. In this approximation, successfully tested for this molecule,26 the variation of the spin–orbit operator with the nuclei coordinates and the non-adiabatic elements were neglected for the gradient calculation. In the case of degeneration points, an effective gradient was obtained by constraining the energy difference between the spin–orbit states. This was done by optimizing at the same time the square of the energy difference between the two electronic states and the lowest electronic state (projecting out the previous contribution).
3 Results and discussion
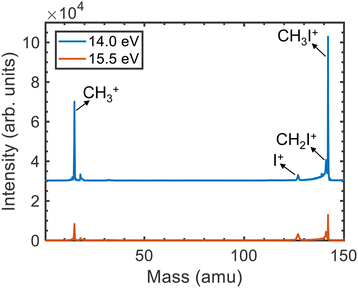
The time-of-flight mass spectra (TOFMS) upon photoionization of CH3I at hν = 14.0 eV and 15.5 eV are displayed in Fig. 1. Four main peaks are observed in both TOFMS. Besides the dominant parent ion CH3I+ at m/z = 142, photoionization leads mainly to the formation of CH3+, as reflected by the peak at m/z = 15. Two additional peaks are observed corresponding to the formation of CH2I+ (m/z = 141) and I+ (m/z = 127). The small structure lying around m/z = 18 is associated with the photoionization of residual water present in the reaction chamber.The KECDs obtained for (CH3+, e), (I+, e), and (CH2I+, e) photoion–photoelectron coincident events are depicted in Fig. 2 and 3 following photoionization at hν = 14.0 eV and 15.5 eV, respectively. The corresponding KECD associated with the (CH3I+, e) coincident events is not shown, first because as a non-dissociative event only the photoelectron image has relevant information, and second because the parent ion formation is mostly related to the ionization into CH3I+(![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E3/2) and CH3I+(
2E3/2) and CH3I+(![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E1/2) in their respective vibrational ground states, leading to the emission of photoelectrons with high kinetic energy (≥4 eV). The extraction field used here does not allow for a full 4π detection of such high energy photoelectrons.
2E1/2) in their respective vibrational ground states, leading to the emission of photoelectrons with high kinetic energy (≥4 eV). The extraction field used here does not allow for a full 4π detection of such high energy photoelectrons.
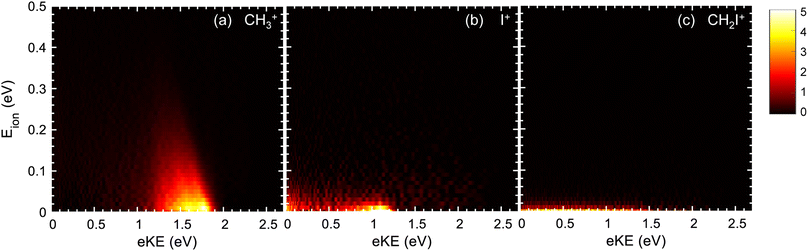
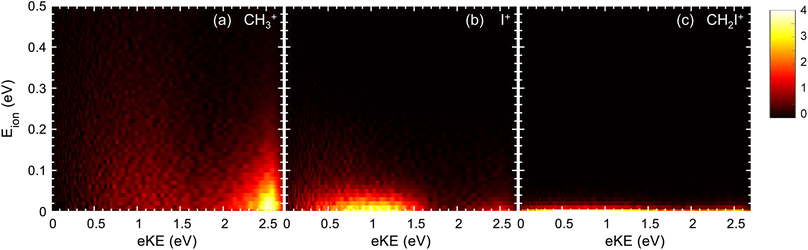
The formation of CH3+ following photoionization at hν = 14 eV is characterized by a single structure centered at ∼1.6 eV photoelectron kinetic energy (eKE) (see Fig. 2a), which arises from photoionization into CH3I+(Ã2A1). At hν = 15.5 eV, two structures are recovered in the corresponding KECD (see Fig. 3a). The dominant structure, centered at eKE of ∼2.5 eV, reflects photoionization into the à cationic state, while the second broad structure, with eKEs in the range 0–1.5 eV, can be attributed to photoionization into the CH3I+(![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2E) state manifold. We note that the extraction field used in Fig. 2 and 3 allows full transmission of electrons with a maximum eKE around 2.5 eV. The dominant structure in Fig. 3(a) associated with the photoionization into the à state is therefore highly affected by electrons flying outside the detector. Fig. 3 should indeed be employed to focus on the dynamics upon photoionization in the
2E) state manifold. We note that the extraction field used in Fig. 2 and 3 allows full transmission of electrons with a maximum eKE around 2.5 eV. The dominant structure in Fig. 3(a) associated with the photoionization into the à state is therefore highly affected by electrons flying outside the detector. Fig. 3 should indeed be employed to focus on the dynamics upon photoionization in the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state. Fig. 2b depicts the KECD for production of I+ and shows a structure peaking at 1.1 eV with a tail down to 0 eV. The main peak would reflect photoionization into vibrationally excited CH3I+(Ã2A1), while the tail would highlight the beginning of photoionization into the second
state. Fig. 2b depicts the KECD for production of I+ and shows a structure peaking at 1.1 eV with a tail down to 0 eV. The main peak would reflect photoionization into vibrationally excited CH3I+(Ã2A1), while the tail would highlight the beginning of photoionization into the second ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) cationic excited states. At hν = 15.5 eV, a main broad contribution is observed ranging from 0 to 1.5 eV, along with a minor contribution peaking at ∼2.5 eV. Similarly to the results at hν = 14 eV, the former reflects major photoionization into the
cationic excited states. At hν = 15.5 eV, a main broad contribution is observed ranging from 0 to 1.5 eV, along with a minor contribution peaking at ∼2.5 eV. Similarly to the results at hν = 14 eV, the former reflects major photoionization into the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) states manifold and the latter highlights photoionization into the à state prior to dissociation. Finally, the KECDs depicted in Fig. 2c and 3c for (CH2I+, e) show a structureless continuum. The respective maximum eKE corresponds directly to a binding energy equal to the reported appearance threshold recently reported by Bodi et al.60 at ∼12.6 eV, while slightly below the value measured by Eland and coworkers (∼12.74 eV).28 The H-atom elimination seems therefore to be open from both the upper part of the à state and from the
states manifold and the latter highlights photoionization into the à state prior to dissociation. Finally, the KECDs depicted in Fig. 2c and 3c for (CH2I+, e) show a structureless continuum. The respective maximum eKE corresponds directly to a binding energy equal to the reported appearance threshold recently reported by Bodi et al.60 at ∼12.6 eV, while slightly below the value measured by Eland and coworkers (∼12.74 eV).28 The H-atom elimination seems therefore to be open from both the upper part of the à state and from the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) manifold of states.
manifold of states.
The photoion kinetic energy, Eion, distributions characterizing the dissociative photoionization channels leading to CH3+ and to I+ show Boltzmann-type distributions peaking at threshold energies. This would indicate indirect dissociation mechanisms for both channels following photoionization, allowing for a considerable sharing of the available energy between the different degrees of freedom. The Eion distribution for the methyl cation, depicted in Fig. 2a and 3a, is considerably narrow, characterized by a full-width at half-maximum (FWHM) around 0.13 eV, corresponding to a kinetic energy release (KER) ∼0.15 eV. Similar Eion distributions and mean kinetic energies for CH3+ between 0.1 eV and 0.2 eV s were reported by Powis.29 These ion kinetic energy distributions reflect the slow dissociation from C–I bond cleavage in the cationic ground state following internal conversion from the à state. The I+ fragment is characterized by small photoion energies, as observed in Fig. 2b and 3b, but by a larger corresponding KER, up to 1.0 eV, although always peaking at threshold energies. The FWHM increases considerably with the photon energy, in agreement with reported mean kinetic energies29 below 0.1 eV at 14 eV photon energy up to 0.17 eV around 15.5 eV. The Eion distribution for I+ reflects an indirect dissociation mechanism leading to a considerable transfer of energy from translational into ro-vibrational degrees of freedom. The kinetic energy distributions for CH2I+ from Fig. 2c and 3c ranges however from 0 to ∼30 meV which corresponds to a KER up to 4 eV due to the low co-fragment (H atom) mass leading to a high mass factor. Taking into account these kinetic energies, the position resolution of the apparatus does not allow resolving the expected Gaussian kinetic energy distribution associated to direct dissociation for the H-atom loss following ionization in the B band.
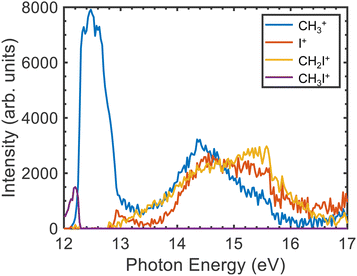
The TPES measured for the parent ion as well as for the three fragments in the photon energy region between 12.0 and 17.0 eV are depicted in Fig. 4. The corresponding breakdown diagram depicted in Fig. 5 shows good agreement with previous results.28 A small signal for the formation of the parent ion is observed at the lower photon energies disappearing at ∼12.25 eV, in coincidence with the threshold for CH3+ formation. This feature, arising in the Franck–Condon (FC) gap between the ground and the first excited state of the cation, is assigned to photoionization into CH3I+(Ã2A1). Bodi et al.40 already reported and discussed in detail this photon energy region. Non-FC photoionization into vibrationally excited CH3I+(![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E3/2,1/2) competing with the photoionization into the à state was discussed in terms of the role of Rydberg states and subsequent autoionization, based on the mechanisms described by Guyon et al.61 and Chupka et al.62 We note that, as observed in Fig. 4 and in agreement with the literature,28 above the fragmentation threshold, photoionization into the excited à and
2E3/2,1/2) competing with the photoionization into the à state was discussed in terms of the role of Rydberg states and subsequent autoionization, based on the mechanisms described by Guyon et al.61 and Chupka et al.62 We note that, as observed in Fig. 4 and in agreement with the literature,28 above the fragmentation threshold, photoionization into the excited à and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) cationic states leads to complete fragmentation, i.e. no parent ions survive.
cationic states leads to complete fragmentation, i.e. no parent ions survive.
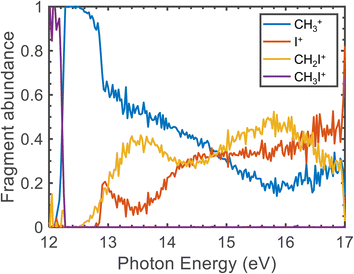 | ||
| Fig. 5 Fragment abundance as a function of the photon energy (eV). The measured data correspond to photon energy steps of 0.25 meV. | ||
The CH3+ fragment shows a threshold at 12.25 ± 0.03 eV, in agreement with the high-resolution value of 12.248 ± 0.003 eV reported by Bodi et al.40 Although the long range/low resolution of the TPES shown in Fig. 4 does not allow us to resolve the C–I stretching vibrational progression on the parent cation, it unexpectedly shows a series of peaks lying between 12 and 13 eV unrelated to this progression. In order to explain the origin of this structure, a zoom on the A band is presented in Fig. 6 recorded with a 2.5 meV energy step, in the form of a 2D energy correlation diagram showing the CH3+ signal correlated to threshold photoelectrons as a function of the center-of-mass kinetic energy release (CoM-KER) and the photon energy. The associated threshold photoelectron spectrum is plotted as a white curve, obtained by integrating the CH3+ signal associated with a CoM-KER below 25 meV. The figure shows a long vibrational progression corresponding to excitation of the ν3 C–I stretching mode in the CH3I+ parent ion. This agrees with the previous high-resolution PES from photoionization using the HeI radiation from Karlsson et al.31 that reported a broad continuum with superimposed vibrational progressions related with the preferred C–I stretching mode (294.2 cm−1), in combination with the ν1 and ν2 vibrational modes. Locht et al.43 also reported the TPES in this energy region and obtain a structureless band, while no vibrational activity was resolved, perhaps due to their higher experimental temperature—room temperature (RT) with respect to the currently measured molecular beam temperature of 70 K—although Bodi et al.40 observe vibrational structure in their RT TPES recorded with an effusive beam up to 12.3 eV. Interestingly, on top of the C–I stretching progression, Fig. 6 shows a modulation of the CoM-KER with the photon energy, i.e., cationic state, with colder ions being produced at periodic intervals that are consistent with the presence of dissociation limits converging towards the formation of CH3+ vibrationally excited in the out-of-plane bending mode. This modulation is also seen in the 1D TPES plotted alongside, especially when correlated with the production of translationally cold fragments (CoM-KER < 25 meV). The excitation of the out-of-plane bending motion in the methyl cation ν2 (1404 cm−1) is analogous to the ν5 scissoring mode in the parent ion (1394 cm−1), which is intriguing since this would not directly reflect the FC factors expected in direct ionization, although Lee and Kim39 reported combination bands involving this vibrational mode in their high-resolution spectroscopic study of the Ã2A1 state. The data in Fig. 6 suggests indeed a certain vibrational selectivity for production of CH3+ which is perhaps not seen in earlier works due to the different sample temperature, and the lack of the fragment KER information. Note that, with respect to the fixed photon energy PES of Karlsson et al.,31 a potential difference could be the effect of autoionizations in the shape of the photon energy scans. However, extracting the TPES at different electron kinetic energy bandwidths to separate indirect from direct ionization, did not point towards the presence of autoionizations.63 The TPES obtained here for different resolutions and CoM-KERs are compared in the supplementary information to the ones previously reported in the literature. The TPES appears to be considerably sensitive to the translational energy of the CH3+ fragment, which is expected because, as seen in Fig. 6, translational cold ions are produced close to the dissociation limits. The vibrational selectivity for production of CH3+ along with the role of the ν5 CH2 scissors mode in the parent ion will be discussed in more detail below, in conjunction with the theoretical calculations carried out in the present work.
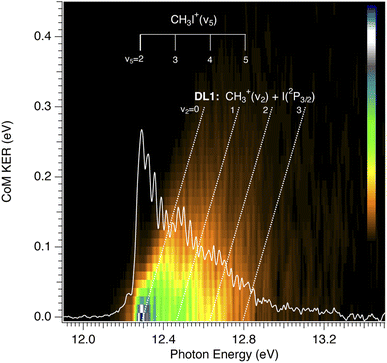 | ||
| Fig. 6 CH3+ signal correlated to threshold photoelectrons (eKE < 15 meV), as a function of centre-of-mass kinetic energy release (CoM-KER) and photon energy. The photon energy axis corresponds to the ionization energy since only threshold electrons are considered. The associated threshold photoelectron spectrum is plotted as a white curve, obtained by integrating the CH3+ signal associated with a CoM-KER below 25 meV. The ν5 vibrational mode of the CH3I+ parent ion with respect to the adiabatic ionization energy of the A band from Karlsson et al.31 is depicted in the figure. The first dissociation limit, from Bodi et al.,40 DL1, corresponding to the production of methyl cation in its electronic ground state plus I(2P3/2) is also shown, along with the limits converging to vibrationally excited methyl cations in the out-of-plane bending, ν2, mode. The represented slope is only qualitative. | ||
The threshold for I+ formation is observed at 12.85 ± 0.03 eV, while the one for CH2I+ is at 12.82 ± 0.03 eV, in qualitative agreement with Eland and co-workers.28 Both values are associated to photoionization into highly-vibrationally excited CH3I+(Ã2A1). The appearance of I+ correlates to a remarkable drop in the CH3+ yield. Formation of CH2I+ is observed between 13.2 and 13.5 eV in the FC gap between the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) cationic excited states, while photoionization into CH3I+(
cationic excited states, while photoionization into CH3I+(![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2E) is observed in the measured TPES for the three fragment ions as a structureless band lying between 13.5 and 16.0 eV.
2E) is observed in the measured TPES for the three fragment ions as a structureless band lying between 13.5 and 16.0 eV.
Table 1 shows the calculated vertical excitation energies (VEEs) at the FC geometry of the CH3I neutral ground state for the three levels of theory used thus far, i.e., a comparison of the present results at CASPT2(11,10) with those reported previously at CASPT2(5,4)26 and MRCI(5,4)25. The norms of the Dyson orbitals calculated at CASPT2(11,10) and CASPT2(5,4) levels of theory are also included. Experimental VEEs are also included in Table 1.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ), at three levels of theory. Present work: CASPT2(11,10). Previous work: CASPT2(5,4) (ref. 26) and MRCI(5,4) (ref. 25). Experimental VEEs are also included (from ref. 31)
), at three levels of theory. Present work: CASPT2(11,10). Previous work: CASPT2(5,4) (ref. 26) and MRCI(5,4) (ref. 25). Experimental VEEs are also included (from ref. 31)
| CH3I+ State | Experimental VEE (eV) | CASPT2(11,10) VEE (eV) | Dyson | CASPT2(5,4)26 VEE (eV) | Dyson | MRCI(5,4)25 VEE (eV) |
|---|---|---|---|---|---|---|
![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2
E
3/2
2
E
3/2
|
9.54 | 9.33 | 0.951 | 9.22 | 0.951 | 9.10 |
![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2
E
1/2
2
E
1/2
|
10.02 | 9.89 | 0.954 | 9.81 | 0.952 | 9.78 |
| Ã 2 A 1 | 12.5 | 12.53 | 0.949 | 12.34 | 0.974 | 12.37 |
| 4 | 14.44 | 0.002 | 14.50 | 0.006 | 14.43 | |
| 5 | 14.54 | 0.004 | 14.61 | 0.003 | 14.57 | |
| 6 | 14.7 | 15.09 | 0.854 | 15.15 | 0.002 | |
| 7 | 15.10 | 0.313 | 15.53 | 0.001 | ||
| 8 | 15.4 | 15.13 | 0.553 | 15.75 | 0.002 | |
| 9 | 15.39 | 0.001 | 16.31 | 0.001 |
The first ionization threshold calculated at CASPT2(11,10) in the present work is located at 9.33 eV, which is in reasonable agreement with the experimental value of 9.54150 ± 0.00003 eV.32 The spin–orbit splitting between the two first ionic states is found to be 0.56 eV, in line with the value of 0.628 ± 0.008 eV found experimentally.31 The first excited state of the cation, CH3I+(Ã2A1), is located at 12.53 eV in the present calculations. Above the Ã2A1 state, a series of states are present lying from 14.44 eV to 15.39 eV (labeled states 4–9 in Table 1). States 6, 7 and 8 (at 15.09, 15.10 and 15.13 eV, respectively) show large Dyson norms, i.e. large ionization probabilities, compared to states 4, 5 and 9 (at 14.44, 14.54 and 15.39 eV, respectively). Although the VEEs of the first three electronic states are very similar at CASPT2(11,10) and CASPT2(5,4), the consideration of the C–H bonds in the active space, CAS(11,10), seems to be very important to properly describe the higher electronic states. This can be seen when comparing the norms of the Dyson orbitals obtained at CASPT2(11,10) and CASPT2(5,4) for the states labeled 4–9 in Table 1, which correspond to the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2E manifold. In addition, we notice that the use of MRCI(5,4) is much less efficient to recover the dynamical electron correction in comparison with the CASPT2 method.
2E manifold. In addition, we notice that the use of MRCI(5,4) is much less efficient to recover the dynamical electron correction in comparison with the CASPT2 method.
The calculated dissociation energies at CASPT2(11,10) are shown in Table 2. Experimental appearances energies obtained in this work are also included in Table 2. Asymptotic energies of 12.21 eV and 12.73 eV correspond to the appearance of the CH3+ and I+ fragment cations, respectively. These values are in good agreement with the reported experimental appearance thresholds,28,40 which are found at 12.25 eV and 12.74 eV. These energies are far from being accessible after photoionization into the spin–orbit split ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E3/2,1/2 ground state of CH3I+. As observed experimentally, the parent cation can dissociate only after photoionization into the à or
2E3/2,1/2 ground state of CH3I+. As observed experimentally, the parent cation can dissociate only after photoionization into the à or ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) excited states. In general, we have observed that the dissociation energies mentioned above do not significantly vary neither with the active space chosen, nor with the method employed to correct the CASSCF energies.
excited states. In general, we have observed that the dissociation energies mentioned above do not significantly vary neither with the active space chosen, nor with the method employed to correct the CASSCF energies.
| Dissociation | Experimental appearances energies | CASPT2(11,10) | CASPT2(5,4)26 | MRCI(5,4)25 |
|---|---|---|---|---|
| I(2P3/2) + CH3+ | 12.25 | 12.21 | 12.09 | 12.12 |
| I+(3P2) + CH3 | 12.85 | 12.73 | 12.95 | 12.30 |
| I(2P1/2) + CH3+ | 13.14 | 13.05 | 13.15 | |
| I+(3P1) + CH3 | 13.51 | 13.23 | ||
| I+(3P0) + CH3 | 13.84 | 13.16 | ||
| I+(1D2) + CH3 | 14.49 | 14.15 | ||
| I+(1S0) + CH3 | 16.21 | |||
CH2I+(![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A1) + H 1A1) + H |
12.82 | 12.73 |
In order to estimate the vibrational broadening associated with the photoionization process, we have calculated the semiclassical photoelectron spectrum, which is depicted in Fig. 7. The simulated spectrum is in very good agreement with the experimental photoelectron spectra reported using HeIα radiation31 as well as synchrotron radiation at 85 eV.33 Two narrow peaks are observed at 9.16 and 9.75 eV, corresponding to the ionization into the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E3/2 and
2E3/2 and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E1/2 ground state wells. We note that the simulated spectrum was convoluted with a Gaussian function (FWHM = 0.25 eV) to reproduce a certain width for these two peaks. The bimodal structure observed experimentally is associated to vibrational activity and cannot be observed in the simulation. The second band, corresponding to the photoionization into CH3I+(Ã2A1) spans from 11.6 to 13.2 eV. Finally, a third band can be observed from 13.0 to 16.4 eV assigned to the B band. Table 1 shows that this band is composed by several electronic states ranging from 14.44 to 15.39 eV.
2E1/2 ground state wells. We note that the simulated spectrum was convoluted with a Gaussian function (FWHM = 0.25 eV) to reproduce a certain width for these two peaks. The bimodal structure observed experimentally is associated to vibrational activity and cannot be observed in the simulation. The second band, corresponding to the photoionization into CH3I+(Ã2A1) spans from 11.6 to 13.2 eV. Finally, a third band can be observed from 13.0 to 16.4 eV assigned to the B band. Table 1 shows that this band is composed by several electronic states ranging from 14.44 to 15.39 eV.
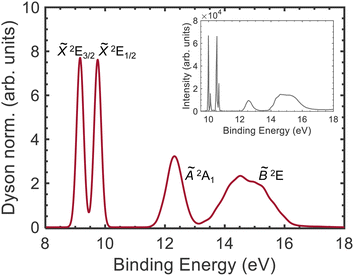 | ||
Fig. 7 Simulated photoelectron spectrum. The Dyson norm for the different states was calculated for a harmonic Wigner distribution in the neutral state and convoluted with a Gaussian function (FWHM = 0.25 eV). The different bands are assigned (from left to right) to the spin–orbit split ground state, ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E3/2 and 2E3/2 and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E1/2, and to the first and second electronic excited states, Ã2A1 and 2E1/2, and to the first and second electronic excited states, Ã2A1 and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2E, of the cation. The experimental photoelectron spectrum measured using HeIα radiation31 is represented in the inset. The structure observed in the two first peaks corresponds to vibrational activity, which is absent in the simulated spectrum. 2E, of the cation. The experimental photoelectron spectrum measured using HeIα radiation31 is represented in the inset. The structure observed in the two first peaks corresponds to vibrational activity, which is absent in the simulated spectrum. | ||
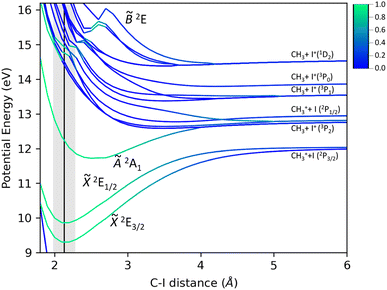
The present potential energy curves (PECs) calculated at the CASPT2(10,11) level of theory as a function of the C–I bond distance are displayed in Fig. 8. The color scale represents the Dyson norm of the corresponding electronic state with respect to the neutral ground state of the molecule, reflecting directly the ionization probability. In agreement with previous work,26 a large Dyson norm characterizes the photoionization into the ground and first excited states of CH3I+. The Dyson norm associated to the second excited state reveals the shape of the potential energy curve. While a main repulsive shape of electronic states constituting the B band is initially observed, the Dyson norm highlights the existence of a bound state in the diabatic picture, associated with the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2E state. According to Fig. 8, no direct ionization into the large number of repulsive electronic states crossing this bound state is expected. The formation of I+ upon photoionization in this absorption band must occur in a classical predissociative mechanism, through a non-adiabatic crossing between the initially populated bound state and the repulsive states leading to the C–I bond cleavage. This could not be observed in the previous calculations,25,26 which primarily focused on the photodynamics in the à state and did not contain the bonding and antibonding orbitals for the C–H bonds in the active space. Moreover, taking into account the role of these orbitals to properly describe the ionization into this state, we would expect a repulsive shape of the
2E state. According to Fig. 8, no direct ionization into the large number of repulsive electronic states crossing this bound state is expected. The formation of I+ upon photoionization in this absorption band must occur in a classical predissociative mechanism, through a non-adiabatic crossing between the initially populated bound state and the repulsive states leading to the C–I bond cleavage. This could not be observed in the previous calculations,25,26 which primarily focused on the photodynamics in the à state and did not contain the bonding and antibonding orbitals for the C–H bonds in the active space. Moreover, taking into account the role of these orbitals to properly describe the ionization into this state, we would expect a repulsive shape of the ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2E state along the C–H bond distance and hence a direct dissociation for the H-atom elimination pathway, yielding CH2I+(
2E state along the C–H bond distance and hence a direct dissociation for the H-atom elimination pathway, yielding CH2I+(![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 1A1) + H.
1A1) + H.
While similar dynamics are often expected for methyl halides (CH3X with X = F, Cl, Br and I), the PECs characterizing the cationic methyl iodide (see Fig. 8) reflect large differences. A fast dissociation leading to the formation of methyl cations following one-photon ionization into the Ã2A1 excited state has been reported for methyl chloride and methyl fluoride.64–66 The corresponding potential energy curves present indeed a repulsive shape. We note that the high spin–orbit coupling characterizing the iodine atom with respect to the small coupling for fluorine and chlorine atoms modifies the energy difference between the two dissociation limits, lying really close in CH3Cl and CH3F. The spin–orbit coupling may therefore play a decisive role in the dissociation dynamics in the Ã2A1 cationic state of methyl iodide.
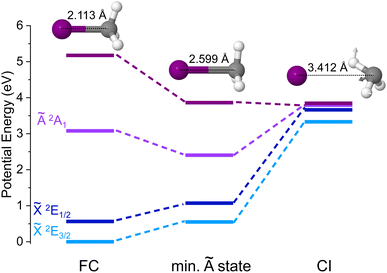
A search of stationary points was carried out following the procedure described in Section 2.2 and a conical intersection between the upper component of the spin–orbit split ground state of CH3I+, ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E1/2, and the first excited state Ã2A1 was found. Its geometry is depicted in Fig. 9 along with the corresponding potential energy, while the arrows shown in the chemical structure indicate the vector associated with the calculated non-adiabatic coupling between the à and
2E1/2, and the first excited state Ã2A1 was found. Its geometry is depicted in Fig. 9 along with the corresponding potential energy, while the arrows shown in the chemical structure indicate the vector associated with the calculated non-adiabatic coupling between the à and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) states at the 2E1/2/2A1 CI (referred henceforth to as non-adiabatic vector). The geometries and potential energies at the Franck–Condon region, associated with one-photon vertical ionization from the ground neutral state, as well as at the minimum of the Ã2A1 cationic state are also depicted. If the spin–orbit coupling is not taken into account in the calculations, the
states at the 2E1/2/2A1 CI (referred henceforth to as non-adiabatic vector). The geometries and potential energies at the Franck–Condon region, associated with one-photon vertical ionization from the ground neutral state, as well as at the minimum of the Ã2A1 cationic state are also depicted. If the spin–orbit coupling is not taken into account in the calculations, the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E3/2 and
2E3/2 and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E1/2 electronic states are degenerate and the CI would not exist. This implies that standard theoretical methods cannot be employed to locate and optimize the geometry of this elusive CI, while the novel procedure used here allows us to identify it. As observed in Fig. 9, this spin–orbit conical intersection is located at a large C–I distance (dC–I = 3.412 Å). A C–I distance of 2.113 Å characterizes the geometry at the Franck–Condon region associated with the ground state of neutral methyl iodide, while a longer C–I distance of 2.599 Å is found at the minimum of the cationic first excited state, Ã2A1. Besides, the I–C–H angles change considerably between the two stationary points. Interestingly, the methyl moiety appears to be somehow rotated at the CI, and the original C3v symmetry is broken. Based on the geometrical modifications required, the CI appears to be located far away from the Franck–Condon region (initially populated following vertical ionization) and also from the energy minimum of the à electronic state. We can assume then that after one-photon ionization the molecule may stay trapped in the à state for a considerable time before it decays into the cationic ground state and further dissociates yielding CH3+ + I(2P3/2).
2E1/2 electronic states are degenerate and the CI would not exist. This implies that standard theoretical methods cannot be employed to locate and optimize the geometry of this elusive CI, while the novel procedure used here allows us to identify it. As observed in Fig. 9, this spin–orbit conical intersection is located at a large C–I distance (dC–I = 3.412 Å). A C–I distance of 2.113 Å characterizes the geometry at the Franck–Condon region associated with the ground state of neutral methyl iodide, while a longer C–I distance of 2.599 Å is found at the minimum of the cationic first excited state, Ã2A1. Besides, the I–C–H angles change considerably between the two stationary points. Interestingly, the methyl moiety appears to be somehow rotated at the CI, and the original C3v symmetry is broken. Based on the geometrical modifications required, the CI appears to be located far away from the Franck–Condon region (initially populated following vertical ionization) and also from the energy minimum of the à electronic state. We can assume then that after one-photon ionization the molecule may stay trapped in the à state for a considerable time before it decays into the cationic ground state and further dissociates yielding CH3+ + I(2P3/2).
The measured photoelectron spectrum28,31 shows a broad continuum associated with photoionization in the first Ã2A1 excited state of the cation while several progressions were observed on top, attributed to excitation in the ν1, ν2 and ν3 vibrational modes, i.e. the CH3 stretch, the umbrella and the C–I stretch, respectively. A broad continuum was also obtained in the photoelectron spectrum measured by one-XUV-photon ionization in the recent femtosecond XUV-IR pump–probe experiment.26 In this work, the excitation of the ν2 mode in the methyl fragment is associated with excitation of the CH3I+ν5 scissors mode, which is not particularly promoted by the ionization step to the unfavorable Franck–Condon factors in the one-photon ionization from the neutral ground state. Based on the literature, the preferred vibrational mode activated in the ionization step would be indeed the ν3 C–I stretch mode. Time-resolved experiments could even visualize this induced vibrational motion.26,67 The ν5 scissors vibrational mode must hence favor the formation of methyl ions. The geometry at the CI shows a somehow distorted methyl moiety geometry while the non-adiabatic vector clearly recalls the scissors vibrational mode. This mode is therefore promoting the passing through the CI mediating the internal conversion into the cation ground state leading to C–I bond cleavage. The vibrational progression in this particular mode reflects the small part of molecules which, upon one-photon ionization, reach the à excited state with the appropriate vibrational activity to promptly access the CI and produce methyl cations.
The location of this elusive CI also explains the long lifetimes estimated for the à excited state. After one-photon ionization, the molecule may stay trapped in this state, since the vibrational activity induced in the absorption step, in any mode besides ν5, does not directly lead to the geometrical modifications required to access the CI seam. Intramolecular vibrational redistribution (IVR) could then take place after internal conversion, and fragmentation would occur from a vibrationally hot ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E1/2 state. This dissociation explains the particularly sharp Boltzmann-type distribution obtained for CH3+ in Fig. 2(a) and Fig. 6. We note that direct C–I bond cleavage in the à excited state leading to I+ is clearly more favorable. Once this channel is opened, the branching ratio for CH3+ formation decreases considerably as observed in Fig. 6.
2E1/2 state. This dissociation explains the particularly sharp Boltzmann-type distribution obtained for CH3+ in Fig. 2(a) and Fig. 6. We note that direct C–I bond cleavage in the à excited state leading to I+ is clearly more favorable. Once this channel is opened, the branching ratio for CH3+ formation decreases considerably as observed in Fig. 6.
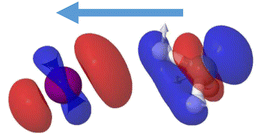
The passage through the CI mediating the internal conversion is in addition leading to a charge transfer. While the à excited state of the cation leads to the formation of iodine ions, I+(3P2), in the asymptotic limit, the cationic ground state is associated with the formation of CH3+. Since the CI is located at large C–I distances, the positive charge is located in the iodine atom before the transfer of population through the CI. Following internal conversion, the positive charge is then located in the methyl group. The charge transfer is mediated by the conical intersection as it can be visualized in Fig. 10. The difference in electronic density between the Ã2A1 and ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E1/2 electronic states computed at the geometry characterizing the conical intersection is shown. A blue color indicates a positive difference in density, reflecting the regions where a higher density is found in the à state while a higher density in the
2E1/2 electronic states computed at the geometry characterizing the conical intersection is shown. A blue color indicates a positive difference in density, reflecting the regions where a higher density is found in the à state while a higher density in the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) 2E1/2 electronic state, i.e. a negative difference, is depicted in red. A higher electronic density is found around the methyl moiety in the à state and around the iodine in the spin–orbit excited ground state. The passage through the CI is thus accompanied by a transfer of electronic density from the methyl moiety into the iodine. This process recalls a classical intramolecular single-electron transfer (SET)68,69 or more specifically a twist intramolecular charge transfer (TICT).70–72 In such case, a twist conformation allows a charge transfer between a donor and an acceptor moiety. The CI requirements impose also here a twisted geometry, breaking the C3v geometry, and allowing the transfer into the ground cationic state and to further dissociate into methyl cation. While intramolecular electron transfer occurs in general in large polyatomic systems, involving aromatic rings facilitating the process, here it takes place in a prototype small system at a considerably large C–I distance.
2E1/2 electronic state, i.e. a negative difference, is depicted in red. A higher electronic density is found around the methyl moiety in the à state and around the iodine in the spin–orbit excited ground state. The passage through the CI is thus accompanied by a transfer of electronic density from the methyl moiety into the iodine. This process recalls a classical intramolecular single-electron transfer (SET)68,69 or more specifically a twist intramolecular charge transfer (TICT).70–72 In such case, a twist conformation allows a charge transfer between a donor and an acceptor moiety. The CI requirements impose also here a twisted geometry, breaking the C3v geometry, and allowing the transfer into the ground cationic state and to further dissociate into methyl cation. While intramolecular electron transfer occurs in general in large polyatomic systems, involving aromatic rings facilitating the process, here it takes place in a prototype small system at a considerably large C–I distance.
4 Conclusions
The valence-shell dissociative photoionization of methyl iodide (CH3I) has been studied using i2 PEPICO spectroscopy in combination with highly-tunable synchrotron radiation. The results are complemented by new high-level ab initio calculations of the potential energy curves. The experimental results consist on electron–ion kinetic energy correlation diagrams upon ionization at fixed photon energies of 14 and 15 eV as well as threshold photoelectron spectra—including a zoom of the A band using a lower step to better resolve the cationic state—and breakdown diagram following photoionization in the 12.0–17.0 photon energy range. In agreement with the literature, three main dissociative photoionization channels are identified, namely the C–I bond cleavage leading to either CH3+ or I+ and the H-atom loss producing CH2I+. Photoionization into the Ã2A1 first excited electronic state leads to complete fragmentation, producing mainly CH3+. The reported threshold photoelectron spectrum and energy correlation diagrams for CH3+ give direct information on the internal conversion process and associated charge transfer between the I and CH3 moieties, leading to the formation of methyl cations vibrationally excited upon photoionization in the à state. It reveals in particular that the ν5 scissors vibrational mode promotes the transfer of population from the initially populated first excited state, CH3I+(Ã2A1), into the ground cationic state, which upon dissociation translates into out-of-plane bending excitation of the CH3+ fragment. The geometry and energy characterizing the elusive spin–orbit conical intersection mediating the internal conversion obtained in a search for stationary points, along with the non-adiabatic coupling vector supports the major role of the ν5 scissors vibrational mode. The passage through this conical intersection requiring a major geometrical modification leads to an intramolecular electron transfer at a considerably large C–I distance. Finally, upon photoionization into the second excited cationic state, CH3I+(![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 2E), the three cationic fragments are also produced. Based on the calculated potential energy curves, a predissociative mechanism leads to the formation of atomic I+ in this band.
2E), the three cationic fragments are also produced. Based on the calculated potential energy curves, a predissociative mechanism leads to the formation of atomic I+ in this band.
Data availability
All the data are available from the corresponding author upon reasonable request.Author contributions
Conceptualization: L. B., S. M. P.; funding acquisition: L. B., S. M. P.; methodology: J. G.-V., G. A. G., L. B., S. M. P.; data curation: J. G.-V., G. A. G., D. V. C., L. B., S. M. P., investigation: J. G.-V., G. A. G., L. B., S. M. P.; software: J. G.-V.; formal analysis: J. G.-V., G. A. G.; writing – original draft preparation: S. M. P.; writing – review and editing: J. G.-V., G. A. G., L. B., S. M. P.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We acknowledge SOLEIL for provision of synchrotron radiation facilities under proposal number 20191887 and the DESIRS beamline staff for their assistance. This work has been financed in part by the Spanish Ministry of Science and Innovation (Grant PID2021-122839NB-I00) and by the Madrid Government (Comunidad de Madrid, Spain) under the Multiannual Agreement with Universidad Complutense de Madrid in the line Research Incentive for Young PhDs, in the context of the V PRICIT (Regional Programme of Research and Technological Innovation) (Grant: PR27/21-010).Notes and references
- M. Bixon and J. Jortner, J. Chem. Phys., 1968, 48, 715–726 CrossRef CAS.
- J.-M. L. Pecourt, J. Peon and B. Kohler, J. Am. Chem. Soc., 2001, 123, 10370–10378 CrossRef CAS PubMed.
- N. H. List, C. M. Jones and T. J. Martínez, Chem. Sci., 2022, 13, 373–385 RSC.
- S. Boldissar and M. S. De Vries, Phys. Chem. Chem. Phys., 2018, 20, 9701 RSC.
- S. Marggi Poullain, D. V. Chicharro, A. Zanchet, L. Rubio-Lago, A. García-Vela and L. Bañares, Phys. Chem. Chem. Phys., 2019, 23017–23025 RSC.
- M. N. Ashfold, R. A. Ingle, T. N. Karsili and J. Zhang, Phys. Chem. Chem. Phys., 2019, 21, 13880–13901 RSC.
- D. W. Chandler and P. L. Houston, J. Chem. Phys., 1987, 87, 1445–1447 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
- L. Rubio-Lago, A. García-Vela, A. Arregui, G. A. Amaral and L. Bañares, J. Chem. Phys., 2009, 131, 174309 CrossRef CAS PubMed.
- M. G. González, J. D. Rodríguez, L. Rubio-Lago, A. García-Vela and L. Bañares, Phys. Chem. Chem. Phys., 2011, 13, 16404–16415 RSC.
- M. G. González, J. D. Rodríguez, L. Rubio-Lago, A. García-Vela and L. Bañares, Phys. Chem. Chem. Phys., 2014, 16, 26330 RSC.
- S. Marggi Poullain, M. G. González, P. Samartzis, T. N. Kitsopoulos, L. Rubio-Lago and L. Bañares, Phys. Chem. Chem. Phys., 2015, 17, 29958 RSC.
- R. de Nalda, J. Durá, A. García-Vela, J. G. Izquierdo, J. González-Vázquez and L. Bañares, J. Chem. Phys., 2008, 128, 244309 CrossRef PubMed.
- G. Gitzinger, M. E. Corrales, V. Loriot, G. A. Amaral, R. de Nalda and L. Bañares, J. Chem. Phys., 2010, 132, 234313 CrossRef CAS PubMed.
- G. Gitzinger, M. E. Corrales, V. Loriot, R. de Nalda and L. Bañares, J. Chem. Phys., 2012, 135, 074303 CrossRef PubMed.
- M. L. M. L. Murillo-Sánchez, J. González-Vázquez, M. E. Corrales, R. de Nalda, E. Martínez-Núñez, A. García-Vela and L. Bañares, J. Chem. Phys., 2020, 152, 014304 CrossRef PubMed.
- M. E. Corrales, G. Gitzinger, J. González-Vázquez, V. Loriot, R. de Nalda and L. Bañares, J. Phys. Chem. A, 2012, 116, 2669 CrossRef CAS PubMed.
- M. Corrales, J. González-Vázquez, R. De Nalda and L. Bañares, J. Phys. Chem. Lett., 2018, 10, 138–143 CrossRef PubMed.
- K. F. Chang, H. Wang, S. Marggi Poullain, D. Prendergast, D. M. Neumark and S. R. Leone, J. Chem. Phys., 2021, 154, 234301 CrossRef CAS PubMed.
- K. F. Chang, H. Wang, S. Marggi Poullain, J. González-Vázquez, L. Bañares, D. Prendergast, D. M. Neumark and S. R. Leone, J. Chem. Phys., 2021, 156, 114304 CrossRef PubMed.
- M. E. Corrales, V. Loriot, G. Balerdi, J. González-Vázquez, R. de Nalda, L. Bañares and A. H. Zewail, Phys. Chem. Chem. Phys., 2014, 16, 8812 RSC.
- M. E. Corrales, J. González-Vázquez, G. Balerdi, I. R. Solá, R. de Nalda and L. Bañares, Nat. Chem., 2014, 6, 785 CrossRef CAS PubMed.
- I. R. Solá, J. González-Vázquez, R. de Nalda and L. Bañares, Phys. Chem. Chem. Phys., 2015, 17, 13183 RSC.
- M. E. Corrales, R. de Nalda and L. Bañares, Nat. Commun., 2017, 8, 1345 CrossRef PubMed.
- S. M. Poullain, D. V. Chicharro, J. González-Vázquez, L. Rubio-Lago and L. Bañares, Phys. Chem. Chem. Phys., 2017, 19, 7886–7896 RSC.
- M. L. Murillo-Sánchez, G. Reitsma, S. M. Poullain, P. Fernández-Milán, J. González-Vázquez, R. de Nalda, F. Martín, M. J. Vrakking, O. Kornilov and L. Bañares, New J. Phys., 2021, 23, 073023 CrossRef.
- B. P. Tsai, T. Baer, A. S. Werner and S. F. Lin, J. Phys. Chem., 1975, 79, 570–574 CrossRef.
- J. H. D. Eland, R. Frey, A. Kuestler, H. Schulte and B. Brehm, Int. J. Mass Spectrom. Ion Processes, 1976, 22, 155–170 CrossRef CAS.
- I. Powis, Chem. Phys., 1983, 74, 421–432 CrossRef CAS.
- D. M. Mintz and T. Baer, J. Chem. Phys., 1976, 65, 2407–2415 CrossRef CAS.
- L. Karlsson, R. Jadrny, L. Mattsson, F. T. Chau and K. Siegbahn, Phys. Scr., 1977, 16, 225 CrossRef CAS.
- M. Grütter, J. M. Michaud and F. Merkt, J. Chem. Phys., 2011, 134, 054308 CrossRef PubMed.
- D. M. P. Holland, I. Powis, G. Öhrwall, L. Karlsson and W. von Niessen, Chem. Phys., 2006, 326, 535–550 CrossRef CAS.
- S. P. Goss, J. D. Morrison and D. l. Smith, J. Chem. Phys., 1981, 75, 757–762 CrossRef CAS.
- S. P. Goss, D. C. McGilvery, J. D. Morrison and D. L. Smith, J. Chem. Phys., 1981, 75, 1820–1828 CrossRef CAS.
- W. A. Chupka, S. D. Colson, M. S. Seaver and A. M. Woodward, Chem. Phys. Lett., 1983, 95, 171–176 CrossRef CAS.
- A. Woodward, S. Colson, W. Chupka and M. White, J. Phys. Chem., 1986, 90, 274–278 CrossRef CAS.
- Y. Song, X.-M. Qian, K.-C. Lau, C. Y. Ng, J. Liu and W. Chen, J. Chem. Phys., 2001, 115, 4095–4104 CrossRef CAS.
- M. Lee and M. S. Kim, J. Chem. Phys., 2007, 127, 124313 CrossRef PubMed.
- A. Bodi, N. S. Shuman and T. Baer, Phys. Chem. Chem. Phys., 2009, 11, 11013–11021 RSC.
- A. Eppink and D. H. Parker, J. Chem. Phys., 1999, 110, 832–844 CrossRef CAS.
- W. Vonniessen, L. Asbrink and G. Bieri, J. Electron Spectrosc. Relat. Phenom., 1982, 26, 173–201 CrossRef CAS.
- R. Locht, D. Dehareng, K. Hottmann, H. Jochims, H. Baumgärtel and B. Leyh, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 105101 CrossRef.
- L. Nahon, N. de Oliveira, G. A. García, J.-F. Gil, B. Pilette, O. Marcouillé, B. Lagarde and F. Polack, J. Synchrotron Radiat., 2012, 19, 508–520 CrossRef CAS PubMed.
- X. Tang, G. A. García, J.-F. Gil and L. Nahon, Rev. Sci. Instrum., 2015, 86, 123108 CrossRef PubMed.
- G. García, B. Cunha de Miranda, M. Tia, S. Daly and L. Nahon, Rev. Sci. Instrum., 2013, 84, 053112 CrossRef PubMed.
- B. Mercier, M. Compin, C. Prevost, G. Bellec, R. Thissen, O. Dutuit and L. Nahon, J. Vac. Sci. Technol., A, 2000, 18, 2533–2541 CrossRef CAS.
- G. A. García, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989–4996 CrossRef.
- J. Poully, J. Schermann, N. Nieuwjaer, F. Lecomte, G. Gregoire, C. Desfrançois, G. Garcia, L. Nahon, D. Nandi and L. Poisson, et al. , Phys. Chem. Chem. Phys., 2010, 12, 3566–3572 RSC.
- E. Nishitani, I. Tanaka, K. Tanaka, T. Kato and I. Koyano, J. Chem. Phys., 1984, 81, 3429–3437 CrossRef CAS.
- I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov and R. K. Carlson, J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef PubMed.
- F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey and I. F. Galván, J. Chem. Phys., 2020, 152, 214117 CrossRef CAS PubMed.
- B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 10945–10956 CrossRef CAS PubMed.
- B. Schimmelpfennig, AMFI, an atomic mean-field spin-orbit integral program, University of Stockholm, 1996 Search PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Du\lak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Phys. Rev. Lett., 2006, 97, 170201 CrossRef PubMed.
- M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258 CrossRef CAS PubMed.
- J. González-Vázquez, Sharcdyn, Zenodo, 2022 Search PubMed.
- A. Bodi, A. Hafliðason and Á. Kvaran, Phys. Chem. Chem. Phys., 2023, 25, 7383–7393 RSC.
- P. M. Guyon, T. Baer and I. Nenner, J. Chem. Phys., 1983, 78, 3665–3672 CrossRef CAS.
- W. A. Chupka, P. J. Miller and E. E. Eyler, J. Chem. Phys., 1988, 88, 3032–3036 CrossRef CAS.
- P. Bréchignac, G. A. Garcia, C. Falvo, C. Joblin, D. Kokkin, A. Bonnamy, P. Parneix, T. Pino, O. Pirali and G. Mulas, et al. , J. Chem. Phys., 2014, 141, 164325 CrossRef PubMed.
- X. Tang, G. A. Garcia and L. Nahon, J. Phys. Chem. A, 2017, 121, 5763–5772 CrossRef CAS PubMed.
- X. Tang, X. Zhou, M. Wu, S. Liu, F. Liu, X. Shan and L. Sheng, J. Chem. Phys., 2012, 136, 034304 CrossRef PubMed.
- H.-W. Xi, M.-B. Huang, B.-Z. Chen and W.-Z. Li, J. Phys. Chem. A, 2005, 109, 4381–4387 CrossRef CAS PubMed.
- Y. Malakar, W. Pearson, M. Zohrabi, B. Kaderiya, F. Ziaee, S. Xue, A. Le, I. Ben-Itzhak, D. Rolles and A. Rudenko, et al. , Phys. Chem. Chem. Phys., 2019, 21, 14090–14102 RSC.
- D. Escudero, Acc. Chem. Res., 2016, 49, 1816–1824 CrossRef CAS PubMed.
- Y. Okada and K. Chiba, Chem. Rev., 2018, 118, 4592–4630 CrossRef CAS PubMed.
- Z. Grabowski and J. Dobkowski, Pure Appl. Chem., 1983, 55, 245–252 CrossRef CAS.
- Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Chem. Rev., 2003, 103, 3899–4032 CrossRef PubMed.
- C. Wang, W. Chi, Q. Qiao, D. Tan, Z. Xu and X. Liu, Chem. Soc. Rev., 2021, 50, 12656–12678 RSC.
| This journal is © The Royal Society of Chemistry 2024 |